- 1Dongying Hualian Petrochemical Plant Co., Ltd, Dongying, Shandong, China
- 2College of Safety and Ocean Engineering, China University of Petroleum-Beijing, Beijing, China
- 3School of Shipping and Maritime, Zhejiang Ocean University, Zhoushan, Zhejiang, China
- 4National and Local Joint Engineering Research Center of Harbor Oil and Gas Storage and Transportation Technology, Zhejiang Key Laboratory of Petrochemical Environmental Pollution Control, Zhejiang Ocean University, Zhoushan, China
Petroleum is the pillar industry of the national economy, but safety accidents are frequent all over the world. The government attaches more importance to the safety production management of enterprises to reduce the occurrence of accidents that infringe on personal safety. The management of emergency supplies, which can effectively respond to the occurrence of safety production accidents, is a key measure for handling emergency accidents. Rapid response to accidents means reducing accident rescue costs and protecting personal and property safety. This paper proposes a material stochastic model with the randomness of accident demand for materials. The enterprise and the government can obtain the material management scheme and the quantitative evaluation standard of accident preventive measures from the model results respectively. The model covers as many accident scenarios as possible through multi-scenario modeling to reduce the impact of accident uncertainty. Finally, the feasibility is proved by an example of a petroleum enterprise in Zhoushan City. When the accident demand fluctuates randomly between 80% and 120%, the model proposes a material management scheme that the dispatching time of materials and the cost in rescue work do not exceed 31.33 min and 11.68 million CNY respectively. With the assistance of the model, the enterprise saves the cost of safe production and improves the efficiency of rescue. The government has strengthened the supervision and evaluation of enterprise safety production management. Finally, the mission of protecting the property and life safety of the people will be realized.
1 Introduction
The number of natural disasters in the world is increasing year by year (Boonmee et al., 2017), and China is one of the countries suffering the most natural disasters (Wang, 2021). The safety accidents in the production process of petrochemical enterprises also show the same trend in the world (Chen, 2021b; Bai et al., 2023). Chemical accidents usually cause casualties and environmental pollution, which seriously affect people’s lives. On 12 August 2015, an explosion at a dangerous goods facility in Tianjin Port killed 165 people, injured 798 others, and caused direct economic losses of 980 million dollars (Anon, 2024). Gradually, people stay away from petroleum companies for fear that accidents at any time threaten their safety. However, the petroleum industry has become one of the basic industries of all countries to improve people’s quality of life. Demand for oil in all countries has soared in recent years, with a total global consumption of 9.384 million tones of oil equivalent in 2015 (Zhu et al., 2020). For a dangerous and important industry, most countries take appropriate preventive measures to balance production accidents with economic development. In China, the production of the petrochemical industry has been strictly controlled by the government to reduce the frequency and likelihood of accidents. The inspection of emergency materials is an important part of accident prevention. Thus, equipped with emergency supplies and setting up special safety funds are all things that must be done before production through laws and regulations in China. However, enterprises always have unreasonable behavior of emergency materials, because the law is widely used and not applicable. The quantity and type of preset materials will vary with the influence of geographical location, pro-duction technology, population density, enterprise production conditions and other factors. Before an accident occurs, the location of the accident and the materials required for the accident are uncertain; After an accident occurs, the development and evolution of the accident changes greatly according to the on-site environment, resulting in the uncertainty of the accident. For example, the chemical reaction between the rescue material and the raw material caused the accident to worsen. Therefore, an emergency material management scheme, considering the accident demand of randomness and uncertainty, is essential for the enterprise to allocate materials in the pre-disaster phase.
Emergency materials management has become one of the main research directions of accident prevention. Dou et al. carried out qualitative research on emergency rescue to solve the low efficiency of cooperative dispatch of materials, and optimized emergency material management through multi-organization coordination (Dou et al., 2012). Qualitative research can point out the direction of enterprise preparation rescue work, but there is still in-sufficient guidance for practical operation. Businesses and governments are increasingly looking to quantitative studies to evaluate the effectiveness of material management and safety measures. Scholars try to optimize the management of emergency materials in the pre-disaster and post-disaster phases by quantitative methods. Knott proposed a concrete and feasible emergency material management scheme by simulating the rescue process (Knott, 1987). Zhang et al. optimized the single-objective model through a variety of algorithms to obtain further optimization for supply management in the pre-disaster phase (Zhang et al., 2011). However, the early models had some drawbacks, which more or less affected the recognition of enterprises and governments.
Many researchers have developed a series of optimization models, including objective function, constraint conditions, external cooperation, randomness, multi-period, multi-scenario and so on. Liu et al. proposed that material presetting is an important link in material management, which involves three levels of material management objects, namely rescue center, warehouse and accidents (Liu et al., 2021). Multi-level dispatch of emergency materials can help rescue workers carry out rescue operations to the greatest extent (Najafi et al., 2013; Bodaghi, 2020; Zahedi et al., 2020). Multi-objective material dispatch optimization is one of the hot spots in optimizing material dispatch after a disaster. The model takes efficiency, fairness or public expectation as the objective function, and considers the constraints of suppliers, multi-materials, multi-vehicles, uncertainty or other constraints to formulate material management schemes (Sheu, 2007; Yi and Özdamar 2007; Zhan et al., 2014; Tang et al., 2021). The material management model has gradually formed a comprehensive emergency material management model based on multi-objective optimization. However, what is most easily overlooked is the preparation of materials in the pre-disaster stage. Material preparation can optimize material dis-patching and improve rescue efficiency. Similarly, the government also requires companies to prepare a certain amount of supplies in case of a sudden accident (Tzeng et al., 2007; Rawls and Turnquist, 2010). Yang et al. optimized the distribution of emergency supplies in the pre-disaster phase. With the information shortage and demand uncertainty, the model takes time, satisfaction and cost as the objective functions to develop a reasonable logistics facility layout (Yang et al., 2022). Liu et al. also adopted the approach to deal with the occurrence of environmental accidents, which showed that the layout of materials reserves can affect the speed of accident response (Liu et al., 2016). Material management in both pre-disaster and post-disaster stages plays a vital role in emergency rescue work. Some scholars have considered the stages as a whole to achieve further optimization. Yu developed a two-stage material management model with the randomness and uncertainty of the accident. The first stage of the model determines the location of the warehouse and the quantity of materials in reserve. In the post-disaster stage, the stochastic model and robust model are used to optimize the material scheduling to get a better scheduling scheme (Yu, 2021). The material management model can closely link the pre-disaster preparation work with the post-disaster rescue work to improve rescue efficiency.
Many researchers are starting to incorporate random and uncertain factors into models to simulate real-world accidents (Boonmee et al., 2017; Chen, 2021a). Because accidents happen suddenly without a little preparation, expert predictions and empirical analysis become vulnerable when accidents happen. Wang et al. solved the problem of warehouse location in the pre-disaster stage by introducing an operational research model with uncertain parameters, which is mainly reflected in the uncertainty of the severity of the disaster (Wang, 2021). A material model presented by Barbarosoǧlu and Arda, which can represent the randomness of the accident demand, is used to deal with resource scheduling to improve the vulnerability of the transportation system and ensure the efficiency of material transportation in the post-disaster stage (Barbarosoǧlu and Arda, 2004). Salmerón and Apte takes into account the uncertain impact of the location and severity of the incident to optimize logistics issues in the post-disaster phase by expanding resources such as supplies warehouses and medical facilities (Salmerón and Aruna, 2010). Abazari et al. (2021) proposed a multi-objective nonlinear programming with uncertain parameters. A material management scheme, including the location of the rescue center, material preparation scheme and quantity of supplies delivered in the post-disaster, is derived from the model which takes the distance and cost as the objective function (Abazari et al., 2021). Whether it is the problem of warehouse location and material storage in the pre-disaster stage, or the optimization of logistics in the post-disaster stage, the introduction of randomness makes the model optimization more practical and accurate. The study of individual stages can better focus on the optimization of individual problems, but the segmented stages of material management make it impossible to optimize the model from a holistic perspective. As far as accidents are concerned, the accident scenes in which they occur are ever-changing. Especially in the post-disaster stage, the material management model usually only considers the occurrence of a single accident scenario, and then carries out optimization and analysis for the scenario. In other words, the location and the material demand of the accident are not fixed.
Many researchers conduct multiple simulations of accidents at different periods to ensure the comprehensiveness of accidents (Zhou et al., 2017; Vahdani et al., 2018; Wang et al., 2020; Yang et al., 2021). Wex et al. tried to accommodate more accident scenarios by weighting the objective function with the severity of the incident to ensure the comprehensiveness of the accident (Wex et al., 2014). Vahdani et al. (2018) developed a multi-objective mathematical model to deal with the contingencies and unpredictability of natural disasters through a multi-cycle modeling approach Vahdani et al. (2018). The time-based multi-scenario model brings light to the continuous operation of the accident, which can carry out continuous material scheduling to ensure the continuity of the rescue process. Unfortunately, the model is not a good guide for material preparation and emergency rescue in the pre-disaster phase. Nezhadroshan et al. (2021) proposed a scenario-based modeling method, trying to make the model accommodate more accident scenarios to ensure comprehensive consideration (Nezhadroshan et al., 2021). The model can improve the reliability of material preparation in pre-disaster, and the efficiency of the logistics network in post-disaster. Therefore, the scenario-based modeling method can accommodate more complex accident scenes, which is valued and recognized by most researchers.
To summarize the research on operation control methods for a material management model with stochastic conditions, a detailed review of the state of the art is performed in Table 1.
Scholars improve the mathematical model to optimize material management and improve rescue efficiency, such as the whole stage, third-party emergency force, objective function, disaster type, accident uncertainty, etc. However, different parameters have a great impact on the results of the model, so the establishment of a comprehensive mathematical model has always been the direction pursued by scholars. These studies did not fully consider the impact parameters. For example, the combination of accident demand randomness and accident site uncertainty is not even considered. In particular, the domino effect has made most of the current material management models ineffective. If the randomness and uncertainty of the accident are ignored, the application range of the model results is narrow and one-sided. Therefore, it is expected that randomness and uncertainty should be incorporated into the emergency materials management model with external coordination.
This paper presents a stochastic programming model for the pre-disaster and post-disaster stages with external coordination, aiming at optimizing emergency material management to improve rescue efficiency. The model will focus on three characteristics: external coordination, the randomness of accident demand and the uncertainty of accident scene. First of all, external coordination is considered because the military, volunteer corps and other enterprises are important forces in the rescue process. These rescue forces can reduce the cost of accident prevention without affecting the conduct of rescue operations. Secondly, the accident demand itself has randomness, that is, the accident demand is different for each occurrence. The accident scene is complex and changeable, such as the accident that occurred with the Domino scenario. The accident scenario may be an accident in one location, an accident in multiple locations, or an accident in consecutive different locations. Thus, models with randomness and uncertainty cover more actual scenarios, and reduce the impact of unexpected accidents on the model for enterprises and governments to the management of materials. Finally, through the verification of examples, this paper proves that the proposed material management scheme can not only reduce the material allocation cost for enterprises in the pre-disaster stage without affecting the priority rescue tasks, but also provide a reference for the government to evaluate the safety precautions of enterprises.
The main contributions of this paper are summarized as follows.
• An integrated material management model with external coordination in the post-disaster phase;
• Randomness and uncertainty are introduced to reduce the impact of unexpected accidents on the model;
• The model takes into account a variety of accident scenarios to ensure a more comprehensive decision.
The rest of this paper is organized as follows. In Section 2, the problem description is provided. In addition, accident background and assumptions are presented. Section 3 develops a stochastic programming model that considers randomness. In Section 4, a realistic application is introduced and analyzed. Some conclusions and future research are summarized in Section 5.
2 Problem description
2.1 Necessary material management
Petrochemical accidents, like natural accidents, have brought great hidden dangers to people’s lives and property. At the time of the accident, the amount of material required was random. The demand will be affected by a variety of factors (the cause of the accident, the site environment, etc.), which is also called the randomness of the accident. By analogy, the location of the accident and the occurrence of secondary disasters are uncertain. But the industry is also an important pillar industry of the national economy. Therefore, the government and enterprises must do a good job in accident control and be ready for accident rescue at any time. Emergency material management is the main prevention and rescue measures of accident rescue, including material preparation in the pre-disaster stage to improve the efficiency of material dis-patch, and material dispatch optimization in the post-disaster stage.
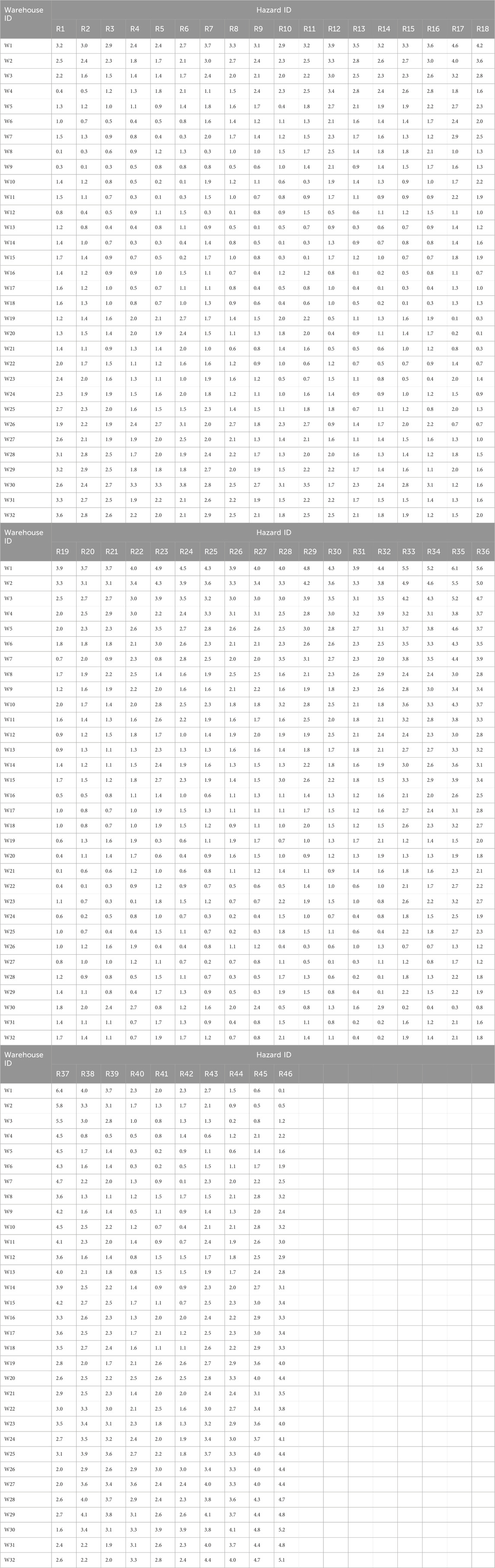
The occurrence of an accident is a probability event, whose probability often in-creases with the degree of danger. Many mathematical models treat the occurrence of an accident as a definite event. In the scene of multiple accidents interweaving, it is easy to ignore the possibility of other accidents by the models, such as the domino effect. The domino effect will make the accident analysis more complicated, such as the randomness of the accident location and the secondary injury caused by the accident (Li et al., 2023; Gholamizadeh et al., 2024). The accident scenario with randomness makes the previous material management model less reliable. As shown in Figures 1, 4, accidents are possible at all hazardous locations, and the probability of accidents is not the same at each risk point. The filling pattern in the figure indicates that the probability of an accident is high, but it does not mean that an accident will occur. Thus, randomness is not conducive to the establishment and decision-making of mathematical models. Enterprises cannot make accurate judgments based on the results, and the government cannot quantify the initial accident preparation work of enterprises.
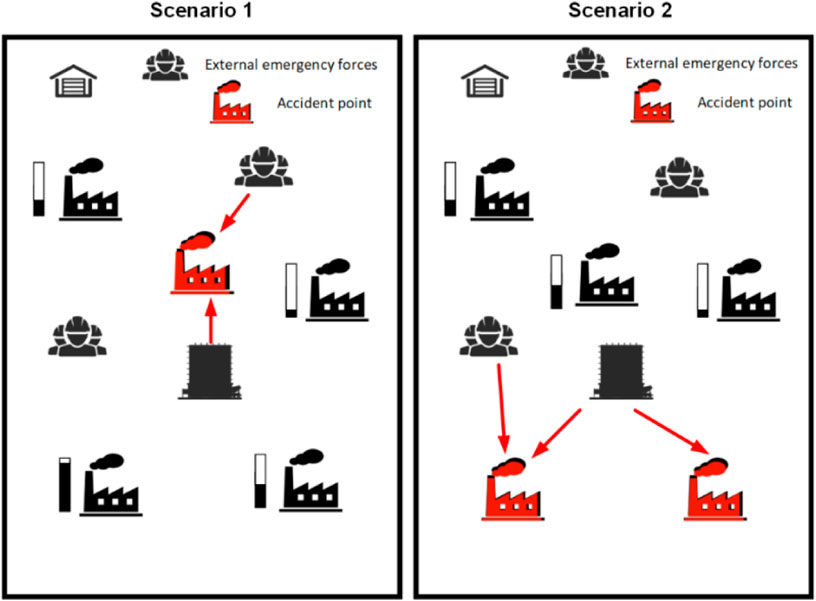
Planning for the dispatch of materials in the post-disaster phase can improve the efficiency of rescue, because it is directly involved in the rescue work. However, the diversification of accident scenarios in the post-disaster stage will weave a huge net under different accident scenarios. The dispatch of materials in different accident scenarios is not the same, and it will also affect the reserve of materials in the pre-disaster stage. As is shown in Figure 2, complex accident scenarios can be disastrous for both quantitative analysis and mathematical modeling, resulting in explosive data growth that slows down operations and weakens the credibility of the resulting scenarios. But it is extremely important. The diversity of accident scenarios will affect the dispatch and preparation of materials, which is not acceptable or lacking. Therefore, the variety of accident scenarios should be taken into account in a sound material management scheme.
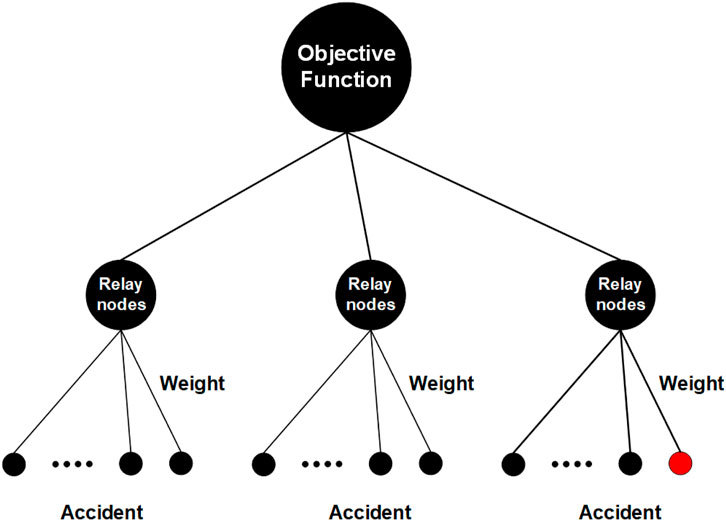
Multi-scene modeling is one of the effective means to deal with the diversity of accident scenes (Zhao et al., 2023). As shown in Figure 3, the black dot represents a scenario in which an accident is possible, with the red representing the scenario in which an accident occurs. The weights are used to distinguish the probability of an accident scenario and are added to the relay nodes. The relay nodes can preferentially discard the branches with the least probability to ensure the smooth operation of the model due to the explosive growth of data. The model must operate in the post-disaster phase to avoid affecting the rescue process. The whole modeling process is completed by weighting the relay nodes to the objective function in the same way. Naturally, the objective function can be multivariate.
2.2 Model requirement
2.2.1 Assumptions
To improve the solution efficiency, the following assumptions are made.
• The relationship between the geographical location of external forces, warehouses and accidents does not change with time (Sheu, 2007).
• All material management units are integers (Bozorgi-Amiri and Jabalameli, 2011).
• The effect of the number of rescuers on the model is not taken into account, which means that the number of people is sufficient in any case.
• The demand for the accident is going to fluctuate randomly (Hu et al., 2016).
2.2.2 Given
• Accident information: accident theoretical material demand, accident probability.
• Rescue information: the amount and type of supplies for external coordination, and the location of pre-construction warehouses.
• Cost information: the unit price of storage, transportation and construction.
• Geographic information: the maximum transport capacity of the road, the shortest distance between the accident and the emergency response force.
• Time information: the loading and shipping time of the materials.
• Other information: randomness of demand, accident scenarios.
2.2.3 Determine
• Material preparation scheme in the pre-disaster stage: warehouse construction lo-cation and scale, the type and quantity of materials stored in advance, and wiring diagram.
• Material dispatching scheme in the post-disaster stage: material dispatching route.
• State variables: the storage capacity of the warehouse at a certain time, whether there are vehicles on the path.
3 Mathematical model
The stochastic programming model with time and cost as the target is used to find the optimal scheme of material management, which integrates the characteristics of external coordination, accident randomness and accident scenario uncertainty. With the integration of these characteristics, the model can cover more accident scenarios and meet the actual demand for materials when accidents occur. The time in objective function includes two parts: material scheduling and preparation; and the cost includes three parts: warehouse construction, material storage and dispatch. In addition, more accident scenarios are considered in the model to reflect the uncertainty of the accident through multi-scenario modeling. The total time and cost are calculated in the model according to the weights of different scenarios in multiple scenarios. Storage, logistics, balance, and other constraints are applied in the model to reduce computational complexity and optimize the material management scheme.
3.1 Objective function
3.1.1 Cost
The cost objective function has two parts, as shown in formulas 1, 2: the material preparation cost in the pre-disaster stage, and the dispatch cost in the post-disaster stage (
3.1.2 Time
The time objective function includes material preparation and transportation, as shown in formulas 3, 4. The time of material preparation mainly includes the loading and unloading time required for materials, which is composed of the product of transportation time (
3.2 Constraints
3.2.1 Storage constraints
The storage of materials is affected by the warehouse scale and transportation conditions, as shown in formula 5. The state variable of the warehouse (
The amount of materials stored (
Warehouses of different scales can be freely combined to suit different needs in the model, as shown in formula 7. When an accident occurs, the emergency force (
3.2.2 Logistical constraints
The maximum capacity of the road (
When the roads are clear (
There will be a convoy on the road (
3.2.3 Balance constraints
Material balance is one of the keys to maintaining the dynamic balance of the model. The premise of running the model is that the materials from the warehouse (
This is the objective function of the conventional model. However, this model takes into account the random influence of accident probability to simulate the situation of realistic accident probability. Each accident is accompanied by different needs, that is, each accident demand is different in terms of quantity. The model can better represent the random process of accident demand through random factors (
The material balance in the warehouse is to ensure the unity of the whole process among the material reserves of the warehouse (
3.2.4 Other constraints
Multiple variables in the model must have the same meaning, as shown in formula 20. The unification of material transportation and path state ensures a balanced relationship between warehouse construction state (
4 Case study
4.1 Basic information
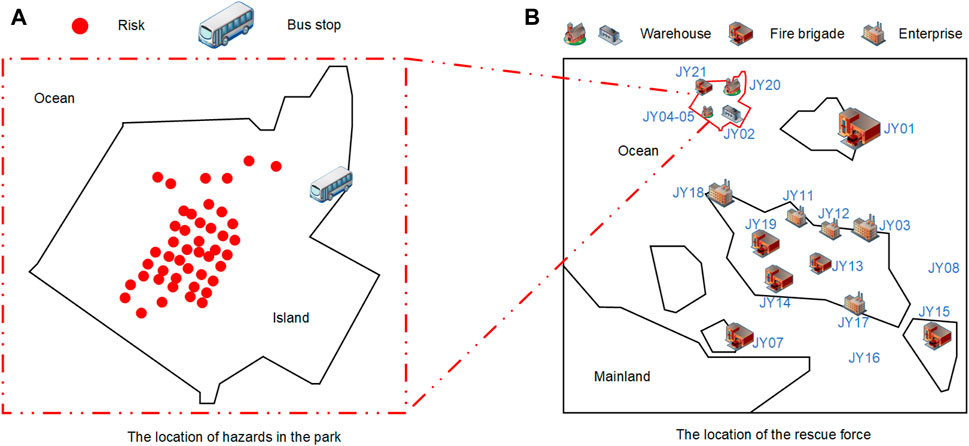
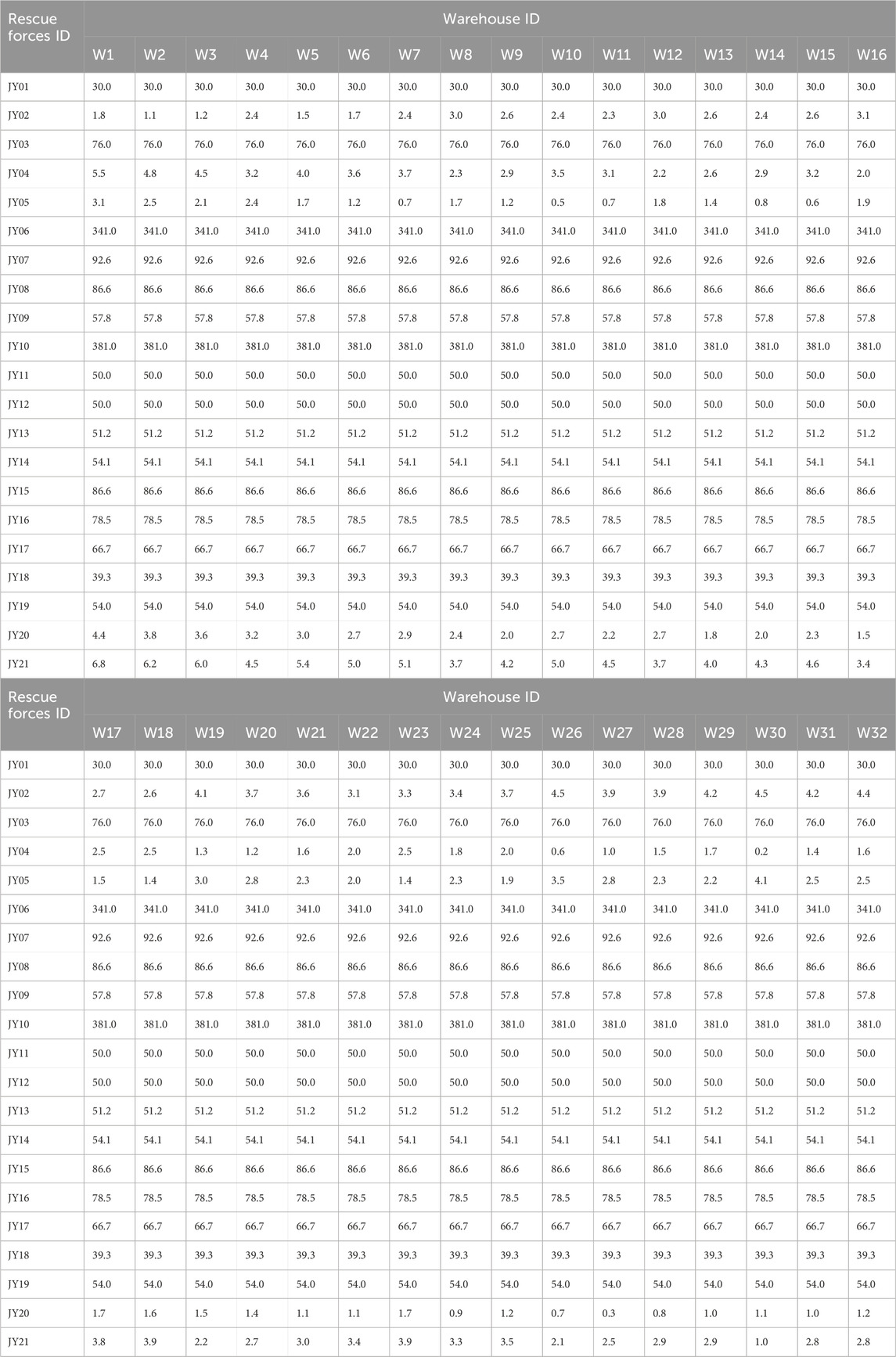
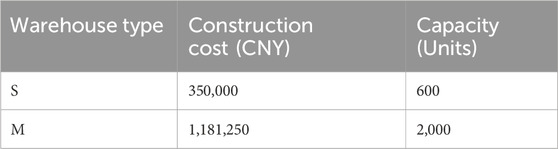
This paper carries on the verification analysis according to the actual production situation of a petrochemical enterprise in Zhoushan City. Fire and explosion accident is one of the key accidents to prevent in this industry, so only the impact of fire and explosion accident be considered in the model. The enterprise has obtained 46 dangerous sources of possible accidents, 32 alternative warehouse locations that can be built, 21 emergency rescue teams that can be called for help (5 of which are established by the enterprise organization), and 4 scales of emergency materials involved in the accident through security experts. The position relationship of them is shown in the Figure 4; Tables 2–5. The warehouse construction scale is divided into small and medium to adapt to different situations, the construction cost and storage capacity of different scales are shown in Table 6. Different attributes of emergency materials lead to different logistics time, such as space, weight and so on. Therefore, the ratio of the path to the speed of the vehicle indicates the time loss, and different kinds of materials can be accommodated in a vehicle. The driving plan is given according to the Autonavi map navigation, and the vehicle speed is determined according to the road speed limit to obtain the shortest time. The dispatching time in the post-disaster is the ratio of distance to speed, and the average speed of each path is shown in Table 7. The costs in the material management, including storage costs and dispatch costs, are shown in Table 8. Finally, due to the small amount of chemical accident case data, the accident randomness of this case follows normal distribution (
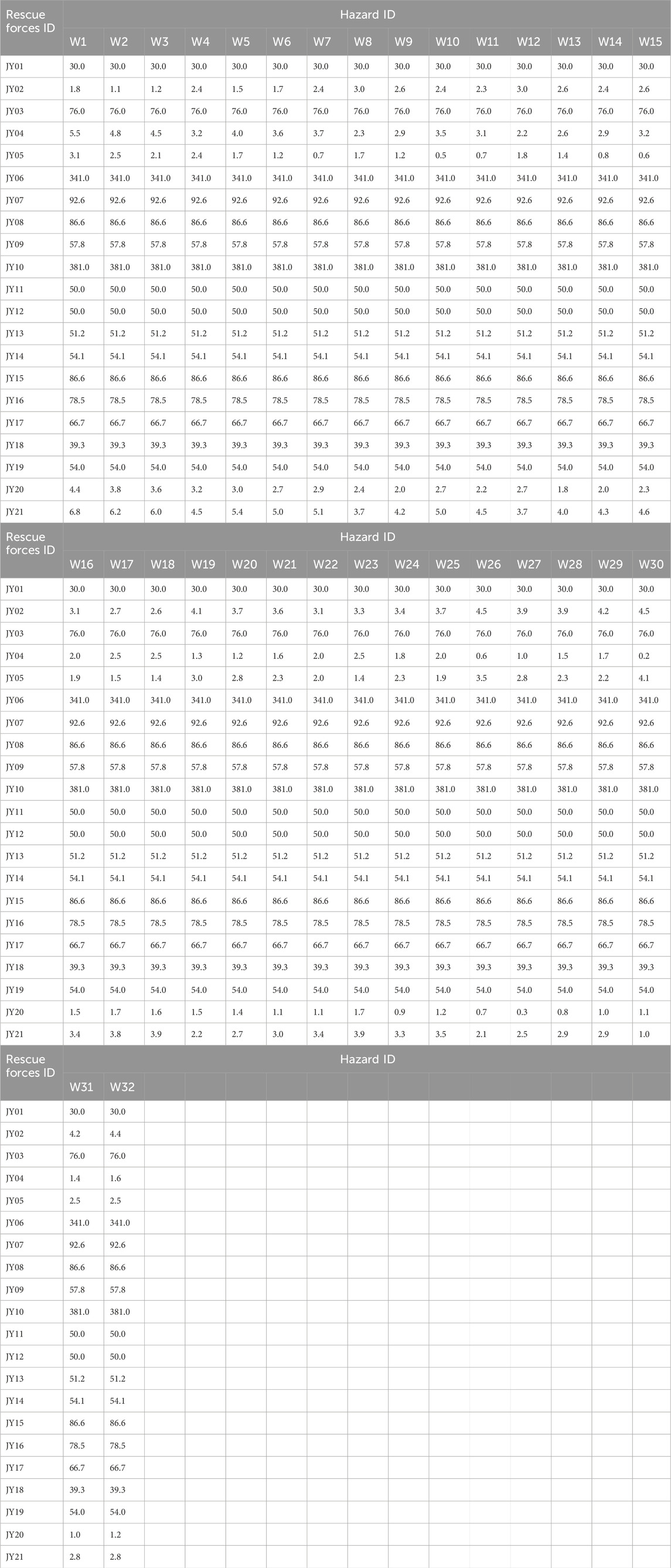
Table 5. The distance (kilometer) between the emergency force (JY) and the source of the hazard (R).
4.2 Flexibility analysis
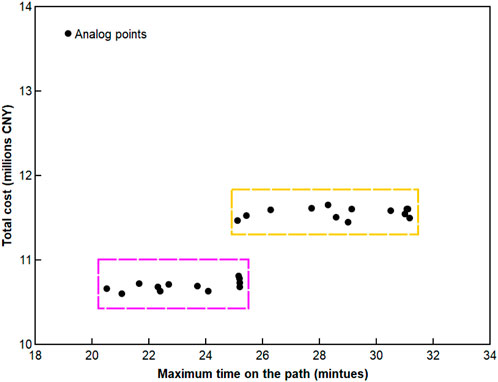
When the accident demand fluctuates randomly between 80% and 120%, the time and cost of the scheme are shown in Figure 5. The cost rises in steps at intervals, and the maximum time on the path shows a continuous upward trend. The colored boxes rep-resent different warehouse schemes, including the scale and quantity of the warehouse to be built. The scheme in the purple box will construct 28 small warehouses on average whose cost is about 9.8 million CNY. And the orange box will construct 27 small ware-houses and 1 large warehouse on average whose cost is about 10.63 million CNY. The difference between the two is 0.83 million, which is just in line with the cost increase interval. The model will change the warehouse construction scheme according to the fluctuation of accident demand to cover more accident scenarios. Compared with 32 warehouses in the actual situation of the enterprise, the model scheme reduces the number of warehouses by 12.5%, which means the reduction of the number of warehouse construction and the saving of investment capital in the pre-disaster stage.
4.3 Sensitivity analysis
The normal distribution (
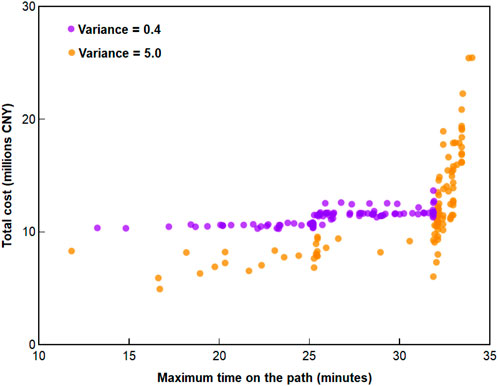
Normal distributions with different variances were used to represent different degrees of randomness of accident demand, and the model results obtained are shown in Figure 6. With the increase of the floating range of accident demand, the frequency of extreme values (purple and red dots) and the values of the objective function in the schemes given by the model increase. If the minimum in all schemes is taken as the result of the model, then the time in the scheme is 13.25 min, 15.76 min, 12.82 min, 7.63 min, 9.48 min, 12.10 min, 8.03 min, and 11.8 min respectively with the variance increases. The results of the model will produce drastic fluctuations and affect the decisions of the enterprise. It is not appropriate to arbitrarily choose one of the many schemes as the overall scheme.
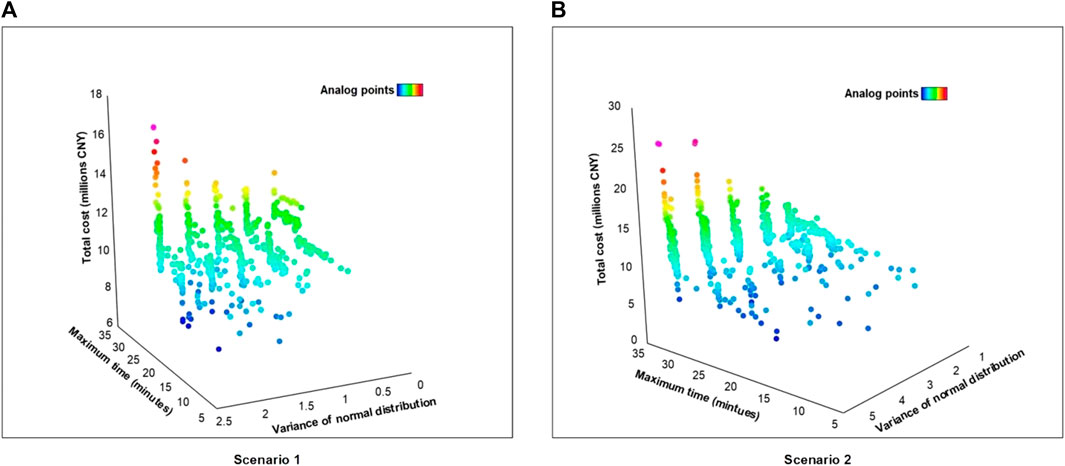
Figure 6. (A) Maximum time on the path and total cost on different randomness in scenario 1; (B) Maximum time on the path and total cost on different randomness in scenario 2.
The STD standard is used to represent the overall solution of a situation. STD-X refers to a scheme in which the amount of material stored in the pre-disaster phase can meet X% of the accident requirements. For example, STD-80% refers to the amount of materials that can effectively meet 80% of the accident requirements. This standard can effectively make up for the shortcomings of randomness that cause the scheme to be not unique and the resulting gap is large. The maximum time on the path with different random degrees and different evaluation criteria is shown in Table 9. The time increases slowly as the variance of the normal distribution increases. Since the stability of each scheme is also different, the standard deviation is used to represent the stability of a scheme. The minimum in all scenarios is 0.63 of STD-90%, which is the most stable scheme to cover 90% of accident requirements.
The results of the model with degrees of randomness are shown in Figure 7. The variance factors are 0.4 and 5.0 respectively, where a larger number represents greater randomness. Scenarios with a variance of 0.4 converge into a horizontal purple line, which implies stability in the cost index and instability in the time index. When the warehouse is close to the accident, the maximum time on the path is small, and vice versa. In contrast, a scenario with a variance of 5.0 presents a vertical orange line, which implies stability in the time index and instability in the cost index. Several small warehouses are built in the vertical line, which can easily meet the small and stable demand. In the vertical case, more large warehouses are built to cope with the sudden increase in individual accident demand, resulting in greater cost fluctuations (the price of large warehouses is 3.3 times that of small warehouses). Therefore, when the number and scale of warehouses built in the pre-disaster is less than 28 small warehouses (the intersection of the orange and the purple), priority should be given to time optimization to improve rescue efficiency. On the contrary, the warehouse construction cost in the pre-disaster stage is optimized to save capital investment.
4.4 Economic analysis
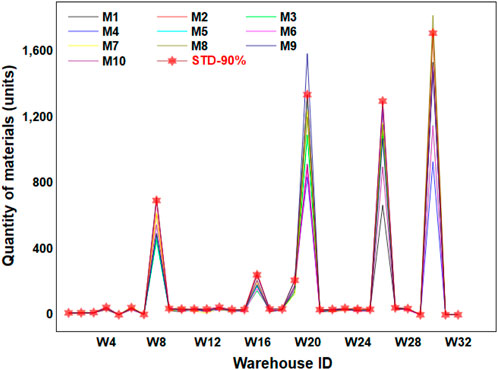
The quantity of materials stored in warehouses with different accident demands is shown in Figure 8 (serial number of materials is W1-W32). The stars in the figure represent the amount of material stored with the STD-90%. The storage quantity of materials is mainly concentrated in 4 warehouses, 4 warehouses do not store any materials, and the remaining warehouses are distributed in small quantities. The average quantity of materials stored in W8, W20, W26 and W30 is higher than that in all warehouses: 81.92, 204.30, 145.36 and 210.94 units, respectively. The quantity of materials stored in warehouses varies greatly with different accidents, which should be paid attention to by enterprises. W5, W29, W31, and W32 do not store any supplies, which means that it is possible to save costs by not building a warehouse. With the STD-90% standard, W20 and W30 warehouses are relatively reduced by about 16.48% and 15.64%. When the material demand does not need to be 100% satisfied, W20 and W30 are the keys that can be optimized.
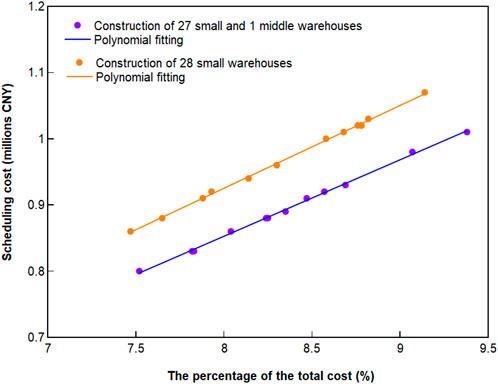
The proportion of material dispatching cost in the total cost in the post-disaster stage with different accident demands is shown in Figure 9. The total cost includes the dispatch cost of materials in the post-disaster stage and the preparation cost in the pre-disaster stage. The preparation cost in the pre-disaster stage includes the storage of materials and the construction of warehouses. The difference between the orange and blue lines in the figure is the scale and number of warehouses being built. In the orange line, the accident demand and the scale of the warehouse are higher than that in blue, but the proportion of material dispatching cost of both is unchanged. In different warehouse schemes, the proportion is linearly fitted to obtain curves,
5 Conclusion
This paper proposes a stochastic model for the pre-disaster stage and post-disaster stage with randomness. The model helps enterprises develop reasonable material management schemes, and helps the government quantify the accident prevention measures for enterprises. The adequacy of preparation determines the efficiency of accident rescue, and the model can improve the preparation to the greatest extent. However, only when an accident occurs can the location of the accident and the demand for the accident be determined. Randomness is considered in the model, which will make the scheme from the results different in each run. Similarly, the single accident scenario will cause the model to interpret the process of chemical accidents unilaterally. Therefore, this paper adopts multi-scenario modeling to eliminate the influence of the diversity of accident scenarios. In this method, the weights of various accident scenarios are given with the possibility, and then the objective functions are formed with the weights. Each accident scenario needs to minimize the two objective functions of time and cost.
A petrochemical enterprise in Zhoushan City was taken as an example to verify the usability of the model. The research shows that it takes at least 31.33 min and costs 11.68 million CNY to meet the requirement of 90% of the accident scenarios. Similarly, if 80% of the accident scenarios need to be satisfied, it will take at least 30.41 min and cost 11.68 million CNY. The scheme will build 28 warehouses, which will reduce the number of warehouses by 12.5% compared to the 32 warehouses in the actual situation of the company.
The accident randomness and uncertainty, it has contributed to the current material management model in the chemical accident scenario. However, the model proposed in this paper still has some limitations: (1) The possibility of accidents still needs to be analyzed and judged by experts, and accident data can only play a supporting role. (2) Rescue workers cannot control the traffic in real-time, lack of further optimization of the accident rescue process. The research can be integrated with computer technology (e.g., big data, neural networks) to reduce the impact of expert experience on the model, which further enhances the objectivity of the model results.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
WJ: Writing–review and editing, Writing–original draft. YY: Writing–review and editing, Data curation, Conceptualization. AH: Writing–review and editing, Methodology, Investigation, Data curation. YL: Writing–original draft, Formal Analysis, Data curation, Conceptualization. SH: Writing–review and editing, Methodology, Investigation, Funding acquisition.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was funded by the Zhejiang Ocean University Project (No. 21028007723).
Conflict of interest
Author WJ was employed by Dongying Hualian Petrochemical Plant Co., Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abazari, S. R., Aghsami, A., and Rabbani, M. (2021). Prepositioning and distributing relief items in humanitarian logistics with uncertain parameters. Socio-Economic Plan. Sci. 74, 100933. doi:10.1016/j.seps.2020.100933
Anon, N. D. (2024). Case study on the catastrophic explosion of a chemical plant for production of M-phenylenediamine | semantic scholar. https://www.semanticscholar.org/paper/Case-study-on-the-catastrophic-explosion-of-a-plant-Yang-Li/6d06049158cf6c32e9a981c7afa0c5f09074f020.
Bai, M., Qi, M., Shu, C.-M., Reniers, G., Khan, F., Chen, C., et al. (2023). Why do major chemical accidents still happen in China: analysis from a process safety management perspective. Process Saf. Environ. Prot. 176, 411–420. doi:10.1016/j.psep.2023.06.040
Barbarosoǧlu, G., and Arda, Y. (2004). A two-stage stochastic programming framework for transportation planning in disaster response. J. Operational Res. Soc. 55 (1), 43–53. doi:10.1057/palgrave.jors.2601652
Bodaghi, B., Shahparvari, S., Fadaki, M., Lau, K. H., Ekambaram, P., and Chhetri, P. (2020). Multi-resource scheduling and routing for emergency recovery operations. Int. J. Disaster Risk Reduct. 50, 101780. doi:10.1016/j.ijdrr.2020.101780
Boonmee, C., Arimura, M., and Asada, T. (2017). Facility location optimization model for emergency humanitarian logistics. Int. J. Disaster Risk Reduct. 24, 485–498. doi:10.1016/j.ijdrr.2017.01.017
Bozorgi-Amiri, A., and Jabalameli, M. S. (2011). A multi-objective robust stochastic programming model for disaster relief logistics under uncertainty. Berlin, Germany: Springer.
Chen, C., Reniers, G., and Yang, F. (2021b). Safety and security of oil and gas pipeline transportation: a systematic analysis of research trends and future needs using WoS. J. Clean. Prod. 279, 123583. doi:10.1016/j.jclepro.2020.123583
Chen, C., Yang, M., and Reniers, G. (2021a). A dynamic stochastic methodology for quantifying HAZMAT storage resilience. Reliab. Eng. Syst. Saf. 215, 107909. doi:10.1016/j.ress.2021.107909
Dou, L., Sun, Y., and Lian, S. (2012). Research on efficiency of collaborative allocation system of emergency material based on synergetic theory. Syst. Eng. Procedia 5, 240–247. doi:10.1016/j.sepro.2012.04.038
Gholamizadeh, K., Zarei, E., Yazdi, M., Ramezanifar, E., and Mirzaei Aliabadi, M. (2024). A hybrid model for dynamic analysis of domino effects in chemical process industries. Reliab. Eng. Syst. Saf. 241, 109654. doi:10.1016/j.ress.2023.109654
Gralla, E., Goentzel, J., and Fine, C. (2013). Assessing tradeoffs among multiple objectives for humanitarian aid delivery using expert preferences. Prod. Operations Manag. 23, 978–989. doi:10.1111/poms.12110
Hu, C. L., Liu, X., and Hua, Y. K. (2016). A Bi-objective robust model for emergency resource allocation under uncertainty. Int. J. Prod. Res. 54 (24), 7421–7438. doi:10.1080/00207543.2016.1191692
Knott, R. (1987). The logistics of bulk relief supplies. Disasters 11 (2), 113–115. doi:10.1111/j.1467-7717.1987.tb00624.x
Li, X., Chen, G., Paul, A., Alauddin, M., and Khan, F. (2023). Modeling and analysis of domino effect in petrochemical storage tank farms under the synergistic effect of explosion and fire. Process Saf. Environ. Prot. 176, 706–715. doi:10.1016/j.psep.2023.06.054
Liu, J., Guo, L., Jiang, J., Jiang, D., Liu, R., and Wang, P. (2016). A two-stage optimization model for emergency material reserve layout planning under uncertainty in response to environmental accidents. J. Hazard. Mater. 310, 30–39. doi:10.1016/j.jhazmat.2016.02.018
Liu, Z., Wu, Z., Ji, Y., Qu, S., and Hassan, R. (2021). Two-stage distributionally robust mixed-integer optimization model for three-level location–allocation problems under uncertain environment. Phys. A Stat. Mech. Its Appl. 572, 125872. doi:10.1016/j.physa.2021.125872
Najafi, M., Eshghi, K., and Dullaert, W. (2013). A multi-objective robust optimization model for logistics planning in the earthquake response phase. Transp. Res. Part E Logist. Transp. Rev. 49 (1), 217–249. doi:10.1016/j.tre.2012.09.001
Nezhadroshan, A. M., Amir, M.F.-F., and Hajiaghaei-Keshteli, M. (2021). A scenario-based possibilistic-stochastic programming approach to address resilient humanitarian logistics considering travel time and resilience levels of facilities. Int. J. Syst. Sci. Operations Logist. 8 (4), 321–347. doi:10.1080/23302674.2020.1769766
Rawls, C. G., and Turnquist, M. A. (2010). Pre-positioning of emergency supplies for disaster response. Transp. Res. Part B Methodol. 44 (4), 521–534. doi:10.1016/j.trb.2009.08.003
Salmerón, J., and Aruna, A. (2010). Stochastic optimization for natural disaster asset prepositioning: stochastic optimization for natural disaster asset prepositioning. Prod. Operations Manag. 19 (5), 561–574. doi:10.1111/j.1937-5956.2009.01119.x
Sheu, J.-B. (2007). An emergency logistics distribution approach for quick response to urgent relief demand in disasters. Transp. Res. Part E Logist. Transp. Rev. 43 (6), 687–709. doi:10.1016/j.tre.2006.04.004
Tang, Z., Li, W., Yu, S., and Sun, J. (2021). A fuzzy multi-objective programming optimization model for emergency resource dispatching under equitable distribution principle. J. Intelligent Fuzzy Syst. 41 (4), 5107–5116. doi:10.3233/JIFS-189996
Tzeng, G.-H., Cheng, H.-J., and Huang, T. D. (2007). Multi-objective optimal planning for designing relief delivery systems. Transp. Res. Part E Logist. Transp. Rev. 43 (6), 673–686. doi:10.1016/j.tre.2006.10.012
Vahdani, B., Veysmoradi, D., Noori, F., and Mansour, F. (2018). Two-stage multi-objective location-routing-inventory model for humanitarian logistics network design under uncertainty. Int. J. Disaster Risk Reduct. 27, 290–306. doi:10.1016/j.ijdrr.2017.10.015
Wang, Bo C., Qian, Q. Y., Gao, J. J., Tan, Z. Y., and Zhou, Y. (2021). The optimization of warehouse location and resources distribution for emergency rescue under uncertainty. Adv. Eng. Inf. 48, 101278. doi:10.1016/j.aei.2021.101278
Wang, F., Pei, Z., Dong, L., and Ju, Ma (2020). Emergency resource allocation for multi-period post-disaster using multi-objective cellular genetic algorithm. IEEE Acces 8, 82255–82265. doi:10.1109/access.2020.2991865
Wex, F., Guido, S., Feuerriegel, S., and Neumann, D. (2014). Emergency response in natural disaster management: allocation and scheduling of rescue units. Eur. J. Operational Res. 235 (3), 697–708. doi:10.1016/j.ejor.2013.10.029
Yang, M., Liu, Y., and Yang, G. (2021). Multi-Period dynamic distributionally robust pre-positioning of emergency supplies under demand uncertainty. Appl. Math. Model. 89, 1433–1458. doi:10.1016/j.apm.2020.08.035
Yang, Y., Ma, C., and Ling, G. (2022). Pre-location for temporary distribution station of urban emergency materials considering priority under COVID-19: a case study of wuhan city, China. Phys. A Stat. Mech. Its Appl. 597, 127291. doi:10.1016/j.physa.2022.127291
Yi, W., and Özdamar, L. (2007). A dynamic logistics coordination model for evacuation and support in disaster response activities. Eur. J. Operational Res. 179 (3), 1177–1193. doi:10.1016/j.ejor.2005.03.077
Yu, W. (2021). Pre-disaster location and storage model for emergency commodities considering both randomness and uncertainty. Saf. Sci. 141, 105330. doi:10.1016/j.ssci.2021.105330
Zahedi, A., Kargari, M., and Ali, H. K. (2020). Multi-objective decision-making model for distribution planning of goods and routing of vehicles in emergency multi-objective decision-making model for distribution planning of goods and routing of vehicles in emergency. Int. J. Disaster Risk Reduct. 48, 101587. doi:10.1016/j.ijdrr.2020.101587
Zhan, S.-lei, Liu, N., and Ye, Y. (2014). Coordinating efficiency and equity in disaster relief logistics via information updates. Int. J. Syst. Sci. 45 (8), 1607–1621. doi:10.1080/00207721.2013.777490
Zhang, L., Lin, Y., Yang, G., and Chang, H. (2011). Emergency resources scheduling based on adaptively mutate genetic algorithm. Comput. Hum. Behav. 27 (5), 1493–1498. doi:10.1016/j.chb.2010.10.013
Zhao, C., Yuanyuan, H., Gong, D., Du, J., Zhang, S., and Zhong, Li (2023). An ensemble learning-based multi-population evolutionary framework for multi-scenario multi-objective optimization problems. Knowledge-Based Syst. 275, 110708. doi:10.1016/j.knosys.2023.110708
Zhou, Y., Liu, J., Zhang, Y., and Gan, X. (2017). A multi-objective evolutionary algorithm for multi-period dynamic emergency resource scheduling problems. Transp. Res. Part E Logist. Transp. Rev. 99, 77–95. doi:10.1016/j.tre.2016.12.011
Zhu, B., Su, B., Li, Y., and Ng, T. S. (2020). Embodied Energy and intensity in China’s (normal and processing) exports and their driving forces, 2005-2015. Energy Econ. 91, 104911. doi:10.1016/j.eneco.2020.104911
Nomenclature
Keywords: emergency logistics, stochastic programming, multi-scenario modeling, petrochemical accident, disaster accident frequency
Citation: Jiang W, Yang Y, Hu A, Liu Y and Hong S (2024) Emergency materials management of petrochemical accidents considering the randomness and uncertainty base on stochastic programming. Front. Energy Res. 12:1370291. doi: 10.3389/fenrg.2024.1370291
Received: 14 January 2024; Accepted: 06 March 2024;
Published: 27 March 2024.
Edited by:
Fei Wang, Qingdao University of Science and Technology, ChinaReviewed by:
Chao Chen, Southwest Petroleum University, ChinaDingli Liu, Changsha University of Science and Technology, China
Copyright © 2024 Jiang, Yang, Hu, Liu and Hong. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yuxiang Yang, eWNoYW83NzM4QGdtYWlsLmNvbQ==
 Wei Jiang
Wei Jiang Yuxiang Yang2*
Yuxiang Yang2*