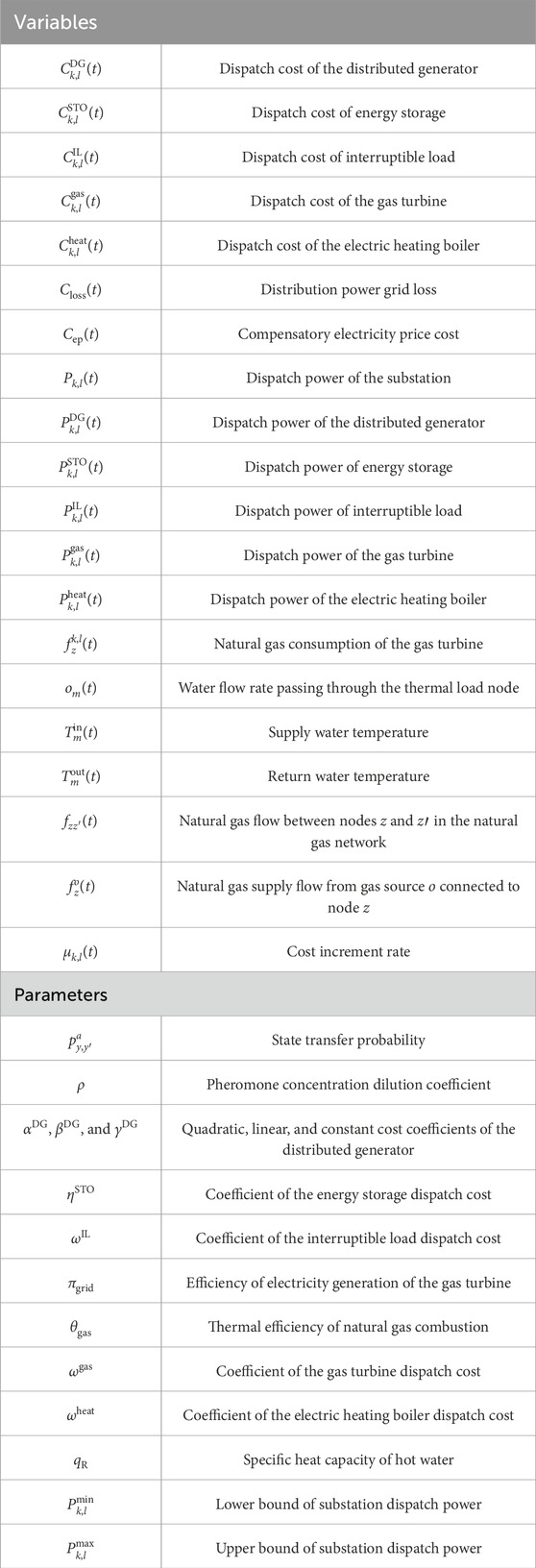
- 1State Grid Dezhou Electric Power Company, Dezhou, China
- 2State Grid Yucheng Electric Power Company, Yucheng, China
In light of the growing urgency surrounding energy and environmental concerns, this paper presents a two-layer iterative energy dispatch strategy tailored for a multi-energy-flow virtual power plant (VPP) operating within the distribution power grid. The proposed strategy unfolds in two key phases. First, it establishes an energy dispatch framework designed specifically for the multi-energy-flow VPP within the distribution power grid. Subsequently, it introduces an improved ant colony algorithm aimed at optimizing the output power of each VPP. In addition, the paper presents an optimization method for substation energy dispatch. This method uses a delay-aware consensus algorithm with the substation dispatch cost increment rate as the consensus variable, taking into account the communication delay between VPPs. Integrating a proportional–derivative (PD) control mechanism enhances the convergence speed of the delay-aware consensus algorithm and enables real-time energy dispatch of the multi-energy-flow VPP. The paper presents its conclusions by validating the efficacy of the proposed approach through simulation, thereby addressing the challenges and adapting to the shifting energy and environmental landscape.
1 Introduction
With increased severity in energy and environmental issues, decarbonization has emerged as an unavoidable trend in the future energy industry (Li et al., 2023). A virtual power plant (VPP) is a system that uses information technology to aggregate and coordinate resources such as distributed generators, energy storage, and interruptible load to enhance the stability and security of the power grid. The global energy system is accelerating its transition to renewable energy (Zhong et al., 2023a; Sarantakos et al., 2023; Wang et al., 2023). As a crucial energy structure for the future, multi-energy flow systems have the capacity to interconnect different types of energy (electricity, heat, gas, etc.); unify the planning, operation, and dispatch of various energy devices; and achieve efficient energy utilization (Chen et al., 2020; Wang et al., 2020). However, with the large-scale integration of renewable energy, encompassing distributed power sources, energy storage, and dispatchable loads, the volatility of multi-energy flow systems is also on the rise (Zhou et al., 2017; Zhong et al., 2023b). A multi-energy flow VPP, as an integrated energy network that connects electricity–gas–thermal energy sources, can coordinate and dispatch various internal units including renewable energy, gas resources, and thermal resources, which can not only provide more economic benefits but also help achieve the goal of energy-saving and emission reduction. At present, the multi-energy flow VPP faces difficulties such as high actual carbon emissions, complex multi-energy flow optimization variables, and multi-optimization objectives. It is urgent to explore how to improve the renewable energy consumption capacity of the multi-energy-flow VPP while reducing carbon emissions. The interconnection of diverse energy devices within multi-energy flow virtual power plants enables coordinated dispatch of electricity, gas, and heat, facilitating complementary utilization of multiple energy flows (Zhang et al., 2019; Gao et al., 2023; Wu et al., 2023). This not only effectively mitigates the fluctuations in multi-energy flow systems, reduces distribution grid losses, and enhances energy utilization efficiency but also promotes supply–demand balance, bringing about significant economic benefits.
Currently, when various types of energy are interconnected and complementarily integrated within a VPP, the involvement of diverse entities with different interests and complex energy and information exchange relationships among these entities pose a series of challenges in multi-energy flow VPP energy dispatch (Yang et al., 2023). A multi-energy flow VPP faces difficulties such as high actual carbon emissions, complex multi-energy-flow optimization variables, and multi-optimization objectives. It is urgent to explore how to improve the renewable energy consumption capacity of multi-energy flow VPPs. Many scholars have undertaken initial investigations into the challenges of energy dispatch in VPPs, with ant colony algorithms and consensus algorithms finding widespread application in the realm of energy dispatch. Ant colony algorithms are suitable for centralized energy dispatch. These algorithms possess global search capabilities and simulate the process of ants searching for food, thus helping in finding the global optimal solution for complex energy dispatch problems. Consensus algorithms, on the other hand, are applicable to distributed energy dispatch. They use real-time status information from neighboring substations and continually update their status to maintain consistency among all substations, thus ensuring the stable operation of the overall energy system.
However, there are still many challenges facing the energy dispatch process in multi-energy flow VPPs:
The energy interaction among electricity, gas, and heat within the VPP, coupled with the interdependence between the VPP, substations, and distribution grids, makes the energy dispatch of multi-energy flow VPPs an extremely complex problem. Complex energy and information exchange relationships exist among multiple entities (Li et al., 2022; Huang et al., 2023). Due to the conflicts of ownership, optimization objectives, and interests among different entities, the increase in the multi-energy flow coupling degree will inevitably make the mutual influence among various energy subsystems more obvious. Traditional single-layer energy dispatch methods usually only consider the optimization of a single energy source when solving the multi-energy flow dispatch model, ignoring the coordination of multi-energy flow. Moreover, the local fluctuations of the system affect the solution of the whole system, resulting in high dispatch costs and high network losses, which are unsuitable for the complex energy dispatch for multi-energy flow VPPs.
In traditional ant colony algorithms, the concentration of pheromones and the heuristic function typically remain static. As the number of iterations increases, there is a gradual rise in the concentration of pheromones, potentially elevating the risk of converging toward local optima. Simultaneously, the value of the heuristic function decreases, possibly resulting in excessive dependence on pheromones. In the context of energy dispatch for multi-energy-flow VPPs, the adaptability of traditional ant colony algorithms decreases. This results in a slow convergence rate when solving the energy dispatch problem for multi-energy flow VPPs, making it challenging to meet the real-time requirements of such dispatch.
Consensus algorithms achieve consistency for all substation states through the transmission of state information among neighboring substations. However, during the consensus iteration process, there is a delay in the transmission of state information among neighboring substations. This leads to traditional consensus algorithms being unable to promptly and accurately obtain state information from neighboring substations, affecting the convergence speed of the consensus iteration, increasing the fluctuation of multi-energy flow within the VPP, and resulting in high dispatch costs and distribution grid losses in the energy dispatch for multi-energy flow VPPs.
During the consensus iteration process, factors such as channel conditions and geographical locations cause a delay in the transmission of state information between neighboring substations. Traditional consensus algorithms overlook the time delay in the transmission of state information, making it challenging to promptly and accurately acquire the state information of neighboring substations. This, in turn, affects the convergence speed of the consensus iteration, increases the fluctuations in multi-energy flow within the VPP, and results in excessively high dispatch costs and distribution grid losses in the energy dispatch for the multi-energy-flow VPPs.
Presently, extensive research is being conducted on the energy dispatch for VPPs. One approach involves conceptualizing VPPs as coalitions of wind generators and electric vehicles, establishing an operational model based on linear programming. This model, as discussed in Vasirani et al. (2013), demonstrates how scheduling the supply to the grid and storage in electric vehicle batteries can enhance the VPP’s profitability. Another highlighted in Yang et al. (2013), Yang et al. proposed a distributed optimal dispatch method using the distributed primal-dual sub-gradient algorithm. This method involves coordinating the individual decision-making of distributed energy resources within the VPP through limited communication, ultimately maximizing the VPP’s profit. In the context of multiple distributed generators within a VPP, a distributed control strategy is introduced in Xin et al. (2013). This strategy aims to guide the VPP to converge and operate at an optimal output power determined by the costs of distributed generations and the required services assigned by the distribution grid. Mohy-ud din et al. (2020) adopts the linearization method to solve the energy transaction management problem of integrated energy systems based on VPPs. The linearization-based optimization method is well-suited for addressing linear optimization objectives of a relatively straightforward nature. However, it encounters challenges when attempting to tackle complex nonlinear optimization targets, such as those related to distribution power grid loss. There is currently much research on the use of intelligent algorithms in the field of VPP energy dispatch. Abdolrasol et al. (2018); Hannan et al. (2021) applied optimization research to solve the application problems of current technologies, adding value by enhancing them in the direction of optimal solutions. Zhang et al. (2023a) focuses on the interaction between electricity and heat, demonstrating the influence of multiple factors on the safe operation of electricity. Yan et al. (2020) focuses on the efficiency and convergence accuracy of the method in solving the electricity and gas system model. However, the above-mentioned literature has not taken into account the coupling of multi-energy flow within VPPs nor has it considered energy dispatch strategies with multiple layers of interaction.
Various studies have explored the multi-energy flow complementation of VPPs. Cui et al. (2016) integrated electric boilers and heat storage equipment into wind power plants, using thermoelectric conversion for consume wind power consumption. Yuan et al., as highlighted in Guili et al. (2017), achieved “thermoelectric decoupling” through use of electric heating equipment, enabling coordinated dispatch of thermoelectric power in the system. Li et al. (2019) analyzed the operation strategy of a multi-energy flow complementary system with the goal of enhancing the system economy. Additionally, there have been advancements in the application of ant colony algorithms. Niknam et al. proposed a novel approach based on the ant colony algorithm for the distribution management system in the context of dispersed generation (Niknam et al., 2005). Trivedi et al. (2015) used the ant colony optimization technique to address multiple environment dispatch problems in microgrids, solving the generation dispatch problem. Hou et al. introduced a versatile optimization algorithm named the generalized ant colony optimization algorithm to tackle discontinuous, nonconvex, nonlinear constrained optimization problems (Hou et al., 2002). Blockchain technology has also been incorporated into VPP systems, as presented by Wang et al. in Jing et al. (2022), where a VPP system architecture based on blockchain was proposed, accompanied by a blockchain partition consensus algorithm for VPP dispatch. Furthermore, consensus-based algorithms have been introduced. Naina and Swarup (2022) proposed a robust, fully distributed consensus-based algorithm utilizing a monotonic decreasing consensus gain function to mitigate the effects of communication delays and noise, allowing the VPP to optimize electricity output and intake based on grid demand. For addressing trust issues in real-time VPP dispatch, Qi et al. designed a hybrid consensus mechanism combining multiple algorithms and proposed a mixed consensus algorithm based on convex optimization problems in Yu et al. (2022), optimizing computational resources and improving VPP dispatch efficiency. Xu et al. (2019) proposed a two-layer distributed coordinated control method for managing VPPs in an active distribution power grid, with the first layer dispatching the total output power of multiple VPPs and the second layer handling the output power of each intelligent agent within the VPPs. Despite these advancements, challenges persist: 1) one notable issue is real-time adjustment of pheromone concentration and heuristic functions. With the increase in the number of iterations, the adaptability of traditional ant colony algorithms diminishes, leading to slow convergence speeds when addressing the energy dispatch problem of multi-energy-flow VPPs. 2) There is a delay in the transmission of state information among neighboring substations, causing traditional consensus algorithms to be unable to promptly and accurately obtain state information from neighboring substations. This affects the convergence speed of the consensus iteration, increases the fluctuation of multi-energy flow within the VPP, and leads to high dispatch costs and distribution grid losses in the energy dispatch for multi-energy flow VPPs.
In response to the aforementioned issues, we propose a two-layer iterative energy dispatch strategy for a multi-energy flow VPP in the distribution power grid. First, we establish an energy dispatch framework for a multi-energy flow VPP in the distribution power grid. Second, we decompose the energy dispatch optimization problem of a multi-energy flow VPP into an upper-layer multi-energy flow VPP energy dispatch sub-problem and a lower-layer distributed substation energy dispatch sub-problem. The upper-layer optimization is designed to minimize distribution grid loss and compensatory electricity price cost, adhering to the constraints of VPP output and power flow balance. Moreover, the lower-layer optimization focuses on minimizing dispatch costs within the constraints of the natural gas pipeline network, thermal network, and inequality. Finally, we propose a two-layer iterative energy dispatch algorithm that incorporates an improved ant colony algorithm and a delay-aware consensus algorithm. This approach reduces the dispatch costs and distribution grid losses of multi-energy flow VPP energy dispatch, enhancing the real-time performance of the energy dispatch process.
The innovation points are given as follows:
A two-layer iterative energy dispatch strategy for a multi-energy flow VPP: the transmission of substation dispatch power occurs from the upper layer to the lower layer, while the lower layer transmits load dispatch ability information to the upper layer. This process enables the realization of a two-layer optimal dispatch method for the multi-energy flow VPP. This strategy achieves coordinated dispatch of electricity, gas, and heat flows, addressing the challenges posed by complex energy and information exchange relationships and conflicting interests among different entities. The two-layer energy dispatch strategy for multi-energy flow in the distribution power grid couples the electric–gas energy sources through gas turbines at the upper layer and couples the electric–thermal energy sources through electric boilers at the upper layer, achieving the complementarity of multi-energy flow. At the lower layer, the two-layer energy dispatch of multi-energy flow only optimizes the output of electric power energy. It improves the flexibility of the VPP, effectively alleviates the fluctuation of the multi-energy flow system, reduces the loss of the distribution power grid, and achieves the coordination and balance of the multi-energy-flow VPP internally.
Multi-energy flow VPP energy dispatch based on the improved ant colony algorithm: in light of real-time operational cost deviations, this paper adjusts the computation of pheromone concentration and heuristic functions dynamically to consider the evolving conditions. This adjustment enhances the algorithm’s adaptability, improves convergence speed, and ensures the real-time performance of multi-energy flow VPP energy dispatch.
Distributed substation energy dispatch based on the delay-aware consensus algorithm: considering the impact of communication delays on consensus convergence. The introduction of a proportional–derivative (PD) controller enables a rapid response to changes in the state information of each substation. Additionally, a time-dependent feedback term is incorporated into the PD controller to adjust dispatch signal updates, improving convergence speed, suppressing fluctuations in multi-energy-flow within the VPP, and reducing the dispatch costs and distribution grid losses of multi-energy flow VPP energy dispatch.
2 System model
Figure 1 shows the energy dispatch framework for a multi-energy flow VPP in the distribution power grid, which consists of a cloud layer, an edge layer, and a device layer. The cloud layer is composed of a regional multi-energy-flow dispatch center, a grid dispatch center, and a power trading center. The edge layer is composed of multiple VPPs, where each VPP is responsible for communicating and interacting with various substations within its jurisdiction. It undertakes substation dispatch, monitoring, and other edge analytics functions. The set of VPPs is represented as
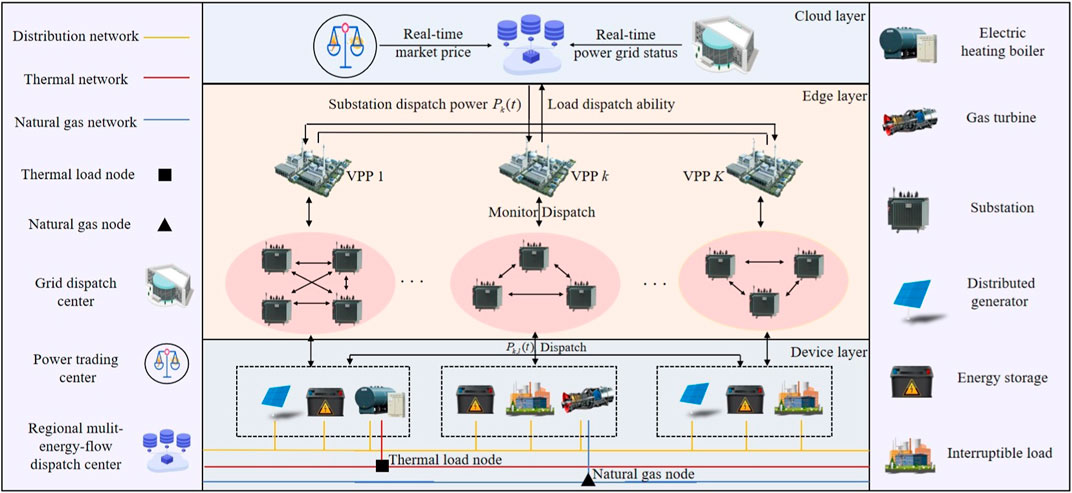
Figure 1. Two-layer iterative energy dispatch framework for a multi-energy flow VPP in the distribution power grid.
The VPPs are connected to the distribution power grid, and there is a coupling relationship between them. The set of distribution grid nodes is denoted as
We use a time-slotted model in which the overall optimization period is segmented into T time slots, each with an equal duration of τ. The set of time slots is denoted as
2.1 Multi-energy-flow VPP model
2.1.1 Distributed generator model
The dispatch cost of the distributed generator
where
2.1.2 Energy storage model
The dispatch cost of energy storage
where
The capacity of energy storage
where
2.1.3 Interruptible load model
There is a clear distinction drawn between controllable and uncontrollable loads in the distribution power grid. Uncontrolled loads are loads that cannot participate in the demand response of the distribution power grid (Liang et al., 2021). In contrast, controllable loads refer to the loads that can participate in the demand response of the distribution power grid. The interruptible load proposed in this paper is one of the controllable loads. The dispatch cost of the interruptible load
where
2.1.4 Gas turbine model
The dispatch power of the gas turbine
where πgrid represents the efficiency of electricity generation by the gas turbine.
The dispatch cost of gas turbine
where ωgas represents the coefficient of the gas turbine dispatch cost.
The gas turbine is linked to the natural gas network, and the model for the gas network is formulated as follows. It is assumed that natural gas flows in the pipeline at a constant temperature and stable flow, and friction coefficients within the pipeline are neglected, i.e., kinetic energy changes during the flow process are ignored.
The balance relationship between natural gas flow refers to the node air flow balance of the natural gas pipeline network, i.e., the natural gas flow injected by the node is equal to the sum of the flow consumed by the node and the gas flowing to the next node (Dai et al., 2018), which is given by Eq. 7.
where fzz′(t) represents the natural gas flow between nodes z and z′ in the natural gas pipeline network.
The natural gas flow fzz′(t) between natural gas nodes z and z′ is given by Eq. 8.
where Kzz′ is the pipeline constant. Dzz′ represents the gas flow direction between nodes z and z′, with Dzz′ = 1 when gas flows from z to z′, and Dzz′ = −1 otherwise. pz(t) and pz′(t) represent the gas pressure at nodes z and z′, respectively.
2.1.5 Electric heating boiler model
As a controllable thermal load, the dispatch cost of electric heating boiler
where ωheat represents the coefficient of the electric heating boiler dispatch cost.
The electric heating boiler is directly connected to the thermal load node m, and the electric heating boiler is connected to the distribution power grid through substation l within VPP k. The interactive power is given by
In a certain range of ambient temperature difference, considering that the heating medium in the thermal network is hot water, minor flow rate changes due to temperature differences in the supply and return pipes are neglected (Zhang et al., 2023b). In this study, it is assumed that the temperature of water in the return pipes is known, and, therefore, the temperature
where ζheat represents the heat production efficiency of the electric heating boiler. qR is the specific heat capacity of hot water. om(t) is the water flow rate passing through thermal load node m during the t-th time slot.
where
2.1.6 Substation model
In order to facilitate resource management, the internal resources of the VPP are divided into multiple substations. We assume that in VPP k, substation l contains the aforementioned five types of resources. The dispatch power of substation Pk,l(t) is given by Eq. 12.
The dispatch power constraint for substation l in VPP k is given by Eq. 13.
where
2.2 Distribution power grid loss model
The distribution power grid loss Closs(t) is given by Eq. 14.
where γloss represents the unit grid loss cost. Rij(t) is the resistance value between the distribution power grid node i and node j during the t-th slot. v(i) represents the set of end nodes of branches in the power grid that have node i as the starting node.
where u(j) represents the set of starting nodes in the distribution power grid with node j as the tail node. v(j) represents the set of end nodes of branches in the power grid with node j as the starting node. Rij and Xij are the resistance and reactance of the line between the distribution power grid node i and node j, respectively. Pj(t) is the net active power at node j. Pjs(t) is the load active power flowing from upstream node j to node s.
where
where Vi and Vj represent the voltage at node i and node j, respectively. The voltage constraint of node i is given by Eq. 18.
where
3 Problem formulation of two-layer iterative energy dispatch
The two-layer iterative energy dispatch problem for a multi-energy flow VPP in the distribution power grid can be decomposed into two optimization sub-problems: the upper-layer multi-energy flow VPP energy dispatch sub-problem and the lower-layer distributed substation energy dispatch sub-problem.
3.1 Upper-layer multi-energy flow VPP energy dispatch sub-problem
During the real-time operational phase, the regional multi-energy-flow dispatch center takes on the task of global optimization and dispatch (Liao et al., 2023). The upper layer multi-energy flow VPP energy dispatch sub-problem is optimized to minimize the distribution power grid loss and the compensatory electricity price cost, and the dispatch power Pk(t) of each VPP participating in the demand response is the optimization variable. The specific formulation of the upper-layer multi-energy flow VPP energy dispatch sub-problem is given by Eq. 19.
where Ctotal(t) represents the distribution power grid dispatch cost, Cep(t) represents the compensatory electricity price cost, αk(t) represents the compensatory electricity price, Pk(t) represents the amount of purchased electricity of VPP k during the t-th time slot, Closs(t) stands for the distribution power grid loss cost, C1 represents the constraints on the upper and lower bounds of substation dispatch power, and C2 represents the constraints on distribution power flow.
3.2 Lower-layer distributed substation energy dispatch sub-problem
The regional multi-energy-flow dispatch center sends the optimized dispatch power values to the substations within VPPs. Within each substation, the dispatch power of the distributed generator, energy storage, interruptible load, gas turbine, and electric heating boiler is optimized and adjusted based on the dispatch power values. The substation energy dispatch sub-problem aims to minimize the dispatch cost of the above resources, with the dispatch power of each resource as the optimization variable. Taking the substation l within VPP k as an example, the specific problem description is given by Eq. 20.
where Ck,l(t) represents the dispatch cost of substation l in VPP k during the t-th time slot. C1 and C6 represent the constraints related to the natural gas network and gas turbine dispatch power, respectively.
4 Two-layer iterative energy dispatch for a multi-energy flow VPP based on the improved ant colony algorithm and the delay-aware consensus algorithm
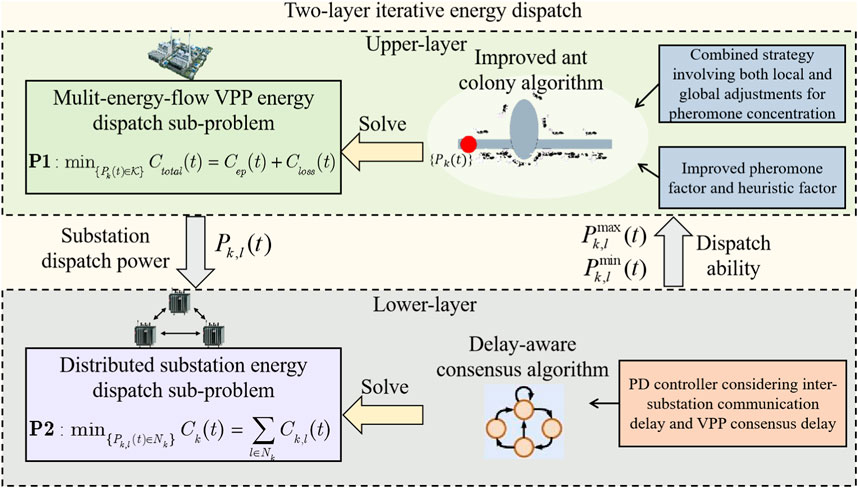
The principle of the proposed algorithm is illustrated in Figure 2. The two-layer iterative energy dispatch strategy incorporates an improved ant colony algorithm in the upper layer and a delay-aware consensus algorithm in the lower layer. First, a combined pheromone update strategy and improved pheromone factor and heuristic factor were adopted to improve the ant colony algorithm for solving the sub-problem of multi-energy flow VPP energy dispatch. This involves adjusting the dispatch power of each VPP according to diverse service requirements. The calculated dispatch power was distributed to each substation for lower-layer optimization. Second, communication interaction was carried out among the substations, with the micro-increment rate of substation dispatch cost serving as the consensus variable for the consensus iteration. To solve the substation energy dispatch sub-problem, the PD controller was introduced into the traditional consensus algorithm. Information exchange occurs between the two layers: the upper layer issues dispatch power to the lower layer for substation scheduling, and the lower layer uploads information on the load dispatch capability.
4.1 Upper-layer multi-energy flow VPP energy dispatch based on the improved ant colony algorithm
The ant colony algorithm falls within the category of heuristic global optimization algorithms, transforming the optimization problem into an ant path problem. However, in traditional ant colony algorithms, the range in variation between pheromone concentration and heuristic function is fixed. As the number of iterations increases, the pheromone concentration gradually increases, and the heuristic function value gradually decreases. This lack of adaptability with the increasing number of iterations results in slow convergence speed when solving the upper-layer multi-energy flow VPP energy dispatch sub-problem, leading to sub-optimal energy dispatch strategies. To address this limitation, this paper introduces real-time operational cost deviation considerations in the computation of pheromone and heuristic factors. This allows for adaptive changes in pheromone concentration and heuristic function based on real-time cost deviations. Such an adaptation accelerates the convergence speed, ensuring the real-time nature of energy dispatch. The specific implementation procedures are summarized in Algorithm 1.
Algorithm 1.Upper-layer energy dispatch for a multi-energy flow VPP based on the improved ant colony algorithm.
1: Initialize maximum iteration hmax, pheromone factor Γ, and heuristic factor ϱ.
2: For h = 1 to hmax do
3: Randomly initialize ant positions.
4: For a = 1 to S do
5: Determine the next optional transfer position according to the tabu list and calculate the state transfer probabilities based on (21).
6: Choose the next position using the roulette wheel method based on the state transfer probabilities.
7: If the selected transfer position does not satisfy constraints (13) and (15)∼(18) do
8: Marks the current position from the tabu list as not optional.
9: The a-th ant returns to the previous position and selects a new transfer position again.
10: Else
11: Update the local pheromone concentration according to (25).
12: End if
13: End for
14: Update the global pheromone concentration according to (23).
15: End for
During the state updating process, it is essential to ensure that the control strategies associated with each position meet various constraint conditions for upper-level multi-energy real-time dispatch. Therefore, this paper initially compares the dispatch strategies associated with each position with various constraint conditions to construct a tabu list, thereby confirming that certain positions cannot be reached. This ensures that the optimization results obtained during the algorithm’s iteration process satisfy all constraint conditions.
The state transfer probabilities are given by Eq. 21.
where
To enhance the convergence speed of the algorithm, this paper proposes the following improvements to the pheromone factor and heuristic factor (Eq. 22):
where ΔCtotal(t) represents the deviation of the real-time operational cost between the t-th time slot and the (t − 1)-th time slot and ΔCtotal(t − 1) represents the deviation of the real-time operational cost between the (t − 1)-th time slot and the(t − 2)-th time slot.
To attain comprehensive performance optimization, this paper proposes a combined strategy involving both local and global adjustments for pheromone concentration. This strategy aims to avoid getting stuck in local optima while increasing the selection probability for better paths as much as possible, in order to accurately and quickly find the global optimum. In each iteration of the improved ant colony algorithm, every ant selects the next position based on a state transfer probability formula, thereby generating a complete path. With an increasing number of iterations, the concentration of pheromones on each path undergoes continuous changes. After all ants have completed their journeys within a single iteration cycle, the adjustment of the pheromone concentration Φy,y′(t) is updated. The updating strategy for pheromone concentration in the ant colony algorithm is given by Eq. 23.
where s represents the number of ants, and there are a total of S ants. ρ represents the improved pheromone concentration dilution coefficient.
In traditional ant colony algorithms, the pheromone concentration dilution coefficient is typically given and relies heavily on historical experience, without the ability to be updated based on real-time conditions. In this paper, the formula for improved pheromone concentration dilution coefficient is introduced by incorporating a negative exponential function that accounts for real-time deviations in operational costs. The improved pheromone concentration dilution coefficient is given by Eq. 24.
where x represents the number of iterations and u represents the influence coefficient of x on ρ. As the number of iterations x increases, the pheromone concentration dilution coefficient ρ decreases to retain a certain degree of prior experience, facilitating global search. The parameter γ serves as the cost weight used to standardize magnitudes. A larger real-time operational cost deviation, indicating a greater distance from the optimal solution, results in a reduction of the pheromone concentration on that path, effectively increasing the pheromone concentration dilution coefficient. In this scenario, ants are more inclined to explore. Conversely, when the real-time operational cost deviation is smaller, indicating proximity to the optimal solution, the pheromone concentration on that path is strengthened by reducing the pheromone concentration dilution coefficient. In such cases, ants are more inclined to exploit the path.
By improving the adaptive selection function in the ant colony algorithm, the pheromone concentration adjustment coefficient is given by Eq. 25.
where G represents the concentration adjustment constant and Ctotal(t) represents the distribution power grid dispatch cost during t-th time slot.
4.2 Lower-layer substation energy dispatch based on the delay-aware consensus algorithm
In the context of processing self-generated information within a substation and receiving data from neighboring substations, traditional consensus algorithms disregard the influence of communication delay on consensus convergence. In scenarios requiring time-sensitive demand–response services, the sluggish convergence rate of traditional algorithms proves inadequate for meeting service demands (Zhou et al., 2022). This paper proposes an enhancement by integrating a proportional–derivative (PD) controller to address the issue of sluggish convergence attributable to communication delay. First, this improvement incorporates the communication delay factor into the algorithm, thereby aligning it more effectively with the requirements of delay-aware service scenarios. Second, the introduction of the PD controller enables the system to respond promptly to changes in substation information, thereby improving both convergence speed and system stability. The fundamental principle of this enhancement involves introducing a time-dependent feedback term into the PD controller to adjust dispatch signal updates for various resource power strategies within each substation. This facilitates the PD controller’s swift and effective response to changes in substation information, mitigating the impact of communication delay on system convergence. The specific implementation procedures are outlined in Algorithm 2.
Algorithm 2.Lower-layer power optimization for substations based on the delay-aware consensus algorithm.
1: Initialize Pk,l(t) in VPP k.
2: While (30) is not satisfied do
3: Calculate μk,l(t) according to (26), (27).
4: Update μk,l(t) according to (28).
5: Calculate Pk,l(t) according to (31).
6: End while
In the algorithm, each substation only acquires the status information of its neighbors at the triggering moment and relies solely on its own status and the status of its neighbors at the triggering moment to update the cost increment rate. There is no need to use real-time status information from neighbors nor is there a need for any global information about the communication topology. The designed dispatch strategy effectively avoids continuous communication. Based on the objective of minimizing dispatch costs of each VPP, the delay-aware consensus algorithm is used to solve the lower-layer distributed substation energy dispatch sub-problem, which is defined in Eq. 20. The substation’s dispatch cost increment rate is defined as the derivative of the dispatch cost with respect to dispatch power over unit time, which is given by Eq. 26.
where μk,l(t) represents the cost increment rate for substation l within VPP k during the t-th time slot.
The cost increment rate for substation l is obtained from (1)–(4), (6), and (9), which is given by Eq. 27.
To accelerate the convergence rate of the consensus algorithm and ensure standardized convergence rates across different substations, the design of the PD controller incorporates considerations for the inter-substation communication delay and the VPP consensus delay. A delay-dependent feedback term is introduced to adapt the cost increment rate update strategy for each substation. The consensus iteration formula post PD correction is given by Eq. 28.
where d is the number of consensus iterations.
If the optimal allocation of dispatch power is achieved among the substations, meaning that the dispatch cost increment rates for all substations tend to be consistent, there exists Eq. 29.
The termination criteria for the iteration are given by Eq. 30.
where ΔPk(t) and Δμk,l(t) are used as the convergence criteria during the computation process of the delay-aware consensus algorithm, with σk and Ωk representing convergence errors within VPP k.
In the proposed consensus algorithm, consideration is given to the communication delay between substations, realizing communication delay awareness. However, due to the introduction of communication delay, the convergence speed of the consensus algorithm is slowed down. Therefore, the algorithm introduces PD control. The PD feedback strength parameter
4.3 Algorithm implementation process
We use the delay-aware consensus algorithm to achieve energy dispatch of multi-energy flow VPPs. The initial values for iteration, i.e., the cost increment rate, are calculated by Eq. 27 and the initial power values for each resource are determined. As the algorithm continues to converge, the power values of each resource in the current time slot gradually approach the optimal value, achieving optimal real-time energy dispatching. Figure 3 shows the specific implementation process:
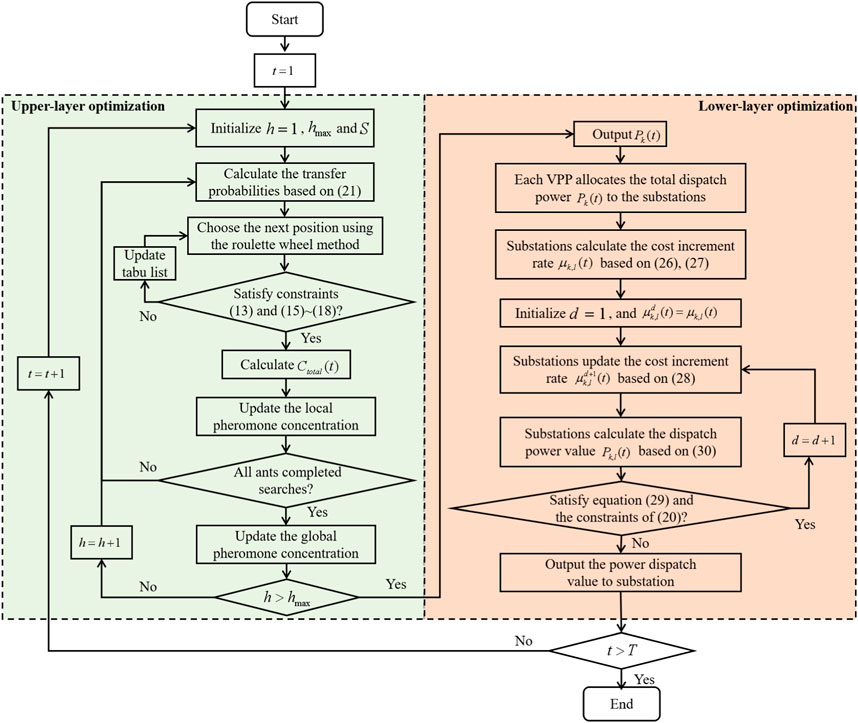
Figure 3. The implementation process of two-layer iterative energy dispatch for a multi-energy flow VPP based on the improved ant colony algorithm and the delay-aware consensus algorithm.
Upper-layer multi-energy-flow VPP energy dispatch based on the improved ant colony algorithm.
Step 1: Initialize t = 1. Initialize the iteration count in the ant colony algorithm and randomly assign ants to different dispatch strategies, including Pk(t). Set the maximum iteration count as hmax.
Step 2: Calculate the transfer probabilities for all ants, determine the probabilities of selecting different dispatch strategies, and choose the next transfer using the roulette wheel method. Verify if the next transfer satisfies all constraints. If it does, proceed to Step 3; otherwise, mark this position in the tabu list, disallowing other ants from transferring to this position. The ant then returns to the previous position and selects a new next position.
Step 3: After an ant completes its current search, use Eq. 19 as the objective function to calculate Ctotal(t) and update the local pheromone levels. Check if constraints (13) and (15∼18) are satisfied. If it is satisfied, continue the implementation process; otherwise, return to Step 2.
Step 4: After all ants have completed their searches for this round, update the global pheromone levels. Check if constraints (13) and (15∼18) are satisfied. If it is satisfied, continue the implementation process; otherwise, return to Step 2.
Step 5: If h⩽hmax, set h = h + 1 and return to Step 1; otherwise, output the optimal result. The regional multi-energy-flow dispatch center allocates optimal dispatch power to each VPP.
Step 6: The total dispatch power of each substation cluster is obtained from the VPP after global optimization calculation.
Lower-layer substation energy dispatch based on the delay-aware consensus.
Step 7: Each VPP allocates the total dispatch power to the substations within its coverage area.
Step 8: Initialize the cost increment rate μk,l(t) based on Eqs (26) and (27), initialize d = 1, and set
Step 9: Update the consensus variables for each substation according to Eq. 28, and calculate the power dispatch value for each substation in this state based on Eq. 31, which can be given by
where
Step 10: Check if Eq. 30 and the constraints of optimization problem P2 are satisfied. If they are not satisfied, continue to execute Step 11. If they are satisfied, output the power dispatch value for the substation, i.e., the dispatch power value of each internal resource, and continue to execute Step 12.
Step 11: Based on the power obtained in Step 9, recalculate the consensus variable. Set d = d + 1, and return to Step 9.
Step 12: If t > T, the optimization process ends; otherwise, set t = t + 1 and return to Step 2.
4.4 Complexity and convergence analysis
4.4.1 Complexity analysis
The computational complexity of the proposed algorithm is analyzed as follows. It consists of two parts, namely, the improved ant colony algorithm and the delay-aware consensus algorithm, which together make up the computational complexity.
The computational complexity of the improved ant colony algorithm consists of six parts. The complexity of calculating transfer probabilities is O(1). The complexity of assessing the constraint conditions during transfers is O(5). The complexity of transferring to the next step is O(v), where O(v) represents the number of required successful transfers in a single step. The complexity of updating local pheromone concentrations is O(1). The complexity of updating global pheromone concentrations is O(S). The complexity of the number of iteration calculations is O(hmax). Therefore, the total computation complexity of the improved ant colony algorithm is O(hmaxS(v + 7)).
The computational complexity of the delay-aware consensus algorithm consists of four parts. The complexity of iteration termination judgment is O(Λ), where O(Λ) represents the number of iterations required to satisfy the constraint and O(Λ) = f(σ, Ω). f(x) represents the fuzzy correlation function. Λ is inversely proportional to σ, so as to Ω. The complexity of calculating the cost increment rate is O(2). The complexity of updating the cost increment rate is O(1). The complexity of calculating the substation power is O(1). Therefore, the total computation complexity of the delay-aware consensus algorithm is O(4Λ).
Totally, the computation complexity of the proposed algorithm is O(hmaxS(v + 7) + 4Λ).
4.4.2 Convergence analysis
In the proposed delay-aware consensus algorithm, we introduce the PD controller to accelerate convergence. The convergence of this algorithm is related to the delay. When the delay is
5 Simulation result
To validate the effectiveness of the proposed algorithm, we use a simulation model based on a modified IEEE 33-node distribution grid system. Figure 4 illustrates the specific topological relations of each VPP. There are three VPPs in the model, each containing multiple substations. Each substation contains different quantities of distributed generators, energy storage, interruptible loads, gas turbines, and electric heating boilers.
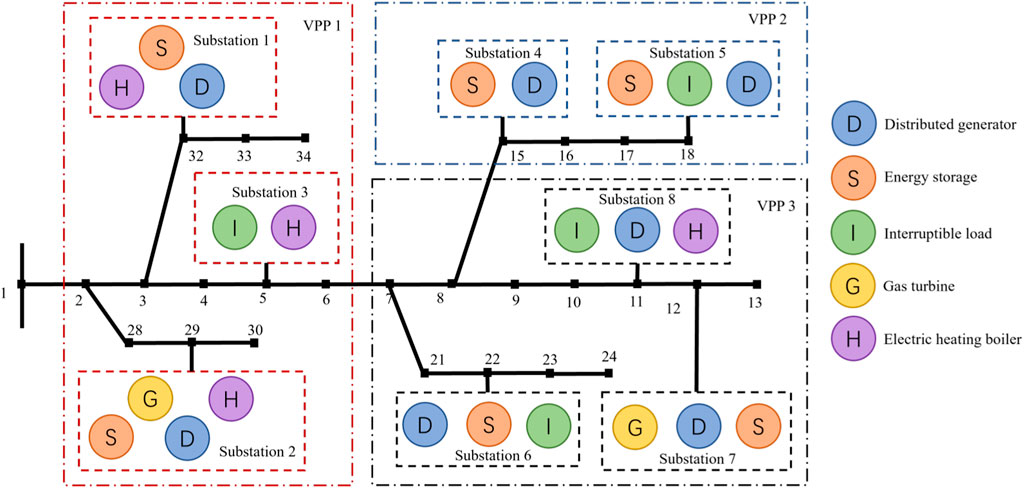
Figure 4. VPP topological relationships based on the modified IEEE 33-node distribution grid system.
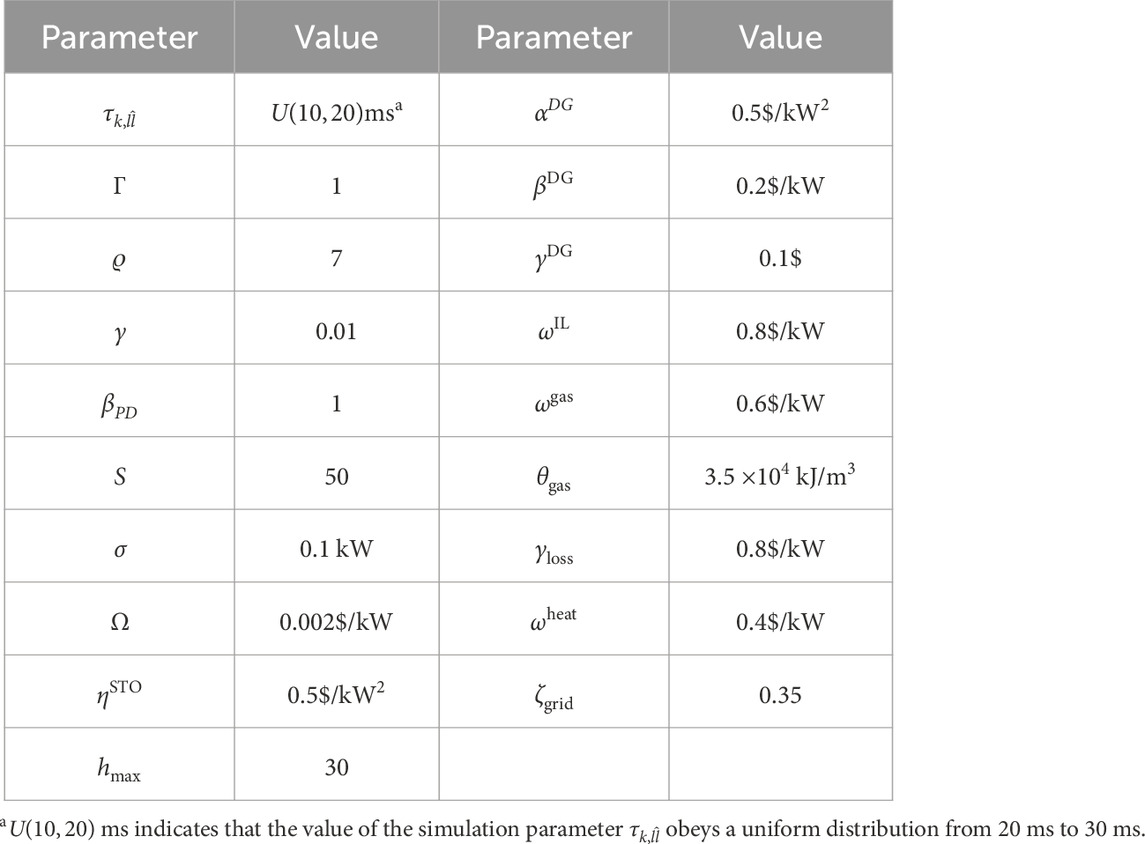
We compare the proposed algorithm with three baselines, with baseline 1 using the DDPG algorithm in the upper layer and the traditional consensus algorithm in the lower layer, baseline 2 using the traditional ant colony algorithm in the upper layer and the traditional consensus algorithm in the lower layer, and baseline 3 using the particle swarm optimization algorithm in the upper layer and the traditional consensus algorithm in the lower layer. Compared with similar deep learning algorithms, the DDPG algorithm has higher training efficiency (Zhang et al., 2023c). Although the desired dispatching value is almost the same as the theoretical optimal value, the real-time requirement of power dispatching is ignored. Table 2 shows the simulation parameters (Pasetti et al., 2018; Gough et al., 2022; Liang and Ma, 2022). The power constraints of various resources in each substation are shown in Tables 3–5. We simulate a 24-hour operation, optimizing dispatch every hour, with a consensus iteration period of 0.1 s.
In Figure 5A, the distribution power grid loss versus time is depicted for the mentioned algorithms. The figure reveals that the proposed algorithm consistently produces lower losses in comparison to the other three algorithms. Taking 4:00 as an example, compared to baseline 1, baseline 2, and baseline 3, the proposed algorithm reduces grid loss by 11.27%, 8.03%, and 3.96%, respectively. The proposed algorithm can adjust the convergence speed according to the delay, thereby reducing the dispatch delay and leading to a decrease in distribution power grid loss.
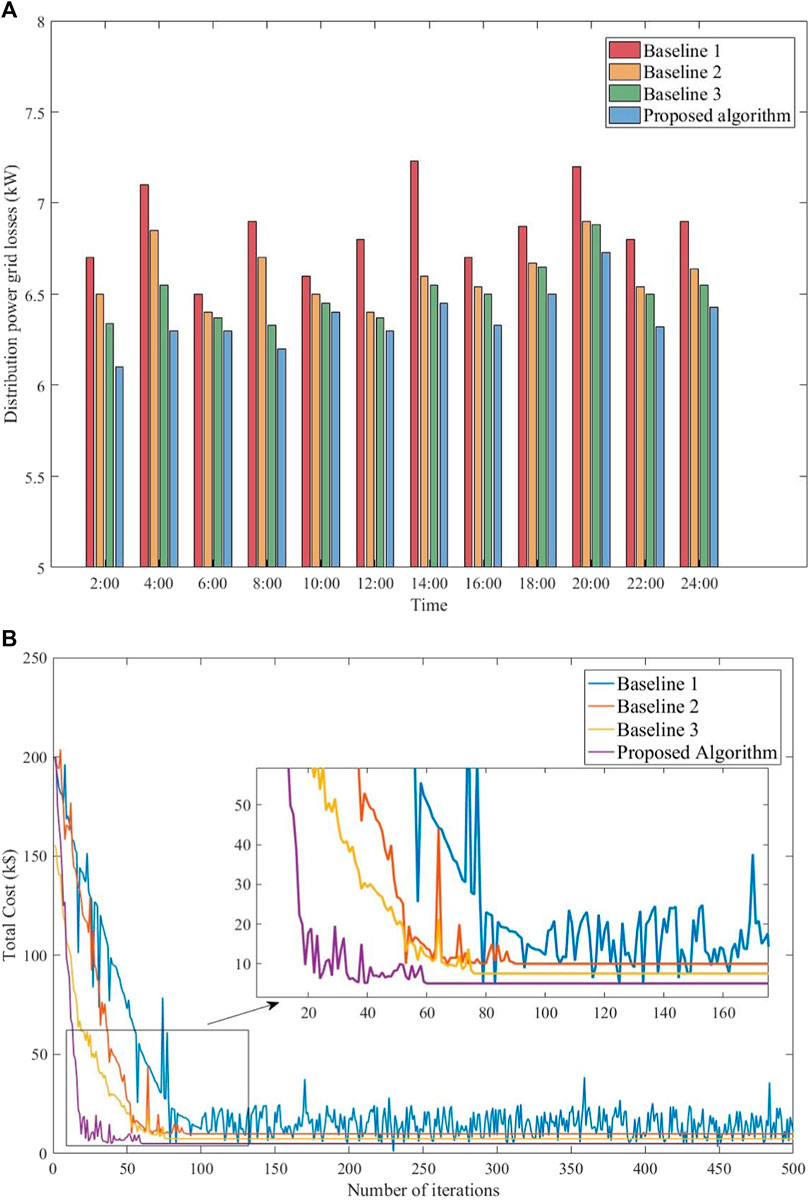
Figure 5. Performance of the total dispatch cost and distribution power grid loss. (A) Distribution power grid losses. (B) Total dispatch costs.
Figure 5B shows the optimized dispatch process of the mentioned algorithms at 16:00. At the beginning of the mentioned algorithms, the total cost is rapidly decreasing. In the end, baseline 1 fluctuates within a certain range and can only achieve dynamic convergence. Baseline 2, baseline 3, and the proposed algorithm reach convergence after 88, 74, and 60 iterations, and their total dispatch costs are $12,000, $9,700, and $7,000, respectively. Compared with baseline 1, baseline 2, and baseline 3, the proposed algorithm reduces the total dispatch cost by 94.38%, 71.42%, and 38.57%, respectively. The proposed algorithm exhibits the fastest convergence speed due to the introduction of changing factors in the ant colony algorithm and PD correction in the consensus algorithm. The change factor and PD correction in the proposed algorithm significantly accelerate the convergence speed.
Figure 6A shows the dispatch power of each substation within VPP I at 16:00. At the beginning of the iteration, the power of substation 1 and substation 3 increases rapidly and the power of substation 2 decreases rapidly, and finally the resources of each substation converge to a stable value. After the PD correction, the convergence of the substations is significantly accelerated. Taking substation 2 as an example, convergence was reached through 38 iterations in 3.8 s before PD correction, and convergence was reached through 23 iterations in 2.3 s after PD correction.
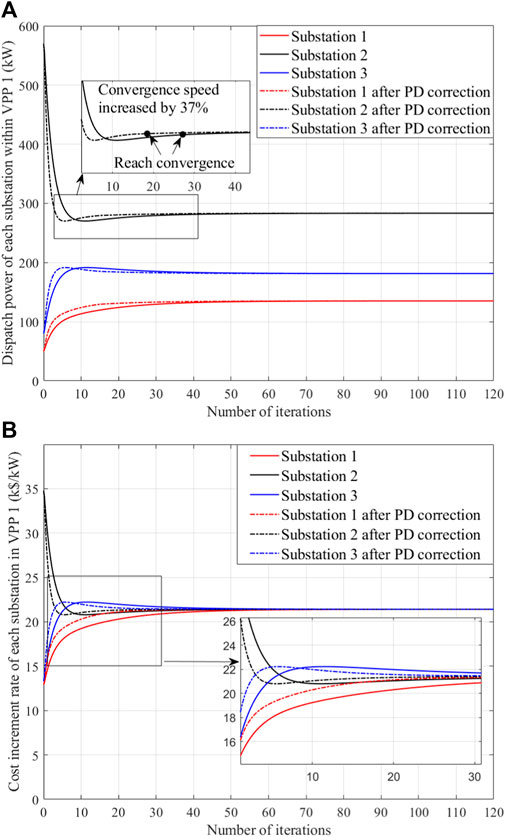
Figure 6. VPP internal optimization dispatch results. (A) Power distribution of each substation within VPP 1. (B) Cost increment rate of each substation in VPP 1.
Figure 6B shows the cost increment rate versus time for each substation within VPP 1 at 16:00. The initial value of the cost increment rate is different for each substation, with a higher initial value for substation 2 and lower initial values for substations 1 and 3. At the beginning of the iteration, the cost increment rate of each substation area changes rapidly. The traditional consensus algorithm reaches convergence for all substations after 55 iterations in 5.5 s. The convergence speed is accelerated after the PD correction, reaching convergence for 45 iterations in 4.5 s with a result of 21.42.
Figure 7A shows the simulation time to reach convergence versus β when σ = 0.1 kW and Ω = 0.02$/kW. In the beginning, increasing β will strengthen PD correction. The algorithm converges with larger fluctuations during each iteration, leading to a decrease in convergence time. The minimum time required for the simulation to reach convergence is 276 ms. Continuously increasing the β will lead to over-correction of PD, making it difficult for the algorithm to converge due to continuous fluctuations, resulting in an extension of convergence time. β has the shortest convergence time at a value of 1.18.

Figure 7. Simulation time to reach convergence versus various algorithm parameters. (A) Simulation time to reach convergence versus β when σ = 0.1 kW and Ω = 0.02k$/kW. (B) Simulation time to reach convergence versus σ and Ω when β = 1. (C) The dispatch cost of the lower layer under different communication delays.
Figure 7B shows the simulation time to reach convergence versus σ and Ω when β = 1. To achieve convergence, two constraints need to be satisfied simultaneously, so a small value for either constraint will result in an extremely long convergence time. The convergence time will only decrease when both σ and Ω are large. When both parameter settings are large, the simulation time required to achieve convergence is 276 ms.
Figure 7C shows the dispatch cost of the proposed algorithm and traditional consensus algorithm at the lower layer under different communication delays. When the communication delay is low, the dispatch cost difference between the two algorithms is not significant. When the delay is large, the proposed algorithm has lower dispatch costs compared to the traditional consensus algorithm. This is because the proposed algorithm introduces PD correction, which can adjust the convergence speed according to the communication delay. In the case of high communication delay, the convergence speed of the proposed algorithm is faster, so the dispatch cost is lower.
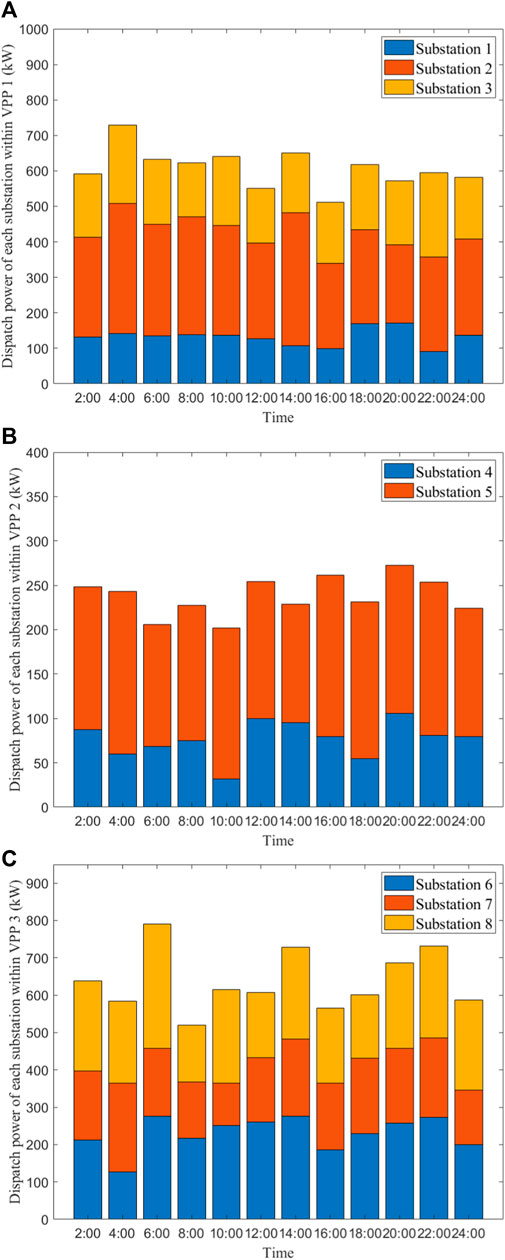
Figure 8 shows the dispatch power of each substation in different VPPs. It can be observed that the power fluctuation of each substation is not large in the time range of 0–24 h. In VPP1, the power of substations 1, 2, and 3 fluctuates around 130, 280, and 190, respectively. In VPP2, the power of substations 4 and 5 fluctuates around 80 and 170, respectively. In VPP3, the power of substations 6, 7, and 8 fluctuates around 230, 170, and 230, respectively.
6 Conclusion
This paper proposes a novel two-layer iterative energy dispatch strategy for multi-energy flow VPPs in distribution power grids. The upper layer sub-problem of multi-energy flow VPP energy dispatch is tackled using an improved ant colony algorithm, while the lower layer substation energy dispatch is addressed through a delay-aware consensus algorithm. To enhance the convergence speed of the delay-aware consensus algorithm and enable real-time energy dispatch of the multi-energy flow VPP, a PD control mechanism is integrated. Simulation results demonstrate that the proposed algorithm significantly reduces the total dispatch cost by 61.11% and 45.45% compared to the two baseline algorithms. Moreover, the convergence speed is increased by 18.18% compared to the traditional consensus algorithm after incorporating the PD control mechanism. In the future, we plan to explore energy cooperative dispatch between electric vehicles and multi-energy flow VPPs.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
WL: conceptualization, data curation, investigation, software, and writing–original draft. ZZ: conceptualization, data curation, and writing–original draft. YZ: conceptualization, data curation, methodology, and writing–original draft. GJ: conceptualization, data curation, formal analysis, and writing–original draft. WW: data curation, formal analysis, validation, and writing–original draft. YR: investigation, methodology, and writing–original draft. YW: conceptualization, formal analysis, methodology, and writing–review and editing. YL: conceptualization, data curation, and writing–original draft. CL: formal analysis, methodology, and writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The authors declare that this study received funding from Science and Technology Project of State Grid Shandong Electric Power Company (Key Technical Research and Application of Real-time Data Sharing Capability Construction for Large-scale Power Gird Nodes, 520608230007). The funder had the following involvement in the study: study design, collection, analysis, interpretation of data, the writing of this article, and the decision to submit it for publication.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abdolrasol, M. G. M., Hannan, M. A., Mohamed, A., Amiruldin, U. A. U., Abidin, I. B. Z., and Uddin, M. N. (2018). An optimal scheduling controller for virtual power plant and microgrid integration using the binary backtracking search algorithm. IEEE Trans. Industry Appl. 54, 2834–2844. doi:10.1109/TIA.2018.2797121
Chen, G., and Zhao, Z. (2018). Delay effects on consensus-based distributed economic dispatch algorithm in microgrid. IEEE Trans. Power Syst. 33, 602–612. doi:10.1109/TPWRS.2017.2702179
Chen, Y., Zhao, J., and Ma, J. (2020). Fast decoupled multi-energy flow calculation for integrated energy system. J. Mod. Power Syst. Clean Energy 8, 951–960. doi:10.35833/MPCE.2018.000598
Cui, Y., Chen, Z., Yan, G., and Tang, Y. (2016). Coordinated wind power accommodating dispatch model based on electric boiler and CHP with thermal energy storage. Proc. CSEE 36, 4072–4081. doi:10.13334/j.0258-8013.pcsee.152406
Dai, W., Yu, J., and Li, W. (2018). “Equivalent optimal power flow method considering natural gas network constraints,” in 2018 5th International Conference on Electric Power and Energy Conversion Systems (EPECS), Kitakyushu, Japan, 23-25 April 2018, 1–5. doi:10.1109/EPECS.2018.8443539
Gao, H., Zhang, F., Xiang, Y., Ye, S., Liu, X., and Liu, J. (2023). Bounded rationality based multi-VPP trading in local energy markets: a dynamic game approach with different trading targets. CSEE J. Power Energy Syst. 9, 221–234. doi:10.17775/CSEEJPES.2021.01600
Gough, M., Santos, S. F., Lotfi, M., Javadi, M. S., Osório, G. J., Ashraf, P., et al. (2022). Operation of a technical virtual power plant considering diverse distributed energy resources. IEEE Trans. Ind. Appl. 58, 2547–2558. doi:10.1109/TIA.2022.3143479
Guili, Y., Linbo, W., and Baoyuan, W. (2017). Optimal dispatch of heat-power load and economy benefit analysis based on decoupling of heat and power of virtual power plant. Proc. CSEE 37, 4974–4985. doi:10.13334/j.0258-8013.pcsee.161300
Hannan, M. A., Abdolrasol, M. G. M., Mohamed, R., Al-Shetwi, A. Q., Ker, P. J., Begum, R. A., et al. (2021). Ann-based binary backtracking search algorithm for vpp optimal scheduling and cost-effective evaluation. IEEE Trans. Industry Appl. 57, 5603–5613. doi:10.1109/TIA.2021.3100321
Hou, Y. H., Wu, Y. W., Lu, L. J., and Xiong, X. Y. (2002). Generalized ant colony optimization for economic dispatch of power systems. Proc. Int. Conf. Power Syst. Technol. 1, 225–229. doi:10.1109/ICPST.2002.1053539
Huang, H., Li, Z., Sampath, LPMI, Yang, J., Nguyen, H. D., Gooi, H. B., et al. (2023). Blockchain-enabled carbon and energy trading for network-constrained coal mines with uncertainties. IEEE Trans. Sustain. Energy 14, 1634–1647. doi:10.1109/TSTE.2023.3240203
Jing, W., Xuefeng, B., and Bin, L. (2022). “Research on consensus algorithm of hierarchical partition blockchain for virtual power plant transactions,” in 2022 2nd International Conference on Advance Computing and Innovative Technologies in Engineering (ICACITE), Greater Noida, 28-29 April 2022, 1613–1617. doi:10.1109/ICACITE53722.2022.9823468
Li, J., Liu, J., Chen, X., and Chen, Z. (2019). Capacity allocation of multi-energy complementary system including renewable energy. Power Syst. Technol. 43, 4387–4398. doi:10.13335/j.1000-3673.pst.2019.0151
Li, Z., Wu, L., Xu, Y., Moazeni, S., and Tang, Z. (2022). Multi-stage real-time operation of a multi-energy microgrid with electrical and thermal energy storage assets: a data-driven MPC-ADP approach. IEEE Trans. Smart Grid 13, 213–226. doi:10.1109/TSG.2021.3119972
Li, Z., Xu, Y., Wang, P., and Xiao, G. (2023). Restoration of multi energy distribution systems with joint district network recon figuration by a distributed stochastic programming approach. IEEE Trans. Smart Grid, 1. doi:10.1109/TSG.2023.3317780
Liang, B., Yang, J., Hou, B., and He, Z. (2021). A pricing method for distribution system aggregators considering differentiated load types and price uncertainty. IEEE Trans. Power Syst. 36, 1973–1983. doi:10.1109/TPWRS.2020.3032593
Liang, H., and Ma, J. (2022). Data-driven resource planning for virtual power plant integrating demand response customer selection and storage. IEEE Trans. Ind. Inf. 18, 1833–1844. doi:10.1109/TII.2021.3068402
Liao, H., Zhou, Z., Jia, Z., Shu, Y., Tariq, M., Rodriguez, J., et al. (2023). Ultra-low AoI digital twin-assisted resource allocation for multi-mode power IoT in distribution grid energy management. IEEE J. Sel. Areas Commun. 41, 3122–3132. doi:10.1109/JSAC.2023.3310101
Mohy-ud din, G., Muttaqi, K. M., and Sutanto, D. (2020). “A bi-level energy management model for energy transactions from vpp based integrated energy systems under system uncertainties,” in 2020 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Jaipur, India, 16-19 December 2020, 1–6. doi:10.1109/PEDES49360.2020.9379387
Naina, P. M., and Swarup, K. S. (2022). Double-consensus-based distributed energy management in a virtual power plant. IEEE Trans. Industry Appl. 58, 7047–7056. doi:10.1109/TIA.2022.3201060
Niknam, T., Ranjbar, A. M., Shirani, A. R., and Ostadi, A. (2005). “A new approach based on ant colony algorithm to distribution management system with regard to dispersed generation,” in CIRED 2005 - 18th International Conference and Exhibition on Electricity Distribution, Turin, 6-9 June 2005, 1–5. doi:10.1049/cp:20051242
Pasetti, M., Rinaldi, S., and Manerba, D. (2018). A virtual power plant architecture for the demand-side management of smart prosumers. Appl. Sci. 8, 432–452. doi:10.3390/app8030432
Sarantakos, I., Bowkett, A., Allahham, A., Sayfutdinov, T., Murphy, A., Pazouki, K., et al. (2023). Digitalization for port decarbonization: decarbonization of key energy processes at the port of tyne. IEEE Electrification Mag. 11, 61–72. doi:10.1109/MELE.2022.3233114
Trivedi, I. N., Thesiya, D. K., Esmat, A., and Jangir, P. (2015). “A multiple environment dispatch problem solution using ant colony optimization for micro-grids,” in 2015 International Conference on Power and Advanced Control Engineering (ICPACE), Bengaluru, India, 12-14 August 2015, 109–115. doi:10.1109/ICPACE.2015.7274927
Vasirani, M., Kota, R., Cavalcante, R. L., Ossowski, S., and Jennings, N. R. (2013). An agent-based approach to virtual power plants of wind power generators and electric vehicles. IEEE Trans. Smart Grid 4, 1314–1322. doi:10.1109/TSG.2013.2259270
Wang, C., Gao, N., Wang, J., Jia, N., Bi, T., and Martin, K. (2020). Robust operation of a water-energy nexus: a multi-energy perspective. IEEE Trans. Sustain. Energy 11, 2698–2712. doi:10.1109/TSTE.2020.2971259
Wang, Y., Guo, Q., and Yu, Y. (2023). Cooperative pricing for vehicle-traffic-power nexus to support city decarbonization: a federated deep reinforcement learning framework. IEEE Trans. Industrial Cyber-Physical Syst. 1, 182–191. doi:10.1109/TICPS.2023.3317012
Wu, S., Lin, J., Li, J., Liu, F., Song, Y., Xu, Y., et al. (2023). Multi-timescale trading strategy for renewable power to ammonia virtual power plant in the electricity, hydrogen, and ammonia markets. IEEE Trans. Energy Mark. Policy Regul. 1, 322–335. doi:10.1109/TEMPR.2023.3287857
Xin, H., Gan, D., Li, N., Li, H., and Dai, C. (2013). Virtual power plant-based distributed control strategy for multiple distributed generators. IET Control Theory & Appl. 7, 90–98. doi:10.1049/iet-cta.2012.0141
Xu, Y., Cheng, Z., Hu, S., Dai, Y., Bi, J., Shen, Y., et al. (2019). Distributed coordination control of multiple VPPs in an active distribution network. IEEE, 5429–5432. doi:10.1109/CAC48633.2019.8996259
Yan, S., Li, T., Huang, D., Zhang, C., Hao, J., and Zhou, D. (2020). “Dynamic modeling and simulation of the large-scale regional integrated electricity and natural gas system,” in 2020 4th International Conference on Smart Grid and Smart Cities (ICSGSC), Osaka, Japan, August 18-21, 2020, 6–13. doi:10.1109/ICSGSC50906.2020.9248547
Yang, H., Yi, D., Zhao, J., and Dong, Z. (2013). Distributed optimal dispatch of virtual power plant via limited communication. IEEE Trans. Power Syst. 28, 3511–3512. doi:10.1109/TPWRS.2013.2242702
Yang, Y., Li, Z., Mandapaka, P. V., and Lo, E. Y. (2023). Risk-averse restoration of coupled power and water systems with small pumped-hydro storage and stochastic rooftop renewables. Appl. Energy 339, 120953. doi:10.1016/j.apenergy.2023.120953
Yu, Q., Cai, Y., Qi, L., Ai, Q., and Wang, D. (2022). “Improved hybrid consensus mechanism based on virtual power plant dispatching,” in 2022 IEEE 6th Conference on Energy Internet and Energy System Integration (EI2), Chengdu, China, October 28th to 30th 2022, 2176–2181. doi:10.1109/EI256261.2022.10116511
Zhang, C., Xu, Y., Li, Z., and Dong, Z. Y. (2019). Robustly coordinated operation of a multi-energy microgrid with flexible electric and thermal loads. IEEE Trans. Smart Grid 10, 2765–2775. doi:10.1109/TSG.2018.2810247
Zhang, S., Gu, W., Wang, J., Zhang, X. P., Meng, X., Lu, S., et al. (2023a). Steady-state security region of integrated energy system considering thermal dynamics. IEEE Trans. Power Syst. 39, 4138–4153. doi:10.1109/TPWRS.2023.3296080
Zhang, S., Liu, W., Zhang, Y., Wu, H., and Wan, H. (2023b). Reliability assessment of regional integrated energy system considering with multiple thermal inertia characteristics. Trans. CHINA Electrotech. Soc. 38, 3289–3305. doi:10.19595/j.cnki.1000-6753.tces.220367
Zhang, S., Ye, F., Zhou, J., Xiao, Q., Zhang, M., Wang, H., et al. (2023c). “Efficient virtual power plant dispatch model for distributed energy resources using deep reinforcement learning,” in 2023 IEEE 13th International Conference on CYBER Technology in Automation, Control, and Intelligent Systems (CYBER), Qinhuangdao, China, July 11-14, 2023, 510–514. doi:10.1109/CYBER59472.2023.10256633
Zhong, J., Li, Y., Cao, Y., Tan, Y., Peng, Y., Zhou, Y., et al. (2023a). Robust coordinated optimization with adaptive uncertainty set for a multi-energy microgrid. IEEE Trans. Sustain. Energy 14, 111–124. doi:10.1109/TSTE.2022.3203299
Zhong, J., Li, Y., Wu, Y., Cao, Y., Li, Z., Peng, Y., et al. (2023b). Optimal operation of energy hub: an integrated model combined distributionally robust optimization method with stackelberg game. IEEE Trans. Sustain. Energy 14, 1835–1848. doi:10.1109/TSTE.2023.3252519
Zhou, Z., Gong, J., He, Y., and Zhang, Y. (2017). Software defined machine-to-machine communication for smart energy management. IEEE Commun. Mag. 55, 52–60. doi:10.1109/MCOM.2017.1700169
Keywords: two-layer iterative energy dispatch, multi-energy-flow virtual power plant, distribution power grid, improved ant colony algorithm, delay-aware consensus algorithm
Citation: Li W, Zhou Z, Zhang Y, Jin G, Wang W, Ren Y, Wan Y, Liu Y and Liu C (2024) Two-layer iterative energy dispatch for a multi-energy-flow VPP in the distribution power grid. Front. Energy Res. 12:1361593. doi: 10.3389/fenrg.2024.1361593
Received: 26 December 2023; Accepted: 25 March 2024;
Published: 09 May 2024.
Edited by:
Hugo Morais, University of Lisbon, PortugalReviewed by:
Suhan Zhang, Hong Kong Polytechnic University, Hong Kong SAR, ChinaZhenyu Zhou, Waseda University, Japan
Chaowei Wang, Beijing University of Posts and Telecommunications (BUPT), China
Chunyu Chen, China University of Mining and Technology, China
Bin Gou, Southwest Jiaotong University, China
Copyright © 2024 Li, Zhou, Zhang, Jin, Wang, Ren, Wan, Liu and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yimin Liu, bGl1eWltaW5nMTk5OG5uQDE2My5jb20=
 Wanbin Li1
Wanbin Li1 Yimin Liu
Yimin Liu Chunxiu Liu
Chunxiu Liu