- 1Science and Technology on Reactor System Design Technology Laboratory, Nuclear Power Institute of China, Chengdu, China
- 2The College of Nuclear Technology and Automation Engineering, Chengdu University of Technology, Chengdu, China
In order to improve the core power density of liquid metal reactors, narrow rectangular fuel assemblies are typically used, which have obvious advantages in heat transfer capacity. However, the flow and heat transfer characteristics in coolant passage need to be studied. In this article, the numerical simulation analysis model obtained earlier was applied to calculate the Nusselt number, friction factor, with different Reynolds number, Prandtl number, or Peclet number of lead bismuth flow in a narrow rectangular channel under high heat flux. A heating correction factor was proposed and a flow resistance model was established for high heat flux. The influencing factors of ultra-high flux reactor core, such as gap size, flow direction, single and double sided heating conditions, on the flow and heat transfer in narrow rectangular channels were explored. The results showed that gap size and aspect ratio have a certain impact on the Nu and f of narrow rectangular channels, but the influence is relatively small within the narrow rectangular channel condition range. The influence of flow direction on flow and heat transfer is minimal, the single and double sided heating conditions will bring about a difference of about 20% in Nu and a difference of about 2.5% in f. In addition, the type of liquid metal will also affect the results. The research can provide reference for the thermal design and optimization of ultra-high flux reactor cores.
1 Introduction
Fast neutron reactors are the main reactor type of the fourth generation advanced nuclear energy system in the world. Compared with previous generations of nuclear energy systems, they have obvious advantages such as good safety, less waste (Böröczki et al., 2022). The performance of nuclear fuels and structural materials, especially their irradiation performance, has always been an important foundation for the development of new nuclear energy systems (Feng et al., 2021; Saoudi et al., 2022). The irradiation test capability of the research reactor is mainly determined by the Neutron flux level. In the above context, our institute proposed a liquid metal high flux fast neutron research reactor design, namely, the Ultra High Flux Reactor (UFR), to accelerate the development of fast reactor material technology (Zhang et al., 2022a).
Under high-performance design requirements, the narrow rectangular-fuel assembly was adopted in UFR with higher heat exchange capacity (Park et al., 2021). Unlike the coolant channel form of rod bundle fuel assemblies, the coolant channel is narrow rectangular with a channel gap of only 2–3 mm. The flow and heat transfer mechanism of liquid metal, a low Prandtl number fluid, in narrow slits is bound to be significantly different from conventional situations (Zhang et al., 2020). The flow and heat transfer characteristics of liquid metal in narrow rectangular channels are crucial for this new core design. In addition, the heat flux of the coolant flow channel in the core can reach up to 3 MW/m2. This can be said to be a very high heat flux in the field of reactor thermal engineering. The high heat flux can cause significant changes in the viscosity of the fluid near the wall, which may affect flow and heat transfer performance.
The important parameters that reflect the flow and heat transfer characteristics are the Nusselt number and frictional resistance coefficient, respectively. Usually, due to the high thermal conductivity of liquid metal and the small wall temperature difference caused by heat flow, the pressure drop of liquid metal in the heating pipeline is calculated using a pressure drop model under adiabatic conditions. For the Nusselt number, it is greatly influenced by the type of coolant and flow channel and boundary condition. Jaeger et al. (Jaeger et al., 2015) summarized the flow and heat transfer experiments of the liquid metal in narrow rectangular channels, which are reflected in a review. Research suggests that a aspect ratio of 10 can be used as a boundary for dividing the heat transfer characteristics of narrow rectangular channels, and two empirical formulas for predicting Nu have been proposed, which are applicable to different aspect ratio ranges (Sineath, 1949; Tidball, 1953; Duchatelle and Vautrey, 1964; Crye et al., 2002). Takahashi et al. (Takahashi et al., 1998) studied the pressure drop and heat transfer characteristics of lithium single-phase fluid in a simple horizontally heated rectangular channel under a horizontal transverse magnetic field in a lithium cooled magnetic confinement fusion reactor. Jiang et al. (Jiang et al., 2023) carried out the numerical analysis on flow and heat transfer characteristics of LBE in narrow rectangular channels. Keshmiri et al. (Keshmiri et al., 2008; Keshmiri et al., 2012)conducted numerical simulations on forced convection heat transfer and mixed convection heat transfer phenomena in the coolant channels of gas cooled reactors, exploring the predictive effects of different RANS models, and comparing direct numerical simulations, large eddy simulations, and RAN methods. The focus of the analysis is on the impacts of the collocation of various models on the Nusselt number, the flow redistribution phenomena, as well as the difference in flow and heat transfer capacity in channels. Our research team recently conducted research on simulation methods for flow and heat transfer of liquid metal in narrow channels, optimized turbulence models, evaluated the applicability of existing Prt models (Aoki, 1963; Reynolds, , 1974; Jischa and Rieke, 1979; Cheng and Tak, 2006; Keshmiri et al., 2008), and proposed a local Prt model and a global Prt model, respectively (Zhang et al., 2022b). The comparison results showed that the local Prt model had better applicability to changes in the cross-section of the flow channel. At present, there is still a lack of research on the flow and heat transfer of liquid metal in narrow rectangular channels. Especially when the heat flux density is very high, conducting experiments is even more difficult. In addition, factors such as single and double sided heating, different channel sizes, and flow directions that occur during core operation can also affect flow and heat transfer. Currently, the mechanism is not clear enough.
Hence, this study will apply the obtained simulation method of liquid metal turbulent heat transfer in narrow rectangular channels obtained from our previous work to conduct a study on the flow and heat transfer characteristics of lead-bismuth fluid in narrow rectangular channels under high heat flux, obtaining the relationship between the Nu, friction resistance with Re, Pr or Pe. Additionally, the influencing factors presenting in ultra high flux reactor core, such as gap size, heating modes and flow directions, etc., on the flow and heat transfer in narrow rectangular channels will be explored. This study will help in refining the pressure drop and heat transfer model, providing a foundational model for the analytical method of core thermal engineering.
2 Numerical methods
The selection of numerical models and grid partitioning have been thoroughly discussed and validated in previous studies (Zhang et al., 2022b), and a simplified introduction will also be provided here.
2 1 Turbulent model and solution methods
The standard k-epsilon model, combined with the enhanced wall treatment model was selected to handle boundary layer and mainstream. The turbulent Prandtl number model adopted in this work is the model which proposed in our previous work. It was implanted by UDF. For the solution method, the numerical calculation is based on the Fluent 18.0, which is a typical commercial CFD software. The SIMPLE is adopted as the pressure-velocity coupling scheme. The spatial discretization of pressure adopt the second-order format and of momentum adopt the bounded central differencing format. Using steady-state calculation method, the residual convergence standard is set to 10−6.
2.2 Geometry and boundary conditions
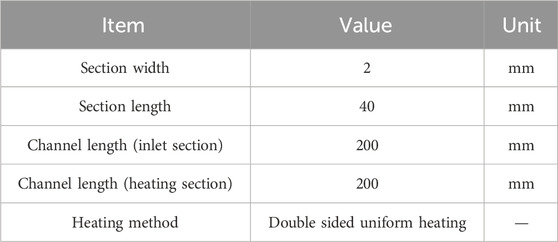
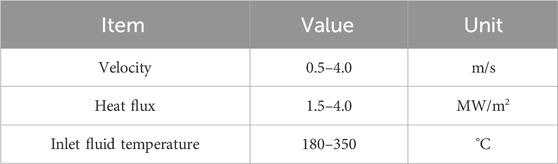
A three-dimensional narrow rectangular channel model is established. The specific geometric dimensions (Reference case) are shown in Table 1. The flowing working fluid is lead-bismuth, and the boundary conditions are shown in Table 2. Physical Parameters of Lead-Bismuth (Concetta, 2015) are shown in Table 3:
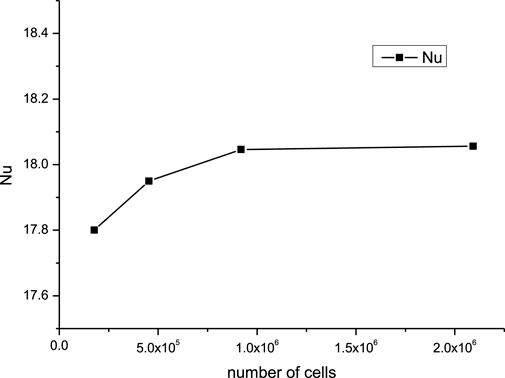
The geometric model needs to be meshed before calculation. A structural grid division method was adopted and the boundary layer grid was divided according to the requirements of the numerical model used. The grid independence verification was carried out for the meshing, as follow in Figure 1.
A set of 900,000 grids was selected for calculation finally, balancing economy and accuracy, the grid division method is as follows: evenly divide 300 nodes along the flow direction of the channel; A total of 120 segments are divided in the long side direction of the cross-section, and densification is performed near the wall. The thickness of the first layer of grid is 0.0005 mm, with a growth rate of 1.2; The narrow edge of the cross-section is divided into a total of 40 segments, with a first layer grid thickness of 0.0005 mm and a growth rate of 1.1.
3 Results and discussions
Firstly, the flow and heat transfer characteristics of lead bismuth in a narrow rectangular channel under high heat flux were obtained, and then the influence of some factors in core design on the flow and heat transfer characteristics was analyzed.
3.1 Characteristics of heat transfer
Figure 2 shows the distribution of temperature and velocity within the narrow gap under different heat fluxes. Figure 3 shows the distribution of temperature and velocity within the narrow gap under different inlet flow velocities. The position of the value is 350 mm along the flow direction. The results show that heat flux has a significant impact on the temperature difference between the heating wall and the mainstream, has a small impact on the distribution of flow velocity. And the inlet velocity has a small impact on the temperature difference between the heating wall and the mainstream.
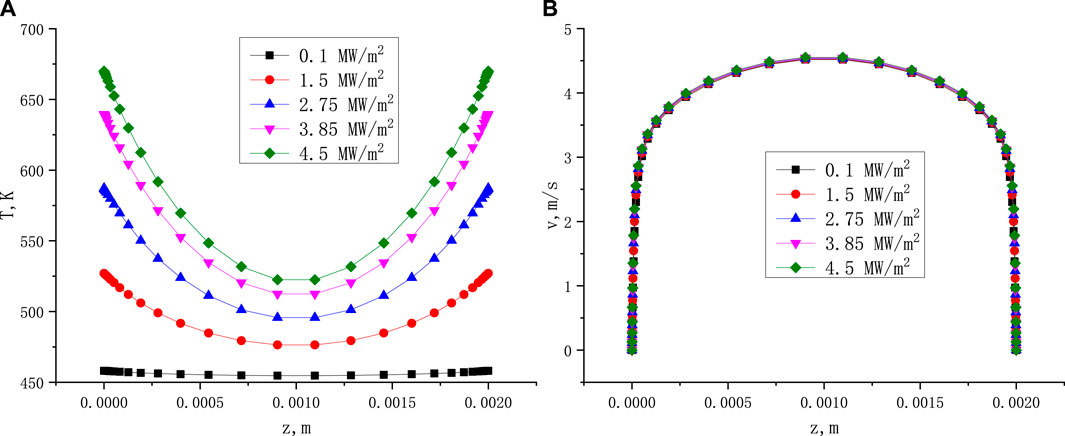
FIGURE 2. The temperature distribution (A) and velocity distribution (B) in narrow gap under different heat fluxes (Tin = 180°C, Vin = 4 m/s, x = 350 mm).
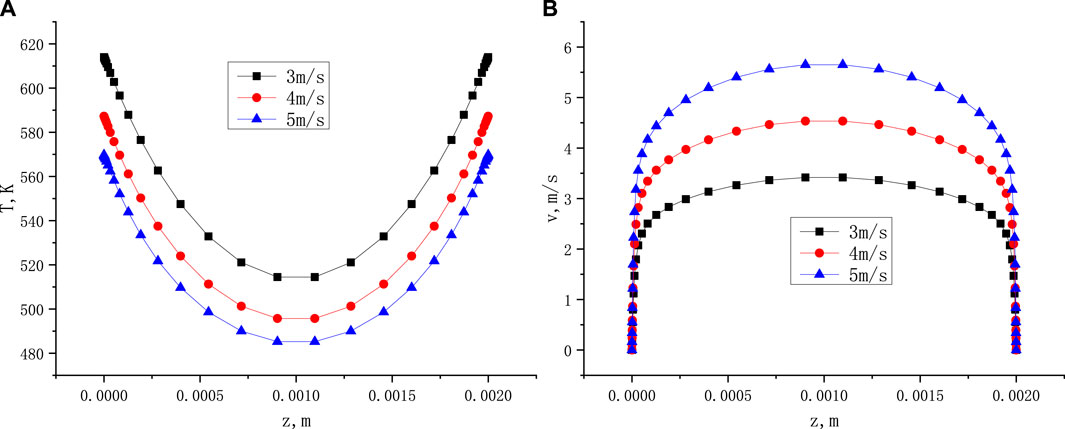
FIGURE 3. The temperature distribution (A) and velocity distribution (B) in narrow gap with different inlet velocity (Tin = 180°C, Q = 2.75 kW/m2, x = 350 mm).
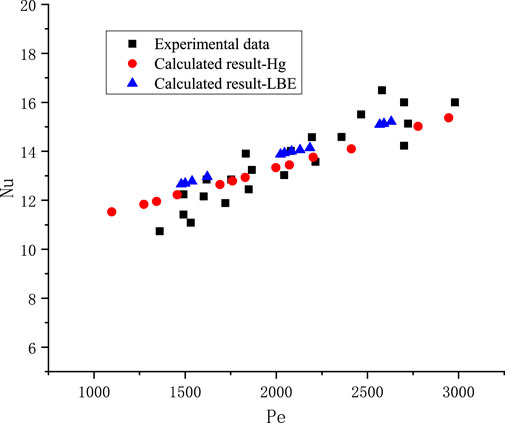
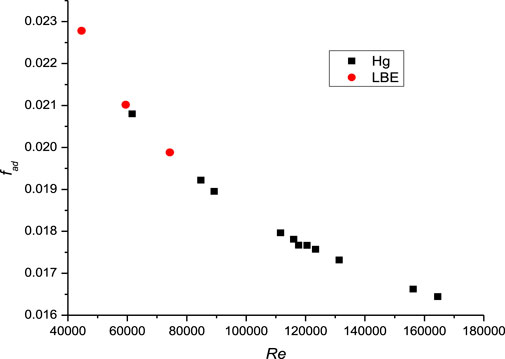
It is known that the Nusselt number is a function of Peclet number. Hence, the Nusselt numbers for the lead bismuth flowing in a narrow rectangular channel with different Peclet numbers were calculated, as shown in Figure 4. In addition, the reliability of this simulation method can be demonstrated by comparing the simulation results with the experimental data of mercury flow and heat transfer in a narrow rectangular channel. The results show that there is still a positive correlation between the Nusselt number and the Peclet number, showing similar characteristics to the mercury (Crye et al., 2002). The impact of high heat flux on heat transfer is not reflected.
3.2 Characteristics of pressure drop
The pressure drop characteristic is mainly reflected in the friction factor, which is mainly divided into adiabatic friction factor and non adiabatic friction factor of the channel. Generally, the friction factor under heating conditions is modeled based on the adiabatic friction factor. Therefore, it is necessary to first obtain an adiabatic friction factor prediction model, and then analyze the friction factor calculation results under heating conditions.
3.2.1 The adiabatic friction factor
The pressure drop of a channel with fluid flow can be calculated by Eq. 1.
The acceleration pressure drop
The single-phase friction factor can be calculated by the Darcy-Weishbach formula as Eq. 3:
As well known, some correlations were proposed to predict the single-phase adiabatic friction factor. The commonly used for turbulent flow are as Eqs 4, 5:
McAdams correlation:
Blasius correlation:
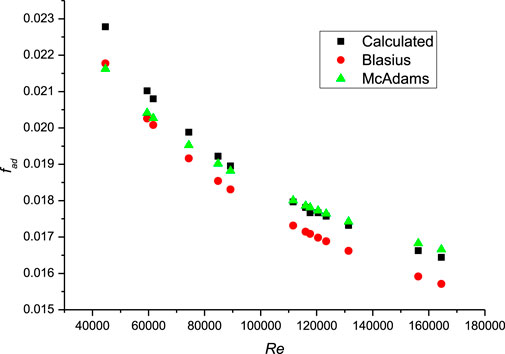
The friction factors of lead bismuth flow in an adiabatic narrow rectangular channel obtained in this study at different Reynolds numbers were compared with the calculation results of existing relationship equations, as shown in Figure 5.
Through the comparison, it can be seen that the CFD calculation value of the adiabatic friction factor is close to the predicted value by Blasius correlation in the region with low Re, and more consistent with the predicted value by McAdams correlation in the region with high Re. Based on the calculated data, an adiabatic friction factor correlation suitable for liquid lead bismuth in narrow rectangular channels was proposed. It is referred to the form of Blasius correlation and McAdams correlation, and fitted according to the following formula as Eq. 6:
The final formula obtained is as Eq. 7, with an error of less than 1.5% compared to the original data.
3.2.2 The friction factor for the heating channel
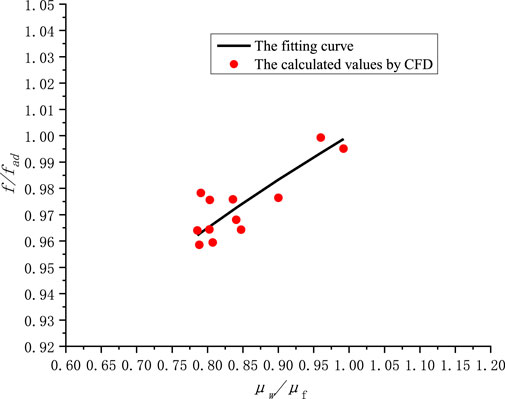
Currently, considering the good thermal conductivity of liquid metals and the small temperature difference at the wall, calculations for the non-adiabatic friction resistance coefficient in round or square tubes in engineering are based on the adiabatic friction resistance coefficient model. However, for the core of ultra-high flux reactors, which have a high power density, the wall temperature difference reaches up to 100°C. The viscosity of the fluid at the wall decreases at high temperatures, increasing the viscosity difference between the wall and the main fluid. This results in the non-adiabatic friction coefficient being less than the adiabatic friction coefficient at the same Reynolds number. Therefore, it is necessary to consider the temperature difference phenomenon caused by wall heat flux and adjust the friction coefficient formula. Referring to the friction resistance coefficient calculation method for heated water channels, the model form is as Eq. 8, with a correction factor being a power function of the viscosity ratio between the wall and main fluid.
From calculations, it can be known that when the wall temperature difference is around 100°C, the viscosity ratio between the wall and the main fluid is 0.79,
Viscosity ratio range between the wall and main fluid: 0.75–1.
The friction factor in the heating section obtained from this work is compared with values calculated using the adiabatic friction factor model and the new model, as depicted in Figure 7. The results indicate a significant improvement in prediction for the friction resistance coefficient when using the modified model compared to the original one.
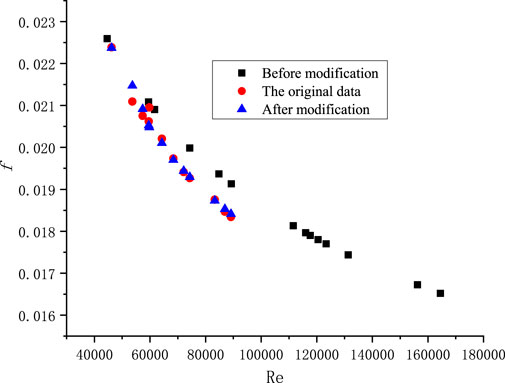
FIGURE 7. Comparison of the heating section friction factor with calculation results by the model before and after modification.
3.3 Sensitivity analysis of some influencing factors
In this section, several factors existing in the reactor core, including the size of channel, single and double-sided heating conditions, flow directions, type of liquid metal were considered, and their effects on the flow and heat transfer characteristics of lead-bismuth in the narrow rectangular channel with high flux were studied.
3.3.1 Impact of the cross-sectional dimensions
In terms of the size characteristics of narrow rectangular channel, there are two main parameters: firstly, the size of narrow gap, and secondly, the aspect ratio of the cross-section.
3.3.1.1 Impact of the narrow gap
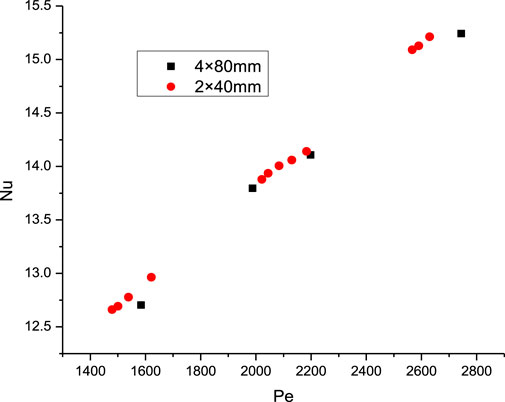
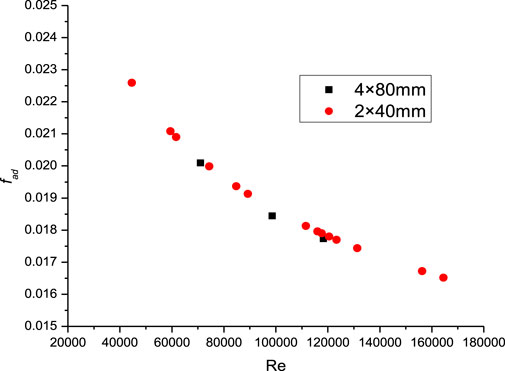
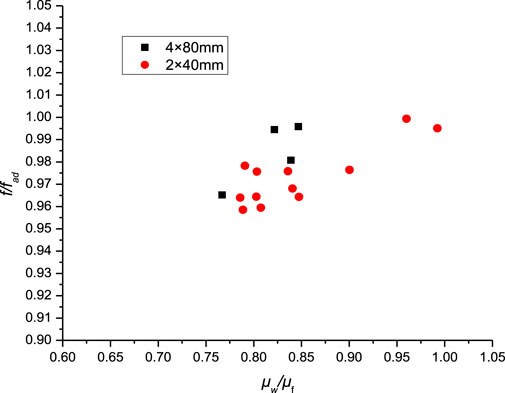
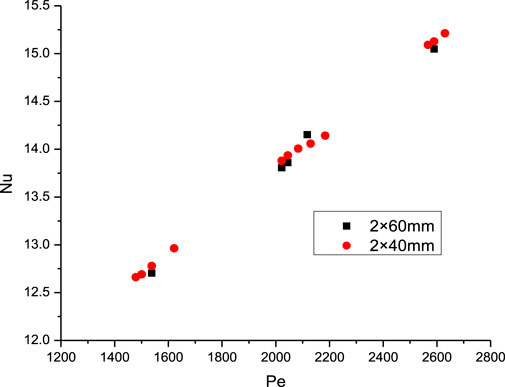
To eliminate the influence of the aspect ratio, the aspect ratio was kept constant. The cross-sectional dimensions of the narrow rectangular channel were set at 2 × 40 mm and 4 × 80 mm. Adjust the length of the inlet section and heating section proportionally according to the size change of the cross-section. Comparison of the Nu and f under different conditions are illustrated in Figure 8, Figure 9, Figure 10.
From the figures, it can be seen that when only increasing the gap without changing the aspect ratio, there’s a slight decrease in Nu, but the effect is very minimal. The impact on fad is also negligible and can be ignored. By observing the relationship between f/fad and
3.3.1.2 Impact of the aspect ratio
To eliminate the influence of the narrow gap, the narrow gap was kept constant. The cross-sectional dimensions of the narrow rectangular channel were set to 2 × 40 mm and 2 × 60 mm, with aspect ratios of 20 and 30, respectively. Both the inlet and heating sections were set to 200 mm. Comparison of Nu and f under different conditions are illustrated in Figure 11, Figure 12, Figure 13.
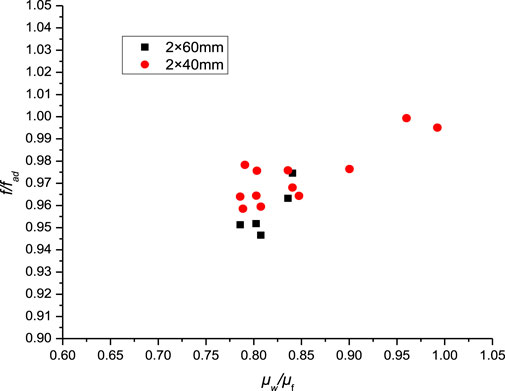
FIGURE 13. Impact of aspect ratios on
Taking into account the combined effects of gap width and aspect ratio, within the confines of a narrow rectangular structure, without altering the aspect ratio, increasing the gap width reduces Nu, whereas decreasing the gap width enhances heat transfer. However, the impact on Nu remains quite minimal. When only increasing the aspect ratio without altering the width, Nu remains unaffected and the heat transfer performance is not compromised. Regarding resistance characteristics, under non-heating conditions, neither parameter has a significant impact on the frictional resistance coefficient. However, under heating conditions, either decreasing the gap width or increasing the aspect ratio will amplify the influence from
3.3.2 Impact of the heating modes
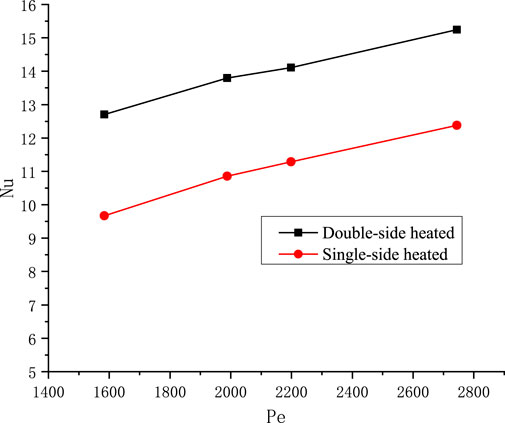
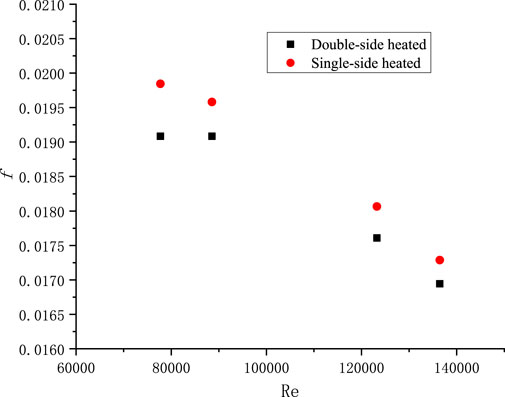
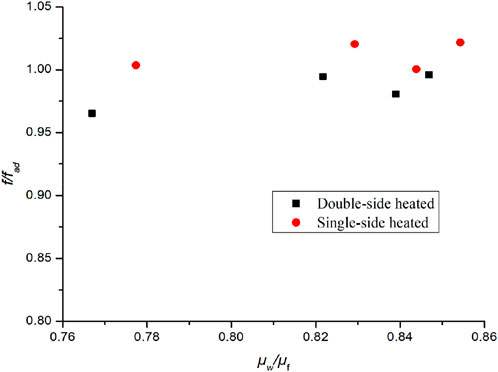
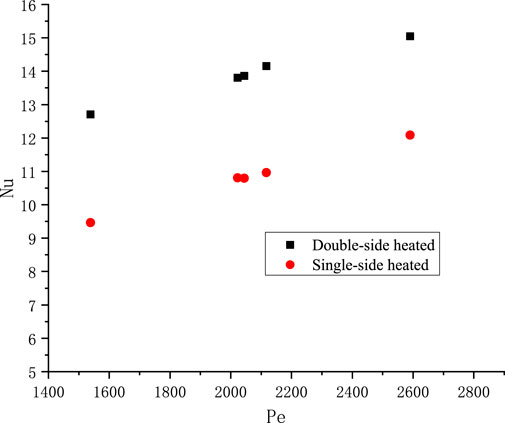
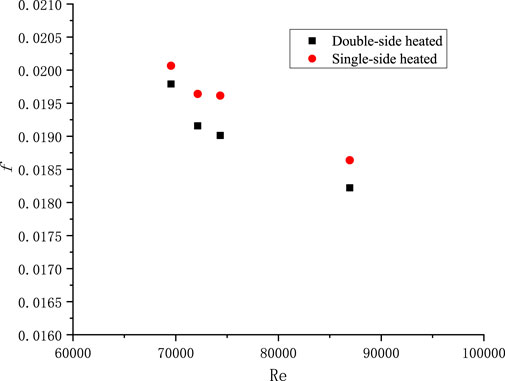
For narrow rectangular fuel assemblies, the edge coolant channel is only heated on one side. Previous studies have focused on double side heating conditions. To analyze the influence of single side and double side heating conditions on flow and heat transfer, the Nu and f for different Re and Pe numbers were calculated for single side and double side heating. Figure 14 shows the effect of single vs double sided heating conditions on Nu, and it can be seen that the Nu of single sided heating is smaller than that of double sided heating. Figure 15 and Figure 16 show the effects of single vs double-sided heating on the friction factor.
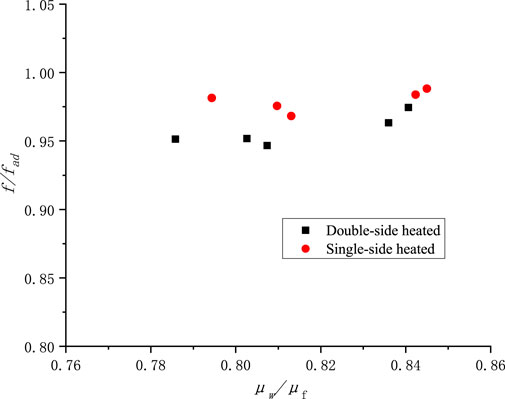
It can be seen that the friction factor of double-sided heating is lower than that of single-sided heating, and is more affected by the wall viscosity ratio. Combined with its impact on Nu, it can be concluded that the flow and heat transfer characteristics of double-sided heating are better than those of single-sided heating. To further investigate, the effect of single and double sided heating on flow and heat transfer in a channel with cross-sectional size 2 × 60 mm was compared, as illustrated in Figure 17, Figure 18, Figure 19.
From the above, it can be deduced that in narrow rectangular channels with cross-sections of 4 × 80 mm and 2 × 60 mm, the Nu for single-sided heating is about 20% lower than that of double-sided heating, and the friction factor is approximately 2.5% higher. Consequently, under the same power, the fluid heat transfer performance of single-sided heating is noticeably inferior to double-sided heating. Furthermore, by comparing the relationship of f/fad and
3.3.3 Impact of the flow direction
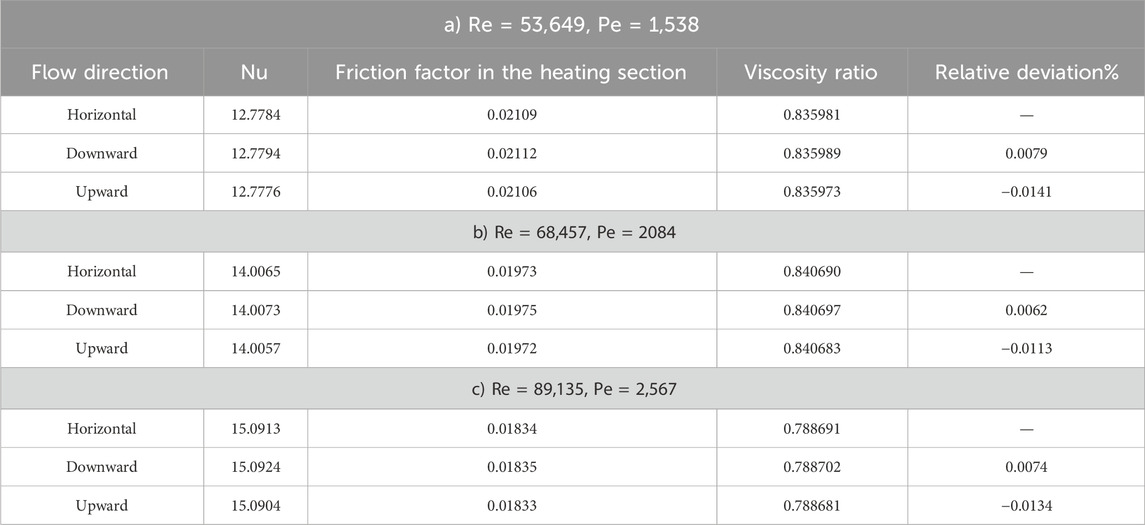
In the design of ultra-high-flux reactor cores, downward flow is adopted under forced circulation, while upward flow is used under natural circulation. The downward flow is not commonly found in current research, and it remains unclear whether the direction of flow has an impact on flow and heat transfer. This section analyzed the effect of flow direction. Calculations were performed for three different Re and Pe number cases under upward, downward, and horizontal flow directions. The comparative results for Nu and f are presented in Table 4.
The relative deviation in the table refers to the deviation from the Nu calculation results for horizontal fluid. Through the comparison, it can be observed that the flow direction has certain effects on Nu and the friction factor. Among them, the upward fluid has the smallest Nu and the least friction factor. Downward fluid has the largest Nu and the highest friction factor. However, there is no clear pattern regarding the effects of Re and Pe on relative deviation. Within the conditions studied in this paper, while the flow direction does have an impact, the degree of influence is very minimal and can be disregarded in engineering practices.
3.3.4 Impact of the kinds of liquid metals
This section explores the impact of different kinds of liquid metals on the flow and heat transfer in a rectangular channel. The Nu and f for liquid lead-bismuth (Pr ≈ 0.03) and mercury (Pr ≈ 0.02) under the same channel (Figure 20; Figure 21). It is evident that the kind of liquid metal does not impact on the adiabatic friction factor, but it does have certain effects on the heat transfer coefficient. The Nu for lead-bismuth is higher than that for mercury, with a relative difference of about 3%.
4 Conclusion
In this study, the flow and heat transfer characteristics of lead-bismuth fluid in narrow rectangular channels under high heat flux, obtaining the relationship between the Nu, friction resistance with Re, Pr or Pe was investigated. Additionally, the impact of several factors existing in ultra high flux reactor core, such as gap size, heating modes and flow directions, etc., on the flow and heat transfer in narrow rectangular channels were explored. The conclusions gained as follows.
1) It is necessary to consider the temperature difference phenomenon caused by the high heat flux at wall and adjust the friction factor formula. Results indicate a significant improvement in prediction for the friction factor when using the modified factor compared to the original one.
2) Decreasing the gap width can enhance heat transfer. Under heating conditions, either decreasing the gap width or increasing the aspect ratio will amplify the influence from
3) Under the same power, the fluid heat transfer performance of single-sided heating is noticeably inferior to double-sided heating. and it is evident that the influence from
4) Within the conditions studied in this paper, the impact of flow direction is very minimal and can be disregarded in engineering practices.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
XZ: Formal Analysis, Funding acquisition, Validation, Writing–original draft. WF: Conceptualization, Investigation, Software, Writing–review and editing. HY: Funding acquisition, Supervision, Writing–review and editing. JD: Funding acquisition, Supervision, Writing–review and editing. SD: Data curation, Methodology, Writing–review and editing. XW: Investigation, Writing–review and editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The authors are grateful for the support of NSAF (Grant No. 12305193), NSFSC (Grant No. 23NSFSC6149), and Postdoctoral Foundation in China (Grant No. 2022M722996).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Aoki, S. (1963). A consideration on the heat transfer in liquid metal. Bull. Tokyo Inst. Tech. 54, 63–73.
Böröczki, Z. I., Aranyosy, Á., and Szieberth, M. (2022). Comparison of calculation methods for lead cooled fast reactor reactivity effects. Ann. Nucl. Energy 171, 109042. doi:10.1016/j.anucene.2022.109042
Cheng, X., and Tak, N. I. (2006). Investigation on turbulent heat transfer to lead-bismuth eutectic flows in circular tubes for nuclear applications. Nucl. Eng. Des. 236 (4), 385–393. doi:10.1016/j.nucengdes.2005.09.006
Concetta, F. (2015). Handbook on lead-bismuth eutectic Alloy and lead Properties, materials compatibility, thermal-hydraulics and technologies: 2015 edition - introduction. Paris (France): OECD.
Crye, J. M., Ruggles, A. E., Pointer, W. D., Felde, D. K., Jallouk, P. A., McFee, M. T., et al. (2002). Measurement of the heat transfer coefficient for mercury flowing in a narrow channel. J. Heat Transf. 124 (6), 1034–1038. doi:10.1115/1.1518500
Duchatelle, L., and Vautrey, L. (1964). Determination des coefficients de convection d'un alliage nak en ecoulement turbulent entre plaques planes paralleles. Int. J. Heat Mass Transf. 7 (9), 1017–1031. doi:10.1016/0017-9310(64)90043-2
Feng, W., Zhang, X., Cao, L., Wang, S., and Chen, H. (2021). Development of oxygen/corrosion product mass transfer model and oxidation-corrosion model in the lead-alloy cooled reactor core. Corros. Sci. 190, 109708. doi:10.1016/j.corsci.2021.109708
Jaeger, W., Hering, W., Lux, M., and Portes, F. (2015). “ICONE23-1101 liquid metal thermal hydraulics in rectangular ducts: review, proposal and validation of empirical models,” in Proceedings of ICONE-23 23rd International Conference on Nuclear Engineering, Kyoto, Japan, May 17-21, 2015 (The Japan Society of Mechanical Engineers).
Jiang, Y., Li, X., Tian, R., Lu, C., and Song, Z. (2023). Numerical analysis on flow and heat transfer characteristics of lbe in narrow rectangular channels. ICONE30.
Jischa, M., and Rieke, H. B. (1979). About the prediction of turbulent Prandtl and schmidt numbers from modeled transport equations. Int. J. Heat Mass Transf. 22, 1547–1555. doi:10.1016/0017-9310(79)90134-0
Keshmiri, A., Cotton, M. A., Addad, Y., and Laurence, D. (2012). Turbulence models and Large Eddy Simulations applied to ascending mixed convection flows. Flow, Turbul. Combust. 89 (3), 407–434. doi:10.1007/s10494-012-9401-4
Keshmiri, A., Cotton, M. A., Addad, Y., Rolfo, S., and Billard, F. (2008). “RANS and LES investigations of vertical flows in the fuel passages of gas-cooled nuclear reactors,” in Proc. 16th Int. Conf. on Nuclear Engineering, ICONE16, Orlando, Florida, USA, June 24, 2009 (American Society of Mechanical Engineers Digital Collection), 297–306. doi:10.1115/ICONE16-48372
Park, J. P., Park, C., and Park, S. (2021). A numerical analysis for a damage propagation in a plate-type fuel assembly of a research reactor. Ann. Nucl. Energy 153, 108071. doi:10.1016/j.anucene.2020.108071
Reynolds, A. J. (1974). The prediction of turbulent Prandtl and Schmidt numbers. Rep. HT74-2. Int. J. Heat Mass Transf. 18, 1055–1069. doi:10.1016/0017-9310(75)90223-9
Saoudi, M., Barry, A., Lang, J., Boyer, C., Rogge, R. B., Corbett, S., et al. (2022). Post-irradiation examination of U-7Mo/Mg and U-10Mo/Mg dispersion fuels irradiated in the NRU reactor. J. Nucl. Mater. 558, 153343. doi:10.1016/j.jnucmat.2021.153343
Sineath, H. H. (1949). “Heat transfer to mercury,”. M.S. thesis (Tennessee: University of Tennessee).
Takahashi, M., Aritomi, M., Inoue, A., and Matsuzaki, M. (1998). MHD pressure drop and heat transfer of lithium single-phase flow in a rectangular channel under transverse magnetic field. Fusion Eng. Des. 42 (1-4), 365–372. doi:10.1016/s0920-3796(98)00380-9
Zhang, X., Feng, W., Chen, H., Guo, S., and Ding, W. (2020). Experimental study on flow instability for downward flow in a narrow rectangular channel with flow pattern transition. Int. Commun. Heat Mass Transf. 114C, 104586. doi:10.1016/j.icheatmasstransfer.2020.104586
Zhang, X., Yu, H., Deng, J., Du, S., Zhang, X., Zou, Z., et al. (2022b). “Investigation on the simulation of turbulent heat transfer of liquid metal flow in a narrow rectangular channel,” in International Conference on Nuclear Engineering, November 23, 2022 (New York: ASME).
Keywords: liquid metal, narrow rectangular channel, flow and heat transfer, high heat flux, numerical simulation
Citation: Zhang X, Feng W, Yu H, Deng J, Du S and Wang X (2024) Study on flow and heat transfer characteristics of liquid metal flow in narrow rectangular channels under high heat flux. Front. Energy Res. 12:1350144. doi: 10.3389/fenrg.2024.1350144
Received: 05 December 2023; Accepted: 15 January 2024;
Published: 02 February 2024.
Edited by:
Hitesh Bindra, Kansas State University, United StatesReviewed by:
Yacine Addad, Khalifa University, United Arab EmiratesShanfang Huang, Tsinghua University, China
Copyright © 2024 Zhang, Feng, Yu, Deng, Du and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hongxing Yu, eXVob25nX3hpbmdAMTI2LmNvbQ==
 Xue Zhang
Xue Zhang Wenpei Feng2
Wenpei Feng2 Sijia Du
Sijia Du