- 1Center for Advanced Studies in Energy (CAS-E), University of Engineering and Technology Peshawar Pakistan, Peshawar, Pakistan
- 2Department of Electrical and Computer Engineering, Comsats University Islamabad Kamra Road Attock Campus Pakistan, Islamabad, Pakistan
- 3Department of Electrical Engineering, College of Engineering, Imam Mohammad Ibn Saud Islamic University (IMSIU), Riyadh, Kingdom of Saudi Arabia
- 4Renewable Energy and Environmental Technology Center, University of Tabuk, Tabuk, Saudi Arabia
- 5Electrical Engineering Department, Faculty of Engineering, University of Tabuk, Tabuk, Saudi Arabia
- 6Department of Electrical Engineering, Air University Islamabad, Aerospace and Aviation Campus Kamra, Islamabad, Pakistan
The modern power generation systems are increasing their reliance on high penetrations of distributed energy resources (DERs). However, the optimal dispatching mechanisms mainly rely on central controls which receive the load demand information from the electricity utility providers and allocate the electricity production targets to participating generating units. The lack of transparency and control over the DER fuel inputs makes the physical power purchase agreements (PPAs) a cumbersome task. This research work proposes an innovative fractal moth flame optimization (FMFO) approach to tackle the problem of integrated load dispatch (ILD). The proposed methodology provides a mechanism to integrate the information of the proposed optimizer, i.e., FMFO into the smart contracts enabled by the blockchain technology. This problem entails the allocation of loads to power-generating units in a manner that minimizes the total generation cost in a decentralized manner. To improve the efficiency of dispatch operations in the presence of a substantial integration of wind energy, this study proposes a novel framework based on the principles of fractal heritage, drawing inspiration from the classical MFO method. To assess the effectiveness and adaptability of the algorithm suggested, various non-convex scenarios in the context of optimization for ILD are considered. These scenarios incorporate valve-point loading effects (VPLEs), capacity limitations, power plants with multiple fuel options, and the presence of stochastic wind (SW) power uncertainty, following a Weibull distribution. The findings demonstrate exceptional performance in terms of minimizing fuel generation costs compared to traditional algorithms.
1 Introduction
Decentralized optimal power flow (D-OPF) in distribution networks represents a cutting-edge approach to enhancing the efficiency and reliability of power distribution, and integrating blockchain technology into this framework further elevates its capabilities. The traditional power flow management systems often face challenges in handling the increasing complexity of modern distribution networks with diverse energy sources (AlSkaif and Van Leeuwen, 2019; Ullah et al., 2022; Younesi et al., 2022; Jangir et al., 2023; Nappu et al., 2023). D-OPF, by distributing decision-making processes across the network nodes, allows for real-time optimization of power flows, ensuring optimal utilization of resources and minimization of losses such as reduction in fuel generation cost, active power line losses, overall operational costs, improved network voltage profile, security, and stability. These objectives are achieved by finding the optimal value for each of the operational variables, such as the active power generation, generator voltages, the tap position of the transformers, the shunt capacitor bank, and flexible alternating current transmission system (FACTS) devices. In addition, reactive power planning, which involves the optimum size and allocation of reactive power sources, is another essential framework that must be used to attain the highest possible level of technological and economic advantages during the operation of a power system.
Blockchain technology plays a pivotal role in ensuring the security, transparency, and trustworthiness of the decentralized decision-making process. By using a distributed ledger, every participant in the network can access a secure and tamper-resistant record of transactions and decisions. Smart contracts, executed automatically based on pre-defined rules, facilitate the seamless execution of optimization strategies. The transparency provided by blockchain not only ensures the integrity of the decision-making process but also encourages collaboration among different stakeholders in the distribution network.
The synergy between D-OPF and blockchain technology not only improves the operational efficiency of distribution networks but also addresses issues related to data privacy and security. The decentralized nature of the system reduces the vulnerability to cyberattacks and unauthorized access. Additionally, the incorporation of blockchain enables the creation of decentralized energy markets, allowing prosumers to participate actively in the energy trading process.
The D-OPF problems are divided into two subcategories: distributed economic load dispatch (D-ELD) and optimal reactive power dispatch (ORPD). The presented research concentrates on the solution of the D-ELD problem by considering the integration of distributed energy resources (DERs), with the primary goal of reducing the total cost of generation. Due to the complexity, non-stationarity, and non-linearity of power systems, however, it is difficult to discover the optimal global solution to a power system. A multitude of conventional, computational intelligence algorithms and mathematical models are introduced to solve OPF problems in power networks. To be more specific, we may refer to numerical techniques such as the Newton method, interior point methods, gradient-based algorithm (Granville, 1994), linear programming (Aoki et al., 1988; Deeb and Shahidehpour, 1988), and quadratic programming (Lo and Zhu, 1991).
The primary objective of this investigation is to propose the concept of fractional calculus for possible exploration and application in the optimization ingenuity of swarming and evolutionary techniques. Researchers will be able to upgrade the efficacy of traditional algorithms developed for engineering applications, particularly for the solution of OPF issues pertaining to electric power systems, which have been a challenging area of research for the past few decades. In the proposed research, the global optimum capabilities through a novel approach of the biological-inspired metaheuristics paradigm of the fractal moth flame optimization (FMFO) algorithm are effectively applied on hybrid energy-generating units of thermal and wind power. According to a recent survey, the metaheuristic strategy of FMFO has not been applied so far on integrated load dispatch (ILD) problems. The salient features of the proposed research can be categorized as follows:
• For the large-scale ILD issue that incorporates SW, a computational heuristic optimization approach that is based on the FMFO algorithm is presented.
• The process of identifying a near-optimum solution for an ILD system involves assessing the effectiveness of the suggested FMFO technique. This assessment entails exploring and exploiting variations in historical data terms and the fractional derivative order.
• Comparative studies of FMFO heuristics outcomes with state-of-the-art solvers for validating and verifying the strength of the proposed scheme.
The structure of this paper is as follows: “Literature review " provides a general overview of relevant studies from the literature. The objective/fitness function for ELD and the mathematical modeling of multiple fuel options and cost function for SW power availability is established in “System mathematical model.” "Design methodology” provides an overview of the proposed scheme of the FMFO algorithm. “Simulations and results” and “Statistical analysis” analyze several simulations using the proposed method, involving a comprehensive comparison with other approaches and a statistical analysis. “Discussion and limitations” provides the strengths and weaknesses of the proposed method. “Conclusions” summarizes the principal conclusions.
2 Literature review
Smart contracts serve as the fundamental basis for blockchain decentralized apps. These structures facilitate transactions in contexts where trust is not required, using consensus techniques and software-controlled verification criteria. Currently, there is a lack of research on the portability of smart contracts, and the ability to reuse their source code is mostly restricted to cloning. Górski (2022) investigated the process of designing and implementing smart contracts, specifically focusing on the explicit description of verification requirements. The author presented two benefits of the pattern: the first aspect is the ability to modify the set of smart contract validation criteria during runtime in order to accommodate different sorts of transactions. Furthermore, the application of verification criteria may be extended across multiple versions of the smart contracts. Kirli et al. (2022) gave a thorough evaluation of the literature with peer review, highlighting the usage of smart contracts for applications related to energy. Energy applications are categorized into two primary categories: energy and flexibility trading and distributed control. The former includes 65% of the material that was evaluated. According to the authors, this percentage is expected to grow further as energy markets become more distributed with individual prosumers gaining more control over their own energy production, storage, and consumption. The most popular areas of smart contract utilization were found to be peer-to-peer trading, market architecture, EV collaboration, grid administration, and DR control. Smart contracts are considered a viable alternative for addressing the challenges associated with implementing local energy management methods, particularly in terms of automating negotiations, invoicing, settlement, and other related processes.
Conventional numerical techniques are not able to solve constrained optimization problems, owing to the stiff situations introduced because of considering practical constraints in conventional OPF problems. These techniques are unable to produce global optimum outcomes and are often trapped in local optimum regions. On the other hand, stochastic search-based computing processes are developed to handle optimization challenges that arise during the study of power systems. These methods evaluate the global optimum while dealing with non-linear, discontinuous, and non-convex fitness functions with success. With the recent development and application of metaheuristic computational strategies, solutions to OPF problems have become vastly superior.
Over the course of many decades, many researchers have developed several optimization strategies with applicability to real-world issues. Some of these strategies include emission, combined emission and ELD, integrated power plant systems, and smart grids. They have gone through fundamental ideas, theoretical frameworks, and methodological approaches for dealing with complex non-linear systems. It is impossible to deny the importance of gradient-free solvers in the field of integrated power plant systems, yet the research community only makes limited use of the few metaheuristic algorithms that are of crucial value. Particle swarm optimization (PSO) is metaheuristic nature-inspired global technique adopted to find optimal results of ELD integrated with SW forming hybrid energy-generating units (Pandit et al., 2015). The genetic algorithm (GA) is exploited to deal with ELD integrated with physical constraints where numerical techniques failed to give global optimum outcomes. More stable and précised results were recorded using a refined genetic algorithm (RGA) by appropriate scheduling of active power generation outputs (Durairaj et al., 2005; Chopra and Kaur, 2012a). Additionally, recently developed metaheuristics-based searching algorithms have been applied in power and energy sectors reported in the work of Abbassi et al. (2019), El-Fergany et al. (2019), Mohseni et al. (2019), Fathy (2020), Yang et al. (2020), and Zhang et al. (2020).
The development of a biological-inspired metaheuristic strategy of gray wolf optimization (GWO) developed by Mirjalili et al. (2014) and Faris et al. (2018) is a fascinating methodology to be applied to stiff scenarios of a practical ELD problem. Numerous preponderant problems of optimization are addressed using GWO (Alzubi et al., 2020; Salgotra et al., 2020; Sattar et al., 2020) that includes feature selection (Chantar et al., 2020), vehicular ad hoc networks (Fahad et al., 2018), power system stabilizer design (Shakarami and Davoudkhani, 2016), hydropower prediction (Dehghani et al., 2019), and energy management (Nimma et al., 2018). Nature-inspired rainfall optimization (RFO) has been adopted to address the fuel generation cost in the case of the standard IEEE 40 generating unit test system. The main inspiration behind the RFO algorithm is the trickling behavior of raindrops from any peak toward sea level according to gravitational force. The RFO algorithm simulates the behavior of these random-generated initial populations of raindrops to find global outcomes in terms of the deepest position of raindrops in the sea where a differential of cost function rather than gradient has been applied to find solutions. The proposed methodology outperformed in terms of convergence characteristics compared to GA and PSO (Kabolia, 2023).
Greater emissions of toxic gases such as CO, SO, and NOx have been observed because of electrical power generation from fossil fuel-operated thermal power-generating units. Due to these hazardous environmental concerns, mathematical formulations have been developed to reduce the generation cost and emission levels of the abovementioned toxic gases simultaneously. The addition of alternate energy resources such as wind and solar energies has largely rectified the concerns of higher generation costs and emission levels of toxic gases. The integration of renewable energy sources (RES) into thermal power plants has led to modifications of the conventional quadratic fuel cost characteristic equation by adding beta and Weibull distribution functions that address the stochastically varying behavior of solar and wind power availability, respectively. A recently developed improved firework algorithm with a non-uniform operator (IFWA-NMO) is applied on the standard IEEE 15 generating unit test system with probabilistic varying behavior of solar and wind power energies (Pandey et al., 2018). Many practical constraints, such as multi-fuel options, spinning reserves, and transmission losses, have made the ELD problem a highly non-convex optimization problem. Moreover, the economic emission dispatch (EED) has transformed the single objective of the ELD problem to a multi-objective problem with two contradictory objectives. In order to improve robustness, convergence speed, and accuracy, the roulette wheel mechanism and wavelet mutation have been included in the conventional harmony search algorithm (HSA) called modified HSA. The effectiveness of the proposed modified strategy scheme has been applied on seven highly non-linear and multi-objective test systems and results proved even better compared to the classical HSA (Jeddi and Vahidinasab, 2014).
The hybridization approach of various optimization techniques has shown greater potential and generated the best global solutions to real-world problems. The best global solutions are promised because the hybridization approach takes advantage of exploiting the best features of individual algorithms simultaneously (Hu et al., 2015). Over the last decade, hybrid techniques have been deliberately applied on power systems. The rising trend of these techniques in the power system is the main motivation for an extensive literature survey in the power system domain. Hybrid algorithms take advantage of simultaneously searching for the best solutions in the search space and rectifying any potential disadvantages. A recently developed hybrid strategy of gravitational acceleration enhanced particle swarm optimization (GAEPSO) has been adopted to optimize the fuel generation cost, emission, and compromise solution of both. The hybrid computational approach of GAEPSO has adopted the exploration feature of PSO and the exploitation property of the gravitational search algorithm (GSA) simultaneously to give global solutions (Jiang et al., 2015). More stable and precise results were recorded using the hybrid genetic algorithm (HGA) by appropriate scheduling of active power generation outputs (Chopra and Kaur, 2012a). Hybrid imperialistic competitive sequential quadratic programming (HIC-SQP) has been applied to optimize the stochastic behavior in terms of direct cost, overestimated cost, and underestimated cost of wind power availability integrated with thermal power-generating units in order to reduce the generation cost and emission of toxic gases simultaneously. Naderi et al. (2017) solved the multi-objective problem involving the fuel generation cost, emission levels, and transmission losses of the ELD problem by considering the valve-point loading effect (VPLE), prohibited operating zones (POZs), and multi-fuel options for 10-, 40-, and 160-unit test systems by formulating the fuzzy-based PSO hybrid with differential evolution (DE) known as FBPSO-DE. The performance of the proposed hybrid approach of PSO was analyzed by comparing it with seven constrained benchmark functions based on 100 independent trials and showed better convergence and robustness against PSO and its different hybrid approaches. The continuous greedy randomized adaptive search procedure (CGRASP) algorithm hybrid with self-adaptive differential evolution (SaDE) known as CGRASP-SaDE is adopted to optimize fuel generation cost considering VPLE (Neto et al., 2017). The effectiveness of the proposed hybrid approach is validated by considering 13, 40, and 140 generating units. The simulation results of the proposed CGRASP-SaDE are well promising and effective compared with standalone strategies of GRASP and CGRASP. Enhanced mutation, additive competition, and discrete difference operators were integrated in the hybrid strategy of the harmony search algorithm with differential evolution (HSDE) by Zhang et al. (2016) and applied on the day-ahead scheduling model of micro grid containing photovoltaic, wind power, diesel generator sets, and battery storage by considering IEEE 9, IEEE 39, and IEEE 57 bus systems. The effectiveness of the proposed hybrid approach of HSDE is validated by comparing it with state-of-the-art counterparts by considering the normal and faulty conditions of IEEE bus systems.
Recently, it has been proposed that the incorporation of fractional calculus (FC) and the foundational concepts of fractional derivatives into the underlying mathematical model of a system will yield far superior results in other disciplines of science and engineering. These methods have been effectively implemented in a variety of issues including feature selection (Wang et al., 2018), image processing (Wang et al., 2019), hyperspectral images (Ghamisi et al., 2013a), controllers for estimating the robotic path (Łegowski and Niezabitowski, 2016), Kalman filters (Zhu et al., 2014a), and fractional-order filters (Ates et al., 2016). This research suggests that FC tools should be embedded with evolutionary techniques in order to solve optimization challenges in the energy industry. We can refer to fractional-order robotic PSO, FPSO with fractional-order velocity (Couceiro et al., 2012a; Ghamisi et al., 2013b; Ghamisi et al., 2014; Ates et al., 2017; Machado and Kiryakova, 2017; Shahri et al., 2019), localization and segmentation of optical disc (Zhu et al., 2014b), parameter adaptation for Kalman filtering algorithms (Zhu et al., 2014a), land-cover monitoring (Yokoya and Ghamisi, 2016), feature selection (Wang et al., 2018), classification of hyperspectral images (Paliwal et al., 2017), and robot path controllers design (Łegowski and Niezabitowski, 2016). Other applications include the design of a multi-band power system stabilizer based on a lead–lag compensator using a hybrid dynamic GA-PSO (Kuttomparambil Abdulkhader et al., 2018), non-linear systems identification (Kosari and Teshnehlab, 2018), continuous non-linear observer using sliding mode PID (Azar and Serrano, 2018), fractional robust control of coupled tank systems (Katal and Narayan, 2017), and reference model-based PID controllers for AVR systems (Li et al., 2017). These studies motivate the integration of FC tools with metaheuristics algorithms for power and energy sector optimization problems.
3 System mathematical model
The main goal of the ILD issue is to optimize the distribution of load among power-producing units to minimize the overall fuel generation cost. This purpose considers the specific restrictions associated with substantial multi-fueled power plants and incorporates the integration of RES to ensure the provision of sustainable energy.
3.1 Convex fuel cost function formulation
The phenomenon of ELD may be classified as a constrained optimization problem since it aims to minimize the overall cost associated with power-producing systems within a certain time frame. A quadratic function can potentially be used to simulate the primary objective function of ELD, which reflects input output characteristics between active power production and fuel-generating cost (Balamurugan et al., 2014).
‘FCost’ is the total fuel cost generation in dollars per hour ($/hr.), whereas ‘TU’ is the total number of thermal power-generating units. Generation coefficients reflecting the social, economic, and other related terms are being shown by coefficients ‘α’, ‘β’, and ‘δ’ for the mth thermal power-generating unit in quadratic fuel cost function formulation.
3.2 Non-convex fuel cost function
The efficiency of power-producing systems including a steam generator, steam turbine, and alternator often exhibits a quadratic relationship with respect to load demand. The quadratic equation demonstrates the relationship between the increase in load demand and the corresponding increase in the generating cost rate, expressed in $/hr. Nevertheless, contemporary thermal power generation systems have also taken into consideration the physical phenomena associated with fluctuations in load demand. The regulation of the electrical power output from an alternator, in accordance with the load demand, often involves the use of controlled valves. These valves are responsible for managing the quantity of steam that is permitted to be sprayed onto turbines via a series of distinct nozzle groups. Optimal efficiency is attained by each nozzle when it operates at maximum output. The attainment of optimal efficiency for enhanced production is achieved by opening valves in a sequential manner. In the VPLE system, the turbine operates at its peak efficiency prior to the activation of the subsequent valve in the prescribed sequence. The physical phenomena under consideration may be represented by incorporating absolute and sine terms into a quadratic fuel cost function, resulting in a non-smooth function owing to the presence of ripples associated with the VPLE (Decker and Brooks, 1958).
where
3.3 Convex cost function involving multiple fuel options
Power plants are provided with a diverse range of fuel sources, including coal, oil, and natural gas. However, to optimize economic efficiency within a certain operational range, power plants choose the most financially advantageous fuel type. The following expression denotes the cost function pertaining to the ELD problem, including a wide range of fuel alternatives (Liu et al., 2022).
where ‘αm,k’, ‘βm,k’, and ‘δm,k’ are the generation coefficients of the mth power plant.
3.4 Non-convex cost function involving multiple fuel options
To obtain a reliable and feasible ELD solution, we must simultaneously evaluate multi-fuel options and VPLE. The cost function may, thus, be expressed as follows:
where
3.5 Wind power cost function formulation
The significant advantage of integrating SW power in thermal power-generating units is reflected by economic and environment-friendly electrical power generation. In the power generation system comprising both thermal and wind power-generating units, various models have been developed for characterizing the scheduling of real power generation and operational generation cost. Due to the inherent random speed of wind power, the power generation operator is uncertain regarding its availability. He may overestimate wind power availability where actual power is less than that of power predicted, and extra power is purchased to fulfill the load requirements. Sometimes due to the underestimation of wind power availability, some extra power is available, and compensation is provided to the wind power supplier’s cost for not using the complete wind power available. The total generation cost of wind power can be modeled as follows (Khan et al., 2021):
‘FW.P(Cost)’ is the total wind power generation cost, and ‘WU’ is the total number of wind power generation units. ‘CW.P(DIR,n)’, ‘CW.P(OE,n)’, and ‘CW.P(UE,n)’ are terms associated with direct cost, overestimated cost, and underestimated cost associated with wind power-generating units, respectively.
Output wind power generation is directly proportional to ‘CW.P(DIR,n)’ and can be expressed mathematically for nth wind power generation unit as follows:
In Eq. 6, ‘qn’ is the coefficient expressing direct electrical energy cost from the nth wind power-generating unit in $/MWh, whereas ‘W.Pn’ is real electrical output power in MW from the nth wind power-generating unit. ‘CW.P(OE,n)’ is the unbalanced overestimated cost as a result of the overestimation of wind power availability, so some extra real power in MW is purchased due to electrical power shortage from wind power-generating units and can be expressed mathematically as follows:
‘Crw,n’ is the cost coefficient for overestimation in $/MWh for the nth wind power-generating unit, whereas ‘X(VOE,n)’ is the expected value of wind power overestimation for the nth wind power-generating unit and can be expressed mathematically as follows:
‘VIN’, ‘VOUT’, and ‘Vr’ are the cut-in, cut-out, and rated speed of wind in meters per second, respectively, whereas V1 = VIN+(Vr-VIN) *W. Pn/W. Pr is the intermediary parameter. ‘Cn’ and ‘Kn’ are the coefficients of the Weibull distribution reflecting scale and shape factor, respectively, for the nth wind power-generating unit. ‘W. Pn’ and ‘W. Pr’ are the generated and rated electrical power in MW for the nth wind power-generating unit, respectively.
Moreover, the symbol Γ in Eq. 8 represents the incomplete gamma function having two parameters (Liu et al., 2022) and can be mathematically expressed as follows:
A standard gamma function involves a single parameter expressed as follows:
‘CW. P (UE, n)’ is the penalty cost imposed because of underestimating the availability of wind power where the actual active power available out of wind power-generating units is more than that of predicted active power. Compensation in this regard is provided to the wind power supplier’s cost for not using all the wind power available and can be mathematically expressed as follows:
‘Cew, n’ is the cost coefficient for underestimation in $/MWh for the nth wind power-generating unit and ‘Y (VUE, n)’ is the expected value of wind power underestimation for the nth wind power-generating unit and can be expressed as follows:
3.6 Total generation fuel cost function
The overall objective function can be modeled by combining the quadratic fuel cost function involving the VPLE and wind power generation availability cost function in $/hr., as expressed in the following equation:
where ‘FCost’ and ‘FW.P(Cost)’ can be found from Eq. 4 and Eq. (5), respectively, and are presented in the following equation:
3.7 Operational constraints
Traditional constraints in ELD analysis include inequality constraints, such as active and reactive power production, as well as equality constraints, such as active and reactive power balancing equations. All these limitations are taken into consideration in a steady state, without taking into account any network disruptions that may occur momentarily. The operational variables and constraints related to ELD are documented in the following sections.
3.7.1 Load demand constraint
The most important constraint to be handled properly while optimizing the total generation cost is that the total active power generation output from different thermal and wind power-generating units at each bus should be equal to the total load demand plus active power losses, respectively, as shown in the following equations:
Similarly, the expression for the loss of reactive power is given by
"Bop” and “Gop” refer to the susceptance and conductance of the transmission lines interconnecting the oth and pth buses, respectively.
3.7.2 Generation constraint
Active power generation output from each thermal and wind power-generating unit should be less than or equal to its maximum active power generation limits such that
3.8 Penalty function method to incorporate the violation of control variables
In the power system, considerable damage will occur to power network if control variables violate its limits. In this regard, the penalty function methodology has been incorporated to take care of the violation of control variables. The penalty function term will become zero if control variables are within its pre-defined limits and objective function incorporating ILD can be expressed as shown in the following equation:
Here, ‘PF(X,ra,rb)’ is penalty function expressions for optimizing total generation cost. X = x ∈ [P, W. P] represents the set of independent variables for thermal power generation and wind power generation. ‘ra’ represents penalty multipliers for equality constraints in case of optimizing the total generation cost, whereas ‘rb’ represents penalty multipliers for inequality constraints. The penalty multiplier ‘rb’ includes ‘rp’ and ‘rw.p’, which are penalty multipliers for independent variables in the case of thermal power generation and wind power generation, respectively. The strategy adopted for constraint violations of controlled variables is summarized in the following equation:
4 Design methodology
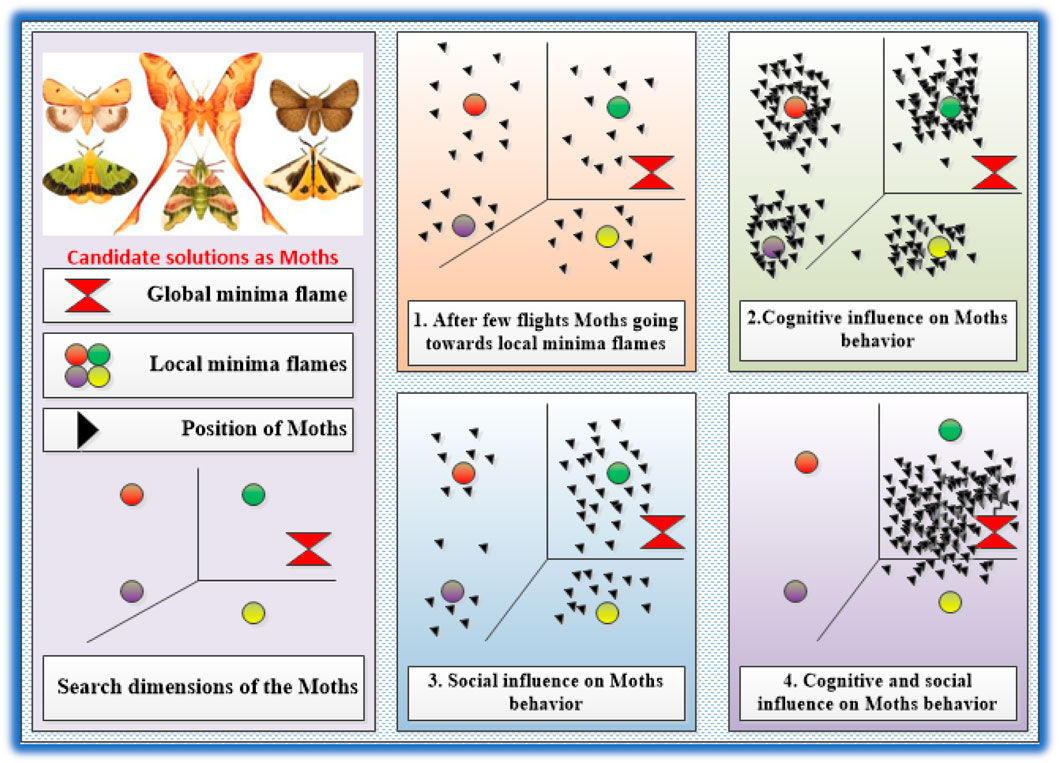
This section introduces a unique way to enhance the local search strategy of the traditional MFO algorithm. Mirjalili (2015), inspired by the transverse positioning of moths during nocturnal navigation, proposed the MFO method for the first time. MFO uses spiral trajectory functions to represent dying behavior in a mathematical model, unlike other nature-inspired algorithms. Moths use transverse orientation as a navigational strategy to facilitate more efficient nocturnal migration over extended distances, whereby they maintain a constant angle relative to the moonlight (Figure 1A). The presence of nocturnal artificial lights or flames often causes moths to deviate from their intended trajectory. This phenomenon may be attributed to the fact that moths tend to be in greater proximity to artificial lights than moonlight. As seen in Figure 1B, moths die as they fall toward artificial light due to a lethal spiral orientation.
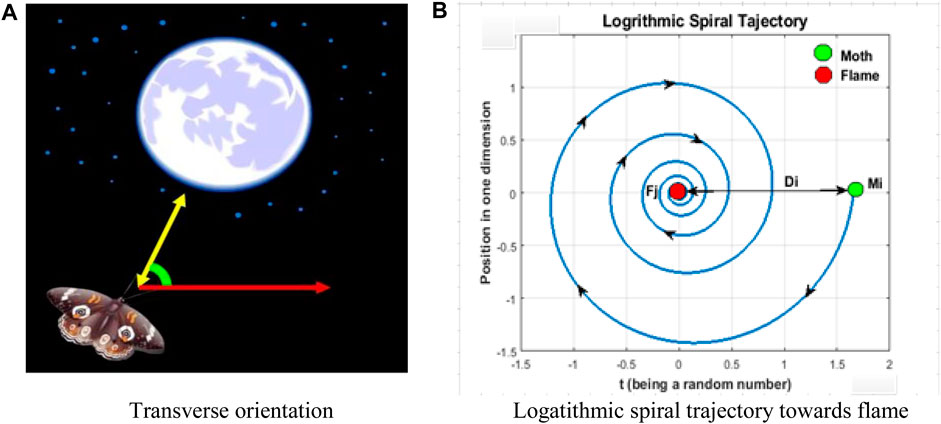
FIGURE 1. Transverse orientation strategy with reference to moonlight and logarithmic spiral trajectory toward artificial light or flame.
The MFO algorithm is a search algorithm that operates on a population-based approach. In this system, every moth serves as a search agent, with the orientation of each agent indicating the quantity of controllable variables. This approach aims to discover the optimum solutions. The framework incorporates an initial solution for moths, denoted as ‘M’, which consists of ‘n’ candidate solutions and ‘d’ dimensions representing controllable variables. These candidate solutions are evaluated based on an objective function, and their fitness is represented by the matrix ‘OM’.
A matrix is developed for flames, denoted as ‘F’, which has a resemblance to the matrix structure seen in moths. The matrix contains encoded fitness values represented as ‘OF’. Moths choose the most advantageous position, and subsequent search agents adjust their placements in accordance with the ideal position that has been reached so far.
The ‘S’ spiral function is used to adjust the position of every nth moth relative to the kth flame.
Historically, the MFO method has replicated the spiral flight trajectory of moths using a logarithmic spiral function, and the alignment has been enhanced using Eq. 26. The variable ‘Dn’ represents the linear distance among the nth moth and the kth. Here, ‘k’ is the form factor of the logarithmic spiral, and ‘r’ represents a randomly generated value within the range of −1 to 1.
The proposed method integrates FC with the fundamental MFO to generate a fractional-order MFO algorithm in order to control the accelerated convergence tendency and achieve acceptable results. MFO has a reasonable predisposition for global search, but its ineffectual local search results in a subpar reduction in convergence speed. To circumvent the aforementioned limitation, the proposed method integrates the FC into the fundamental MFO in order to use the FC retention feature of the earlier solutions to guarantee information sharing across solutions during the exploitation phase. Consequently, both the response accuracy and convergence speed are altered. FC is well-suited to describing intriguing phenomena, such as irreversibility and disorder, due to the characteristics it reveals and its inherent memory component. According to this theory, the dynamic nature of an MFO trajectory creates a unique situation, whereas FC instruments are a suitable complement.
FC has garnered the interest of numerous academicians due to its applicability in a vast array of scientific disciplines, including engineering, computer mathematics, and computational physics. FC is an extension of integer-order calculus, accomplishing what the latter could not. As a natural extension of integer (or classical) derivatives, fractional derivatives are a suitable method for describing the memory and inherited properties of processes.
There are several alternative approaches for representing the notion of fractional-order derivatives (Sabatier et al., 2007; Teodoro et al., 2019). Using the Grünwald–Letnikov theory for fractional-order derivatives, it is possible to derive the FC-based mathematical equations for MFO. We consider any random signal s(t) for which the Grünwald–Letnikov fractional-order derivative is given in the following equation (Couceiro et al., 2012b):
Although an integer-order derivative only implies a finite series, a fractional-order derivative necessitates an infinite number of terms. Derivatives of integers are, hence, “local” operators. In contrast, fractional derivatives inherently “remember” all prior events. Nevertheless, the influence of prior events diminishes over time. The discrete time calculation is inspired by the following expression:
where ‘T’ is the sampling period and ‘r’ is the order of truncation. [s(t)] is a discrete variable, and for a special case, where δ is equal to one, the equation is transformed to an integer-order or ordinary first-order derivative and can be expressed as follows:
In order to use the previously described definition of FC to enhance the classical MFO’s local search capabilities, the position of each moth is updated based on its velocity, as shown in the following equation:
Moths exhibit PSO motion, with the local optima representing the moth’s associated flame (LB. Fpos) and the global optima being the best flame (GB. Fpos). The position of each moth is updated at each iteration depending on its current velocity and position. Both initial velocity and the cognition and social behavioral patterns of moths are consistent with the revised velocity. In contrast, the mathematical model of cognitive behavior is the distance between the greatest local flames and their current location.
where
Here,
The order of a velocity derivative can indeed be generalized to something like a real number ranging from 0 to 1, resulting in a smoother fluctuation and a prolonged memory effect, based on the FC notion. Considering the discrete-time fractional differential, Eq. 30 can be rewritten as follows:
The expression of the fractional velocity for the nth moth particle with the rth term is as follows: tr = 1, 2, 3, r.
Considering only four terms, Eq. 33 can be rewritten as follows:
The operating idea of the proposed FMFO algorithm is shown in Figure 2, while the pseudocode for FMFO is given in Algorithm 1.
Algorithm 1.FMFO.
INPUT: Standard test data for 13 generating units, Taiwan 40 generating units, and Korean 140 generating units are loaded.
OUTPUT: Fuel generation cost optimum outcomes because of fitness assessment for objective function as stated in the system mathematical model.
FOMFO Algorithm
Random initialization of the search agent’s (moths) population: n search agents are randomly introduced whose dimensions correlate to the task's controllable variables into the 'M' population of moths.
Fitness evaluation: The evaluation of the fitness value of each search agent is conducted by subjecting it to the requisite objective function pertaining to fuel generation cost minimization.
Sorting initial search agent population: The collective number of search agents is primarily sorted based on their distinctive fitness function scores and then allocated to the flame population 'F' in conjunction with their individual fitness function values 'OF'.
Updating the position of search agents: A logarithmic spiral function is used to adjust the position of a moth relative to the optimal flame.
Velocity calculation of each search agent based on the fractional-order strategy: The velocity for every nth moth is calculated through fractional order “varying from 0.1 to 0.9 as defined inEq. 36.
Fractional-order velocity strategy adopted to further update position: Each moth's location is updated using the following equation, which considers the moth's fractional velocity with respect to its prior position.
Stopping criteria: The FOMFO algorithm's halting criterion is based on a predetermined number of iterations.
Storage of results: The minimal fuel generation cost determines the ELD problem's control variables, which are predicated on the global best outcome of moths/search agents.
Statistical analysis: One hundred independent trials are analyzed statistically using boxplot and CDF-based analysis.
4.1 Integration of FMFO into a blockchain smart contract
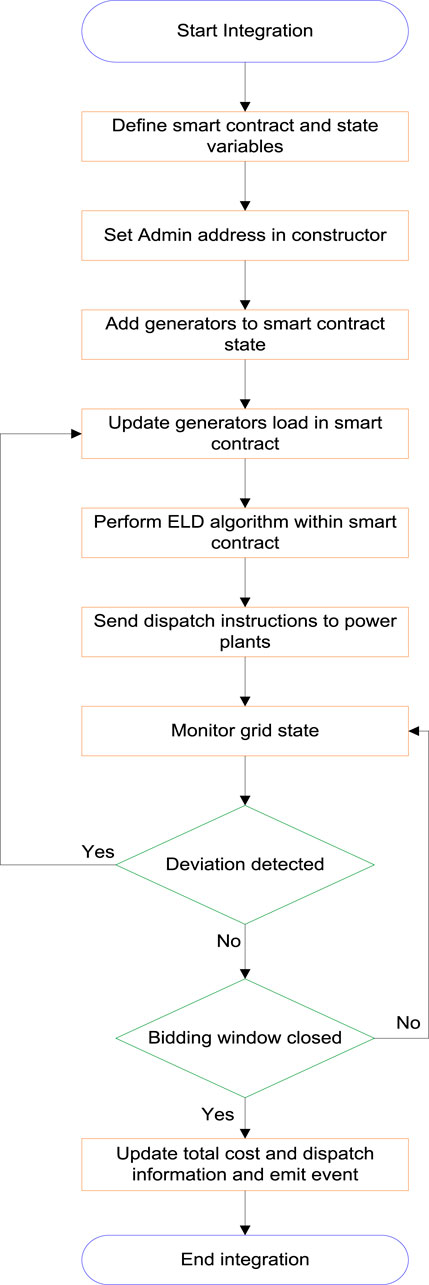
Integrating ELD into a blockchain smart contract involves combining traditional power system optimization techniques with blockchain technology (Górski, 2022). ELD is a crucial aspect of power system management that aims to minimize the cost of generating electricity while satisfying various operational constraints. The proposed work uses FMFO to solve the ELD problem and integrates it into a blockchain smart contract. The flowchart outlining a high-level framework for this integration is shown in Figure 3. The integrating framework is designed by considering the runtime reconfigurability and the reusability of the various constructs of the smart contract (Kirli et al., 2022).
The flowchart in Figure 3 outlines the steps involved in integrating ELD into an Ethereum smart contract. It starts with defining the contract and state variables, setting the administrator’s address in the constructor, adding a generator to the contract state, updating the generator load, performing the ELD algorithm, and finally, updating the total cost and emitting an event. In case, if any of the generators fails to fulfill the unit commitment or if there is any change in the load demand, a request is sent back to update the generator's load in the smart contract. The flowchart emphasizes the sequential nature of the integration process. The information related to the Ethereum interactions, error handling, and security features is not considered for this work.
The pseudocode focuses on the core logic of the FMFO optimizer in the blockchain contract. The data-gathering step fetches demand, power plant, and grid constraint data from appropriate sources. This is followed by the ELD calculations using the FMFO optimizer. The optimized results are then stored on the blockchain platform and communicated to the power plants through off-chain mechanisms. The grid state (both the load and the generator side) is continuously monitored and triggers re-optimization if deviations occur. It should also be noted that the proposed framework also follows an auction-based approach, and the time taken by the bidding window depends upon the convergence time taken by the FMFO optimizer to get the most optimal results. This research mainly focuses on cost optimization; however, the time optimization of the FMFO is an interesting dimension to consider in future works.
5 Simulation results
The effectiveness and applicability of the proposed FMFO for active power planning are evaluated using three test systems based on 13 generating units, practical Taiwan 40 generating units, and a Korean large-scale test system of 140 generating units. Determining a solution that minimizes the number of financial resources spent on generation is one of the most important factors that the intended function takes into consideration. The numerical values of the primary controlling parameter are used as the basis for determining how successful the proposed algorithms are when it comes to managing the system. Even a little shift in the proportions of these elements has the potential to bring about early saturation, which will lead to a result that is less than ideal. The parameters of the FMFO, including the number of particles, swarm size, fractional order of the moth’s velocity, social and cognitive acceleration vectors, maximum iterations, and independent variables, are determined through experimentation and thorough analysis of an optimization problem. The basic parameters that need to be adjusted to increase the overall effectiveness of the recommended algorithms are shown in Table 1. To optimize the efficiency of the suggested approach, the algorithms are conducted using varying percentages of fractional orders, depending on the specific case being analyzed. Ten fractional-order values that range from 0.1 to 0.9 have been assessed. Typically, a stochastic method is used to determine the optimal fractional order for fractional evolutionary or swarming techniques. Nevertheless, choosing a fractional order that has a clear physical rationale is always challenging, and Monte Carlo statistics is used to determine the best sequence to follow. To ascertain the robustness of the FMFO’s optimization, a statistical analysis of 100 trials through all test cases is conducted.
5.1 Case study A: the 13-generating-unit test system
This case study incorporates a collection of 13 thermal power-generating units. The coefficients for the generation fuel costs were sourced from the work of Raja et al. (2019). The power demand under consideration for this analysis is 2420 MW. The incorporation of the VPLE was undertaken to account for the accurate representation of power system dynamics. A total of 10 distinct variants of the FMFO method, denoted as FMFO-I to FMFO-IX, were used in the analysis of case study A. These variants included a range of fractional-order derivatives, spanning from 0.1 to 0.9. The stochastic variability of the optimized simulation results of the FMFO method cannot be disregarded. To rigorously monitor the frequency of variations in optimized outcomes, 100 independent trials were conducted for each form of the FMFO algorithm, using 300 iterations. Table 2 presents the simulation results of the fuel cost value in $/hr. for each fractional-order derivative values of the FMFO algorithm over 100 separate trials, while the values for determining variables in relation to the output of active power production in megawatts for the FMFO variants are also presented in Table 2. Among the 10 different variants of the FMFO algorithm, it has been observed that FMFO-I exhibits the most favorable simulation outcomes in relation to the least fuel cost, which amounts to 23938.71 $/hr. The efficacy of the approach, as shown in Figure 4, over best fractional-order values that range from 0.1 to 0.9 has been assessed, all of which are necessary to get the optimal alpha value. The minimal fuel cost outlined by FMFO and their state-of-the-art equivalents from the literature, including GA-SQP, FA, PSO, CSA, and FO-FA (Raja et al., 2019), are summarized in Table 3. The percentage fuel cost includes 3.21% for GA-SQP, 0.76% for FA, 2% for PSO, 2.6% for CSA, and 2.3% for FO-FA, while the proposed FMFO is 27.06%, as illustrated in Figure 5.
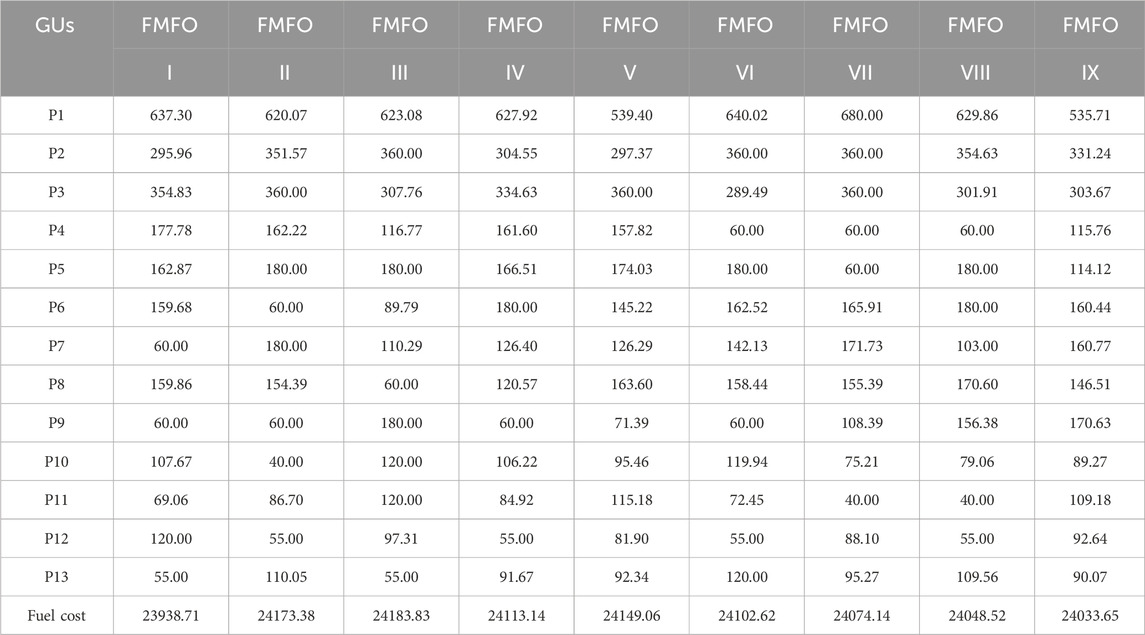
TABLE 2. Comparative analysis of the proposed FMFO algorithm for the 13-generating-unit test system for fractional-order values that range from 0.1 to 0.9.
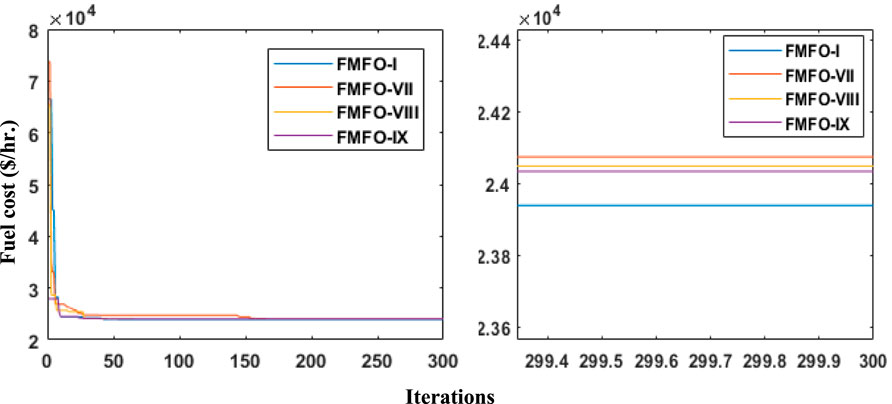
FIGURE 4. Comparing the learning curves of the proposed FMFO algorithm for the best fractional orders in case of the 13-generating-unit test system.

TABLE 3. Comparative analysis of the proposed FMFO algorithm for the 13-generating-unit test system with state-of-the-art algorithms from the literature.
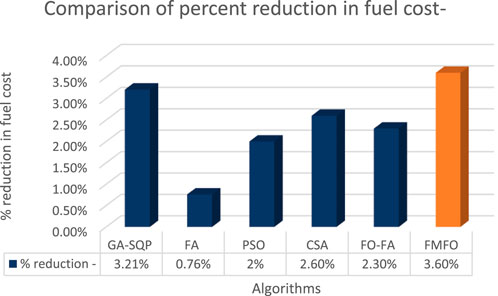
FIGURE 5. Comparison of percentage reduction in the fuel cost of the proposed FMFO algorithm for the 13-generating-unit test system with state-of-the-art algorithms from the literature.
5.2 Case study B: the Taiwan 40-generating-unit test system
In the present case, a revised examination of the ELD problem in Taiwan’s 40-unit test system is undertaken. The study involves the substitution of the final three thermal power-generating units, namely, units 38, 39, and 40, with wind power-generating units. The use of a system model in the formulation of Eq. 5 enables the integration of SW into the ELD-VPLE. The data pertaining to thermal generators were extracted from the work of Morshed and Asgharpour (2014b). The data pertaining to wind power units were sourced from the work of Morshed and Asgharpour (2014b) and are shown in Table 4. The load demand for case study B remains constant at 10500 MW.
Nine distinct variants of the FMFO algorithm, namely, FMFO-I to FMFO-IX, including fractional-order derivatives within the range of 0.1–0.9, were used in the analysis of case study B. A total of 100 separate trials were conducted for each variant of the FMFO algorithm, with each trial consisting of 1,000 iterations. Table 5 presents the tabulated results of the optimal total cost value in $/hr. and its corresponding fuel cost value for each variant of the FMFO algorithm over 100 separate trials. The values for determining variables in relation to the output of active power generation in megawatts for the FMFO variations are also provided in Table 5. Out of the nine distinct variants of the FMFO algorithm, it was found that FMFO-IX demonstrates the most favorable simulation results in terms of the lowest total cost, which is recorded at 135440.17 $/hr. The effectiveness of the methodology is seen in Figure 6 over several fractional alpha order intervals (ranging from 0.1 to 0.9), all of which are essential for determining the ideal alpha value. The minimal total cost outlined by FMFO and their state-of-the-art equivalents from the literature, including HIC-SQP (Morshed and Asgharpour, 2014b), PWTED1 (Morshed and Asgharpour, 2014b), DWTED1 (Morshed and Asgharpour, 2014b), GA-SQP, PSO, and COOT (Mehmood et al., 2023), are summarized in Table 6. The percentage total cost reduction includes 5% for HIC-SQP, 3.9% for PWTED1, 4.45% for DWTED1, 4.8% for GA-SQP, and 3.19% for PSO and COOT, while the proposed FMFO is 5.67%, as illustrated in Figure 7.
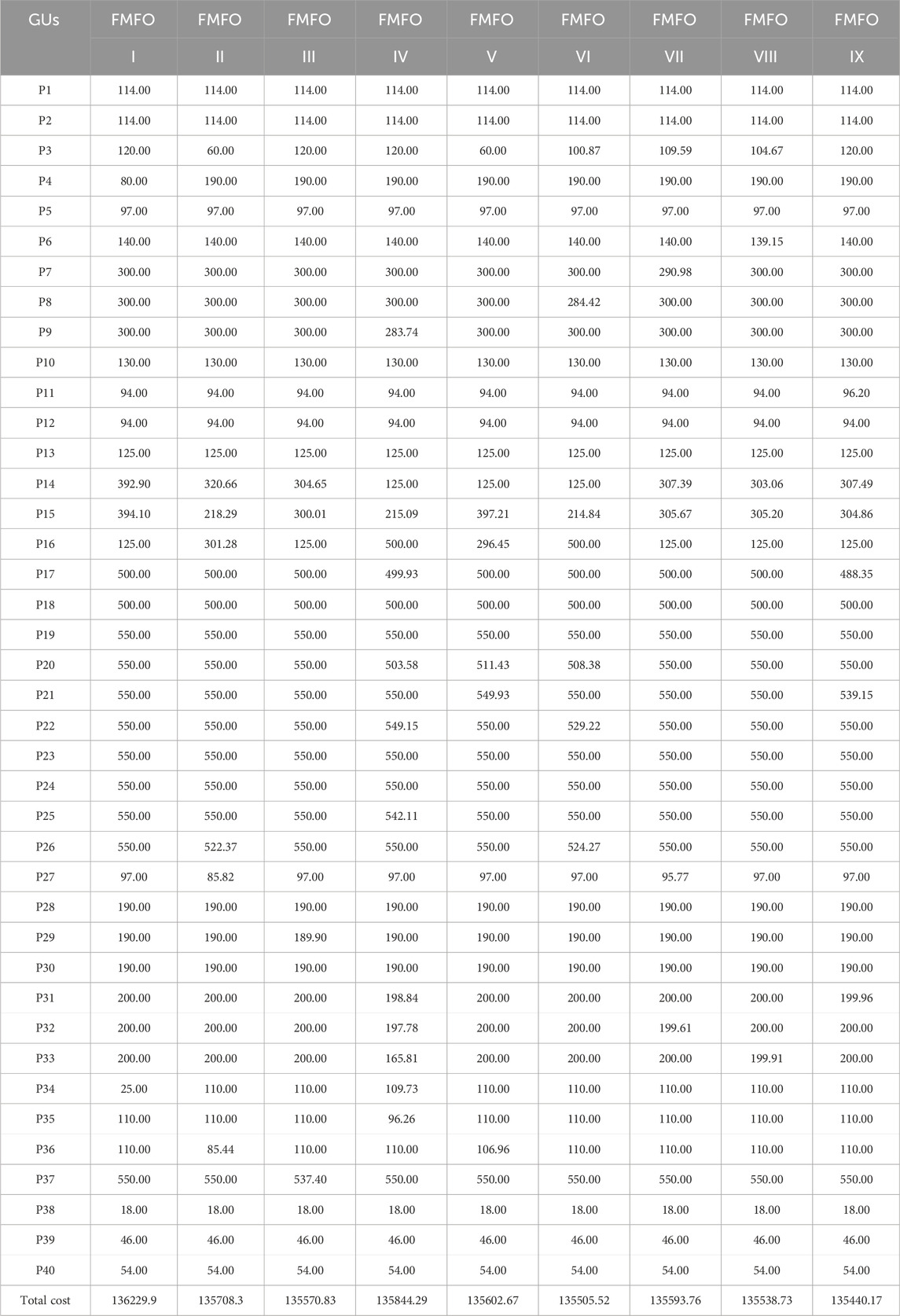
TABLE 5. Comparative analysis of the proposed FMFO algorithm for the Taiwan 40-generating-unit test system for fractional-order values that range from 0.1 to 0.9.
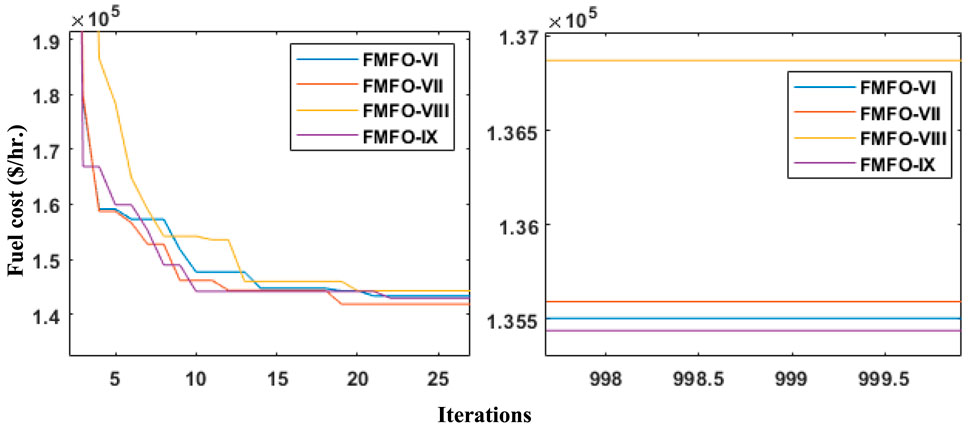
FIGURE 6. Comparing the learning curves of the proposed FMFO algorithm for the best fractional orders in case of the Taiwan 40-generating-unit test system.

TABLE 6. Comparative analysis of the proposed FMFO algorithm for the Taiwan 40-generating-unit test system with state-of-the-art algorithms from the literature.
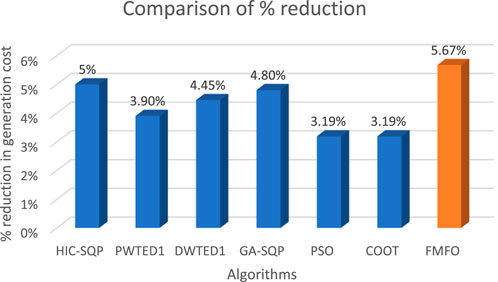
FIGURE 7. Comparison of percentage reduction in the fuel cost of the proposed FMFO algorithm for the Taiwan 40-generating-unit test system with state-of-the-art algorithms from the literature.
5.3 Case study C: the Korean 140-generating-unit test system
The test system comprises a fully operational power plant located in Korea. The system is comprised of a total of 140 units, which can be classified into the following categories: there are a total of 40 thermal generating units, 51 gas units, 20 nuclear units, and 29 oil units. In addition, it is worth noting that there are six heat units, four gas units, and two oil units that exhibit non-convex fuel cost functions (Zhang et al., 2019). The analysis of case study C included the use of nine variations of the FMFO method, specifically denoted as FMFO-I to FMFO-IX. One hundred trials were undertaken for each variation of the FMFO algorithm, with each trial including 100 iterations. The tabulated findings of the ideal fuel cost value in $/hr. for each variation of the FMFO algorithm across 100 independent trials for all case studies are shown in Table 7. Among the nine various forms of the FMFO algorithm, it has been observed that FMFO-VII exhibits the most favorable simulation outcomes in relation to the lowest overall cost, which has been documented as 1405421.20 $/hr. The efficacy of the technique is shown in Figure 8 over many fractional alpha-order intervals (ranging from 0.1 to 0.9), all of which are crucial for ascertaining the optimal alpha value. Table 8 provides a summary of the minimum total cost as presented by FMFO and other contemporary approaches in the literature, such as GA-SQP, FA, PSO, CSA, COOT, and FO-FA (Mehmood et al., 2023). The overall cost reduction percentage comprises many components, including 11.8% for GA-SQP, 11.5% for FA, 8.9% for CSA, 7.3% for COOT, and 11.84% for FO-FA. Additionally, the suggested FMFO shows a cost reduction of 19.22%, as illustrated in Figure 9.
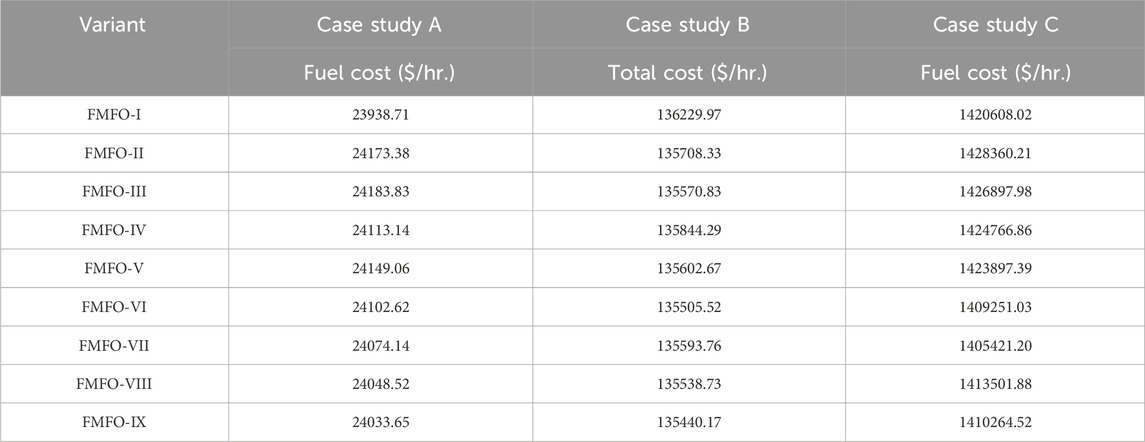
TABLE 7. Comparative analysis of the proposed FMFO algorithm for fractional orders ranging from 0.1 to 0.9 in case of case studies A, B, and C.
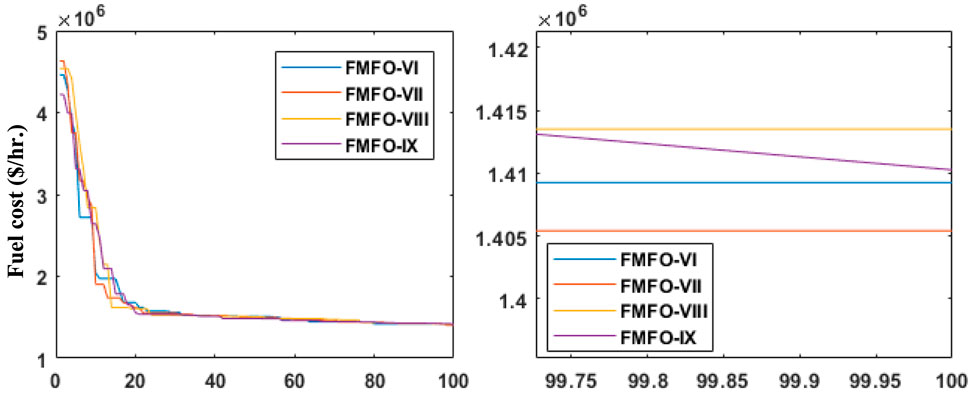
FIGURE 8. Comparing the learning curves of the proposed FMFO algorithm for the best fractional orders in case of the Korean 140-generating-unit test system.

TABLE 8. Comparative analysis of the proposed FMFO algorithm for the Korean 140-generating-unit test system with state-of-the-art algorithms from the literature.
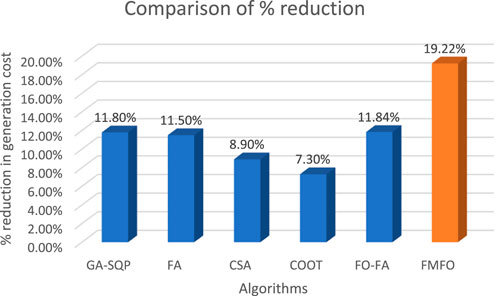
FIGURE 9. Comparison of percentage reduction in the fuel cost of the proposed FMFO algorithm for the Taiwan 40-generating-unit test system with state-of-the-art algorithms from the literature.
6 Statistical analysis
The stability, accuracy, and robustness of the proposed scheme are evaluated by 100 independent trials for each variation in fractional order inside the FMFO algorithm for all three test systems of the ILD problem. The statistical results for ILD case study A are shown in Figures 10A,D, while the results for ILD case study B can be found in Figures 10B,E. Similarly, the statistical results for ILD case study C are displayed in Figures 10C,F. The accuracy of the suggested scheme is confirmed by examining empirical cumulative distribution function plots of the planned technique for optimal values in fractional-order magnitudes, which demonstrate a probability of independent trials above 0.8. Additionally, to further validate the robustness of the suggested approach, boxplots are generated. The results of this study illustrate the efficacy of the scheme by examining the central tendencies of box plots, which are free from any extreme values and reveal median values that closely align with the mean. Each of these illustrations provides evidence supporting the appropriateness of the envisioned solution to the ILD issue.
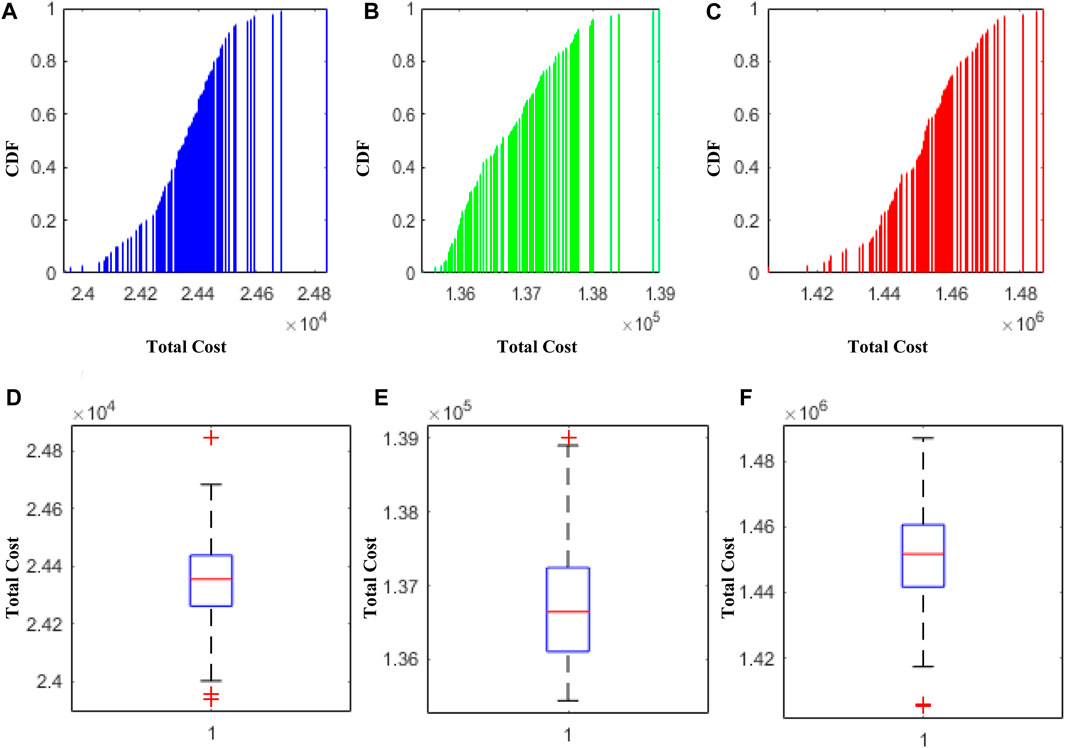
FIGURE 10. Statistical analysis of the proposed FMFO algorithm in terms of CDF. (A) CDF: FMFO-I for case study A. (B) CDF: FMFO-IX for case study B. (C) CDF: FMFO-VII for case study C. (D) Boxplot: FMFO-I for case study A. (E) Boxplot: FMFO-IX for case study B. (F) Boxplot: FMFO-VII for case study C.
7 Discussion and limitations
The implementation of the FMFO algorithm in blockchain smart contracts exemplifies the convergence of sophisticated optimization techniques in a synergistic manner. The fractal-order dynamics that are intrinsic to FMFO provide improved capabilities for exploration and exploitation, thereby facilitating more efficient optimization of the ELD problem. The integration of FMFO into blockchain smart contracts enhances the transparency, immutability, and decentralization of the optimization process. This promotes stakeholder confidence and guarantees the security and integrity of the optimization results. Furthermore, the use of blockchain smart contracts brings about enhanced levels of transparency, traceability, and responsibility to the process of optimizing energy load dispatch. The unchangeable and resistant to tampering characteristics of blockchain technology improve the ability to confirm optimization outcomes, reducing concerns about the integrity of data and faith in centralized optimization authority. Smart contracts enable the automatic implementation and enforcement of optimization criteria, simplifying the energy dispatch processes and decreasing operating costs. Moreover, the use of FOPSO in blockchain smart contracts shows potential for promoting innovations in energy market processes and grid management techniques. Smart contracts enabled by FMFO provide real-time optimization and dynamic modification of energy loads, resulting in enhanced resource utilization, decreased energy expenses, and enhanced grid stability. Blockchain technology’s decentralized nature enables peer-to-peer energy trading, decentralized energy marketplaces, and demand-side management programs. This empowers consumers and prosumers to actively engage in the energy ecosystem.
The FMFO performance is highly influenced by parameter configurations, such as fractional-order settings, inertial weights, and accelerating coefficients. Inadequate parameter settings might result in early convergence, lack of progress, or fluctuating behavior, requiring meticulous adjustment and optimization. Blockchain technology has intrinsic advantages when it comes to transparency and security, but it also brings about additional costs in regards to processing, storage, and communication. Storing and running smart contracts on the blockchain results in resource expenses and needs agreement among network members, thereby impacting the scalability and cost-efficiency of the optimization solution. Blockchain smart contracts function on a clear and unchangeable record, which gives rise to worries about the privacy and confidentiality of data, especially in sensitive areas like energy management. It is crucial to include privacy-preserving methods in smart contracts while also maintaining openness and auditability in order to solve these issues.
8 Conclusion
A novel optimization approach called the FMFO is proposed to address the challenges of economic load dispatch problems including stochastic wind power generation and inequity generator capacity constraints, while ensuring power balance. Using a hybrid system with thermal and wind power plans, FMFO’s ability to identify the lowest possible generating cost was investigated. Three separate test systems including 13 generating units, Taiwan 40 generating units, and Korean 140 generating unit test systems were optimized to reduce fuel generation cost as the objective function using the proposed optimization approach. FMFO was compared to various optimization algorithms that have been used in the past for the same issue, both in terms of its rate of convergence and the final optimized value it supplied. The tests on three different systems, including a large-scale Korean electricity network, all revealed that FMFO performed best. In case study A, the fuel cost calculated by FMFO is 3.6% lower than that in the base case. In contrast, the solvers GA-SQP, FA, PSO, CSA, and FO-FA achieve fuel cost reductions of 3.21%, 0.76%, 2%, 2.6%, and 2.3%, respectively. In case study B, specifically the Taiwan 40-generating-unit test system, the fuel cost calculated by FMFO is 5.67% lower than that in the base case. In comparison, other solvers such as HIC-SQP, PWTED1, DWTED1, GA-SQP, PSO, and COOT achieve fuel cost reductions of 5%, 3.9%, 4.45%, 4.8%, 3.19%, and 3.2%, respectively. In case study C, which involves a test system with 140 generating units, the fuel cost calculated using FMFO is $1,405,421.20 per hour. This represents a reduction of 19.22% compared to the base case. In contrast, other solvers such as GA-SQP, FA, CSA, COOT, and FO-FA achieve fuel cost reductions of 11.8%, 11.5%, 8.9%, 7.3%, and 11.84%, respectively. The consistency and stability of the FMFO are confirmed by statistical analysis, which involves examining the minimum values for fitness over 100 separate trials. Additionally, empirical CDF and box-plotting depictions are used to quantify the variance and central tendency of the lowest fitness values for solving ELD issues. The statistical data analysis of various situations of ELD demonstrates that FMFO is a dependable and efficient alternative optimization strategy in the energy sector as it exhibits stability, robustness, and consistency.
Fractional swarming, an evolutionary computing paradigm, may soon replace traditional simulations for multi-model, non-linear optimization problems such as rigorous wind speed forecasting, multi-objective routing problems, parameter estimation for photovoltaic cells, and active noise control over distributed networks. Further exploration into the efficacy of the power system requires including the future renewable energy generating (REG) components and using them in both steady and dynamic modes. The selection of an appropriate fractional order in FMFO with respect to the underlying rationale of the physics seems to hold promise for further exploration into a novel optimization problem.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
BK: writing–original draft, visualization, validation, writing–review and editing, methodology, and conceptualization. AQ: visualization, validation, supervision, investigation, funding acquisition, and writing–review and editing. AW: writing–review and editing, methodology, conceptualization, visualization, and validation. KA: writing–review and editing, resources, investigation, formal analysis, and data curation. AA-S: writing–review and editing, resources, project administration, investigation, and data curation.
Funding
The authors declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (grant number IMSIURG23022).
Acknowledgments
The authors appreciate the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) for supporting and supervising this project.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abbassi, R., Abbassi, A., Heidari, A. A., and Mirjalili, S. (2019). An efficient salp swarm-inspired algorithm for parameters identification of photovoltaic cell models. Energy Convers. Manag. 179, 362–372. doi:10.1016/j.enconman.2018.10.069
AlSkaif, T., and Van Leeuwen, G. (2019). “Decentralized optimal power flow in distribution networks using blockchain,” in 2019 International Conference on Smart Energy Systems and Technologies (SEST), Porto, Portugal, September, 2019 (IEEE), 1–6.
Alzubi, Q. M., Anbar, M., Alqattan, Z. N., Al-Betar, M. A., and Abdullah, R. (2020). Intrusion detection system based on a modified binary grey wolf optimisation. Neural Comput. Appl. 32, 6125–6137. doi:10.1007/s00521-019-04103-1
Aoki, K., Fan, M., and Nishikori, A. (1988). Optimal VAR planning by approximation method for recursive mixed-integer linear programming. IEEE Trans. power Syst. 3 (4), 1741–1747. doi:10.1109/59.192990
Ates, A., Alagoz, B. B., Kavuran, G., and Yeroglu, C. (2017). Implementation of fractional order filters discretized by modified fractional order darwinian particle swarm optimization. Measurement 107, 153–164. doi:10.1016/j.measurement.2017.05.017
Ates, A., Kavuran, G., Alagoz, B. B., and Yeroglu, C. (2016). “Improvement of IIR filter discretization for fractional order filter by discrete stochastic optimization,” in 2016 39th International Conference on Telecommunications and Signal Processing (TSP), Vienna, Austria, June, 2016, 583–586.
Azar, A. T., and Serrano, F. E. (2018). “Fractional order sliding mode PID controller/observer for continuous nonlinear switched systems with PSO parameter tuning,” in International conference on advanced machine learning technologies and applications, Cairo, Egypt, January, 2018, 13–22.
Balamurugan, K., Muralisachithnndam, R., and Krishnan, S. R. (2014). Differential evolution based solution for combined economic and emission power dispatch with valve loading effect. Int. J. Electr. Eng. Inf. 6 (1), 74–92. doi:10.15676/ijeei.2014.6.1.6
Chantar, H., Mafarja, M., Alsawalqah, H., Heidari, A. A., Aljarah, I., and Faris, H. (2020). Feature selection using binary grey wolf optimizer with elite-based crossover for Arabic text classification. Neural Comput. Appl. 32, 12201–12220. doi:10.1007/s00521-019-04368-6
Chopra, L., and Kaur, R. (2012a). Economic load dispatch using simple and refined genetic algorithm. Int. J. Adv. Eng. Technol. 5 (1), 584–590.
Chopra, L., and Kaur, R. (2012b). Economic load dispatch using simple and refined genetic algorithm. Int. J. Adv. Eng. Technol. 5 (1), 584–590.
Couceiro, M. S., Rocha, R. P., Ferreira, N. F., and Machado, J. T. (2012a). Introducing the fractional-order darwinian PSO. Signal, Image Video Process. 6 (3), 343–350. doi:10.1007/s11760-012-0316-2
Couceiro, M. S., Rocha, R. P., Ferreira, N. F., and Machado, J. T. (2012b). Introducing the fractional-order darwinian PSO. Signal, Image Video Process. 6 (3), 343–350. doi:10.1007/s11760-012-0316-2
Decker, G. L., and Brooks, A. D. (1958). Valve point loading of turbines. Trans. Am. Inst. Electr. Eng. Part III Power Apparatus Syst. 77 (3), 501–484. doi:10.1109/ee.1958.6445133
Deeb, N. I., and Shahidehpour, S. M. (1988). An efficient technique for reactive power dispatch using a revised linear programming approach. Electr. power Syst. Res. 15 (2), 121–134. doi:10.1016/0378-7796(88)90016-8
Dehghani, M., Riahi-Madvar, H., Hooshyaripor, F., Mosavi, A., Shamshirband, S., Zavadskas, E. K., et al. (2019). Prediction of hydropower generation using grey wolf optimization adaptive neuro-fuzzy inference system. Energies 12 (2), 289. doi:10.3390/en12020289
Durairaj, S., Kannan, P. S., and Devaraj, D. (2005). Application of genetic algorithm to optimal reactive power dispatch including voltage stability constraint. J. Energy & Environ. 4 (63), 7.
El-Fergany, A. A., Hasanien, H. M., and Agwa, A. M. (2019). Semi-empirical PEM fuel cells model using whale optimization algorithm. Energy Convers. Manag. 201, 112197. doi:10.1016/j.enconman.2019.112197
Fahad, M., Aadil, F., Khan, S., Shah, P. A., Muhammad, K., Lloret, J., et al. (2018). Grey wolf optimization based clustering algorithm for vehicular ad-hoc networks. Comput. Electr. Eng. 70, 853–870. doi:10.1016/j.compeleceng.2018.01.002
Faris, H., Aljarah, I., Al-Betar, M. A., and Mirjalili, S. (2018). Grey wolf optimizer: a review of recent variants and applications. Neural Comput. Appl. 30, 413–435. doi:10.1007/s00521-017-3272-5
Fathy, A. (2020). Butterfly optimization algorithm based methodology for enhancing the shaded photovoltaic array extracted power via reconfiguration process. Energy Convers. Manag. 220, 113115. doi:10.1016/j.enconman.2020.113115
Ghamisi, P., Couceiro, M. S., and Benediktsson, J. A. (2013a), Classification of hyperspectral images with binary fractional order Darwinian PSO and random forests, Image signal Process. remote Sens. XIX, 8892, 215–222.
Ghamisi, P., Couceiro, M. S., and Benediktsson, J. A. (2014). A novel feature selection approach based on FODPSO and SVM. IEEE Trans. Geoscience Remote Sens. 53 (5), 2935–2947. doi:10.1109/tgrs.2014.2367010
Ghamisi, P., Couceiro, M. S., Martins, F. M., and Benediktsson, J. A. (2013b). Multilevel image segmentation based on fractional-order Darwinian particle swarm optimization. IEEE Trans. Geoscience Remote Sens. 52 (5), 2382–2394. doi:10.1109/tgrs.2013.2260552
Górski, T. (2022). Reconfigurable smart contracts for renewable energy exchange with Re-use of verification rules. Appl. Sci. 12 (11), 5339. doi:10.3390/app12115339
Granville, S. (1994). Optimal reactive dispatch through interior point methods. IEEE Trans. power Syst. 9 (1), 136–146. doi:10.1109/59.317548
Hu, Y., Liu, K., Zhang, X., Su, L., Ngai, E. W. T., and Liu, M. (2015). Application of evolutionary computation for rule discovery in stock algorithmic trading: a literature review. Appl. Soft Comput. 36, 534–551. doi:10.1016/j.asoc.2015.07.008
Jangir, P., Manoharan, P., Pandya, S., and Sowmya, R. (2023). MaOTLBO: many-objective teaching-learning-based optimizer for control and monitoring the optimal power flow of modern power systems. Int. J. Industrial Eng. Comput. 14 (2), 293–308. doi:10.5267/j.ijiec.2023.1.003
Jeddi, B., and Vahidinasab, V. (2014). A modified harmony search method for environmental/economic load dispatch of real-world power systems. Energy Convers. Manag. 78, 661–675. doi:10.1016/j.enconman.2013.11.027
Jiang, S., Ji, Z., and Wang, Y. (2015). A novel gravitational acceleration enhanced particle swarm optimization algorithm for wind–thermal economic emission dispatch problem considering wind power availability. Int. J. Electr. Power & Energy Syst. 73, 1035–1050. doi:10.1016/j.ijepes.2015.06.014
Kabolia, S. H. A. (2023). A rain-fall inspired optimization algorithm for optimal load dispatch in power system. United States: Nova Science Publishers.
Katal, N., and Narayan, S. (2017). Design of robust fractional order PID controllers for coupled tank systems using multi-objective particle swarm optimisation. Int. J. Syst. Control Commun. 8 (3), 250–267. doi:10.1504/ijscc.2017.10006533
Khan, B. S., Raja, M. A. Z., Qamar, A., and Chaudhary, N. I. (2021). Design of moth flame optimization heuristics for integrated power plant system containing stochastic wind. Appl. Soft Comput. 104, 107193. doi:10.1016/j.asoc.2021.107193
Kirli, D., Couraud, B., Robu, V., Salgado-Bravo, M., Norbu, S., Andoni, M., et al. (2022). Smart contracts in energy systems: a systematic review of fundamental approaches and implementations. Renew. Sustain. Energy Rev. 158, 112013. doi:10.1016/j.rser.2021.112013
Kosari, M., and Teshnehlab, M. (2018). Non-linear fractional-order chaotic systems identification with approximated fractional-order derivative based on a hybrid particle swarm optimization-genetic algorithm method. J. AI Data Min. 6 (2), 365–373.
Kuttomparambil Abdulkhader, H., Jacob, J., and Mathew, A. T. (2018). Fractional-order lead-lag compensator-based multi-band power system stabiliser design using a hybrid dynamic GA-PSO algorithm. IET Generation, Transm. Distribution 12 (13), 3248–3260. doi:10.1049/iet-gtd.2017.1087
Łegowski, A., and Niezabitowski, M. (2016). “Robot path control based on PSO with fractional-order velocity,” in 2016 International Conference on Robotics and Automation Engineering (ICRAE), Jeju, Korea (South), August, 2016, 21–25.
Li, X., Wang, Y., Li, N., Han, M., Tang, Y., and Liu, F. (2017). Optimal fractional order PID controller design for automatic voltage regulator system based on reference model using particle swarm optimization. Int. J. Mach. Learn. Cybern. 8, 1595–1605. doi:10.1007/s13042-016-0530-2
Liu, T., Xiong, G., Mohamed, A. W., and Suganthan, P. N. (2022). Opposition-mutual learning differential evolution with hybrid mutation strategy for large-scale economic load dispatch problems with valve-point effects and multi-fuel options. Inf. Sci. 609, 1721–1745. doi:10.1016/j.ins.2022.07.148
Liu, X., and Xu, W. (2010). Minimum emission dispatch constrained by stochastic wind power availability and cost. IEEE Trans. Power Syst. 25 (3), 1705–1713. doi:10.1109/tpwrs.2010.2042085
Lo, K. L., and Zhu, S. P. (1991). A decoupled quadratic programming approach for optimal power dispatch. Electr. power Syst. Res. 22 (1), 47–60. doi:10.1016/0378-7796(91)90079-3
Machado, J. T., and Kiryakova, V. (2017). The chronicles of fractional calculus. Fract. Calc. Appl. Analysis 20 (2), 307–336. doi:10.1515/fca-2017-0017
Mehmood, A., Raja, M. A. Z., and Jalili, M. (2023). Optimization of integrated load dispatch in multi-fueled renewable rich power systems using fractal firefly algorithm. Energy 278, 127792. doi:10.1016/j.energy.2023.127792
Mirjalili, S. (2015). Moth-flame optimization algorithm: a novel nature-inspired heuristic paradigm. Knowledge-based Syst. 89, 228–249. doi:10.1016/j.knosys.2015.07.006
Mirjalili, S., Mirjalili, S. M., and Lewis, A. (2014). Grey wolf optimizer. Adv. Eng. Softw. 69, 46–61. doi:10.1016/j.advengsoft.2013.12.007
Mohseni, S., Brent, A. C., and Burmester, D. (2019). A demand response-centred approach to the long-term equipment capacity planning of grid-independent micro-grids optimized by the moth-flame optimization algorithm. Energy Convers. Manag. 200, 112105. doi:10.1016/j.enconman.2019.112105
Morshed, M. J., and Asgharpour, A. (2014a). Hybrid imperialist competitive-sequential quadratic programming (HIC-SQP) algorithm for solving economic load dispatch with incorporating stochastic wind power: a comparative study on heuristic optimization techniques. Energy Convers. Manag. 84, 30–40. doi:10.1016/j.enconman.2014.04.006
Morshed, M. J., and Asgharpour, A. (2014b). Hybrid imperialist competitive-sequential quadratic programming (HIC-SQP) algorithm for solving economic load dispatch with incorporating stochastic wind power: a comparative study on heuristic optimization techniques. Energy Convers. Manag. 84, 30–40. doi:10.1016/j.enconman.2014.04.006
Naderi, E., Azizivahed, A., Narimani, H., Fathi, M., and Narimani, M. R. (2017). A comprehensive study of practical economic dispatch problems by a new hybrid evolutionary algorithm. Appl. Soft Comput. 61, 1186–1206. doi:10.1016/j.asoc.2017.06.041
Nappu, M. B., Arief, A., and Ajami, W. A. (2023). Energy efficiency in modern power systems utilizing advanced incremental particle swarm optimization–based OPF. Energies 16 (4), 1706. doi:10.3390/en16041706
Neto, J. X. V., Reynoso-Meza, G., Ruppel, T. H., Mariani, V. C., and dos Santos Coelho, L. (2017). Solving non-smooth economic dispatch by a new combination of continuous GRASP algorithm and differential evolution. Int. J. Electr. Power & Energy Syst. 84, 13–24. doi:10.1016/j.ijepes.2016.04.012
Nimma, K. S., Al-Falahi, M. D., Nguyen, H. D., Jayasinghe, S. D. G., Mahmoud, T. S., and Negnevitsky, M. (2018). Grey wolf optimization-based optimum energy-management and battery-sizing method for grid-connected microgrids. Energies 11 (4), 847. doi:10.3390/en11040847
Paliwal, K. K., Singh, S., and Gaba, P. (2017). “Feature selection approach of hyperspectral image using GSA-FODPSO-SVM,” in 2017 International Conference on Computing, Communication and Automation (ICCCA), Greater Noida, India, May, 2017 (IEEE), 1070–1075.
Pandey, V. C., Jadoun, V. K., Gupta, N., Niazi, K. R., and Swarnkar, A. (2018). Improved fireworks algorithm with chaotic sequence operator for large-scale non-convex economic load dispatch problem. Arabian J. Sci. Eng. 43, 2919–2929. doi:10.1007/s13369-017-2956-6
Pandit, M., Chaudhary, V., Dubey, H. M., and Panigrahi, B. K. (2015). Multi-period wind integrated optimal dispatch using series PSO-DE with time-varying Gaussian membership function based fuzzy selection. Int. J. Electr. power & energy Syst. 73, 259–272. doi:10.1016/j.ijepes.2015.05.017
Raja, M. A. Z., Ahmed, U., Zameer, A., Kiani, A. K., and Chaudhary, N. I. (2019). Bio-inspired heuristics hybrid with sequential quadratic programming and interior-point methods for reliable treatment of economic load dispatch problem. Neural Comput. Appl. 31, 447–475. doi:10.1007/s00521-017-3019-3
Sabatier, J. A. T. M. J., Agrawal, O. P., and Machado, J. T. (2007). Advances in fractional calculus. Dordrecht: Springer.
Salgotra, R., Singh, U., and Sharma, S. (2020). On the improvement in grey wolf optimization. Neural Comput. Appl. 32, 3709–3748. doi:10.1007/s00521-019-04456-7
Sattar, M. K., Ahmad, A., Fayyaz, S., Ul Haq, S. S., and Saddique, M. S. (2020). Ramp rate handling strategies in dynamic economic load dispatch (DELD) problem using grey wolf optimizer (GWO). J. Chin. Inst. Eng. 43 (2), 200–213. doi:10.1080/02533839.2019.1694446
Shahri, E. S. A., Alfi, A., and Machado, J. T. (2019). Fractional fixed-structure H∞ controller design using augmented Lagrangian particle swarm optimization with fractional order velocity. Appl. Soft Comput. 77, 688–695. doi:10.1016/j.asoc.2019.01.037
Shakarami, M. R., and Davoudkhani, I. F. (2016). Wide-area power system stabilizer design based on grey wolf optimization algorithm considering the time delay. Electr. Power Syst. Res. 133, 149–159. doi:10.1016/j.epsr.2015.12.019
Teodoro, G. S., Machado, J. T., and De Oliveira, E. C. (2019). A review of definitions of fractional derivatives and other operators. J. Comput. Phys. 388, 195–208. doi:10.1016/j.jcp.2019.03.008
Ullah, Z., Wang, S., Wu, G., Hasanien, H. M., Jabbar, M. W., Qazi, H. S., et al. (2022). Advanced studies for probabilistic optimal power flow in active distribution networks: a scientometric review. IET Generation, Transm. Distribution 16 (18), 3579–3604. doi:10.1049/gtd2.12555
Wang, Y. Y., Peng, W. X., Qiu, C. H., Jiang, J., and Xia, S. R. (2019). Fractional-order Darwinian PSO-based feature selection for media-adventitia border detection in intravascular ultrasound images. Ultrasonics 92, 1–7. doi:10.1016/j.ultras.2018.06.012
Wang, Y. Y., Zhang, H., Qiu, C. H., and Xia, S. R. (2018). A novel feature selection method based on extreme learning machine and fractional-order Darwinian PSO. Comput. Intell. Neurosci. 2018, 1–8. doi:10.1155/2018/5078268
Yang, B., Wang, J., Zhang, X., Yu, T., Yao, W., Shu, H., et al. (2020). Comprehensive overview of meta-heuristic algorithm applications on PV cell parameter identification. Energy Convers. Manag. 208, 112595. doi:10.1016/j.enconman.2020.112595
Yokoya, N., and Ghamisi, P. (2016). “Land-cover monitoring using time-series hyperspectral data via fractional-order darwinian particle swarm optimization segmentation,” in 2016 8th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Los Angeles, CA, USA, August, 2016 (IEEE), 1–5.
Younesi, A., Shayeghi, H., Wang, Z., Siano, P., Mehrizi-Sani, A., and Safari, A. (2022). Trends in modern power systems resilience: state-of-the-art review. Renew. Sustain. Energy Rev. 162, 112397. doi:10.1016/j.rser.2022.112397
Zhang, H., Heidari, A. A., Wang, M., Zhang, L., Chen, H., and Li, C. (2020). Orthogonal Nelder-Mead moth flame method for parameters identification of photovoltaic modules. Energy Convers. Manag. 211, 112764. doi:10.1016/j.enconman.2020.112764
Zhang, J., Wu, Y., Guo, Y., Wang, B., Wang, H., and Liu, H. (2016). A hybrid harmony search algorithm with differential evolution for day-ahead scheduling problem of a microgrid with consideration of power flow constraints. Appl. energy 183, 791–804. doi:10.1016/j.apenergy.2016.09.035
Zhang, Q., Zou, D., Duan, N., and Shen, X. (2019). An adaptive differential evolutionary algorithm incorporating multiple mutation strategies for the economic load dispatch problem. Appl. Soft Comput. 78, 641–669. doi:10.1016/j.asoc.2019.03.019
Zhu, Q., Yuan, M., Liu, Y. L., Chen, W. D., Chen, Y., and Wang, H. R. (2014a). Research and application on fractional-order Darwinian PSO based adaptive extended Kalman filtering algorithm. IAES Int. J. Robotics Automation 3 (4), 245. doi:10.11591/ijra.v3i4.6014
Keywords: stochastic wind, Weibull distribution, blockchain smart contracts, integrated load dispatch, fractional calculus, moth flame optimization
Citation: Khan BS, Qamar A, Wadood A, Almuhanna K and Al-Shamma AA (2024) Integrating economic load dispatch information into the blockchain smart contracts based on the fractional-order swarming optimizer. Front. Energy Res. 12:1350076. doi: 10.3389/fenrg.2024.1350076
Received: 05 December 2023; Accepted: 21 February 2024;
Published: 19 March 2024.
Edited by:
Fazal Akbar, University of Edinburgh, United KingdomReviewed by:
Tomasz Górski, University of Gdansk, PolandHafeez Anwar, National University of Sciences and Technology (NUST), Pakistan
Copyright © 2024 Khan, Qamar, Wadood, Almuhanna and Al-Shamma. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Affaq Qamar, YWFxYW1hckBpbWFtdS5lZHUuc2E=; Abdul Wadood, d2Fkb29kQHV0LmVkdS5zYQ==
 Babar Sattar Khan
Babar Sattar Khan Affaq Qamar
Affaq Qamar Abdul Wadood
Abdul Wadood Khalid Almuhanna3
Khalid Almuhanna3