Stackelberg game-based optimal electricity trading method for distribution networks with small-micro industrial parks

In order to improve the operating benefits of the distribution network (DN) and reduce the energy consumption costs of small-micro industrial parks (SMIPs), a two-layer optimal electricity trading method for DN with SMIPs is proposed. First, based on the Stackelberg game, a multi-objective two-layer optimal trading model for DN and SMIP is established. In the upper layer, the DN agent is regarded as the leader, and a trading model is established with the goal of maximizing the profits of agents. In the lower layer, an energy optimization model is proposed for the SMIP operators, which are regarded as the followers, with the goal of minimizing the operating costs. According to the buying and selling electricity prices at the upper and lower layers, a dynamic pricing strategy is formulated. The Karush–Kuhn–Tucker condition (KKT) is introduced to transform the two-layer model into a single-layer model, and based on linear transformations, the model is further converted into a mixed-integer linear programming model. The transformations aim to address the non-linear issues arising from multivariable coupling between the upper and lower-layer trading models. The simulation results show that the trading strategy proposed in this paper can effectively increase the profit of DNs while reducing the operating costs of SMIPs and can provide a reference for decision-making in the electricity market (EM) with the participation of SMIP.

1 Introduction

In recent years, small and micro enterprises have developed rapidly in Zhejiang Province, China. In order to facilitate the prosperous development of such enterprises, Zhejiang Province has standardized and renovated the existing small-micro industrial parks (SMIPs) based on the actual operation. However, the SMIPs do not dispatch enough power generation and energy storage (ES) devices, which results in a low capacity to withstand the operating risks. With the rapid development of SMIPs, the demand for electricity trading between SMIPs and distribution networks (DNs) is constantly increasing. On one hand, trading electricity with the DNs can help the SMIPs to withstand the operating risks. On the other hand, an optimal trading electricity strategy can help the SMIPs to save the operating costs. Then, how to optimize the electricity trading between the DNs and SMIPs is currently a highly important issue (He et al., 2021).

As the electricity market (EM) continues to expanding, the operators and agents in the DNs gradually participate in EM competition (Jin et al., 2022), and the economic operation of the DNs has been significantly improved (Li et al., 2023a). A market simulator for peer-to-peer electricity trading is proposed in Kuno et al. (2022), and a market agent is designed to perform power bidding and contract processing. Guo et al. (2022) showed that all agents can freely trade in an asynchronous mode without waiting for idle or inactive neighboring agents, and the sublinear regret upper bound is proved for the asynchronous mode, which can maximize the social welfare in the EM. A real-time congestion management strategy is applied by Klsch et al. (2022), and the strategy can enable grid-supportive operation of the operators without interventions. Considering the characteristic that natural gas can blend with hydrogen, Ding et al. (2023) proposed a multi-agent electricity–heat–hydrogen trading model by taking hydrogen produced on the load side. Tan et al. (2022) treated carbon as a direct trading object and proposed an internal multi-energy trading mechanism, which adopts an auction based on the demands for cooling, heating, electricity, and carbon. To further explore the multi-energy coupling capacity and carbon reduction potential of the integrated energy systems, Yang M. et al. (2023) proposed a cooling–heat–electricity–gas collaborative optimization model of integrated energy systems, given the ladder carbon trading mechanism and multi-energy demand response. Li Z. et al. (2023) proposed a medium-term, multi-stage, distributionally robust optimization scheduling approach for the price-taking of hydro–wind–solar complementary systems in the EM. A multi-agent deep reinforcement learning approach combining the multi-agent actor-critic algorithm with the twin-delayed deep deterministic policy gradient algorithm is proposed by Chen et al. (2022), and the proposed approach can handle the high-dimensional continuous action space and aligns with the nature of peer-to-peer energy trading. Yang et al. (2022) analyzed the impact of different bidding decisions on the distribution of wind farm revenues in a process where the interest of two markets is played against each other. Khaligh et al. (2022) introduced a stochastic agent-based model for the coordinated scheduling of multi-vector microgrids, considering interactions between electricity, hydrogen, and gas agents. Considering the power loss, flexible load demand, and other operating indicators, to maximize the user and supplier benefits, the real-time transaction electricity price model of the user side and the power supply side is constructed by Lyu et al. (2022). In order to meet the challenge of global low-carbon development, a multi-objective optimal scheduling model considering the participation of the park-level integrated energy system in the EM is proposed by Wang L. et al. (2022), which takes into account multiple uncertainties on the renewable energy and load. Li et al. (2023c) analyzed the impact of uncertainties for the multi-energy virtual power plant on the peak-regulation market, and the operation mechanism for the multi-energy virtual power plant in the peak-regulation market is proposed by considering the integrated demand response. As a user-side system, SMIPs can participate in electricity trading under the management of SMIP operators (Davoudi and Moeini-Aghtaie, 2022), which can develop the hierarchical structure of the EM (Pownall et al., 2021). Meanwhile, the agents in DNs can link the SMIP with EM (Anwar et al., 2022), which exerts a significant influence on the energy costs of such parks (Yuan et al., 2022). As SMIPs participate in electricity trading, how to balance the benefits between agents and operators, achieve the expected profit of agents, and reduce the operating costs of operators has become a key concern in current EM.

Different stakeholders have different optimization goals in EM trading (Xiao et al., 2021), and a coupling relationship exists among the EM trading models (Yang et al., 2021). Finding the balanced benefits in EM trading has become a key way to keep the stability of the alliances (Cao et al., 2021). To find the balanced benefits in EM trading, Stackelberg game theory has become an effective tool (Li et al., 2022). To solve the inherent conflict among the players, a Stackelberg game-based technique is proposed by Haghifam et al. (2020), and the distribution system operator attempts to minimize its operating costs as the leader, while the distributed energy resource aggregator tends to maximize its profit as the follower. Huang et al. (2022) proposed a Stackelberg game-based optimization model for energy service providers and integrated energy systems based on the collaborative optimization of integrated energy systems and carbon transaction cost, where the energy service provider acts as a leader while the integrated energy systems serve as followers. A Stackelberg game model between the load aggregator and distribution system operator was proposed by Xu et al. (2022); the distribution system operator issues subsidies to decrease the frequency of voltage violations, and the load aggregator schedules the demand to maximize profits. A trading model based on the Stackelberg game model was proposed by Wei et al. (2022) to balance the interests of the supply side and demand side and reduce carbon emissions. To solve the problems of environmental pollution and conflict of interests among multiple stakeholders in the integrated energy system, Wang R. et al. (2022) proposed a novel collaborative optimization strategy for a low-carbon economy in the integrated energy system based on the carbon trading mechanism and Stackelberg game theory. Envelope et al. (2022) proposed a Stackelberg game-based optimal scheduling model for electro-thermal integrated energy systems, which seeks to maximize the revenue of the integrated energy operator and minimize the cost of users. Pu et al. (2023) constructed a two-stage supply chain consisting of a manufacturer and a retailer based on the dual-credit policy, considered three different power structure models, including the vertical Nash game model, the manufacturer Stackelberg game model, and the retailer Stackelberg game model, and explored the operational strategy issues of new energy vehicle enterprises under the dual-credit policy. Zhang et al. (2022) took the integrated energy system operator as the leader and each integrated energy system as the follower to construct the Stackelberg operation model, and the proposed model is constructed and solved by the double mutation differential evolution algorithm. Hua et al. (2023) proposed a framework of local energy markets to manage this transactive energy and facilitate the flexibility provision; the decision-making and interactions between a DN operator and multiple microgrid traders are formulated as the Stackelberg game-theoretic problem. Fattaheian et al. (2022) applied the Stackelberg game to model incentivizing resource scheduling optimization in post-contingency conditions, and a strong duality condition is used to re-cast the preliminary bi-level model into a one-level mathematical problem. The pricing strategies in existing research studies mainly belong to fixed pricing mechanisms (Du et al., 2022). In the future, as more SMIPs participate in EM trading, the fixed pricing mechanisms will not be satisfied to the flexible EM model. In this context, studying the dynamic pricing strategies for DN trading with SMIPs to enhance the economic operation of DNs is highly necessary.

As described previously, a two-layer optimal electricity trading method for DNs with SMIPs is proposed based on the Stackelberg game. The main contributions of this paper are summarized as follows.

(1) A two-layer optimization trading model is established for DNs and SMIPs, and the competitive game relationship between different stakeholders in the trading process is characterized by the Stackelberg game. The paper shows that through the proposed scheme, the profit of DNs increases by 14.8% in a typical day, and the operating costs of SMIPs decreased by 2.5% and 3.8%, respectively.

(2) The Karush–Kuhn–Tucker (KKT) condition and linear relaxation technique are utilized to transform the proposed non-linear model into a mixed-integer linear programming model. This method solves the coupling–nesting problem of interactive power and electricity price in the proposed model without any approximation.

(3) To address the disadvantage of fixed pricing mechanisms, a dynamic pricing strategy is formulated in this paper. The DN agent sets the dynamic prices to lead the trading behavior of SMIP operators, and the SMIP operators choose the trading time to follow the guidance of the DN agent without passive price reception. Then, the overall profits of both the DN agent and SMIP operators are greatly improved.

The remainder of this paper is organized as follows. A two-layer game optimization trading framework for multi-stakeholders is proposed in Section 2. In addition, a two-layer game optimization trading model based on the Stackelberg game is proposed in Section 3. In Section 4, the solution process of the proposed model is introduced. In Section 5, the case study is analyzed. The discussion and conclusion are described in Section 6.

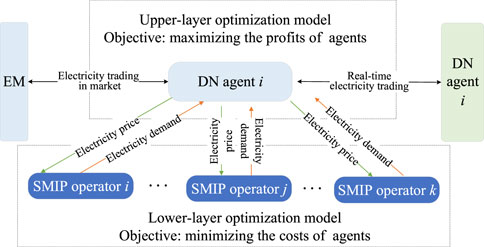
2 Two-layer optimization trading framework

In order to improve the operating benefits of DN and reduce the energy costs of SMIPs, a two-layer optimization trading framework for multi-stakeholders is established, as shown in Figure 1.

FIGURE 1

FIGURE 1. Two-layer trading model framework.

In the trading framework, the stakeholders include the EM, DN agent, and SMIP operators. The trading framework is divided into two layers, with EM and DN agent located in the upper layer and SMIP operators located in the lower layer. The stakeholders in the upper and lower layers have different benefits goals, and they mutually influence each other. In the upper layer, the DN agent makes decisions on the volume of purchased electricity or sold electricity based on the needs of EM and SMIPs. If EM supply cannot meet the demand, electricity trading occurs between two adjacent DN agents. Additionally, the DN agent will use dynamic trading prices to encourage the trading of lower-layer SMIP operators. In the lower layer, SMIP operators will dynamically adjust the outputs of internal generation units based on the trading prices set by DN agents, as well as the electricity demand on the user side. Simultaneously, SMIP operators provide real-time feedback to the upper layer DN agents regarding the electricity usage strategies. DN agents, based on the energy consumption situation, dynamically adjust the trading prices. Through the iterative process between the upper and lower layers, a balance point that aligns with the interests of both stakeholders is ultimately determined.

3 Two-layer optimization trading model based on the Stackelberg game

3.1 Upper-layer optimization model for the DN agent

In two-layer game optimization trading, the DN agent is regarded as the leader of the Stackelberg game (Liu et al., 2023), and an optimization model with the goal of maximizing profits is established for the DN agent.

$\max \left[{\displaystyle \sum _t}{c}_t^{\text{sell}}{P}_t^{\text{sell}}\Delta t-{\displaystyle \sum _t}{c}_t^{\text{buy}}{P}_t^{\text{buy}}\Delta t+\left. \left({\displaystyle \sum _t}{\pi }_t^{-}{R}_t^{-}\Delta t-{\displaystyle \sum _t}{\pi }_t^{+}{R}_t^{+}\Delta t-{\displaystyle \sum _t}{\pi }_t{R}_t\Delta t\right)-{\displaystyle \sum _t}{c}_t^{\text{tra}}{P}_t^{\text{sop}}\Delta t\right]\right. .(1)$

The optimization model for DNs mainly imposes constraints on power balance, ES operation, trading of the DN agent, and pricing. The constraints are as follows:

(1) Power balance constraints

$P_t^{\text{buy}}-P_t^{\text{sell}}+R_t+R_t^{+}-R_t^{-}+P_t^{\text{sop}}-E_t+e_t=0.(2)$

(2) ES operation constraints

$\left\{\begin{array}{l}{P}^{\text{ESS},\min }\le E_t\le P^{\text{ESS},\max }\\ P^{\text{ESS},\min }\le e_t\le P^{\text{ESS},\max }\end{array}\right.,(3)$

$S_t^{\text{ESS}}=S_{t-1}^{\text{ESS}}+{\eta }^{\mathrm{E}}{E}_t,(4)$

$S_t^{\text{ESS}}=S_{t-1}^{\text{ESS}}-\frac{e_t}{{\eta }^{\mathrm{e}}}.(5)$

Considering the service life of the ESs, the constraints on the number of ES charging and discharging cycles are shown in Eqs (6) and (7):

$0\le w_t^{\mathrm{E}}+w_t^{\mathrm{e}}\le 1,(6)$

${\displaystyle \sum _{t=1}^{24}}\left|w_t^{\mathrm{E}}-w{w}_{t-1}^{\mathrm{E}}\right|\le \xi .(7)$

(3) Trading constraints of DN agents

The day-ahead market contract electricity quantity and real-time EM trading must meet the constraints of upper and lower limits of trading power, as shown below:

$0\le R_t\le R_t^{\max },(8)$

$\left\{\begin{array}{l}0\le R_t^{+}\le {\kappa }_t^{+}{R}^{\max }\\ 0\le R_t^{-}\le {\kappa }_t^{-}{R}^{\max }\end{array}\right.,(9)$

$0\le {\kappa }_t^{+}+{\kappa }_t^{-}\le 1.(10)$

(4) Pricing constraints

The DN agent formulates dynamic electricity prices to lead trading among SMIP operators. Therefore, it is necessary to impose constraints on pricing as follows:

$\left\{\begin{array}{l}{c}^{\text{buy},\min }\le c_t^{\text{buy}}\le c^{\text{buy},\max },\\ c^{\text{sell},\min }\le c_t^{\text{sell}}\le c^{\text{sell},\max }.\end{array}\right.(11)$

To encourage the active participation of SMIP operators in energy trading, the real-time electricity trading price of the DN agent needs to be constrained by the average value of the electricity price as

${\displaystyle \sum _{t=1}^{\mathrm{T}}}\frac{c_t^{\text{sell}}}{\mathrm{T}}\le c^{\text{av}},(12)$

${\displaystyle \sum _{t=1}^{\mathrm{K}}}\frac{c_t^{\text{buy}}}{\mathrm{K}}\ge c^{\text{av}}.(13)$

3.2 Lower-layer optimization model for SMIP operators

In the lower-layer model, SMIP operators provide real-time feedback to the upper-layer agents based on the electricity trading prices provided by DNs and the real-time energy demands of the users (Lei et al., 2023). The optimization objective is to minimize the operating costs as follows:

$\min \left[{\displaystyle \sum _t}{c}_t^{\text{sell}}{P}_t^{\text{sell}}\Delta t-{\displaystyle \sum _t}{c}_t^{\text{buy}}{P}_t^{\text{buy}}\Delta t+{\displaystyle \sum _t}{\displaystyle \sum _{\mathrm{m}}}{c}^{\mathrm{DEG}}{P}_{m,t}^{\mathrm{DEG}}\Delta t\right].(14)$

The optimization model for the lower-layer SMIP operators mainly imposes constraints on power balance, DEG operation, SMIP operator trading, and opportunity constraints. Each constraint is as follows:

(1) Power balance constraints in the SMIP area:

${\displaystyle \sum _m}{P}_{m,t}^{\mathrm{DEG}}+P_t^{\text{PV}}+P_t^{\text{WT}}+P_t^{\text{sell}}=P_t^{\text{load}}+P_t^{\text{buy}}.(15)$

(2) DEG operation constraints

$P_m^{\mathrm{DEG},\min }\le P_{m,t}^{\mathrm{DEG}}\le P_m^{\mathrm{DEG},\max }.(16)$

(3) SMIP operator trading constraints

$P_t^{\text{sell},\min }\le P_t^{\text{sell}}\le P_t^{\text{sell},\max },(17)$

$P_t^{\text{buy},\min }\le P_t^{\text{buy}}\le P_t^{\text{buy},\max }.(18)$

(4) Opportunity constraints

The prediction of the load, WTs, and PVs is susceptible to uncontrollable factors such as weather, resulting in forecasting errors. The level of error is approximately represented by a normal distribution (Li et al., 2023d). In order to deal with the prediction errors caused by such uncertainties, the system should have a backup capacity in operation, which is described in probability with a given confidence level:

$\text{P}\left\{{\displaystyle \sum _{\text{m}}}\left[{\text{P}}_{\text{m},\text{t}}^{\text{DEG}}+{\text{R}}_{\text{m},\text{t}}^{\text{DEG}}\right]+\left[{\text{P}}_{\text{t}}^{\text{PV}}+{\delta }_{\text{t}}^{\text{PV}}\right]+\left[{\text{P}}_{\text{t}}^{\text{WT}}+{\delta }_{\text{t}}^{\text{WT}}\right]+{\text{P}}_{\text{t}}^{\text{sell}}\ge {\text{P}}_{\text{t}}^{\text{load}}+{\delta }_{\text{t}}^{\text{load}}+{\text{P}}_{\text{t}}^{\text{buy}}\}\right.\ge \alpha ,(19)$

where P{} represents the probability at a given confidence level. The proposed model cannot be solved because of the presence of random variables; then, the opportunity constraint is converted into a deterministic equivalent constraint as

${\displaystyle \sum _{\text{m}}}\left[{\text{P}}_{\text{m},\text{t}}^{\text{DEG}}+{\text{R}}_{\text{m},\text{t}}^{\text{DEG}}\right]+{\text{P}}_{\text{t}}^{\text{PV}}+{\text{P}}_{\text{t}}^{\text{WT}}+{\text{P}}_{\text{t}}^{\text{sell}}\ge {\text{P}}_{\text{t}}^{\text{load}}+{\text{P}}_{\text{t}}^{\text{buy}}+{\text{F}}^{-1}\left(\alpha \right)\sqrt{{\left({\sigma }^{\text{PV}}\right)}^2+{\left({\sigma }^{\text{WT}}\right)}^2+{\left({\sigma }^{\text{load}}\right)}^2},(20)$

where F⁻¹(α) represents the quantile point $\alpha$ under the standard normal distribution function.

4 Solution process of the proposed model

In the constructed two-layer optimization model, the upper and lower optimization models are coupled through the electricity trading price. The upper-layer DN agent, acting as the leader in the Stackelberg game, optimizes the electricity trading with EM and SMIP operators based on their own internal demand. The lower-layer SMIP operators, as followers in the Stackelberg game, optimize their internal energy consumption based on the electricity trading price provided by the DN agent.

Due to coupling in the two-layer model in this paper, the KKT condition transformation (Yang X. et al., 2023) is employed to convert the original coupled two-layer optimization model into a single-layer linear programming model. The specific process is as follows:

$c_t^{\text{sell}}\Delta t-{\lambda }_t^{2,\min }+{\lambda }_t^{2,\max }-{\lambda }_t^4=0,(21)$

$-c_t^{\text{buy}}\Delta t-{\lambda }_t^{3,\min }+{\lambda }_t^{3,\max }+{\lambda }_t^4=0,(22)$

$c^{\mathrm{DEG}}-{\rho }_{m,t}^{\min }+{\rho }_{m,t}^{\max }-{\lambda }_t^4=0.(23)$

The dual variables above need to satisfy the following conditions:

${\rho }_{m,t}^{\min }\perp \left(P_{m,t}^{\mathrm{DEG}}-P_m^{\mathrm{DEG},\min }\right),(24)$

${\rho }_{m,t}^{\max }\perp \left(P_m^{\mathrm{DEG},\max }-P_{m,t}^{\mathrm{DEG}}\right),(25)$

${\lambda }_t^{2,\min }\perp \left(P_t^{\text{sell}}-P_t^{\text{sell},\min }\right),(26)$

${\lambda }_t^{2,\max }\perp \left(P_t^{\text{sell},\max }-P_t^{\text{sell}}\right),(27)$

${\lambda }_t^{3,\min }\perp \left(P_t^{\text{buy}}-P_t^{\text{buy},\min }\right),(28)$

${\lambda }_t^{3,\max }\perp \left(P_t^{\text{buy},\max }-P_t^{\text{buy}}\right),(29)$

${\lambda }_t^4\perp \left(P_t^{\text{load}}+P_t^{\text{buy}}+F^{-1}\left(\alpha \right)\sqrt{{\left({\sigma }^{\text{PV}}\right)}^2+{\left({\sigma }^{\text{WT}}\right)}^2+{\left({\sigma }^{\text{load}}\right)}^2}-{\displaystyle \sum _m}\left[P_{m,t}^{\mathrm{DEG}}+R_{m,t}^{\mathrm{DEG}}\right]-P_t^{\text{PV}}-P_t^{\text{WT}}-P_t^{\text{sell}})\right..(30)$

In the above equations, x⊥y represents that x and y have at most one non-zero value. To linearize the model, this paper relaxes the above equations by introducing Boolean variables:

$0\le {\rho }_{m,t}^{\min }\le \mathrm{M}{\theta }_{m,t}^{\min },(31)$

$0\le P_{m,t}^{\mathrm{DEG}}-P_m^{\mathrm{DEG},\min }\le \mathrm{M}\left(1-{\theta }_{m,t}^{\min }\right),(32)$

$0\le P_m^{\mathrm{DEG},\max }-P_{m,t}^{\mathrm{DEG}}\le \mathrm{M}\left(1-{\theta }_{m,t}^{\max }\right),(33)$

$0\le {\rho }_{m,t}^{\max }\le \mathrm{M}{\theta }_{m,t}^{\max },(34)$

$0\le {\lambda }_t^{2,\min }\le \mathrm{M}{\theta }_t^{2,\min },(35)$

$0\le P_t^{\text{sell}}-P_t^{\text{sell},\min }\le \mathrm{M}\left(1-{\theta }_t^{2,\min }\right),(36)$

$0\le {\lambda }_t^{2,\max }\le \mathrm{M}{\theta }_t^{2,\max },(37)$

$0\le P_t^{\text{sell},\max }-P_t^{\text{sell}}\le \mathrm{M}\left(1-{\theta }_t^{2,\max }\right),(38)$

$0\le {\lambda }_t^{3,\min }\le \mathrm{M}{\theta }_t^{3,\min },(39)$

$0\le P_t^{\text{buy}}-P_t^{\text{buy},\min }\le \mathrm{M}\left(1-{\theta }_t^{3,\min }\right),(40)$

$0\le {\lambda }_t^{3,\max }\le \mathrm{M}{\theta }_t^{3,\max },(41)$

$0\le P_t^{\text{buy},\max }-P_t^{\text{buy}}\le \mathrm{M}\left(1-{\theta }_t^{3,\max }\right),(42)$

$0\le {\lambda }_t^4\le M{\theta }_t^4,(43)$

$0\le \left(P_t^{\text{load}}+P_t^{\text{buy}}+F^{-1}\left(\alpha \right)\sqrt{{\left({\sigma }^{\text{PV}}\right)}^2+{\left({\sigma }^{\text{WT}}\right)}^2+{\left({\sigma }^{\text{load}}\right)}^2}-{\displaystyle \sum _m}\left[P_{m,t}^{\mathrm{DEG}}+R_{m,t}^{\mathrm{DEG}}\right]-P_t^{\text{PV}}-P_t^{\text{WT}}-P_t^{\text{sell}}\right.)\le \mathrm{M}\left(1-{\theta }_t^4\right).(44)$

In the above equations, ${\theta }_{\mathrm{m},t}^{\min }$, ${\theta }_{\mathrm{m},t}^{\max }$, ${\theta }_{2,t}^{\min }$, ${\theta }_{2,t}^{\max }$, ${\theta }_{3,t}^{\min }$, ${\theta }_{3,t}^{\max },$ and ${\theta }_{4,t}$ are the Boolean variables. M is the maximum value. After the transformation, the objective function still contains two non-linear terms: ${\displaystyle \sum _t}{c}_t^{\text{sell}}{P}_t^{\text{sell}}\Delta t$ and ${\displaystyle \sum _t}{c}_t^{\text{buy}}{P}_t^{\text{buy}}\Delta t$. To facilitate the solution, the strong duality principle (Ouyang et al., 2023) is employed to process the objective function, resulting in the transformation of the objective function into a linear programming model.

$\begin{array}{l}\text{max}\left[{\displaystyle \sum _{\text{t}}}{\text{c}}_{\text{t}}^{\text{sell}}{\text{P}}_{\text{t}}^{\text{sell}}\Delta \text{t}-{\displaystyle \sum _{\text{t}}}{\text{c}}_{\text{t}}^{\text{buy}}{\text{P}}_{\text{t}}^{\text{buy}}\Delta \text{t}+\left({\displaystyle \sum _{\text{t}}}{\pi }_{\text{t}}^{-}{\text{R}}_{\text{t}}^{-}\Delta \text{t}-{\displaystyle \sum _{\text{t}}}{\pi }_{\text{t}}^{+}{\text{R}}_{\text{t}}^{+}\Delta \text{t}-{\displaystyle \sum _{\text{t}}}{\pi }_{\text{t}}{\text{R}}_{\text{t}}\Delta \text{t}\right)-{\displaystyle \sum _{\text{t}}}{\text{c}}_{\text{t}}^{\text{tra}}{\text{P}}_{\text{t}}^{\text{sop}}\Delta \text{t}\right]\\ \Rightarrow \text{max}\left[\begin{array}{l}{\displaystyle \sum _{\text{t}}}{\displaystyle \sum _{\text{m}}}\left({\rho }_{\text{m},\text{t}}^{\text{min}}{\text{P}}_{\text{m}}^{\text{DEG},\text{min}}-{\rho }_{\text{m},\text{t}}^{\text{max}}{\text{P}}_{\text{m}}^{\text{DEG},\text{max}}\right)+{\displaystyle \sum _{\text{t}}}\left({\lambda }_{\text{t}}^{2,\text{min}}{\text{P}}_{\text{t}}^{\text{sell},\text{min}}-{\lambda }_{\text{t}}^{2,\text{max}}{\text{P}}_{\text{t}}^{\text{sell},\text{max}}\right)+{\displaystyle \sum _{\text{t}}}\left({\lambda }_{\text{t}}^{3,\text{min}}{\text{P}}_{\text{t}}^{\text{buy},\text{min}}-{\lambda }_{\text{t}}^{3,\text{max}}{\text{P}}_{\text{t}}^{\text{buy},\text{max}}\right)\\ +{\displaystyle \sum _{\text{t}}}{\lambda }_{\text{t}}^4\left({\text{F}}^{-1}\left(\alpha \right)\sqrt{{\left({\sigma }^{\text{PV}}\right)}^2+{\left({\sigma }^{\text{WT}}\right)}^2+{\left({\sigma }^{\text{load}}\right)}^2}+{\text{P}}_{\text{t}}^{\text{load}}-{\text{P}}_{\text{t}}^{\text{PV}}-{\text{P}}_{\text{t}}^{\text{WT}}-{\text{R}}_{\text{m},\text{t}}^{\text{DEG}}\right)-{\displaystyle \sum _{\text{t}}}{\displaystyle \sum _{\text{m}}}{\text{c}}^{\text{DEG}}{\text{P}}_{\text{m},\text{t}}^{\text{DEG}}\Delta \text{t}\\ +\left({\displaystyle \sum _{\text{t}}}{\pi }_{\text{t}}^{-}{\text{R}}_{\text{t}}^{-}\Delta \text{t}-{\displaystyle \sum _{\text{t}}}{\pi }_{\text{t}}^{+}{\text{R}}_{\text{t}}^{+}\Delta \text{t}-{\displaystyle \sum _{\text{t}}}{\pi }_{\text{t}}{\text{R}}_{\text{t}}\Delta \text{t}\right)-{\displaystyle \sum _{\text{t}}}{\text{c}}_{\text{t}}^{\text{tra}}{\text{P}}_{\text{t}}^{\text{sop}}\Delta \text{t}\end{array}\right].\end{array}(45)$

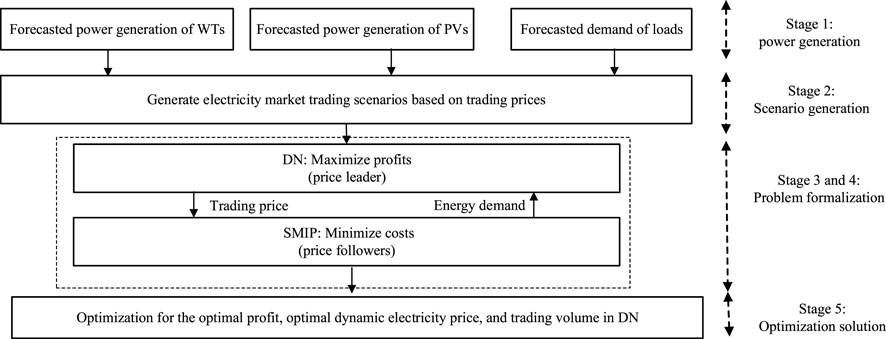
By employing the above method, the non-linear dual-layer game model can be transformed into a mixed-integer linear single-layer optimization model. The optimal solution can be obtained using the commercial solver CPLEX (Zhao et al., 2022). The overall solving process of the model established in this paper is illustrated as follows and is shown in Figure 2:

FIGURE 2

FIGURE 2. Solving process of the model.

Step 1:. The outputs of WTs, PVs, and user load demand are forecasted within the SMIP.

Step 2:. The data obtained from the previous step are utilized to generate EM trading scenarios, including the electricity generation volume and trading prices in EM.

Step 3:. A two-layer optimization trading model is established, with the upper-layer DN agent as the price leaders and the lower-layer SMIP operators as the price followers, thus forming the Stackelberg game optimization model.

Step 4:. KKT conditions are applied to transform the dual-layer problem into a single-layer problem. Dual theory, linear relaxation, and other methods are combined to convert the optimization model into a more easily solvable mixed-integer linear programming model. In this step, the specific electricity trading volume of each stakeholder can be calculated through the nested solution of electricity price and trading volume.

Step 5:. Through the real-time dynamic optimization processes, the optimal electricity price and trading volume are obtained, and an optimal solution for all stakeholders in the Stackelberg game is achieved.

5 Case study

5.1 Case study system

In order to verify the effectiveness of the proposed method, an actual DN with SMIPs in Zhejiang Province, China, is utilized to analyze. The topology of this system is illustrated in Figure 3. Within this system, DNs and SMIPs are connected through the public connection point (PCC). The DNs are connected through intelligent software switches. In this topology, DN agents, SMIP operators, and the EM conduct mutual trading to meet their respective demands.

FIGURE 3

FIGURE 3. Physical topology of the system.

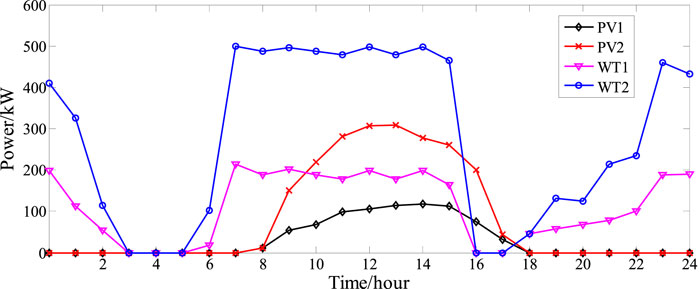
In the optimization of trading strategies in this paper, the upper-layer DN maximizes their profits primarily by adjusting the ESs. Meanwhile, the two lower-layer SMIP operators minimize their operational costs by adjusting various distributed resources such as PVs, WTs, DEGs, and loads. The installed capacity of the distributed resources is shown in Table 1. The predicted data for the output of photovoltaics and wind power in SMIPs are shown in Figure 4.

TABLE 1

TABLE 1. Installed capacity of the distributed resources.

FIGURE 4

FIGURE 4. Forecasted power of WTs and PVs.

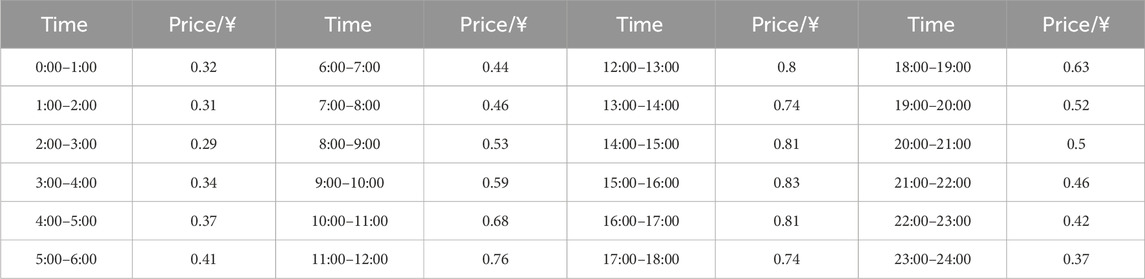
The day-ahead contract electricity price of the DN agent is shown in Table 2, which is denoted as π_t. Due to the flexibility in actual trading, the real electricity trading price is generally higher than the day-ahead contract electricity price. Therefore, in this paper, the real-time buying and selling prices, π+ t and π-t, respectively, are set at 1.2 π_t. The trading price between DN agents is set at 0.9 π_t.

TABLE 2

TABLE 2. Day-ahead contract electricity price.

As shown in Table 2, the day-ahead contract electricity price of the DN agent exhibits continuous fluctuations throughout the day. The price steadily increases from 2:00, experiences a slight decrease around noon at 12:00, and reaches its peak in the afternoon at 16:00. Then, the price gradually decreases to reach the lowest point. This pattern of price variation indicates that in EM, the electricity price during different time periods may be influenced by supply and demand dynamics, peak loads, and other factors. The fluctuations in prices can have a significant impact on EM stakeholders when formulating trading strategies. Based on these fluctuations, the leader–follower model needs to undergo a corresponding electricity trading strategy design to maximize the interests of the stakeholders involved.

5.2 Analysis of the pricing strategy and energy usage optimization

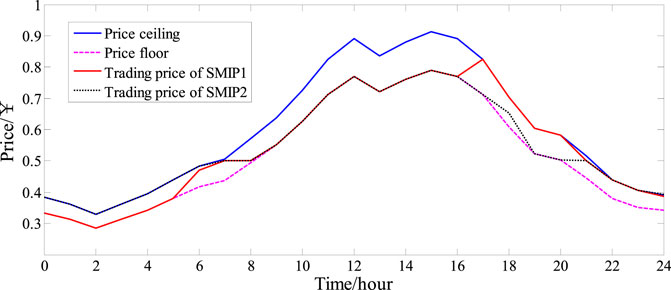
For the study of pricing strategies of the DN agent and energy optimization for SMIP operators, considering the variations in electricity consumption across regions, the DN agent provides pricing methods that align with the differences in electricity consumption. The pricing strategy of the DN agent for SMIP operators is illustrated in Figure 5.

FIGURE 5

FIGURE 5. Pricing strategies of the DN agent.

As shown in Figure 5, due to the constraints imposed by the average price, the interests of SMIP operators are protected. Under this premise, the DN agent formulates trading prices tailored to the electricity demand of different SMIP operators to maximize their own benefits, thus achieving a win–win situation.

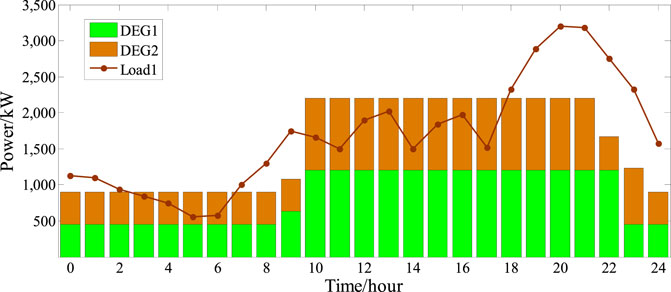
The internal energy optimization for SMIP operators 1 and 2 is shown in Figure 6 and Figure 7, respectively. Figure 6 and Figure 7 show that the lower-layer SMIP operators provide feedback to dynamic trading prices after optimizing the output of internal generation units. For SMIP operator 1, where the user exhibits significant fluctuations, the DN agent sets the dynamic electricity price close to the price floor during periods of relatively low electricity consumption, such as the time period from 1:00 to 6:00. During the time period from 7:00 to 9:00, when the energy demand within SMIP operators begins to increase but the outputs of WTs and PVs are relatively low, the DN agent increases the trading price to maximize profits while still meeting the average price constraint. During the time period from 10:00 to 18:00, when the energy consumption in SMIP operator 1 is relatively stable and the outputs of WTs and PVs are high, SMIPs do not need the electricity urgently, so the trading price is close to the price floor. During the time period from 19:00 to 24:00, as the outputs of WTs and PVs cannot meet the required energy demand and the user-side electricity demand is high, the DN agent sets the trading price to the price ceiling to maximize its own profits.

FIGURE 6

FIGURE 6. Internal energy optimization of SMIP operator 1.

FIGURE 7

FIGURE 7. Internal energy optimization of SMIP operator 2.

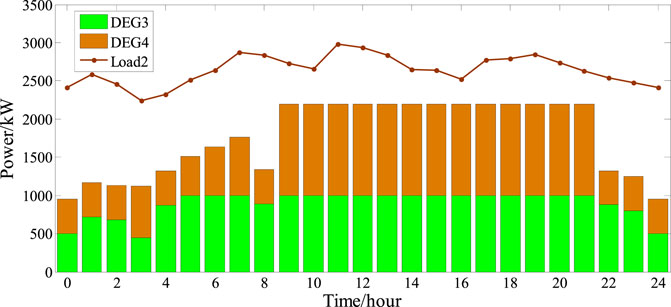
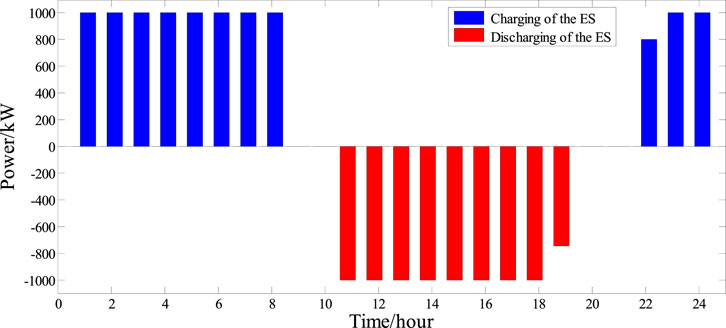
For SMIP operator 2, which is characterized by stable load fluctuations, the pricing strategy of the DN agent is less influenced by the load. In this situation, the pricing strategy is determined more by the outputs of WTs and PVs. During the periods that the outputs of WTs and PVs are high, such as the time period from 10:00 to 18:00, the demand for electricity purchase in the SMIP has decreased, and then, the trading price is set close to the price floor. Conversely, during the time periods from 1:00 to 9:00 and 17:00 to 20:00, the outputs of WTs and PVs are low, the demand for electricity purchase in the SMIP has increased, and then the trading price is set close to the price ceiling. Figure 8 shows the optimal trading strategy between the DN agent and SMIP operators. The agents determine the day-ahead contract electricity volume based on the day-ahead data. During the time periods between 1:00–8:00 and 21:00–24:00, due to the lower day-ahead contract electricity prices, the DN agent increases the day-ahead contract electricity volume for trading with EM based on the past experiences. Meanwhile, as shown in Figure 9, a portion of the purchased electricity is charged and stored in the ES, and the stored energy is discharged during time periods with relatively higher electricity prices, allowing for maximum profit. Additionally, to ensure their own benefits, SMIP operators increase their electricity purchases from the upper layer during these time periods. During periods with higher day-ahead electricity prices, such as from 9:00 to 16:00, the DN agent reduces the day-ahead contract electricity volume and release stored energy. The electricity is sold to the adjacent DN agent as a means of balancing electricity prices. Meanwhile, SMIP operators increase the generation output of internal distributed power sources and sell electricity to the upper-layer DN agent. Through this strategy, the DN agent and SMIP operators achieve a balance of benefits.

FIGURE 8

FIGURE 8. Optimal trading between the DN agent and SMIP operators.

FIGURE 9

FIGURE 9. Operation of the ES.

The optimization results based on the dynamic pricing strategy under the Stackelberg game are compared with the conventional fixed-value time-of-use pricing, as shown in Table 3. Under the former strategy, the profit of DN has increased, and the operating costs of SMIP operators have decreased. The reason is that the dynamic pricing strategy under the Stackelberg game can formulate electricity prices according to the varying electricity demands of different SMIP operators. The role of lower-layer SMIP operators has undergone a significant transformation as they are no longer passive recipients of electricity prices. DN can influence dynamic trading prices indirectly by autonomously planning energy demands. By formulating dynamic electricity prices, the initiative of lower-layer SMIP operators is enhanced, allowing them to actively participate in the optimization scheduling of the EM. Simultaneously, this also improves the overall economic efficiency of DN optimization to a certain extent.

TABLE 3

TABLE 3. Comparison of pricing strategies.

The profits of the upper-layer DN agent in a typical day increased from the original price of 5724.6 $\yen$ to 6572.7 $\yen$, showing an overall increase of 14.8%. The operating costs of lower-layer SMIP operators decreased from 17936.55 $\yen$ and 26661.23 $\yen$ to 17486.31 $\yen$ and 25631.24 $\yen$, resulting in an overall reduction of 2.5% and 3.8%, respectively. The dynamic pricing can improve the benefits of different stakeholders. As indicated in Table 1, under the Stackelberg game-based dynamic pricing strategy, the benefits of the DN agent and SMIP operators are effectively balanced. On one hand, the DN agent can dynamically adjust the trading electricity price based on the electricity demand of SMIP operators, as well as the output of WTs and PVs, thereby increasing their own profits. On the other hand, SMIP operators optimize the outputs of internal power generation, as well as purchasing strategies through responding to the dynamic trading prices, thereby reducing operating costs. This indicates that under the Stackelberg game-based dynamic pricing strategy, the DN agent and SMIP operators have achieved maximum benefits, fulfilling the goal of a win–win situation. The dynamic pricing strategy allows for timely adjustments based on electricity buying and selling conditions in the market, enabling the market to respond more rapidly and flexibly. Moreover, the prices can be adjusted according to different market conditions, thereby enabling the stakeholders to pinpoint their market positions and adapt more effectively to market changes. Furthermore, the prices can also be adjusted based on market demand, supply conditions, and the strategies of competitors. This can enable the business to maximize profits, meet market demands, and gain a greater competitive advantage.

6 Discussion and conclusion

With the rapid development of SMIP, the demand for electricity trading between SMIPs and DNs is constantly increasing. An optimal trading electricity strategy with the DN can help the SMIPs to withstand the operating risks, as well as help the SMIPs to save the operating costs. For the electricity trading between the DNs and SMIPs, the existing methods have the following issues that need to be addressed:

• The electricity trading mode between the DN and SMIP is unclear. How to characterize the competitive game relationship between the DN and SMIP in the trading process needs to be solved.

• In existing electricity trading methods, due to different optimization objectives of different stakeholders, there are multivariable nested problems such as the trading price and trading quantity, which are often difficult to solve.

• The pricing strategies in existing research studies mainly belong to fixed pricing mechanisms. As the SMIPs continue to develop, a fixed pricing mechanism will not be able to adapt to the flexible trend of the EM. Proposing a dynamic pricing strategy to further improve the profits of stakeholders is necessary.

To address the above issues, a Stackelberg game-based optimal electricity trading method for DNs with SMIPs is proposed. Our conclusions are as follows:

• The proposed two-layer optimization trading model can characterize the competitive game relationship between the DNs and SMIPs. Furthermore, under the proposed scheme, the profit of DNs increases by 14.8% in a typical day, and the operating costs of SMIPs decreased by 2.5% and 3.8%, respectively.

• The proposed solution method transforms the proposed non-linear model into a mixed-integer linear programming model, which solves the coupling–nesting problem of interactive power and electricity price in the proposed model without any approximation.

• A dynamic pricing strategy is formulated to address the disadvantage of fixed pricing mechanisms. Under the dynamic pricing strategy, the DN agent sets the dynamic prices to lead the trading behavior of SMIP operators, and the SMIP operators choose the trading time to follow the guidance of the DN agent without the passive price reception.

The trading strategy proposed in this paper can effectively increase the profits of the DN agent while reducing the operating costs of SMIP operators. In future research, a two-layer robust optimization trading method for the DN agent and SMIP operators will be developed with the consideration of the uncertainty of PVs and WTs to make the methods more comprehensive.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

LC: writing–original draft. QY: writing–review and editing. XW: writing–review and editing. YC: writing–original draft. WW: writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The study in this paper was supported by the Project Supported by Zhejiang Electric Power Industry Corporation Technology Project (CF058810002022001).

Conflict of interest

Authors LC, QY, XW, YC, and WW were employed by State Grid Pingyang Power Supply Company.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Anwar, B., Stephen, G., Dalvi, S., Frew, B., Ericson, S., Brown, M., et al. (2022). Modeling investment decisions from heterogeneous firms under imperfect information and risk in wholesale electricity markets. Appl. Energy 306, 117908. doi:10.1016/j.apenergy.2021.117908

CrossRef Full Text | Google Scholar

Cao, S., Zhang, H., Cao, K., Chen, M., Wu, Y., and Zhou, S. (2021). Day-ahead economic optimal dispatch of microgrid cluster considering shared energy storage system and P2P transaction. Front. energy Res. 9 (9), 645017. doi:10.3389/fenrg.2021.645017

CrossRef Full Text | Google Scholar

Chen, T., Bu, S., Liu, X., Kang, J., Yu, F. R., and Han, Z. (2022). Peer-to-peer energy trading and energy conversion in interconnected multi-energy microgrids using multi-agent deep reinforcement learning. IEEE Trans. smart grid 13 (1), 715–727. doi:10.1109/tsg.2021.3124465

CrossRef Full Text | Google Scholar

Davoudi, M., and Moeini-Aghtaie, M. (2022). Local energy markets design for integrated distribution energy systems based on the concept of transactive peer-to-peer market. IET generation, Transm. distribution (1), 16. doi:10.1049/gtd2.12274

CrossRef Full Text | Google Scholar

Ding, J., Gao, C., Song, M., Yan, X., and Chen, T. (2023). Optimal operation of multi-agent electricity-heat-hydrogen sharing in integrated energy system based on Nash bargaining. Int. J. Electr. power energy Syst. 148 (6), 108930. doi:10.1016/j.ijepes.2022.108930

CrossRef Full Text | Google Scholar

Du, X., Li, X., Hao, Y., and Chen, L. (2022). Sizing of centralized shared energy storage for resilience microgrids with controllable load: a bi-level optimization approach. Front. energy Res. 10 (10), 954833. doi:10.3389/fenrg.2022.954833

CrossRef Full Text | Google Scholar

Envelope, L., Envelope, R., Envelope, Y., and Xu, C. (2022). Stackelberg game-based optimal scheduling of integrated energy systems considering differences in heat demand across multi-functional areas. Energy Rep. 8, 11885–11898. doi:10.1016/j.egyr.2022.08.199

CrossRef Full Text | Google Scholar

Fattaheian, S., Tavakkoli, M., Abbaspour, A., Fotuhi-Firuzabad, M., and Lehtonen, M. (2022). Optimal energy management of distribution networks in post-contingency conditions. Int. J. Electr. power energy Syst. 141 (11), 108022. doi:10.1016/j.ijepes.2022.108022

CrossRef Full Text | Google Scholar

Guo, Z., Pinson, P., Wu, Q., Chen, S., Yang, Q., and Yang, Z. (2022). An asynchronous online negotiation mechanism for real-time peer-to-peer electricity markets. IEEE Trans. power Syst. 37 (3), 1868–1880. doi:10.1109/tpwrs.2021.3111869

CrossRef Full Text | Google Scholar

Haghifam, S., Zare, K., Abapour, M., Muñoz-Delgado, G., and Contreras, J. (2020). A Stackelberg game-based approach for transactive energy management in smart distribution networks. Energies 13 (14), 3621. doi:10.3390/en13143621

CrossRef Full Text | Google Scholar

He, C., Tang, J., Zhang, W., Zhang, Z., Lin, Z., Li, Y., et al. (2021). Optimal planned electricity allocation model for power exchange under the plan-market double-track mechanism. Front. energy Res. 9 (9), 679365. doi:10.3389/fenrg.2021.679365

CrossRef Full Text | Google Scholar

Hua, W., Xiao, H., Pei, W., Chiu, W., Jiang, J., Sun, H., et al. (2023). Transactive energy and flexibility provision in multi-microgrids using Stackelberg game. CSEE J. power energy Syst. 9 (2), 505–515. doi:10.17775/CSEEJPES.2021.04370

CrossRef Full Text | Google Scholar

Huang, Y., Wang, Y., Liu, N., et al. (2022). Low-carbon economic dispatch and energy sharing method of multiple integrated energy systems from the perspective of system of systems. Energy 244, 122717. doi:10.1016/j.energy.2021.122717

CrossRef Full Text | Google Scholar

Jin, L., Liu, Q., Yu, J., Wang, M., and Wu, W. (2022). Research on the development of electricity market based on performance guarantee. Front. energy Res. 10 (10), 900901. doi:10.3389/fenrg.2022.900901

CrossRef Full Text | Google Scholar

Khaligh, V., Ghezelbash, A., Mazidi, M., Liu, J., Ryu, J. H., and Na, J. (2022). A stochastic agent-based cooperative scheduling model of a multi-vector microgrid including electricity, hydrogen, and gas sectors. J. power sources 546 (10), 231989–232014. doi:10.1016/j.jpowsour.2022.231989

CrossRef Full Text | Google Scholar

Klsch, L., Zellmann, L., Vyas, R., Pfeifer, M., and Hohmann, S. (2022). Optimal distributed frequency and voltage control for zonal electricity markets. IEEE Trans. Power Syst. 37 (4), 2666–2678. doi:10.1109/tpwrs.2021.3123088

CrossRef Full Text | Google Scholar

Kuno, S., Tanaka, K., and Yamada, Y. (2022). Effectiveness and feasibility of market makers for P2P electricity trading. Energies 15 (12), 4218. doi:10.3390/en15124218

CrossRef Full Text | Google Scholar

Lei, Z., Liu, M., and Shen, Z. (2023). Analysis of strategic bidding of a DER aggregator in energy markets through the Stackelberg game model with the mixed-integer lower-level problem. Int. J. Electr. power energy Syst. 152 (12), 109237. doi:10.1016/j.ijepes.2023.109237

CrossRef Full Text | Google Scholar

Li, S., Zhang, L., Nie, L., and Wang, J. (2022). Trading strategy and benefit optimization of load aggregators in integrated energy systems considering integrated demand response: a hierarchical Stackelberg game. Energy 249, 123678. doi:10.1016/j.energy.2022.123678

CrossRef Full Text | Google Scholar

Li, Y., Deng, Y., Wang, Y., Jiang, L., and Shahidehpour, M. (2023c). Robust bidding strategy for multi-energy virtual power plant in peak-regulation ancillary service market considering uncertainties. Int. J. Electr. power energy Syst. 151 (9), 109101. doi:10.1016/j.ijepes.2023.109101

CrossRef Full Text | Google Scholar

Li, Y., Lin, Y., He, Y., Zhang, G., Zhang, L., Yang, J., et al. (2023a). Part-load performance analysis of a dual-recuperated gas turbine combined cycle system. Energy 269, 126744. doi:10.1016/j.energy.2023.126744

CrossRef Full Text | Google Scholar

Li, Y., Sun, Y., Wang, Q., Sun, K., Li, K. J., and Zhang, Y. (2023d). Probabilistic harmonic forecasting of the distribution system considering time-varying uncertainties of the distributed energy resources and electrical loads. Appl. Energy 329, 120298. doi:10.1016/j.apenergy.2022.120298

CrossRef Full Text | Google Scholar

Li, Z., Yang, P., Guo, Y., and Lu, G. (2023b). Medium-term multi-stage distributionally robust scheduling of hydro–wind–solar complementary systems in electricity markets considering multiple time-scale uncertainties. Appl. Energy 347, 121371. doi:10.1016/j.apenergy.2023.121371

CrossRef Full Text | Google Scholar

Liu, X., Chen, X., Jin, T., Liu, Z., Liu, Y., Su, M., et al. (2023). Network-constrained peer-to-peer energy trading for multiple microgrids considering zoning pricing. Int. J. Electr. power energy Syst. 147 (5), 108837. doi:10.1016/j.ijepes.2022.108837

CrossRef Full Text | Google Scholar

Lyu, Z., Lai, Y., Yang, X., Li, Y., and Yi, J. (2022). Cooperative game consistency optimal strategy of multi-microgrid system considering flexible load. Energy sources. 44 (3), 7378–7399. doi:10.1080/15567036.2022.2109779

CrossRef Full Text | Google Scholar

Ouyang, S., Huang, Y., and Yang, M. (2023). Reliability modeling of multi-terminal DC circuit breaker and its impact on multi-terminal DC distribution network. Int. J. Electr. power energy Syst. 7 (1), 32–41. doi:10.1016/j.ijepes.2022.108888

CrossRef Full Text | Google Scholar

Pownall, T., Soutar, I., and Mitchell, C. (2021). Re-designing GB’s electricity market design: a conceptual framework which recognises the value of distributed energy resources. Energies 14 (4), 1124. doi:10.3390/en14041124

CrossRef Full Text | Google Scholar

Pu, J., Chun, W., Wang, Z., and Chen, W. (2023). Operation strategy for new energy vehicle enterprises based on dual credit policy. J. industrial Manag. Optim. 19 (8), 5724–5748. doi:10.3934/jimo.2022192

CrossRef Full Text | Google Scholar

Tan, J., Li, Y., and Zhang, X. (2022). Optimization and trading of district multi-energy system in university community considering carbon emission. Int. J. Electr. power energy Syst. 137 (5), 107450. doi:10.1016/j.ijepes.2021.107450

CrossRef Full Text | Google Scholar

Wang, L., Dong, H., Lin, J., and Zeng, M. (2022a). Multi-objective optimal scheduling model with IGDT method of integrated energy system considering ladder-type carbon trading mechanism. Int. J. Electr. power energy Syst. 143 (12), 108386. doi:10.1016/j.ijepes.2022.108386

CrossRef Full Text | Google Scholar

Wang, R., Cheng, S., Zuo, X., and Liu, Y. (2022b). Optimal management of multi stakeholder integrated energy system considering dual incentive demand response and carbon trading mechanism. Int. J. energy Res. 46 (5), 6246–6263. doi:10.1002/er.7561

CrossRef Full Text | Google Scholar

Wei, M., Deng, Y., Long, M., Wang, Y., and Li, Y. (2022). Transaction model based on Stackelberg game method for balancing supply and demand sides of multi-energy microgrid. Energies 15 (4), 1362–1420. doi:10.3390/en15041362

CrossRef Full Text | Google Scholar

Xiao, C., Ding, M., Sun, L., and Chung, C. (2021). Network partition-based two-layer optimal scheduling for active distribution networks with multiple stakeholders. IEEE Trans. industrial Inf. 17 (9), 5948–5960. doi:10.1109/tii.2020.3038668

CrossRef Full Text | Google Scholar

Xu, L., Xie, Q., Zheng, L., Hua, Y., Shao, L., and Cui, J. (2022). Stackelberg-game-based demand response for voltage regulation in distribution network with high penetration of electric vehicles. Energies 15 (10), 3654. doi:10.3390/en15103654

CrossRef Full Text | Google Scholar

Yang, D., Wang, M., Yang, R., Zheng, Y., and Pandzic, H. (2021). Optimal dispatching of an energy system with integrated compressed air energy storage and demand response. Energy 234 (19), 121232. doi:10.1016/j.energy.2021.121232

CrossRef Full Text | Google Scholar

Yang, M., and Liu, Y. (2023a). Research on multi-energy collaborative operation optimization of integrated energy system considering carbon trading and demand response. Energy 283, 129117. doi:10.1016/j.energy.2023.129117

CrossRef Full Text | Google Scholar

Yang, X., Fan, L., Gao, X., and Liu, H. (2022). Analysis of wind farm participation in frequency regulation considering multi-market interests. J. Renew. Sustain. energy 14 (1), 013304. doi:10.1063/5.0073140

CrossRef Full Text | Google Scholar

Yang, X., Song, Z., Wen, J., Ding, L., Zhang, M., Wu, Q., et al. (2023b). Network-constrained transactive control for multi-microgrids-based distribution networks with soft open points. IEEE Trans. Sustain. energy 14 (3), 1769–1783. doi:10.1109/tste.2023.3246360

CrossRef Full Text | Google Scholar

Yuan, W., Zhang, S., Su, C., Wu, Y., Yan, D., and Wu, Z. (2022). Optimal scheduling of cascade hydropower plants in a portfolio electricity market considering the dynamic water delay. Energy 252, 124025. doi:10.1016/j.energy.2022.124025

CrossRef Full Text | Google Scholar

Zhang, Y., Zhao, H., Li, B., and Wang, X. (2022). Research on dynamic pricing and operation optimization strategy of integrated energy system based on Stackelberg game. Int. J. Electr. power energy Syst. 143 (12), 108446. doi:10.1016/j.ijepes.2022.108446

CrossRef Full Text | Google Scholar

Zhao, Y., Xiong, W., Yuan, X., and Zou, X. (2022). A fault recovery strategy of flexible interconnected distribution network with SOP flexible closed-loop operation. Int. J. Electr. power energy Syst. 142 (11), 108360. doi:10.1016/j.ijepes.2022.108360

CrossRef Full Text | Google Scholar

Glossary