A position allocation approach to the scheduling of battery-electric bus charging

Robust charging schedules for a growing market of battery-electric bus (BEB) fleets are critical to successful adoption. In this paper, we present a BEB charging scheduling framework that considers spatiotemporal schedule constraints, route schedules, fast and slow charging options, and battery dynamics, modeled as a mixed-integer linear program (MILP). The MILP is based on the berth allocation problem (BAP), a method that optimally assigns vessels for service, and is adapted in a modified form known as the position allocation problem (PAP), which assigns electric vehicles (EVs) for charging. Linear battery dynamics are included to model the charging of buses while at the station. To account for the BEB discharges over their respective routes, we assume that each BEB experiences an average kWh charge loss while in transit. The optimization coordinates BEB charging to ensure that each vehicle maintains a state-of-charge (SOC) above a specified level. The model also minimizes the total number of chargers utilized and prioritizes slow charging for battery health. The validity of the model is demonstrated using a set of routes sampled from the Utah Transit Authority (UTA) for 35 buses and 338 visits to the charging station. The model is also compared to a heuristic algorithm based on charge thresholds, referred to as the Qin-modified method. The results show that the MILP framework encourages battery health by assigning slow chargers to BEBs more readily than the Qin-modified method. The MILP utilized one fast charger and six slow chargers, whereas the Qin-modified method utilized four fast chargers and six slow chargers. Moreover, the MILP maintained a specified minimum SOC of 25% throughout the day and achieved the required minimum SOC of 70% at the end of the working day, whereas the Qin-modified method failed to maintain the SOC above 0% without any constraints applied. Furthermore, it is shown that the spatiotemporal constraints are met while considering the battery dynamics and minimizing both the charger count and consumption cost.

1 Introduction

The public transportation system is crucial in any urban area; however, the increased awareness and concern over the environmental impacts of petroleum-based public transportation have fueled efforts to reduce the pollution footprint (De Filippo et al., 2014; Xylia and Silveira, 2018; Guida and Abdulah, 2017; Li, 2016). One key solution is the electrification of public bus transportation via battery power, i.e., battery-electric buses (BEBs), which has received significant attention (Li, 2016). Although this technology provides benefits beyond a reduction in emissions, such as lower driving costs, lower maintenance costs, and reduced vehicle noise, battery-powered systems introduce new challenges, such as higher upfront costs and, potentially, long “refueling” periods, which can last several hours (Xylia and Silveira, 2018; Li, 2016). Furthermore, the problem is exacerbated by the constraints of the transit schedule to which the fleet must adhere, the limited number of chargers available, and the adverse effects of fast charging on battery health (Lutsey and Nicholas, 2019). This paper aims to remedy these problems by presenting a framework for optimally assigning BEBs to charging queues, assuming fixed routes, while considering multiple charger types and utilizing linear charging dynamics. This method also ensures that the state-of-charge (SOC) remains above a specified percentage throughout the day and ensures a minimum SOC at the end of the working day.

Recently, many efforts have been made to simultaneously solve the problems of route scheduling, charging fleets, and determining the infrastructure upon which they rely (Wei et al., 2018; Sebastiani et al., 2016; Hoke et al., 2014; Wang X. et al., 2017). Several simplifications are made to make these problems computationally feasible. Simplifications to the charge scheduling model include utilizing only fast chargers while planning (Wei et al., 2018; Sebastiani et al., 2016; Wang Y. et al., 2017; Zhou et al., 2020; Yang et al., 2018; Wang X. et al., 2017; Qin et al., 2016; Liu and Ceder, 2020). If slow chargers are used, they are only used at the depot and not at the station (He et al., 2020; Tang et al., 2019). Some approaches also simplify by assuming that full charge is always achieved (Wei et al., 2018; Wang X. et al., 2017; Zhou et al., 2020; Wang Y. et al., 2017). Others have assumed that the charge received is proportional to the time spent on the charger (Liu and Ceder, 2020; Yang et al., 2018), which can be a valid assumption when the battery SOC is below 80% (Liu and Ceder, 2020).

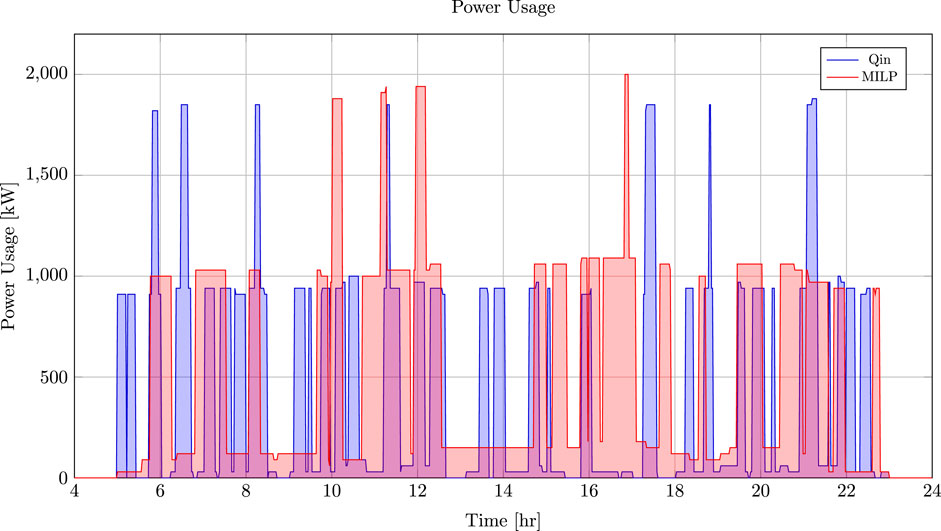
This work builds upon the position allocation problem (PAP) (Qarebagh et al., 2019), a modification of the well-studied berth allocation problem (BAP), as a means to schedule the charging of electric vehicles (Buhrkal et al., 2011; Frojan et al., 2015; Imai et al., 2001; Rodrigues and Agra, 2022). The BAP is a continuous time model that solves the problem of allocating space for incoming vessels to be berthed and serviced. Each arriving vessel requires both time and space for service and, thus, must be carefully assigned to avoid delay (Imai et al., 2001). Vessels are lined up parallel to the berth to be serviced and are horizontally queued, as shown in Figure 1. As the vessels are serviced, they move from left to right, creating space for the queued vessels, which move vertically downward into their respective berthing locations. The PAP utilizes this queuing concept for scheduling vehicles to be charged, as shown in Figure 2. The vehicles are queued in several lines and move from left to right to receive their charge before exiting the system. The PAP is formulated as a rectangle packing problem and assumes that each vehicle has a predefined charge time, and the number of vehicles that can be charged at any given moment is limited by the physical width of each vehicle and the length of the charging block. The PAP also assumes that each vehicle in the system is unique (Qarebagh et al., 2019).

Figure 1

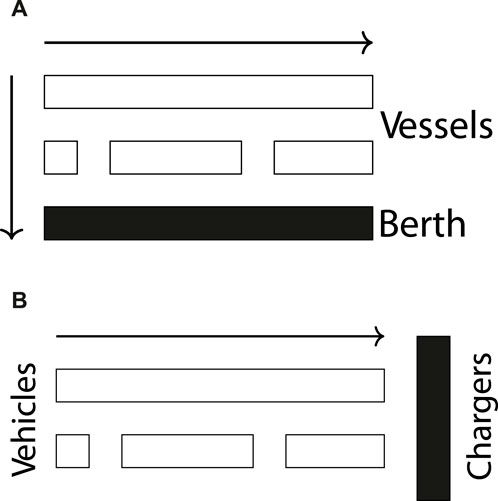
Figure 1. (A) Example of berth allocation. Vessels are docked in berth locations (horizontal) and queued over time (vertical). The vertical arrow represents the movement direction of the queued vessels, and the horizontal arrow represents the direction of departure. (B) Example of position allocation. Vehicles are placed in queues to be charged and move in the direction indicated by the arrow.

Figure 2

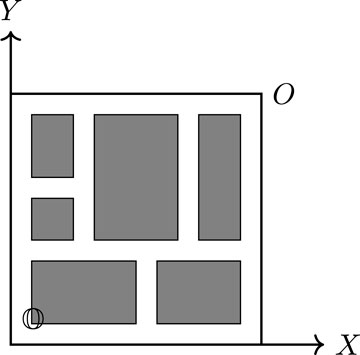
Figure 2. Example of the rectangle packing problem. The large square represented by $O$ indicates the constrained area that the set of shaded rectangles $\mathbb{O}$ must be placed within.

The main contribution of this work is the extension of the PAP’s novel approach to BEB charger scheduling. This incorporates a proportional charging model into the mixed-integer linear program (MILP) framework, considers multiple charger types, and considers each route in the schedule. The last contribution is of importance because both the BAP and PAP consider each arrival to be unique; thus, the tracking of battery charge from one visit to the next must be considered. Furthermore, the input parameters for the model can be predefined in such a manner as to minimize the number of fast and slow chargers utilized and minimize the energy consumption. That is, the model will simultaneously minimize the number of chargers and the total consumed energy. The result is a MILP formulation that coordinates charging times and charger type for every visit while considering a dynamic charge model with scheduling constraints.

The remainder of the paper is structured as follows: in Section 2, the PAP is introduced with a formulation of the resulting MILP; Section 3 constructs the MILP for BEB scheduling, including modifications to the PAP queuing constraints and the development of a dynamic charging model; Section 4 demonstrates an example of using the formulation to coordinate 35 buses over 338 total visits to the station; and Section 5 presents the concluding remarks.

2 Position allocation problem

This section provides a brief overview of the BAP and a detailed formulation of the PAP, as presented by Qarebagh et al. (2019).

2.1 Overview of the BAP

The BAP is a rectangle packing problem where a set of rectangles, denoted as $\mathbb{O}$, are optimally placed in a larger rectangle, denoted as $O$, as shown in Figure 3. The rectangle packing problem is an NP-hard problem and can be used to describe many real-life problems (de Bruin, 2013; Murata et al., 1995). In some of these problems, the dimensions of $\mathbb{O}$ are held constant, such as in the problem of packing modules on a chip, where the widths and heights of the rectangles correspond to the physical widths and heights of the modules (Murata et al., 1995). Other problems, such as the one presented in this work, allow either the horizontal or vertical edge of each rectangle in $\mathbb{O}$ to vary. For example, suppose the vessel lengths are predefined (i.e., vertical edges are static), but the service time is allowed to vary (i.e., horizontal edges are dynamic) (Buhrkal et al., 2011).

Figure 3

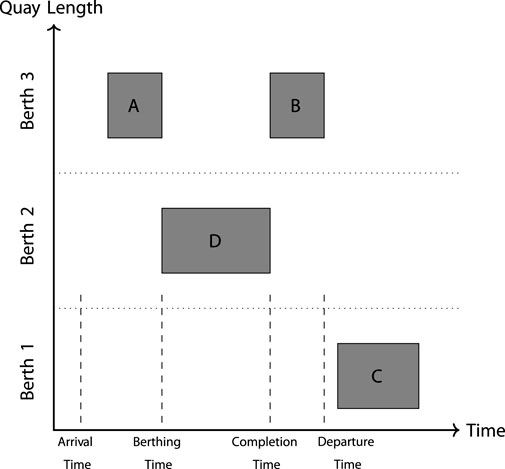
Figure 3. Representation of the berth–time space. The x- and y-axes represent time and space, respectively. Along the y-axis, the dashed lines represent discrete berthing locations. These locations may be chosen to be continuous. The shaded rectangles represent scheduled vessels to be serviced. The height of each shaded rectangle represents the space taken on the berth, and the width represents the time required to service the said vessel. The vertical dashed lines are associated with vessel D and represent the arrival time, berthing time, service completion time, and departure time. Note that the arrival time may be before the berthing time and the completion time may be before the departure time.

The BAP solves the problem of optimally assigning incoming vessels to berthing positions in order to be serviced, as shown in Figure 1. To relate to the rectangle packing problem, the width and height of $O$ represent the time horizon $T$ seconds and the berth length $L$ meters, respectively. Similarly, the widths and heights of each element in $\mathbb{O}$ represent the time spent to service vessel $i$ and the space taken by docking vessel $i$, respectively. In the BAP, the vessel characteristics (length of the vessel, arrival time, handling time, and desired departure time) are assumed to be known for all vessels. A representation of a BAP solution is shown in Figure 4. The x- and y-axes represent the time horizon and berthing space, respectively. The gray squares, labeled A, B, C, and D, represent scheduled vessels. The width of the boxes represents the time spent being serviced, and the height of the boxes represents the amount of space the vessel requires on the berth. The vertical line adjacent to the “arrival time” represents the time at which the vessel arrives and is available to be berthed. The “berthing time” is the time the vessel is berthed and begins to be serviced. The “completion time” represents the time at which the berthing space becomes available again.

Figure 4

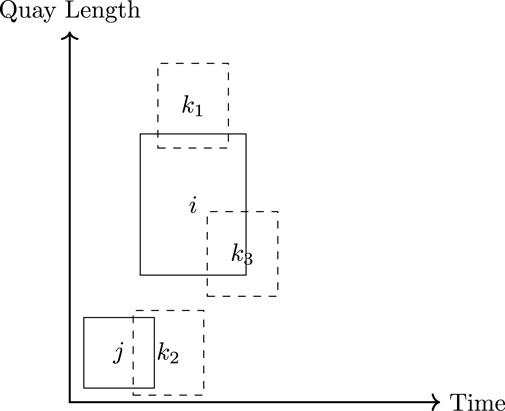
Figure 4. Examples of different methods of overlapping. Space overlap: $v_{k_1}<v_i+l_i\therefore {\psi }_{k_{1}i}=0$. Time overlap: $u_{k_1}<u_j+s_j\therefore {\sigma }_{k_{2}j}=0$. Both space and time overlap: ${\sigma }_{k_{3}i}=0$ and ${\psi }_{k_{3}j}=0$.

2.2 PAP formulation

The BAP forms the basis of the PAP; however, there are some differences in the way the variables are interpreted. The relevant variables are given in Table 1. The starting service time, $u_i$ s, is viewed as the initial charge time, and the service time is the total elapsed time spent on the charger. Similarly, for the spatial term, $v_i\in [0,L]$, the berth location is interpreted as the initial position on the charger. There are also a few clarifying concepts about how the system is modeled. The PAP models the set of chargers as one continuous line; that is, the natural behavior of the PAP model is to allow vehicles to be queued anywhere along $[0,L]$. Similarly, the charge times are continuous and can be placed anywhere on the time horizon, $[0,T]$, as long as the allocated times do not interfere with other scheduled charge times.

Table 1

Table 1. Notation used throughout the paper. Values and units are provided when available.

The PAP formulation’s parameters can be divided into two categories: input parameters and decision variables. The following parameters are assumed to be known inputs for the MILP. $L$ defines the length of the charger in meters. As stated previously, it is modeled as a continuous bar, meaning that a vehicle can be placed anywhere in the range $[0,L]$. It is assumed that the time horizon, $T$ s, is known so that vehicles may be placed temporarily in the range $[0,T]$. The total number of visits to the station over the time horizon is represented by $n_V$. The arrival time for each visit is represented by $a_i$ s, and the required charge time is represented by $s_i$ s. The width of vehicle $i$ is represented by $l_i$ m.

The decision variables provide the means by which the solver may optimize the problem. The initial and final charge times for vehicle $i$ are $u_i$ and $d_i$ s, respectively. The starting position on the charger is denoted as $v_i\in [0,L]$ m. The temporal ordering of vehicles $i$ and $j$ is determined by ${\sigma }_{ij}\in \{\mathrm{0,1}\}$, where ${\sigma }_{ij}=1\Rightarrow i$ arrives before $j$ for all $1\le i,j\le n_V$. Similarly, ${\psi }_{ij}\in \{\mathrm{0,1}\}$ determines the relative position of vehicles $i$ and $j$ on the charger: ${\psi }_{ij}=1\Rightarrow v_i<v_j$ for all $1\le i,j\le n_V$.

To determine the values for each of these decision variables, a MILP was formulated by Qarebagh et al. (2019). The formulation is shown in its entirety for completeness. The problem to be solved is

$\min {\displaystyle \sum _{i=1}^{n_v}}\left(d_i-a_i\right),(1)$

subject to

$u_j-u_i-s_i-\left({\sigma }_{ij}-1\right)T\ge 0,(\mathrm{2a})$

$v_j-v_i-l_i-\left({\psi }_{ij}-1\right)L\ge 0,(\mathrm{2b})$

${\sigma }_{ij}+{\sigma }_{ji}+{\psi }_{ij}+{\psi }_{ji}\ge 1,(\mathrm{2c})$

${\sigma }_{ij}+{\sigma }_{ji}\le 1,(\mathrm{2d})$

${\psi }_{ij}+{\psi }_{ji}\le 1,(2e)$

$s_i+u_i=d_i,(\mathrm{2f})$

$a_i\le u_i\le \left(T-s_i\right),(\mathrm{2g})$

${\sigma }_{ij}\in \left\{\mathrm{0,1}\right\},{\psi }_{ij}\in \left\{\mathrm{0,1}\right\},(\mathrm{2h})$

$v_i\in \left[0,L\right],(\mathrm{2i})$

$i,j=1\dots n_V;i\ne j.(\mathrm{2j})$

The objective function, Equation 1, minimizes the idle and service time by summing over the differences between the departure time, $d_i$, and arrival time, $a_i$, for all visits. In other words, the objective function is to search for the schedule that removes each vehicle from the service queue as quickly as possible.

Equations 2a–e are used to ensure that individual rectangles do not overlap. In terms of the PAP, this implies that there are no conflicts in the schedule spatially or temporally. Equation 2a establishes temporal ordering when active $({\sigma }_{ij}=1)$ in the manner described previously by utilizing big-M notation. Similarly, Equation 2b establishes spatial ordering when active $({\psi }_{ij}=1)$. Equations 2c, e enforce spatial and temporal ordering between each queue/vehicle pair. Equation 2d and Equation 2e enforce the validity of the assignments. For example, if Equation 2d resulted in a value of 2, that would imply that both vehicles $i$ and $j$ are scheduled before and after each other temporally, which is impossible. In the case of Equation 2e being equal to 2, it would mean that vehicles $i$ and $j$ are scheduled both before and after one another on the charging strip, which is again impossible.

The last constraints force relationships between arrival time, initial charge time, and departure time. Equation 2f states that the initial charge time, $u_i$, plus the total charge time, $s_i$, must equal the departure time, $d_i$. Equation 2g enforces the arrival time, $a_i$, to be less than or equal to the service start time, $u_i$, which, in turn, must be less than or equal to the latest time the vehicle may begin charging and stay within the time horizon. Equation 2h simply states that ${\sigma }_{ij}$ and ${\psi }_{ij}$ are binary terms. Equations 2i, 2j ensures that the assigned value of $v_i$ is within the range $[0,L]$.

3 Rectangle packing formulation for BEB charging

Applying the PAP to BEB charging requires four fundamental changes. The first is that the time that a BEB spends charging must be allowed to vary. That is, $u_i$, $d_i$, and $s_i$ become variables of optimization. This is done primarily because chargers of various speeds are to be introduced. Second, in the PAP, each visit is assumed to be a different vehicle. For the BEB charging problem, each bus may make multiple visits to the station throughout the day. Thus, the resulting SOC for a bus at a given visit is dependent upon each of the prior visits. The third fundamental change is related to the first two. The SOC of each bus must be tracked to ensure that charging across multiple visits is sufficient to allow each bus to execute its route throughout the day. Finally, as previously stated, the PAP models the charger as one continuous bar. For the BEB, it will be assumed that a discrete number of chargers exist. Moreover, it is assumed that these chargers may have different charge rates.

A few assumptions are made in the derivation of the algorithm. As this work is not focused on estimating the discharge of a BEB during its route, the discharge for each route will be pre-calculated by assuming a fixed discharge rate kW multiplied by the route duration in hours. Second, it is assumed that the initial SOC of each BEB at the beginning of the day, ${\alpha }_b{\kappa }_b$, is larger than the minimum required SOC at the end of the day, ${\beta }_b{\kappa }_b$. Therefore, it must be assumed that the difference in the SOC can reach ${\alpha }_b{\kappa }_b$ by the beginning of the next working day.

The discussion of the four changes is separated into two sections. Subsection 3.1 discusses the changes in the spatiotemporal constraint formulation to form a queuing constraint. Subsection 3.2 discusses the addition of bus charge management. This section ends with a brief discussion of a modified objective function and the statement of the full problem in Subsection 3.3. The notation is explained throughout and summarized in Table 1.

3.1 Queuing constraints

The queuing constraints ensure that the buses entering the charging queues are assigned feasibly. There are three sets to differentiate between different entities. $\mathbb{B}=\{1,\dots ,n_B\}$ is the set of bus indexes, with index $b$ used to denote an individual bus, $\mathbb{Q}=\{1,\dots ,n_Q\}$ is the set of queues, with index $q$ used to denote an individual queue, and $\mathbb{V}=\{1,\dots ,n_V\}$ is a set of visits to the station, with $i$ and $j$ used to refer to individual visits. The mapping $\mathrm{\Gamma }:\mathbb{V}\to \mathbb{B}$ is used to map a visit index, $i$, to a bus index, $b$. The notation ${\mathrm{\Gamma }}_i$ is used as a shorthand to refer to bus index $b$ for visit $i$.

The actual physical dimensions of the BEB are ignored, and it is assumed that each BEB will be assigned to charge at a particular charger. Because of this assumption, the PAP spatial variable, $l_i$, may be removed, and $v_i$ is made to be an integer corresponding to which queue visit $i$ will be used, $v_i\in \mathbb{Q}$. That is, the queue position is now discretized over $n_Q$ queues, where a BEB occupies a single charge queue. Thus, when ${\psi }_{ij}=1$, vehicle $j$ is placed in a charging queue with a larger index than that of vehicle $i$, i.e., $v_j>v_i$. The charger length $L$ is likewise replaced with $n_Q$. Note that $n_Q=n_B+n_C$, where $n_B$ is the number of buses and $n_C$ is the number of chargers. The rationale for adding additional idle queues is to allow BEBs to be “set aside” if no additional charge is required. Adding one idle queue for each BEB ensures that the constraints will be satisfied if multiple buses sharing overlapping times at the station are placed in idle queues. This method will be applied when defining the parameters in Section 4. The modified queuing constraints can be written as shown in Equation 3:

$v_i-v_j-\left({\psi }_{ij}-1\right)n_Q\ge 1(\mathrm{3a})$

$d_i\le {\tau }_i,(\mathrm{3b})$

$s_i\ge 0,(\mathrm{3c})$

$v_i\in \mathbb{Q}.(\mathrm{3d})$

The constraint in Equation 3a is nearly identical to Equation 2b, but rather than viewing the charger as a continuous strip of length $L$, it is discretized into $n_Q$ queues, each with a width of unit length 1. A BEB is also assigned a unit length of 1, which is reflected in Equation 3a by $\cdot \ge 1$. Equation 3b ensures that the time the BEB is detached from the charger, $d_i$, is before its departure time, ${\tau }_i$ s. Note that the introduction of the new variable ${\tau }_i$ exists to allow the final charge time to be independent, similar to the manner in which to the initial charge time is independent of the arrival time, $a_i\le u_i\le d_i\le {\tau }_i$. Equation 3c ensures that the change time is non-negative. Equation 3d defines $v_i$ to be an element from the set of queues.

3.2 Battery charge dynamic constraints

This section introduces the battery dynamic constraints. Two constraints are enforced on the SOC for each BEB: the SOC must always remain above a specified percentage to guarantee sufficient charge to execute their respective routes, and each bus must end the day with a SOC above a specified threshold, in preparation for the next day.

The SOC upon arrival for visit $i$ is denoted as ${\eta }_i$ kWh. Because the SOC for visit $i$ is dependent on its previous visits, the mapping $\mathrm{\Upsilon }:\mathbb{V}\to \mathbb{V}\bigcup \{\varnothing \}$ is used to determine the next visit that corresponds to the same bus, with ${\mathrm{\Upsilon }}_i$ being the shorthand notation. Thus, ${\mathrm{\Gamma }}_j$ and ${\mathrm{\Gamma }}_{{\mathrm{\Upsilon }}_i}$, for ${\mathrm{\Upsilon }}_i=j$, would both map to the same bus index as long as ${\mathrm{\Upsilon }}_i$ is not the null element, $\varnothing$. The null element is reserved for BEBs that have no future visits.

To define the time spent on the charger, $s_i$, as well as the initial, final, and intermediate bus charges for each visit $i$, the sets for the initial and final visits must be defined. Let the mapping of the first visit by each bus be denoted as ${\mathrm{\Gamma }}^0:\mathbb{B}\to \mathbb{V}$. The resulting value of the mapping ${\mathrm{\Gamma }}^0$ represents the index for the first visit of bus $b$. Similarly, let ${\mathrm{\Gamma }}^f:\mathbb{B}\to \mathbb{V}$ map the indexes for the final visits for each bus $b\in \mathbb{B}$. Let the shorthand for each mapping be denoted as ${\mathrm{\Gamma }}_b^0$ and ${\mathrm{\Gamma }}_b^f$. The initial and final bus charge percentages, $\alpha$ and $\beta$, can then be represented by the constraint equations ${\eta }_{{\mathrm{\Gamma }}_b^0}={\alpha }_b{\kappa }_b$ and ${\eta }_{{\mathrm{\Gamma }}_b^f}={\beta }_b{\kappa }_b$, respectively. The intermediate charges must be determined during runtime.

It is assumed that the charge received is proportional to the time spent charging. The rate for charger $q$ is denoted as $r_q$ kW. Note that a value of $r_q=0$ corresponds to a queue where no charging occurs. A bus in such a queue simply waits at the station for the departure time. The queue indexes are ordered such that the first $n_B$ queues have $r_q=0$ to allow an arbitrary number of buses to sit idle at any given moment in time. The next $n_C$ queues are reserved for the slow and fast chargers. The amount of discharge between visits $i$ and ${\mathrm{\Upsilon }}_i$, the next visit of the same bus, is denoted as ${\mathrm{\Delta }}_i$ kWh. If visit $i$ occurred at charger $q$, the SOC of the BEB’s next arrival, ${\mathrm{\Upsilon }}_i$, would be ${\eta }_{{\mathrm{\Upsilon }}_i}={\eta }_i+s_i{r}_q-{\mathrm{\Delta }}_i$.

The binary decision variable $w_{iq}\in \{\mathrm{0,1}\}$ is introduced to indicate the active charger for visit $i$ in vector form. The form of the SOC for the next visit, ${\mathrm{\Upsilon }}_i$, can be written using the following constraints:

${\eta }_{{\mathrm{\Upsilon }}_i}={\eta }_i+{\displaystyle \sum _{q=1}^{n_Q}}{s}_i{w}_{iq}{r}_q-{\mathrm{\Delta }}_i,(\mathrm{4a})$

${\displaystyle \sum _{q=1}^{n_Q}}{w}_{iq}=1,(\mathrm{4b})$

$w_{iq}\in \left\{\mathrm{0,1}\right\}.(\mathrm{4c})$

Where Equation 4a represents the SOC for the next visit of BEB $b$, Equation 4b ensures that the BEB for visit $i$ is assigned to a single queue, and Equation 4c specifies that $w_{iq}$ is a binary value.

The choice of queue for visit $i$ becomes a slack variable and is defined in terms of $w_{iq}$ as

$v_i={\displaystyle \sum _{q=1}^{n_Q}}q{w}_{iq}.(5)$

Maximum and minimum values for the charges are included to ensure that the battery is not overcharged and guarantee sufficient charge for subsequent visits. The upper and lower battery charge bounds for bus $b$ are ${\kappa }_b$ and ${\nu }_b{\kappa }_b$, respectively, where ${\kappa }_b$ is the battery capacity and ${\nu }_b$ is a percent value. The upper and lower bounds for the current SOC are written as follows:

${\eta }_i+{\displaystyle \sum _{q=1}^{n_Q}}{s}_i{w}_{iq}{r}_q\le {\kappa }_{{\mathrm{\Gamma }}_i},(\mathrm{6a})$

${\eta }_i\ge {\nu }_{{\mathrm{\Gamma }}_i}{\kappa }_{{\mathrm{\Gamma }}_i}.(\mathrm{6b})$

Equation 6a ensures that the BEB SOC does not exceed the battery capacity, and Equation 6b ensures that the initial SOC for each visit is above the threshold of ${\nu }_{{\mathrm{\Gamma }}_i}{\kappa }_{{\mathrm{\Gamma }}_i}$. Note that the term $s_i{w}_{iq}$ is a bilinear term. A standard method for linearizing a bilinear term that contains an integer variable is by introducing a slack variable with an either/or constraint (Chen et al., 2010; Rodriguez and Vecchietti, 2013). Allowing the slack variable $g_{iq}$ s to be equal to $s_i{w}_{iq}$, $g_{iq}$ can be defined as

$g_{iq}=\left\{\begin{array}{cc}{s}_i\hfill & w_{iq}=1\hfill \\ 0\hfill & w_{iq}=0\hfill \end{array}\right..(7)$

Equation 7 can be expressed as a mixed-integer constraint using big-M notation with the following four constraints:

$s_i-\left(1-w_{iq}\right)M\le g_{iq},(\mathrm{8a})$

$s_i\ge g_{iq},(\mathrm{8b})$

$M{w}_{iq}\ge g_{iq},(\mathrm{8c})$

$0\le g_{iq},(\mathrm{8d})$

where $M$ is a large unitless value. If $w_{iq}=1$, then Equations 8a, b become $s_i\le g_{iq}$ and $s_i\ge g_{iq}$, forcing $s_i=g_{iq}$, with Equation 8c being inactive. If $w_{iq}=0$, Equation 8a is inactive, and Equations 8c, d force $g_{iq}=0$.

3.3 BEB charging problem

The goal of the MILP is to utilize chargers as little as possible to reduce energy costs, with fast charging being penalized more to avoid its adverse effects on battery health and to account for the higher usage costs. Thus, assignment cost $m_q$ and usage cost ${ϵ}_q$ are associated with each charger, $q$. These unitless weights can be adjusted based on the charger type or time of day when the visit occurs. The assignment term takes the form $w_{iq}{m}_q$, and the usage term takes the form $g_{iq}{ϵ}_q$. The resulting BEB charging problem is defined in Equation 9:

$\min {\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{q=1}^{n_Q}}\left(w_{iq}{m}_q+g_{iq}{ϵ}_q\right),(9)$

subject to the constraints

$u_j-u_i-s_i-\left({\sigma }_{ij}-1\right)T\ge 0,(\mathrm{10a})$

$v_j-v_i-\left({\psi }_{ij}-1\right)n_Q\ge 1,(\mathrm{10b})$

${\sigma }_{ij}+{\sigma }_{ji}+{\psi }_{ij}+{\psi }_{ji}\ge 1,(\mathrm{10c})$

${\sigma }_{ij}+{\sigma }_{ji}\le 1,(\mathrm{10d})$

${\psi }_{ij}+{\psi }_{ji}\le 1,(10e)$

$s_i+u_i=d_i,(\mathrm{10f})$

${\eta }_{{\mathrm{\Gamma }}_b^0}={\alpha }_{{\mathrm{\Gamma }}_i}{\kappa }_{{\mathrm{\Gamma }}_i},(\mathrm{10g})$

$a_i\le u_i\le \left(T-s_i\right),(\mathrm{10h})$

$d_i\le {\tau }_i,(\mathrm{10i})$

${\eta }_i+{\displaystyle \sum _{q=1}^{n_Q}}{g}_{iq}{r}_q-{\mathrm{\Delta }}_i={\eta }_{{\gamma }_i},(\mathrm{10j})$

${\eta }_i+{\displaystyle \sum _{q=1}^{n_Q}}{g}_{iq}{r}_q-{\mathrm{\Delta }}_i\ge {\nu }_{{\mathrm{\Gamma }}_i}{\kappa }_{{\mathrm{\Gamma }}_i},(\mathrm{10k})$

${\eta }_i+{\displaystyle \sum _{q=1}^{n_Q}}{g}_{iq}{r}_q\le {\kappa }_{{\mathrm{\Gamma }}_i},(\mathrm{10l})$

${\eta }_{{\mathrm{\Gamma }}_b^f}\ge {\beta }_{{\mathrm{\Gamma }}_f}{\kappa }_{{\mathrm{\Gamma }}_f},(\mathrm{10m})$

$s_i-\left(1-w_{iq}\right)M\le g_{iq},(\mathrm{10n})$

$s_i\ge g_{iq},(\mathrm{10o})$

$M{w}_{iq}\ge g_{iq},(\mathrm{10p})$

$0\le g_{iq},(\mathrm{10q})$

$v_i={\displaystyle \sum _{q=1}^{n_Q}}q{w}_{iq},(\mathrm{10r})$

${\displaystyle \sum _{q=1}^{n_Q}}{w}_{iq}=1,(\mathrm{10s})$

$w_{iq},{\sigma }_{ij},{\psi }_{ij}\in \left\{\mathrm{0,1}\right\},(\mathrm{10t})$

$v_i,q_i\in \mathbb{Q},(\mathrm{10u})$

$i\in \mathbb{V}.(\mathrm{10v})$

Equations 10a–i are reiterations of the queuing constraints from Equation 2; Equation 3. Equations 10g–m provide the battery charge constraints. Equations 10n–q define the charge duration of every visit/queue pairing. Equations 10r, 10s are reiterations of Equation 4b and Equation 5, respectively. Equations 10t–v define the sets of valid values for each variable.

4 Example

We present an example to demonstrate the utility of the developed MILP charge scheduling technique. A description of the scenario is first presented, followed by a description of an alternative heuristic-based planning strategy called Qin-modified method, which is used as a comparison with the MILP PAP. The results are then presented, analyzed, and discussed for each of the planning strategies.

4.1 BEB scenario

To display the capabilities of the model, an example scenario is presented. The scenario was run over a time horizon of $T=24$ h, utilizing $n_B=35$ buses with $n_V=338$ visits divided between the $n_B$ buses. As stated before, the route times are sampled from a set of routes provided by the Utah Transit Authority (UTA). Each bus has a battery capacity of ${\kappa }_b=$ 388 kWh, which is required to stay above an SOC of ${\nu }_b=$ 20% (77.6 kWh) $\forall b\in \mathbb{B}$ to ensure that each BEB can complete its next route while maintaining battery health. Each bus is assumed to begin the working day with an SOC of $alph{a}_b=$ 90% $\forall i\in \mathbb{V}$ (349.2 kWh). Additionally, each bus is required to end the day with a minimum SOC of ${\beta }_b=$ 70% (271.6 kWh) $\forall b\in \mathbb{B}$. This assumes that overnight charging can account for the 20% SOC deficit. Furthermore, the value selected for ${\beta }_b\forall b\in \mathbb{B}$ is primarily for illustrative purposes and has no particular significance other than to demonstrate the user’s ability to specify the desired end-of-day SOCs. Each bus is assumed to discharge at a rate of ${\zeta }_b=$ 30 kW. Note that many factors play a role in the rate of discharge; however, for the sake of simplicity, since the discharge calculation is beyond the scope of this work, an average rate is used. A total of $n_C=30$ chargers are utilized, where 15 of the chargers are slow charging (30 kW) and 15 are fast charging (911 kW). The technique to minimize the total charger count is used.

To encourage the MILP PAP to utilize the fewest number of chargers, the value of $m_q$ in the objective function, Equation 9, is set as follows: $\forall q\in \{\mathrm{1,2},\dots ,n_B\};m_q=0$ and $\forall q\in \{n_B+1,n_B+2,\dots ,n_B+n_C\};m_q=1000q$. The charge duration scalar, ${ϵ}_q$, is defined as ${ϵ}_q=r_q$ to create a consumption cost term, $g_{iq}{ϵ}_q$ kWh. By consumption cost, it is meant that the total energy consumed by the charge schedule will be accounted for in the objective function. This method encourages the model to minimize active charger times, particularly for the fast chargers.

Another heuristic-based optimization strategy, referred to as the Qin-modified method, is also used to compare the results of the MILP PAP. The Qin-modified strategy is based on the threshold strategy proposed by Qin et al. (2016). The strategy has been modified slightly to accommodate the case of multiple charger types without an exhaustive search for the best charger type. The heuristic is based on a set of rules that revolve around the initial SOC of the bus visit $i$. There are three different thresholds, low (85%), medium (90%), and high (95%). Buses below the low threshold ($\text{SOC}\le 85$%) are prioritized to fast chargers and are then allowed to utilize slow chargers if no fast chargers are available. Buses between the low and medium threshold (85% $<\text{SOC}\le$ 90%) prioritize slow chargers first and utilize fast chargers only if no slow chargers are available. Buses above the medium threshold and below the high threshold (90% $<\text{SOC}\le$ 95%) will only be assigned to slow chargers. Buses above the high threshold ($\text{SOC}>$ 95%) will not be placed in a charging queue. Once a bus has been assigned to a charger, it remains on the charger for the duration of the time it is at the station or reaches an SOC of 95% charge, whichever comes first.

The total number of constraints resulted in 7,511 continuous and 328,282 integer/binary constraints. The optimization was performed using the Gurobi MIP solver (Gurobi Optimization, LLC, 2021) on a machine equipped with an AMD Ryzen 9 5900 × 12 Processor (24 core) running at 4.95 GHz. The solver was allowed to run for $7.200$ s.

4.2 Results

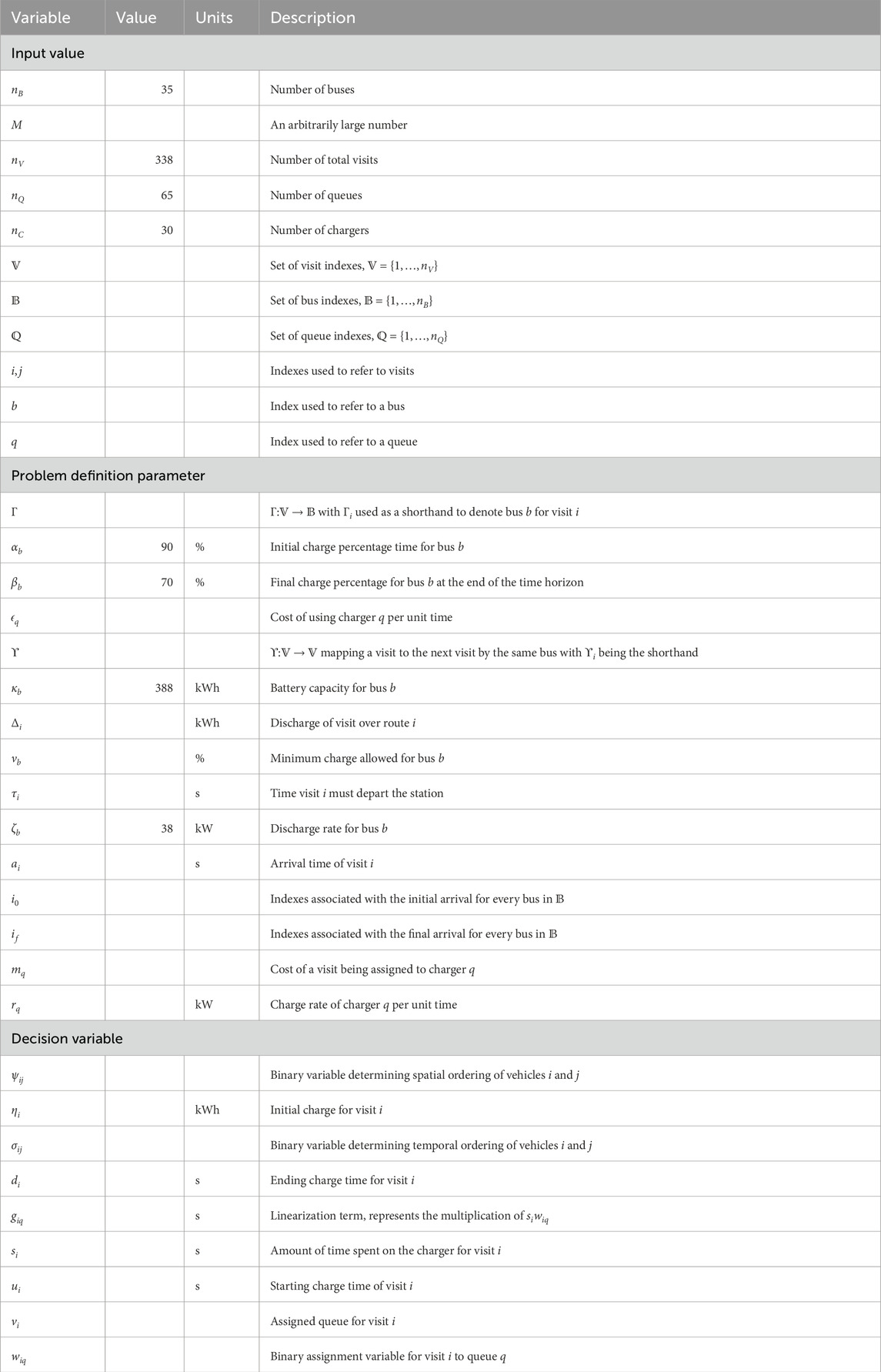
The schedule generated by the Qin-modified strategy and the MILP PAP is shown in Figures 5A, B, respectively. The x-axis represents the time in hours. The y-axis represents the assigned charging queue. Rows between 0 and 14 are active times for slow chargers, and rows in the range of 15 and 29 are active times for fast chargers. The unique color/symbol-styled vertices represent the starting charge time for a bus $b$, with the line to the vertical tick signifying the region of time the charger is active. The lines connecting the points represent the charge sequence for each BEB.

Figure 5

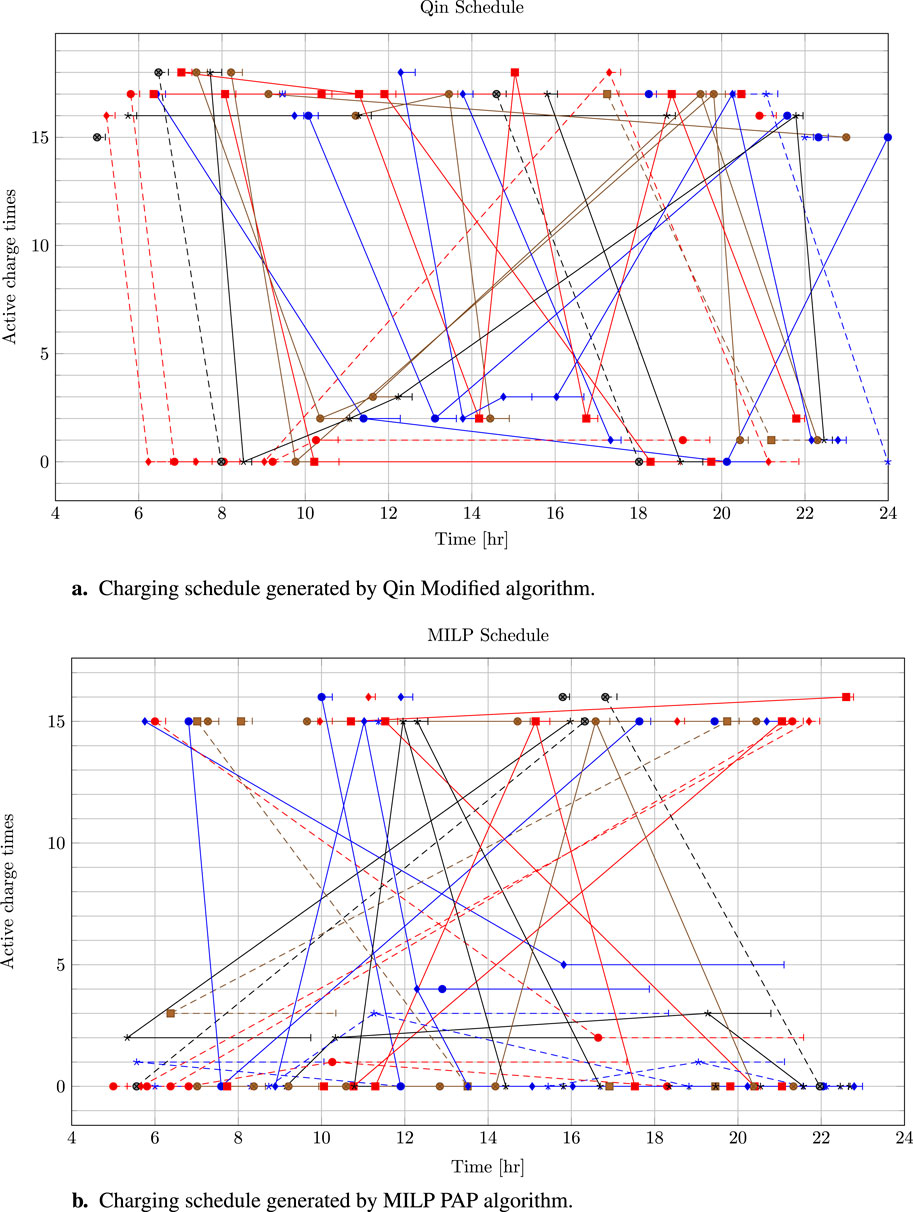
Figure 5. (A) Charging schedule generated by the Qin-modified algorithm. (B) Charging schedule generated by the MILP PAP algorithm.

The first observation is in the choice of preferred chargers between the Qin-modified and MILP scheduler. Figures 6A, B show that the Qin-modified schedule uses at most four fast chargers and three slow chargers at the same time, whereas the MILP schedule uses at most one fast charger and six slow chargers at the same time. Both the Qin-modified and MILP schedule used the fast chargers in short bursts (˜0.2–0.5 h). The main difference lies in the utilization strategy of the slow chargers. The Qin-modified method, for the most part, opted for shorter bursts for the slow chargers (˜0.3–0.7 h), most heavily placed on the first slow charger. The MILP utilized the slow chargers in short bursts; however, the solver recognized moments where a BEB being placed in a slow-charging queue for a longer duration was more cost-effective (with respect to the objective function) than the BEB placed in a fast-charging queue. Although one of the objectives of the MILP was to minimize the amount of chargers used, the Qin-modified schedule ended up using fewer chargers than the MILP. Note that the MILP schedule packed the first queue for the fast and slow chargers more effectively than the Qin-modified schedule. Although both schedules generated are valid, no comparison of the quality of the schedule can be made directly from Figures 5A, B.

Figure 6

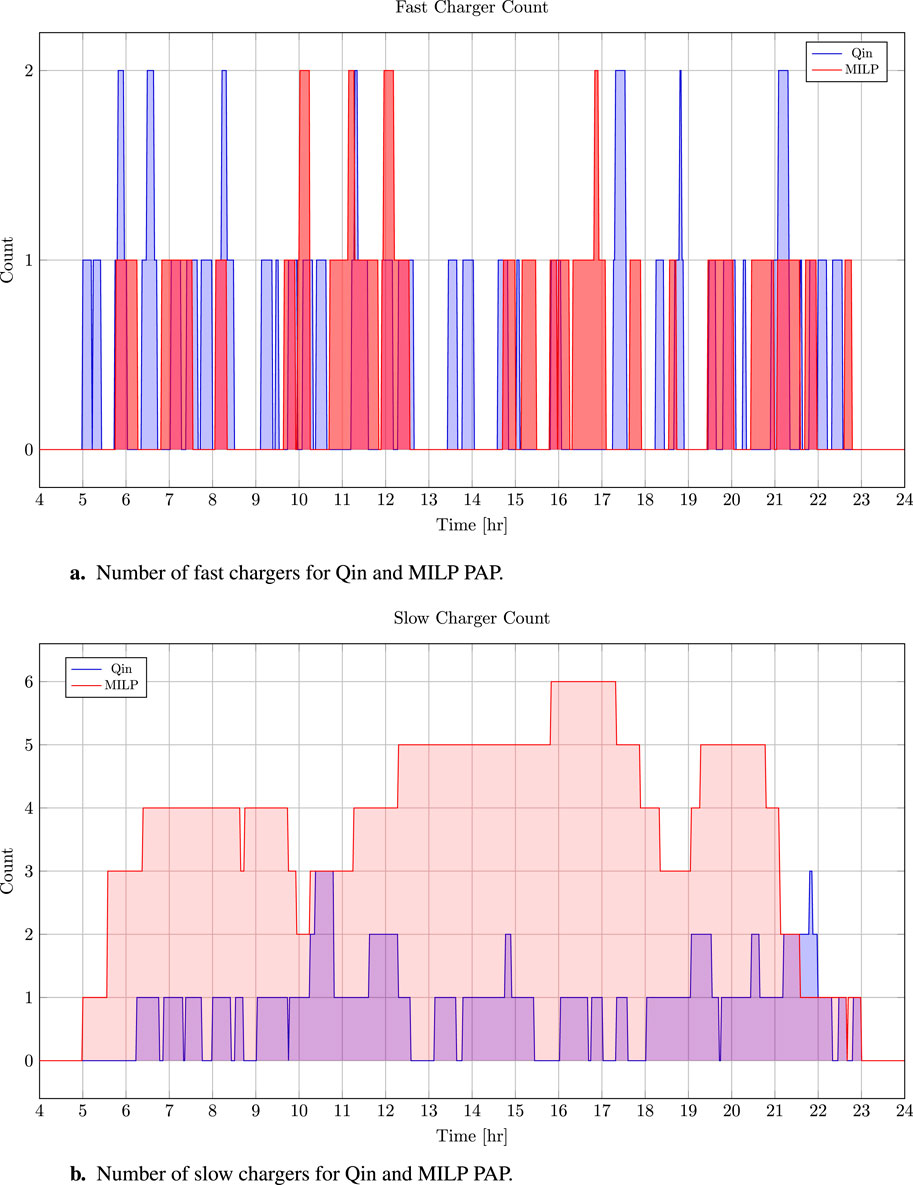
Figure 6. (A) Number of fast chargers for Qin-modified and MILP PAP methods. (B) Number of slow chargers for Qin-modified and MILP PAP methods.

Figures 7A, B depict the charge for every bus over the time horizon for the Qin-modified and MILP schedules, respectively. Every vehicle begins with a SOC of ${\alpha }_b=$ 90%, finishes with a SOC of ${\beta }_b=$ 70% in the MILP PAP schedule, and never goes below 20% in the intermediate arrivals, as stated in Equation 10. There is no guarantee for this in the Qin-modified strategy, which can be observed by some intermediate charges reaching a SOC of 0% and the distribution of final charges, the minimum being 0% and the maximum being 94.845%. It is of note that the SOC plummeting to 0% is due to the reactive nature of the Qin-modified method. Specifically, the schedule utilized in this example contains some BEBs that begin with routes that deplete the SOC by small amounts but do not fall below the threshold. These routes are followed by small charge windows, which are then preceded by large routes depleting the SOC by a significant amount, resulting in the SOC reaching 0%. The only guarantee that the Qin-modified method supplies is its predictability for the intermediate visits due to its heuristic nature (i.e., if the BEB charge is within the low threshold, a fast charger will be prioritized), whereas MILP places a bus in the queue that “makes sense” in the context of the larger picture. The MILP PAP does not have an obvious decision-making process because its weighted objective function is affected by the accumulation of previous decisions.

Figure 7

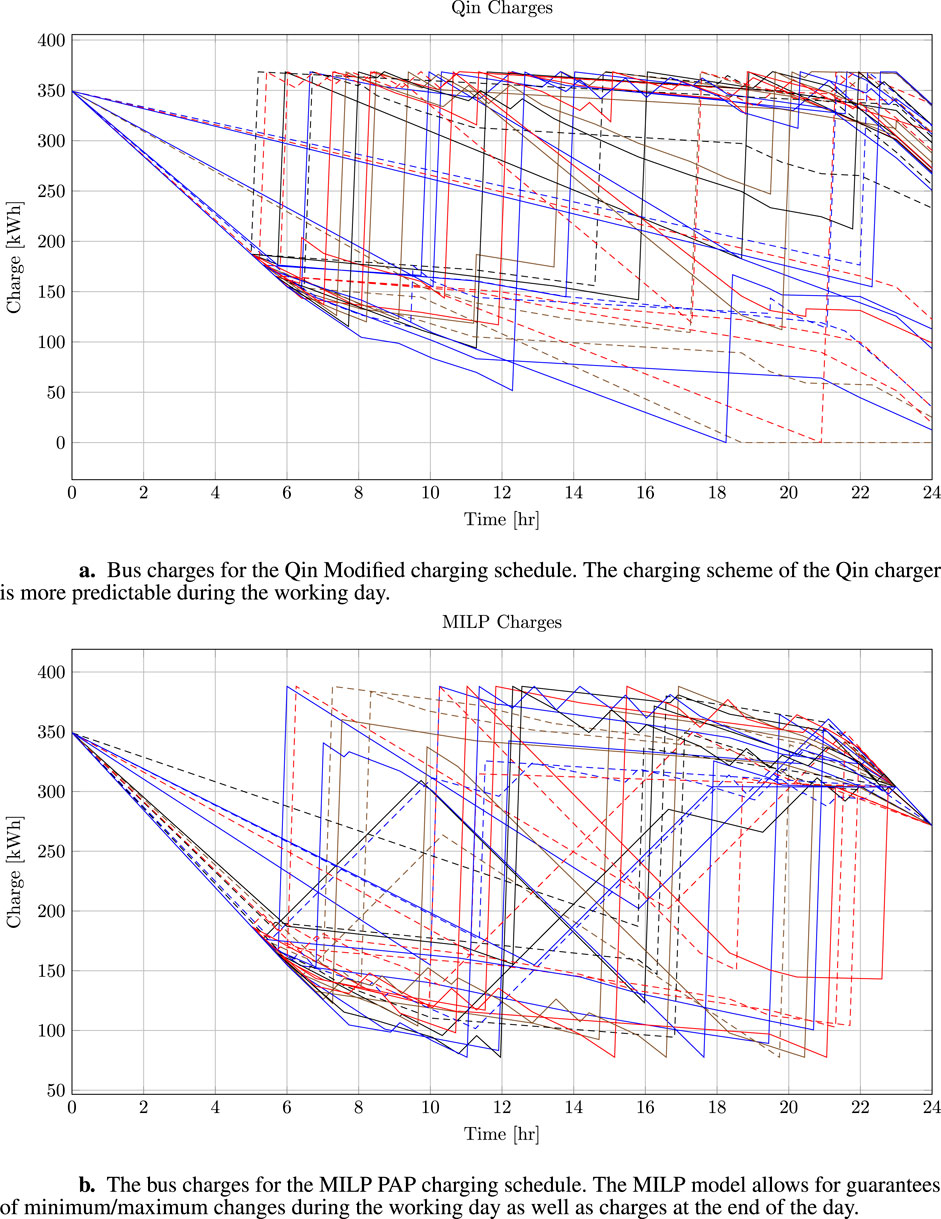
Figure 7. (A) Bus charges for the Qin-modified charging schedule. The charging scheme of the Qin charger is more predictable during the working day. (B) Bus charges for the MILP PAP charging schedule. The MILP model allows for guarantees of minimum/maximum changes during the working day and charges at the end of the day.

Another important measure for the chargers is to compare the amount of power and energy consumed. Figure 8 depicts the power consumption throughout the time horizon. It can be seen that the Qin-modified power consumption is steadily less or the same as that of the MILP schedule. This can be accounted for by the MILP’s constraints to keep the bus SOC above 20% and to reach a final SOC of 70% at the end of the working day. Similarly, the accumulated energy consumed is shown in Figure 9. The MILP schedule is more efficient up until about the 11th hour. Again, this can be accounted for by the fact that the MILP accommodates the extra constraints. Due to these constraints, the MILP PAP consumes approximately $0.1\cdot 10^4$ kWh more than the Qin-modified method. The overlap of the MILP PAP can be accounted for by referencing Figures 6A, B. Between the 5th and 10th hours, the MILP schedule mainly uses slow chargers, increasing the rate at which power is being consumed. Afterward, the MILP schedule continues to use at least the same number of chargers as the Qin-modified schedule. However, due to the added constraints, the MILP schedule must utilize more resources to remain within the specified bounds.

Figure 8

Figure 8. Amount of power consumed by the Qin-modified and MILP schedules over the time horizon.

Figure 9

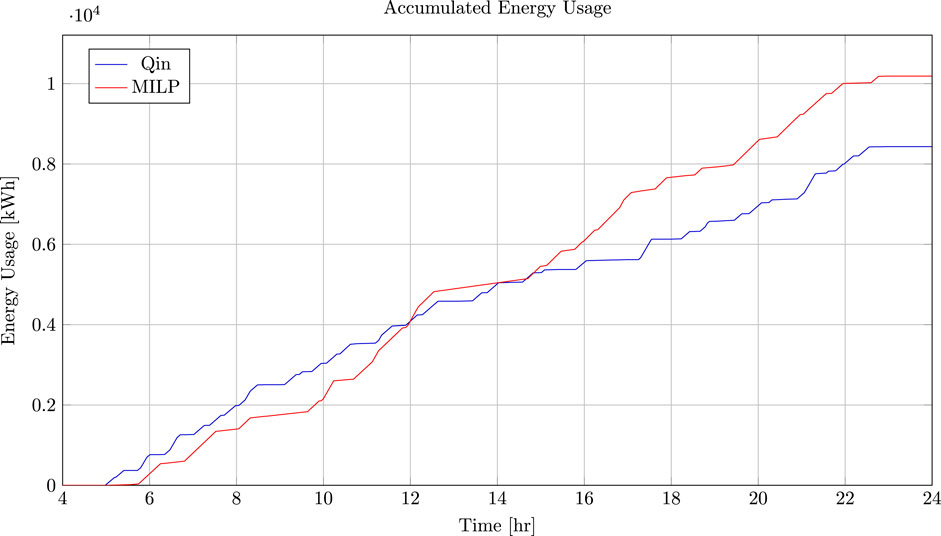
Figure 9. Total accumulated energy consumed by the Qin-modified and MILP schedules throughout the time horizon.

5 Conclusion

This work developed a MILP scheduling framework that optimally assigns fast and slow chargers to a BEB fleet, assuming a constant schedule. The BAP was briefly introduced, followed by a description and formulation of the PAP. The PAP was modified to allow the charge time to be variable. Because the modified PAP no longer requires a predefined charge time, linear battery dynamics were introduced to model the propagation of each BEB’s SOC. Additional constraints were also introduced to provide upper and lower limits for the battery dynamics.

An example of the MILP PAP formulation was then presented and compared to a heuristic-based schedule, referred to as the Qin-modified method. The MILP PAP optimization was run for 7,200 s to a non-optimal solution. The Qin-modified and MILP schedule utilized four and one fast charger(s), respectively. Furthermore, the MILP and Qin-modified method utilized the fast chargers for similar durations ranging from approximately 0.2 to 0.5 h; however, the MILP schedule demonstrated battery health considerations by recognizing visits that could utilize slow chargers for longer durations while satisfying the constraints. The MILP PAP schedule utilized approximately $0.1\cdot 10^4$ kWh more than the Qin-modified method, but the SOC for the MILP schedule remained above the constrained minimum SOC of 20% and charged all the buses to 70% at the end of the working day. That is, the constraints applied to the MILP model consumed more energy to satisfy the SOC threshold requirements. The Qin-modified schedule, on the other hand, allowed the SOC of certain BEBs to decrease to 0%. The SOC at the end of the day for the Qin-modified method varied from 0% to 94.85%, whereas the results of the MILP showed that the BEBs converged to the specified minimum SOC of 70%.

Further fields of interest include utilizing the formulation (Equation 9; Equation 10) with nonlinear battery dynamics, calculation and utilization of the demand and consumption cost in the objective function, and utilizing this formulation in a metaheuristic solver. Furthermore, “fuzzifying” the initial and final charge times is of interest to allow flexibility in the arrival and departure times.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

AB: conceptualization, software, and writing–original draft. GD: supervision and writing–review and editing. JG: supervision and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported in part by the Department of Energy through a Prime Award with ABB Ltd., under Grand DE-EE0009194, and in part by PacifiCopr Under Contract 3590. The funder had no involvement in the study design, data collection and analysis, or preparation of the manuscript. They did review and approve the publication prior to the decision to publish.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2024.1347442/full#supplementary-material

References

Buhrkal, K., Zuglian, S., Ropke, S., Larsen, J., and Lusby, R. (2011). Models for the discrete berth allocation problem: a computational comparison. Transp. Res. Part E Logist. Transp. Rev. 47, 461–473. doi:10.1016/j.tre.2010.11.016

CrossRef Full Text | Google Scholar

Chen, D.-S., Batson, R. G., and Dang, Y. (2010). Applied integer programming. Wiley.

Google Scholar

de Bruin, F. (2013). Rectangle Packing. Master’s thesis. Amsterdam (Netherlands): University of Amsterdam.

Google Scholar

De Filippo, G., Marano, V., and Sioshansi, R. (2014). Simulation of an electric transportation system at the Ohio state university. Appl. Energy 113, 1686–1691. doi:10.1016/j.apenergy.2013.09.011

CrossRef Full Text | Google Scholar

Frojan, P., Correcher, J. F., Alvarez-Valdes, R., Koulouris, G., and Tamarit, J. M. (2015). The continuous berth allocation problem in a container terminal with multiple quays. Expert Syst. Appl. 42, 7356–7366. doi:10.1016/j.eswa.2015.05.018

CrossRef Full Text | Google Scholar

Guida, U., and Abdulah, A. (2017). ZeEUS eBus Report# 2-An updated overview of electric buses in Europe. Tech. Rep. 2, International Association of Public Transport (UITP)

Google Scholar

Gurobi Optimization, LLC (2021). Gurobi optimizer reference manual

Google Scholar

He, Y., Liu, Z., and Song, Z. (2020). Optimal charging scheduling and management for a fast-charging battery electric bus system. Transp. Res. Part E Logist. Transp. Rev. 142, 102056. doi:10.1016/j.tre.2020.102056

CrossRef Full Text | Google Scholar

Hoke, A., Brissette, A., Smith, K., Pratt, A., and Maksimovic, D. (2014). Accounting for lithium-ion battery degradation in electric vehicle charging optimization. IEEE J. Emerg. Sel. Top. Power Electron. 2, 691–700. doi:10.1109/JESTPE.2014.2315961

CrossRef Full Text | Google Scholar

Imai, A., Nishimura, E., and Papadimitriou, S. (2001). The dynamic berth allocation problem for a container port. Transp. Res. Part B Methodol. 35, 401–417. doi:10.1016/s0191-2615(99)00057-0

CrossRef Full Text | Google Scholar

Li, J.-Q. (2016). Battery-electric transit bus developments and operations: a review. Int. J. Sustain. Transp. 10, 157–169. doi:10.1080/15568318.2013.872737

CrossRef Full Text | Google Scholar

Liu, T., and Ceder, A. (2020). Battery-electric transit vehicle scheduling with optimal number of stationary chargers. Transp. Res. Part C Emerg. Technol. 114, 118–139. doi:10.1016/j.trc.2020.02.009

CrossRef Full Text | Google Scholar

Lutsey, N., and Nicholas, M. (2019). Update on electric vehicle costs in the United States through 2030. The International Council on Clean Transportation 2.

Google Scholar

Murata, H., Fujiyoshi, K., Nakatake, S., and Kajitani, Y. (1995). “Rectangle-packing-based module placement,” in Proceedings of IEEE international conference on computer aided design (ICCAD), 472–479. doi:10.1109/.ICCAD.1995.480159

CrossRef Full Text | Google Scholar

Qarebagh, A. J., Sabahi, F., and Nazarpour, D. (2019). “Optimized scheduling for solving position allocation problem in electric vehicle charging stations,” in 2019 27th Iranian conference on electrical engineering (ICEE), 593–597. doi:10.1109/IranianCEE.2019.8786524

CrossRef Full Text | Google Scholar

Qin, N., Gusrialdi, A., Paul Brooker, R., and T-Raissi, A. (2016). Numerical analysis of electric bus fast charging strategies for demand charge reduction. Transp. Res. Part A Policy Pract. 94, 386–396. doi:10.1016/j.tra.2016.09.014

CrossRef Full Text | Google Scholar

Rodrigues, F., and Agra, A. (2022). Berth allocation and quay crane assignment/scheduling problem under uncertainty: a survey. Eur. J. Operational Res. 303, 501–524. doi:10.1016/j.ejor.2021.12.040

CrossRef Full Text | Google Scholar

Rodriguez, M. A., and Vecchietti, A. (2013). A comparative assessment of linearization methods for bilinear models. Comput. Chem. Eng. 48, 218–233. doi:10.1016/j.compchemeng.2012.09.011

CrossRef Full Text | Google Scholar

Sebastiani, M. T., Lüders, R., and Fonseca, K. V. O. (2016). Evaluating electric bus operation for a real-world brt public transportation using simulation optimization. IEEE Trans. Intelligent Transp. Syst. 17, 2777–2786. doi:10.1109/TITS.2016.2525800

CrossRef Full Text | Google Scholar

Tang, X., Lin, X., and He, F. (2019). Robust scheduling strategies of electric buses under stochastic traffic conditions. Transp. Res. Part C Emerg. Technol. 105, 163–182. doi:10.1016/j.trc.2019.05.032

CrossRef Full Text | Google Scholar

Wang, X., Yuen, C., Hassan, N. U., An, N., and Wu, W. (2017a). Electric vehicle charging station placement for urban public bus systems. IEEE Trans. Intelligent Transp. Syst. 18, 128–139. doi:10.1109/TITS.2016.2563166

CrossRef Full Text | Google Scholar

Wang, Y., Huang, Y., Xu, J., and Barclay, N. (2017b). Optimal recharging scheduling for urban electric buses: a case study in davis. Transp. Res. Part E Logist. Transp. Rev. 100, 115–132. doi:10.1016/j.tre.2017.01.001

CrossRef Full Text | Google Scholar

Wei, R., Liu, X., Ou, Y., and Fayyaz, S. K. (2018). Optimizing the spatio-temporal deployment of battery electric bus system. J. Transp. Geogr. 68, 160–168. doi:10.1016/j.jtrangeo.2018.03.013

CrossRef Full Text | Google Scholar

Xylia, M., and Silveira, S. (2018). The role of charging technologies in upscaling the use of electric buses in public transport: experiences from demonstration projects. Transp. Res. Part A Policy Pract. 118, 399–415. doi:10.1016/j.tra.2018.09.011

CrossRef Full Text | Google Scholar

Yang, C., Lou, W., Yao, J., and Xie, S. (2018). On charging scheduling optimization for a wirelessly charged electric bus system. IEEE Trans. Intelligent Transp. Syst. 19, 1814–1826. doi:10.1109/TITS.2017.2740329

CrossRef Full Text | Google Scholar

Zhou, Y., Liu, X. C., Wei, R., and Golub, A. (2020). Bi-objective optimization for battery electric bus deployment considering cost and environmental equity. IEEE Trans. Intelligent Transp. Syst. 22, 2487–2497. doi:10.1109/tits.2020.3043687

CrossRef Full Text | Google Scholar