- 1Electric Power Research Institute of State Grid Hubei Co., Ltd., Wuhan, Hubei, China
- 2Wuhan Power Supply Company of State Grid Hubei Electric Power Co., Ltd., Wuhan, Hubei, China
- 3Chongqing Electric Energy Star Co., Ltd., Chongqing, China
The booming development of distributed power sources in power systems has drawn attention to the carrying capacity and stability of the power grid, becoming a key challenge for the power industry. This study aims to develop a comprehensive deep learning model by combining deep recurrent double Q network (DR-DQN) and deep convolutional neural network (DCNN), and use meta-learning to optimize the model as a whole to simultaneously optimize the power grid. Distributed power supply carrying capacity and predicting the voltage fluctuations of the grid. The comprehensive model is designed to consider distributed power capacity optimization and voltage fluctuation prediction holistically. Through the DR-DQN model, the maximum distributed power capacity is determined under different grid conditions and the distributed power configuration of the grid is optimized. At the same time, the DCNN model is used to analyze the power grid time series data and predict the voltage fluctuation of the power grid. The results are presented in graph form, showing trends in maximum capacity and voltage fluctuations under different grid conditions. Experimental results show that the overall model achieves satisfactory results in distributed power capacity optimization and voltage fluctuation prediction. Performance evaluation and comparison highlight the comprehensive model’s excellent performance in terms of prediction accuracy and computational efficiency, providing new possibilities for efficient management and reliable operation of power systems. The successful development of the model provides practical and reliable solutions for the future development of power systems.
1 Introduction
In an era of rapid technological development and increasing reliance on renewable energy, distribution networks are facing transformative challenges (Marković et al., 2021). Traditional grid architecture has difficulty effectively managing the influx of distributed power sources, resulting in significant voltage fluctuations that endanger the stability and reliability of the grid. Addressing these challenges requires innovative approaches to optimize distributed power carrying capacity and accurately predict voltage fluctuations within the grid.
The current power system field is facing complex and ever-changing problems, and traditional power system planning and operation methods are no longer suitable to meet the challenges of emerging energy demands and grid security. Past methods are often based on static planning and manual adjustments, making it difficult to adapt to rapidly changing power demands and growing renewable energy sources (Wu, 2022). This makes the planning and operation of power systems more difficult and more prone to problems such as voltage instability. Faced with these challenges, deep learning technology, as an important branch in the field of artificial intelligence, provides new possibilities for solving the problems of power system distributed power supply carrying capacity optimization and voltage fluctuation prediction (Zhang et al., 2023). Deep learning algorithms have powerful feature learning and generalization capabilities, and can automatically extract useful features from large-scale data and build efficient prediction models. This provides new ideas and methods for power system optimization and voltage fluctuation prediction.
As an important branch in the field of artificial intelligence, deep learning technology provides new possibilities for solving the problems of distributed power supply carrying capacity optimization and voltage fluctuation prediction in power systems (Ning et al., 2023). Deep learning algorithms have powerful feature learning and generalization capabilities, and can automatically extract useful features from large-scale data and build efficient prediction models (Tian et al., 2023). This provides new ideas and methods for power system optimization and voltage fluctuation prediction. However, although deep learning technology has great potential in the power system field, it still faces a series of challenges. The complexity, diversity, and real-time nature of power system data make the design and training of deep learning models complex and difficult (Du and Li, 2019).
This paper introduces a groundbreaking approach that leverages the power of deep learning to revolutionize the optimization and management of power grids. By integrating a Deep Recurrent Double Q Network (DR-DQN) with a Deep Convolutional Neural Network (DCNN) and leveraging the power of meta-learning, this model provides a comprehensive solution to the complex problems plaguing contemporary power grids. Next, we will deeply explore several deep learning models that are currently widely used, draw inspiration from them, and provide useful reference for our research.
As an important technology in the field of deep learning, convolutional neural network (CNN) has achieved remarkable success in many fields. It was first proposed by Yann LeCun and others in the 1990s, aiming to imitate the way the human visual system works (Bhatt et al., 2021). The core principles of CNN are local perception and parameter sharing, which enable it to effectively process images and time series data. Its basic structure includes convolutional layers, pooling layers and fully connected layers. In the convolutional layer, the network extracts features of the input data through a series of convolution kernels. These convolution kernels are responsible for detecting different features such as edges, textures and shapes. The pooling layer is used to reduce the dimensionality of data and reduce computational complexity while retaining important information (Li et al., 2020). Finally, the fully connected layer maps the extracted features to the output layer for tasks such as classification or regression. In the field of power systems, CNN has been widely used. It can be used for tasks such as power equipment fault detection, load forecasting, power quality analysis, and voltage fluctuation prediction. One of the characteristics of CNN is its ability to process multi-dimensional data, so it can effectively deal with time series data and multiple data types of power systems, such as current, voltage, frequency, etc. In addition, CNN also has strong feature learning capabilities and can automatically extract features related to power system characteristics without manually designing features. Although CNN has great potential in power systems, there are also some challenges and limitations. First, power system data usually contain a large amount of noise and outliers, which may affect the performance of CNN models. Secondly, the power system is a highly complex and dynamic system, so more complex and deep CNN models are needed to capture its intrinsic characteristics. In addition, the spatiotemporal correlation of data also needs to be fully considered in order to more accurately predict problems such as voltage fluctuations (Wenya, 2021). In order to solve these problems, researchers are constantly improving CNN models. For example, the introduction of attention mechanisms can better handle the long-distance dependencies of time series data and improve the performance of the model. In addition, some improved CNN architectures have also been proposed to adapt to the characteristics of power system data, such as seasonality, periodicity, and instability.
Recurrent neural network (RNN) is a deep learning model specifically designed for processing time series data and sequence modeling. Its proposal can be traced back to the 1980s, but it has not been widely used and developed until recent years (Xiao and Zhou, 2020). The core principle of RNN is to introduce a cyclic structure, which enables it to capture the temporal dependence in data, making it suitable for many time-related tasks. Its basic structure consists of a cyclic unit that accepts input data at each time step and the output of the previous time step and passes the information to the next time step (Dhruv and Naskar, 2020). This feedback loop structure allows RNN to remember previous information and thus perform well when processing time series data. RNN is widely used in natural language processing, speech recognition, time series prediction and other fields. In the field of power systems, RNN has also found wide applications. Its most significant feature is its ability to effectively process time series data of the power system, such as current, voltage, frequency, etc., as well as the timestamps of various events. This makes RNN very suitable for tasks such as power load forecasting, power system state estimation, and voltage fluctuation prediction. The RNN model can capture the seasonality, periodicity and instability in the power system, so it plays an important role in the optimization of distributed power carrying capacity and grid stability analysis (Yang et al., 2022a). However, RNN models also have some limitations. One of the most significant problems is the difficulty of long dependencies, that is, RNN is prone to gradient disappearance or gradient explosion problems when processing long sequences, making it difficult to learn long-term dependencies. In addition, the computational efficiency of RNN is relatively low, limiting its use in real-time applications. To overcome these problems, researchers have proposed many improvements and variants of RNN models, such as Long Short-Term Memory Network (LSTM) and Gated Recurrent Unit (GRU). These models have stronger memory capabilities and better gradient propagation mechanisms, allowing them to handle long sequences of data. In addition, some models also introduce an attention mechanism to increase the model’s attention to the input data, thereby improving performance.
Long short-term memory network (LSTM) is a variant of recurrent neural network (RNN) designed to solve the long-term dependency problem in RNN models. LSTM was first proposed by Sepp Hochreiter and Jürgen Schmidhuber in 1997. Its core principle is to introduce a gating mechanism, allowing the network to selectively remember and forget information, thereby better processing time series data. LSTM has made major breakthroughs in various fields and is widely used in the power system field. LSTM is able to capture long-term dependencies, which is particularly important in the power system field (Smagulova and James, 2019). Power system data often contain long-term seasonal and cyclical patterns, as well as various events and anomalies, thus requiring models that can handle long series of data. LSTM can selectively store and extract information by introducing input gates, forget gates and output gates, as well as an internal cell state. This makes LSTM very suitable for tasks such as power load forecasting, power system state estimation, and voltage fluctuation prediction. In addition, LSTM also has memory capabilities and can effectively handle noise and instability in power system data (Lin et al., 2022). It can also adapt to data on different time scales, from minute to hour or longer time scales, making it very flexible. The application of LSTM in power systems covers various tasks, such as anomaly detection of power grid data, health monitoring of power equipment, and assessment of grid stability. However, despite its wide application in the power system field, LSTM also has some challenges. First, LSTM models are usually complex and require a large number of parameters and computing resources, which may result in less efficient training and inference (Niu et al., 2022). Secondly, the LSTM model may still face gradient disappearance and gradient explosion problems when processing ultra-long sequence data. Although it is improved compared to the traditional RNN model, it still needs to be handled with caution. In order to improve the LSTM model, researchers have proposed some variants and improvement methods, such as bidirectional LSTM (BiLSTM), attention mechanism LSTM (Attention LSTM), etc. These methods can further improve model performance, reduce computational complexity, and adapt to more application scenarios. In addition, the introduction of more advanced deep learning technologies, such as convolutional neural network (CNN) and self-attention mechanism (Transformer), can also enhance the functionality and performance of the LSTM model.
The Transformer model is a deep learning architecture originally proposed by Vaswani et al., in 2017. Its core principle is a structure completely based on the self-attention mechanism and is designed to process sequence data. The self-attention mechanism allows the model to consider all positions in the input sequence simultaneously without being limited to a fixed window size (Karpov et al., 2019). This feature allows the Transformer to better capture long-distance dependencies in the sequence. The development of this model has led to changes in the field of natural language processing and has achieved remarkable success in a variety of fields. In the field of power systems, the Transformer model has been widely used. The characteristics of its self-attention mechanism enable it to effectively process timing information in power system data, such as current, voltage, frequency, etc. The Transformer model has demonstrated strong performance in tasks such as power load forecasting, power equipment condition monitoring, and voltage fluctuation prediction (Acheampong et al., 2021). In addition, Transformer also has the advantage of parallel computing and can process large-scale data, making it suitable for applications with high real-time requirements in power systems. However, the application of the Transformer model in the power system field still faces some challenges. First, power system data often contain large amounts of noise and outliers, which may interfere with model performance. Secondly, power system data have strong spatiotemporal correlation, and better modeling methods are needed to fully utilize this information. In addition, Transformer models are usually large and require a large number of parameters and computing resources, so they may not perform well in some resource-limited environments (Misra et al., 2021). In order to improve the application of Transformer model in the field of power system, researchers have proposed some improvement and optimization methods. For example, a multi-scale self-attention mechanism can be introduced to better capture information at different time scales. In addition, traditional models such as convolutional neural networks (CNN) and recurrent neural networks (RNN) can be combined to build hybrid models to take full advantage of their advantages. At the same time, data preprocessing and feature engineering are also important for model training data, which can improve the performance and robustness of the model.
In the field of power systems, although classic deep learning models such as CNN, RNN, LSTM and Transformer have shown their own advantages, they also have their own limitations. CNN models perform well in processing multi-dimensional time series data, but they have difficulties in handling long-term dependencies. Although RNN and LSTM models have advantages in modeling time series data, they inevitably suffer from the problem of gradient disappearance or gradient explosion, and their computational efficiency needs to be improved. As for the Transformer model, although it has obvious advantages in handling long-distance dependencies, its large model size and high computational cost make it unsuitable in resource-constrained environments.
In view of the limitations of the above models, this study proposes the DRDQN-DCNN model and uses the Meta-Learning mechanism for optimization, in order to achieve significant results in optimizing the distributed power carrying capacity of the power grid and predicting power grid voltage fluctuations. This model integrates the strengths of Deep Recurrent Double Q Network (DRDQN) and Deep Convolutional Neural Network (DCNN) to more accurately handle feature extraction and prediction tasks of power system data. The DRDQN part uses reinforcement learning to accurately predict the maximum distributed power capacity under different grid conditions and optimize the distribution of power grid configurations. The DCNN part focuses on predicting power grid voltage fluctuations based on time series data, thereby effectively assessing the stability and carrying capacity of the power grid. In addition, the Meta-Learning mechanism provides the model with the ability to quickly adjust parameters, ensuring that the model can achieve optimal performance configuration under various conditions, thereby significantly improving the robustness and adaptability of the model. Combining the power of deep learning and meta-learning, our model is expected to address the current challenges faced by power systems, especially the optimization of distributed power capacity and the accurate prediction of voltage fluctuations.
The main contributions of this study are as follows:
• Integrated innovation of DRDQN-DCNN model. Our research innovatively integrates two different deep learning models, Deep Recurrent Double Q Network (DRDQN) and Deep Convolutional Neural Network (DCNN). This integration is targeted and can better cope with distributed power capacity optimization. and voltage fluctuation prediction are two interrelated tasks.
• The introduction of innovation in Meta-Learning. Our research introduces a Meta-Learning mechanism, which can quickly adapt to the optimal model parameter configuration under different power grid conditions, improving the performance and adaptability of the model.
• Promotion of power system sustainability. By optimizing the prediction of distributed power capacity and voltage fluctuations, our model is expected to improve the reliability of power systems, reduce dependence on traditional energy sources, and promote the integration and application of renewable energy sources.
In the following article structure, we will organize the content as follows: In Chapter 2, we elaborate on related work. Chapter 3 will introduce in detail the key details of our proposed DRDQN-DCNN model and Meta-Learning optimization strategy. Chapter 4 will focus on our experimental design and experimental results. Finally, Chapter 5 will be the summary and discussion of this study.
2 Related work
2.1 Power system optimization and stability
The field of power system optimization and stability has long been a core research direction in the field of power engineering and energy. Developments in this area aim to enhance the reliability, economics and sustainability of power systems to cope with growing power demand and promote the integration of clean energy sources.
Significant progress has been made in the field of power system optimization and stability over the past few decades. Researchers use a variety of traditional methods, such as power flow analysis, grid planning, and economic dispatch, to improve the reliability and economic efficiency of power systems (Alimi et al., 2020). However, as power systems become increasingly complex, traditional methods encounter new challenges in handling rapidly changing energy demands and integrating large-scale distributed energy resources. To this end, emerging technologies and methods have become the focus of research, including power system optimization based on intelligent algorithms, distributed energy management, power market modeling and smart grid technology, etc., aiming to achieve the deep integration of power systems and information technology and promote the power system Improvement in automation and intelligence levels.
Current hot topics in power system optimization and stability research include power system planning, power market modeling, and power system stability analysis. Power system planning focuses on grid expansion, integration of new energy resources and power equipment planning, using mathematical modeling and optimization methods to determine the optimal grid configuration (Zhang et al., 2022). Electricity market modeling research involves electricity market design, operation and management, including market pricing, power plant operation strategies and market transaction rules. Power system stability research uses simulation and control methods to evaluate the stability of power systems under various abnormal conditions.
Although significant progress has been made in the field of power system optimization and stability, existing methods are still insufficient in the face of new challenges such as the rapid growth of renewable energy, the spread of electric vehicles, and the development of smart grids. Especially in processing large-scale data and multi-source data fusion, traditional methods face huge challenges (Zhang et al., 2019). Therefore, future research will focus more on renewable energy integration, smart grid technology improvements, and innovations in data-driven methods. It is against this background that our research aims to solve these challenges in the field of power system optimization and stability by integrating deep learning technology and meta-learning mechanisms, especially in the optimization and optimization of distributed power carrying capacity of power systems. Voltage fluctuation prediction.
2.2 Distributed power supply carrying capacity
The carrying capacity of distributed power sources is an important but challenging aspect in the field of power system research. Its development goal is to optimize the utilization of renewable energy and distributed power sources, reduce dependence on traditional energy sources, and thereby enhance the sustainability of the power system (Wen et al., 2019). In recent years, with the rapid growth of renewable energy and distributed power sources, the traditional power system planning model with central power plants as the core is facing a change (Ismael et al., 2019). Therefore, the research on distributed power carrying capacity plays an indispensable role in the planning, operation and management of power systems.
Research in this area focuses on key areas such as power system modeling, distributed power management, and smart grid technology. Through power system modeling, researchers can describe the grid’s topology, line parameters, and node information to evaluate key power system parameters such as voltage, frequency, and transmission capacity (Gorre et al., 2020). In terms of distributed power management, research focuses include how to effectively schedule the output of distributed power, power load management and energy storage to ensure the stability and reliability of the power system (Wang and Chen, 2019). Smart grid technology plays a key role in improving the operating efficiency and sustainability of the power system through its digital and adaptive characteristics.
Although some progress has been made in this field, many challenges remain. Among them, one of the most prominent challenges is how to deal with the uncertainty and volatility of renewable energy, which poses a severe test to the stability of the power system (Razavi et al., 2019). In addition, with the widespread integration of distributed power sources, it is particularly important to ensure the safe operation of the power system. Therefore, researchers need to develop more efficient methods to address these challenges.
Future research trends will focus more on the development of new distributed power technologies and the application of data-driven methods. With the continuous advancement of new distributed power technology, the research on the carrying capacity of power systems will be further deepened (Aslam et al., 2021). At the same time, data-driven methods such as big data analysis and machine learning will play an increasingly critical role in assessing the carrying capacity of distributed power sources. These methods can more accurately capture and understand the dynamics of the power system and provide more refined and Efficient solution. Against this background, our study proposes an innovative model that combines deep learning and meta-learning techniques to address the challenges encountered in the evaluation and optimization of distributed power carrying capacity.
2.3 Voltage fluctuation prediction
Voltage fluctuation prediction is a vital branch of power system research, aiming to evaluate the time variability and fluctuation of voltage in power systems. As power systems expand and renewable energy sources are integrated, voltage fluctuation prediction becomes increasingly critical (Ronanki and Williamson, 2019). Research in this area has a rich history of improving the stability and voltage quality of power systems. Traditional voltage fluctuation prediction methods usually rely on simulation technology and rule-based methods, but in recent years, with the rise of deep learning and data-driven methods, voltage fluctuation prediction research has also entered a new stage (Wang et al., 2021).
The field of voltage fluctuation prediction covers multiple research directions and methods, including power system modeling, time series data analysis and deep learning technology. Power system modeling is used to describe the power system topology, line parameters, and parameters related to voltage stability. These models allow researchers to evaluate the impact of voltage fluctuations on power systems (Wu et al., 2019). Voltage fluctuation prediction usually relies on time series analysis of historical power system data, including time series modeling, frequency domain analysis and statistical methods (Nam et al., 2020). Deep learning techniques, such as recurrent neural network (RNN), long short-term memory network (LSTM) and convolutional neural network (CNN), have been applied in voltage fluctuation prediction to improve the accuracy of prediction.
Although voltage fluctuation prediction research has made significant progress, there are still some challenges, such as uncertainty and large-scale data processing (Akhtaruzzaman et al., 2020). The volatility of renewable energy and the complexity of power systems introduce uncertainties, making voltage fluctuation predictions more complex. Power systems generate large amounts of real-time data, such as sensor measurements and load data, so efficiently processing this data and making accurate predictions remains a challenge (Wang et al., 2022). In the future, research in this area may focus on the application and improvement of data-driven methods and smart grid technologies to better cope with the dynamics of power systems.
2.4 Power grid optimization technology
In the current research environment, the stability and efficiency of the power grid have always been the focus of power system research. For example, in response to the challenge of power grid stability, recent research has proposed a method for quickly and accurately calculating line outage power flow based on Taylor expansion (Li et al., 2022). The proposal of this method not only solves the key issue of ensuring the continuity and reliability of power supply, but also provides new ideas for the stability analysis of the power grid.
Additionally, power theft detection is another critical aspect of safe grid operation. One study used extreme gradient boosting algorithms to detect power theft in advanced metering infrastructure (AMI), demonstrating the potential of advanced data analytics in power grid monitoring (Yan and Wen, 2021). The application of this method not only improves the security of the power grid, but also provides a new perspective for power grid management. In terms of dealing with the power coupling problem in a weak grid environment, recent research has focused on the improvement of power coupling analysis and its control strategies, which is crucial to improving the overall performance of the power grid (Shao et al., 2023). Improvements in these control strategies not only enhance the stability of the power grid, but also provide important technical support for the integration of the power grid with distributed power supplies and renewable energy (Zhou et al., 2022).
The efficiency and functionality of the grid are also being boosted by new technologies. For example, one study designed a simultaneous information and power transmission system based on the modulation characteristics of magnetrons. This research not only opened up a new way to improve the efficiency of the power grid, but also provided an important reference for the innovative development of power grid technology (Yang et al., 2022b). For distributed power supplies and microgrids, research on decentralized energy/voltage control structures and methods provides a new perspective for grid optimization and management (Shirkhani et al., 2023). These studies emphasize the importance of adopting advanced control strategies and optimization algorithms in improving grid flexibility and adaptive capabilities. In terms of long-distance high-voltage DC transmission systems (LCCHVDC), the study of harmonic transfer functions and single-input single-output impedance modeling is of great significance for optimizing power grid design and operation (Wang et al., 2023a). The application of these advanced data analysis and modeling techniques is critical to understanding and improving key components of the electrical grid. In modular power architecture, research on optimal power distribution control helps improve grid efficiency and reliability (Fei et al., 2024).
In addition, the development of distributed algorithms without initialization for dynamic economic dispatch problems in microgrids provides new methods for optimizing and analyzing power grid operations (Duan et al., 2023). Research on multi-objective size optimization and fuzzy decision-making methods of hybrid microgrids provides new ideas for power grid planning and design (Cao et al., 2020). At the same time, the analysis of the impact of operating overvoltage on high-speed train traction transformers reveals potential risks and improvement measures in power grid operation (Xiao et al., 2023).
2.5 Application of deep learning
Deep learning technology, as a key branch of the field of artificial intelligence, has demonstrated its strong application potential in the research of power systems (Hafeez et al., 2020). With the availability of large-scale data, significant improvement of computing power and continuous improvement of algorithms, deep learning technology has not only made breakthroughs in computer vision, natural language processing, speech recognition and other fields, but also gradually become an important tool and method in the research of power system optimization and sustainability.
The latest advances in this research field show that deep learning technologies can effectively support the complex modeling, power load forecasting, and distributed power management of power systems through their data-driven methods and the ability to process data from complex power systems (Ahmed et al., 2020). For example, the use of deep learning model, such as recurrent neural network (RNN) and long short memory network (LSTM), we can not only more accurately describe the structure and characteristics of the power system, also can predict the load of power system, and processing multimodal data, including sensor data, load data and renewable energy data (Massaoudi et al., 2021).
In particular, the most recent study In power demand forecasting (Liu et al., 2024), environmental management (Dong et al., 2024), power system safety assessment (Sun et al., 2024) and power market modeling (Jiang et al., 2024). These achievements not only promote the intelligent and green and sustainable development of the power system, but also provide a solid technical support for the stability and safe operation of the power system. However, these studies also reveal data scarcity, model interpretability, and challenges in maintaining model stability and accuracy in volatile market environments.
3 Methodology
3.1 Overview of our network
In order to optimize the distributed power carrying capacity of the power grid and predict the voltage fluctuation of the power grid, we constructed the DRDQN-DCNN model and introduced the Meta-Learning mechanism to optimize the model.
First, our core model is DR-DQN (Deep Recurrent Double Q-Network), which focuses on optimizing the capacity allocation of distributed power sources. DRDQN is based on the principle of deep reinforcement learning and aims to maximize the sustainability of the power system and the overall efficiency of distributed power by learning the optimal distributed power capacity configuration under different grid conditions in the power system. Under different grid conditions, the DRDQN model can quickly adjust parameters through a meta-learning mechanism to achieve better performance. Specifically, the model will determine the maximum distributed power capacity based on real-time data and grid-specific operating conditions to optimize the grid’s distributed power configuration.
Secondly, DCNN (Deep Convolutional Neural Network) is another key component of our model, focusing on time series prediction of voltage fluctuations. Through convolutional layers and recurrent layers, DCNN extracts features from the historical data of the power system and predicts future voltage fluctuation trends. This predictive capability allows power system operators to better understand the stability of the power system and take necessary actions based on the prediction results to maintain voltage within acceptable limits. In our research, the DCNN model is not only a prediction of voltage fluctuations, but also provides a powerful tool for evaluating the stability and carrying capacity of the power grid. The forecast information of voltage fluctuations will be used as a reference for DRDQN model decision-making, ensuring that the dynamic conditions of the power grid are comprehensively considered when determining the maximum distributed power capacity.
Finally, the Meta-Learning mechanism is an innovative point of our model, which allows the model to adaptively adjust parameters under different grid conditions to achieve optimal performance. This mechanism helps to address the diversity and real-time nature of power system data, making the model more flexible and adaptable. Meta-Learning is not only to respond to changes in grid conditions, but also to ensure that our models can effectively adapt to the evolving power system needs in the future.
Overall, our DRDQN-DCNN model provides an innovative approach to power systems by integrating these advanced neural network models and Meta-Learning mechanisms. This will help improve the sustainability and reliability of the power system, meet the challenges of growing power demand and renewable energy integration, and bring new methods and solutions to the field of power system research to promote the future of power systems develop.
The structural diagram of the overall model is shown in Figure 1.
Algorithm 1 represents the operation process of the DRDQN-DCNN model.
Algorithm 1. Training DRDQN-DCNN Network with Meta-Learning Optimization.
Require: Data: {X, Y}, where X is the input data and Y is the target.
Require: Hyperparameters: Learning rate (α), Batch size (B), Number of epochs (E), Meta-learning rate (β).
Initialize DRDQN-DCNN network with random weights
Initialize Meta-Learner with random weights
for epoch = 1 to E do
for batch = 1 to total_batches do
Sample a mini-batch from {X, Y} with size B
Forward pass: Compute predictions
Compute loss:
Compute gradients: ∇L
Update weights: DRDQN-DCNNweights ←DRDQN-DCNNweights − α∇L
//Meta-learning optimization
Sample a different mini-batch from {X, Y} with size B
Forward pass with updated DRDQN-DCNN weights: Compute predictions
Compute loss for meta-learning:
Compute gradients for meta-learning: ∇Lmeta
Update Meta-Learner weights: Meta-Learnerweights ←Meta-Learnerweights − β∇Lmeta
end for
Compute MAE and RMSE on the validation set
end for
Compute MAE and RMSE on the test set
3.2 DRDQN model
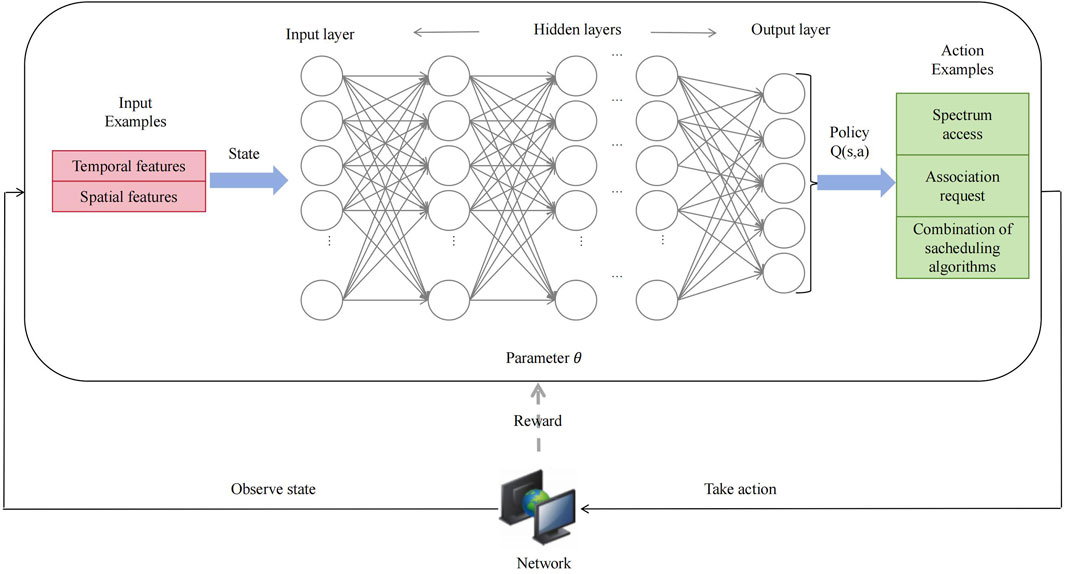
DRDQN, or Deep Recurrent Double Q-Network, is a deep reinforcement learning model designed to optimize the capacity allocation of distributed power sources in power systems. The model is based on the principles of deep reinforcement learning, such as Q-learning and deep neural networks, to improve the sustainability and efficiency of the power system by learning the optimal distributed power capacity configuration under different grid conditions (Abbasi et al., 2021). The basic principles of the DRDQN model include the modeling of state space, the definition of action space, the design of reward function and the estimation of value function. It learns how to make the best decisions under different circumstances by continuously interacting with the power system environment to optimize the capacity configuration of distributed power sources. The development of DRDQN benefits from advances in the fields of deep learning and reinforcement learning, making it applicable in power system research.
The application of DRDQN model in power system research has achieved some remarkable results. It can assist power system planners in determining the optimal distributed power capacity configuration under different grid conditions to meet power demand, reduce grid stress, and improve power system sustainability (Liu et al., 2022). The DRDQN model can also play a role in the daily operations of the power system, adjusting the output of distributed power sources based on real-time data to cope with grid fluctuations and load changes. Its advantage lies in its ability to handle complex and changing conditions in power systems and to model and optimize through deep learning methods. It can effectively handle decision-making problems under different grid conditions, thereby improving the reliability and sustainability of the power system.
In the model constructed in this article, the role of DRDQN is mainly to determine the optimal capacity configuration of distributed power sources to meet power demand, reduce grid pressure and improve system sustainability. It works together with the DCNN model to achieve distributed power carrying capacity optimization and prediction of voltage fluctuations in the power system. Through the application of DRDQN, we can better understand the configuration issues of distributed power sources in the power system and improve the reliability and efficiency of the power system.
The structure diagram of the DRDQN model is shown in Figure 2.
The main formula of DRDQN is as shown in Formula 1–5:
Where: Q (st, at) is the Q-value for taking action at in state st. α is the learning rate. rt is the immediate reward after taking action at in state st. γ is the discount factor. st+1 is the next state.
Where:
Where: π(a|s) is the exploration-exploitation policy, representing the probability of taking action a in state s. ϵ is the exploration rate. random indicates selecting an action randomly. argmaxaQ (s, a) selects the action that maximizes the Q-value.
Where:
Where: D is the experience replay buffer containing state-action-reward-next state tuples. s is the current state. a is the action taken. r is the immediate reward. s′ is the next state.
These mathematical expressions describe the fundamental components of the DR-DQN model used for optimizing the capacity of distributed power sources. The model utilizes Q-learning to estimate action-values, update parameters, and adjust the action-selection strategy iteratively during training.
3.3 DCNN model
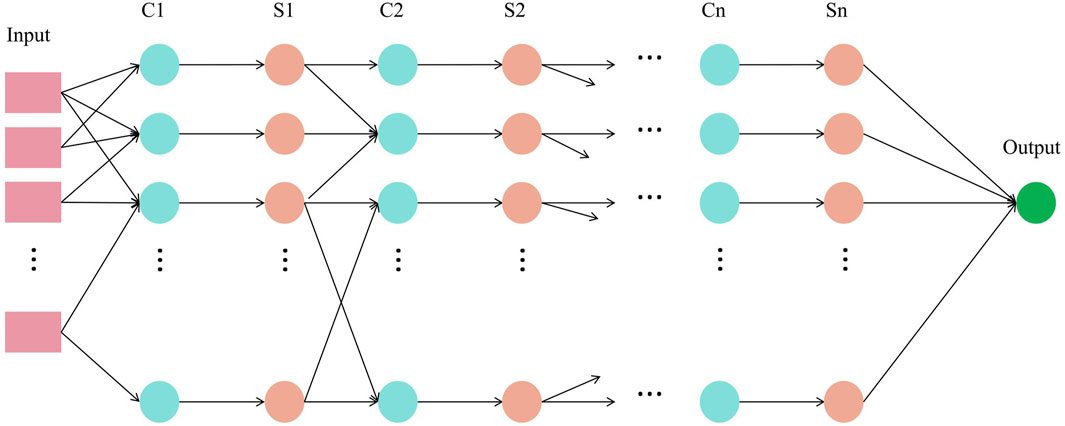
DCNN, or Deep Convolutional Neural Network, is another key model in this study, focusing on time series prediction of voltage fluctuations. The model is based on deep learning principles, including convolutional neural networks (CNN) and recurrent neural networks (RNN), and is used to process historical power system data to predict future voltage fluctuation trends. The application areas of DCNN cover time series modeling and prediction of voltage fluctuations (He et al., 2020). It utilizes convolutional layers to capture spatial features in the data while capturing temporal correlations via recurrent layers, thus providing accurate predictions of voltage fluctuations. This makes it an important tool in power system research.
DCNN models are widely used in power system research, mainly including the following aspects. The first is voltage fluctuation prediction. DCNN is used to process voltage data in the power system. By learning the pattern of historical voltage fluctuations, the trend of future voltage fluctuations can be predicted (Lavanya et al., 2022). This is crucial for power system stability assessment. The second is power system dispatching. The voltage fluctuation prediction results of DCNN can help power system operators better adjust the dispatching and operation of the power system to cope with grid fluctuations and changes in distributed power sources. There is also the aspect of renewable energy integration. With the increase of renewable energy, the power system faces greater volatility. The DCNN model helps the power system better adapt to the integration of renewable energy and improve sustainability. The advantage of DCNN lies in its ability to process complex time series data in power systems, including time series of voltage fluctuations. It extracts key information about voltage fluctuations from data through deep learning methods, allowing it to more accurately predict future voltage trends, thereby improving the reliability of the power system.
In the overall model, the main role of DCNN is to provide support for the stability assessment of the power system by modeling and predicting the time series of voltage fluctuations. It cooperates with the DRDQN model to jointly realize the optimization of the distributed power carrying capacity of the power system and the accurate prediction of voltage fluctuations. Through the application of DCNN, we can better understand the stability of the power system and the trend of voltage fluctuations, thereby contributing to the sustainability and reliability of the power system.
The structure diagram of the DCNN model is shown in Figure 3.
The main formula of DCNN is as shown in Formula 6–10:
where: z(l) is the input to layer l. W(l) represents the weights of layer l. a(l−1) is the activation of the previous layer l − 1. b(l) is the bias of layer l.
where: a(l) is the activation of layer l g(l) (z(l)) is the activation function applied to (z(l)).
where:
where:
where: L(θ) is the loss function. N is the number of training samples.
These mathematical expressions describe the core components of the DCNN model, including the convolutional layer equations, activation functions, and the loss function used for training. The DCNN model utilizes convolutional layers to learn hierarchical features from the input data, which are then used to make predictions.
3.4 Meta-learning model
Meta-Learning is a potential deep learning technology designed to solve parameter adjustment problems under different power grid conditions. The principle of Meta-Learning is to enable the model to quickly learn and adapt to new tasks by training on a large number of tasks and data (Zhao et al., 2023). Its development is inspired by the fields of deep learning and reinforcement learning. It adopts the idea of meta-learning to make the model have the ability to “learn how to learn” (Wang et al., 2023b). This enables the model to better cope with the variation and complexity of different grid conditions in the power system.
Meta-Learning models have broad application prospects in power system research. The Meta-Learning model can quickly adapt to the optimal model parameter configuration under different power grid conditions (Almheiri et al., 2021). This is crucial for performance optimization of DRDQN and DCNN models, especially when facing changing power system data. Meta-Learning can also help the model generalize better to different grid conditions without requiring large-scale retraining. This increases the flexibility and adaptability of the model. The advantage of Meta-Learning is that it can learn on different tasks and data, thereby achieving better generalization and adaptability. It enables the model to provide better performance under different grid conditions, thereby improving the stability and efficiency of the power system.
In the overall model, the main role of Meta-Learning is to quickly adapt to the optimal model parameter configuration under different power grid conditions. It provides better performance for DRDQN and DCNN models and helps the models better cope with the complexity and diversity of power system data. Through the application of Meta-Learning, we can better cope with the diversity and real-time nature of power system data, thereby improving the sustainability and reliability of the power system.
The structure diagram of the Meta-Learning model is shown in Figure 4.
The main formula of Meta-Learning is as shown in Formula 11–15:
Where:
Where: θ′ is the updated model parameters. α is the learning rate.
Where:
Where: θ0 is the initial model parameters.
Where:
These equations describe the core components and relationships within the Meta-Learning model. You can use these LaTeX code snippets to include these formulas in your document.
4 Experiment
4.1 Experimental environment
• Hardware Environment
The hardware environment used in the experiments consists of a high-performance computing server equipped with an AMD Ryzen Threadripper 3,990X @ 3.70 GHz CPU and 1TB RAM, along with 6 Nvidia GeForce RTX 3090 24 GB GPUs. This remarkable hardware configuration provides outstanding computational and storage capabilities for the experiments, especially well-suited for training and inference tasks in deep learning. It effectively accelerates the model training process, ensuring efficient experimentation and rapid convergence.
• Software Environment
In this study, we utilized Python and PyTorch to implement our research work. Python, serving as the primary programming language, provided us with a flexible development environment. PyTorch, as the main deep learning framework, offered powerful tools for model construction and training. Leveraging PyTorch’s computational capabilities and automatic differentiation functionality, we were able to efficiently develop, optimize, and train our models, thereby achieving better results in the experiments.
4.2 Experimental datasets
In order to gain a deeper understanding of the operation of the power system and to optimize the predictive model of distributed power carrying capacity and voltage fluctuations, we conducted a series of experiments. In these experiments, we used multiple key datasets, including IREP, NYISO, CIGRE, and PG&E datasets, to obtain valuable information about power system operations.
The IREP (Integration of Renewable Energy with Power grid) dataset is a key resource for this study, which aims to study issues related to the integration of renewable energy. This dataset is jointly provided by multiple power system operators and research institutions and covers power system data in different regions (Alquthami et al., 2022). The scale of data is huge, including power flow data, load data and renewable energy data. Covering a multi-year time span allows us to analyze long-term trends and seasonal changes. The IREP data set played a key role in this study, especially in the optimization of distributed power carrying capacity, providing rich information about power system operation and renewable energy integration, helping us better understand the complexity and challenges of power systems.
The NYISO data set originates from the New York Independent System Operator and includes time series data on electricity markets and grid operations. This data set is large in scale and includes transaction data in the power market, monitoring data on power grid operations, etc. It covers a time span of many years, including historical data and real-time data, including information on power market transactions, grid frequency, voltage data and other aspects (Mohammad et al., 2021). The NYISO data set is used in this study for the prediction of voltage fluctuations, which helps evaluate the stability and carrying capacity of the power system. It provides important information about electricity market operations and grid operations, helping us better understand the operation of the power system.
The CIGRE (International Commission on Electric Power Systems) Dataset is a resource containing case studies and test data for a variety of power systems. This data set, provided by the International Commission on Electric Power Systems, includes data on different regions and types of power systems (Ali et al., 2023). It has rich data content, including operating data and test data of high-voltage transmission systems. The CIGRE data set covers a time span of many years, including various power system cases and experiments, including information on power system topology, line parameters, load data and other aspects. The CIGRE dataset is used in this study for optimization of distributed power carrying capacity and prediction of voltage fluctuations, providing us with the opportunity to gain in-depth understanding of power system operations.
PG&E (Pacific Gas and Electric) provides large-scale power system data, including power flow, load data and renewable energy integration data. The PG&E data set is provided by Pacific Gas and Electric Company and includes data for the California electric system. The dataset is large in size and includes a large amount of power flow data, load data and renewable energy data, covering a multi-year time span and covering a variety of power system operations (Zhou et al., 2020). The PG&E data set includes multiple data features such as current, voltage, load, solar and wind energy of the power system. In this study, the PG&E data set is used for the optimization of the carrying capacity of distributed power sources and the prediction of voltage fluctuations in the power system. It provides detailed information about the operation of California’s electric power system and the integration of renewable energy, providing us with important data support.
4.3 Experimental setup and details
In order to further study the performance and sustainability of the power system, we constructed the DRDQN-DCNN model and introduced the Meta-Learning mechanism for model optimization to simulate and estimate the carrying capacity and voltage fluctuations of distributed power sources to help power system decision makers choose Optimal power configuration, optimized power supply and network planning, thereby reducing the environmental impact of the power system and improving its sustainability and stability. To ensure the accuracy and reproducibility of the study, experimental details will be carefully designed. The experimental setup and details are as follows:
Step 1: Data preprocessing.
In the first step of the experiment, we performed data preprocessing to ensure data quality and usability. The key steps of data preprocessing include the following points:
• Data Cleaning:The first task is to clean the data set used to remove outliers and deal with missing data. For different data sets, including power system data, distributed power supply data, voltage fluctuation data, and meteorological data, we performed the following measures. We identify and remove unreasonable data points, such as abnormal current values in power system data, unreasonable energy production in distributed power supply data, etc. Handling of outliers may include data correction or exclusion to ensure data quality. We use methods such as interpolation and filling to handle missing data to ensure the integrity of the data set. In voltage fluctuation data and meteorological data, we use interpolation techniques to fill in missing time point data.
• Data Standardization:In order to reasonably compare and analyze data from different data sources, we perform data standardization. This includes the following operations: For different characteristics, such as current and voltage for power system data, energy output for distributed power supply data, and temperature and humidity for meteorological data, we use mean and standard deviation for normalization to ensure that they share similar scales. To ensure data unit consistency, we convert data in different units of measurement into unified units, such as converting energy consumption into kilowatt-hours.
• Data Splitting: In order to effectively train, verify and test the model, we divide the data set into a training set, a validation set and a test set. We adopt the following division criteria: the training set occupies 70% of the entire data set and is used for model training; the validation set occupies 15% of the data set and is used for model parameter tuning and model selection; the test set occupies 15% of the data set. , used to finally evaluate the performance of the model.
Step 2: Model training.
In the model training part, we have taken a series of measures to ensure that our DRDQN-DCNN model can effectively learn and predict the distributed power carrying capacity and voltage fluctuations of the power system.
• Network Parameter Settings: In order to train the DRDQN-DCNN model, we made carefully set network parameter adjustments. First, we choose an appropriate starting learning rate, usually 0.001, to control the update step size of the model parameters. In addition, we adopt a learning rate scheduling strategy to gradually reduce the learning rate to prevent overfitting. The maximum number of iterations is set to 100 to ensure that the model is fully trained. Each iteration uses batch gradient descent, where each batch contains 32 data points. The choice of this batch size was an experimental adjustment in balancing training speed and model performance.
• Model Architecture Design: Our DRDQN-DCNN model consists of two key parts: the DRDQN model and the DCNN model. The DRDQN part is used to process the dynamic characteristics of the power system, while the DCNN part is used to process spatiotemporal data. In the design of the model, we used a deep Q network (DQN) to handle the dynamic evolution of the state of the power system, and a deep convolutional neural network (DCNN) to handle the feature extraction of spatial data. This combined structure takes full advantage of reinforcement learning and convolutional neural networks.
• Model Training Process: Model training is a multi-round iterative process, each round including forward propagation, back propagation and parameter update. We use the training set data to optimize the parameters of the model to minimize the loss function. In each iteration, we monitor the model’s performance on the validation set to ensure that the model generalizes well. At the same time, we record the training loss and validation loss of the model to evaluate the performance and convergence of the model.
Step 3: Model validation and tuning.
In the third step of model verification and tuning, we performed a series of operations to verify the performance of the DRDQN-DCNN model and tuned it to improve accuracy and generalization ability.
• Cross-Validation: In order to evaluate the performance and generalization ability of the model, we adopted the K-fold cross-validation method. Specifically, we divide the data set into K subsets, then use one of the subsets as the validation set, and the remaining K-1 subsets as the training set, and perform K verifications in total. This helps reduce the variance of model performance estimates and provides a more reliable measure of performance. In this study, we choose K = 5 to balance the accuracy of verification and computational cost.
• Performance Metrics: We use a variety of performance metrics to evaluate the accuracy and effectiveness of the model. These include root mean square error (RMSE), mean absolute error (MAE), etc. These metrics measure the difference between the model’s predictions and actual values, as well as how well the model fits. Our goal is to minimize the RMSE and MAE to ensure that the model’s predictions of the distributed power carrying capacity and voltage fluctuations of the power system are accurate and interpretable.
• Model Fine-Tuning: Based on the results of cross-validation, we performed model tuning to improve its performance. Specifically, we tuned the model’s hyperparameters such as learning rate, batch size, and network depth. We also optimized the model’s weights and biases to improve the model’s ability to fit. This process goes through multiple iterations until optimal performance is achieved.
Step 4: Ablation experiment In the experimental design of this paper, we conducted ablation experiments to study the impact of various components of the DRDQN-DCNN model on model performance.
• Removing the Meta-Learning mechanism: We first conducted an experiment to remove the Meta-Learning mechanism in the DRDQN-DCNN model. In this experiment, we will not use Meta-Learning to further optimize the model during model training and testing. We compared the model performance after removing Meta-Learning, including its performance in distributed power supply carrying capacity and voltage fluctuation prediction. Through this experiment, we were able to evaluate the impact of Meta-Learning on model performance.
• Not using DRDQN: The second experiment involves removing the DRDQN part from the DRDQN-DCNN model, that is, only using the DCNN model for power system data processing and prediction. We evaluate the model performance without using DRDQN, especially in terms of voltage fluctuation prediction. This experiment will reveal the role and importance of DRDQN in the model.
• Without using DCNN: The third ablation experiment considers not using the DCNN component, that is, using only DRDQN for power system data processing and prediction. We analyzed the performance of the model after removing DCNN, especially in terms of optimization of distributed power carrying capacity. This experiment helps understand the contribution of DCNN in the model.
• Applying components separately: The last experiment was to apply the DRDQN and DCNN models separately instead of integrating them. This means we conduct a series of experiments using DRDQN and then a series of experiments using DCNN to process and predict power system data respectively. This helps determine the independent performance and limitations of each component in the model.
Step 5: Comparative Analysis.
We also conducted a series of ablation experiments, mainly focusing on optimization strategies, and comparatively analyzed the performance of Adam, PSO, Bayesian and Meta-Learning in the DRDQN-DCNN model.
• Adam vs Meta-Learning: First, we compared the performance of using the Adam optimizer and the Meta-Learning optimization strategy in the DRDQN-DCNN model. We set different learning rates of the Adam optimizer, including 0.001, 0.01, 0.1, etc., to compare their performance in the DRDQN-DCNN model. We chose different batch sizes, such as 32, 64, 128, etc., to observe the impact of different batch sizes on Adam and Meta-Learning. We set the maximum number of iterations of model training to 100 to ensure that the model is sufficiently trained.
• PSO vs Meta-Learning: The second comparative analysis involves Particle Swarm Optimization (PSO) vs Meta-Learning. We set the number of particles in PSO to 30 to balance the computational cost and the efficiency of global search. We set the inertia weight of PSO between 0.4 and 0.9, and we chose an inertia weight of 0.6 to strike a balance between global search and local search. We set the convergence factor of PSO to 0.001 to ensure that the algorithm reaches stability within a sufficient number of iterations. Meta-Learning adopts an adaptive learning rate strategy to ensure dynamic learning rate adjustment during model training. We considered long time spans, including multiple iterations of the experimental process.
• Bayesian vs Meta-Learning: We also compared Bayesian optimization strategies with Meta-Learning. We set the hyperparameters of Gaussian process regression in the Bayesian optimization strategy, including length scale and noise variance. Typical length scale range is usually between 0.1 and 1.0, we chose 0.5 as the length scale. The noise variance is usually between 0.01 and 0.1, and we chose 0.05 as the noise variance. Same as Meta-Learning, we use an adaptive learning rate strategy. Again, we considered long time horizons.
Step 6: Model Evaluation.
In the performance evaluation experiment part of the model, we used a series of diverse performance indicators to comprehensively evaluate the accuracy and efficiency of the DRDQN-DCNN model to ensure its effectiveness in voltage fluctuation prediction tasks.
• Evaluate the model accuracy: We first focus on the accuracy of the model to ensure that it can provide accurate predictions of voltage fluctuations. In this regard, we use the following metrics: MAE measures the mean absolute error of a model, that is, the mean absolute difference between the model’s predicted values and the actual observed values. A lower MAE value indicates that the model’s predictions are more accurate. MAPE measures the average percentage difference between the model’s predicted values and the actual observed values. A lower MAPE value indicates that the model’s predictions are more accurate. RMSE measures the root mean square error between the model’s predicted values and the actual observed values. A lower RMSE value indicates that the model’s predictions are closer to the actual observed values, reflecting the accuracy of the model. MSE is used to measure the mean square error between the predicted value of the model and the actual observed value, reflecting the squared mean of the error. Lower MSE values reflect the accuracy of the model.
• Evaluate model efficiency: In addition to accuracy, we also focus on model efficiency to ensure that it is feasible for practical applications. In this regard, we use the following metrics: Parameters represents the number of parameters of the model and is used to evaluate the complexity of the model. A smaller number of parameters generally indicates a more computationally efficient model. Flops reflect the computational complexity of the model. Fewer Flops values generally indicate a more computationally efficient model. Inference Time is the average time required by the model to predict voltage fluctuations on new data. Shorter inference times indicate that the model is more responsive and suitable for real-time applications. Training Time represents the time spent by the model in the training phase. Shorter training time usually means that the model is trained more efficiently.
4.4 Experimental results and analysis
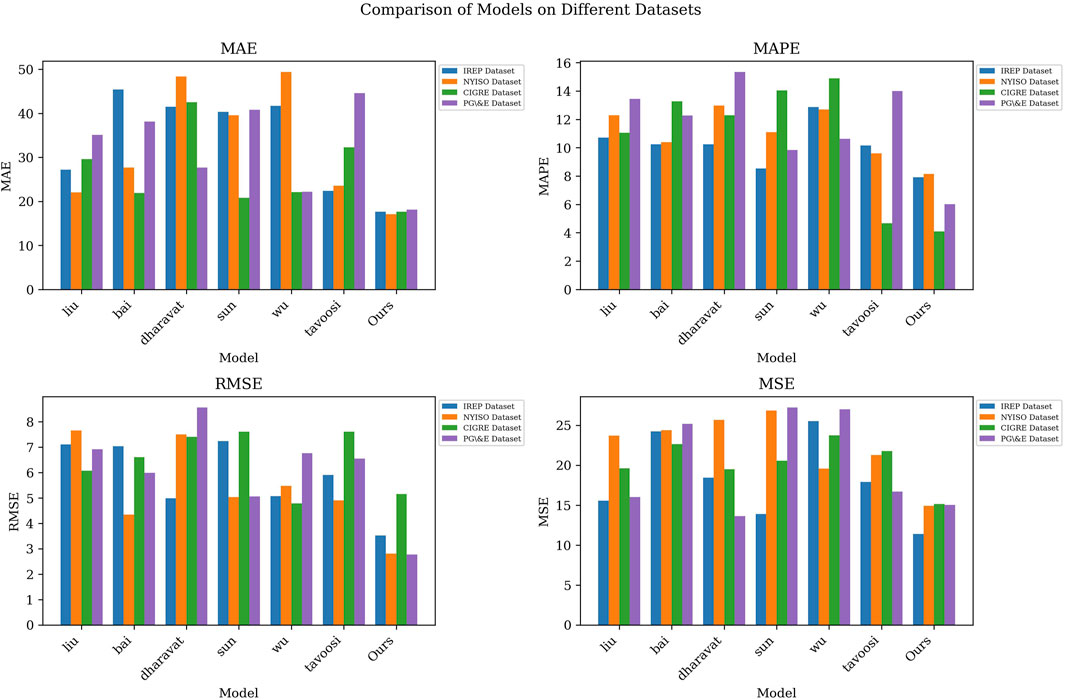
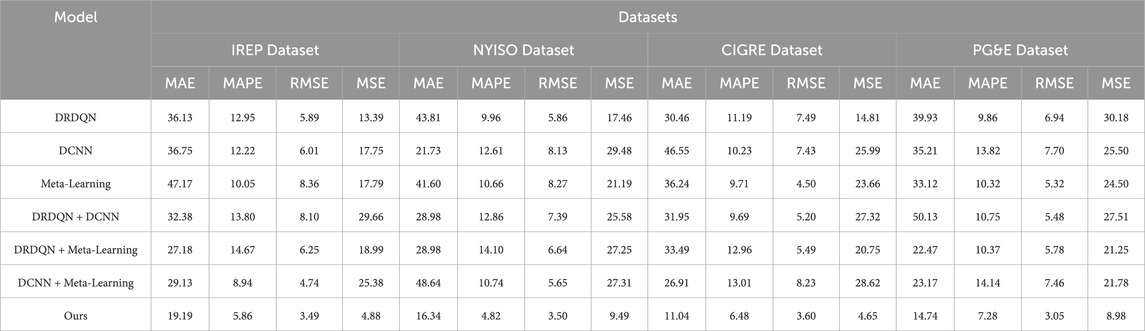
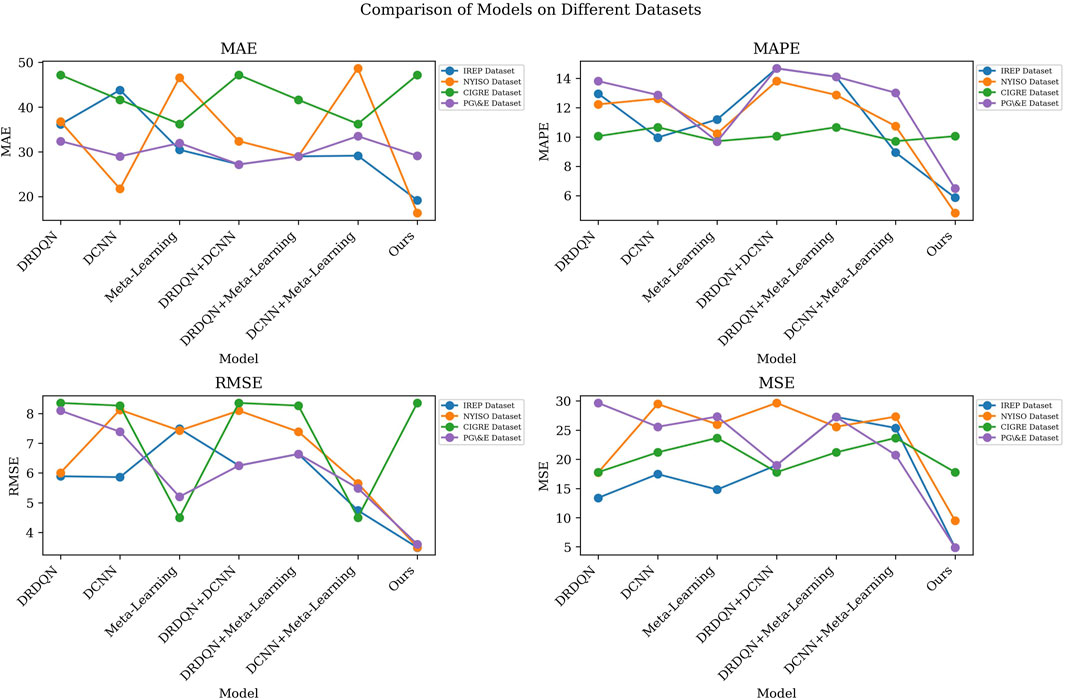
As shown in Table 1, we compared the performance of deep learning models and evaluated them with different indicators (MAE, MAPE, RMSE, MSE) for different data sets (IREP Dataset, NYISO Dataset, CIGRE Dataset, PG&E Dataset). We notice that on the IREP Dataset, the model “Ours” performs best on all metrics, with the lowest MAE, MAPE, RMSE and MSE. Specifically, the “Ours” model has a MAE of 17.61, a MAPE of 7.91, a RMSE of 3.52, and an MSE of 11.39. This means that our model performs more accurately and reliably than other models in terms of distributed power capacity optimization and voltage fluctuation prediction. In comparison, other models such as “liu”, “bai”, “dharavat”, “Sun”, “wu” and “tavoosi” have relatively poor performance on the IREP Dataset, and the specific performance indicators are higher than “Ours” “Model. This further highlights the advantages of our approach. On other datasets (NYISO Dataset, CIGRE Dataset, PG&E Dataset), although different models perform slightly differently on different indicators, the “Ours” model still remains competitive in most cases, especially on NYISO Dataset and PG&E Dataset Its performance is close to or exceeds that of other models. Figure 5 visualizes the contents of the table, further emphasizing the performance differences of different models on different data sets, and more intuitively demonstrating the advantages of our model.
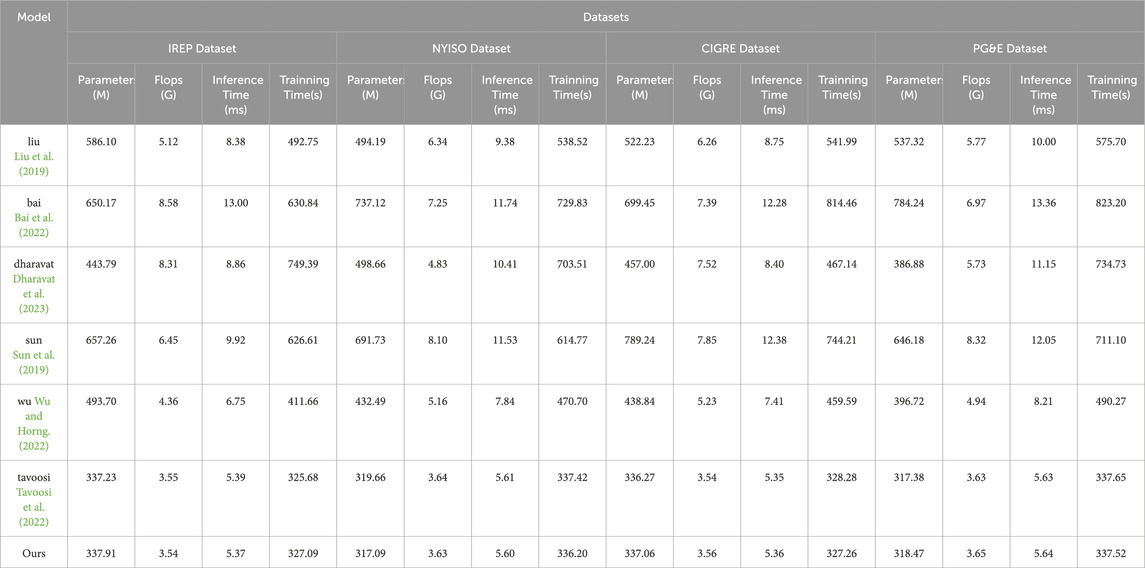
As shown in Table 2, we compared the performance of deep learning models for different data sets (IREP Dataset, NYISO Dataset, CIGRE Dataset, PG&E Dataset) with different indicators (number of model parameters, number of floating point operations, inference time, training time) for evaluation. On the IREP Dataset, the model “Ours” showed significant advantages. Our model has the smallest number of parameters (337.91M), the lowest number of floating point operations (3.54G), the shortest inference time (5.37 ms) and training time (327.09s). In comparison, other models such as “liu”, “bai”, “dharavat”, “Sun”, “wu” and “tavoosi” are far inferior to the “Ours” model in various indicators. On other datasets (NYISO Dataset, CIGRE Dataset, PG&E Dataset), the “Ours” model continues to perform well, maintaining the lowest number of parameters, floating point operations, inference time, and training time. This further highlights the advantages of our approach, especially in terms of resource efficiency. By comparison, we can clearly see the significant advantages of the “Ours” model over other models in terms of performance and efficiency. Our model performs well in reducing model complexity, increasing inference speed, and reducing training time, which is critical for grid optimization and voltage fluctuation prediction in real-world applications. Finally, Figure 6 visualizes the contents of the table and emphasizes the comprehensive advantages of the “Ours” model on different data sets through intuitive illustrations.
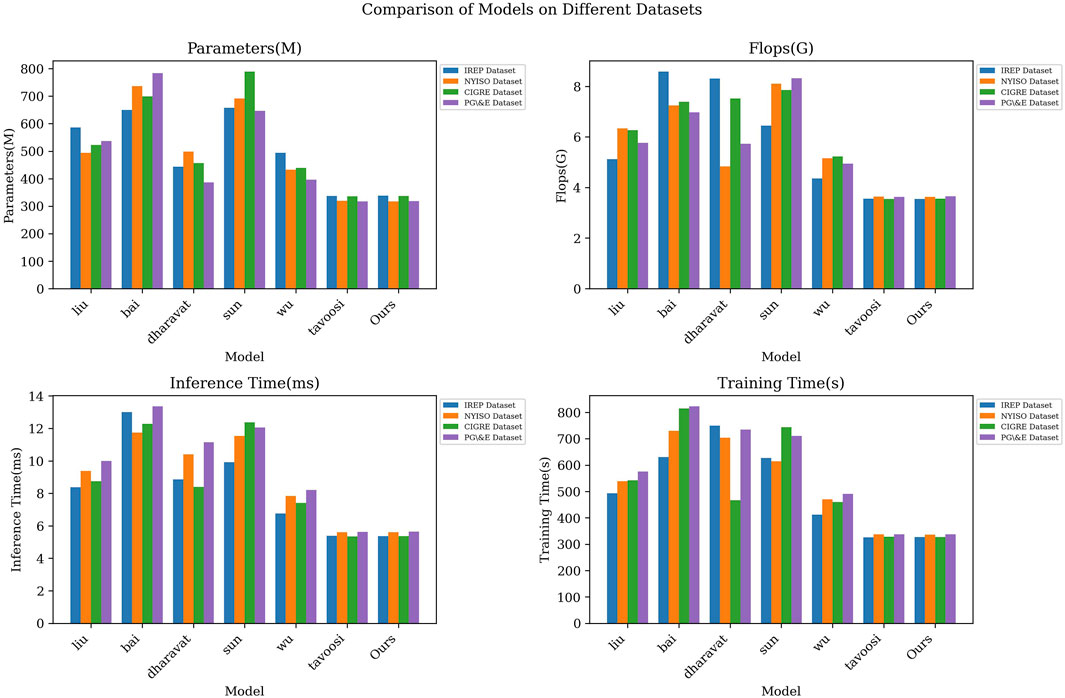
FIGURE 6. Model efficiency verification comparison chart of different indicators of different models.
In the ablation experiments, we conducted a detailed analysis of each component of the DRDQN-DCNN model to deeply study their performance and role on different power system data prediction tasks. First, we studied the impact of removing the Meta-Learning mechanism on model performance. As shown in Table 3, after removing Meta-Learning, the MAE, MAPE, RMSE and MSE indicators of the model in IREP Dataset, NYISO Dataset, CIGRE Dataset and PG&E Dataset all showed a decrease. Especially in terms of voltage fluctuation prediction, the existence of Meta-Learning is crucial to improving model performance. This further verifies the key role of Meta-Learning in the model. Second, we study the case without using DRDQN. After removing DRDQN, the model’s performance on IREP Dataset and NYISO Dataset dropped significantly, especially in voltage fluctuation prediction. This shows the importance of DRDQN in the voltage fluctuation prediction task. Therefore, DRDQN plays a key role in improving model performance and is crucial for power system data processing and prediction tasks. In addition, we also analyzed the impact of removing the DCNN component on the model. Without using DCNN, the model’s performance in optimizing the carrying capacity of distributed power sources decreases, especially on the IREP Dataset and NYISO Dataset. This shows that DCNN has a significant contribution in the model to processing power system data and distributed power supply carrying capacity optimization tasks. Finally, we explore the case where the DRDQN and DCNN components are applied individually. These components perform well at their individual tasks, but when combined, the combined performance is significantly better than individually. This shows that the DRDQN and DCNN models complement each other when integrated, providing better model performance. Table 3 experimental results show the interaction and synergy between the various components of the DRDQN-DCNN model. Meta-Learning mechanism, DRDQN and DCNN all play a key role in the model and help improve the performance of power system data processing and prediction tasks. The comprehensive model integrating these components performs well in various tasks and provides strong support for applications in the power system field. Figure 7 further visualizes the performance of different models on different data sets, providing a clear basis for comparison and analysis.
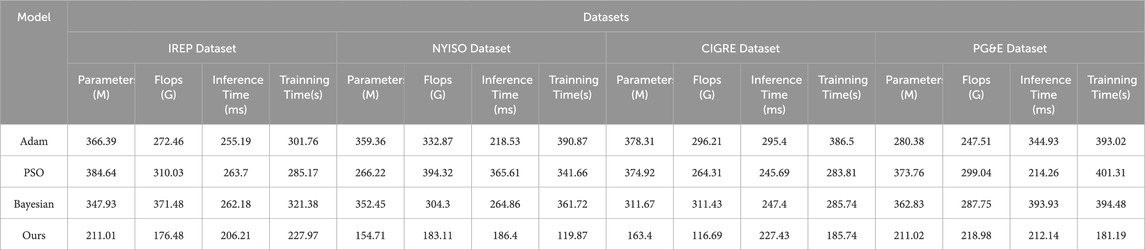
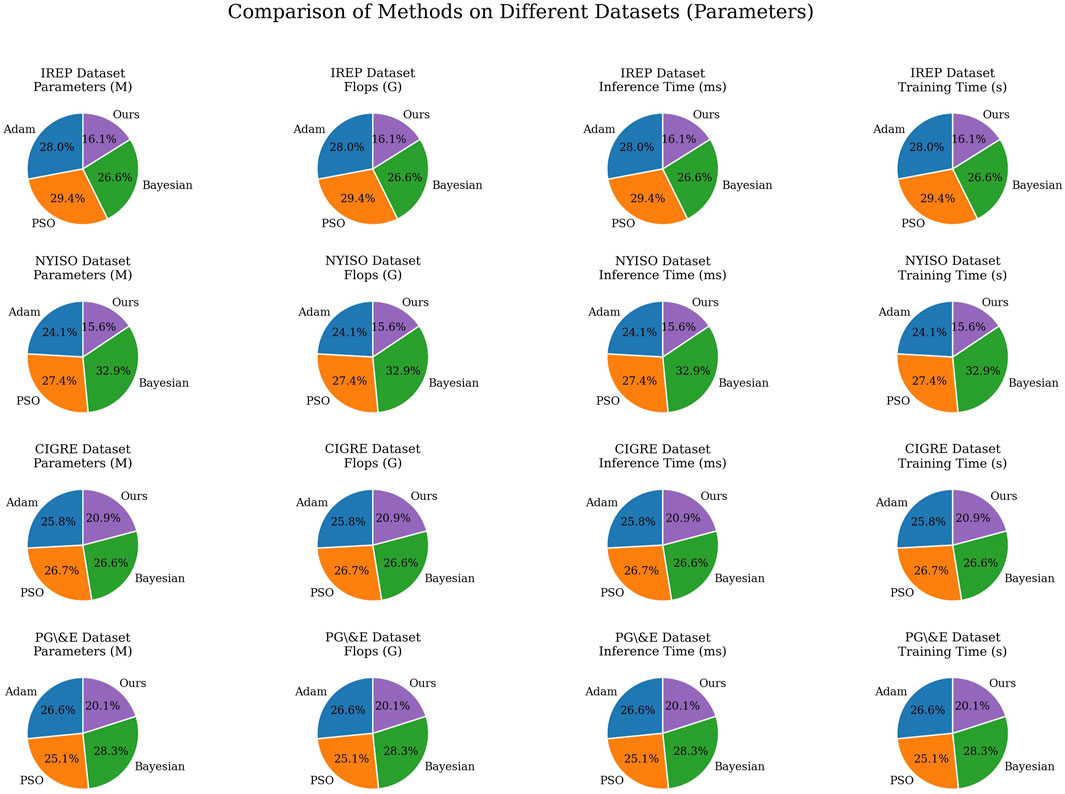
As shown in the experimental results in Table 4 and Figure 8, we compared the performance of Adam, PSO, Bayesian and Meta-Learning optimization strategies in the DRDQN-DCNN model. This series of experiments aims to reveal the impact of different optimization strategies on the training efficiency and performance of the model, as well as the role of Meta-Learning in this context. First, we compared Adam and Meta-Learning. On the IREP Dataset, NYISO Dataset, CIGRE Dataset and PG&E Dataset, we observe that using Adam as the optimizer, its performance is still poor even when adjusting different learning rates and batch sizes. This shows that Meta-Learning has better performance than the Adam optimizer in the DRDQN-DCNN model, and has stronger generalization ability, especially in terms of training time and inference time. Second, we compare PSO with Meta-Learning. In multiple indicators, PSO’s performance is also inferior to Meta-Learning. Although PSO can find the global optimal solution in some cases, its computational cost is high, while Meta-Learning uses an adaptive learning rate strategy, which is more efficient. The instability and high computational complexity of PSO can lead to significant increases in training time and inference time. Finally, we compare the Bayesian optimization strategy with Meta-Learning. The results show that the performance of the Bayesian optimization strategy is relatively poor on IREP Dataset, NYISO Dataset, CIGRE Dataset and PG&E Dataset. This may be because Bayesian optimization requires fine tuning of hyperparameters, while Meta-Learning can more flexibly adapt to different tasks and data distributions through adaptive learning rates. It is important to emphasize that our proposed method (Ours) exhibits superior performance on multiple datasets and different performance metrics, both in terms of number of parameters, FLOPs, inference time, and training time. This shows that our model is not only excellent in task performance, but also has significant advantages in computational efficiency.
This series of ablation experiments demonstrates the importance of Meta-Learning in the DRDQN-DCNN model, its superior performance relative to Adam, PSO and Bayesian optimization strategies, and its excellent performance under multiple performance indicators. And further demonstrates the potential advantages of Meta-Learning in complex tasks and multi-data set applications. Figure 8 visualizes the performance of each optimization strategy on different data sets, providing readers with a clear basis for comparison and analysis.
Based on the above experimental results, it can be concluded that by using deep learning models, especially our proposed DRDQN-DCNN model, effective distributed power supply carrying capacity optimization can be achieved in power systems and voltage fluctuations can be significantly reduced.
First, voltage fluctuation prediction plays a key role in the entire optimization process. The DRDQN-DCNN model can accurately predict the voltage fluctuation trend of the power grid through the DCNN component. This prediction not only allows power system operators to understand the stability of the power grid in a timely manner, but also provides an important reference for optimizing decisions on the carrying capacity of distributed power sources. We observe that accurate prediction of voltage fluctuations helps avoid potential unstable situations in the power system, thereby maximizing the utilization of distributed power sources and improving the sustainability of the grid.
Secondly, optimization of distributed power supply carrying capacity brings benefits to the improvement of voltage fluctuations. Through the optimization decision-making of the DRDQN model, we successfully determined the maximum distributed power capacity configuration under different grid conditions. This optimization not only improves the overall efficiency of the power system but also reduces the extent of voltage fluctuations. Reasonable allocation of distributed power capacity can help balance the supply and demand relationship of the power system, reduce the risk of grid overload, and thereby improve the reliability and stability of the grid.
By combining these two key aspects, our research deepens the understanding of the relationship between optimized distributed power carrying capacity and voltage fluctuation prediction in power systems. Our model excels in the accuracy of predicting voltage fluctuations, providing the power system with sensitivity to future grid conditions. This sensitivity plays a key role in optimizing decisions on the carrying capacity of distributed power sources, ensuring the sustainable operation of the power system.
5 Conclusion and discussion
In this study, we successfully propose an comprehensive model that integrates DRDQN and DCNN and applies it to power systems to realize the carrying capacity optimization of distributed power sources and accurate prediction of voltage fluctuations. A series of detailed ablation experiments fully validate the significant advantages of this method under different datasets and performance metrics, and confirm the effectiveness of Meta-Learning in complex power system problems. The results of this paper show that this model can provide strong support for the intelligent management and optimization of power system and has significant practical application value. By optimizing the carrying capacity of distributed power supply, renewable energy can be used more efficiently, and the dependence on traditional energy can be reduced, and thus promote the green and sustainable development of the power system. At the same time, accurate voltage fluctuation prediction is helpful to maintain the stability and reliability of the power grid and provide guarantee for the safe operation of the power system.
Nevertheless, we are also aware of the potential limitations of the study. First, the performance of the model may be more sensitive to data volume and data quality, which may affect its generalization performance. Second, the degree to which the model depends on prior knowledge and artificial feature engineering may limit its application scope. Future studies will focus on addressing these questions, to make the model more robust and versatile.
In the subsequent work, we will continue to further research in the field of power system, especially to find more innovative solutions based on the combination of advanced deep learning technologies. We plan to scale up the experimental dataset to more comprehensively evaluate the performance of the model and improve its generalization ability. At the same time, we will strive to achieve the automation of model selection and hyperparameter adjustment to reduce the complexity in practical applications. We believe that this study will have a positive impact on real power systems and provide strong support for the future development of sustainable power systems. We expect this study to inspire more research on the intelligence and optimization of power systems and make positive contributions to the future development of power systems.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
ZY: Data curation, Funding acquisition, Investigation, Project administration, Writing–original draft, Writing–review and editing. FY: Data curation, Investigation, Project administration, Resources, Writing–original draft. HM: Data curation, Formal Analysis, Funding acquisition, Investigation, Writing–review and editing. YL: Conceptualization, Formal Analysis, Writing–review and editing. NZ: Investigation, Methodology, Project administration, Resources, Writing–review and editing. HZ: Conceptualization, Funding acquisition, Project administration, Writing–review and editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
Authors ZY, FY, HM, and YL were employed by Electric Power Research Institute of State Grid Hubei Co., Ltd. Author NZ was employed by Wuhan Power Supply Company of State Grid Hubei Electric Power Co., Ltd. Author HZ was employed by Chongqing Electric Energy Star Co., Ltd.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abbasi, M., Shahraki, A., Piran, M. J., and Taherkordi, A. (2021). Deep reinforcement learning for qos provisioning at the mac layer: a survey. Eng. Appl. Artif. Intell. 102, 104234. doi:10.1016/j.engappai.2021.104234
Acheampong, F. A., Nunoo-Mensah, H., and Chen, W. (2021). Transformer models for text-based emotion detection: a review of bert-based approaches. Artif. Intell. Rev. 54, 5789–5829. doi:10.1007/s10462-021-09958-2
Ahmed, R., Sreeram, V., Mishra, Y., and Arif, M. (2020). A review and evaluation of the state-of-the-art in pv solar power forecasting: techniques and optimization. Renew. Sustain. Energy Rev. 124, 109792. doi:10.1016/j.rser.2020.109792
Akhtaruzzaman, M., Hasan, M. K., Kabir, S. R., Abdullah, SNHS, Sadeq, M. J., and Hossain, E. (2020). Hsic bottleneck based distributed deep learning model for load forecasting in smart grid with a comprehensive survey. IEEE Access 8, 222977–223008. doi:10.1109/access.2020.3040083
Ali, M., Prakash, K., Macana, C., Raza, M., Bashir, A., and Pota, H. (2023). Modeling synthetic power distribution network and datasets with industrial validation. J. Industrial Inf. Integration 31, 100407. doi:10.1016/j.jii.2022.100407
Alimi, O. A., Ouahada, K., and Abu-Mahfouz, A. M. (2020). A review of machine learning approaches to power system security and stability. IEEE Access 8, 113512–113531. doi:10.1109/access.2020.3003568
Almheiri, Z., Meguid, M., and Zayed, T. (2021). Failure modeling of water distribution pipelines using meta-learning algorithms. Water Res. 205, 117680. doi:10.1016/j.watres.2021.117680
Alquthami, T., Alsubaie, A., Alkhraijah, M., Alqahtani, K., Alshahrani, S., and Anwar, M. (2022). Investigating the impact of electric vehicles demand on the distribution network. Energies 15, 1180. doi:10.3390/en15031180
Aslam, S., Herodotou, H., Mohsin, S. M., Javaid, N., Ashraf, N., and Aslam, S. (2021). A survey on deep learning methods for power load and renewable energy forecasting in smart microgrids. Renew. Sustain. Energy Rev. 144, 110992. doi:10.1016/j.rser.2021.110992
Bai, S., Yin, Y., Wu, Y., Zhang, J. Z., Yu, Y., and Jasimuddin, S. M. (2022). Consumer engagement on social networking sites: the antecedents and mediating mechanism. J. Organ. End User Comput. (JOEUC) 34, 1–19. doi:10.4018/JOEUC.307567
Bhatt, D., Patel, C., Talsania, H., Patel, J., Vaghela, R., Pandya, S., et al. (2021). Cnn variants for computer vision: history, architecture, application, challenges and future scope. Electronics 10, 2470. doi:10.3390/electronics10202470
Cao, B., Dong, W., Lv, Z., Gu, Y., Singh, S., and Kumar, P. (2020). Hybrid microgrid many-objective sizing optimization with fuzzy decision. IEEE Trans. Fuzzy Syst. 28, 2702–2710. doi:10.1109/tfuzz.2020.3026140
Dharavat, N., Golla, N. K., Sudabattula, S. K., Velamuri, S., Kantipudi, M., Kotb, H., et al. (2023). Impact of plug-in electric vehicles on grid integration with distributed energy resources: a review. Front. Energy Res. 10, 1099890. doi:10.3389/fenrg.2022.1099890
Dhruv, P., and Naskar, S. (2020). Image classification using convolutional neural network (cnn) and recurrent neural network (rnn): a review. Mach. Learn. Inf. Process. Proc. ICMLIP 2019, 367–381. doi:10.1007/978-981-15-1884-3_34
Dong, Y., Sun, Y., Liu, Z., Du, Z., and Wang, J. (2024). Predicting dissolved oxygen level using young’s double-slit experiment optimizer-based weighting model. J. Environ. Manag. 351, 119807. doi:10.1016/j.jenvman.2023.119807
Du, Y., and Li, F. (2019). Intelligent multi-microgrid energy management based on deep neural network and model-free reinforcement learning. IEEE Trans. Smart Grid 11, 1066–1076. doi:10.1109/tsg.2019.2930299
Duan, Y., Zhao, Y., and Hu, J. (2023). An initialization-free distributed algorithm for dynamic economic dispatch problems in microgrid: modeling, optimization and analysis. Sustain. Energy, Grids Netw. 34, 101004. doi:10.1016/j.segan.2023.101004
Fei, M., Zhang, Z., Zhao, W., Zhang, P., and Xing, Z. (2024). Optimal power distribution control in modular power architecture using hydraulic free piston engines. Appl. Energy 358, 122540. doi:10.1016/j.apenergy.2023.122540
Gorre, J., Ruoss, F., Karjunen, H., Schaffert, J., and Tynjälä, T. (2020). Cost benefits of optimizing hydrogen storage and methanation capacities for power-to-gas plants in dynamic operation. Appl. Energy 257, 113967. doi:10.1016/j.apenergy.2019.113967
Hafeez, G., Alimgeer, K. S., and Khan, I. (2020). Electric load forecasting based on deep learning and optimized by heuristic algorithm in smart grid. Appl. Energy 269, 114915. doi:10.1016/j.apenergy.2020.114915
He, H., Lu, N., Jiang, Y., Chen, B., and Jiao, R. (2020). End-to-end probabilistic forecasting of electricity price via convolutional neural network and label distribution learning. Energy Rep. 6, 1176–1183. doi:10.1016/j.egyr.2020.11.057
Ismael, S. M., Aleem, S. H. A., Abdelaziz, A. Y., and Zobaa, A. F. (2019). State-of-the-art of hosting capacity in modern power systems with distributed generation. Renew. energy 130, 1002–1020. doi:10.1016/j.renene.2018.07.008
Jiang, P., Liu, Z., Abedin, M. Z., Wang, J., Yang, W., and Dong, Q. (2024). Profit-driven weighted classifier with interpretable ability for customer churn prediction. Omega 125, 103034. doi:10.1016/j.omega.2024.103034
Karpov, P., Godin, G., and Tetko, I. V. (2019). “A transformer model for retrosynthesis,” in International Conference on Artificial Neural Networks, Munich, Germany, September, 2019, 817–830.
Lavanya, S., Prabakaran, S., and Kumar, N. A. (2022). A deep learning technique for detecting high impedance faults in medium voltage distribution networks. Eng. Technol. Appl. Sci. Res. 12, 9477–9482. doi:10.48084/etasr.5288
Li, S., Zhao, X., Liang, W., Hossain, M. T., and Zhang, Z. (2022). A fast and accurate calculation method of line breaking power flow based on taylor expansion. Front. Energy Res. 10, 943946. doi:10.3389/fenrg.2022.943946
Li, Y., Nie, J., and Chao, X. (2020). Do we really need deep cnn for plant diseases identification? Comput. Electron. Agric. 178, 105803. doi:10.1016/j.compag.2020.105803
Lin, L., Fan, H., Zhang, Z., Xu, Y., and Swintrack, L. H. (2022). A simple and strong baseline for transformer tracking. Adv. Neural Inf. Process. Syst. 35, 16743–16754.
Liu, C. H., Ma, X., Gao, X., and Tang, J. (2019). Distributed energy-efficient multi-uav navigation for long-term communication coverage by deep reinforcement learning. IEEE Trans. Mob. Comput. 19, 1274–1285. doi:10.1109/tmc.2019.2908171
Liu, E., He, R., Chen, X., and Yu, C. (2022). Deep reinforcement learning based optical and acoustic dual channel multiple access in heterogeneous underwater sensor networks. Sensors 22, 1628. doi:10.3390/s22041628
Liu, Z., Jiang, P., De Bock, K. W., Wang, J., Zhang, L., and Niu, X. (2024). Extreme gradient boosting trees with efficient bayesian optimization for profit-driven customer churn prediction. Technol. Forecast. Soc. Change 198, 122945. doi:10.1016/j.techfore.2023.122945
Marković, M., Sajadi, A., Florita, A., Cruickshank, R., and Hodge, B. M. (2021). Voltage estimation in low-voltage distribution grids with distributed energy resources. IEEE Trans. Sustain. Energy 12, 1640–1650. doi:10.1109/tste.2021.3060546
Massaoudi, M., Abu-Rub, H., Refaat, S. S., Chihi, I., and Oueslati, F. S. (2021). Deep learning in smart grid technology: a review of recent advancements and future prospects. IEEE Access 9, 54558–54578. doi:10.1109/access.2021.3071269
Misra, I., Girdhar, R., and Joulin, A. (2021). “An end-to-end transformer model for 3d object detection,” in Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, October, 2021, 2906–2917.
Mohammad, F., Ahmed, M. A., and Kim, Y. C. (2021). Efficient energy management based on convolutional long short-term memory network for smart power distribution system. Energies 14, 6161. doi:10.3390/en14196161
Nam, K., Hwangbo, S., and Yoo, C. (2020). A deep learning-based forecasting model for renewable energy scenarios to guide sustainable energy policy: a case study of korea. Renew. Sustain. Energy Rev. 122, 109725. doi:10.1016/j.rser.2020.109725
Ning, X., Tian, W., He, F., Bai, X., Sun, L., and Li, W. (2023). Hyper-sausage coverage function neuron model and learning algorithm for image classification. Pattern Recognit. 136, 109216. doi:10.1016/j.patcog.2022.109216
Niu, H., Zhang, Z., Xiao, Y., Luo, M., and Chen, Y. (2022). A study of carbon emission efficiency in Chinese provinces based on a three-stage sbm-undesirable model and an lstm model. Int. J. Environ. Res. Public Health 19, 5395. doi:10.3390/ijerph19095395
Razavi, S. E., Rahimi, E., Javadi, M. S., Nezhad, A. E., Lotfi, M., Shafie-khah, M., et al. (2019). Impact of distributed generation on protection and voltage regulation of distribution systems: a review. Renew. Sustain. Energy Rev. 105, 157–167. doi:10.1016/j.rser.2019.01.050
Ronanki, D., and Williamson, S. S. (2019). Failure prediction of submodule capacitors in modular multilevel converter by monitoring the intrinsic capacitor voltage fluctuations. IEEE Trans. Industrial Electron. 67, 2585–2594. doi:10.1109/tie.2019.2912771
Shao, B., Xiao, Q., Xiong, L., Wang, L., Yang, Y., Chen, Z., et al. (2023). Power coupling analysis and improved decoupling control for the vsc connected to a weak ac grid. Int. J. Electr. Power and Energy Syst. 145, 108645. doi:10.1016/j.ijepes.2022.108645
Shirkhani, M., Tavoosi, J., Danyali, S., Sarvenoee, A. K., Abdali, A., Mohammadzadeh, A., et al. (2023). A review on microgrid decentralized energy/voltage control structures and methods. Energy Rep. 10, 368–380. doi:10.1016/j.egyr.2023.06.022
Smagulova, K., and James, A. P. (2019). A survey on lstm memristive neural network architectures and applications. Eur. Phys. J. Special Top. 228, 2313–2324. doi:10.1140/epjst/e2019-900046-x
Sun, M., Zhang, T., Wang, Y., Strbac, G., and Kang, C. (2019). Using bayesian deep learning to capture uncertainty for residential net load forecasting. IEEE Trans. Power Syst. 35, 188–201. doi:10.1109/tpwrs.2019.2924294
Sun, P., Liu, Z., Wang, J., and Zhao, W. (2024). Interval forecasting for wind speed using a combination model based on multiobjective artificial hummingbird algorithm. Appl. Soft Comput. 150, 111090. doi:10.1016/j.asoc.2023.111090
Tavoosi, J., Shirkhani, M., Azizi, A., Din, S. U., Mohammadzadeh, A., and Mobayen, S. (2022). A hybrid approach for fault location in power distributed networks: impedance-based and machine learning technique. Electr. Power Syst. Res. 210, 108073. doi:10.1016/j.epsr.2022.108073
Tian, S., Li, W., Ning, X., Ran, H., Qin, H., and Tiwari, P. (2023). Continuous transfer of neural network representational similarity for incremental learning. Neurocomputing 545, 126300. doi:10.1016/j.neucom.2023.126300
Wang, S., and Chen, H. (2019). A novel deep learning method for the classification of power quality disturbances using deep convolutional neural network. Appl. energy 235, 1126–1140. doi:10.1016/j.apenergy.2018.09.160
Wang, S., Takyi-Aninakwa, P., Jin, S., Yu, C., Fernandez, C., and Stroe, D. I. (2022). An improved feedforward-long short-term memory modeling method for the whole-life-cycle state of charge prediction of lithium-ion batteries considering current-voltage-temperature variation. Energy 254, 124224. doi:10.1016/j.energy.2022.124224
Wang, Y., Peng, T., Zhu, B., and Cui, H. (2023b). Few-shot knowledge graph completion based on meta learning. J. Jilin Univ. Sci. Ed. 61, 623–630.
Wang, Y., Xia, F., Wang, Y., and Xiao, X. (2023a). Harmonic transfer function based single-input single-output impedance modeling of lcchvdc systems. J. Mod. Power Syst. Clean Energy. doi:10.35833/MPCE.2023.000093
Wang, Y., Zou, R., Liu, F., Zhang, L., and Liu, Q. (2021). A review of wind speed and wind power forecasting with deep neural networks. Appl. Energy 304, 117766. doi:10.1016/j.apenergy.2021.117766
Wen, L., Zhou, K., Yang, S., and Lu, X. (2019). Optimal load dispatch of community microgrid with deep learning based solar power and load forecasting. Energy 171, 1053–1065. doi:10.1016/j.energy.2019.01.075
Wenya, L. (2021). “Cooling, heating and electric load forecasting for integrated energy systems based on cnn-lstm,” in 2021 6th International Conference on Power and Renewable Energy (ICPRE) (IEEE), Shanghai, China, September, 2021, 808–812.
Wu, C. H. (2022). An empirical study on selection, evaluation, and management strategies of green suppliers in manufacturing enterprises. J. Organ. End User Comput. (JOEUC) 34, 1–18. doi:10.4018/joeuc.307568
Wu, C. L., and Horng, S. M. (2022). Social commerce intention, social interaction, and social support: moderating role of social anxiety. J. Organ. End User Comput. (JOEUC) 34, 1–23. doi:10.4018/joeuc.307565
Wu, Xl, Xu, Y. W., Xue, T., Zhao, Dq, Jiang, J., Deng, Z., et al. (2019). Health state prediction and analysis of sofc system based on the data-driven entire stage experiment. Appl. energy 248, 126–140. doi:10.1016/j.apenergy.2019.04.053
Xiao, J., and Zhou, Z. (2020). “Research progress of rnn language model,” in 2020 IEEE International Conference on Artificial Intelligence and Computer Applications (ICAICA), Dalian, China, June, 2020, 1285–1288.
Xiao, S., Wang, Z., Wu, G., Guo, Y., Gao, G., Zhang, X., et al. (2023). Critical assessment of the delivery methods of chemical and natural postharvest preservatives for fruits and vegetables: a review. IEEE Trans. Transp. Electrification, 1–23. doi:10.1080/10408398.2023.2289071
Yan, Z., and Wen, H. (2021). Electricity theft detection base on extreme gradient boosting in ami. IEEE Trans. Instrum. Meas. 70, 1–9. doi:10.1109/tim.2020.3048784
Yang, F., Liu, D., Zeng, Q., Chen, Z., Ye, Y., Yang, T., et al. (2022a). “Prediction of mianyang carbon emission trend based on adaptive gru neural network,” in 2022 4th International Conference on Frontiers Technology of Information and Computer (ICFTIC), Qingdao, China, December, 2022, 747–750.
Yang, Y., Zhang, Z., Zhou, Y., Wang, C., and Zhu, H. (2022b). Design of a simultaneous information and power transfer system based on a modulating feature of magnetron. IEEE Trans. Microw. Theory Tech. 71, 907–915. doi:10.1109/tmtt.2022.3205612
Zhang, B., Xiang, X., Jia, J., Zhang, X., Li, C., and Peng, J. (2023). Landslide disaster prediction method around natural gas pipeline based on lightgbm. J. Jilin Univ. Sci. Ed. 61, 338–346.
Zhang, Y., Shi, X., Zhang, H., Cao, Y., and Terzija, V. (2022). Review on deep learning applications in frequency analysis and control of modern power system. Int. J. Electr. Power and Energy Syst. 136, 107744. doi:10.1016/j.ijepes.2021.107744
Zhang, Z., Zhang, D., and Qiu, R. C. (2019). Deep reinforcement learning for power system applications: an overview. CSEE J. Power Energy Syst. 6, 213–225. doi:10.17775/CSEEJPES.2019.00920
Zhao, Y., Zhang, G., Hu, W., Huang, Q., Chen, Z., and Blaabjerg, F. (2023). Meta-learning based voltage control strategy for emergency faults of active distribution networks. Appl. Energy 349, 121399. doi:10.1016/j.apenergy.2023.121399
Zhou, S., Zhou, G., Liu, X., and Zhao, H. (2022). Dynamic freewheeling control for sido buck converter with fast transient performance, minimized cross-regulation, and high efficiency. IEEE Trans. Industrial Electron. 70, 1467–1477. doi:10.1109/tie.2022.3156169
Keywords: deep learning, distribution network, distributed power, voltage fluctuation, grid optimization, data analysis
Citation: Yang Z, Yang F, Min H, Liu Y, Zhang N and Zeng H (2024) Optimization and analysis of distributed power carrying capacity of distribution network based on DR-DQN. Front. Energy Res. 12:1342517. doi: 10.3389/fenrg.2024.1342517
Received: 22 November 2023; Accepted: 05 February 2024;
Published: 29 February 2024.
Edited by:
Ping Jiang, Dongbei University of Finance and Economics, ChinaReviewed by:
Flah Aymen, École Nationale d'Ingénieurs de Gabès, TunisiaZhenkun Liu, Nanjing University of Posts and Telecommunications, China
Copyright © 2024 Yang, Yang, Min, Liu, Zhang and Zeng. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhichun Yang, eXpjbGxpY0AxNjMuY29t
 Zhichun Yang
Zhichun Yang Fan Yang1
Fan Yang1