Electricity market clearing for multiple stakeholders based on the Stackelberg game

In order to improve the operating benefits of the distribution network and reduce the energy consumption costs of small–micro-industrial parks, an electricity market clearing considering small–micro-industrial parks is proposed based on the Stackelberg game. First, an optimal operating model of multiple stakeholders is established for integrated energy suppliers, the electricity market, and small–micro-industrial parks. In this model, an optimal electricity supply model for integrated energy suppliers is established with the goal of maximizing the operating benefits. A market clearing optimization model is established for the electricity market with the goal of maximizing the social surplus profit. In addition, an energy utilization optimization model is established for the small–micro-industrial parks with the goal of minimizing the energy procurement costs. Second, with the electricity market as the leader, the integrated energy suppliers and the small–micro-industrial parks as the followers, a leader–follower game strategy is proposed based on the Stackelberg game theory to achieve the maximizing benefits for multiple stakeholders. Finally, the simulation indicates that the proposed strategy can find the best profit point during the game process and achieve a balance between supply and demand.

1 Introduction

In recent years, small and micro-enterprises have developed rapidly in Zhejiang Province, China. In order to facilitate the prosperous development of such enterprises, Zhejiang Province has standardized and renovated the existing small–micro-industrial parks (SMIPs) based on the actual operation. However, the SMIPs do not dispatch enough power generation and energy storage (ES) devices, which results in a low capacity to withstand the operating risks. With the rapid development of SMIPs, the demand for electricity trading between SMIPs and distribution networks (DNs) is constantly increasing. On one hand, trading electricity with the DNs can help the SMIPs withstand operating risks. On the other hand, an optimal trading electricity strategy can help the SMIPs save operating costs. Then, how to optimize the electricity trading between the DNs and SMIPs is currently a highly important issue.

As the electricity market (EM) continues to open up, operators and agents in the DNs gradually participate in the competition within the EM (He et al., 2021). As a user-side autonomous system, SMIPs can participate in power trading in the EM under the management of operators (Davoudi and Moeini-Aghtaie, 2022), which can deepen the hierarchical structure of the EM trading framework (Pownall et al., 2021). Meanwhile, agents, as the link between SMIP operators and the EM, directly affect the energy costs of these parks. Talaeizadeh et al. (2022) explored the procurement of flexibility services in the power system by the collaboration between distribution system operators and transmission system operators. With the coordination among the operators, the flexibility sources were exploited to procure flexibility services. Anwar et al. (2022) introduced an electricity market and investment suite-agent-based simulation, which modeled the evolution of the electricity generation mix under various market structures while explicitly capturing the aforementioned investment factors and imperfect information. To improve power generation profits, Yuan et al. (2022) proposed an optimized scheduling model for cascade hydropower plants, simultaneously participating in both the day-ahead spot market and the daily contract market. Considering the characteristic that natural gas can blend with hydrogen, Ding et al. (2023) proposed a multi-agent electricity–heat–hydrogen trading model by taking hydrogen produced on the load side. Tan et al. (2022) treated carbon as a direct trading object and proposed an internal multi-energy trading mechanism, which adopts an auction based on the demands for cooling, heating, electricity, and carbon. To further explore the multi-energy coupling capacity and carbon reduction potential of the integrated energy systems, Yang et al. (2023) proposed a cooling–heat–electricity–gas collaborative optimization model of integrated energy systems given a ladder carbon trading mechanism and multi-energy demand response. Li et al. (2023) proposed a medium-term multi-stage distributionally robust optimization scheduling approach for a price-taking of hydro–wind–solar complementary systems in the EM. A multi-agent deep reinforcement learning approach combining the multi-agent actor–critic algorithm with the twin delayed deep deterministic policy gradient algorithm was proposed by Chen et al. (2022), and the proposed approach can handle the high-dimensional continuous action space and aligns with the nature of peer-to-peer energy trading. Yang et al. (2022) analyzed the impact of different bidding decisions on the distribution of wind farm revenues in a process where the interest of two markets is played against each other. Khaligh et al. (2022) introduced a stochastic agent-based model for the coordinated scheduling of multi-vector microgrids considering interactions between electricity, hydrogen, and gas agents. Considering the power loss, flexible load demand, and other operating indicators to maximize the user and supplier benefits, the real-time transaction electricity price model of the user side and the power supply side was constructed by Lyu et al. (2022). In the EM trading that SMIPs participate in, how to coordinate the benefit relationship between agents and operators (Green and Newman, 2017), increasing the profit of agents while reducing the electricity costs for the operators (Zare et al., 2015), has become a hotspot in the research direction of the EM.

In EM trading, the optimization goals of multiple stakeholders are different (Yu and Hong, 2016), but there exists a coupling relationship among the optimization models (Mahdavi et al., 2018). Finding a point of balanced benefits has become a key factor for the stability of the alliances in EM trading (Cao et al., 2021). Stackelberg game theory is frequently employed as an effective tool in solving optimization problems within the electricity market (Du et al., 2022). To solve the inherent conflict among the players, a Stackelberg game-based technique is proposed by Haghifam et al. (2020). To achieve comprehensive optimal benefits for different stakeholders, Liu et al. (2018) established a two-layer optimization model considering the involvement of different stakeholders, and the stakeholders achieve the maximization of the overall benefits by aggregating the generation units within microgrids. However, in this method, the electricity price during the trading process is a fixed time-of-use price, which cannot reflect the flexibility of EM trading. Cherukuri and Cortes (2020) proposed a bidding iterative auction mechanism in the EM but did not analyze the factors affecting the electricity price of the agents. Furthermore, the operation of the generation units can only be optimized after obtaining the market clearing results, so it has lower flexibility. A trading model based on the Stackelberg game model is proposed by Wei et al. (2022) to balance the interests of the supply side and demand side and reduce the carbon emissions. To solve the problems of environmental pollution and conflict of interests among multiple stakeholders in the integrated energy system, Wang et al. (2022) proposed a novel collaborative optimization strategy for a low-carbon economy in the integrated energy system based on the carbon trading mechanism and Stackelberg game theory. Envelope et al. (2022) proposed a Stackelberg game-based optimal scheduling model for electro–thermal integrated energy systems, which seeks to maximize the revenue of the integrated energy operator and minimize the cost of users. Pu et al. (2023) constructed a two-stage supply chain consisting of a manufacturer and a retailer based on a dual-credit policy, considering three different power structure models, namely, the vertical Nash game model, the manufacturer Stackelberg game model, and the retailer Stackelberg game model, and explored the operational strategy issues of new energy vehicle enterprises under the dual-credit policy. Zhang et al. (2022) took the integrated energy system operator as the leader and each integrated energy system as the follower to construct the Stackelberg operation model, and the proposed model is constructed and solved by the double mutation differential evolution algorithm. Hua et al. (2023) proposed a framework of local energy markets to manage this transactive energy and facilitate the flexibility provision, the decision-making, and interactions between a DN operator, and multiple microgrid traders are formulated as the Stackelberg game-theoretic problem. Fattaheian et al. (2022) applied the Stackelberg game to model the incentivizing resource scheduling optimization under post-contingency conditions, and a strong duality condition is used to re-cast the preliminary bi-level model into a one-level mathematical problem. The pricing mechanisms in existing research are mainly day-ahead fixed pricing mechanisms; as SMIP types participate in market trading in the future, fixed pricing strategies will not be able to adapt to the increasingly flexible EM. In this context, it is highly necessary to study the dynamic pricing strategies for EM trading to enhance the economic operation of the multiple stakeholders in the power system.

In light of the abovementioned strategies, an EM clearing considering SMIP is proposed based on the Stackelberg game. The main contributions of this paper are summarized as follows:

(1) To improve the DN operating benefits, as well as reduce the energy costs of SMIPs, an optimal operating model for multiple stakeholders in the EM clearing is established, which contains an optimal electricity supply model for integrated energy suppliers (IESs), a market clearing optimization model for the EM, and an energy utilization optimization model for the SMIPs.

(2) To characterize the benefit relationship among multiple stakeholders, with the EM as the leader and the IESs and SMIPs as the followers, a leader–follower game model based on the Stackelberg game is proposed to maximize the benefits for multiple stakeholders.

(3) To find the balanced benefits, an iterative optimization method is proposed to solve the leader–follower game model. In addition, by the iterative optimization among the multiple stakeholders, the best profit point during the game process can be found, and a dynamic optimal pricing strategy for EM trading is obtained.

The remainder of this paper is organized as follows: an EM clearing framework for multiple stakeholders is proposed in Section 2; an optimized operating model for multiple stakeholders in the EM clearing is introduced in Section 3; in Section 4, a leader–follower game strategy is proposed for multiple stakeholders; in Section 5, the case study is analyzed; and the conclusion is given in Section 6.

2 The EM clearing framework for multiple stakeholders

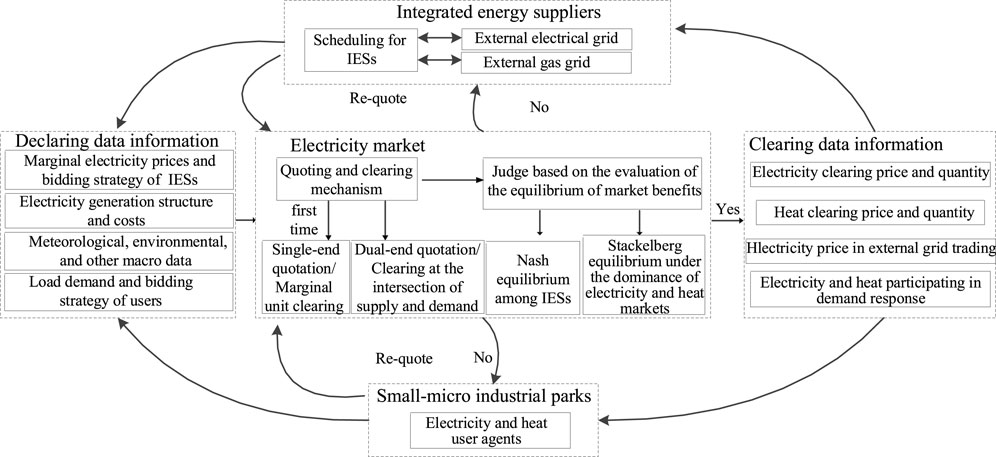
The EM clearing framework for bilateral bidding between IESs and SMIPs is shown in Figure 1. The IESs have their own scheduling strategies and market quotation–bidding strategies. The SMIPs offer quotations to the market through an agency and engage in bidding with IESs.

Figure 1

Figure 1. EM clearing framework.

At the beginning of the first quotation, the IESs and SMIPs declare the prices to the market side, and then the declared prices are processed according to the quotation clearing mechanism. The price clearing data are prepared by the evaluation of the market benefits. If the equilibrium of benefits does not meet the standard, the IESs and SMIPs will carry on a re-quote based on the latest clearing results. When the equilibrium of benefits meets the standard, the final clearing data will be exported and transmitted to the IESs and SMIPs.

3 The optimal operating model for multiple stakeholders

The optimal operating model for multiple stakeholders in the EM clearing contains an optimal electricity supply model for IESs, a market clearing optimization model for the EM, and an energy utilization optimization model for the SMIPs.

3.1 The optimal electricity supply model for IESs

The electricity supply of IESs should consider the income from selling energy F_sell, trading costs with external electricity grids F_util, and various energy supply costs. The energy supply costs include the natural gas fuel cost F_f and the equipment maintenance cost F_om. The optimal electricity supply model is as follows:

$\max F=F_{\text{sell}}-\left(F_{\mathrm{f}}+F_{\text{util}}+F_{\text{om}}\right).(1)$

The IESs can earn profits by selling the produced electricity and heat to SMIPs. The price and power of the sold energy are obtained based on the electricity market clearing. Then, the income from selling energy F_sell is given as follows:

$F_{\text{sell}}={\displaystyle \sum _{t=1}^{\mathrm{T}}}{P}_{el}\left(t\right)C_e\left(t\right)+{\displaystyle \sum _{t=1}^{\mathrm{T}}}{Q}_{hl}\left(t\right)C_h\left(t\right),(2)$

where P_el(t) and Q_hl(t) represent the electricity power and heat power, respectively, at time t under the response to the demand of the SMIPs. C_e(t) and C_h(t) represent the electricity prices and heat prices, respectively, at time t cleared by the EM. T represents the optimization time.

IESs can arbitrage through trading with external grids. When the electricity price of the power grid is low, the IESs purchase the electricity and sell electricity when its price is high, and then the profits can be obtained. The trading costs with the external electricity grid F_util is given as follows:

$F_{\text{util}}={\displaystyle \sum _{t=1}^{\mathrm{T}}}{P}_{util}\left(t\right)C_{util}\left(t\right),(3)$

where P_util(t) is the interactive power between the IESs and the external electricity grid at time t. When P_util(t) > 0, it means that the IESs purchase electricity from the external electricity grid. When P_util(t) < 0, it means that the IESs sell electricity from the external electricity grid. C_util(t) is the interactive electricity price between the IESs and the external electricity grid at time t.

The energy provided by IESs is divided into two categories. The first category is wind turbines (WTs) and photovoltaic (PV) power generation, and this type of energy does not need to be purchased. The second category is gas turbines and gas boilers, which burn natural gas to generate electricity and heat, respectively. For this category, the purchasing cost of natural gas needs to be included in the cost, which is called fuel cost. The fuel cost F_f is given as follows:

$\left.F_f=\frac{C_{gas}}{L}\cdot {\displaystyle \sum _{t=1}^{\mathrm{T}}}\left[\frac{P_{GT}\left(t\right)}{{\eta }_{GT}}+\right.\frac{Q_{GB}\left(t\right)}{{\eta }_{GB}}\right],(4)$

where C_gas is the price of natural gas and L is the low calorific value of natural gas, which represents the heat released by burning a certain volume of natural gas. P_GT(t) and Q_GB(t) represent the output powers of the gas turbine and gas boiler at time t, respectively. η_GT and η_GB represent the efficiencies of the gas turbine and gas boiler, respectively.

The distributed energy equipment in the system needs maintenance, and the equipment maintenance cost F_om is given as follows:

$F_{om}={\displaystyle \sum _{i=1}^{\mathrm{I}}}{\displaystyle \sum _{t=1}^{\mathrm{T}}}{{\xi }_i}^S{P}_{DGi}\left(t\right),(5)$

where I is the number of power generation equipment. ${{\xi }_i}^S$ is the cost coefficient of the ith power generation equipment. P_DGi(t) represents the supply power of the ith power generation equipment at time t. In the IES optimization model, the constraints of various parameters are given as follows:

(1) Constraints on electricity and heat power balance

$P_{el}\left(t\right)={\displaystyle \sum _{i=1}^{\mathrm{I}}}{P}_{DGi}\left(t\right)+P_{GT}\left(t\right)+P_{util}\left(t\right),(6)$

$P_{el}\left(t\right)=L_e\left(t\right)+P_{EDR}\left(t\right),(7)$

$Q_{hl}\left(t\right)=Q_{WH}^{out}\left(t\right)+Q_{GB}^h\left(t\right),(8)$

$Q_{hl}\left(t\right)=L_h\left(t\right)+Q_{HDR}\left(t\right).(9)$

Formulas 6, 7 are the constraints on electricity power balance, and Formulas 8, 9 are the constraints on heat power balance. L_e(t) and L_h(t) represent the original electricity and heat loads of SMIPs at time t, respectively. Q(t) is the heat power recovered from the gas boiler at time t. P_EDR(t) and Q_eHDR(t) represent the electricity and heat load responding to the demand of SMIPs at time t, respectively.

(2) Constraints on the output of distributed energy generation equipment

$P_{DGi,\min }\le P_{DGi}\left(t\right)\le P_{DGi\max },(10)$

where P_{i min}(t) and P_{i max}(t) represent the upper and lower limits of the power of the ith distributed energy equipment, respectively.

(3) Constraints on the power exchange with the external electricity grid

$P_{\max }^{sell}\le P_{util}\left(t\right)\le P_{\max }^{buy},(11)$

where $P_{\max }^{sell}$ and $P_{\max }^{buy}$ are the upper limits of the power sold to and bought from the external electricity grid by the IESs, respectively.

(4) Constraints on the power of energy equipment participating in the electricity market clearing

$P_{k,e}^{\prime }\left(t\right)\le P_{k,e}\left(t\right),(12)$

$Q_{s,h}^{\prime }\left(t\right)\le Q_{s,h}\left(t\right),(13)$

where P^'_k,e(t) and Q^'_s,h(t) represent the powers cleared in the EM for each electric and thermal unit at time t, respectively. P_k,e(t) and Q_s,h(t) represent the actual power generated by each electric and thermal unit at time t, respectively.

3.2 The energy utilization optimization model for the SMIPs

The energy utilization optimization model of SMIPs takes minimizing the energy purchase cost as the objective function. In addition to paying the energy purchase fee F_sell to the IESs, SMIPs can also obtain income compensation F_DR by reducing a certain amount of load through demand response. Therefore, the objective function is established as follows:

$\min F_{user}=F_{sell}-F_{DR},(14)$

$F_{sell}={\displaystyle \sum _{t=1}^{\mathrm{T}}}\left[L_e\left(t\right)+P_{EDR}\left(t\right)\right]\cdot C_e\left(t\right)+{\displaystyle \sum _{t=1}^{\mathrm{T}}}\left[L_h\left(t\right)+Q_{HDR}\left(t\right)\right]\cdot C_h\left(t\right),(15)$

$\left.F_{DR}={\displaystyle \sum _{t=1}^{\mathrm{T}}}\left[v_e{P}_{EDR}\left(t\right)\right]+{\displaystyle \sum _{t=1}^{\mathrm{T}}}\left[v_h{Q}_{HDR}\left(t\right)\right.\right],(16)$

where v_e and v_h represent the reduction compensation coefficients for the electricity and heat demand response of SMIPs, respectively. For the demand response to SMIPs, various constraints need to be considered as follows:

(1) Constraints on the income of SMIPs

The benefits of users after demand response $F_{user}^{DR}$ should be greater than the benefits before the response F₀. The mathematical formula is

$F_{user}^{DR}\ge F_0.(17)$

(2) Constraints on the power of load transfer

During the optimization process, the SMIPs can participate in price-based demand response. Thus, the power of electricity and heat load transfer cannot exceed the limit value $P_{EDR}^{\mathit{max}}$ and $Q_{HDR}^{\mathit{max}}$. The mathematical formula is

$P_{EDR}\left(t\right)\le P_{EDR}^{\max },(18)$

$Q_{HDR}\left(t\right)\le Q_{HDR}^{\max }.(19)$

3.3 The market clearing optimization model for the EM

The EM aims at maximizing the social surplus profit, which reflects the balance of benefits between the supply and demand. The maximum social surplus profit in this paper consists of the profit surplus of IESs and profit surplus of the users. The objective function of the model is established as follows:

$\max H={\displaystyle \sum _{t=1}^{\mathrm{T}}}\left[H_{emo}\left(t\right)+H_{user}\left(t\right)\right],(20)$

$H_{emo}\left(t\right)={\displaystyle \sum _{k=1}^{\mathrm{K}}}\left[\left(C_e\left(t\right)-C_{e,\min }\left(t\right)\right)P_{k,e}^{\prime }\left(t\right)\right]+{\displaystyle \sum _{s=1}^{\mathrm{S}}}\left[\left(C_h\left(t\right)-C_{h,\min }\left(t\right)\right)Q_{s,h}^{\prime }\left(t\right)\right],(21)$

where H_emo(t) and H_user(t) represent the surplus profits of the IESs and the surplus profits of SMIPs at time t, respectively. K represents the number of electricity power generation equipment. S represents the number of heat power generation equipment. C_e,min(t) and C_h,min(t) represent the lower limits of the electricity and heat bidding prices of the IESs, respectively. C_e,max(t) and C_h,max(t) represent the upper limits of electricity and heat bidding prices of SMIPs, respectively.

The price and power of the electricity and heat cleared by the EM need to be constrained to ensure that the clearing data are within a reasonable range. The formulas are as follows:

$P_{e,\min }^{\prime }\hspace{0.17em}\left(t\right)\le P_e^{\prime }\left(t\right)\le P_{e,\max }^{\prime }\hspace{0.17em}\left(t\right),(22)$

$Q_{h,\min }^{\prime }\hspace{0.17em}\left(t\right)\le Q_h^{\prime }\left(t\right)\le Q_{h,\max }^{\prime }\hspace{0.17em}\left(t\right),(23)$

$C_{e,\min }\left(t\right)\le C_e\left(t\right)\le C_{e,\max }\left(t\right),(24)$

$C_{h,\min }\left(t\right)\le C_h\left(t\right)\le C_{h,\max }\left(t\right),(25)$

where P′_k.e(t) represents the electricity power cleared by the EM. Q′_s.h(t) represents the heat power cleared by the EM. P′_e,min(t) represents the essential need of electricity load. Q′_s.h(t) represents the essential need of heat load. P′_e,max(t) represents the electricity load after the demand response. Q′_h,max(t) represents the heat load after the demand response. To solve the proposed optimal electricity supply model for IESs, the energy utilization optimization model for the SMIPs, and the market clearing optimization model for the EM, an improved particle swarm optimization algorithm (Xiao et al., 2017) is utilized to conduct the optimization.

4 The leader–follower game strategy for the multiple stakeholders

4.1 The leader–follower game model for the multiple stakeholders

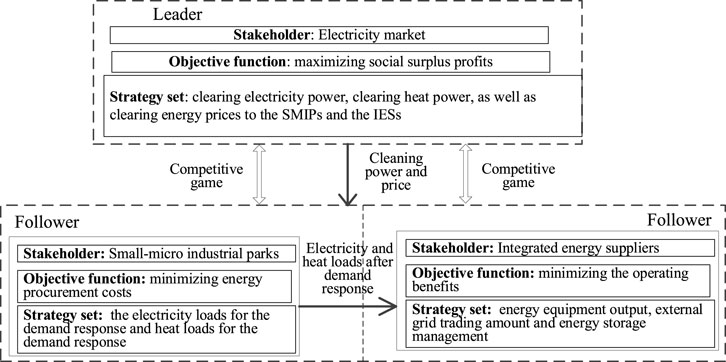
To characterize the benefit relationship among multiple stakeholders, a leader–follower game model based on the Stackelberg game is proposed in this paper to maximize benefits for multiple stakeholders. In the proposed leader–follower game mode, there are three stakeholders: the EM, SMIPs, and the IESs. The EM is the leader in the game, while the SMIPs and IESs are followers. The SMIPs and the IESs respond to the decisions of the EM and adjust the strategy according to their objective functions. The EM aims to maximize social surplus profits, and the strategy set includes clearing electricity power, heat power, and energy prices to the SMIPs and the IESs. The IESs aim to maximize operating benefits, and the strategy set includes energy equipment output, external grid trading amount, and energy storage management. The SMIPs aim to minimize energy procurement costs, and the strategy set includes the electricity loads for the demand response and heat loads for the demand response. The interactive framework of the leader–follower game is shown in Figure 2.

Figure 2

Figure 2. Leader–follower game interaction framework.

For the Stackelberg equilibrium of a non-cooperative game, when Eq. 26 is satisfied, it indicates that the game has reached equilibrium. At this point, the followers make the best response according to the strategy of the leader. In addition, each stakeholder cannot obtain more profits by changing their own strategy set.

$\left\{\begin{array}{l}{E}_{mar}\left[I_{mar},F_{emo}^{*},L_{user}^{*}\right]\le E_{mar}\left[I_{mar}^{*},F_{emo}^{*},L_{user}^{*}\right]\\ E_{user}\left[I_{mar}^{*},F_{emo},L_{user}^{*}\right]\le E_{user}\left[I_{mar}^{*},F_{emo}^{*},L_{user}^{*}\right]\\ E_{\mathrm{e}mo}\left[I_{mar}^{*},F_{emo}^{*},F_{emo}\right]\le E_{emo}\left[I_{mar}^{*},F_{emo}^{*},F_{emo}^{*}\right]\end{array}\right.,(26)$

where E_mar represents the profits of the EM. E_user represents the profits of the SMIPs. E_emo represents the profits of the IESs. L_user, F_emo, and I_mar represent the strategy sets for the SMIPs, the IESs, and the EM, respectively. L*_user, F^*_emo, and I*_mar represent the optimal strategy sets for the SMIPs, the IESs, and the EM, respectively.

4.2 The solution process of the proposed method

To solve the proposed method, an iteration search method proposed by Chuang et al. (2001) is employed to find the Nash equilibrium point. The solution of the proposed scheduling model is summarized as follows:

Step 1. The strategies of all the stakeholders are initialized as D^old = [I⁰_mar, L⁰_user, F⁰_emo], and the profits of all stakeholders are calculated as F^old = [E⁰_mar, E⁰_user, E⁰_emo].

Step 2. The scheduling model for each stakeholder is solved based on the exchanged game strategies from other stakeholders.

Step 3. The game strategy of each stakeholder is updated as D^new = [I¹_mar, L¹_user, F¹_emo], and the operating cost of all stakeholders is calculated as F^new = [E¹_mar, E¹_user, E¹_emo].

Step 4. The operating cost difference of F^new and F^old is calculated. If the cost difference is smaller than its threshold, the procedure is terminated, and the new strategies D^new is output. Otherwise, D^old is reset as D^new, and Step 2 onwards is repeated.

5 Case study

5.1 Basic data of the case study

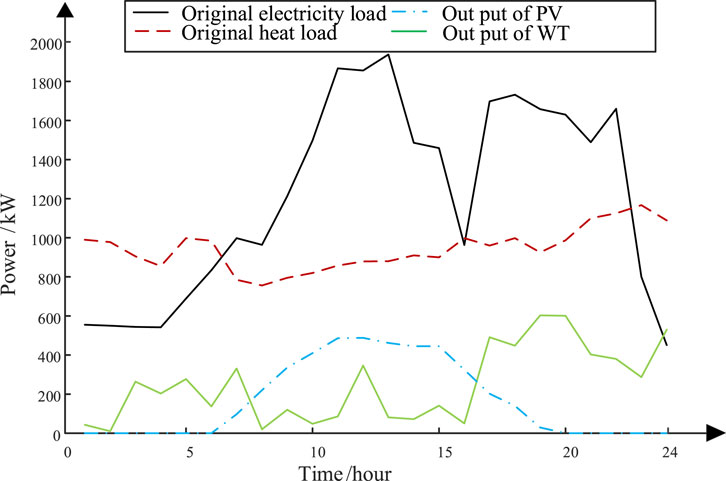
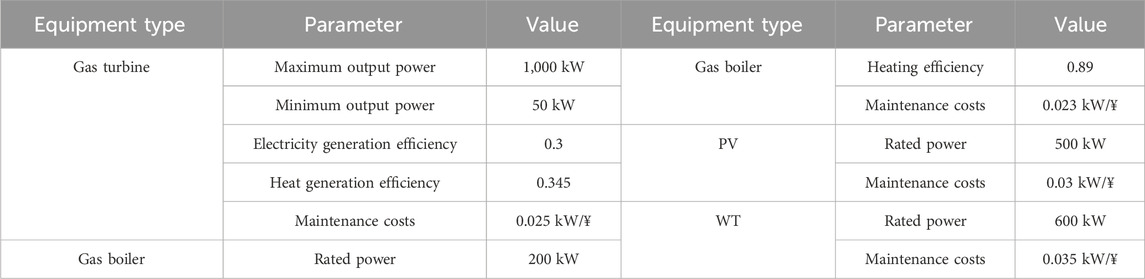
This paper conducted a simulation analysis of the day-ahead EM clearing with SMIPs as an example. The WT and PV forecast data, as well as the electricity and heat load power of users, are shown in Figure 3. Table 1 shows the time-of-use energy prices of the electricity and gas grids. Table 2 shows the parameters for IESs and SMIPs.

Figure 3

Figure 3. Loads and renewable energy outputs.

Table 1

Table 1. Time-of-use energy price for electricity and gas grids.

Table 2

Table 2. Parameters of the IESs and SMIPs.

In order to analyze the advantages of the proposed method, three scenarios are set up. In scenario 1, the objective function of the operation is maximizing the profits of IESs, electricity and heat prices are fixed, and users do not participate in the demand response. In scenario 2, the objective function of the operation is still maximizing the profits of IESs, but the user side will actively respond according to the change in energy prices. In scenario 3, the EM, IES, and SMIP carry out the operation with the proposed strategy of this paper, and the power and price of energy are determined by market clearing through market-side quoting and bidding.

5.2 Analysis of the case study

Table 3 shows the operation results of the three scenarios. It shows that under the proposed method, there have been varying degrees of improvement in social surplus profits, profits of the IESs, and profits of the SMIPs, with the most notable increase in social surplus profits.

Table 3

Table 3. Comparison of the three scenarios.

Compared to scenario 1, in scenario 2, the social surplus increase in the profits of the IES decrease slightly, and the energy purchase costs for SMIPs decrease significantly. This is because through price-based demand response, the user side can peak-shave and valley-fill to smooth the electricity and heat load curves, thereby obtaining extra compensation benefits. As the load demand curve becomes smoother, the arbitrage space obtained by IESs through energy storage will be correspondingly reduced, leading to a decrease in profits. As the load demand becomes flat, the marginal cost of the energy equipment output is reduced, and the social surplus profits increase. In scenario 3, the profits of all stakeholders increase significantly, and the energy purchase costs of SMIPs have been reduced. This is because under the guidance of the EM mechanism, the energy trading price between IESs and SMIPs is determined based on the clearing of the supply and demand relationship at each moment. Thus, the price can better reflect the degree of energy surplus or scarcity within the SMIPs. The proposed method can also increase efficiency in energy storage arbitrage and trading with the external electricity grid, as well as improve the precision of user demand response.

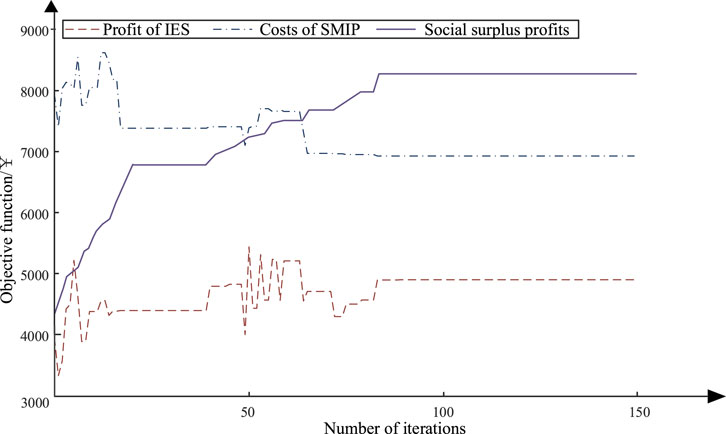
Figure 4 shows the convergence diagram of profits for each stakeholder in scenario 3. It well reflects the game process between various stakeholders throughout the entire iteration process, and finally, equilibrium is achieved at about 80 iterations, which takes 16.3 min. In the game process, the declared energy power and prices from other stakeholders are constantly cleared by the EM. In addition, the EM, as the leader in the entire game process, shows a gradual upward trend in its profits. The SMIPs and IESs adjust their own strategy sets continuously and rationally based on the clearing results of the EM. The SMIPs and IESs, as followers, also engage in game interaction at the same time and finally reach convergence. When the leader and two followers reach the Stackelberg equilibrium, their strategy sets no longer change.

Figure 4

Figure 4. Convergence diagram of profits for each stakeholder.

The energy clearing prices are shown in Figure 5. The electricity clearing price in the EM peaks from 18:00 to 22:00. During this period, the PV output is low, and the demand for electricity load is high. To meet the demand, the IES will utilize more gas turbines. At the same time, the gas turbines have the highest marginal cost among all units, so their prices are the highest. Meanwhile, the demand response from the SMIPs is low, and the electric load demand curve is flat. Therefore, the EM will clear the electricity generated by gas turbines at high prices. The heat clearing price in the EM shows a significant peak from 00:00 to 04:00. Therefore, during this period, the output of gas boilers needs to be scheduled to meet the heat needs of the SMIPs. The cost of gas boilers is higher than that of other heat sources, so the heat clearing price in the EM shows a short-term peak.

Figure 5

Figure 5. Energy clearing prices.

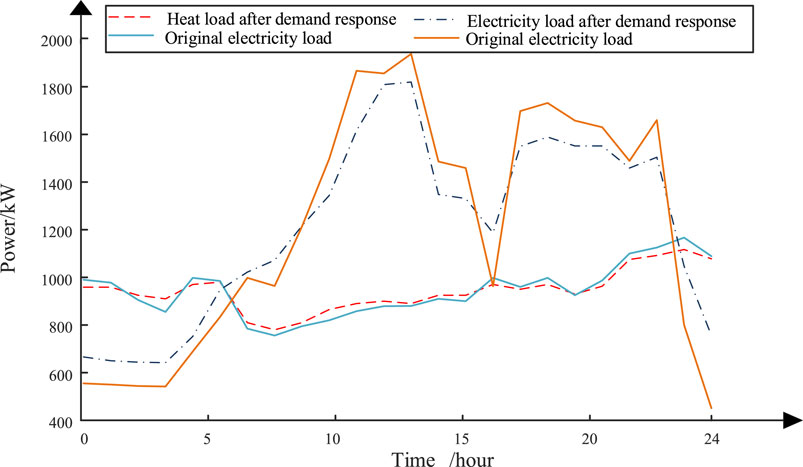
Figure 6 shows the comparison of the before and after demand response of the SMIPs under the proposed strategy. It indicates that the fluctuations in electricity and heat loads have been significantly reduced, and the effects of peak-shaving and valley-filling are obvious. SMIPs respond more accurately to the energy price in the EM clearing, which brings a lot of hidden benefits to the DN. After the demand response, the electricity and heat load curves are smoothed within an appropriate range, and the energy purchase costs on the user side are reduced. At the same time, the energy supply pressure of the IESs is eased.

Figure 6

Figure 6. Demand response of SMIPs.

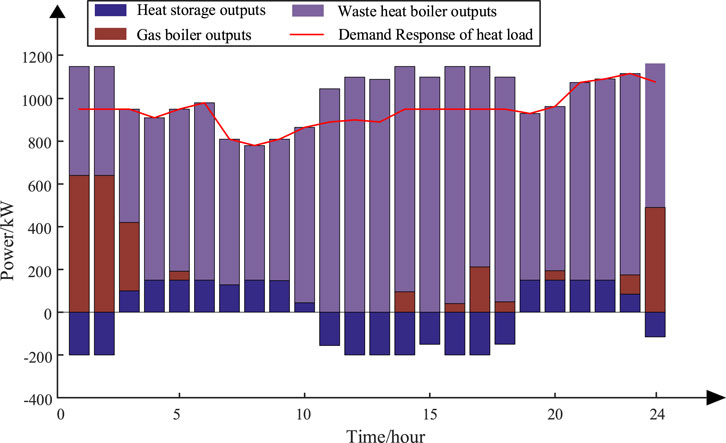
The final optimized electricity and heat power of the IESs are shown in Figures 7, 8. According to the following optimization results, several key time periods with obvious characteristics are analyzed:

1) From 0:00 to 9:00, the electric load demand is low. During this period, the electricity clearing price of the EM is low, so the SMIPs follow the price-based demand response and increase electricity usage when the electricity price is low. The output of the WT is relatively high, and only a minimal amount of gas turbine output is needed to supplement the electricity supply alongside the WT. At the same time, the energy prices of the upper-layer electricity and gas grids are relatively low. Therefore, with the complete consumption of the WT, the IESs can use a small amount of gas turbine power while purchasing electricity from the external electricity grid. Then, the electrical energy is stored under the premise of meeting the electrical load demand.

2) From 10:00 to 13:00, the electricity load demand is at its peak. During this period, the electricity clearing price in the EM is relatively high, so the SMIPs follow a price-based demand response and reduce electricity consumption. The output of the PV increases, the output of the WT is very low, and the output of gas turbines needs to be increased to meet the electrical load. At the same time, the energy prices of the electricity and gas grids are relatively high. With the complete consumption of the WT, the IESs need to increase the output of the gas turbines to meet the load demand. If the load demand failed to be met, electricity needs to be purchased from the external electricity grid, and the battery power is released to complete the supply.

3) From 17:00 to 22:00, the electricity and heat load demands are both high. During this period, the electricity and heat clearing prices in the EM are relatively high, so users follow a price-based demand response and reduce electricity and heat usage. The outputs of the WT are very high, the outputs of the PV decreased significantly, and the output of the gas turbines needs to be increased to meet the electrical load demand. The heat outputs of the waste heat boiler are relatively high and can basically meet the heat load demands of SMIPs. During this period, the energy prices of the electricity and gas grids are both relatively high. Therefore, with the complete consumption of the WT, IESs can choose to increase the output of gas turbines to meet the electrical load demand. If the load demand is still unable to be met, electricity needs to be purchased from the external electricity grid, and the battery power is released to complete the electric load supply.

Figure 7

Figure 7. Optimized electricity power of the integrated energy supplier.

Figure 8

Figure 8. Optimized heat power of the IESs.

6 Conclusion

In order to improve the flexibility of SMIPs to participate in market trading, a Stackelberg game-based EM clearing is proposed for multiple stakeholders in DNs. First, an optimal operating model for multiple stakeholders is established, which contains an optimal electricity supply model for the IES, a market clearing optimization model for the EM, and an energy utilization optimization model for the SMIPs. With the EM as the leader, and the IESs and the SMIPs as the followers, a leader–follower game model is proposed to achieve the maximizing benefits for multiple stakeholders. Finally, an iterative optimization method is proposed to find a point of balanced benefits of multiple stakeholders. The proposed strategy can enhance the benefits of all participating stakeholders and achieve a balance between supply and demand. It should be noted that the uncertainty of WTs, PVs, and loads in the operation is not considered. In the future, considering the uncertainty, the real-time quoting and clearing will be conducted in the EM.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

XW: writing–original draft. QY: writing–review and editing. LC: writing–review and editing. HL: writing–review and editing. WW: writing–review and editing.

Funding

The authors declare that financial support was received for the research, authorship, and/or publication of this article. The study in this paper was supported by the project supported by Zhejiang Electric Power Industry Corporation Technology Project (CF058810002022001).

Conflict of interest

Authors XW, QY, LC, HL, and WW were employed by State Grid Pingyang Power Supply Company.

The authors declare that this study received funding from the Zhejiang Electric Power Industry Corporation. The funder had the following involvement in the study design, collection, analysis, the writing of this article.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Anwar, B., Stephen, G., Dalvi, S., Frew, B., Ericson, S., Brown, M., et al. (2022). Modeling investment decisions from heterogeneous firms under imperfect information and risk in wholesale electricity markets. Appl. Energy 306, 117908. doi:10.1016/j.apenergy.2021.117908

CrossRef Full Text | Google Scholar

Cao, S., Zhang, H., Cao, K., Chen, M., Wu, Y., and Zhou, S. (2021). Day-ahead economic optimal dispatch of microgrid cluster considering shared energy storage system and P2P transaction. Front. Energy Res. 9 (9), 645017. doi:10.3389/fenrg.2021.645017

CrossRef Full Text | Google Scholar

Chen, T., Bu, S., Liu, X., Kang, J., Yu, F. R., and Han, Z. (2022). Peer-to-peer energy trading and energy conversion in interconnected multi-energy microgrids using multi-agent deep reinforcement learning. IEEE Trans. Smart Grid 13 (1), 715–727. doi:10.1109/tsg.2021.3124465

CrossRef Full Text | Google Scholar

Cherukuri, A., and Cortes, J. (2020). Iterative bidding in electricity markets: rationality and robustness. IEEE Trans. Netw. Sci. Eng. 7 (3), 1265–1281. doi:10.1109/tnse.2019.2921056

CrossRef Full Text | Google Scholar

Chuang, A., Wu, F., and Varaiya, P. (2001). A game-theoretic model for generation expansion planning: problem formulation and numerical comparisons. IEEE Power Eng. Rev. 21 (10), 63. doi:10.1109/mper.2001.4311103

CrossRef Full Text | Google Scholar

Davoudi, M., and Moeini-Aghtaie, M. (2022). Local energy markets design for integrated distribution energy systems based on the concept of transactive peer-to-peer market. IET Generation, Transm. Distribution (1), 16. doi:10.1049/gtd2.12274

CrossRef Full Text | Google Scholar

Ding, J., Gao, C., Song, M., Yan, X., and Chen, T. (2023). Optimal operation of multi-agent electricity-heat-hydrogen sharing in integrated energy system based on Nash bargaining. Int. J. Electr. Power Energy Syst. 148 (6), 108930. doi:10.1016/j.ijepes.2022.108930

CrossRef Full Text | Google Scholar

Du, X., Li, X., Hao, Y., and Chen, L. (2022). Sizing of centralized shared energy storage for resilience microgrids with controllable load: a bi-level optimization approach. Front. Energy Res. 10 (10), 954833. doi:10.3389/fenrg.2022.954833

CrossRef Full Text | Google Scholar

Envelope, L., Envelope, R., Envelope, Y., and Xu, C. (2022). Stackelberg game-based optimal scheduling of integrated energy systems considering differences in heat demand across multi-functional areas. Energy Rep. 8, 11885–11898. doi:10.1016/j.egyr.2022.08.199

CrossRef Full Text | Google Scholar

Fattaheian, S., Tavakkoli, M., Abbaspour, A., Fotuhi-Firuzabad, M., and Lehtonen, M. (2022). Optimal energy management of distribution networks in post-contingency conditions. Int. J. Electr. Power Energy Syst. 141 (11), 108022. doi:10.1016/j.ijepes.2022.108022

CrossRef Full Text | Google Scholar

Green, J., and Newman, P. (2017). Citizen utilities: the emerging power paradigm. Energy Policy 105, 283–293. doi:10.1016/j.enpol.2017.02.004

CrossRef Full Text | Google Scholar

Haghifam, S., Zare, K., Abapour, M., Muñoz-Delgado, G., and Contreras, J. (2020). A Stackelberg game-based approach for transactive energy management in smart distribution networks. Energies 13 (14), 3621. doi:10.3390/en13143621

CrossRef Full Text | Google Scholar

He, C., Tang, J., Zhang, W., Zhang, Z., Lin, Z., Li, Y., et al. (2021). Optimal planned electricity allocation model for power exchange under the plan-market double-track mechanism. Front. Energy Res. 9 (9), 679365. doi:10.3389/fenrg.2021.679365

CrossRef Full Text | Google Scholar

Hua, W., Xiao, H., Pei, W., et al. (2023). Transactive energy and flexibility provision in multi-microgrids using Stackelberg game. CSEE J. Power Energy Syst. 9 (2), 505–515. doi:10.17775/CSEEJPES.2021.04370

CrossRef Full Text | Google Scholar

Khaligh, V., Ghezelbash, A., Mazidi, M., Liu, J., Ryu, J. H., and Na, J. (2022). A stochastic agent-based cooperative scheduling model of a multi-vector microgrid including electricity, hydrogen, and gas sectors. J. Power Sources 546 (10), 231989–232014. doi:10.1016/j.jpowsour.2022.231989

CrossRef Full Text | Google Scholar

Li, Z., Yang, P., Guo, Y., and Lu, G. (2023). Medium-term multi-stage distributionally robust scheduling of hydro–wind–solar complementary systems in electricity markets considering multiple time-scale uncertainties. Appl. Energy 347, 121371. doi:10.1016/j.apenergy.2023.121371

CrossRef Full Text | Google Scholar

Liu, Y., Guo, L., and Wang, C. (2018). Economic dispatch of microgrid based on two stage robust optimization. Proc. CSEE 38 (14), 4013–4022. doi:10.13334/j.0258-8013.pcsee.170500

CrossRef Full Text | Google Scholar

Lyu, Z., Lai, Y., Yang, X., Li, Y., and Yi, J. (2022). Cooperative game consistency optimal strategy of multi-microgrid system considering flexible load. Energy Sources. 44 (3), 7378–7399. doi:10.1080/15567036.2022.2109779

CrossRef Full Text | Google Scholar

Mahdavi, S., Hemmati, R., and Jirdehi, M. (2018). Two-level planning for coordination of energy storage systems and wind-solar-diesel units in active distribution networks. Energy 151, 954–965. doi:10.1016/j.energy.2018.03.123

CrossRef Full Text | Google Scholar

Pownall, T., Soutar, I., and Mitchell, C. (2021). Re-designing GB’s electricity market design: a conceptual framework which recognises the value of distributed energy resources. Energies 14 (4), 1124. doi:10.3390/en14041124

CrossRef Full Text | Google Scholar

Pu, J., Chun, W., Wang, Z., and Chen, W. (2023). Operation strategy for new energy vehicle enterprises based on dual credit policy. J. Industrial Manag. Optim. 19 (8), 5724–5748. doi:10.3934/jimo.2022192

CrossRef Full Text | Google Scholar

Talaeizadeh, V., Aghaei, J., and Shayanfar, H. (2022). Day-ahead flexibility market clearing mechanism for interactive collaboration of transmission and distribution system operators. IET Generation, Transm. Distribution 16 (13), 2587–2599. doi:10.1049/gtd2.12474

CrossRef Full Text | Google Scholar

Tan, J., Li, Y., and Zhang, X. (2022). Optimization and trading of district multi-energy system in university community considering carbon emission. Int. J. Electr. Power Energy Syst. 137 (5), 107450. doi:10.1016/j.ijepes.2021.107450

CrossRef Full Text | Google Scholar

Wang, R., Cheng, S., Zuo, X., and Liu, Y. (2022). Optimal management of multi stakeholder integrated energy system considering dual incentive demand response and carbon trading mechanism. Int. J. Energy Res. 46 (5), 6246–6263. doi:10.1002/er.7561

CrossRef Full Text | Google Scholar

Wei, M., Deng, Y., Long, M., Wang, Y., and Li, Y. (2022). Transaction model based on Stackelberg game method for balancing supply and demand sides of multi-energy microgrid. Energies 15 (4), 1362–1420. doi:10.3390/en15041362

CrossRef Full Text | Google Scholar

Xiao, C., Zhao, B., Ding, M., Li, Z., and Ge, X. (2017). Zonal voltage control combined day-ahead scheduling and real-time control for distribution networks with high proportion of PVs. Energies 10 (10), 1464. doi:10.3390/en10101464

CrossRef Full Text | Google Scholar

Yang, M., Liu, Y., Lund, H., et al. (2023). Research on multi-energy collaborative operation optimization of integrated energy system considering carbon trading and demand response. Energy 283, 129117. doi:10.1016/j.energy.2023.129117

CrossRef Full Text | Google Scholar

Yang, X., Fan, L., Gao, X., and Liu, H. (2022). Analysis of wind farm participation in frequency regulation considering multi-market interests. J. Renew. Sustain. Energy 14 (1), 013304. doi:10.1063/5.0073140

CrossRef Full Text | Google Scholar

Yu, M., and Hong, S. H. (2016). Supply–demand balancing for power management in smart grid: a Stackelberg game approach. Appl. Energy 164, 702–710. doi:10.1016/j.apenergy.2015.12.039

CrossRef Full Text | Google Scholar

Yuan, W., Zhang, S., Su, C., Wu, Y., Yan, D., and Wu, Z. (2022). Optimal scheduling of cascade hydropower plants in a portfolio electricity market considering the dynamic water delay. Energy 252, 124025. doi:10.1016/j.energy.2022.124025

CrossRef Full Text | Google Scholar

Zare, K., Abapour, S., and Mohammadi-Ivatloo, B. (2015). Dynamic planning of distributed generation units in active distribution network. Generation Transm. Distribution Iet 9 (12), 1455–1463. doi:10.1049/iet-gtd.2014.1143

CrossRef Full Text | Google Scholar

Zhang, Y., Zhao, H., Li, B., and Wang, X. (2022). Research on dynamic pricing and operation optimization strategy of integrated energy system based on Stackelberg game. Int. J. Electr. Power Energy Syst. 143 (12), 108446. doi:10.1016/j.ijepes.2022.108446

CrossRef Full Text | Google Scholar