
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res. , 28 February 2024
Sec. Sustainable Energy Systems
Volume 12 - 2024 | https://doi.org/10.3389/fenrg.2024.1336205
This article is part of the Research Topic Building Energy System Retrofit and Optimization in Small Energy Communities View all 4 articles
Endeavoring to enhance the penetration rate of renewable energy sources, concurrently ensuring economic and operational stability, this study proposes a novel bi-layer optimization method of the wind–solar-storage AC/DC microgrid (MG). First, by incorporating a superordinate electric and seasonal hydrogen hybrid energy storage system (E&SHESS), the topology structure of the microgrid is established. Subsequently, to rectify the intrinsic limitations of the conventional beluga whale optimization (BWO) algorithm, this paper proposes a multi-strategy hybrid improvement to BWO (MHIBWO). This innovative improvement integrates an MTent strategy, a step size adjustment mechanism, and a crisscross strategy. Then, constructing a bi-layer iterative model based on the topology, annual net income and grid-connected friendliness are introduced as optimization objectives for the outer and inner layers, respectively, utilizing MHIBWO and CPLEX for resolution. Through a nested iteration of the two layers, the model outputs the capacity scheme with the best performance of economy and stability. Finally, the simulation unequivocally demonstrated the superiority of MHIBWO and the model proposed. In addition, based on the real data of the Elia power station, the validity of the method in operation is tested using the fuzzy C-means algorithm (FCMA) to extract and aggregate typical days, thereby presenting a sophisticated solution for the field of microgrids optimization configuration.
In recent years, there has been a rapid and significant advancement in microgrids (MGs). The integration of distributed generations (DGs) into MGs has been steadily increasing, driven by their benefits of energy utilization efficiency and dependable power supply (Singh and Sharma, 2017; Zhao et al., 2023). However, the inherent instability of the energy sources in MGs leads to voltage and frequency fluctuations that adversely affect both the economy and the system reliability (Xu et al., 2021; He et al., 2022). Consequently, there is an urgent need to optimize and strategically configure the MG, with the primary objectives of improving grid-connection friendliness and ensuring economic efficiency.
The optimal capacity determination for the MG relies on constructing an effective model and solving associated optimization problems (Lu Z. et al., 2023). The MG comprises various components, including DGs, energy storage systems (ESSs), loads, and power busbars. To meet the increasing requirements of modern power systems, this paper proposes an electric and seasonal hydrogen hybrid energy storage system (E&SHESS). This system combines the advantages of an electric ESS in terms of response time and a hydrogen ESS in terms of capacity and conversion efficiency, which enables the system to adapt to power demands across various periods and frequency ranges. Compared to a single busbar, AC/DC hybrid busbars can handle different types of loads and offer advantages such as high-power output efficiency and improved system stability (Ferahtia et al., 2022). Unlike single-layer models that predominantly focus on cost reduction in the objective function construction, this paper addresses the challenges of balancing operation stability and reliability, recognizing the limitations and poor ergodicity, and introduces a bi-layer optimal model. The outer-layer objective is economy, while the inner-layer objective is stability. The coordination between planning and operation is achieved through nested iterations of the two layers, resulting in the derivation of an optimal global performance configuration. To solve the bi-layer model, an efficient meta-heuristic algorithm, Beluga Whale optimization (BWO), is proposed. Furthermore, to overcome the shortcomings of poor population initialization and the tendency to converge to local optima in the later stages, a multi-strategy hybrid improvement method is used. This method incorporates the MTent strategy, step size adjustment strategy, and crisscross approach, enhancing the diversity of the initial population of beluga whales and improving their optimization-seeking ability in the middle and late stages.
In general, this paper introduces a bi-layer capacity optimization method for wind–solar-storage AC/DC MG, considering grid-connected friendliness (GCF). The contributions of this study are four-fold.
1. An E&SHESS responding to the demand for different levels of energy and power is proposed. The topological structure of the MG and information mathematical model are built using the E&SHESS.
2. A bi-layer iteration model of the MG is constructed. The net income and GCF are introduced as the outer and inner objectives, respectively. This optimization methodology combines cost, environmental sustainability, and system stability with more practical significance.
3. The multi-strategy hybrid improvement method and MHIBWO are introduced. The proposed method exhibits superior optimization performance to five common algorithms in terms of optimization speed and accuracy.
4. The FCMA is used to aggregate typical operational and uncertainty analysis days and validate the proposed optimization method.
Planning and configuration are crucial in ensuring the financial and operational stability of MGs. Consequently, researchers have devoted significant attention to constructing comprehensive models for the MG and addressing the problem of optimizing capacity (Souza Junior and Freitas, 2022; Huang et al., 2023).
The construction of an MG model serves as a fundamental step in achieving optimal efficiency. The ESS can effectively alleviate the strain on the grid caused by generation power and enhance the overall power supply quality (Erdemir and Dincer, 2023). However, the primary ESSs, batteries, are susceptible to capacity limitations, particularly in managing the high proportion of long-time scale energy generation on the grid (Lyden et al., 2022). To solve the above problems, an ideal seasonal ESS should have the advantages of a large storage capacity, long service life, and low self-discharge rate (Xie et al., 2023). Seasonal hydrogen ESSs have emerged as a promising solution, attracting significant attention due to their potential for large-scale energy storage (Zhou et al., 2022; Yamashita et al., 2019). In a previous work, Lu et al. developed an optimal configuration model for a “hydrogen production–hydrogen storage” system in the incredible energy season and a hybrid hydrogen gas turbine in the depleted energy season (Lu M. F. et al., 2023). In 2023, Shao et al. introduced a multi-time grid method to optimize the operation of seasonal ESSs. However, their planning model still uses the full-time series, which increases the computational effort for system optimization planning (Shao et al., 2023). Compared to single DC or AC microgrids, hybrid AC/DC MGs combine both advantages (Yue et al., 2022). Xie et al. learned through simulation analysis that an AC/DC MG ensures power quality during the grid-connected process and significantly improves the system stability of the MG compared to a single MG (Xie et al., 2022).
The optimization problem of MGs has the characteristics of non-convexity, nonlinearity, multi-objectivity, discrete/integer variables, and nonlinear/linear constraints (Mohseni et al., 2019). The modality of optimization problems is a multimodal system with multiple local optima and a globally optimal solution (Ogbonnaya et al., 2019). To realize the optimal operation of an island group energy system with an energy transmission-constrained environment, the energy demand and energy supply are guaranteed. Yang et al. proposed an island energy hub model that can realize energy cascade utilization and used the hybrid policy-based reinforcement learning (HPRL) adaptive energy management method to solve the problem. An HPRL method that can deal with discrete–continuous mixing behavior is proposed to solve the energy management problem of island groups. For complex models with discrete–continuous mixed actions, it is better to avoid simplifying the model to obtain an optimization strategy (Yang et al., 2023). The methods for solving MG optimization problems are shown in Supplementary Table S1. Capacity optimization models are mainly divided into two categories. One category is the single-layer, single/multi-objective model, and the other is the two-stage, two-layer model (Huang et al., 2021; Chen et al., 2022). The single-layer model makes it difficult to consider the economics and dispatching problems, and the output decision scheme is more localized and weaker in terms of global interests (Chen et al., 2022). To avoid these issues, the two-stage two-layer optimization model is applied (Luo et al., 2022). This model can better coordinate the interests of multiple parties within the MG and develop a reasonable strategy and an optimal operation plan for the MG. Among these, the one with the strongest computing power is the two-layer heuristic algorithm, with the upper layer often being a meta-heuristic algorithm. Currently, research on artificial intelligence (AI) has produced a series of programs that can be directly applied or used to solve complex energy-related problems, such as energy system planning, design, operation, and investment. Metaheuristics or heuristic optimization is a branch of AI. By using appropriate computational variants of Systema Naturae, we can calculate the globally optimal solution of non-deterministic polynomial time-hard problems that do not cooperate with precise mathematical optimization technology. To adapt to the problem of complex bi-layer model structures, multiple variables, and nonlinear constraints in the optimization configuration process of microgrids, it is necessary to improve the upper-level heuristic algorithm for the optimization objective in the two-layer optimization method to further enhance the global search ability and optimization accuracy (Almadhor et al., 2021). To improve the performance of existing metaheuristic optimization, Raghav et al. used the quantum teaching learning-based optimization (QTLBO) algorithm, devised for the first time to optimize energy flow in microgrids, solving the multidimensional nonlinear problem of microgrid scheduling, and compared it with existing metaheuristic algorithms, such as the real-number encoding genetic algorithm, differential evolution algorithm, and TLBO. The simulation demonstrated the superiority of QTLBO in terms of convergence and overcoming premature convergence of global optimal solutions and has improved the system economy (Raghav et al., 2021). To study the issues of day-ahead and real-time cooperative energy management for multi-energy systems formed by many energy bodies, Li et al. proposed an event-triggered distributed algorithm. By implementing this algorithm, energy entities can effectively collaborate, maximize social welfare for a day, smooth real-time load changes, and suppress fluctuations in renewable resources (Li et al., 2019). Optimization objectives often focus on economic efficiency, and the literature also considers indicators such as power supply reliability, environmental benefits, and safety (Dong et al., 2022; Ma et al., 2023).
Wind turbines (WTs) and photovoltaic (PV) modules constitute the power generation system. In an E&SHESS, the battery is selected as the electric ESS; the hydrogen ESS consists of an electrolyzer (EL), a hydrogen storage tank (HT), and a fuel cell (FC). The converter equipment realizes energy flow and system stability support through bidirectional AC/DC. The topology of the MG system is shown in Figure 1.
The bi-layer optimal model, with a hierarchical structure, is a particular case of the multi-layer model. The architecture of the bi-layer optimal model in this paper is shown in Figure 2. The nomenclature is shown in Supplementary Table S2. Sections 3.1, 3.2 present the outer and inner optimization model functions, respectively.
The outer-layer optimal model considers the economics and environment, with the objective function of the highest annual comprehensive economy (ACE). This includes the annual operating economy (AOE) and the annual polluting gas penalties (APGPs). The decision variables in this layer are the capacity and power of the devices in the system. The objective function is expressed as Eq. 1:
The AOE includes electricity income (EI), oxygen income (OI), electricity cost (EC), power generation system cost (PGSC), and hybrid energy storage system cost (HESSC). It can be expressed as Eq. 2 and Eq. 3:
Here, S(P, E)1 is the initial investment cost, S(P, E)2 is the cost of operation and maintenance, S(P, E)3 is the repayment cost for the construction loan, and SE4 is the replacement cost. The expressions are as given in Eqs 4–6:
where kCRF is the recovery factor, kCRF = r(1+r)N/(1+r)N-1, and SW+P=KWTPWT+KPVPPV.
Pollutants generated by purchasing electricity from the utility grid are converted into a penalty, expressed as Eq. 7:
During operation, power balance must be ensured. The constraints are expressed as Eq. 8:
where ΔP = PPV(t)+PWT(t)-PLOAD(t) is the difference between DG and load power.
The power, transactions, and capacity must be satisfied within a certain range. The constraints are expressed as Eqs 9, 10:
The inner optimization objective is GCF, which is represented by the DG daily output fluctuation rate (DOFR) and daily output peaks and valley gap (DOPVG). The power output of each device is the decision variable of this layer. Using the linear weighted aggregation method to transform multi-objective optimization into single-objective optimization, the aggregate multi-objective function is constructed as shown in Eq. 11.
The parameters of λ1 and λ2 are determined using the objective function fitness departure ranking method.
The power fluctuation of the complementary DG is shown in Eqs 12, 13:
The peaks and valley gap power of DG is shown in Eq. 14:
The charge state and operation of the electric ESS are shown in Eqs 15–17.
This system operates daily to accommodate the high-frequency power response and extend its service life. The system is charged and discharged at different times. a is the working flag bit. When a = 1, it is charging; when a = 0, it is discharging. n is the positive integer.
The capacity and operation are expressed in Eqs 18–19.
This system operates on an annual cycle to accommodate the massive electrical demand. The staggered operation of the EL and FC in the system was investigated. b is the working flag bit. When b = 1, EL is working; when b = 0, FC is working.
The self-balancing rate is the ratio of the power provided by the DG to the load, as shown in Eq. 20:
BWO is a new meta-heuristic algorithm proposed by Zhong et al. (2022). The behaviors of beluga whales inspire BWO. Balance factor Bf determines the transition from the exploration to the exploitation phase, which is expressed as Eq. 21:
where T is the current iteration, Tmax is the maximum iteration, and B0 randomly changes between (0 and 1). The processes are as follows:
The exploration phase considers the pair of swimming beluga whales. The positions are updated as given in Eq. 22:
where Xi,jT+1 is the new position for the ith beluga whale on the jth dimension. Pj is a random number selected from the d-dimension (j = 1, 2, . . ., d). Xi,PjT and Xr,P1T are the positions of the ith and rth beluga whales, respectively. r1 to r7 is a random number between (0 and 1).
The preying behavior inspires the exploitation phase, which is expressed in Eq. 23:
where XiT and XrT are the positions for the ith beluga whale and a random beluga whale, respectively, XiT+1 is the new position, XbestT is the best position, C1 is the random jump strength, and LF is the Levy flight function. The expression is given in Eqs 24, 25:
where
During migration and foraging, a small number of beluga whales do not survive and fall into the deep seabed. Xstep is the step size of whale fall. The model is expressed as Eqs 26, 27:
where ub and lb are the upper and lower boundaries of the variable, C2 is the step factor, and C2 = 2Wf × n. Wf is the probability of whale fall, Wf = 0.1–0.05 T/Tmax.
Due to the mutual constraints and influences between the inner and outer layers in the established bi-layer optimal model, the computational complexity is high. Therefore, three methods are proposed to strengthen BWO, given as follows.
In this paper, the traditional Tent is improved, and MTent is proposed. MTent is used to replace the original initialization method of BWO to enhance the population diversity. The formula is expressed in Eq. 28:
where Xn represents the initial value and ranges between (0 and 1). rand() is a random number between [0 and 1]. The bifurcation diagram and population initialization are shown in Figures 3A, B. By using the MTent approach proposed in this study for population initialization, a comparison between the two methods leads to the observation that the populations generated by the Tent map predominantly conglomerate at the boundary, exhibiting limited ergodicity and randomness. In contrast, the initial population derived from MTent demonstrates improved ergodicity and randomness, resulting in a more diverse generated population.

FIGURE 3. Algorithm improvement ideas. (A) Bifurcation diagram of MTent. (B) Population initialization. (C) Inertia weight curve.
The step size adjustment strategy enriched the individual diversity of the population. The nonlinear decreasing search factor is shown in Eq. 29:
where η is the adjustment coefficient and A is the random number rand. The range is between (0 and 1). As shown in Figure 3C, in the early stage, the weight is relatively large, and the decreasing speed is slow, which is conducive to improving the global optimization ability. When the weight factor is small, it enhances the advantage of the algorithm in local development and accelerates the speed of obtaining the optimal solution.
Horizontal crossover operation is the process of performing crossover operations on two different white whales in a population in the same dimension, enabling them to learn from each other and improve the global optimization ability of the algorithm. Lateral crossover is performed on the parent individuals xi and xj to generate the offspring individuals MxTi and MxTj, respectively, as shown in Eq. 30:
where m1 and m2 are random numbers among [0,1]; N1 and N2 are random numbers in [-1,1]; xTi,d and xTj,d are the dth dimensions of the parent individuals xi and xj, respectively; and MxTi,d and MxTj,d are the children generated by crossing xi and xj in the dth dimension, respectively.
Vertical crossover operations are crossover operations performed on all dimensions of newborn individuals, improving the ability of the algorithm to avoid local optima. The vertical crossover operation performs crossover operations on two dimensions of the global optimal solution xTi. d1st and d2nd dimensions of xTi are crossed vertically and horizontally, as shown in Eq. 31:
MxTi,d is the offspring generated from the d1 and d2 dimensions of individuals xTi,d1 and xTi,d2, respectively, by longitudinal crossover; m∈[0,1].
In this section, the optimization process of MHIBWO is introduced in detail, and Figure 4 shows the specific flowchart.
Step 1:. Parameter initialization.
The algorithm parameters of the BWO are initialized, and the population size, n, and the maximum number of iterations, Tmax are set. The initial positions of all beluga whales are randomly generated within the search space, and the fitness values are obtained based on the objective function.
Step 2:. Population initialization.
The Tent is used to initialize the beluga whale population and randomly generate the individual beluga whale population, and the position of a beluga whale is updated using Eq. 28.
Step 3:. Fitness calculation.
The initial fitness values of the beluga whale population and the individuals are calculated and compared to find the optimal individual.
Step 4:. Update on the exploration and exploitation phases.
Each beluga whale enters the exploration phase or exploitation phase based on the balance factor Bf = B0(1-T/2Tmax). The step size adjustment strategy is used in Eq. 31, and the subsequent stages, (22) and (23), are applied.
(1) If Bf > 0.5, the updating mechanism enters the exploration phase as Eq. 22. Then, the crisscross strategy is used to improve, and the position of the beluga whale is updated by Eqs 30, 31.
(2) If Bf < 0.5, the updating is controlled by the exploitation phase as Eq. 23.
Calculating and sorting the fitness values of new positions helps in finding the optimum result in the current iteration.
Step 5:. Update on the whale fall phase.
Calculating the probability of whale fall Wf in each iteration, the updating mechanism is entered into the whale fall phase as Eq. 26.
Step 6:. Terminating condition check.
If the current iteration is larger than the maximum iterative number, the MHIBWO stops; otherwise, step 4 is repeated.
In this paper, nine benchmark functions are used to test the optimization performance of particle swarm optimization (PSO), gray wolf optimization (GWO), improved gray wolf optimization (IGWO), seagull optimization algorithm (SOA), and BWO. All algorithms are tested 20 times (Luo et al., 2022). The test function results are shown in Tables 1, 2, and Figure 5. The benchmark function is shown in Supplementary Table S4, and the three-dimensional results of the test results are shown in Supplementary Figure S1. The parameters of the algorithms are shown in Supplementary Table S3.
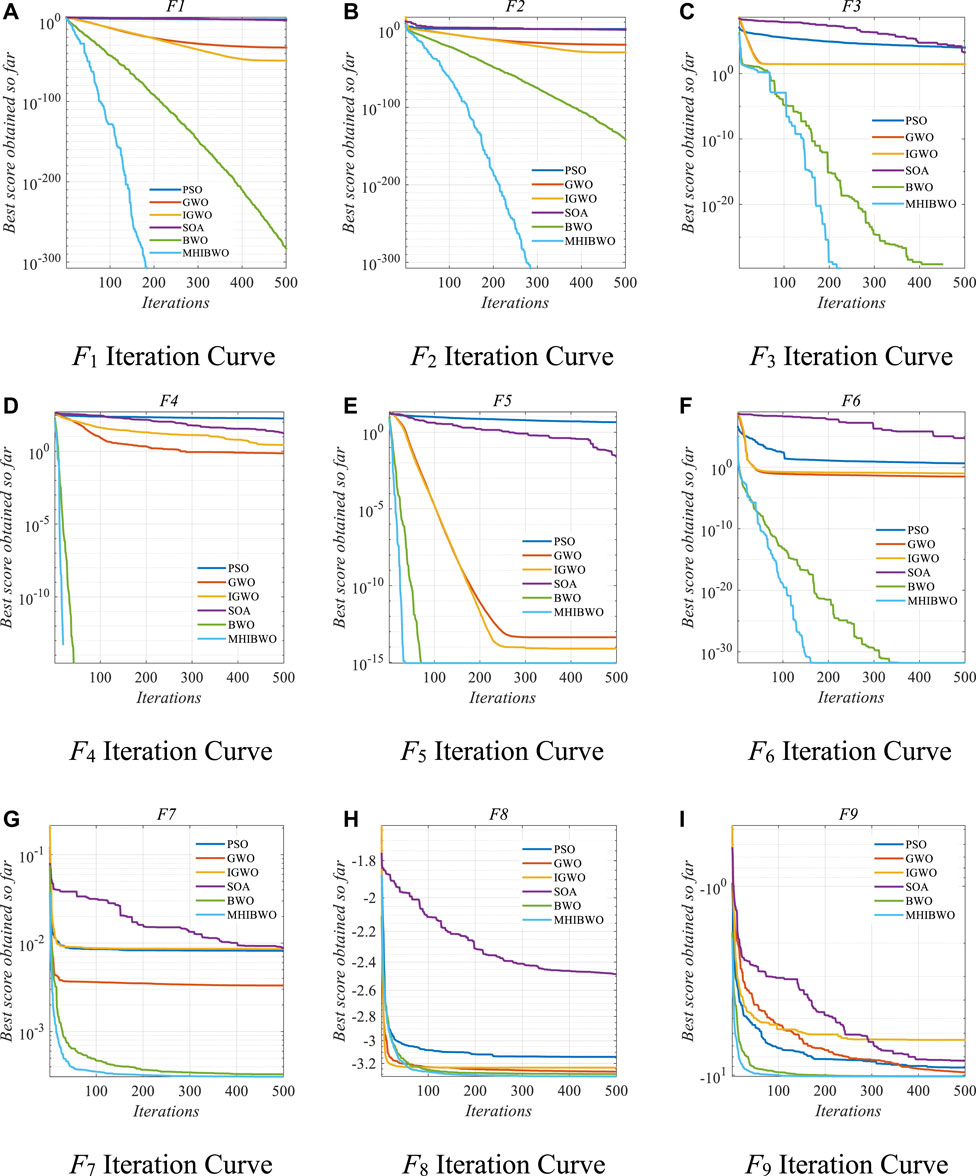
FIGURE 5. Benchmark function test results. (A) F1 iteration curve. (B) F2 iteration curve. (C) F3 iteration curve. (D) F4 iteration curve. (E) F5 iteration curve. (F) F6 iteration curve. (G) F7 iteration curve. (H) F8 iteration curve. (I) F9 iteration curve.
In the case of the benchmark test functions, it is evident that MHIBWO not only successfully identifies the optimal function value but also significantly improves the convergence speed. This outcome reflects the effectiveness of the proposed method in enhancing the global search capability and convergence speed of the algorithm. Furthermore, while both BWO and MHIBWO consistently identify the minimum value of the function, it is notable that MHIBWO exhibits a shorter search time and higher accuracy. These results unequivocally highlight the superiority of the proposed method in terms of search accuracy and speed.
A total of 8,760 sets of measurement light intensity, wind speed, and load data are shown in Supplementary Figure S2 (ELIA, 2024). Supplementary Table S5 gives the MG equipment investment parameter. Supplementary Table S6 presents the electricity time-of-use price. Supplementary Table S7 provides the pollutant emission factors for power purchase. The following five scenarios are given in Table 3. The solution process of the system is shown in Supplementary Figure S3. In this paper, the analytical calculations of the system were carried out on the MATLAB R2021a platform based on YALMIP/CPLEX12.8.
PSO, BWO, and MHIBWO are used to solve scenario 5. The convergence curves are shown in Figure 6, and the optimized results are shown in Table 4:
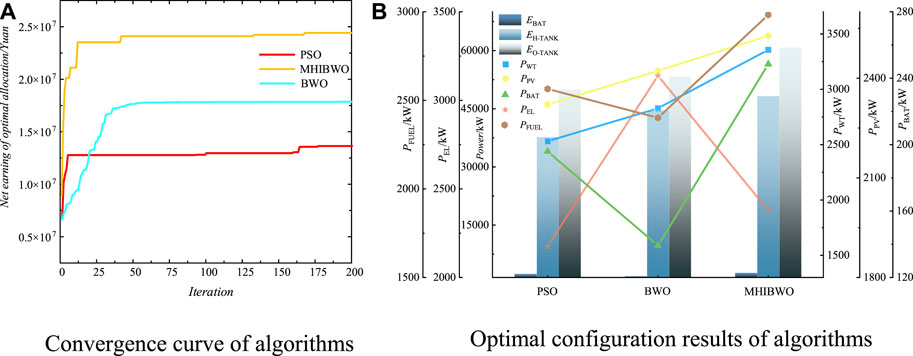
FIGURE 6. Comparative analysis of algorithms. (A) Convergence curve of algorithms. (B) Optimal configuration results of algorithms
As shown in Figure 6, MHIBWO has the highest net value, a faster convergence speed, and requires fewer iterations to reach the convergence state. As can be analyzed from Table 4, the results of capacity optimization configuration using MHIBWO output have achieved good net income and grid stability results. Compared with PSO and BWO, the economy has increased by 53.2% and 33.9%, respectively. Under the configuration scheme, the SBR degree of the MG has also been significantly improved, which proves the excellent ability of MHIBWO to solve the model. Therefore, the algorithms used below are MHIBWO.
The configuration schemes under five different scenarios are shown in Table 5, and the results are shown in Figure 7.
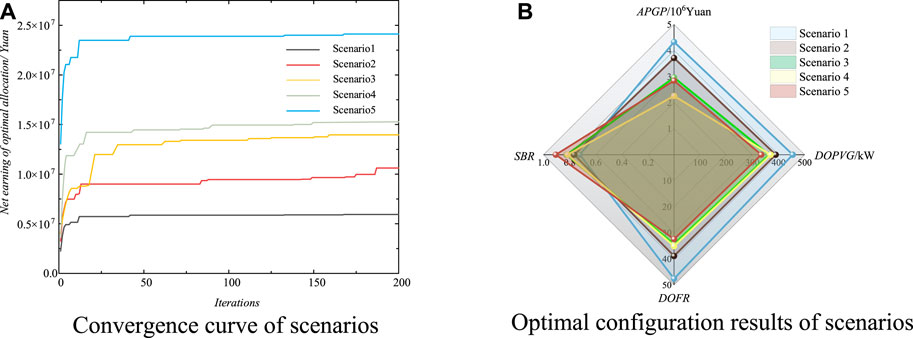
FIGURE 7. Comparative analysis of multi-scenarios. (A) Convergence curve of scenarios. (B) Optimal configuration results of scenarios.
Combining all of the experimental results, configuring a hybrid ESS that couples a seasonal hydrogen ESS and electrical ESS can effectively improve the environmental protection and stability of the system. Compared to single-layer optimization models, double-layer optimization models have better uniformity and globality. The reason is that the double-layer model achieves model architecture optimization, and its outer decision variable dimension is exponentially reduced compared to those of the single-layer model, allowing the solution to spread throughout the entire solution set space to the maximum extent possible.
The FCMA is used to extract and aggregate 4 typical days. The operation curve of the system on typical days is shown in Figure 8.
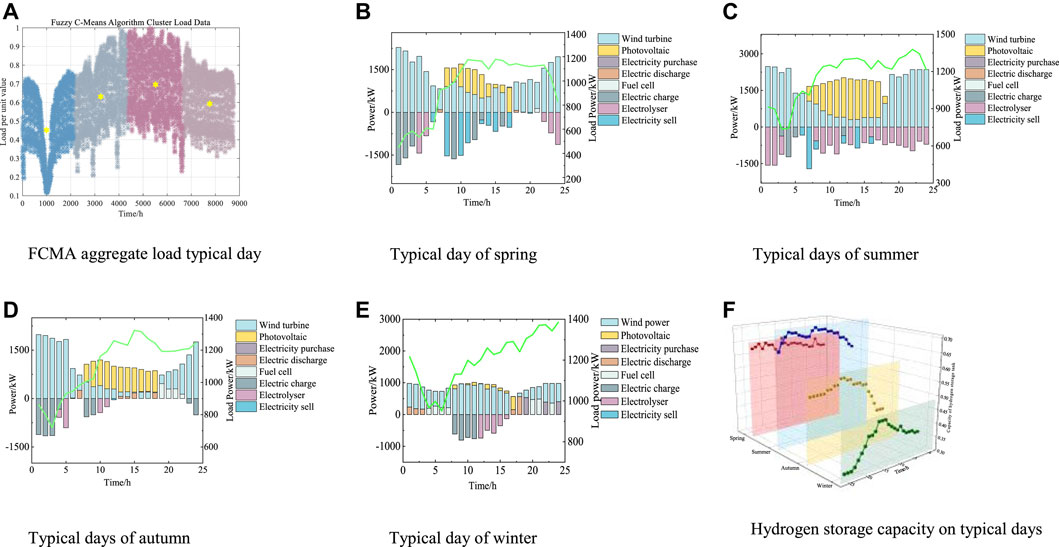
FIGURE 8. Operation curve on the typical days. (A) Fuzzy C-means algorithm (FCMA) aggregate load on a typical day. (B) Typical day of spring. (C) Typical day of summer. (D) Typical day of autumn. (E) Typical day of winter. (F) Hydrogen storage capacity on typical days.
The wind and solar energy resources in spring and summer are relatively abundant, and the electricity consumption is not high. The system is self-sufficient. When there is surplus power generation, the E&SHESS operates to store or sell the surplus electricity to the utility grid and regularly sells excess energy to further increase economic efficiency. The resources in autumn and winter have significantly decreased, and the peak load has increased. The start-up of EL is reduced, and the electric ESS participates in peak shaving, while FC compensates for the shortage of PV power generation. At night and during peak load, the electric ESS and FC are discharged in an orderly manner, and any shortage of electricity is purchased from the utility grid. In addition, the hydrogen storage level of the HT on typical days is in the range of 30%–80%, which is the optimal operating range of the hydrogen storage tank, further proving the rationality of the configuration scheme.
This paper presents a bi-layer optimization method for microgrid capacity optimization, aiming to achieve a balance between the economy and operational stability while considering engineering practicality.
1) The MG with the E&SHESS could meet the response requirements of various power sources and loads.
2) A bi-layer capacity optimization model of MGs is proposed. By iterating through outer and inner layers, the dimensionality of decision variables is reduced to optimize the architectural model, improving the ergodicity and globality of the solution.
3) By comparing the test functions with five other common algorithms, the superiority of MHIBWO in terms of convergence speed and optimization accuracy was verified.
4) Through typical daily operations, it was proved that power allocation can be effectively carried out between systems, achieving overall economic and stable operation.
The subsequent work explores the new generation of high-quality energy. Studying the beneficial interaction between the grid and users further improves the economy and reliability of the system.
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
XZ: investigation, software, validation, and writing–original draft. XS: conceptualization, formal analysis, funding acquisition, project administration, resources, and writing–review and editing. YW: methodology, supervision, validation, and writing–review and editing.
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This project was supported by the National Natural Science Foundation of China under Grant 61961017 and Key R&D Plan Projects in Hubei Province 2022BAA060.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2024.1336205/full#supplementary-material
Almadhor, A., Rauf, H. T., Khan, M. A., Kadry, S., and Nam, Y. (2021). A hybrid algorithm (BAPSO) for capacity configuration optimization in a distributed solar PV based microgrid. Energy Rep. 7, 7906–7912. doi:10.1016/j.egyr.2021.01.034
Chen, X., Dong, W., and Yang, Q. (2022). Robust optimal capacity planning of grid-connected microgrid considering energy management under multi-dimensional uncertainties. Appl. Energy 323, 119642. doi:10.1016/j.apenergy.2022.119642
Dong, J., Dou, Z., Si, S., Wang, Z., and Liu, L. (2022). Optimization of capacity configuration of wind–solar–diesel–storage using improved sparrow search algorithm. J. Electr. Eng. Technol. 17, 1–14. doi:10.1007/s42835-021-00840-3
ELIA (2024). For a successful energy transition in a sustainable world. Available at: https://www.elia.be/.
Erdemir, D., and Dincer, I. (2023). Development and assessment of a novel hydrogen storage unit combined with compressed air energy storage. Appl. Therm. Eng. 219, 119524. doi:10.1016/j.applthermaleng.2022.119524
Ferahtia, S., Djeroui, A., Rezk, H., Houari, A., Zeghlache, S., and Machmoum, M. (2022). Optimal control and implementation of energy management strategy for a DC microgrid. Energy 238, 121777. doi:10.1016/j.energy.2021.121777
He, P., Gong, Z. J., Jin, H. R., Dong, J., and Ming, L. (2022). Review of peak-shaving problem of electric power system with high proportion of renewable energy. Electr. Power Constr. 43 (11), 108–121. doi:10.12204/i.issn.1000-7229.2022.11.011
Huang, N., Wang, W., and Cai, G. (2023). Optimal configuration planning of multi. energy microgrid based on source load-temperature scenarios deep joint generation. Csee J. Power Energy Syst. 9 (3). doi:10.17775/CSEEJPES.2020.01090
Huang, Y., Lin, Z., Liu, X., Yang, L., Dan, Y., Zhu, Y., et al. (2021). Bi-level coordinated planning of active distribution network considering demand response resources and severely restricted scenarios. J. Mod. Power Syst. Clean Energy 9 (5), 1088–1100. doi:10.35833/mpce.2020.000335
Li, Y., Zhang, H., Liang, X., and Huang, B. (2019). Event-triggered-based distributed cooperative energy management for multienergy systems. IEEE Trans. Industrial Inf. 15 (4), 2008–2022. doi:10.1109/tii.2018.2862436
Lu, M. F., Li, X. S., Li, F., Xiong, W., and Xin, L. (2023b). Two-stage stochastic programming of seasonal hydrogen energy storage and mixed hydrogen-fueled gas turbine system. Proc. CSEE. doi:10.13334/j.0258-8013
Lu, Z., Gao, Y., Xu, C., and Li, Y. (2023a). Configuration optimization of an off-grid multi-energy microgrid based on modified NSGA-II and order relation-TODIM considering uncertainties of renewable energy and load. J. Clean. Prod. 383, 135312. doi:10.1016/j.jclepro.2022.135312
Luo, Y., Wang, Y., Liu, C., and Fan, L. (2022). Two-stage robust optimal scheduling of wind power-photovoltaic-thermal power-pumped storage combined system. IET Renew. Power Gener. 16 (13), 2881–2891. doi:10.1049/rpg2.12544
Lyden, A., Brown, C. S., Kolo, I., Falcone, G., and Friedrich, D. (2022). Seasonal thermal energy storage in smart energy systems: district-level applications and modelling approaches. Renew. Sustain. Energy Rev. 167, 112760. doi:10.1016/j.rser.2022.112760
Ma, X., Liu, S., Zhao, S., Zong, Q., and Liu, H. (2023). The optimal configuration of distributed generators for CCHP micro-grid based on double-layer operation strategy and improved NSGA-III algorithm. Energy Build. 293, 113182. doi:10.1016/j.enbuild.2023.113182
Mohseni, S., Brent, A. C., and Burmester, D. (2019). A demand response-centred approach to the long-term equipment capacity planning of grid-independent micro-grids optimized by the moth-flame optimization algorithm. Energy Convers. Manage 200, 112105. doi:10.1016/j.enconman.2019.112105
Ogbonnaya, C., Turan, A., and Abeykoon, C. (2019). Energy and exergy efficiencies enhancement analysis of integrated photovoltaic-based energy systems. J. Storage Mater 26, 101029. doi:10.1016/j.est.2019.101029
Raghav, L., Kumar, R., Raju, D., and Singh, A. (2021). Optimal energy management of microgrids using Quantum teaching learning based algorithm. IEEE Trans. Smart Grid 12 (6), 4834–4842. doi:10.1109/tsg.2021.3092283
Shao, Z., Cao, X., Zhai, Q., and Guan, X. (2023). Risk-constrained planning of rural-area hydrogen-based microgrid considering multiscale and multi-energy storage systems. Appl. Energy 334, 120682. doi:10.1016/j.apenergy.2023.120682
Singh, B., and Sharma, J. (2017). A review on distributed generation planning. Renew. Sustain. Energy Rev. 76, 529–544. doi:10.1016/j.rser.2017.03.034
Souza Junior, M. E. T., and Freitas, L. C. G. (2022). Power electronics for modern sustainable power systems: distributed generation, microgrids and smart grids—a review. Sustainability 14 (6), 3597. doi:10.3390/su14063597
Xie, P., Jia, Y., Lyu, C., Wang, H., Shi, M., and Chen, H. (2022). Optimal sizing of renewables and battery systems for hybrid AC/DC microgrids based on variability management. Appl. Energy 321, 119250. doi:10.1016/j.apenergy.2022.119250
Xie, X. R., Ma, N., Liu, W., Zhao, W., Xu, P., and Li, H. Z. (2023). Functions of energy storage in renewable energy dominated power systems: review and prospect. Proc. CSEE 43 (01), 158–169. doi:10.13334/i.0258-8013.pcsee.220025
Xu, X. Y., Wang, H., Yan, Z., Lu, Z. X., Kang, C. Q., and Xie, K. G. (2021). Overview of power system uncertainty and its solutions under energy transition. Automation Electr. Power Syst. 45 (16), 2–13. doi:10.7500/AEPS20210301003
Yamashita, D., Tsuno, K., Koike, K., Fujii, K., Wada, S., and Sugiyama, M. (2019). Distributed control of a user-on-demand renewable-energy power-source system using battery and hydrogen hybrid energy-storage devices. Int. J. Hydrogen Energy 44 (50), 27542–27552. doi:10.1016/j.ijhydene.2019.08.234
Yang, L., Li, X., Sun, M., and Sun, C. (2023). Hybrid policy-based reinforcement learning of adaptive energy management for the energy transmission-constrained island group. IEEE Trans. Industrial Inf. 19 (11), 10751–10762. doi:10.1109/tii.2023.3241682
Yue, Y., Feng, L., Cai, Y. P., and Wang, X. (2022). AC-DC hybrid microgrid operation control Technology. Sci. Technol. Eng. 22 (28), 12242–12252. doi:10.3969/j.issn.1671-1815.2022.28.002
Zhao, J., Wang, W., and Guo, C. (2023). Hierarchical optimal configuration of multi-energy microgrids system considering energy management in electricity market environment. Int. J. Electr. Power & Energy Syst. 144, 108572. doi:10.1016/j.ijepes.2022.108572
Zhong, C., Li, G., and Meng, Z. (2022). Beluga whale optimization: a novel nature-inspired metaheuristic algorithm. Knowledge-Based Syst. 251, 109215. doi:10.1016/j.knosys.2022.109215
Keywords: wind–solar-storage AC/DC microgrid, hybrid energy storage system, optimal configuration, bi-layer optimal model, multi-strategy hybrid improvement of Beluga Whale Algorithm
Citation: Zhong X, Sun X and Wu Y (2024) A bi-layer optimization method of the grid-connected microgrid based on the multi-strategy of the beluga whale algorithm. Front. Energy Res. 12:1336205. doi: 10.3389/fenrg.2024.1336205
Received: 10 November 2023; Accepted: 12 February 2024;
Published: 28 February 2024.
Edited by:
Michael Carbajales-Dale, Clemson University, United StatesReviewed by:
Minh Quan Duong, University of Science and Technology, The University of Danang, VietnamCopyright © 2024 Zhong, Sun and Wu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xianbo Sun, c3VueGlhbmJvQHdodXQuZWR1LmNu
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.