Predicting short-term energy usage in a smart home using hybrid deep learning models

The forecasting of home energy consumption is a crucial and challenging topic within the realm of artificial intelligence (AI)-enhanced energy management in smart grids (SGs). The primary goal of this study is to provide accurate energy consumption forecasts for a smart home. Two deep learning models are implemented: ConvLSTM, which combines convolutional operations with Long Short-Term Memory (LSTM), and the CNN-LSTM model, which synergizes Convolutional Neural Networks (CNN) and LSTM networks. Both hybrid models offer a comprehensive approach to modeling complex relationships in spatial and temporal patterns. Additionally, two baseline models—LSTM and CNN—are employed for comparative analysis. Utilizing real data from a smart home in Houston, Texas, the results demonstrate that both the hybrid models deliver highly accurate predictions for energy consumption. However, the ConvLSTM model outperforms all proposed models, improving predictions in terms of mean absolute percentage error by 4.52%, 9.59%, and 10.53% for 1 day, 3 days, and 6 days in advance, respectively.

1 Introduction

As energy consumption around the world increases more rapidly, developing an intelligent and reliable power grid has become a necessity. Smart grids (SGs) appear to be the most effective tool for minimizing the energy gap between generation and demand. A research field that has emerged as an indispensable tool of SGs is energy consumption forecasting. Accurate energy forecasting is crucial for providing relevant energy, income analysis, capital expenditure, and market control (Raza and Khosravi, 2015; Wei et al., 2019; Kaur et al., 2020). Although prediction uncertainties have impaired the attention of some researchers, new techniques with more precise and reliable energy consumption predictions are still in development.

In the literature, energy consumption prediction is split into three categories based on the time interval of the forecast. The three classes are short-, medium-, and long-term energy consumption forecasting (Ghalehkhondabi et al., 2017). The first aims to estimate energy forecasting for the next half hour up to the following 2 weeks. It helps energy system managers to make several decisions, including supply planning, demand-side management, and security systems (Gerwig, 2017). Medium-term energy consumption deals with a horizon prediction of weeks to months. It is usually used to plan power grid capacity, schedule maintenance, and manage energy resources (Shirzadi et al., 2021). Long-term energy prediction generally covers forecasting timeframes from 1 to 10 years and can extend for several decades. This kind of prediction is fundamental for strategic decisions, infrastructure planning, and internal resources (Carvallo et al., 2018). Thus, electricity consumption forecasting must carefully avoid mistaken planning or financial burden.

Many studies have examined forecasting at high aggregated levels. Few, however, deal with residential energy consumption forecasting due to the great uncertainties resulting from the varied lifestyles and behavior of householders. Energy consumption forecasting represents a time series problem. Due to the seasonal variation and irregular trends in time series data, traditional machine learning techniques fail to accurately forecast energy consumption (Ahmad, 2017). Traditional machine learning (ML) is thus defective for complex systems. However, deep learning (DL) methods have been widely studied in energy forecasting and have achieved higher accuracy (Kaur and Ahuja, 2017).

Several studies have been made of energy consumption forecasting. Generally, there are three types of forecasting models: ML, DL, and hybrid models (HM) (Sun et al., 2020; Sun et al., 2021).

Artificial neural networks (ANNs), support vector regression (SVR), and other statistical models, such as autoregressive integrated moving average (ARIMA) and multiple linear regression (MLR), are commonly used algorithms applied in energy consumption forecasting (Amasyali and El-Gohary, 2018). Deb et al. (2015) compare the performance of ANNs to the those of Adaptive Neuro-Fuzzy Interface System (ANFIS) for predicting the cooling load energy of three institutional constructions in Singapore. The simulation outcomes reveal that both methods can predict energy consumption with good accuracy. ANNs are also used in Elbeltagi and Wefki (2021) to predict energy usage in household construction. The advanced ANN model is tested and validated to accurately forecast energy use. Similarly, Li et al. (2021) suggest an ANN model to accurately predict electrical loads. Compared to LSTM and the Random Forest approach, the proposed model proved more accurate, with an MSE of 4.486, and can be used for long-term prediction. ANNs were also used in Ahmad et al. (2016) for short-term industrial energy prediction. Simulation outcomes indicate that the suggested model provides 98.5% accurate predictions compared to bi-level strategy. However, prediction accuracy is enhanced by feeding the forecast module’s output of the optimization module, which takes more time to execute. Short-term load prediction is also performed in Al-Musaylh et al. (2018), who compare the performance of SVR, Multivariate Adapter Regression Spline (MARS), and ARIMA models in predicting electricity usage in Queensland, Australia. The results obtained show that for the forecasting horizon 0.5 h and 1.0 h, MARS outperforms SVR and ARIMA with lowest mean absolute error. However, for 24 h, the SVR model was superior. A multiple regression (MR) technique was developed in Amber et al. (2017) to assess daily energy usage in university buildings. Their findings show that surrounding temperature, weekday index, and building type significantly impact energy consumption. Furthermore, the error obtained by adopting the proposed method is set between 12% for administrative construction and 13% for academic construction.

Convolutional neural networks (CNNs) and long short-term memory (LSTM) are two types of DL neural networks that have recently received much attention. Amarasinghe et al. (2017) investigated the effectiveness of the CNN model for electricity forecasting of a residential building. The results achieved from the CNNs were compared with LSTM, ANNs, and SVM. The CNN model outperforms SVM while having comparable results to ANNs and LSTM. CNNs are further implemented in Khan et al. (2019) to forecast the electricity consumption for every day of the week in Victoria, Australia. To test the effectiveness of the suggested model, a comparison was made with ARIMA, recurrent neural networks (RNNs), and extreme learning machines (ELMs). Their outcomes show that the suggested CNN records the lowest prediction error. CNNs are also proposed in Tudose et al. (2020) to deal with day-ahead power prediction. The testing and validation of the elaborated model were performed based on a set of data from the Romanian power system. A comparison between the results obtained and the Romanian TSO’s forecasting demonstrates the suggested approach’s great capability in precise forecasting and high generalization potential. In Cai et al. (2019), CNNs and RNNs are suggested for day-ahead commercial power consumption. The performance of the suggested models is compared with the seasonal ARIMAX model. The CNN model proved best, with an accuracy of 22.6% compared to ARIMAX. Nazir et al. (2021) attempted to predict a month forward of daily power usage considering four different household daily datasets. Their experiment demonstrated that the ConvLSTM model outperforms LSTM in respect of average forecasting accuracy and efficiency. Mpawenimana et al. (2020) proposed a system for forecasting the power consumption in a smart house under LSTM and ARIMA. The exactness of these models was compared for the short- and medium-terms, with the outcomes demonstrating that LSTM outperformed ARIMA. Kong et al. (2017) applied the LSTM model to address the forecasting of domestic power usage. They compared their results with K-Nearest Neighbor regression (KNN), backpropagation neural networking (BPNN), and ELM to enhance forecasting exactness by utilizing LSTM. It was also examined in Cui et al. (2020) for load prediction. A comparison between real and forecasted data demonstrated that the LSTM prediction model greatly increased the accuracy of power forecasting for single- and multi-point loads. LSTM was also adopted for predicting energy consumption by Asri et al. (2021) to check the quality of forecasting outcomes and evaluated accuracy; their results showed LSTM to be very precise in its predictions. LTSM was also studied by Xu et al. (2022) for probabilistic residential electrical load forecasting by comparing Gated Recurrent Unit (GRU) and RNN models. Their results once again demonstrated the efficiency of LSTM in making predictions with the smallest error values over other methods.

Hybrid models have shown encouraging results in forecasting household energy consumption. For instance, Nepal et al. (2020) proposed a predicting method for energy usage in university buildings based on a hybrid model that combined a clustering technique with the ARIMA model. This blending was confirmed to raise the efficiency of prediction more than using ARIMA alone. Pooniwala and Sutar (2021) blended the seasonal ARIMA and LSTM time-series forecasting techniques to predict power load. The resulting hybrid network decreased the MAE by almost 13.08% compared to the two models separately. Peng et al. (2022) applied enhanced LSTM prediction based on empirical wavelet transform to predict monthly energy usage. Compared to basic LSTM and other existing models, the outcomes demonstrated that their suggested model had better forecasting accuracy. Memarzadeh and Keynia (2021) investigated short-term energy and pricing using a hybrid LSTM-NN model. The efficiency of this approach was accurately validated on energy and price data gathered from the Pennsylvania–New Jersey–Maryland (PJM) and Spanish electricity markets. In Sulaiman et al. (2022), a hybrid blend of Empirical Mode Decomposition (EMD) and ELM boosted the prediction accuracy of residential loads. Compared to ANN, SVR, and ELM, this model effectively predicted peaks in residential loads and thus enhanced forecast accuracy. Sajjad et al. 2020) developed a hybrid CNN and GRU for short-term domestic load prediction. Their test evaluation revealed that their model had a lower error rate than other baseline models. Kim and Cho (2019) hybridized CNN with LSTM to predict electricity consumption. Compared to other baseline methods, CNN-LSTM recorded the lowest error rates because it learned from both spatial and temporal features. CNN-LSTM was also deployed in Guo et al. (2020) for short-term energy forecasting based on real time electricity price. The results demonstrated that this method provides better prediction than LSTM, SVM, ARIMA, and Random Forest (RF). CNN was hybridized with the LSTM autoencoder model (LSTM-AE) in Khan et al. (2020) to predict energy consumption in domestic and commercial construction. Their findings showed that their hybrid model outperformed other models such as CNN and LSTM. In the same context, Shao et al. (2020) proposed a hybrid model that blended CNN and LSTM in order to analyze the dataset and improve the strength of the conventional CNN-LSTM model. The CNN and LSTM blend was used along with six statistical parameters and three real datasets from American companies. Similarly, CNN-LSTM was investigated in Rafi et al. (2021) for short-term electrical load forecasting. Compared to LSTM, their method had the lowest errors over all the study cases: monthly, weekly, 48 h, and 24 h. CNN-LSTM was also assessed in (40) to successfully forecast household electric power consumption based on real-time electricity prices. This proposed approach reached an ideal prediction performance that was previously difficult to forecast with the smallest error values when compared using traditional forecasting methods. A synthesis of all this research is presented in Table 1.

Table 1

Table 1. Related works synthesis.

Motivated by such research, the present study proposed two hybrid forecasting methods for smart home energy usage: ConvLSTM and CNN-LSTM. These models were developed in response to the growing need for accurate, scalable, and efficient forecasting techniques, which are especially crucial given rising energy demands and sustainability objectives. To demonstrate the efficiency of the suggested models, LSTM and CNN were used for comparison. To check the quality of forecasting outcomes, the accuracy evaluation was established, and the obtained results established that the two hybrid methods are very precise in their predictions. However, the ConvLSTM model outperformed all other models and has higher efficiency. Thus, the main contributions of this research can be outlined as follows.

• Time-series forecasting of home energy consumption is conducted using the Hybrid ConvLSTM and CNN-LSTM models.

• Three scenarios with different time-period predictions are studied in simulation for better analyzes.

• The performance of the suggested models is compared with other baseline models, LSTM and CNN, using three error metrics: mean absolute error (MAE), mean absolute percentage error (MAPE), and root mean squared error (RMSE).

The rest of this research paper is structured as follows: The proposed methodology is elaborated in Section 2. The forecasting evaluation and case study are outlined in Section 3. The analysis results of the presented forecasting techniques compared with other baseline models are discussed in Section 4. Lastly, conclusions are given in Section 5.

2 Proposed methodology

This section outlines and clarifies the proposed hybrid models used in the simulation. Each proposed hybrid model is composed of an encoder part that encrypts the input data and a decoder part that decodes the encoded data and builds prediction for every single day.

2.1 Convolutional neural networks with long short-term memory (CNN-LSTM)

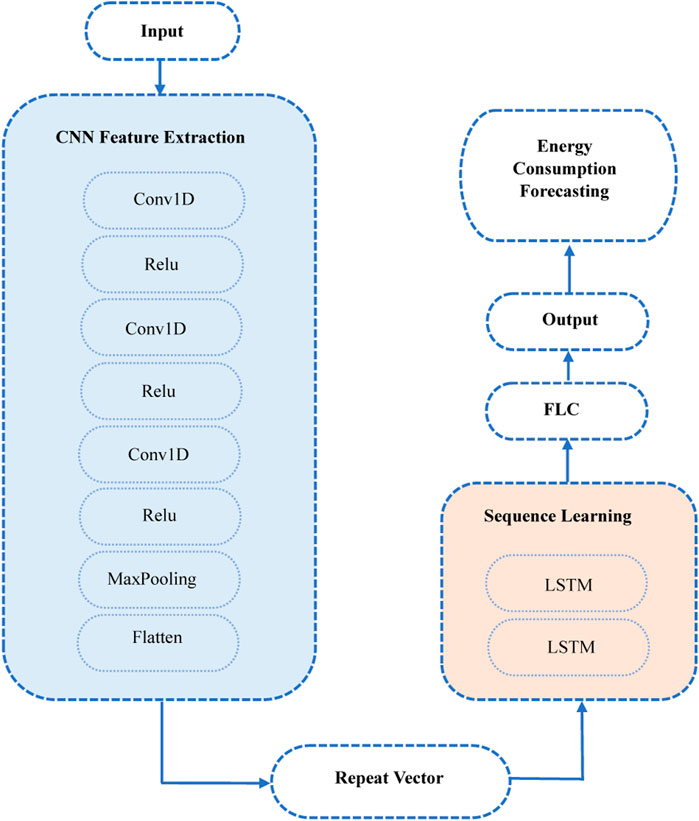
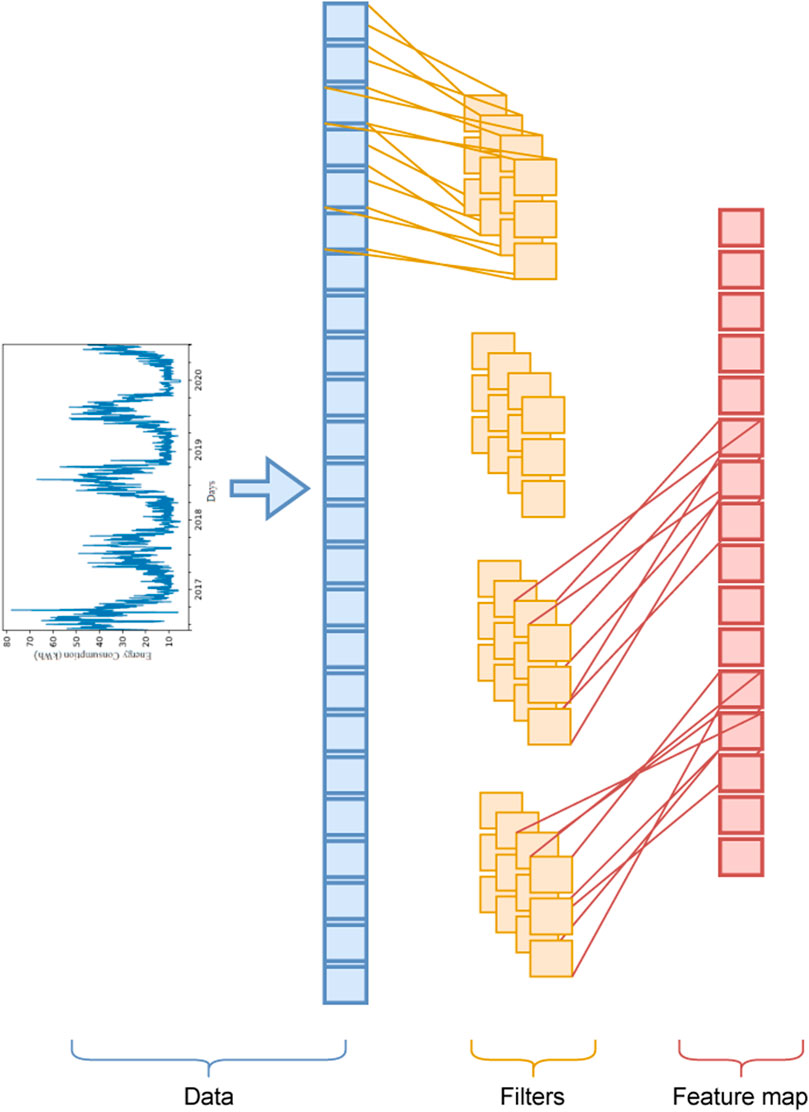
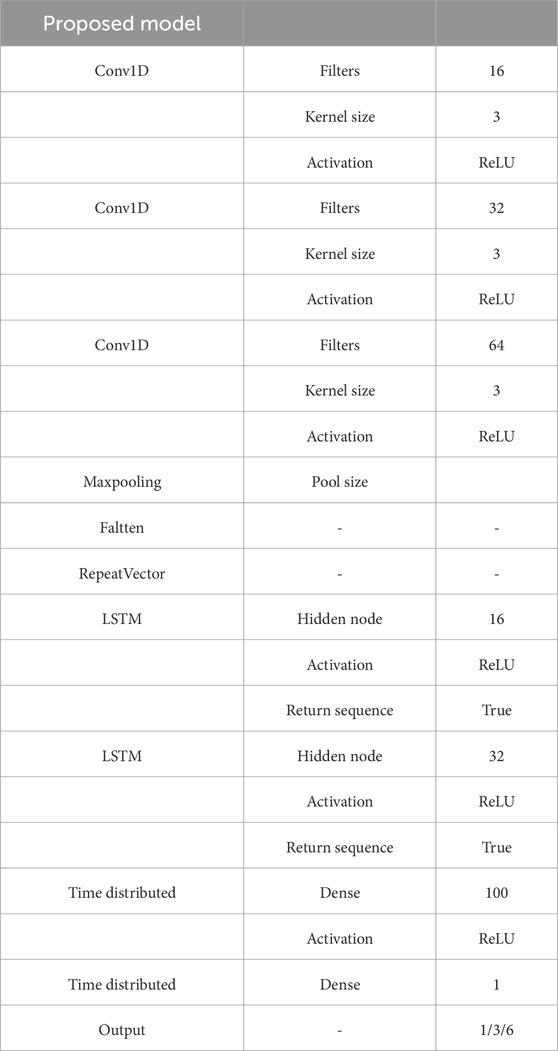
The CNN-LSTM model is composed of a sequence of layers of CNN and LSTM. The structure of the CNN-LSTM framework used is illustrated in Figure 1. The CNN feature extraction box consists of three sequences of one-dimensional conventional layer (Conv1D) (Figure 2) and three rectified linear units (ReLU). The model can be represented using Equations 1–13. The result of the vector output from the Conv1D can be expressed as follows (Agga et al., 2021):

$y_{ij}^l=\sigma \left(a_j^l+{\displaystyle \sum _{n=1}^N}\left(w_{n,j}^l{x}_{i+n-1,j}^0\right)\right),(1)$

where σ is the activation function, a is the bias for the j feature map, N is the number of units per window, n is the index rate of the filter, w is the kernel weight, and x is the energy consumption input vector.

Figure 1

Figure 1. CNN-LSTM framework.

Figure 2

Figure 2. 1D-CNN model framework.

To decrease the computational cost of the upper layers and sustain the most prominent information, the max-polling layer is used. The functioning of this layer is described thus:

$y_{ij}^l=\underset{r\in R}{\max }{f}_{i\times T+r,j}^{l-1},(2)$

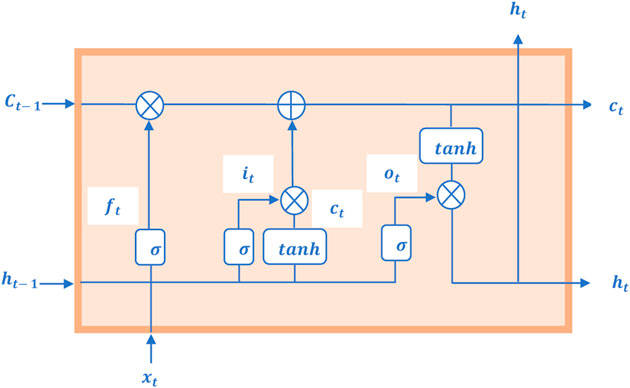
where T is the stage that defines the distance of the entering data area to be affected and R is the pooling size lower than the input size y. The obtained results after the pooling layer are then flattened into a vector and fed to the LSTM decoder through the Repeat Vector layer. The decoder part is composed of LSTM layers that save time information about daily energy consumption derived through CNN. The structure of the LSTM model is illustrated in Figure 3.

Figure 3

Figure 3. LSTM framework.

The obtained values by the CNN layer are sent to the gate units. The gate unit is a mechanism that defines the state of each single memory cell via multiplication operating. The operation of the input gate i, the forget gate f, and the output gate o is explained thus by Eq. 41:

$i_t=\sigma \left(W_{pi}{p}_t+W_{hi}{h}_{t-1}+W_{ci}◦c_{t-1}+b_i\right),(3)$

$f_t=\sigma \left(W_{pf}{p}_t+W_{hf}{h}_{t-1}+W_{cf}◦c_{t-1}+b_f\right),(4)$

$o_t=\sigma \left(W_{po}{p}_t+W_{ho}{h}_{t-1}+W_{co}◦c_{t-1}+b_o\right),(5)$

where W is the weight matrix of each gate unit, p_t is the output of the pooling layer at time t, and b is the bias vector. The output layers at time t are the cell state c_t and the hidden state h_t. They can be expressed as follows:

$c_t=f_t◦c_{t-1}+i_t\sigma \left(W_{pc}{p}_t+W_{hc}{h}_{t-1}+b_c\right),(6)$

$h_t=o_t◦\sigma \left(c_t\right).(7)$

The final layer of CNN-LSTM is composed of a fully connected layer (FLC). The output vector obtained from the FCL can be expressed as follows:

$d_i^l={\displaystyle \sum _j}{W}_{ij}^{l-1}\left(\sigma \left(h_i^{l-1}\right)+b_i^{l-1}\right).(8)$

The configuration of all layers of the indicated model is provided in Table 2.

Table 2

Table 2. Configuration of CNN-LSTM layers.

2.2 Convolutional LSTM network (ConvLSTM)

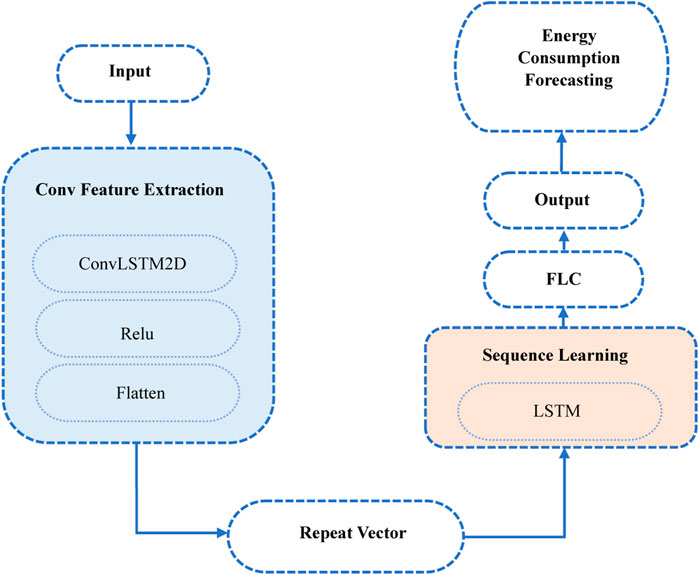
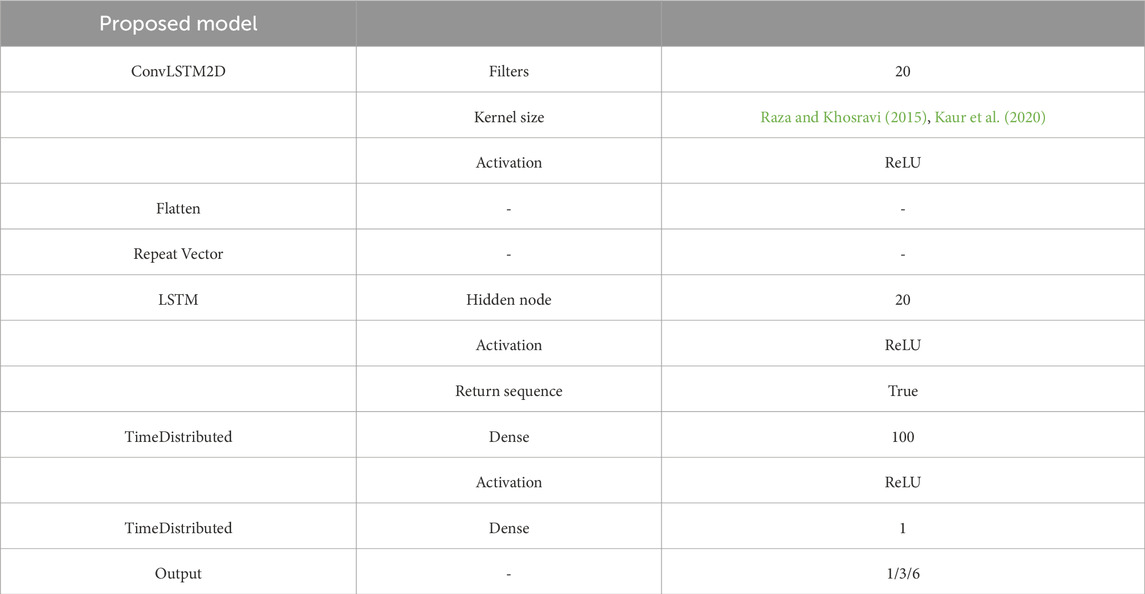
The structure of the suggested ConvLSTM is illustrated in Figure 4. The encoder part is composed of a two-dimensional conventional LSTM layer (ConvLSTM2D) followed by a ReLU and a flattened layer. The mathematical theory of the ConvLSTM model looks like the LSTM model with some mathematical symbol changes. Thus, it can be summarized by the following formulations (Zhang et al., 2022).

$i_t=\sigma \left(W_{i-xi}\otimes x_t+W_{i-hi}\otimes h_{t-1}+W_{i-ci}◦c_{t-1}+b_i\right),(9)$

$f_t=\sigma \left(W_{f-fx}\otimes x_t+W_{f-hx}\otimes h_{t-1}+W_{f-cf}◦c_{t-1}+b_f\right),(10)$

$o_t=\sigma \left(W_{o-xo}\otimes x_t+W_{o-ho}\otimes h_{t-1}+W_{o-co}◦c_t+b_o\right),(11)$

$c_t=\tanh \left(W_{c-xc}\otimes x_t+W_{c-hc}\otimes h_{t-1}+b_c\right),(12)$

$h_t=o_t◦\tanh \left(c_t\right),(13)$

where ⊗ denotes the convolution operator. To match the 2D output of the upper layer and the 3D input of the lower layer, a RepeatVector is employed. The obtained vectors are fed into the LSTM decoder. The FCL is then charged to repeat each time step in the output sequence before the final output layer. The configuration of all layers of the proposed model is provided in Table 3.

Figure 4

Figure 4. ConvLSTM framework.

Table 3

Table 3. Configuration of the ConvLSTM layers.

3 Forecasting evaluation and case study

3.1 Forecasting evaluation

To test the effectiveness of the earlier described methods, three common forecasting accuracy tests are employed—MAE, RMSE, and MAPE—where the mathematical equations are formulated using Equations 14–16:

$MAE={\displaystyle \sum _{m=1}^M}\frac{|E_m-\check{E}|}{M},(14)$

$RMSE=\sqrt{\frac{{\sum }_{m=1}^M{\left(E_m-\check{E}\right)}^2}{M}},(15)$

$MAPE={\displaystyle \sum _{m=1}^M}|\frac{E_m-\check{E}}{E_m}|\times 100,(16)$

where E_i is the actual energy consumption, $\check{E}$ is the forecasted energy consumption, and M represents the number of forecasting samples.

3.2 Case study

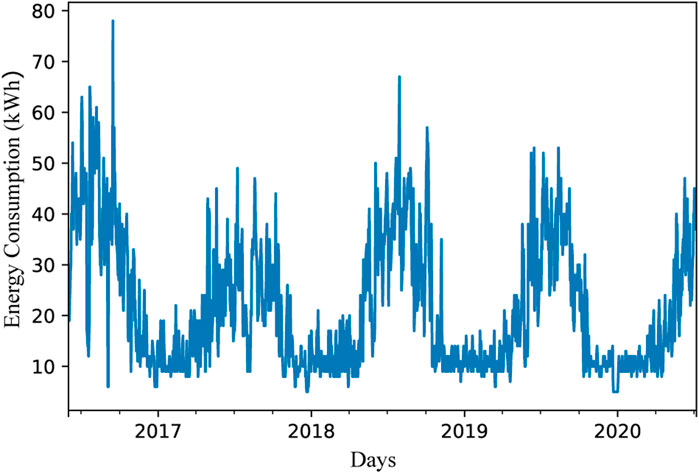
Energy consumption data were gathered from a household situated in Houston, Texas, United States (Residential power usage, 2022). Smart meters were employed to obtain energy usage data from each electrical appliance such as televisions, washing machines, dryers, and air conditioner. The dataset involved the daily energy usage in (kWh) from June 2016 to August 2020 (Figure 5). The household was equipped with security DVR and POI cameras, as well as two refrigerators. Additionally, there were two 50-gallon water heaters that operated during the daytime. At night, electrical appliances such as light bulbs, TVs, washing machines, dryers, and air conditioners operated from 6 pm in the evening until 8 am in the morning.

Figure 5

Figure 5. Daily energy consumption (kWh).

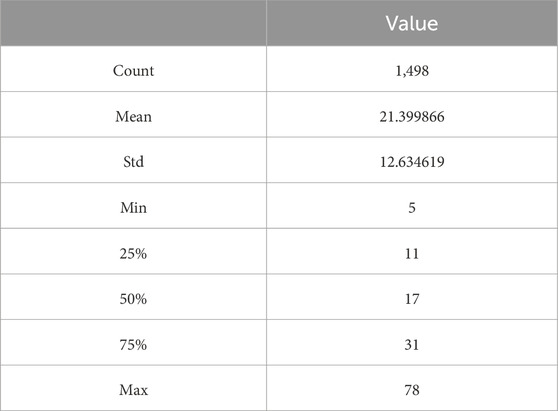
Figure 5 illustrates that the energy consumption values ranged from as low as 5 kWh to as high as 78 kWh, with most of the data points falling between these extremes. Consumption rarely reached the maximum, with such instances possibly representing days of extreme weather conditions or other anomalies. Additional specifics on the dataset are provided in the Table 4.

Table 4

Table 4. Dataset description.

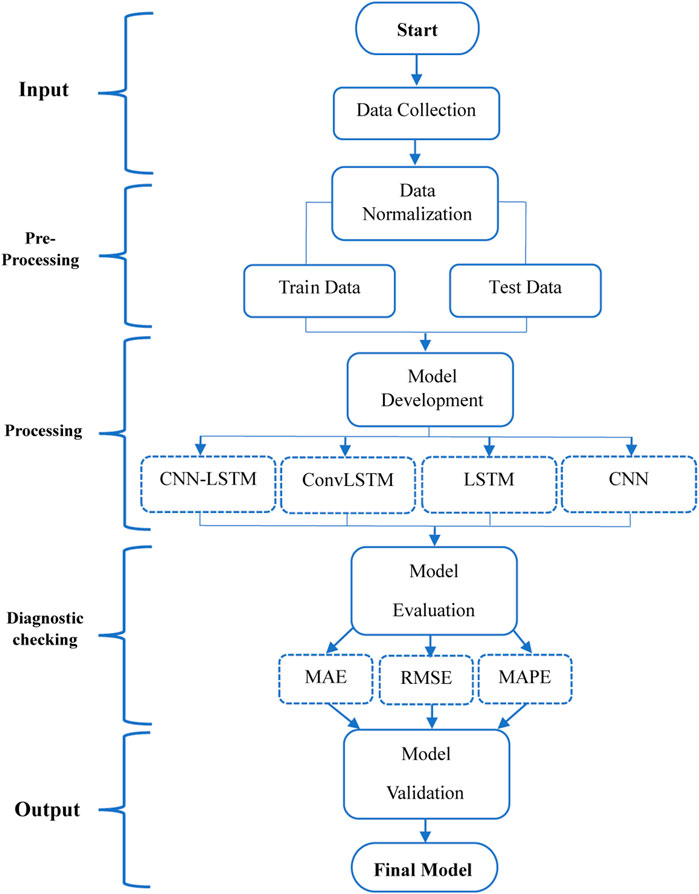
The overall systematic forecasting process considered in this study is represented in Figure 6. After collecting the dataset, a pre-processing step was necessary in order to normalize the obtained data. The normalized dataset was divided into training and testing sets and then exploited to develop the ConvLSTM, CNN-LSTM, CNN, and LSTM models. To evaluate each model, a diagnostic check was established using the forecasting evaluation earlier described.

Figure 6

Figure 6. Schematic representation of the forecasting process.

4 Results, analysis, and discussion

The study aimed to evaluate the performance of the two hybrid models under study using the daily energy consumption dataset of a smart home. Different time intervals were considered in the simulation test to obtain the k-step-ahead energy prediction. To evaluate the efficiency of these models, baseline models such as LSTM and CNN were used for comparison. The results obtained were analyzed by evaluating the metrics, leading to the following results.

4.1 Scenario 1: 1-day-ahead energy consumption forecasting

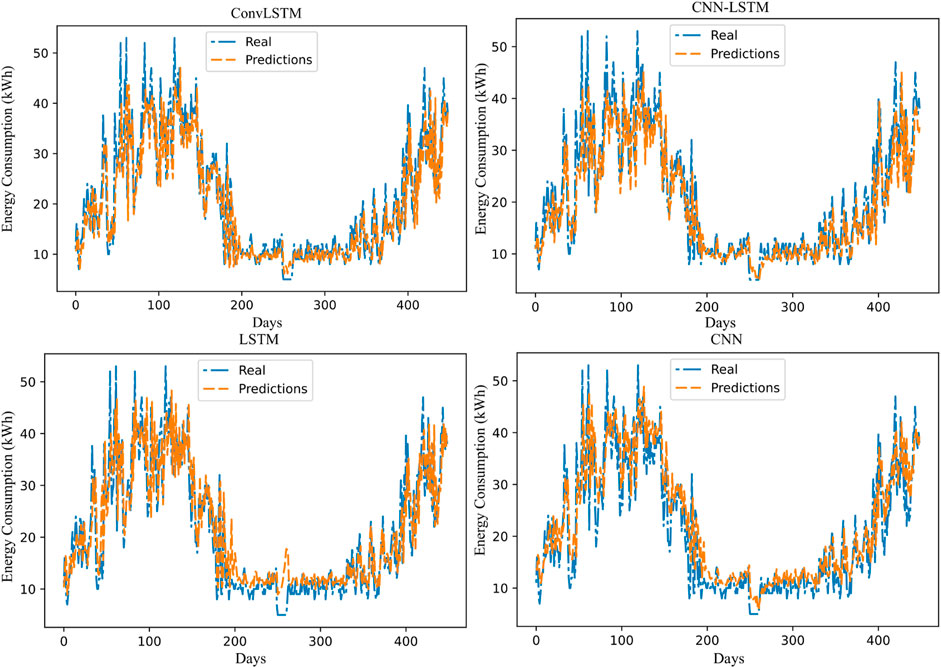
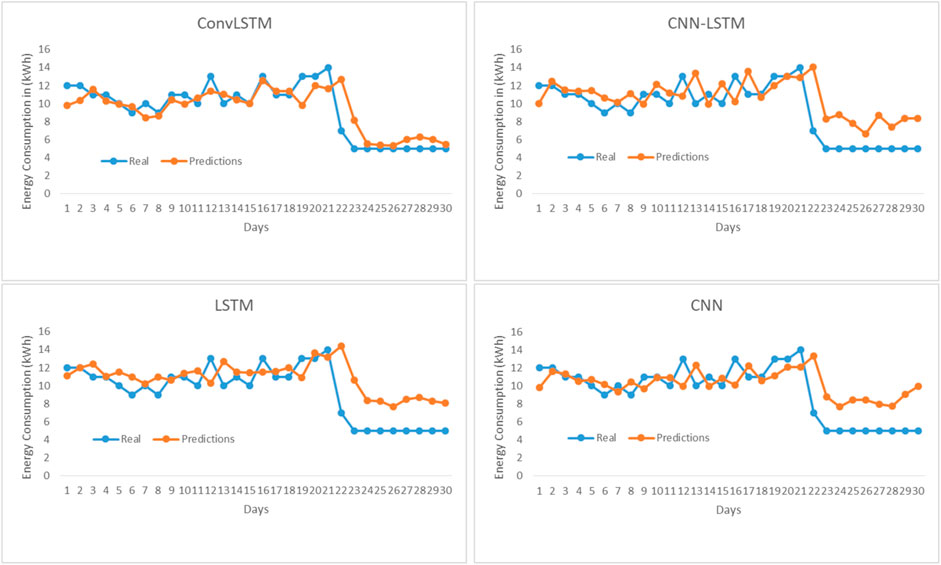
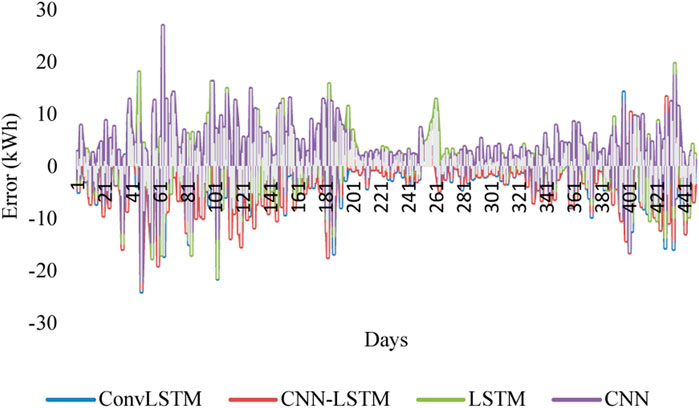
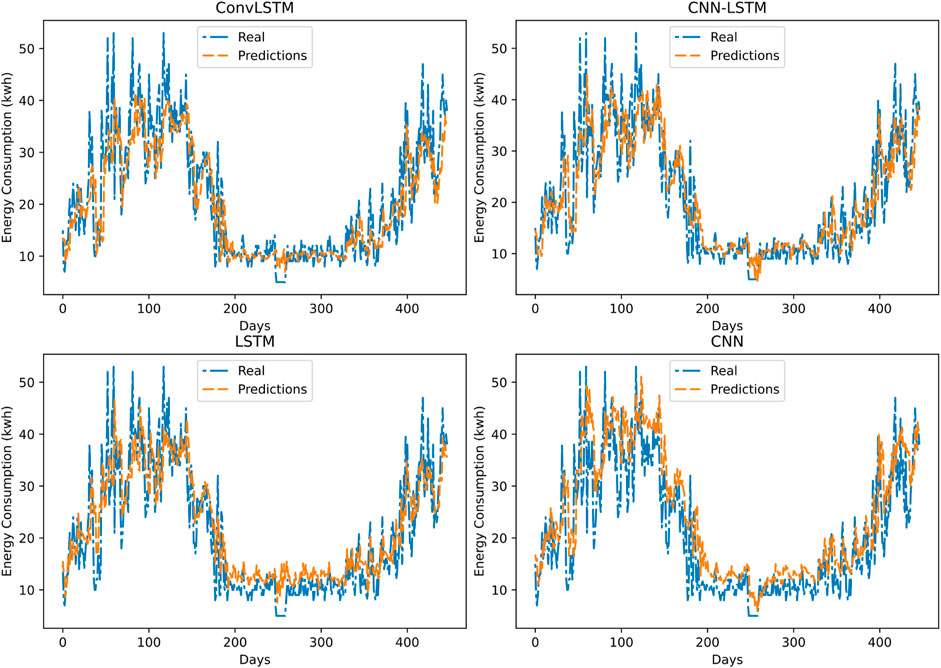
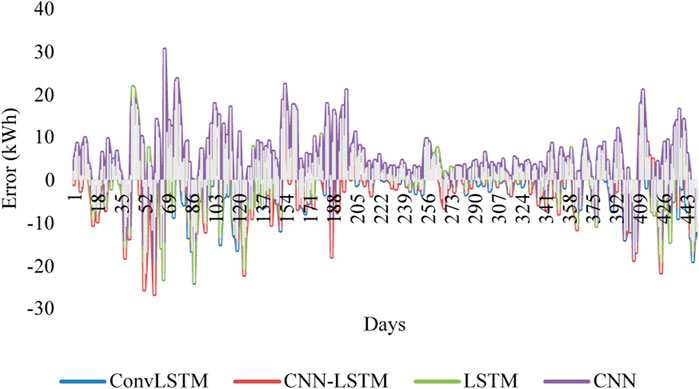
The 1-day-ahead energy consumption prediction using ConvLSTM, CNN-LSTM, LSTM, and CNN is illustrated in Figure 7, and a zoom-in of 30 days from days 230–240 using the abovementioned models is plotted in Figure 8. The real energy usage curves are shown in blue, and the forecasting results, in orange. As can be seen, the two curves match well for all the studied models. However, it is hard to distinguish which one perfectly predicts energy consumption and thus provides lower error and higher accuracy. Thus, the difference between the real and predicted data is calculated and displayed in Figure 9. This shows that the CNN model performs the most important fluctuations, followed by the LSTM model. However, the error graph of the ConvLSTM and the CNN-LSTM models are relatively small.

Figure 7

Figure 7. 1-day-ahead energy consumption forecasting.

Figure 8

Figure 8. 1-day-ahead energy consumption forecasting; zoom-in between days 230 and 260.

Figure 9

Figure 9. 1-day-ahead energy consumption errors.

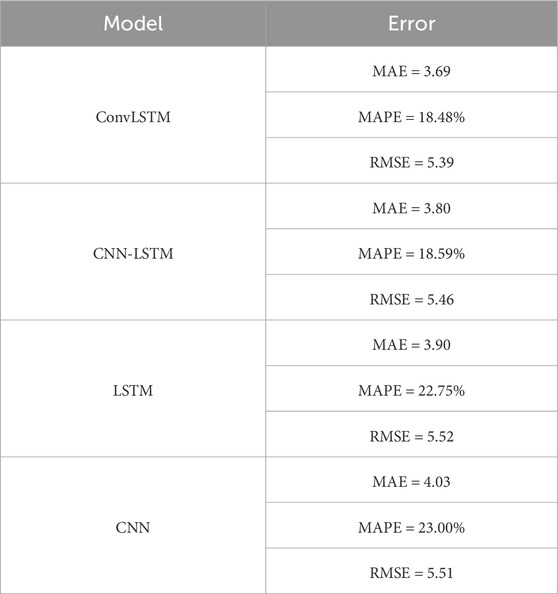
To better quantify the performance of the investigated models, accuracy tests are provided, and the results obtained are depicted in Table 5. It is clear that the two hybrid models predict well the 1-day energy consumption. The ConvLSTM model achieves the smallest MAPE of 18.48% and the lowest MAE of 3.69. In addition, CNN-LSTM reaches a MAPE of 18.59% and RMSE of 5.46. The LSTM model performs quite well for energy consumption compared to the CNN model. For instance, the MAPE of LSTM was 22.75% and the RMSE 5.52. However, CNN had some difficulty predicting the energy consumption 1 day before, resulting in MAE of 4.03 and MAPE of 23%.

Table 5

Table 5. Scenario 1 prediction errors.

4.2 Scenario 2: 3-day-ahead energy consumption forecasting

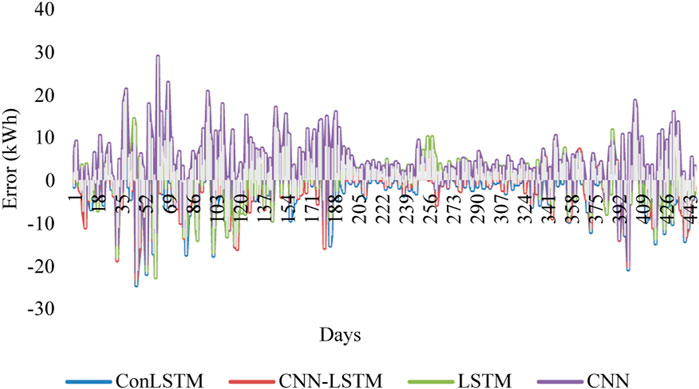
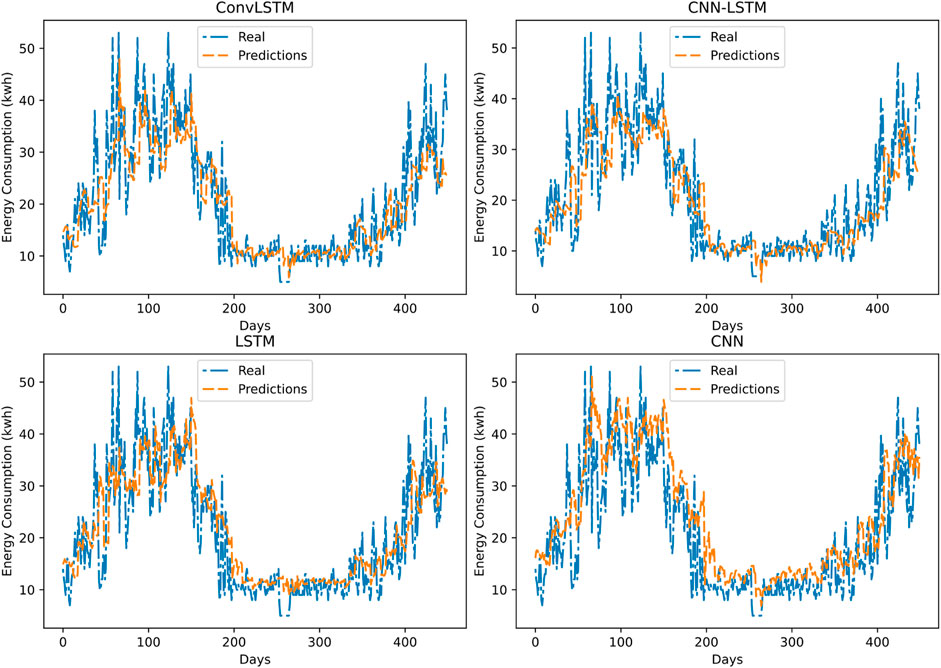
To investigate the efficiency of the proposed forecasting models, the time interval prediction was increased. Figure 10 represents in detail the 3-day-ahead energy consumption prediction using the same previous models. The difference between the real and predicted values is illustrated in Figure 11. As is apparent from these figures, the energy consumption prediction is quite accurate compared to the previous scenario. Moreover, the real and the predicted curves do not match well for all the models. To identify the accurate energy forecasting model, the difference between the real and the predicted data is illustrated in Figure 11. Once again, the CNN model scores the highest error fluctuations, followed by the LSTM model. However, the error graphs of the ConvLSTM and the CNN-LSTM models are relatively small. The error metrics are highly recommended for determining the most accurate model.

Figure 10

Figure 10. 3-day-ahead energy consumption forecasting.

Figure 11

Figure 11. 3-day-ahead energy consumption errors.

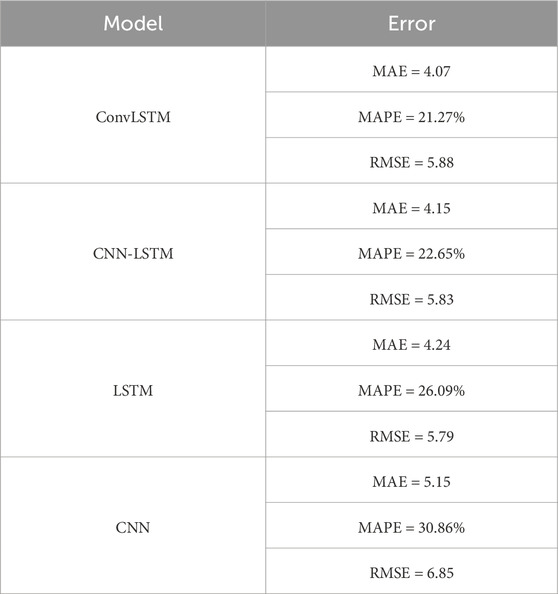
The error metrics of the studied methods with a time interval prediction of 3 days are provided in Table 6. As expected, both

Table 6

Table 6. Scenario 2 prediction errors.

hybrid models made better predictions than the other baseline models. However, ConvLSTM outperformed CNN-LSTM with the smallest MAPE of 21.27%, although CNN-LSTM scored a MAPE of 22.65%. Once again, the proposed model shows more robustness even when the time interval is increased. Furthermore, in this scenario, LSTM shows its weakness in long-time interval predictions, resulting in a MAPE of 26.09% and MAE of 4.24. The CNN model scores the worst results, with a MAPE of 30.86% and RMSE of 6.85.In accordance with the partially obtained error metrics results, it can be deduced that the proposed ConvLSTM and CNN-LSTM are promising models that perform well even for 3 days ahead.

4.3 Scenario 3: 6-days-ahead energy consumption forecasting

In this third scenario, the forecasting time interval is raised to 6 days. Figure 12 displays in detail the 6-days-ahead energy consumption prediction using the aforementioned models. The errors between the real and predicted data for all methods are represented in Figure 13. In comparing the previous and current scenarios, it is clear that accuracy declines and the difference between the real and the predicted data is high. However, both hybrid methods still realize some good results compared with the baseline methods.

Figure 12

Figure 12. 6-day-ahead energy consumption forecasting.

Figure 13

Figure 13. 6-day-ahead energy consumption errors.

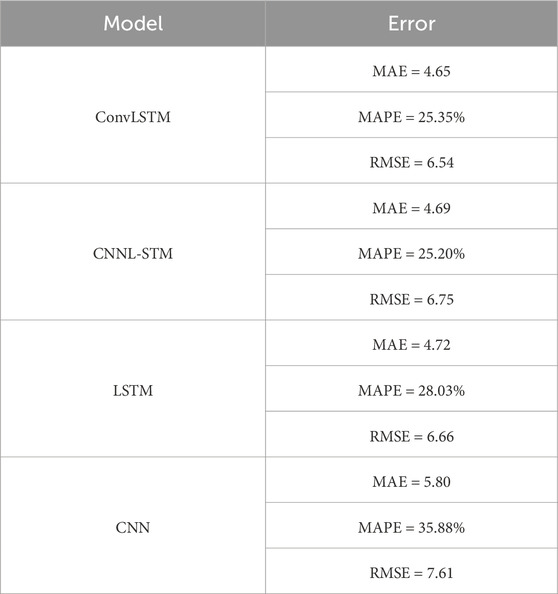
Table 7 presents the error metrics results for all methods with a time interval prediction of 6 days. As expected, the ConvLSTM model achieves the best prediction results with the smallest MAPE of 25.35%. Moreover, the hybrid CNN-LSTM demonstrates quite better results than the other baseline models, with MAE of 4.69 and MAPE of 25.20%. However, the baseline models demonstrate some difficulties in predicting the energy consumption 6 days ahead. These results indicate that LSTM achieves a MAPE of 28.03% and RMSE of 6.66. However, CNN scores worst, with a MAPE of 35.88%.

Table 7

Table 7. Scenario 3 prediction errors.

Once again, ConvLSTM outperforms CNN-LSTM, confirming the strength of the proposed model in predicting energy consumption even over long time intervals.

4.4 Results analysis

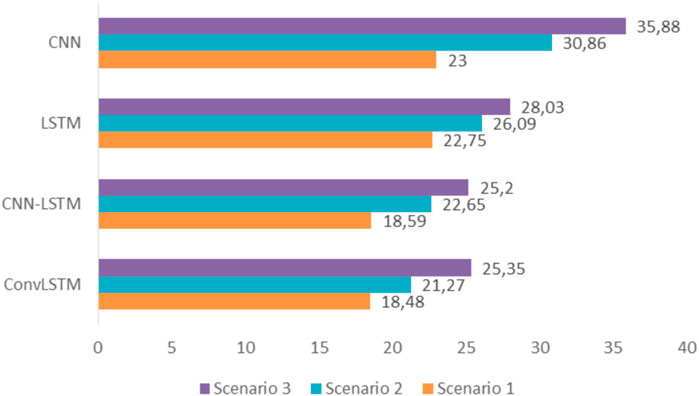
A comparison of each model’s performance through the three scenarios based on the MAPE is provided in Figure 14. It is obvious from this figure that an increase in the time prediction interval decreases the performance of the forecasting models. For all the models, the MAPE increases from scenario 1 to 3. The first scenario is recognized as the most reliable, with accurate predictions and lower errors. However, scenario 3 scores worst with the highest errors. Over all scenarios, the proposed ConvLSTM outperforms all other models. In the first scenario, it improves predictions by 4.52%. However, in the second and third scenarios, the predictions are enhanced by 9.59% and 10.53%, respectively. The CNN-LSTM model provides good results as well, ranking second after ConvLSTM, improving prediction by 4.41%, 8.21%, and 10.68% for the first, second, and third scenarios, respectively. Moreover, the LSTM model had enhanced results. For instance, the first scenario only had a 0.25% improvement, but in the second and third scenarios, 4.77% and 7.85% were reached, respectively. Meanwhile, the CNN model had the lowest performance improvement over all scenarios, scoring the highest MAPE: 23% in scenario 1, 30.86% in scenario 2, and 35.88% in scenario 3.

Figure 14

Figure 14. MAPE values for all scenarios.

As mentioned earlier, an increase in the time prediction interval resulted in decreasing the performance of the models. However, hybrid models outperformed baseline models owing to the blending of the different robustness of each model. According to the error metrics analyzed above, the proposed ConvLSTM and CNN-LSTM models outperform all the other models in all studied scenarios.

5 Conclusion

This research proposes hybrid ConvLSTM and CNN-LSTM models to predict the k-step-ahead energy consumption in a smart home. First, the two hybrid methods were tested to predict 1-day-ahead energy consumption, and the obtained results were compared with other baseline models such as LSTM and CNN. Then, 3- and 6-days-ahead are added to the simulation for better analysis. The findings indicate that the more the prediction period increases, the more the model’s accuracy decreases. However, ConvLSTM outperformed all the proposed models in predicting energy consumption over all three scenarios. In the first scenario, predictions were improved by 4.52%. However, in the second and third scenarios, the predictions were enhanced by 9.59% and 10.53%, respectively. Meanwhile, CNN-LSTM was also able to make good predictions, ranking second after ConvLSTM. It attained a MAPE of 18.59% in the first scenario, 22.65% in the second, and 25.20% in the third scenario. However, the baseline models worked quite well in the first scenario, but in scenarios 2 and 3, their performance dropped significantly, reaching a MAPE of 28.03% for LSTM and 35.88% for CNN in scenario 3. In future work, our focus will be on predicting the hourly energy consumption in a smart home while investigating other hybrid methods.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding authors.

Author contributions

IO: conceptualization, formal analysis, investigation, methodology, resources, software, writing–original draft, and writing–review and editing. AA: conceptualization, formal analysis, methodology, software, and writing–review and editing. MO: methodology, resources, supervision, validation, writing–review and editing, and project administration. MM: supervision, validation, writing–review and editing, and project administration. AE: funding acquisition, supervision, validation, visualization, writing–review and editing, and project administration. HK: supervision, visualization, and writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

The authors extend their appreciation to the Deanship of Scientific Research at Northern Border University, Arar, KSA, for funding this research work through the project number “NBU-FFR-2024-332-03”.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Agga, A., Abbou, A., Labbadi, M., and El Houm, Y. (2021). Short-term self consumption PV plant power production forecasts based on hybrid CNN-LSTM, ConvLSTM models. Renew. Energy 177, 101–112. doi:10.1016/j.renene.2021.05.095

CrossRef Full Text | Google Scholar

Ahmad, A., Javaid, N., Guizani, M., Alrajeh, N., and Khan, Z. A. (2016). An accurate and fast converging short-term load forecasting model for industrial applications in a smart grid. IEEE Trans. Industrial Inf. 13 (5), 2587–2596. doi:10.1109/tii.2016.2638322

CrossRef Full Text | Google Scholar

Ahmad, M. I. (2017). Seasonal decomposition of electricity consumption data. Rev. Integr. Bus. Econ. Res. 6 (4), 271.

Google Scholar

Al-Musaylh, M. S., Deo, R. C., Adamowski, J. F., and Li, Y. (2018). Short-term electricity demand forecasting with MARS, SVR and ARIMA models using aggregated demand data in Queensland, Australia. Adv. Eng. Inf. 35, 1–16. doi:10.1016/j.aei.2017.11.002

CrossRef Full Text | Google Scholar

Amarasinghe, K., Marino, D. L., and Manic, M. (2017). “Deep neural networks for energy load forecasting,” in 2017 IEEE 26th International Symposium on Industrial Electronics (ISIE), China, 2017, June (IEEE), 1483–1488.

CrossRef Full Text | Google Scholar

Amasyali, K., and El-Gohary, N. M. (2018). A review of data-driven building energy consumption prediction studies. Renew. Sustain. Energy Rev. 81, 1192–1205. doi:10.1016/j.rser.2017.04.095

CrossRef Full Text | Google Scholar

Amber, K. P., Aslam, M. W., Mahmood, A., Kousar, A., Younis, M. Y., Akbar, B., et al. (2017). Energy consumption forecasting for university sector buildings. Energies 10 (10), 1579. doi:10.3390/en10101579

CrossRef Full Text | Google Scholar

Asri, M. A. N. M., Zaini, N., and Latip, M. F. A. (2021). “Development of an LSTM-based model for energy consumption prediction with data pre-analysis,” in 2021 11th IEEE International Conference on Control System, Computing and Engineering (ICCSCE), China, 2021, August (IEEE), 228–233.

CrossRef Full Text | Google Scholar

Cai, M., Pipattanasomporn, M., and Rahman, S. (2019). Day-ahead building-level load forecasts using deep learning vs. traditional time-series techniques. Appl. energy 236, 1078–1088. doi:10.1016/j.apenergy.2018.12.042

CrossRef Full Text | Google Scholar

Carvallo, J. P., Larsen, P. H., Sanstad, A. H., and Goldman, C. A. (2018). Long term load forecasting accuracy in electric utility integrated resource planning. Energy Policy 119, 410–422. doi:10.1016/j.enpol.2018.04.060

CrossRef Full Text | Google Scholar

Cui, C., He, M., Di, F., Lu, Y., Dai, Y., and Lv, F. (2020). “Research on power load forecasting method based on LSTM model,” in 2020 IEEE 5th Information Technology and Mechatronics Engineering Conference (ITOEC), USA, 2020, June (IEEE), 1657–1660.

CrossRef Full Text | Google Scholar

Deb, C., Eang, L. S., Yang, J., and Santamouris, M. (2015). Forecasting energy consumption of institutional buildings in Singapore. Procedia Eng. 121, 1734–1740. doi:10.1016/j.proeng.2015.09.144

CrossRef Full Text | Google Scholar

Elbeltagi, E., and Wefki, H. (2021). Predicting energy consumption for residential buildings using ANN through parametric modeling. Energy Rep. 7, 2534–2545. doi:10.1016/j.egyr.2021.04.053

CrossRef Full Text | Google Scholar

Gerwig, C. (2017). “Short term load forecasting for residential buildings—an extensive literature review,” in International Conference on Intelligent Decision Technologies, Cham, 2017, June (Springer), 181–193.

Google Scholar

Ghalehkhondabi, I., Ardjmand, E., Weckman, G. R., and Young, W. A. (2017). An overview of energy demand forecasting methods published in 2005–2015. Energy Syst. 8 (2), 411–447. doi:10.1007/s12667-016-0203-y

CrossRef Full Text | Google Scholar

Guo, X., Zhao, Q., Zheng, D., Ning, Y., and Gao, Y. (2020). A short-term load forecasting model of multi-scale CNN-LSTM hybrid neural network considering the real-time electricity price. Energy Rep. 6, 1046–1053. doi:10.1016/j.egyr.2020.11.078

CrossRef Full Text | Google Scholar

Kaur, D., Islam, S. N., Mahmud, M., and Dong, Z. (2020). Energy forecasting in smart grid systems: a review of the state-of-the-art techniques. arXiv Prepr. arXiv:2011.12598.

Google Scholar

Kaur, H., and Ahuja, S. (2017). “Time series analysis and prediction of electricity consumption of health care institution using ARIMA model,” in Proceedings of Sixth International Conference on Soft Computing for Problem Solving, Singapore, 24 December 2016 (Springer), 347–358.

CrossRef Full Text | Google Scholar

Khan, S., Javaid, N., Chand, A., Khan, A. B. M., Rashid, F., and Afridi, I. U. (2019). “Electricity load forecasting for each day of week using deep CNN,” in Workshops of the International Conference on Advanced Information Networking and Applications, Cham, 2019, March (Springer), 1107–1119.

CrossRef Full Text | Google Scholar

Khan, Z. A., Hussain, T., Ullah, A., Rho, S., Lee, M., and Baik, S. W. (2020). Towards efficient electricity forecasting in residential and commercial buildings: a novel hybrid CNN with a LSTM-AE based framework. Sensors 20 (5), 1399. doi:10.3390/s20051399

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, T. Y., and Cho, S. B. (2019). Predicting residential energy consumption using CNN-LSTM neural networks. Energy 182, 72–81. doi:10.1016/j.energy.2019.05.230

CrossRef Full Text | Google Scholar

Kong, W., Dong, Z. Y., Jia, Y., Hill, D. J., Xu, Y., and Zhang, Y. (2017). Short-term residential load forecasting based on LSTM recurrent neural network. IEEE Trans. Smart Grid 10 (1), 841–851. doi:10.1109/tsg.2017.2753802

CrossRef Full Text | Google Scholar

Li, A., Xiao, F., Fan, C., and Hu, M. (2021). Development of an ANN-based building energy model for information-poor buildings using transfer learning. Build. Simul. 14 (1), 89–101. doi:10.1007/s12273-020-0711-5

CrossRef Full Text | Google Scholar

Memarzadeh, G., and Keynia, F. (2021). Short-term electricity load and price forecasting by a new optimal LSTM-NN based prediction algorithm. Electr. Power Syst. Res. 192, 106995. doi:10.1016/j.epsr.2020.106995

CrossRef Full Text | Google Scholar

Mpawenimana, I., Pegatoquet, A., Roy, V., Rodriguez, L., and Belleudy, C. (2020). “A comparative study of LSTM and ARIMA for energy load prediction with enhanced data preprocessing,” in 2020 IEEE Sensors Applications Symposium (SAS), China, 2020, March (IEEE), 1–6.

CrossRef Full Text | Google Scholar

Nazir, S., Ab Aziz, A., Hosen, J., Aziz, N. A., and Murthy, G. R. (2021). Forecast energy consumption time-series dataset using multistep LSTM models. J. Phys. Conf. Ser. 1933 (1), 012054. doi:10.1088/1742-6596/1933/1/012054

CrossRef Full Text | Google Scholar

Nepal, B., Yamaha, M., Yokoe, A., and Yamaji, T. (2020). Electricity load forecasting using clustering and ARIMA model for energy management in buildings. Jpn. Archit. Rev. 3 (1), 62–76. doi:10.1002/2475-8876.12135

CrossRef Full Text | Google Scholar

Peng, L., Wang, L., Xia, D., and Gao, Q. (2022). Effective energy consumption forecasting using empirical wavelet transform and long short-term memory. Energy 238, 121756. doi:10.1016/j.energy.2021.121756

CrossRef Full Text | Google Scholar

Pooniwala, N., and Sutar, R. (2021). “Forecasting short-term electric load with a hybrid of ARIMA model and LSTM network,” in 2021 International Conference on Computer Communication and Informatics (ICCCI), USA, 2021, January (IEEE), 1–6.

CrossRef Full Text | Google Scholar

Rafi, S. H., Deeba, S. R., and Hossain, E. (2021). A short-term load forecasting method using integrated CNN and LSTM network. IEEE Access 9, 32436–32448. doi:10.1109/access.2021.3060654

CrossRef Full Text | Google Scholar

Raza, M. Q., and Khosravi, A. (2015). A review on artificial intelligence-based load demand forecasting techniques for smart grid and buildings. Renew. Sustain. Energy Rev. 50, 1352–1372. doi:10.1016/j.rser.2015.04.065

CrossRef Full Text | Google Scholar

Residential power usage: 2022 Available at: https://www.kaggle.com/srinuti/residential-power-usage-3years-data-timeseries visited 01-01-2022

Google Scholar

Sajjad, M., Khan, Z. A., Ullah, A., Hussain, T., Ullah, W., Lee, M. Y., et al. (2020). A novel CNN-GRU-based hybrid approach for short-term residential load forecasting. IEEE Access 8, 143759–143768. doi:10.1109/access.2020.3009537

CrossRef Full Text | Google Scholar

Shao, X., Kim, C. S., and Sontakke, P. (2020). Accurate deep model for electricity consumption forecasting using multi-channel and multi-scale feature fusion CNN–LSTM. Energies 13 (8), 1881. doi:10.3390/en13081881

CrossRef Full Text | Google Scholar

Shirzadi, N., Nizami, A., Khazen, M., and Nik-Bakht, M. (2021). Medium-term regional electricity load forecasting through machine learning and deep learning. Designs 5 (2), 27. doi:10.3390/designs5020027

CrossRef Full Text | Google Scholar

Sulaiman, S. M., Jeyanthy, P. A., Devaraj, D., and Shihabudheen, K. V. (2022). A novel hybrid short-term electricity forecasting technique for residential loads using Empirical Mode Decomposition and Extreme Learning Machines. Comput. Electr. Eng. 98, 107663. doi:10.1016/j.compeleceng.2021.107663

CrossRef Full Text | Google Scholar

Sun, H., Burton, H. V., and Huang, H. (2021). Machine learning applications for building structural design and performance assessment: state-of-the-art review. J. Build. Eng. 33, 101816. doi:10.1016/j.jobe.2020.101816

CrossRef Full Text | Google Scholar

Sun, Y., Haghighat, F., and Fung, B. C. (2020). A review of the-state-of-the-art in data-driven approaches for building energy prediction. Energy Build. 221, 110022. doi:10.1016/j.enbuild.2020.110022

CrossRef Full Text | Google Scholar

Tudose, A. M., Sidea, D. O., Picioroaga, I. I., Boicea, V. A., and Bulac, C. (2020). “A CNN based model for short-term load forecasting: a real case study on the Romanian power system,” in 2020 55th International Universities Power Engineering Conference (UPEC), USA, 2020, September (IEEE), 1–6.

CrossRef Full Text | Google Scholar

Wei, N., Li, C., Peng, X., Zeng, F., and Lu, X. (2019). Conventional models and artificial intelligence-based models for energy consumption forecasting: a review. J. Petroleum Sci. Eng. 181, 106187. doi:10.1016/j.petrol.2019.106187

CrossRef Full Text | Google Scholar

Xu, L., Hu, M., and Fan, C. (2022). Probabilistic electrical load forecasting for buildings using Bayesian deep neural networks. J. Build. Eng. 46, 103853. doi:10.1016/j.jobe.2021.103853

CrossRef Full Text | Google Scholar

Zhang, A., Bian, F., Niu, W., Wang, D., Wei, S., Wang, S., et al. (2022). “Short term power load forecasting of large buildings based on multi-view ConvLSTM neural network,” in 2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2), China, 1 November 2020 (IEEE), 4154–4158.

Google Scholar