An improved optical length research on the physical boundary of particle-dispersed fuel

The Volumetric Homogenization Method (VHM) is one of the most commonly used methods for neutronics calculation in reactors or components. However, the use of VHM for the Double-Heterogeneous (DH) System may lead to a large deviation in reactivity calculation. The deviation of DH System using the VHM can be expressed by the theoretically modified optical length. When the theoretically modified optical length is less than 10⁻⁴, the deviation caused by the VHM will be less than 100 pcm. This paper points out that the existing theoretically modified optical length for some cases of DH systems is not accurate, and this method is only for pin cell. In this paper, by calculating a series of DH models and their corresponding VHM models, it is found that the water-uranium ratio and the shape of fuel region seriously affects the reactivity calculation deviation of particle-dispersed fuel, the original modified optical length does not take this into account, resulting in unacceptable errors. On this basis, the application of optical length to physical boundaries for DH system is further discussed and the shape correction factor is taken into consideration. Therefore, an improved optical length is proposed, which greatly expands the range of application of the physical boundary judgment methods for the double heterogeneity of dispersed particle fuel. The numerical results show that the accuracy of the improved optical length in defining the physical boundary of double heterogeneous system is higher than the theoretically modified optical length.

1 Introduction

Dispersed fuel particles have the characteristics of containing fission products at high temperature and deep depletion, and blocking the release of fission gas and fission debris out of the fuel pellets. So they are widely used in high temperature gas reactors (HTR) (Zhai et al., 2004) and Fully Ceramic Micro-encapsulated fuel (FCM) design in light-water reactor (LWR) (Powers et al., 2013; Terrani et al., 2012).

DH system mainly includes particle-dispersed burnable poison and particle-dispersed fuel, which has a complex geometric structure due to the random distribution of its dispersed particle (Weng et al., 2021). The double heterogeneity leads to high computational costs for fine calculations, and DH system cannot be described by traditional neutronic calculation programs (Sanchez and Pomraning, 1991; Hébert, 1993; Kim et al., 2005). To solve the problem, many equivalent solutions of neutronics calculation are proposed, such as Reactivity-equivalent Physical Transformation (RPT)method (Lei et al., 2020; Li et al., 2018), the equivalent homogenization method (She et al., 2017) implemented in VSOP (Teuchert et al., 1994) and PANGU (She et al., 2018; She et al., 2021), the volumetric homogenization method (VHM), subgroup method for the resonance treatment, the Sanchez–Pomraning method (Sanchez and Pomraning, 1991; Hébert, 1993) implemented in Dragon and Apollo. These methods often require fine calculations to generate the initial solution, and the fine computational processing is more complex and time-consuming (Wu et al., 2021). Among these methods, the VHM is simpler and faster than others.

In the VHM method, the original DH System is transformed into a conventional single-heterogeneous one, which is directly processed by deterministic programs. It is one of the most commonly used methods to deal with DH System.

The VHM process of the DH System is shown in Figure 1, where the dispersed particle material is mixed with the matrix material according to a volume fraction and then filled into the fuel zone. Then, a transition from a DH System to a conventional single-heterogeneous system has done.

FIGURE 1

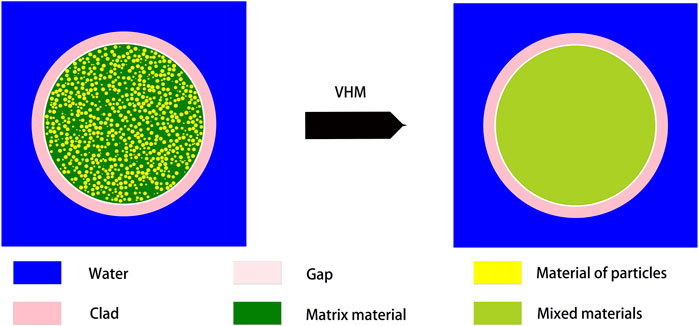
FIGURE 1. Process diagram of using Volumetric Homogenization Method for Double Heterogeneous System.

At different scales of geometries (i.e., fuel pin, fuel block, full core) which based on the Modular High-Temperature Gas-cooled Reactor, the impact of VHM on the reactor physics parameters was evaluated by Golesorkhi et al. (Golesorkhi et al., 2023), It is found that the calculation time is greatly reduced by using VHM for the calculation object, but it also brings errors. This is because of the spatial self-shielding effect under the special spatial structure of the DH system. When a neutron enters a fuel particle, the neutron is first absorbed by the outer layer. This means that the elements on the outside of the particle can preferentially absorb more neutrons than the inside, and fewer neutrons can enter the inside of the fuel particle, which means that the inside is shielded by the outside, resulting in the neutron collision probability error. Accurate modeling and analysis are essential for this kind of DH system. When the VHM is not applicable, the program with double heterogeneity processing ability must be used for analysis and calculation (Alrwashdeh et al., 2020).

To solve this problem, many treatment methods have been proposed and applied to reactor core physical analysis. For example, Alameri et al. analyzed the effect of integral fuel burnable absorber (IFBA) coated the tri-structural isotropic (TRISO) on prismatic-core advanced high temperature reactor by collision of probability calculation method (Alameri and Alrwashdeh, 2021; Alrwashdeh et al., 2020). In addition, the RPT method is also an extension of the VHM and it has been proved to be effective in burnup calculation for DH system (Alrwashdeh et al., 2019). However, these methods require program with double heterogeneity processing capabilities for calculation. Compared with these methods, the volume homogenization method is undoubtedly the most simple and effective.

The DH System is complex and diverse, and the deviation caused by the VHM is also different. Therefore, a determination method is needed to quantify the error caused by the VHM, which can determine whether the DH System can be directly treated by the VHM.

The Nuclear Power Institute of China comprehensively considers the cross-section of dispersed particles and materials, particle size, and the mutual shielding effect between particles, and proposes the theoretically modified optical length (Lei et al., 2022) to define the DH physical boundary of the dispersed particle system.

The theoretically modified optical length is pointed out when the VHM can be used directly and when the DH of the system must be considered. The model shows that for the vast majority of particle-dispersed burnable poison, the double heterogeneity of system must be considered. However, for the dispersed particle fuel, the theoretically modified optical length has two shortcomings. Firstly, when the volumetric fraction is less than 10%, the existing theory model is invalid. Second, the theoretically modified optical length cannot explain that, the homogenization method will produce positive deviation in some cases, while it will produce negative deviation in other cases. Therefore, the model needs to be further improved. In this paper, it is found that the water-uranium ratio and the shape of the fuel region will affect the double heterogeneity of the dispersed particle fuel, which is one of the key factors affecting the volumetric homogenization method deviation of dispersed particle-type fuel.

In this paper, the OpenMC is used to model the dispersed particle-type fuel with an explicit method (Romano and Forget, 2012), and the double heterogeneity of the dispersed particle system is further discussed. In this study, the particle model was used as the benchmark solution. In order to eliminate the calculation differences between different programs, the model after volumetric homogenization method was also calculated by OpenMC as a comparison. Aiming at the characteristic that the water-uranium ratio and the shape of fuel region will significantly affect the double heterogeneity of the dispersed particle system, the deviation effect caused by the volumetric homogenization method under the three variables: volumetric fraction, water-uranium ratio and particle size is explored. At the same time, the discussion scope is extended to the dispersion fuel plate, and the shape correction factor is proposed.

The numerical results show that the improved optical length solves the problem that the original modified optical length is not suitable for the determination of the double heterogeneity of the dispersion fuel plate, and improves the prediction accuracy of the modified optical length for the volumetric homogenization reactivity calculation deviation of the dispersion fuel with different volumetric fraction and different fuel region shapes.

2 Calculation object

In this paper, the fuel cell with total reflection boundary condition is studied. The main parameters of fuel pin are shown in Table 1, the parameters of fuel plate are shown in Table 2, and the parameters of random dispersion particle are shown in Table 3. The model diagram is shown in Figure 2. The calculation examples cover the types of fuel pin and fuel plate with particle sizes of 100–500 μm under different water-uranium ratios and volumetric fraction of dispersed particles. DH systems with different particle sizes but the same UO₂ ratio correspond to the same VHM model. For a given DH system with a specified UO₂ ratio, we calculated only one VHM model as the benchmark and compared it with DH models with different particle sizes. Since the hydrogen nucleus in the moderator water plays a major role in the neutron slowing-down process, the ratio of the number of hydrogen nuclei per unit volume to the number of heavy metal nuclei (H/HM) is used as the water-uranium ratio. In this paper, it is recorded as R, and the specific calculation method is Eq. 1

$R=\frac{2\bullet \left({\rho }_{H_{2}o}\bullet \frac{N_A}{M_{H_{2}O}}\right)\bullet V_M}{\left({\rho }_{U_{2}o}\bullet \frac{N_A}{M_{U_{2}O}}\right)\bullet V_F\bullet V_P}(1)$

TABLE 1

TABLE 1. Main parameters of fuel pin.

TABLE 2

TABLE 2. Main parameters of fuel plate.

TABLE 3

TABLE 3. Parameters of dispersion particle model.

FIGURE 2

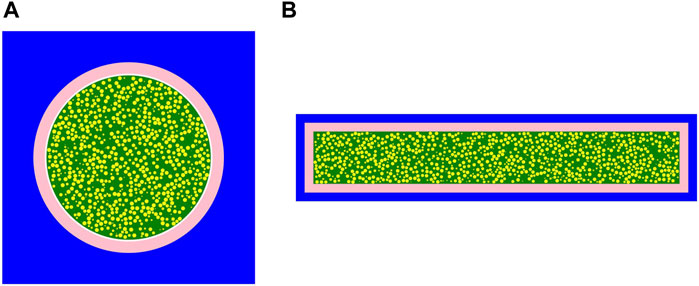
FIGURE 2. Schematic diagram of random distribution of dispersed particles. (A) Top View of Fuel Pin. (B) Top View of Fuel Plate.

In this formula, $V_M$ and $V_F$ are the volume of moderator and fuel zone respectively. $V_P$ is dispersed particle volumetric fraction, ${\rho }_{H_{2}o}$, ${\rho }_{U_{2}o}$ are the density of water and fuel, $M_{H_{2}O},M_{U_{2}O}$ is atom of water and fuel, $N_A$ represents the Avogadro constant, all units are international.

3 Volumetric homogenization method deviation analysis of dispersed fuel

The Monte Carlo program OpenMC developed by MIT (Romano and Forget, 2012) is used to model the random distribution of dispersed particles. A schematic diagram of the random distribution of dispersed particles in the matrix is shown in Figure 2.

To analyze the calculation deviation caused by the volumetric homogenization method of the DH System, the volumetric fraction in this paper is selected from 5%–30% volumetric fraction, the pitch length is selected from 1.0 to 1.6  cm, and the particle radius is from 100 to 500 μm. The numerical simulation calculation and analysis of the particle model are as follows.

3.1 Effect of particle size

The main calculation results are shown in Figure 3, in which 1.0–1.6 indicates that the pitch of cell is 1.0–1.6 cm. Each figure shows the reactivity calculation deviation curve with particle size between the VHM and particle model of the Monte Carlo program under different fuel volumetric fractions and different pitch of cell.

FIGURE 3

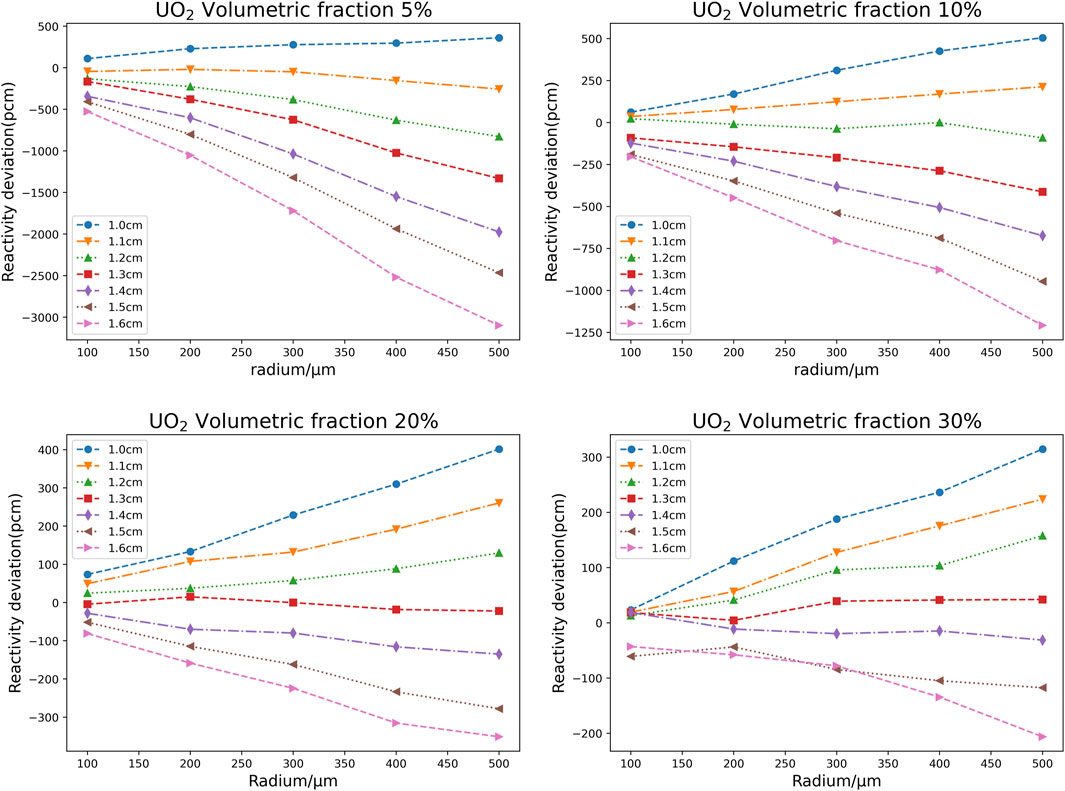
FIGURE 3. Reactivity calculation deviation curve with particle sizes under different UO₂ volumetric fraction and pitch of cell.

It can be inferred from Figure 3 that the larger the particle radius, the larger the deviation will be. This is due to the spatial self-screening effect, the larger the particle radius is, the more intense the self-screening effect is, so the deviation of the VHM model is larger. Moreover, there must be a certain pitch for the fuel pin. Under the water-uranium ratio corresponding to the pitch, no matter how the particle size changes, the reactivity calculation deviation of the VHM will always be close to 0, and the water-uranium ratio corresponding to the pitch is called the minimum deviation point. We adopt the linear interpolation method to determine the minimum deviation point. The steps are as follows. Taking Figure 4 as an example, we first use the linear interpolation method to obtain the intersection point of each specific particle size curve and the x-axis, and then calculate the average value of these intersection points x coordinates. The minimum deviation point is obtained. When the water-uranium ratio is at the minimum deviation point, the particle size has little effect on the reactivity calculation deviation of VHM for the dispersed fuel particles. When the water-uranium ratio obviously deviates from the minimum deviation point, the absolute value of the calculation deviation will increase with particle size. When the water-uranium ratio is close to the minimum deviation point, the calculation deviation of reactivity caused by the volumetric homogenization method is still less than 100pcm even if the particle radius increases to 500 μm.

FIGURE 4

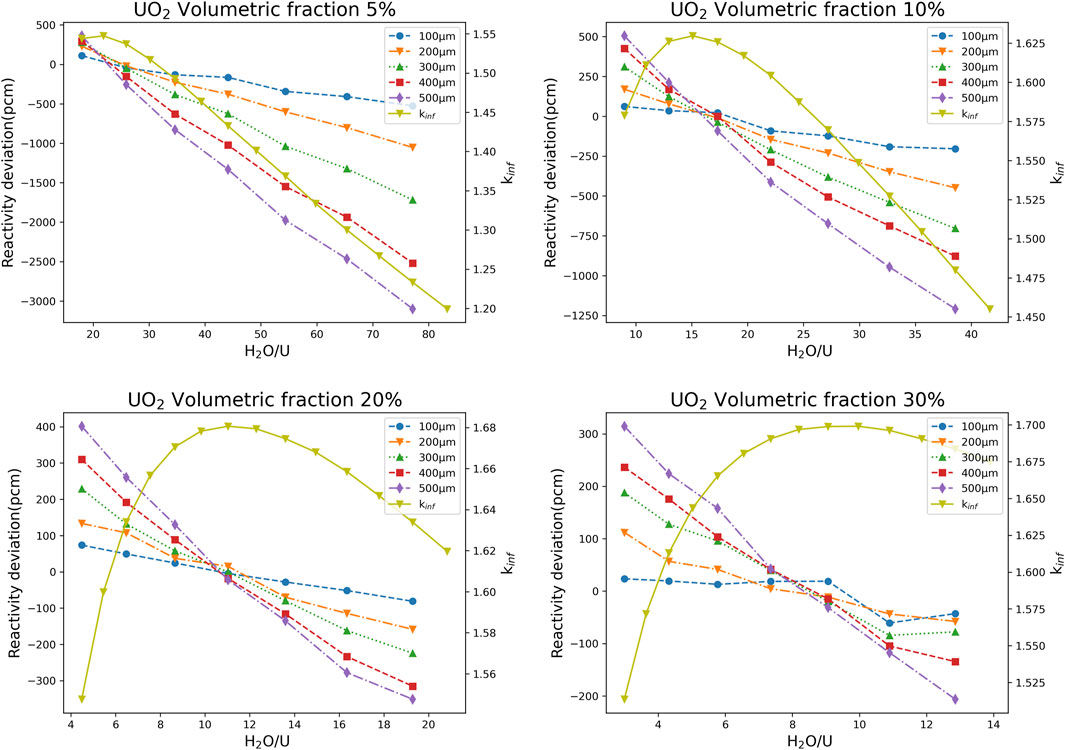
FIGURE 4. Reactivity calculation deviation curve with water-uranium ratio under different UO₂ volumetric fraction and particle sizes.

3.2 Effect of water-uranium ratio

To investigate the inconsistency of positive and negative values of reactivity calculation deviation caused by volumetric homogenization method at different volumetric fraction of dispersed particles, the volumetric fraction is kept constant and the ratio of water to uranium is changed. The numerical results show that the volumetric fraction change will lead to the deviation caused by the VHM from positive to negative, which is mainly caused by the water-uranium ratio rather than the volumetric fraction. Compared to the VHM model, the DH model will have a less overall neutron absorption due to the spatial self-screening effect. That mean the lower the probability of neutron collision with the fuel in the DH model. In fuel particles, the shielding effect of thermal neutrons is higher than that of resonance neutrons. Therefore, with the increase of the water-uranium ratio, the thermal neutrons start to become more numerous, and the self-screening effect is further aggravated, which leads to the decrease of the k_inf of the DH model, so the calculation deviation will gradually decrease. It can be seen from Figure 4 that when the water-uranium ratio is less than the minimum deviation point, the volume homogenization will cause a positive deviation. When it is greater than the minimum deviation point, volume homogenization will cause a negative deviation. And the farther the water-uranium ratio deviates from the minimum deviation point, the larger the homogenization deviation is. For fuel pin, the deviation between the minimum deviation point and the optimum water-uranium ratio is within 10%. Therefore, the effect of water-uranium ratio must be considered when quantifying the deviation caused by the volumetric homogenization method of the double heterogeneous system.

The minimum deviation point calculation method is calculated by linear interpolation. Firstly, the particle size and volumetric fraction are determined, and the intersection point with the x-axis is obtained by linear interpolation, which is the minimum deviation point under the particle size, recorded as $R_i$. Then the average value $\overline{R}$ is the minimum deviation point value under the volumetric fraction. Table 4 lists the relationship between the optimal water-uranium ratio and the minimum deviation point under each volumetric fraction. In this paper, the optimal water-uranium ratio is determined by the uniform sample point method. The sampling points are shown in the k_inf curve in Figure 4, and the maximum value is taken as the optimal water-uranium ratio.

TABLE 4

TABLE 4. Relationship between optimal water - uranium ratio and minimal deviation point for fuel pin with different volumetric fraction.

3.3 Effect of volumetric fraction

Figure 4 shows the relationship between the deviation and each factor for 5, 10, 20, and 30 volumetric fraction in turn. From the four subplots, it can be seen that the curves for the different radii have an intersection point, which corresponds to a calculated deviation of exactly 0. Volumetric fraction affects the calculation deviation by influencing the Water-Uranium Ratio. It can be seen from Figure 4 that as the volumetric fraction increases, the pitch corresponding to the optimal water-uranium ratio also changes, and the deviation caused by volumetric homogenization method is also decreasing. For a specific size of the fuel pin, as the volumetric fraction increases, the optimal water-uranium ratio corresponding to the cell pitch also changes. The cell transits from undermoderation to overmoderation, and the deviation will also change from negative to positive.

3.4 Effect of fuel region shape

The change in water-uranium ratio will cause a change in neutron energy spectrum distribution, and the previous discussion shows that the distribution of the neutron energy spectrum will affect the reactivity calculation deviation of VHM for the dispersed fuel particles model. The double heterogeneity caused by dispersed fuel particles under different reactor structures is not consistent, so another fuel region shape in PWR--fuel plate is discussed.

To explore whether the fuel plate has the same characteristics of double heterogeneity as the fuel pin, the plate dispersion fuel model with different pitch, different volumetric fraction and different particle sizes is explored. The specific description of the example is shown in Table 2.

It can be seen from Figure 5 and Figure 6 that the variation trend of the calculation deviation of the homogenization for the dispersion fuel plate with the water-uranium ratio, particle size, volumetric fraction, and other factors is almost the same as that of the fuel pin. The reactivity calculation deviation of VHM for dispersion fuel plate will increase with the increase of particles, and the water-uranium ratio will also significantly affect the trend of reactivity calculation deviation of VHM. Similar fuel pin, the reactivity calculation deviation of VHM for dispersion fuel plate also has a minimum deviation point at a specific water-uranium ratio, but the difference is that the minimum deviation point is not exactly equal to the optimal water-uranium ratio point. According to numerical experience, the minimum deviation point is about 1.25 times the optimal water-uranium ratio for dispersion fuel plate The relationship between the minimum deviation point and the optimal water uranium ratio under the volumetric fraction of the fuel plate and the fuel pin is shown in Table 4 and Table 5.

FIGURE 5

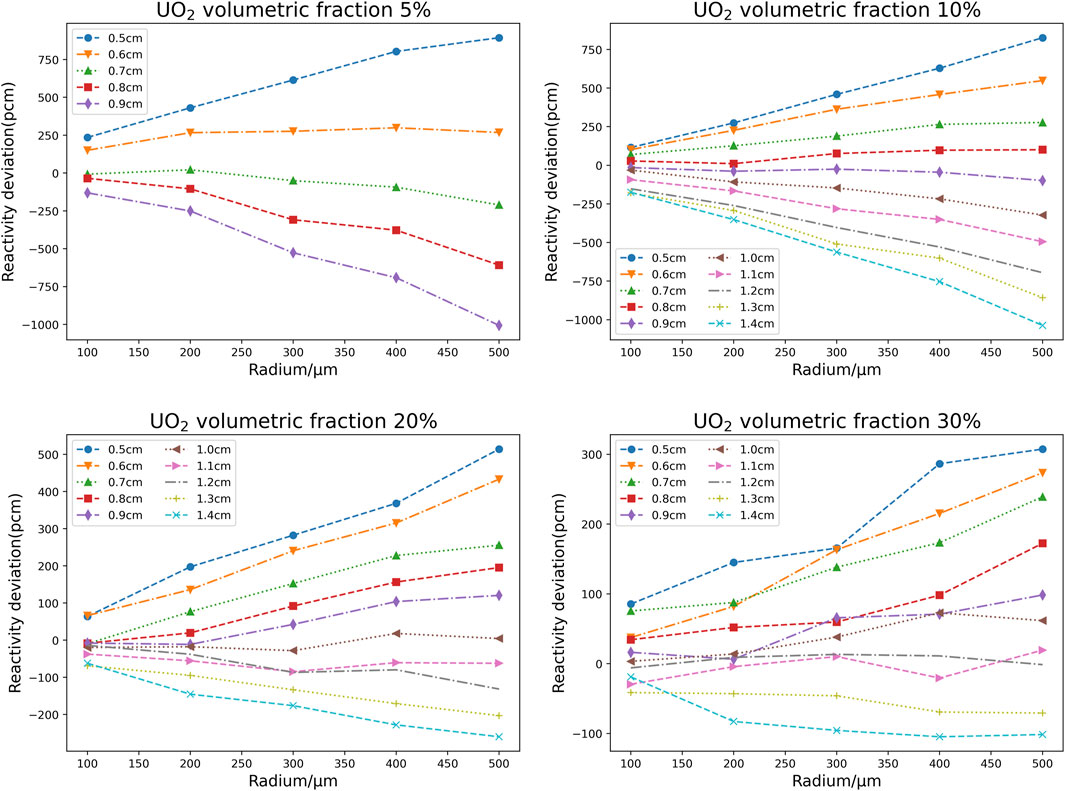
FIGURE 5. Reactivity calculation deviation curve for fuel plate with particle sizes under different UO₂ volumetric fraction and pitch of cell.

FIGURE 6

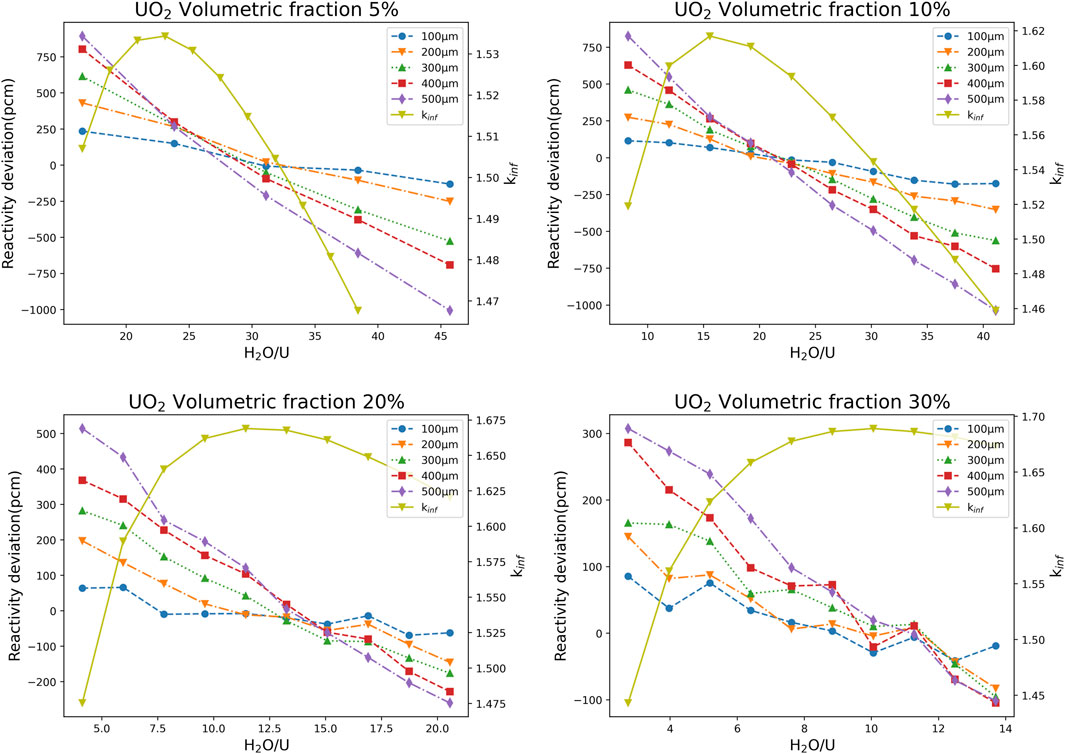
FIGURE 6. Reactivity calculation deviation curve for fuel plate with water-uranium ratio under different UO₂ volumetric fraction and particle sizes.

TABLE 5

TABLE 5. Relationship between optimal water - uranium ratio and minimal deviation point for fuel plate with different volumetric fraction.

From Table 4, it can be seen that the optimal water-uranium ratio is closest to the minimum deviation point when the UO₂ ratio is 20%. To ensure the safety of PWR, the current reactor water-uranium ratio is usually lower than the optimal water-uranium ratio, which means that the k_inf of GM model is larger than the VHM model., a negative deviation is introduced by using the VHM method. As the water-uranium ratio in the reactor increases with depletion, the deviation caused by the VHM method decreases. In addition, during the depletion, due to the spatial self-shielding effect, the fuel element consumption in the outer layer of the particle is higher than that in the inner layer, which leads to the decrease of the particle radius, and the error induced by the VHM method will also decrease.

4 Judgment formula for physical boundary of dispersion fuel system

Since the theoretically modified optical length does not take into account the reactivity calculation deviation of VHM under different water-uranium ratios, the determination effect of dispersed particle fuel with different volumetric fraction of dispersed particles under fixed pitch is not satisfactory, especially in the case of low volumetric fraction, and the influence of different reactor structures is not considered. Therefore, it is necessary to propose a new correction method for the double heterogeneity boundary judgment formula of dispersed particle fuel systems.

4.1 Relationship between self-shielding effect and theoretically modified optical length

The reactivity deviation calculation of the volumetric homogenization method is related to many factors. For the dispersed particle fuel, whether the system needs to consider double heterogeneity can be judged by theoretically modified optical length (Lei et al., 2022), as shown in Eq (2).

$\left|{\mathrm{\Sigma }}_m-{\mathrm{\Sigma }}_p\right|d_p\frac{\sqrt{V_P}}{10}>\stackrel{\sim }{\epsilon }(2)$

In the formula, ${\mathrm{\Sigma }}_m$ is the macroscopic section of the matrix material, and the unit is ${cm}^{-1}$ ; ${\mathrm{\Sigma }}_p$ is the macroscopic cross section of granular material, the unit is ${cm}^{-1}$ ; $d_p$ is the particle radius, and the unit is ${cm}^{-1}$. $V_P$ is the volumetric fraction of the dispersed particles, ranging from 0 to 1.0, and $\stackrel{\sim }{\epsilon }$ is the modified optical length limit.

The physical meaning of the judgment equation is that the macro cross-section difference between the particle material and the matrix material will cause the neutron flux difference between the materials, and the particle size will also cause the spatial self-shielding effect and affect the flux gradient inside the particles. At the same time, the volumetric fraction of dispersed particles will also cause the mutual shielding effect between the particles. When the flux difference between the matrix and the interior of the particles reaches a certain degree, at which the theoretically modified optical length reaches 10⁻⁴, the reactivity calculation deviation of VHM for the dispersed fuel particles will exceed 100pcm.

4.2 Relationship between self-shielding effect and the improved optical length

The above theoretically modified optical length considers not only the effect between the matrix and a single particle but also the mutual shielding effect between particles. However, the formula is not ideal for the fitting of dispersed fuel particles with different volumetric fraction of dispersed particles The reason is that the change of water-uranium ratio caused by the change of volumetric fraction is ignored, and the shape of the fuel cell will also affect the double heterogeneity of the system. The original theoretically modified optical length separately discusses the influence of volumetric fraction on the calculation deviation, so sqrt (Vp) is used as the correction term. It can be seen from Figure 7 that the fitting effect is not ideal. It can be seen from the discussion in Section 3 that the volumetric fraction is not the fundamental factor affecting the calculation deviation. The reason why the volumetric fraction affects the calculation deviation is that the change of the volumetric fraction leads to the change of the water-uranium ratio and the minimum deviation point, and the calculation deviation is related to the degree of the current water-uranium ratio deviating from the minimum deviation point. The improved optical length introduces R/R_best to quantify the degree of deviation. When discussing the fuel plate, it is found that the optimal water-uranium ratio does not coincide with the minimum deviation point, so the shape coefficient k is introduced to correct it. Finally, it can be seen from Figure 4 and Figure 6 that the effect of water-uranium ratio on the calculation deviation is non-linear. The smaller the water-uranium ratio, the greater the effect of the water-uranium ratio on the calculations deviation, the results of this data are consistent with the characteristics of a logarithmic function, so the logarithmic function is introduced as a correction. In addition, in order to be the same as the theoretically modified optical length limit used to determine the dispersed particle poison, the constant term is adjusted. Thus, Eq. 3 can be derived. Combined with the above research, Eq. 2 can be modified to Eq. 3.

$\left|{\mathrm{\Sigma }}_m-{\mathrm{\Sigma }}_p\right|d_p\frac{R_{dev}}{20}>\stackrel{\sim }{\epsilon }(3)$

$R_{dev}={\log }_e\left(\frac{R}{k\bullet R_{best}}\right)(4)$

FIGURE 7

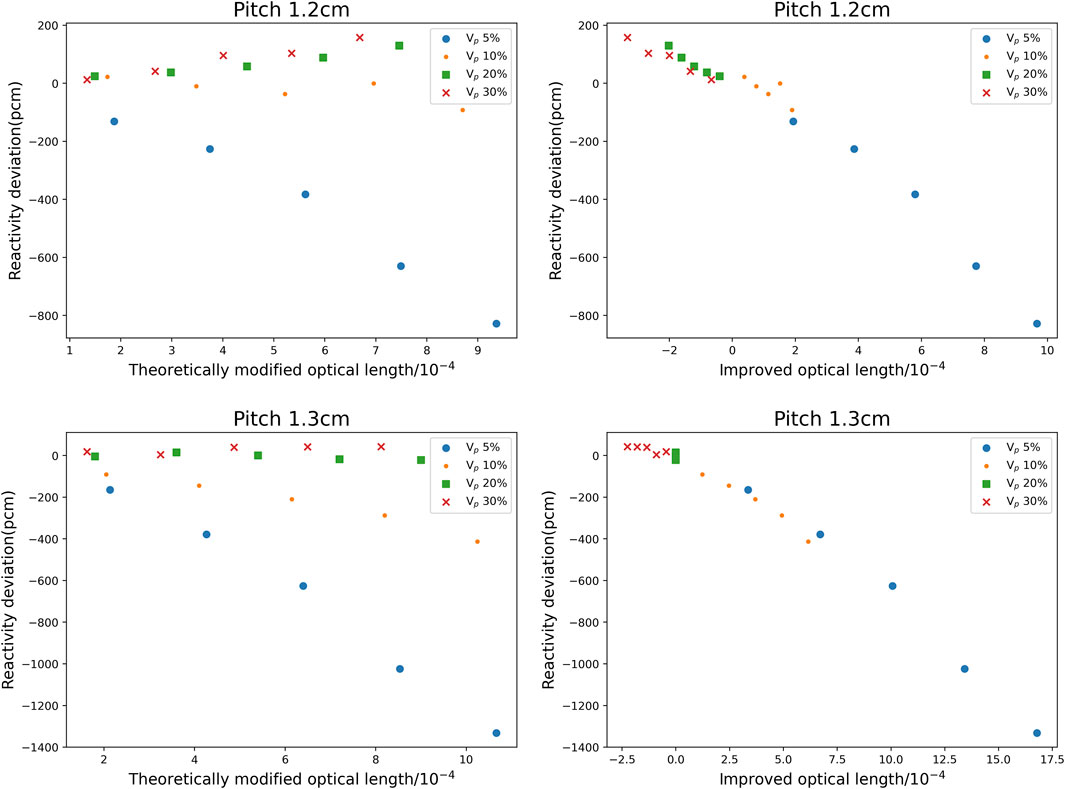
FIGURE 7. Relationship between reactivity deviation and theoretically modified optical length or improved optical length under different UO₂ volumetric fraction.

In this formula, k is the shape coefficient which defined as the ratio of the minimum deviation point to the optimal water-uranium ratio for the fuel cell and $R_{dev}$ is the deviation of water-uranium ratio; $R$ is the water-uranium ratio of the current cell; $R_{best}$ is the best water-uranium ratio corresponding to the current fuel cell.

The improved optical length takes into account the influence of the water-uranium ratio of the cell, and the influence of the volumetric fraction is re-corrected. The shape correction factor k is also given for different fuel region shapes. The numerical analysis shows that for the dispersed fuel particles, the larger the volumetric fraction of dispersed particles, the smaller the absolute value of the deviation of VHM when the pitch and particle size remain unchanged. The change in fuel region shape will lead to the deviation of minimum deviation point. Therefore, the shape coefficient k is used to correct the water-uranium ratio deviation coefficient.

4.3 Numerical results

For the dispersion fuel particle system described in this paper, the relationship between the reactivity calculation deviation of the volumetric homogenization method and the theoretically modified optical length and the improved optical length under different volumetric fractions after fixing the pitch is shown in Figure 7. Then Figure 8 shows the relationship between the reactivity calculation deviation of the volumetric homogenization method and the modified optical length and the improved optical length under different pitch after the volumetric fraction of dispersed particles is fixed. Finally, Figure 9 shows the relationship between the reactivity calculation deviation of VHM for the fuel plate and the theoretically modified optical length and the improved optical length by fixing the volume of dispersed particles and changing the plate spacing.

FIGURE 8

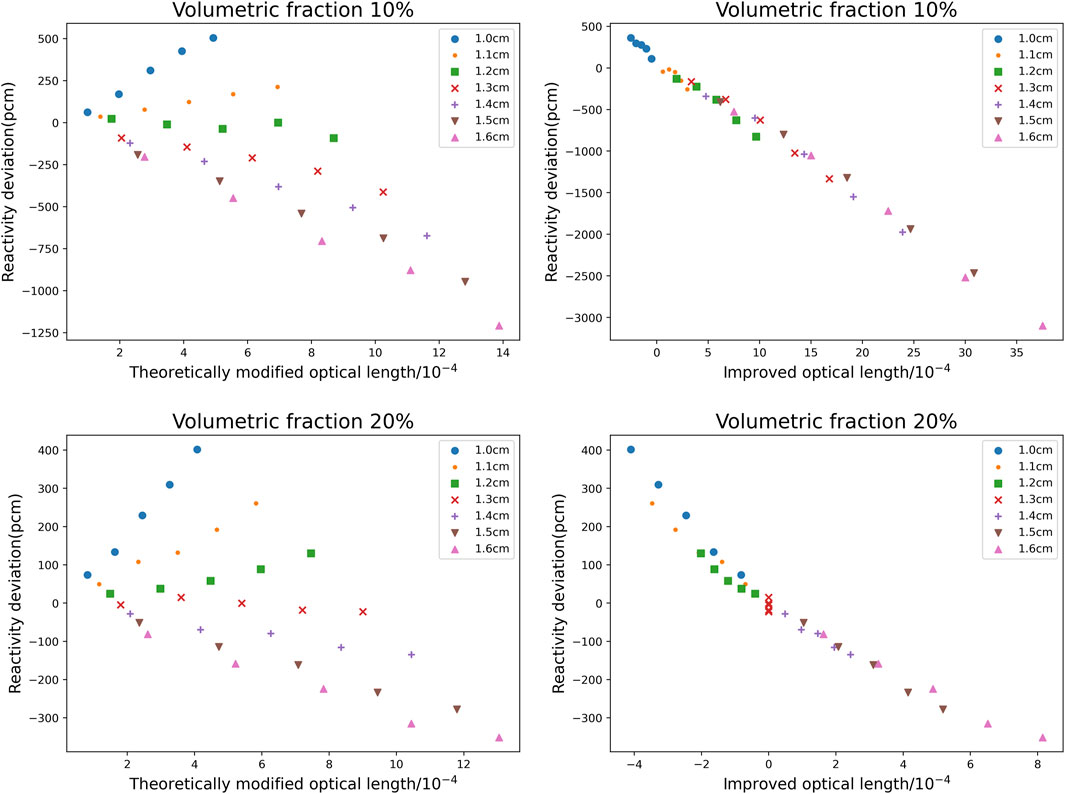
FIGURE 8. Relationship between reactivity deviation and theoretically modified optical length or improved optical length under different pitch of cell.

FIGURE 9

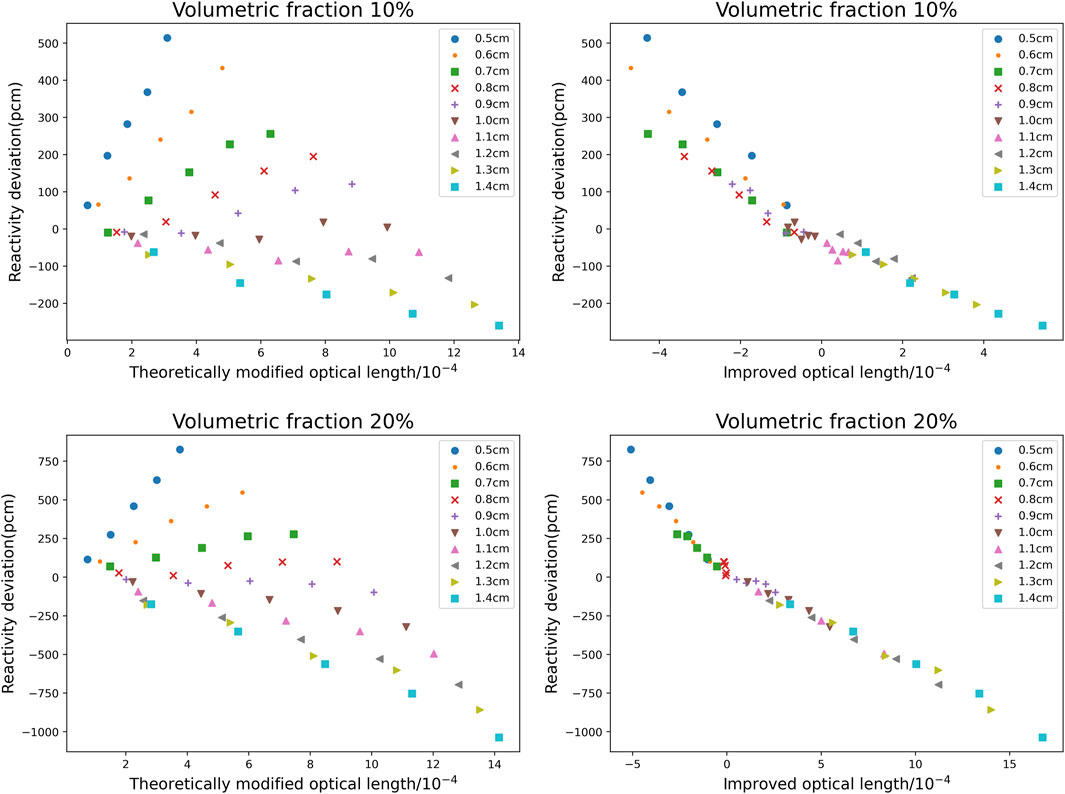
FIGURE 9. Relationship between reactivity deviation and theoretically modified optical length or improved optical length for fuel plate.

It can be seen from Figure 7 that when the pitch is fixed, the volumetric fraction of the dispersed particle fuel is changed, and the size of the dispersed particles is changed. The improved optical length is almost linearly related to the reactivity calculation deviation of VHM. The larger the improved optical length, the larger the deviation of the volumetric homogenization method. The improved optical length fits better with the reactivity calculation deviation of the homogenization for the dispersed particle fuel under low volumetric fraction, and can correctly reflect the positive and negative values of the deviation. The improved optical length can better reflect the law under different volumetric fraction of dispersed particles than the original.

It can be seen from Figure 8 that when the volumetric fraction of dispersed particles remains constant, the pitch of the dispersed particle fuel is changed, and the size of the dispersed particles is changed at the same time. The improved optical length is almost linear with the deviation of the homogenization reactivity calculation. Compared with the original theoretically modified optical length, the improved optical length expands the application range of the judgment method for the double heterogeneity. The improved optical length can better reflect the reactivity calculation deviation law of the homogenization for the dispersed fuel particle system under different water-uranium ratios.

The noteworthy phenomenon in Figure 8 is the behaviour of the improved optical length for the 1.3 cm case. They are stuck at 0 (in the x-axis). There are two reasons for this phenomenon. First, the error caused by the limitation of the number of sampling points. In this paper, the sampling method is used to find the optimal water-uranium ratio. There is an error in this method. For the case where the volumetric fraction is 20% and the pitch is 1.3 in Figure 8, the water-uranium ratio reaches the optimal when the pitch is 1.3 cm. Therefore, the improved optical length corresponding to all cases under this pitch is 0, but the actual optimal water-uranium ratio is slightly deviated, which results in this phenomenon. Second, the statistical error of Monte Carlo method. It can be seen from the original data that in the case that pitch is 1.3cm, the deviation values corresponding to different particle sizes are −4.4pcm, 15.0pcm, 0.2pcm, −18.2pcm, −22.2pcm. The fluctuation is within ±20pcm. This phenomenon is within the statistical fluctuation of Monte Carlo calculation. Therefore, if it is necessary to improve the accuracy of determination, it is necessary to accurately find the best water-uranium ratio and improve the accuracy of Monte Carlo calculation.

As can be seen from Figure 9, for the dispersion fuel plate, the new judge method makes up for the problem that the theoretically modified optical length cannot accurately define the DH physical boundary of the dispersion fuel plate. After using the new judgment formula, the reactivity calculation deviation of the VHM for the dispersion fuel plate is almost linear with the improved optical length.

The numerical results show that for the dispersed particle fuel, the impact when the particles was introduced on the neutronics calculation depends not only on the properties of the particles, but also on the cell parameters. Through the analysis of Eq. 3, it can be seen that the deviation caused by VHM is not constant, but is closely related to the water-uranium ratio and size of particle. It can be seen from Figure 4 that for fuel plate, VHM overestimates the reactivity when the cell is on undermoderation, and the situation is opposite when it is on overmoderation. When the water-uranium ratio is optimal, no matter how the particle size and volumetric fraction change, the reactivity deviation calculated by VHM does not change much. It can be seen from Figure 5 that for fuel plate, the calculation deviation caused by VHM has the same trend, but the minimum deviation point is about 1.2 times of the optimal water-uranium ratio. When the volumetric fraction of fuel and water-uranium ratio are constant, the particle size directly affects the calculation deviation caused by VHM. From Figure 3 and Figure 5, it can be seen that whether it is a fuel pin or a plate, the larger the particle size, the greater the deviation caused. The positive and negative deviation values caused by VHM are determined by the water-uranium ratio, and the greater the water-uranium ratio deviation from the minimum deviation point, the greater the deviation change rate caused by the corresponding particle size change. The particle size and water-uranium ratio jointly affect the error caused by the VHM.

In quantifying the size of the double heterogeneity introduced by the dispersed particles, the improved optical length is more accurate than the theoretically modified optical length, but there are also some limitations. The linear fitting effect of the plate cell is not as good as that of the pin cell. In some extreme cases (such as the pitch is small, the water-uranium ratio is low, as shown in Figure 9), the accuracy of the improved optical length has decreased, but the deviation trend presented by the improved optical length still does not change. Due to the extremely low water-uranium ratio is not common in reactor design, the improved optical length still has a good range in neutronics analysis of DH systems.

5 Conclusion

In this paper, it is found that the water-uranium ratio and the shape of the fuel region will seriously affect the reactivity calculation deviation of the volumetric homogenization method for dispersion fuel system, and the original modified optical length does not consider this, so it causes unacceptable errors.

The numerical results show that the volumetric fraction change will lead to the deviation caused by the VHM from positive to negative, The reason for this phenomenon is mainly due to the change of water uranium ratio caused by the change of volumetric fraction, rather than the effect of pure volumetric fraction.

The relationship between the reactivity calculation deviation of VHM for the dispersion fuel system and various factors under different water-uranium ratios is reanalyzed, and the influence of some parameters is corrected. The factors such as the size of dispersed fuel particles, the water-uranium ratio of the cell, the volumetric fraction of the particle, and the particle size are integrated into the improved optical length.

An improved optical length is proposed, which can better reflect the reactivity calculation deviation of VHM for the dispersed fuel particles under different volumetric fraction of dispersed particles. Moreover, the new formula can also reflect the positive and negative deviation values caused by the volumetric homogenization method. In addition, this paper also analyzes another fuel cell type in PWR—fuel plate, and integrates the shape coefficient into the improved optical length. When the absolute value of the improved optical length exceeds 10⁻⁴, the reactivity calculation deviation of the VHM for the dispersed particle fuel will exceed 100pcm, which needs to be considered by the double heterogeneity calculation program. The improved optical length not only solves the problem that the original one cannot linearly characterize the reactivity calculation deviation of the VHM for the dispersion fuel system under different volumetric fractions but also makes the judgment formula capable to predict the double heterogeneity of the fuel plate, which improves the accuracy of the judgment formula for the double heterogeneity of dispersion fuel and expands the range of it. The numerical results show that the accuracy of the improved optical length in defining the physical boundary of double heterogeneous system is higher than the theoretically modified optical length.

For some reactors that contain a large number of particle-dispersed fuels, the improved optical length can help designers quickly simplify the grating geometries in the assembly during simulation, thereby avoiding the consumption of computing for processing double heterogeneity, it plays an important role in improving the efficiency of simulation for the reactors that contain a large number of particle-dispersed fuels.

In addition, the improved optical length also represents the size of the double heterogeneity of the particle-dispersed fuel system, revealing the factors related to the size of the double heterogeneity introduced by the particle material. When designing the algorithm for processing double heterogeneity, the dispersed particle system on different improved optical lengths can be selected for calculation to verify the accuracy of the algorithm in various cases.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

PL: Writing–original draft, Writing–original draft, YC: Writing–review and editing, Writing–review and editing, SL: Writing–review and editing, Writing–review and editing, LL: Writing–review and editing, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alameri, S. A., and Alrwashdeh, M. (2021). Preliminary three-dimensional neutronic analysis of IFBA coated TRISO fuel particles in prismatic-core advanced high temperature reactor. Ann. Nucl. Energy 163, 108551. doi:10.1016/j.anucene.2021.108551

CrossRef Full Text | Google Scholar

Alrwashdeh, M., Alamaeri, S. A., Alkaabi, A. K., and Ali, M. (2019). Homogenization of TRISO fuel using reactivity equivalent physical transformation method. Transactions 121 (1), 521–1522. Khalifa Univ. doi:10.13182/t30850

CrossRef Full Text | Google Scholar

Alrwashdeh, M., Alameri, S. A., and Alkaabi, A. K. (2020). Preliminary study of a prismatic-core advanced high-temperature reactor fuel using homogenization double-heterogeneous method. Nucl. Sci. Eng. 194, 163–167. doi:10.1080/00295639.2019.1672511

CrossRef Full Text | Google Scholar

Golesorkhi, S., Kelly, S., and Trottier, A. (2023). Impact of the TRISO fuel homogenisation approximation in the MHTGR. Ann. Nucl. Energy 183, 109634. doi:10.1016/j.anucene.2022.109634

CrossRef Full Text | Google Scholar

Hébert, A. (1993). A collision probability analysis of the double-heterogeneity problem. Nucl. Sci. Eng. 115 (2), 177–184. doi:10.13182/nse115-177

CrossRef Full Text | Google Scholar

Kim, Y., Kim, K., and Noh, J. (2005). Reactivity-equivalent physical transformation for homogenization of double-heterogeneous fuels.

Google Scholar

Lei, L., Dong, Y., Chai, X., Peng, X., Li, M., Li, W., et al. (2020). A novel reactivity-equivalent physical transformation method for homogenization of double-heterogeneous systems. Ann. Nucl. Energ. 142, 107396. doi:10.1016/j.anucene.2020.107396

CrossRef Full Text | Google Scholar

Lei, L., Xiaoming, C., Dong, Y., Lianjie, W., Mancang, L., Liang, C., et al. (2022). Theoretically modified optical length research on the physical boundary of the double-heterogeneous system. Front. Energy Res. 9, 773067. doi:10.3389/fenrg.2021.773067

CrossRef Full Text | Google Scholar

Li, J., She, D., and Shi, L. (2018). An improved reactivity-equivalent physical transformation for treating FCM fuel with burnable poisons. Ann. Nucl. Energ. 121 (11), 577–581. doi:10.1016/j.anucene.2018.08.024

CrossRef Full Text | Google Scholar

Powers, J. J., Lee, W. J., Venneri, F., Snead, L. L., Jo, C. K., Hwang, D. H., et al. (2013). Fully ceramic microencapsulated (FCM) replacement fuel for LWRs (No. ORNL/TM-2013/173, 1087039). doi:10.2172/1087039

CrossRef Full Text | Google Scholar

Romano, P. K., and Forget, B. (2012). The OpenMC Monte Carlo particle transport code. Ann. Nucl. Energy 51, 274–281. doi:10.1016/j.anucene.2012.06.040

CrossRef Full Text | Google Scholar

Sanchez, R., and Pomraning, G. C. (1991). A statistical analysis of the double heterogeneity problem. Ann. Nucl. Energ. 18 (7), 371–395. doi:10.1016/0306-4549(91)90073-7

CrossRef Full Text | Google Scholar

She, D., Guo, J., Liu, Z., and Shi, L. (2018). PANGU code for pebble-bed HTGR reactor physics and fuel cycle simulations. Ann. Nucl. Energ. 126, 48–58. doi:10.1016/j.anucene.2018.11.005

CrossRef Full Text | Google Scholar

She, D., Liu, Z., and Shi, L. (2017). An equivalent homogenization method for treating the stochastic media. Nucl. Sci. Eng. 185, 351–360. doi:10.1080/00295639.2016.1272363

CrossRef Full Text | Google Scholar

She, D., Xia, B., Guo, J., Wei, C. L., Zhang, J., Li, F., et al. (2021). Prediction calculations for the first criticality of the HTR-PM using the PANGU code. Nucl. Sci. Tech. 32 (9), 90–97. doi:10.1007/s41365-021-00936-5

CrossRef Full Text | Google Scholar

Terrani, K. A., Snead, L. L., and Gehin, J. C. (2012). Microencapsulated fuel technology for commercial light water and advanced reactor application. J. Nucl. Mater. 427, 209–224. doi:10.1016/j.jnucmat.2012.05.021

CrossRef Full Text | Google Scholar

Teuchert, E., Haas, K. A., Rütten, H. J., Brockmann, H., Gerwin, H., Ohlig, U., et al. (1994). V.S.O.P. (94) computer code system for reactor physics and fuel cycle simulation. Jülich, Germany: Forschungszentrum Jülich.

Google Scholar

Weng, M., Liu, S., Liu, Z., Qi, F., Zhou, Y., and Chen, Y. (2021). Development and application of Monte Carlo and COMSOL coupling code for neutronics/thermohydraulics coupled analysis. Ann. Nucl. Energy 161, 108459. doi:10.1016/j.anucene.2021.108459

CrossRef Full Text | Google Scholar

Wu, Y., Liu, S., Li, M., Xiao, P., Wang, L., and Chen, Y. (2021). Monte Carlo simulation of dispersed coated particles in accident tolerant fuel for innovative nuclear reactors. Int. J. Energy Res. 45, 12110–12123. doi:10.1002/er.6127

CrossRef Full Text | Google Scholar

Zhai, T., Kadak, A. C., and No, H. C. (2004). LOCA and air ingress accident analysis of a pebble bed reactor, MIT center for advanced nuclear energy systems. MIT-ANP-TR-102.

Google Scholar