An evolutionary planning method for distribution networks considering prosumers and shared energy storage

This research provides a rolling planning method for distribution networks, which takes into account shared energy storage capacity configuration and grid topology optimization due to the stochastic unpredictability of the planning scenarios and the interaction between multi-agents. First, the grid topology and the investment capacity of the shared energy storage are optimized by the gird company with the aim of minimizing the overall cost within the planning time scale, and a distribution network planning model that precisely satisfies the reliability requirements is built. Second, the operational utility model of prosumers is suggested based on the planning strategy of the grid company. The cooperation of grid company corporations with prosumers is established in the evolutionary game model. The differential evolution algorithm is used to realize the dynamic solution of the planning strategy by creating the replicator dynamic equation of the grid company. The IEEE-33 bus system is taken as an example for simulation analysis for demonstrating the usefulness of the suggested evolution game-based planning model, which can reduce network planning costs and system operational costs while optimizing prosumers’ load curves.

1 Introduction

The development of a new power system with renewable energy as its mainstay has emerged as the key to the modern energy system’s transformation in light of the dual carbon objective (Yu et al., 2022). Large-scale access of distributed energy makes the distribution network planning goal to change from the traditional, meeting load growth and grid development needs for alleviating the power imbalance after access of large-scale renewable energy (FU et al., 2022; Lishen et al., 2024). To decouple energy supply and demand in space and time and further encourage their complementarity, energy storage can be used as a linked energy coupling storage and conversion medium (Bai et al., 2022). Therefore, it is important to study the synergistic planning of the distribution grid structure and energy storage in the context of new power systems to enhance the consumption of renewable energy, optimize the load curve of prosumers, and reduce the grid investment cost (Li et al., 2022).

Both domestic and international research studies have been done on the planning of distribution network grid structures (Shi et al., 2019; Wang et al., 2020; HUANG et al., 2021; Li et al., 2021) and energy storage (Xu et al., 2017; Asensio et al., 2018; Wang Q. et al., 2022). For the distribution network expansion planning problem, an Euclidean–Steiner minimal tree problem is built to fit it, which is solved by the simulated annealing algorithm (Shi et al., 2019). Considering the system reliability, a multistage expansion planning model for mesh distribution networks is constructed with customized investment/reliability preferences (Li et al., 2021). In addition, uncertainties associated with demand and renewable-based power production are considered in the distribution system expansion planning problem through a set of scenarios (HUANG et al., 2021). For the energy storage planning problem, a bi-level formulation is proposed to optimize the location and size of energy storage in the market environment (Xu et al., 2017). In Wang Q. et al. (2022), the energy storage planning problem is formulated as a Bayesian distributionally robust optimization model, faced with the interrelated and uncertainty output of renewable energy on the supply side. The interaction between grid planning and energy storage configuration is modeled in a joint distribution and generation expansion problem that includes the demand response (Asensio et al., 2018). However, the aforementioned literature only takes into account the grid company’s independent planning approach with cost minimization, and there is limited research on the distribution network planning and optimization method with multi-investment entities involved.

Groups of prosumers with distributed power and demand response capabilities emerge as a result of the widespread acceptance of distributed power on the customer side and take part in the distribution grid investment planning process. A shared energy storage investment model is suggested (Dai et al., 2021) and applied to enhance system resilience (Wang Wenyong et al., 2022), stable distributed energy output (Zhao et al., 2015), and energy storage profit (Wang et al., 2014; Tushar et al., 2016). According to concept of the shared energy storage investment, the business model of shared energy storage can be divided into single-user investment, multi-user co-investment, and operator or grid company investment. The single-user investment in energy storage ownership for a single user is done when the user has the properties of the producer and consumer, and energy storage can be shared between producers and consumers through the auction mechanism (Tushar et al., 2016). However, in this investment model, a single user must invest heavily, and it is difficult to guarantee that it will be used. As a result, multiple users must invest in public energy storage, which creates a new sharing model. Liu N. et al. (2018) proposed an energy-sharing model based on public energy storage for PV prosumers, and Zhong et al. (2020) proposed a Lyapunov optimization framework-based online management method for virtual energy storage capacity in users. Although the ownership of energy storage belongs to all users, an upper-level manager is still required to coordinate the users’ capacity allocation and to ensure regular operation of the energy storage system. To address this issue, a shared energy storage business model with investments from operators or grid companies has emerged. In order to encourage market participants to honestly disclose their needs for shared energy storage leasing and increase cost recovery, a combined auction operation model is built coupled with the multidimensional parameters of shared energy storage (Wu et al., 2022). In addition, a new shared energy storage pattern named cloud energy storage is proposed (Liu J. et al., 2017; Liu J. et al., 2018), which replaces the physical energy storage on the prosumer side with virtual energy storage capacity in the cloud to enable on-demand use of grid-level shared energy storage resources by prosumers. Thereby, users will not have to pay the cost of the investment, but operators will have to deal with the risk associated with both the investment and operation. As a result, a challenging issue in the current research is how to realistically plan the shared energy storage investment capacity while lowering the risk associated with the uncertainty of multiple sources in medium- and long-term planning.

In conclusion, the majority of current studies on distribution network planning concentrate on the investment cost–benefit model of grid companies, ignoring the impact of prosumers’ energy-sharing modes on the planning process, while only a small number of companies dynamically take prosumers’ dispatching strategies into account in the planning process to achieve rolling optimization of the planning strategy under uncertainty. Accordingly, this paper proposes a differential evolutionary algorithm under the evolutionary game based on this and dynamically corrects the planning strategy to find the best solution through the two processes of planning. The evolutionary game emphasizes the dynamic evolutionary process in which a finite number of rational participants repeat the game through continuous learning. In this paper, we propose a distribution grid evolution planning method that takes into account two types of interests: grid companies and prosumers with photovoltaics (PV) and storage. This method accounts for the uncertainty of prosumers’ load and PV increment. The contribution of this paper can be summarized in the following three points.

1) A distribution network evolutionary planning framework is constructed that considers energy-sharing between prosumers and grid companies. The energy-sharing behavior between prosumers is considered in the planning process, and the energy consumption preference is considered in the operation model of prosumers.

2) A dynamic programming model based on the evolutionary game theory is proposed, which can dynamically modify the planning strategy through planning optimization and dynamic evolution and realize the rolling optimization of the planning strategy under the uncertainty prediction error.

3) A differential evolution algorithm is proposed to solve the proposed dynamic programming model. The IEEE-33 bus system is used as an example to demonstrate the effectiveness of the model suggested in this paper.

2 A bi-level planning and operation framework

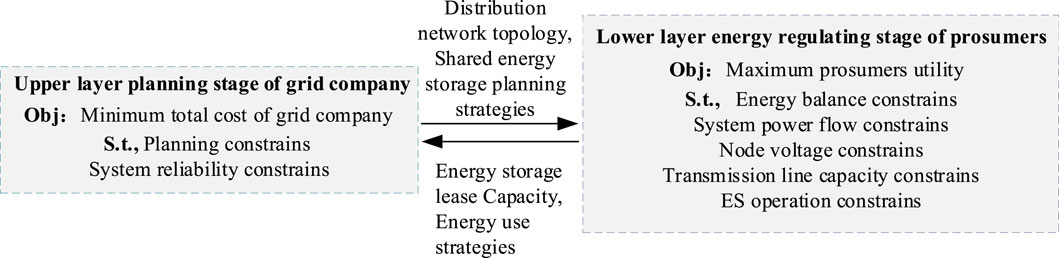
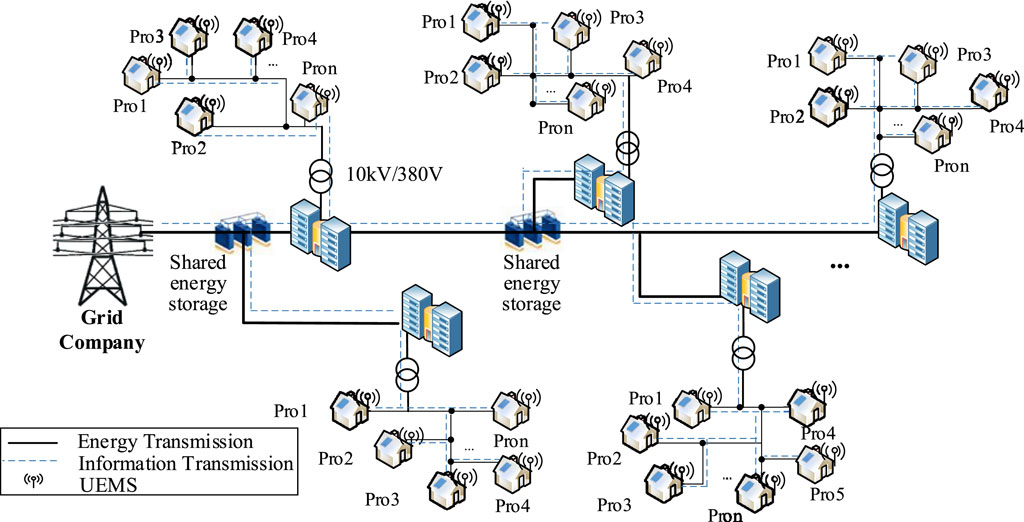
The bi-level planning and operation optimization framework, which considers the interaction between the planning strategy of the grid company and the energy dispatch strategy of the prosumers, is shown in Figure 1. The research object of this paper is the 10-kV voltage level regional distribution network, and the schematic diagram of the research object is shown in Figure 2. At the same time, taking into account factors such as distribution network structure planning and system operation reliability, the grid company is set as the investor of the shared energy storage. The upper layer of the model is the grid company, which optimizes the distribution network structure and the shared energy storage capacity of each node with the goal of minimizing the total planning cost, and the planning process of the grid company is constrained by the investment capacity and system reliability. Based on the grid company’s planning strategy, the prosumers at the lower nodes optimize their energy storage leasing capacity and energy utilization strategy to maximize the benefits. At the same time, prosumers need to meet the constraints of their own energy balance, energy storage operational constraints, and the constraints of the safe and stable operation of the system. Prosumers lease shared energy storage to the grid company to bring part of the revenue to the grid company; in addition, there is a purchase and sale of electricity between the prosumers and the grid company, which affects the total cost of the grid company. The investment of the grid company in the construction of shared energy storage capacity in each node affects the upper limit of the capacity of the prosumers’ leased energy storage, which in turn changes the energy consumption strategy of the prosumers.

Figure 1

Figure 1. Bi-level planning and operation framework.

Figure 2

Figure 2. Diagram of the 10-kV network in the research.

3 Grid-side energy storage configurations

3.1 Objective function

The grid company plans the network topology of the distribution network with the shared energy storage investment capacity at each node, and its objective function within the planning stage k can be expressed as follows:

$P_k=P_k^{\text{ESS}\text{inv}}+P_k^{\text{line}\text{inv}}+P_k^{main}-{\sum }_{y=1}^{{\mathrm{Y}}_k}{I}_{k,y}^{grid},(1)$

where $P_k$ is the cost function of the grid company in the planning period k; $P_k^{\text{ESS}\text{inv}}$ is the annual equivalent cost of the shared energy storage investment cost within the planning period k; $P_k^{\text{line}\text{inv}}$ is the annual equivalent cost of the line investment cost within the planning period k; $P_k^{main}$ is the annual equivalent cost of the operation and maintenance cost within the planning period k; $I_{k,y}^{grid}$ is the operational benefit of the interaction between the grid company and the prosumers in year y; and Y_k is the number of years to be considered within the planning period k.

In the equation, the annual equivalent investment cost can be expressed as

$P_k^{\text{ESS}\text{inv}}={\sum }_i{\mathrm{\lambda }}_{ESS}{C}_{k,i}^{ESS}\cdot \frac{\mathrm{r}{\left(1+\mathrm{r}\right)}^{{\mathrm{m}}_{\text{ESS}}}}{{\left(1+\mathrm{r}\right)}^{{\mathrm{m}}_{\text{ESS}}}-1}(2)$

$P_k^{\text{line}\text{inv}}={\sum }_i{\mathrm{\lambda }}_{\text{line}}{L}_k^{ij}\cdot \frac{\mathrm{r}{\left(1+\mathrm{r}\right)}^{{\mathrm{m}}_{\text{line}}}}{{\left(1+\mathrm{r}\right)}^{{\mathrm{m}}_{\text{line}}}-1}(3)$

where ${\mathrm{\lambda }}_{ESS}$ and ${\mathrm{\lambda }}_{\text{line}}$ are the fixed investment costs of investing in shared energy storage per unit capacity and building new lines per unit length, respectively; $C_{k,i}^{ESS}$ is the shared energy storage capacity of investment node i in the kth planning stage; $L_k^{ij}$ is the length of the new line between nodes i and j in the kth planning stage; r is the discount rate; and m_ESS and m_line are the useful lives of the energy storage and the line, respectively.

The annual equivalent maintenance cost can be expressed as

$P_k^{main}={\mathrm{\mu }}_1\cdot P_k^{\text{ESS}\text{inv}}+{\mathrm{\mu }}_2\cdot P_k^{\text{line}\text{inv}}(4)$

where μ1 and μ2 are the proportionality coefficients between energy storage and line investment costs and maintenance costs, respectively.

The grid company sets the lease price of the shared energy storage capacity and the cost of charging and discharging usage based on technical and economic analyses. The prosumers purchase energy storage capacity based on electricity usage strategy analysis and issue charging and discharging commands to the shared energy storage capacity purchased based on its own energy storage usage demand in actual operation.

The revenue of the transaction between the grid company and the prosumers is derived from the revenue of the purchase and sale of electricity between the grid company and the prosumers, as well as the fees paid by the prosumers for leasing the shared energy storage capacity and using the energy storage:

$I_{k,y}^{grid}={\sum }_{i=1}^N\left\{\frac{365}{\mathrm{S}}\cdot {\sum }_{s=1}^S{\sum }_{t=1}^T\left(\begin{array}{l}{\lambda }_{k,t,s}^{buy}{E}_{y,i,t,s}^{gb}-{\lambda }_{k,t,s}^{sell}{E}_{y,i,t,s}^{gs}\\ +{\lambda }_k^{ESS}\left|E_{y,i,t,s}^{ESS}\right|\end{array}\right)+{\lambda }_k^{ESS\_C}{C}_{k,y,i}^{ESS}\right\}(5)$

where S is the number of typical scenarios. This paper forms several typical scenarios based on the historical data of consumers and producers through the K-means clustering method. ${\lambda }_k^{ESS}$ and ${\lambda }_k^{ESS\_C}$ are the storage capacity tariffs and electricity tariffs, respectively. $E_{y,i,t,s}^{gb}$ and $E_{y,i,t,s}^{gs}$ are the load deficits and feed-in tariffs of prosumers at node i at stage k, respectively. $C_{k,y,i}^{ESS}$ and $E_{y,i,t,s}^{ESS}$ are the capacity of the prosumers leasing shared energy storage at node i in year y under phase k and the charging and discharging amount of the energy storage in each time period, respectively.

3.2 Planning constraints

Limitations on the scale of investment in energy storage equipment, taking into account the limitations of construction space and investment costs:

${\mathrm{C}}^{\text{ESS}\_\min }\le C_i^{\text{ESS}}\le {\mathrm{C}}^{{\text{ESS}}_{\max }}(6)$

where C^ESS_max and C^ESS_min are the upper and lower limits of the installed capacity of the node energy storage, respectively.

At the same time, the total energy storage capacity leased annually by all prosumers shall be no greater than the shared energy storage capacity planned by the grid company:

${\sum }_{i=1}^N{C}_{k,y,i}^{\text{ESS}}\le C_k^{\text{ESS}}(7)$

For each planning phase, the next phase is based on the realized planning of the previous phase:

$C_{k-1}^{\text{ESS}}\le C_k^{\text{ESS}}(8)$

$L_{k-1}^{ij}\le L_k^{ij}(9)$

The routes constructed shall be in the buildable route planning set with the following constraints:

$L_k^{ij}=0,ij\notin \mathrm{\Phi }(10)$

where $\mathrm{\Phi }$ is the set of all plannable line solutions, i is the line start point, and j is the line end point.

For the load nodes in the distribution network, their node failure characteristics can be represented by node failure rate and node failure duration. In this paper, the Monte Carlo sampling method is used to evaluate and analyze the system reliability, and the system average interruption frequency index (SAIFI), system average interruption duration index (SAIDI), and average service availability index (ASAI) are selected and constrained as the reliability evaluation indexes for distribution network planning:

$SAIFI=\frac{\sum {\pi }_i\cdot N_i}{N_i}\le SAIF{I}_{\max }(11)$

$SAIDI=\frac{\sum D_i\cdot N_i}{N_i}\le SAID{I}_{\max }(12)$

$ASAI=\frac{8760-SAIDI}{8760}\ge ASA{I}_{\min }(13)$

where N_i is the number of consumers connected to node i; ${\pi }_i$ is the outage rate of load node i; D_i is the outage time of load node i; SAIFI_max, SAIDI_max, and ASAI_min are the maximum SAIFI and SAIDI and minimum ASAI constraints, respectively, under reliable operation of the distribution network.

4 Prosumer operational benefit model

4.1 Objective function

With the objective of maximizing their own benefits, prosumers decide on the annual lease capacity, the charge and discharge energy of energy storage in each time period, and the flexible load based on the time-sharing tariff of the distribution network, which is calculated as follows:

$\max U_i=\frac{365}{\mathrm{S}}{\sum }_{s=1}^S{\sum }_{t=1}^T\left({\lambda }_{k,t,s}^{sell}\cdot E_{k,i,t,s}^{gs}-{\lambda }_{k,t,s}^{buy}\cdot E_{k,i,t,s}^{gb}-{\lambda }_k^{ESS\_ch}\cdot \left|E_{k,i,t,s}^{ESS}\right|+{\omega }_{i,t}\cdot \ln \left(1+E_{k,i,t,s}^{load}\right)\right)-{\lambda }_k^{ES{S}_C}\cdot C_{k,y,i}^{ESS}(14)$

where U_i is the objective function of prosumers at node i. $\ln \left(1+E_{k,i,t,s}^{load}\right)$ denotes the utility of prosumers at node i in time t. Prosumers have different preferences for load consumption at different times, and the diverse preferences are considered in the form of preference coefficients in the utility function (Ma et al., 2019).

4.2 Operational constraints

To ensure the stable operation of the distribution network, the following constraints should be satisfied:

The energy balance constraints of prosumers can be expressed as

$\left\{\begin{array}{l}{E}_{y,i,t,s}^{gb}+E_{y,i,t,s}^{ESS}+E_{y,i,t,s}^{PV}=E_{y,i,t,s}^{load}i\in N_b\\ E_{y,j,t,s}^{gs}+E_{y,j,t,s}^{ESS}+E_{y,j,t,s}^{load}=E_{y,j,t,s}^{PV}j\in N_s\end{array}\right.(15)$

where $E_{k,i,t,s}^{ESS}$ is the charging and discharging state of prosumers at node i, where the charging state is positive and the discharging state is negative. $E_{k,i,t,s}^{\text{load}}$ is the demand of prosumers at node i in time t. $E_{k,i,t,s}^{PV}$ is the PV output of prosumer i at time t.

System power flow constraints:

$\left\{\begin{array}{l}{P}_i=U_i^0{\sum }_{j=1}^n{U}_j^0\left(G_{ij}\cos {\theta }_{ij}+B_{ij}\sin {\theta }_{ij}\right)\\ Q_i=U_i^0{\sum }_{j=1}^n{U}_j^0\left(G_{ij}\sin {\theta }_{ij}-B_{ij}\cos {\theta }_{ij}\right)\end{array}\right.(16)$

where $P_i$ and $Q_i$ are the active and reactive powers injected at node i, respectively; $U_i^0$ and $U_j^0$ are the voltage amplitude of nodes i and j, respectively; $G_{ij}$ and $B_{ij}$ are the electrical conductance and susceptance values of branch ij, respectively; and ${\theta }_{ij}$ is the voltage phase angle difference between nodes i and j.

Node voltage constraint:

$U^{\min }\le U_i^0\le U^{\max }(17)$

where U^max and U^min are the upper and lower limits of node voltage amplitude, respectively.

Transmission line capacity constraint:

$S^{\min }\le S_i\le S^{\max }(18)$

where S^max and S^min are the upper and lower limits of transmission line power transmission, respectively.

Energy storage operational constraints:

$0\le \left|E_{y,i,t,s}^{ESS}\right|\le E^{ESS,\max }(19)$

$0\le {{\displaystyle \sum }}_{i=1}^N{Q}_{y,i,t,s}\le C_{k,y,i}^{ESS}(20)$

$SO{C}_{y,t,s}=SO{C}_{y,t-1,s}-\frac{{{\displaystyle \sum }}_{i=1}^N\left\{\max \left(0,{\eta }_0\cdot E_{y,i,t,s}^{ESS}\right)+\min \left(0,\frac{E_{y,i,t,s}^{ESS}}{{\eta }_0}\right)\right\}}{C_k^{ESS}}(21)$

$SO{C}_{\min }\le SO{C}_{y,t,s}\le SO{C}_{\max }(22)$

where E^ESS,max is the upper limit of the charge/discharge energy of the energy storage. Considering the safe operation of the energy storage, its charge/discharge energy cannot exceed E^ESS,max. Q_k,t,s is the capacity of the shared energy storage at time t. SOC_k,t,s is the charge state of the shared energy storage at time t, which is the ratio of its current capacity to the rated capacity. SOC_max and SOC_min are the upper and lower limits of the charge state of the energy storage, respectively. η0 is the charging and discharging efficiency of the energy storage.

5 Differential evolutionary solution algorithm under an evolutionary game

5.1 Basic model of the evolutionary game

Evolutionary games emphasize the dynamic evolutionary process in which a finite and rational participant population repeats the game through continuous learning, i.e., participants can dynamically evolve by repeating the game through continuous learning. In this paper, the demand-side prosumers in the medium and long term are affected by economic conditions and climate change, so the upper layer planning process of the grid company needs to take into account the dynamic change process of the demand side. The dynamic evolution process of the set of planning strategies under multisource uncertainty is similar to the evolution process, so this paper proposes a differential evolution algorithm under the evolution game. The dynamic correction of the planning strategies is carried out through the two processes of optimization of the planning and dynamic evolution, which are used to realize the rolling optimization of the planning strategies under the prediction error of uncertainties.

Based on the three basic elements of the evolutionary game (participants, strategy set, and payment function), the evolutionary game model between the grid company and demand-side prosumers is constructed.

5.1.1 Participants

In this paper, we consider one participant, i.e., the grid company. Since the planning strategy is formulated by the grid company, the operational scheduling strategy of the prosumers considered in the planning process is formed by the forecast of the grid company, which is modified according to the actual situation in the evolution process. The subject of the grid company game is mapped to the population P in the evolutionary game, and there are multiple individuals in the population P, which corresponds to different planning strategies under different stochastic scenarios, and the individuals generate differentiated decisions based on their respective payment functions.

5.1.2 Strategy set

The grid company maximizes its own revenue by planning the shared energy storage capacity at each stage, and the distribution grid network structure. The demand-side prosumers adjust the flexible load, the leasing capacity, and the storage charging and discharging strategies based on the planning strategy to achieve the maximum utility. Each individual of population P randomly generates multiple sets of decision strategies under the constraints, where the set of strategies generated by P is denoted as S. There are S strategies in S, and S can be expressed as

$\mathbf{S}=\left\{{\mathbf{C}}^{ESS},\mathbf{L}\right\}(23)$

5.1.3 Payment function

The payment function in the evolutionary game represents the cost paid by the participant in selecting the current strategy. In the framework of the evolutionary game constructed in this paper, the population P payment function is the utility function P in Eq. 1.

5.2 Dynamic characteristics of the evolutionary game

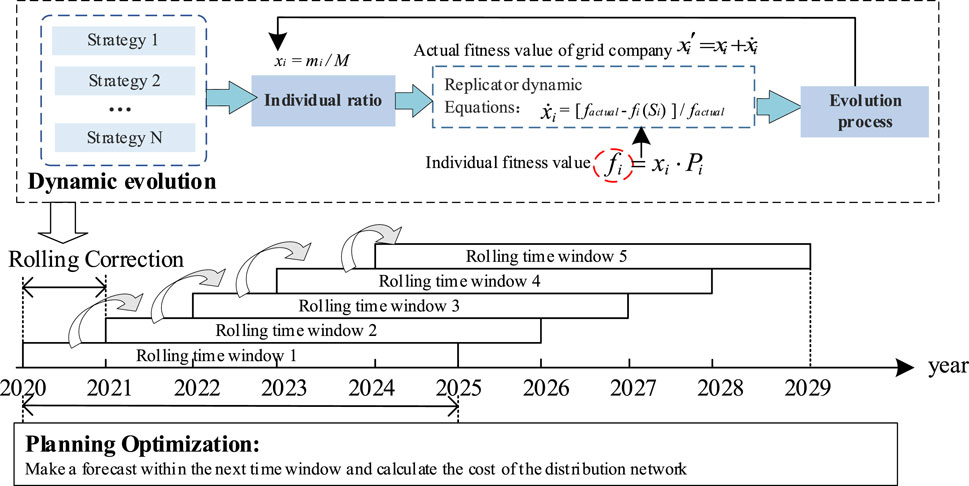
The decision process of participants in the evolutionary game has dynamic characteristics, where participants can evolve dynamically by continuously learning to repeat the game. In this paper, the demand-side prosumers’ behavior of electricity consumption in the long term is affected by economic conditions and climate change. So the upper-level planning process of the grid company needs to consider the dynamic change process of the demand side, so the rolling decision behavior of the grid company is modeled as a replicator dynamic equation for analysis (Harper, 2011).

The number of individuals choosing strategy S_i in the population at moment t is x_i, and the proportion of the number of individuals to the total number of individuals in the population x_i is chosen as the state variable, which can be expressed as

$x_i=\frac{m_i}{M}(24)$

where m_i is the number of individuals selecting strategy S_i, and when the proportion of individuals is 0, it means that the individual is declining and ${\sum }_{i=1}^S{x}_i=1$.

Considering the uncertainty of prosumers’ load and PV growth in long-term planning, the optimal strategy for the current time period is obtained by constructing a dynamic equation for the grid company and the dynamic evolution of different individual strategy choices within the grid company, where the individual average fitness function f_i for selecting strategy S_i in the advance planning process of the grid company can be expressed as

$f_i=x_i\cdot P_{S_i}(25)$

The fitness function f_actual is the grid company’s utility function expressed in Eq. 1.

Differentiation of the population state variables in evolution time: since the fitness function is the grid company utility function, if the individual fitness of the selection strategy S_i is greater than the actual fitness, the individual growth rate of the selection strategy is negative. The difference equation between the grid company dynamic equation and the individual occupancy rate can be expressed as

$\dot{x}=\left[f_{actual}-f_i\left(s_i\right)\right]/f_{actual},i\in \left\{1,2,...,N\right\}(26)$

$x\left(t+1\right)=\dot{x}+x\left(t\right)(27)$

where the time granularity of t is the optimization year, which is set to 1 year in this paper. In Eq. 25, the evolutionary process of the individual share of the strategy from year to year is presented.

The planning strategies of the grid company will eventually stabilize, and the evolutionary game will eventually reach a stable equilibrium state. The stable equilibrium strategy of the evolutionary game is defined as follows:

For $\forall \delta \in \mathit{S}$ and $\delta \ne S_i$, there exists some positive number ${\overline{\epsilon }}_{\delta }\in \left(0,1\right)$, such that the population fitness function f of the selection strategy S_i satisfies

$f\left[S_i,\epsilon \delta +\left(1-\epsilon \right)S_i\right]>f\left[\delta ,\epsilon \delta +\left(1-\epsilon \right)S_i\right]\forall \epsilon \in \left(0,{\overline{\epsilon }}_{\delta }\right)(28)$

At this point, the strategy S_i is the evolutionary stable strategy of the grid company.

5.3 Differential evolution algorithm-based solving process

The primary analytical mechanism that sets apart the evolutionary game from traditional games’ static Nash equilibrium analysis is its emphasis on the dynamic nature of the players’ choosing strategies. In contrast to other heuristic algorithms, this method can alter strategies dynamically based on the discrepancy between actual and predicted data. Traditional uncertainty is frequently transformed into a deterministic problem for the best possible solution in a probabilistic manner, and the probability distribution is frequently out of sync with the actual lack of accuracy, while the uncertainty is more challenging to accurately predict in the face of long-term forecasts. To overcome the aforementioned difficulty to evaluate the uncertainty problem, this research proposes a differential evolution algorithm within an evolutionary game that evolves dynamically from year to year.

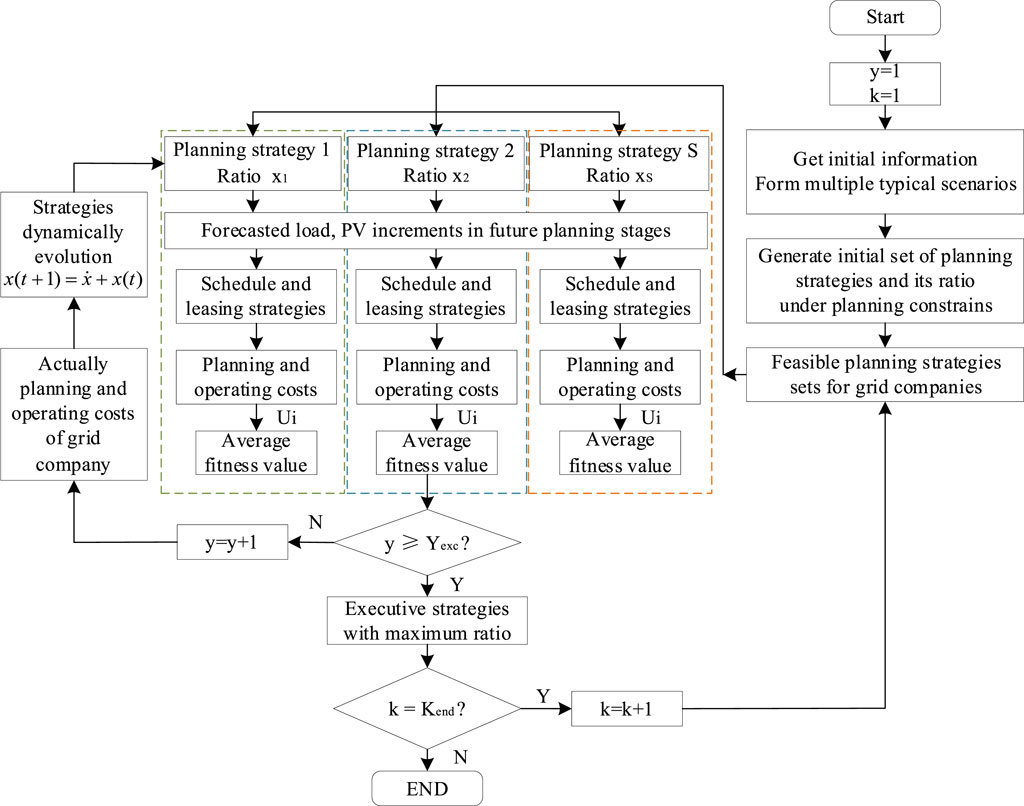
This paper divides the entire planning time frame into multiple planning stages using the differential evolution algorithm, which is based on the evolutionary game framework and includes two processes of planning optimization and dynamic evolution. At the beginning of the entire planning time frame, the grid company initially generated multiple sets of planning strategies. When the initial set of strategies cannot meet the planning constraints (5)–(13), this strategy is eliminated, where m_i = x_i = 0. The grid company chooses and implements the current optimal planning strategy in the first year of each phase. Performing planning optimization and dynamic optimization processes in the subsequent years of each planning stage was done to continuously improve the optimal planning strategy. The planning process is schematically depicted in Figure 3, and the specific solution process is depicted in Figure 4.

Figure 3

Figure 3. Schematic diagram of the rolling planning process.

Figure 4

Figure 4. Flowchart for the proposed solution algorithm under the evolution game.

The planning optimization process refers to the prediction of load and PV increment in the subsequent forecast cycle based on the known distribution network topology and prosumers’ load. Under the constraints of Eqs 15–22, the demand-side prosumers’ operation strategies are simulated with Eq. 14 with the aim of maximizing prosumers’ benefits. Eq. 1 yields the value of the grid company’s utility function, which is the value of the fitness function for selecting each individual strategy in the evolutionary game, under multiple planning strategies in this forecast cycle.

In order to minimize deviations from the optimal solution caused by prediction errors on uncertain factors, the grid company's planning strategy must be adjusted as much as possible. The dynamic optimization process is conducted yearly, where the gap between the actual value and the predicted value is taken into account. The individual share in the strategies set is adjusted and evaluated according to Eq. 27. The aforementioned evolutionary process is continuously repeated until the current planning stage is completed.

6 Case study

6.1 Case description

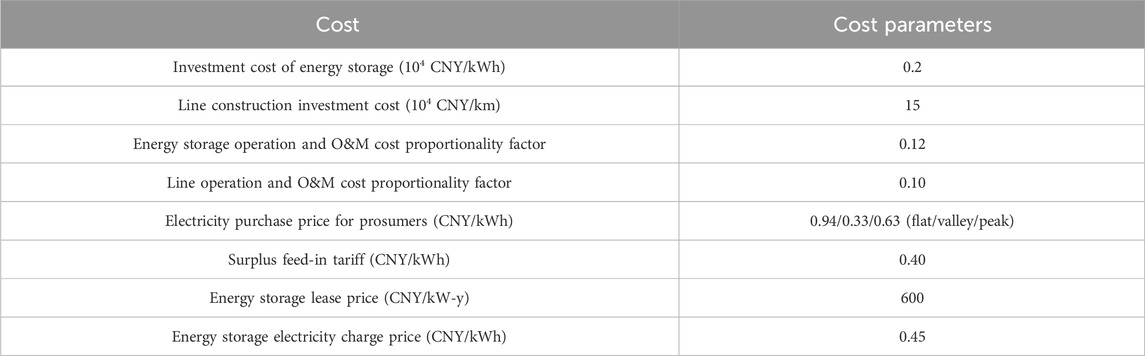
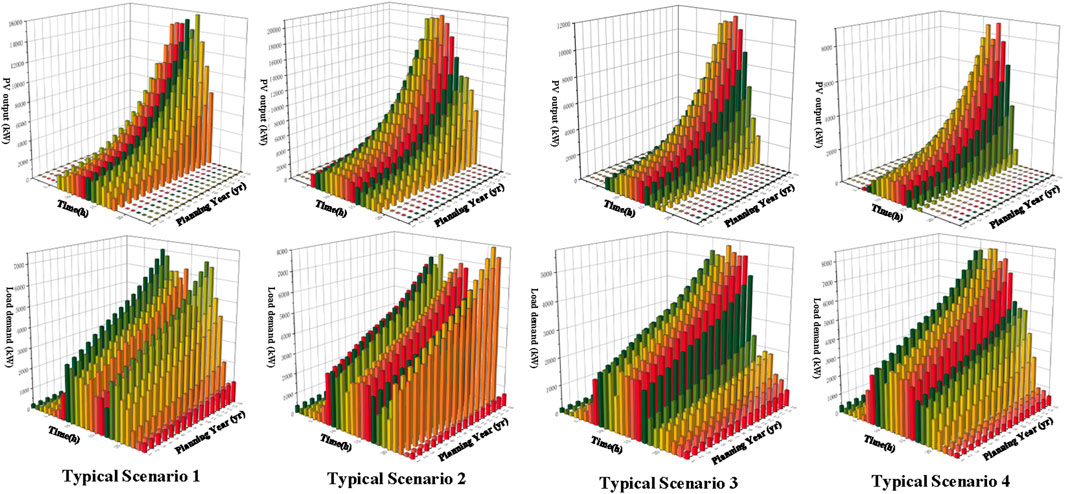
In this paper, the IEEE-33 bus distribution system is used to verify the effectiveness of the model proposed in this paper. The case study is implemented by a computer with Intel Core i5-1135G7 CPU 2.40 GHz, 16 G memory, and MATLAB 2017a was used as the test environment. The service life of shared energy storage and construction of 110 kV lines is 20 years, and the relevant cost parameters are shown in Table 1 (Chen et al., 2016; Han et al., 2016; Liu H. et al., 2022; Ma et al., 2022). The energy storage charging and discharging efficiency is set to 0.95, the initial SOC is 0.5, and the charging and discharging depth is limited to 10%–90%. Based on the actual data of the demand-side prosumers’ net load of the distribution network for clustering analysis, the typical days were selected in turn to form four typical planning scenarios. The growth trend of the prosumers’ load and prosumers’ self-built PV in 15 years was assumed based on the load prediction results, as shown in Figure 5. The growth trend of the consumer load and consumer-built PV in 15 years was assumed based on the load prediction results, as is shown in Figure 5, where the annual growth rate of the load increased to 9.46% (Ahyeji, 2024), and the annual growth rate of PV grew 13.68% from 2020 to 2025, 8.75% from 2025 to 2030, and 6.07% from 2030 to 2035 (Zhang, 2021).

Table 1

Table 1. Parameter setting of the case study.

Figure 5

Figure 5. Annual growth tendency of prosumers’ load and self-built PV under the typical scenario.

6.2 IEEE-33 bus system case analysis

6.2.1 Grid company planning strategy

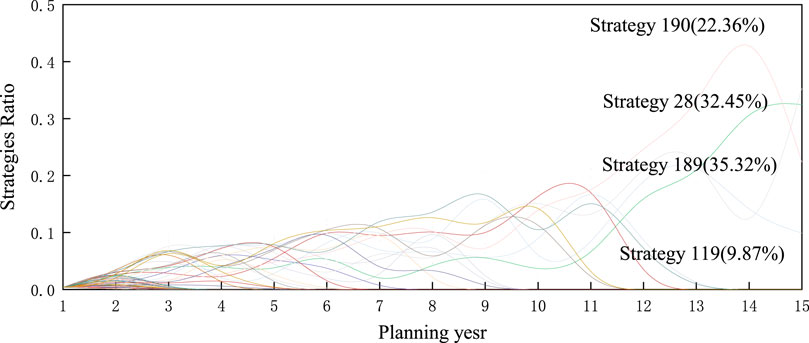
In this paper, a differential evolutionary algorithm is used to solve the planning decision of the grid company considering the dynamic changes of the prosumers’ decision, and the distribution grid topology and the shared energy storage investment capacity and situation are randomly generated. A total of 255 initial strategy sets are set, the evolution time is set to 15 years, and the evolution time interval is 1 year. The 255 strategy sets correspond to the initial year planning of the grid company in each planning stage, and the evolution process of the planning strategy in the evolution game is shown in Figure 6. This paper assumes that the initial percentage of each strategy is the same. With the evolution of the game, individuals with survival advantages will maintain a positive growth trend with the evolution, and individuals with survival disadvantages show a negative growth trend. The grid company in each planning stage of the initial year selected the highest percentage, that is, the current optimal strategy implementation, and finally, in the 15-year evolution process, only three individual strategies survived, with strategy numbers and percentage ratios of 190 (22.36%), 28 (32.45%), 189 (35.32%), and 119 (9.87%), respectively. The final grid companies’ planning results for shared energy storage are shown in Table 2.

Figure 6

Figure 6. Population evolution process.

Table 2

Table 2. Planning strategy of shared energy storage.

As can be seen from Table 2, the storage capacity of stage 2 is significantly reduced compared with that of stage 1 and stage 3. In the method presented in this paper, the installed capacity of stage 2 is reduced by 12.51% compared with that of stage 1; this is a 27.03% reduction in capacity compared to stage 3. This is because, at stage 1, PV is growing at a large scale, and the load is growing at a smaller rate than that of of PV growth. At this stage, the storage can absorb the excess PV and participate in market arbitrage, thus obtaining greater profits. At stage 2, the load is still increasing, and as distributed PV becomes more and more popular, the additional energy storage capacity is reduced, and the cost of energy storage installation is higher than the income of energy storage arbitrage.

In addition, the planning stage 1 strategies are selected to analyze the system reliability. The system reliability indexes SAIFI, SAIDI, and ASAI are calculated to be 1.46 times y, 15.23 h y, and 99.83%, respectively.

6.2.2 Prosumer operational strategies

The load distribution of demand-side prosumers under different planning scenarios is used to analyze the influence of the planning strategies on the operational strategies of prosumers. In this paper, a typical scenario 2 of the load distribution of the prosumer at node 3 in year 1, year 6, and year 15 is selected as an example. Since the study is about the operation and scheduling strategy of the same node-generator under different planning time scales, its initial net load has the same trend within 24 h, but the power increases according to a certain trend.

As shown in Figure 7, the net load of the prosumer decreases significantly in 1–5 h and 19–23 h. Due to the configuration of the energy storage, prosumers charge in the low-load period 6 h–7 h and in the high PV generation periods 11–12 h and 14–15 h and discharge at the peak load periods 8–13 h and 19–22 h. At the same time, the prosumers schedule the flexible load during the day so that its load peaks are effectively reduced, in which the prosumers’ load peaks are reduced by 717, 1,041, and 2,627 kW in years 1, 6, and 15, respectively. In addition, the peak–valley difference of the prosumers’ load is further reduced, in which the prosumers’ load peaks are reduced by 1781.68, 1,090.85, and 2,627 kW in years 1, 6, and 15, respectively. The peak and valley differences of prosumers’ loads are further reduced, which are reduced by 1781.68, 1,090.85, and 1779.08 kW in years 1, 6, and 15, respectively.

Figure 7

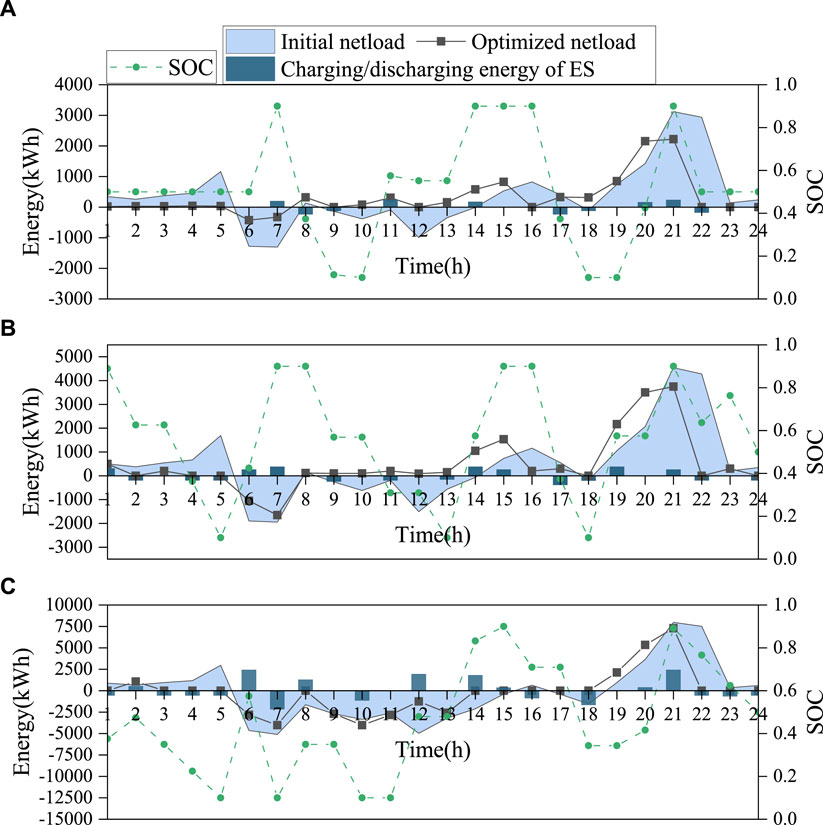
Figure 7. Prosumers’ energy scheduling strategies (A) in the planning year 1; (B) in the planning year 6; (C) in the planning year 15.

6.2.3 Comparison case

To verify the effectiveness of the proposed collaborative dynamic planning method and the evolutionary game method, two cases are set as follows:

Static planning method: the static planning model of grid company and prosumers under the Stackelberg game (Liu H. et al., 2017).

Single planning entities: the planning optimization model considering only the planning cost and operational reliability in the grid side, ignoring the participation of prosumers (Liu S. et al., 2022).

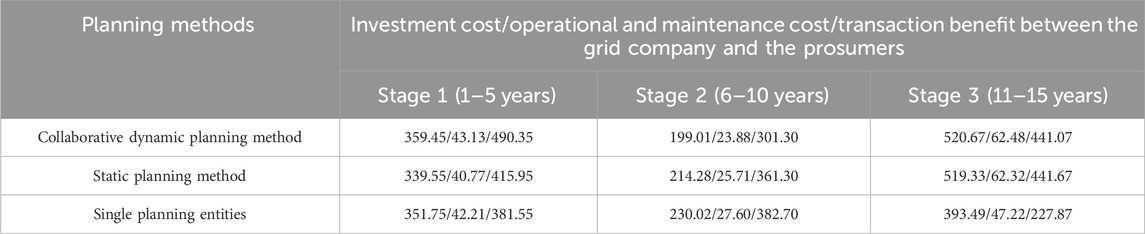
The planning strategies of the grid company under the two cases are shown in Table 3. The comparison of the planning cost is shown in Table 4.

Table 3

Table 3. Shared energy storage planning strategy.

Table 4

Table 4. Comparison of planning costs of shared energy storage.

The total cost of planning under the static planning method case and single planning entity case is −16.97 and 1.018 million RMB, respectively, in the planning years. The total cost of the grid company is reduced by 7.13 million RMB for the planning methods proposed by this paper compared to the planning strategies in the static planning method case. However, the investment cost of the proposed planning method is higher than that of the static planning method case by 6.67 million RMB, as can be seen from Table 2. The investment capacity of the proposed planning methods in planning stage 1 is larger than that of the static planning method case, indicating that in the early investment process, the proposed planning methods paid more investment cost. However, considering the increase of prosumers’ load and PV in the later stage, the grid company can get higher revenue from leasing by prosumers, thus reducing the total planning cost.

Comparing the proposed planning methods and the single planning entities without considering the operation strategies of the prosumers, when the prosumers’ operation is not considered, the grid company only considers the investment and maintenance cost and reliability requirements, the shared energy storage investment capacity under the single planning entities case is reduced by 6.52 MW compared with that of the proposed planning methods, and the investment and maintenance cost is reduced by 1.163 million RMB. However, because the energy storage invested on the grid side is only used for load smoothing on the grid side, the benefits of prosumers are not taken into account, so the revenue obtained by the grid company from the prosumers side in the single planning entity case is 2.460 million RMB less than that in the proposed case. The total cost of the grid company in the planning period is 1.427 million RMB higher than that in the proposed case.

Based on the comparison between cases, it can be seen that when the cost of shared energy storage decreases, the grid company tends to invest in larger capacity energy storage equipment, but its cost–benefit is affected by the investment cost and is also related to the leasing strategy of the prosumers. When it is difficult for prosumers to self-balance their energy, they tend to lease a certain capacity of energy storage from the grid company to cut the high cost of buying electricity directly from the grid. In addition, the self-provided PV capacity owned by prosumers is often affected by weather factors and has strong volatility and uncertainty. In order to avoid the uncertainty of self-provided PV capacity for their energy self-balancing, consumers tend to choose to lease a certain capacity of energy storage to ensure their scheduling flexibility, and the higher the generation ratio, the more capacity is leased by prosumers.

7 Conclusion

The paper proposes a rolling planning method for a distribution network considering shared energy storage capacity allocation and grid structure optimization. A capacity planning strategy for shared energy storage is constructed for prosumers based on their load demand. To address long-term uncertainty from prosumers, a population dynamic equation for grid companies is built considering the uncertainties from prosumers. From the simulation results, it is concluded that the method can reduce the planning cost of the grid company and reduce the peak load and the peak-to-valley difference of the system while satisfying the reliability and safety constraints. At the same time, the proposed rolling planning method based on the evolutionary game can be used for the formulation and modification of the rolling optimization strategy considering any dynamic uncertainty. However, there is a mutual influence on the behavior of leasing and shared energy storage between prosumers, and this paper lacks consideration of the interactions of the behavior between prosumers. Furthermore, the planning strategy of the grid company in this paper ignores the social behavior of prosumers, and it will be a future research direction to consider such uncertainty in the planning method.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

JH: writing–original draft and writing–review and editing. XF: writing–original draft and writing–review and editing. ZC: writing–review and editing and writing–original draft. PH: investigation and writing–review and editing. HZ: investigation and writing–review and editing. YC: writing–review and editing. NL: supervision and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

Authors JH and XF were employed by State Grid Hebei Economic and Technological Research Institute Co., Ltd. Authors ZC, PH, and HZ were employed by State Grid Hebei Electric Power Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The authors declare that this study received funding from the Technology Project (Research on key technologies of digital active power Grid Intelligent planning in Xiongan New Area) of Hebei Electric Power Company with No. SGHEJY00GHJS2000103. The funder had the following involvement in the study: Hebei Electric Power Company was involved in the study design, collection, analysis, interpretation of data, and the writing of this article through the authors ZC, PH, and HZ.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahyeji (2024). Liuan city yeji district electricity special planning (2016-2030) liu'an city yeji district people's government (ahyeji.gov.cn).

Google Scholar

Asensio, M., Meneses de Quevedo, P., Muñoz-Delgado, G., and Contreras, J. (2018). Joint distribution network and renewable energy expansion planning considering demand response and energy storage—Part I: stochastic programming model. IEEE Trans. Smart Grid 9 (2), 655–666. doi:10.1109/tsg.2016.2560339

CrossRef Full Text | Google Scholar

Bai, J., Zhao, Y., Jiang, H., Wei, M., and Yu, S. (2022). Load frequency control of power system with energy storage based on disturbance observer. Energy Rep. 8 (8), 615–622. doi:10.1016/j.egyr.2022.09.181

CrossRef Full Text | Google Scholar

Chen, J., Liu, Y., Zhang, W., and Bao, G. (2016). Analysis of multi-level microgrid optimal configuration in distribution network based on game theory. Power Syst. Autom. 40 (01), 45–52. doi:10.7500/AEPS20150130005

CrossRef Full Text | Google Scholar

Dai, R., Esmaeilbeigi, R., and Charkhgard, H. (2021). The utilization of shared energy storage in energy systems: a comprehensive review. IEEE Trans. Smart Grid 12 (4), 3163–3174. doi:10.1109/tsg.2021.3061619

CrossRef Full Text | Google Scholar

Fu, X., Wu, X., Zhang, C., Fan, S., and Liu, N. (2022). Planning of distributed renewable energy systems under uncertainty based on statistical machine learning. Prot. Control Mod. Power Syst. 7 (1), 41. doi:10.1186/s41601-022-00262-x

CrossRef Full Text | Google Scholar

Han, X., Wang, L., Gao, B., and Xiu, X. (2016). Power planning for grid-connected optical storage microgrid system based on cost and benefit analysis. J. Electr. Eng. Technol. 31 (14), 31–39+66. doi:10.3969/j.issn.1000-6753.2016.14.004

CrossRef Full Text | Google Scholar

Harper, M. (2011). Escort evolutionary game theory. Phys. D. Nonlinear Phenom. 240 (18), 1411–1415. doi:10.1016/j.physd.2011.04.008

CrossRef Full Text | Google Scholar

Huang, Y., Lin, Z., Lin, X., Yang, L., Dan, Y., Zhu, Y., et al. (2021). Bi-Level coordinated planning of active distribution network considering demand response resources and severely restricted scenarios. J. Mod. Power Syst. Clean Energy 9 (5), 1088–1100. doi:10.35833/mpce.2020.000335

CrossRef Full Text | Google Scholar

Li, P., Ji, J., Chen, S., Ji, H., Xu, J., Zhao, J., et al. (2022). Multi-stage expansion planning of energy storage integrated soft open points considering tie-line reconstruction. Prot. Control Mod. Power Syst. 7 (1), 45. doi:10.1186/s41601-022-00268-5

CrossRef Full Text | Google Scholar

Li, Z., Wu, W., Tai, X., and Zhang, B. (2021). A reliability-constrained expansion planning model for mesh distribution networks. IEEE Trans. Power Syst. 36 (2), 948–960. doi:10.1109/tpwrs.2020.3015061

CrossRef Full Text | Google Scholar

Lishen, W., Ai, X., and Fang, J. (2024). A survey of application and solution techniques of time series production simulation for New Power System [ J/OL ]. Power Syst. autom. 1-19. doi:10.7500/AEPS20230630012

CrossRef Full Text | Google Scholar

Liu, H., Fan, B., Tang, C., Ge, S., Wang, Y., and Guo, L. (2017b). Game theory-based alternate optimization of active distribution network expansion planning and photovoltaic storage site selection and capacity. Power Syst. Autom. 41 (23), 38–45+116. doi:10.7500/AEPS20170118013

CrossRef Full Text | Google Scholar

Liu, H., Jiao, S., Liu, H., Mo, Z., and Liang, R. (2022a). “Joint optimization method of distribution network frame planning and multi-module intelligent terminal configuration[J/OL],” in Power automation equipment, 1–10. doi:10.16081/j.epae.202207022

CrossRef Full Text | Google Scholar

Liu, J., Zhang, N., Kang, C., Kirschen, D., and Xia, Q. (2017a). Cloud Energy Storage for residential and small commercial consumers: a business case study. Appl. Energy 188, 226–236. doi:10.1016/j.apenergy.2016.11.120

CrossRef Full Text | Google Scholar

Liu, J., Zhang, N., Kang, C., Kirschen, D. S., and Xia, Q. (2018b). Decision making models for the participants in cloud Energy Storage. IEEE Trans. Smart Grid 9 (6), 5512–5521. doi:10.1109/tsg.2017.2689239

CrossRef Full Text | Google Scholar

Liu, N., Cheng, M., Yu, X., Zhong, J., and Lei, J. (2018a). Energy-sharing provider for PV prosumer clusters: a hybrid approach using stochastic programming and Stackelberg game. IEEE Trans. Industrial Electron. 65 (8), 6740–6750. doi:10.1109/tie.2018.2793181

CrossRef Full Text | Google Scholar

Liu, S., Wang, M., Ding, T., Hu, Y., and Lian, X. (2022b). “Active power planning for distribution networks considering the optimal admissible domain of net load [J/OL],” in Power grid Technology, 1–13. doi:10.13335/j.1000-3673.pst.2022.1606

CrossRef Full Text | Google Scholar

Ma, L., Liu, N., Zhang, J., and Wang, L. (2019). Real-time rolling horizon energy management for the energy-hub-coordinated prosumer community from a cooperative perspective. IEEE Trans. Power Syst. 34 (2), 1227–1242. doi:10.1109/tpwrs.2018.2877236

CrossRef Full Text | Google Scholar

Ma, Y., Wu, C., Lin, X., Chen, C., Li, Z., Wei, P., et al. (2022). A cloud Energy Storage peer-to-peer trading strategy based on semi-distributed structured topology [J/OL]. Chin. J. Electr. Eng. 1-15. doi:10.13334/j.0258-8013.pcsee.211263

CrossRef Full Text | Google Scholar

Shi, P. J., Lei, Y., Zhang, L. Y., Wang, Q. L., Liu, X., Tang, Y. Q., et al. (2019). A distribution grid network planning method with Steiner point finding capability in feasible domain. Power Constr. 40 (12), 104–112. doi:10.3969/j.issn.1000-7229.2019.12.013

CrossRef Full Text | Google Scholar

Tushar, W., Chai, B., Yuen, C., Huang, S., Smith, D. B., Poor, H. V., et al. (2016). Energy storage sharing in Smart grid: a modified auction-based approach. IEEE Trans. Smart Grid 7 (3), 1462–1475. doi:10.1109/tsg.2015.2512267

CrossRef Full Text | Google Scholar

Wang, Q., Zhang, X., Yi, C., Li, Z., and Xu, D. (2022a). A novel shared energy storage planning method considering the correlation of renewable uncertainties on the supply side. IEEE Trans. Sustain. Energy 13 (4), 2051–2063. doi:10.1109/tste.2022.3179837

CrossRef Full Text | Google Scholar

Wang, S., Dong, Z. Y., Chen, C., Fan, H., and Luo, F. (2020). Expansion planning of active distribution networks with multiple distributed energy resources and EV sharing system. IEEE Trans. Smart Grid 11 (1), 602–611. doi:10.1109/tsg.2019.2926572

CrossRef Full Text | Google Scholar

Wang, W., Huo, Q., Zhang, N., Yin, J., Ni, J., Zhu, J., et al. (2022b). Flexible energy storage power station with dual functions of power flow regulation and energy storage based on energy-sharing concept. Energy Rep. 8, 8177–8185. doi:10.1016/j.egyr.2022.06.035

CrossRef Full Text | Google Scholar

Wang, Y., Saad, W., Han, Z., Poor, H. V., and Başar, T. (2014). A game-theoretic approach to energy trading in the Smart grid. IEEE Trans. Smart Grid 5 (3), 1439–1450. doi:10.1109/tsg.2013.2284664

CrossRef Full Text | Google Scholar

Wu, Z., Zhou, M., Wang, J., Li, A., Chen, L., and Li, G. (2022). A Sharing Energy Storage operation method for urban energy systems based on combined auction. Power Syst. Autom. 46 (17), 83–90.

Google Scholar

Xu, B., Wang, Y., Dvorkin, Y., Fernandez-Blanco, R., Silva-Monroy, C. A., Watson, J. P., et al. (2017). Scalable planning for energy storage in energy and reserve markets. IEEE Trans. Power Syst. 32 (6), 4515–4527. doi:10.1109/tpwrs.2017.2682790

CrossRef Full Text | Google Scholar

Yu, X., Wang, B., Wang, W., Guo, X., Han, J., and Chen, X. (2022). Analysis of renewable resources in Central China under the “double carbon” strategy. Energy Rep. 8 (8), 361–373. doi:10.1016/j.egyr.2022.09.147

CrossRef Full Text | Google Scholar

Zhang, W. H. (2021). Research on high percentage renewable energy power planning for system flexibility. Beijing: North China Electric Power University.

Google Scholar

Zhao, H., Wu, Q., Hu, S., Xu, H., and Rasmussen, C. N. (2015). Review of Energy Storage system for wind power integration support. Appl. Energy 137, 545–553. doi:10.1016/j.apenergy.2014.04.103

CrossRef Full Text | Google Scholar

Zhong, W., Xie, K., Liu, Y., Yang, C., Xie, S., and Zhang, Y. (2020). Online control and near-optimal algorithm for distributed energy storage sharing in Smart grid. IEEE Trans. Smart Grid 11 (3), 2552–2562. doi:10.1109/tsg.2019.2957426

CrossRef Full Text | Google Scholar