- 1Department of Electrical Engineering and Computer Science, University of Liège, Liège, Belgium
- 2Haulogy, Braine-Le-Comte, Belgium
- 3LTCI, Telecom Paris, Institut Polytechnique de Paris, Paris, France
Introduction: The control of Renewable Energy Communities (REC) with controllable assets (e.g., batteries) can be formalised as an optimal control problem. This paper proposes a generic formulation for such a problem whereby the electricity generated by the community members is redistributed using repartition keys. These keys represent the fraction of the surplus of local electricity production (i.e., electricity generated within the community but not consumed by any community member) to be allocated to each community member. This formalisation enables us to jointly optimise the controllable assets and the repartition keys, minimising the combined total value of the electricity bills of the members.
Methods: To perform this optimisation, we propose two algorithms aimed at solving an optimal open-loop control problem in a receding horizon fashion. Moreover, we also propose another approximated algorithm which only optimises the controllable assets (as opposed to optimising both controllable assets and repartition keys). We test these algorithms on Renewable Energy Communities control problems constructed from synthetic data, inspired from a real-life case of REC.
Results: Our results show that the combined total value of the electricity bills of the members is greatly reduced when simultaneously optimising the controllable assets and the repartition keys (i.e., the first two algorithms proposed).
Discussion: These findings strongly advocate the need for algorithms that adopt a more holistic standpoint when it comes to controlling energy systems such as renewable energy communities, co-optimising or jointly optimising them from both a traditional (very granular) control standpoint and a larger economic perspective.
1 Introduction
Decarbonising the electricity generation sector is currently one of the primary goals towards curbing anthropogenic emissions of greenhouse gases. To that end, various energy policies around the world have set out to provide guidelines and pathways toward achieving this goal (Code de l’énergie Français, 2017; European Union, 2018; Service public de Wallonie, 2019; Torabi Moghadam et al., 2020). A key enabler of decarbonisation is the decentralisation of power generation, which now enables the electricity to be generated closer to where it is consumed. The production assets are, in this case, typically small, such as solar photovoltaic (PV) panels, and are directly connected to the distribution networks. However, this decentralisation does not come without challenges. Several technical as well as regulatory challenges emerge when a significant proportion of the electricity consumed by the end customer is produced near or at the consumption centres (e.g., by prosumers) as addressed by (Manuel de Villena et al., 2021). These problems exist due to, among other reasons, the lack of regulatory frameworks defining how the electricity can be traded in decentralised settings. In this regard, various trading alternatives have been studied and described in existing literature, the most relevant ones based on peer-to-peer (P2P) electricity trading and on trading via a centralised entity. Concerning the first one (P2P trading), a substantial amount of research already exists, including these two literature reviews (Tushar et al., 2018; Sousa et al., 2019), which encapsulate the existing works in the context of these types of exchange. The former review deals with P2P mechanisms using game-theoretical approaches, whilst the latter provides a motivation for the existence of these markets, identifying several challenges, market designs, and potential future developments in this field. As for trading through a central entity, the literature is less abundant and focuses mainly on aggregator or retailer models [see for instance (Mathieu et al., 2019)]. Over the last few years though, a new concept has entered the arena: the Renewable Energy Communities (RECs). Some literature (Moret and Pinson, 2018; Cornélusse et al., 2019; Manuel de Villena et al., 2020a) exists on how the control of energy consumption and production of consumers inside a REC can be computed; however, the lack of adequate regulation has made it difficult to apply any of those mechanisms in practice.
In an effort to provide a framework to boost these new decentralised markets, in the latest Energy Package, the European Commission has embraced the concept of a REC and has introduced, for the first time, a formal definition of these communities along with some basic working principles (European Union, 2018). According to this definition, RECs constitute a type of consumer-centric electricity market comprised of consumers, prosumers, and generation and storage assets that may be shared by all or a subset of the REC members. In this context, electricity surplus generated from prosumers and reinjected into the network can be allocated to the community and shared among the REC members. Thus, a fraction of the total electricity surplus can be allocated to each REC member at a lower price than the retail one. In this paper, this surplus is denoted as local production surplus. As per European regulation, RECs are managed by a central entity: the energy community manager (ECM), whose responsibilities include ensuring the adequate functioning of the REC. Although the rules of participation in a REC are precisely outlined in this European regulation1, there is no provision dictating how to share the local production surplus within the REC. Furthermore, to date and to the best of our knowledge, little or no research has addressed the issue of performing the control of flexible assets such as storage devices within a REC context, which often modifies this local production surplus within the REC, as further explained in Section 2.
To fill this gap, the main contribution of this paper consists of providing a new methodology to simultaneously control, in an optimal manner, the generation and storage devices of RECs with the allocation of the local production surplus to the REC members. Our methodology provides a generic formulation of the decision process associated with the control of RECs, one sufficiently flexible to work with any composition of a REC and to the specific rules applying to it. This decision process, for which the formulation is detailed in Section 3, describes the dynamics of the controllable assets of each member (e.g., batteries), as well as the distribution of local production surplus among the REC members. To that end, it exploits the concept of repartition keys, which are introduced in (Manuel de Villena et al., 2020b). Repartition keys represent the fraction of the total production surplus which is allocated to each REC member—there is one key per member and time-step of the simulation. These keys are computed in the framework of our decision process. Along with the decision process, we propose two algorithms, described in Section 4, which directly exploit the specification of the decision process itself to jointly optimise the control of the controllable assets and the repartition keys in a finite time window. The goal of these algorithms is to jointly minimise the cost related to the controllable assets and the combined total value of the electricity bills of the members that is dependent on the repartition keys (e.g., the combined total value of the electricity bills of the members after allocating the local production surplus to the REC members). Then, a test case is provided in Section 5, where a REC is constructed from synthetic data—the two algorithms described in the previous section are here benchmarked against a third one, that does not optimise the repartition keys, illustrating the relevance of jointly optimising the repartition keys when controlling RECs. Finally, Section 6 concludes this paper.
1.1 Gap targeted and summary of the hypotheses
In this paper, we target a centralised optimisation of the REC electricity bill where we simultaneously command the controllable assets and periodically re-allocate the electricity production surplus of the whole REC. The main hypotheses are as follows.
• The controllable assets of each member are managed at a fixed time rate (e.g., 15 min),
• The dynamics and the operational costs of the controllable assets of each member are known at runtime and assumed, in the experiments of this paper, to be linear,
• Any electricity production surplus of any member can be either redistributed to net consumers inside the REC or sold to the retailer,
• The network topology is not taken into account.
2 Related work
Although the exact rules defining how to exploit and control RECs are still “a work in progress,” as seen in (European Union, 2018; Heaslip et al., 2016; Reijnders et al., 2020; Code de l’énergie Français, 2017; Service public de Wallonie, 2019) research into this topic is already gathering momentum. In (Ciocia et al., 2020), the authors propose a sizing and simulation optimisation framework of a microgrid composed of nanogrids, which is a structure similar to RECs, which follows the Italian market framework. However, this is not addressed as a control problem since the optimisation stage is directly performed with the full history of production and consumption of each member of this microgrid. The literature on these control problems is, by and large, scarce, and typically focuses on single-entity problems where a unique agent (i.e., a single end customer such as a microgrid) is optimised with respect to a specific objective, usually a cost minimisation. In this regard, model predictive control approaches, based on mixed integer linear programming (MILP) or dynamic programming (DP), have been used to optimise the control of microgrids, which can be seen as a particular case of RECs with a single member. In (Parisio and Glielmo, 2011), the authors present an MILP as a solution to perform online planning in a microgrid with the goal of minimising the sum of the operational costs related to electricity exchanges with the main network and to the usage of complex devices (e.g., an energy generator with start-up and shut-down commands). Similarly, in (Francois et al., 2016), linear programming techniques are employed to optimise the control of microgrids by balancing the usage of short-term and long-term storage systems in order to minimise the levelised cost of electricity generated by the microgrid control. In (Hooshmand et al., 2012) the authors propose an algorithm that combines dynamic programming and empirical mean of the objective function to control a microgrid under stochastic scenarios of wind turbine production so as to maximise the local energy consumption. In (Cominesi et al., 2017), the authors propose a bilevel optimisation scheme, in a receding time horizon to control a microgrid comprised of a battery, a microturbine, a PV system, and a load. In their work, an optimal daily planning of each controllable component of the microgrid is computed at a time scale of 15 min. Then, a lower-level controller adjusts the control of the microgrid to be as close as the optimal daily plan as possible while respecting the real-time operational constraints. The optimal control of microgrids can be achieved by adopting other techniques, like reinforcement learning (RL) algorithms, which often do not require an assumption relating to the knowledge of the dynamics of the microgrids. In (Tomin et al., 2019), the authors propose to train deep neural networks with RL, specifically with the Q-Learning algorithm (Sutton and Barto, 2018) by exploiting historical data of production and consumption in order to sample control trajectories. Another work using RL, (Nakabi and Toivanen, 2020), benchmarks several deep reinforcement learning algorithms against a microgrid with flexible demand. In (Boukas et al., 2018), the authors propose using Deep Q-Learning to construct a policy that controls a microgrid which places orders in a continuous real-time market while taking into account operational constraints.
The decision processes relating to the control of multi-entity problems, such as the REC, are only covered to a very limited extent by the existing literature. For instance, in (Zhou et al., 2019) the authors adapt the Q-learning algorithm to train an autonomous centralised controller with the objective of minimising the combined total value of the electricity bills within a REC composed of buildings (members) that are equipped with batteries and PV panels. In (Prasad and Dusparic, 2019), a multi-agent deep reinforcement learning algorithm, previously developed in (François-Lavet et al., 2018), is employed to train each member of the REC to cooperate in order to minimise the volume of the energy imported from the main network, that is, the proportion of the REC consumption that is not covered by local generation.
3 Decision process associated with renewable energy communities
This section explains in detail the modelling framework proposed in our work, formalising the decision process associated with RECs. This decision process aims to control the dynamics of the electricity consumption and production of the REC members, as well as the electricity exchanges between them. Each REC member is characterised by i) a non-controllable electricity consumption, ii) a non-controllable electricity production (when it exists) with e.g., PV panels or wind turbines, and iii) a controllable electricity consumption/production (when it exists) with devices such as flexible loads, batteries or hydrogen tanks equipped with fuel cells and electrolysers. Periodically (e.g., each month), REC members are billed for their electricity consumption depending on their metered consumption/production. According to the last European regulation (European Union, 2018), the electricity surplus of a REC member can either be sold to other REC members or can be injected into the main grid via sales to the retailer. On the other hand, the energy consumption needs of REC members may be covered first by their own energy production (if they are prosumers), with the surplus of other REC members via the local REC market, or through a traditional retailer contract. In the context of RECs as described in (European Union, 2018), the ECM of the REC is in charge of distributing the local electricity surplus among the REC members as required. This allocation of the local production surplus can be performed according to different objectives such as the minimisation of the total combined value of the individual REC members’ electricity bills. To that end, we introduce a methodology of local production surplus allocation based on a sequential decision-making optimisation framework. This methodology is based on repartition keys, as described in (Manuel de Villena et al., 2020b). For each member, a repartition key is defined by two values: the first one, namely the export key, determines the fraction of each member’s own local production surplus to be sold in the internal market of the REC, whereas the second one, the import key, determines the fraction of the total local production surplus to be allocated to each member. An illustration of the REC design used in our decision process can be found in Figure 1.
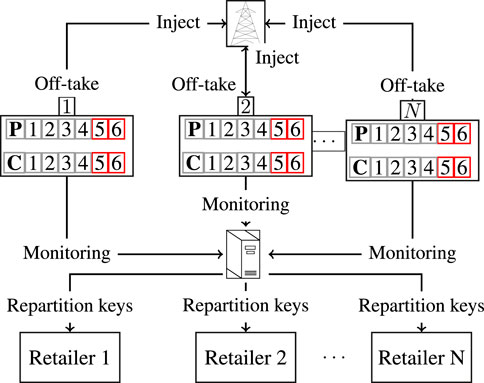
FIGURE 1. Illustration of a REC. Each member
3.1 Mathematical formulation of the decision process
The decision process introduced previously can be formalised as a discrete-time dynamical system with a finite time horizon T. Within this dynamical system denoted by
•
•
• Ξ denotes its exogenous space and is composed of the exogenous values with non-observable dynamics to which dynamical systems associated with RECs are typically subject (e.g., PV panel production).
With these spaces, we can define the dynamics, denoted f(s, u, e), as the transition from a state-action-exogenous triplet
3.1.1 Discretisation of the time horizon
The time horizon constituting the dynamical system is split into discrete time steps 0, …, t, …, T − 1. We assume a constant duration equals to ΔC (e.g., 15 min) for all time intervals
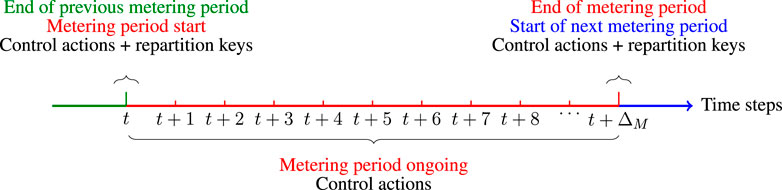
FIGURE 2. Illustration of the time discretization strategy of the decision process described in the problem statement starting from a given time step t and ending at t + ΔM, where t mod ΔM = 0. These two discrete time steps both corresponds to the end of a metering period.
3.1.2 State space
Every state
3.1.3 Action space
Every action
3.1.4 Exogenous space
Every exogenous variable e ∈ Ξ contains, for all members
3.1.5 Local production surplus
The local production surplus to be shared among the REC members at the end of a metering period is denoted by Φ and defined as follows:
The fraction of this local production surplus allocated to member i is defined by
3.1.6 Constraints on the controllable assets actions and on the repartition keys
We assume that the set of admissible actions that can be taken given the current state and the current exogenous variable is given by the mapping
3.1.6.1 At the end of a metering period
The repartition keys are set to values between 0 and 1. The amount of the electricity production surplus of the REC imported by a member cannot exceed its consumption. The sum of the import keys among the members is equal to 1. Finally.
3.1.6.2 At others discrete time steps
The only value that can be set for the repartition keys is ∅, i.e., the repartition keys are not defined at these discrete time steps.
The equation below summarises the above-mentioned constraint:
3.1.7 Net electricity consumption and production during a control period
The net electricity production or consumption is the amount of power injected to or withdrawn from the grid during a given control period, and are denoted by
3.1.8 Transition dynamics
We assume the following known discrete-time transition dynamics for the state space for all
3.1.8.1 Controllable assets dynamics
The transition dynamics of the controllable assets of the members, known at runtime, are defined as follows:
where
3.1.8.2 Metering period counter dynamics
The transition dynamics of the counter of the remaining discrete time steps in the current metering period is defined as follows:
3.1.8.3 Meters dynamics
The transition dynamics of the production and consumption meters for the current metering period are defined as follows:
We merge these functions for conciseness into a single function f such that
3.1.9 Cost functions
We assume the following known instantaneous cost functions.
3.1.9.1 Operational costs on controllable assets
Let
3.1.9.2 Total combined value of the individual electricity bills
The cost function related to the total combined value of the electricity bills of the REC members, known at runtime, is defined by the function
We merge these two costs functions into a single cost function ρ as follows:
3.2 Optimal policy search
A mapping from a given state and exogenous variables to an action space is known as a policy. In this subsection, we define i) the structure of the policies as well as how to evaluate their performance; and ii) the objective function to define the set of optimal policies.
3.2.1 Formal definition and evaluation of policies
We assume that the dynamics of the exogenous variables may not follow a Markov Decision Process (i.e, the value at t + 1 cannot be predicted given the value at t). Therefore, we define a policy π as a mapping from a state and a history of exogenous variables to an action. Accordingly, the entire set of admissible policies Π can be defined as:
where
Given a realisation of exogenous variables ET ∈ ΞT, we can determine the cumulative cost C of a policy π as the sum of the observed costs at every time step t of such a trajectory:
3.2.2 Searching optimal policies
To find the optimal policy we choose as optimisation criterion the expected return of the policy represented by an objective function Obj3 derived from the cumulative cost C defined by Eq. 9. This objective function requires the knowledge of the probability distribution
From this objective function, the goal is to find an optimal policy π* such that
However, since
4 Policies for the control of RECs
In the previous section, we have formalised the problem faced by an ECM to find an optimal policy that minimises the total combined value of the individual electricity bills of REC members (this problem is summarised by Eq. 11). To find this optimal policy, the distributions
The three policies introduced in this section compute open-loop sequences of actions that minimise the objective function described in Eq. 10. This is done to find the next action to be applied to the dynamical system. Assuming that the policies can access to the current state st and exogenous variable et of the system, they perform the following steps.
1) Prediction of the values of the future exogenous variables over a look-ahead horizon K, which we refer to as the policy horizon;
2) Joint optimisation of the sequence of control actions and the sequence of repartition keys that minimise the sum of the costs ρ from the time step t to t + K;
3 )Application, to the REC, of the first action of the sequence.
The first of our policies simply applies these three steps. We refer to this one as the look-ahead policy. A shortcoming of this policy is that, the predicted sequence of exogenous variables does not necessarily end up in a time step that corresponds with the end of a metering period (i.e., T′(t) mod ΔM ≠ 0). As a consequence, electricity prices are predicted up to t + K, but the policy computes optimal actions—w.r.t the predicted values—taking into account only prices up to t + ΔM. This means that this policy often (when T′(t) mod ΔM ≠ 0) will not consider the billing costs related to the repartition keys when computing the actions. To improve the solution of this policy, we introduce a second policy that can compute virtual repartition keys up to t + K, thereby making use of all the available information when computing optimal control actions. We call this policy the look-ahead-billing policy. Finally, to compare the look-ahead and the look-ahead-billing policies against the case where no joint optimisation of control actions and repartition keys is performed, we create a third policy that we call the look-ahead decoupling policy. This last policy computes the sequence of control actions and repartition keys in two stages. In the first stage, it disables the re-allocation of the local production surplus among the REC members while optimising the control actions. In the second stage, it optimises the repartition keys by constraining the sequence of control actions to be equal to the actions computed at the first stage. This policy is inspired by the approach described in (Manuel de Villena et al., 2020b), where an independent ex-post optimisation process is performed at the end of the simulation period to compute the repartition keys so as to minimise the combined total value of the electricity bills of the members.
4.1 Look-ahead policy
The first of the policies introduced in our work, the look-ahead policy, is formally described in this section. We assume that this policy can predict exogenous variables up to a given time horizon K, denoted by policy horizon,
Algorithm 1. Look-ahead policy for decision process

Algorithm 2. REC control process with a given policy.

4.2 Look-ahead-billing policy
Improving upon the look-ahead policy, this section introduces the look-ahead-billing policy. When using the look-ahead policy, the billing costs related to the repartition keys for the last metering period of the optimisation time horizon are often not taken into account. Indeed, let
Algorithm 3. Look-ahead-billing policy for decision process

4.3 Look-ahead-decoupling policy
Depending on the complexity of the optimisation problem to be solved at each discrete time step–especially when K is rather large–the computation time needed for the look-ahead and look-ahead-billing policies might not be compatible with real-time constraints of the control actions. Indeed, these two policies jointly optimise both control actions and repartition keys, and this optimisation procedure creates greater complexity than optimising only the control actions. If computational constraints are an issue, the two optimisations can be decoupled so that the control actions are first optimised and then, based on them, an ex-post optimisation of the repartition keys can be performed, in a similar fashion than (Manuel de Villena et al., 2020b). This optimising procedure is computationally less intensive, but at the expense of the quality of the solution. Consequently, a trade-off between them emerges, which can only be assessed on a case-by-case analysis.
According to these principles, a new policy can be defined, namely the look-ahead-decoupling policy. This policy requires the export key
Algorithm 4. Look-ahead-decoupling policy for decision process

4.4 Computing open-loop sequences of actions for the three policies
To compute open-loop sequences of actions for each of the policies, we assume that, at each discrete time step t, all the policies have access to the exogenous variables et, …, eT′(t) for all look-ahead horizons
4.4.1 Linearisation of the transition dynamics functions
Let us first define the indicator function 1=0(x), indicating whether x is zero:
Since the value of sτ is known, the transition functions
4.4.2 Linearisation of the constraints
Let us derive
We then can replace, for all
4.4.3 Linearisation of the whole cost function
Since the value of fτ(sτ) is known, the cost function ρ can be transformed into an equivalent linear function as follows:
5 Testing the policies on a REC decision process constructed from synthetic data
In this section, we illustrate and test the three policies proposed in Section 4. To that end, we employ various policy horizons and three different RECs (Cases 0, I and II). The former, detailed in Section 5.1, is a simple REC with two members, a producer equipped with a battery and a consumer, so as to illustrate the working principle of the three policies. The two others are constructed from synthetic data, and inspired from a real-life case of REC that was in operation from 2017 till 2021 in the municipality of Méry, Belgium (Cornélusse et al., 2017).
Case I The first REC includes six members: four consumers, one producer based on a solar photovoltaic (PV) installation, and the owner of a large lithium-ion battery. The latter is, therefore, the only controllable asset of the REC.
Case II The second case is similar to the first, but differs on specific points: i) the lithium-ion battery is replaced by a long-term storage device with larger capacity but less power capacity, and ii) the PV producer also owns a small lithium-ion battery, suitable for short-term storage. Hydrogen-based storage systems can be used as long-term storage whereby relatively large amounts of energy can be economically stored since the container is inexpensive. However, due to the high costs of electrolytes and cells, their power is usually limited. On the other hand, lithium-ion batteries are relatively expensive at high capacities, but they provide relatively inexpensive input and output power, which make them good candidates for short-term electricity storage. This second REC is inspired by the single user off-grid microgrid set-up described in (Francois et al., 2016).
Finally, we display and discuss the results, particularly highlighting the difference in terms of performances between jointly optimising the controllable assets and the repartition keys, and optimising only the controllable assets. We also report the runtime of the three policies tested in the two REC cases with a Dell XPS 15, equipped with a Intel Core i7 3.5 GHz CPU and 16 GB of DDR4 RAM. Note that the computational complexity of each policy correspond to the underlying linear solver we have used (Cplex, 2009) which itself has a complex behaviour depending on the number of variables and the general shape of the model.
Due to the scarcity of the available data and the fact that the computation of the policies are deterministic at runtime, we focus our experiments on a single consumption and production profiles for each REC member. However, as shown by results in Sections 5.2.4 and 5.3.3, the performance of the policies are sufficiently different to compare them, particularly between the look-ahead policy and the look-ahead-decoupling policy.
5.1 Description of case 0
In this section, we formalise a simple REC composed of N = 2 members. The first member, named C, is a consumer. The second member, named PVB, is a PV producer equipped with a battery.
5.1.1 Discretisation of the time horizon
We assume that the duration between two discrete time steps ΔC is set to 1 h and that the number of time steps in a metering period ΔM is 4. We assume that the time horizon T is 24 h.
5.1.2 State space
The member C has no controllable asset, so
5.1.3 Action space
Since the member C has no controllable asset, the action
5.1.4 Exogenous space
Figure 3 shows the consumption profile of member C and the production profile of member PVB. The values of the exogenous variables
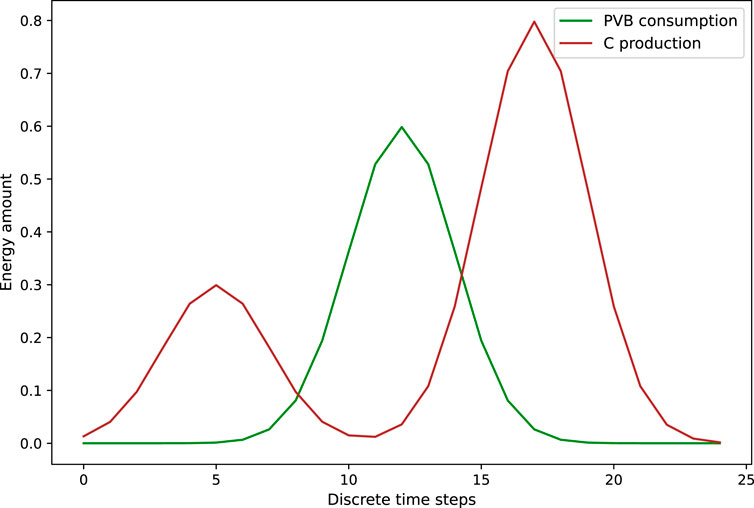
FIGURE 3. Consumption profile of the member C and production profile of the member PVB for the REC of Case 0.
The retailer contracts of the members C and PVB specify that they are charged at 1€/kWh and 2€/kWh for electricity consumption, respectively. These retailer contracts also specify that the surplus of electricity production of these members injected into the network is not bought back. In other words, the selling prices are 0.
The values of
5.1.5 Constraints on the action space
The actions related to the battery of member PVB are bounded by the content and power capacities as follows.
5.1.6 Net electricity consumption/production during a control period
The net electricity production and consumption of the member C are based on its consumption profile. More formally, the values of
5.1.7 Transition dynamics
Since the member C has no controllable asset, no transition dynamics is associated to him. The transition function associated to the member PVB, which continuously charge and discharge its battery, is defined as follows:
The initial state
5.1.8 Cost functions
Since the member C has no controllable asset, the operational cost
The total combined value of the individual electricity bills depending on the repartition keys ρe is defined as:
See Section 5.2.3 for the linearisation of this cost function.
5.1.8.1 Illustrating the policies through case 0
Table 1 shows the results of testing the three policies with

TABLE 1. Size (in financial terms) of the electricity bill of member C by testing the three policies with several policy horizons for the simple REC, compared with the optimal policy (equivalent to the look-ahead policy with K = T = 24). The electricity bill of PVB is not shown in this table; its value is 0 for all policies tested.
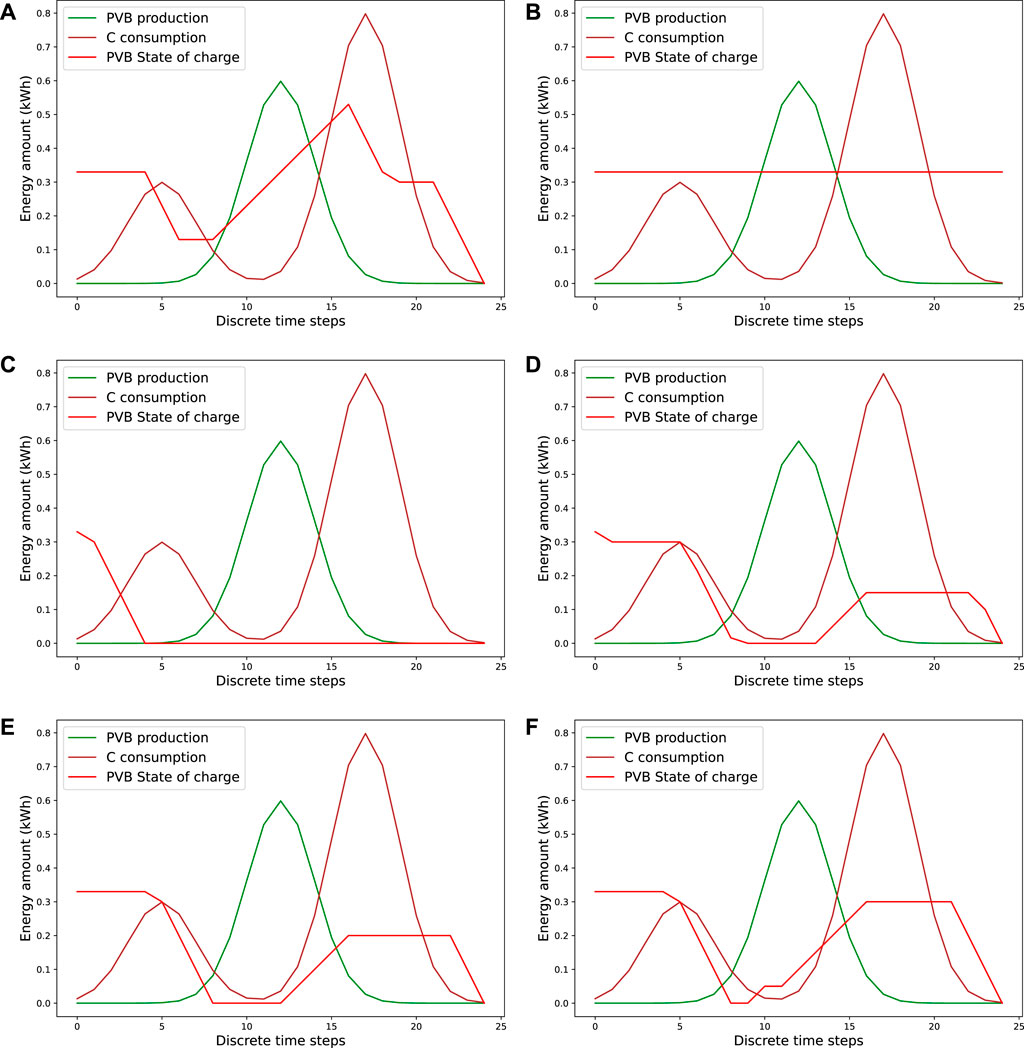
FIGURE 4. State of the battery and total electricity consumption covered by surplus of electricity production (local electricity net consumption) at each discrete time step for Case 0.
The optimal policy handles at best the intermittence of the solar production of the member PVB by charging at most during the production peak and discharging at the consumption peak that occurs later in the day. In the other hand the look-ahead-decoupling policy, which has the worst performance, does not use at all the battery. In this case, the look-ahead-billing policy is consistently, slightly better than the look-ahead policy. At K = 4, the look-ahead policy completely discharges the battery to satisfy the first consumption peak and do not use the battery afterwards, while the look-ahead-billing policy uses a little fraction of the production peak to charge the battery before discharging at the end of the day. As K grows, the behaviour of the two policies gets closer to the optimal policy.
5.2 Description of case I
5.2.1 Formal description of the decision process
This section completes the formulation of the decision process associated with the first REC, composed of N = 6 members, where i) 1, …, 4 are the indexes referring to four consumers named C1, …, C4, ii) the 5th member is a PV producer named PV, and iii) the 6th member is a battery owner named B who does not consume or produce electricity via non-controllable assets.
5.2.1.1 Discretisation of the time horizon
We assume that ΔC = 0.25 h and that ΔM = 4. We assume that T = 720, which corresponds to 7.5 days.
5.2.1.2 State space
The state
5.2.1.3 Action space
The action
5.2.1.4 Exogenous space
The exogenous variable
5.2.1.5 Constraints on the action space
The set of admissible actions U(s, e) for all pairs of states and exogenous variables
where
5.2.1.6 Net electricity consumption/production during a control period
The values of
5.2.1.7 Transition dynamics
Transition dynamics for all members except member 6, are defined as follows:
Transition dynamics specific to the charging/discharging dynamics of the battery of the member 6 are defined as follows:
5.2.1.8 Cost functions
We define the operational cost functions of all members
The total combined value of the individual electricity bills depending on the repartition keys ρe is defined as:
5.2.2 Values from synthetic data for case I
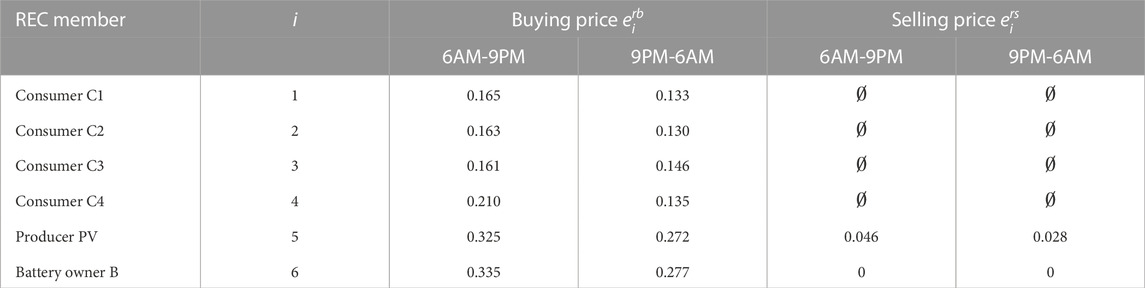
The sequences of exogenous variables related to the energy buying prices from retailers
The values for parameters described in Section 5.2.1 and initial states are:
5.2.3 Computing open-loop sequences of actions for each policy
The total combined value of the individual electricity bills defined by Eq. 31 can be transformed into an equivalent linear function using action space
5.2.4 Testing the policies for case I and discussion on results
The three policies discussed in Section 4 are tested in this section for Case I with varying policy horizons
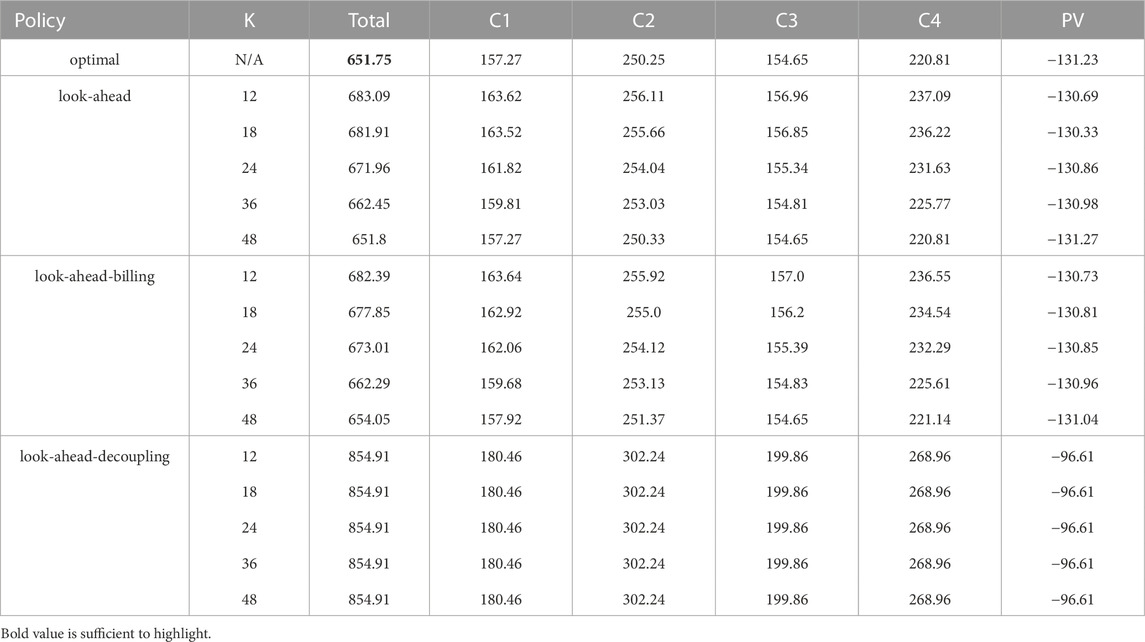
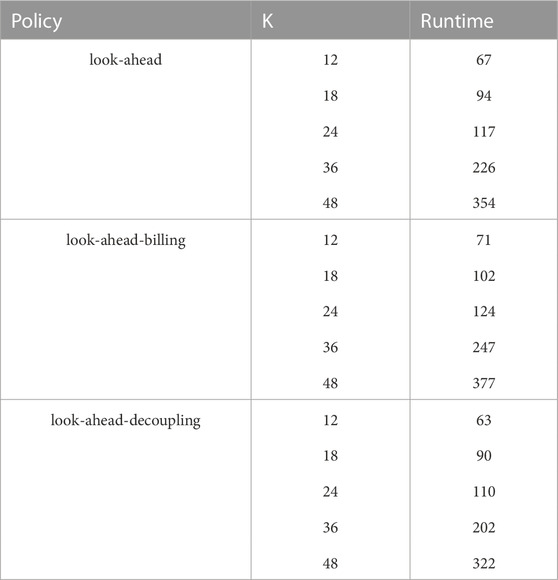
TABLE 4. Size (in financial terms) of the electricity bill in total and also for each member by testing the three policies with several policy horizons for the first REC, compared with the optimal policy (equivalent to the look-ahead policy with K = T = 720). Since the size of the electricity bill of the member 6 is 0 regardless of the tested policy, the corresponding column is not reported.
The combined total value of the electricity bills of the members obtained by using the look-ahead policy with the policy horizon K = 12 is close to the one obtained using the optimal policy—the difference being less than 30€, and this difference decreases as K grows. At K = 48, the difference with the optimal policy is less than 0.05€. These results suggest that near-optimal open-loop sequences of actions can be computed with the look-ahead policy with a rather small policy horizon, provided that the prediction error on the exogenous variables is low.
The combined total value of the electricity bills of the members obtained by using the look-ahead-billing policy with the policy horizon K = 12 is lower than the look-ahead policy (by around 1€). This suggests that the look-ahead-billing policy, which computes virtual repartition keys at the last time step T′(t) might output better quality actions than the look-ahead policy. When K grows, we make the same observations as in the results of Case I.
Regardless of the policy horizon K, the combined total value of the electricity bills of the members obtained by using the look-ahead-decoupling policy is significantly higher than the one obtained using the optimal policy (by around 200€). Since this amount is also significantly higher compared to the other policies within the same REC configuration, it clearly shows the importance, for any efficient open-loop policy, of computing sequences of actions by jointly optimising the controllable assets and the repartition keys through the control process of a REC.
To better understand the difference in terms of the combined total value of the electricity bills of the members across the policies, Figure 5 shows the evolution of the state of charge of the battery of member 6. We notice that, while the optimal policy and the look-ahead policy make use of the battery of member 6 the look-ahead-decoupling policy does not use it at all. This is expected since the look-ahead-decoupling policy cannot compute the repartition keys in real time, and therefore cannot use the demand and production of the community to charge and discharge the battery.
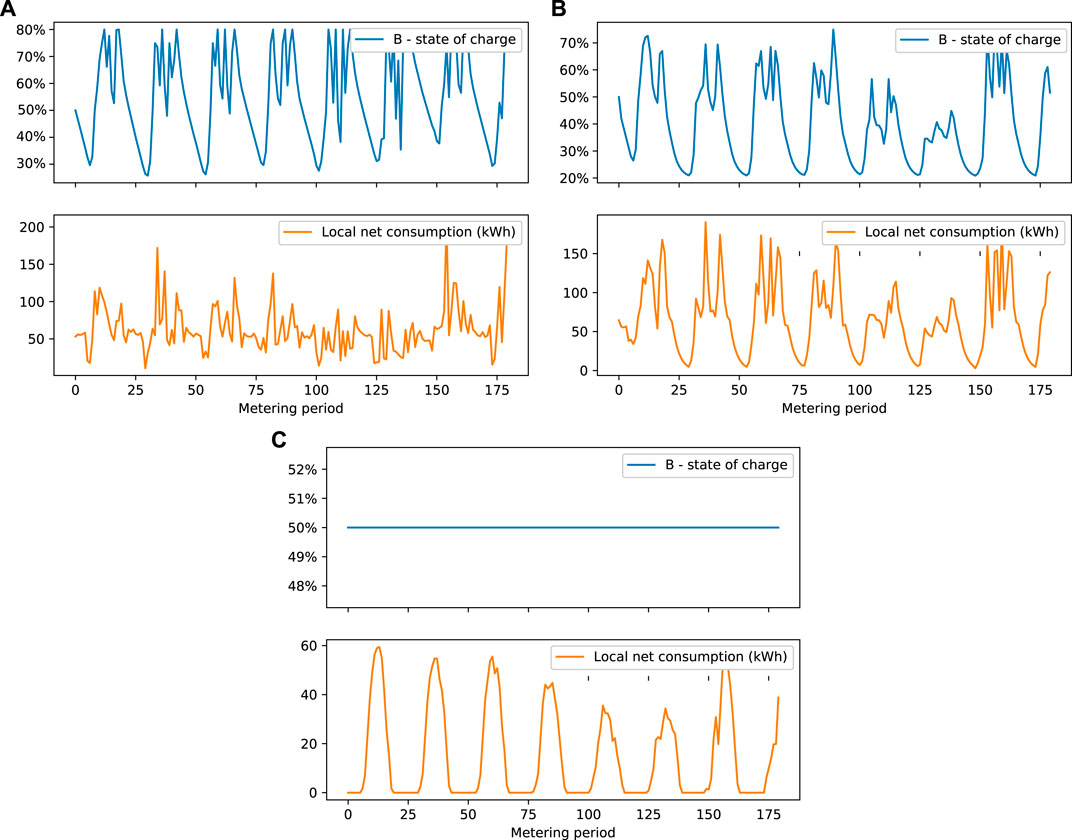
FIGURE 5. State of the battery and total electricity consumption covered by surplus of electricity production (local electricity net consumption) at each discrete time step for Case I.
Results also show the individual electricity bills. Note that repartition keys implicitly define a rule to redistribute the global electricity bill among the members. At the end of each metering period, the look-ahead policy, look-ahead-billing policy and the optimal policy redistribute the local production surplus generated by members 5 and 6 to the other members. The way they redistribute it depends on their consumption profiles and their retailer tariffs. Indeed, according to Eq. 31, the import key allocated to members with higher retailer tariffs should be higher than the others, following a global minimisation criterion of the combined total value of the electricity bills.
5.3 Description of case II
5.3.1 Differences with the decision process of case I
This section describes the decision process associated with the second REC (case II), which only differs from the first one in that member 5 of the REC (i.e., the solar-based electricity producer) owns a small battery, and that the configuration of the battery of member 6 differs in terms of capacity, power and energy efficiency. More precisely, we describe the components of the decision process associated with this second REC which differs from the first one.
Spaces State
Constraints Upper and lower bounds on
Production The variable
Consumption The variable
Dynamics The transition dynamics function
Cost functions The cost function
5.3.2 Values from synthetic data for case II
The values for parameters described in Sections 5.2.1 and 5.3.1 as well as initial states are set as follows.
5.3.3 Testing the policies for case II and discussion on results
As in Section 5.2.4, we test the three policies discussed in Section 4 in the second REC (case II) with varying policy horizons
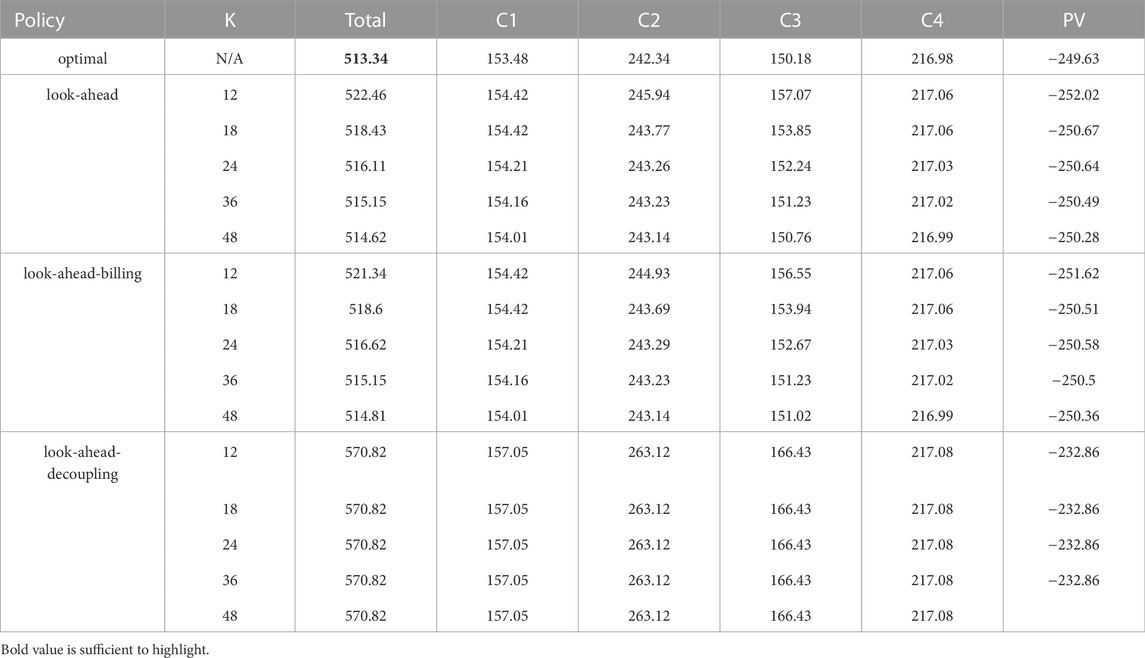
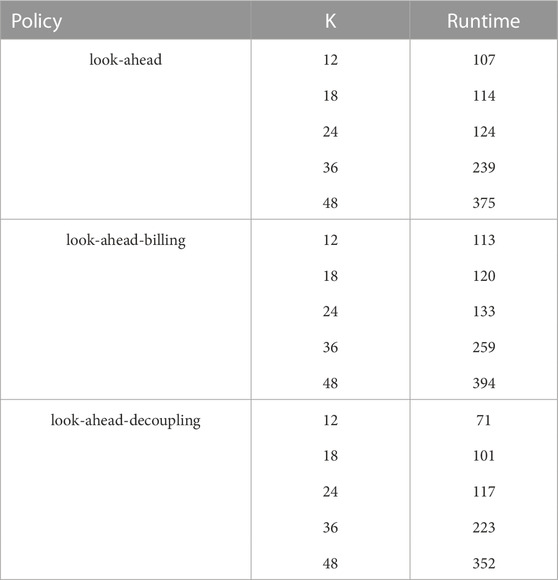
TABLE 6. Size (financial) of the overall electricity bill and those for each individual member by testing the three policies with several policy horizons for Case II, compared with the optimal policy (equivalent to the look-ahead policy with K = T = 720). Since the size of the electricity bill of the member 6 is 0 regardless of the tested policy, the corresponding column is not reported.
The combined total value of the electricity bills of the members, obtained by using the look-ahead policy with the policy horizon K = 12 is similar to the one obtained using the optimal policy—the difference is less than 10€, and this difference decreases as K grows. At K = 48, the difference with the optimal policy is less than 1€. This corroborates that the near-optimal open-loop sequences of actions can be computed with the look-ahead policy with a rather small policy horizon, provided that there is a low prediction error of the exogenous variables.
The combined total value of the electricity bills of the members, obtained by using the look-ahead-billing policy with the policy horizon K = 12 is lower than the look-ahead policy (around 1€). As in the previous policy, as K grows, the difference between their sub-optimalities decreases. Indeed, the combined total value of the electricity bills of the members obtained by using the look-ahead billing policy with the policy horizon K = 48 is lower than that obtained through the look-ahead policy. It is also interesting to note that across the values of K, the combined total value of the electricity bills obtained by the look-ahead billing policy is lower than the one obtained by the look-ahead policy, which validates the hypothesis that the look-ahead billing policy can improve the quality of the control actions compared to the look-ahead policy.
Regardless of the policy horizon K, the combined total value of the electricity bills of the members obtained by using the look-ahead-decoupling policy is significantly higher than the one obtained using the optimal policy (by around than 50€).
To better understand the difference in terms of the combined total value of the electricity bills of the members across the policies, Figure 6 shows the evolution of the state of charge of the battery of member 6. As in the first REC, we notice that the look-ahead-decoupling policy does not use the battery at all, unlike the two other policies. However, the battery owned by member 5 is also used by this policy, and it is used in a different way to the two other policies. The pattern of the state of charge of the battery suggests that this battery discharges its energy to sell it to its own retailer when the selling price is higher than outside this time interval.
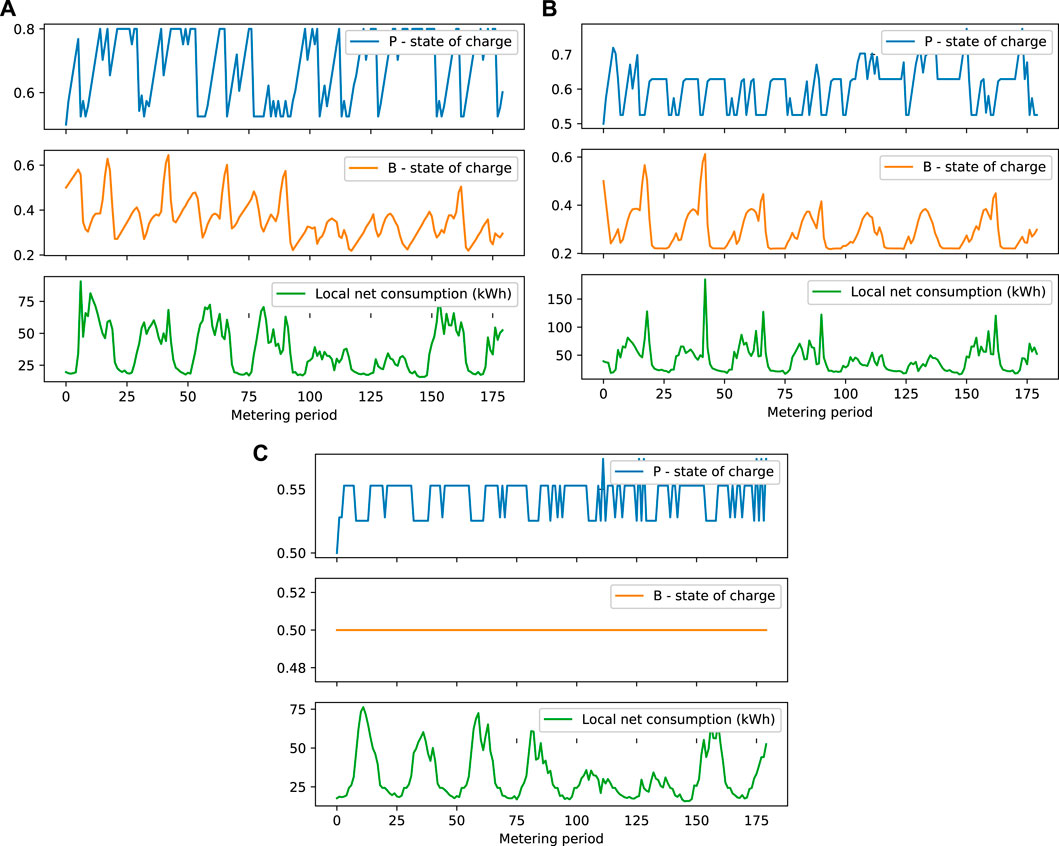
FIGURE 6. State of the batteries and total electricity consumption covered by surplus of electricity production (local electricity net consumption) at each discrete time step for Case II.
6 Conclusion and perspectives
In this paper, we have proposed a generic formulation of the decision process associated with renewable energy communities, which enables one to jointly optimise the controllable assets of each member and the repartition keys used to allocate the local production among the members in order to minimise the total combined value of their individual electricity bills. We have proposed two policies that exploit both the structure of the REC and the available predictions of the future production and consumption of each member to perform this joint optimisation in a time-receding horizon fashion. Furthermore, a third policy that only optimises the controllable assets is proposed. We have tested these algorithms on two REC control problems constructed from synthetic data with 6 members–4 consumers, one producer and a battery. Our results highlight the importance of the joint optimisation of the controllable assets and the repartition keys, as higher total combined value of individual electricity bills have been observed for the third policy.
The contribution of this paper could be extended along several directions. First, let us observe that the control policies we have proposed have been using linear programming techniques since the dynamics and the cost functions associated with the REC constructed from synthetic data were linear - this is often not the case for real RECs. In such context, we could use more advanced techniques such as non-linear programming techniques (e.g., interior point methods) in these open-loop policies or even use closed-loop policies. Reinforcement learning techniques (Bellman, 1954), especially by exploiting the expressiveness of deep neural networks (François-Lavet et al., 2018) (Mnih et al., 2015) (Lillicrap et al., 2015), are excellent candidates to construct these closed-loop policies, since these techniques have been successfully tested on challenging control problems related to microgrids and power systems (Tomin et al., 2019; François-Lavet et al., 2016; Glavic et al., 2017). Another interesting avenue for future research would also be to conduct a extensive benchmark on the look-ahead and the look-ahead-billing policies to extract an insight on which situations one of the policies is more efficient than the other one.
Finally, the repartition keys, introduced by the decision process developed in Section 3, implicitly describe a mechanism to redistribute the revenues generated from the REC, which corresponds to the difference between the combined total value of the individual electricity bills without the REC and the combined total value of the individual electricity bills with the REC. However, this redistribution of the REC revenues is biased by the electricity tariffs imposed by the retailers on each member. Indeed, as observed by the simulation results in Section 5, whenever the buying retail tariff of a member is higher compared to other members, the size of its individual electricity bill is lower compared to these members. By design, other factors that could influence this redistribution in another way (e.g., investment participation of a member to build the REC, subsides brought by some members) are not taken into account at optimisation stage. An ex-post procedure could be developed to compute alternative redistributions schemes as to better incentivise the members to join the RECs.
Data availability statement
Publicly available datasets were analyzed in this study. This data can be found here: https://zenodo.org/record/6047543#.Yg_VBdvjLd5 (only first column of each file).
Author contributions
SA and DE designed the research. QG has helped with the research and the design of the software architecture to conduct the experiments. SA performed the research. SA and MdV collected the data. SA, MdV, and GD drafted the manuscript. MdV, MC, GD, QG, and DE provided feedback on the research and manuscript. All authors contributed to the article and approved the submitted version.
Funding
The authors gratefully acknowledge the support of the Walloon region through the funding of the Merygrid and Integcer projects.
Conflict of interest
QG was employed by Haulogy.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1According to the latest European regulation, any end customer–consumer or prosumer–may participate in a REC without losing the previous status.
2
3The objective function might be a different one (e.g., expected value at risk).
4Consumption and production profiles are publicly available on Zenodo, see (Aittahar et al., 2022). Consider only the column 1st week of each file.
References
Aittahar, S., de Villena, M. M., Derval, G., Castronovo, M., Boukas, I., Gemine, Q., et al. (2022). Optimal control of renewable energy communities with controllable assets: Consumption and production profiles. doi:10.5281/zenodo.6047543
Bellman, R. (1954). The theory of dynamic programming. Tech. rep. Washington: Rand corp santa monica ca.
Boukas, I., Ernst, D., and Cornélusse, B. (2018). CIRED 2018 ljubljana workshop on microgrids and local energy communities.Real-time bidding strategies from micro-grids using reinforcement learning.
Ciocia, A., Di Leo, P., Malgaroli, G., and Spertino, F. (2020). “Subhour simulation of a microgrid of all-electric nzebs based on Italian market rules,” in 2020 IEEE international conference on environment and electrical engineering and 2020 IEEE industrial and commercial power systems europe (EEEIC/ICPS europe), 1–6. doi:10.1109/EEEIC/ICPSEurope49358.2020.9160517
Code de l’énergie Français (2017). Article D315-6, créé par Décret 2017-676 du 28 avril 2017 - art, 2.
Cominesi, S. R., Farina, M., Giulioni, L., Picasso, B., and Scattolini, R. (2017). A two-layer stochastic model predictive control scheme for microgrids. IEEE Trans. Control Syst. Technol. 26, 1–13.
Cornélusse, B., Ernst, D., Warichet, L., and Legros, W. (2017). Efficient management of a connected microgrid in Belgium. CIRED-Open Access Proc. J. 2017, 1729–1732. doi:10.1049/oap-cired.2017.0211
Cornélusse, B., Savelli, I., Paoletti, S., Giannitrapani, A., and Vicino, A. (2019). A community microgrid architecture with an internal local market. Appl. Energy 242, 547–560. doi:10.1016/j.apenergy.2019.03.109
Ernst, D., Glavic, M., Capitanescu, F., and Wehenkel, L. (2009). Reinforcement learning versus model predictive control: A comparison on a power system problem. IEEE Trans. Syst. Man, Cybern. Part B Cybern. 39, 517–529. doi:10.1109/TSMCB.2008.2007630
European Union(2018). Directive 2018/2001 of the European Parliament and of the Council of 11 december 2018 on the promotion of the use of energy from renewable sources. Official J. Eur. Union 4, 82–209.
Francois, V., Gemine, Q., Ernst, D., and Fonteneau, R. (2016). Towards the minimization of the levelized energy costs of microgrids using both long-term and short-term storage devices, 295–319. doi:10.1201/b19664-17
François-Lavet, V., Henderson, P., Islam, R., Bellemare, M. G., and Pineau, J. (2018). An introduction to deep reinforcement learning. CoRR abs/1811.12560.
François-Lavet, V., Taralla, D., Ernst, D., and Fonteneau, R. (2016). “Deep reinforcement learning solutions for energy microgrids management,” in European workshop on reinforcement learning, Barcelona (EWRL).
Glavic, M., Fonteneau, R., and Ernst, D. (2017). Reinforcement learning for electric power system decision and control: Past considerations and perspectives. IFAC-PapersOnLine 50, 6918–6927. doi:10.1016/j.ifacol.2017.08.1217
Heaslip (nee Hassett), E., Costello, G., and Lohan, J. (2016). Assessing good-practice frameworks for the development of sustainable energy communities in Europe: Lessons from Denmark and Ireland. J. Sustain. Dev. Energy, Water Environ. Syst. 4, 307–319. doi:10.13044/j.sdewes.2016.04.0024
Hooshmand, A., Poursaeidi, M. H., Mohammadpour, J., Malki, H. A., and Grigoriads, K. (2012). “Stochastic model predictive control method for microgrid management,” in 2012 IEEE PES innovative smart grid technologies (ISGT), 1–7. doi:10.1109/ISGT.2012.6175660
Lillicrap, T. P., Hunt, J. J., Pritzel, A., Heess, N., Erez, T., Tassa, Y., et al. (2015). Continuous control with deep reinforcement learning. arXiv preprint arXiv:1509.02971.
Manuel de Villena, M., Boukas, I., Mathieu, S., Vermeulen, E., and Ernst, D. (2020a). “A framework to integrate flexibility bids into energy communities to improve self-consumption,” in 2020 IEEE general meeting (IEEE), 1–5.
Manuel de Villena, M., Gautier, A., Ernst, D., Glavic, M., and Fonteneau, R. (2021). Modelling and assessing the impact of the DSO remuneration strategy on its interaction with electricity users. Int. J. Electr. Power & Energy Syst. 126, 106585. doi:10.1016/j.ijepes.2020.106585
Manuel de Villena, M., Mathieu, S., Vermeulen, E., and Ernst, D. (2020b). Allocation of locally generated electricity in renewable energy communities. arXiv preprint arXiv:2009.05411.
Mathieu, S., Manuel de Villena, M., Vermeulen, E., and Ernst, D. (2019). “Harnessing the flexibility of energy management systems: A retailer perspective,” in 2019 IEEE milan PowerTech (IEEE), 1–6.
Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Veness, J., Bellemare, M. G., et al. (2015). Human-level control through deep reinforcement learning. Nature 518, 529–533. doi:10.1038/nature14236
Moret, F., and Pinson, P. (2018). Energy collectives: A community and fairness based approach to future electricity markets. IEEE Trans. Power Syst. 34, 3994–4004. doi:10.1109/tpwrs.2018.2808961
Nakabi, T. A., and Toivanen, P. (2020). Deep reinforcement learning for energy management in a microgrid with flexible demand. Sustain. Energy, Grids Netw. 25, 100413. doi:10.1016/j.segan.2020.100413
Oreshkin, B. N., Dudek, G., Pełka, P., and Turkina, E. (2021). N-beats neural network for mid-term electricity load forecasting. Appl. Energy 293, 116918. doi:10.1016/j.apenergy.2021.116918
Parisio, A., and Glielmo, L. (2011). “Energy efficient microgrid management using model predictive control,” in 2011 50th IEEE conference on decision and control and European control conference (IEEE), 5449–5454.
Prasad, A., and Dusparic, I. (2019). IEEE PES innovative smart grid technologies europe (ISGT-Europe). 1–5. doi:10.1109/ISGTEurope.2019.8905628Multi-agent deep reinforcement learning for zero energy communities
Reijnders, V. M., van der Laan, M. D., and Dijkstra, R. (2020). “Chapter 6 - energy communities: A Dutch case study,” in Behind and beyond the meter. Editor F. Sioshansi (Academic Press), 137–155. doi:10.1016/B978-0-12-819951-0.00006-2
Service public de Wallonie (2019). Mai 2019 – Décret modifiant les décrets des 12 avril 2001 relatif à l’organisation du marché régional de l’électricité, du 19 décembre 2002.
Sousa, T., Soares, T., Pinson, P., Moret, F., Baroche, T., and Sorin, E. (2019). Peer-to-peer and community-based markets: A comprehensive review. Renew. Sustain. Energy Rev. 104, 367–378. doi:10.1016/j.rser.2019.01.036
Tomin, N., Zhukov, A., and Domyshev, A. (2019). Deep reinforcement learning for energy microgrids management considering flexible energy sources. EPJ Web Conf. 217, 01016. doi:10.1051/epjconf/201921701016
Torabi Moghadam, S., Di Nicoli, M. V., Manzo, S., and Lombardi, P. (2020). Mainstreaming energy communities in the transition to a low-carbon future: A methodological approach. Energies 13, 1597. doi:10.3390/en13071597
Tushar, W., Yuen, C., Mohsenian-Rad, H., Saha, T., Poor, H. V., and Wood, K. L. (2018). Transforming energy networks via peer-to-peer energy trading: The potential of game-theoretic approaches. IEEE Signal Process. Mag. 35, 90–111. doi:10.1109/msp.2018.2818327
Keywords: optimisation, renewable energy, carbon neutral, linear programming, energy communities, local electricity market, repartition keys, revenue sharing
Citation: Aittahar S, de Villena MM, Derval G, Castronovo M, Boukas I, Gemine Q and Ernst D (2023) Optimal control of renewable energy communities with controllable assets. Front. Energy Res. 11:879041. doi: 10.3389/fenrg.2023.879041
Received: 18 February 2022; Accepted: 09 January 2023;
Published: 03 February 2023.
Edited by:
Yunfei Mu, Tianjin University, ChinaReviewed by:
Seyedali Mirjalili, Torrens University Australia, AustraliaEnrico Pons, Polytechnic University of Turin, Italy
Copyright © 2023 Aittahar, de Villena, Derval, Castronovo, Boukas, Gemine and Ernst. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Samy Aittahar, c2FpdHRhaGFyQHVsaWVnZS5iZQ==
 Samy Aittahar
Samy Aittahar Miguel Manuel de Villena
Miguel Manuel de Villena Guillaume Derval1
Guillaume Derval1