Multi-objective particle swarm optimization for optimal scheduling of household microgrids

Addressing the challenge of household loads and the concentrated power consumption of electric vehicles during periods of low electricity prices is critical to mitigate impacts on the utility grid. In this study, we propose a multi-objective particle swarm algorithm-based optimal scheduling method for household microgrids. A household microgrid optimization model is formulated, taking into account time-sharing tariffs and users’ travel patterns with electric vehicles. The model focuses on optimizing daily household electricity costs and minimizing grid-side energy supply variances. Specifically, the mathematical model incorporates the actual input and output power of each distributed energy source within the microgrid as optimization variables. Furthermore, it integrates an analysis of capacity variations for energy storage batteries and electric vehicle batteries. Through arithmetic simulation within the Pareto optimal solution set, the model identifies the optimal solution that effectively mitigates fluctuations in energy input and output on the utility side. Simulation results confirm the effectiveness of this strategy in reducing daily household electricity costs. The proposed optimization approach not only improves the overall quality of electricity consumption but also demonstrates its economic and practical feasibility, highlighting its potential for broader application and impact.

1 Introduction

The increasing demand for household electricity and energy consumption issues in recent years has led to the emergence of distributed renewable energy sources (Li et al., 2023a). With advancements in science and technology, home microgrid management systems utilizing distributed energy sources like photovoltaic power generation and battery storage are gaining increasing attention from consumers (Jiang and Fei, 2015). With the increasing popularity of electric vehicles and the continuous development of battery technology, the rise in electric vehicle ownership has been driven by the use of electricity instead of fuel, lower energy consumption costs, and the use of clean energy. The variability of photovoltaic (PV) power systems and electric vehicle (EV) can affect grid scheduling and user comfort when connected to home microgrids (Khan et al., 2017; Lou et al., 2021). Energy storage batteries have the capability to mitigate PV fluctuations and enhance home energy reliability (Liu et al., 2015; Zhang et al., 2018). Combining renewable energy sources, such as hydropower (Xu et al., 2023; Zhu et al., 2023), with electric vehicles and battery storage not only enables internal consumption of distributed energy (Jin et al., 2023) but also enhances the utilization of distributed energy while reducing the cost of daily household electricity consumption (Yang et al., 2022a; Li et al., 2023b).

Within the energy management domain, home microgrids are gaining prominence as essential elements of distributed energy frameworks (Zhou et al., 2023). These microgrids bolster both flexibility and efficiency in energy consumption, introducing complexities and advantages through the integration of multi-objective optimization tactics. Utilizing diverse energy sources alongside Energy Storage Systems (ESS), home microgrids play a critical role in harmonizing and refining energy use, especially as renewable energy adoption surges (Yang et al., 2023). Yang et al. (2022b) present the first study dedicated to solving SCUC problems. They introduce a sophisticated data-driven SCUC expert system that relies on an enhanced sequence-to-sequence (E-Seq2Seq) model. This system is tailored to handle intricate mapping samples within dynamic, multi-sequence environments. It meticulously considers numerous input factors that impact SCUC decision-making, guaranteeing remarkable versatility, heightened solution accuracy, and eminent efficiency compared to traditional methods.

The essence of multi-objective optimization in home microgrid design and operation cannot be understated. It transcends the singular objective of cost reduction, encompassing variables like renewable energy source fluctuations and user comfort in energy consumption. This optimization strategy adeptly manages multiple, sometimes conflicting goals: cutting electricity costs, curbing environmental footprints, and ensuring grid resilience while maintaining household power continuity.

Intelligent scheduling within this framework strikes a delicate balance between cost-efficiency and reliable supply. Consider, for example, scenarios where solar panels produce excess energy on sunny days; multi-objective optimization algorithms facilitate decisions on immediate usage or future storage. Likewise, during renewable energy supply shortages, these algorithms can dynamically adjust loads, curbing wastage and ensuring sustained power via intelligent storage solutions.

As technology evolves, the role of home microgrids in shaping energy management becomes increasingly pivotal. The deployment of multi-objective optimization not only bolsters the economic and ecological viability of energy infrastructures but also furnishes households with more dependable and efficient energy alternatives. A burgeoning community of researchers is fervently exploring innovative optimization paradigms, driving home microgrid advancements and steering energy landscapes towards sustainability and intelligence.

The landscape of research on home microgrid system optimization is expansive, encompassing both domestic and international perspectives (Yang et al., 2022c). Li and Yang (2019) proposes a strategy for optimizing home renewable energy, which involves using dual battery packs based on time-of-day tariffs. This strategy aims to reduce the impact of the uncertainty of renewable energy sources on energy scheduling through the two-battery storage system, while also aiming to reduce the cost of electricity, albeit without considering battery lifespan implications. Ben Slama (2021) proposes an integrated home microgrid management system that utilizes vehicle-to-home (V2H) technology. This system orchestrates energy demand by scheduling automated devices but overlooks potential system impacts from electric vehicle usage. Zheng and Huang (2021) proposed a home energy management system utilizing a power router to connect distributed energy sources, the grid (Li et al., 2022), and home loads. This system addresses scheduling issues arising from renewable energy sources, enhances energy utilization, and ensures system reliability.

Han et al. (2021), Merrington et al. (2022) describes a home microgrid system that integrates domestic dwellings and distributed energy sources. While validated through simulations, the model lacks insights into load-to-grid fluctuations during periods of economical electricity prices. Sun et al. (2019) delved into the optimization of EV predictive control to counteract EV-related uncertainties in home microgrid operations. Although their approach showcases effectiveness via numerical examples, research on electricity price fluctuations remains limited. Fouladfar et al. (2021) championed the integration of electric vehicles in home microgrids to bolster user demand response. Their study highlighted enhanced microgrid demand response performance through differential evolution (DE) methods. Elkazaz et al. (2020) effectively reduces energy costs and power losses by predicting household energy consumption and forecasting photovoltaic power generation. It also verifies the feasibility of this method when combined with simulation.

Wang et al. (2016) employed an innovative small-habitat evolutionary multi-objective immune algorithm (IA) to optimize distributed power sources within microgrids. However, certain intricacies like electric vehicle charging/discharge indexes and microgrid energy storage devices were overlooked. Ding et al. (2016) utilized a classical genetic algorithm (GA) to navigate specific dynamic scheduling challenges. While their study offered valuable insights into equipment capacity and power generation costs, it lacked considerations for advanced microgrid configurations and electric vehicle impacts. Qin et al. (2023) formulated a coordinated optimal scheduling model tailored for active distribution networks, addressing diverse objectives like dispatch cost and load curve variance within a multi-energy system framework (Ma et al., 2022). Nonetheless, traditional PSO algorithms utilized in their model posed challenges related to convergence and real-time scheduling demands (Yang et al., 2022d). Overall, while these studies contribute significantly to the field of home microgrid optimization, each presents its unique set of insights and limitations, underscoring the evolving nature of research in this domain.

In the present study, we advance the existing research landscape by introducing a multi-objective optimal dispatch framework meticulously crafted for residential microgrids. This model intricately weaves together PV power systems, energy storage batteries, and electric vehicles (EVs). Embracing time-of-day tariffs as its foundational pillar, our innovative methodology strives not merely for economic efficiency but also for steadfast grid reliability (Li et al., 2023c).

Harnessing the prowess of the multi-objective particle swarm optimization algorithm (celebrated for its robust search capabilities and swift optimization prowess) we seamlessly integrate the mobility patterns of EV users with diverse distributed energy resources (Li et al., 2020). This harmonization decisively attenuates the disparities between peak and off-peak loads on the grid, setting the stage for a more balanced energy ecosystem. Our primary objective pivots on mitigating the adverse impacts exerted by household loads and EVs on grid-centric operations. Through rigorous MATLAB simulations, serving as our empirical foundation, we scrutinize the time-of-day transitions between diverse energy resources and the power demand emanating from residential loads. Our empirical analyses corroborate the efficacy of the proposed multi-objective optimization paradigm. Specifically, it substantially curtails the strain exerted by centralized electricity consumption (stemming from household loads and EVs) on grid infrastructures. Moreover, this optimization strategy culminates in noteworthy reductions in daily electricity expenditures within the residential microgrid, while concurrently streamlining the scheduling intricacies of its constituent components.

2 Home microgrid system

2.1 Structure of the home microgrid system

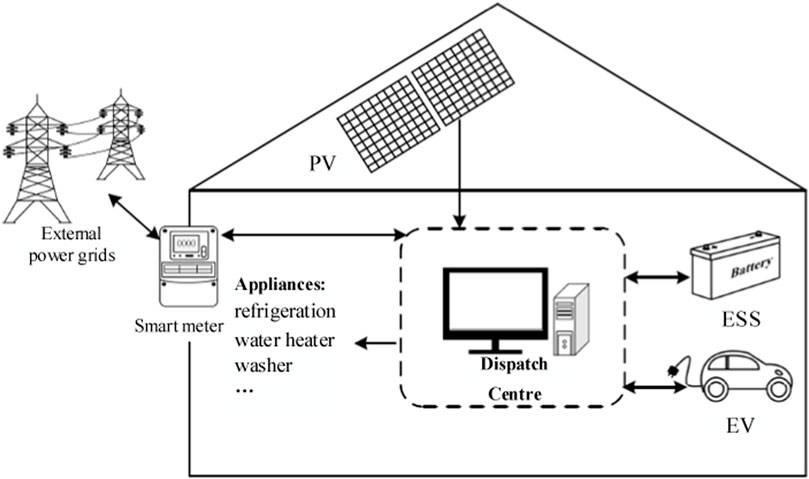
Figure 1 provides an overview of the essential framework of the home microgrid system investigated in this study. The system comprises a photovoltaic power generation system, an electric vehicle, an energy storage battery system, household loads, an external grid, and an energy dispatch center. When the distributed energy source is connected to an energy dispatch center within the system, it collects information about the energy consumed by household loads, electric vehicles, the charging and discharging of storage batteries, and the power generated by the solar power system. This collated information is used to regulate the power flow between the components within the system, including the exchange of energy between the distributed source and household loads.

FIGURE 1

FIGURE 1. Home microgrid system structure diagram.

2.2 Renewable energy system

The output power of a photovoltaic power generation system is related to solar radiation, which is divided into beam radiation and diffuse radiation. It is generally calculated using the modified Hottel equation and the Liu-Jordan equation, as shown in Eq. 1.

$\xi \left(t\right)=\left({\tau }_b+{\tau }_d\right)G_{on}(1)$

where ${\tau }_b$ is solar beam radiation; ${\tau }_d$ is diffuse solar radiation; and $G_{on}$ is other radiation received on a given day of the year.

After obtaining the solar radiation incident on the PV panels, the output power of the PV power generation system can be calculated using the following Eq. 2 (Gu et al., 2012):

$P_{pv}\left(t\right)=\xi \mathit{cos}\theta {\eta }_m{A}_p{\eta }_p(2)$

where $P_{pv}$ is the electrical energy generated by the PV system; $\xi$ is the total solar radiation; $\theta$ is the angle of incidence calculated based on the panel; ${\eta }_m$ is the efficiency calculated based on the maximum power tracking point (MTTP); $A_p$ is the area of the PV panel; and ${\eta }_p$ is the efficiency of the PV panel.

The energy storage battery system is modeled using the KiBaM model, which is commonly utilized in simulating lead-acid batteries (Jongerden and Haverkort, 2017). In this model, the power of the storage battery is obtained through the mutual conversion of available charge and bound charge. When the storage battery discharges to the outside, the bound charge is converted into available charge at a certain rate. Meanwhile, the maximum charging and discharging power of the storage battery is related to its energy storage state, which is calculated by the following Eq. 3:

$\left\{\begin{array}{c}{P}_{ess}^{jmax}\left(t\right)=\frac{k{E}_{\mathrm{1,0},t}{\left(t\right)e}^{-k∆t}+E_{0,t}\left(t\right)kb\left(1-e^{-k∆t}\right)}{1-e^{-k∆t}+b\left(k∆t-1+e^{-k∆t}\right)}\\ P_{ess}^{imax}\left(t\right)=\frac{-k{E}_{ess}^{\mathit{max}}\left(t\right)+k{E}_{\mathrm{1,0},t}{\left(t\right)e}^{-k∆t}+E_{0,t}\left(t\right)kb\left(1-e^{-k∆t}\right)}{1-e^{-k∆t}+b\left(k∆t-1+e^{-k∆t}\right)}\end{array}\right.(3)$

Where $P_{ess}^{jmax}\left(t\right)$ and $P_{ess}^{imax}\left(t\right)$ are the maximum discharge power and charging power at the initial time of time period $t$, respectively; $k$ is a constant indicating the rate of conversion of bound charge to usable charge; $E_{\mathrm{1,0},t}\left(t\right)$ and $E_{\mathrm{1,0},t}\left(t\right)$ are the initial usable power and the total stored power at time period $t$, respectively; $b$ is the ratio of usable charge to the total charge; and $E_{ess}^{\mathit{max}}\left(t\right)$ is the maximum stored power of the storage battery at time period $t$.

Assuming that the electric vehicle is charged in constant power mode and the power is allowed to vary within a small range when discharged, the state of charge (SOC) of the battery in the charging and discharging states of the electric vehicle is calculated as follows Eqs 4, 5 (Zhang et al., 2016):

${SOC}_{ev}\left(t+1\right)={SOC}_{ev}\left(t\right)+P_{ev}^i\left(t\right)\bullet ∆t\bullet \frac{{\eta }_{ev}^i}{C_{ev}}(4)$

$\left.{SOC}_{ev}\left(t+1\right)={SOC}_{ev}\left(t\right)-\left(P_{ev}^j\left(t\right)\bullet ∆t\right)/{\left(\eta \right.}_{ev}^j\bullet C_{ev}\right)(5)$

Where ${SOC}_{ev}\left(t\right)$ is the SOC of EV in time period $t$; $P_{ev}^i\left(t\right)$ and $P_{ev}^i\left(t\right)$ are the input and output power of EV in time period $t$, respectively; ${\eta }_{ev}^i$ is the charging efficiency; ${\eta }_{ev}^j$ is the discharging efficiency; and $C_{ev}$ is the rated capacity of EV battery.

2.3 Power distribution strategies for home microgrid systems

The time-of-use (TOU) tariff strategy delineates a dynamic pricing paradigm, predicated on differential electricity pricing across distinct demand epochs, namely, peak and off-peak periods. Notably, operational costs of electricity generation escalate during peak consumption intervals, rendering electricity tariffs substantially higher than those during off-peak intervals. Consequently, households are incentivized to realign their electricity consumption patterns, optimizing usage during off-peak periods to capitalize on reduced tariffs, as elucidated in prior research (Ruan et al., 2012; Sun et al., 2014). However, a potential repercussion of this strategy is the inadvertent emergence of elevated consumption peaks during these ostensibly low-cost periods. As the paradigm of distributed energy resources gains traction within residential energy frameworks, it underscores the imperative for users to adeptly navigate the nuances of time-of-use tariffs (Nan et al., 2018). This necessitates the formulation of astute strategies delineating optimal electricity procurement and consumption patterns. Within this context, two scenarios could be consideration: i) during diurnal intervals when occupants are absent, the EV remains disengaged from the home microgrid, mitigating its energy interactions within the system. ii) Conversely, upon the user’s nocturnal return, inherent constraints render the EV system ineffectual in electricity generation, necessitating strategic resource management to ensure optimal microgrid functionality and user-centric energy provisioning.

(1) When the EV is away from home during times of low electricity pricing, there arises a necessity to procure additional power from the grid. Conversely, during peak electricity price intervals, precedence is accorded to the utilization of photovoltaic systems and storage batteries for electricity generation. This strategic approach ensures the optimal and cost-efficient fulfillment of household electricity requirements, defined as Eq. 6.

$P_{buy}\left(t\right)=P_{load}\left(t\right)-P_{ess}^j\left(t\right)-P_{pv}\left(t\right)(6)$

where $P_{buy}\left(t\right)$ is the purchased electricity; $P_{load}\left(t\right)$ is the electricity required by the household load; $P_{ess}^j\left(t\right)$ is the output of the storage battery; and $P_{pv}\left(t\right)$ is the electricity generated by the PV system.

When the power generated by the PV system is adequate for the household’s energy needs, the storage battery can be linked to the PV system for recharging. The relationship between them is shown in Eq. 7.

$P_{ess}^i\left(t\right)=P_{pv}\left(t\right)-P_{load}\left(t\right)(7)$

where $P_{ess}^i\left(t\right)$ is the input electrical energy of the storage battery.

If the PV system can supply power to the household loads and there is still surplus power after charging the storage battery, the excess power is sold to the grid. The sold power can be calculated using Eq. 8.

${P_{sold}\left(t\right)=P}_{pv}\left(t\right)-P_{load}-P_{ess}^i\left(t\right)(8)$

where $P_{sold}\left(t\right)$ is the portion of electrical energy sold to the grid.

(2) When the EV is at home and the PV system is no longer supplying power, it is necessary to buy the missing load power from the grid at a low electricity price and charge the EV simultaneously. The size of the buy power can be determined using Eq. 9.

$P_{buy}\left(t\right)=P_{load}\left(t\right)+P_{ev}^i\left(t\right)-P_{ess}^j\left(t\right)(9)$

where $P_{ev}^i\left(t\right)$ is the electrical energy input to the electric vehicle.

During peak electricity prices, the home energy system relies primarily on electric vehicles and storage batteries for energy. Therefore, the buy power at this time is represented by Eq. 10.

$P_{buy}\left(t\right)=P_{load}\left(t\right)-P_{ess}^j\left(t\right)-P_{ev}^j\left(t\right)(10)$

where $P_{ev}^j\left(t\right)$ is the electrical energy output of the electric vehicle.

In order to determine the input and output ranges of the storage battery and the state of charge (SOC) of the battery, the following calculations will be performed for the battery at each interval as shown in Eqs 11–13:

$P_{ess}^{in}\left(t\right)={\epsilon }_{ess}\left({SOC}_{ess}^{\mathit{max}}-{SOC}_{ess}\left(t\right)\right)/∆t(11)$

$P_{ess}^{out}\left(t\right)={\epsilon }_{ess}\left({SOC}_{ess}\left(t\right)-{SOC}_{ess}^{\mathit{min}}\right)/∆t(12)$

$S_{ess}\left(t+∆t\right)=S_{ess}\left(t\right)+\frac{\left(P_{ess}^i\left(t\right)\bullet {\xi }_{ess}^i-P_{ess}^j\left(t\right)/{\xi }_{ess}^j\right)∆t}{{\xi }_{ess}^{\mathit{max}}}(13)$

where $P_{ess}^{in}\left(t\right)$ is the input power limit of the battery; $P_{ess}^{out}\left(t\right)$ is the output power limit of the battery; ${\epsilon }_{ess}$ is the capacity of the battery; ${\xi }_{ess}^i$ is the charging efficiency of the battery; ${\xi }_{ess}^j$ is the discharging efficiency of the battery; ${SOC}_{ess}\left(t\right)$ is the real-time capacity of the battery; ${SOC}_{ess}^{\mathit{max}}$ is the maximum SOC limit of the battery; ${SOC}_{ess}^{\mathit{min}}$ is the minimum SOC limit of the battery.

3 Multi-objective optimization model for home microgrids

3.1 Objective function

3.1.1 Objective function 1: minimization of electricity consumption costs

In the home microgrid system analyzed within this study, the primary objective function revolves around minimizing the electricity costs. Given the presence of time-of-use tariffs, the paramount goal is to curtail electricity expenses, thereby enhancing the economic viability for users. This cost computation incorporates both the maintenance expenditures related to distributed energy components and the net daily expenditure attributed to household energy consumption. Mathematically, the objective function for minimizing electricity costs is represented in formula (14) as:

$f_1=\mathit{min}\left(COE\right)={Cost}_u+{Cost}_w(14)$

Here $COE$ represents the cost of electricity; ${Cost}_u$ is the maintenance cost of distributed energy components; ${Cost}_w$ denotes the cost of electricity exchanged with the grid.

The electricity cost for the system is derived from the difference between the expenditures associated with maintaining the distributed energy equipment and the revenue generated, such as from the sale of electricity. Consequently, Cost_u is computed by multiplying the maintenance, replacement, and conservation costs of distributed energy resources with their respective unit quantities. It is essential to distinguish between maintenance and replacement costs: maintenance costs pertain to the periodic upkeep of equipment at each time interval t, whereas replacement costs are incurred when components require substitution while the system remains operational. Additionally, protective costs emerge when equipment approaches the end of its operational lifecycle. Thus, the comprehensive cost structure for the system is articulated in Eq. 15:

${Cost}_u=X_{pv}\left(V_{pv}^m+V_{pv}^r+V_{pv}^s\right)+X_{ess}\left(V_{ess}^m+V_{ess}^r+V_{ess}^s\right)+X_{ev}\left(V_{ev}^m+V_{ev}^r+V_{ev}^s\right)(15)$

Here:

• X represents the respective unit quantities.

• pv denotes the photovoltaic power generation system.

• $V_{pv}^m$ signifies the maintenance cost for the PV system, encompassing periodic upkeep and service expenses.

• $V_{pv}^r$ stands for the replacement cost of PV modules, accounting for necessary upgrades to sustain efficiency amidst evolving technology and market dynamics.

• $V_{pv}^s$ represents safety and insurance expenditures vital for the reliable operation of the PV system.

• ess refers to the energy storage system, mirroring the PV system’s cost structure with its own maintenance, replacement, and protective costs.

• ev designates an electric vehicle, with its associated costs segmented into maintenance, replacement, and protective facets.

Additionally, a pivotal metric for the energy storage battery’s lifecycle is its capacity degradation. When the battery’s capacity diminishes to 80% of its initial value, it is deemed to have reached its lifecycle’s conclusion. This capacity degradation is quantified by the Depth of Discharge (DOD) of the battery, defined in formula (16):

${DOD}_{ess}\left(t\right)=1-{SOC}_{ess}\left(t\right)(16)$

Here ${DOD}_{ess}$ denotes the depth of discharge of the battery.

The capacity degradation of the battery posts each operational cycle is determined employing the rain flow algorithm, represented in Eq. 17:

$V_{ess}\left(\beta \right)=\frac{20}{33000\bullet e^{-0.06576\bullet {DOD}_{ess}\left(\beta \right)}+3277}(17)$

Where $V_{ess}$ is the degree of capacity degradation for the battery; $\beta$ denotes the entire lifespan cycle of the battery.

Within this framework, the battery’s lifecycle termination is defined when its capacity diminishes to 20%.

The net cost of exchanging electricity with the grid ${Cost}_w$ can be calculated from the total cost of electricity used by the household and the cost of electricity purchased and sold. This can be determined using the following formula (18):

${Cost}_w={\displaystyle {\sum }_{t=1}^H}TOU\left(t\right)\bullet P_{buy}\left(t\right)-{\displaystyle {\sum }_{t=1}^H}FTT\left(t\right)\bullet P_{sold}\left(t\right)(18)$

where $H$ indicates the total number of hours within a given day; $TOU\left(t\right)$ represents the electricity purchasing price from the grid at time t; and $FTT\left(t\right)$ stands for the electricity selling price to the grid at time t.

3.1.2 Objective function 2: minimizing variability in grid-side energy supply

When a substantial number of electric vehicles charge during the grid’s off-peak periods, the methodology of mobile charging can profoundly influence the grid. Such a scenario might inadvertently lead to the emergence of a new peak load during typically off-peak times, potentially disrupting the seamless electricity consumption experience within households. In light of this challenge, the formulation of an objective function aimed at minimizing grid-side supply variance is advocated as the second focal point of this study. Moreover, integrating distributed energy sources into the household grid is posited as a strategy to attenuate these unexpected load fluctuations.

By prioritizing the reduction of real-time energy exchange variability between the utility grid and the household, there’s an opportunity to amplify the contribution of distributed energy supply within the home microgrid framework. This strategic shift not only bolsters the incorporation of renewable energy sources but also refines the load profile, diminishing network losses. Consequently, this optimization approach elevates the overall quality and reliability of household electricity consumption.

It is worth noting that prioritizing the minimization of grid-side supply variance as an objective function, as opposed to merely focusing on reducing network losses, offers distinct advantages. Specifically, this approach obviates the need for iterative computations, resulting in expedited computational times. Such efficiency is pivotal for addressing the nuanced load power allocation challenges delineated in this research.

The mathematical representation for minimizing the grid-side energy variance is delineated in formula (19):

$f_2=\frac{1}{H}{\displaystyle {\sum }_{t=1}^H}{\left[P_{grid}\left(t\right)-\frac{1}{H}{\displaystyle {\sum }_{t=1}^H}{P}_{grid}\left(t\right)\right]}^2(19)$

where $P_{grid}\left(t\right)$ signifies the power exchanged between the household and the utility grid over time t.

3.2 Constraint

(1) PV power limitation is shown in formula (20)

${0\le P}_{pv}\left(t\right)\le P_{pv}^{\mathit{max}}(20)$

(2) Constraints on energy storage battery input and output are represented in formula (21)

${0\le P}_{ess}^{in}\left(t\right),P_{ess}^{out}\left(t\right)\le P_{ess}^{\mathit{max}}(21)$

where $P_{ess}^{\mathit{max}}$ signifies the maximum output power capacity of the energy storage battery.

(3) EV battery power limitations are represented as shown in formula (22)

${0\le P}_{ev}^{in}\left(t\right),P_{ev}^{out}\left(t\right)\le P_{ev}^{\mathit{max}}(22)$

where $P_{ev}^{\mathit{max}}$ represents the maximum output power capacity of the electric vehicle battery.

(4) Energy storage battery SOC constraints are defined by formula (23)

${SOC}_{ess}^{\mathit{min}}\le {SOC}_{ess}\left(t\right)\ll {SOC}_{ess}^{\mathit{max}}(23)$

where ${SOC}_{ess}^{\mathit{min}}$ and ${SOC}_{ess}^{\mathit{max}}$ define the minimum and maximum SOC limits of the energy storage battery, respectively.

(5) EV battery SOC constraints can be found in formula (24)

${SOC}_{ev}^{\mathit{min}}\le {SOC}_{ev}\left(t\right)\ll {SOC}_{ev}^{\mathit{max}}(24)$

where ${SOC}_{ev}^{\mathit{min}}$ and ${SOC}_{ev}^{\mathit{max}}$ represent the minimum and maximum SOC limits of the electric vehicle battery, respectively.

(6) System power balance constraints

When the EV is not at home during the day, the output and purchased electricity from the PV system and storage batteries need to be sufficient to support the household load. Any excess electricity generated by the distributed energy sources is used to sell to the municipal grid. In this scenario, the power of the load adheres to the relationship described by Eq. 25.

$P_{pv}\left(t\right)+P_{ess}^j\left(t\right)+P_{buy}\left(t\right)-P_{sold}\left(t\right)=P_{load}\left(t\right)(25)$

When the EV is connected to the home energy system as a distributed energy source at night while it is at home, the power output from the distributed energy source and the purchased power need to be sufficient to support the home load simultaneously. Any excess power generated by the distributed energy source is then sold to the utility grid. In this scenario, the power of the load aligns with the conditions set by Eq. 26.

$P_{ess}\left(t\right)+P_{ev}\left(t\right)+P_{buy}\left(t\right)-P_{sold}\left(t\right)=P_{load}\left(t\right)(26)$

3.3 Optimization process

To address the complex multi-objective optimization challenges presented in this study, we have harnessed the power of computational algorithms. Specifically, the Multi-objective Particle Swarm Optimization (MOPSO) algorithm, implemented within the MATLAB environment, serves as our chosen tool to navigate this intricate optimization landscape.

The formulation of our mathematical model for the multi-objective optimization problem can be succinctly represented in formula (27):

$\begin{array}{c}\mathit{min}y=F\left(x\right)=\left(f_1\left(x\right),f_2\left(x\right),f_3\left(x\right),\cdots ,f_m\left(x\right)\right)\\ s.t.\left\{\begin{array}{c}{g}_i\left(x\right)\le 0,i=\mathrm{1,2,3},\cdots ,q\\ h_j\left(x\right)=0,j=\mathrm{1,2,3},\cdots ,p\\ x\in \left[x_{\mathit{min}},x_{\mathit{max}}\right]\end{array}\right.\end{array}(27)$

where $X$ is an n-dimensional decision space, $Y$ is an m-dimensional target space, and $y=\left(f_1\left(x\right),f_2\left(x\right),f_3\left(x\right),\cdots ,f_m\left(x\right)\right)$ is an m-dimensional target vector; The objective function $F\left(x\right)$ defines $m$ mapping functions from the decision space to the objective function; $g_i\left(x\right)\le 0,\left(i=\mathrm{1,2},\cdots ,q\right)$ and $h_j\left(x\right)\le 0,\left(j=\mathrm{1,2},\cdots ,p\right)$ define the $q$ inequality constraints and $P$ equality constraints of the multi-objective optimisation problem, respectively; $x_{\mathit{min}}$ and $x_{\mathit{max}}$ are the upper and lower bounds of the vector search.

The Particle Swarm Optimization (PSO) algorithm stands out in the realm of optimization techniques due to its remarkable computational efficiency, swift execution pace, and reduced sensitivity to initial conditions. This method’s prowess has led to the evolution of the Multi-objective Particle Swarm Optimization (MOPSO) algorithm, specifically tailored to tackle multi-objective optimization challenges. A distinguishing feature of MOPSO is its incorporation of the Pareto sorting mechanism. This mechanism facilitates the identification of the global optimal solution and paves the way for capturing the Pareto optimal frontier. However, despite its merits, MOPSO exhibits a potential pitfall: its rapid convergence rate. When MOPSO converges swiftly, the exploration scope contracts, restricting the algorithm’s capacity to discover the global optimal frontier. Instead, it may inadvertently settle for a local Pareto optimal frontier, thus compromising the overarching objective of identifying the best trade-offs across multiple criteria.

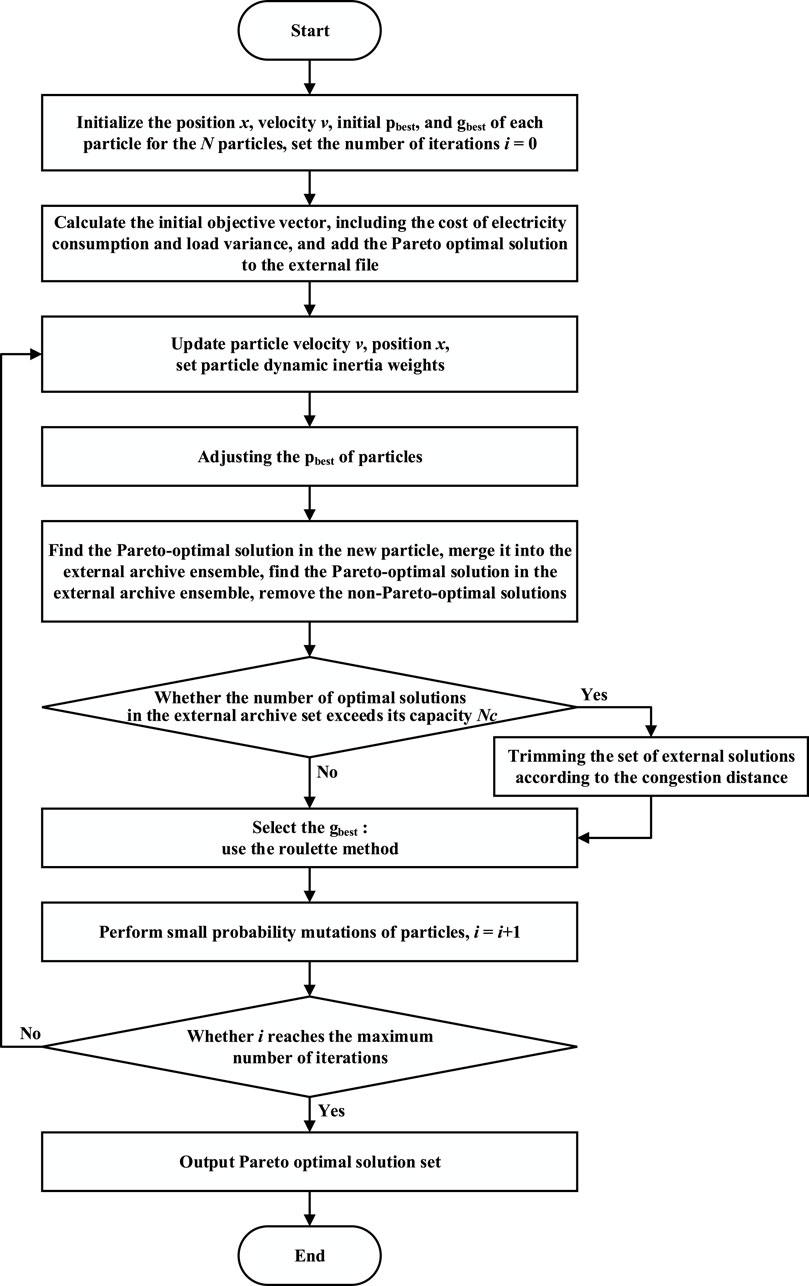
To circumvent this limitation, our study introduces a nuanced enhancement: the incorporation of a probabilistic random mutation mechanism within the particle swarm evolution dynamics. This strategic inclusion injects controlled perturbations into the particle positions, rejuvenating the algorithm’s exploratory prowess and fortifying its ability to navigate the solution landscape more comprehensively. Figure 2 delineates the flowchart illustrating the multi-objective optimal scheduling framework tailored for home microgrids.

FIGURE 2

FIGURE 2. Multi-objective optimization scheduling process of home microgrid.

The operational workflow of the enhanced Multi-objective Particle Swarm Optimization (MOPSO) algorithm is delineated as follows:

Step 1. Parameter Initialization:

Initiate the optimization process by initializing four crucial parameters: particle position(x), velocity (v), initial personal best (p_best), and global best (g_best). Herein, the g_best symbolizes the anticipated optimal solution to be discerned during the optimization journey, while p_best represents the most optimal solution achieved by an individual particle up to that instance.

Step 2. Target Vector Computation:

Compute the target vector after setting the initial p_best for each particle and determining the overarching g_best for the entire ensemble. This phase necessitates directing each particle toward minimizing both electricity cost and load error. To achieve this objective, ascertain the fitness value for every particle, encapsulating a composite metric of electricity cost and load error. Consequently, particles with superior fitness scores amalgamate to constitute the Pareto front, thereby delineating the Pareto optimal surface.

Step 3. Particle Position and Velocity Adjustment:

Modify the position(x) and velocity(v) of particles while concurrently evaluating each particle’s fitness function and updating its p_best. These iterative adjustments facilitate the expansion of the search space through position modifications and expedite exploration via velocity alterations.

Step 4. Periodic Update of Personal Best (p_best):

At regular intervals, recalibrate the p_best of particles by identifying those in proximity to the g_best, subsequently updating the g_best to optimize the algorithm’s performance.

Step 5. Selection and Archival of New g_best:

From the established Pareto front, cherry-pick a novel g_best. Integrate this fresh g_best into an external archival repository. Should multiple viable g_best candidates emerge, select an optimal solution from this archival ensemble.

Step 6. Integration of Random Mutation Mechanism:

Embed a stochastic random mutation mechanism within the algorithmic framework. This introduces nuanced perturbations to each particle’s position, fortifying the algorithm’s prowess in global optimization by diversifying the exploration trajectory.

Step 7. Decision-making via Roulette Selection:

Implement a roulette-based decision-making paradigm. This culminating phase involves either endorsing the prevailing algorithmic state or triggering termination protocols, thereby finalizing the optimization loop based on predetermined criteria.

Step 8. Conclusion and Output:

Upon attaining the pre-defined maximum generation threshold, culminate the iterations. Conclusively, output the g_best solution set, emblematic of the optimal trade-off achieved between minimizing electricity cost and mitigating load variability.

4 Case study

4.1 Experimental methods and data acquisition

To validate the efficacy of the proposed strategy delineated in this research, an illustrative family residing in East China was chosen as a representative case for rigorous simulation and subsequent analysis. For computational tractability and clarity, the simulation framework employed in this study adopts a concise 1-day scheduling cycle, meticulously segmented into 24 distinct time intervals. These simulations were adeptly executed leveraging the computational prowess of MATLAB.

The empirical foundation for this case study is anchored on the average daily electricity consumption metrics observed over a span of 1 month during the summertime in East China. This comprehensive dataset serves as the foundational bedrock for our analytical calculations and simulations.

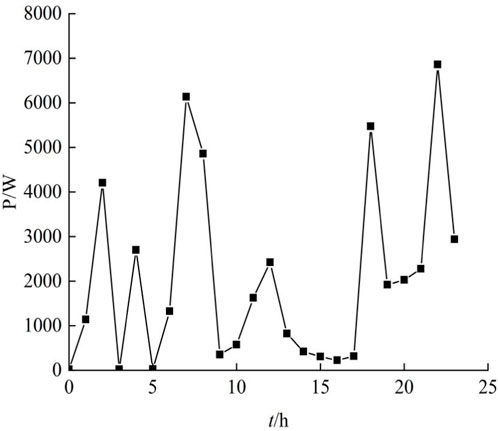
When integrating the electric EVs into the family’s broader electricity consumption matrix, the resultant load curve is vividly portrayed in Figure 3. This graphical representation lucidly elucidates the diurnal distribution of household electricity consumption, intricately factoring in the demands associated with EV charging protocols.

FIGURE 3

FIGURE 3. Household daily load curve.

Furthermore, a granular analysis of this load curve facilitates discerning specific temporal peaks in electricity consumption. These pronounced peaks are intrinsically tethered to the circadian rhythms and habitual patterns exhibited by household occupants. Notably, the load profile conspicuously exhibits substantial peaks, surging to an impressive 6856 W during the evening intervals. This surge predominantly emanates from the confluence of household members returning home and initiating the charging protocols for their EVs, underscoring the significance of such empirical insights in devising optimized microgrid management strategies.

In this paper, the number of particle swarms is selected to be 80, the maximum number of iterations is 100, the number of external archive ensemble size is 100, the learning factor $c_1$ is taken to be 0.1, $c_2$ is taken to be 0.2, the maximum inertia weight ${\omega }_{\mathit{max}}$ is 0.8, the minimum inertia weight ${\omega }_{\mathit{max}}$ is 0.4, and the variation rate is 0.1. The parameters of each distributed energy source of the home microgrid are as follows: the PV generation system operates in MPPT mode and its maximum output power is 10 kW; the maximum output power of the energy storage battery is 3 kW, the rated power is 3.6 kW, and the capacity is 3 kWh; the maximum output power of the electric vehicle is taken to be 5 kW; the maximum input power is taken to be 7 kW; and the battery capacity of the electric vehicle is 30 kWh. The maintenance costs and power parameters of distributed energy are shown in Table 1.

TABLE 1

TABLE 1. Distributed energy parameters.

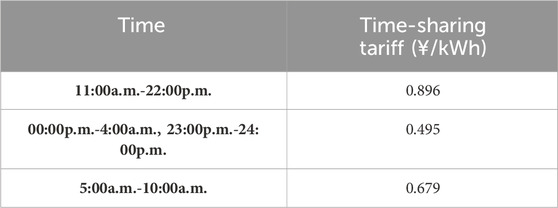
The storage batteries incorporated within the system are multifunctional, providing both charging and discharging capabilities that synergize seamlessly with the electric vehicle’s operations. Specifically, during instances where the photovoltaic power generation system faces constraints due to factors such as insufficient light, the storage batteries become instrumental. They supply power to household loads, especially during peak electricity pricing periods. Conversely, when the distributed energy sources are unable to meet the demand and necessitate recharging, the system strategically dispatches them to the grid during periods characterized by lower electricity prices. This strategic maneuvering significantly curtails household electricity expenses. To provide a comprehensive understanding of the financial dynamics, the time-of-day tariff structure employed in this study is meticulously delineated in Table 2. This table enumerates the tariff rates corresponding to distinct time intervals. For instance: The morning peak period, spanning from 07:00 to 09:00, incurs a tariff of ¥0.679 per kWh. The daytime bracket, ranging from 11:00 to 17:00, attracts a tariff of ¥0.896 per kWh. During the nighttime window, extending from 23:00 to 05:00, the tariff stands at ¥0.495 per kWh. The delineated time-based tariff structure underscores a strategic financial approach. It encourages households to leverage lower-cost charging opportunities during nighttime and off-peak hours. Conversely, prudent consumption practices during peak hours are advocated to mitigate overall electricity expenditure.

TABLE 2

TABLE 2. Timely electricity price data by household location.

4.2 Multi-objective optimization results for home microgrids

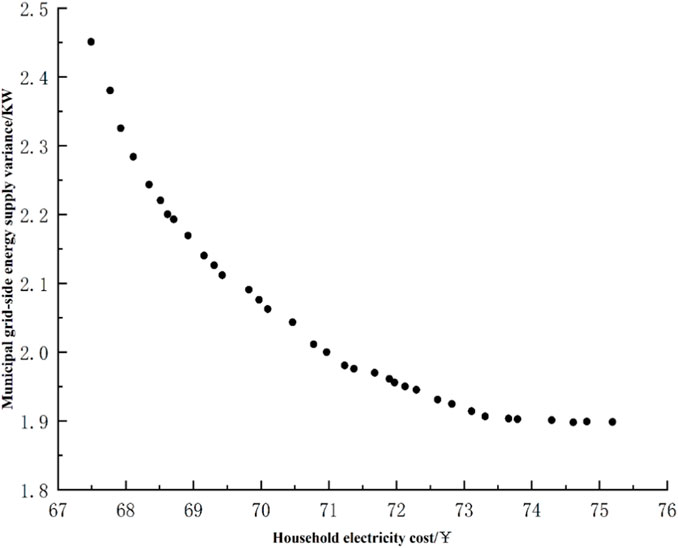
This algorithm produces 34 Pareto-optimal solutions after 100 iterations, and the resulting Pareto-optimal frontier is shown in Figure 4.

FIGURE 4

FIGURE 4. Pareto frontier calculated by MOPSO.

The Pareto frontier, characterized by its smooth and evenly distributed curves, underscores the algorithm’s aptitude in addressing multi-objective optimization challenges within this research framework. A discernible negative correlation emerges between household electricity expenses and grid-side output variance, accentuating the intricacies of load management during tariff variations.

The aggregation of electricity consumption during low-cost periods diminishes household expenses but concurrently instigates heightened demand on the grid. This behavior could jeopardize grid stability and reliability, amplifying supply system burdens and compromising user electricity consumption comfort. Through meticulous MATLAB-based optimization, these concerns are alleviated. Specifically, the optimization ensures distributed energy sources mitigate consumption peaks, regulate grid-side load fluctuations, and cater to demand-side preferences.

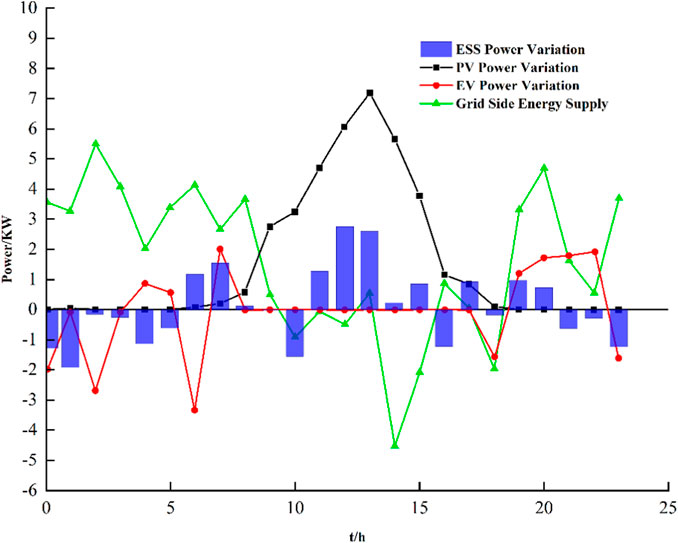
Comparison with Table 3 data reveals a 14% reduction in household electricity expenses post-optimization. Moreover, grid-side energy supply variance diminishes by 61.9%, underscoring enhanced grid reliability. Figure 5 elucidates each energy source’s operational dynamics within the household microgrid, emphasizing the PV system’s daytime prominence, battery storage’s peak-demand support, and the EV’s dual role based on its charge status. The operational model maintains a harmonious balance among consumption, cost-efficiency, and grid resilience, validating the optimization framework’s efficacy.

TABLE 3

TABLE 3. Results of multi-objective optimal scheduling for home microgrid.

FIGURE 5

FIGURE 5. Operating power of each energy source after optimal dispatch.

It can be observed that the PV system contributes significantly during the daytime when solar radiation is available, the battery storage system provides power during peak demand periods, and the EV is both a load and possibly a potential energy source depending on its state of charge. It is assumed that the owner of the EV leaves home for work at 8:00 p.m. during the day, and that the EV is connected to the home microgrid system to start working at 5:00 p.m., while ensuring that the depth of discharge of the EV does not exceed 80%, thus increasing the lifetime of both the storage battery and the EV. Figure 5 summarizes the dynamic equilibrium behavior between energy consumption, cost savings, and grid stability, highlighting the effectiveness of the optimization model in improving the operational efficiency of the home microgrid.

5 Discussions

5.1 Changes in household electricity load capacity before and after optimization

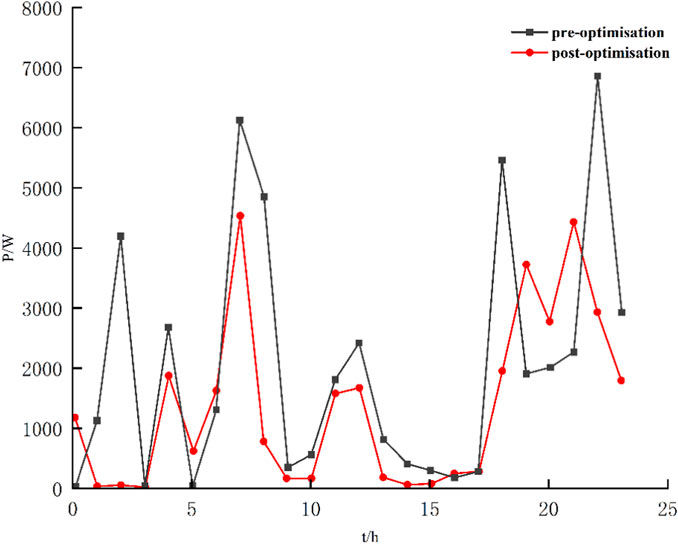
The visual representation in Figure 6 delineates the variations in the household electricity load before and after optimization efforts. It is evident that prior to optimization, the electric vehicle in the household microgrid is in the charging state. The peak periods of home power consumption are 7:00-8:00 a.m. and 10:00-11:00 p.m., with maximum power demand reaching 6133 W and 6856 W, respectively. Additionally, when the EV is disconnected from the home microgrid, 12:00 p.m. becomes another peak period for home power consumption, with a maximum demand of 2422 W.

FIGURE 6

FIGURE 6. Changes of household load curve before and after optimization.

Following the optimization process, the household load demand decreases to 4559 W at 7:00, with the storage battery outputting 1.8 kWh. At 12:00, the household load demand decreases to 1693W, with the PV system outputting 6 kWh. Meanwhile, at 22:00, the household electricity demand drops to 4450W, while the electric vehicle battery discharges 2 kWh.

Under the scheduling strategy of the optimization algorithm, the required electrical energy difference for household loads during the day is primarily supplied by the photovoltaic power generation system and the energy storage battery. At night, when electric vehicles are used as the energy supply source, the required power difference is mainly supplied by electric vehicles and energy storage batteries. This reduces the impact of the grid peak on the utility and alleviates the pressure on household electricity consumption by effectively optimizing the scheduling of household flexible loads.

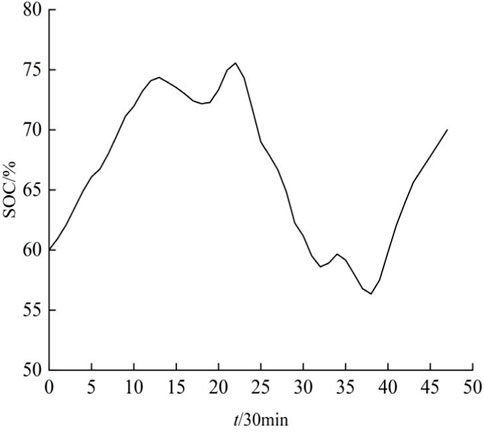
5.2 Changes in storage battery capacity after optimization

The depicted daily power dynamics of the home’s energy storage battery, as showcased in Figure 7, elucidate its performance post the optimization of the home microgrid system. Initially configured at a 60% capacity threshold, the battery’s operational behavior is meticulously managed through the optimization paradigm.

FIGURE 7

FIGURE 7. Changes of home energy storage battery capacity.

During daylight hours, when ambient light levels are conducive, the PV power generation system orchestrates a dual function: recharging the storage battery while simultaneously fulfilling the energy requirements of the household loads. This synergy ensures that surplus energy harnessed during optimal light conditions is efficiently stored for subsequent utilization, enhancing overall system sustainability and reducing dependency on external grid resources.

Conversely, during nocturnal hours when solar irradiance wanes, rendering the PV system less effective, the storage battery seamlessly transitions into its role as a micro-power hub. It continues to serve the home microgrid system, supplying requisite power and ensuring uninterrupted energy provisioning to critical household functionalities.

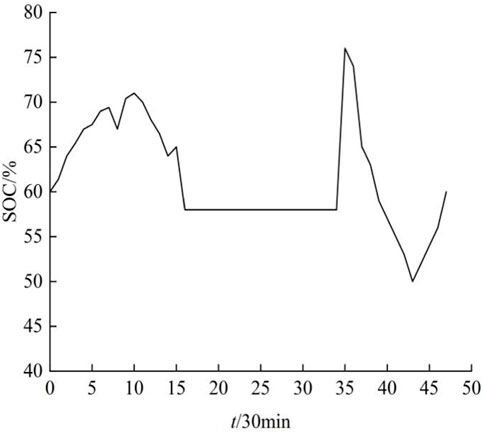
5.3 Changes in battery capacity of EV after optimization

Figure 8 delineates the transformation in the EV battery capacity, initialized at a 60% threshold, throughout the optimized operational scenario. The graph offers insights into the nuanced interplay between the EV’s battery state and the overarching home microgrid system dynamics.

FIGURE 8

FIGURE 8. Changes of electric vehicle battery capacity.

During daylight intervals, the PV system takes on the pivotal role of recharging the EV’s battery while it remains stationed at home. This solar-powered charging mechanism not only capitalizes on renewable energy sources but also primes the EV for subsequent commutes, optimizing its operational efficiency.

However, upon the owner’s departure for work, the EV transitions out of the home microgrid’s operational ambit, marking a divergence in its energy dynamics until its return. Upon reconnecting to the home microgrid during nocturnal hours, an intriguing pattern emerges: the EV’s power consumption registers a reduction of approximately 10% compared to its off-grid operational metrics.

A salient feature of the optimized strategy manifests when electricity tariffs oscillate. During periods of elevated electricity prices, the EV pivots from being a passive consumer to an active energy contributor. It seamlessly integrates into the home microgrid ecosystem, channeling its stored energy to power essential household loads. This strategic shift not only curtails reliance on the power grid during peak demand cycles but also amplifies the system’s resilience by diversifying energy sources.

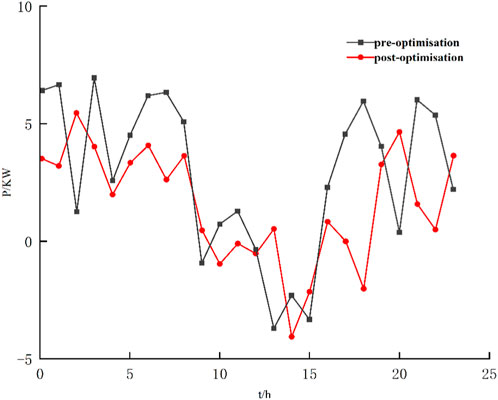
5.4 Changes in grid-side power supply before and after optimization

Figure 9 delineates the alterations in grid-side energy supply pre and post-optimization. The graphical representation vividly illustrates that prior to optimization, the period characterized by the lowest tariffs aligns with the household’s peak electricity consumption window, registering an average consumption close to 5 kW. Such a pattern induces erratic fluctuations in grid energy supply, consequently compromising the quality of household electricity supply.

FIGURE 9

FIGURE 9. Changes of grid-side energy supply power before and after optimization.

Conversely, with the implementation of the optimized scheduling management strategy, the average energy draw during peak tariff hours diminishes substantially to around 2 kW. Leveraging the capabilities of the PV power generation system and the storage battery, surplus electricity is channeled back to the grid at strategic intervals, notably at 14:00 and 18:00, facilitating efficient energy reclamation.

Furthermore, the integration of EV into the household microgrid system proves advantageous. They play a pivotal role in attenuating the household’s reliance on the grid during low-tariff periods, thereby augmenting electricity consumption comfort while curtailing costs. A comparative analysis of grid-side energy supply pre and post-optimization underscores the efficacy of this strategy in peak shaving and valley filling. Remarkably, the daily grid-side electricity consumption within the home microgrid system post-optimization is halved compared to its pre-optimized counterpart.

This optimized approach not only amplifies the efficacy of distributed renewable energy utilization and curtails electricity consumption costs but also refines the grid-side energy supply curve. The resultant benefits include bolstered security and stability in grid operations, culminating in an enhanced quality of household electricity consumption.

6 Conclusion

In this study, we have introduced a sophisticated multi-objective optimization framework tailored explicitly for home microgrids. The primary objectives encapsulated within this model are the minimization of electricity consumption costs and the mitigation of grid-side variances. By focusing on enhancing centralized electricity consumption within home microgrids, our model encapsulates an intricate strategy that meticulously integrates each distributed energy source with household loads.

A pivotal aspect of our model revolves around considering daily electricity demands juxtaposed against time-of-day tariffs and user comfort preferences. Through rigorous examination, we delineated the transformative impact of this optimization strategy on both the components of the home microgrid and the overarching grid-side power supply dynamics. Empirical validations affirm the salient effectiveness and guiding prowess of our proposed methodology.

The computational framework leverages the Multi-Objective Particle Swarm Optimization (MOPSO) algorithm, calibrated meticulously with constraints that synchronize distributed energy source power limitations with corresponding battery charging and discharging paradigms. Our analytical assessments, rooted in the arithmetic examples, elucidate that the delineated strategy yields tangible reductions in daily household electricity consumption expenditures.

Furthermore, judicious allocation strategies for distributed energy sources within the household microgrid not only fortify grid-side operational reliability but also optimize energy utilization metrics. This approach synergistically augments the quality and efficiency of household electricity consumption profiles.

While our research framework unveils promising outcomes, it is imperative to acknowledge its current limitations, notably the limited spectrum of integrated distributed energy models and nascent explorations into home load forecasting. Future research trajectories could encompass the integration of diversified distributed energy systems, such as wind power generation. Concurrently, an expanded research ambit focusing on refining home load forecasting methodologies would augment the model’s predictive robustness and real-world applicability.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

YH: Writing–original draft. GH: Writing–review and editing, Funding acquisition. ZP: Software. YZ: Data curation. QL: Methodology. CD: Resources.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported in part by the China Southern Power Grid Corporation Technology Project (066600KK52222044/GZKJXM20222165).

Conflict of interest

Authors YH, ZP, YZ, and CD were employed by Electric Power Research Institute of Guizhou Power Grid Co., Ltd. Author GH was employed by China Southern Power Grid. Author QL was employed by Duyun Power Supply Bureau of Guizhou Power Grid Co Ltd.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ben Slama, S. (2021). Design and implementation of home energy management system using vehicle to home (H2V) approach. J. Clean. Prod. 312, 127792. doi:10.1016/j.jclepro.2021.127792

CrossRef Full Text | Google Scholar

Ding, M., Zhang, Y., Mao, M., Yang, W., and Liu, X. (2016). Steady model and operation optimization for microgrids under centralized control. Automation Electr. Power Syst. 33 (24), 78–82. doi:10.3321/j.issn:1000-1026.2009.24.018

CrossRef Full Text | Google Scholar

Elkazaz, M., Sumner, M., Pholboon, S., Davies, R., and Thomas, D. (2020). Performance assessment of an energy management system for a home microgrid with PV generation. Energies 13, 3436. doi:10.3390/en13133436

CrossRef Full Text | Google Scholar

Fouladfar, M. H., Saeed, N., Marzband, M., and Franchini, G. (2021). Home-microgrid energy management strategy considering EV's participation in DR. Energies 14, 5971. doi:10.3390/en14185971

CrossRef Full Text | Google Scholar

Gu, W., Wu, Z., and Wang, R. (2012). Multi-objective operation optimization of combined heat and power microgrid considering polluting gas emissions. Automation Electr. Power Syst. 36 (14), 177–185. doi:10.3969/j.issn.1000-1026.2012.14.033

CrossRef Full Text | Google Scholar

Han, F., Zeng, C., and Miao, H. (2021). Home microgrid energy management system considering EV and renewable energy. J. Electr. Power Sci. Technol. 36 (01), 79–86. doi:10.19781/j.issn.1673-9140.2021.01.009

CrossRef Full Text | Google Scholar

Jiang, B., and Fei, Y. (2015). Smart home in smart microgrid: a cost-effective energy ecosystem with intelligent hierarchical agents. IEEE Trans. Smart Grid 6 (1), 3–13. doi:10.1109/tsg.2014.2347043

CrossRef Full Text | Google Scholar

Jin, M., Zhu, X., and Zhou, Q. (2023). Quantitative assessment of influence of renewable energy on peak regulation characteristics of power grid and its application. High. Volt. Appar. 59 (04), 70–76. doi:10.13296/j.1001-1609.hva.2023.04.010

CrossRef Full Text | Google Scholar

Jongerden, M. R., and Haverkort, B. R. (2017). Which battery model to use? Softw. Iet 3 (6), 445–457. doi:10.1049/iet-sen.2009.0001

CrossRef Full Text | Google Scholar

Khan, O., Xiao, W., and Moursi, M. S. E. (2017). A new PV system configuration based on submodule integrated converters. IEEE Trans. Power Electron. 32 (5), 3278–3284. doi:10.1109/tpel.2016.2633564

CrossRef Full Text | Google Scholar

Li, J., Ding, Z., You, H., and Yang, B. (2023b). Research on stable operation of new power system supported by grid-forming energy storage system. High. Volt. Appar. 59 (07), 1–11. doi:10.13296/j.1001-1609.hva.2023.07.001

CrossRef Full Text | Google Scholar

Li, J., Mu, G., Zhang, J., Li, C., Yan, G., Zhang, H., et al. (2023c). Dynamic economic evaluation of hundred megawatt-scale electrochemical energy storage for auxiliary peak shaving. Prot. Control Mod. Power Syst. 8, 50. doi:10.1186/s41601-023-00324-8

CrossRef Full Text | Google Scholar

Li, Z., Xu, Y., Wang, P., and Xiao, G. (2023a). Restoration of multi energy distribution systems with joint district network recon figuration by a distributed stochastic programming approach. IEEE Trans. Smart Grid 23, 1–13. doi:10.1109/TSG.2023.3317780

CrossRef Full Text | Google Scholar

Li, S., and Yang, J. (2019). Real-time optimization strategy of household renewable energy based on dual battery packs. Renew. Energy 37 (07), 1007–1014. doi:10.3969/j.issn.1671-5292.2019.07.011

CrossRef Full Text | Google Scholar

Li, Z., Wu, L., Xu, Y., and Zheng, X. (2022). Stochastic-weighted robust optimization based bilayer operation of a multi-energy building microgrid considering practical thermal loads and battery degradation. IEEE Trans. Sustain. Energy 13 (2), 668–682. doi:10.1109/TSTE.2021.3126776

CrossRef Full Text | Google Scholar

Li, Z., Xu, Y., Fang, S., Wang, Y., and Zheng, X. (2020). Multiobjective coordinated energy dispatch and voyage scheduling for a multienergy ship microgrid. IEEE Trans. Industry Appl. 56 (2), 989–999. doi:10.1109/TIA.2019.2956720

CrossRef Full Text | Google Scholar

Liu, H., Lu, D., Yang, B., Yao, Y., Ye, J., and Xue, J. (2015). Dispatching strategy of energy storage power station that can suppress power fluctuation of distributed photovoltaic power generation with high penetration. High. Volt. Technol. 41 (10), 3213–3223. doi:10.13336/j.1003-6520.hve.2015.10.005

CrossRef Full Text | Google Scholar

Lou, W., Zhai, H., and Xu, L. (2021). Research on combined frequency regulation control strategy of wind power-storage-electric vehicle. Renew. Energy 39 (12), 1648–1654. doi:10.3969/j.issn.1671-5292.2021.12.014

CrossRef Full Text | Google Scholar

Ma, Y., Xie, J., and Zhao, S. (2022). Multi-objective optimal dispatching for active distribution network considering park-level integrated energy system. Automation Electr. Power Syst. 46 (13), 53–61. doi:10.7500/aeps20210909001

CrossRef Full Text | Google Scholar

Merrington, S., Khezri, R., and Mahmoudi, A. (2022). Optimal planning of solar photovoltaic and battery storage for electric vehicle owner households with time-of-use tariff. IET generation, Transm. Distribution 3, 16. doi:10.1049/gtd2.12300

CrossRef Full Text | Google Scholar

Nan, Y., Di, Y., Zhou, Z., Jiazhan, C., Daojun, C., and Xiaoming, W. (2018). Research on modelling and solution of stochastic SCUC under AC power flow constraints. IET Generation Transm. Distribution 12 (15), 3618–3625. doi:10.1049/iet-gtd.2017.1845

CrossRef Full Text | Google Scholar

Qin, M., Yang, Y., Zhao, X., Xu, Q., and Yuan, L. (2023). Low-carbon economic multi-objective dispatch of integrated energy system considering the price fluctuation of natural gas and carbon emission accounting. Prot. Control Mod. Power Syst. 8, 61. doi:10.1186/s41601-023-00331-9

CrossRef Full Text | Google Scholar

Ruan, W., Wang, B., and Yang, L. (2012). Research on user response behavior under peak and valley time-of-use electricity prices. Grid Technol. 36 (07), 86–93.

Google Scholar

Sun, H., Chen, Z., and Wu, G. (2019). Real-time energy scheduling strategy for household microgrid considering the uncertainty of electric vehicles. Grid Technol. 43 (07), 2544–2551. doi:10.13335/j.1000-3673.pst.2018.2847

CrossRef Full Text | Google Scholar

Sun, J., Wan, Y., and Zheng, P. (2014). Orderly charging and discharging strategy of electric vehicles based on demand side management. J. Electrotech. Technol. 29 (08), 64–69.

Google Scholar

Wang, X., Qian, A., and Xu, W. (2016). Multi-objective optimal energy management of microgrid with distributed generation. Power Syst. Prot. Control 37 (20), 79–83. doi:10.3969/j.issn.1674-3415.2009.20.017

CrossRef Full Text | Google Scholar

Xu, P., Fu, W., Lu, Q., Zhang, S., Wang, R., and Meng, J. (2023). Stability analysis of hydro-turbine governing system with sloping ceiling tailrace tunnel and upstream surge tank considering nonlinear hydro-turbine characteristics. Renew. Energy 210, 556–574. doi:10.1016/j.renene.2023.04.028

CrossRef Full Text | Google Scholar

Yang, N., Dong, Z., Wu, L., Zhang, L., Shen, X., Chen, D., et al. (2022a). A comprehensive review of security-constrained unit commitment. J. Mod. Power Syst. Clean Energy 10 (3), 562–576. doi:10.35833/mpce.2021.000255

CrossRef Full Text | Google Scholar

Yang, N., Qin, T., Wu, L., Huang, Y., Huang, Y., Xing, C., et al. (2022b). A multi-agent game based joint planning approach for electricity-gas integrated energy systems considering wind power uncertainty. Electr. Power Syst. Res. 204, 107673. doi:10.1016/j.epsr.2021.107673

CrossRef Full Text | Google Scholar

Yang, N., Yang, C., Wu, L., Shen, X., Jia, J., Li, Z., et al. (2022c). Intelligent data-driven decision-making method for dynamic multisequence: an E-Seq2Seq-based SCUC expert system. IEEE Trans. Industrial Inf. 18 (5), 3126–3137. doi:10.1109/tii.2021.3107406

CrossRef Full Text | Google Scholar

Yang, N., Yang, C., Xing, C., Ye, D., Jia, J., Chen, D., et al. (2022d). Deep learning-based SCUC decision-making: an intelligent data driven approach with self-learning capabilities. IET Generation, Transm. Distribution (Wiley-Blackwell) 16 (4), 629–640. doi:10.1049/gtd2.12315

CrossRef Full Text | Google Scholar

Yang, Y., Li, Z., Mandapaka, P. V., and Lo, E. Y. M. (2023). Risk-averse restoration of coupled power and water systems with small pumped-hydro storage and stochastic rooftop renewables. Appl. Energy 339, 120953. doi:10.1016/j.apenergy.2023.120953

CrossRef Full Text | Google Scholar

Zhang, M., Yan, T., Lai, X., Chen, J., Niu, M., and Xu, S. (2018). Development vision and technicalpath of energy storage technology under the new functional form of power grid. Grid Technol. 42 (05), 1370–1377. doi:10.13335/j.1000-3673.pst.2017.2475

CrossRef Full Text | Google Scholar

Zhang, Y., Zeng, P., and Chuanzhi, C. (2016). Optimal scheduling algorithm of home energy management system in smart grid environment. Power Syst. Prot. Control 44 (02), 18–26. doi:10.7667/j.issn.1674-3415.2016.02.003

CrossRef Full Text | Google Scholar

Zheng, W., and Huang, S. (2021). Home energy management system based on power router. J. Power Supply 19 (03), 86–92. doi:10.13234/j.issn.2095-2805.2021.3.86

CrossRef Full Text | Google Scholar

Zhou, D., Xie, P., Huang, Y., Cheng, G., Tang, W., Zou, K., et al. (2023). Optimization method of power grid material warehousing and allocation based on multi-level storage system and reinforcement learning. Comput. Electr. Eng. 109, 108771. doi:10.1016/j.compeleceng.2023.108771

CrossRef Full Text | Google Scholar

Zhu, B., Yang, Y., Wang, K., Liu, J., and Vilathgamuwa, M. (2023). High transformer utilization ratio and high voltage conversion gain flyback converter for photovoltaic application. IEEE Trans. Industry Appl. 99, 1–13. doi:10.1109/TIA.2023.3310488

CrossRef Full Text | Google Scholar