- 1Electric Power Research Institute of State Grid Liaoning Electric Power Co., Ltd., Shenyang, China
- 2State Grid Liaoning Electric Power Supply Co., Ltd., Shenyang, China
- 3School of Automation, Chengdu University of Information Technology, Chengdu, China
The increasing integration of various energy sources and the adoption of smart grid technologies have revolutionized the way we generate, distribute, and consume energy. While these advancements offer numerous benefits, they also introduce vulnerabilities to cyber–physical attacks. To this aim, this paper investigates a resilient energy management strategy for integrated energy systems. By adopting a switched control approach and incorporating a local estimation mechanism, we have developed a resilient distributed energy management strategy to tackle the energy management problem (EMP) in integrated energy systems (IESs). This methodology demonstrates strong robustness and resilience, successfully detecting data integrity attacks and denial-of-service (DoS) attacks. Finally, we provide a case study to demonstrate the effectiveness of our proposed strategy in a real-world scenario.
1 Introduction
Integrated energy systems (IESs), encompassing various energy sources, storage systems, and smart grid technologies (Liu et al., 2023; Liu et al., 2022), have significantly improved the efficiency and sustainability of energy generation and distribution. The energy management problem (EMP) is the core research problem in IESs (Li et al., 2020; Li et al., 2020; Li et al., 2022). EMP can be conceptualized as an optimization challenge constrained by the goal of minimizing overall costs or maximizing societal benefit (Li et al., 2021; Zhang et al., 2023). This optimization aims to achieve these objectives while simultaneously ensuring a balance between energy supply and demand and adhering to operational constraints.
The algorithms designed for EMP can be broadly categorized as either centralized or distributed methods. Traditional centralized algorithms, such as the reinforcement learning algorithm (Yang et al., 2022) and cuckoo algorithm, have been extensively explored in previous research. However, a significant limitation of these algorithms lies in their centralized nature, demanding a central controller to collect and process all relevant information to compute optimal solutions. With the integration of distributed energy resources, there is a growing inclination to shift computationally intensive tasks toward the edge (Teng et al., 2023). Additionally, distributed participants are hesitant to divulge personal data to a centralized controller due to concerns regarding security and financial gain. To address this issue, distributed methods have been proposed, which attract significant attention. The distributed algorithms possess several advantages: 1) Scalability: Distributed methods are highly scalable. They can efficiently handle large-scale problems by dividing the computational workload among multiple agents or nodes. 2) Flexibility: Distributed optimization can adapt to dynamic environments and changing conditions more effectively. Each node can respond to local changes independently, which is particularly useful in rapidly changing or unpredictable environments. 3) Privacy: In distributed optimization, each node or agent can keep its data local, which is beneficial for privacy-sensitive applications. The distributed methods primarily encompass the alternating direction method of multipliers (ADMM)-based approaches and consensus-based methods. As an illustration, a distributed energy management framework and model were introduced in Zhang et al. (2017), taking into account interrelated power, heat, and gas systems. In this context, an innovative distributed consensus-ADMM algorithm was devised to ascertain the global optimal operation for each participating entity. Utilizing a similar approach, the distributed consensus-ADMM algorithm was subsequently extended to address the multi-period energy management problem (EMP) for manufacturing execution systems (MESs), incorporating certain linearized network constraints (Xu et al., 2020). Building upon the foundation laid in Zhang et al. (2017), an asynchronous event-triggering-based distributed energy management algorithm was introduced in Li et al. (2019). This algorithm adeptly manages the distinctive timescales inherent in various energy network types. Furthermore, the concept of the We-Energy (WE) model, akin to the multi-energy prosumer concept, was unveiled in Sun et al. (2019). Concurrently, a distributed double-consensus (DDC) algorithm was introduced to facilitate cooperative energy management among multiple WE entities. Recently, various distributed optimization algorithms have been developed to cater to diverse application requirements. These include the adoption of a Newton-based method to expedite convergence (Li et al., 2021), a federated reinforcement learning algorithm (Lee and Choi, 2022), and a double-side coordinative method (Zhou et al., 2023).
The prior research mentioned above has effectively addressed EMP for IESs, yielding satisfactory results. However, it is worth noting that the efficacy of these methods relies on a fundamental assumption: the reliability of the communication network. The distributed algorithms are executed within a communication network that is susceptible to various malicious cyberattacks. In recent years, notable efforts have been undertaken to investigate the impact of different cyberattacks on distributed energy management algorithms. To elaborate, Zeng et al. (2017), Zhao et al. (2017), and Duan and Chow (2019) delved into the vulnerability of the distributed lambda iteration algorithm in the context of data integrity attacks. In such scenarios, the energy management system’s operation may be compromised by the injection of false data into exchanged information or local utilization data. In contrast, denial-of-service (DoS) attacks are aimed at obstructing and disrupting information sharing among agents. These attacks can have severe consequences for IES security operations, as communication is disrupted during the DoS attack period, resulting in a fractured structure of the distributed communication network. In this scenario, agents cannot exchange real-time and accurate data with their neighbors, potentially causing a global supply and demand mismatch, leading to system failures and substantial economic losses. Developing effective dispatch strategies to withstand such attacks becomes imperative. In response, Zhang et al. (2019) introduced a DoS-attack-robust strategy that combats DoS attacks by implementing a mixed-integer linear programming method to allocate the load demand. Li et al. (2017) proposed a novel robust distributed economic dispatch strategy capable of identifying and isolating misbehaving distributed generators to safeguard the rest of the system. Most recently, Huang et al. (2022) introduced a privacy-preserving protocol-based distributed robust dispatch approach for MESs. This method proficiently addresses both colluding and non-colluding attacks. Additionally, Li et al. (2022) analyzed the impact of DoS attacks and proposed an effectively double-gradient-descent algorithm to resist the DoS attacks.
Although the existing research has investigated EMP under diverse cyberattacks, they still suffer from two key challenges: 1) the existing distributed and resilient energy management strategies are mainly designed to deal with a single type of cyberattack, such as data integrity or DoS attacks. It is highly needed to develop new algorithms that are compatible with integrity and DoS attacks simultaneously; 2) the existing distributed energy management strategies, considering cyberattacks, work on connected communication networks. However, in reality, the communication networks may not be two-way. It is necessary to design distributed algorithms that can handle directed graphs.
To tackle those challenges, we propose an attack-resilient distributed energy management strategy that is capable of handling integrity and DoS attacks and working under a directed communication network. The contributions of this paper are summarized as follows:
1) By introducing a switched control and local estimation mechanism, an attack-resilient distributed energy management strategy can be developed to solve EMP in IESs. The proposed method can well resist both integrity and DoS attacks, resulting in strong robustness and resilience.
2) The proposed energy management strategy fits well with the directed communication network. Compared with the existing distributed studies (Zeng et al., 2017; Zhao et al., 2017; Li et al., 2018; Duan and Chow, 2019; Zhang et al., 2019; Li et al., 2022; Huang et al., 2022), it possesses strong expansibility and universality.
2 Formulation of EMP in IES
An IES consists of numerous interconnected energy bodies (EBs) and principal networks. Each EB integrates a diverse array of energy generation and conversion devices. This includes renewable generators (RGs), renewable heating devices (RHDs), fuel generators (FGs), fuel heating devices (FHDs), combined heat and power (CHP) devices, electricity storage systems (ESSs), heat storage systems (HSs), and gas producers (GPs). Furthermore, every EB encompasses energy loads consisting of power, heat, and gas loads. These loads further comprise must-run and schedulable loads that are connected to their respective energy buses. The EMP of IES is more complex than that of smart grids due to the following two parts. On the one hand, IES typically encompasses a wider array of energy resources compared to a smart grid. While smart grids primarily focus on electrical energy, integrating aspects like renewable energy sources, demand response, and storage, IES includes not only electricity but also other forms of energy, such as heat, gas, and sometimes cooling systems. Managing these diverse energy types, each with its own dynamics and constraints, adds complexity to EMP. On the other hand, the objectives of managing IES are more diverse and complex. In addition to ensuring the reliability and efficiency of each energy system, IES must optimize the overall system operation considering economic factors and the balance between different energy sources. This multifaceted objective set goes beyond the primary electrical focus of smart grids.
2.1 Model of EB
Considering the energy generation and consumption of single EB, electricity is produced from RG, FG, and CHP, represented as
Beyond the supply–demand balance constraints, each EB adheres to a series of localized operational constraints. Primarily, these constraints fall under six categories:
1) Capability constraints for FG, FHD, and GP are given by
where the superscripts “min” and “max” indicate the respective minimum and maximum permissible values.
2) Forecasting error-adjusted confidence constraints for RG and RHD are given by
3) The operational feasibility region of CHO is composed of four linear inequality constraints defined as
where
4) Consideration of permissible charging/discharging processes and accumulated energy for ES and HS is given by
where
5) Restrictions on energy loads and associated proportions are given by
where
Next, the calculation of benefits for each individual EB, which directs optimal operational behavior, encompasses the following six components:
1) Derived from fuel costs, the FG and FHD cost functions, along with CHP, are expressed as
where
2) When contemplating the balance between optimality and generative likelihood, the cost functions of RG and RHD are
where
3) The cost functions of ES and HS can be represented as
where
4) The expression of GP’s cost function is
where
5) With demand response in focus, the energy load’s utility function is
where
The reasons for why we chose the second-order form of the load utility function are as follows: first, the second-order utility function provides a more accurate representation of user satisfaction in scenarios where it is not just the service itself but the rate of change in service quality that impacts user perception. Second, the second-order utility function provides the flexibility needed to model various user behaviors and preferences under different conditions. Third, this form of utility function offers a good balance between complexity and analytical tractability. It allows us to derive meaningful insights and results without overly complicating the mathematical framework.
2.2 Model of EMP
The overall objective of EMP of IES is to maximize the social welfare. Its mathematical expression is given by
For the sake of analysis, we stipulate that the three-dimensional vector
where
Note that the cost function for each component is the convex function within the corresponding local operation region. Meanwhile, the global supply and demand constraint shown in Eq. 19 is the affine function. Thus, our studied problem is a convex problem. According to the convex theory, there is only one optimal point. Thus, in our considered model, there exists only one equilibrium point, which is the optimal point.
3 Attack-resilient distributed energy management strategy
3.1 Attack models
This study delves into the utilization of a distributed algorithm to address EMP. As the operational framework of such algorithms is deeply rooted in a distributed communication network, it becomes inherently vulnerable to diverse cyberattacks. In this paper, we consider data integrity and DoS attacks. The major mechanisms affected by the two types of cyberattacks on EMP are as follows:
1) Data integrity attacks in energy management algorithms refer to cyberattacks where adversaries manipulate or tamper with the data being used by these algorithms, leading to faulty decision-making. Energy management systems rely on accurate data to efficiently control and distribute energy resources. By compromising the integrity of these data, attackers can cause operational inefficiencies, financial losses, system instabilities, and even safety hazards.
2) DoS attacks, in the context of computer networks, refer to attempts to make a machine, service, or network resource unavailable to its intended users by flooding the targeted system with superfluous requests in an effort to overload systems and prevent some or all legitimate requests from being fulfilled. The potential disruption by multiple adversaries targeting the communication flow between EBs is recognized, which can lead to an enduring compromise of essential shared data.
In order to divide the attack and non-attack zones, we provide the following definitions: Starting at a reference point
3.2 Directed communication network
We study a directional communication network, represented by
3.3 Main algorithm
In this section, we propose a discrete-time attack-resilient distributed energy management algorithm to solve EMP, considering data integrity and DoS attacks. First, we define the following switched control variables:
where
Next, the updating rules of the discrete-time attack-resilient distributed energy management algorithm are given by
where
We elaborate the updating processes, including the following steps:
Step (1) Each agent tries to send the information of
Step (2) Each agent should identify whether it is subjected to data integrity attacks and DoS attacks based on the methods proposed in Li T. et al. (2022) and Huang et al. (2022), respectively. Then, each agent is able to identify the current categories for
Step (3) Each agent updates
Step (4) Each agent updates
Step (5) Repeat Steps (1–4) until the algorithm converges to stable values.
Based on the aforementioned processes, it can be observed that each agent only needs to share the information of
In this paper, we design a discrete-time algorithm to solve EMP. The reasons are as follows: first, by using the discrete-time algorithm, agents are executed at discrete time steps, making it easier to synchronize information sharing across distributed agents. This is particularly useful in IES, where coordinating the timing of operations is crucial. Second, discrete-time algorithms can be more resource-efficient in certain contexts. They can be designed to operate only at specific intervals, reducing the need for continuous computation and potentially saving on energy and computational resources. Last but not least, discrete-time algorithms offer flexibility in implementation, especially in digital systems where time is naturally discretized. This makes them well-suited for implementation in digital computers and microcontrollers.
4 Simulation analysis
4.1 Setting of the test system
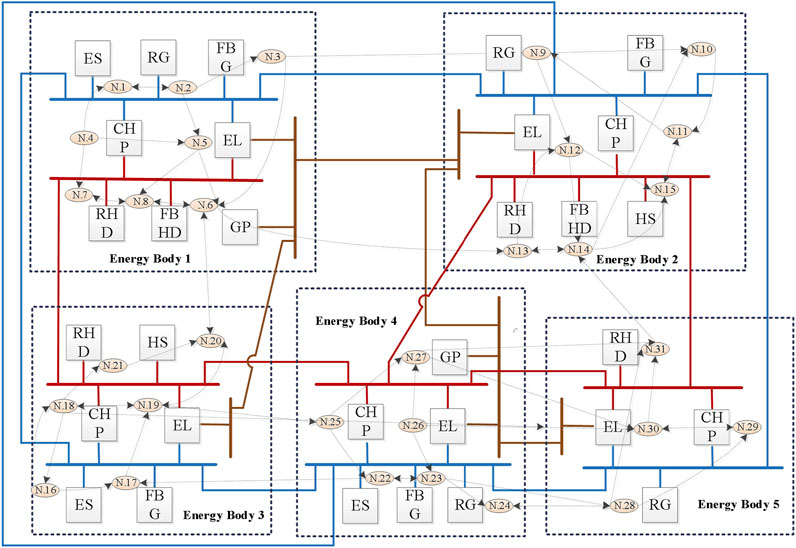
The effectiveness of the proposed method will be tested in IES with five EBs. Its physical and communication structures are shown in Figure 1, as described previously in Zhang et al. (2017). We also follow Zhang et al. (2017) to set the parameters of each EB. The communication interval is 0.01 s. We consider that the system is subjected to data integrity attacks during [0.40 s, 0.66 s] and [2.3 s, 2.55 s] and is subjected to DoS attacks during [6.1 s, 6.2 s] and [11.1 s, 11.12 s]. The scales of energy and price are unified as 1 p.u. = 1 MW for power or heat, 1 p.u. = 84 SCM/h for gas, and 1 p.u. = 1 $/MWh for price.
4.2 Convergence analysis
In this section, the proposed attack-resilient distributed energy management algorithm is performed to solve EMP. The simulation outcomes are shown in Figures 2–7.
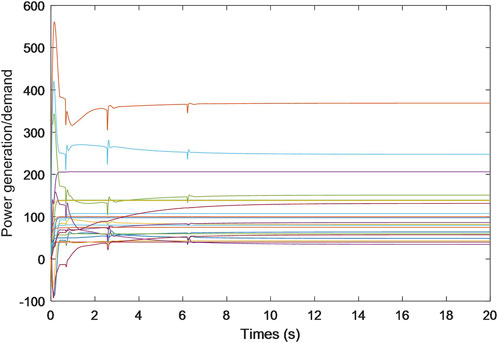
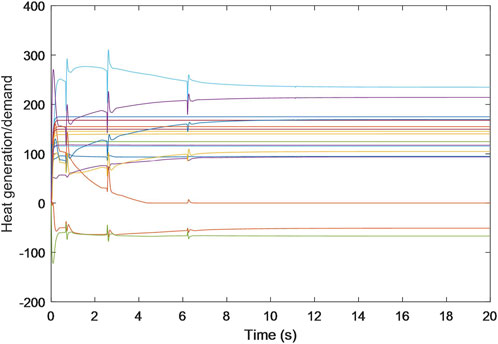
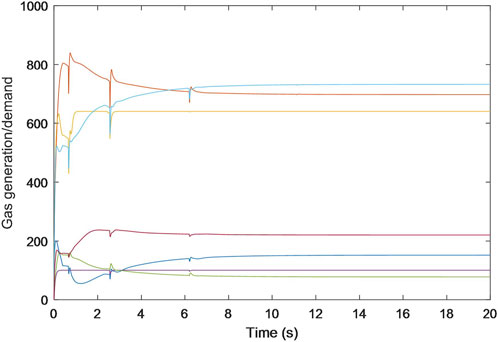
Specifically, Figures 2–4 exhibit the estimated calculations for power generation/demand, heat generation/demand, and gas generation/demand across all participating entities. Distinct colors within each graph are employed to differentiate between the various curves, each representing computational and convergence trajectory of each participant. These visual representations indicate that despite the data integrity and DoS attacks, the energy generation/demand (encompassing power, heat, and gas) for every participant is capable of stabilizing at a consistent value.
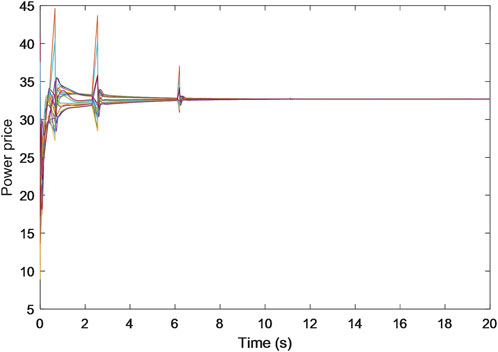
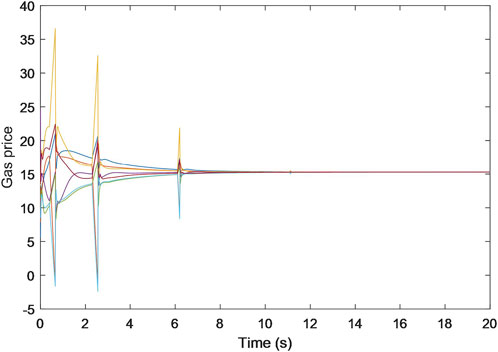
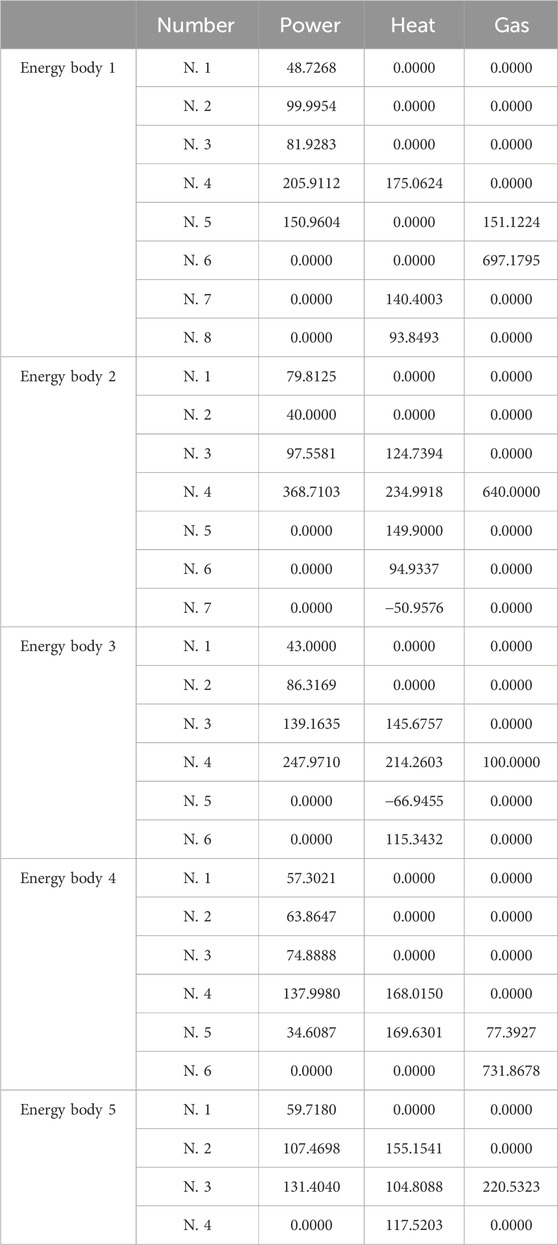
Additionally, the trajectories for the estimated prices of power, heat, and gas are shown in Figures 5–7, each progressively settling at three common values, ultimately representing the final market clearing prices for power, heat, and gas, respectively. This occurrence persists even in the face of data integrity and DoS attacks. The final settled values are marked at $32.6887 (p.u.) for the power price, $23.6611 (p.u.) for the heat price, and $15.2825 (p.u.) for the gas price. In addition, the final energy generation and demands are listed in Table 1. These values are consistent with those derived in scenarios devoid of attacks, as referenced from Zhang et al. (2017).
These findings collectively underscore the resilience and robustness of the S-NRBDEM algorithm, affirming its capacity to empower each participant to persistently seek optimal operational states and market clearing prices for energy.
5 Discussion
This paper addresses the pressing need for resilient energy management in the context of IESs; this necessity has become even more urgent due to the ever increasing integration of diverse energy resources and the rapid adoption of IES technologies. Through rigorous investigation and analysis, we have introduced and validated an attack-resilient distributed energy management strategy, augmented by a local estimation mechanism and switched control. This strategy has been meticulously designed to address not only data integrity attacks but also DoS attacks. The simulations conducted in IES with five EBs show that our proposed method enables estimated energy prices and energy generation/demand to converge to the corresponding optimal solutions, although there are both data integrity attacks and DoS attacks. The findings and insights garnered from this case study underscore the potential of our proposed strategy to serve as a reliable safeguard against cyber–physical threats, ensuring uninterrupted and secure energy management.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
TL: methodology, validation, and writing–original draft. FS: conceptualization, investigation, and writing–original draft. JC: formal analysis, validation, and writing–original draft. LW: conceptualization, formal analysis, and writing–original draft. ZY: formal analysis, project administration, and writing–review and editing. RL: data curation and writing–review and editing. JQ: writing–original draft and writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Science and Technology Project of Electric Power Research Institute of State Grid Liaoning Electric Power Supply Co., Ltd. and Research on Network Security Risk Analysis and Attack Recovery Strategies for Integrated Energy Information Systems Facing the Distribution Network Side (2023YF-155).
Conflict of interest
Authors TL, FS, JC, ZY, and RL were employed by Electric Power Research Institute of State Grid Liaoning Electric Power Co., Ltd. Author LW was employed by State Grid Liaoning Electric Power Supply Co., Ltd.
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Duan, J., and Chow, M. Y. (2019). A novel data integrity attack on consensus-based distributed energy management algorithm using local information. IEEE Trans. Industrial Inf. 15 (3), 1544–1553. doi:10.1109/TII.2018.2851248
Huang, B., Li, Y., Zhan, F., Sun, Q., and Zhang, H. (2022). A distributed robust economic dispatch strategy for integrated energy system considering cyber-attacks. IEEE Trans. Industrial Inf. 18 (2), 880–890. doi:10.1109/TII.2021.3077509
Lee, S., and Choi, D. H. (2022). Federated reinforcement learning for energy management of multiple smart homes with distributed energy resources. IEEE Trans. Industrial Inf. 18 (1), 488–497. doi:10.1109/TII.2020.3035451
Li, P., Liu, Y., Xin, H., and Jiang, X. (2018). A robust distributed economic dispatch strategy of virtual power plant under cyber-attacks. IEEE Trans. Industrial Inf. 14 (10), 4343–4352. doi:10.1109/TII.2017.2788868
Li, T., Chen, L., Jensen, C. S., and Pedersen, T. B. (2021a). TRACE: real-time compression of streaming trajectories in road networks. Proc. VLDB Endow. 14 (7), 1175–1187. doi:10.14778/3450980.3450987
Li, T., Chen, L., Jensen, C. S., Pedersen, T. B., Gao, Y., and Hu, J. (2022a). “Evolutionary clustering of moving objects,” in 2022 IEEE 38th International Conference on Data Engineering, Kuala Lumpur, Malaysia, 09-12 May 2022, 2399–2411.
Li, T., Huang, R., Chen, L., Jensen, C. S., and Pedersen, T. B. (2020b). Compression of uncertain trajectories in road networks. Proc. VLDB Endow. 13 (7), 1050–1063. doi:10.14778/3384345.3384353
Li, Y., Gao, D. W., Gao, W., Zhang, H., and Zhou, J. (2020a). Double-mode energy management for multi-energy system via distributed dynamic event-triggered Newton-raphson algorithm. IEEE Trans. Smart Grid 11 (6), 5339–5356. doi:10.1109/TSG.2020.3005179
Li, Y., Gao, D. W., Gao, W., Zhang, H., and Zhou, J. (2021b). A distributed double-Newton descent algorithm for cooperative energy management of multiple energy bodies in energy internet. IEEE Trans. Industrial Inf. 17 (9), 5993–6003. doi:10.1109/TII.2020.3029974
Li, Y., Li, T., Zhang, H., Xie, X., and Sun, Q. (2022b). Distributed resilient double-gradient-descent based energy management strategy for multi-energy system under dos attacks. IEEE Trans. Netw. Sci. Eng. 9 (4), 2301–2316. doi:10.1109/TNSE.2022.3162669
Li, Y., Zhang, H., Liang, X., and Huang, B. (2019). Event-Triggered-based distributed cooperative energy management for multienergy systems. IEEE Trans. Industrial Inf. 15 (4), 2008–2022. doi:10.1109/TII.2018.2862436
Liu, Z., Huang, B., Hu, X., Du, P., and Sun, Q. (2023). Blockchain-based renewable energy trading using information entropy theory. IEEE Trans. Netw. Sci. Eng., 1–12. doi:10.1109/TNSE.2023.3238110
Liu, Z., Xu, Y., Zhang, C., Elahi, H., and Zhou, X. (2022). A blockchain-based trustworthy collaborative power trading scheme for 5G-enabled social internet of vehicles. Digital Commun. Netw. 8 (6), 976–983. doi:10.1016/j.dcan.2022.10.014
Mellal, M. A., and Williams, E. J. (2020). Cuckoo optimization algorithm with penalty function and binary approach for combined heat and power economic dispatch problem. Energy Rep. 6, 2720–2723. doi:10.1016/j.egyr.2020.10.004
Sun, Q., Fan, R., Li, Y., Huang, B., and Ma, D. (2019). A distributed double-consensus algorithm for residential we-energy. IEEE Trans. Industrial Inf. 15 (8), 1–4842. doi:10.1109/TII.2019.2921431
Teng, F., Zhang, Y., Yang, T., Li, T., Xiao, Y., and Li, Y. (2023). Distributed optimal energy management for we-energy considering operation security. IEEE Trans. Netw. Sci. Eng., 1–11. doi:10.1109/TNSE.2023.3295079
Xu, D., Wu, Q., Zhou, B., Li, C., Bai, L., and Huang, S. (2020). Distributed multi-energy operation of coupled electricity, heating, and natural gas networks. IEEE Trans. Sustain. Energy 11 (4), 2457–2469. doi:10.1109/TSTE.2019.2961432
Yang, L., Sun, Q., Zhang, N., and Li, Y. (2022). Indirect multi-energy transactions of energy internet with deep reinforcement learning approach. IEEE Trans. Power Syst. 37 (5), 4067–4077. doi:10.1109/TPWRS.2022.3142969
Zeng, W., Zhang, Y., and Chow, M. Y. (2017). Resilient distributed energy management subject to unexpected misbehaving generation units. IEEE Trans. Industrial Inf. 13 (1), 208–216. doi:10.1109/TII.2015.2496228
Zhang, H., Li, Y., Gao, D. W., and Zhou, J. (2017). Distributed optimal energy management for energy internet. IEEE Trans. Industrial Inf. 13 (6), 3081–3097. doi:10.1109/TII.2017.2714199
Zhang, X., Li, Y., Li, T., Gui, Y., Sun, Q., and Gao, D. W. (2023). Digital twin empowered PV power prediction. J. Mod. Power Syst. Clean Energy. doi:10.35833/MPCE.2023.000351
Zhang, Z., Yue, D., Dou, C., Cheng, Z., and Chen, L. (2019). A robust consensus-based economic dispatch strategy under dos attack. IEEE Int. Conf. Industrial Cyber Phys. Syst. (ICPS) 127–132. doi:10.1109/ICPHYS.2019.8780286
Zhao, C., He, J., Cheng, P., and Chen, J. (2017). Analysis of consensus-based distributed economic dispatch under stealthy attacks. IEEE Trans. Industrial Electron. 64 (6), 5107–5117. doi:10.1109/TIE.2016.2638400
Keywords: cyberattacks, energy management, integrated energy systems, smart grid, distributed optimization
Citation: Li T, Sun F, Chen J, Wang L, Yang Z, Liu R and Qi J (2024) An attack-resilient distributed energy management strategy for integrated energy systems. Front. Energy Res. 11:1341984. doi: 10.3389/fenrg.2023.1341984
Received: 21 November 2023; Accepted: 26 December 2023;
Published: 11 January 2024.
Edited by:
Yushuai Li, University of Oslo, NorwayReviewed by:
Bi Liu, Anhui University, ChinaYihuan Li, North China Electric Power University, China
Xiao Wang, The University of Manchester, United Kingdom
Copyright © 2024 Li, Sun, Chen, Wang, Yang, Liu and Qi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jun Qi, MTM4OTgxNzc0NTJAMTYzLmNvbQ==
 Tong Li1
Tong Li1 Jun Qi
Jun Qi