Krill herd technique for dynamic economic dispatch problems with the integration of wind power generation

The krill herd (KH) approach is proposed in this article for tackling the dynamic economic dispatch (DED) problem with the integration of wind power generation, including constraints such as valve-point loadings and prohibited operating zones (PoZs). The purpose of resolving the DED problem is to determine the optimum feasible combination of power outputs for all allocated generating units within a given period while simultaneously meeting dynamic operational constraints and power demand. Due to the addition of valve points and PoZs to the cost characteristics of the generating unit, the DED issue becomes a highly non-linear and non-convex optimization issue. When transmission losses are taken into account, the DED problem becomes significantly more complex to solve. KH is a swarm-inspired algorithm based on krill individual herding behavior. KH employs two global and two local tactics, and these work in parallel, making KH a powerful algorithm. The effectiveness of the KH method is investigated and validated through extensive testing on various test systems, including 5-, 6-, 10-, 16-, and 30-unit test systems. Extensive studies are conducted to evaluate the efficacy of the proposed KH algorithm; the present research work compares the convergence properties of the suggested approach with those of the other recently published methods. In addition to reduced generation costs compared to other results published in recent literature, the numerical findings of the KH approach reveal that it has strong convergence qualities.

1 Introduction

Coal and gas, which are nonrenewable resources, are responsible for the generation of more than three-fourth of the world’s electricity. Because of their scarcity, these resources must be used wisely. As a result, optimizing the generating unit problem is critical. Supply–demand balancing is the equivalent constraint in this issue, which aims to reduce fuel costs. This issue is called the economic dispatch problem (Happ, 1977). In the 1920s, this issue was considered static because demand is constant for a specific period of time. Currently, the situation is more complicated because demand changes over time, necessitating the adjustment of the supply of each power plant in order to meet that change. In order to overcome the above issue, dynamic economic dispatch (DED) is implemented by taking into consideration the dynamic costs associated with switching from one generating level to the next. In addition to maintaining the thermal stress on the generating equipment, such as turbines and boilers, inside the permissible limits, the DED issue takes into account the generator valve-point loading effects and prohibited operating zones (PoZs) (Zaman et al., 2016).

In recent decades, conventional power generation plants such as thermal, gas, and oil facilities have traditionally served as the primary sources of electricity production, despite being significant contributors to environmental pollution. The increasing demand for power, the depletion of traditional energy resources, and the urgent need to curtail greenhouse gas emissions (such as CO₂, NOx, and SOx) have encouraged scientists to focus on renewable energy sources (RESs) (Ullah et al., 2019). Within the context of national energy conservation efforts and emissions reduction, RESs have demonstrated immense potential for reducing fuel consumption and emissions of pollutants. In this context, wind and solar energy production has experienced consistent growth over the past two decades due to its cost-effectiveness, environmental friendliness, and widespread availability, among other RES options (Perera, 2017).

DED is a dynamic issue because of the constantly shifting electrical grid and the wide range of possible load conditions. To address this issue, the whole dispatch period may discretize into a series of shorter periods, during each of which the load is believed to remain constant, and the system is observed as being under a condition of temporal steady state. However, some of the researchers have assumed that the cost functions are linear in order to simplify the mathematical formulation of the issue and make use of many of the standard optimization methods (Zaman et al., 2016). Several optimization strategies and processes have been utilized to solve the ED and DED issues with complicated objective functions or limitations since the 1980s when they were first described. This topic has been addressed using a variety of traditional approaches such as the gradient method (Granelli et al., 1989), linear programming (Somuah and Khunaizi, 1990), and dynamic programming (DP) (Xia and Elaiw, 2010). Although they provide certain advantages such as tremendous computation efficiency and being theoretically optimum (Xia and Elaiw, 2010), they have numerous downsides. For example, Ullah et al. (2019) did not take into account the basic constraints such as line flow limits and load voltage levels. Perera (2017) considered the line flows, but the main drawbacks of the LP method are the piece-wise linear cost approximation and algorithm complexity. DP (Somuah and Khunaizi, 1990) has a drawback that the computing needs of this method vary with the size of the discrete capacity step. Therefore, as the alternative for conventional approaches, evolutionary methods have gained great attention and demonstrated their usefulness as powerful optimizers for the DED problem in the last few decades, such as genetic algorithm (Li et al., 1997; Li and Aggarwal, 2000; Zhang et al., 2006; Basu, 2008; Preeti et al., 2022), simulated annealing (SA) (Panigrahi et al., 2006), evolutionary programming (EP) (Basu, 2007), particle swarm optimization (PSO) (Gaing, 2004; Yuan et al., 2009; Zhang et al., 2014), fuzzy optimization (Attaviriyanupap et al., 2004), the artificial immune system (Hemamalini and Simon, 2011), harmony search (Pandi and Panigrahi, 2011; Sahoo et al., 2021), and biography-based optimization (BBO) (Xiong and Shi, 2018).

Zhang et al. (2006) developed a novel hybrid real-coded genetic algorithm with quasi-simplex approaches for solving the constructed DED model. In the current work, a new strategy for generating the first population is proposed to enhance the search process. The economic scheduling of electric power production over a defined time period under different systems and operational limitations was presented by Li et al. (1997), using the hybrid genetic algorithm (HGA). The suggested hybrid system is designed such that a basic GA is used as the first level of search, making a rapid choice to focus the search on the best area, and then, a local search approach (gradient technique) is used to fine-tune the results. Li and Aggarwal (2000) developed a relaxed hybrid genetic algorithm and gradient method (RHGAGM) to allocate the generated power economically, rapidly, precisely, and without stress. The suggested hybrid method is built such that a GA conducts a preliminary search and makes fast judgments to guide the local GT in its ascent of the possible hill. By permitting a loose match between power production and load demand at the base search and compensating for any mismatch at the beginning of the local search, the suggested technique further assures the dispatch quality, as well as speed. Thus, a GA may devote the same amount of time and resources to finding the optimal cost/power trade-off as it does to finding the best possible answers. The strategy’s goal was to achieve cost savings in a sensible amount of time. A non-dominated sorting genetic algorithm II for the DED issue was solved by Basu (2008). To enhance the exploration capability of the GA, a three-parent crossover mechanism was implemented by Preeti et al. (2022) to solve the DED problem. The proposed technique achieved better results than the GA with a two-parent crossover mechanism. The suggested method performs well in terms of both identifying a broad range of options and landing on a set that is close to the genuine Pareto optimality.

Panigrahi et al. (2006) used DED with a SA approach to find the optimal dispatch strategy for a given region. In this scenario, network losses are included through loss coefficients, load-balance limitations, operational limits, valve-point loading, and ramp constraints. The effectiveness and versatility of the suggested technique have been shown using numerical results for a model test system. The novel hybrid approach was developed by combining EP with sequential QP to solve the DED issue by Basu (2007). Here, initially, a simple EP is employed as a basis level search in the suggested technique, which may provide a good direction to the optimum global area, and SQP is utilized for fine tuning in the local search to provide the best feasible solutions. PSO was utilized by Gaing (2004) to address a constrained DED issue in a power system management. Both the solution quality and the computational efficiency of the proposed PSO approach are compared to those of the other stochastic methods to exhibit the quality of the PSO method. However, when solving complicated optimization problems, sometimes, the g-best particle, which PSO uses as its optimum solution, may be found at a local minimum, which might cause the algorithm to converge too soon. Therefore, to overcome the above issue, the authors developed (Yuan et al., 2009) an improved PSO (IPSO) method to solve dynamic load dispatch with valve-point effects. For efficiently dealing with restrictions, the suggested IPSO technique uses rules based on feasibility and heuristic tactics with a probability-based priority list. The population may be swiftly directed to the viable area by using the constraint-handling approach rather than the penalty function method, which requires penalty factors and other parameters. In particular, DED’s equality restrictions may be met accurately. An improved bare-bones PSO (IBBPSO) method (Zhang et al., 2014) to solve DED with valve points was developed. In BBPSO, most of the particles in the swarm stop updating in the early stages, which leads to being stuck at a local optima solution. To enhance the search toward a global direction, a directionally chaotic search (DCS) is added with BBPSO and developed IBBPSO. Attaviriyanupap et al. (2004) suggested a fuzzy optimization technique to solve DED, taking into account uncertainty in deregulated energy markets. The system was created with the goal of maximizing profit and hedging risks as a participant in the energy market and the 10-min spinning reserve market in mind. The uncertainties in the current paper are represented by fuzzy numbers and include the demand and reserves necessary in each market, the prices cleared in each market, and the likelihood that reserves are relied upon in real operations.

A clonal selection-relied artificial immune algorithm was developed by Hemamalini and Simon (2011) to solve the DED issue with valve points and the inclusion of ramp rate constraints. However, the algorithm has a large number of parameters, and identifying the right values of the respective parameter is a difficult task; otherwise, it leads to a suboptimal solution. A derivative-free evolutionary technique harmony search (HS) was applied to solve the DED problem by Sahoo et al. (2021), and the correlation in music can be likened to the solution vector, while the process of a musician’s improvisation bears resemblance to both local and global search strategies. However, the proper adjustment of tuning parameters such as the pitch adjustment rate (PAR) is a difficult task. Therefore, Pandi and Panigrahi (2011) implemented a hybrid HS by dynamically varying the PAR value, which is more efficient than a classical HS technique. A hybrid technique named BBOSB was developed by Xiong and Shi (2018) by combining the good exploiting capability of BBO and exploring the capability of brain storm optimization (BSO) to solve DED issues with valve effects.

A reference point technique was incorporated in the original TLBO and a many-objective TLBO was developed to solve OPF by Pradeep et al. (2012). A new hybrid moth flame technique is developed to solve the OPF issue with the inclusion of wind power, along with FACTS devices (Sundaram et al., 2022a). Sunilkumar et al. (2023) solved the OPF issue with the integration of hybrid power systems such as thermal, solar, and wind power systems and addressed the issues related to the integration of RESs. A techno-economic investigation coordinating with RESs solved OPF by using an equilibrium optimizer technique (Sundaram et al., 2022b). The wind power in the current work was predicted with the probability distribution function of Weibull. These swarm intelligence-based evolutionary algorithms (EAs) are very effective and adaptable to include different RESs in the existing power system for resolving DED problems. However, the dispatched solutions these EAs produce may not be the most cost-effective if the complexity of the problem is enhanced while adding more constraints.

Gandomi and Alavi (2012) created the krill herd (KH) method, a novel creature-based evolutionary method inspired by the process of increasing individual density and achieving large concentrations of food following predation. There are three primary movements in the KH algorithm: motions that are triggered by other krill, foraging motions, and physical diffusion. To solve DED, krill must be placed in such a way that they can get to the food supply, and each krill’s fitness is determined by how far away the food source and its greatest density are from it. Individuals that are closer in proximity to greater krill density and food concentration have the greatest fitness value. The KH algorithm has two local and global searches, which makes it efficient and useful in solving a wide range of real-world problems, including numerical optimization (Hu et al., 2016), economic dispatch (Harish et al., 2019), and optimal power flow (Harish et al., 2016; Harish et al., 2017).

This paper introduces several significant contributions.

1 It focuses on the DED problem rather than the conventional ED problem. This shift allows for the consideration of dynamic constraints, valve-point loading effects, and prohibited operating zones, which enhances the complexity of the optimization process.

2. The problem formulation presents the conventional DED issue with the inclusion of an RES (wind power).

3. The DED issue is solved with the novel krill herd algorithm. The effectiveness of the KH method is verified by considering five different test systems.

This paper is organized as follows: a mathematical model of the DED issue including valve points is given in Section 2, after which the KH technique is discussed in Section 3. Section 4 shows the results attained with the proposed technique, and conclusions are given in Section 5.

2 Mathematical model

There must be DED for all thermal generators that are subjected to various constraints on a regular basis over an extended period of time. The next sections go further deep into the integration of thermal cost characteristics with solar PV and wind energy units and related constraints.

2.1 Optimization of total cost

In general, the DED problem reduces the overall manufacturing cost for committed units over the course of an operational horizon, which is obtained using Eq. 1 as follows (Behnam et al., 2012):

$\mathit{min}f={\sum }_{t=1}^T{\sum }_{m=1}^{NG}{a}_m+b_m{P}_{Gm,t}+C_m{P}_{Gm,t}^2,(1)$

where f indicates the total cost (TC) of all thermal units, $P_{Gm,t}$ represents the real power of the $m\text{th}$ unit at the $t\text{th}$ hour, and $NG$ indicates the number of generators.

2.2 Optimization of TC with valve points

Modern large power-producing units that use multi-valve steam turbines exhibit non-convexity in the input–output characteristic functions, demonstrating a substantial variance in the characteristic curves. Valve-point effects and mixing of various fuels cause the former to be non-convex. When each steam valve starts to open, ripples appear at the valve point. When valve-point effects are included, the ED cost objective function is often characterized as a superposition of a sinusoidal function and a quadratic function as shown in Eq. 2. In the current research, a non-convex function is used to evaluate the influence of the valve points (Behnam et al., 2012).

$\mathit{min}f={\sum }_{t=1}^T{\sum }_{m=1}^{NG}{a}_m+b_m{P}_{Gm,t}+C_m{P}_{Gm,t}^2+\left|d_m\times \sin \left(e_m\left(P_{Gm,t}^{\min }-P_{Gm,t}\right)\right)\right|,(2)$

where $a_m,b_m,c_m,d_m\&e_m$ refer to the cost characteristics of the $m\text{th}$ generator and $P_{Gm,t}^{\min }$ indicates the minimum values of the real power of the $m\text{th}$ unit at the $t\text{th}$ hour.

2.3 Wind energy

The cost function of wind generation is subject to the investment cost of the equipment and the operation and maintenance (O&M) cost of the generated energy (Behnam et al., 2012) and is given using Eq. 3 as follows:

$F\left(P_{wp}\right)=a{I}^p{P}_{wp}+G^E{P}_{wp},(3)$

where P_wP denotes the wind power generation (kW), a indicates the annuitization coefficient, and I_p and G^E represent the investment costs and O&M cost per unit generated ($/kW), respectively. However, the investment cost of land will be considered as constant. Only the O&M cost is considered in the current work (Behnam et al., 2012). It is assumed that the investment costs and O&M cost are considered as $1,400 and 1.6 cents per kW, respectively. In the current research work, the wind generation data on a location in the east coast of the United States of America are considered. It gives constant wind power at each and every hour (Augustine et al., 2020).

2.4 Total cost including renewable energy sources

The comprehensive cost function is obtained using Eq. 4 as follows:

$\text{TC}=minf+F\left(P_{wp}\right),(4)$

where TC indicates the total cost.

2.5 Constraints

The constraints considered in the current work are described in brief below (Faisal et al., 2020).

2.5.1 Equality constraints

The active power balance constraint in this case is a crucial factor and can be expressed using Eq. 5 as follows:

${\sum }_{n=1}^{N_G}{P}_{Gnt}=P_D\left(t\right)t=\mathrm{1,2},...T.(5)$

2.5.2 Inequality constraints

The expression of these limits is provided below using Eq. 6, encompassing both their low and high values:

$P_{Gn}^{\mathit{min}}\le P_{Gnt}\le P_{Gn}^{\mathit{max}}n=\mathrm{1,2},\dots ,N_{G}t=\mathrm{1,2},\dots ,T.(6)$

Here, $P_{Gn}^{\min }\&P_{Gk}^{\max }$ are the low and high real power limits of the $n\text{th}$ generator, respectively.

2.5.3 Prohibited operating zones

A prohibited operating zone defines the area of the real power output of a generator that is impacted by the technical functioning of the shaft. Modification of electricity is often not permitted within the forbidden spans of time. The operational range of the generator is specified using Eq. 7 as follows (Harish et al., 2016):

$\begin{array}{l}{P}_{Gn}^{\mathit{min}}\le P_{Gn,t}\le P_{Gn,1}^{lower}n=\mathrm{1,2},\dots ,N_G\\ P_{Gn,m-1}^{upper}\le P_{Gn,t}\le P_{Gn,m}^{lower}t=\mathrm{1,2},\dots ,T\\ P_{Gn,M_n}^{upper}\le P_{Gn,t}\le P_{Gn}^{\mathit{max}}m=\mathrm{2,3},\dots M_n\end{array},(7)$

where $P_{Gn,1}^{lower}\&P_{Gn,m-1}^{upper}$ indicate the lower and upper boundaries of the jth PoZ of the nth unit, respectively. M_n denotes the number of PoZs of the nth unit. m indicates the number of PoZs. The main aim of the current work is to determine the optimum generation schedule (P_i,t) as in 1 and 2, which leads to minimizing the cost of power production, by satisfying the constraints mentioned in 3–9 used with various combinations in different cases.

3 Krill herd algorithm

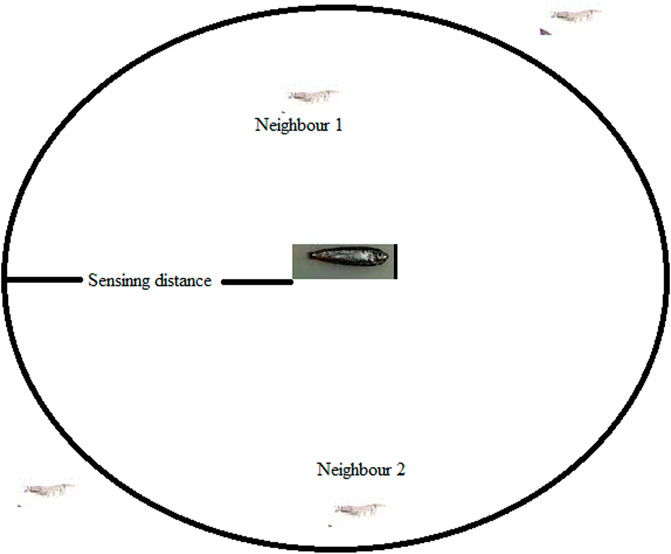
Krill become divided individually when attacked by predators including seals, penguins, and seagulls. This reduces the density of the krill. Later, the formation of the krill herd relies on numerous parameters. The process of increasing the krill density is adopted in the current work (Gandomi and Alavi, 2012). The krill herd eventually forms around the global minima because of the density-dependent attraction of krill and food availability. It is feasible to find a solution by measuring the distance from each individual krill to the source of food with the maximum density. The fittest krill is the one that is closest to a density population of krill and a greater concentration of food. Foraging motion, physical diffusion, and motion generated by other individual krill all contribute to the krill’s rotation in a multi-dimensional search space, which is discussed below (Gandomi and Alavi, 2012).

3.1 Motion induced by other individual krill

Individual krill constantly travel in an n-dimensional search area with a specific velocity to attain high krill density, and their orientation is controlled by the local impact supplied by neighboring krill and the goal effect. The $i\text{th}$ krill velocity is given as follows (Gandomi and Alavi, 2012):

${N_i}^{k+1}=N^{\max }\left({\displaystyle \sum _{j=1}^{NN}}{\widehat{F}}_{ij}{\widehat{X}}_{ij}+2\left(rand+I/I_{\max }\right){\widehat{X}}_{i,best}{\widehat{F}}_{i,best}\right)+{\omega }_n{N}_i^k,(8)$

where $N_i^{k+1}\&N_i^k$ indicate the motion induced by other krill to the $i\text{th}$ krill in the $\left(k+1\right)\text{th}$ and $k\text{th}$ generations, respectively, $N^{\max }$ denotes the maximum induced speed, ${\widehat{F}}_{ij}$ indicates the normalized fitness difference between the $i\text{th}\&j\text{th}$ krill, ${\widehat{X}}_{ij}$ indicates the normalized position variation between the $i\text{th}\&j\text{th}$ krill; $F^{worst},F^{best}$ are the worst and best fitness values, respectively, and $NN$ denotes the number of neighbors. Different methods may be used to choose a neighbor. It is easy to calculate the number of krill that are within a certain distance of each other using the neighborhood ratio. The sensing distance (d_s) surrounding an individual krill, as given in Figure 1, should be computed using the actual behavior of the individual krill, and the neighbors should be located. The sensing distance is calculated as follows:

$d_{si}=\frac{1}{5N}{\sum }_{k=1}^N‖X_i-X_k‖,(9)$

where $d_{s,i}$ denotes the sensing distance of the $i\text{th}$ krill. N indicates the number of krill. If the sensing distance between two krill is less than a certain value, then the two krill are considered neighbors.

FIGURE 1

FIGURE 1. Representation of neighboring krill of a krill.

3.2 Foraging motion

It is divided into two sections, one for the present iteration and the other for prior versions. A good food location is a mix of food attraction and the local best food placement that is utilized to attract individual krill to the global ideal solution. The foraging action of the krill is given as follows (Gandomi and Alavi, 2012):

${F_i}^{k+1}=V_f\left(2\left(1-I/I_{\max }\right){\widehat{F}}_{i,best}{\widehat{X}}_{i,best}+{\widehat{F}}_{i,food}{\widehat{X}}_{i,food}\right)+{\omega }_f{F}_i^k,(10)$

where $F_i^{k+1}\&F_i^k$ denote the foraging motion of the $i\text{th}$ krill, $V_f$ indicates the foraging speed, ${\omega }_f$ indicates the inertia weight, ${\widehat{F}}_{i,best}\&{\widehat{X}}_{i,best}$ are the normalized fitness and position variation between the $i\text{th}$ and best individual krill, respectively, and ${\widehat{F}}_{i,food}\&{\widehat{X}}_{i,food}$ are the normalized fitness and position variation between the $i\text{th}$ krill and the center of food, respectively.

3.3 Physical diffusion

The physical spread of individual krill is considered a random phenomenon. This movement can be characterized by utilizing a random directional vector and a maximum diffusion speed. It is possible to put it this way using Eq. 11 (Gandomi and Alavi, 2012) as follows:

$D_i=D^{\max }\delta .(11)$

$D_i$ indicates the physical diffusion of the $i\text{th}$ krill in the $k\text{th}$ generation, $D^{\max }$ denotes the maximum diffusion speed, and $\delta$ indicates a random directional vector.

When a krill approaches closer to the global optimum solution, less random orientation is required. To account for this, a new term is introduced to the physical diffusion formula. Foraging motion and motion caused by other individual krill have a diminishing influence with time (iterations). A random vector of physical diffusion is shown in Eq. 8 and does not steadily decrease with the increase in the number of iterations. This results in the addition of an additional term Eq. 9 to Eq. 8. Random speed is reduced linearly with time and is given below:

$D_i=\left(1-I/I_{\max }\right)D^{\max }\delta .(12)$

3.4 Update krill position

Each krill’s position is revised as given below:

$X_i\left(t+\Delta t\right)=X_i\left(t\right)+C_t{\displaystyle \sum _{k=1}^{CV}}\left(U{L}_k-L{L}_k\right)\left(N_i+F_i+D_i\right).(13)$

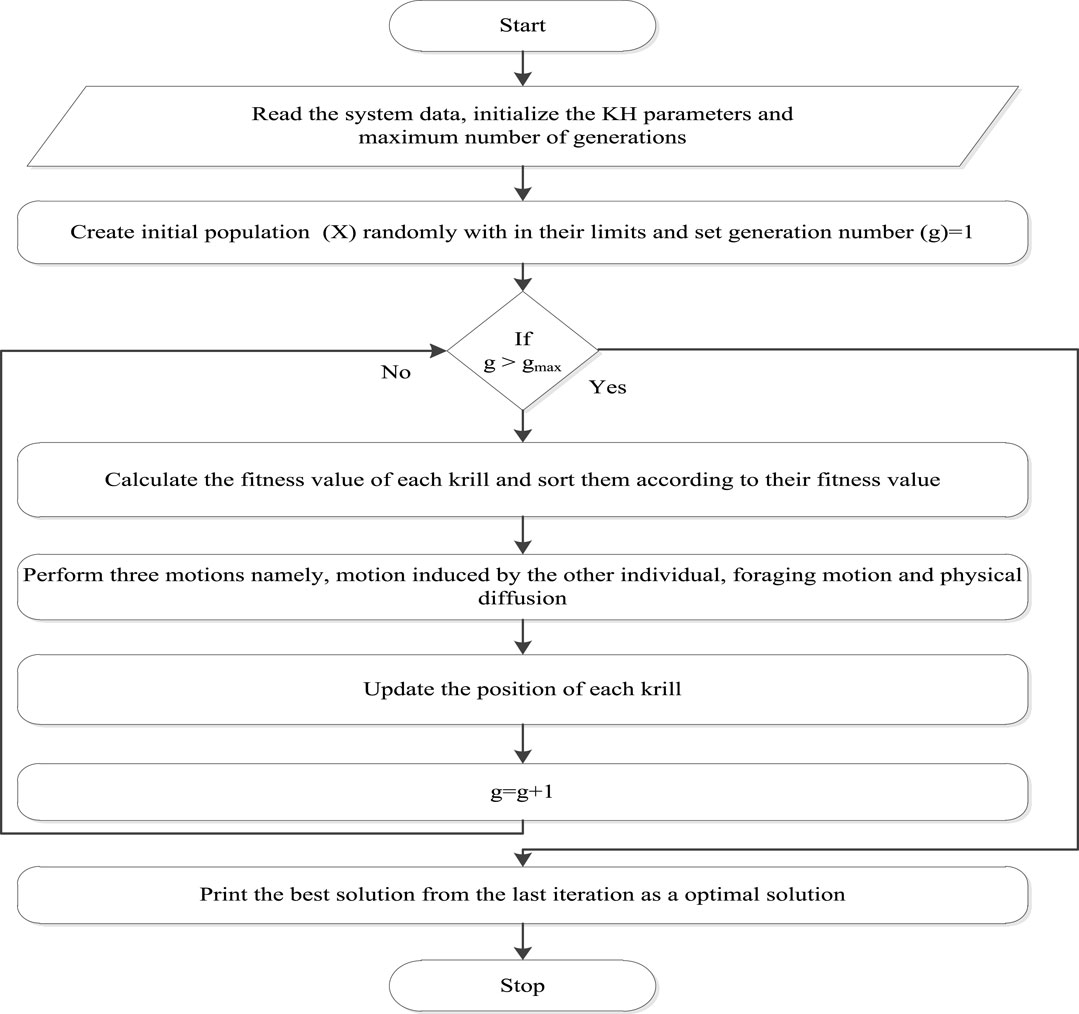
3.5 The procedure of KH to solve the DED problem

Step 1:. KH variables and max generations (G_max) are initialized.

Step 2:. The unknown variable of this ED problem is generator-active power output. In the KH, all these variables constitute the individual position of several chromosomes that indicate a complete solution set. The position of any chromosome, X_k, is represented using Eq. 14 as follows:

$X_k=\left[P_{g\mathrm{1,1},k}^m,P_{g\mathrm{1,2},k}^m,\dots \dots ,P_{g\mathit{1},t,k}^g,\right].(14)$

The complete search space for population NP is expressed using Eq. 15 as follows:

$X_k^m=\left[\begin{array}{cccc}{P}_{g\mathrm{1,1},k}^m& P_{g\mathrm{1,2},k}^m& \cdots & P_{g\mathit{1},t,k}^g\\ P_{g\mathrm{2,1},k}^m& P_{g\mathrm{2,2},k}^m& \cdots & P_{g2,t,k}^m\\ ⋮& ⋮& \ddots & ⋮\\ P_{gNg,\mathit{1},k}^m& P_{gNg,2,k}^m& \cdots & P_{gNg,t,k}^m\end{array}\right]\begin{array}{l}k=\mathrm{1,2}\dots NP\\ g=\mathrm{1,2}\dots G_{\mathit{max}}\end{array}.(15)$

Step 3:. The fitness of each krill can be evaluated by applying Eq. 12.

$\left|F\right|=f+w_P{\left(\left|P_{G\mathit{1}}-{P_G}_{\mathit{1}}^{\mathit{lim}}\right|\right)}^2.(16)$

Step 4:. The three movements mentioned in Eqs 8, 10, 12 are applied, and the newly created individual krill are updated using Eq. 13.

Step 5:. If the current limitations of a variable are exceeded, it will be set to an explicit low or high value.

Step 6:. If utmost generations have been reached, the process is stopped, and the optimum result from the previous generation is used as the best solution. Otherwise, we proceed to step 3.

The flowchart of the proposed algorithm is given in Figure 2.

FIGURE 2

FIGURE 2. Flowchart of the proposed KH algorithm.

4 Simulation results

To examine the scalability and effectiveness of the KH approach described in the solution to the DED problem, various modules are explored here to prove the efficiency of the KH algorithm. In all modules, the number of krill and maximum iterations are taken as 30 and 500, respectively, and the schedule time is set to 24 h. A Pentium IV Computer with a clock speed of 2.33 GHz and a memory capacity of 3.25 GB with MATLAB 2016a was used to run all simulations.

4.1 Selection of control parameters

The quality of the answer and the pace at which the algorithm converges are both heavily influenced by the choice of appropriate algorithmic parameters. In order to achieve the optimal population size for various tests, the minimal cost for various populations was computed. The best value for the population size achieved for all the test cases is 30. In addition, multiple trials have been conducted to identify an appropriate number of maximum iterations. The associated test cases indicate that the best value for the maximum number of iterations is 500. A total of 20 independent trials were conducted for each system to verify the reliability and efficacy of the proposed KH method. The KH method input variables used in this simulation research are considered from the study by Gandomi and Alavi (2012), which are follows: maximum induced speed N^max = 0.01; foraging speed (V_f) = 0.05; and maximum diffusion speed D^max = 0.01. It is important to note that the inertia weights (w_n, w_f) are initially set at 0.9 to highlight the capacity of the search process to explore the search space, but these values are gradually decreased to 0.1 at the conclusion of the search process to maximize the amount of space that can be explored.

4.2 Five-unit system

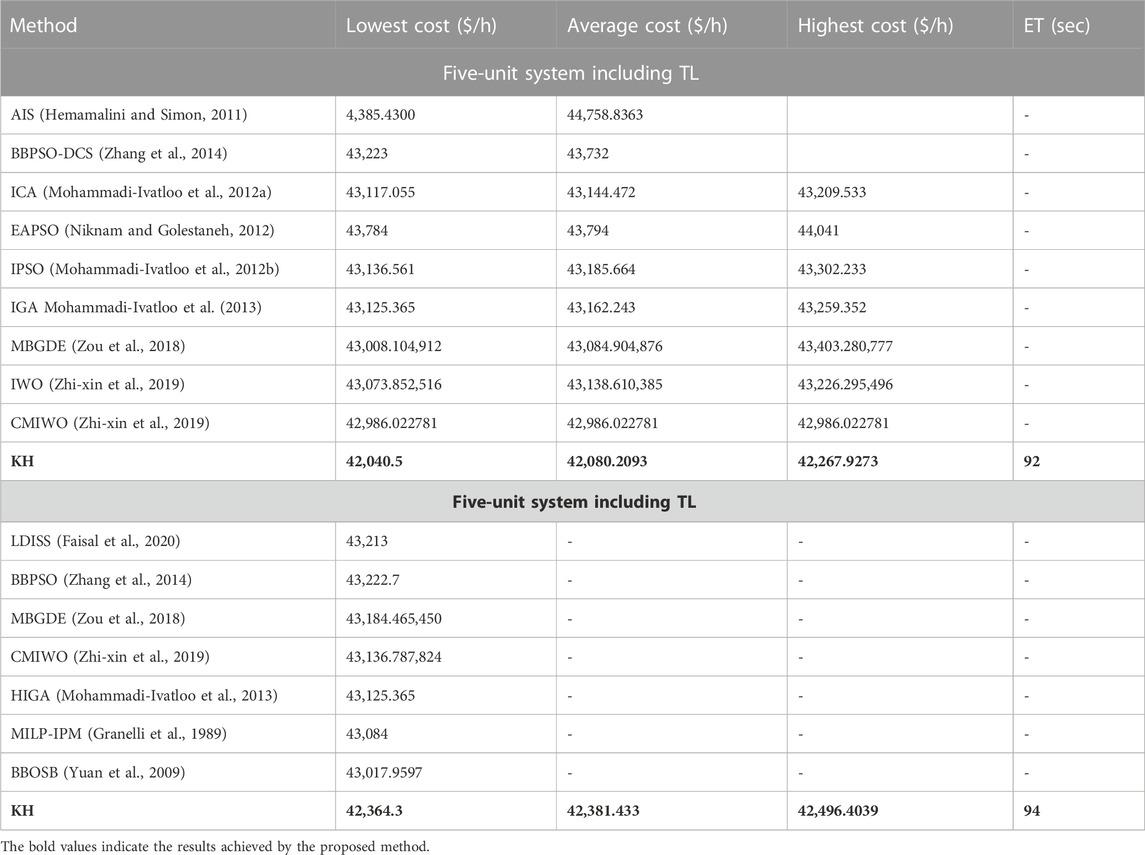
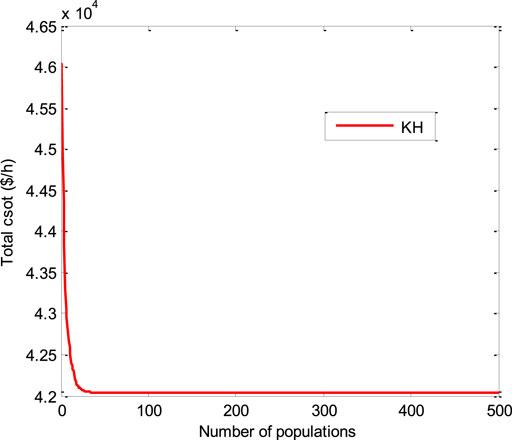
It contains five generators, and the full data on the system are obtained from the study by Faisal et al. (2020), which consist of the cost coefficients of generators and their limits, PoZ limits, and load in every period. For a five-unit system, two test scenarios were considered. In scenario 1, only transmission loss (TL) was considered. In scenario 2, TL with PoZ was considered. In the above two scenarios, the best combination of real powers obtained with the proposed KH method is given in Table 1. Table 2 represents statistical values obtained for the two test scenarios with the KH method compared with the artificial immune system (AIS) (Hemamalini and Simon, 2011), bare-bones PSO (Zhang et al., 2014), imperialist competitive algorithm (ICA) (Mohammadi-Ivatloo et al., 2012a), enhanced adaptive PSO (Niknam and Golestaneh, 2012), time-varying acceleration-improved PSO TVA-IPSO (Mohammadi-Ivatloo et al., 2012b), immunity GA (IGA) (Mohammadi-Ivatloo et al., 2013), HIGA (Mohammadi-Ivatloo et al., 2013), memory-based global DE (MBGDE) (Zou et al., 2018), IWO (Zhi-xin et al., 2019), CMIWO (Zhi-xin et al., 2019), MILP-IPM (Granelli et al., 1989), and BBOSB (Pandi and Panigrahi, 2011). These results proved that the KH method achieved the best results in the two scenarios compared to other methods. The convergence curves obtained with the proposed KH algorithm are given in Figure 3 and Figure 4, respectively, and it is shown that the KH technique converged quickly to the optimal solution.

TABLE 1

TABLE 1. Optimal solution of the five-unit system with TL and with TL and PoZs obtained using the KH technique.

TABLE 2

TABLE 2. Statistical analysis of KH compared with other methods.

FIGURE 3

FIGURE 3. Convergence curve of five-unit system test scenario 1.

FIGURE 4

FIGURE 4. Convergence curve of five-unit test scenario 2.

4.3 Six-unit system

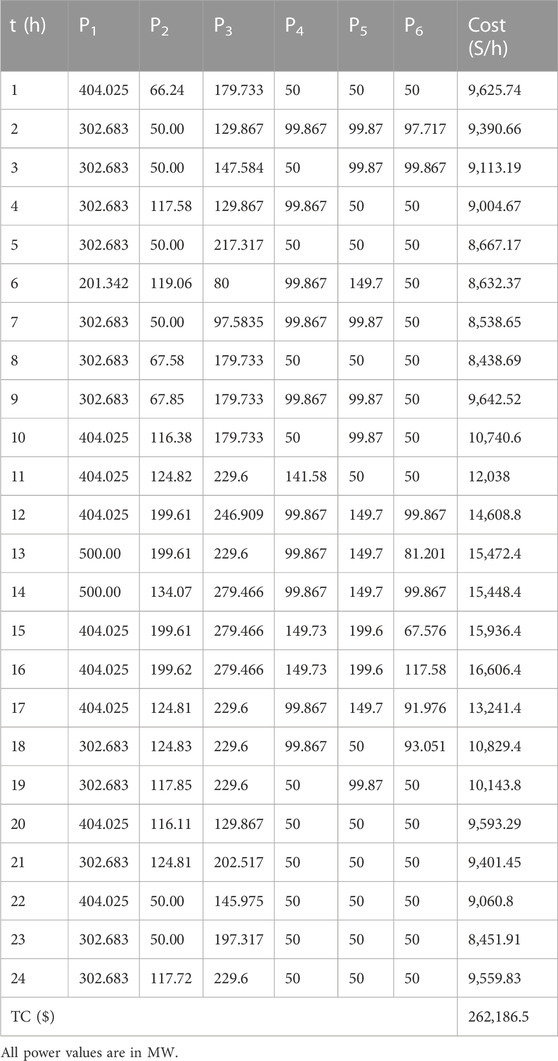
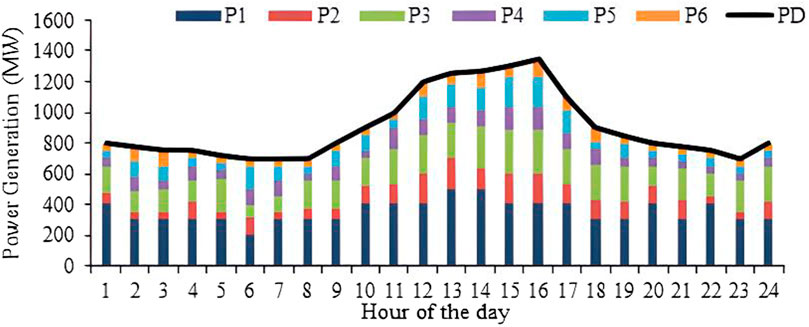
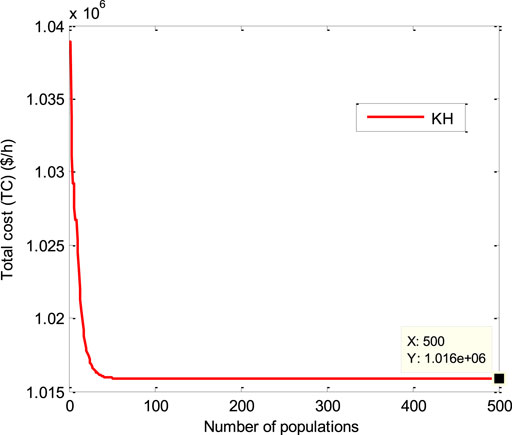
It contains six generators, and the whole data for this system are obtained from the study by Faisal et al. (2020), which include the cost characteristics of generators, generator limitations, and load demand in each period. Table 3 shows the optimum set of real powers found for this system using the KH algorithm, and a graphical illustration is given in Figure 5. Table 4 compares these findings with those of BA (Faisal et al., 2020) and DBA (Faisal et al., 2020), and these results show that the proposed technique is a better procedure to identify the best solutions to such complicated DED challenges, with the lowest, average, and highest costs, as shown in the table. Using the formulation of KH, a minimum value of 262,186.5 ($/day) was attained, demonstrating the extraordinary nature of the KH technique. In addition, the KH cost characteristics are given in Figure 6. This graph shows that the proposed KH converged very quickly, which indicates that it achieved optimum results in less time.

TABLE 3

TABLE 3. Optimal solution of the six-unit system with VPL obtained using KH.

FIGURE 5

FIGURE 5. Power production and load demand schedule throughout 24 h in a day for a six-unit system.

TABLE 4

TABLE 4. Statistical analysis of the six-unit system compared with other methods.

FIGURE 6

FIGURE 6. Convergence curve of a six-unit system.

4.4 M2: 10-unit system

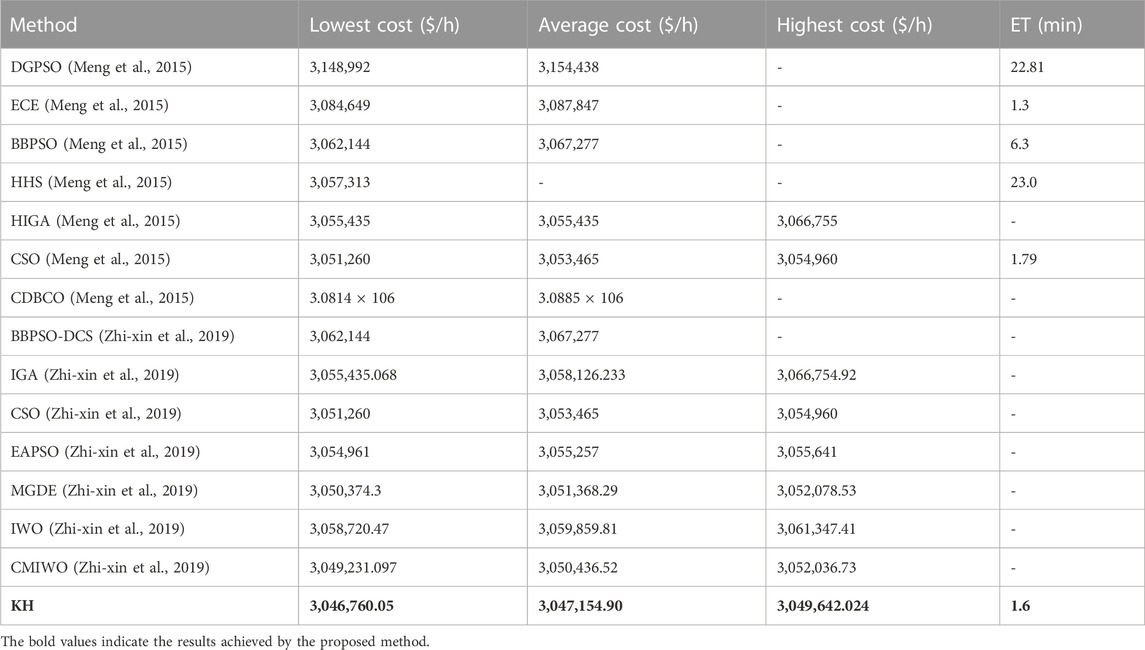
It this test case, the valve-point loading effect and generation limits were considered. The complete test data on this system are obtained from the study by Harish et al. (2016), which include the cost coefficients of thermal limits and their limits and the load in every period. Table 5 presents the optimum combination of real powers found for this system using the KH method. The statistical values achieved with the present method are compared with those obtained by the AIS (Zhang et al., 2014), BBPSO-DCS (Zhang et al., 2014), ICA (Mohammadi-Ivatloo et al., 2012a), TVAC-IPSO (Mohammadi-Ivatloo et al., 2012b), chaotic differential bee colony optimization (CDBCO) (Lu et al., 2014), crisscross optimization algorithm (CSO) (Meng et al., 2015), EAPSO (Niknam and Golestaneh, 2012), IGA (Mohammadi-Ivatloo et al., 2013), MBGDE (Zou et al., 2018), IWO (Zhi-xin et al., 2019), and CMIWO (Zhi-xin et al., 2019) and are given in Table 6. It is observed that the proposed method provided a superior strategy for identifying solutions. In addition, the KH cost characteristics are given in Figure 7, and it is shown that the proposed KH converged very quickly, which indicates that it achieved optimum results in less execution time (ET).

TABLE 5

TABLE 5. Optimal solution of the 10-unit system obtained using KH.

TABLE 6

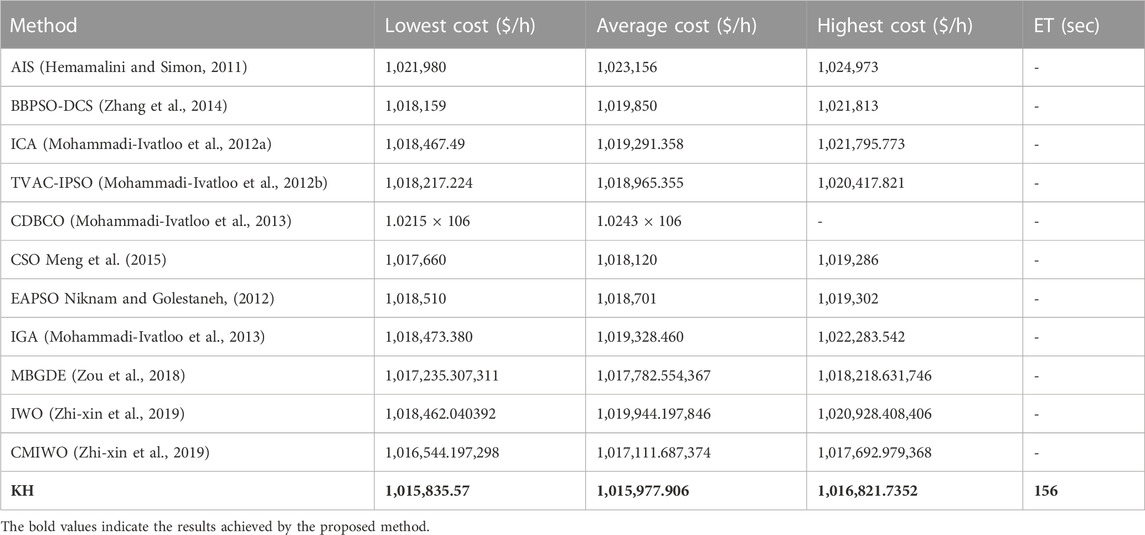
TABLE 6. Comparison of the statistical analysis of the KH technique with other methods for the 10-unit system without TLs and PoZs.

FIGURE 7

FIGURE 7. Convergence characteristics of a 10-unit system.

4.5 15-unit system

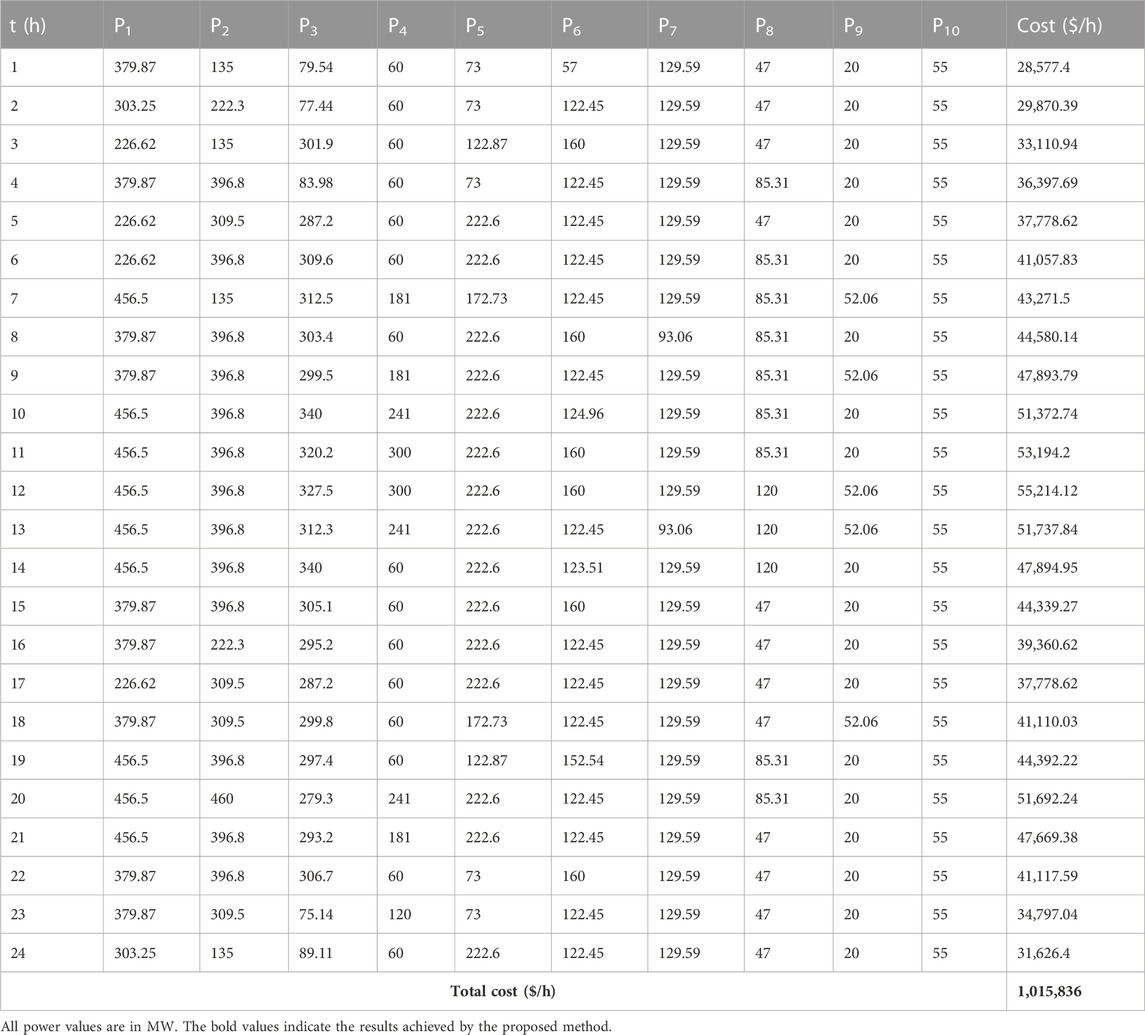
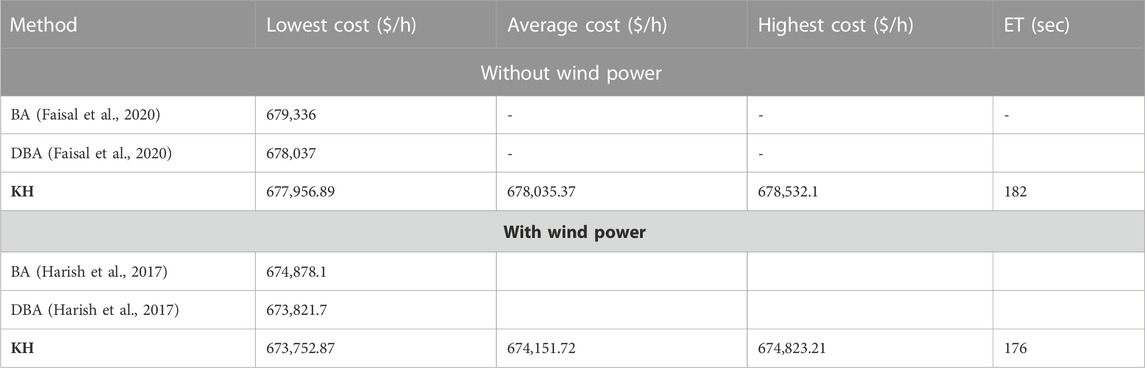
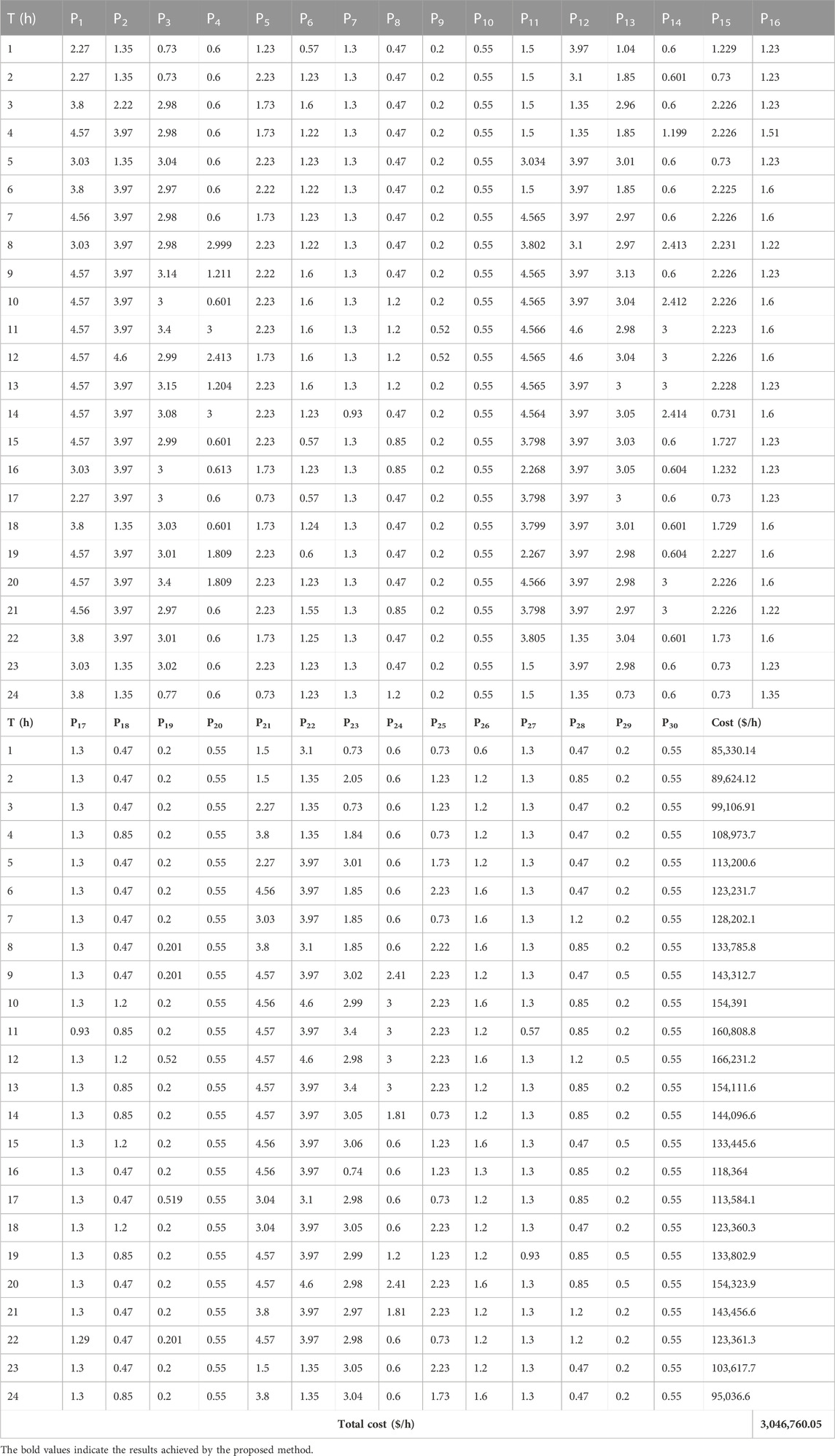
The efficiency of the KH algorithm is determined by examining 15-unit systems while addressing the DED issue with the inclusion of wind power. This system obtained complete data from the study by Hu et al. (2016). Table 7 shows the optimum set of real powers derived using the KH algorithm for this system in the first scenario (without wind power). In the second scenario involving renewables, the KH algorithm was employed in the same unit system incorporating one wind farm for a 24-h period. The best combination of real power values obtained in this case is given in Table 8. Table 9 presents the statistical results obtained for this system with and without the inclusion of wind power, compared with other methods published in the literature. This includes the lowest, average, and highest cost, along with the corresponding ET, and it is proven that the suggested technique produced better optimal results than the BA (Faisal et al., 2020) and DBA methods (Faisal et al., 2020). The cost characteristics of the KH technique are given in Figure 8. Overall, these results show that the KH algorithm is effective in the presence of renewable energy sources as well.

TABLE 7

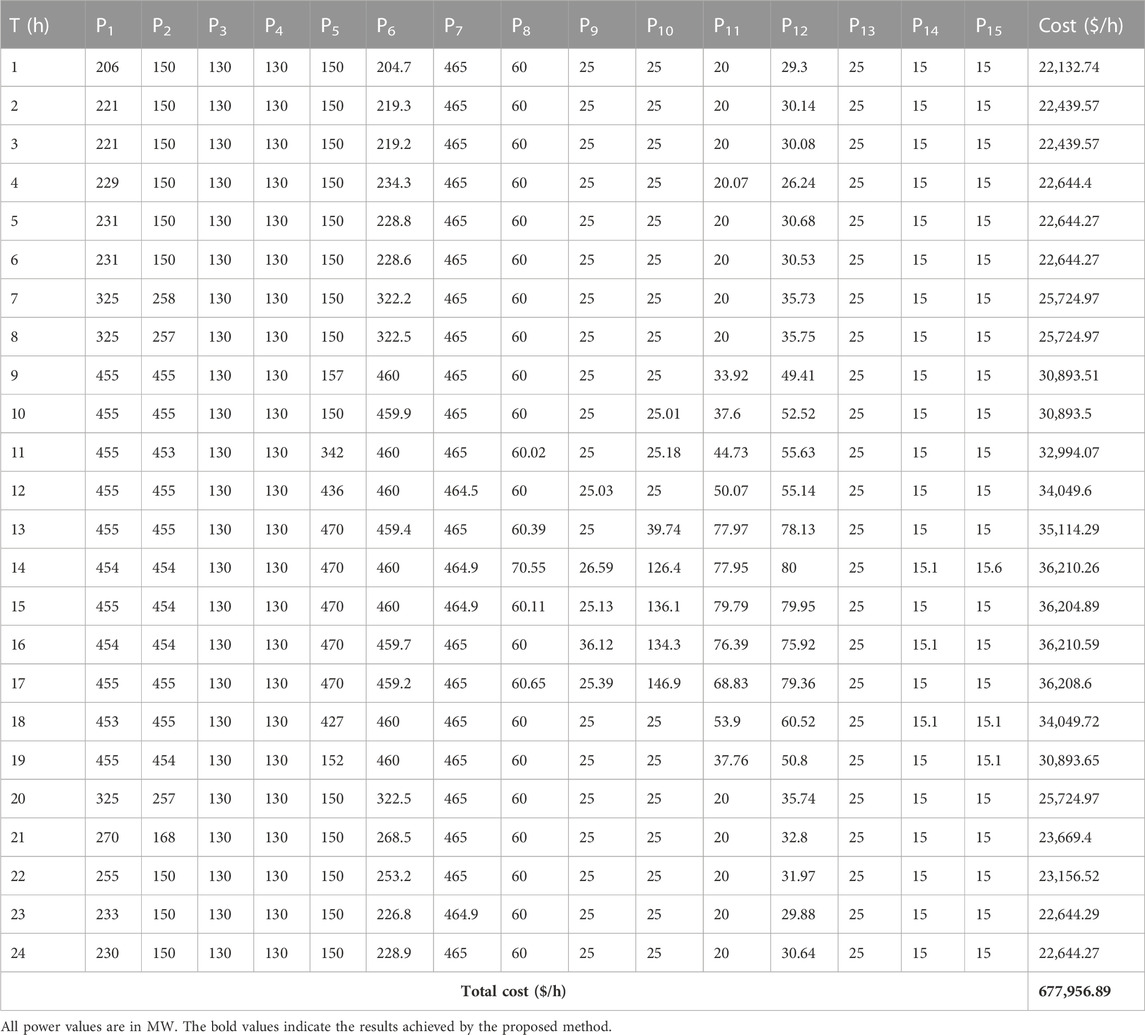
TABLE 7. Optimal solution of the 15-unit system obtained using the proposed KH technique without wind power.

TABLE 8

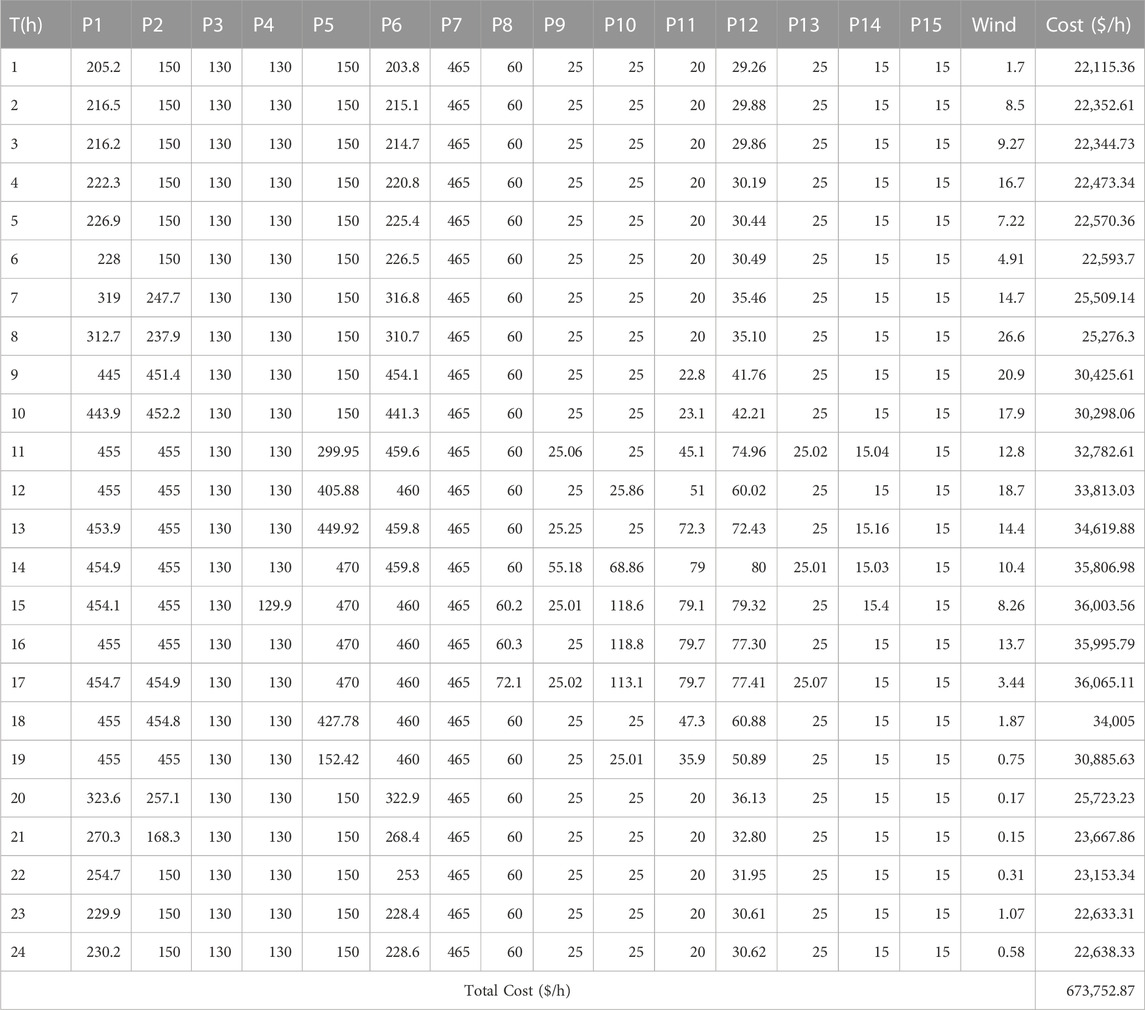
TABLE 8. Optimal solution of the 15-unit system obtained using the proposed KH technique with wind power.

TABLE 9

TABLE 9. Statistical analysis comparison for the 15-unit system with other algorithms.

FIGURE 8

FIGURE 8. Convergence characteristics of a 15-unit system.

4.6 30-unit system

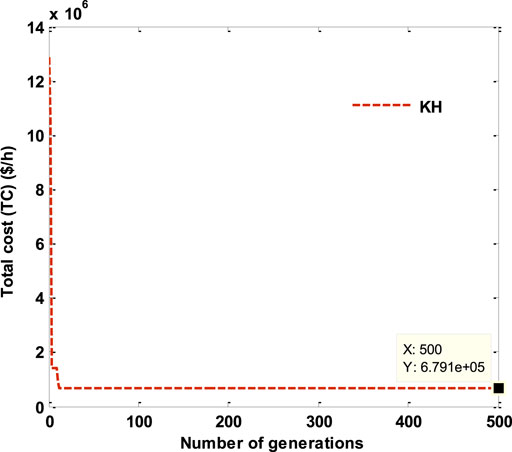
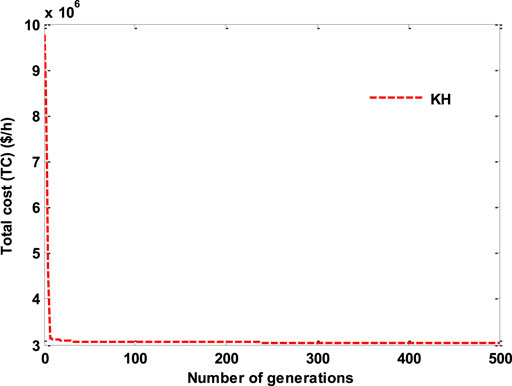
This research simulated the scheduling of a 30-unit system without taking into account TL and PoZs to demonstrate the dispatch performance of the KH technique on large-scale systems. The data for the 30-unit system are obtained by multiplying the information for a 10-unit system by 3, and the data of a 10-unit system are obtained from the study by Zhi-xin et al. (2019). Table 10 displays the most cost-effective dispatch solution produced by the KH algorithm and also displays the ideal solution of the KH algorithm, which confirms that the self-adaptive repair approach is effective since it fulfills the power demand balance, generating capacity restrictions. Table 11 compares the optimum dispatch results obtained by the KH algorithm with those obtained by other techniques from the literature. The suggested KH technique achieves the lowest generation costs compared to state-of-the-art approaches. The KH cost characteristics are given in Figure 9. The graph shows that the proposed KH converged very quickly, which shows that the KH technique achieved optimum results in less time. As a result, the suggested KH algorithm provides superior performance in terms of lowering generating costs during the dispatch of large-scale systems.

TABLE 10

TABLE 10. Optimal solution of the 30-unit system obtained using the proposed KH technique.

TABLE 11

TABLE 11. Statistical analysis comparison of the 30-unit system with other algorithms.

FIGURE 9

FIGURE 9. Convergence characteristics of a 30-unit system.

4.7 Statistical assessment

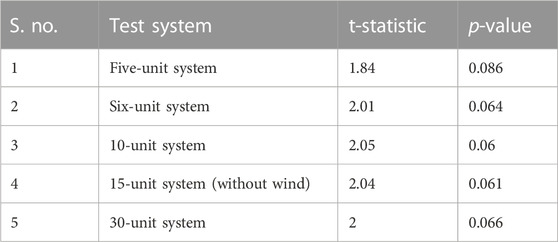
A well-known one-sample t-test (Mowafaq, 2022) is performed on all the test systems to evaluate the stability of the suggested KH technique for solving the DED issue. The significance level used in this test is 0.05. Statistical analysis provides us the data to keep or discard any hypothesis. The comparison of statistical data using significance analysis may be used to reject or retain any hypothesis. If the statistical value is larger than the threshold of significance, the hypothesis is accepted; otherwise, it is rejected. The results of the all-sample t-test are shown in Table 12 to demonstrate the validity of the null hypothesis.

TABLE 12

TABLE 12. Statistical analysis of all the systems.

5 Conclusion

In this work, the KH technique is utilized to solve dynamic economic dispatch issues during a 24-h time span by including various constraints such as valve-point loading effects and prohibited operating zones, as well as wind power generation. In KH, the initial search space is reduced through motion induced by other krill and foraging motion. Later, random diffusion is utilized to pick good-quality solutions to improve the system accuracy and dependability while dealing with optimization issues. In the current work, the KH algorithm is applied on five different systems to solve the optimization of the total cost with and without valve-point loading effects. The results of the test scenarios show that the KH technique is reliable, resilient, and capable of consistently providing high-quality DED solutions with actual operating restrictions such as transmission loss, valve-point effects, and prohibited operating zones. Compared to other methods, KH performance in terms of cost reduction and dispatch schedule optimization is found to be fairly competitive, and it can be securely employed as an effective algorithm for small-to-medium-sized, simple-to-complicated DED situations. Furthermore, KH is applied to solve multi-objective DED issues in hybrid power systems, and combined heat and power dispatch, stochastic DED, and power state estimation would be a possible extension of the present work.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author contributions

HP: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing–original draft, and writing–review and editing. GN: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing–original draft, and writing–review and editing. BV: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing–original draft, and writing–review and editing. BS: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing–original draft, and writing–review and editing. CR: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing–original draft, and writing–review and editing. HK: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing–original draft, and writing–review and editing. KA: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing–original draft, and writing–review and editing. AE: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing–original draft, and writing–review and editing.

Funding

The authors declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Attaviriyanupap, P., Kita, H., Tanaka, E., and Hasegawa, J. (2004). A fuzzy-optimization approach to dynamic economic dispatch considering uncertainties. IEEE Trans. Power Syst. 19 (3), 1299–1307. doi:10.1109/tpwrs.2004.831272

CrossRef Full Text | Google Scholar

Augustine, N., Suresh, S., Moghe, P., and Sheikh, K. (2020). “Economic dispatch for a microgrid considering renewable energy cost functions,” in Proceedings of the 2012 IEEE PES Innovative Smart Grid Technologies, Washington, DC, USA, 16–20 January (ISGT), 1–7.

Google Scholar

Basu, M. (2007). Dynamic economic emission dispatch using evolutionary programming and fuzzy satisfying method. Int. J. Emerg. Elect. Power Syst. 8 (4), 1–15. doi:10.2202/1553-779x.1146

CrossRef Full Text | Google Scholar

Basu, M. (2008). Dynamic economic emission dispatch using nondominated sorting genetic algorithm-II. Int. J. Elctr. Power Energy Syst. 30, 140–149. doi:10.1016/j.ijepes.2007.06.009

CrossRef Full Text | Google Scholar

Behnam, M., Mehdi, E., and Ehsan, M. (2012). Time-varying acceleration coefficients IPSO for solving dynamic economic dispatch with non-smooth cost function. Energy Convers. Manage 56, 175–183. doi:10.1016/j.enconman.2011.12.004

CrossRef Full Text | Google Scholar

Faisal, T., Salem, A., Ghulam, A., Ayman, Q., and Mohammad, R. (2020). Solving renewables-integrated economic load dispatch problem by variant of metaheuristic bat-inspired algorithm. Energies 13, 1–36. doi:10.3390/en13236225

CrossRef Full Text | Google Scholar

Gaing, Z. L. (2004). Constrained dynamic economic dispatch solution using particle swarm optimization. Proc. IEEE Power Eng. Soc. General Meet., 153–158. doi:10.1109/PES.2004.1372777

CrossRef Full Text | Google Scholar

Gandomi, A. H., and Alavi, A. H. (2012). Krill herd: a new bio-inspired optimization algorithm. Commun. Nonlinear Sci. Numer. Simul. 17, 4831–4845. doi:10.1016/j.cnsns.2012.05.010

CrossRef Full Text | Google Scholar

Granelli, G. P., Marannino, P., Montagna, M., and Silvestri, A. A. (1989). Fast and efficient gradient projection algorithm for dynamic generation dispatching. IEEE Proc. Gener. Transm. Distrib. 136, 295–302. doi:10.1049/ip-c.1989.0039

CrossRef Full Text | Google Scholar

Happ, H. H. (1977). Optimal power dispatch-a comprehensive survey. IEEE Trans. Power Appa. Syst. 96, 841–854. doi:10.1109/t-pas.1977.32397

CrossRef Full Text | Google Scholar

Harish, P., Goutham, N., Mohan, U., Preeti, , and Mekala, G. (2019). Krill herd algorithm for solution of economic dispatch with valve-point loading effect. Appl Comput. Automation Wirel. Syst Electr Eng 553, 383–392. doi:10.1007/978-981-13-6772-4_33

CrossRef Full Text | Google Scholar

Harish, P., Naresh, R., and Veena, S. (2016). Application of stud krill herd algorithm for solution of optimal power flow problems. Int. Trans. Electr. Eng. 1-18. doi:10.1007/s00500-016-2319-3

CrossRef Full Text | Google Scholar

Harish, P., Naresh, R., and Veena, S. (2017). A solution network based on stud krill herd algorithm for optimal power flow problems. Soft Copmut 22, 159–176. doi:10.1002/etep.2316

CrossRef Full Text | Google Scholar

Hemamalini, S., and Simon, S. P. (2011). Dynamic economic dispatch using artificial immune system for units with valve-point effect. Int. J. Electr.Power Energy Syst. 33 (4), 868–874. doi:10.1016/j.ijepes.2010.12.017

CrossRef Full Text | Google Scholar

Hu, S., He, L., Si, X., Zhang, Y., and Hao, P. (2016). An effective krill herd algorithm for numerical optimization. Int. J. Hybrid. Inf. Tech. 9, 127–138. doi:10.14257/IJHIT.2016.9.7.13

CrossRef Full Text | Google Scholar

Li, F., and Aggarwal, R. K. (2000). Fast and accurate power dispatch using a relaxed genetic algorithm and a local gradient technique. Expert Syst. Appl. 19, 159–165. doi:10.1016/s0957-4174(00)00030-0

CrossRef Full Text | Google Scholar

Li, F., Morgan, R., and Williams, D. (1997). Hybrid genetic approaches to ramping rate constrained dynamic economic dispatch. Elect. Power Syst. Res. 43, 97–103. doi:10.1016/s0378-7796(97)01165-6

CrossRef Full Text | Google Scholar

Lu, P., Zhou, J., Zhang, H., Zhang, R., and Wang, C. (2014). Chaotic differential bee colony optimization algorithm for dynamic economic dispatch problem with valve-point effects. Int. J. Electr. Power Energy Syst. 62, 130–143. doi:10.1016/j.ijepes.2014.04.028

CrossRef Full Text | Google Scholar

Meng, A., Hu, H., Yin, H., Peng, X., and Guo, Z. (2015). Crisscross optimization algorithm for large-scale dynamic economic dispatch problem with valve-point effects. Energy 93, 2175–2190. doi:10.1016/j.energy.2015.10.112

CrossRef Full Text | Google Scholar

Mohammadi-Ivatloo, B., Rabiee, A., and Ehsan, M. (2012b). Time-varying acceleration coefficients IPSO for solving dynamic economic dispatch with non-smooth cost function. Energy Convers. Manag. 56, 175–183. doi:10.1016/j.enconman.2011.12.004

CrossRef Full Text | Google Scholar

Mohammadi-Ivatloo, B., Rabiee, A., and Soroudi, A. (2013). Nonconvex dynamic economic power dispatch problems solution using hybrid immune-genetic algorithm. IEEE Syst. J. 7 (4), 777–785. doi:10.1109/jsyst.2013.2258747

CrossRef Full Text | Google Scholar

Mohammadi-Ivatloo, B., Rabiee, A., Soroudi, A., and Ehsan, M. (2012a). Imperialist competitive algorithm for solving non-convex dynamic economic power dispatch. Energy 44 (1), 228–240. doi:10.1016/j.energy.2012.06.034

CrossRef Full Text | Google Scholar

Mowafaq, M. (2022). The Use of one sample t-Test in the real data. J. Adv. Math. 21, 1–6. doi:10.24297/jam.v21i.9279

CrossRef Full Text | Google Scholar

Niknam, T., and Golestaneh, F. (2012). Enhanced adaptive particle swarm optimisation algorithm for dynamic economic dispatch of units considering valve-point effects and ramp rates. IET Gener. Transm. Distr. 6 (5), 424–435. doi:10.1049/iet-gtd.2011.0219

CrossRef Full Text | Google Scholar

Pandi, V. R., and Panigrahi, B. K. (2011). Dynamic economic load dispatch using hybrid swarm intelligence based harmony search algorithm. Expert Syst. Appl. 38, 8509–8514. doi:10.1016/j.eswa.2011.01.050

CrossRef Full Text | Google Scholar

Panigrahi, C. K., Chattopadhyay, R. N., and Chakrabarti, M. B. (2006). Simulated annealing technique for dynamic economic dispatch. Elect. Power Components Syst. 34 (5), 577–586. doi:10.1080/15325000500360843

CrossRef Full Text | Google Scholar

Perera, F. (2017). Pollution from fossil-fuel combustion is the leading environmental threat to global pediatric health and equity: solutions exist. Int. J. Envi. Res. Public Health 15, 16. doi:10.3390/ijerph15010016

CrossRef Full Text | Google Scholar

Pradeep, J., Premkumar, M., Sundaram, P., and Ravichandran, S. (2012). MaOTLBO: many-objective teaching-learning-based optimizer for control and monitoring the optimal power flow of modern power systems. I. J. Ind. Eng. Comput. 14 (2), 293–308. doi:10.5267/j.ijiec.2023.1.003

CrossRef Full Text | Google Scholar

Preeti, P. H., Vedik, B., and Kumar, T. A. (2022). “A new genetic algorithm variant designed for dynamic economic dispatch,” in Proceedings of 3rd International Conference on Machine Learning, Advances in Computing, Renewable Energy and Communication, Singapore. Editors A. Tomar, H. Malik, P. Kumar, and A. Iqbal (Springer). Lecture Notes in Electrical Engineering, vol 915. doi:10.1007/978-981-19-2828-4_37

CrossRef Full Text | Google Scholar

Sahoo, A. K., Panigrahi, T. K., Paramguru, J., and Hota, A. (2021). “Dynamic economic dispatch using harmony search algorithm,” in Advances in machine learning and computational intelligence. Algorithms for intelligent systems. Editors S. Patnaik, X. S. Yang, and I. Sethi (Singapore: Springer). doi:10.1007/978-981-15-5243-4_3

CrossRef Full Text | Google Scholar

Somuah, C. B., and Khunaizi, N. (1990). Application of linear programming redispatch technique to dynamic generation allocation. IEEE Trans. Power Syst. 5, 20–26. doi:10.1109/59.49081

CrossRef Full Text | Google Scholar

Sundaram, B., Pandya, S. R., Premkumar, M., Pradeep, J., and Hassan, H. (2022b). Multi-objective optimization framework for optimal power flow problem of hybrid power systems considering security constraints. IEEE Access 1–19. doi:10.1109/ACCESS.2022.3209996

CrossRef Full Text | Google Scholar

Sundaram, P., Pradeep, J., and Indrajit, N. T. (2022a). Multi-objective Moth flame optimizer: a fundamental visions for wind power integrated optimal power flow with FACTS devices. Smart Sci. 10 (2), 118–141. doi:10.1080/23080477.2021.1964693

CrossRef Full Text | Google Scholar

Sunilkumar, A., Sundaram, P., Pradeep, J., Kanak, K., and Shankar, C. (2023). A multi-objective thermal exchange optimization model for solving optimal power flow problems in hybrid power systems. Dec. Analy. J. 8, 1–18. doi:10.1016/j.dajour.2023.100299

CrossRef Full Text | Google Scholar

Ullah, Z., Wang, S., Radosavljevic, J., and Lai, J. (2019). A solution to the optimal power flow problem considering WT and PV generation. IEEE Access 7, 46763–46772. doi:10.1109/access.2019.2909561

CrossRef Full Text | Google Scholar

Xia, X., and Elaiw, A. M. (2010). Optimal dynamic economic dispatch of generation: a review. Electr. Power Syst. Res. 80 (8), 975–986. doi:10.1016/j.epsr.2009.12.012

CrossRef Full Text | Google Scholar

Xiong, G., and Shi, D. (2018). Hybrid biogeography-based optimization with brain storm optimization for non-convex dynamic economic dispatch with valve-point effects. Energy 157, 424–435. doi:10.1016/j.energy.2018.05.180

CrossRef Full Text | Google Scholar

Yuan, X., Su, A., Yuan, Y., Nie, H., and Wang, L. (2009). An improved PSO for dynamic load dispatch of generators with valve-point effects. Energy 34 (1), 67–74. doi:10.1016/j.energy.2008.09.010

CrossRef Full Text | Google Scholar

Zaman, M. F., Elsayed, S. M., Raym, T., and Sarker, R. A. (2016). Evolutionary algorithms for dynamic economic dispatch problems. IEEE Trans. Power Syst. 31 (2), 1486–1495. doi:10.1109/tpwrs.2015.2428714

CrossRef Full Text | Google Scholar

Zhang, G. L., Lu, H. Y., Li, G. Y., and Xie, H. (2006). “A new hybrid real-coded genetic algorithm and application in dynamic economic dispatch,” in Proc. 6th World Congr. Intell. Control and Autom., Dalian, China, 3627–3632.

Google Scholar

Zhang, Y., Gong, D. W., Geng, N., and Sun, X. Y. (2014). Hybrid bare-bones PSO for dynamic economic dispatch with valve-point effects. Appl. Soft Comput. J. 18, 248–260. doi:10.1016/j.asoc.2014.01.035

CrossRef Full Text | Google Scholar

Zhi-xin, Z., Jun-qing, L., and Yu-yan, H. (2019). An improved invasive weed optimization algorithm for solving dynamic economic dispatch problems with valve-point effects. J. Experi. Theor. Arti. Intel. 5, 805–829. doi:10.1080/0952813X.2019.1673488

CrossRef Full Text | Google Scholar

Zou, D., Li, S., Kong, X., Ouyang, H., and Li, Z. (2018). Solving the dynamic economic dispatch by a memory-based global differential evolution and a repair technique of constraint handling. Energy 147, 59–80. doi:10.1016/j.energy.2018.01.029

CrossRef Full Text | Google Scholar