A hybrid RBF neural network based model for day-ahead prediction of photovoltaic plant power output

Renewable energy resources like solar power contribute greatly to decreasing emissions of carbon dioxide and substituting generators fueled by fossil fuels. Due to the unpredictable and intermittent nature of solar power production as a result of solar radiance and other weather conditions, it is very difficult to integrate solar power into conventional power systems operation economically in a reliable manner, which would emphasize demand for accurate prediction techniques. The study proposes and applies a revised radial basis function neural network (RBFNN) scheme to predict the short-term power output of photovoltaic plant in a day-ahead prediction manner. In the proposed method, the linear as well as non-linear variables in the RBFNN scheme are efficiently trained using the whale optimization algorithm to speed the convergence of prediction results. A nonlinear benchmark function has also been used to validate the suggested scheme, which was also used in predicting the power output of solar energy for a well-designed experiment. A comparison study case generating different outcomes shows that the suggested approach could provide a higher level of prediction precision than other methods in similar scenarios, which suggests the proposed method can be used as a more suitable tool to deal such solar energy forecasting issues.

1 Introduction

In addition to reducing fossil fuel use and assisting electric grid operators in meeting peak demand during peak hours, solar photovoltaic (PV) energy has become a rapidly expanding renewable energy source and major energy supply (Hong et al., 2019; Jaihuni et al., 2022). With the advent of this kind of renewable relevant technology, solar power production is being integrated more efficiently into the electrical grid with operation features (Wentz et al., 2022). Nevertheless, solar PV system operators face challenges when their output power varies due to climate patterns (such as cloudy, rainy, and sunny days; abrupt weather changes; winter weather; and so on). It is essential for the system to operate reliably and securely in these cases when solar PV power generated is forecasted accurately with good enough precision (Li et al., 2019; Succetti et al., 2020). Especially for the short-term forecasting that involves numerous uncertainty sources, which become extremely hard for conventional methods depends heavily on the time series modeling (Inman et al., 2013; Tuohy et al., 2015). On the other hand, PV plant power output forecasting is the process of forecasting solar energy production at the intersection of different domain knowledge in different fields, such as the energy industry, meteorology, data science, and machine learning (Inman et al., 2013; Gutierrez-Corea et al., 2016; Reindl et al., 2017). By forecasting solar irradiance, grid operators, power traders or solar farms can plan and manage better electricity production and consumption. This is essential to ensure the stable operation of the power grid, reducing operating costs, and promote the widespread usage of renewable energy sources (Islam et al., 2008; Ellabban et al., 2014). There are a variety of methods for solar irradiance and energy prediction (Blaga et al., 2019; Han et al., 2022), including physical model-based methods, statistical methods and machine learning methods that are mostly dealing with short-term forecasting issue. Within these methods, physical model-based approaches depend a lot on modeling and simulation of physical factors such as solar radiation, clouds, and atmospheric conditions, which are even highly dynamic during any short time periods. In comparison, statistical methods, presented in most current works, build data-driven probabilistic models that can be based on historical data to predict short-term future solar energy production (Blaga et al., 2019; Snegirev et al., 2019; Han et al., 2022) either in long-term or short-term time period. Machine learning methods, especially deep learning techniques, are also playing an increasingly important role in solar energy prediction. These methods learn and automatically extract complex patterns in the solar power relevant data to provide more accurate predictions. However, due to the complexity and uncertainty of weather conditions, solar forecasting remains a challenging task (Zhang et al., 2013). In order to improve the accuracy of prediction, it is necessary to consider a variety of factors, such as geographical location, climatic conditions, seasonal changes, equipment performance and so on (Sangrody et al., 2017; Sobri et al., 2018). In addition, real-time data acquisition and processing, model selection and optimization, uncertainty estimation are also key issues in solar energy prediction.

In general, solar forecasting is a complex and important task that involves knowledge and technology from multiple fields. With the popularization of renewable energy and the advancement of intelligent grid, solar energy prediction will play an even more important role in the future (Vanderstar et al., 2018; Wentz et al., 2022). The work in (Hong et al., 2019) describes a number of solar power prediction methods that mostly deal with short-term forecasting issues. A significant research trend is that recent works have focused heavily on deep learning techniques that are purely data-driven with model-free design, especially for short-term small-scale forecasting problem. Ref (Jaihuni et al., 2022) demonstrates the effectiveness of deep Recurrent Neural Networks (RNNs) in estimating 1-week solar radiance using highly accurate Canadian solar data. Ref (Wentz et al., 2022) shows that the power prediction technique using a radiance metric and Long Short-Term Memory (LSTM) has a Mean Absolute Percentage Error (MAPE) of 6.95% that is highly below the average MAPE of conventional methods. Ref (Succetti et al., 2020) uses a multiple variable network with associated parameters such as temperature, wind speed, humidity, solar radiation, and PV power output, and achieves a Normalized Mean Absolute Error (NMAE) of 7.91%, which can be taken as good enough record in day-ahead short-term PV power output forecasting.

In addition to ANN and Fuzzy Logic, soft computing methods were applied to obtain accurate energy predictions. A Recurrent Neural Network method for estimating insolation was presented in ref (Li et al., 2019) A number of ANN methods were employed in ref (Obiora et al., 2021) for predicting solar irradiation, while both multivariate and univariate methods were employed for forecasting power. A weather-driven hybrid approach was used in ref (Akhter et al., 2022) for forecasting solar power output daily, and for decreasing adverse effects the following day. A climate-driven prediction model was used in Ref (Gao et al., 2019) for predicting solar plants for a day ahead, overcoming the effects of fluctuation. Further, ref (Sridharan, 2023) examined how multi-linear regression, polynomial regression, logarithmic regression, and artificial neural networks can be employed for predicting PV power using data from the prior year. Ref (Sangrody et al., 2017) applied Backpropagation Neural Network (BPNN) using Lavenberg - Marquardt algorithms to update weights.

A solar power prediction method based on echo state networks and principal component analysis was examined in ref (Ling et al., 2023). ANNs are not the only models used to forecast solar power; deep learning is likewise used. In ref (Zhang et al., 2019), deep recurrent neural networks using long short-term memory units (DRNN-LSTM) were used to forecast solar power and loads using day-ahead and weekly-ahead historical data. A radiance prediction algorithm based on LSTM deep neural networks was used in ref (Jaihuni et al., 2022) to analysis the radiance impact on solar energy. In neural network modeling, training non-linear variables requires considerable effort, despite the fact that many neural network schemes are available. In spite of their problems with complexities and formulations, meta-heuristic algorithms (MAs) serve as efficient optimization methods that can help improve the parameter-tuning. Therefore, numerous MAs are widely applied for optimizing neural network nonlinear variables, including grey wolf optimizations, monarch butterfly optimizations (MBOs), genetic algorithms (GA), biogeography-based optimizations (BBOs), particle swarm optimizations (PSO), glowworm swarm optimizations (GSOs), and whale optimization problems (WOAs), so on. Radical basis function neural networks are known for their simplicity and ability to approximate non-linear behavior. An artificial bee colony method was used in (Alzaeemi and Sathasivam, 2020) for training fuzzy RBFNNs using data granulation. In (Tsoulos and Charilogis, 2023), a combined PSO-GA approach was employed for optimizing the evolution of RBF neural network to predict rain.

The study proposes and implements a whale optimization-driven RBF neural network to solve the solar production problem. The study’s main contributions are as follows, 1) the study uses Whale optimization-driven RBF scheme to train non-linear variables in RBF scheme for the first time. 2) Efficiency of suggested WOA-driven model training techniques was evaluated against conventional MA techniques on a number of nonlinear model problems.

Following are the sections in the study. Section 2 presents the general framework and preliminary methods for the PV plant power output forecasting scenarios, including the proposed WOA-driven RBF approach. Section 3 presents the simulations and case study results to implement the test cases with demonstration of the numerical values for the performance validation. Section 4 concludes and discusses the major founding with suggestion of the future research work.

2 Preliminaries of the framework

The following part discusses preliminary techniques such as competitive swarm optimization and the canonical RBFNN, which provides good fundamental for the proposed PV plant power output forecasting framework.

2.1 RBFNN

Traditionally, RBF neural networks are multi-input and single-output (MISO) neural network structures, using Gaussian functions acting as the activation function. Figure 1 shows three layers of RBF neural networks, consisting of input layer, hidden layer, and output layer. The basic structure could be represented as the following Eq. 1:

$y\left(t\right)={\displaystyle \sum _{i=1}^n}{w}_i.{\varnothing }_i\left(X\right)(1)$

FIGURE 1

FIGURE 1. RBF network framework.

In which, $y\left(t\right)$ shows the neural network model output during $t$. $w_i$ shows the linear output weight of the $i^{th}$ node hidden layer. For input vector, the radial basis function ${\phi }_i$ can be determined as standard Gaussian function formulation in the following way of Eq. 2:

${\varnothing }_i\left(X\right)=\exp \left(-\frac{1}{2{\sigma }_i^2}{‖X-c_i‖}^2\right),i=\mathrm{1,2},\dots ,n(2)$

Where, ${\sigma }_i$ shows the Gaussian distributed width and $c_i$ shows center of the $i^{th}$ hidden node. $n$ shows the number of hidden layers. Euclidean distance formulas and denominator contain non-linear function variables, requiring efficient optimization methods. The weighting parameters of RBF-based neural network can be efficiently computed via combination with any computationally tractable heuristic optimization method, which makes it easily for parameter tuning compared with other hyper-parameter sensitive methods.

2.2 Whale optimization algorithm (WOA)

WOA is an optimization algorithm derived from bubble-net hunt methods used in meta-heuristic algorithms (Mi et al., 2016). In this algorithm, it is described how humpback whales hunt. Humpback whales follow the usual bubbles when they encircle preys, creating a circle or ‘9-shaped path’. Basically, bubble-net hunting or feeding is explained by humpback whales diving 10–15 m in water and subsequently starting to generate bubbles encasing preys, followed by following the bubbles and moving up. According to the algorithm presented in (Mi et al., 2016), Whale Optimization algorithm (WOA) is modeled in the following ways.

2.2.1 An encircled prey formula

After encircling the target, the humpback whales update their location to reach the optimum solution over a series of iterations.

$\overrightarrow{D}=\left|C.\overrightarrow{X}\left(t\right)-X\left(t\right)\right|(3)$

$\overrightarrow{X}\left(t+1\right)=\overrightarrow{X}\left(t\right)-\overrightarrow{A}.\overrightarrow{D}(4)$

In which, $\overrightarrow{A}$, $\overrightarrow{D}$ show coefficient vectors. $t$ shows present iteration. ${\overrightarrow{X}}^{*}\left(t\right)$ shows the position vector of optimal solution. $X\left(t\right)$ shows the position vector. $\overrightarrow{A}$, $\overrightarrow{D}$ can be described in the following way:

$\overrightarrow{A}=2\overrightarrow{a}\ast r-\overrightarrow{a}(5)$

$\overrightarrow{A}=2\ast r(6)$

In which, $\overrightarrow{a}$ reduces linearly from two to zero over during iteration and r shows a randomly selected number between [0, 1]. In this way, Eqs 3–6 could control the optimal search direction and learning rate of the global optimality convergence.

2.2.2 Bubble-net attack approach

Humpback whale bubble-net behaviors can be mathematically described using 2 approaches:

A. Method for shrinking encirclement: In the method, $\overrightarrow{a}$ was linearly decreased from two to zero. Random value for vector in domain amongst $\left[-1,1\right]$.

B. Spiral updating position: As a result of the helix-shaped motion of the humpback whales and target, the following formula can be derived as Eq. 7:

$\overrightarrow{X}\left(t+1\right)={\overrightarrow{D}}^{\prime }\ast e^{bt}\ast \cos \left(2\pi l\right)+\overrightarrow{X}\left(t\right)(7)$

In which, $l$ represents a randomly selected number between $\left[-1,1\right]$. $b$ shows fixed logarithmic shape. ${\overrightarrow{D}}^{\prime }=\left|{\overrightarrow{X}}^{*}\left(t\right)-X\left(t\right)\right|$ shows the distance among $i^{th}$ whale to the target mean optimal solution.

During optimization, whales are assumed to follow either a shrinking encirclement or logarithmic path 50%–60% of the time. The mathematical model is based on the following Eq. 8:

$\overrightarrow{X}\left(t+1\right)=\left\{\begin{array}{c}\overrightarrow{X}\left(t\right)-\overrightarrow{A}\overrightarrow{D}ifp<0.5\\ {\overrightarrow{D}}^{\prime }.e^N.\cos \left(2\pi l\right)+\overrightarrow{X}\left(t\right)p\ge 0.5\end{array}\right.(8)$

In which, $p$ is a randomly selected parameter in the value range of $\left[0,1\right]$. $\overrightarrow{A}$, $\overrightarrow{D}$ still indicate the coefficient vectors to tune the learning rate of optimal solutions.

2.2.3 Searching for target

Exploration is done using $\overrightarrow{A}$ to find the target. Additionally, $\overrightarrow{A}$ accepts values above 1 or below −1. There are 2 requirements for exploration.

$\overrightarrow{D}=\left|\overrightarrow{C}.\overrightarrow{X_{rand}}-\overrightarrow{X}\right|(9)$

$\overrightarrow{X}\left(t+1\right)=\overrightarrow{X_{rand}}-\overrightarrow{A}\overrightarrow{D}(10)$

Lastly, the following should be followed (Zhang et al., 2013):

• $\left|\overrightarrow{A}\right|>1$ would enforce exploration to WOA algorithm for determining global optimal avoid local optimal.

• $\left|\overrightarrow{A}\right|<1$ should be chosen in order to update the location of present searching agent/optimal solution.

3 Suggested WOA optimized RBF neural network

An RBF neural network’s architecture and variables must be defined, just like any other neural network scheme. A scheme training process can be divided into three main categories depending on the flexibility of its determination. The first one involves determining the model structure and non-linear variables via trial and error and subsequently obtaining linear weights using minimum squares or various approximations. The second one involves fixing the model structure including input and hidden node number and allowing the optimization approach for training the non-linear and linear variables. Lastly, the third one involves simultaneous training of the model structure and variables. As part of the Model Training Type 2 presented in the study, the WOA approach has been used to train the non-linear and linear variables based on an established neural network model framework. As a fitness function for optimizing RBF networks, the root mean square error (RMSE) has been used, as shown in Eqs 5, 6)

$\min f=\sqrt{\frac{1}{N_m}.{\displaystyle \sum _{i=1}^{N_m}}{\left(\widehat{y}-y_m\right)}^2}(11)$

In which, $\widehat{y}$ shows the forecast value and $y_m$ shows the measured information set. It is important to calculate each parameter in advance of computing $\widehat{y}$, as expressed in Eq. (12):

$\widehat{\text{y}}={\displaystyle \sum _{\text{i}=1}^{{\text{n}}_{\text{h}}}}{\text{w}}_{\text{i}}.\text{exp\hspace{0.17em}}\left(-\frac{1}{2{\sigma }_{\text{i}}^2}{‖\text{X}-{\text{c}}_{\text{i}}‖}^2\right),\text{i}=\mathrm{1,2},\dots ,\text{n}(12)$

An RBF neural network training procedure can likewise be considered an unrestricted optimization problem along with the objective function. The decision parameters are expressed in the following manner, assuming $i$ and $j$ are the input node and hidden node in Eq. (13):

$\text{particle}\left(\text{i}\right)=\left[{\text{c}}_{11},{\text{c}}_{21},\dots ,{\sigma }_1,{\text{w}}_1,c_{12},c_{22},\dots ,c_{j2},{\sigma }_2,w_2,,\dots c_{1k},c_{2k},\dots ,c_{jk},{\sigma }_k,w_k\right](13)$

There is full encoding of non-linear variables in all hidden nodes and their associated linear weighting factors. Figure 2 shows the in-depth process of this suggested WOA-driven RBF model approach:

1) Initialization:

(a) Input information vectors are selected and adopted into the RBF neural networks; b) The number of hidden nodes for RBF neural networks is determined and pre-defined according to empirical analysis; c) The decision parameters based on the current framework are encoded according to the solar power predication factors; d) Decision parameter values of the entire population are initialized by random values;

2) Optimization procedure:

(a) The mean value $X_k^{\prime }\left(t\right)$ of the entire population is calculated; b) The entire population is divided into two categories containing the same number of particles; c) one population from every category is selected at the random group and the fitness function Eq. 11 for the two particles is calculated; d) The loser based on Eqs 9, 10 is updated; e) The new loser and the winner are added to the upcoming generation population; f) The step 2)-(c) to step 2)-(e) should be repeated until there are no whales left.

3) Finalization procedure:

(a) The maximum number of iterations should be determined according pre-defined tolerance; b) The step 2)-(a) should be repeated until the max number of iterations has been reached; c) The procedure is terminated via iteration limitation or convergence tolerance with the optimal value generated.

FIGURE 2

FIGURE 2. Process of WOA optimized RBF network.

4 Simulation and case study

Even though PV power output is mainly determined by radiance, other weather conditions and associated parameters (the temperature of the module, surrounding temperature, the direction and speed of the wind) are also important and have impact on the ultimate PV plant power output. For instance, the open circuit voltage of crystalline silicon PV modules reduces in response to increasing temperature, reaching a value of −0.45%/K, and short-circuit current ranges from 0.4%/K to 0.9%/K. Consequently, wind speed is usually used as a predicting variable to account for the cooling impact, heat dissipation, and PV panel cleaning. Those weather and environmental conditions could be coded as corresponding variables in the RBFNN as modified input data. The short-term forecasting for PV plant power output should include considerable determining factors to guarantee the accuracy and forecasting reliability.

4.1 Simulation setup

Table 1 shows the plant information. Information is captured by the SCADA system daily and is used to monitor and record weather conditions. A weather variable’s output is correlated using Pearson Correlation Coefficient (PCC). The Pearson Correlation Coefficient is described by Eq. (14) in which x-axis shows the time series of output power, y-axis shows the time series for all climate dependent parameters.

$PCC=\frac{n\left(\sum xy\right)-\left(\sum x\right)\left(\sqrt{y}\right)}{\sqrt{\left[n\sum x^2-{\left(\sqrt{x}\right)}^2\right]\left[n\sum y^2-{\left(\sum y\right)}^2\right]}}(14)$

TABLE 1

TABLE 1. PV Power plant information.

The PCC parameter setting for a weather variable is shown in Table. 2 to illustrate the association among the variable and the plant’s power output. An example of a radiance and power output profile is shown in Figure 3A, in which a near-unity PCC value predicts that radiance and power output are heavily correlated. In contrast, variables such as module temperature, ambient temperature, and the direction and speed of the wind show less correlation with power output (see Figures 3B, C, D). Wind variables can be key to forecasting unplanned blackouts in coastal areas such as Odisha due to adverse climate conditions.

TABLE 2

TABLE 2. PCC among the plant output power and various weather variables within 2022 data.

FIGURE 3

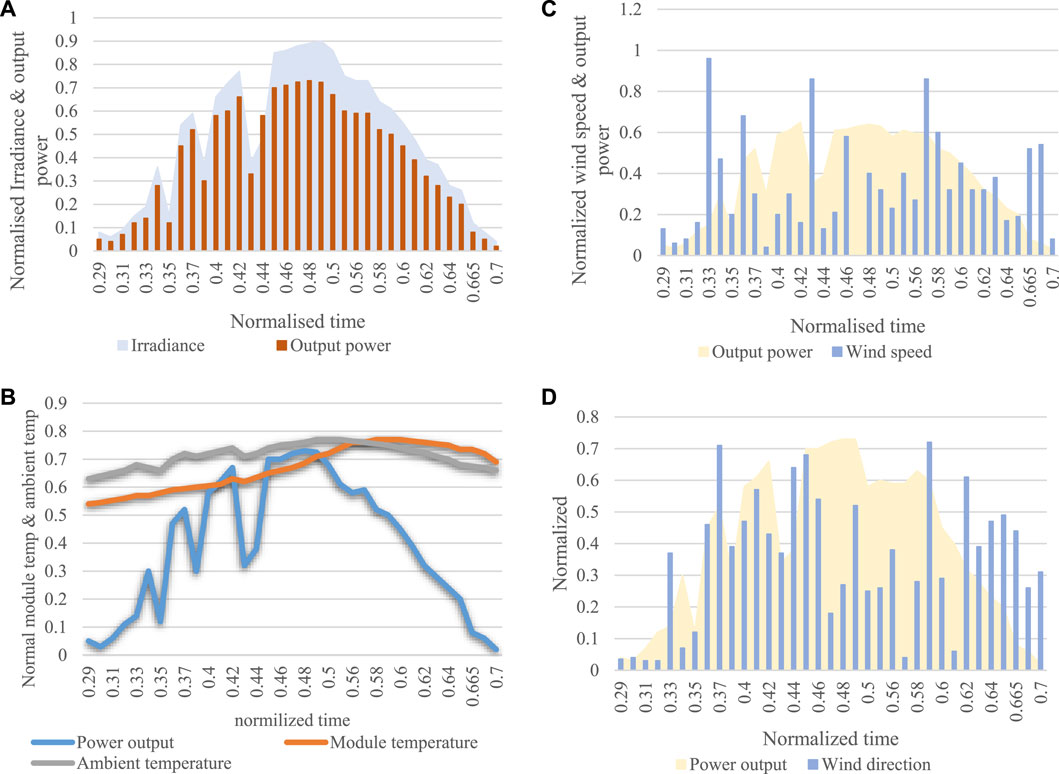
FIGURE 3. A representation of normalized weather variables and plant output power against normalized time for 8 January 2022 (A) Radiance (B) Ambient and Module temperatures (C) Wind speed and (D) Wind direction.

The networks are trained using information from 2012 to 2013. The information from 2022 to 2023 is either inaccurate (for example, incorrect SCADA reading) or indicates unusual circumstances (for example, blackouts). In the absence of power generation, the information is eliminated using a MATLAB program. MATLAB’s ‘nntool’ function is used to train the network during July 2022 and 2023 datasets to produce forecasts in July 2024. A comparison of the trained ANN’s output with the calculated 2024 information set helps to determine how effective the algorithm is.

4.2 Method performance

A neural network schema is trained for information gathered in July 2022 and July 2023 and evaluated for information gathered in July 2024. A comparison of the approach with the real output information of 18 July 2014 is shown in Figure 4. The optimum Sigma (${\sigma }_{opt}$) of RBF training monthly is shown in Figure 5. In Figure 6, the proposed approach and others are simulated alongside the PV power generation of the plant measured on 18 July 2024.

FIGURE 4

FIGURE 4. RMSE versus sigma for RBF.

FIGURE 5

FIGURE 5. Optimum Sigma (${\sigma }_{opt}$) for RBF training monthly.

FIGURE 6

FIGURE 6. Comparing the output of RBF, FFNN, decision-driven algorithm and the real power production of the plant.

As a result of the proposed approach’s low RMSE, it produces an improved fit compared with other existing methods that usually range from 0.7–0.9 for RMSE. As well as a low RMSE, the algorithm has also produced an irregular envelope around the real output with limited upper bound and lower bound. In this way, WOA-RBF actually increases power output envelope by having greater RMSE than the proposed approach. Although the proposed approach has the lowest RMSE among others, simulated output power drops sharply around 0.5 during normalized time. There is a possibility that at the RBFEF training, one point of the dataset was anomalous near the input data point, which can cause unexpected drops in simulated output.

4.3 Analysis in different application scenarios

With the consideration of different weather condition effect, the proposed method has also been tested in different application scenarios via RBFNN parameter tuning according to the clear-sky day forecasting or cloudy day forecasting applications in different seasons.

By tuning the optimal hyper-parameters of RBFNN, Table 3 shows the minimal forecasting RMSE error of PV plant power output for different weather conditions in different seasons. Compared with other forecasting methods, the proposed one could deal with more different scenarios since it depends little on any specific features that should be pre-defined. It is easily observed that generally speaking most short-term PV power output forecasting results are better in clear-sky day conditions than cloudy day conditions due to the uncertain shadowing effect of massive cloud impact on the sunny irradiance. It is worth mentioning that this phenomenon is also observed in other existing methods. The specific forecasting RMSE error also varies with the season change over the whole year, since the temperature or humidity condition will play a role as well in determining the specific energy generation level of PV plant power output.

TABLE 3

TABLE 3. The minimal forecasting RMSE error for different weather conditions in different seasons.

In Figure 7, we also try the normal distribution fitting for the forecasting errors to observe the error reduction and error growth phenomenon in application scenarios of different aggregated PV plant power output capacity. It can be found that for smaller 60 MW PV plant power output forecasting, the fitting error has a more stochastic error distribution since the internal aggregation of PV cell units usually suffers less counteracting effect compared with larger 230 MW PV plant power output forecasting.

FIGURE 7

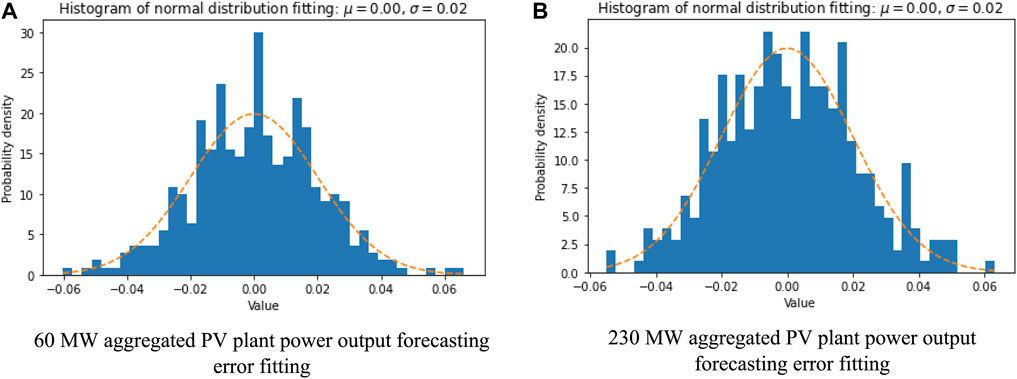
FIGURE 7. The forecasting error with normal distribution fitting for different large-scale aggregated PV plant. (A) 60 MW aggregated PV plant power output forecasting error fitting. (B) 230 MW aggregated PV plant power output forecasting error fitting.

On the other hand, the operation of larger PV plant would provide larger resource capacity and better forecasting reliability margin to deal with the manual feature extraction issues. It is believed that with proper design of the hyper-parameter of RBFNN framework and gradient calculation of WOA optimization, the short-term PV plant power output forecasting could be self-adaptive to the changes of external environmental weather conditions and power dispatch scheduling of each PV generation unit.

5 Conclusion

The work proposes a whale optimization algorithm combined with RBFNN to forecast solar production. The suggested approach framework allows for simultaneous determination of linear and non-linear variables in RBFs. Several non-linear evaluations and a forecast task for solar production have confirmed its competitiveness. This paper also proposes the whale optimization algorithm using RBF to help forecast PV power plant output directly day-ahead in advance with acceptable forecasting errors. A comparison study case is experimented to generate different outcomes that shows the proposed approach could provide a higher level of prediction precision than other conventional methods in similar scenarios, especially for PV plant power output in various conditions. According to the specific application scenarios, this work suggests and concludes the proposed method can be used as a more suitable tool to deal with such solar energy and PV plant power output forecasting problems. In the future work, we will consider more sources of uncertainty and combine the current method with some auto-encoder framework to efficiently extract the significant features of the forecasting problem, which would further improve the short-term prediction accuracy for large-scale PV plant capacity. The proposed method can also be combined with the coupled operation framework to facilitate the end-to-end decision-making of forecasting-based power system operation.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

QZ: Conceptualization, Investigation, Software, Writing–original draft, Writing–review and editing. NT: Conceptualization, Data curation, Investigation, Methodology, Writing–review and editing. JL: Conceptualization, Data curation, Investigation, Methodology, Software, Supervision, Writing–review and editing. WW: Formal Analysis, Project administration, Validation, Writing–original draft, Writing–review and editing. LW: Formal Analysis, Funding acquisition, Resources, Visualization, Writing–review and editing. WK: Funding acquisition, Methodology, Resources, Supervision, Validation, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work is supported by NARI Technology Co., Ltd. Technology Project under No. 524608220177. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.

Conflict of interest

Authors QZ, NT, JL, WW, LW and WK were employed by NARI Research Institute, NARI Technology Co, Ltd.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akhter, M. N., Mekhilef, S., Mokhlis, H., Ali, R., Usama, M., Muhammad, M. A., et al. (2022). A hybrid deep learning method for an hour ahead power output forecasting of three different photovoltaic systems. Appl. Energy 307, 118185. doi:10.1016/j.apenergy.2021.118185

CrossRef Full Text | Google Scholar

Alzaeemi, S. A., and Sathasivam, S. (2020). Artificial immune system in doing 2-satisfiability based reverse analysis method via a radial basis function neural network. Processes 8 (10), 1295. doi:10.3390/pr8101295

CrossRef Full Text | Google Scholar

Blaga, R., Sabadus, A., Stefu, N., Dughir, C., Paulescu, M., and Badescu, V. (2019). A current perspective on the accuracy of incoming solar energy forecasting. Prog. energy Combust. Sci. 70, 119–144. doi:10.1016/j.pecs.2018.10.003

CrossRef Full Text | Google Scholar

Ellabban, O., Abu-Rub, H., and Blaabjerg, F. (2014). Renewable energy resources: current status, future prospects and their enabling technology. Renew. Sustain. energy Rev. 39, 748–764. doi:10.1016/j.rser.2014.07.113

CrossRef Full Text | Google Scholar

Gao, M., Li, J., Hong, F., and Long, D. (2019). Day-ahead power forecasting in a large-scale photovoltaic plant based on weather classification using LSTM. Energy 187, 115838. doi:10.1016/j.energy.2019.07.168

CrossRef Full Text | Google Scholar

Gutierrez-Corea, F. V., Manso-Callejo, M. A., Moreno-Regidor, M. P., and Manrique-Sancho, M. T. (2016). Forecasting short-term solar irradiance based on artificial neural networks and data from neighboring meteorological stations. Sol. Energy 134, 119–131. doi:10.1016/j.solener.2016.04.020

CrossRef Full Text | Google Scholar

Han, R., Hu, Q., Cui, H., Chen, T., Quan, X., and Wu, Z. (2022). An optimal bidding and scheduling method for load service entities considering demand response uncertainty. Appl. Energy 328, 120167. doi:10.1016/j.apenergy.2022.120167

CrossRef Full Text | Google Scholar

Hong, T., Xie, J., and Black, J. (2019). Global energy forecasting competition 2017: hierarchical probabilistic load forecasting. Int. J. Forecast. 35 (4), 1389–1399. doi:10.1016/j.ijforecast.2019.02.006

CrossRef Full Text | Google Scholar

Inman, R. H., Pedro, H. T., and Coimbra, C. F. (2013). Solar forecasting methods for renewable energy integration. Prog. energy Combust. Sci. 39 (6), 535–576. doi:10.1016/j.pecs.2013.06.002

CrossRef Full Text | Google Scholar

Islam, M. R., Islam, M. R., and Beg, M. R. (2008). Renewable energy resources and technologies practice in Bangladesh. Renew. Sustain. Energy Rev. 12 (2), 299–343. doi:10.1016/j.rser.2006.07.003

CrossRef Full Text | Google Scholar

Jaihuni, M., Basak, J. K., Khan, F., Okyere, F. G., Sihalath, T., Bhujel, A., et al. (2022). A novel recurrent neural network approach in forecasting short term solar irradiance. ISA Trans. 121, 63–74. doi:10.1016/j.isatra.2021.03.043

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, G., Wang, H., Zhang, S., Xin, J., and Liu, H. (2019). Recurrent neural networks based photovoltaic power forecasting approach. Energies 12 (13), 2538. doi:10.3390/en12132538

CrossRef Full Text | Google Scholar

Ling, Y., Li, X., Li, C., and Chen, T. (2023). “An intelligent adversarial deep forecasting model for load demand using hybrid modified DA-GAN,” in IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia) (IEEE), 1340–1345.

CrossRef Full Text | Google Scholar

Mirjalili, S., and Lewis, A. (2016). The whale optimization algorithm. Adv. Eng. Softw. 95, 51–67. doi:10.1016/j.advengsoft.2016.01.008

CrossRef Full Text | Google Scholar

Obiora, C. N., Hasan, A. N., Ali, A., and Alajarmeh, N. (2021). Forecasting hourly solar radiation using artificial intelligence techniques. IEEE Can. J. Electr. Comput. Eng. 44 (4), 497–508. doi:10.1109/icjece.2021.3093369

CrossRef Full Text | Google Scholar

Reindl, T., Walsh, W., Yanqin, Z., and Bieri, M. (2017). Energy meteorology for accurate forecasting of PV power output on different time horizons. Energy Procedia 130, 130–138. doi:10.1016/j.egypro.2017.09.415

CrossRef Full Text | Google Scholar

Sangrody, H., Sarailoo, M., Zhou, N., Tran, N., Motalleb, M., and Foruzan, E. (2017). Weather forecasting error in solar energy forecasting. IET Renew. Power Gener. 11 (10), 1274–1280. doi:10.1049/iet-rpg.2016.1043

CrossRef Full Text | Google Scholar

Snegirev, D. A., Eroshenko, S. A., Khalyasmaa, A. I., Dubailova, V. V., and Stepanova, A. I. (2019). “Day-ahead solar power plant forecasting accuracy improvement on the hourly basis,” in In2019 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus) (IEEE), 1088–1091.

CrossRef Full Text | Google Scholar

Sobri, S., Koohi-Kamali, S., and Rahim, N. A. (2018). Solar photovoltaic generation forecasting methods: a review. Energy Convers. Manag. 156, 459–497. doi:10.1016/j.enconman.2017.11.019

CrossRef Full Text | Google Scholar

Sridharan, M. (2023). Generalized regression neural network model based estimation of global solar energy using meteorological parameters. Ann. Data Sci. 10 (4), 1107–1125. doi:10.1007/s40745-020-00319-4

CrossRef Full Text | Google Scholar

Succetti, F., Rosato, A., Araneo, R., and Panella, M. (2020). Deep neural networks for multivariate prediction of photovoltaic power time series. IEEE Access 8, 211490–211505. doi:10.1109/access.2020.3039733

CrossRef Full Text | Google Scholar

Tsoulos, I. G., and Charilogis, V. (2023). Locating the parameters of RBF networks using a hybrid particle swarm optimization method. Algorithms 16 (2), 71. doi:10.3390/a16020071

CrossRef Full Text | Google Scholar

Tuohy, A., Zack, J., Haupt, S. E., Sharp, J., Ahlstrom, M., Dise, S., et al. (2015). Solar forecasting: methods, challenges, and performance. IEEE Power Energy Mag. 13 (6), 50–59. doi:10.1109/mpe.2015.2461351

CrossRef Full Text | Google Scholar

Vanderstar, G., Musilek, P., and Nassif, A. (2018). “Solar forecasting using remote solar monitoring stations and artificial neural networks,” in In2018 IEEE Canadian conference on electrical & computer engineering (CCECE) (IEEE), 1–4.

CrossRef Full Text | Google Scholar

Wentz, V. H., Maciel, J. N., Gimenez Ledesma, J. J., and Ando Junior, O. H. (2022). Solar irradiance forecasting to short-term PV power: accuracy comparison of ann and LSTM models. Energies 15 (7), 2457. doi:10.3390/en15072457

CrossRef Full Text | Google Scholar

Zhang, J., Hodge, B. M., Florita, A., Lu, S., Hamann, H. F., and Banunarayanan, V. (2013). Metrics for evaluating the accuracy of solar power forecasting. Golden, CO (United States): National Renewable Energy Lab.NREL.

Google Scholar

Zhang, X., Pipattanasomporn, M., Chen, T., and Rahman, S. (2019). An IoT-based thermal model learning framework for smart buildings. IEEE Internet Things J. 7 (1), 518–527. doi:10.1109/jiot.2019.2951106

CrossRef Full Text | Google Scholar

Zhang, Y., Qian, W., Ye, Y., Li, Y., Tang, Y., Long, Y., et al. (2023). A novel non-intrusive load monitoring method based on ResNet-seq2seq networks for energy disaggregation of distributed energy resources integrated with residential houses. Appl. Energy 349, 121703. doi:10.1016/j.apenergy.2023.121703

CrossRef Full Text | Google Scholar