Large-scale deep reinforcement learning method for energy management of power supply units considering regulation mileage payment

To improve automatic generation control (AGC) performance and reduce the wastage of regulation resources in interconnected grids including high-proportion renewable energy, a multi-area integrated AGC (MAI-AGC) framework is proposed to solve the coordination problem of secondary frequency regulation between different areas. In addition, a cocktail exploration multi-agent deep deterministic policy gradient (CE-MADDPG) algorithm is proposed as the framework algorithm. In this algorithm, the controller and power distributor of an area are combined into a single agent which can directly output the power generation command of different units. Moreover, the cocktail exploration strategy as well as various other techniques are introduced to improve the robustness of the framework. Through centralized training and decentralized execution, the proposed method can nonlinearly and adaptively derive the optimal coordinated control strategies for multiple agents and is verified on the two-area LFC model of southwest China and the four-area LFC model of the China Southern Grid (CSG).

1 Introduction

The development of interconnected power systems (Li et al., 2021; Li et al., 2022) and the increasing application of large-scale renewable energy and generating units with multiple energy coupling characteristics have led to more frequent random disturbances in power systems, which generate significant coordination problems with regard to frequency control within such power systems (Qu et al., 2023). Nowadays, the two major coordination problems affecting secondary frequency regulation in multi-area power systems (hereinafter referred to as the “two coordination problems”) are as follows: (1) there is a coordination problem between the automatic generation control (AGC) controller and distributor, which reduces the frequency regulation efficiency of the system and reduces the adjustment resources of the system; (2) the coordination problems of AGC in various areas will affect each other, resulting in frequency oscillation and regulation waste and reduced control performance. In this situation, conventional AGC (Qu et al., 2022) cannot meet the network demand due to its failure to allow for the above problems (Huan et al., 2023).

In the AGC controller and distributor, the existing AGC-related algorithms can be divided into two categories. One is the control algorithm of AGC, which consists of the PID-based algorithm (Li et al., 2023a), neural network (Li et al., 2023b), sliding mode control, and (Yu et al., 2011a) learning (Yu et al., 2011b). The purpose of these control algorithms is to minimize deviations in the control frequency.

The other category is the optimization algorithm for the distributor, which consists of the intelligent optimization algorithm (Yu et al., 2015), the fixed pattern dispatch (Yu et al., 2012), group optimization algorithm (Xi et al., 2020), and traditional optimization algorithm (Mirjalili et al., 2014). The optimization algorithm is used to send commands to each unit in order to minimize the regulation payment.

The payment calculated dynamically based on regulation mileage has replaced the original fixed regulation payment in the AGC, which aggravates the coordination problem between the controller and the distributor. Thus, the combination of these two categories of algorithms (hereafter termed “combinatorial algorithm”) increases the frequency deviation and the regulation payment, which will lead to poor AGC performance.

Regarding the coordination problem affecting secondary frequency regulation between different areas, the independent supplier operator (ISO) of each area has a certain interest independence, whereby the ISO of each area wants to restore the frequency but has no intention to pay too much frequency regulation payment during mutual support (Bahrami et al., 2014; Mirjalili, 2016; Xi et al., 2016).

An increasing number of researchers have opined that a data-driven control scheme based on multi-agent deep reinforcement learning (MA-DRL) holds significant potential. For example, Yu et al. have demonstrated a novel MA-DRL algorithm, which is designed for solving the coordinated control problem (Yu et al., 2016). However, an increase in the number of agents leads to a lower convergence probability of the algorithm; this property limits its application in real-world systems. Moreover, Xi et al. have developed a “wolf climbing” MA-DRL algorithm (Xi et al., 2015) and solved the problem of multi-area control. However, because the action space of the algorithm is discrete, there arises the problem of the dimensionality curse, which makes it difficult to realize continuous control. Xi et al. have proposed a multi-agent coordination method for inter-area AGC (Xi et al., 2020); however, continuous control of inter-area AGC cannot be realized for the discrete action space (Li et al., 2023c; Li and Zhou, 2023). However, the current MA-DRL-based data-driven control method still has the following problems: the comprehensive coordination of multi-agent was not achieved; low robustness. In order to solve the “two coordination problems” and further improve the AGC performance and reduce wastage of regulation resources in a multi-area power system, a multi-area integrated AGC (MAI-AGC) framework is proposed. In this framework, a novel deep reinforcement learning algorithm, known as cocktail exploration multi-agent deep deterministic policy gradient (CE-MADDPG), has been proposed, which uses the cocktail exploring strategy and other techniques to improve the robustness of the MADDPG. Based on this algorithm, the controller and distributor are combined into a single agent which can output the commands of the various units. Due to the employment of centralized training and decentralized execution, each agent only needs local information in its control area for delivering optimal control signals. The simulation of the LFC model shows that the method achieves the comprehensive optimization of performance and economy.

The innovations demonstrated in this paper are as follows:

(1) An MAI-AGC framework based on multi-area coordination is proposed to achieve coordination between the controller and distributor, which reduces the cost and fluctuation of frequency regulation, and enables each agent to make optimal decisions based on local information without relying on the global status of the whole power grid (Yu et al., 2011a; Yu et al., 2011b; Yu et al., 2012; Bahrami et al., 2014; Mirjalili et al., 2014; Yu et al., 2015; Mirjalili, 2016; Xi et al., 2016; Yu et al., 2016; Xi et al., 2020).

(2) A CE-MADDPG algorithm is introduced to improve the robustness of the MAI-AGC framework, which employs cocktail exploration and other techniques to overcome the problem of sparse rewards of conventional deep reinforcement learning methods and to achieve multi-objective optimization of control performance and regulation mileage payment (Xi et al., 2015; Xi et al., 2020; Li et al., 2023c).

The MAI-AGC model is elaborated in in Section 2, CE-MADDPG is introduced in Section 3; in Section 4, a new approach was used throughout the event, and the conclusion is given in Section 5.

2 MAI-AGC framework

2.1 Performance-based frequency regulation market

Frequency regulation mileage is a novel technical indicator for identifying the actual regulating variable of each unit (Li et al., 2021). According to the calculation rules of China Southern Grid (CSG) in China, the frequency regulation mileage payment of each unit is as Eqs (1)–(10) (Li et al., 2021):

$D_i={\displaystyle \sum _{k=1}^N}\lambda \cdot k_i^{\mathrm{p}}\cdot M_i\left(k\right)={\displaystyle \sum _{k=1}^N}\lambda \cdot k_i^{\mathrm{p}}\cdot \left|\Delta P_{Gi}\left(k+1\right)-\Delta P_{Gi}\left(k\right)\right|,(1)$

$\left\{\begin{array}{l}{S}_i^{\text{rate}}=\frac{\Delta P_i^{\text{rate}}}{\Delta P_a^{\text{rate}}}\\ S_i^{\text{delay}}=1-\frac{T_i^{\mathrm{d}}}{5\mathit{min}}\\ S_i^{\text{pre}}=1-\frac{1}{N}{\displaystyle \sum _{k=1}^N}\left|\frac{\Delta P_{\text{order}-i}\left(k\right)-\Delta P_{Gi}\left(k+1\right)}{\Delta P_{i,\mathrm{a}}}\right|\\ S_i^{\mathrm{p}}={\omega }_1{S}_i^{\text{rate}}+{\omega }_2{S}_i^{\text{delay}}+{\omega }_3{S}_i^{\text{pre}}\\ {\omega }_1+{\omega }_2+{\omega }_3=1,{\omega }_1\ge 0,{\omega }_2\ge 0,{\omega }_3\ge 0\end{array}\right.,(2)$

where ${\int }_0^t\Delta f_{A}dt$, $e_{ACE}^A$, and ${\int }_0^t{e}_{ACE}^{A}dt$ are 0.50, 0.25, and 0.25, respectively.

2.2 Frequency operating standards

CPS1 can best represent the performance of AGC (Qu et al., 2023). The calculation method of the area control error (e_ACE) is as follows:

$e_{\text{ACE}}=\Delta P_{\text{tie}}-10B\Delta f.(3)$

The CPS1 indicator is as follows:

$C_{\text{CPS}1}=\left(2-C_{\text{CF}1}\right)\times 100\%,(4)$

where

$C_{\text{CF}1}=\frac{\sum \left(e_{{\text{ACE}}_{\text{AVE}\cdot \min }}*\Delta f_{\text{AVE}-\min }\right)}{-10B_i{n}_{\text{time}}{\epsilon }_1^2}.(5)$

2.3 Control framework of MAI-AGC

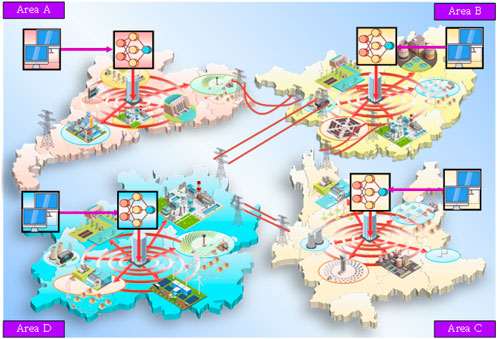
As shown in Figure 1, in the MAI-AGC framework, the AGC controller and power distributor of each area are replaced by a centralized agent, which can output the power generation commands of multiple units in the area simultaneously and obtain the optimal coordinated strategy via training so that during online application, the coordination with agents in other areas can be realized while reducing the frequency deviation and payment in different areas.

FIGURE 1

FIGURE 1. MAI-AGC framework.

2.4 Objective function

The aim was to achieve the optimum performance of AGC and its economic efficiency. The objective of the agent in the ith area is expressed as follows:

$\min f_i={\mu }_1{\displaystyle \sum _{k=1}^N}\Delta f_i{\left(k\right)}^2+{\mu }_2{\displaystyle \sum _{k=1}^N}\left|e_i^{ACE}\left(k\right)\right|+{\mu }_3{\displaystyle \sum _{j=1}^n}{D}_i^j.(6)$

2.5 Constraint conditions

The constraint conditions for the coal-fired unit, LNG units, oil-fired unit, hydro unit, and DERs in the SVPP are represented as Eq. 12. The constraint of DERs in the FVPP, which employs DC/DC convert to control the energy, excludes the generation climbing speed constraint.

$\left\{\begin{array}{l}{\displaystyle \sum _{j=1}^n}\Delta P_j^{\text{in}}\left(k\right)=\Delta P_{\text{order}-\sum }\left(k\right)\\ \Delta P_{\text{order}-\sum }\left(k\right)*\Delta P_j^{\text{in}}\left(k\right)\ge 0\\ \Delta P_j^{\min }\le \Delta P_j^{\text{in}}\left(k\right)\le \Delta P_j^{\max }\\ \left|\Delta P_j^{\text{out}}\left(k+1\right)-\Delta P_j^{\text{out}}\left(k\right)\right|\le \Delta P_j^{\text{rate}}\end{array}\right..(7)$

3 Principle of the MAI-AGC-based CE-MADDPG algorithm

3.1 Design of MAI-AGC based on the EE-MAPDDG algorithm

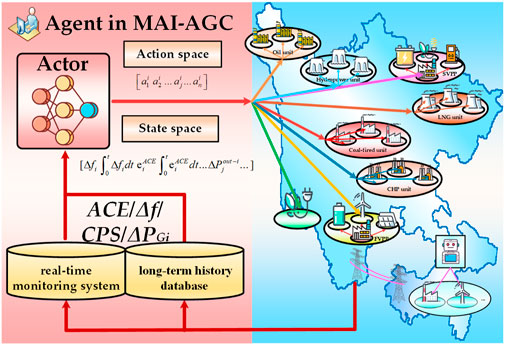
There are n agents in this MA-DRL framework of one area, with agent_i corresponding to the agent of the ith area. The method comprises offline centralized training and online application.

The global optimal coordinated control strategy can be obtained by fully off-line training agents. In online applications, the policy function π_ϕⁱ (s) of agent_i is responsible for outputting the actions under that particular state, i.e., the generation factor for each unit in the ith area. The control interval of agent_i is set to 4 s. The control objective is to eliminate the ACE and reduce the mileage payment of each area. The control framework is shown in Figure 2.

FIGURE 2

FIGURE 2. MAI-AGC system based on the CE-MADDPG algorithm.

3.1.1 Action space

For any time t, in the ith area, the AGC generation factor of n units and VPP are selected as action, and there are a total of n actions, as shown in the following equation:

$\left\{\begin{array}{l}\left[a_1^i{a}_2^i\dots a_j^i\dots a_n^i\right],a_j^i\le 1\\ ∆P_{\text{order}-j}^i=a_j^i*P_{jG}^{\max -i}\end{array}\right..(8)$

3.1.2 State space

A state refers to an ordered collection of the smallest number of variables that can determine the state of the system in the system, and the state space of the agent of area i is shown as Figure 3:

$\left[∆f_i{\int }_0^t∆f_{i}dt{\mathrm{e}}_i^{ACE}{\int }_0^t{\mathrm{e}}_i^{ACE}dt{∆P}_1^{out-i}\dots ∆P_j^{out-i}\dots ∆P_n^{out-i}\right].(9)$

FIGURE 3

FIGURE 3. Training flow of CE-MADDPG.

3.1.3 State space of the EIE-MATD3 algorithm

By referring to Eq. 11, the reward of the agent in the ith area is expressed as follows:

$r_i\left(t\right)=-\left[{\mu }_1\Delta f_i{\left(k\right)}^2+{\mu }_2\left|e_{ACE}^i\left(k\right)\right|+{\mu }_3{\displaystyle \sum _{j=1}^n}{d}_j^i\left(k\right)\right]+A,(10)$

$d_j^i\left(k\right)=\lambda *S_j^{\mathrm{p}}*\left|\Delta P_j^{\text{out}-i}\left(k\right)-\Delta P_j^{\text{out}-i}\left(k+1\right)\right|,(11)$

$A_i=\left\{\begin{array}{cc}0& \left|\Delta f_i\left(k\right)\right|<0.05Hz\\ -10& \left|\Delta f_i\left(k\right)\right|\ge 0.05Hz.\end{array}\right.(12)$

3.2 Deep reinforcement learning

3.2.1 MA-DDPG

The MADDPG algorithm (Lowe et al., 2017) is an algorithm that extends the DDPG algorithm into a multi-agent environment. In training, each agent can obtain the state and actions of all agents. The loss of agents is calculated as Eq. (13) and Eq. (14):

$L\left({\theta }^Q\right)=\frac{1}{K}{\displaystyle \sum _{j=1}^K}{\left(y_j-Q\left(s_j,a_1,a_2,\cdots a_N,{\theta }^Q\right)\right)}^2.(13)$

The policy gradient is as follows:

${\nabla }_{{\varphi }^{\pi }}J=\frac{1}{K}{\displaystyle \sum _{j=1}^K}{\nabla }_{{\varphi }^{\pi }}\pi \left(o,{\varphi }^{\pi }\right){\nabla }_{a}Q\left(s,a_1,a_2,\cdots a_N,{\theta }^Q\right).(14)$

3.3 Training framework of CE-MADDPG

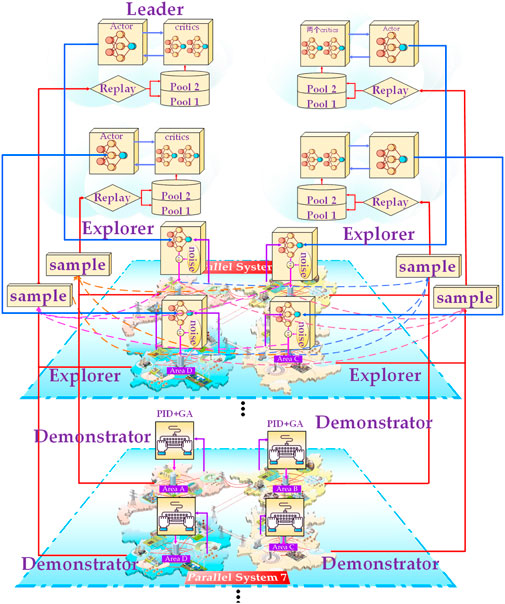
CE-MADDPG is an MA-DRL algorithm, which is a modification of MA-DDPG. CE-MADDPG adopts the cocktail exploration distributed MA-DRL training framework, and this algorithm improves the efficiency of MADDPG. The training framework adopts centralized training and decentralized execution for parallel optimization. According to Figure 4, taking the four-area LFC model as an example, the framework includes several explorers, integrators, and four leaders.

FIGURE 4

FIGURE 4. Training framework of the CE-MADDPG algorithm.

The purpose of this novel scheme is to improve the detection capability and robust performance of the proposed method, in which there are 10 parallel systems, and each of them is associated with a different power disturbance. In the case of an LFC model having four areas, each of the parallel systems 1–6 is provided with four explorers, which serve as an AGC integration agent for four areas, to output a command for the respective unit in the area. These four explorers adopt the same exploration principle. Each of the parallel systems 7–12 has four integrators, and each integrator contains a combination of different control algorithms and optimization algorithms. During training, the explorers in different areas simultaneously explore the environment in parallel, and each explorer generates a sample. Each integrator generates an integration sample. Different parallel spaces are shown in Eq. 15.

3.3.1 Explorer

The explorer in different systems employs different exploration actions. The action of the explorer in parallel systems 1–2 is shown as Eq. (15):

$a_{\epsilon }^l=\{\begin{array}{cc}{\pi }_{\varphi }^l\left(s\right)& \text{With\hspace{0.17em}}\epsilon \text{\hspace{0.17em}probability}\\ a_{\text{rand}}^l& \text{With\hspace{0.17em}}1-\epsilon \text{\hspace{0.17em}probability }\end{array},(15)$

where l refers to the lth agent.

The action of the explorer in parallel systems 3–4 is as Eq. (16):

$a_{OU}^j={\pi }_{\varphi }^j\left(s\right)+N_{OU}^j,(16)$

where j refers to the jth agent.

The action of the explorer in two parallel systems is as Eq. (17):

$a_{\text{Gaussian}}^j={\pi }_{\varphi }^j\left(s\right)+N_{\text{Gaussian}}^j.(17)$

An SAC explorer is set in parallel systems 9–12 to create the samples in collaboration with three demonstrators.

In this paper, the demonstrator adopts various controllers on different principles. PSO-fuzzy-PI is used in parallel systems 5 and 9; GA-fuzzy-PI is used in parallel systems 6 and 10; TS-fuzzy-PI is used in parallel systems 7 and 11; type-II fuzzy-PI is used in parallel systems 8 and 12. The target function of the controllers is as Eq. (18):

$F\left(t\right)={\int }_0^{\infty }t{\left(e_i^j\left(t\right)\right)}^2\mathrm{d}t.(18)$

3.3.2 Integrators

The design of the CE-MADDPG incorporates imitation learning. The integrator includes a controller and a distributor. The controllers and power distributors among different integrators employ different principles. During training, every integrator gives a reasonable result according to its own controller and power distributor, converts it into a sample, and puts it into the experience pool, which makes the public experience pool to make valuable samples.

In the integrators, PI, PSO-PI, FOPI, PSO-tuned fuzzy-PI, and fuzzy-PI algorithm are adopted in the controller. Due to the frequent occurrence of big amplitude disturbances in area A, when PSO-PI and PSO-fuzzy-PI factors in area A are optimized, the other control parameters are adjusted manually. The objective of the integrators for the controller is shown as Eq. (19):

$\min F_C\left(t\right)={\int }_0^{\infty }t{\left(e_i^{ACE}\left(t\right)\right)}^2\mathrm{d}t.(19)$

The principles of the power distributor for generation power command dispatch corresponding to each integrator are as follows: PROP, GA, and PSO. Various learning samples are provided for the public experience pool through the integrator interacting with the environment.

In the integrator, only ACE is taken into account in the control algorithm, and the regulation payment is considered in the dispatch algorithm for the distributor. In optimization, the fitness function for the distributor is shown in Eq. 20. The fitness function is as Eq. (20):

$\min F_D\left(t\right)={\displaystyle \sum _{t=1}^T}\left({\mu }_1{\displaystyle \sum _{i=1}^N}\Delta P_{\text{error}-i}^2\left(t\right)+{\mu }_2{\displaystyle \sum _{i=1}^N}{d}_i^j\left(t\right)\right).(20)$

3.3.3 Classified prioritized replay

Classified prioritized replay is adopted in the experience replay mechanism. In CE-MADDPG, two experience pools are employed. The samples obtained by the explorers are put into pool 1, and those collected by the integrators are put into pool 2.

The probability ξ is shown in Eq. 21:

$\xi =\left\{\begin{array}{cc}0.8& \text{Episodes}\le 1000\\ 0.9& 1000<\text{Episodes}\le 2000.\\ 1& \text{Episodes}>2000\end{array}\right.(21)$

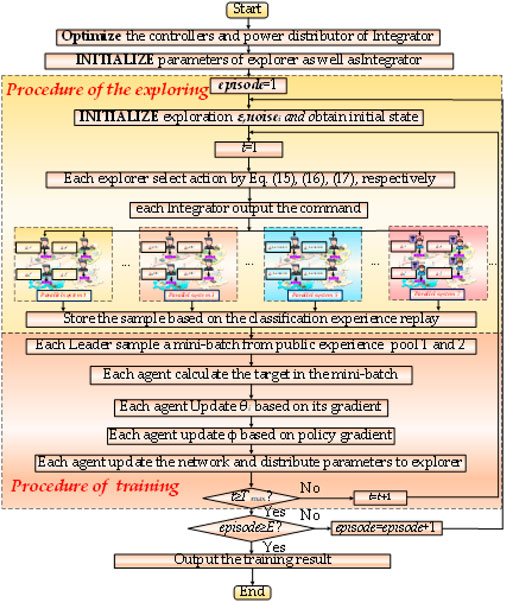
3.3.4 Training flow

The training flow of the CE-MADDPG algorithm is shown as follows:

3.4 Case studies

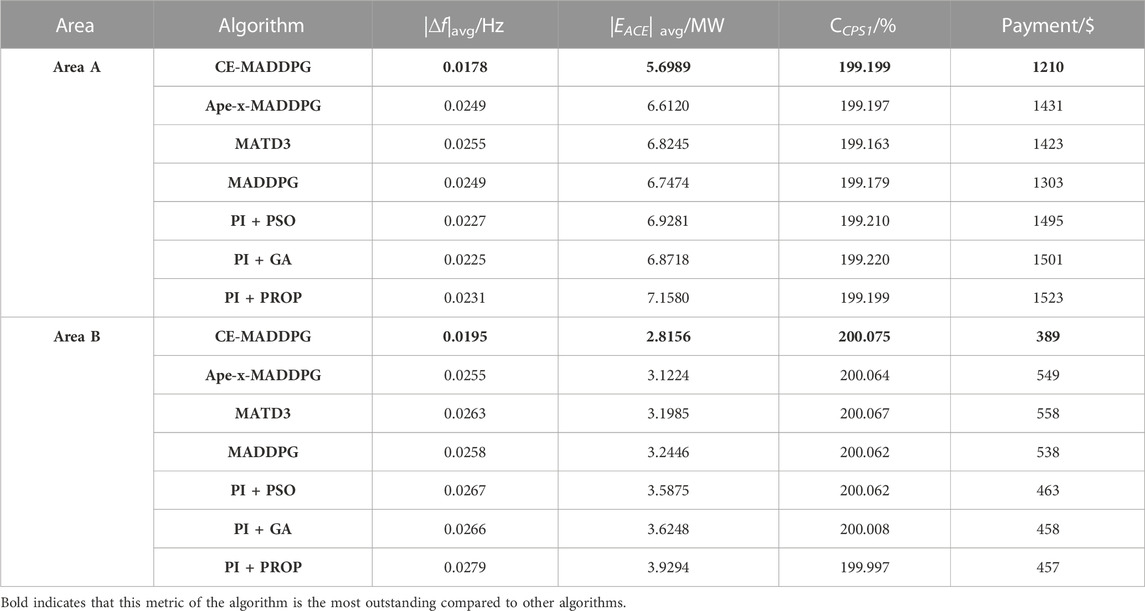
In case studies, the performance of the CE-MADDPG algorithm is compared with that of other MA-DRL algorithms (Ape-x-MADDPG, MATD3, and MADDPG) and combinatorial algorithms, which include controllers with power distributors (PI + PROP, PI + PSO, PI + GA) in the two cases.

3.4.1 Case 1: stochastic step disturbance

In case 1, three random step perturbations were introduced to test the effectiveness of the method.

1) Performance of MA-DRL algorithms. From Table 2, it can be known that the CPS1 indexes of CE-MADDPG in areas A and B are 199.199 and 200.075, respectively, which are the largest among these algorithms. In addition, |∆f |_avg and |E_ACE| _avg of CE-MADDPG are the smallest in MA-DRL algorithms. In addition, the payments of CE-MADDPG in the two areas are $1,210 and $389, respectively, which are much lower than those of other MA-DRL algorithms.

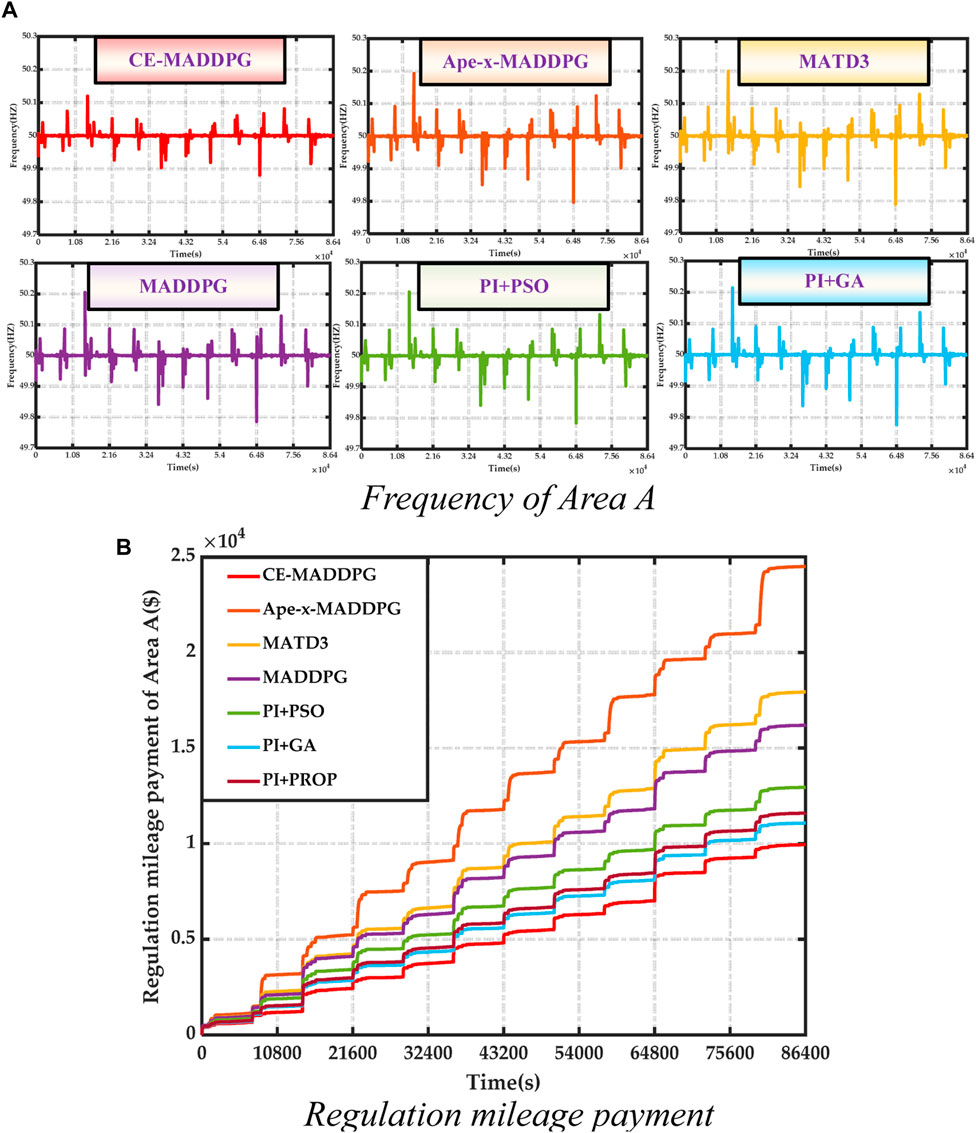
Based on the above results, it can be argued that CE-MADDPG uses more techniques for improving its exploration capability and training efficiency, and thus a better coordinated control strategy can be obtained. Therefore, when confronted with different disturbances, the CE-MADDPG algorithm exhibits better performance; conversely, due to the lack of corresponding techniques, in each case, a suboptimal coordinated control strategy is obtained by other MA-DRL algorithms, thereby leading to suboptimal coordinated control performance. According to Figures 5A, B and Figure 5G, the coordinated control strategy adopted by the CE-MADDPG algorithm calls more rapid-regulating units for frequency regulation. In addition, other MA-DRL algorithms are subjected to larger overshoot, which leads to serious frequency regulation resource wastage and increases the payment. As shown in Figures 5C, E, the CE-MADDPG achieves more stable frequency deviation and ACE.

FIGURE 5

FIGURE 5. Case 1 results.

2) Performance of combinatorial algorithms. According to Table 1, in area A, for combinatorial algorithms, the CE-MADDPG algorithm can reduce |∆f |_avg by 26.4%–29.5%, |E_ACE| _avg by 20.58%–25.6%, and the regulation mileage payment by 22.8%–24.82%; it also has the largest CPS1 index value. In area B, the CE-MADDPG algorithm can reduce |∆f |_avg by 36.03%–42.6%,| E_ACE | _avg by 27.4%–39.6%, and the regulation mileage payment by 17.46%–29.05%.

TABLE 1

TABLE 1. Result of case 1.

Based on the above results, it can be argued that as shown in Figure 6B, the other combinatorial algorithms are also subjected to larger overshoot due to the PI controller being contained in these combinatorial algorithms. When the parameters are not set properly, there will arise instability in terms of total generation power command and overshoot, which will lead to degradation of performance and increased payment (Figures 5D, F, G, H). By contrast, the CE-MADDPG algorithm can significantly improve the response capability of AGC, which, in turn, reduces the occurrence of “overshoot,” thereby reducing its payment.

FIGURE 6

FIGURE 6. Results of case 2.

3.4.2 Case 2: four-area LFC model under disturbance with large-scale DERs

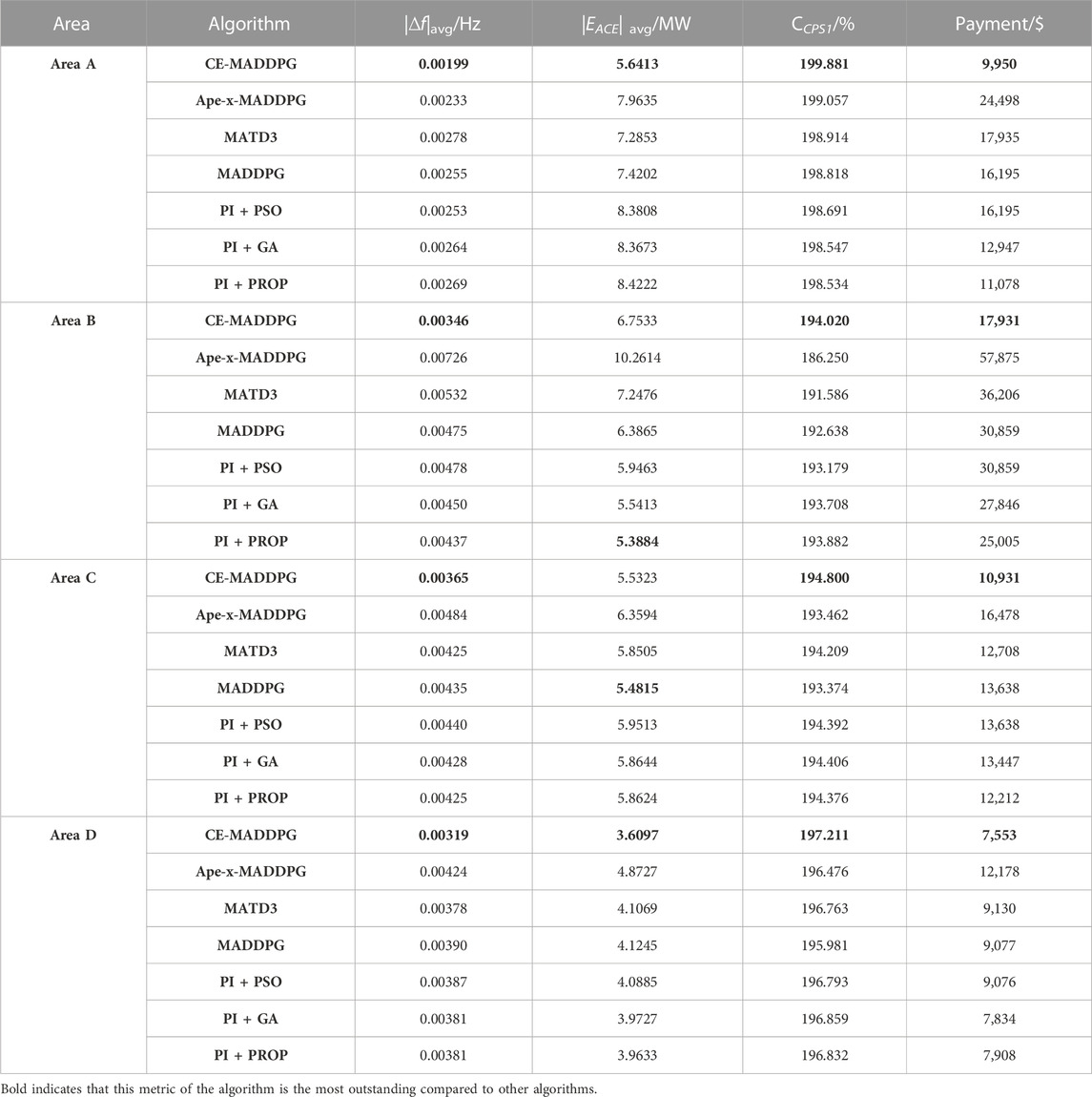
In case 2, WT disturbance, PV disturbance, and stochastic disturbance occur across the four areas.

As shown in Table 2, in area A, CE-MADDPG reduces |∆f |_avg by 16.79%–39.69%, |E_ACE| _avg by 29.14%–48.56%, and the payment by 11.33%–146.21%; it also attains the largest CPS1 index value. In addition, CE-MADDPG exhibits the minimum |∆f |_avg and payment in other areas. However, since other areas will give emergency support when a disturbance occurs in one of the areas, the |E_ACE| _avg of the CE-MADDPG algorithm is not the lowest in areas B and C (which provide more support). However, the CPS1 index of the CE-MADDPG algorithm across the different areas is the largest.

TABLE 2

TABLE 2. Statistical results of case 2.

According to Figures 6A, B, for the CE-MADDPG algorithm, when a disturbance occurs in an area, the AGC of that area can respond rapidly, and the influence of coordination among controllers in multiple areas is considered while at the same time avoiding the degradation of performance caused by the combinatorial algorithm. Therefore, the CPS1 of AGC in all the areas is better; also, the peak value of its frequency is smaller, which reduces unnecessary load shedding caused by the operation of the emergency control device due to frequency fluctuation.

It can, therefore, be argued that in the event of a disturbance, and with large-scale DERs, compared with the MA-DRL algorithms and combinatorial algorithms, the CE-MADDPG algorithm is advantageously characterized by better performance and can realize multi-area secondary frequency regulation coordination.

4 Conclusion

Based on the study, we can draw the following conclusions:

1) In this paper, an MAI-AGC framework is designed in the performance-based frequency regulation market. The controller and the distributor are integrated into a single agent, which can resolve the cooperative problem of the controller and distributor.

2) A CE-MADDPG algorithm is proposed as the framework algorithm from the perspective of AGC. This algorithm uses multiple groups of explorers with different exploration strategies combined with integrators to improve training efficiency. It introduces a variety of techniques to guide the strategy objectives in striking a balance between exploration and utilization and then realizing the optimal coordinated control of AGC with greater robustness. Moreover, the utilization framework of decentralized execution is adopted to realize the coordination control of different areas.

3) The results of two cases show that, compared with the three MA-DRL and three combinatorial algorithms, the proposed algorithm exhibits enhanced performance and economic efficiency.

4) Future work: We will conduct research based on practical examples in the future.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

TQ: conceptualization, data curation, investigation, methodology, software, supervision, writing–original draft, and writing–review and editing. CY: formal analysis, investigation, and writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2023.1333827/full#supplementary-material

References

Bahrami, S., Hooshmand, R.-A., and Parastegari, M. (2014). Short term electric load forecasting by wavelet transform and grey model improved by PSO (particle swarm optimization) algorithm. Energy 72, 434–442. doi:10.1016/j.energy.2014.05.065

CrossRef Full Text | Google Scholar

Huan, J., Ding, Q., Zhou B, Yu T., Yang, B., and Cheng, Y. (2023). Multi-stage low-carbon planning of an integrated energy system considering demand response. Front. Energy Res. 11. doi:10.3389/fenrg.2023.1259067

CrossRef Full Text | Google Scholar

Li, J., Cui, H., and Jiang, W. (2023a). Distributed deep reinforcement learning-based gas supply system coordination management method for solid oxide fuel cell. Eng. Appl. Artif. Intell. 120, 105818. doi:10.1016/j.engappai.2023.105818

CrossRef Full Text | Google Scholar

Li, J., Cui, H., Jiang, W., and Yu, H. (2023c). Optimal dual-model controller of solid oxide fuel cell output voltage using imitation distributed deep reinforcement learning. Int. J. Hydrogen Energy 48 (37), 14053–14067. doi:10.1016/j.ijhydene.2022.12.194

CrossRef Full Text | Google Scholar

Li, J., Yu, T., and Zhang, X. (2022). Coordinated automatic generation control of interconnected power system with imitation guided exploration multi-agent deep reinforcement learning. Int. J. Elec Power 136, 107471. doi:10.1016/j.ijepes.2021.107471

CrossRef Full Text | Google Scholar

Li, J., Yu, T., Zhang, X., Li, F., Lin, D., and Zhu, H. (2021). Efficient experience replay based deep deterministic policy gradient for AGC dispatch in integrated energy system. Appl. Energ. 285, 116386. doi:10.1016/j.apenergy.2020.116386

CrossRef Full Text | Google Scholar

Li, J., and Zhou, T. (2023). Evolutionary multi agent deep meta reinforcement learning method for swarm intelligence energy management of isolated multi area microgrid with internet of things. IEEE Internet Things J. 10, 12923–12937. doi:10.1109/JIOT.2023.3253693

CrossRef Full Text | Google Scholar

Li, J., Zhou, T., and Cui, H. (2023b). Brain-inspired deep meta-reinforcement learning for active coordinated fault-tolerant load frequency control of multi-area grids. IEEE Trans. Automation Sci. Eng. 2023, 1–13. doi:10.1109/TASE.2023.3263005

CrossRef Full Text | Google Scholar

Lowe, R., Wu, Y., Tamar, A., Harb, J., Abbeel, P., and Mordatch, I. (2017). Multi-agent actor-critic for mixed cooperative-competitive environments. arXiv preprint arXiv:170602275. Available at: https://doi.org/10.48550/arXiv.1706.02275.

Google Scholar

Mirjalili, S. (2016). SCA: a Sine Cosine Algorithm for solving optimization problems. Knowl-Based Syst. 96, 120–133. doi:10.1016/j.knosys.2015.12.022

CrossRef Full Text | Google Scholar

Mirjalili, S., Mirjalili, S. M., and Lewis, A. (2014). Grey wolf optimizer. Adv. Eng. Softw. 69, 46–61. doi:10.1016/j.advengsoft.2013.12.007

CrossRef Full Text | Google Scholar

Qu, K., Zheng, X., Li, X., Lv, C., and Yu, T. (2022). Stochastic robust real-time power dispatch with wind uncertainty using difference-of-convexity optimization. IEEE Trans. Power Syst. 37 (6), 4497–4511. doi:10.1109/TPWRS.2022.3145907

CrossRef Full Text | Google Scholar

Qu, K., Zheng, X., and Yu, T. (2023). Environmental-economic unit commitment with robust diffusion control of gas pollutants. IEEE Trans. Power Syst. 38 (1), 818–834. doi:10.1109/TPWRS.2022.3166264

CrossRef Full Text | Google Scholar

Xi, L., Yu, L., Xu, Y., Wang, S., and Chen, X. (2020). A novel multi-agent DDQN-AD method-based distributed strategy for automatic generation control of integrated energy systems. IEEE Trans. Sustain Energ 11 (4), 2417–2426. doi:10.1109/TSTE.2019.2958361

CrossRef Full Text | Google Scholar

Xi, L., Yu, T., Yang, B., and Zhang, X. (2015). A novel multi-agent decentralized win or learn fast policy hill-climbing with eligibility trace algorithm for smart generation control of interconnected complex power grids. Energ Convers. Manage 103, 82–93. doi:10.1016/j.enconman.2015.06.030

CrossRef Full Text | Google Scholar

Xi, L., Zhang, Z., Yang, B., Huang, L., and Yu, T. (2016). Wolf pack hunting strategy for automatic generation control of an islanding smart distribution network. Energ Convers. Manage 122, 10–24. doi:10.1016/j.enconman.2016.05.039

CrossRef Full Text | Google Scholar

Yu, T., Wang, H. Z., Zhou, B., Chan, K. W., and Tang, J. (2015). Multi-agent correlated equilibrium Q(λ) learning for coordinated smart generation control of interconnected power grids. IEEE Trans. Power Syst. 30 (4), 1669–1679. doi:10.1109/TPWRS.2014.2357079

CrossRef Full Text | Google Scholar

Yu, T., Xi, L., Yang, B., Xu, Z., and Jiang, L. (2016). Multiagent stochastic dynamic game for smart generation control. J. Energ Eng. 142 (1), 04015012. doi:10.1061/(ASCE)EY.1943-7897.0000275

CrossRef Full Text | Google Scholar

Yu, T., Zhou, B., Chan, K. W., Chen, L., and Yang, B. (2011b). Stochastic optimal relaxed automatic generation control in non-markov environment based on multi-step $Q(\lambda)$ learning. IEEE Trans. Power Syst. 26 (3), 1272–1282. doi:10.1109/TPWRS.2010.2102372

CrossRef Full Text | Google Scholar

Yu, T., Zhou, B., Chan, K. W., and Lu, E. (2011a). Stochastic optimal CPS relaxed control methodology for interconnected power systems using Q-learning method. J. Energ Eng. 137 (3), 116–129. doi:10.1061/(asce)ey.1943-7897.0000017

CrossRef Full Text | Google Scholar

Yu, T., Zhou, B., Chan, K. W., Yuan, Y., Yang, B., and Wu, Q. H. (2012). R(λ) imitation learning for automatic generation control of interconnected power grids. Automatica 48 (9), 2130–2136. doi:10.1016/j.automatica.2012.05.043

CrossRef Full Text | Google Scholar

Nomenclature