Numerical simulation of CO2-enhanced oil recovery in fractured shale reservoirs using discontinuous and continuous Galerkin finite element methods

Introduction: This study explores the potential of enhancing shale oil recovery and reducing CO₂ emissions through CO₂ injection in fractured shale reservoirs. The importance of this approach lies in its dual benefit: improving oil extraction efficiency and addressing environmental concerns associated with CO₂ emissions.

Method: We employed a discrete fracture-matrix model to simulate CO₂ flooding in fractured shale reservoirs, utilizing both discontinuous Galerkin (DG) and continuous Galerkin (CG) finite element methods. The DG-CG FEM’s accuracy was validated against the McWhorter problem, ensuring the reliability of the simulation results. Our model also considered various factors, including reservoir heterogeneity, fracture permeability, CO₂ injection volume, and gas injection patterns, to analyze their impact on shale oil recovery.

Result: Our simulations revealed that fractured reservoirs significantly enhance shale oil production efficiency compared to homogeneous reservoirs, with an approximate 48.9% increase in production. A notable increase in shale oil production, by 15.8%, was observed when fracture permeability was increased by two orders of magnitude. Additionally, a fourfold increase in CO₂ injection rate resulted in a 31.5% rise in shale oil production. Implementing a step-by-step reduction in injection volume while maintaining the total CO₂ injection constant proved to be more effective than constant-rate injections.

Discussion: The study demonstrates the effectiveness of CO₂ flooding in fractured shale reservoirs for enhancing shale oil recovery.

1 Introduction

The effective exploitation of unconventional oil and gas is of great strategic significance to alleviate the contradiction between oil and gas supply and demand, promoting the low-carbon transformation of energy structure (JIN et al., 2021a). In China, shale oil resources are abundant and exhibit extensive geographical distribution. Nonetheless, notable challenges persist, notably concerning the low recovery and limited production experienced by individual wells (JIN et al., 2021b). The shale oil development goal of China is to achieve a production output of 6.5 million metric tons by 2025, with increasing shale oil recovery rate serving as a crucial support for realizing the objective (Yang and Huang, 2019). Since supercritical CO₂ can rapidly penetrate into the microporosity of reservoir rocks, CO₂ injection for enhanced recovery has been applied industrially in the field of oil and gas development (LU et al., 2021; MA et al., 2017). Not only does CO₂ injection enhance the oil and gas recovery rate, but it also facilitates CO₂ geological storage, mitigates the global greenhouse effect, and aids China in reaching its “carbon peak, carbon neutral” goals. Therefore, the development of CO₂ injection shale oil technology has a broad application prospect and strategic significance.

At present, CO₂ enhanced oil recovery from shale mainly focuses on two aspects: shale core flooding test and numerical simulation of gas injection enhanced recovery (MEI et al., 2018; JIA et al., 2019; FAN et al., 2022; Li et al., 2022; Wan et al., 2022; Huang et al., 2023). In terms of experimental research, core-scale CO₂ shale oil replacement tests have been carried out (ALHARTHY et al., 2018; ELWEGAA et al., 2019; FAKHER and IMQAM, 2020; LANG et al., 2021) and the results show that CO₂ injection can improve shale oil recovery. Moreover, the efficiency of this replacement process is influenced by factors such as the duration of CO₂ exposure, shale permeability, porosity, and the maturity of organic matter. Chen et al. (Cheng et al., 2014), Zhu et al. (ZHU et al., 2018) and Yu et al. (YU et al., 2021) adopted numerical simulations to show that volumetric fracturing penetrates the internal fractures of the reservoir, and then injecting CO₂ effectively improve the recovery rate. If CO₂ is directly injected into the reservoir with low permeability, the recovery rate of shale oil is reduced. The existing studies focus on the impact of secondary fractures generated by fracturing on gas injection and oil recovery, while ignoring the impact of primary fractures widely present inside the reservoir.

Fractures in reservoirs profoundly affect fluid flow paths and mass transport. The models describing fluid flow in fractured rock are generally categorized into equivalent continuous models, discrete fracture network models, and discrete fracture-matrix models (GLÄSER et al., 2017; BERRE et al., 2019). Among them, the equivalent continuum model is subdivided into single-pore medium model, dual-pore medium model, and multi-pore medium model (BERRE et al., 2019). The assumptions of the single-pore medium model are based on the effective medium theory, which ignores the properties of the fracture network and calculates the effective permeability of the fracture network based on the shape, size, pore size and orientation distribution of the fracture as well as the matrix permeability. The dual-pores medium model and the multi-pore medium model mathematically describe the pores and fracture, and the fluid-mass balance equations are established within the fracture and matrix systems respectively. At any point in space, hydraulic parameters (permeability, porosity, etc.) have single or multiple values. Fracture-matrix interactions are represented by fluid exchange terms that incorporate microscale effects at the macroscale and do not geometrically characterize the fracture. Therefore, it is possible to carry out relevant studies directly using the method of simulating the flow in porous media (WANG et al., 2000; LIU and ZHANG, 2008; Yang et al., 2008). Currently, the common oil and gas numerical simulation software ECLIPSE, TOUGH2 and CMG are using equivalent continuous models (PRUESS et al., 1999; GUIDE, 2002; LAW et al., 2002; LAW et al., 2003; GeoQuest, 2010). Although this method is computationally efficient, it is more difficult to geometrically realize discrete fractures in porous media and their effects on local fluid paths. In the discrete fracture network and discrete fracture matrix models, the matrix and the fracture are retained as separate geometrical objects, and the fracture region is explicitly created within the overall framework. The discrete-fracture model ignores the permeability of the matrix and considers only the fluid behavior in the fracture network. In the discrete fracture matrix model, diffusion, desorption, or two-phase seepage of the fluid within the matrix is ab considered. Meanwhile, the model downscales to deal with fractures and explicitly constructs low-dimensional fractures. The discrete fracture matrix model allows the effect of fractures on the flow topology to be explicitly modeled compared to the dual-porosity and dual-permeability model in an equivalent continuous medium (KHOEI et al., 2016a; CHEN et al., 2017; ZHANG et al., 2017; MENG et al., 2018; CUSINI et al., 2021).

Based on the discrete fracture matrix model, this paper establishes a two-phase fluid flow model for CO₂ enhanced shale oil recovery. The model incorporates the two-phase seepage governing equations for CO₂ and shale oil, accounting for their behavior in both the porous regions and low-dimensional discrete fracture within the reservoir, including the fluid-mass transfer between the fractures and the pores. We apply this established model to a randomly fractured shale reservoir for numerical simulation purposes. Through this application, we analyze the effects of reservoir inhomogeneity, fracture permeability, CO₂ injection volume, and the injection scheme on the field, as well as on the efficiency and volume of shale oil extraction.

2 Mathematical model

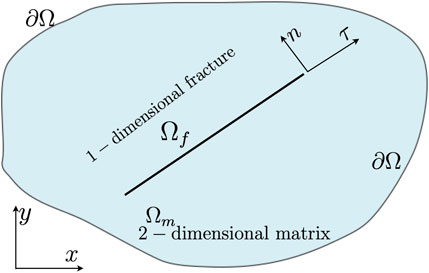
The discrete fracture matrix model utilizes explicit low-dimensional interfaces to equivalently replace the high-dimensional regions occupied by fractures. The matrix and low-dimensional fractures are retained as separate geometric objects, and the discrete fracture network is explicitly modeled within the overall framework, as shown in Figure 1. The two-dimensional computational domain $\mathrm{\Omega }$ is equivalently described as a two-dimensional matrix region ${\mathrm{\Omega }}_m$ and a one-dimensional fracture region ${\mathrm{\Omega }}_f$. Therefore, the method is also known as mixed-dimensional or hybrid-dimensional discrete fracture model. The fracture computational domain contains any set of fully or partially interconnected fractures, and thus ${\mathrm{\Omega }}_f$ is expressed as ${\mathrm{\Omega }}_f={\cup }_1^i{\mathrm{\Omega }}_{fi}$, $i$ being the total number of fractures. where $\partial \mathrm{\Omega }$ is the boundary of the computational domain, and $\tau$ and $n$ are the tangent and normal directions of the fractures.

FIGURE 1

FIGURE 1. Geometric diagram of discrete fracture model.

2.1 Governing equations for two-phase flow

The basic assumptions of the mathematical model are as follows: 1) the fluid process is isothermal; 2) CO₂ and shale oil are immiscible fluids; 3) the velocities of the free-state fluids in the matrix and the fracture satisfy Darcy’s law; 4) the mass exchange of CO₂ and shale oil in the matrix and fracture satisfies the linear mass-transfer equations; and 5) the differential capillary pressure effect between the matrix and the fracture is neglected. Based on the above assumptions, the governing equations for the two-phase fluids of CO₂ and shale oil in the reservoir matrix ${\mathrm{\Omega }}_m$ are expressed as (ZHANG et al., 2017; MA et al., 2021a):

${{\varphi }^{m}S}_o^m{\rho }_o^m{c}_o\frac{\partial p_g^m}{\partial t}+\left({\varphi }^m{\rho }_o^m-{\varphi }^m{S}_o^m{\rho }_o^m{c}_o\left|p_c^m\right|\right)\frac{\partial S_o^m}{\partial t}+\nabla \cdot \left(-{\rho }_o^m\frac{{\mathit{k}}^{\mathit{m}}{k}_{ro}^m}{{\mu }_o}\nabla p_g^m\right)-\nabla \cdot \left(-{\rho }_o^m\frac{{\mathit{k}}^{\mathit{m}}{k}_{ro}^m}{{\mu }_o}\left|p_c^m\right|\nabla S_o^m\right)=0(1)$

${{\varphi }^{m}S}_g^m{\rho }_g^m{c}_g\frac{\partial p_g^m}{\partial t}-{\varphi }^m{\rho }_g^m\frac{\partial S_o^m}{\partial t}+\nabla \cdot \left(-{\rho }_g^m\frac{{\mathit{k}}^{\mathit{m}}{k}_{rg}^m}{{\mu }_g}\nabla p_g^m\right)=0(2)$

The two-phase flow in the reservoir fracture ${\mathrm{\Omega }}_f$ is expressed as (LAW et al., 2003; MENG et al., 2018):

$d_f{{\varphi }^{f}S}_o^f{\rho }_o^f{c}_o\frac{\partial p_g^f}{\partial t}+d_f\left({\varphi }^f{\rho }_o^f-{\varphi }^f{S}_o^f{\rho }_o^f{c}_o\left|p_c^f\right|\right)\frac{\partial S_o^f}{\partial t}+{\nabla }_T\cdot \left(-d_f{\rho }_o^f\frac{{\mathit{k}}^{\mathit{f}}{k}_{ro}^f}{{\mu }_o}\nabla p_g^f\right)-{\nabla }_T\cdot \left(-d_f{\rho }_o^f\frac{{\mathit{k}}^{\mathit{f}}{k}_{ro}^f}{{\mu }_o}\left|p_c^f\right|\nabla S_o^f\right)=[[{\rho }_o^m{\mathit{u}}_{\mathit{o}}^{\mathit{m}}\bullet \mathit{n}]](3)$

$d_f{{\varphi }^{f}S}_g^f{\rho }_g^f{c}_g\frac{\partial p_g^f}{\partial t}-d_f{\varphi }^f{\rho }_g^f\frac{\partial S_o^f}{\partial t}+{\nabla }_T\cdot \left(-d_f{\rho }_g^f\frac{{\mathit{k}}^{\mathit{f}}{k}_{rg}^f}{{\mu }_g}\nabla p_g^m\right)=[[{\rho }_g^m{\mathit{u}}_{\mathit{g}}^{\mathit{m}}\bullet \mathit{n}]](4)$

where superscript $\alpha \in \left\{m,f\right\}$ denotes matrix and fractures. Subscript $\beta \in \left\{o,g\right\}$ denotes shale oil and CO₂. ${\varphi }^{\alpha }$ is the porosity, $S_{\beta }^{\alpha }$ is the fluid saturation, ${\rho }_{\beta }^{\alpha }=-1/c_{\beta }\left(\mathrm{d}{\rho }_{\beta }^{\alpha }/\mathrm{d}{p}_{\beta }^{\alpha }\right)$ is the fluid density, $c_{\beta }$ is the fluid compressibility coefficient, $p_{\beta }^{\alpha }$ is the fluid pressure, and $p_c^{\alpha }$ is the capillary pressure. Absolute permeability tensor ${\mathit{k}}^{\alpha }=k^{\alpha }$ I, $k^{\alpha }$ is the absolute permeability, $\mathbf{I}$ is the unit matrix, $k_{r\beta }^{\alpha }$ is the relative permeability, ${\mu }_{\beta }$ is the fluid viscosity; $d_f$ is the fracture aperture. The source-sink term $[[{\rho }_{\beta }^m{\mathit{u}}_{\beta }\bullet \mathit{n}]]$ describes the jump in fluid normal flux in the matrix grids adjacent to the fracture, and the normal velocity of the fluid at the matrix grid is expressed as (Brenner et al., 2018):

${\mathit{u}}_{\mathit{\beta }}^{\mathit{m}}\bullet \mathit{n}=-\frac{k_n^f{k}_{r\beta }^f}{{\mu }_{\beta }}\left(\frac{p_{\beta }^m-p_{\beta }^f}{d^f/2}\right)(5)$

The weak forms of the discontinuous Galerkin method for Equations 1, 2 are shown below (MA et al., 2021a; MA et al., 2021b):

$\begin{array}{c}{\displaystyle \sum _{E\in {\mathrm{\Omega }}_m}}{\displaystyle \underset{E}{\int }}\left[{{\varphi }^{m}S}_o^m{\rho }_o^m{c}_o\frac{\partial p_o^m}{\partial t}+\left({\varphi }^m{\rho }_o^m-{\varphi }^m{S}_o^m{\rho }_o^m{c}_o\left|p_c^m\right|\right)\frac{\partial S_o^m}{\partial t}\right]\stackrel{\sim }{S_o^m}dV+{\displaystyle \sum _{E\in {\mathrm{\Omega }}_m}}{\displaystyle \underset{E}{\int }}{\lambda }_o^m\left(\left|p_c^m\right|\nabla S_o^m-\nabla p_g^m\right)\nabla \stackrel{\sim }{S_o^m}dV-\hfill \\ {\displaystyle \sum _{e\in \partial {\mathrm{\Omega }}_o}}{\displaystyle \underset{e}{\int }}{\lambda }_o^m\left(\left|p_c^m\right|\left\{\nabla S_o^m\right\}-〈\nabla p_g^m〉\right)[[\stackrel{\sim }{S_o^m}]]dS+{\displaystyle \sum _{e\in \partial {\mathrm{\Omega }}_o}}{\displaystyle \underset{e}{\int }}\left({\lambda }_o^m\left|p_c^m\right|\left\{\nabla \stackrel{\sim }{S_o^m}\right\}[[S_o^m]]+\frac{{\delta }_o}{h}[[S_o^m]]\cdot [[\stackrel{\sim }{S_o^m}]]\right)dS+\hfill \\ {\displaystyle \sum _{e\in \partial {\mathrm{\Omega }}_o}}{\displaystyle \underset{e}{\int }}\left({\lambda }_o^m\left\{\nabla \stackrel{\sim }{S_o^m}\right\}[[p_g^m]]+\frac{{\delta }_o}{h}[[p_g^m]]\cdot [[\stackrel{\sim }{S_o^m}]]\right)dS+{\displaystyle \sum _{e{\in \mathrm{\Omega }}_f}}{\displaystyle \underset{e}{\int }}{\rho }_o^{m+}{\mathit{u}}_{\mathit{o}}^{\mathit{m}+}\bullet {\mathit{n}}^{+}\stackrel{\sim }{S_o^{m+}}+{\rho }_o^{m-}{\mathit{u}}_{\mathit{o}}^{\mathit{m}-}\bullet {\mathit{n}}^{-}\stackrel{\sim }{S_o^{m-}}dS=0\hfill \end{array}(6)$

$\begin{array}{c}{\displaystyle \sum _{E\in {\mathrm{\Omega }}_m}}{\displaystyle \underset{E}{\int }}\left({{\varphi }^{m}S}_g^m{\rho }_g^m{c}_g\frac{\partial p_g^m}{\partial t}-{\varphi }^m{\rho }_g^m\frac{\partial S_g^m}{\partial t}\right)\stackrel{\sim }{p_g^m}dV+{\displaystyle \sum _{E\in {\mathrm{\Omega }}_m}}{\displaystyle \underset{E}{\int }}{\lambda }_g^m\nabla p_g^m\cdot \nabla \stackrel{\sim }{p_g^m}dV-{\displaystyle \sum _{e\in \partial {\mathrm{\Omega }}_o}}{\displaystyle \underset{e}{\int }}{\lambda }_g^m\nabla p_g^m\cdot \nabla \stackrel{\sim }{p_g^m}dS+\hfill \\ {\displaystyle \sum _{e\in \partial {\mathrm{\Omega }}_o}}{\displaystyle \underset{e}{\int }}\left({\lambda }_g^m\left\{\nabla \stackrel{\sim }{p_g^m}\right\}[[p_g^m]]+\frac{{\delta }_g}{h}[[p_g^m]]\cdot [[\stackrel{\sim }{g}]]\right)dS+{\displaystyle \sum _{e{\in \mathrm{\Omega }}_f}}{\displaystyle \underset{e}{\int }}{\rho }_g^{m+}{\mathit{u}}_{\mathit{g}}^{\mathit{m}+}\bullet {\mathit{n}}^{+}\stackrel{\sim }{g}+{\rho }_g^{m-}{\mathit{u}}_{\mathit{g}}^{\mathit{m}-}\bullet {\mathit{n}}^{-}\stackrel{\sim }{p_g^{m-}}dS=0\hfill \end{array}(7)$

The weak form of the continuous Galerkin method in Equations 3, 4 is shown below (MA et al., 2021b):

${\displaystyle \sum _{e{\in \mathrm{\Omega }}_f}}{\displaystyle \underset{e}{\int }}\left[d^f{{\varphi }^{f}S}_o^f{\rho }_o^f{c}_o\frac{\partial p_g^f}{\partial t}+d^f\left({\varphi }^f{\rho }_o^f-{\varphi }^f{S}_o^f{\rho }_o^f{c}_o\left|p_c^f\right|\right)\frac{\partial S_o^f}{\partial t}-[[{\rho }_o^m{\mathit{u}}_{\mathit{o}}^{\mathit{m}}\bullet \mathit{n}]]\right.]\times \stackrel{\sim }{S_w^f}dS+{\displaystyle \sum _{e{\in \mathrm{\Omega }}_f}}{\displaystyle \underset{e}{\int }}\left(d^f{\lambda }_o^f\left|p_c^f\right|{\nabla }_T{S}_o^f-d^f{\lambda }_o^f\nabla p_g^f\right)\cdot {\nabla }_T\stackrel{\sim }{S_o^f}dS=0(8)$

${\displaystyle \sum _{e{\in \mathrm{\Omega }}_f}}{\displaystyle \underset{e}{\int }}\left[d^f{{\varphi }^{f}S}_g^f{\rho }_g^f{c}_g\frac{\partial p_g^f}{\partial t}-d^f{\varphi }^f{\rho }_g^f\frac{\partial S_g^f}{\partial t}-[[{\rho }_g^m{\mathit{u}}_{\mathit{g}}^{\mathit{m}}\bullet \mathit{n}]]\right]\stackrel{\sim }{p_g^f}dS+{\displaystyle \sum _{e{\in \mathrm{\Omega }}_f}}{\displaystyle \underset{e}{\int }}{d}^f{\lambda }_g^f{\nabla }_T{p}_g^f\cdot {\nabla }_T\stackrel{\sim }{p_g^f}dS=0(9)$

where $\stackrel{\sim }{p_g^{\alpha }}$ and $\stackrel{\sim }{S_o^{\alpha }}$ are the trial functions, ${\lambda }_{\beta }^m=-{\rho }_{\beta }\frac{{\mathit{k}}^{\mathit{m}}{k}_{r\beta }}{{\mu }_{\beta }}$, The penalization factor ${\delta }_o$ is set to $0.01$, and $h$ is the grid size. The proposed model can consider the effect of low-permeability barriers on fluids, whereas we focus on high-permeability fractures. In other words, the fractures described herein have a higher permeability compared to the matrix, resulting in a relatively small gradient of pore pressure in the direction normal to the fracture. Thus, the pore pressures of matrix adjacent to the fractures is approximated equivalently as continuous when crossing the fracture.

2.2 Relative permeability and capillary pressure

The same relative permeability and capillary pressure models are selected for the matrix and fractures in shale reservoirs with the following expressions (MA et al., 2021a):

$k_{ro}^{\alpha }=\left\{\begin{array}{l}\sqrt{S_e^{\alpha }}{\left[1-{\left(1-{S_e^{\alpha }}^{1/{\omega }^{\alpha }}\right)}^{{\omega }^{\alpha }}\right]}^2,S_o^{\alpha }<1\\ 1,S_o^{\alpha }>1\end{array}\right.(10)$

$k_{rg}^{\alpha }=\left\{\begin{array}{l}1-k_{ro}^{\alpha },S_{rg}^{\alpha }=0\\ {\left(1-S_e^{\alpha }\right)}^2\left(1-{S_e^{\alpha }}^2\right),S_{rg}^{\alpha }>0\end{array}\right.(11)$

$p_c^{\alpha }=p_g^{\alpha }-p_o^{\alpha }=p_e^{\alpha }{\left(S_e^{\alpha }\right)}^{-\frac{1}{{\lambda }^{\alpha }}}(12)$

In the above equation: $k_{ro}^{\alpha }$ and $k_{rg}^{\alpha }$ are the relative permeability of shale oil and CO₂; $S_e^{\alpha }$ is the effective saturation; $p_c^{\alpha }$ is the capillary pressure; ${\omega }^{\alpha }$ is the van Genuchten coefficient, and ${\lambda }^{\alpha }$ is the pore size distribution index.

2.3 Initial and boundary conditions

The initial conditions in the matrix and fractures of the shale reservoir are set as follows:

$p_g^{\alpha }\left(x,t=0\right)=p_{gi}^{\alpha }(13)$

$S_o^{\alpha }\left(x,t=0\right)=S_{oi}^{\alpha }(14)$

where $p_{gi}^{\alpha }$ and $S_{oi}^{\alpha }$ denote the initial CO₂ pressure and oil phase saturation of the reservoir.

The production well is set up as Dirichlet boundary conditions with constant pore pressures and saturation, which are expressed as follows:

$p_g\left(x,y\right)=p_g^b(15)$

$S_o\left(x,y\right)=S_o^b(16)$

The injection well is set as a constant flow boundary:

$-{\rho }_g\frac{{\mathit{k}}^{\mathit{m}}{k}_{rg}}{{\mu }_g}\nabla p_g=Q_g(17)$

where $p_g^b$ and $S_o^b$ are the CO₂ pressure and oil-phase saturation at the production well, $Q_g$ is the CO₂ injection volume.

The difference in initial values of the variables between the production well and the shale reservoir increases the nonlinear characteristics of the two-phase flow equations. To further improve the convergence and stability of the model, the method of adding penalty function is introduced in this study to set Dirichlet boundary conditions (MA et al., 2021a), then equations Eq. 15 and Eq. 16 are rewritten as:

$p_g\left(x,y\right)={\displaystyle \underset{\partial {\mathrm{\Omega }}_o}{\int }}{\lambda }_g^m\nabla \stackrel{\sim }{p_g^m}\cdot \mathit{n}\left(p_g-p_g^b\right)dS+{\displaystyle \underset{\partial {\mathrm{\Omega }}_o}{\int }}\frac{{\delta }_o}{h}\left(p_g-p_g^b\right)\stackrel{\sim }{p_g^m}dS(18)$

$S_o\left(x,y\right)={\displaystyle \underset{\partial {\mathrm{\Omega }}_o}{\int }}\left({\lambda }_o^m\left|p_c^m\right|\right)\nabla \stackrel{\sim }{S_o^m}\cdot \mathit{n}\left(S_o-S_o^b\right)dS+{\displaystyle \underset{\partial {\mathrm{\Omega }}_o}{\int }}\frac{{\delta }_o}{h}\left(S_o-S_o^b\right)\stackrel{\sim }{S_o^m}dS(19)$

3 Model implementation

We use ADFNE software to generate the coordinate information of random fractures. Subsequently, we utilize COMSOL Livelink in conjunction with MATLAB to import this random fracture information into the COMSOL Multiphysics software, allowing us to generate the corresponding geometric model. Following this, we incorporate the two-phase flow equations (6) to (9) for both pores and fractures into the built-in PDE weak form and low-dimensional PDE weak form modules of the COMSOL Multiphysics finite element software, respectively. We also set the model boundary and initial conditions. In the time domain, we choose to discretize the equations using the q-order backward difference method. For solving the nonlinear algebraic system, we selecte the MUMPS direct solver based on LU decomposition, applying the damped Newton method. To achieve higher computational accuracy, we set the relative tolerance to 0.001. The algorithm employs an adaptive approach for time discretization, in contrast to the pre-established time step method which selects time steps randomly. By default, this method initiates with the first step being 0.1% of the total end time.

4 Model validation

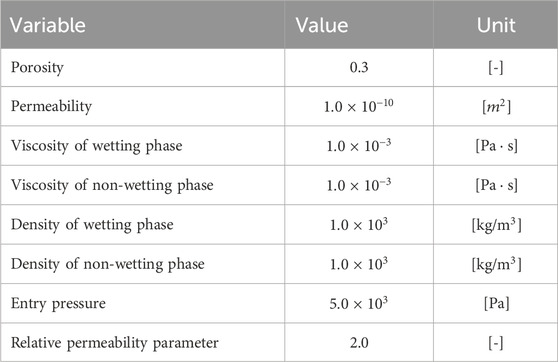
In this section, the model and its numerical results are validated through the McWhorter problem, in which the capillary effects of immiscible and incompressible two-phase flow in porous media are considered. The geometry, boundary and initial conditions of the model are shown in Figure 2. The length of the model is 2.6 m. At the initial moment, the simulated region is fully saturated by the non-wetting phase fluid and the reservoir pressure is $2\times {10}^5$ Pa. The left boundary has the water saturation of 1 and the pressure is $2\times {10}^5$ Pa, while the other boundaries are no-flow boundaries. Brooks-Corey functions for capillary pressure and relative permeability are implemented in the model. The relevant parameter settings in the simulation are shown in Table 1. The comparisons between the semi-analytical solution of the McWhorter problem and the numerically calculated water saturation curves are given in Figure 3. The results show that the water is transported from the left boundary by about 1.5 m after 10,000 s. Meanwhile, the numerical and theoretical results match well, proving the applicability and accuracy of the numerical method in two-phase flow.

FIGURE 2

FIGURE 2. Geometric model, boundary conditions and initial conditions for the McWhorter problem. The subscripts w and nw refer to the wetting phase and non-wetting phase, respectively.

TABLE 1

TABLE 1. Parameter settings in McWhorter problems.

FIGURE 3

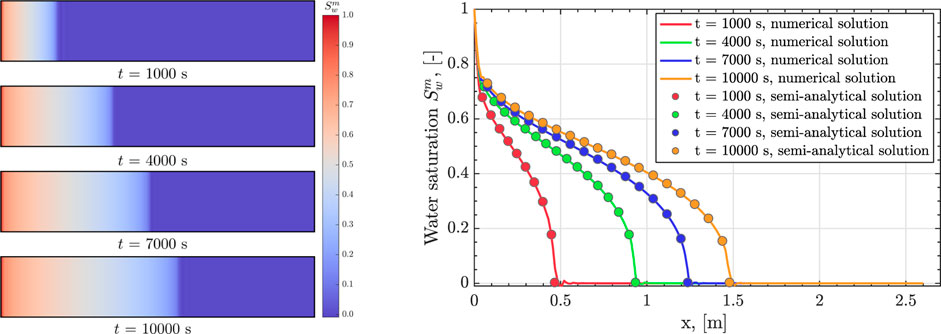
FIGURE 3. The left panel illustrates the spatial distribution of water saturation at various time steps, whereas the right panel presents the line distribution of water saturation from numerical (lines) and semi-analytical (dots) solution.

5 Model setup

Given the challenge of directly obtaining the distribution characteristics and attribute information of fractures within the reservoir, we employ the ADFNE program to generate two sets of two-dimensional random fractures (Alghalandis, 2017), with fracture lengths following an exponential distribution. The fractures are oriented at 45° and 135° to the horizontal direction, and the minimum and maximum values of the fracture lengths are 1 m and 5 m, respectively. The model is shown in Figure 4, and the 10 m $\times$ 10 m simulation geometry area is divided into about 4,700 triangular cells. The initial reservoir pressure $p_{gi}^m$ of the model is 8 MPa and the initial saturation $S_{oi}^m$ is 0.9, and the extraction well and gas injection well are placed in the upper right and lower left sections of the model, respectively. The pore pressure $p_g^b$ and saturation $S_o^b$ in the extraction wells are 4 MPa and 0.9, respectively, and the gas injection wells are set at a constant flow rate with a CO₂ injection of $1.5\times {10}^{-5}\text{ kg}/{\mathrm{m}}^2\bullet \mathrm{s}$, and the rest of the boundaries are zero-flow boundaries. The whole simulation time is set to 600 days, and the basic physical parameters of the model are shown in Table 2.

FIGURE 4

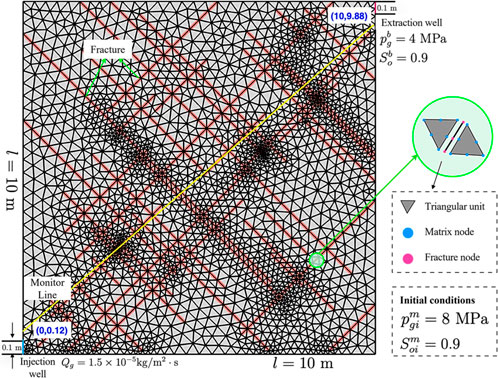
FIGURE 4. Geometric model, boundary conditions and initial conditions of a fractured shale reservoir.

TABLE 2

TABLE 2. Simulation parameters for CO₂ enhanced shale oil in a fractured reservoir.

6 Simulation results

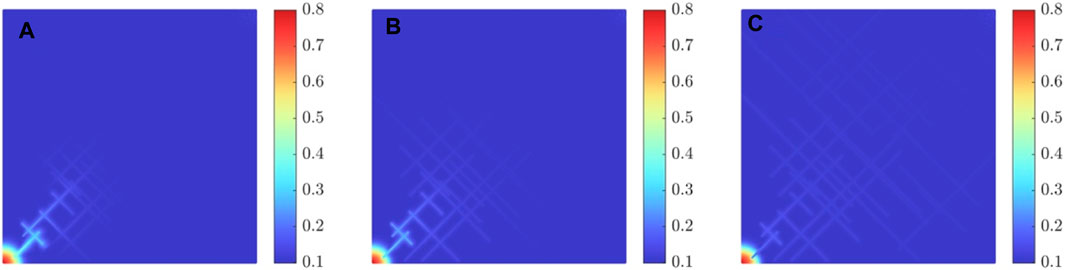
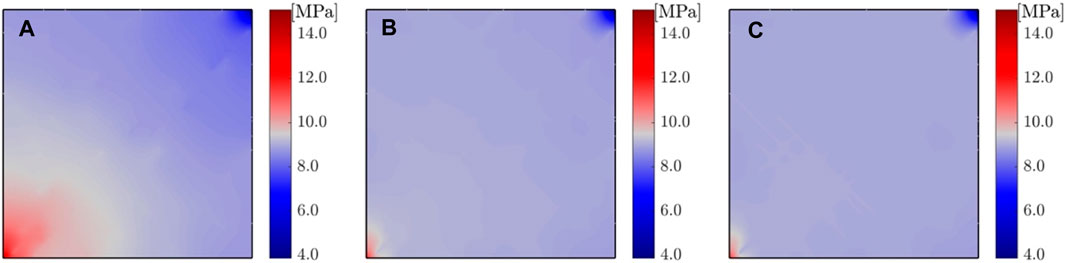
Figures 5, 6 represent the spatial distribution of pore pressure ($p^{\alpha }=p_g^{\alpha }{S}_g^{\alpha }+p_w^{\alpha }{S}_w^{\alpha }$) and CO₂ saturation at different time steps (t = 50th, 300th and 600th day) of CO₂ injection into the fractured reservoir for enhanced shale oil recovery, respectively. During shale oil extraction, pore pressures near the gas injection wells increase, while those near the extraction wells decrease, resulting in an expanding range of pressure fluctuations. The higher permeability of the fractures, compared to the surrounding matrix, facilitates a more substantial flow of CO₂ into the interior of the reservoir along the fracture regions.

FIGURE 5

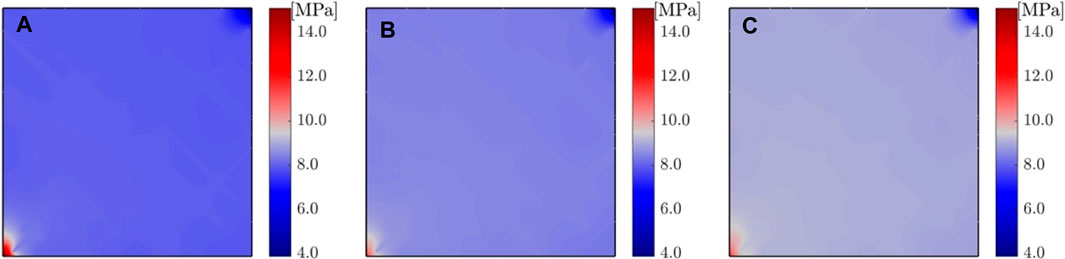
FIGURE 5. Pore pressure distribution at t = 50th, 300th and 600th day for CO₂ injection into fractured reservoirs.

FIGURE 6

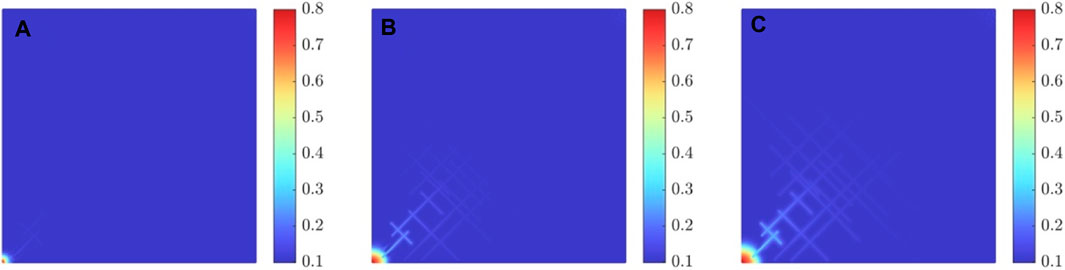
FIGURE 6. Saturation distribution at t = 50th, 300th and 600th day for CO₂ injection into fractured reservoirs.

7 Sensitivity analysis

7.1 Effects of heterogeneity in shale reservoirs

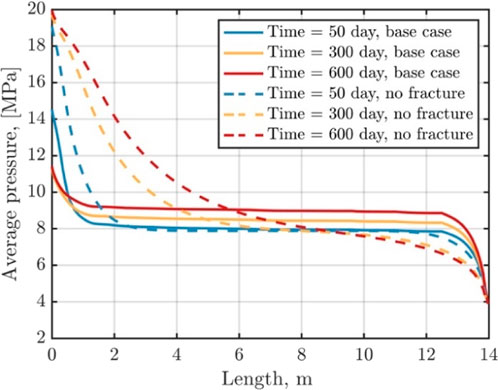
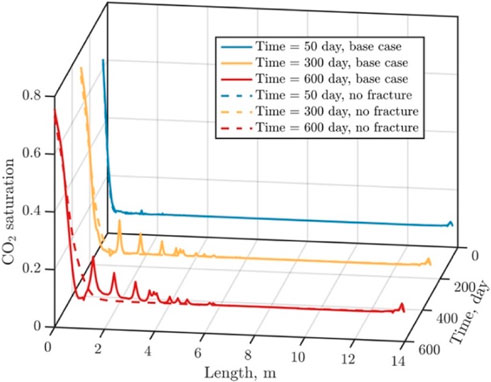
In shale oil reservoirs, a considerable number of weak structural surfaces, such as laminae and natural fractures, are developed (JIN et al., 2021a; JIN et al., 2021b). Although fractures account for a small portion of the volume of the underlying shale oil reservoir, the fractures contribute to the heterogeneity of reservoir, profoundly affecting fluid transport and shale oil extraction efficiency (LEI et al., 2021). To accurately understand the impact of shale oil reservoirs heterogeneity properties on internal fluid transport, we investigate the effects of CO₂ injection into fractured and homogeneous reservoirs. Figures 7, 8 shows the distribution of reservoir pore pressure and CO₂ saturation along the monitoring line at different time steps (t = 50th, 300th and 600th day) during CO₂ injection into both the fractured and homogeneous reservoirs. The fractures enhance the overall permeability of the shale oil reservoir, increasing the mobility of both CO₂ and shale oil. As a result, the CO₂ saturation within the fractured reservoir at the same location is significantly higher than that in the homogeneous reservoir. Due to the lower permeability of matrix in the homogeneous reservoir, CO₂ tends to accumulate near the well, leading to slightly higher CO₂ saturation in its vicinity than at the wellhead of the fractured reservoir. The pore pressure near the injection well in the homogeneous reservoir is about 14.5 MPa at 600 days into the injection; however, in the fractured reservoir, the pore pressure near the injection well is about 20.1 MPa, due to the injection of a larger volume of CO₂.

FIGURE 7

FIGURE 7. Distribution of pore pressure along the monitoring line at different time steps.

FIGURE 8

FIGURE 8. Distribution of CO₂ saturation at different moments along the monitoring line.

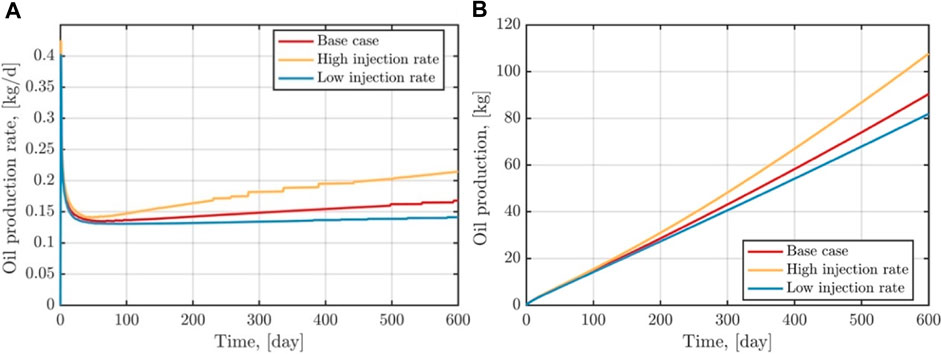
Figure 9 illustrates the shale oil extraction rate and cumulative production resulting from CO2 injection into both fractured and homogeneous reservoirs. At the outset of gas injection and production, the production rate of shale oil surges rapidly due to the significant pressure difference between the gas extraction well and the reservoir. During the process of production, the production rate of shale oil follows a general trend of increasing initially and then decreasing. On the 50th day of gas injection, the production rate of shale oil in the fractured reservoir experiences a rebound, attributable to the injection of a larger quantity of CO₂. By the 600th day of gas injection, the production rates of shale oil in the homogeneous and fractured reservoirs are approximately 0.09 kg/d and 0.17 kg/d, respectively, while the cumulative production amounts to approximately 60.8 kg and 90.4 kg, respectively. Throughout the entirety of the simulation process, the presence of natural fractures contributes to a 48.9% increase in the cumulative production of shale oil.

FIGURE 9

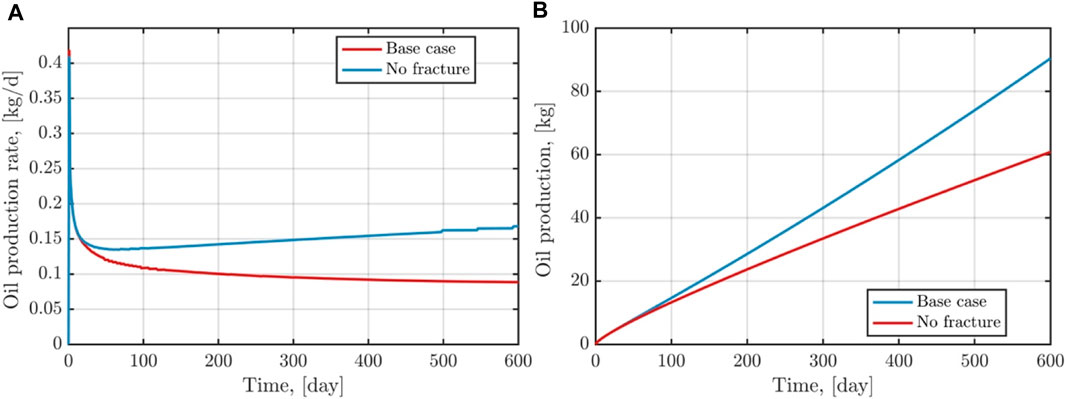
FIGURE 9. The evolutions of shale oil production rate and cumulative production for CO₂ injection into both fractured and homogeneous reservoirs.

7.2 Effect of fracture permeability

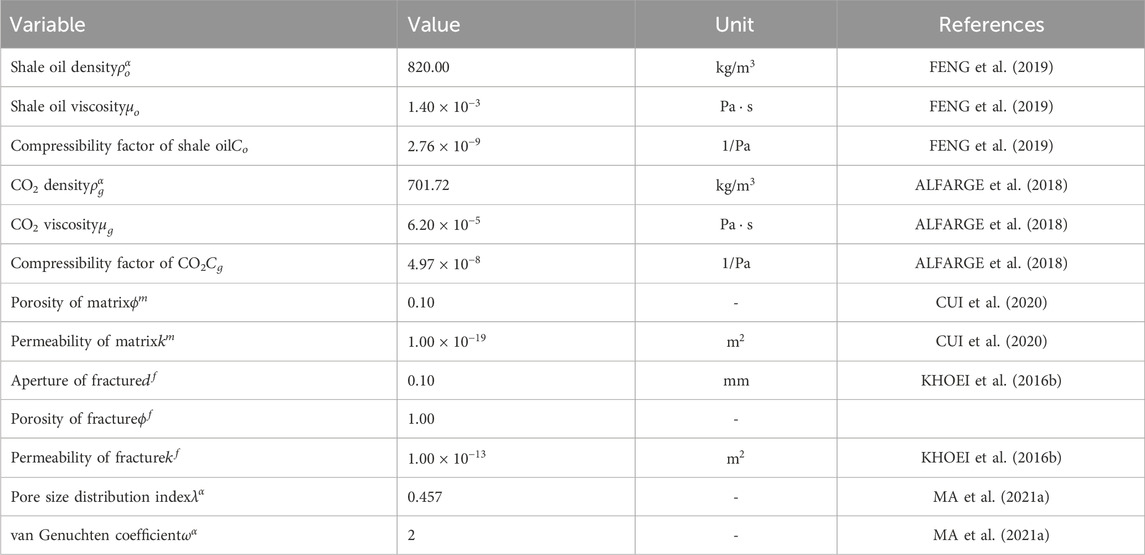
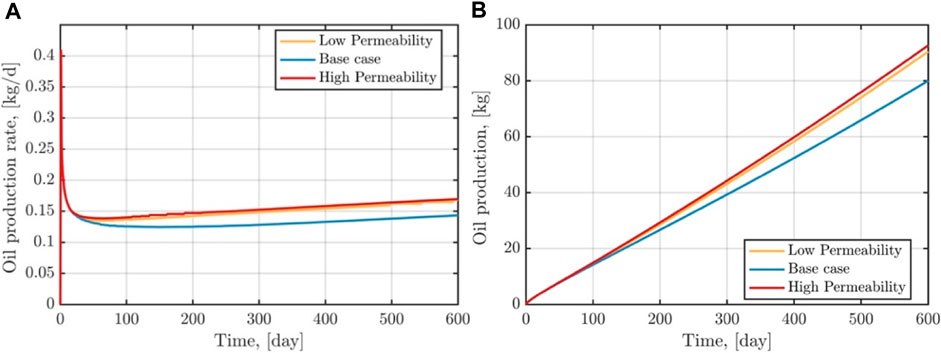
Fracture permeability is typically one of the key factors influencing the efficiency of CO₂ enhanced shale oil recovery (ALFARGE et al., 2018; FENG et al., 2019). Here, we focus on analyzing the effect of fracture permeability on the behavior of fluid flow, as well as on shale oil recovery efficiency and production volume. Figures 10, 11 show the distribution of CO₂ saturation and pore pressure on the 600th day under different fracture permeability conditions ($k^f=1.00\times {10}^{-14},1.00\times {10}^{-13},1.00\times {10}^{-12}{m}^2$).

FIGURE 10

FIGURE 10. Distribution of CO₂ saturation at t = 600th day with different fracture permeabilities.

FIGURE 11

FIGURE 11. Distribution of pore pressure at t = 600th day with different fracture permeabilities.

Figures 12, 13 demonstrate the distribution of CO₂ saturation and pore pressure along the monitoring line, as well as the shale oil production rate and total production volume under different fracture permeability conditions. As fracture permeability increases, CO₂ is more readily able to penetrate into the interior of the reservoir, leading to an increase in both CO₂ saturation and reservoir pressure near the gas injection wells. A higher fracture permeability facilitates the flow of shale oil, enhancing the production rate and the total volume of shale oil produced. When the fracture permeability increases from $1.00\times {10}^{-14}{\mathrm{m}}^2$ to $1.00\times {10}^{-13}{\mathrm{m}}^2$, total shale oil production increases from 80.0 kg to 90.4 kg. However, as fracture permeability further increases from $1.00\times {10}^{-13}{\mathrm{m}}^2$ to $1.00\times {10}^{-12}{\mathrm{m}}^2$, the total shale oil production increases slightly, from 90.4 kg to 92.6 kg, amounting to an increase of 2.4%.

FIGURE 12

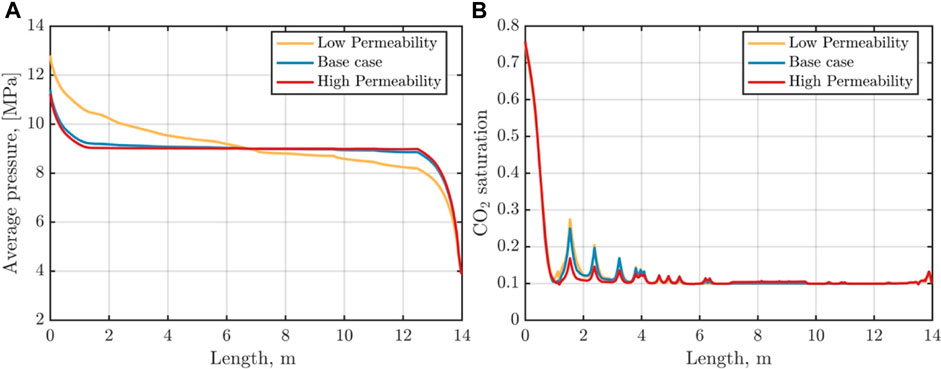
FIGURE 12. Distribution of pore pressure and CO₂ saturation along the monitoring line at t = 600th day with different fracture permeabilities.

FIGURE 13

FIGURE 13. Shale oil production rate and total production with different fracture permeabilities.

7.3 Effect of CO2 injection rate

Figures 14, 15 show the distribution of pore pressure and CO₂ saturation along the monitoring line, as well as the shale oil extraction rate and total amount of production, under the conditions of CO₂ injection rate ($Q_g=7.5\times {10}^{-6},1.5\times {10}^{-5},3.0\times {10}^{-5}\text{\hspace{0.17em}kg}/{\mathrm{m}}^2\bullet \mathrm{s}$). Given the same parameters and grid conditions, a larger CO₂ injection rate results in a higher volume of CO₂ being injected into the reservoir at any given time. When the injection rate increases from $7.5\times {10}^{-6}\text{\hspace{0.17em}kg}/{\mathrm{m}}^2\bullet \mathrm{s}$ to $3.0\times {10}^{-5}\text{\hspace{0.17em}kg}/{\mathrm{m}}^2\bullet \mathrm{s}$, the pressure near the injection well rises from 9.88 MPa to 14.1 MPa, and the CO₂ saturation also increases. Furthermore, a higher injection rate enhances the efficiency of shale oil displacement, leading to an increase in both the production rate and total extraction of shale oil. The production efficiencies of the three scenarios are 0.14 kg/d, 0.17 kg/d and 0.22 kg/d, while the recoveries are 81.9 kg, 90.4 kg and 107.7 kg, respectively. The simulation results indicate that a higher gas injection rate yields greater production benefits. However, it is crucial to note that higher pore pressure may increase the likelihood of damage or even rupture in the reservoir and caprock. New fractures in the caprock could provide pathways for CO₂ leakage, escalating the risk of gas escape, diminishing the CO₂ sequestration capacity of the reservoir, and potentially contaminating groundwater, among other issues. Therefore, the mechanical properties of both the reservoir and caprock warrant further investigation.

FIGURE 14

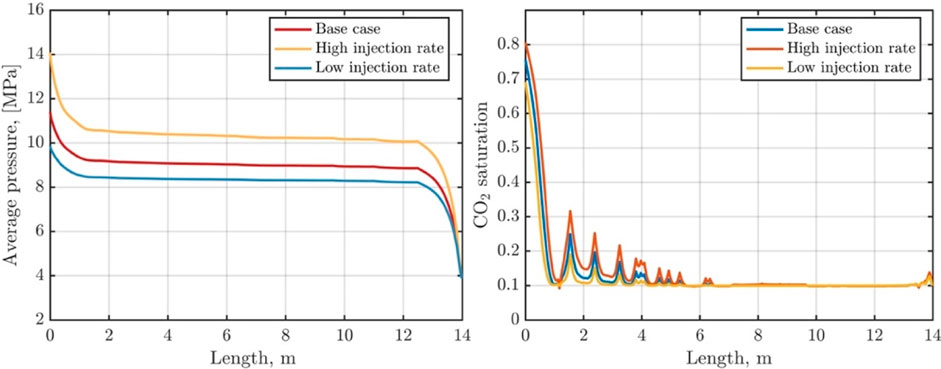
FIGURE 14. Distribution of pore pressure and CO₂ saturation along the monitoring line under different CO₂ injection rate conditions.

FIGURE 15

FIGURE 15. Shale oil extraction rate and total production under different CO₂ injection rates.

7.4 Effect of different gas injection schemes

To examine the impact of various gas injection strategies, three distinct cases are designed, as depicted in Figure 16. In case 1, the CO₂ injection rate undergoes a stepwise reduction, starting from $1.5\times {10}^{-5}\text{\hspace{0.17em}kg}$ and decreasing to $0.25\times {10}^{-5}\text{\hspace{0.17em}kg}$. In case 2, there is a stepwise increase in the CO₂ injection rate, ranging from $0.25\times {10}^{-5}\text{\hspace{0.17em}kg}$ to $1.5\times {10}^{-5}\text{\hspace{0.17em}kg}$. Lastly, Case 3 maintains a constant CO₂ injection rate of $8.75\times {10}^{-6}\text{\hspace{0.17em}kg}$ throughout the simulation. These designs ensure that the total gas injection rate remains the same for all three schemes during the entire simulation period.

FIGURE 16

FIGURE 16. Evolution of shale oil production in different gas injection cases.

The spatial distribution of CO₂ saturation at t = 600 days for different gas injection schemes is illustrated in Figure 17. After 600 days of gas injection and extraction, the CO₂ distribution within the shale reservoir is generally similar across all three injection schemes. Figures 18, 19 highlight variations in pore pressure, extraction rate, and total production near the injection and production wells under different gas injection scenarios. The pore pressures near the injection wellheads for case 1 and 3 quickly peak at 13.5 MPa and 11.5 MPa, respectively, at the onset of gas injection and extraction. Thereafter, the pore pressure decreases under the influence of the production wells. In Case 2, the pore pressure gradually increases to 10.2 MPa. Across all three injection cases, the pore pressure near the production wells follows a pattern of rapid decline followed by a rebound. In the middle stage of extraction, case 1 exhibits the highest pore pressure and extraction rate near the injection wells, while Case 2 has the lowest. The total production in Case 1 surpasses that of the other two cases, indicating that the choice of gas injection influences shale oil production, even when the same amount of CO₂ is injected. Therefore, optimizing the gas injection scheme presents tangible economic benefits for enhancing production capacity.

FIGURE 17

FIGURE 17. Distribution of CO₂ saturation at t = 600th day in different gas injection cases.

FIGURE 18

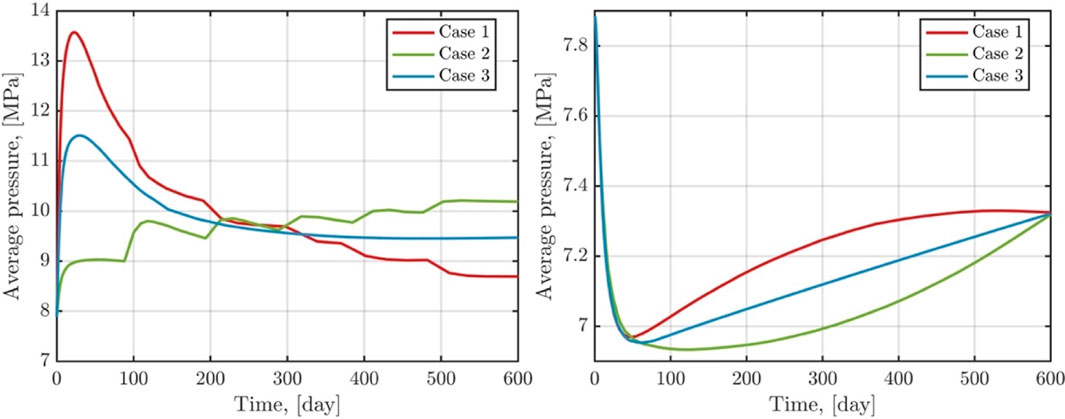
FIGURE 18. Evolution of pore pressure near injection and production wells in different gas injection cases.

FIGURE 19

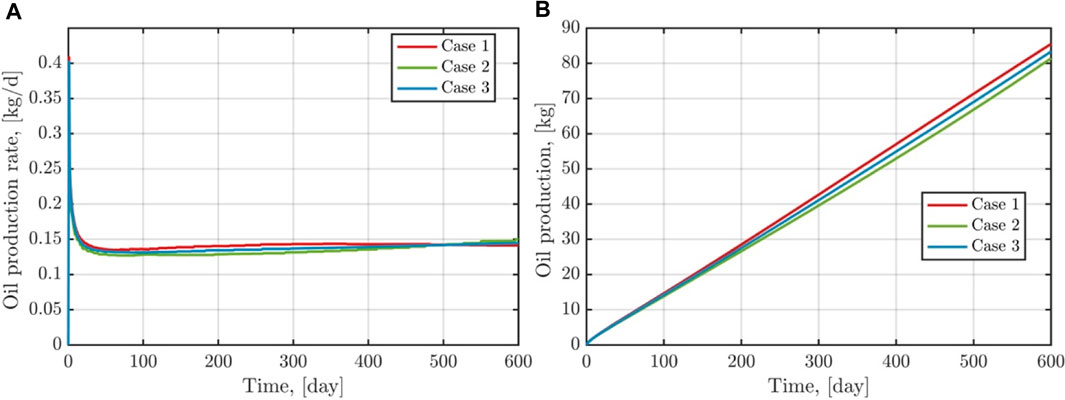
FIGURE 19. Evolution of shale oil recovery rates and total production in different gas injection cases.

8 Conclusion

In this paper, we conducted a comprehensive analysis of the fluid dynamics and production characteristics of shale oil in response to CO₂ injection. We presented the discrete fracture matrix model, incorporating both discontinuous and continuous Galerkin finite element methods. The main conclusions are drawn as follows:

(1) Fractures in shale oil reservoirs play a crucial role in boosting both the efficiency of shale oil production and the production volumes. When compared to homogeneous reservoirs, fractured reservoirs exhibit an approximate 48.9% increase in cumulative shale oil production. Enhancing the permeability of fractures contributes to improved fluid flow capacity within the reservoir, subsequently fostering an increase in both the shale oil extraction rate and production volume. However, it is important to note that solely increasing the fracture permeability has a limited effect on augmenting the reservoir’s shale oil production capacity.

(2) A higher CO₂ injection rate enhances both the replacement efficiency and shale oil production. As the CO₂ injection rate increases from $7.5\times {10}^{-6}\text{\hspace{0.17em}kg}/{\mathrm{m}}^2$ to $3.0\times {10}^{-5}\text{\hspace{0.17em}kg}/{\mathrm{m}}^2\bullet \mathrm{s}$, the shale oil recovery rate improves from 0.14 kg/d to 0.22 kg/d, and the recovery volume increases from 82 kg to 109 kg. Furthermore, when considering the same total volume of CO₂ injection, the chosen gas injection scheme significantly influences shale oil recovery. Simulation results indicate that gradually decreasing the CO₂ injection rate yields more favorable outcomes for shale oil production compared to a constant flow rate injection.

(3) Higher CO₂ injection rates and a stepwise reduction in CO₂ injection result in higher reservoir pore pressures, increasing the possibility of damage or even destruction of the rock near the well. New fractures created could cause CO₂ leakage, which affects the overall gas injection effect and leads to environmental problems.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

TM: Conceptualization, Funding acquisition, Methodology, Visualization, Writing–original draft. LJ: Formal Analysis, Visualization, Writing–original draft. YL: Funding acquisition, Writing–review and editing, Writing–original draft. CG: Funding acquisition, Methodology, Writing–review and editing. WS: Investigation, Writing–review and editing. YX: Methodology, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This study is supported by the National Natural Science Foundation of China (No. 12202483, 12172362, 42002255 and 42372286), the Natural Science Foundation of Chongqing (cstc2021jcyj-msxmX0564), the Opening Fund from the State Key Laboratory of Gas Disaster Detecting, Preventing and Emergency Controlling (Grant No. 2021SKLKF04), PetroChina Innovation Foundation (No. 2021DQ02-0204), and China Postdoctoral Science Foundation (2022M713374), the Chinese Academy of Geological Sciences through Chinese Geological Survey Projects (DD20221819) and the Fund from SinoProbe Laboratory (SinoProbe Lab 202210).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alfarge, D., Wei, M., and Bai, B. (2018). Data analysis for CO2-EOR in shale-oil reservoirs based on a laboratory database. J. Petroleum Sci. Eng. 162, 697–711. doi:10.1016/j.petrol.2017.10.087

CrossRef Full Text | Google Scholar

Alghalandis, Y. F. (2017). ADFNE: open-source software for discrete fracture network engineering, two- and three-dimensional applications. Comput. Geosciences 102, 1–11. doi:10.1016/j.cageo.2017.02.002

CrossRef Full Text | Google Scholar

Alharthy, N., Teklu, T., Kazemi, H., Graves, R., Hawthorne, S., Braunberger, J., et al. (2018). Enhanced oil recovery in liquid–rich shale reservoirs: laboratory to field. SPE Reserv. Eval. Eng. 21 (01), 137–159. doi:10.2118/175034-pa

CrossRef Full Text | Google Scholar

Berre, I., Doster, F., and Keilegavlen, E. (2019). Flow in fractured porous media: a review of conceptual models and discretization approaches. Transp. Porous Media 130 (1), 215–236. doi:10.1007/s11242-018-1171-6

CrossRef Full Text | Google Scholar

Brenner, K., Hennicker, J., Masson, R., and Samier, P. (2018). Hybrid-dimensional modelling of two-phase flow through fractured porous media with enhanced matrix fracture transmission conditions. J. Comput. Phys. 357, 100–124. doi:10.1016/j.jcp.2017.12.003

CrossRef Full Text | Google Scholar

Cheng, CHEN, Balhoff, M., and Mohanty, K. K. Effect of reservoir heterogeneity on primary recovery and CO₂ huff ‘n’puff recovery in shale-oil reservoirs[J]. SPE Reserv. Eval. Eng., 2014, 17(03): 404–413. doi:10.2118/164553-pa

CrossRef Full Text | Google Scholar

Chen, S., Yang, T., Ranjith, P., and Wei, C. (2017). Mechanism of the two-phase flow model for water and gas based on adsorption and desorption in fractured coal and rock. Rock Mech. Rock Eng. 50 (3), 571–586. doi:10.1007/s00603-016-1119-5

CrossRef Full Text | Google Scholar

Cui, G., Tan, Y., Chen, T., Feng, X. T., Elsworth, D., Pan, Z., et al. (2020). Multidomain two-phase flow model to study the impacts of hydraulic fracturing on shale gas production. Energy and Fuels 34 (4), 4273–4288. doi:10.1021/acs.energyfuels.0c00062

CrossRef Full Text | Google Scholar

Cusini, M., White, J. A., Castelletto, N., and Settgast, R. R. (2021). Simulation of coupled multiphase flow and geomechanics in porous media with embedded discrete fractures. Int. J. Numer. Anal. Methods Geomechanics 45 (5), 563–584. doi:10.1002/nag.3168

CrossRef Full Text | Google Scholar

Elwegaa, K., Emadi, H., Soliman, M., Gamadi, T., and Elsharafi, M. (2019). Improving oil recovery from shale oil reservoirs using cyclic cold carbon dioxide injection–An experimental study. Fuel 254, 115586. doi:10.1016/j.fuel.2019.05.169

CrossRef Full Text | Google Scholar

Fakher, S., and Imqam, A. (2020). Application of carbon dioxide injection in shale oil reservoirs for increasing oil recovery and carbon dioxide storage. Fuel 265, 116944. doi:10.1016/j.fuel.2019.116944

CrossRef Full Text | Google Scholar

Fan, L., Chen, J., Zhu, J., Nie, X., Li, L. I. B., and Shi, Z. (2022). Experimental study on enhanced shale oil recovery and remaining oil distribution by CO₂ flooding with nuclear magnetic resonance technology. Energy and Fuels 36 (4), 1973–1985. doi:10.1021/acs.energyfuels.1c02982

CrossRef Full Text | Google Scholar

Feng, Q., Xu, S., Wang, S., Li, Y., Gao, F., and Xu, Y. (2019). Apparent permeability model for shale oil with multiple mechanisms. J. Petroleum Sci. Eng. 175, 814–827. doi:10.1016/j.petrol.2019.01.038

CrossRef Full Text | Google Scholar

GeoQuest, S. (2010). ECLIPSE reservoir simulator, Manual and technical description. USA, ECLIPSE Technical Description.

Google Scholar

Gläser, D., Helmig, R., Flemisch, B., and Class, H. (2017). A discrete fracture model for two-phase flow in fractured porous media. Adv. Water Resour. 110, 335–348. doi:10.1016/j.advwatres.2017.10.031

CrossRef Full Text | Google Scholar

Guide, S. (2002). Advanced process and thermal reservoir simulator. Alberta Canada: Computer Modelling Group Ltd.

Google Scholar

Huang, XING, Tian, Z., Zuo, X., Xiang, L. I., Yang, W., and Lu, J. (2023). The microscopic pore crude oil production characteristics and influencing factors by DME-assisted CO₂ injection in shale oil reservoirs. Fuel 331, 125843. doi:10.1016/j.fuel.2022.125843

CrossRef Full Text | Google Scholar

Jia, B., Tsau, J. S., and Barati, R. (2019). A review of the current progress of CO₂ injection EOR and carbon storage in shale oil reservoirs. Fuel 236, 404–427. doi:10.1016/j.fuel.2018.08.103

CrossRef Full Text | Google Scholar

Jin, Z., Wang, G., Liu, G., et al. (2021a). Research progress and key scientific issues of continental shale oil in China. Acta Pet. Sin. 42 (7), 821–835. doi:10.7623/syxb202107001

CrossRef Full Text | Google Scholar

Jin, Z., Zhu, R., Liang, X., and Shen, Y. (2021b). Several issues worthy of attention in current lacustrine shale oil exploration and development. Petroleum Explor. Dev. 48 (6), 1471–1484. doi:10.1016/s1876-3804(21)60303-8

CrossRef Full Text | Google Scholar

Khoei, A. R., Hosseini, N., and Mohammadnejad, T. (2016b). Numerical modeling of two-phase fluid flow in deformable fractured porous media using the extended finite element method and an equivalent continuum model. Adv. water Resour. 94, 510–528. doi:10.1016/j.advwatres.2016.02.017

CrossRef Full Text | Google Scholar

Khoei, A., Hosseini, N., and Mohammadnejad, T. (2016a). Numerical modeling of two-phase fluid flow in deformable fractured porous media using the extended finite element method and an equivalent continuum model. Adv. Water Resour. 94, 510–528. doi:10.1016/j.advwatres.2016.02.017

CrossRef Full Text | Google Scholar

Lang, D., Lun, Z., Lyu, C., Wang, H., Zhao, Q., and Sheng, H. (2021). Nuclear magnetic resonance experimental study of CO₂ injection to enhance shale oil recovery. Petroleum Explor. Dev. 48 (3), 702–712. doi:10.1016/s1876-3804(21)60056-3

CrossRef Full Text | Google Scholar

Law, H. S., Meer, L. G. H. V. D., and Gunter, W. D. (2003). Comparison of numerical simulators for greenhouse gas storage in coal beds, part ii: flue gas injection, 563–568.

CrossRef Full Text | Google Scholar

Law, D., Meer, L. G. H. V. D., and Gunter, W. D. (2002). Numerical simulator comparison study for enhanced coalbed methane recovery processes, part i: pure carbon dioxide injection. SPE Gas. Technol. Symp. doi:10.2118/75669-MS

CrossRef Full Text | Google Scholar

Lei, Q., Weng, D., Xiong, S., et al. (2021). Progress and development directions of shale oil reservoir simulation technology of China National Petroleum Corporation. Petroleum Explor. Dev. 48 (5), 1035–1042. doi:10.1016/S1876-3804(21)60102-7

CrossRef Full Text | Google Scholar

Li, S., Zhang, S., Xing, H., and Zou, Y. (2022). CO₂–brine–rock interactions altering the mineralogical, physical, and mechanical properties of carbonate-rich shale oil reservoirs. Energy 256, 124608. doi:10.1016/j.energy.2022.124608

CrossRef Full Text | Google Scholar

Liu, Z., and Zhang, Q. (2008). A review on the state of art of the saturated seepage-stress coupling models in rock mass. Adv. Mech. 38 (5), 585–600. doi:10.6052/1000-0992-2008-5-J2007-054

CrossRef Full Text | Google Scholar

Lu, Y., Zhou, J., Xian, X., et al. (2021). Research progress and prospect of the integrated supercritical CO2 enhanced shale gas recovery and geological sequestration. Nat. Gas. Ind. 41 (06), 60–73. doi:10.3787/j.issn.1000-0976.2021.06.007

CrossRef Full Text | Google Scholar

Ma, T., Rutqvist, J., Oldenburg, C. M., and Liu, W. (2017). Coupled thermal–hydrological–mechanical modeling of CO₂-enhanced coalbed methane recovery. Int. J. Coal Geol. 179, 81–91. doi:10.1016/j.coal.2017.05.013

CrossRef Full Text | Google Scholar

Ma, T., Shen, W., Liu, W., et al. (2021a). Discontinuous Galerkin FEM method for the coupling of compressible two-phase flow and poromechanics. Chin. J. Theor. Appl. Mech. 53 (8), 2235–2245. doi:10.6052/0459-1879-21-177

CrossRef Full Text | Google Scholar

Ma, T., Zhang, K., Shen, W., Guo, C., and Xu, H. (2021b). Discontinuous and continuous Galerkin methods for compressible single-phase and two-phase flow in fractured porous media. Adv. Water Resour. 156, 104039. doi:10.1016/j.advwatres.2021.104039

CrossRef Full Text | Google Scholar

Mei, H., He, L., Zhang, M., et al. (2018). Status and feasibility analysis on improved shale-oil recovery by gas injection. Reserv. Eval. Dev. 8 (6), 77–82.

Google Scholar

Meng, S., Li, Y., Wang, L., Wang, K., and Pan, Z. (2018). A mathematical model for gas and water production from overlapping fractured coalbed methane and tight gas reservoirs. J. Petroleum Sci. Eng. 171, 959–973. doi:10.1016/j.petrol.2018.08.036

CrossRef Full Text | Google Scholar

Pruess, K., Oldenburg, C., and Moridis, G. (1999). TOUGH2 user’s guide version 2. China, Lawrence Berkeley National Laboratory.

Google Scholar

Wan, T. A. O., Zhang, J., and Jing, Z. (2022). Experimental evaluation of enhanced shale oil recovery in pore scale by CO₂ in Jimusar reservoir. J. Petroleum Sci. Eng. 208, 109730. doi:10.1016/j.petrol.2021.109730

CrossRef Full Text | Google Scholar

Wang, Y., Xu, Z., and Su, B. (2000). Full coupling analysis of seepage and stress elastic-plastic in complex fractured rock mass. Chin. J. Rock Mech. Eng. 019 (2), 177–181. doi:10.3321/j.issn:1000-6915.2000.02.011

CrossRef Full Text | Google Scholar

Yang, L. I. U., Li, S., and Liu, X. (2008). A coupled model of seepage stress in dual media based on continuum discrete element. Chin. J. Rock Mech. Eng. 030 (005), 951–959.

Google Scholar

Yang, Y., and Huang, D. (2019). Geological characteristics and new understandings of exploration and development of Jurassic lacustrine shale oil and gas in the Sichuan Basin. Nat. Gas. Ind. 39 (06), 22–33. doi:10.3787/j.issn.1000-0976.2019.06.003

CrossRef Full Text | Google Scholar

Yu, H., Xu, H., Fu, W., Lu, X., Chen, Z., Qi, S., et al. (2021). Extraction of shale oil with supercritical CO₂: effects of number of fractures and injection pressure. Fuel 285, 118977. doi:10.1016/j.fuel.2020.118977

CrossRef Full Text | Google Scholar

Zhang, Q., Huang, C., Yao, J., Wang, Y., and Li, Y. (2017). Two-phase numerical simulation of discrete fracture model based on multiscale mixed finite element method. Chin. Sci. Bull. 62 (13), 1392–1401. doi:10.1360/n972016-00584

CrossRef Full Text | Google Scholar

Zhu, C., Lizhao, Y. Q., Gong, H., Sang, Q., Zou, H., et al. (2018). Experimental study and simulation of CO₂ transfer processes in shale oil reservoir. Int. J. Coal Geol. 191, 24–36. doi:10.1016/j.coal.2018.03.002

CrossRef Full Text | Google Scholar