Archimedes optimization algorithm based parameter extraction of photovoltaic models on a decent basis for novel accurate RMSE calculation

Solar photovoltaic (PV) technology stands as a promising alternative to conventional fossil fuel-based power generation, offering pollution-free and low-maintenance energy production. To harness its potential effectively, understanding the power generation process and accurately modeling solar PV systems are essential. Unfortunately, manufacturers often do not provide the necessary parameters for modeling solar cells, making it challenging for researchers. This research employs the Archimedes Optimization Algorithm (AOA), an optimization technique, to determine unknown parameters for the PVM752 GaAs thin film solar cell and the RTC France solar cell. The modeling of these solar cells utilizes both a Single Diode Model (SDM) and a Double Diode Model (DDM). Performance evaluations are conducted using the sum of individual absolute errors (SIAE) and a novel root mean square error (RMSE) method. Comparing the effectiveness of the AOA with other optimization methods, The RMSEs for the AOA applied to the SDM and DDM of RTC France solar cell were 3.7415 × 10^–3 and 1.0033 × 10^–3. Similarly, for PVM752 GaAs thin film solar cell were 1.6564 × 10^–3, and 0.00106365, respectively. The SIAE values for both solar diode models of RTC France cells were 0.071845 and 0.021268, respectively. For the PVM752 GaAs thin film, the corresponding SIAE values were 0.031488 and 0.040224. The results highlight the efficiency of the AOA-based approach, showcasing consistent convergence and a high level of accuracy in obtained solutions. The suggested approach produces superior results with a lower RMSE compared to other algorithms, demonstrating its efficacy in determining solar PV parameters for modeling purposes.

1 Introduction

The usage of fossil fuels has rapidly increased in recent years due to both population growth and the construction of infrastructure to make life simpler. Fossil fuels, which are non-renewable resources and contribute to global warming via pollution, are the main sources of electricity production. Fossil fuels are scarce and might become extinct 1 day. Getting fossil fuels has been a natural process that has undertaken tens of thousands of years and is still going on today. The primary fossil fuels are natural gas, coal, and oil. In the process of producing power, they are burned. The world is currently shifting towards the growth of renewable energy sources due to the depletion of fossil fuels and concerns about global warming (Kataria and Khan, 2021).

Solar photovoltaic (PV) is a popular renewable energy source (along with geothermal, hydropower, solar, wind, and biomass energy). After wind and hydropower, PV is the third most widely used renewable energy technology. 1) As fossil fuel usage is rising rapidly and may eventually run out, PVs are being encouraged because their resources are plentiful and limitless. 2) While PVs themselves do not contribute to air pollution, the fossil fuels used to power conventional power plants do. 3) While PVs help to decrease the issue of global warming, fossil-fuel units exacerbate it. 4) Low operating and maintenance expenses; 5) Ability to produce electricity on the demand side; 6) PV installation and operation require less labor than conventional generating units. The greatest power density between renewable energy sources is offered by PVs. These causes caused a startling rise in research and investment in renewable energy sources, primarily solar photovoltaic systems. There is a lot of research being done to improve the thermal and electrical efficiency of PV. Recent years have seen a surge in interest in the study of how AI can be applied to the solar system. Applications in residential use, transportation, street lighting, and defect detection are all included in the investigation scope.

According to the Renewables 2022 Global Status Report (GSR 2022) from the Renewable Energy Policy Network (REN21) for the 21st Century, India’s renewable energy installations are third in the world, behind only China and Russia. For new solar PV capacity, India was the second-largest market throughout Asia and the third-largest market overall (Holeczek, 2014). India is home to four of the world’s seven largest solar power facilities, with Rajasthan Bhadla Solar Park being among the largest with a total capacity of 2.2 GW. These solar installations were completed as part of India’s National Solar Mission (NSM). With a goal of 20 GW by 2022, the Government of India established the National Solar Mission in 2010. The Government of India increased the goal to 100 GW in the 2015 Union Budget, with 40% of those projects being rooftop installations and the other 60% being large- and medium-scale grid-connected solar power plants (MNRE, 2019). India generated more than 70.24 billion units (BU) of solar energy in the first 9 months of 2022, a 36% increase when compared with 51.67 BU at the same time last year, according to the Mercom India Research study (Mercom, 2022).

An accurate assessment and performance forecasts for quality control and maximum power tracking are required before a PV system can be deployed, as underestimating power means not having enough to meet demands and overestimating power means having too much and wasting it. One of the primary issues with sun photovoltaic systems is the intricate, nonlinear, and implicit relationship between photovoltaic current and voltage. Temperature, dust accumulation, solar radiation, shading, soiling, and cable losses are just some of the environmental elements that have a major impact on the efficiency of photovoltaic systems. This makes it harder to create an accurate mathematical model that can capture the relationship between voltage and current in a photovoltaic system as it actually operates. The single diode model (SDM) and the double diode model (DDM) are the most popular equivalent circuits for designing PV systems based on electrical attributes, and they describe the non-linear features of voltage and current. The I-V characteristics described by these models are specific to residential applications. The three-diode model (TDM), which is lately being used has a potential for usage in the manufacturing sector (Oliva et al., 2019).

In many real-world scenarios, precise model parameter data is crucial. For example, PV system simulation is used to estimate energy yield and categorize power converter gear. 2) Used to manage and track the PV system’s maximum power point (MPPT) (Hussain et al., 2023a). 3) To maintain quality throughout the production process. 4) used to examine the degradation of PV cells Since the manufacturers’ data is measured under standard test settings (STC), actual PV systems are operated under less than perfect circumstances. Numerous approaches are suggested for figuring out the unknown parameters, which may be roughly categorized into numerical and analytical approaches. I-V curve data is used by analytical methods to mathematically formulate model parameters. It takes information from the I-V characteristic curve or data sheet for a number of important points, including the open circuit voltage, short-circuit current, voltage at maximum power, current at maximum power, and slopes of the intersecting curves. However, the analytical approach for predicting PV-cell characteristics has several drawbacks. 1) Frequently, the controlling equation contains difficult-to-solve exponential components. 2) In some cases, an initial guess at a parameter value is necessary. 3) A few formulas are dependent on information that the makers don't provide. 4) A number of assumptions have been made that lower the accuracy of model parameters.

The numerical extraction approach gets around these restrictions. The method of numerical extraction is, at heart, an optimization technique. The primary objective is to improve the accuracy of the calculated I-V curve relative to the experimental dataset. Since the parameters are evaluated using an analytical technique based on a relatively small sample size, the solutions are more vulnerable to the effects of measurement error. From this point on, it is acknowledged that the analytical technique is less trustworthy than the numerical extraction approach (Chin and Salam, 2019). The optimization method itself may be further broken down into the two categories of stochastic and deterministic. Newton’s method, iterative curve fitting, Levenberg-Marquardt’s algorithm, and the conductivity method are all examples of deterministic approaches that rely on gradients. Its early solution was crucial to its success. The deterministic approach brings with it a number of limitations, such as the requirement that the goal function be differentiable, convex, and continuous. The more parameters there are, the less likely it is that you will get the right answer (Chin and Salam, 2019). As a consequence, the outcomes are unpredictable. Stochastic approaches are used to get around these limitations. There are no restrictions on how you formulate an issue, make it computationally and conceptually simple, or be admirable in multimodal situations. They are probability-based and draw their design cues from nature. They are effective at resolving challenging engineering issues. They are the following: the genetic algorithm (GA) (Holland, 1992), the particle swarm optimization (PSO) (Ye et al., 2009), the whale optimization algorithm (WA) (Mirjalili and Lewis, 2016), the artificial bee colony (ABC) (Karaboga and Akay, 2009), the simulated annealing (SA) (Kirkpatrick et al., 1983), the teaching-learning-based optimization (TLBO) (Rao et al., 2011), the differential evolution (DE) (Price and Storn, 1997), the harmony search (HS) (Geem et al., 2001), the cuckoo search (CS) (Yang and Deb, 2009), and the pattern search (PS) (Torczon, 1997).

Xiong et al., 2021 confirmed that a GSK-based technique can be used to retrieve the unknown PV model parameters. The programmed simulates the lifelong process of learning and communicating knowledge. Single diode and double diode variants of RTC France cells are used alongside three different PV modules in this GSK procedure: the Pho-towatt-PWP201, STM6-40/36, and STP6-120/36. The GSK algorithm’s strength lies in its ability to perform well across a wide range of population densities. (Ganesh Pardhu and Kota, 2021). validated the Radial Movement Optimization (RMO) method for extracting the unknown parameters using a dedicated Kyocera KC200GT 200W panel. RMO is a swarm-based stochastic optimization approach in which every time a particle moves in three dimensions with a changing velocity, its location is updated. In comparison to other strategies, this one provides the fastest reaction. Parameters for the STM_40_36, STP6_120_36, and PWP 201 PV modules, among others, were extracted using the Supply Demand Optimization (SDO) method by in (Ginidi et al., 2021). This algorithm was conceived with economics in mind. In this situation, the root mean square error was calculated to account for the discrepancy between the optimized estimated data and the experimental data. In order to determine the five unknown solar cell parameters, (Abdulrazzaq et al., 2022), used a complex numerical method. A modified version of the Newton-Raphson method is used to solve the system of equations resulting from the best curve fitting using the least squares methodology. Parameters can be derived even without a data sheet if the solar module’s I-V characteristic curves are known. In this case, a highly sensitive first estimate value is generated by an optimum method. Crystalline solar cells, polycrystalline modules, and amorphous modules were all tested with this method to ensure their reliability at varying temperatures and amounts of sunlight. In (Khan et al., 2021), SA Khan et al. used the Chaos Induced Coyote Algorithm (CICA) to determine previously unknown parameters for the thin-film RTC France, monocrystalline, and polycrystalline solar cell single-, double-, and three-diode models. The introduction of disorder during population expansion is a conceptual influence for this method. The results in this study are organized in terms of the RMSE in comparison to previous research. HFM (Mateo Romero et al., 2022) investigate the application of AI to solar photovoltaic systems. Applications of artificial intelligence are discussed in this article for monitoring maximum power points, calculating energy output, estimating unmeasured properties, and identifying issues with PV panels. However, there are multiple published studies on obtaining these parameters. Most of this literature, unfortunately, emphasizes the superior performance of the algorithms employed. Algorithms were ranked in the aforementioned literature using metrics like average CPU time, final RMSE value, and RMSE boxplot representation. It's strange that most RMSE calculations in the literature are off (Ćalasan et al., 2020). Moreover, recent work proposed in (Abbassi et al., 2023) which introduces an enhanced Mountain Gazelle Optimizer (MGO) designed for optimizing the unknown parameters of PV generation units. Inspired by the social structure and hierarchy observed in mountain gazelles in their natural habitat, the MGO was evaluated against several contemporary algorithms, including the Grey Wolf Optimizer (GWO), Squirrel Search Algorithm (SSA), Differential Evolution (DE) algorithm, Bat–Artificial Bee Colony Optimizer (BABCO), Bat Algorithm (BA), Multiswarm Spiral Leader Particle Swarm Optimization (M-SLPSO), Guaranteed Convergence Particle Swarm Optimization algorithm (GCPSO), Triple-Phase Teaching–Learning-Based Optimization (TPTLBO), Criss-Cross-based Nelder–Mead simplex Gradient-Based Optimizer (CCNMGBO), quasi-Opposition-Based Learning Whale Optimization Algorithm (OBLWOA), and Fractional Chaotic Ensemble Particle Swarm Optimizer (FC-EPSO). Through comprehensive experimental findings and statistical analyses, it was established that the MGO demonstrated superior performance over the rival techniques when identifying parameters for the SDM and the DDM of PV models, specifically Photowatt-PWP201 (polycrystalline) and STM6-40/36 (monocrystalline). Furthermore, in the process of parameter extraction for the SDM with five unknown parameters in solar PV models another recent work proposed in (Premkumar et al., 2023). In this work a common practice involves utilizing a non-linear equation to describe the PV cell current has been used. Subsequently, the RMSE is employed as the objective function to quantify the error between the estimated and measured currents. This study introduces an iterative method based on the Lambert-W function for computing the PV cell current within the SDM. Additionally, a Weighted Velocity-Guided Grey Wolf Optimizer (WVGGWO) is incorporated as an optimization algorithm to discern the unknown lumped parameters of both the cell and module within the SDM. To assess the effectiveness of the proposed algorithm and Lambert-W function, four case studies are examined for validation. The performance of the introduced approach is then benchmarked against seven established optimization algorithms. The comparative analysis reveals that the suggested method consistently yields superior results when compared to various optimization techniques, establishing its efficacy in accurately extracting parameters for the SDM in PV models. Another recent work proposed in (Chandrasekaran et al., 2023) aims to investigate traditional methods for solving equations in PV models. Introducing an enhanced variant, Augmented Mountain Gazelle Optimizer (AMGO_IB3H), the study focuses on improving the convergence of the MGO using an upgraded Berndt-Hall-Hall-Hausman method. AMGO_IB3H demonstrates advancements in exploring and exploiting phases of MGO and objective function design. Additionally, a hybrid method is proposed for efficiently identifying unknown parameters in the three-diode PV model, utilizing actual laboratory data. Simulation results show that AMGO_IB3H achieves zero errors under various statistical standards and environmental conditions, outperforming state-of-the-art algorithms in terms of reliability, accuracy, and convergence rate within a reasonable processing time. Likewise, (Premkumar et al., 2022), presents an enhanced Gradient-Based Optimizer (GBO), termed Criss-Cross Nelder–Mead GBO (CCNMGBO), for estimating uncertain parameters in diverse PV models. By combining the Criss-Cross algorithm and Nelder–Mead simplex strategy with GBO, CCNMGBO demonstrates superior performance. The algorithm is validated on benchmark numerical optimization problems and applied to parameter estimation in PV models with five, seven, and nine unknown parameters. Comparative results against state-of-the-art algorithms confirm CCNMGBO’s effectiveness in handling numerical optimization and obtaining accurate parameters for different PV models under varied operating conditions. Similarly, the study in (Hussain et al., 2023b) evaluates the performance of artificial neural network (ANN) algorithms for maximum power point tracking (MPPT) in solar PV systems. This investigation contributes valuable insights to the optimization landscape, complementing the innovative approach proposed in the primary study. The inclusion of the article enhances the comprehensive understanding of optimization techniques and their applications in photovoltaic research.

In this proposed study, the real RMSE is estimated using the characteristics of 30 suggested methods that were collected from existing literature for SDM, with a focus on RTC France solar cells. The RTC France solar cell of SDM was chosen since it is the most widely used in the literature that has been published. Then, an AOA optimization approach for obtaining unknown solar photovoltaic parameters is suggested. This method is based on a physics concept known as Archimedes’ Law of Buoyancy (Hashim et al., 2021). Its performance was assessed by comparing it with other methods. In this study, the real RMSE is estimated using the characteristics of 30 suggested methods that were collected from existing literature for SDM, with a focus on RTC France solar cells. The RTC France solar cell of SDM was chosen since it is the most widely used in the literature that has been published. Next, an AOA approach to extracting unknown solar photovoltaic parameters is suggested. The AOA, one of the newest algorithms derived from nature, is based on a physics concept known as Archimedes’ Law of Buoyancy (Hashim et al., 2021). Its performance was assessed by comparing it with other methods.

The remaining portions of the paper are organized as follows: Solar photovoltaic models are discussed in Section 2, problem formulation is discussed in Section 3, the AOA method is explained in detail in Section 4, simulation and results are discussed in Section 5, and a conclusion is presented in Section 6.

2 Modeling of solar PV module

Sunlight is converted into energy via solar PV cells, sometimes referred to as photovoltaic cells. They include semiconductor materials, usually silicon, which receive photons from the sun and emit electrons as a result. Electrons generated through exposure to sunlight are captured and directed through a circuit, establishing an electric current. Photovoltaic (PV) cells, which exist in diverse shapes and sizes, commonly employ the traditional silicon solar cell structure. In this process, a silicon wafer is infused with impurities to form a p-n junction. Sunlight triggers the movement of electrons from the p-side to the n-side, inducing an electric current. PV cells are moderately efficient, typically converting only 15%–20% of incident sunlight into electricity. However, enhancing efficiency involves connecting multiple PV cells into a PV array, arranged both in series and parallel configurations. The most prevalent arrangement is the “series-parallel” configuration, elevating voltage and overall current output. Efficiency can further be heightened by deploying various PV cell types. Multi-junction cells, characterized by multiple semiconductor layers, widen the sunlight spectrum captured, enhancing efficiency. Integrating PV cells with other technologies amplifies their effectiveness. Concentrators focus sunlight onto PV cells using lenses or mirrors, intensifying sunlight absorption. Trackers move PV arrays to align with the sun’s trajectory, optimizing sunlight capture and boosting efficiency. PV cells and arrays are increasingly favored as renewable energy sources due to their low maintenance, absence of emissions, and independence from fuel for electricity generation. Furthermore, PV cells and arrays offer the advantage of easy integration into buildings and structures, enabling on-site electricity generation. However, there are notable limitations associated with their use. One constraint is their reliance on sunlight, rendering them ineffective during cloudy weather or at night. Moreover, the initial installation cost of a PV array can be substantial, although it has been decreasing in recent years. Another challenge is their durability; materials like silicon, which compose PV cells, are delicate and susceptible to damage from extreme weather conditions such as hail or strong winds. Over time, these cells can also degrade, leading to reduced efficiency and eventual replacement, incurring significant ongoing expenses for large arrays. Considering the environmental impact, the production process involves materials and chemicals that can be harmful if not disposed of responsibly. Additionally, the transportation and installation of PV arrays can contribute to environmental strain. To address these concerns, it is crucial to ensure that the production and disposal of PV cells and arrays adhere to environmentally responsible practices. Furthermore, the cost of installation and maintenance remains a significant factor limiting widespread adoption. Despite these challenges, technological advancements are rapidly driving down installation costs and enhancing PV cell efficiency. Given the escalating demand for clean and renewable energy sources, PV cells and arrays are expected to continue playing a pivotal role in the energy landscape. Governments and private organizations should persist in investing in research and development to improve technology and make it accessible to a broader population. Encouraging policies that promote the use of PV cells and arrays will further accelerate their adoption. Through these efforts, PV cells and arrays can contribute significantly to creating a more sustainable and resilient energy future for all.

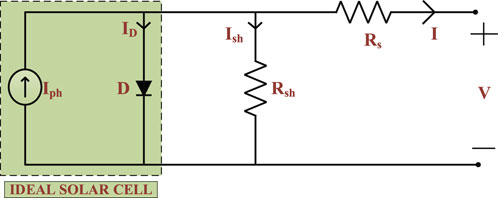
2.1 Single diode model

The Single Diode Model (SDM) serves as a mathematical representation of a solar PV cell’s behavior, enabling the prediction of its performance under different conditions like temperature, irradiance, and bias voltage. This model is grounded in the fundamental principles of photovoltaics and considers factors such as internal resistance, recombination losses, and the diode ideality factor. Figure 1 illustrates the equivalent circuit diagram of the SDM.

FIGURE 1

FIGURE 1. Equivalent circuit of SDM for a PV cell.

The SDM is defined by a series of equations that describe the current-voltage (I-V) characteristics of a solar PV cell. The current through the cell is determined by the Shockley diode equation, encompassing recombination-induced current, saturation current, and photocurrent. The cell’s voltage is calculated using Ohm’s law, accounting for the internal resistance.

Crucially, the SDM allows the prediction of essential parameters such as open-circuit voltage, short-circuit current, and maximum output power of a solar PV cell. Additionally, it facilitates the evaluation of the cell’s efficiency across diverse operating conditions like temperature, irradiance, and bias voltage. Despite its simplicity, the Single Diode Model proves to be a valuable tool, providing reasonably accurate predictions of a solar PV cell’s performance. However, it does not take into account some of the complexities of a real solar PV cell, such as the non-uniformity of the cell and the recombination losses at the contacts. More complex models, such as the two-diode model, can be used to account for these complexities and provide more accurate predictions of the performance of a solar PV cell.

In the absence of irradiation from the sun, the PV-cell, which is constructed by mixing p-type and other n-type material, performs the same function as a normal P-N junction diode, the characteristics of which are indicated by Shockley Eq. 1 (Shockley, 1949).

${\mathit{I}}_{\mathit{D}}={\mathit{I}}_{\mathit{S}}\left({\mathit{e}}^{\frac{{\mathit{V}}_{\mathit{D}}}{\mathit{n}{\mathit{V}}_{\mathit{T}}}}-\mathbf{1}\right)(1)$

The single diode model (SDM) incorporates both series resistance (R_s) and shunt resistance (R_sh) to accommodate non-idealities within photovoltaic cells. The single diode captures the diffusion of charge carriers, while R_s represents losses caused by the semiconductor material’s bulk resistance and resistance from connecting wires and metals. Conversely, R_sh addresses leakage current in the p-n junction, leading to power losses primarily caused by manufacturing defects (Vankadara et al., 2022).

The KCL notation for the I_ph, I_D, and I_sh components of a PV cell’s SDM output current, I, is as follows:

$\mathit{I}={\mathit{I}}_{\mathit{p}\mathit{h}}-{\mathit{I}}_{\mathit{D}}-{\mathit{I}}_{\mathit{s}\mathit{h}}(2)$

And applying KVL;

${\mathit{I}}_{\mathit{s}\mathit{h}}=\frac{\mathit{V}+\mathit{I}{\mathit{R}}_{\mathit{s}}}{{\mathit{R}}_{\mathit{s}\mathit{h}}}(3)$

The statement of the relationship between the output current and output voltage of the SDM, by putting Eq. 1 and Eq. 3 in Eq. 2, may be expressed as follows:

$\mathit{I}={\mathit{I}}_{\mathit{p}\mathit{h}}-{\mathit{I}}_{\mathit{S}}\left({\mathit{e}}^{\frac{\mathit{V}+\mathit{I}{\mathit{R}}_{\mathit{s}}}{\mathit{n}{\mathit{V}}_{\mathit{T}}}}-\mathbf{1}\right)-\frac{\mathit{V}+\mathit{I}{\mathit{R}}_{\mathit{s}}}{{\mathit{R}}_{\mathit{s}\mathit{h}}}(4)$

It is possible to see from Eq. 4 that there are five unidentified parameters (I_ph, I_s, n, R_s, and R_sh) that must be determined for the current-voltage characteristics.

${\mathit{V}}_{\mathit{T}}=\frac{\mathit{k}\mathit{T}}{\mathit{q}}(5)$

where, k = 1.380649 * 10–23 J/K is a Boltzmann constant (NIST, 2018) and q = 1.602176634 * 10–19°C is the charge of an electron. T is the temperature in kelvin, I_ph is the photogenerated current, I_D is the diode current, V_D is the voltage across the diode, I_S is the diode saturation current, V_T is the junction thermal voltage, R_s and R_sh are the series and shunt resistance, respectively, and the ideality factor is represented by n.

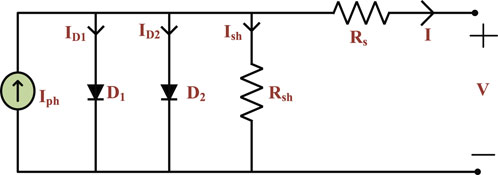
2.2 Double diode model

The DDM is a more complex mathematical representation of the behavior of a solar PV cell compared to the SDM and it requires more parameters to be fitted. However, it pro-vides more accurate predictions of the performance of a solar PV cell, especially when the cell has non-uniformities or recombination losses at the contacts, which can affect its performance. The DDM is based on the basic ideas of photovoltaics and is an augmentation of the SDM. The DDM is represented by a set of equations that describe the I-V characteristics of a solar PV cell. The equation for the current through the cell is given by two Shock-ley diode equations, one for the front and one for the back of the cell. The voltage across the cell is given by the Ohm’s law, which takes into account the internal resistance of the cell. Estimating the maximum power output of a solar PV cell, as well as its open-circuit volt-age and short-circuit current, may be done with the help of the DDM. It can also be used to determine the efficiency of a solar PV cell under different operating conditions. The equivalent circuit diagram of SDM is shown in Figure 2.

FIGURE 2

FIGURE 2. Equivalent circuit of DDM for a PV cell.

It's worth noting that when it comes to the modelling of PV systems, a more sophisticated model like the DDM can provide more accurate results than the SDM. However, it also requires more data and a more complex fitting procedure.

Using KCL, one can express the output current (I) of an ideal PV cell as the following in terms of I_ph, I_sh, I_D1, and I_D2 as follows:

$\mathit{I}={\mathit{I}}_{\mathit{p}\mathit{h}}-{\mathit{I}}_{\mathit{D}\mathbf{1}}-{\mathit{I}}_{\mathit{D}\mathbf{2}}-{\mathit{I}}_{\mathit{s}\mathit{h}}(6)$

The two diode currents (I_D1 and I_D2) may be represented as follows using Shockley Eq. 1:

${\mathit{I}}_{\mathit{D}\mathbf{1}}={\mathit{I}}_{\mathit{S}\mathbf{1}}\left({\mathit{e}}^{\frac{\mathit{V}+\mathit{I}{\mathit{R}}_{\mathit{s}}}{{\mathit{n}}_{\mathbf{1}}{\mathit{V}}_{\mathit{T}}}}-\mathbf{1}\right)(7)$

${\mathit{I}}_{\mathit{D}\mathbf{2}}={\mathit{I}}_{\mathit{S}\mathbf{2}}\left({\mathit{e}}^{\frac{\mathit{V}+\mathit{I}{\mathit{R}}_{\mathit{s}}}{{\mathit{n}}_{\mathbf{2}}{\mathit{V}}_{\mathit{T}}}}-\mathbf{1}\right)(8)$

where I_s1 and I_s2 are the currents that reach saturation in the opposite direction during the diffusion and recombination processes, respectively. The ideality factors of recombination and diffusion diodes, respectively, are denoted by the integers n₁ and n₂, which are both whole numbers. By inserting Eq. 7 and Eq. 8 into Eq. 6, one can derive the following expression for the relationship between the SDM’s output current and output voltage:

$\mathit{I}={\mathit{I}}_{\mathit{p}\mathit{h}}-{\mathit{I}}_{\mathit{S}\mathbf{1}}\left({\mathit{e}}^{\frac{\mathit{V}+\mathit{I}{\mathit{R}}_{\mathit{s}}}{{\mathit{n}}_{\mathbf{1}}{\mathit{V}}_{\mathit{T}}}}-\mathbf{1}\right)-{\mathit{I}}_{\mathit{S}\mathbf{2}}\left({\mathit{e}}^{\frac{\mathit{V}+\mathit{I}{\mathit{R}}_{\mathit{s}}}{{\mathit{n}}_{\mathbf{2}}{\mathit{V}}_{\mathit{T}}}}-\mathbf{1}\right)-\frac{\mathit{V}+\mathit{I}{\mathit{R}}_{\mathit{s}}}{{\mathit{R}}_{\mathit{s}\mathit{h}}}(9)$

It is clear from Eq. 9 that there are 7 unknown parameters for the current-voltage characteristics that need to be estimated: I_ph, I_s1, I_s2, n₁, n_2, R_s, and R_sh.

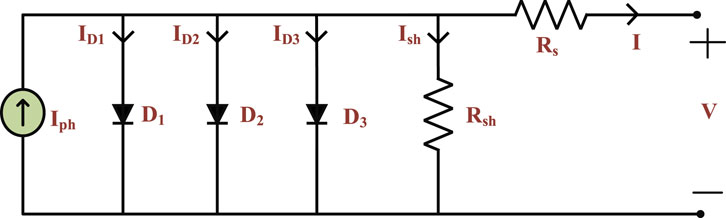
2.3 Three diode model

The TDM is an even more advanced mathematical representation of the behaviour of a so-lar PV cell, compared to the SDM and DDM. It provides the most accurate predictions of the performance of a solar PV cell, especially when the cell has non-uniformities or re-combination losses at the contacts and in the bulk of the cell. This model provides a more detailed and accurate representation of the PV cell behaviour under different operating circumstances.

The TDM is represented by a set of equations that describe the I-V characteristics of a solar PV cell. The equation for the current through the cell is given by three Shockley diode equations, one for the front and one for the back of the cell and one for the bulk recombination. The voltage across the cell is given by the Ohm’s law, which takes into account the internal resistance of the cell. The TDM can be used to determine the maximum power output of a solar PV cell, the short-circuit current and the open-circuit voltage. This model is mostly used in research and development of PV cells and module, and it's less common in real-world applications where the single or double diode models are more commonly used (Khanna et al., 2015). The equivalent circuit diagram of SDM is shown in Figure 3.

FIGURE 3

FIGURE 3. Equivalent circuit of TDM for a PV cell.

Using Kirchhoff’s Current Law, the output current ($\left.\mathit{I}\right)$ can be determined as:

$\mathit{I}={\mathit{I}}_{\mathit{p}\mathit{h}}-{\mathit{I}}_{\mathit{D}\mathbf{1}}-{\mathit{I}}_{\mathit{D}\mathbf{2}}-{\mathit{I}}_{\mathit{D}\mathbf{3}}-{\mathit{I}}_{\mathit{s}\mathit{h}}(10)$

The relationship between the output current and voltage of the SDM may be expressed as follows usingEqs 1, 7, 8:

$\mathit{I}={\mathit{I}}_{\mathit{p}\mathit{h}}-{\mathit{I}}_{\mathit{s}\mathbf{1}}\left[\mathit{exp}\left(\frac{\mathit{V}+\mathit{I}{\mathit{R}}_{\mathit{S}}}{{\mathit{n}}_{\mathbf{1}}{\mathit{V}}_{\mathit{T}}}\right)-\mathbf{1}\right]-{\mathit{I}}_{\mathit{s}\mathbf{2}}\left[\mathit{exp}\left(\frac{\mathit{V}+\mathit{I}{\mathit{R}}_{\mathit{S}}}{{\mathit{n}}_{\mathbf{2}}{\mathit{V}}_{\mathit{T}}}\right)-\mathbf{1}\right]-{\mathit{I}}_{\mathit{s}\mathbf{3}}\left[\mathit{exp}\left(\frac{\mathit{V}+\mathit{I}{\mathit{R}}_{\mathit{S}}}{{\mathit{n}}_{\mathbf{3}}{\mathit{V}}_{\mathit{T}}}\right)-\mathbf{1}\right]-\frac{\mathit{V}+\mathit{I}{\mathit{R}}_{\mathit{s}\mathit{h}}}{{\mathit{R}}_{\mathit{s}\mathit{h}}}(11)$

where I_s1, I_s2, and I_s3 are the reverse saturation currents, and the ideality factors of the diodes D₁, D₂, and D₃ are, respectively, n₁, n₂, and n₃. Using Eq. 11, the nine unknown parameters of the solar cell model with three diodes are R_s, R_sh, I_s1, I_s2, I_s3, n₁, n₂, and n₃ and I_ph are supposed to be found in order to bring the characteristics of the solar cell closer to those of the actual one.

3 Problem formulation

The objective of the parameter extraction problem in solar photovoltaics is to identify unidentified model parameters that precisely predict the system performance. This is accomplished by converting the task into an optimization problem, where the goal is to reduce the discrepancy between predicted and actual data. The error functions for the SDM, DDM, and TDM are presented in Eqs 12–14, and the goal is to minimize these error functions to a near zero value.

$\mathit{J}\left(\mathit{V},\mathit{I},\mathit{x}\right)={\mathit{I}}_{\mathit{p}\mathit{h}}-{\mathit{I}}_{\mathit{S}}\left({\mathit{e}}^{\frac{\mathit{V}+\mathit{I}{\mathit{R}}_{\mathit{s}}}{\mathit{n}{\mathit{V}}_{\mathit{T}}}}-\mathbf{1}\right)-\frac{\mathit{V}+\mathit{I}{\mathit{R}}_{\mathit{s}}}{{\mathit{R}}_{\mathit{s}\mathit{h}}}-\mathit{I}(12)$

$\mathit{J}\left(\mathit{V},\mathit{I},\mathit{x}\right)={\mathit{I}}_{\mathit{p}\mathit{h}}-{\mathit{I}}_{\mathit{S}\mathbf{1}}\left({\mathit{e}}^{\frac{\mathit{V}+\mathit{I}{\mathit{R}}_{\mathit{s}}}{{\mathit{n}}_{\mathbf{1}}{\mathit{V}}_{\mathit{T}}}}-\mathbf{1}\right)-{\mathit{I}}_{\mathit{S}\mathbf{2}}\left({\mathit{e}}^{\frac{\mathit{V}+\mathit{I}{\mathit{R}}_{\mathit{s}}}{{\mathit{n}}_{\mathbf{2}}{\mathit{V}}_{\mathit{T}}}}-\mathbf{1}\right)-\frac{\mathit{V}+\mathit{I}{\mathit{R}}_{\mathit{s}}}{{\mathit{R}}_{\mathit{s}\mathit{h}}}-\mathit{I}(13)$

$\mathit{J}\left(\mathit{V},\mathit{I},\mathit{x}\right)={\mathit{I}}_{\mathit{p}\mathit{h}}-{\mathit{I}}_{\mathit{s}\mathbf{1}}\left[{\mathit{e}}^{\frac{\mathit{V}+\mathit{I}{\mathit{R}}_{\mathit{s}}}{{\mathit{n}}_{\mathbf{1}}{\mathit{V}}_{\mathit{T}}}}-\mathbf{1}\right]-{\mathit{I}}_{\mathit{s}\mathbf{2}}\left[{\mathit{e}}^{\frac{\mathit{V}+\mathit{I}{\mathit{R}}_{\mathit{s}}}{{\mathit{n}}_{\mathbf{2}}{\mathit{V}}_{\mathit{T}}}}-\mathbf{1}\right]-{\mathit{I}}_{\mathit{s}\mathbf{3}}\left[{\mathit{e}}^{\frac{\mathit{V}+\mathit{I}{\mathit{R}}_{\mathit{s}}}{{\mathit{n}}_{\mathbf{3}}{\mathit{V}}_{\mathit{T}}}}-\mathbf{1}\right]-\frac{\mathit{V}+\mathit{I}{\mathit{R}}_{\mathit{s}\mathit{h}}}{{\mathit{R}}_{\mathit{s}\mathit{h}}}-\mathit{I}(14)$

Existence of the solution vector ‘x' is a fundamental requirement for all optimization techniques. The second requirement is the search range, as shown in Table 1. The third requirement is the objective function, whose final form is shown in Eq. 15,

$\mathit{O}\mathit{b}\mathit{j}\mathit{e}\mathit{c}\mathit{t}\mathit{i}\mathit{v}\mathit{e}\mathit{F}\mathit{u}\mathit{n}\mathit{c}\mathit{t}\mathit{i}\mathit{o}\mathit{n}=\sqrt{\frac{\mathbf{1}}{\mathit{N}}{\displaystyle \sum _{\mathit{i}=\mathbf{1}}^{\mathit{N}}}{\mathit{J}\left(\mathit{V},\mathit{I},\mathit{x}\right)}^{\mathbf{2}}}(15)$

TABLE 1

TABLE 1. Vector of solutions for models.

The number of data points that were measured is represented by N. Once the steps or the error tolerance has reached the predetermined value, iteration ends. The objective function chosen in this case has been rated as RMSE in several published literature.

The typical RMSE formula, which also evaluates the objective function, is as follows:

$\mathit{R}\mathit{M}\mathit{S}\mathit{E}\left(\mathit{c}\mathit{o}\mathit{n}\mathit{v}\mathit{e}\mathit{n}\mathit{t}\mathit{i}\mathit{o}\mathit{n}\mathit{a}\mathit{l}\right)=\sqrt{\frac{\mathbf{1}}{\mathit{N}}{\displaystyle \sum _{\mathit{i}=\mathbf{1}}^{\mathit{N}}}{\mathit{J}\left(\mathit{V},\mathit{I},\mathit{x}\right)}^{\mathbf{2}}}(16)$

The RMSE function may be expressed by pseudo-substituting Eq. 12 in Eq. 16 and V= V_exp and I= I_exp as:

$\mathit{R}\mathit{M}\mathit{S}\mathit{E}=\sqrt{\frac{\mathbf{1}}{\mathit{N}}{\displaystyle \sum _{\mathit{i}=\mathbf{1}}^{\mathit{N}}}{\left({\mathit{I}}_{\mathit{p}\mathit{h}}-{\mathit{I}}_{\mathit{S}}\left({\mathit{e}}^{\frac{{\mathit{V}}_{\mathit{exp}}+{\mathit{V}}_{\mathit{exp}}{\mathit{R}}_{\mathit{s}}}{\mathit{n}{\mathit{V}}_{\mathit{T}}}}-\mathbf{1}\right)-\frac{{\mathit{V}}_{\mathit{exp}}+{\mathit{I}}_{\mathit{exp}}{\mathit{R}}_{\mathit{s}}}{{\mathit{R}}_{\mathit{s}\mathit{h}}}-{\mathit{I}}_{\mathit{exp}}\right)}^{\mathbf{2}}}(17)$

The issue with this RMSE calculation is that it uses the observed or experimental current value rather than the calculated value of current, I. The precise RMSE equation employed in this study is shown in Eq. 18, where current is computed at each value of output voltage where it is observed utilising other retrieved relevant parameters.

$\mathit{R}\mathit{M}\mathit{S}\mathit{E}\left(\mathit{x}\right)=\sqrt{\frac{\mathbf{1}}{\mathit{N}}{\displaystyle \sum _{\mathit{i}=\mathbf{1}}^{\mathit{N}}}{\left({\mathit{I}}_{\mathit{i}}^{\mathit{e}\mathit{x}\mathit{p}\mathit{e}\mathit{r}\mathit{i}\mathit{m}\mathit{e}\mathit{n}\mathit{t}\mathit{a}\mathit{l}}-{\mathit{I}}_{\mathit{i}}^{\mathit{e}\mathit{s}\mathit{t}\mathit{i}\mathit{m}\mathit{a}\mathit{t}\mathit{e}\mathit{d}}\right)}^{\mathbf{2}}}(18)$

Eq. 18 makes it clear that the model’s parameters are recovered with greater accuracy the lower the RMSE value. The fitting error is calculated using the sum of each individual absolute error, as illustrated by equation:

$\mathit{S}\mathit{I}\mathit{A}\mathit{E}={\displaystyle \sum _{\mathit{i}=\mathbf{1}}^{\mathit{N}}}\left|{\mathit{I}}_{\mathit{i}}^{\mathit{e}\mathit{x}\mathit{p}\mathit{e}\mathit{r}\mathit{i}\mathit{m}\mathit{e}\mathit{n}\mathit{t}\mathit{a}\mathit{l}}-{\mathit{I}}_{\mathit{i}}^{\mathit{e}\mathit{s}\mathit{t}\mathit{i}\mathit{m}\mathit{a}\mathit{t}\mathit{e}\mathit{d}}\right|(19)$

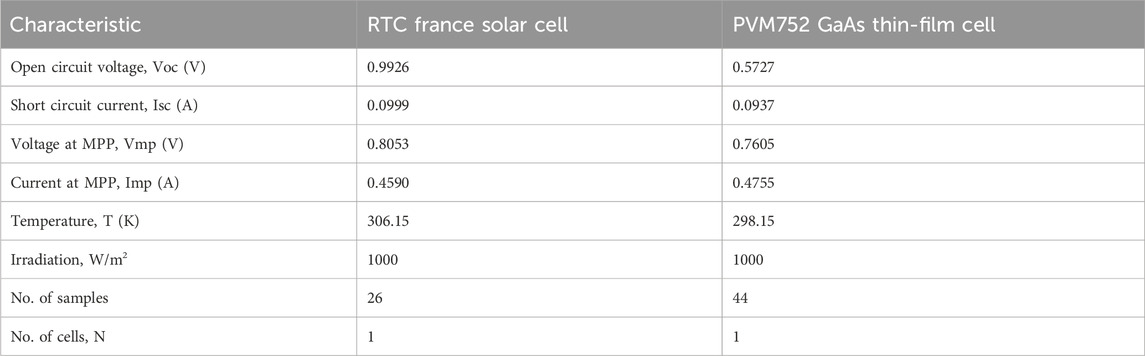
The experimental data sheet for the two types of solar cell such as, PVM752 GaAs thin film and RTC France, is sourced from (Easwarakhanthan et al., 1986; Jordehi, 2016). The purpose of this study is to compare AOA with existing optimization techniques for extracting solar photovoltaic characteristics and to verify AOA, which is a novel approach.

4 Archimedes optimisation algorithm

4.1 Basics of archimedes optimisation algorithm

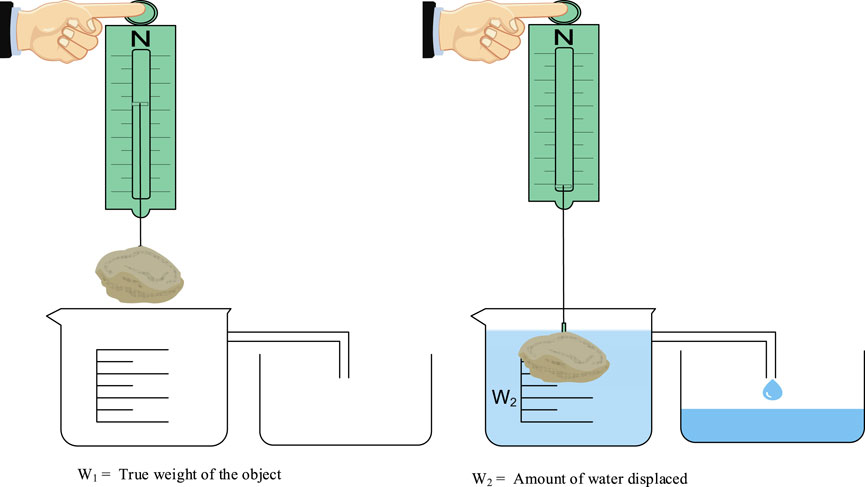
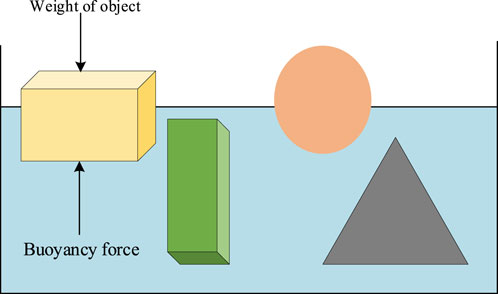
Archimedes principle describes the Archimedes Law of buoyancy. It imitates the idea of buoyant force, which is proportionate to the weight of the fluid being displaced and ap-plied to an object that is partly or entirely immersed in a fluid (water). When the weight of the liquid displaced is more than the weight of the item, the object floats, and when it is less than the weight of the liquid displaced, the object sinks. The objects which are sub-merged in the fluid are the population individual in the Archimedes Optimization algorithm (AOA). These substances possess volume, acceleration, and density, all of which contribute to an object’s buoyancy. The objective of AOA is to reach a position where the fluid net force is zero and objects remain neutrally buoyant (Hashim et al., 2021).

When an object (W1) is partially or fully immersed in a fluid, Archimedes’ principle states that the fluid exerts an upward force on the object, equivalent to the weight of the fluid displaced by the object. As illustrated in Figure 4, when an object is submerged in fluid, it experiences an upward force known as the buoyant force (W2), which is equal to the fluid it displaces.

FIGURE 4

FIGURE 4. The volume of water moved when an object is immersed in the liquid.

4.2 Mathematical modelling of archimedes optimisation algorithm

Let’s assume in the same liquid a large number of objects are submerged (Figure 5) and each one of them is aiming to achieve an equal equilibrium state. The submerged objects have distinct volumes and densities which cause distinct acceleration.

FIGURE 5

FIGURE 5. Various items submerged in same liquid.

If the weight of the object (${\mathit{W}}_{\mathit{o}\mathit{b}\mathit{j}}$) is the same as the buoyancy force (${\mathit{F}}_{\mathit{b}\mathit{y}}$) then the object will reach an equilibrium state.

$\begin{array}{c}{\mathit{F}}_{\mathit{b}\mathit{y}}={\mathit{W}}_{\mathit{o}\mathit{b}\mathit{j}}\\ {\mathit{\delta }}_{\mathit{b}\mathit{y}}{\mathit{V}}_{\mathit{b}\mathit{y}}{\mathit{A}}_{\mathit{b}\mathit{y}}={\mathit{\delta }}_{\mathit{o}\mathit{b}\mathit{j}}{\mathit{V}}_{\mathit{o}\mathit{b}\mathit{j}}{\mathit{A}}_{\mathit{o}\mathit{b}\mathit{j}}\end{array}(20)$

Where “${\mathit{\delta }}_{\mathit{b}\mathit{y}}$” denotes density, “V” denotes volume and “A” denotes acceleration or gravity. obj and by subscripts are for submerged objects and fluid, respectively.

Further Eq. 1 can be written as,

${\mathit{A}}_{\mathit{o}\mathit{b}\mathit{j}}=\frac{{\mathit{\delta }}_{\mathit{b}\mathit{y}}{\mathit{V}}_{\mathit{b}\mathit{y}}{\mathit{A}}_{\mathit{b}\mathit{y}}}{{\mathit{\delta }}_{\mathit{o}\mathit{b}\mathit{j}}{\mathit{V}}_{\mathit{o}\mathit{b}\mathit{j}}}(21)$

Suppose, the object is affected by another force, such as a contact with another nearby objects.

Then Eq. 1 will modify as,

$\begin{array}{c}{\mathit{F}}_{\mathit{b}\mathit{y}}={\mathit{W}}_{\mathit{o}\mathit{b}\mathit{j}}\\ {\mathit{W}}_{\mathit{b}\mathit{y}}-{\mathit{W}}_{\mathit{s}}={\mathit{W}}_{\mathit{o}\mathit{b}\mathit{j}}\\ {\mathit{\delta }}_{\mathit{b}\mathit{y}}{\mathit{V}}_{\mathit{b}\mathit{y}}{\mathit{A}}_{\mathit{b}\mathit{y}}-{\mathit{\delta }}_{\mathit{s}}{\mathit{v}}_{\mathit{s}}{\mathit{A}}_{\mathit{s}}={\mathit{W}}_{\mathit{o}\mathit{b}\mathit{j}}\end{array}(22)$

The AOA is one of the most modern algorithms that draws inspiration from nature and is based on Archimedes’ Law of Buoyancy, a physics principle. AOA is based on population and in this suggested method, the submerged objects are the individual population. Like all other meta-heuristics algorithms which are based on population, AOA starts the search with a random population of particles (also known as the solution of the candidate) with stochastic densities, acceleration and volumes.

The object possesses a distinct entity during this position. Object’s random position in the fluid is initialized at this instant. Next, initial fitness calculations of population fitness, AOA continues the iterations up-to the condition meets of improve termination. After every one iteration, AOA improves the object’s density and the volume.

Based on circumstances of impact with some other nearest object, the object’s acceleration is corrected. The improved acceleration, density and volume helps to find out the object’s new position.

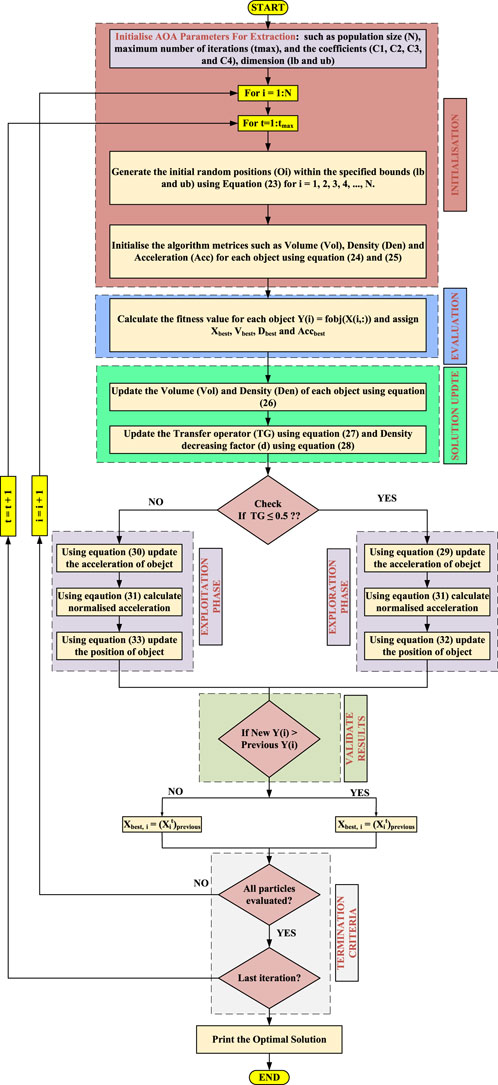
The steps of the suggested algorithm are mathematically represented as follows: STEP-1 (Initialization)

With the help of Eq. 23 each object position can be initialized.

${\mathit{O}}_{\mathit{I}}={\mathit{l}\mathit{b}}_{\mathit{I}}+\mathit{R}\mathit{a}\mathit{n}\mathit{d}\left({\mathit{u}\mathit{b}}_{\mathit{I}}-{\mathit{l}\mathit{b}}_{\mathit{I}}\right)(23)$

For $\mathit{I}=\mathbf{1,2,3,4},\dots .\mathit{N}$

Where, ${\mathit{O}}_{\mathit{I}}$ denotes ${\mathit{i}}^{\mathit{t}\mathit{h}}$ object in a population of the total number of N objects. ${\mathit{u}\mathit{b}}_{\mathit{I}}\mathit{a}\mathit{n}\mathit{d}{\mathit{l}\mathit{b}}_{\mathit{I}}$ are the search-space of upper bounds and lower bounds respectively of ${\mathit{i}}^{\mathit{t}\mathit{h}}$ object.

With the help of Eq. 24 and Eq. 25, the density $\left(\mathit{D}\mathit{e}\mathit{n}\right)$ and volume $\left(\mathit{V}\mathit{o}\mathit{l}\right)$ of every iteration of ${\mathit{i}}^{\mathit{t}\mathit{h}}$ object can be initialized.

$\begin{array}{c}{\mathit{D}\mathit{e}\mathit{n}}_{\mathit{I}}=\mathit{R}\mathit{a}\mathit{n}\mathit{d}\\ {\mathit{V}\mathit{o}\mathit{l}}_{\mathit{I}}=\mathit{R}\mathit{a}\mathit{n}\mathit{d}\end{array}(24)$

Where, $\mathit{R}\mathit{a}\mathit{n}\mathit{d}$ is a D dimensional vector which generates a random number in the middle of $\left[\mathbf{0},\mathbf{1}\right]$.

Lastly, with the help of Eq. 25 the acceleration (Acc) of ${\mathit{i}}^{\mathit{t}\mathit{h}}\mathit{o}\mathit{b}\mathit{j}\mathit{e}\mathit{c}\mathit{t}$ can be initialised as,

${\mathit{A}\mathit{c}\mathit{c}}_{\mathit{I}}={\mathit{l}\mathit{b}}_{\mathit{I}}+\mathit{R}\mathit{a}\mathit{n}\mathit{d}\times \left({\mathit{u}\mathit{b}}_{\mathit{I}}-{\mathit{l}\mathit{b}}_{\mathit{I}}\right)(25)$

In this initialization step, the value of the best fitness object is picked and allotted as ${\mathit{A}\mathit{c}\mathit{c}}_{\mathit{b}\mathit{e}\mathit{s}\mathit{t}},{\mathit{D}\mathit{e}\mathit{n}}_{\mathit{b}\mathit{e}\mathit{s}\mathit{t}},{\mathit{X}}_{\mathit{b}\mathit{e}\mathit{s}\mathit{t}}\mathit{a}\mathit{n}\mathit{d}{\mathit{V}\mathit{o}\mathit{l}}_{\mathit{b}\mathit{e}\mathit{s}\mathit{t}}$.

STEP-2 (Update Volumes and Densities)

The volume and density of ${\mathit{i}}^{\mathit{t}\mathit{h}}$ object for t+ $\mathbf{1}$ iterations is improved using Eq. 26.

$\begin{array}{c}{\mathit{D}\mathit{e}\mathit{n}}_{\mathit{I}}^{\mathit{t}+\mathbf{1}}={\mathit{D}\mathit{e}\mathit{n}}_{\mathit{I}}^{\mathit{t}}+\mathit{R}\mathit{a}\mathit{n}\mathit{d}\times \left({\mathit{D}\mathit{e}\mathit{n}}_{\mathit{b}\mathit{e}\mathit{s}\mathit{t}}-{\mathit{D}\mathit{e}\mathit{n}}_{\mathit{I}}^{\mathit{t}}\right)\\ {\mathit{V}\mathit{o}\mathit{l}}_{\mathit{I}}^{\mathit{t}+\mathbf{1}}={\mathit{V}\mathit{o}\mathit{l}}_{\mathit{I}}^{\mathit{t}}+\mathit{R}\mathit{a}\mathit{n}\mathit{d}\times \left({\mathit{V}\mathit{o}\mathit{l}}_{\mathit{b}\mathit{e}\mathit{s}\mathit{t}}-{\mathit{V}\mathit{o}\mathit{l}}_{\mathit{I}}^{\mathit{t}}\right)\end{array}(26)$

Where, ${\mathit{D}\mathit{e}\mathit{n}}_{\mathit{b}\mathit{e}\mathit{s}\mathit{t}}$ and ${\mathit{V}\mathit{o}\mathit{l}}_{\mathit{b}\mathit{e}\mathit{s}\mathit{t}}$ denote density and volume related with the best object notice up to this point and $\mathit{R}\mathit{a}\mathit{n}\mathit{d}$ is an arbitrarily generated number.

STEP-3 (Density Factor and Transfer Operator)

At first, there are collisions with nearby items, but over time, the objects work to reach an equilibrium condition. In AOA, the Transfer Operator (TG), which transforms inquiries between exploration and exploitation, can be utilised to do this.

$\mathit{T}\mathit{G}=\mathit{exp}\left[\frac{{\mathit{t}}_{\mathit{n}}-{\mathit{t}}_{\mathit{Max}}}{{\mathit{t}}_{\mathit{Max}}}\right](27)$

where, Transfer Operator (TG) moderately increases with the time till reaching 1. t_n and t_Max denote number of iterations and maximum iterations respectively. Similarly, using density decreasing factor(d), the AOA is a betted on global search to local search.

With the help of Eq. 28, it reduces with time

${\mathit{d}}^{\mathit{t}+\mathbf{1}}=\mathit{exp}\left(\frac{{\mathit{t}}_{\mathit{Max}}-{\mathit{t}}_{\mathit{n}}}{{\mathit{t}}_{\mathit{Max}}}\right)-\left(\frac{{\mathit{t}}_{\mathit{n}}}{{\mathit{t}}_{\mathit{Max}}}\right)(28)$

${\mathit{d}}_{\mathit{t}+\mathbf{1}}$ reduces over time, causing it to converge in a predefined acceptable zone. It is important to remember that precise control of this parameter will assure a good balance between exploration and exploitation.

STEP-4.1 (Occurrence of collision between adjacent objects, i.e., exploration phase)

If TG is less than or equal to value 0.5 (TG ≤ 0.5) collision between adjacent objects occurs. Choose a random material (rm) and by taking help of Eq. 29, the acceleration of each object for t+1 iteration can be improved.

${\mathit{A}\mathit{c}\mathit{c}}_{\mathit{I}}^{\mathit{t}+\mathbf{1}}=\frac{{\mathit{D}\mathit{e}\mathit{n}}_{\mathit{r}\mathit{m}}+{\mathit{V}\mathit{o}\mathit{l}}_{\mathit{r}\mathit{m}}\times {\mathit{A}\mathit{c}\mathit{c}}_{\mathit{r}\mathit{m}}}{{\mathit{D}\mathit{e}\mathit{n}}_{\mathit{I}}^{\mathit{t}+\mathbf{1}}\times {\mathit{V}\mathit{o}\mathit{l}}_{\mathit{I}}^{\mathit{t}+\mathbf{1}}}(29)$

Where ${\mathit{A}\mathit{c}\mathit{c}}_{\mathit{I}}$, ${\mathit{D}\mathit{e}\mathit{n}}_{\mathit{I}}$ and ${\mathit{V}\mathit{o}\mathit{l}}_{\mathit{I}}$ are acceleration, density and volume of ${\mathit{i}}^{\mathit{t}\mathit{h}}$ object. Whereas ${\mathit{D}\mathit{e}\mathit{n}}_{\mathit{r}\mathit{m}}$, ${\mathit{V}\mathit{o}\mathit{l}}_{\mathit{r}\mathit{m}}$ and ${\mathit{A}\mathit{c}\mathit{c}}_{\mathit{r}\mathit{m}}$ are the density, volume and acceleration of randomly chosen material. It’s worth remembering that Transfer Operator $\left(\mathit{T}\mathit{G}\le \mathbf{0.5}\right)$ assures exploration for one-third of iterations. The behavior of exploration and exploitation can be altered when a value other than 0.5 is used.

STEP-4.2 (Occurrence of no collision between adjacent objects, i.e., exploitation phase)

If Transfer Operator (TG) is greater than the value 0.5 (TG > 0.5), there is no collision with neighboring objects. In this case acceleration of each object for t+1 iteration is improved using Eq. 30.

${\mathit{A}\mathit{c}\mathit{c}}_{\mathit{I}}^{\mathit{t}+\mathbf{1}}=\frac{{\mathit{D}\mathit{e}\mathit{n}}_{\mathit{b}\mathit{e}\mathit{s}\mathit{t}}+{\mathit{V}\mathit{o}\mathit{l}}_{\mathit{b}\mathit{e}\mathit{s}\mathit{t}}\times {\mathit{A}\mathit{c}\mathit{c}}_{\mathit{b}\mathit{e}\mathit{s}\mathit{t}}}{{\mathit{D}\mathit{e}\mathit{n}}_{\mathit{I}}^{\mathit{t}+\mathbf{1}}\times {\mathit{V}\mathit{o}\mathit{l}}_{\mathit{I}}^{\mathit{t}+\mathbf{1}}}(30)$

Here, ${\mathit{A}\mathit{c}\mathit{c}}_{\mathit{b}\mathit{e}\mathit{s}\mathit{t}},{\mathit{D}\mathit{e}\mathit{n}}_{\mathit{b}\mathit{e}\mathit{s}\mathit{t}}\mathit{a}\mathit{n}\mathit{d}{\mathit{V}\mathit{o}\mathit{l}}_{\mathit{b}\mathit{e}\mathit{s}\mathit{t}}$ are the acceleration, density and volume of the best object.

STEP- 4.3 (Normalization of Acceleration)

Using Eq. 31 acceleration can be normalized to determine percentage of change.

${\mathit{A}\mathit{c}\mathit{c}}_{\mathit{i}-\mathit{n}\mathit{o}\mathit{r}\mathit{m}}^{\mathit{t}+\mathbf{1}}=\frac{\mathit{u}\times {\mathit{A}\mathit{c}\mathit{c}}_{\mathit{I}}^{\mathit{t}+\mathbf{1}}-{\mathit{A}\mathit{c}\mathit{c}}_{\mathit{min}}}{{\mathit{A}\mathit{c}\mathit{c}}_{\mathit{max}}-{\mathit{A}\mathit{c}\mathit{c}}_{\mathit{min}}}(31)$

where, the normalization ranges u and l are fixed at 0.9 and 0.1, respectively.

The percentage of steps that each agent will alter is specified by ${\mathit{A}\mathit{c}\mathit{c}}_{\mathit{i}-\mathit{n}\mathit{o}\mathit{r}\mathit{m}}^{\mathit{t}+\mathbf{1}}$. The value of acceleration will be high when object i is distant from the global optimum representing that it is in the exploration phase rather than exploitation phase. This depicts the transition from exploration to exploitation in the search process. In a typical case, the acceleration factor starts off large and gradually decreases. This supports search agents in straying from local solutions and heading for the best global solution. It's important to keep in mind that the same search agent can take longer than normal. As a consequence, AOA achieves stability between exploration and extraction.

STEP-5 (Position Update)

Considering the exploration phase, i.e., TG $\le$ 0.5, the position of ith object is updated for following t+1 iterations using Eq. 32.

${\mathit{X}}_{\mathit{I}}^{\mathit{t}+\mathbf{1}}={\mathit{X}}_{\mathit{I}}^{\mathit{t}}+{\mathit{A}\mathit{c}\mathit{c}}_{\mathit{i}-\mathit{n}\mathit{o}\mathit{r}\mathit{m}}^{\mathit{t}+\mathbf{1}}\times \mathit{R}\mathit{a}\mathit{n}\mathit{d}\times {\mathit{B}}_{\mathbf{1}}\times \mathit{d}\times \left({\mathit{X}}_{\mathit{R}\mathit{a}\mathit{n}\mathit{d}}-{\mathit{X}}_{\mathit{I}}^{\mathit{t}}\right)(32)$

Here, ${\mathit{B}}_{\mathbf{1}}$ is a constant whose value is equal to 2. Similarly, considering the Transfer Operator is greater than the value 0.5 $\left(\mathit{T}\mathit{G}>\mathbf{0.5}\right)$ i.e., exploitation phase. In this case using Eq. 33, the object updates their position for following $\mathit{t}+\mathbf{1}$ iterations.

${\mathit{X}}_{\mathit{I}}^{\mathit{t}+\mathbf{1}}={\mathit{X}}_{\mathit{b}\mathit{e}\mathit{s}\mathit{t}}^{\mathit{t}}+{\mathit{A}\mathit{c}\mathit{c}}_{\mathit{i}-\mathit{n}\mathit{o}\mathit{r}\mathit{m}}^{\mathit{t}+\mathbf{1}}\times \mathit{R}\mathit{a}\mathit{n}\mathit{d}\times \mathit{F}\times {\mathit{B}}_{\mathbf{2}}\times \mathit{d}\left(\mathit{T}\times {\mathit{X}}_{\mathit{b}\mathit{e}\mathit{s}\mathit{t}}-{\mathit{X}}_{\mathit{I}}^{\mathit{t}}\right)(33)$

Here, ${\mathit{B}}_{\mathbf{2}}$ is another constant whose value is equals to 6. can be defined with Transfer Operator relation, i.e., $\mathit{T}={\mathit{B}}_{\mathbf{3}}\times \mathit{T}\mathit{G}$. It may be inferred from this relationship that $\mathit{T}$ first deducts a certain amount from the best position before rising in the range of $\left(\mathbf{0.3}\times {\mathit{B}}_{\mathbf{3}},\mathbf{1}\right)$ over time. The random walk’s step size is huge since it starts off with a low percentage, which causes a big gap between the best and current position. This proportion steadily increases as the search goes on, closing the gap between the best and current position. A good balance between exploration and exploitation may be reached as a consequence.

Letter $\mathit{F}$ is used for flag which changes motion’s directions using Eq. 34

$\mathit{F}=\left\{\begin{array}{c}+\mathbf{1}\mathit{i}\mathit{f}\mathit{P}\le \mathbf{0.5}\\ -\mathbf{1}\mathit{i}\mathit{f}\mathit{P}>\mathbf{0.5}\end{array}\right.(34)$

Here, $\mathit{P}=\mathbf{2}\times \mathit{R}\mathit{a}\mathit{n}\mathit{d}-{\mathit{B}}_{\mathbf{4}}$

STEP-6 (Evaluation)

Using objective function $\left(\mathit{f}\right)$ to compute each object and take into account the best solution computed until now. Allocate ${\mathit{V}\mathit{o}\mathit{l}}_{\mathit{b}\mathit{e}\mathit{s}\mathit{t}}$, ${\mathit{X}}_{\mathit{b}\mathit{e}\mathit{s}\mathit{t}},{\mathit{A}\mathit{c}\mathit{c}}_{\mathit{b}\mathit{e}\mathit{s}\mathit{t}}$ and ${\mathit{D}\mathit{e}\mathit{n}}_{\mathit{b}\mathit{e}\mathit{s}\mathit{t}}$.

The flowchart for the proposed AOA for parameter extraction has been shown in Figure 6.

FIGURE 6

FIGURE 6. Flowchart of the proposed AOA for parameter extraction.

5 Simulation results

This section displays the outcomes of computations performed using a MATLAB R2018a application on an Intel(R) Core (TM) i5-10210U CPU running at 2.11 GHz and 8 GB of memory. This section tests and validates the suggested AOA approach that was utilized to extract the solar photovoltaic parameters of SDM and DDM. Using the most modern and accurate metaheuristic algorithms, the results are compared. The best (minimum), average (mean), worst (maximum), and standard deviation of the RMSE values are computed after 50 iterations of the method. Before that, SIAE and RMSE were computed for the single diode model and in particular for the RTC France solar cell based on the extracted parameters of reported 30 approaches from different published literature.

Since many writers used various methods to calculate the RMSE, practically all of the literature says that the algorithms they employed performed better than others. This leads us to the conclusion that no approach can definitively show that it is the best and most effective one to use for the extraction of unknown solar parameters. Based on the characteristics of 30 suggested methods that were taken from different published literature, the actual RMSE is determined in this study. Because of its popularity and extensive usage in published literature, the RTC France single-diode solar cell type has been employed. First, the RMSE is computed using Eq. 16, which was often used to extract parameters in significant publications published before 2019. Next, using Eq. 4, the current is computed for the appropriate voltage value, and Eq. 18 is used to get the RMSE. For all computed current values and experimental current values derived from data sheets, the innovative RMSE Eq. 18 is implemented. The estimated RMSE and the RMSE that has been reported in the literature are compared. The findings for the stated parameters of the RTC France solar cell in the different published literature are shown and contrasted in Table 2 using the traditional RMSE formula, the accurate RMSE formula, and the computed SIAE. The same experimental current-voltage (I-V) characteristics are used as the basis for all comparison techniques.

TABLE 2

TABLE 2. The results of traditional and correct RMSE and SIAE for the parameters reported for the RTC France solar cell in a variety of published sources.

Table 2 shows that there is a discrepancy between the estimated RMSE and the reported RMSE in published articles. A result mismatch might be caused by.

• A crude approximation, traditional Eq. 16, may have been used to determine RMSE. • Instead of using the lengthier form (NIST, 2018; N.I.Technology, 2023) of the value, some writers may have used the compact value of the electron charge q, q = 1.6*10⁻¹⁹ C or maybe q = 1.6021*10⁻¹⁹ C, and k = 1.38*10⁻²³ J/K or k = 1.3806*10⁻²³ J/K is the Boltzmann constant. • It's possible that some writers didn't utilize all of the I-V characteristic measurement points. For the RTC France solar cell, N = 26 samples. • It’s possible that the RMSE calculation was done incorrectly.

The SIAE plays a crucial role in providing insight into the effectiveness of the strategy. This demonstrates the comparison between the experimental value and the estimated value. The curve between experimental and predicted values fits well with the lower SIAE. Table 2 demonstrates that the performance of each method has a lower RMSE when the SIAE value is closer to 0.01 than other values. Whereas, the characteristics data for RTC France Solar cell and PVM752 GaAs has been shown in Table 3.

TABLE 3

TABLE 3. Characteristics data of RTC France Solar Cell and PVM752 GaAs.

The goal of this research is to lay a solid groundwork for future work that uses proper analysis and applies an optimization technique to the problem of determining unknown solar parameters. There is no use in comparing two approaches and asserting that one is superior if the RMSE is not calculated properly. If we just considered the RMSE number that has been previously reported in the literature, it would be easy for us to give proper credit to the AOA method we used. This, however, is inaccurate, as their method and strategy may have flaws. Therefore, we first compared the efficacy of AOA by estimating the new value of RMSE with a rigorous formula. The AOA method is tested on two types of solar modules: an RTC France silicon solar cell operating at 1000 W/m2 irradiance at 33°C temperature and a PVM752 GaAs thin-film solar cell operating at 1000 W/m2 irradiance at 25°C temperature.

5.1 Parameters of RTC france solar cell

The process of determining the parameters of a single diode model of a 57-mm-diameter silicon solar cell (RTC France) begins by applying the AOA (Archimedes Optimization algorithm). The data used for this analysis was taken from a measured data sheet (Easwarakhanthan et al., 1986) commonly used in related literature. The temperature for the analysis was 33°C, and the irradiance was 1000 W/m2. The search range for the parameters of the RTC France cell under the Single Diode Model (SDM) and Double Diode Model (DDM) is outlined in Table 4.

TABLE 4

TABLE 4. Search range of parameters of RTC France Solar cell for SDM and DDM.

The comparison of the extracted parameters of the single diode model (SDM) and the double diode model (DDM) by the AOA algorithm with those obtained using other algorithms such as Memetic Adaptive Differential Evolution (MADE) (Li et al., 2019), Time Varying Acceleration Coefficients Particle Swarm Optimization (TVACPSO) (Jordehi, 2016), Simulated Annealing (SA) (El-Naggar et al., 2012b), Tree Growth Algorithm (TGA) (Diab et al., 2020), and Artificial Bee Colony (ABC) (Diab et al., 2020) is presented in Table 5 and Table 6, respectively. To assess the accuracy of the AOA algorithm in determining the unknown parameters, the RMSE and the SIAE were calculated and compared with the published parameters obtained from other algorithms. Table 7 demonstrates the similarity between the predicted results and the experimental results.

TABLE 5

TABLE 5. Assessment of SDM (RTC France Solar Cell) parameters derived using the AOA method and other method.

TABLE 6

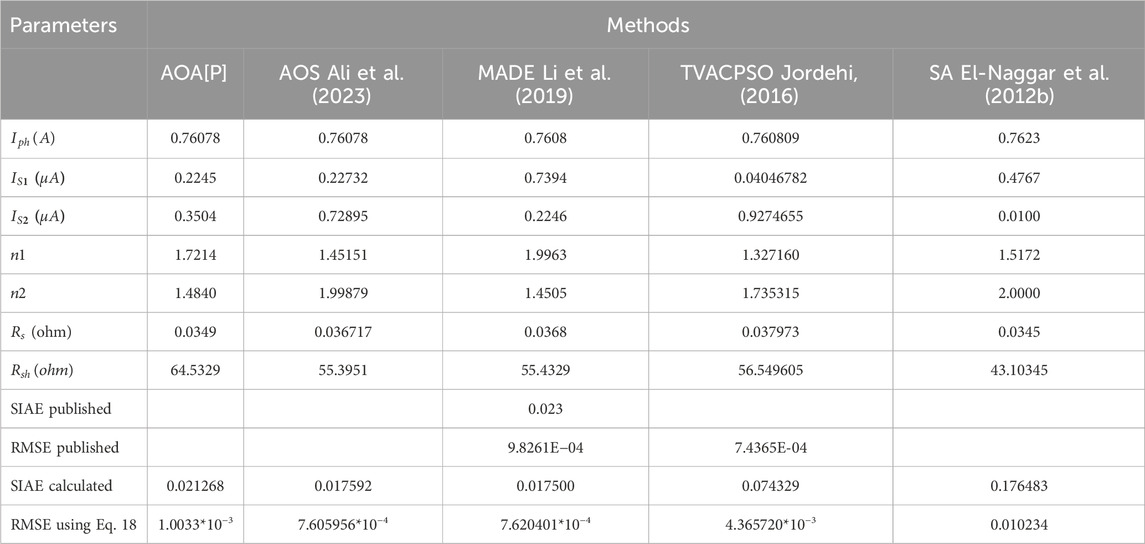
TABLE 6. Parameter extraction for DDM (RTC France Solar cell) utilizing the AOA approach compared to other methods.

TABLE 7

TABLE 7. Fitting Results for SDM and DDM of RTC France Solar cell.

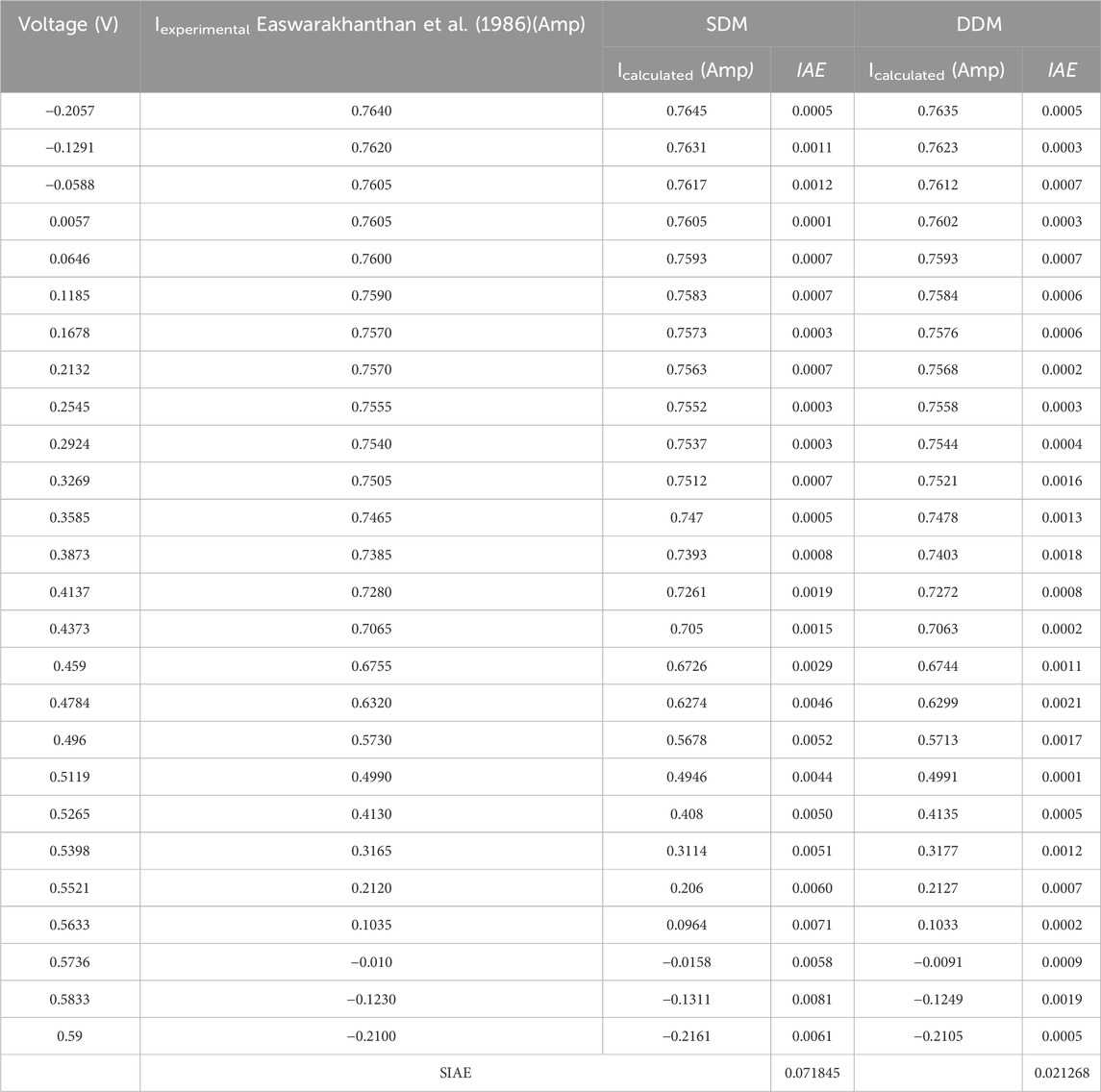
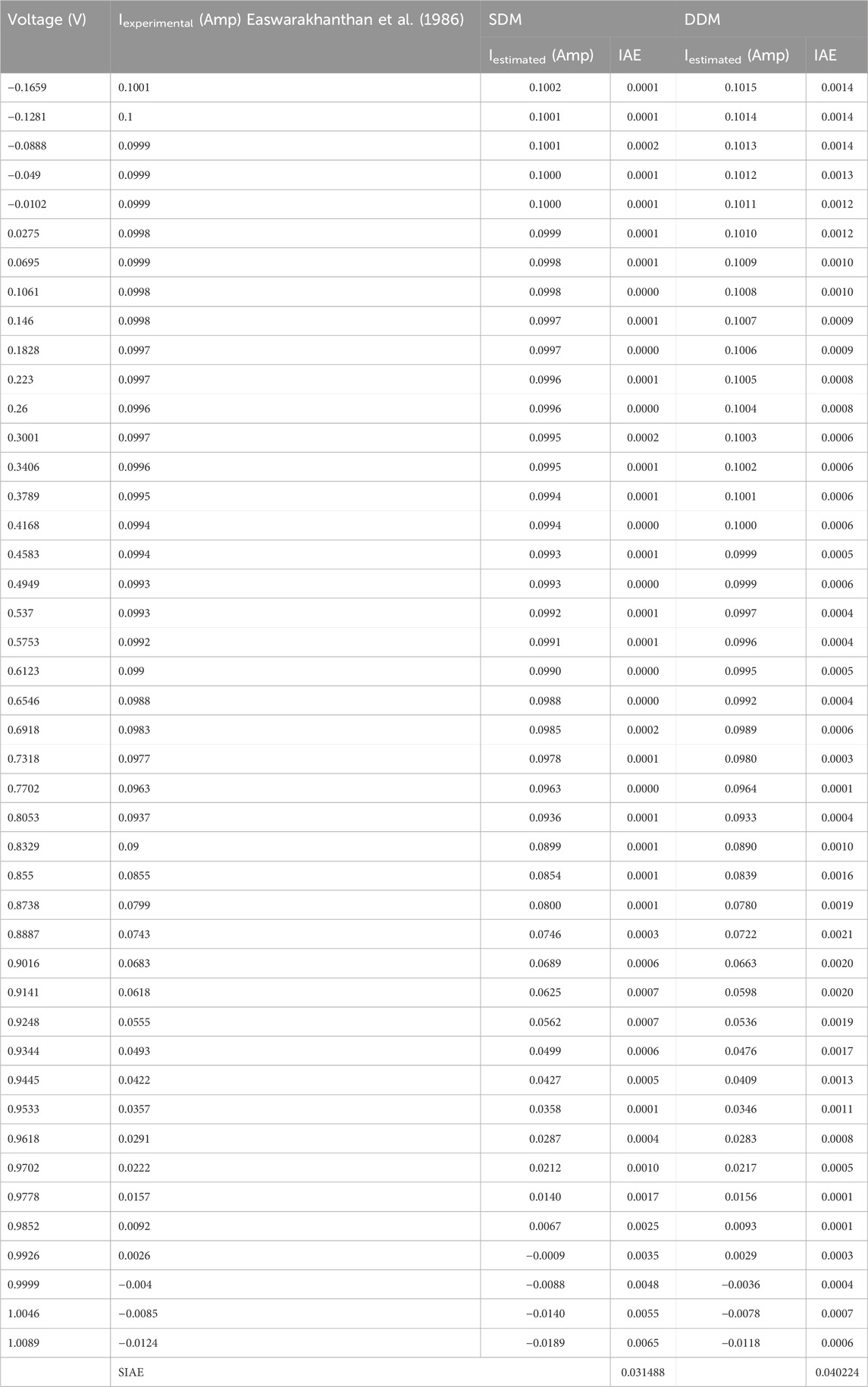
Table 7 also shows the outcomes of the SDM and DDM fittings for the RTC France solar cell. Calculated and experimental data for SDM and DDM of RTC France solar cells are used to depict I-V characteristics and compare the two sets of data. It reveals how well the theoretical outcomes correlate with the empirical findings. Individual absolute error (IAE) was used to quantify the discrepancy between the actual current in an experiment and the theoretical current that was obtained by putting in the extracted parameters. The SIAE is a metric used to evaluate the accuracy of a model by comparing the predicted values with the actual values. A lower SIAE value indicates that the model has better accuracy in predicting the behaviour of the device. All of the SDM IAE values are less than 0.00159633, and all of the DDM values are less than 0.00150183. This demonstrates the high accuracy of the derived parameters. It should have been set up such that when the model parameters are increased, the RMSE lowers from a SDM to a DDM. After comparing the results of SDM and DDM, and we discover that DDM (1.0033*10-3) provides the lowest and best RMSE value, while SDM (3.7415*10-3) provides the highest RMSE. This could be because SDM requires the extraction of just five unknown parameters, while DDM requires seven. The best and least SIAE values are provided by DDM (0.021268), while the highest SIAE values are provided by SDM (0.071845).

The SIAE value for the DDM is less than the SDM, it signifies that the DDM is a better fit for the measured data. The DDM is a more complex model that takes into account additional parameters, such as the shunt resistance, that the Single Diode Model does not con-sider. This additional complexity may allow the DDM to better capture the underlying physics of the device and provide a more accurate prediction of its behaviour. These findings demonstrate that DDM is appropriate for RTC France solar cells.

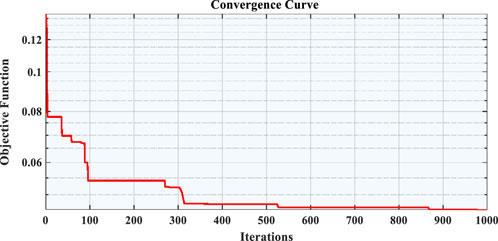
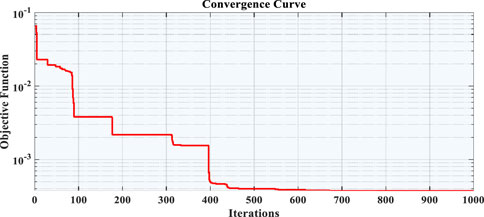
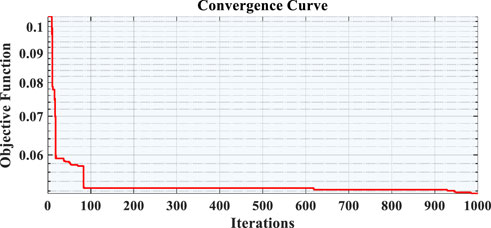
The comparison between estimated data and experimentally recorded data for SDM and DDM for the RTC France solar cell are shown in Figures 7, 8. This is done to check for consistency between experimental and predicted results. Further, the convergence curve during its best run for both model such as SDM and DDM are shown in Figures 9, 10, respectively. From figure, we can see how quickly SDM and DDM converged on their best run with the smallest RMSE. It also demonstrates that the SDM converge quickly at the start of iterations than DDM. The objective functions of SDM converge to the optimal values with little variation after 350–400 iterations whereas, the objective functions of DDM converge to the optimal values after 400 iterations.

FIGURE 7

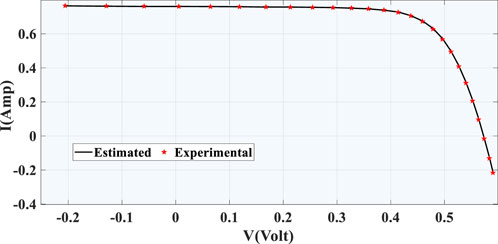
FIGURE 7. Comparison between estimated data and experimentally recorded data for SDM (RTC France solar cell).

FIGURE 8

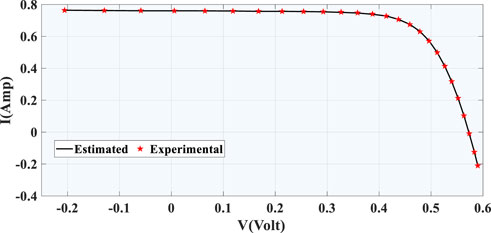
FIGURE 8. Comparison between estimated data and experimentally recorded data for DDM (RTC France solar cell).

FIGURE 9

FIGURE 9. Convergence curve of SDM for RTC France.

FIGURE 10

FIGURE 10. Convergence curve of DDM for RTC France.

5.2 Parameters of PVM752 GaAs thin film solar cell

The AOS method is used to figure out the unknown values of the PVM752 GaAs thin-film solar cell at 25°C and 1000 W/m². The PVM752 GaAs solar PV cell’s recorded data sheet, which is made up of 44 I-V measurements, is from (Jordehi, 2016). The search range for the PVM752 GaAs solar cell’s PV cell characteristics for both model SDM and DDM are shown in Table 8. The comparison of the extracted parameters of the single diode model (SDM) and the double diode model (DDM) by the AOA algorithm with those obtained using other algorithms such as to atomic orbital search (AOS) (Ali et al., 2023), Tree Growth Algorithm (TGA) (Diab et al., 2020), Coyote Optimization Algorithm (COA) (Chin and Salam, 2019) and Artificial Bee Colony (ABC) (Karaboga and Akay, 2009) are shown in Table 9 and Table 10, respectively.

TABLE 8

TABLE 8. Search range of parameters of PVM752 (Oliva et al., 2019) as thin film solar cell.

TABLE 9

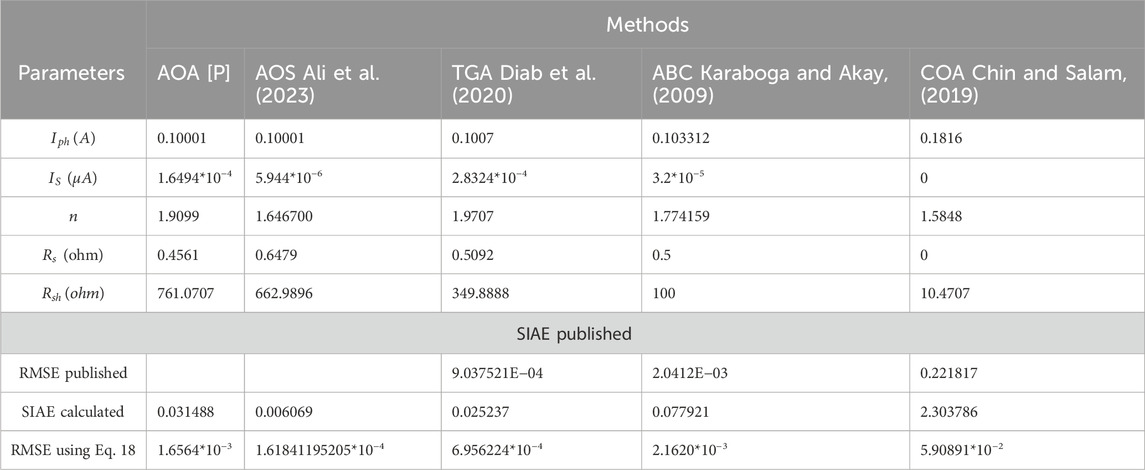
TABLE 9. Parameters derived by the AOA algorithm for SDM (PVM752 GaAs THIN FILM SOLAR CELL) for SDM compared to those extracted by other methods.

TABLE 10

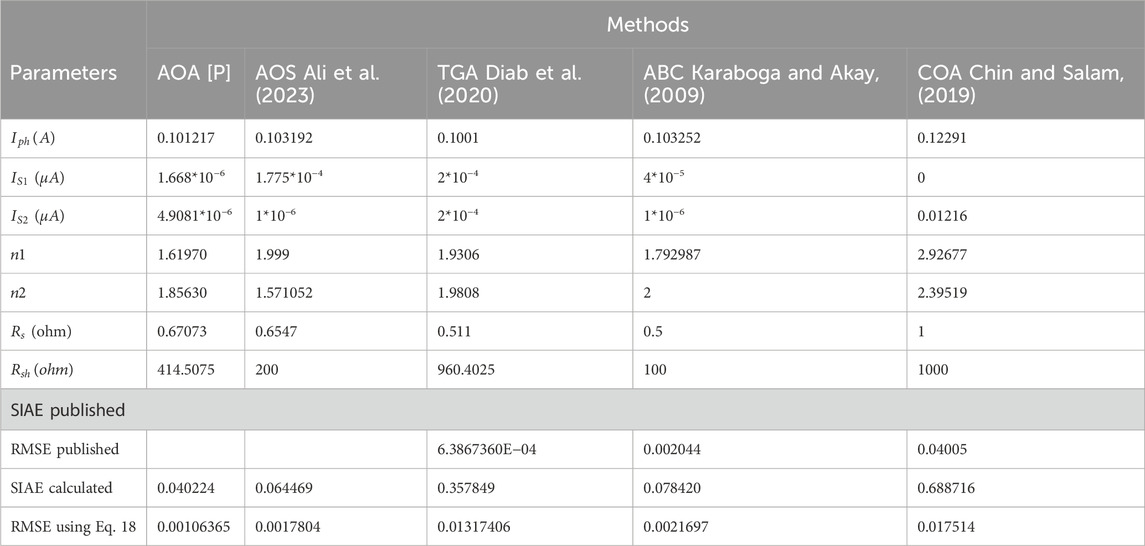
TABLE 10. DDM (PVM752 GaAs THIN FILM SOLAR CELL) parameters extraction using the AOA algorithm compared to other method.

Tables 9 and 10 show the SDM and DDM values that were taken from the PVM752 GaAs thin film solar cell. In terms of RMSE and SIAE, it is clear that the proposed algorithm AOA does better than AOS (Mirjalili and Lewis, 2016), TGA (Diab et al., 2020), ABC (Karaboga and Akay, 2009), and COA (Chin and Salam, 2019). The PVM752 GaAs thin film solar cell’s SDM results gave the best RMSE of everything that has been done so far. SDM provides the best and lowest RMSE (1.6564*10-3) for the PVM752 GaAs solar cell, whereas DDM provides the greatest RMSE (0.00106365). The SDM and DDM of the PVM752 GaAs solar cell, both measured and predicted, are compared in Figures 11, 12, respectively. The best-performing PVM GaAs solar cell SDM and DDM convergence curves are depicted in Figures 13, 14, respectively. This demonstrates that, unlike DDM, SDM’s goal function tends to decrease over time. SDM and DDM fitting results for the PVM752 GaAs thin film solar cell are also shown in Table 11. It demonstrates how well the expected and actual outcomes match up.

FIGURE 11

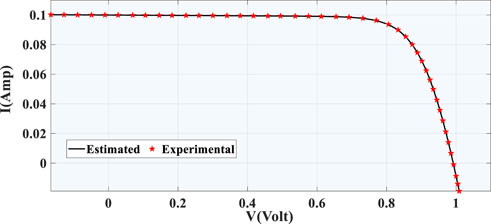
FIGURE 11. Comparison between estimated data and experimentally recorded data for SDM (PVM752 GaAs thin film solar cell).

FIGURE 12

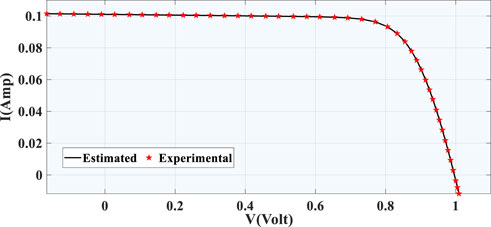
FIGURE 12. Comparison between estimated data and experimentally recorded data for DDM (PVM752 GaAs thin film solar cell).

FIGURE 13

FIGURE 13. Convergence Curve of SDM for PVM752 GaAs thin film.

FIGURE 14

FIGURE 14. Convergence Curve of DDM for PVM752 GaAs thin film.

TABLE 11

TABLE 11. Fitting results for SDM and DDM of PVM752 GaAs THIN FILM SOLAR CELL.

Using extracted numbers, one may calculate the difference between the actual and expected currents, denoted by the individual absolute error (IAE). The Standardised Intrinsic Accuracy Evaluation (SIAE) compares a model’s predicted and observed values to determine how well the model performs. The more accurately the model can anticipate the device’s behaviour, the less the SIAE value will be. The lowest SDM IAE value is 0.0002670, while the lowest DDM IAE value is 0.00358210. This demonstrates that the extracted parameters are reliable. When comparing the SIAE values, SDM (0.031488) is the best and lowest, while DDM (0.040224) is the worst. These findings support the use of SDM in the production of PVM GaAs thin-film solar cells. We may conclude that the optimisation algorithms have a more difficult time extracting data from the PVM752 GaAs thin film cell than from the RTC France solar cell. It's possible that the difference stems from the usage of 44 pairs of I-V measured data, as opposed to the 26 pairs utilised for the RTC France solar cell.

6 Conclusion

This research introduces the Archimedes optimization method (AOA) as a novel metaheuristic approach for the precise extraction of solar unknown parameters. The method is applied to both single- and double-diode variants of the RTC France solar cell and the PVM 752 GaAs thin film solar cell. The effectiveness of the Archimedes optimization method is evaluated using the RMSE value and compared with other optimization techniques. We provide a novel and precise formula for calculating RMSE for the RTC French solar cell single diode model. In our analysis, we review 30 alternative methods from diverse literature and note variations in RMSE calculation methodologies. The study emphasizes the importance of proper RMSE calculation for accurate performance evaluation and comparison of optimization algorithms. The proposed AOA, when used on RTC France solar cells, gave RMSE values of 3.7415 × 10⁻³ for the SDM and 1.0033 × 10⁻³ for the DDM. For PVM752 GaAs thin film solar cells, the RMSE values were 1.6564 × 10⁻³ and 0.00106365, respectively. The SIAE values for RTC France cells were 0.071845 for the SDM and 0.021268 for the DDM. For PVM752 GaAs thin film, the SIAE values were 0.031488 and 0.040224. Comparing AOA’s performance, we find that it outperforms state-of-the-art methods, exhibiting a smaller RMSE and superior curve fitting between recovered parameters (I-V characteristics) and experimental data. se results suggest that the AOA method has the potential to estimate unknown parameters in various modules. It can be utilized in applications of parameter extraction in photovoltaics, including performance evaluation under diverse operating conditions, design optimization for enhanced efficiency and reduced costs, and quality control in production to detect defects and variations. In the future, the scope of parameter extraction entails developing new modeling techniques, refining measurement methods, and integrating artificial intelligence and machine learning algorithms. These advancements aim to significantly enhance the accuracy and efficiency of solar parameter extraction. The research contributes to the field by introducing a robust optimization method and emphasizing the importance of rigorous RMSE calculation in solar cell parameter extraction studies.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

MTH: Conceptualization, Formal Analysis, Investigation, Methodology, Validation, Visualization, Writing–original draft. MRH: Conceptualization, Formal Analysis, Investigation, Methodology, Validation, Visualization, Writing–original draft. MT: Conceptualization, Formal Analysis, Investigation, Methodology, Supervision, Validation, Visualization, Writing–review and editing. AS: Conceptualization, Formal Analysis, Investigation, Methodology, Supervision, Validation, Visualization, Writing–review and editing. SA: Formal Analysis, Funding acquisition, Methodology, Project administration, Writing–review and editing. MP: Formal Analysis, Methodology, Visualization, Writing–review and editing. HM: Formal Analysis, Funding acquisition, Methodology, Project administration, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research has received funding from King Saud University through Researchers Supporting Project number (RSP2024R387), King Saud University, Riyadh, Saudi Arabia.

Acknowledgments

The authors extend their appreciation to King Saud University for funding this work through Researchers Supporting Project number (RSP2024R387), King Saud University, Riyadh, Saudi Arabia.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abbassi, R., Saidi, S., Urooj, S., Alhasnawi, B. N., Alawad, M. A., and Premkumar, M. (2023). An accurate metaheuristic Mountain Gazelle optimizer for parameter estimation of single- and double-diode photovoltaic cell models. Mathematics 11, 4565. doi:10.3390/math11224565

CrossRef Full Text | Google Scholar

Abdulrazzaq, A. K., Bognár, G., and Plesz, B. (2022). Accurate method for PV solar cells and modules parameters extraction using I–V curves. J. King Saud. Univ. - Eng. Sci. 34, 46–56. doi:10.1016/j.jksues.2020.07.008

CrossRef Full Text | Google Scholar

Alam, D. F., Yousri, D. A., and Eteiba, M. B. (2015). Flower pollination algorithm based solar PV parameter estimation. Energy Convers. Manag. 101, 410–422. doi:10.1016/j.enconman.2015.05.074

CrossRef Full Text | Google Scholar

AlHajri, M. F., El-Naggar, K. M., AlRashidi, M. R., and Al-Othman, A. K. (2012). Optimal extraction of solar cell parameters using pattern search. Renew. Energy 44, 238–245. doi:10.1016/j.renene.2012.01.082

CrossRef Full Text | Google Scholar

Ali, E. E., El-Hameed, M. A., El-Fergany, A. A., and El-Arini, M. M. (2016). Parameter extraction of photovoltaic generating units using multi-verse optimizer. Sustain. Energy Technol. Assessments 17, 68–76. doi:10.1016/j.seta.2016.08.004

CrossRef Full Text | Google Scholar

Ali, F., Sarwar, A., Ilahi Bakhsh, F., Ahmad, S., Ali Shah, A., and Ahmed, H. (2023). Parameter extraction of photovoltaic models using atomic orbital search algorithm on a decent basis for novel accurate RMSE calculation. Energy Convers. Manag. 2023, 116613. doi:10.1016/j.enconman.2022.116613

CrossRef Full Text | Google Scholar

Askarzadeh, A., and Rezazadeh, A. (2012). Parameter identification for solar cell models using harmony search-based algorithms. Sol. Energy 86, 3241–3249. doi:10.1016/j.solener.2012.08.018

CrossRef Full Text | Google Scholar

Cai, Z., and Gong, W. (2013). Parameter extraction of solar cell models using repaired adaptive differential evolution. Sol. Energy 94, 209–220. doi:10.1016/j.solener.2013.05.007

CrossRef Full Text | Google Scholar

Ćalasan, M., Abdel Aleem, S. H. E., and Zobaa, A. F. (2020). On the root mean square error (RMSE) calculation for parameter estimation of photovoltaic models: a novel exact analytical solution based on Lambert W function. Energy Convers. Manag. 210, 112716. doi:10.1016/j.enconman.2020.112716

CrossRef Full Text | Google Scholar

Chandrasekaran, K., Thaveedhu, A. S. R., Manoharan, P., and Periyasamy, V. (2023). Optimal estimation of parameters of the three-diode commercial solar photovoltaic model using an improved Berndt-Hall-Hall-hausman method hybridized with an Augmented Mountain Gazelle optimizer. Environ. Sci. Pollut. Res. 30, 57683–57706. doi:10.1007/s11356-023-26447-x

CrossRef Full Text | Google Scholar

Chen, X., Yu, K., Du, W., Zhao, W., and Liu, G. (2016a). Parameters identification of solar cell models using generalized oppositional teaching learning based optimization. Energy 99, 170–180. doi:10.1016/J.ENERGY.2016.01.052

CrossRef Full Text | Google Scholar

Chen, Z., Wu, L., Lin, P., Wu, Y., and Cheng, S. (2016b). Parameters identification of photovoltaic models using hybrid adaptive Nelder-Mead simplex algorithm based on eagle strategy. Appl. Energy 182, 47–57. doi:10.1016/j.apenergy.2016.08.083

CrossRef Full Text | Google Scholar

Chin, V. J., and Salam, Z. (2019). Coyote optimization algorithm for the parameter extraction of photovoltaic cells. Sol. Energy 194, 656–670. doi:10.1016/j.solener.2019.10.093

CrossRef Full Text | Google Scholar

Diab, A. A. Z., Sultan, H. M., Aljendy, R., Al-Sumaiti, A. S., Shoyama, M., and Ali, Z. M. (2020). Tree growth based optimization algorithm for parameter extraction of different models of photovoltaic cells and modules. IEEE Access 8, 119668–119687. doi:10.1109/ACCESS.2020.3005236

CrossRef Full Text | Google Scholar

Easwarakhanthan, T., Bottin, J., Bouhouch, I., and Boutrit, C. (1986). Nonlinear minimization algorithm for determining the solar cell parameters with microcomputers. Int. J. Sol. Energy 4, 1–12. doi:10.1080/01425918608909835

CrossRef Full Text | Google Scholar

El-Fergany, A. (2015). Efficient tool to characterize photovoltaic generating systems using mine blast algorithm. Electr. Power Components Syst. 43, 890–901. doi:10.1080/15325008.2015.1014579

CrossRef Full Text | Google Scholar

El-Naggar, K. M., AlRashidi, M. R., AlHajri, M. F., and Al-Othman, A. K. (2012a). Simulated annealing algorithm for photovoltaic parameters identification. Sol. Energy 86, 266–274. doi:10.1016/j.solener.2011.09.032

CrossRef Full Text | Google Scholar

El-Naggar, K. M., AlRashidi, M. R., AlHajri, M. F., and Al-Othman, A. K. (2012b). Simulated annealing algorithm for photovoltaic parameters identification. Sol. Energy 86, 266–274. doi:10.1016/J.SOLENER.2011.09.032

CrossRef Full Text | Google Scholar

Ganesh Pardhu, B. S. S., and Kota, V. R. (2021). Radial movement optimization based parameter extraction of double diode model of solar photovoltaic cell. Sol. Energy 213, 312–327. doi:10.1016/j.solener.2020.11.046

CrossRef Full Text | Google Scholar

Gao, X., Cui, Y., Hu, J., Xu, G., Wang, Z., Qu, J., et al. (2018). Parameter extraction of solar cell models using improved shuffled complex evolution algorithm. Energy Convers. Manag. 157, 460–479. doi:10.1016/j.enconman.2017.12.033

CrossRef Full Text | Google Scholar

Geem, Z. W., Kim, J. H., and Loganathan, G. V. (2001). A new heuristic optimization algorithm: harmony search. Simulation 76, 60–68. doi:10.1177/003754970107600201

CrossRef Full Text | Google Scholar

Ginidi, A. R., Shaheen, A. M., El-Sehiemy, R. A., and Elattar, E. (2021). Supply demand optimization algorithm for parameter extraction of various solar cell models. Energy Rep. 7, 5772–5794. doi:10.1016/j.egyr.2021.08.188

CrossRef Full Text | Google Scholar

Hashim, F. A., Hussain, K., Houssein, E. H., Mabrouk, M. S., and Al-Atabany, W. (2021). Archimedes optimization algorithm: a new metaheuristic algorithm for solving optimization problems. Appl. Intell. 51, 1531–1551. doi:10.1007/s10489-020-01893-z

CrossRef Full Text | Google Scholar

Holeczek, H. (2014). Renewables: global Status Report 2014. Global CCS Institute. Available at: https://www.globalccsinstitute.com/resources/publications-reports-research/the-global-status-of-ccs-2014/.

Google Scholar

Holland, J. H. (1992). Genetic algorithms. Sci. Am. 267, 66–72. doi:10.1038/scientificamerican0792-66

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, W., Jiang, C., Xue, L., and Song, D. (2011). “Extracting solar cell model parameters based on Chaos particle swarm algorithm,” in 2011 International Conference on Electric Information and Control Engineering, Wuhan, 15-17 April 2011 (IEEE), 398–402. doi:10.1109/ICEICE.2011.5777246

CrossRef Full Text | Google Scholar

Hussain, M. T., Sarwar, A., Tariq, M., Urooj, S., BaQais, A., and Hossain, M. A. (2023b). An evaluation of ANN algorithm performance for MPPT energy harvesting in solar PV systems. Sustain 15, 11144. doi:10.3390/su151411144

CrossRef Full Text | Google Scholar

Hussain, M. T., Tariq, M., Sarwar, A., Urooj, S., BaQais, A., and Hossain, M. A. (2023a). Atomic orbital search algorithm for efficient maximum power point tracking in partially shaded solar PV systems. Processes 11, 2776. doi:10.3390/pr11092776

CrossRef Full Text | Google Scholar

Jordehi, A. R. (2016). Time varying acceleration Coefficients particle swarm optimisation (TVACPSO): a new optimisation algorithm for estimating parameters of PV cells and modules. Energy Convers. Manag. 129, 262–274. doi:10.1016/j.enconman.2016.09.085

CrossRef Full Text | Google Scholar

Karaboga, D., and Akay, B. (2009). A comparative study of Artificial Bee Colony algorithm. Appl. Math. Comput. 214, 108–132. doi:10.1016/j.amc.2009.03.090

CrossRef Full Text | Google Scholar

Kataria, A., and Khan, T. I. (2021). “Necessity of paradigm shift from non-renewable sources to renewable sources for energy demand,” in Urban growth environ. Issues India (Spinger), 337–352. doi:10.1007/978-981-16-4273-9

CrossRef Full Text | Google Scholar

Khan, S. A., Ahmad, S., Sarwar, A., Tariq, M., Ahmad, J., Asim, M., et al. (2021). Chaos induced Coyote algorithm (cica) for extracting the parameters in a single, double, and three diode model of a mono-crystalline, polycrystalline, and a thin-film solar pv cell. Electron 10, 2094. doi:10.3390/electronics10172094

CrossRef Full Text | Google Scholar

Khanna, V., Das, B. K., Bisht, D., Vandana, S., and Singh, P. K. (2015). A three diode model for industrial solar cells and estimation of solar cell parameters using PSO algorithm. Renew. Energy 78, 105–113. doi:10.1016/j.renene.2014.12.072

CrossRef Full Text | Google Scholar

Kharchouf, Y., Herbazi, R., and Chahboun, A. (2022). Parameter’s extraction of solar photovoltaic models using an improved differential evolution algorithm. Energy Convers. Manag. 251, 114972. doi:10.1016/j.enconman.2021.114972

CrossRef Full Text | Google Scholar

Kirkpatrick, S., Gelatt, C. D., and Vecchi, M. P. (1983). Optimization by simulated annealing. Science 220, 671–680. doi:10.1126/science.220.4598.671

PubMed Abstract | CrossRef Full Text | Google Scholar

Kler, D., Sharma, P., Banerjee, A., Rana, K. P. S., and Kumar, V. (2017). PV cell and module efficient parameters estimation using evaporation rate based water cycle algorithm. Swarm Evol. Comput. 35, 93–110. doi:10.1016/j.swevo.2017.02.005

CrossRef Full Text | Google Scholar

Li, S., Gong, W., Yan, X., Hu, C., Bai, D., and Wang, L. (2019). Parameter estimation of photovoltaic models with memetic adaptive differential evolution. Sol. Energy 190, 465–474. doi:10.1016/j.solener.2019.08.022

CrossRef Full Text | Google Scholar

Long, W., Cai, S., Jiao, J., Xu, M., and Wu, T. (2020). A new hybrid algorithm based on Grey Wolf optimizer and cuckoo search for parameter extraction of solar photovoltaic models. Energy Convers. Manag. 203, 112243. doi:10.1016/j.enconman.2019.112243

CrossRef Full Text | Google Scholar

Ma, J., Man, K. L., Guan, S. U., Ting, T. O., and Wong, P. W. H. (2016). Parameter estimation of photovoltaic model via parallel particle swarm optimization algorithm. Int. J. Energy Res. 40, 343–352. doi:10.1002/er.3359

CrossRef Full Text | Google Scholar

Mateo Romero, H. F., González Rebollo, M. Á., Cardeñoso-Payo, V., Alonso Gómez, V., Redondo Plaza, A., Moyo, R. T., et al. (2022). Applications of artificial intelligence to photovoltaic systems: a review. Appl. Sci. 12, 10056. doi:10.3390/app121910056

CrossRef Full Text | Google Scholar

Merchaoui, M., Sakly, A., and Mimouni, M. F. (2018). Particle swarm optimisation with adaptive mutation strategy for photovoltaic solar cell/module parameter extraction. Energy Convers. Manag. 175, 151–163. doi:10.1016/j.enconman.2018.08.081

CrossRef Full Text | Google Scholar

Mercom (2022). India’s solar power generation rises by 36% YoY to 70.2 BU in 9M 2022. Mercom India. Available at: https://www.mercomindia.com/indias-solar-power-generation-rises-by-36-yoy-in-9m-2022.

Google Scholar

Mirjalili, S., and Lewis, A. (2016). The whale optimization algorithm. Adv. Eng. Softw. 95, 51–67. doi:10.1016/j.advengsoft.2016.01.008

CrossRef Full Text | Google Scholar

MNRE (2019). Annual Report ministry of new and renewable energy. Report.

Google Scholar

NIST (2018). NIST CODATA value: Boltzmann constant NIST ref. Constants, units. Uncertain. Available at: https://physics.nist.gov/cgi-bin/cuu/Value?k.

Google Scholar

N.I.Technology (2023). CODATA value: elementary charge. NIST ref. Constants, units. Uncertain. Available at: https://physics.nist.gov/cuu/Constants/.

Google Scholar

Oliva, D., Abd El Aziz, M., and Ella Hassanien, A. (2017). Parameter estimation of photovoltaic cells using an improved chaotic whale optimization algorithm. Appl. Energy 200, 141–154. doi:10.1016/j.apenergy.2017.05.029

CrossRef Full Text | Google Scholar

Oliva, D., Elaziz, M. A., Elsheikh, A. H., and Ewees, A. A. (2019). A review on meta-heuristics methods for estimating parameters of solar cells. J. Power Sources 435, 126683. doi:10.1016/j.jpowsour.2019.05.089

CrossRef Full Text | Google Scholar

Premkumar, M., Jangir, P., Ramakrishnan, C., Kumar, C., Sowmya, R., Deb, S., et al. (2022). An enhanced gradient-based optimizer for parameter estimation of various solar photovoltaic models. Energy Rep. 8, 15249–15285. doi:10.1016/j.egyr.2022.11.092

CrossRef Full Text | Google Scholar

Premkumar, M., Shankar, N., Sowmya, R., Jangir, P., Kumar, C., Abualigah, L., et al. (2023). A reliable optimization framework for parameter identification of single-diode solar photovoltaic model using weighted velocity-guided Grey Wolf optimization algorithm and Lambert-W function. IET Renew. Power Gener. 17, 2711–2732. doi:10.1049/rpg2.12792

CrossRef Full Text | Google Scholar

Price, K., and Storn, R. (1997). Differential evolution – a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 11, 341–359. doi:10.1023/a:1008202821328

CrossRef Full Text | Google Scholar

Rao, R. V., Savsani, V. J., and Vakharia, D. P. (2011). Teaching-learning-based optimization: a novel method for constrained mechanical design optimization problems. Cad. Comput. Aided Des. 43, 303–315. doi:10.1016/j.cad.2010.12.015

CrossRef Full Text | Google Scholar

Shockley, W. (1949). The theory of P-n junctions in semiconductors and P-n junction transistors. Bell Syst. Tech. J. 28, 435–489. doi:10.1002/j.1538-7305.1949.tb03645.x

CrossRef Full Text | Google Scholar

Torczon, V. (1997). On the convergence of pattern search algorithms. SIAM J. Optim. 7, 1–25. doi:10.1137/S1052623493250780

CrossRef Full Text | Google Scholar

Vankadara, S. K., Chatterjee, S., and Balachandran, P. K. (2022). An accurate analytical modeling of solar photovoltaic system considering rs and Rsh under partial shaded condition. Int. J. Syst. Assur. Eng. Manag. 13, 2472–2481. doi:10.1007/s13198-022-01658-6

CrossRef Full Text | Google Scholar

Xiong, G., Li, L., Mohamed, A. W., Yuan, X., and Zhang, J. (2021). A new method for parameter extraction of solar photovoltaic models using gaining–sharing knowledge based algorithm. Energy Rep. 7, 3286–3301. doi:10.1016/j.egyr.2021.05.030

CrossRef Full Text | Google Scholar

Xiong, G., Zhang, J., Shi, D., Zhu, L., and Yuan, X. (2020). Parameter extraction of solar photovoltaic models with an either-or teaching learning based algorithm. Energy Convers. Manag. 224, 113395. doi:10.1016/j.enconman.2020.113395

CrossRef Full Text | Google Scholar

Xiong, G., Zhang, J., Yuan, X., Shi, D., and He, Y. (2018). Application of symbiotic organisms search algorithm for parameter extraction of solar cell models. Appl. Sci. 8, 2155. doi:10.3390/app8112155

CrossRef Full Text | Google Scholar

Xu, S., and Qiu, H. (2022). A modified stochastic fractal search algorithm for parameter estimation of solar cells and PV modules. Energy Rep. 8, 1853–1866. doi:10.1016/j.egyr.2022.01.008

CrossRef Full Text | Google Scholar

Yang, X. S., and Deb, S. (2009). “Cuckoo search via lévy flights,” in 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 09-11 December 2009 (IEEE) 210–214. doi:10.1109/NABIC.2009.5393690

CrossRef Full Text | Google Scholar

Ye, M., Wang, X., and Xu, Y. (2009). Parameter extraction of solar cells using particle swarm optimization. J. Appl. Phys. 105, 82. doi:10.1063/1.3122082

CrossRef Full Text | Google Scholar

Yu, K., Liang, J. J., Qu, B. Y., Chen, X., and Wang, H. (2017). Parameters identification of photovoltaic models using an improved JAYA optimization algorithm. Energy Convers. Manag. 150, 742–753. doi:10.1016/j.enconman.2017.08.063

CrossRef Full Text | Google Scholar

Yu, K., Qu, B., Yue, C., Ge, S., Chen, X., and Liang, J. A. (2019). A performance-guided JAYA algorithm for parameters identification of photovoltaic cell and module. Appl. Energy 237, 241–257. doi:10.1016/j.apenergy.2019.01.008

CrossRef Full Text | Google Scholar