Unlocking inter-regional flexibility for the HVDC-connected two-area system with a multistage model

In recent years, the deployment of high-voltage direct current (HVDC) tie-lines in power grids has become a prevalent solution in some countries to transmit renewable energy from remote locations to load centers. However, the variability and uncertainty associated with renewable energy generation pose challenges to effectively utilizing this technology. This work proposes a novel multistage planning-operation model, aiming to unlock the potential flexibility in the HVDC transmission system and increase the renewable penetration. By incorporating flexibility, which is essential for accommodating the uncertainty in renewable generation, our model optimally shares the inter-regional flexibility between the sending- and receiving-end grids. One of the key features of our proposed model is its robustness and non-anticipativity, meaning it can account for different levels of uncertainty and make decisions that are suitable for multiple scenarios. This work develops two solution approaches to solve this challenging multistage model with variable uncertainty sets. We validate the proposed approach through a case study conducted on a real-world inter-regional grid. The numerical results demonstrate that our approach effectively unlocks more inter-regional flexibility and assists in increasing the renewable hosting capacity.

1 Introduction

The global adoption of high-voltage direct current (HVDC) systems has been rapidly increasing in regions such as Europe, North and South America, and China. This widespread installation of HVDC systems is driving a significant revolution in the strategy for accommodating renewable energy. With the characteristics of wind and solar energy, large-capacity wind and PV farms are often located far away from major load centers. This geographical separation creates a need for long-distance transmission solutions, and HVDC has emerged as one of the favorable options. HVDC offers advantages in terms of capital cost for long-distance transmission and has a transmission capability that remains relatively constant, regardless of the distance traveled (Li et al., 2021). In addition to the cost and distance advantages, HVDC also provides power flow controllability, which helps in effectively managing and avoiding loop flows in the transmission system. This controllability feature further enhances the suitability of long-distance HVDC transmission for accommodating renewable energy. A prime example of the importance of long-distance HVDC transmission for renewable energy accommodation can be seen in China. The vast renewable resources in western China are efficiently delivered to the load-centralized eastern regions through HVDC transmission (Lin et al., 2020).

The traditional approach to HVDC tie-line scheduling assumes that the transmission system operator (TSO) or independent system operator (ISO) has accurate load forecasts and the ability to schedule generation accordingly (Guo et al., 2018). However, the growing penetration of renewable energy sources has challenged this fundamental assumption. Renewable generation, such as wind and solar energy, is inherently variable and not fully controllable. This variability introduces uncertainty into power system operation, requiring TSOs/ISOs to consider and manage this uncertainty effectively. As tie-lines connect inter-regional power grids, it becomes crucial to collaboratively address the uncertainty associated with the tie-line power flow. In response to these challenges, there is a need to develop new HVDC tie-line scheduling approaches that account for the uncertainty stemming from renewable energy. By jointly managing the uncertainty across regions, TSOs/ISOs can enhance the system’s ability to accommodate renewable energy and maintain grid stability.

In recent years, significant research has been conducted on the topic of the scheduling and operation of HVDC systems with large-scale renewable penetration. Zhong et al. (2015) developed an operation model of HVDC tie-line for enhancing the capacity of renewable energy integration. Zhao et al. (2022) proposed a distributed multi-objective day-ahead generation and HVDC transmission joint scheduling model. Zhou et al. (2018) presented a distributed dispatch model aimed at facilitating the integration of wind power within the bulk AC/DC hybrid system. Guo et al. (2018) presented a robust optimization framework for efficient tie-line scheduling. Zeng et al. (2017) proposed a sequential simulation method considering HVDC tie-line operation and unit aggregation to analyze the wind accommodation in the 1-year horizon. Li et al. (2016) proposed a two-stage adaptive robust optimization model that takes into account uncertainties related to wind energy in tie-line scheduling problems. Wang et al. (2019a) proposed a stochastic optimization model to address cross-regional system scheduling, with a primary focus on minimizing renewable energy curtailment. In the aforementioned works, detailed unit and network models are often employed in the problem formulations (Li et al., 2016; Guo et al., 2018; Zhou et al., 2018; Zhao et al., 2022). However, the model size is often large in the real-world power systems, and these models may be computationally expensive. Thus, some research studies simplify the transmission system topology (Zhong et al., 2015; Zeng et al., 2017; Wang et al., 2019a) and aggregate units within each area (Zhong et al., 2015; Zeng et al., 2017) to reduce the complexity. Recently, distributed optimization techniques, such as the synchronous alternating direction method of multipliers (SADMMs) (Zhao et al., 2022) and analytical target cascading (ATC) (Zhou et al., 2018), have also been employed to speed up solving. These interesting works show promising performance in computational efficiency.

Renewable energy resources have led to the wide utilization of energy storage (ES) devices to alleviate potential congestion and minimize curtailment of renewable sources. Extensive research has been conducted on both transmission expansion planning (Yifan et al., 2015; Yin and Wang, 2022) and ES planning (Wogrin and Gayme, 2015). More recently, there has been a growing interest in developing collaborative planning models that address the challenges of high renewable penetration in the transmission system. Moradi-Sepahvand and Amraee (2021) proposed a multi-year planning model of a hybrid AC/DC transmission system to optimize the operation and investment cost of ES. Wang et al. (2019b) proposed a robust formulation for ES and transmission line co-planning. Qiu et al. (2017) proposed a co-planning model of transmission expansion and ES under high renewable penetration.

Nonetheless, it is difficult to find an optimal robust scheduling strategy and recourse action for ES when considering non-anticipativity constraints. This complexity primarily arises due to ES’s state of charging (SOC). It has been proven that many approaches, such as the two-stage robust model, scenario-based model, and chance-constrained models, fall short in ensuring feasibility when accommodating uncertainty (Lorca et al., 2016; Lorca and Sun, 2017; Zhai et al., 2017; Zhou et al., 2021). On the other hand, the recently proposed multistage optimization method in Zhou et al. (2021); Lorca and Sun (2017) Lorca et al. (2016); G. Cobos et al. (2018); and Hreinsson et al. (2019) proves to be an effective approach for ES-accommodating uncertainties. Decisions derived from the multistage model are guaranteed in terms of non-anticipativity and robustness. In other words, the operators’ actions are restricted to only depend on an uncertainty realized up to the current decision period, which is defined as non-anticipativity (Lorca and Sun, 2017). In addition, these actions have to be feasible for any uncertainty realization within an uncertainty set, which is denoted by robustness (Zhou et al., 2021). Nevertheless, it is worth noting that the uncertainty set associated with renewable generation will vary as capacity increases, often rendering the existing multistage optimization method computationally challenging.

This paper aims to advance the integration of renewable energy into the power system by unlocking cross-area flexibility with HVDC tie-lines, taking into account the renewable uncertainty. To achieve this, the authors propose a novel multistage HVDC tie-line planning-operation model that specifically addresses the challenges associated with high levels of renewable penetration. The model developed in this paper considers several important factors, including the scheduling of HVDC tie-line power, thermal plant operations, demand response, planning of energy storage, and the uncertainty associated with renewable energy generation. Drawing inspiration from the surrogate affine approximation (SAA) approach (Ye, 2018) and implicit decision method (IDM) (Zhai et al., 2017; Zhou et al., 2021), the authors propose the two-solution method for the model that accounts for the variable uncertainty set. These approaches allow for effective decision-making in the face of uncertainty, ensuring a robust and efficient operation of the HVDC tie-line system. The contributions of this paper are threefold:

• We propose a novel HVDC tie-line planning-operation model that takes into account the variable uncertainty set associated with renewable generation. One of the key decision variables in the model is the renewable installation capacity, which directly impacts the uncertainty range. The model optimally determines how much renewable and uncertainty that the inter-regional flexibility can accommodate. In addition to the renewable installation capacity, the model also determines storage capacity and HVDC tie-line power, considering thermal plant dispatch and demand response. It is noted that this work focuses on the flexibility and thus employs the simplified planning model used in practice.

• This work proposes two solution approaches to the model with the variable uncertainty set. Unlike most multistage models that assume a constant uncertainty set, we recognize the need to model a variable uncertainty set that is determined by the renewable installation capacity. This introduces challenges in solving the model as the uncertainty set is no longer fixed. To address this, we employ a surrogate affine policy-based solution method and implicit decision-based solution method. Both methods allow us to effectively handle the variable uncertainty set and make informed decisions regarding the renewable installation capacity. As a result of the two solution approaches, we obtain closed-form re-dispatch strategies and safe ranges of re-dispatch strategies, respectively. These strategies provide valuable insights into how to respond to uncertain renewable generation, ensuring a reliable and efficient operation of the HVDC tie-line system.

• We conduct comprehensive studies with a real-world case, offering an in-depth analysis and discussion of an inter-regional power system within China. It shows potential to offer valuable insights into inter-regional renewable energy accommodation.

The rest of this paper is organized as follows: Section II introduces the multistage HVDC model. Section III presents the proposed solution approach. Case studies are provided in Section IV. Section V concludes this paper.

2 Problem formulation

In this section, we first present the deterministic HVDC-connected two-area system planning-operation model. To place emphasis on the HVDC tie-line, we streamline the models for both the sending and receiving ends. The sending-end grid comprises thermal power plants, wind and PV farms, and storage. Meanwhile, the receiving end incorporates storage, loads, and demand response. Planning and operation decisions are determined in the model simultaneously. The planning decision includes the renewable installation capacity, storage capacity, and medium-term HVDC tie-line power contract. The operation decision involves HVDC tie-line power scheduling, thermal unit dispatch, renewable energy output, storage SOC, and load shedding. Then, we present the multistage optimization model to guarantee the solution non-anticipativity and robustness. Recourse actions are modeled in the multistage model to accommodate the uncertainty.

2.1 Deterministic HVDC-connected two-area system planning-operation model

In the proposed HVDC planning-operation model, the objective is to maximize the installation capacity of renewable energy and minimize investment and operation costs. Let ω denote the weight factor that could be any value between 0 and 1. Then, the objective function is formulated as

$\begin{array}{ll}\hfill \min \left(1-\omega \right)& \left\{F^c\left(C^{pv},C^w,C^{\mathit{sto}}\right)+{\displaystyle \sum _{t\in \mathcal{T}}}\left[F_t^g\left(p_t^g\right)\right.\right.\hfill \\ \hfill & \left.\left.+F_t^n\left(p_t^n\right)+F_t^l\left(p_t^{ls}\right)\right]\right\}-\omega \left(C^{pv}+C^w\right).\hfill \end{array}(1)$

It is subject to

$\begin{array}{ll}\hfill & -{\kappa }_t^{\mathit{hvdc}}{R}^{\mathit{hvdc}}\le p_t^{\mathit{hvdc}}-p_{t-1}^{\mathit{hvdc}}\le {\kappa }_t{R}^{\mathit{hvdc}},\hfill \\ \hfill & {\kappa }_t^{\mathit{hvdc}}\in \left\{\mathrm{0,1}\right\},\forall t\in \mathcal{T},\hfill \end{array}(2)$

${\underline{p}}^{\mathit{hvdc}}\le p_t^{\mathit{hvdc}}\le {\bar{p}}^{\mathit{hvdc}},\forall t\in \mathcal{T},(3)$

${\displaystyle \sum _t^{t+T^{\mathit{hvdc}}}}{\kappa }_t^{\mathit{hvdc}}\le 1,\forall t\in \mathcal{T},(4)$

${\displaystyle \sum _{t\in \mathcal{T}}}{\kappa }_t^{\mathit{hvdc}}\le X^{\mathit{hvdc}},(5)$

${\displaystyle \sum _{t\in \mathcal{T}}}{p}_t^{\mathit{hvdc}}\mathrm{\Delta }t=Q^{\mathit{hvdc}},(6)$

${\beta }^g{C}^g\le p_t^g\le C^g,\forall t\in \mathcal{T},(7)$

$-R^g\mathrm{\Delta }t\le p_t^g-p_{t-1}^g\le R^g\mathrm{\Delta }t,\forall t\in \mathcal{T},(8)$

$p_t^{f,pv}+p_t^{f,w}+p_t^{s,dis}-p_t^{s,ch}+p_t^g=p_t^{\mathit{hvdc}},\forall t\in \mathcal{T},(9)$

$E_{t+1}^s=E_t^s+({\mu }^{s,ch}{p}_t^{s,ch}-p_t^{s,dis}/{\mu }^{s,dis})\mathrm{\Delta }t,\forall t\in \mathcal{T},(10)$

$\left(1-{\alpha }^{s,sto}\right)C^{s,sto}\le E_t^s\le C^{s,sto},\forall t\in \mathcal{T},(11)$

$0\le p_t^{s,ch}\le {\eta }^{s,ch}{C}^{s,sto},\forall t\in \mathcal{T},(12)$

$0\le p_t^{s,dis}\le {\eta }^{s,dis}{C}^{s,sto},\forall t\in \mathcal{T},(13)$

$E_0^s=E_T^s,(14)$

$p_t^{f,pv}=k_t^{f,pv}{C}^{pv},\forall t\in \mathcal{T},(15)$

$p_t^{f,w}=k_t^{f,w}{C}^w,\forall t\in \mathcal{T},(16)$

$p_t^{r,dis}-p_t^{r,ch}+p_t^{\mathit{hvdc}}+p_t^n=p_t^l-p_t^{ls},\forall t\in \mathcal{T},(17)$

${\underline{p}}_t^n\le p_t^n\le {\bar{p}}_t^n,\forall t\in \mathcal{T},(18)$

$-R^n\mathrm{\Delta }t\le p_t^n-p_{t-1}^n\le R^n\mathrm{\Delta }t,\forall t\in \mathcal{T},(19)$

$E_{t+1}^r=E_t^r+({\mu }^{r,ch}{p}_t^{r,ch}-p_t^{r,dis}/{\mu }^{r,dis})\mathrm{\Delta }t,\forall t\in \mathcal{T},(20)$

$0\le p_t^{r,ch}\le {\eta }^{r,ch}{C}^{r,sto},\forall t\in \mathcal{T},(21)$

$0\le p_t^{r,dis}\le {\eta }^{r,dis}{C}^{r,sto},\forall t\in \mathcal{T},(22)$

$\left(1-{\alpha }^{r,sto}\right)C^{r,sto}\le E_t^r\le C^{r,sto},\forall t\in \mathcal{T},(23)$

$E_0^r=E_T^r,(24)$

$0\le p_t^{ls}\le {\gamma }^{ls}{p}_t^l,\forall t\in \mathcal{T}.(25)$

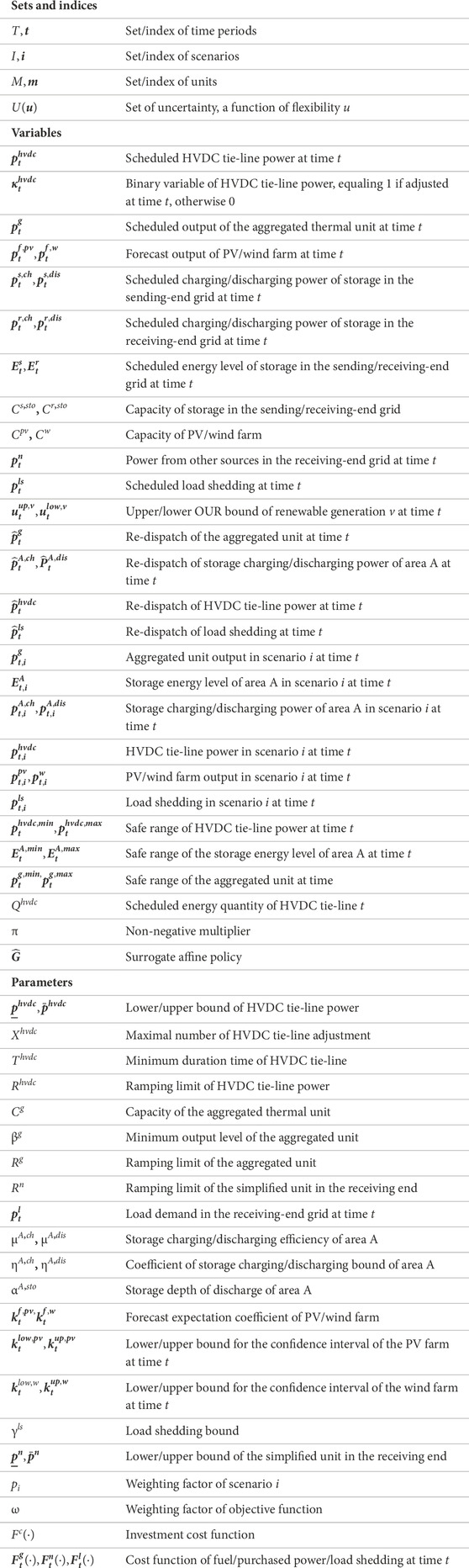
Eqs 2–6 are operation constraints of the HVDC tie-line. Specifically, Eq. 2 represents the ramping limits of HVDC tie-line power. Eq. 3 denotes the lower and upper limits of HVDC tie-line power. The minimum duration time for HVDC tie-line power is modeled in Eq. 4. Eq. 5 represents the maximal adjustment constraint of HVDC tie-line power each day. Eq. 6 shows that the total energy transferred by the HVDC tie-line is determined by the cross-border trading contract. It is worth mentioning that the energy transferred by HVDC is formulated in this model, following the planning practice. The transferred energy between regions is affected by many factors. Among them is the energy cost difference. Figure 1 illustratively depicts an intersection of two supply curves in an inter-regional grid. Without considering the renewable installation capacity and other constraints, the intersection is the optimal point, which yields the resulting energy quantity to be inter-regional transferred.

FIGURE 1

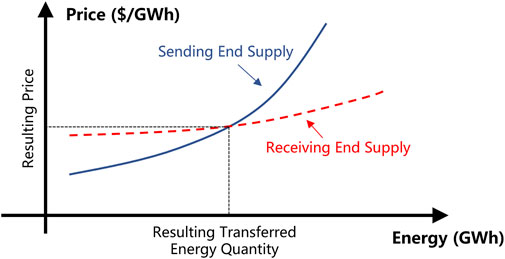
FIGURE 1. Illustrative intersection of sending- and receiving-end supply curves in an inter-regional grid without network congestion. The intersection is the energy price–quantity pair without considering other constraints.

Eqs 7–16 denote sending-end constraints. Specifically, Eq. 7 stands for the lower and upper bounds of the aggregated thermal unit output. Eq. 8 represents the ramp-up/ramp-down limit of the aggregated thermal unit. Eq. 9 represents the power balance equation. Eqs 10 and 11 denote the SOC change and lower/upper limit of the SOC level of the storage, respectively. Charging and discharging power of storage are modeled in Eqs 12 and 13, respectively. Eq. 14 shows that SOC at the last time period equals to its initial level. Eqs 15 and 16 define the scheduled outputs of PV and wind farm, respectively.

Eqs 17–25 denote receiving-end constraints. Specifically, Eq. 17 represents the power balance equation. Eq. 18 stands for the lower and upper bounds of the simplified unit. Eq. 19 shows the ramp-up/ramp-down limit of the simplified unit. Eqs 20–24 denote storage constraints, which are similar to those in the sending end. Eq. 25 represents the upper bound of load shedding.

2.2 Multistage optimization model with the variable uncertainty set

2.2.1 Uncertainty modeling

In this study, the deviations from renewable forecast output are considered an uncertainty. Without loss of generality, an uncertainty is assumed to follow Gaussian distribution with a mean value of 0 and variance of σ. Then, the materialized renewable generation is defined as

${\widehat{p}}_t^v=p_t^{f,v}+{ϵ}_t^v,{ϵ}_t^v\sim N(0,{{\sigma }^v}^2),\forall t\in \mathcal{T},\forall v\in \{pv,w\}.(26)$

Generally, the renewable output is proportional to its capacity. Hence, the confidence interval of ${ϵ}_t^v$ can be denoted as $[-k_t^{\mathit{low,v}}{C}^v,k_t^{up,v}{C}^v]$, given a certain confidence level. Traditionally, the uncertainty is usually modeled as a box set with a fixed boundary in the multistage model (Lorca and Sun, 2017; Zhai et al., 2017; Zhou et al., 2021). However, the installation capacity of renewables is to be determined in this study, resulting in a non-constant uncertainty set. Thus, we formulate the variable uncertainty set (Cartesian product):

$\mathcal{U}(\mathit{u})={\mathcal{U}}_1({\mathit{u}}_1)\times {\mathcal{U}}_2({\mathit{u}}_2)\times \dots \times {\mathcal{U}}_T({\mathit{u}}_T),(27)$

where ${\mathcal{U}}_t({\mathit{u}}_t)$ is a polyhedral convex set of uncertainty at time t. ${\mathcal{U}}_t({\mathit{u}}_t)$ can be formulated as a box set with the variable boundary,

${\mathcal{U}}_t\left({\mathit{u}}_t\right)\triangleq \left\{{\left({ϵ}_t^{pv},{ϵ}_t^w\right)}^T:-u_t^{\mathit{low,v}}\le {ϵ}_t^v\le u_t^{up,v};v\in \left\{pv,w\right\}\right\},(28)$

which denotes the range of uncertainty that the inter-regional flexibility is capable of accommodating. ${\mathcal{U}}_t({\mathit{u}}_t)$ can also be called an optimal uncertainty range (OUR). It is related to renewable installation capacity, and we formulate constraints as follows:

$u_t^{up,v}\ge k_t^{up,v}{C}^v,\forall t\in \mathcal{T},\forall v\in \left\{pv,w\right\},(29)$

$u_t^{\mathit{low,v}}\ge k_t^{\mathit{low,v}}{C}^v,\forall t\in \mathcal{T},\forall v\in \left\{pv,w\right\},(30)$

which guarantee that uncertainty in the confidence interval can always be accommodated in OUR. Figure 2 shows the comparison of the uncertainty confidence interval, OUR, and installation capacity of renewable generation.

FIGURE 2

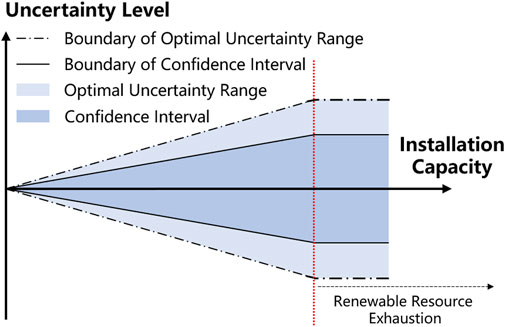
FIGURE 2. Comparison of the uncertainty confidence interval, optimal uncertainty range (OUR), and installation capacity of renewable generation. OUR is the uncertainty range that the inter-regional flexibility can accommodate, and the confidence interval of generation uncertainty always falls within OUR. The harnessed renewable energy, such as wind, may reach the maximal level, regardless of installation capacity.

2.2.2 Uncertainty accommodation

The recourse actions of flexible resources can be formulated as

$\begin{array}{ll}\hfill & {\left[{\widehat{p}}_t^g,{\widehat{p}}_t^{A,ch},{\widehat{p}}_t^{A,dis},{\widehat{p}}_t^{\mathit{hvdc}},{\widehat{p}}_t^{ls}\right]}^T\hfill \\ \hfill & ={\left[p_t^g,p_t^{A,ch},p_t^{A,dis},p_t^{\mathit{hvdc}},p_t^{ls}\right]}^T+{\mathit{y}}_{\mathit{t}}\left({\mathit{ϵ}}_{\left[\mathit{t}\right]}\right),\forall t\in \mathcal{T},\forall {\mathit{ϵ}}_{\mathit{t}}\in {\mathcal{U}}_{\mathit{t}}\left({\mathit{u}}_{\mathit{t}}\right),\hfill \\ \hfill & \forall A\in \left\{s,r\right\},\hfill \end{array}(31)$

which respect constraints (2–25). ϵ_[t] represents the uncertainty vector and ϵ_[t] = {ϵ₁, ϵ₂, …, ϵ_t}. ${\mathit{y}}_{\mathit{t}}\left({\mathit{ϵ}}_{[\mathit{t}]}\right)$ is the recourse function that maps uncertainty to re-dispatch decisions. Unlike the two-stage robust-based and scenario-based method, the proposed recourse actions (31) can guarantee the non-anticipativity and robustness of the solution simultaneously.

2.2.3 Multistage optimization model

With aforementioned equations, the multistage optimization model can be formulated as

$\begin{array}{ll}\hfill \left(\text{P}\right)\min \left(1-\omega \right)& \left\{F^c\left(C^{pv},C^w,C^{\mathit{sto}}\right)\right.\hfill \\ \hfill & \left.+{\displaystyle \sum _{t\in \mathcal{T}}}\left[F_t^g\left(p_t^g\right)+F_t^n\left(p_t^n\right)+F_t^l\left(p_t^{ls}\right)\right]\right\}-\omega \left(C^{pv}+C^w\right)\hfill \\ \hfill & \text{s.t.}\left(4\right)-\left(5\right),\left(18\right)-\left(19\right),\left(26\right),\left(29\right)-\left(31\right),\hfill \\ \hfill & -{\kappa }_t^{\mathit{hvdc}}{R}^{\mathit{hvdc}}\le {\widehat{p}}_t^{\mathit{hvdc}}-{\widehat{p}}_{t-1}^{\mathit{hvdc}}\le {\kappa }_t^{\mathit{hvdc}}{R}^{\mathit{hvdc}},\forall t\in \mathcal{T},\hfill \end{array}(32)$

${\underline{p}}^{\mathit{hvdc}}\le {\widehat{p}}_t^{\mathit{hvdc}}\le {\bar{p}}^{\mathit{hvdc}},\forall t\in \mathcal{T},(33)$

${\displaystyle \sum _{t\in T}}{\widehat{p}}_t^{\mathit{hvdc}}\mathrm{\Delta }t=Q^{\mathit{hvdc}},(34)$

${\widehat{p}}_t^{pv}+{\widehat{p}}_t^w+{\widehat{p}}_t^{s,dis}-{\widehat{p}}_t^{s,ch}+{\widehat{p}}_t^g={\widehat{p}}_t^{\mathit{hvdc}},\forall t\in \mathcal{T},(35)$

$\begin{array}{ll}\left(1-{\alpha }^{A,sto}\right)C^{A,sto}\le \hfill & {\displaystyle \sum _{\tau =1}^t}\left({\mu }^{A,ch}{\widehat{p}}_{\tau }^{A,ch}-{\widehat{p}}_{\tau }^{A,dis}/{\mu }^{A,dis}\right)\hfill \\ \hfill & +E_0^A\le C^{A,sto},\forall t\in \mathcal{T},\forall A\in \left\{s,r\right\},\hfill \end{array}(36)$

$0\le {\widehat{p}}_t^{A,ch}\le {\eta }^{A,ch}{C}^{A,sto},\forall t\in \mathcal{T},\forall A\in \left\{s,r\right\},(37)$

$0\le {\widehat{p}}_t^{A,dis}\le {\eta }^{A,dis}{C}^{A,sto},\forall t\in \mathcal{T},\forall A\in \left\{s,r\right\},(38)$

${\displaystyle \sum _{t\in \mathcal{T}}}\left({\mu }^{A,ch}{\widehat{p}}_t^{A,ch}-{\widehat{p}}_t^{A,dis}/{\mu }^{A,dis}\right)\mathrm{\Delta }t=0,\forall A\in \left\{s,r\right\},(39)$

${\beta }^g{C}^g\le {\widehat{p}}_t^g\le C^g,\forall t\in \mathcal{T},(40)$

$-R^g\mathrm{\Delta }t\le {\widehat{p}}_t^g-{\widehat{p}}_{t-1}^g\le R^g\mathrm{\Delta }t,\forall t\in \mathcal{T},(41)$

${\widehat{p}}_t^{r,dis}-{\widehat{p}}_t^{r,ch}+{\widehat{p}}_t^{\mathit{hvdc}}+p_t^n=p_t^l-{\widehat{p}}_t^{ls},\forall t\in \mathcal{T},(42)$

$0\le {\widehat{p}}_t^{ls}\le {\gamma }^{ls}{p}_t^l,\forall t\in \mathcal{T}.(43)$

The problem (P) is a highly non-convex optimization problem. First, the model has plenty of infinite constraints due to uncertainty. Second, the recourse actions are non-linear and non-convex. Moreover, the model has a variable uncertainty set that is relevant to the renewable installation capacity. To address these difficulties, we propose two tractable methods in the following section.

3 Solution approach

3.1 Surrogate affine approximation

In this section, affine policies are adopted to implement the recourse actions. Re-dispatch decisions of the aggregated unit, HVDC, load shedding, and storages are functions of renewable realizations. We define the recourse actions as

${\mathit{y}}_{\mathit{t}}\left({\mathit{ϵ}}_{[\mathit{t}]}\right)={\mathit{G}}_{\mathit{t}}{\mathit{ϵ}}_{[\mathit{t}]},\forall t\in \mathcal{T},\forall {\mathit{ϵ}}_{\mathit{t}}\in {\mathcal{U}}_t({\mathit{u}}_{\mathit{t}}),(44)$

where G_t is the matrix of affine policy. Following (31) and (44), the problem (P) can be rewritten into a compact form as follows:

$(\text{AP}-\text{P})\underset{\mathit{x},\mathit{u},\mathit{G}}{\min }{\mathit{c}}^T\mathit{x},(45)$

$\text{s.t.}\mathit{A}\mathit{x}+\mathit{E}\mathit{u}\le \mathit{b},(46)$

$\mathit{K}\mathit{x}+\mathit{L}\mathit{ϵ}+\mathit{M}\mathit{G}\mathit{ϵ}\le \mathit{d},\forall \mathit{ϵ}\in \mathcal{U}(\mathit{u}),(47)$

$\mathit{F}\mathit{x}+\mathit{H}\mathit{ϵ}+\mathit{J}\mathit{G}\mathit{ϵ}=\mathit{h},\forall \mathit{ϵ}\in \mathcal{U}(\mathit{u}),(48)$

where x represents scheduled variables including tie-line power and adjustment of HVDC, output of the aggregated unit, capacity and output of renewables and storages, purchased power, and load shedding. The variable u denotes the OUR bound of renewables. G represents the affine policy matrix. Eq. 45 denotes the objective function (1). Eq. 46 denotes constraints (4)–(5), (18)–(19), and (29)–(30). Eq. 47 denotes inequality inter-regional grid constraints with ϵ. Equality inter-regional grid constraints with ϵ are represented by (48).

Although the affine policy reduces the model complexity, (AP-P) is still computationally intractable due to the variable bound of uncertainty set in Eqs 47 and 48. To deal with this difficulty, we employ SAA (Ye, 2018) by introducing a set of surrogate variables

$\mathbf{0}\le {\mathit{\delta }}^{\text{LB}}\le \mathbf{1},\mathbf{0}\le {\mathit{\delta }}^{\text{UB}}\le \mathbf{1},(49)$

and surrogate affine policy

$\widehat{\mathit{G}}=\mathit{G}\left[-{\mathit{U}}^{\text{LB}},{\mathit{U}}^{\text{UB}}\right],\forall t,(50)$

where ${\mathit{U}}^{\text{LB}}=\mathrm{diag}\left({\mathit{u}}^{\mathit{low}}\right)$ and ${\mathit{U}}^{\text{UB}}=\mathrm{diag}\left({\mathit{u}}^{\mathit{u}\mathit{p}}\right)$. Following strong duality, Eq. 47 is recast as

$\mathit{K}\mathit{x}+\mathit{\pi }\cdot \mathbf{1}\le \mathit{d},(51)$

$\mathit{M}\widehat{\mathit{G}}+\mathit{L}[-{\mathit{U}}^{\text{LB}},{\mathit{U}}^{\text{UB}}]\le \mathit{\pi },(52)$

$\mathit{\pi }\ge \mathit{0},(53)$

where π is a matrix of non-negative multipliers. The recourse action in Eq. 44 can be rewritten as

$\begin{array}{ccc}\hfill \mathit{G}\mathit{ϵ}=\mathit{G}[-{\mathit{U}}^{\text{LB}},{\mathit{U}}^{\text{UB}}]\left[\begin{array}{cc}\hfill & {\mathit{\delta }}^{\text{LB}}\hfill \\ \hfill & {\mathit{\delta }}^{\text{UB}}\hfill \end{array}\right]=\widehat{\mathit{G}}\left[\begin{array}{cc}\hfill & {\mathit{\delta }}^{\text{LB}}\hfill \\ \hfill & {\mathit{\delta }}^{\text{UB}}\hfill \end{array}\right].& \hfill & \hfill \end{array}(54)$

Following the recourse action (54), Eq. 48 is equivalent to the following equations:

$\mathit{F}\mathit{x}=\mathit{h},(55)$

$\mathit{H}[-{\mathit{U}}^{\text{LB}},{\mathit{U}}^{\text{UB}}]+\mathit{J}\widehat{\mathit{G}}=\mathit{0}.(56)$

With aforementioned constraints, the SAA model is formulated as

$(\text{SAA}-\text{P})\underset{\mathit{x},\mathit{u},\widehat{\mathit{G}},\mathit{\pi }}{\min }{\mathit{c}}^T\mathit{x},(57)$

$\text{s.t.}\left(46\right)\text{,\hspace{0.17em}}\left(51\right)-\left(53\right)\text{,\hspace{0.17em}}\left(55\right)-\left(56\right).(58)$

(SAA-P) is an MILP problem and can be solved using the off-the-shelf solvers.

3.2 Implicit decision method

IDM uses carefully selected scenarios and predefined (i.e., non-anticipative) constraints to reformulate the multistage model, while guaranteeing solution non-anticipativity and robustness. Based on Zhai et al. (2017), the selected scenarios include three categories: base scenario (BS), selective vertex scenarios (SVS), and extreme ramping scenarios (ERS). BS represents the forecast scenario of the renewable. SVS denotes vertex scenarios of the uncertainty set. ERS comprises two scenarios that capture extreme fluctuations in renewable generation.

Non-anticipativity and robustness of thermal output, storage charging/discharging power and HVDC tie-line power shall be guaranteed. For thermal units, we use $p_t^{g,\mathit{min}}$ and $p_t^{g,\mathit{max}}$ to formulate non-anticipativity constraints (NCs) as in Eqs 59–61. For storage, $E_t^{A,\mathit{min}}$ and $E_t^{A,\mathit{max}}$ are introduced to formulate the NCs, as shown in Eqs 62–64. Furthermore, we develop $p_t^{\mathit{hvdc,max}}$ and $p_t^{\mathit{hvdc,min}}$ to constitute the NCs of HVDC tie-line power, as shown in Eqs 65–67.

$\beta C^g\le p_t^{g,\mathit{min}}\le p_{t,i}^g\le p_t^{g,\mathit{max}}\le C^g,\forall t\in \mathcal{T},\forall i\in \mathcal{I},(59)$

$-R^g\mathrm{\Delta }t\le p_t^{g,\mathit{max}}-p_{t-1}^{g,\mathit{min}}\le R^g\mathrm{\Delta }t,\forall t\in \mathcal{T},(60)$

$-R^g\mathrm{\Delta }t\le p_t^{g,\mathit{min}}-p_{t-1}^{g,\mathit{max}}\le R^g\mathrm{\Delta }t,\forall t\in \mathcal{T},(61)$

$\begin{array}{ll}\hfill & \left(1-{\alpha }^A\right)C^{A,sto}\le E_t^{A,\mathit{min}}\le E_{t,i}^A\le E_t^{A,\mathit{max}}\le C^{A,sto},\forall t\in \mathcal{T},\hfill \\ \hfill & \forall i\in \mathcal{I},\forall A\in \left\{s,r\right\},\hfill \end{array}(62)$

$\begin{array}{ll}\hfill & -{\eta }^{A,dis}{C}^{A,sto}/{\mu }^{A,dis}\le \left(E_t^{A,\mathit{max}}-E_{t-1}^{A,\mathit{min}}\right)/\hfill \\ \hfill & \mathrm{\Delta }t\le {\eta }^{A,ch}{\mu }^{A,ch}{C}^{A,sto},\forall t\in \mathcal{T},\forall A\in \left\{s,r\right\},\hfill \end{array}(63)$

$\begin{array}{ll}\hfill & -{\eta }^{A,dis}{C}^{A,sto}/{\mu }^{A,dis}\le \left(E_t^{A,\mathit{min}}-E_{t-1}^{A,\mathit{max}}\right)/\hfill \\ \hfill & \mathrm{\Delta }t\le {\eta }^{A,ch}{\mu }^{A,ch}{C}^{A,sto},\forall t\in \mathcal{T},\forall A\in \left\{s,r\right\},\hfill \end{array}(64)$

${\underline{p}}^{\mathit{hvdc}}\le p_t^{\mathit{hvdc,min}}\le p_{t,i}^{\mathit{hvdc}}\le p_t^{\mathit{hvdc,max}}\le {\bar{p}}^{\mathit{hvdc}},\forall t\in \mathcal{T},\forall i\in \mathcal{I},(65)$

$\begin{array}{ll}\hfill & -{\kappa }_t^{\mathit{hvdc}}{R}^{\mathit{hvdc}}-\left(1-{\kappa }_t^{\mathit{hvdc}}\right){\bar{p}}^{\mathit{hvdc}}\le p_t^{\mathit{hvdc,min}}\hfill \\ \hfill & -p_{t-1}^{\mathit{hvdc,max}}\le {\kappa }_t^{\mathit{hvdc}}{R}^{\mathit{hvdc}}+\left(1-v_t\right){\bar{p}}^{\mathit{hvdc}},\forall t\in \mathcal{T},\hfill \end{array}(66)$

$\begin{array}{ll}\hfill & -{\kappa }_t^{\mathit{hvdc}}{R}^{\mathit{hvdc}}-\left(1-{\kappa }_t^{\mathit{hvdc}}\right){\bar{p}}^{\mathit{hvdc}}\le p_t^{\mathit{hvdc,max}}\hfill \\ \hfill & -p_{t-1}^{\mathit{hvdc,min}}\le {\kappa }_t^{\mathit{hvdc}}{R}^{dc}+\left(1-{\kappa }_t^{\mathit{hvdc}}\right).{\bar{p}}^{\mathit{hvdc}},\forall t\in \mathcal{T}.\hfill \end{array}(67)$

Based on BS, SVS, ERS, and the proposed NCs, the multistage model of HVDC with IDM is established as

$\begin{array}{ll}\hfill \min -\omega \left(C^{pv}+C^w\right)& +\left(1-\omega \right){\displaystyle \sum _{i\in \mathcal{I}}}{p}_i\left\{F^c\left(C^w,C^{pv},C^{\mathit{sto}}\right)\right.\hfill \\ \hfill & \left.+{\displaystyle \sum _{t\in \mathcal{T}}}\left[F_t^g\left(p_{t,i}^g\right)+F_t^n\left(p_t^n\right)+F_t^l\left(p_{t,i}^{ls}\right)\right]\right\},\hfill \end{array}(68)$

$\begin{array}{ll}\hfill & \mathrm{s.t.}(4)-(5),(18)-(19),(59)-(67),\hfill \\ \hfill & {\displaystyle \sum _{t\in \mathcal{T}}}{p}_{t,i}^{\mathit{hvdc}}\mathrm{\Delta }t=Q^{\mathit{hvdc}},\forall i\in \mathcal{I},\hfill \end{array}(69)$

$p_{t,i}^{pv}+p_{t,i}^w+p_{t,i}^{s,dis}-p_{t,i}^{s,ch}+p_{t,i}^g=p_{t,i}^{\mathit{hvdc}},\forall t\in \mathcal{T},\forall i\in \mathcal{I},(70)$

$p_{t,i}^{r,dis}-p_{t,i}^{r,ch}+p_{t,i}^{\mathit{hvdc}}+p_t^n=p_t^l-p_{t,i}^{ls},\forall t\in \mathcal{T},\forall i\in \mathcal{I},(71)$

$\begin{array}{ll}\hfill & E_{t+1,i}^A=E_{t,i}^A+\left({\mu }^{A,ch}{p}_{t,i}^{A,ch}\right.\hfill \\ \hfill & \left.-p_{t,i}^{A,dis}/{\mu }^{A,dis}\right)\mathrm{\Delta }t,\forall t\in \mathcal{T},\forall i\in \mathcal{I},\forall A\in \{s,r\},\hfill \end{array}(72)$

$E_{0,i}^A=E_{T,i}^A,\forall i\in \mathcal{I},\forall A\in \{s,r\},(73)$

$0\le p_{t,i}^{ls}\le {\gamma }^{ls}{p}_t^l,\forall t\in \mathcal{T},\forall i\in \mathcal{I}.(74)$

4 Case study

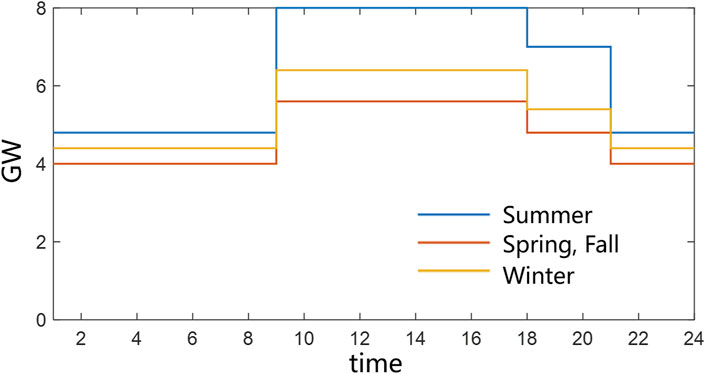
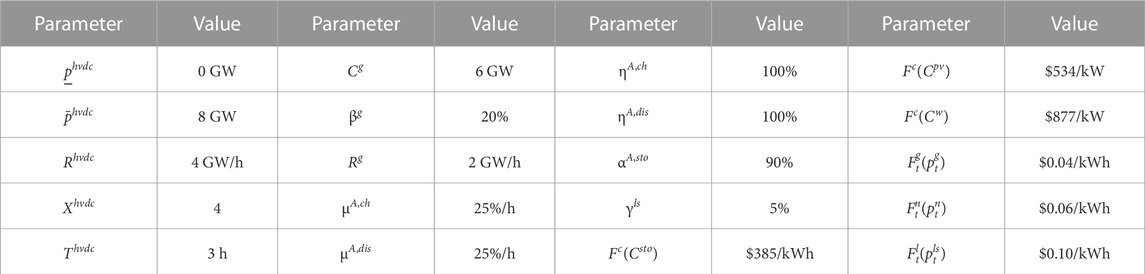
We perform the case studies based on a real-world two-area interconnected system in China. Load and renewable forecast profiles are obtained from real historical data on two provinces. The existing daily trading electricity of HVDC tie-line is 112.8 GWh, 150.6 GWh, 112.8 GWh, and 126.6 GWh from spring to winter. Figure 3 shows the existing scheduled profile of the HVDC tie-line in various seasons. The planning horizon is considered 10 years. We use four seasonal typical days for the planning, and the time resolution is set as 2 h. The major techno-economical parameters are presented in Table 1. The simulations are executed using MATLAB 2021b and Gurobi 9.5 in a server with Intel Xeon Gold 6140 (2.30 GHz).

FIGURE 3

FIGURE 3. Existing scheduled HVDC tie-line profiles for each season.

TABLE 1

TABLE 1. Major techno-economical parameters.

4.1 Effectiveness of the proposed model

4.1.1 Inter-regional flexibility

The following HVDC operation modes are compared to demonstrate the effectiveness of the proposed model for unlocking inter-regional flexibility:

• Mode 1: HVDC tie-line power is fixed based on the current practice in the industry.

• Mode 2: HVDC tie-line power is optimized without a recourse action.

• Mode 3: HVDC tie-line power is optimized with a recourse action.

For a fair comparison, all three modes utilize an identical amount of energy transferred by HVDC. IDM is used to solve the proposed model in this case. The second column of Table 2 shows the maximum installation capacity of renewable generation obtained by the proposed model with ω = 1. Mode 3 achieves the highest renewable installation capacity, amounting to 9.81 GW. This is primarily due to mode 3’s ability to unlock the inter-regional flexibility. Recourse actions of HVDC tie-line can be taken when uncertainty is materialized. Then, flexible resources in the receiving end are adjusted to accommodate power fluctuations transmitted by the HVDC tie-line. This utilization of inter-regional flexibility effectively mitigates the impact of uncertainty; thus, more renewable resources can be accommodated. In mode 2, the renewable installation capacity stands at 8.24 GW, representing a decrease of 1.57 GW in comparison to mode 3 (1.57 = 9.81–8.24). This reduction can be attributed to mode 2’s inability to leverage inter-regional flexibility without a recourse action. However, it is worth noting that mode 2 outperforms mode 1, primarily due to its optimized HVDC tie-line power. These results demonstrate that the proposed model can unlock inter-regional flexibility, thus enhancing the penetration of renewable energy. The third column of Table 2 shows the minimum 10-year cost obtained by the proposed model with ω = 0. Mode 3 has the lowest 10-year cost, amounting to $628.074 billion, while mode 1 has the highest 10-year cost, reaching $634.034 billion. This observation highlights the cost-saving potential achieved through unlocking inter-regional flexibility.

TABLE 2

TABLE 2. Maximum installation capacity of renewable generation and minimum 10-year cost obtained by the proposed model under different operation modes of the HVDC tie-line.

4.1.2 Optimizing the contracted energy

To demonstrate the benefit of optimizing contracted energy transferred by HVDC, the results under different cross-border contracts are compared. SAA is employed to solve the proposed model. We set ω = 0. Table 3 shows the resulting 10-year cost and transferred energy quantity. Column “Q” presents the energy transferred by HVDC. It is observed that 458.8 TWh energy is transferred, according to current industry practice. In contrast, the proposed approach has 532.88 TWh energy transferred by HVDC. The column “Total” presents the total cost in two approaches. The proposed approach saves $1.949 billion (i.e. 1.949 = 628.16–626.211), 10-year cost, compared with the current practice. The data indicate that the proposed approach improves HVDC utilization and also performs better in economic efficiency.

TABLE 3

TABLE 3. Resulting 10-year transferred energy quantity and cost under different cross-border contracts.

4.1.3 All-scenario-feasible verification

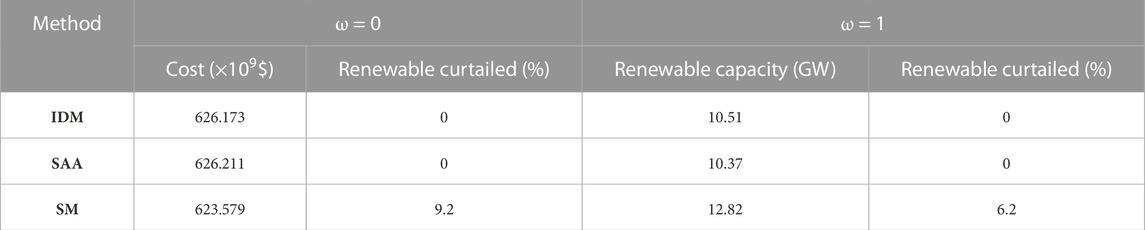
In this section, we compare IDM, the SAA model, and scenario-based model (SM) (Wang et al., 2019a). Both IDM and SAA can guarantee solution non-anticipativity and robustness simultaneously, while SM does not. Furthermore, SM is performed based on 100 scenarios generated by Monte Carlo sampling.

Table 4 shows the testing results. In this case, we use 500 out-of-sample scenarios to verify the solution feasibility. “Renewable curtailed” denotes the percentage of scenarios where curtailment of renewable energy occurs. When ω = 0, SM has the lowest cost of $624 billion. However, the renewable curtailment occurs in 9.2% scenarios for SM. In contrast, SAA does not have any curtailment scenario. This suggests that SM tends to be over-optimistic. Consequently, the planning outcome might become infeasible when restrictions on renewable curtailment are in place, resulting in substantial economic losses during actual operations. Meanwhile, IDM-based results have the similar cost to those based on SAA and also have zero renewable curtailment. Similar trends can be found in the results with ω = 1.

TABLE 4

TABLE 4. Planning results with different methods.

4.2 Comparison of solution approaches

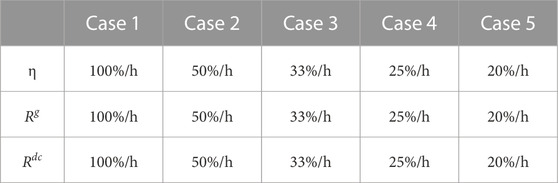
In this paper, we find that the flexibility parameters are the dominant factors affecting the feasible region of SAA and IDM. NCs in the IDM shrink the safe region to guarantee solution robustness and non-anticipativity. SAA has no pre-specified constraints or bounds for re-dispatch. However, the surrogate affine policy is used as recourse actions in SAA, which may somewhat compromise the optimality of re-dispatch. Therefore, it is difficult to judge the two approaches directly. Thus, we perform a sensitivity study of flexibility parameters to compare the solution approaches. The parameters used are shown in Table 5, where η = η^A,c = η^A,d. From case 1 to case 5, we decrease the charging/discharging capacity, ramping capability of unit, and HVDC. Figure 4 presents the results attained by SAA and IDM with ω = 1. Both curves show that the maximum installation capacity decreases with the reducing ramping limits or efficiency. When the flexibility parameters are all equal to 100%/h (i.e., Case 1), the installation capacities attained by SAA and IDM are 10.4 GW and 10.67 GW, respectively. When they decrease to 20%/h, the result solved by SAA and IDM reduced by 14% and 24%, respectively. It indicates that IDM is more sensitive to flexibility parameters than SAA. This is mainly because the reduction in flexibility shrinks the safe region more in IDM and leads to more conservative results. Figure 5 shows the results obtained by the proposed methods with ω = 0 in mode 3. Similarly, IDM obtains a better result than SAA at the initial stage, and SAA surpasses IDM when the flexibility parameters are less than 33%/h.

TABLE 5

TABLE 5. Cases for sensitivity analysis with different parameters.

FIGURE 4

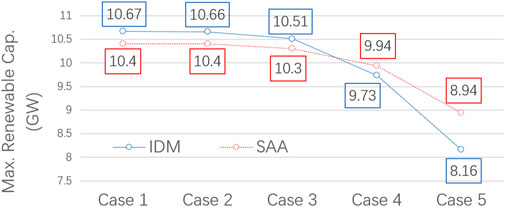
FIGURE 4. Maximal renewable installation capacity with various flexibilities. The renewable installation capacity decreases with the reducing flexibility. SAA surpasses IDM after case 3 in terms of capacity.

FIGURE 5

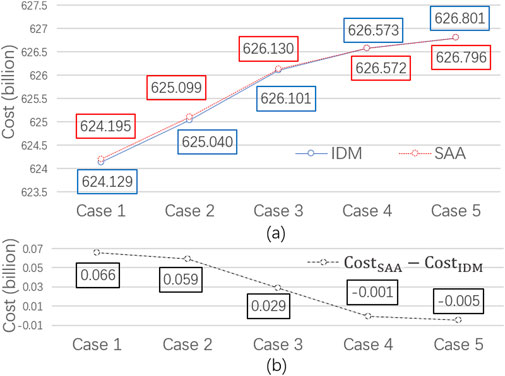
FIGURE 5. Minimum 10-year cost solved by IDM and SAA under different cases. (A) Cost of two methods. (B) Cost of SAA minus the cost of IDM.

The solution time of SAA is approximately 9,000 s, while the solution time of IDM is less than 1 s. Thus, IDM has better computation performers. However, it is worth mentioning that an explicit re-dispatch policy can be provided by SAA, while the IDM has to solve an extra economic dispatch (ED) problem in the re-dispatch progress. The re-dispatch policy is an analogy to the participation coefficient in AGC, except that it is optimally determined. Flexible resources can be re-dispatched based on a closed-form solution when the uncertainty is materialized.

5 Conclusion

This paper introduces a novel multistage HVDC tie-line planning-operation model that incorporates a variable uncertainty set. The model considers the uncertain nature of renewable generation and incorporates a multistage re-dispatch strategy to ensure solution feasibility in practice. To solve the multistage model, we propose a surrogate affine-based method and implicit decision-based method, which effectively handle the variable uncertainty set. To validate the effectiveness of the proposed approaches, we conducted simulation cases using a real-world two-area system. Numerical tests show that the proposed approaches can unlock inter-regional flexibility and help increase renewable accommodation. In addition, we also find that the flexibility parameters are the dominant factors affecting the feasible region of the solution approaches. SAA outperforms IDM in a system with low flexibility, while IDM shows better performance in a system with high flexibility. IDM has better computation efficiency than SAA, while SAA can provide an extra closed-form re-dispatch policy. The closed-form re-dispatch policy allows for fast calculations and decision-making, ensuring that adjustments to the HVDC tie-line system can be made promptly and effectively. Planners and operators can easily determine the appropriate actions to take in real time based on the uncertainty of renewable generation. Utility can choose the proposed methods under different realistic conditions.

In future studies, we plan to extend the current model to include more HVDC tie-lines, enabling a more comprehensive analysis of the system. Additionally, we aim to improve the computation efficiency of the proposed approaches to make them more practical and scalable for larger-scale power systems.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

NW: writing–original draft and writing–review and editing. LZ: writing–review and editing. SL: writing–review and editing. HY: writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work is financially supported by State Grid Science and Technology Project No. 5100-202156006A-0-0-00.

Conflict of interest

Authors NW and SL were employed by State Grid Economic and Tech. Research Institute. Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Cobos, G., Arroyo, J. M., Alguacil, N., and Street, A. (2018). Network-constrained unit commitment under significant wind penetration: a multistage robust approach with non-fixed recourse. Appl. Energy 232, 489–503. doi:10.1016/j.apenergy.2018.09.102

CrossRef Full Text | Google Scholar

Guo, Y., Bose, S., and Tong, L. (2018). On robust tie-line scheduling in multi-area power systems. IEEE Trans. Power Syst. 33, 4144–4154. doi:10.1109/TPWRS.2017.2775161

CrossRef Full Text | Google Scholar

Hreinsson, K., Scaglione, A., and Analui, B. (2019). Continuous time multi-stage stochastic unit commitment with storage. IEEE Trans. Power Syst. 34, 4476–4489. doi:10.1109/TPWRS.2019.2923207

CrossRef Full Text | Google Scholar

Li, Z., Song, Q., An, F., Zhao, B., Yu, Z., and Zeng, R. (2021). Review on dc transmission systems for integrating large-scale offshore wind farms. Energy Convers. Econ. 2, 1–14. doi:10.1049/enc2.12023

CrossRef Full Text | Google Scholar

Li, Z., Wu, W., Shahidehpour, M., and Zhang, B. (2016). Adaptive robust tie-line scheduling considering wind power uncertainty for interconnected power systems. IEEE Trans. Power Syst. 31, 2701–2713. doi:10.1109/TPWRS.2015.2466546

CrossRef Full Text | Google Scholar

Lin, W., Yang, Z., and Yu, J. (2020). Flexibility of interconnected power system operation: analysis, evaluation and prospection. Energy Convers. Econ. 1, 141–150. doi:10.1049/enc2.12013

CrossRef Full Text | Google Scholar

Lorca, A., and Sun, X. A. (2017). Multistage robust unit commitment with dynamic uncertainty sets and energy storage. IEEE Trans. Power Syst. 32, 1678–1688. doi:10.1109/TPWRS.2016.2593422

CrossRef Full Text | Google Scholar

Lorca, A., Sun, X. A., Litvinov, E., and Zheng, T. (2016). Multistage adaptive robust optimization for the unit commitment problem. Operations Res. 64, 32–51. doi:10.1287/opre.2015.1456

CrossRef Full Text | Google Scholar

Moradi-Sepahvand, M., and Amraee, T. (2021). Hybrid AC/DC transmission expansion planning considering HVAC to HVDC conversion under renewable penetration. IEEE Trans. Power Syst. 36, 579–591. doi:10.1109/TPWRS.2020.2988195

CrossRef Full Text | Google Scholar

Qiu, T., Xu, B., Wang, Y., Dvorkin, Y., and Kirschen, D. S. (2017). Stochastic multistage coplanning of transmission expansion and energy storage. IEEE Trans. Power Syst. 32, 643–651. doi:10.1109/tpwrs.2016.2553678

CrossRef Full Text | Google Scholar

Wang, H., Qin, H., Zhou, C., Feng, L. I., Xiaohui, X. U., and Pan, X. (2019a). Cross-regional day-ahead to intra-day scheduling model considering forecasting uncertainty of renewable energy. Automation Electr. Power Syst. 43, 60–67. doi:10.7500/AEPS20190122003

CrossRef Full Text | Google Scholar

Wang, S., Geng, G., and Jiang, Q. (2019b). Robust Co-planning of energy storage and transmission line with mixed integer recourse. IEEE Trans. Power Syst. 34, 4728–4738. doi:10.1109/TPWRS.2019.2914276

CrossRef Full Text | Google Scholar

Wogrin, S., and Gayme, D. F. (2015). Optimizing storage siting, sizing, and technology portfolios in transmission-constrained networks. IEEE Trans. Power Syst. 30, 3304–3313. doi:10.1109/TPWRS.2014.2379931

CrossRef Full Text | Google Scholar

Ye, H. (2018). Surrogate affine approximation based co-optimization of transactive flexibility, uncertainty, and energy. IEEE Trans. Power Syst. 33, 4084–4096. doi:10.1109/tpwrs.2018.2790170

CrossRef Full Text | Google Scholar

Yifan, Y. L., McCalley, J. D. M, and James, D. (2015). Design of a high capacity inter-regional transmission overlay for the u.s. IEEE Trans. Power Syst. 30, 513–521. doi:10.1109/tpwrs.2014.2327093

CrossRef Full Text | Google Scholar

Yin, S., and Wang, J. (2022). Generation and transmission expansion planning towards a 100% renewable future. IEEE Trans. Power Syst. 37, 3274–3285. doi:10.1109/tpwrs.2020.3033487

CrossRef Full Text | Google Scholar

Zeng, F., Bie, Z., Han, Z., Li, X., Zhi, Y., and Zhang, Y. (2017). Long-term wind accommodation of interconnected power grids via hvdc tie-line based on aggregate unit model. In 2017 IEEE Conference on Energy Internet and Energy System Integration (EI2). 1–6. doi:10.1109/EI2.2017.8245394

CrossRef Full Text | Google Scholar

Zhai, Q., Li, X., Lei, X., and Guan, X. (2017). Transmission constrained UC with wind power: an all-scenario-feasible MILP formulation with strong nonanticipativity. IEEE Trans. Power Syst. 32, 1805–1817. doi:10.1109/TPWRS.2016.2592507

CrossRef Full Text | Google Scholar

Zhao, J., Zhang, Y., Liu, Z., Hu, W., and Su, D. (2022). Distributed multi-objective day-ahead generation and hvdc transmission joint scheduling for two-area hvdc-linked power grids. Int. J. Electr. Power and Energy Syst. 134, 107445. doi:10.1016/j.ijepes.2021.107445

CrossRef Full Text | Google Scholar

Zhong, H., Xia, Q., Ding, M., and Zhang, H. (2015). A new mode of hvdc tie-line operation optimization for maximizing renewable energy accommodation. Auto. Electr. Power Syst. 39, 36–42. doi:10.7500/AEPS20140529005

CrossRef Full Text | Google Scholar

Zhou, M., Zhai, J., Li, G., and Ren, J. (2018). Distributed dispatch approach for bulk ac/dc hybrid systems with high wind power penetration. IEEE Trans. Power Syst. 33, 3325–3336. doi:10.1109/TPWRS.2017.2762358

CrossRef Full Text | Google Scholar

Zhou, Y., Zhai, Q., and Wu, L. (2021). Multistage transmission-constrained unit commitment with renewable energy and energy storage: implicit and explicit decision methods. IEEE Trans. Sustain. Energy 12, 1032–1043. doi:10.1109/TSTE.2020.3031054

CrossRef Full Text | Google Scholar

Nomenclature