- 1School of Electric Power Engineering, South China University of Technology, Guangzhou, China
- 2CSG Electric Power Research Institute China Southern Power Grid, Guangzhou, China
In this paper, a resilient control strategy is proposed to improve the stability of frequency and voltage recovery for the islanded microgrid (MG) under hybrid cyber attacks. To deal with the common false data injection attacks (FDI) and denial of service attacks (DoS) in MGs, the proposed resilient control strategy utilizes the observers to accurately estimate the potential FDI signals on both the sensors and actuators of each distributed generation unit (DG) and reconstruct the unavailable states in the system to enhance the system’s ability actively. The ultimate uniform boundedness (UUB) of the system under hybrid cyber attacks is proved by the Lyapunov stability theory. Finally, an islanded MG system is established in MATLAB/SIMULINK, and multiple scenarios are simulated to verify the effectiveness of the method.
1 Introduction
With the development of smart grid technologies, MGs are evolving into typical cyber-physical systems (CPS) by integrating more and more renewable energy sources, monitoring devices, communication facilities, and control systems. MGs can operate in both grid-connected mode and islanded mode (Albarakati et al., 2022). In islanding mode, due to the lack of support from the main grid, MGs are sensitive to disturbances such as power fluctuations, load switching, and cyber attacks, which can cause system instability or even large-scale blackouts. To improve system operation performance, MGs widely adopt the hierarchical control structure in islanded mode (Kang et al., 2018). The primary layer is the lowest control layer in MGs, including voltage and current control loops. In the primary control, each DG only uses its own measurements, so the control layer will cause steady-state errors in frequency and voltage. The secondary layer is responsible for voltage/frequency recovery and active/reactive power sharing between DGs (Dörfler et al., 2015). The tertiary layer is responsible for implementing economic dispatching, operation dispatching, and power flow between MGs and the main grid in the grid-connected mode (Liu et al., 2023).
Centralized and distributed control strategies are common approaches to achieving secondary control objectives in AC MGs. In recent years, centralized algorithms have been increasingly replaced by distributed schemes for secondary controllers since distributed techniques offer better robustness (no single point of failure) and scalability (Feng and Ma, 2022; Yang et al., 2022). Distributed consensus algorithms based on multiagent systems (MAS) have been widely studied in the secondary control of MGs (Ma et al., 2017). Since MAS-controlled AC MGs are typical CPS, researchers mainly concentrated on challenges related to unmodeled dynamics (Shotorbani et al., 2017; Hu et al., 2023), physical disturbances (Hu and Bhowmick, 2020), communication failures (Shahab et al., 2019), stability analysis (Majumder et al., 2009; Zhang and Fan, 2022), high integration of DGs (Sharma et al., 2018), economical and reliable operation of MGs (Albarakati et al., 2022; Liu et al., 2023), and synchronization problems in grid-connected mode (Hossain et al., 2019; Elshenawy et al., 2022), etc.
In addition to the objective and common problems mentioned above, MG CPS is very vulnerable to extreme human-made attacks such as cyber attacks. For example, in 2015, the power grid of Ukraine suffered from the coordinated attack of multiple types of cyber-attacks, leading to large-scale power failure (Dibaji et al., 2019). Common cyber-attacks include disruption attacks and deception attacks, etc (Dibaji et al., 2019; Chen et al., 2019). Among them, DoS and FDI attacks are considered to be the most prevalent and destructive forms of attacks (Uddin et al., 2023). Specifically, FDI attacks are typically deception attacks that inject or modify real data from sensors, actuators, and communication links in the secondary layer to degrade performance (Beg et al., 2017; Ding et al., 2018). DoS attacks can prevent data transmission in communication links (Lian et al., 2022). In a closed-loop feedback control system that uses distributed algorithms, such as MGs, FDI and DoS attacks have always been regarded as persistent security threats (Tan et al., 2020). In Zhang et al. (2006), the authors have concluded that the IEC 61850 protocol and its extensions are recommended when modeling the communication infrastructure for the MG. However, IEC 61850 and TCP/IP protocols are still potentially threatened by FDI attacks, which are tested by the remote monitoring based adaptive LTC controller (Wang and Yang, 2018) and a TCP/IP-based networked dc servo system (Yu et al., 2019). Industrial control systems security mechanisms such as industrial firewalls and white lists cannot effectively deal with these threats. If the cyber attacks on the MG’s communication system are not detected and corrective actions are not implemented in time, the DGs in the MG will be unable to supply the required power, which deviate from the system operating point and endanger the security and stability (Wang et al., 2023). Furthermore, note that FDI and DoS attacks may occur concurrently, resulting in a more devastating impact and lower detection probability, seriously jeopardizing the system’s security and stability (Liu et al., 2019; Tadepalli and Pullaguram, 2022). Therefore, it is crucial to investigate the resilient distributed control problems that arise from the simultaneous presence of DoS and FDI attacks.
In previous works, resilient control strategies for islanded MGs under FDI and DoS attacks are generally studied separately. Several detection, identification, and mitigation schemes have been proposed for DGs under FDI attacks in MGs. In Peng et al. (2019), Abhinav et al. (2017), the influence of FDI attacks is alleviated by detecting the attacked DG and correcting the confidence factor of the communication links. Although these methods can resist various attacks on communication links, additional assumptions about the connectivity of the communication topology and the number of compromised DGs are usually required. Recently, several artificial intelligence algorithms, including reinforcement learning and unsupervised learning, have been used to detect and mitigate cyber attacks (Tian et al., 2022; Ramotsoela et al., 2023). However, the effectiveness of these data-driven schemes depends on sufficient historical data sets, which may have challenges such as a high amount of calculation, poor compatibility, and limited resistance to parameter changes. In addition, estimating attack signals or reconfiguring the system states by designing the state observers is also an essential technique to enhance system resilience. In Afshari et al. (2020), deception attack, dynamic interference, and uncertainty are regarded as bounded disturbances and an adaptive control is introduced to compensate for the influence of disturbances. In Jiang et al. (2021), Mohiuddin and Qi (2021), Shi et al. (2021), Barzegari et al. (2022), Muktiadji et al. (2022), Zhou et al. (2023), the distributed observer frameworks are used to estimate the real states of the system, respectively. In Wang et al. (2022a), Wang et al. (2022b), Zhan et al. (2023), the virtual layer-based compensation strategies are proposed to mitigate FDI attacks. For DoS attacks, a resilient controller based on sampling and communication mechanisms is employed to enhance the DC MGs against DoS attacks by rigorously limiting the frequency and duration of attacks (Lian et al., 2021). In Xu and Ma (2020), Li et al. (2022), Liu and Che (2022), distributed control schemes based on security event triggering mechanisms are proposed to ensure the secondary control objectives and secure economic dispatch of MG under DoS attacks, which establish a connection between the triggering mechanism and DoS attacks.
To summarize, the aforementioned methods mainly focus on the effects of MGs under FDI or DoS attacks, and few studies have investigated the resilient control of MGs that are simultaneously subjected to FDI and DoS attacks. Currently, to resist the influence of various cyber attacks, (Wang et al., 2023), proposes an adaptive control strategy to deal with the bounded sensor FDI attacks and tolerate the intermittent DoS attacks on the communication links. In Liu et al. (2021), the authors develop an adaptive gain-based control scheme to cope with intermittent DoS and impulse signal FDI attacks. However, these methods either do not address both sensor and actuator attacks in a unified framework or assume that these FDI signals are regarded as bounded natural disturbances, etc. Furthermore, the control strategies in Wang et al. (2023), Liu et al. (2021) do not consider the impact of DoS attacks on the controller, i.e., the control inputs are forced to zero when the communication links under DoS attacks. Although these studies have some effect, the resilience under attacks is not satisfactory. Therefore, the main goal of this paper is to develop a resilient distributed method to effectively address both FDI and DoS attacks in MGs. The core challenges that need to be addressed to achieve this goal include:
(1) How to develop an effective distributed resilient method to eliminate or mitigate the effects of attacks when FDI signals are unknown and even unbounded, and sensors and actuators of numerous DGs may be attacked simultaneously?
(2) How to cleverly design the resilient method to avoid the divergence or even infinite growth of the system states when MGs subjected to hybrid attacks, while ensuring the realization of secondary control objectives?
As a result, it is essential to consider designing a general and resilient framework to resist the impact of hybris attacks. Compared with the existing research, the main contributions can be summarized as follows:
1) Compared to most recent works that focus solely on the impact of single cyber attacks on islanded MGs, this paper further proposes a distributed control framework incorporating resilience against simultaneous sensor, actuator, and DoS attacks for MG systems. It is more practical for island MGs in complex working environments.
2) The proposed resilient control strategy utilizes the observer to accurately estimate the potential FDI signals on both the sensors and actuators of each DG and is capable of accommodating unbounded FDI attacks on any number of DGs, thus enhancing its robustness against potential attacks. During DoS attacks, the open-loop observer is used to reconstruct the unavailable neighbor DG state to enhance the system’s ability to resist DoS attacks actively.
3) The system’s stability is demonstrated using the Lyapunov function, which shows that the system can achieve UUB when subjected to hybrid cyber attacks.
2 Modeling of AC MGs and cyber attacks
2.1 Notations and graph theory
In this paper,
2.2 Dynamic modeling of MGs
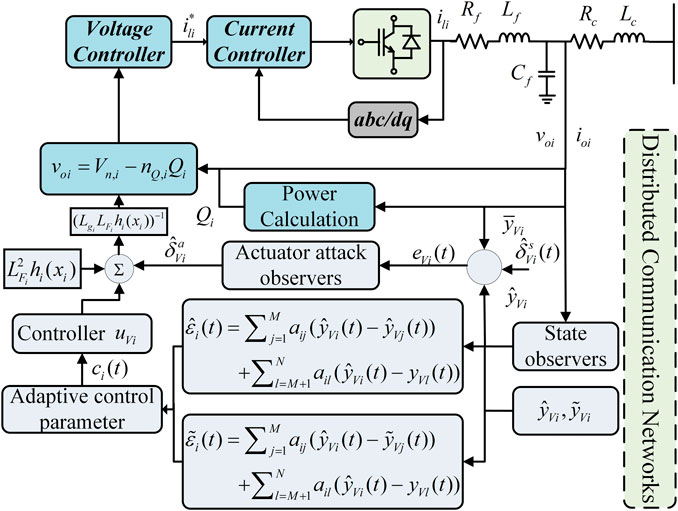
In this paper, a typical inverter-based islanded MG is taken as the research object, and the control framework of a grid-forming converter is shown in Figure 1. In the grid-forming converters, the islanded MG includes two parts: 1) physical layer, including inverter-based DGs and their controllers, LC filter, coupling inductor (Pogaku et al., 2007), transmission lines, and loads; 2) the control layer, including the hierarchical control structure; 3) communication layer, which usually contains only communication links composed of directed or undirected graphs.
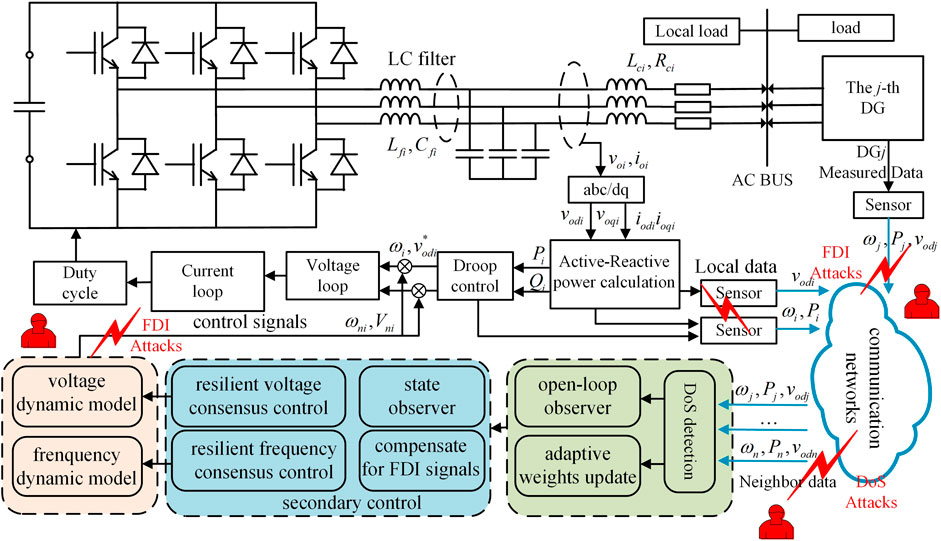
FIGURE 1. The MG layers schematic, including the physical, control, and communication layers. The control layer gives the schematic diagram of the proposed resilient control framework.
The secondary control is usually achieved by introducing additional regulation terms for voltage/frequency consensus as well as power sharing, as follows (Hennane et al., 2023):
where
In MG dynamic modeling and control system design, the model of the MG system can safely ignore the fast switching model in Dehkordi et al. (2016), so the nonlinear dynamics model of the grid-forming DGs in the d-q reference system can be expressed as.
where
Since the dynamic characteristics of the current and voltage controllers are much faster than the primary controller, the dynamic characteristics of the current and voltage controllers can be ignored in the study of the secondary controller. Therefore, the secondary control problem is transformed into a tracking control problem using the input-output feedback linearization technique. For the secondary voltage control of MGs, let
where
where
Similar to the voltage dynamic model, according to Eq. 3, the system frequency dynamics can be obtained using feedback linearization as:
The above equation can be written in the following form:
2.3 Modeling of FDI attacks
Complex FDI attacks can modify real data in sensors, actuators, and communication links simultaneously. In this paper, we consider the case of unknown cyber attacks that occur in sensors and actuators in a MG system as shown in Figure 1. The sensor FDI corrupts the measured states or output signals, while the actuator attacks modify the control signals generated by the secondary controller. Therefore, the following typical FDI attack model is used for the islanded MG system:
where
Assumption 1. Sensor attack signals
Remarks 1:. Malicious signals are often modeled in the papers as random disturbances such as constants, steps, sines, and noise (Afshari et al., 2020; Barzegari et al., 2022). However, unlike random disturbances such as power fluctuations or noise, FDI signals should not be regarded as unintentionally caused bounded signals. Moreover, the attacker carefully designs cyber attacks and does not need information about the system dynamics to perform FDI. Therefore, inspired by Wang et al. (2022b), this paper argues that malicious cyber attacks can be unbounded time-varying signals, i.e., the amplitude of a FDI signal is allowed to be sufficiently large, but as long as its derivatives are constrained, the malicious signals will not grow at an infinitely fast rate. Due to these aspects, the designs available in Afshari et al. (2020), Barzegari et al. (2022) may not be directly applicable. Additionally, the model is universal for the problem of frequency and voltage restoration in MGs with bounded disturbances (attacks, disturbances, uncertainties, etc.).
2.4 Modeling of DoS attacks
The MG system based on the MAS distributed control strategy is shown in Figure 2. The communication network of the MG is usually not sufficiently resistant to DoS attacks. Once the DG fails to receive the states sent by all its neighbors, the control objective of the system will not be accomplished. Consider a class of non-periodic DoS attacks and assume that one DoS attack over a period of time can be denoted as
Assumption 2. There exist constants
Remark 2. Assumption 2 limits the duration of DoS attacks considering the limited attack resources and the self-healing mechanisms of real systems, which are widely used in Xu and Ma (2020)).
3 Distributed resilient voltage control under hybrid attack
This section proposes a resilient control scheme for hybrid network attacks in secondary control of MGs. The proposed resilient control framework is shown in Figure 2, and the UUB stability of the whole system is guaranteed.
3.1 Design of resilient voltage controller
The real states of MGs is usually not available due to FDI attacks. Therefore, this paper first introduces state observers to reconstruct the real states of the system and estimate the sensor and actuator FDI signals. To compensate for the effect of FDI on MGs, the following state observers are designed:
where
where
where
To achieve frequency and voltage restoration and active power and reactive power sharing among DGs, we design the auxiliary control inputs
where
When the communication link (i, j) suffers from DoS attacks, the states sent by the j th DG during DoS cannot be received by the i th DG. Therefore, to mitigate or cope with the impact of DoS attacks on the secondary controller as much as possible, inspired by the literature (Xiao and Dong, 2020), the following open-loop observer is introduced to reconstruct the unavailable state of the MG system during DoS as follows
where
Remark 3. Proj{·} denotes the projection operator, which has been used to design fully distributed controllers and fault-tolerant controls (Xiao and Dong, 2020). Since it is difficult for the open-loop observer to recover the lost data perfectly, introducing the projection operator and the adaptive controller constrain the tracking error during DoS, preventing the system’s consensus error from diverging or even being unbounded. In addition, the open-loop estimator is activated only during the attack. If a particular DG’s states are unavailable, the neighboring DGs are aware of the attacks. The last estimate is kept until the communication state of the MG returns to normal.
3.2 Stability analysis
Before moving forward, the estimated errors of the FDI signals are defined as
Let
where
Let
Next, the stability analysis of MGs under hybrid attack is discussed. The main results are as follows.
Theorem 1. Assuming that the communication topology
such that
where
The block diagram for the proposed resilient control scheme is depicted in Figure 2. Proof of stability for the proposed scheme is also presented in the Supplementary Appendix SA1.
Remarks 4. The main differences between this paper and related work are clarified in the following two aspects: i) Compared with most recent work that only considers a single cyber attack, this paper proposes a resilient control framework that resists both FDI and DoS attacks. ii) In Wang et al. (2023), Liu et al. (2021), although resilient control strategies are designed to resist FDI and DoS attacks, the ability of the system to actively resist DoS attacks has not been investigated, that is, when the communication network is subjected to DoS attacks, the control input is forced to zero. In addition, the type of FDI attacks is limited to bounded actuator attacks. On the contrary, this paper proposes a resilient control strategy that can effectively compensate for the unbounded FDI attacks of sensors and actuators and reconstruct the unavailable neighbor DG state to resist DoS attacks actively.
Remark 5. Similar to the resilient voltage control, the frequency consensus error can be UUB under hybrid attacks by applying similar schemes (10)–(16). The proof is similar to Theorem 1.
4 Simulation analysis
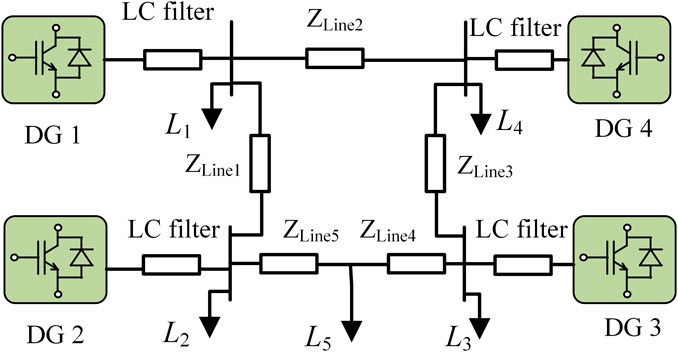
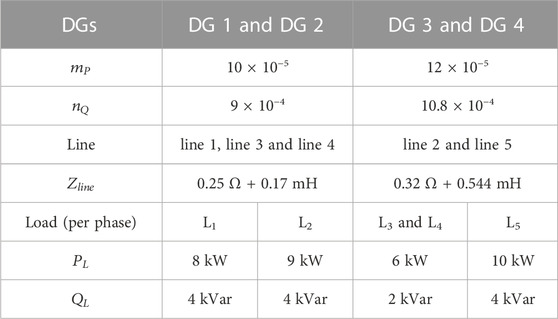
In order to verify the performance of the proposed resilient distributed control strategy, a 380V/50Hz islanded MG with four inverter-based DGs is taken as the test system, as shown in Figure 3. The simulation is analyzed in the MATLAB/Simulink platform. The parameters of load, transmission line, and DG controller can be found in Table 1. The effectiveness of the proposed control strategy is verified through several scenarios such as load fluctuation, plug-and-play (P&P) of DG, and hybrid cyber attacks.
4.1 Distributed resilient control strategy without attacks
In this section, the performance of the proposed resilient distributed frequency and voltage controller is analyzed by simulation without considering any cyber attacks. The parameters of the controllers are chosen as
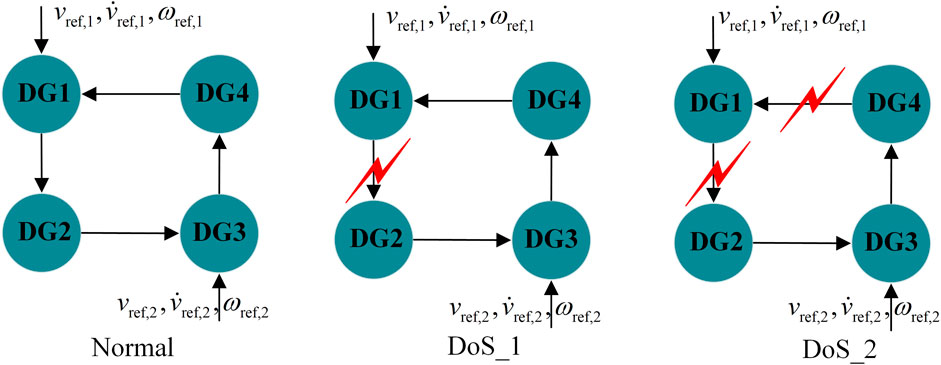
The results are discussed in time sequence as below: i) at t = 1.0 s, the proposed resilient controller starts up, and the communication topology between DGs is shown in Figure 4, given the voltage reference value
The simulation results are shown in Figure 5. When the proposed resilient control is adopted, the islanded MG frequency is restored to 50Hz and the output voltage of DGs returns to the range of 380∼390 V. The load fluctuation and P&P of DG4 occur in the MG system during 2.0∼6.0 s. Under these system disturbances, the frequency and active power can quickly maintain consistency and respond rapidly. However, due to factors such as MG line impedance mismatch, there is a deviation in the voltage and reactive power consensus. Figure 5D gives the reactive power dynamic characteristics of the system under load fluctuations. The reactive power deviation rises at t = 5 s as the MG’s load distribution becomes more unbalanced. During the P&P of DG4, the frequency, voltage, active power, and reactive power of MG remain stable within a reasonable range. The simulation results show that the proposed method will not influence the normal operation of the MG system.
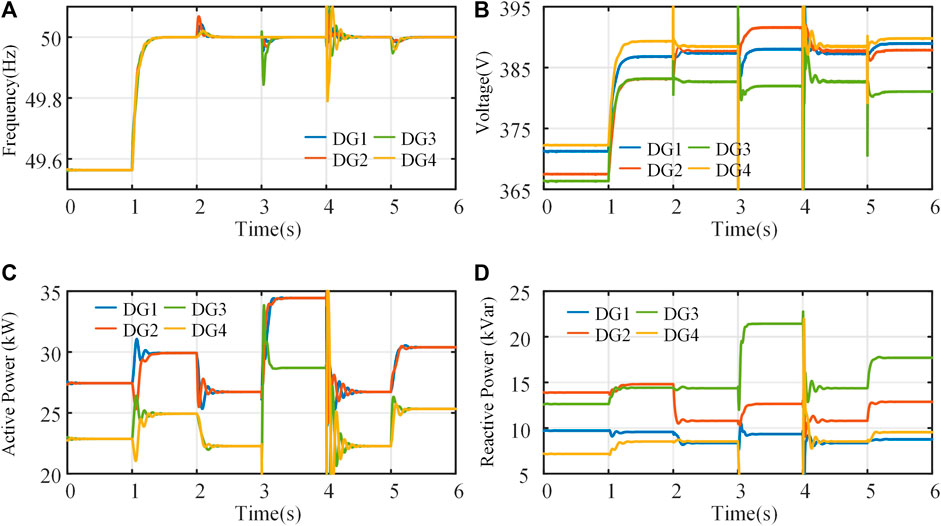
FIGURE 5. Performance evaluation of the proposed method without cyber attacks: (A) frequency, (B) voltage, (C) active power, (D) reactive power.
4.2 Distributed resilient control strategies under hybrid attacks
In this subsection, the MG system is considered to suffer from both FDI attacks and DoS attacks. Also, the performance of the MG system with distributed controllers using traditional consensus algorithms is tested to show the impact of hybrid attacks. It will also serve as a benchmark for comparison with the proposed approach. The effectiveness of the proposed resilient control strategy in secondary frequency and voltage control is evaluated for the sensor and actuator attacks and intermittent interruptions of the communication network in Figure 4, respectively. The duration of the DoS attacks is designed to
Simulation events are set as follows: i) at t = 0 s, the MG operates in an islanded mode, and the DoS attacks persist and lead to two communication topologies as shown in Figure 4. ii) at t = 0.5 s, the proposed resilient controller is activated and an actuator is attacked at DG3 with
Figures 6A, B depict the dynamic characteristics of the proposed resilient control strategy in secondary voltage control. It can be found that the existence of DoS attacks will affect the control performance, resulting in system voltage and power fluctuations. However, if the duration of the DoS attacks satisfies (25), the system’s stability will not be threatened. Furthermore, the communication topology after DoS attacks is complete, which can guarantee system convergence under the proposed resilient approach. During 0.5∼6 s, the system suffers from sinusoidal form and linear growth FDI attacks, respectively, and the simulation results show that as long as the derivatives of the injected FDI signals are bounded [the growth rate of the malicious signals satisfies (30)], the resilient control strategy ensures that the system achieves UUB. The estimated values of the FDI attack signals are shown in Figure 7. It can be seen that the proposed control strategy can better estimate the FDI attack signals in the system, which will accurately and effectively alleviate the impact of FDI attacks on the MG. Besides, the effectiveness of the proposed method can be clearly demonstrated by comparing the results of Figure 6 and Figure 8.
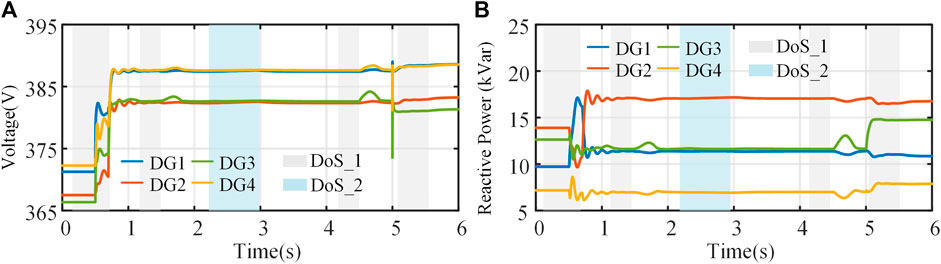
FIGURE 6. The test results of the proposed resilient voltage control under hybrid attack: (A) voltage, (B) reactive power.
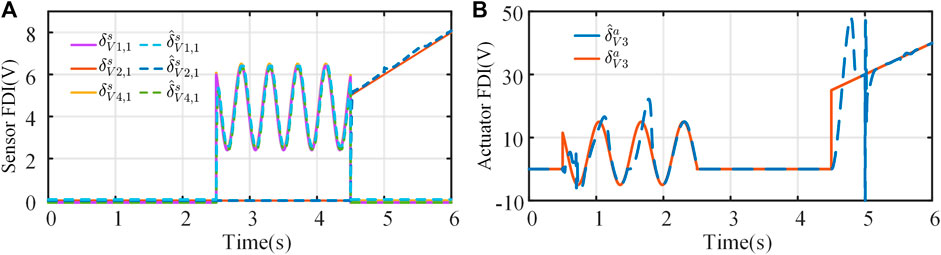
FIGURE 7. Sensor and actuator attack signals (solid lines) and their estimated values (dashed lines): (A) sensor FDI, (B) actuator FDI.
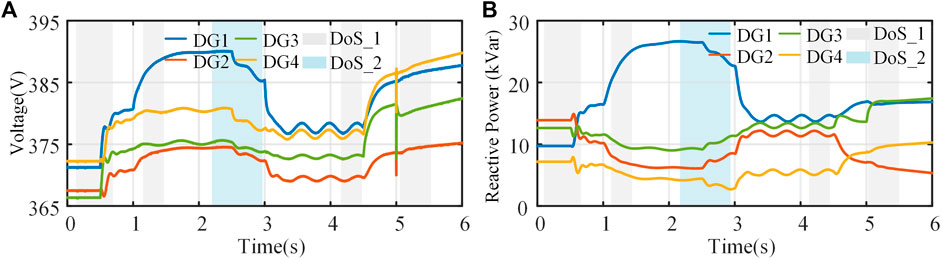
FIGURE 8. The test results of the traditional voltage consensus algorithms under hybrid attack: (A) voltage, (B) reactive power.
Figure 9 shows the performance of the proposed control strategy in secondary frequency control. In the case of load fluctuation and mixed network attack, the proposed method can still ensure the system’s normal operation. In addition, the proposed algorithm can effectively deal with bounded or unbounded sensor and actuator attacks. Compared with the results of the traditional consensus algorithm shown in Figure 10, the proposed strategy effectively suppresses the frequency and active power fluctuations caused by hybrid attacks in frequency control and performs better.
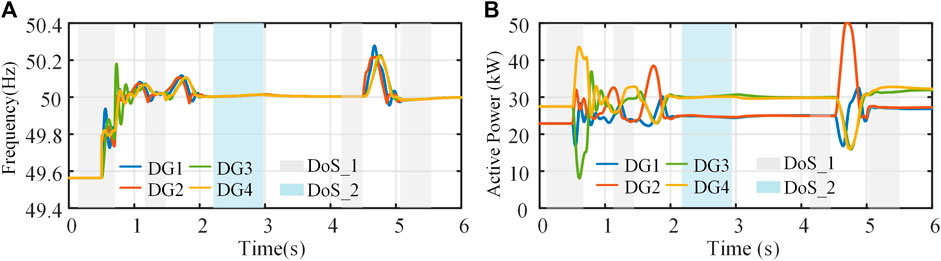
FIGURE 9. The test results of resilient frequency control under hybrid attack: (A) frequency, (B) active power.
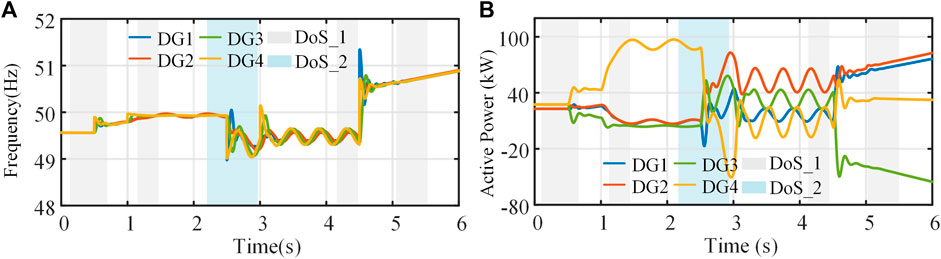
FIGURE 10. The test results of the traditional frequency consensus algorithms under hybrid attack: (A) frequency, (B) active power.
4.3 Comparison with other resilient control methods
In this section, the proposed control method is compared with a cyber-resilient control approach in the latest work (Wang et al., 2023). The cyber-resilient control approach is based on an adaptive strategy to compensate for bounded FDI attacks on the secondary controller, and it can also tolerate DoS attacks on the communication link. Considering the characteristics of the cyber-resilient controller, the following modifications and clarifications are made in this paper: 1) the cyber-resilient controller only targets bounded actuator attacks, and it utilizes adaptive techniques to mitigate hybrid network attacks and does not reconstruct or estimate unavailable states and FDI attack signals in the system; 2) the cyber-resilient control approach is designed for secondary frequency control. This section only compares the frequency results of the MG system under hybrid attacks.
Figure 11 shows the performance of the cyber-resilient controller in the secondary frequency control. Compared with the resilient control strategy proposed in this paper, both of them have better performance under bounded actuator FDI signals and DoS attacks. During 0.5–2.5 s, both the cyber-resilient and the proposed controller can effectively resist the influence of the bounded sensor FDI signals, and the frequency and active power of the system only fluctuate or shift slightly. After t = 2.5 s, the system suffers from sensor FDI and linear growth FDI signals, respectively. Compared with the traditional consensus algorithm, the cyber-resilient controller can alleviate the impact of unbounded FDI signals but cannot effectively compensate for attacks. The system with the cyber-resilient controller is awful under unbounded FDI attacks. Therefore, the resilience strategy proposed in this paper can better resist the influence of multiple concurrent attacks and improve the stability of the islanded MG system under hybrid attacks.
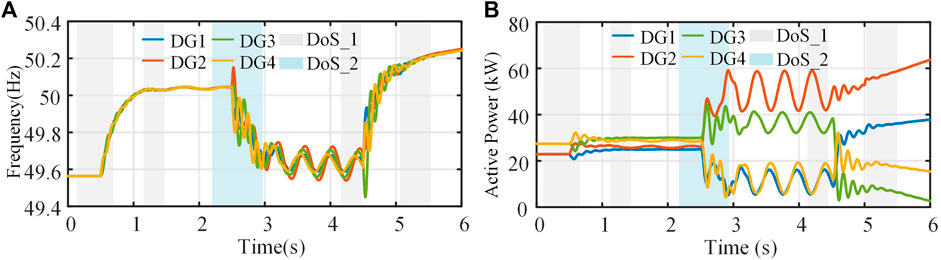
FIGURE 11. Performance evaluation of cyber-resilient controller under hybrid attack: (A) frequency, (B) active power.
5 Conclusion
To deal with the frequency and voltage restoration problem of islanded MGs under hybrid FDI and DoS attacks, this paper proposes a resilient distributed control protocol to improve the robustness of frequency and voltage restoration. Using the state observers, the proposed control strategy can effectively estimate the potential FDI attack signals on each DG. The open-loop observer is utilized to reconstruct the neighbor information during DoS attacks, and the adaptive parameters are used to constrain the consensus error. In addition, the proposed control strategy can improve the system’s ability to resist unbounded FDI attacks on sensors and actuators and is more practical in real-world security applications. The stability of the system is proved by the Lyapunov function, which shows that the system can realize UUB under hybrid attacks. The simulation results verify that the proposed control method can effectively mitigate or cope with the impact of concurrent DoS and FDI attacks on MGs. Future work will further explore the coordinated control framework of the AC MG system under other attack scenarios, such as replay attacks, communication delays, and failures.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
YL: Writing–original draft, Writing–review and editing. ZD: Writing–original draft, Writing–review and editing. YC: Writing–original draft, Writing–review and editing. HZ: Writing–original draft, Writing–review and editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was supported by the State Key Laboratory of HVDC (Project No. SKLHVDC-2022-KF-14).
Conflict of interest
Author YC was employed by CSG Electric Power Research Institute China Southern Power Grid.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2023.1320968/full#supplementary-material
References
Abhinav, S., Modares, H., Lewis, F. L., Ferrese, F., and Davoudi, A. (2017). Synchrony in networked microgrids under attacks. IEEE Trans. Smart Grid 9 (6), 6731–6741. doi:10.1109/tsg.2017.2721382
Afshari, A., Karrari, M., Baghaee, H. R., and Gharehpetian, G. B. (2020). Resilient synchronization of voltage/frequency in AC microgrids under deception attacks. IEEE Syst. J. 15 (2), 2125–2136. doi:10.1109/jsyst.2020.2992309
Albarakati, A. J., Boujoudar, Y., Azeroual, M., Eliysaouy, L., Kotb, H., Aljarbouh, A., et al. (2022). Microgrid energy management and monitoring systems: a comprehensive review. Front. Energy Res. 10, 1097858. doi:10.3389/fenrg.2022.1097858
Barzegari, Y., Zarei, J., Razavi-Far, R., Saif, M., and Palade, V. (2022). Resilient consensus control design for DC microgrids against false data injection attacks using a distributed bank of sliding mode observers. Sensors 22 (7), 2644. doi:10.3390/s22072644
Beg, O. A., Johnson, T. T., and Davoudi, A. (2017). Detection of false-data injection attacks in cyber-physical DC microgrids. IEEE Trans. industrial Inf. 13 (5), 2693–2703. doi:10.1109/tii.2017.2656905
Cao, G., Jia, R., and Dang, J. (2022). Distributed resilient mitigation strategy for false data injection attack in cyber-physical microgrids. Front. Energy Res. 10, 845341. doi:10.3389/fenrg.2022.845341
Chen, L., Wang, Y., Lu, X., Zheng, T., Wang, J., and Mei, S. (2019). Resilient active power sharing in autonomous microgrids using pinning-consensus-based distributed control. IEEE Trans. Smart Grid 10 (6), 6802–6811. doi:10.1109/tsg.2019.2911344
Dehkordi, N. M., Sadati, N., and Hamzeh, M. (2016). Fully distributed cooperative secondary frequency and voltage control of islanded microgrids. IEEE Trans. Energy Convers. 32 (2), 675–685. doi:10.1109/tec.2016.2638858
Deng, C., and Che, W. W. (2019). Fault-tolerant fuzzy formation control for a class of nonlinear multiagent systems under directed and switching topology. IEEE Trans. Syst. Man, Cybern. Syst. 51 (9), 5456–5465. doi:10.1109/tsmc.2019.2954870
Dibaji, S. M., Pirani, M., Flamholz, D. B., Annaswamy, A. M., Johansson, K. H., and Chakrabortty, A. (2019). A systems and control perspective of CPS security. Annu. Rev. control 47, 394–411. doi:10.1016/j.arcontrol.2019.04.011
Ding, D., Han, Q. L., Xiang, Y., Ge, X., and Zhang, X. M. (2018). A survey on security control and attack detection for industrial cyber-physical systems. Neurocomputing 275, 1674–1683. doi:10.1016/j.neucom.2017.10.009
Dörfler, F., Simpson-Porco, J. W., and Bullo, F. (2015). Breaking the hierarchy: distributed control and economic optimality in microgrids. IEEE Trans. Control Netw. Syst. 3 (3), 241–253. doi:10.1109/tcns.2015.2459391
Elshenawy, M., Fahmy, A., Elsamahy, A., El Zoghby, H. M., and Kandil, S. A. (2022). Improving frequency response for AC interconnected microgrids containing renewable energy resources. Front. Energy Res. 10, 1035097. doi:10.3389/fenrg.2022.1035097
Feng, Y., and Ma, J. (2022). Controller design for distributed secondary voltage restoration in the islanded microgrid. Front. Energy Res. 10, 826921. doi:10.3389/fenrg.2022.826921
Hennane, Y., Berdai, A., Pierfederici, S., and Meibody-Tabar, F. (2023). A consensus-based control for precise reactive power-sharing in AC microgrids. Sustain. Energy Technol. Assessments 60, 103510. doi:10.1016/j.seta.2023.103510
Hossain, M. A., Pota, H. R., Hossain, M. J., and Blaabjerg, F. (2019). Evolution of microgrids with converter-interfaced generations: challenges and opportunities. Int. J. Electr. Power & Energy Syst. 109, 160–186. doi:10.1016/j.ijepes.2019.01.038
Hu, J., and Bhowmick, P. (2020). A consensus-based robust secondary voltage and frequency control scheme for islanded microgrids. Int. J. Electr. Power & Energy Syst. 116, 105575. doi:10.1016/j.ijepes.2019.105575
Hu, S., He, L., Zhao, H., Liu, H., Liu, X., and Qiu, J. (2023). Distributed secondary control of microgrids with unknown disturbances and non-linear dynamics. Front. Energy Res. 10, 1113110. doi:10.3389/fenrg.2022.1113110
Huang, H., Liu, F., Ouyang, T., and Zha, X. (2022). Sequential detection of microgrid bad data via a data-driven approach combining online machine learning with statistical analysis. Front. Energy Res. 10, 861563. doi:10.3389/fenrg.2022.861563
Jiang, Y., Yang, Y., Tan, S. C., and Hui, S. Y. R. (2021). A high-order differentiator based distributed secondary control for DC microgrids against false data injection attacks. IEEE Trans. Smart Grid 13 (5), 4035–4045. doi:10.1109/tsg.2021.3135904
Kang, W., Li, Q., Chen, M., Peng, C., and Chen, F. (2018). A two-layer distributed control method for islanded microgrids by using multi-agent systems. Proc. CSEE 38, 770–781. doi:10.13334/j.0258-8013.pcsee.162194
Li, Y., Ren, R., Huang, B., Wang, R., Sun, Q., Gao, D. W., et al. (2022). Distributed hybrid-triggering-based secure dispatch approach for smart grid against DoS attacks. IEEE Trans. Syst. Man, Cybern. Syst. 53, 3574–3587. doi:10.1109/tsmc.2022.3228780
Lian, Z., Guo, F., Wen, C., Deng, C., and Lin, P. (2021). Distributed resilient optimal current sharing control for an islanded DC microgrid under DoS attacks. IEEE Trans. Smart Grid 12 (5), 4494–4505. doi:10.1109/tsg.2021.3084348
Lian, Z., Wen, C., Guo, F., et al. (2022). Distributed resilient secondary voltage control for AC microgrids under DoS attacks. 2022 IEEE 17th International Conference on Control & Automation (ICCA). Naples, Italy, June, 2022, 80–84.
Liu, L. N., Yang, G. H., and Wasly, S. (2023). Distributed predefined-time dual-mode energy management for a microgrid over event-triggered communication. IEEE Trans. Industrial Inf., 1–11. doi:10.1109/tii.2023.3304025
Liu, S., Siano, P., and Wang, X. (2019). Intrusion-detector-dependent frequency regulation for microgrids under denial-of-service attacks. IEEE Syst. J. 14 (2), 2593–2596. doi:10.1109/jsyst.2019.2935352
Liu, X. K., Wen, C., Xu, Q., and Wang, Y. W. (2021). Resilient control and analysis for DC microgrid system under DoS and impulsive FDI attacks. IEEE Trans. Smart Grid 12 (5), 3742–3754. doi:10.1109/tsg.2021.3072218
Liu, X. Y., and Che, W. W. (2022). Event-based distributed secondary voltage tracking control of microgrids under DoS attacks. Inf. Sci. 608, 1572–1590. doi:10.1016/j.ins.2022.07.012
Ma, X., Yang, P., Dong, H., et al. (2017). “Secondary control strategy of islanded micro-grid based on multiagent consistency,” in 2017 IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, November, 2017, 1–6.
Majumder, R., Chaudhuri, B., Ghosh, A., Ledwich, G., and Zare, F. (2009). Improvement of stability and load sharing in an autonomous microgrid using supplementary droop control loop. IEEE Trans. power Syst. 25 (2), 796–808. doi:10.1109/tpwrs.2009.2032049
Mohiuddin, S. M., and Qi, J. (2021). “Attack resilient distributed control for AC microgrids with distributed robust state estimation,” in 2021 IEEE Texas Power and Energy Conference (TPEC). College Station, TX, USA, 1–6. doi:10.1109/TPEC51183.2021.9384912
Muktiadji, R. F., Ramli, M. A. M., Bouchekara, H. R. E. H., Milyani, A. H., Rawa, M., Seedahmed, M. M. A., et al. (2022). Control of boost converter using observer-based backstepping sliding mode control for DC microgrid. Front. Energy Res. 10, 828978. doi:10.3389/fenrg.2022.828978
Peng, H. Y., Peng, C., and Sun, H. T. (2019). Incremental detection mechanism of a microgrid under false data injection attack. Information and Control 40 (5), 522–527. doi:10.13976/j.cnki.xk.2019.9156
Pogaku, N., Prodanovic, M., and Green, T. C. (2007). Modeling, analysis and testing of autonomous operation of an inverter-based microgrid. IEEE Trans. power Electron. 22 (2), 613–625. doi:10.1109/tpel.2006.890003
Ramotsoela, D. T., Hancke, G. P., and Abu-Mahfouz, A. M. (2023). Practical challenges of attack detection in microgrids using machine learning. J. Sens. Actuator Netw. 12 (1), 7. doi:10.3390/jsan12010007
Shahab, M. A., Mozafari, B., Soleymani, S., Dehkordi, N. M., Shourkaei, H. M., and Guerrero, J. M. (2019). Distributed consensus-based fault tolerant control of islanded microgrids. IEEE Trans. Smart Grid 11 (1), 37–47. doi:10.1109/tsg.2019.2916727
Sharma, A., Kolhe, M., Nils, U. M., et al. (2018). “Comparative analysis of different types of micro-grid architectures and controls,” in 2018 International Conference on Advances in Computing, Communication Control and Networking (ICACCCN), Greater Noida, India, October, 2018, 1200–1208.
Shi, M., Chen, X., Shahidehpour, M., Zhou, Q., and Wen, J. (2021). Observer-based resilient integrated distributed control against cyberattacks on sensors and actuators in islanded AC microgrids. IEEE Trans. Smart Grid 12 (3), 1953–1963. doi:10.1109/tsg.2021.3050203
Shotorbani, A. M., Ghassem-Zadeh, S., Mohammadi-Ivatloo, B., and Hosseini, S. H. (2017). A distributed secondary scheme with terminal sliding mode controller for energy storages in an islanded microgrid. Int. J. Electr. Power & Energy Syst. 93, 352–364. doi:10.1016/j.ijepes.2017.06.013
Tadepalli, P. S., and Pullaguram, D. (2022). Distributed control microgrids: cyber-attack models, impacts and remedial strategies. IEEE Trans. Signal Inf. Process. over Netw. 8, 1008–1023. doi:10.1109/tsipn.2022.3230562
Tan, S., Guerrero, J. M., Xie, P., Han, R., and Vasquez, J. C. (2020). Brief survey on attack detection methods for cyber-physical systems. IEEE Syst. J. 14 (4), 5329–5339. doi:10.1109/jsyst.2020.2991258
Tian, E., Wu, Z., and Xiangpeng, X. (2022). Codesign of FDI attacks detection, isolation, and mitigation for complex microgrid systems: an HBF-NN-based approach. IEEE Trans. Neural Netw. Learn. Syst., 1–10. doi:10.1109/tnnls.2022.3230056
Uddin, M., Mo, H., Dong, D., Elsawah, S., Zhu, J., and Guerrero, J. M. (2023). Microgrids: a review, outstanding issues and future trends. Energy Strategy Rev. 49, 101127. doi:10.1016/j.esr.2023.101127
Wang, F., Shan, Q., Teng, F., He, Z., Xiao, Y., and Wang, Z. (2022a). Distributed secondary control strategy against bounded FDI attacks for microgrid with layered communication network. Front. Energy Res. 10, 914132. doi:10.3389/fenrg.2022.914132
Wang, F., Shan, Q., Zhu, J., and Xiao, G. (2022b). Discrete-time resilient-distributed secondary control strategy against unbounded attacks in polymorphic microgrid. Front. Energy Res. 10, 961488. doi:10.3389/fenrg.2022.961488
Wang, J. S., and Yang, G. H. (2018). Data-driven methods for stealthy attacks on TCP/IP-based networked control systems equipped with attack detectors. IEEE Trans. Cybern. 49 (8), 3020–3031. doi:10.1109/tcyb.2018.2837874
Wang, Y., Deng, C., Liu, Y., and Wei, Z. (2023). A cyber-resilient control approach for islanded microgrids under hybrid attacks. Int. J. Electr. Power & Energy Syst. 147, 108889. doi:10.1016/j.ijepes.2022.108889
Xiao, S., and Dong, J. (2020). Distributed fault-tolerant containment control for linear heterogeneous multiagent systems: a hierarchical design approach. IEEE Trans. Cybern. 52 (2), 971–981. doi:10.1109/tcyb.2020.2988092
Xu, G., and Ma, L. (2020). Resilient self-triggered control for voltage restoration and reactive power sharing in Islanded microgrids under Denial-of-Service attacks. Appl. Sci. 10, 3780. doi:10.3390/app10113780
Yang, P., Peng, Y., Xia, Y., Wei, W., Yu, M., and Feng, Q. (2022). A unified bus voltage regulation and MPPT control for multiple PV sources based on modified MPC in the DC microgrid. Front. Energy Res. 10, 1010425. doi:10.3389/fenrg.2022.1010425
Yang, Y., Li, Y., Yue, D., Tian, Y. C., and Ding, X. (2020). Distributed secure consensus control with event-triggering for multiagent systems under DoS attacks. IEEE Trans. Cybern. 51 (6), 2916–2928. doi:10.1109/tcyb.2020.2979342
Yu, W., Wang, Y., and Song, L. (2019). A two stage intrusion detection system for industrial control networks based on ethernet/IP. Electronics 8 (12), 1545. doi:10.3390/electronics8121545
Zhan, H., Du, Z., Liu, X., and Li, F. (2023). Resilient distributed control of islanded microgrids under false data injection attacks. Sustain. Energy Technol. Assessments 57, 103145. doi:10.1016/j.seta.2023.103145
Zhang, P., Portillo, L., and Kezunovic, M. (2006). “Compatibility and interoperability evaluation for all-digital protection system through automatic application test,” in 2006 IEEE power engineering society general meeting, Montreal, QC, Canada, June, 2006, 7.
Zhang, S., and Fan, H. (2022). Editorial: stability and primary control, dynamic analysis, and simulation of microgrids with new forms and features. Front. Energy Res. 10, 854473. doi:10.3389/fenrg.2022.854473
Zhou, D., Zhang, Q., Guo, F., Lian, Z., Qi, J., and Zhou, W. (2023). Distributed resilient secondary control for islanded DC microgrids considering unbounded FDI attacks. IEEE Trans. Smart Grid, 1. doi:10.1109/tsg.2023.3286991
Nomenclature
Keywords: islanded microgrids, resilient control, false data injection attack, denial-of-service attack, secondary control
Citation: Liu Y, Du Z, Chen Y and Zhan H (2023) Resilient distributed control of islanded microgrids under hybrid attacks. Front. Energy Res. 11:1320968. doi: 10.3389/fenrg.2023.1320968
Received: 13 October 2023; Accepted: 01 December 2023;
Published: 29 December 2023.
Edited by:
Fuwen Yang, Griffith University, AustraliaReviewed by:
Yushuai Li, University of Oslo, NorwaySahaj Saxena, Thapar Institute of Engineering and Technology, India
Copyright © 2023 Liu, Du, Chen and Zhan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhaobin Du, ZXBkdXpiQHNjdXQuZWR1LmNu
 Yao Liu
Yao Liu Zhaobin Du
Zhaobin Du Yan Chen2
Yan Chen2