Grid interface control of wind–solar generator in Hail region of Saudi Arabia using FOPI controller

This study investigates the performance of a wind–solar generator (WSG) in the Hail region of Kingdom of Saudi Arabia (KSA) with a fractional order PI controller (FOPI) applied to the grid connection line. The proposed hybrid generator consists of a wind turbine with a PMSM machine and a PV panel connected to a secondary distribution grid by a DC link, three-phase inverter, and an RL filter. The line currents injected into the grid and/or loads are controlled by calculating the output reference voltage of an inverter and by the reference active and reactive requested powers. For this purpose, control loops around the RL filter were developed with fractional-order proportional-integral (FOPI) controllers, and a comparison with classic PI controllers was made. The system was simulated using the MATLAB/Simulink software. The results showed that the generator satisfied the power demand under the climatic conditions of the Hail region. They also demonstrated the good performance of the proposed controllers, which had good tracking accuracy and robustness to variations in wind speed and power demanded by loads in a very short time. The FOPI controller exhibited faster dynamic response and less overshoot than the classic PI controller.

1 Introduction

Proportional integral (PI) and proportional integral derivative (PID) controllers are the most widely utilized types of controllers in the industry (Warrier and Shah, 2021a; Kumar et al., 2023a). Fractional controllers have gained popularity in recent years because of their robustness towards plant gain variations and plant uncertainties. In comparison to integer-order (IO) controllers, design characteristics such as gain and phase margins can be modified with greater flexibility utilizing fractional order (FO) controllers. The FO controller provides better resilience with fewer tuning knobs which could be achieved with very high order IO controllers (Chen et al., 2009). The fractional operators, also known as differ-integrals, contain memory, which allows them to save previous states and so improve filtering action. This characteristic aids in the reduction of control effort. As a result, a FO controller produces a smoother control signal than an IO controller (Monje et al., 2010a). FO controllers have more parameters than IO controllers, allowing for additional design standards to be met. As a result, fractional control can be used to create more robust and precise control systems.

The use of fractional calculus in system control and modeling has grown significantly over the last decade. Further, FOPI/FOPID controllers for various power converters (DC shoppers, inverters, rectifiers, etc.), electrical drives, renewable energy applications, and hybrid vehicles have recently attracted a lot of attention (Yichen et al., 2017; Balaska et al., 2019). To illustrate the advantages of the FOPID controller over the PID controller, Khubalkar et al. (2018) deployed FOPID control for a separately excited DC motor. Rajasekhar et al. (2013) suggested an FOPID controller for DC shoppers to control the speed of DC motors with separate excitations. FOPID/FOPI controllers have been used in a variety of other studies, including wound stator DC electrical motors, permanent-magnet stator DC motors, permanent-magnet synchronous motors, and electric drives (Khurram et al., 2018; Vanchinathan and Valluvan, 2018; Zaihidee et al., 2019; Bruzzone et al., 2020). The authors of (Alhelou et al., 2018) proposed an FOPID controller to control electric vehicles with renewable generators. Pan and Das suggested a Kriging-based surrogate modeling optimization technique in their publication (Pan and Das, 2015) to design FOPID controllers for a microgrid system. FOPID/FOPI was used in electrical grid and microgrid systems in (Afghoul et al., 2016; Nasimullah et al., 2017). The use of renewable energy sources (wind, solar, geothermal, etc.) is a result of the world’s rising energy needs, climate change, and desire for a better planet (Kumar et al., 2023b). However, these resources are only available during certain times of the year, and the load needs change over time (Zdiri et al., 2019; Bilel et al., 2020). Iov et al. (2007) provided a comprehensive overview of the use of power electronic devices with renewable sources. Owing to their resistance to nonlinearities, fractional-order approaches have recently been included in traditional MPPT procedures and have proven to be successful. Kamal and Ibrahim (Kamal and Ibrahim, 2018) thoroughly analyzed traditional fractional-order MPPT approaches. Kuo-Nan presented a variable fractional-order incremental conductance technique for MPPT management of a boost DC shopper (Yu et al., 2015). Huang and Hsu developed a fractional open-circuit voltage-based algorithm to evaluate the performance of a high-concentration PV module with a buck converter (Huang and Hsu, 2016).

A photovoltaic inverter was improved using the Yin-Yang technique and controlled using a perturbation-observer-based fractional-order PID controller (POFOPID) (Yang et al., 2018a). For the PV system, Yin-Yang pair optimization defines and optimizes the POFOPID controller (Tam et al., 2011). Yang et al. (2018b) designed a passivity-based FOPID controller. Melício et al. (2010) developed a fractional PI-based approach and sliding mode control for a variable-speed wind source with a PMSG and discussed its use for matrix (AC-AC) converters and multilevel (AC-DC-AC) converter topologies. In (Ghasemi et al., 2014), analytical techniques were used to design a reliable FOPI controller for a wind source with a PMSG, taking advantage of the isodamping properties of fractional-order systems. Seixas et al. (2014) proposed a fractional control method for an offshore wind turbine outfitted with back-to-back Neutral Point Converters and a PMSG (Beddar et al., 2016). Mahvash et al. (2018) suggested an FOPI control technique in a DFIG in a 10 MW wind farm for the pitch compensation control of the DFIG (Mahvash et al., 2019). Asghar and Nasimullah (2018) examined the effectiveness of fault-tolerant fractional and integer controllers in the DFIG control. Owing to the random and unexpected characteristics of their generated electricity, the distribution grid is affected by the variable nature of wind and solar generators, which can significantly affect how well they run (Tran-Quoc and Caire, 2010; Abassi and Chebbi, 2012; Thi Minh Chau, 2012; Samy et al., 2021). Hybrid sustainable resources can help resolve various problems. Because of its minimal influence on the network and several technological and financial benefits, a wind–solar hybrid system is a promising solution (Eid et al., 2016). The connection of a hybrid system to the network must be well-controlled to minimize the impact on the stability of the power system and the balance between production and consumption.

In Saudi Arabia, several programs focus on increasing the use of renewable energy. Due to the availability of solar radiation throughout the year, Saudi Arabia is one of the prime locations for harnessing solar energy. In (Mohana et al., 2021) seven well-known machine learning algorithms were successfully applied to solar PV system data from Abha (Saudi Arabia) to predict the generated power. A comprehensive dynamic voltage stability analysis of the Sakaka PV power plant connected to the Saudi transmission network is presented in (Saidi et al., 2023). Many studies have been conducted on renewable energy in Saudi Arabia (El Khashab and Ghamedi, 2015; Sawle et al., 2016; Alshibani and Alshamrani, 2017; Alharthi et al., 2018a; Barhoumi et al., 2020; Tazy et al., 2020; Younsi et al., 2022a).

In this paper, the region under consideration (Hail, Saudi Arabia) is located at (27 23′11″, 41 38′49″). Hail has a hot desert climate with hot summers and cool winters (Köppen climatic classification). Because of its higher altitude temperature, humidity, and insolation, it has a milder climate than other Saudi cities. Furthermore, Hail is recognized to be one of the most active agricultural regions, making solar energy for pumping water from deep wells economically efficient. In this study, a hybrid generator that collects wind turbines and solar PV panels connected to a secondary distribution grid with an FOPI controller of the grid connection was presented to examine its performance in Hail region. A grid interface was built to manage power transfer from the generator by regulating the line currents. To achieve this, current control loops using FOPI controllers were developed to determine the output voltage of the inverter. The active and reactive powers required by the grid and/or loads were used to calculate the current reference values.

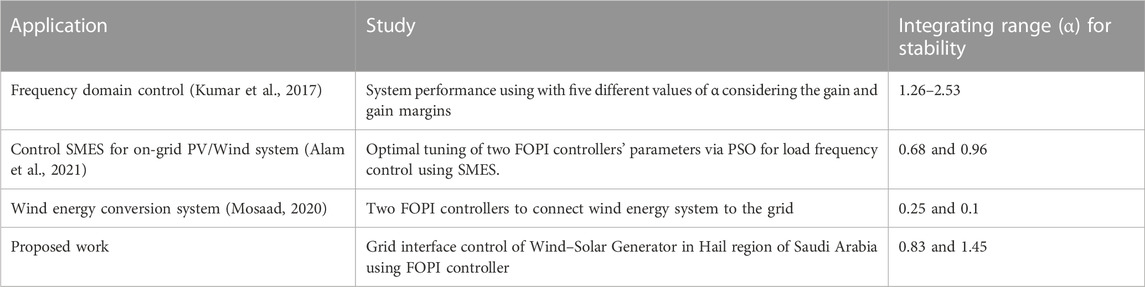
The wind–solar generator (WSG) in the Hail region of Kingdom of Saudi Arabia (KSA) with a fractional order PI controller (FOPI) are nonlinear and complex systems. The conventional methods such as linear programming and simplex methods for FOPI controller gains’ optimal scheduling may not guarantee attaining the best dynamic performance. Thus, metaheuristic-based optimization methods, GA and PSO, can conveniently ensure the system controller’ optimal gain scheduling and enhance their dynamic performance. Table 1 Illustrates the gains’ ranges of the FOPI for different applications in the state of art.

TABLE 1

TABLE 1. Range of the integrating factor of the FOPI in the literature.

To test the performance of the proposed system with FOPI controllers in the Hail region simulations were performed using MATLAB/Simulink with the suggested system under different climatic conditions.

The proposed FOPI controllers were compared with classic PI controllers using simulations to evaluate the performance of the FOPI controller. The results indicated that the generator satisfied the power demand under the climatic conditions of the Hail region. They also demonstrated good controller performance with good tracking accuracy and robustness to variations in wind speed and power demanded by loads in a relatively short period of time. The FOPI controller has a faster dynamic response and less overshoot than a PI controller.

The principal contributions and novelty of this paper are outlined as:

• Exploiting the FOPI controllers to improve grid connection by controlling the Wind–Solar Generator in Hail region.

• Introducing two FOPI controllers for regulating the line currents injected into the grid by determining the reference output inverter voltages.

• Maximizing the dynamic performance enhancement through the gain scheduling of both PI/FOPI controllers using advanced metaheuristic optimization techniques: GA and PSO algorithm;

• Comparing the influence of using FOPI and PI controller on the dynamic

Behavior of the grid interface.

The remainder of this paper is structured as follows. The system is detailed in Section 2. The modeling of the grid connection is presented in Section 3. The control strategies for the grid interface are provided in Section 4. Section 5 presents simulations, results, and discussion. The principal conclusions of this study are presented in Section 6.

2 System description

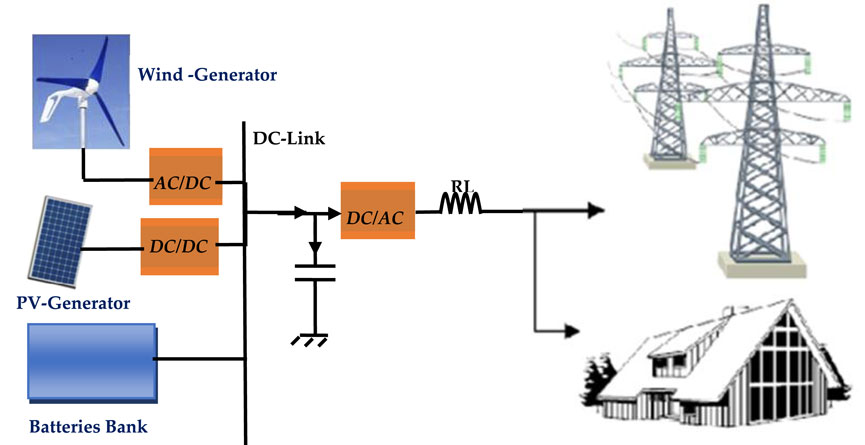
The hybrid system consists of wind turbine and solar panels which are connected to the DC link by an AC/DC converter and a boost DC/DC converter, respectively. The three-phase DC/AC converter and RL filter are used to interface the generator with the low voltage AC secondary distribution grid. The power generated by hybrid generator is directly injected into the grid. The system can also power a separate load; in this case, a battery bank is added to provide an uninterruptible power supply (UPS) in the event that renewable energy sources such as wind and/or solar fail. The system is shown in Figure 1.

FIGURE 1

FIGURE 1. System components.

3 Modeling of the grid connection

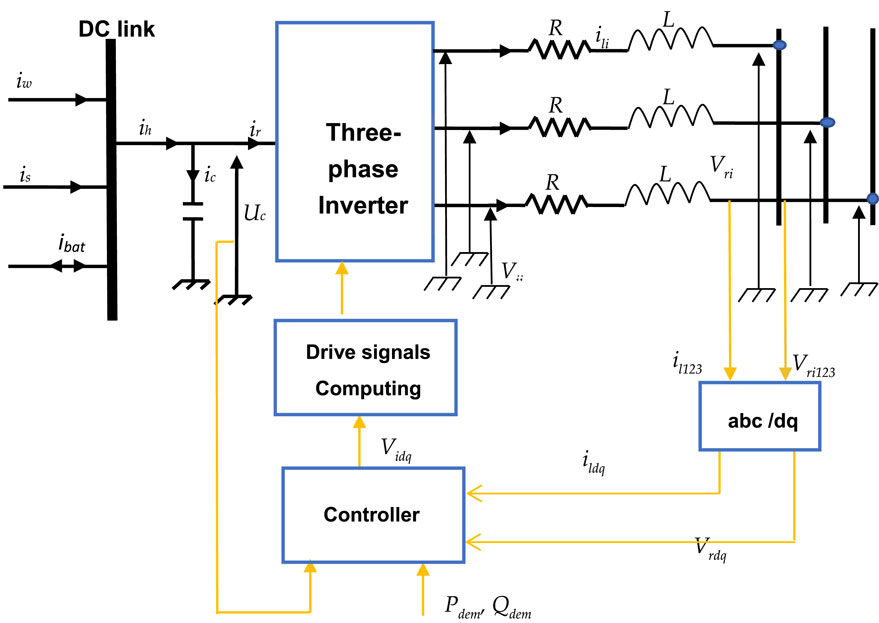
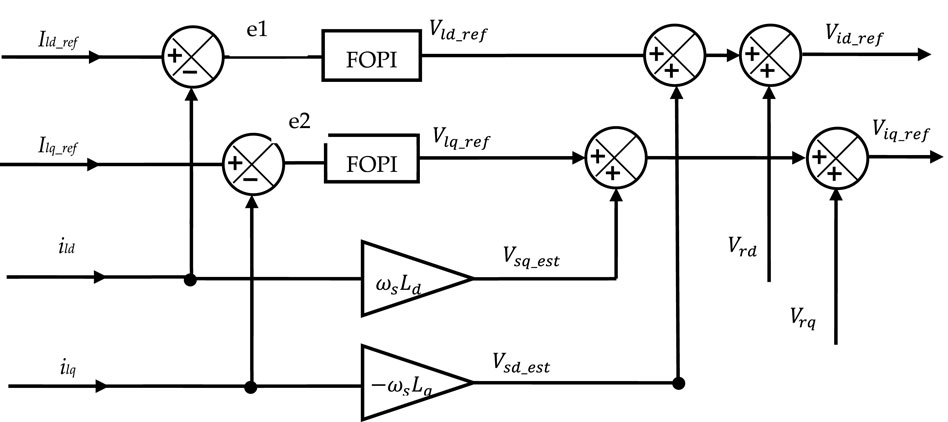
Figure 2 shows the connection between the hybrid system and the three-phase grid, and the control system design. The grid connection line model (as applied to the RL filter) is given in three-phase axis by the following equations:

$\left\{\begin{array}{c}{V}_{i1}=R{i}_{l1}+L\frac{d{i}_{l1}}{dt}+V_{r1}\\ V_{i2}=R{i}_{l2}+L\frac{d{i}_{l2}}{dt}+V_{r2}\\ V_{i3}=R{i}_{l3}+L\frac{d{i}_{l3}}{dt}+V_{r3}\end{array}\right.(1)$

FIGURE 2

FIGURE 2. Control system design.

Using the Park matrix transformation, the voltage equation of the filter on the direct and quadratic axis becames:

$\left\{\begin{array}{c}{V}_{id}=R{i}_{ld}+L\frac{d{i}_{ld}}{i_{ld}}-L{\omega }_s{i}_{lq}+V_{rd}\\ V_{iq}=R{i}_{lq}+L\frac{d{i}_{lq}}{i_{lq}}+L{\omega }_s{i}_{ld}+V_{rq}\end{array}\right.(2)$

Where:V_id and V_iq are the output voltages of inverter in direct and quadratic axis.V_rd and V_rq are the voltages of grid in direct and quadratic axis.R is the resistance of the line filter.L is the inductance of the line filter.${\omega }_s$ is the frequency of line currents.

The active power generated and transferred to the grid is expressed as follows:

$P=V_{rd}{i}_{ld}+V_{rq}{i}_{lq}(3)$

The reactive power generated and transferred to the grid is expressed as follows:

$Q=V_{rq}{i}_{ld}-V_{rd}{i}_{lq}(4)$

4 Control strategies of the grid interface

The grid-interface command approach controls the currents injected into the grid and/or loads. It imposes a control vector $V={\left[\begin{array}{cc}{V}_{id\_ref}& V_{iq\_ref}\end{array}\right]}^T$ reflecting the output voltages of the inverter on Park’s d- and q-axes, allowing the control of both active and reactive power. Control loops were built around the RL filter to control the line currents using the control vector V.

The reference current values are calculated using Eqs 7, 8 using the powers P_dem and Q_dem demanded by the AC grid and/or separate loads (in islanding operation) (Alharthi et al., 2018a; Samy et al., 2021). The control vector $V={\left[\begin{array}{cc}{V}_{id\_ref}& V_{iq\_ref}\end{array}\right]}^T$ is given by,

$\left\{\begin{array}{c}{V}_{id\_ref}=V_{ld\_ref}-L{\omega }_s{i}_{lq}+V_{rd}\\ V_{iq\_ref}=V_{lq\_ref}+L{\omega }_s{i}_{ld}+V_{rq}\end{array}\right.(5)$

The direct and quadratic components of voltage $V_{ldq\_ref}$ are obtained from the control loops on the direct and quadratic line currents and are given by:

$\left\{\begin{array}{c}{V}_{ld\_ref}=C\left(s\right)*\left[i_{ld\_ref}-i_{ld}\right]\\ V_{lq\_ref}=C\left(s\right)*\left[i_{lq\_ref}-i_{lq}\right]\end{array}\right.(6)$

The direct and quadratic components of voltage $I_{ldq\_ref}$ are obtained by:

$i_{ld\_ref}=\frac{P_{dem}.V_{rd}+Q_{dem}.V_{rq}}{V_{rd}^2+V_{rq}^2}(7)$

$i_{lq\_ref}=\frac{P_{dem}.V_{rq}-Q_{dem}.V_{rd}}{V_{rd}^2+V_{rq}^2}(8)$

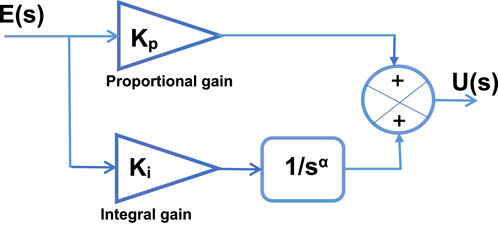
C(s) denotes a fractional-order proportional-integral (FOPI) controller.

Because of its relevance in a wide range of engineering domains, fractional-order calculus and non-integer order systems have grown in importance (Warrier and Shah, 2021b). FOPI has appeared in the theory of dynamical system control. The fractional differential equations are employed in such systems to describe the controlled system or/and its controller. The use of fractional derivatives to describe the system/controller attributes results in a fractional-order system with more complex mathematical modelling and numerical simulations (Pandey et al., 2017).

The FOPID controller, in the form of PI^αD^β, incorporates an integrator and a differentiator with both α and β fractional values. It has limitations owing to parameter fluctuations and uncertainties (Pandey et al., 2017). FOPI takes into account α ∈R and β = 0. The fractional α, together with the integer Kp and Ki gains, should be established for efficient FOPI parameter scheduling. The ideal set of Kp, Ki, and α is evaluated using a pre-defined impartial objective function criterion.

The overall form of the FOPID controller is as follows (Monje et al., 2010b; Visioli, 2012):

$\mathrm{C}\left(\mathrm{s}\right)={\mathrm{K}}_{\mathrm{p}}+{\mathrm{K}}_{\mathrm{I}}{\mathrm{S}}^{-\mathrm{\alpha }}+{\mathrm{K}}_{\mathrm{d}}{\mathrm{S}}^{\mathrm{\beta }}(9)$

In general, the fractional orders range from 0 to 2. It is obvious that α = β = 1 results in the traditional PID controller. Figure 3 shows the FOPI controller, which is given by:

$\mathrm{C}\left(\mathrm{s}\right)={\mathrm{K}}_{\mathrm{p}}+{\mathrm{K}}_{\mathrm{I}}{\mathrm{S}}^{-\mathrm{\alpha }}(10)$

FIGURE 3

FIGURE 3. FOPI controller.

The inverter output currents injected into the grid are represented by the vector $I_l={\left[\begin{array}{cc}{i}_{ld}& i_{lq}\end{array}\right]}^T$. Figure 4 shows the grid connection line control.

FIGURE 4

FIGURE 4. Grid connection line control.

5 Metaheuristic optimization techniques

In the context of determining the near-optimal gains for PI/FOPI controllers, two modern metaheuristic optimization techniques are suggested: Genetic Algorithm (AG) and Particle Swarm Optimization (PSO). For the optimal FOPI parameter scheduling, the fractional α should be determined together with the integer Kp and Ki gains.

These optimization methods are used to fine-tune the controller gains of PI/FOPI controllers, aiming to achieve optimal or near-optimal control system performance. AG and PSO are popular metaheuristic algorithms that can efficiently search for the best set of controller gains by iteratively evaluating different combinations and selecting the ones that yield improved control system performance based on a defined objective or fitness function.

5.1 Algorithm (AG)

The developed optimization algorithm for Grid interface control of Wind–Solar Generator in this section is based on the GA method. The primary idea of GA is to use genetic operators (selection, crossover, and mutation) to generate a population of individuals (Jebali et al., 2016). These operators are applied to each person during each generation to generate a new developed population from the previous one. Each person in GA is represented by a single chromosome. This chromosome corresponds to the gains for PI/FOPI controllers (α, Kp, and Ki) in the studied system. The population is the collection of chromosomes. As a first step in GA implementation, a random population of persons is formed. Each chromosome is then encoded. A real coding strategy, in which each gene corresponds to a gain of FOPI controller, was adopted. Following that, each individual was evaluated. The suggested GA employs three genetic operations: crossover, mutation, and selection. There were two crossover points evaluated. These points were chosen at random, and they divided the chromosome into three segments. In the crossover process, the second portions of two identified chromosomes were exchanged. The crossover rate in this study is 0.8. To avoid a local optimum, the mutation rate is set to 0.02. Individuals are chosen using a tournament approach.

5.2 Particle swarm optimization (PSO)

In PSO, the coordinates of each particle constitute a possible solution that is coupled with two vectors, the position (${\mathrm{x}}_{\mathit{i}}$) and velocity (${\mathrm{v}}_{\mathit{i}}$) vectors (Baghel et al., 2012). The number of particles is equal to the size of vectors vectors ${\mathrm{x}}_{\mathit{i}}$ and ${\mathrm{v}}_{\mathit{i}}$. A swarm is made up of a group of particles or “possible solutions” that move (fly) through the feasible solution space in search of optimal solutions. The position of each particle is updated depending on its best exploration, overall swarm experience, and previous velocity vector. Eqs 11, 12 offer the update procedures with inertial weight for particle i at iteration k + 1.

$v_i^{k+1}={wv}_i^k+c_1{r}_1\left(p_i^k-x_i^k\right)+c_2{r}_2\left(g_i^k-x_i^k\right)(11)$

$x_i^{k+1}=x_i^k+v_i^{k+1}(12)$

$v_i^k,x_i^k$ are the velocity and position of particle i, respectively; w is the inertia weight; c1 and c2 are the acceleration coefficients; r1 and r2 are two random numbers between 0 and 1; $p_i^k$ is the best position found so far for the ith particle, $g_i^k$ is the best position found so far by the entire swarm (Abedinpourshotorbana et al., 2016).

5.3 Objective function

These advanced optimizers are utilized for the minimization of the objective function J that represents the sum of the two errors (e = |e1| + |e2|) given in Figure 4. The objective function J can be expressed as:

$\mathrm{J}=\min \left(\mathrm{e}\right)(13)$

This objective function J is appropriately minimized in case of reaching near-optimal gains’ values for the proposed PI/FOPI controllers.

The design problem for Grid interface control of Wind–Solar Generator can be formulated as the following constrained optimization problem, where the constraints are the FOPI controller gain bounds:

minimize J.

Subject to:

${\alpha }_{\mathit{min}}\le \alpha \le {\alpha }_{\mathit{max}}$

$K_{P\mathit{min}}\le \alpha \le K_{P\mathit{max}}(14)$

$K_{I\mathit{min}}\le \alpha \le K_{I\mathit{max}}$

Where:${\alpha }_{\mathit{min}}$ and ${\alpha }_{\mathit{max}}$ are the search boundaries of $\alpha$$K_{P\mathit{min}}$ and $K_{P\mathit{max}}$ are the search boundaries of $K_P$$K_{I\mathit{min}}$ and $K_{I\mathit{max}}$ are the search boundaries of $K_I$.

6 Simulations and results

Simulations were performed using Simulink software in MATLAB to verify the performance of the system with an FOPI controller developed to control the grid-side inverter and line. In this study, the climatic conditions of the Hail region, northwest KSA, were used.

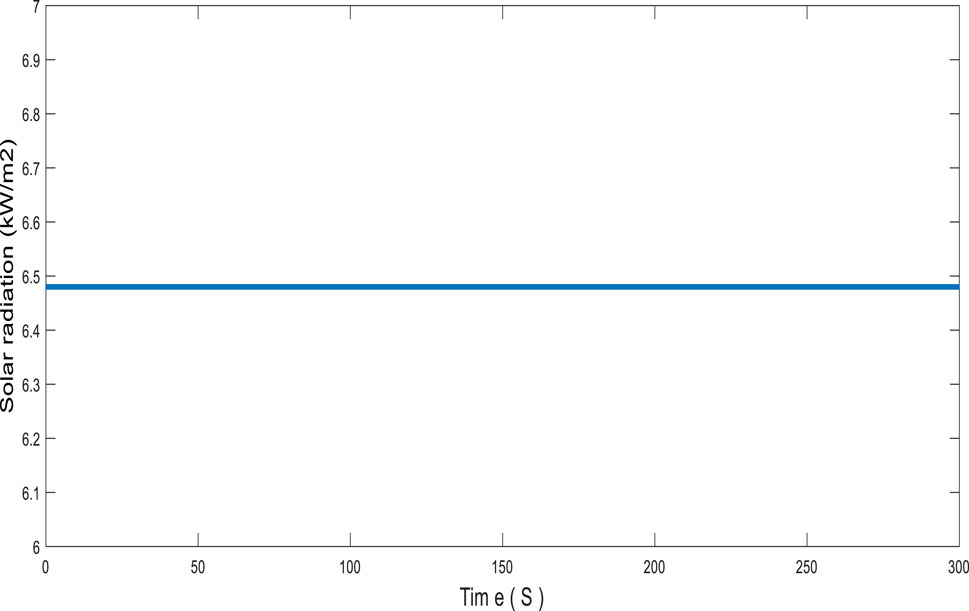
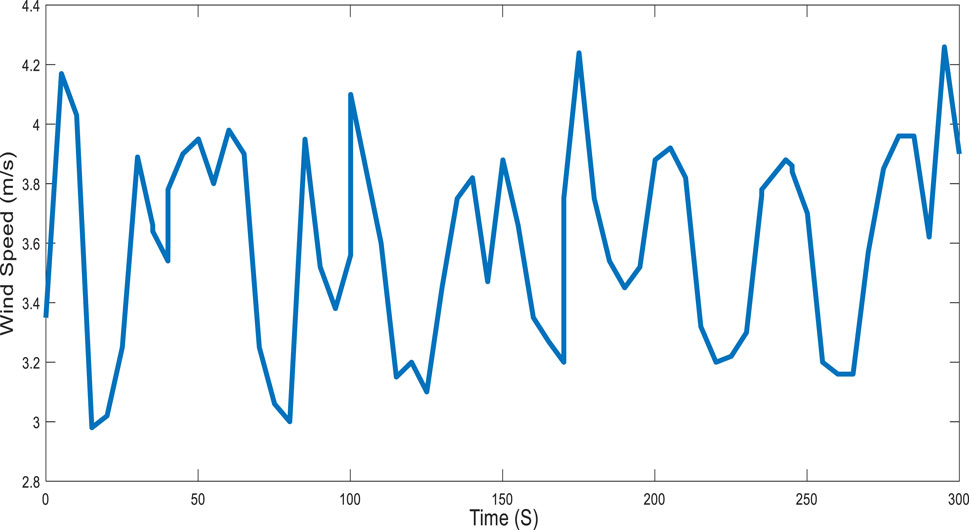
The average solar radiation in Hail is approximately 6.483 kWh/m2 (Zell et al., 2015; Alharthi et al., 2018b; Younsi et al., 2022b), which was built to be equal to the average value shown in Figure 5. The average wind speed was approximately 3.6 m/s (Azorin-Molina et al., 2018; Younsi et al., 2022b; General Authority for statistics, 2023), and was highly variable over a short period of time around the average value, as shown in Figure 6.

FIGURE 5

FIGURE 5. Average solar radiation in Hail.

FIGURE 6

FIGURE 6. Average wind speed in Hail.

The near-optimal PI/FOPI gains alongside with the control measures using the different metaheuristic (AG and PSO) techniques are stated in Tables 2, 3.

TABLE 2

TABLE 2. Optimal gains for PI controllers with different metaheuristic optimizers.

TABLE 3

TABLE 3. Optimal gains for FOPI controllers with different metaheuristic optimizers.

Tables 2, 3 summarizes the characteristics of the two methods developed in order to solve the single-objective optimization problem for searching the optimal gains for PI/FOPI controllers. The PSO approach seems to be the most efficient. It requires less computational effort, compared to the AG.

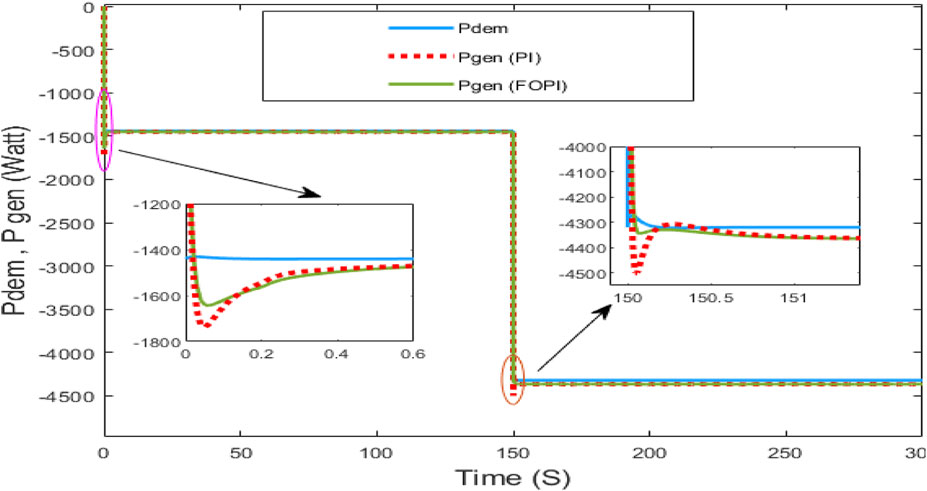
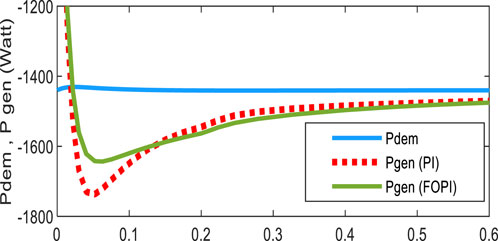
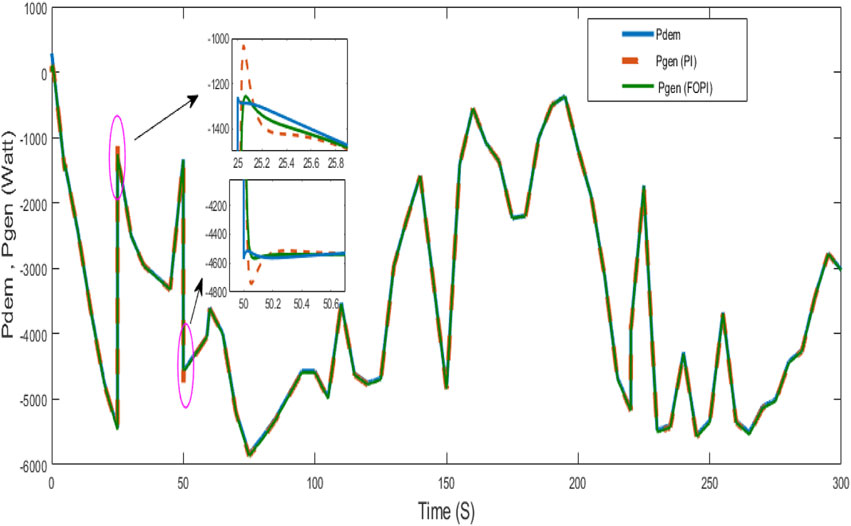
To evaluate the performance of the system with the FOPI controller, the reference power requested by the grid and/or loads was first chosen as a constant with two different steps over two periods, as shown in Figure 7. In the same figure, power is generated by the wind–solar generator (WSG) with PI and FOPI controllers. These results indicate that the power generated by the WSG immediately satisfies the load demand. This indicates that the generator satisfies the power requirements.

FIGURE 7

FIGURE 7. Demanded and generated powers.

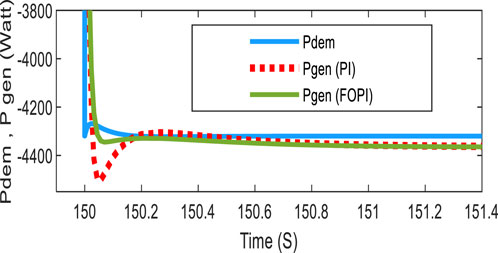
Figures 8, 9 show the response of the system to generate power starting at time 0 s and during a sudden and significant change in the requested power at time 150 s, respectively. These results show good tracking accuracy and robustness to climatic variations in a very short time and to the change in power demanded by the load. They also demonstrated the FOPI controller’s fast dynamic response and lower overshoot compared to those of the PI controller.

FIGURE 8

FIGURE 8. Response of the system at starting time.

FIGURE 9

FIGURE 9. Response of the system at 150 s.

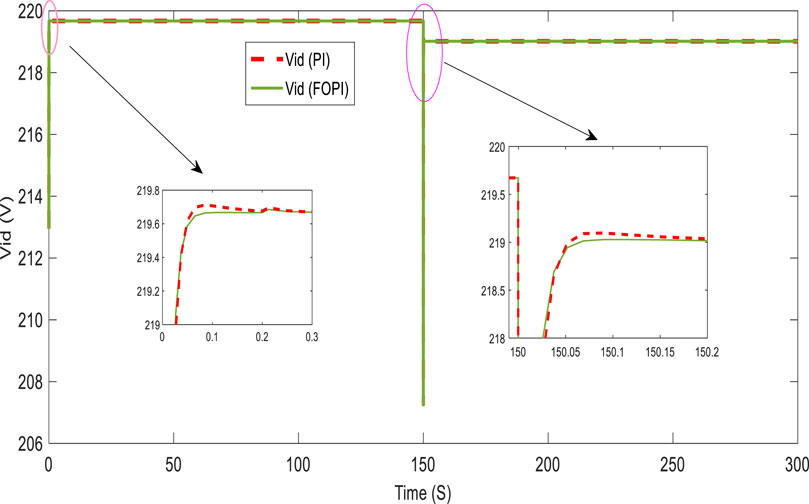
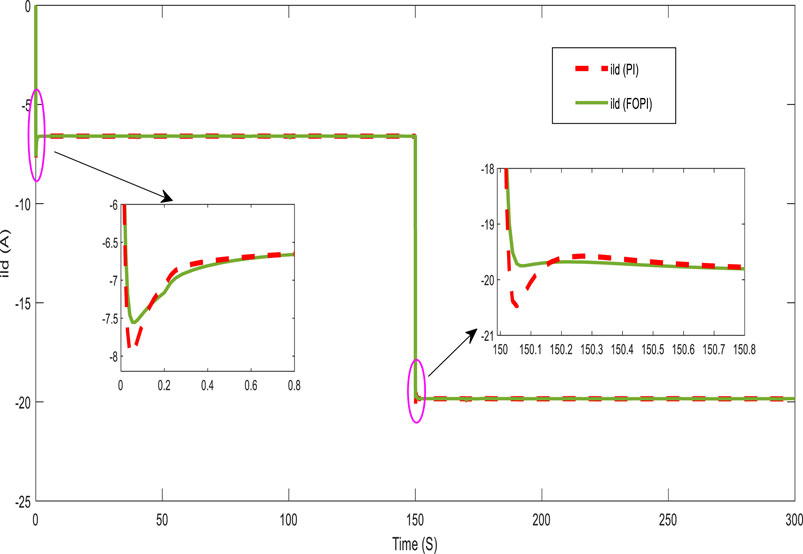
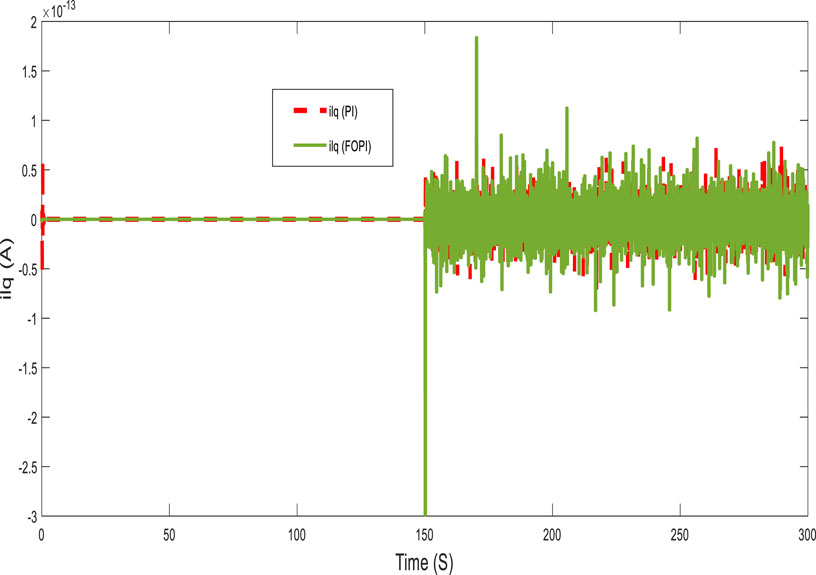
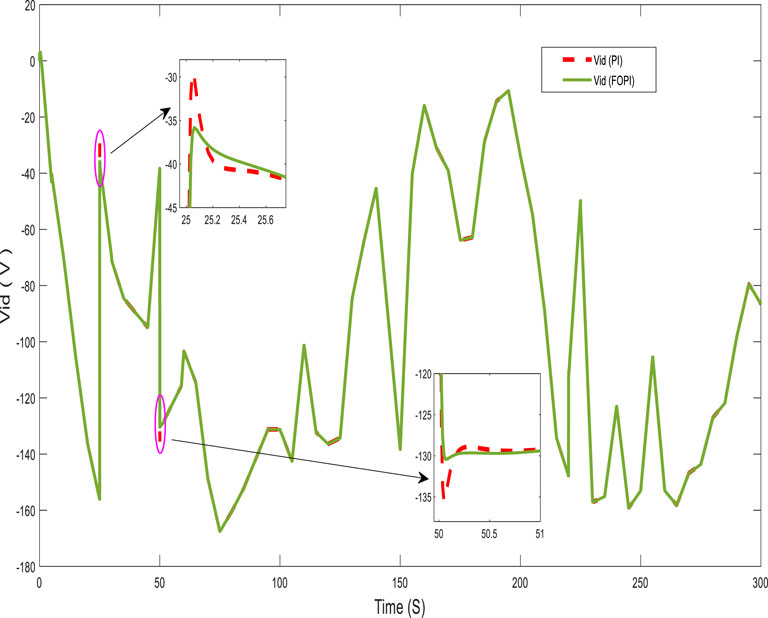
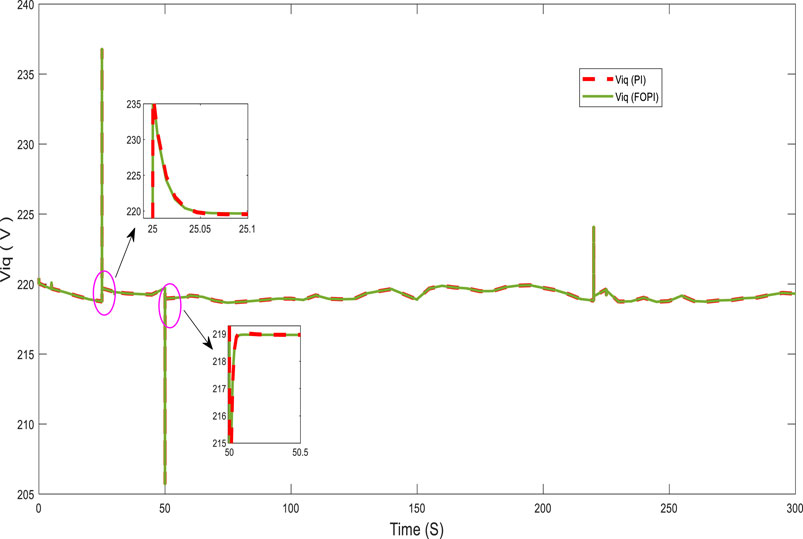
Figures 10, 11 present, respectively, the direct and quadratic output inverter voltages (Vid and Viq). Figures 12, 13 show the direct and quadratic line currents injected into the grid and/or loads ild and ilq, respectively. These results also show that the system has a fast dynamic response and less overshoot with the FOPI controller than with the PI controller at the start and after a significant change in power requested by the grid and/or loads.

FIGURE 10

FIGURE 10. Direct output inverter voltage.

FIGURE 11

FIGURE 11. Quadratic output inverter voltage.

FIGURE 12

FIGURE 12. Direct component of current.

FIGURE 13

FIGURE 13. Quadratic component of current.

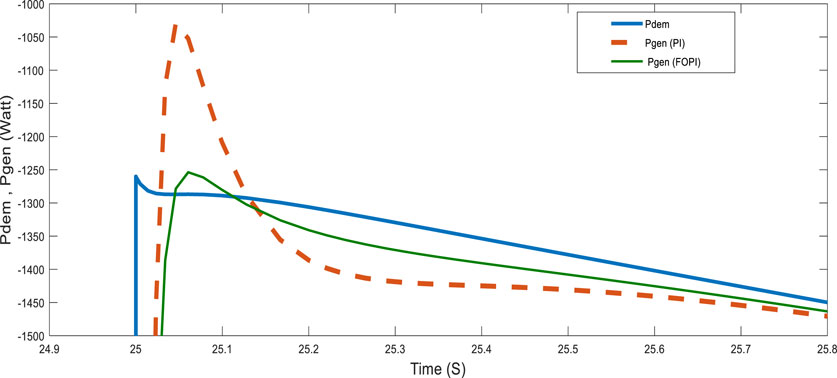
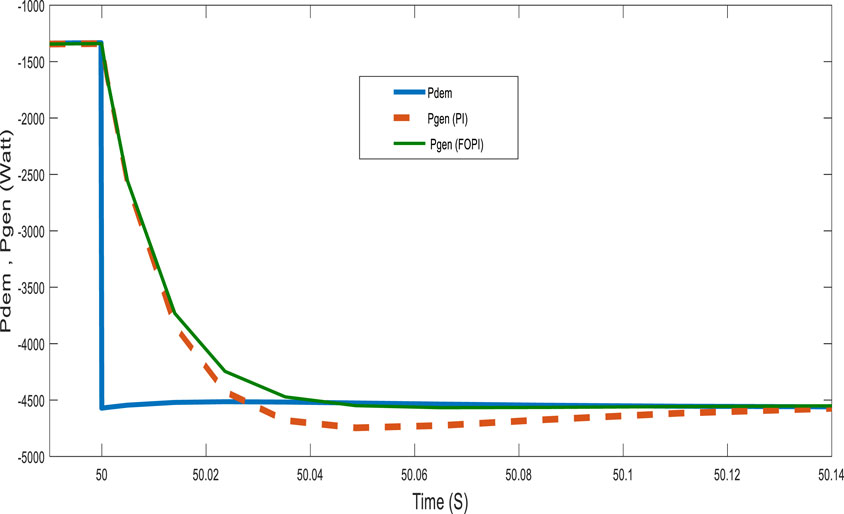
For a more detailed analysis of the controller performance, the system was tested with highly variable power requested by the loads, as shown in Figure 14. The figure also shows the power generated by the generator. These results show that the system generates power with good tracking accuracy and robustness to wind speed and the power demanded by the load, which varies within a very short time. Figures 15, 16 show the response of the system at notable points (t = 25 and t = 50 s) as well as the fast dynamic response and reduced overshoot of the FOPI controller.

FIGURE 14

FIGURE 14. Variable demanded and generated powers.

FIGURE 15

FIGURE 15. Response of system at t = 25 s.

FIGURE 16

FIGURE 16. Response of system at t = 50 s.

Figures 17, 18 show, respectively, the direct and quadratic output inverter voltages (Vid and Viq) for a highly variable power demand. For this operation, Figures 19, 20 show, respectively, the direct and quadratic line currents (ild and ilq) injected into the grid and/or load. These results also demonstrate good performance of the FOPI, which provides a fast response and low overshoot in the system compared with the PI controller at some notable points.

FIGURE 17

FIGURE 17. Direct output inverter voltage.

FIGURE 18

FIGURE 18. Quadratic output inverter voltage.

FIGURE 19

FIGURE 19. Direct line current.

FIGURE 20

FIGURE 20. Quadratic line current.

In this study, the FOPI controller demonstrates satisfactory robustness in the face of the following disturbances:

-Sudden increase in demanded power Pdem.

-Rapid variation in demanded power in a very short time.

-Abrupt changes in wind speed in a very short time.

Figure 7 demonstrates that the FOPI controller responds effectively to rapid changes in power demand, highlighting its capability to maintain system stability despite these sudden shifts. The FOPI controller also effectively manages sudden variations in power demand, as illustrated in Figures 8, 9, demonstrating its suitability for maintaining system stability despite these rapid changes. Additionally, as indicated in Figure 14, the FOPI is capable of managing abrupt fluctuations in wind speed, which is crucial in wind energy generation systems.

In comparison to a Proportional-Integral (PI) controller, the FOPI exhibits a shorter response time and less overshoot. This means that the FOPI can adjust generated power more rapidly in response to disturbances, making it better suited to minimize deviations between generated and demanded power.

In conclusion, the simulation results indicate that the FOPI controller is the preferred choice for control systems facing substantial disturbances, particularly those related to swift variations in power demand and wind speed. It provides a faster response time and superior performance compared to a PI controller.

7 Conclusion

In this study, the performance of a wind–solar generator (WSG) consisting of a wind turbine and solar panels in Hail, Kingdom of Saudi Arabia (KSA), with a fractional-order PI controller (FOPI) applied to the grid connection line, was studied and analyzed. A control loop around the RL filter was developed using an FOPI controller to regulate the line currents injected into the grid by determining the reference output inverter voltages. The reference values of the line currents were obtained using the power requested by a three-phase AC grid and/or loads. The system was simulated using MATLAB/Simulink software based on the wind speed and solar radiation of the Hail region. The results demonstrate the good performance of hybrid wind–solar generators in this region, which satisfy the required power instantly despite being highly variable over a short period of time. A comparison of the system with the FOPI and PI controllers showed good performance of the system with the two controllers, which had good tracking accuracy and robustness to variations in wind speed and power demanded by loads. The FOPI controller offers a fast dynamic response, has a low overshoot, and works well with renewable energy systems that have highly variable characteristics (wind speed and requested power) in a relatively brief period of time.

In the forthcoming studies, particular attention on the experimental validation of the enhanced performance will be considered while using the optimized FOPI controller for Grid interface control of Wind–Solar Generator in Hail region. In addition, the online tuning of the FOPI gains will be considered to cope with real time variations of these systems.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

SY: Writing–original draft. OK: Writing–original draft. HA: Methodology, Writing–review and editing. NA: Validation, Writing–review and editing. MC: Visualization, Writing–original draft.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research has been funded by Scientific Research Deanship at University of Ha’il-Saudi Arabia through project number (RD-21 122).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abassi, R., and Chebbi, S. (2012). Energy management strategy for a grid connected wind-solar hybrid system with battery storage: policy for optimizing conventional energy generation. Int. Rev. Electr. Eng. (IREE) 7 (2).

Google Scholar

Abedinpourshotorbana, H., Shamsuddina, S. M., Beheshtia, Z., and Jawawi, D. N. (2016). Electromagnetic field optimization: a physics inspired metaheuristic optimization algorithm. Swarm Evol. Comput. 26, 8–22. doi:10.1016/j.swevo.2015.07.002

CrossRef Full Text | Google Scholar

Afghoul, H., Chikouche, D., Krim, F., Babes, B., and Beddar, A. (2016). Implementation of fractional-order integral-plus-proportional controller to enhance the power quality of an electrical grid. Electr. Power Compon. Syst. 44 (9), 1018–1028. doi:10.1080/15325008.2016.1147509

CrossRef Full Text | Google Scholar

Alam, M. S., Al-Ismail, F. S., and Abido, M. A. (2021). PV/Wind-Integrated low-inertia system frequency control: PSO-optimized fractional-order PI-based SMES approach. Sustainability 13 (14), 7622. doi:10.3390/su13147622

CrossRef Full Text | Google Scholar

Alharthi, Y. Z., Siddiki, M. K., and Chaudhry, G. M. (2018a). Resource assessment and techno-economic analysis of a grid-connected solar PV-wind hybrid system for different locations in Saudi Arabia. Sustainability 10, 3690. doi:10.3390/su10103690

CrossRef Full Text | Google Scholar

Alharthi, Y. Z., Siddiki, M. K., and Chaudhry, G. M. (2018b). Resource assessment and techno-economic analysis of a grid-connected solar PV-wind hybrid system for different locations in Saudi Arabia. Sustainability 10, 3690. doi:10.3390/su10103690

CrossRef Full Text | Google Scholar

Alhelou, H. H., Hamedani-Golshan, M. E., Heydarian-Forushani, E., Al-Sumaiti, A. S., and Siano, P. (2018). “Decentralized fractional order control scheme for LFC of deregulated nonlinear power systems in presence of EVs and RER,” in Proc. Int. Conf. Smart Energy Syst Technol. (SEST), Seville, Spain, September, 2018, 1–6.

CrossRef Full Text | Google Scholar

Alshibani, A., and Alshamrani, O. S. (2017). ANN/BIM-based model for predicting the energy cost of residential buildings in Saudi Arabia. J. Taibah Univ. Sci. 11 (6), 1317–1329. doi:10.1016/j.jtusci.2017.06.003

CrossRef Full Text | Google Scholar

Asghar, M., and Nasimullah, (2018). Performance comparison of wind turbine based doubly fed induction generator system using fault tolerant fractional and integer order controllers. Renew. Energy 116, 244–264. doi:10.1016/j.renene.2017.01.008

CrossRef Full Text | Google Scholar

Azorin-Molina, C., Rehman, S., Guijarro, J. A., McVicar, T. R., Minola, L., Chena, D., et al. (2018). Recent trends in wind speed across Saudi Arabia, 1978–2013: a break in the stilling. Int. J. Climatol. 38, 966–984. doi:10.1002/joc.5423

CrossRef Full Text | Google Scholar

Baghel, M., Agrawal, S., and Silakari, S. (2012). Survey of metaheuristic algorithms for combinatorial optimization. Int. J. Comput. Appl. 58 (19), 21–31. doi:10.5120/9391-3813

CrossRef Full Text | Google Scholar

Balaska, H., Ladaci, S., Schulte, H., and Djouambi, A. (2019). Adaptive cruise control system for an electric vehicle using a fractional order model reference adaptive strategy. IFAC-Papers 52 (13), 194–199. doi:10.1016/j.ifacol.2019.11.096

CrossRef Full Text | Google Scholar

Barhoumi, E. M., Okonkwo, P. C., Zghaibeh, M., Belgacem, I. B., Alkanhal, T. A., Abo-Khalil, A. G., et al. (2020). Renewable energy resources and workforce case study Saudi Arabia: review and recommendations. J. Therm. Analysis Calorim. 141, 221–230. doi:10.1007/s10973-019-09189-2

CrossRef Full Text | Google Scholar

Beddar, A., Bouzekri, H., Babes, B., and Afghoul, H. (2016). Experimental enhancement of fuzzy fractional order PI+I controller of grid connected variable speed wind energy conversion system. Energy Convers. Man- age. 123, 569–580. doi:10.1016/j.enconman.2016.06.070

CrossRef Full Text | Google Scholar

Bilel, DHOUIB, Alaas, Z., Kahouli, O., and Abdallah, H.HADJ (2020). Determination of optimal location of FACTS device to improve integration rate of wind energy in presence of MBPSS regulator. IET Renew. Power Gener. 14, 3526–3540. doi:10.1049/iet-rpg.2020.0679

CrossRef Full Text | Google Scholar

Bruzzone, L., Fanghella, P., and Baggetta, M. (2020). Experimental assessment of fractional-order PDD1/2 control of a brushless DC Motor with inertial load. Actuators 9 (1), 13–17. doi:10.3390/act9010013

CrossRef Full Text | Google Scholar

Chen, Y., Petras, I., and Xue, D., 2009, Fractional order control_A tutorial, in Proc. Amer. Control Conf., St. Louis, MO, USA, June. 2009, pp. 1397–1411.

Google Scholar

Eid, B. M., Abd Rahim, N., Selvaraj, J., and AhmadEl Khateb, H. (2016). Control methods and objectives for electronically coupled distributed energy resources in microgrids: a review. IEEE Syst. J. 10 (2), 446–458. doi:10.1109/jsyst.2013.2296075

CrossRef Full Text | Google Scholar

El Khashab, H., and Ghamedi, M.Al (2015). Comparison between hybrid renewable energy systems in Saudi Arabia. J. Electr. Syst. Inf. Technol. 2 (1), 111–119. doi:10.1016/j.jesit.2015.03.010

CrossRef Full Text | Google Scholar

General Authority for statistics, (2023). Rate wind speed observed by pme met stations for 2015 A.D. Saudi Arabia: General Authority for statistics- KSA.

Google Scholar

Ghasemi, S., Tabesh, A., and Askari-Marnani, J. (2014). Application of fractional calculus theory to robust controller design for wind turbine generators. IEEE Trans. Energy Convers. 29 (3), 780–787. doi:10.1109/tec.2014.2321792

CrossRef Full Text | Google Scholar

Huang, Y.-P., and Hsu, S.-Y. (2016). A performance evaluation model of a high concentration photovoltaic module with a fractional open circuit voltage based maximum power point tracking algorithm. Comput. Electr. Eng. 51, 331–342. doi:10.1016/j.compeleceng.2016.01.009

CrossRef Full Text | Google Scholar

Iov, F., Ciobotaru, M., Sera, D., Teodorescu, R., and Blaabjerg, F., 2007, Power electronics and control of renewable energy systems,'' in Proc. 7th Int. Conf. Power Electron. Drive Syst., Bangkok, Thailand, pp.6–28. November, 2007

CrossRef Full Text | Google Scholar

Jebali, M., Kahouli, O., and Hadj Abdallah, H., 2016, "Power system stabilizer parameters optimization using genetic algorithm," 2016 5th International Conference on Systems and Control (ICSC), Marrakesh, Morocco, May, 2016, pp. 78–83. doi:10.1109/ICoSC.2016.7507031

CrossRef Full Text | Google Scholar

Kamal, N. A., and Ibrahim, A. M. (2018). “Conventional, intelligent, and fractionalorder control method for maximum power point tracking of a photovoltaic system: a review,” in Fractional order systems (advances in nonlinear dynamics and chaos) (New York, NY, USA: Academic), 603–671.

CrossRef Full Text | Google Scholar

Khubalkar, S. W., Junghare, A. S., Aware, M. V., Chopade, A. S., and Das, S. (2018). Demonstrative fractional order_PID controller-based DC motor drive on digital platform. ISA Trans. 82, 79–93. doi:10.1016/j.isatra.2017.08.019

PubMed Abstract | CrossRef Full Text | Google Scholar

Khurram, A., Rehman, H., Mukhopadhyay, S., and Ali, D. (2018). Comparative analysis of integer-order and fractional-order proportional integral speed controllers for induction motor drive systems. J. Power. Electron. 18 (3), 723–735. doi:10.6113/JPE.2018.18.3.723

CrossRef Full Text | Google Scholar

Kumar, M., Diwania, S., Sen, S., and Rawat, H. S. (2023b). Emission-averse techno-economical study for an isolated microgrid system with solar energy and battery storage. Electr. Eng. 105, 1883–1896. doi:10.1007/s00202-023-01785-8

CrossRef Full Text | Google Scholar

Kumar, M., Sen, S., Prajapati, A. K., and Diwania, S., 2023a, "A comprehensive power management approach for hydrogen fuel-cell-based hybrid EVs using PID controller," 2023 IEEE IAS Global Conference on Renewable Energy and Hydrogen Technologies (GlobConHT), Male, Maldives, March, 2023, pp. 1–6. doi:10.1109/GlobConHT56829.2023.10087669

CrossRef Full Text | Google Scholar

Kumar, M. R., Deepak, V., and Ghosh, S. (2017). Fractional-order controller design in frequency domain using an improved nonlinear adaptive seeker optimization algorithm. Turk. J. Electr. Eng. Comput. Sci. 25, 4299–4310. doi:10.3906/elk-1701-294

CrossRef Full Text | Google Scholar

Mahvash, H., Taher, S. A., Rahimi, M., and Shahidehpour, M. (2018). DFIG performance improvement in grid connected mode by using fractional order [PI] controller. Int. J. Electr. Power Energy Syst. 96, 398–411. doi:10.1016/j.ijepes.2017.10.008

CrossRef Full Text | Google Scholar

Mahvash, H., Taher, S. A., Rahimi, M., and Shahidehpour, M. (2019). Enhancement of DFIG performance at high wind speed using fractional order PI controller in pitch compensation loop. Int. J. Electr. Power Energy Syst. 104, 259–268. doi:10.1016/j.ijepes.2018.07.009

CrossRef Full Text | Google Scholar

Melício, R., Mendes, V. M. F., and Catalão, J. P. S. (2010). Fractional order control and simulation of wind energy systems with PMSG/full-power converter topology. Energy Convers. manage. 51 (6), 1250–1258. doi:10.1016/j.enconman.2009.12.036

CrossRef Full Text | Google Scholar

Mohana, M., Saidi, A. S., Alelyani, S., Alshayeb, M. J., Basha, S., and Anqi, A. E. (2021). Small-scale solar photovoltaic power prediction for residential load in Saudi Arabia using machine learning. Energies 14, 6759. doi:10.3390/en14206759

CrossRef Full Text | Google Scholar

Monje, C., Chen, Y., Vinagre, B., Xue, D., and Feliu, V. (2010a). Fractional order systems and Control_Fundamentals and applications (advances in industrial control). London, U.K.: Springer-Verlag. doi:10.1007/978-1-84996-335-0

CrossRef Full Text | Google Scholar

Monje, C. A., Chen, Y. Q., and Vinagre, B. M. (2010b). Dingyu xue and vicente feliu, fractional-order systems and control: fundamentals and applications. London: Springer.

Google Scholar

Mosaad, M. I. (2020). Direct power control of SRG-based WECSs using optimised fractional order PI controller. IET Electr. Power Appl. 14 (3), 409–417. doi:10.1049/iet-epa.2019.0194

CrossRef Full Text | Google Scholar

Nasimullah, M. A., Khattak, A., Ra_q, M. M., and Rafiq, M. M. (2017). Comparison of integer and fractional order robust controllers for DC/DC converter feeding constant power load in a DC microgrid. Sustain. Energy, Grids Netw. 12, 1–9. doi:10.1016/j.segan.2017.08.003

CrossRef Full Text | Google Scholar

Pan, I., and Das, S. (2015). Kriging based surrogate modeling for fractional order control of microgrids. IEEE Trans. Smart Grid 6 (1), 36–44. doi:10.1109/tsg.2014.2336771

CrossRef Full Text | Google Scholar

Pandey, S., Dwivedi, P., and Junghare, A. S. (2017). A novel 2-DOF fractional-order PI D controller with inherent anti-windup capability for a magnetic levitation system. AEU-Int. J. Electron. Commun. 79, 158–171. doi:10.1016/j.aeue.2017.05.031

CrossRef Full Text | Google Scholar

Rajasekhar, A., Das, S., and Abraham, A. (2013). Fractional order PID controller design for speed control of chopper fed DC motor drive using arti_cial bee colony algorithm. Proc.World Congr. Nat. Biol. Inspired Comput., 259–266. doi:10.1109/NaBIC.2013.6617873

CrossRef Full Text | Google Scholar

Saidi, A. S., Alsharari, F., Ahmed, E. M., Al-Gahtani, S. F., Irshad, S. M., and Alalwani, S. (2023). Investigating the impact of grid-tied photovoltaic system in the aljouf region, Saudi Arabia, using dynamic reactive power control. Energies 16, 2368. doi:10.3390/en16052368

CrossRef Full Text | Google Scholar

Samy, M. M., Mossad, M. I., and Barakat, S. (2021). Reliability support of undependable grid using green energy systems; economic study. IEEE Access J. 9, 14528–14539. doi:10.1109/access.2020.3048487

CrossRef Full Text | Google Scholar

Sawle, Y., Gupta, S. C., and Kumar Bohre, A. (2016). PV-wind hybrid system: a review with case study. Cogent Eng. 3, 1189305. doi:10.1080/23311916.2016.1189305

CrossRef Full Text | Google Scholar

Seixas, M., Melício, R., and Mendes, V. M. F. (2014). Offshore wind turbine simulation: multibody drive train. Back-to-back NPC (neutral point clamped) converters. Fractional-order control. Energy 69, 357–369. doi:10.1016/j.energy.2014.03.025

CrossRef Full Text | Google Scholar

Tam, S. C., Chio, C. H., and Tam, H. K., 2011, Development of a new optimization method, Yin-Yang algorithm, for traveling salesman problem, in Proc. Int. Conf. Syst. Sci. Eng., Macau, China, pp. 245–250. June, 2011

CrossRef Full Text | Google Scholar

Tazy, A. F., Samy, M. M., and Barakat, S. (2020). A techno-economic feasibility analysis of an autonomous hybrid renewable energy sources for university building at Saudi Arabia. J. Electr. Eng. &Technology 15, 2519–2527. doi:10.1007/s42835-020-00539-x

CrossRef Full Text | Google Scholar

Thi Minh Chau, Le (2012). Couplage onduleurs photovoltaïques et réseau, aspects contrôle/commande et rejet de perturbations. Français: THÈSE DE L’UNIVERSITÉ DE GRENOBLE.

Google Scholar

Tran-Quoc, T., and Caire, R. (2010). Chapitre 5 du livre "La distribution d’énergie électrique en présence de production décentralisée. Français: éditeur LAVOISIER.

Google Scholar

Vanchinathan, K., and Valluvan, K. R. (2018). A metaheuristic optimization approach for tuning of fractional-order PID controller for speed control of sensorless BLDC motor. J. Circuits, Syst. Comput. 27 (08), 1850123. doi:10.1142/s0218126618501232

CrossRef Full Text | Google Scholar

Visioli, A. (2012). Research trends for PID controllers. Acta Polytech. 52 (5), 144–150. doi:10.14311/1656

CrossRef Full Text | Google Scholar

Warrier, P., and Shah, P. (2021a). Fractional order control of power electronic converters in industrial drives and renewable energy systems: a review. IEEE Acces 9, 58982–59009. doi:10.1109/access.2021.3073033

CrossRef Full Text | Google Scholar

Warrier, P., and Shah, P. (2021b). Fractional order control of power electronic converters in industrial drives and renewable energy systems: a review. IEEE Access 9, 58982–59009. doi:10.1109/ACCESS.2021.3073033

CrossRef Full Text | Google Scholar

Yang, B., Yu, T., Shu, H., Zhu, D., An, N., Sang, Y., et al. (2018b). Energy reshaping based passive fractional-order PID control design and implementation of a grid-connected PV inverter for MPPT using grouped grey wolf optimizer. Sol. Energy 170, 31–46. doi:10.1016/j.solener.2018.05.034

CrossRef Full Text | Google Scholar

Yang, B., Yu, T., Shu, H., Zhu, D., Zeng, F., Sang, Y., et al. (2018a). Perturbation observer based fractional-order PID control of photovoltaics inverters for solar energy harvesting via Yin-Yang-Pair optimization. Energy Convers. manage. 171, 170–187. doi:10.1016/j.enconman.2018.05.097

CrossRef Full Text | Google Scholar

Yichen, Z., Hejin, X., and Deming, L., 2017, Feedback control of fractional PID for DC/DC buck converters, in Proc. Int. Conf. Ind. Inform.- Comput. Technol., Intell. Technol., Ind. Inf. Integr. (ICIICII), Wuhan, China, pp. 219–222. December, 2017

Google Scholar

Younsi, S., Kahouli, O., Hamrouni, N., Alsaif, H., Ali, , and Hamed, S. (2022a). Performance analysis and multi-mode control of grid connected micro Wind–solar hybrid generator in Saudi Arabia. J. Taibah Univ. Sci. 16 (1), 550–565. doi:10.1080/16583655.2022.2078134

CrossRef Full Text | Google Scholar

Younsi, S., Kahouli, O., Hamrouni, N., Alsaif, H., Ali, , and Hamed, S. (2022b). Performance analysis and multi-mode control of grid connected micro Wind–solar hybrid generator in Saudi Arabia. J. Taibah Univ. Sci. 16 (1), 550–565. doi:10.1080/16583655.2022.2078134

CrossRef Full Text | Google Scholar

Yu, K.-N., Liao, C.-K., and Yau, H.-T. (2015). A new fractional-order based intelligent maximum power point tracking control algorithm for photovoltaic power systems. Int. J. Photoenergy 2015, 1–8. doi:10.1155/2015/493452

CrossRef Full Text | Google Scholar

Zaihidee, F. M., Mekhilef, S., and Mubin, M. (2019). Application of fractional order sliding mode control for speed control of permanent magnet synchronousmotor. IEEE Access 7, 101765–101774. doi:10.1109/access.2019.2931324

CrossRef Full Text | Google Scholar

Zdiri, M. A., Bouzidi, B., Kahouli, O., and Abdallah, H. H., 2019, "Fault detection method for boost converters in solar PV systems," 2019 19th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering (STA), Sousse, Tunisia, March, 2019, pp. 237–242. doi:10.1109/STA.2019.8717239

CrossRef Full Text | Google Scholar

Zell, E., Gasim, S., Wilcox, S., Katamoura, S., Stoel, T., Husain, S., et al. (2015). Assessment of solar radiation resources in Saudi Arabia. Sci. Direct-Solar Energy 119, 422–438. doi:10.1016/j.solener.2015.06.031

CrossRef Full Text | Google Scholar

Nomenclature