Robust model predictive control of wind turbines based on Bayesian parameter self-optimization

This paper studies the effect of different turbulent wind speeds on the operation of wind turbines. The proportion of wind power in the field of new energy generation has increased massively and has gained wide application and attention. However, the smooth operation and the stability of the output power of the wind power generation system are susceptible to wind speed fluctuations. To tackle this problem, this paper takes a 5 MW horizontal axis wind turbine as the research object that proposes a parameter adaptive robust control method to achieve self-optimization of controller parameters by means of Bayesian optimization. The 5 MW wind turbine model is utilized to verify the feasibility of the algorithm by combining the wind speed types commonly found in a high-altitude region in northwestern. The simulation results validate the effectiveness of the proposed scheme. The outcomes demonstrate that Bayesian optimization can significantly decrease the effects of wind speed instability. The output power increases by 1.9% on average at low wind speed and stabilizes on 5 MW at high wind speed. Therefore, the stable controller for wind power output is the robust model predictive controller with parameter improvement.

1 Introduction

As a renewable energy source, wind energy has the properties of high reserves, widely spread, low emission and clean. The promotion of the wind power technology industry is of major significance to China in achieving the goals of peak carbon dioxide emissions and carbon neutrality, promoting energy structure transition, building a new energy system with new energy as the mainstay, and fostering new dynamics of economic development (Rezamand et al., 2020; Qin et al., 2021; Kumar et al., 2023). With the advancement of wind power technique, the safe operation of wind power systems is becoming increasingly crucial. So, the operational quality of wind power systems is a main factor of current research. As one of the most widely used and significant models with high power generation efficiency, 5 MW wind turbines occupy 60%–70% of the market share in the high-altitude areas of western China. In addition, random fluctuation of wind speed not only affects the steady performance of wind power generation, but also requires constant switching of control targets according to different wind speed ranges (Gao et al., 2022). Therefore, this paper focuses on how to minimize the influences of wind speed variations on the steady performance of wind turbines, which will place further demands on the controlling methods of wind power systems (Xu et al., 2019).

Model predictive control (MPC) and robust model predictive control (RMPC) are two common methods which are widely used in the wind power generation systems. (Shang et al., 2020). The traditional method of control for wind power systems is MPC. MPC is a model-based control approach that calculates the optimal control input for a future period by predicting the dynamic model of the system (Chen et al., 2022). The stochastic nature of wind speeds during wind turbine generation has been the subject of intensive research by many scholars. The load of blades and towers of wind power systems were analyzed and an MPC algorithm was proposed to suppress wind speed fluctuations. Simulation results show that MPC can make the active power of the wind turbine stable and reduce the blade load (Zhu et al., 2014). To address the nonlinear control issue of wind turbines, a multi-model predictive control was established for the non-linear multi-coupling characteristics of wind power system, which has obtained good control effect and effectively suppressed the system disturbance (Ye et al., 2015). Multi-timescale dynamic coordination strategies were proposed based on model predictive control for active distribution network operation optimization, enabling flexible regulation of resources. (Dong et al., 2016). During the control of wind power systems, MPC was used for controlling the rotational speed of the wind turbine, the blade angle and the output power of the generator in order to achieve optimal power generation (David et al., 2022). For the power control problem of wind power systems with non-linear characteristics, a non-linear model predictive control based on an input-output feedback linearization strategy was proposed to ensure high efficiency and high load tracking performance (Liu and Kong, 2014). To reduce the unbalanced load on the wind turbine paddles, an integrated control strategy combining MPC with neural networks and adaptive PID was proposed to effectively achieve real-time control of the paddle pitch angle (Wang et al., 2017). A controller that does not require wind speed measurements was designed to correct model uncertainty in the form of magnitude scaling errors. (Mulders et al., 2023).

In addition, MPC is combined with distributed control structures and deep learning algorithms to maximize the power production of wind power systems (Yin and Zhao, 2021). However, the stochastic nature of wind resources is dependent on wind speed and is not removed by model updates and feedback corrections, so effective model predictive control strategies need to be designed to guarantee the steady and reliable performance of wind power systems in the presence of different wind speed variations. To address the impact of real-time wind speed uncertainty on wind power systems, a disturbance observer was designed to estimate unknown disturbances and improve the robustness of the generalized predictive controller (Kamel et al., 2015). A distributed predictive controller was designed to assume bounded disturbances in the wind field (Zhao et al., 2015). Wind power systems have diverse control objectives in the presence of various wind speed ranges (Cui and Liu, 2019). The operation of wind power systems was improved by studying transmission line fault phase selection. (Zhang et al., 2018). A small capacity power conversion interface capable of efficiently introduced to track the maximum power of a wind power systemw (Wu and Wang, 2014). A prediction model was built for doubly-fed wind turbines based on support vector machines to achieve optimal speed tracking, which is meaningful for wind power systems to efficiently use wind energy to generate electricity (Liu et al., 2014). A multivariate control strategy based on model predictive control was presented for variable pitch control of wind energy conversion systems. The proposed scheme enhanced the power quality and lengthen the service time of the wind turbine parts (Soliman et al., 2011). As a matter of fact, the ideal linear time-invariant model in practical control hardly exists. Furthermore, wind power systems always encounter wind speed disturbances with uncertainty (Yang et al., 2023). Nevertheless, the above-mentioned methods of control all indirectly take into account the influence of wind speed instability on the system constraints, making it difficult to design controllers that are accurate in real time. Moreover, the MPC is applied to the control process of wind power systems without directly considering the uncertainty of wind speed. Consequently, the MPC algorithm needs to be improved to enhance the robustness of wind power system operation.

To control wind power systems more effectively, the uncertainty of wind speed needs to be taken into account directly in the controller design process. Existing research in model predictive control theory has used invariant sets, linear matrix inequality (LMI), and others as basic tools, and Lyapunov stability as the analytical method for current predictive control problems (Song et al., 2017). On these foundations, a min-max RMPC strategy was designed for wind power systems (Moamed et al., 2017). By exploiting the boundary of wind speed uncertainty, the active power is rated at full load operation while ensuring system stability and reducing the torque load. In order to cope with the uncertainty caused by the stochastic and fluctuating nature of new energy sources to the load frequency control of interconnected systems, a RMPC strategy implemented based on Tube invariant sets for the optimal operation of wind power systems (Zhang et al., 2020). A RMPC based on a linear time-varying model was devised. It completed the effective control of the turbine by enhancing the robustness of the system when additional disturbances occur (Falugi and Mayne, 2014). Tube was employed based continuous time RMPC to ensure robustness of non-linear wind power systems operating above rated wind speeds (Lasheen et al., 2017). Multi-objective maintenance and closed-loop maintenance strategies were introduced to address the uncertainty awareness of offshore wind turbine decision-making under random wind speeds. The effects of different uncertainties on maintenance performance were quantified (Li et al., 2023; Li et al., 2022). Moreover, microscale obstacle resolution models, such as MITRAS (Salim et al., 2018) and PALM (Maronga et al., 2020), play a crucial role in the parameterization of wind turbines in urban areas (Wurps et al., 2020; Stanly et al., 2022). These models use standard methods, usch as simple actuator disk and blade element momentum theory (Calaf et al., 2010; Wu and Porté-Agel, 2011), to account for the interaction between the wind turbines and the atmosphere. These models account also for the effects of trees (Salim et al., 2015), including wind speed reduction, turbulence generation, dissipation due to plant leaf drag, and radiation absorption and shading (Krč et al., 2021; Salim et al., 2022). The parameterization of turbulence generation in wind turbine wake is achieved by adding an extra part to the turbulent mechanical generation term in the turbulent dynamic energy equation. An open source wind model was developed based on GIS, which is a relatively fast and accurate model that is easy to use and capable of generating wind fields. It can be used both indoors and outdoors for complex urban environments (Bernard et al., 2023).

With the development of wind power technology, RMPC is well used for the control of wind power systems. RMPC is a control methodology that adds robust design to MPC to effectively overcome the effects of model errors and external disturbances on the control system. The combined application of RMPC and stochastic model prediction algorithms to uncertain systems is studied comparatively, visualizing the performance and reliability of RMPC algorithms through simulation examples (Xie et al., 2017). Model-free adaptive control was proposed for doubly-fed wind turbines to improve the overall operational performance of the wind energy conversion system (Mosaad et al., 2020). In wind power systems, the RMPC can be applied to control the speed of the wind turbine, the angle of the blades, the output power of the generator, and so forth, for the purpose of robust control of the system. The RMPC was utilized to control the output power of a wind turbine, which was good at reducing output power fluctuations (Zhang et al., 2022). A finite control set RMPC control strategy was designed, which is important for the power quality improvement and stable operation of doubly-fed wind power systems (Alami et al., 2023). The fan speed and paddle angle were controlled with an RMPC in pursuit of robust control of the system (Lio et al., 2017). Nonlinear model predictive control was proposed for coordinated optimization of wind energy resources in power systems. The efficiency of wind energy capture and conversion is improved. (Sahar et al., 2017). Also, An intelligent maximum power tracking algorithm was developed, which improved the output power to maximize the revenue of wind farms (Huang et al., 2015). An additional feedback control loop is proposed for the active power control of the wind farm. The distribution of regulated power demand between wind turbines were improved. A wind farm example was also simulated using PALM, thus testing the suitability of the controller (Vali et al., 2018). All of the above approaches have been successful in addressing the overall operational performance, structural uncertainty or external disturbance uncertainty of wind power systems. However, wind speed is a random and discontinuous disturbance input and difficult to predict. Minimizing wind speed uncertainty is a prerequisite to ensure that wind power system control can be carried out smoothly. At the same time the robust boundaries for stochastic perturbations are not easy to determine, too small or large a boundary can cause problems of under-robustness and over-conservatism of the control system. Thus, the integrated consideration of different random wind speed disturbance inputs and the optimization of robust boundaries are important issues to be addressed in the control of wind turbine.

Based on the above overview, this paper designs a robust model predictive controller with self-optimizing parameters to increase the efficiency of wind turbine, using a 5 MW wind turbine as the research target. The robust boundaries are optimized based on Bayesian optimization methods to ensure robust and low-conservative controllers. The innovation is reflected in two aspects. On the one hand, the wind turbine needs to switch back and forth between control targets for different wind speeds. Moreover, the use of RMPC makes the wind turbine more stable to complete the switch between different control targets. On the other hand, Bayesian optimization is used to achieve self-optimization of the controller parameters to address the problem of inappropriate setting of the robust model prediction controller weight parameters. In this paper, different wind conditions are simulated in a high-altitude region of northwest China and the reliability of the proposed approach is validated through simulation studies. The results demonstrate that this approach can strengthen the capability of wind power systems, including improving power generation efficiency, reducing mechanical losses and extending equipment life. In conclusion, a robust model predictive controller based on Bayesian optimization is an advanced method to optimize the behavior of wind power systems.

The sections of this paper are structured as follows. Section 2 develops a wind speed model and a non-linear mathematical model of the wind power system. Moreover, it describes the control problems of the wind turbine behind different wind speed. Section 3 introduces the Bayesian algorithm. It designs a robust model predictive controller based on Bayesian parameter self-optimization to establish an RMPC-based control scheme for wind power systems. Section 4 simulates and analyses the control effect of the RMPC on the wind power system under two different wind conditions. Section 5 draws the conclusions of this paper.

2 System models

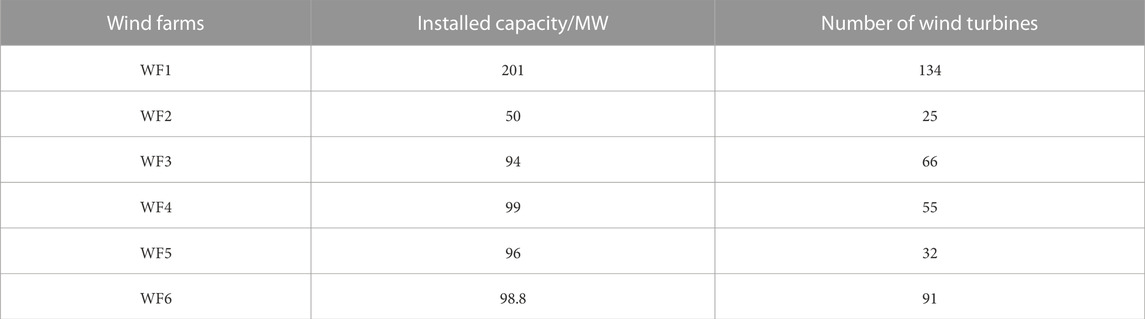
Wind power systems are designed to consist of three components. They are the wind turbine, the drive system and the generator. Figure 1 is a schematic diagram of wind energy conversion. Wind turbine enables the process of converting wind energy into electricity. Firstly, the varying wind speed drives the rotation of the wind wheel, converting the wind energy into mechanical energy. Then, it is transferred to the generator via the drive system in the unit, which turns the rotor to convert the mechanical energy into electrical energy, which is then connected to the grid via a two-way inverter. This paper focuses on the control of megawatt-class variable-speed pitch wind turbines. Figure 2 shows a specific flow chart of the methodology of this study.

FIGURE 1

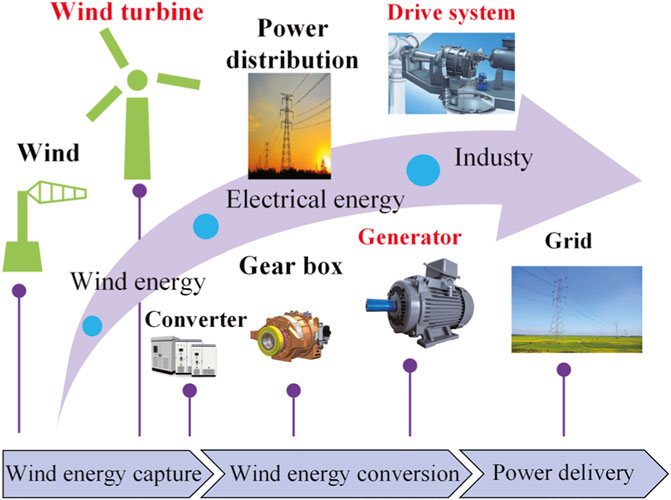
FIGURE 1. Diagram of wind energy conversion. The kinetic energy of the wind is converted into mechanical kinetic energy, which is then converted into electrical kinetic energy.

FIGURE 2

FIGURE 2. Flow chart of the proposed method. The model was linearized and the controller model was built using RMPC. Finally, the controller parameters were optimized using Bayesian.

2.1 Wind speed model for wind farms

Due to the rich wind energy resources at high altitude in northwest China, the wind direction is highly concentrated and the wind energy has a high level of quality. In general, wind speed becomes higher with increasing altitude. Due to the large difference in altitude, the wind speed varies greatly, with the annual average wind speed at 70 m high ranging from about 6 m/s to 10 m/s. High altitude areas have a variety of wind speed types suitable for the establishment and operation of wind farms. The wind speed at an altitude in north-western China is used as the simulated wind speed so that a more realistic wind speed model can be obtained. v_m represents the average wind speed, which conforms to the mathematical expectations of the Weibull distribution. As shown in Eq. 1. Its size is determined by the shape and scale parameters, s₁ is the scale parameter and s₂ is the shape parameter (Usta et al., 2018).

$v_{\text{m}}=\frac{s_2}{s_1}{\left(\frac{v_{\text{m}}}{s_1}\right)}^{s_2-1}\exp \left(-{\left(\frac{v_{\text{m}}}{s_1}\right)}^{s_2}\right)(1)$

A steady wind is a wind field in which the wind speed and direction remain constant in time and space. This wind field is usually caused by the atmospheric circulation and the wind speed and direction are relatively stable without significant fluctuations or disturbances. Uniform winds are a common meteorological condition in areas such as aviation, navigation and construction, and can provide a stable environment for the work involved. Its wind speed model can be described by the Eq. 2 (Cao et al., 2021).

$v_{\text{m}}=v_0+\mathrm{\Delta }v(2)$

where v₀ is the base wind speed and Δv is the wind speed disturbance.

Turbulent winds are wind fields in which the wind speed and direction change randomly in time and space. Such wind fields are usually caused by factors such as topography, buildings and meteorological conditions, with significant fluctuations and disturbances in wind speed and direction. Turbulent winds are a common meteorological condition in aviation, navigation and construction and have a significant impact on the safety and stability of the work involved. The study and prediction of turbulent winds is therefore of great importance. Its wind speed model can be described by the Eq. 3.

$v_{\text{t}}=v_0+\mathrm{\Delta }v+\delta v(3)$

where v_t is the turbulent velocity, v₀ is the basic wind speed, Δv is the wind disturbance and δv is the turbulent wind speed. Turbulent wind speeds are random in magnitude and direction, it can be described by statistical methods.

Turbulent wind speeds obey the Gaussian distribution in Eq. 4.

$v_{\text{t}}\sim N\left(0,{\sigma }^2\right)(4)$

where σ is the standard deviation.

2.2 Wind power system model

Before designing the RMPC, a mathematical model is needed to describe the wind power generation system (WPGS). WPGS consist of a number of components such as wind turbines, generators, transmissions and controllers. Amongst other things, the wind turbine is the core component of the WPGS and its speed and torque have a very significant impact on the performance of the WPGS. Therefore, this paper establishes the mathematical model of the WPGS as shown in Eq. 5.

$\left\{\begin{array}{c}{J}_{\text{r}}{\dot{\omega }}_{\text{r}}=T_{\text{r}}-K_{\text{s}}\theta -D_{\text{s}}\dot{\theta }\hfill \\ \dot{\theta }={\omega }_{\text{r}}-\frac{{\omega }_{\text{g}}}{N_{\text{M}}}\hfill \\ J_{\text{g}}{\dot{\omega }}_{\text{g}}=-T_{\text{g}}+\frac{K_{\text{s}}}{N_{\text{M}}}\theta +\frac{D_{\text{s}}}{N_{\text{M}}}{\dot{\theta }}^{\prime }\hfill \\ P_{\text{g}}={\eta }_{\text{g}}{\omega }_{\text{g}}{T}_{\text{g}}\hfill \end{array}\right.(5)$

where T_r is the rotor torque, as shown in Eq. 6.

$T_{\text{r}}=\frac{1}{2}\rho \pi R^2{C}_{\text{P}}\left(\lambda ,\beta \right)(6)$

where C_P is the power coefficient, which is associated with the pitch angle β and tip velocity ratio λ = Rω_r/v (Lackner, 2011).

$C_{\text{P}}\left({\lambda }_{,}\beta \right)=0.5176\left(\frac{116}{{\lambda }_{\text{s}}}-0.4\beta -5\right)\exp \left(-\frac{21}{{\lambda }_{\text{s}}}\right)+0.006795\lambda (7)$

where λ_s is established using Eq. 8.

$\frac{1}{{\lambda }_s}=\frac{1}{\lambda +0.08\beta }-\frac{0.035}{{\beta }^3+1}(8)$

This paper sets $x={\left[\begin{array}{ccc}\hfill x_1\hfill & \hfill x_2\hfill & \hfill x_3\hfill \end{array}\right]}^{\text{T}}={\left[\begin{array}{ccc}\hfill {\omega }_{\text{r}}\hfill & \hfill \theta \hfill & \hfill {\omega }_{\text{g}}\hfill \end{array}\right]}^{\text{T}}$ as state variables, $u={\left[\begin{array}{cc}\hfill u_1\hfill & \hfill u_2\hfill \end{array}\right]}^{\text{T}}={\left[\begin{array}{cc}\hfill \beta \hfill & \hfill T_{\text{g}}\hfill \end{array}\right]}^{\text{T}}$ as input variables and $y={\left[\begin{array}{cc}\hfill y_1\hfill & \hfill y_2\hfill \end{array}\right]}^{\text{T}}={\left[\begin{array}{cc}\hfill P_{\text{g}}\hfill & \hfill {\omega }_{\text{g}}\hfill \end{array}\right]}^{\text{T}}$ as output. According to Eqs. 5–8, the dynamic model of the WPGS is depicted in Eq. 9 by a non-linear equation of state (Cui et al., 2018).

$\dot{x}\left(t\right)=f\left(x\left(t\right),u\left(t\right),v\left(t\right)\right)(9)$

2.3 Description of control issues requiring improvement

The wind turbine RMPC control block diagram is shown in Figure 3. The reference values are brought into the quadratic programming solver to obtain the optimal pitch angle β_opt and the optimal generator torque T_m,opt. Combining the feedback control law K and the robust invariant set Z, the pitch moment angle and generator torque acting on the actual wind turbine are obtained. The actual value of the optimization problem at the next moment is obtained through the prediction model and the feedback correction session. The difference between the actual value and the reference value is then solved with the quadratic programming solver until the reference value is tracked.

FIGURE 3

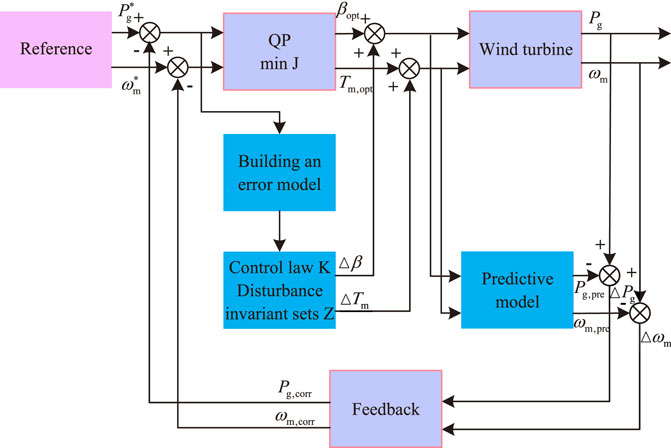
FIGURE 3. Wind Turbine RMPC Control Block Diagram. The optimal pitch moment angle and optimal generator torque were obtained using the quadratic programming solver parameter values. The pitch moment angle and generator torque acting on the actual wind turbine were obtained by combining the feedback control law K and the robust invariant set Z. The actual values of the optimization problem at the next moment were obtained by the prediction model and the feedback correction link. The actual values of the optimization problem at the next moment were obtained through the prediction model and the feedback correction link. Finally, the quadratic programming solver solves for the difference until the reference values were tracked.

In this paper, it is assumed that the wind speed stochastic disturbance is bounded, so that this part of the uncertainty disturbance is regarded as a factor that deviates from the stable operating point of the wind turbine. The purpose of the controller is to make the actual trajectory of the wind turbine closely related to the trajectory of the nominal system of the wind turbine. Under the action of the feedback control law, the deviation between the actual operating state of the wind turbine and the nominal state of the system is limited to the set of perturbation invariants. No matter how the wind speed changes, it will never get out of the set, which is what an invariant set means. Linearizing the mathematical model of the wind turbine, the following equations are obtained.

$\dot{\stackrel{̄}{x}}=A\bar{x}\left(t\right)+B\bar{x}\left(t\right)+Ev\left(t\right)(10)$

Considering Ev(t) as a perturbation, Eq. 10 is discretized and written in Eq. 11.

$\bar{x}\left(k+1\right)=A_d\bar{x}\left(k\right)+B_d\bar{x}\left(k\right)+w\left(k\right)(11)$

Neglecting w(k) then the nominal model of the wind power system without disturbances can be obtained as follows.

$\bar{x}\left(k+1\right)=A_d\bar{x}\left(k\right)+B_d\bar{x}\left(k\right)(12)$

The feedback control rate and invariant set are solved by constructing the Liapunov function. The objective function can be expressed as Eq. 13.

$\begin{array}{ll}\hfill \min J& ={\displaystyle \sum _{i=1}^{N_c=1}}\left(\begin{array}{c}\hfill \tilde{x}{\left(k+i\mid k\right)}^{\text{T}*}{Q}^{*}\tilde{x}\left(k+i\mid k\right)\hfill \\ \hfill \tilde{u}{\left(k+i\mid k\right)}^{\text{T}*}{Q}^{*}\tilde{u}\left(k+i\mid k\right)\hfill \end{array}\right)\hfill \\ \hfill & +\tilde{x}{\left(k+N_{\text{c}}\mid k\right)}^{\text{T}}*F\tilde{x}\left(k+N_{\text{c}}\mid k\right)\hfill \end{array}(13)$

$\begin{array}{ll}\hfill \text{\hspace{0.17em}s.t.\hspace{0.17em}}\tilde{x}\left(k+1\right)& =A_d\tilde{x}\left(k\right)+B_d\tilde{x}\left(k\right)\hfill \\ x\left(k\mid k\right)\hfill & =x_0\left(k\mid k\right)\hfill \\ {\tilde{x}}_{\min }\hfill & \le x\le {\tilde{x}}_{\max }\hfill \\ {\tilde{u}}_{\min }\hfill & \le \tilde{u}\le {\tilde{u}}_{\max }\hfill \end{array}(14)$

where N_c denotes the control time domain, Q and R denote the positive definite weighting matrices, F is the terminal constraint weighting matrix. ${\tilde{x}}_{\min }$, ${\tilde{x}}_{\max }$, ${\tilde{u}}_{\min }$ and ${\tilde{u}}_{\max }$ are the maximum and minimum constraints on the state variables and input variables. Solving the optimization objective function gives the optimal solution.

$\bar{x}\left(k+1\right)=A_d\bar{x}\left(k\right)+B_d\bar{x}\left(k\right)(15)$

Take the first value and apply it to the actual system.

$\bar{x}\left(k+1\right)=A_d\bar{x}\left(k\right)+B_d\bar{x}\left(k\right)(16)$

The obtained state variables are used as inputs to solve the optimization problem from scratch until the control objective is accomplished.

3 Robust controllers with adaptive optimization of parameters

3.1 Design of the RMPC controller

After establishing a mathematical model of the system, the RMPC controller can be designed to optimize the control of the WPGS (Wang et al., 2011; Ping et al., 2022). RMPC of wind turbines sets the optimization objective function by tracking the reference values of wind turbine rotational speed, generator output power, generator rotational speed, and pitch angle (Xie et al., 2021). The optimal control inputs pitch angle and generator torque are solved based on the current objective function and constraints, then applied to the actual system. Specifically, the design of the robust model predictive controller includes the following steps.

1) Establish the wind speed model Eq. 1 and the nonlinear mathematical model Eq. 9 for the wind turbine. Next the nonlinear mathematical model is linearized around the stable operating point (x*, u*, v*). Neglecting wind speed disturbances, the nominal system x(k + 1) = Ax(k) + Bu(k) is obtained (Yang et al., 2022).

2) The error system is obtained and the Lyapunov function S(e(t)) = eT(t)Pe(t) is constructed. The feedback control rate K and the set of perturbation invariants Z are obtained using linear matrix inequalities (Rafael and Darci, 2022).

3) Set the initial state x₀(k|k) of the turbine nominal system at moment k. Set the N_C and N_P values to construct the prediction equation (Zou et al., 2014).

4) A quadratic programming solver is used to solve the optimization objective function and obtain the optimal solution. The input control quantity u(k) = u (k − 1) + u*(k|k) of the nominal system is obtained by decomposing the first term u*(k|k) and combining it with the feedback control law K to obtain the control input of the actual system.

5) Solve for the state variables using the nominal model and substitute them into the optimized objective function for the next solution.

6) Perform k = k + 1 and return to step 4.

3.2 Bayesian parametric self-optimization algorithm

The Bayesian optimization algorithm uses a probabilistic model agent to fit an objective function of the original cost and constructs a collection function based on the posterior probability distribution to select the next optimal evaluation point. In this paper, the probability model is chosen to use Gaussian process regression and the collection function is chosen to use a boosted probability function (Tanoe et al., 2021).

3.2.1 Gaussian process

The Gaussian process is the most commonly used probabilistic model in the use of Bayesian optimization. As a general paradigm for multivariate Gaussian probability distributions, the Gaussian process is mainly composed of a mean function and a covariance function.

$\mathrm{y}=\mathrm{G}\mathrm{P}\left(n\left(x\right),k\left(x,x^{\prime }\right)\right)(17)$

where n(x) is the mean value function, $k\left(x,x^{\prime }\right)$ is the covariance function. The measure of x is finite-dimensionally distributed in a Gaussian process. When fitting discrete data to a sample using a Gaussian process, n(x) is generally set to 0. Because the Matern covariance function depends only on the distance between two points, it is smooth. This paper chooses Matern as $k\left(x,x^{\prime }\right)$.

3.2.2 Acquisition functions

The lift probability is the most commonly used acquisition function. The function determines the next point to be taken from the mean and covariance calculated by Gaussian regression. It is shown in Eq. 18.

$f\left(x\right)=P\left(f\left(x_{\max }\right)+\alpha \right)=\phi \left(\frac{\mu \left(x\right)-f\left(x_{\max }\right)-\alpha }{\sigma \left(x\right)}\right)(18)$

where f(x) is the objective function value, φ(*) is the distribution function, μ(x) is the mean, σ(x) is the variance, and α is the hyperparameter to explore the maximum space. α = 0 makes the value converge to $f\left(x_{\max }\right)$, avoiding a local optimum.

The steps for optimizing the parameters of the RMPC model using the Bayesian algorithm in this paper are shown below.

1) Set parameters to be optimized, with the optimization objective being the minimum global target value.

2) Optimization of the parameters of the RMPC controller using Bayesian.

3) Return the minimum global objective value of the optimization and the parameters of the corresponding RMPC model.

4) The minimum global objective value output by the Bayesian optimization algorithm corresponds to the controller optimization parameters as the final RMPC controller parameters.

3.3 Bayesian optimization of controller parameters

The RMPC controller objective function is shown in Eq. 19.

$J\left(x\left(\tau \right),u\left(\tau \right)\right)=r_1\dot{\beta }{\left(t\right)}^2+r_2{\dot{T}}_{\text{g}}{\left(t\right)}^2+r_3{\left(P_{\text{g}}\left(t\right)-P_{\text{g}}^{*}\right)}^2(19)$

where τ is the time parameter.$\dot{\beta }(t)$ is the Pitch angle change rate, ${\dot{T}}_{\text{g}}(t)$ is rate of change of generator torque. P_g(t) is actual output power, $P_{\text{g}}^{*}$ is rated output power.

The first and second terms of the objective function reflect the control of the pitch angle and generator torque of the system, while the last term accounts for the output power in Eq. 19 (Hyacinthe and Sun, 2020). Pitch angle and generator torque and output power weighting factors in the RMPC controller to be optimally adjusted. The above parameters are optimized using a Bayesian optimization method, as shown in Figure 4.

FIGURE 4

FIGURE 4. Diagram of the Bayesian-based parametric self-optimization framework. The blue section shows a complete RMPC controller process. The green part is the optimization of the RMPC controller parameters using Bayes.

Considering the need for maximum power tracking and constant power maintenance in the wind power system control task, the following global objective function is established as shown in Eq. 20.

$J_G={\displaystyle \sum _{k=1}^{\infty }}\left({\mathrm{w}}_{\text{bo}}\mathrm{\Delta }{\beta }_k+{\mathrm{w}}_{\text{bo},\mathrm{P}}\mathrm{\Delta }{\mathrm{P}}_{\text{g},k}\right)(20)$

where w_bo is the global objective function pitch angle deviation factor and Δβ_k is the pitch angle deviation. w_bo,P is the global objective function output power deviation coefficient and ΔP_g,k is the output power deviation value. The global objective value is minimized by adjusting the optimization parameter matrix ${\mathrm{W}}_{\text{Bo}}={\left[{\omega }_{\text{r}},\theta ,{\omega }_{\text{g}},\alpha \right]}^{\text{T}}$.

$\begin{array}{c}\mathrm{arg\; min}{J}_{\text{G}}\left({\mathrm{W}}_{\text{Bo}}\right)\hfill \\ \text{\hspace{0.17em}s.t.\hspace{0.17em}}{\mathrm{W}}_{\text{Bo}}\in \mathrm{\Omega }\hfill \end{array}(21)$

where Ω is the bounded domain of parameters that guarantee the stability of the controller. Since the gradient and concavity properties of the global objective function are unknown, it is assumed that the global objective function is a Gaussian process, as shown in Eq. 22.

$J_G\sim GP\left(\mu \left({\mathrm{W}}_{\text{Bo}}\right),k\left({\mathrm{W}}_{\text{Bo}},{\mathrm{W}}_{\text{Bo}}^{*}\right)\right)(22)$

where μ(W_Bo) is the posterior mean and $k({\mathrm{W}}_{\text{Bo}},{\mathrm{W}}_{\text{Bo}}^{*})$ is the posterior variance. The global target values are calculated and a Gaussian process regression is performed on the collected sample dataset to obtain μ(W_Bo) and of the Gaussian process of the alternative model, which is obtained from the upper confidence boundary collection function to suggest sampling optimization parameters for the next iteration. The minimum global objective value corresponding to the controller optimization parameter value output by the Bayesian optimization algorithm is used as the final RMPC controller parameter.

4 Simulation analysis

4.1 Simulation parameter settings

Application of MATLAB simulation software for simulation experiments on wind power systems. The sampling time is chosen to be 0.05 s and the predicted time domain is N = 10. The simulation experiment uses a 5 MW horizontal axis wind turbine (Jason et al., 2009). In this paper, three parameters, namely, pitch angle, generator torque and output power, are selected to study the control performance of the proposed approach on WPGS under different wind conditions. In the objective function, the weighting parameters are set to r₁ = 7, r₂ = 1 × 10⁻⁸ and r₃ = 1 × 10⁻¹². The low wind speed region enables the wind turbine to achieve maximum wind energy capture by varying the tip speed ratio of the wind turbine and fixing the pitch angle for maximum aerodynamic efficiency. The blade pitch angle is adjusted in the high wind speed region to ensure that both the output power and generator speed are stabilized at the rated value. In order to verify the effectiveness of the control method proposed in this paper, we simulated different values of wind speed to validate the performance of the controller. The cut-in wind speed of wind turbines is generally 3–5 m/s, so a wind speed of 5 m/s is chosen as a low wind speed. Through the wind speed data of wind farms in northwestern China, the wind speed of 8 m/s occurs more frequently, so the wind speed of 8 m/s is simulated as another low wind speed. The rated wind speed of 5 MW wind turbine is 11.4 m/s. In order to evaluate whether the proposed method can control the turbine to reach the rated output power under the rated wind speed, the wind speed of 11.4 m/s is simulated. After the wind speed research statistics show that the frequency of 12 m/s wind speed is high, so the simulation of 12 m/s wind speed as a high wind speed representative wind speed. In conclusion, these four wind speeds are chosen for this paper.

4.2 Uniform wind control results

Figure 5 shows the comparison curves of pitch angle simulation for two control strategies using RMPC and Bayesian optimized RMPC. From Figures 5A,D, it can be seen that for the disturbance caused by inaccurate wind speed measurement, the proposed method can make the generator torque vary with wind speed with high robustness, which can achieve maximum wind energy capture and the power generated is proportional to the wind speed variation. As shown in Figures 5B,C, both controllers have the same control effect for bounded wind speed disturbances. However, when the measured wind speed changes, the maximum change in pitch angle is reduced under the parameter self-optimizing RMPC controller.

FIGURE 5

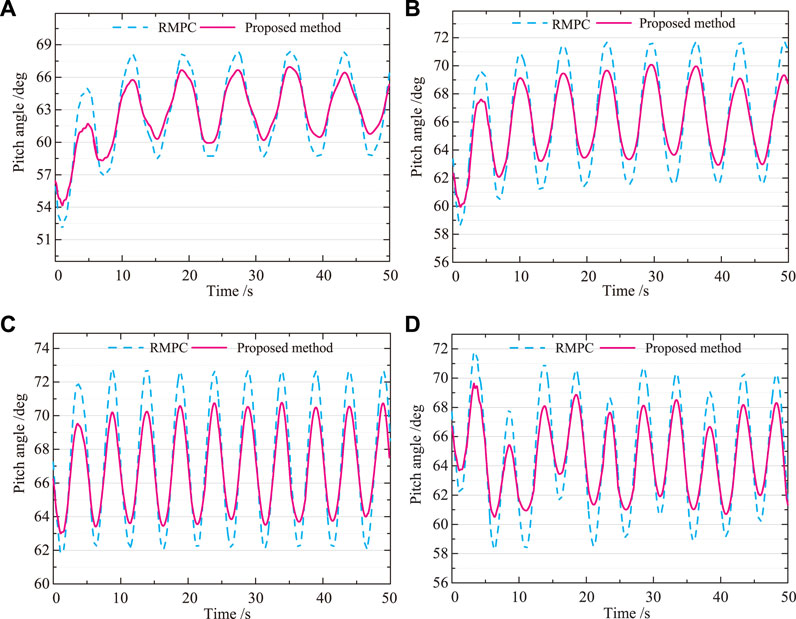
FIGURE 5. Pitch angle. (A) 5 m/s. (B) 8 m/s. (C) 11.4 m/s. (D) 12 m/s. The maximum change in pitch angle is reduced under the parameter self-optimizing RMPC controller, when the measured wind speed changes.

Figure 6 shows a comparison of the generator torque simulation curves using both RMPC and Bayesian optimized RMPC. As can be seen from Figure 6, both control strategies are able to control the generator torque stabilization rating and stay within the set constraints. Pitch angle fluctuations are less under the Bayesian optimized RMPC than under RMPC control. According to Figure 6 it can be concluded that the oscillation of the generator torque is reduced with the RMPC optimization method compared to the RMPC controller. This will reduce internal losses in the system, extend the life of the turbine and gain more economic benefits. Therefore, the proposed control strategy allows the generator power to be stabilized at the rated value with reduced mechanical fatigue losses and improved economic performance.

FIGURE 6

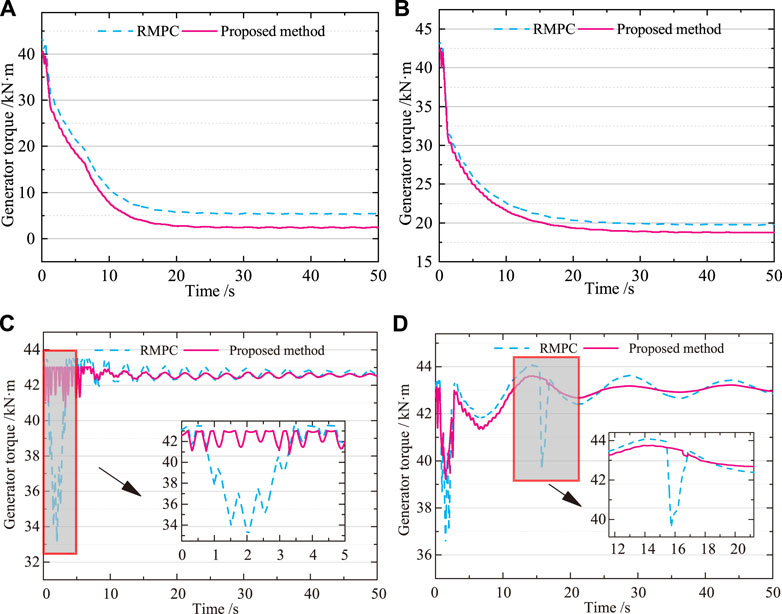
FIGURE 6. Generator torque. (A) 5 m/s. (B) 8 m/s. (C) 11.4 m/s. (D) 12 m/s. The oscillation of the generator torque is reduced with the RMPC optimization method compared to the RMPC controller. This will reduce internal losses in the system, extend the life of the turbine and gain more economic benefits.

From Figure 6C, it can be seen that the generator torque is in an extremely unstable state during 0–5 s when the wind power system is first started. As can be seen from Figure 6, the Bayesian optimized RMPC strategy responds quickly, allowing the generator torque to stabilize quickly around its nominal value. Also from Figure 6D, it can be seen that the generator torque under the RMPC control strategy oscillates greatly during 15–17 s when the wind power system is subject to uncertainty disturbance. With the proposed method the torque fluctuations are greatly reduced and the variation values are much smoother.

Figure 7 shows the comparative generator output power curves for the RMPC and Bayesian optimized RMPC control strategies. As can be seen in Figure 7, the Bayesian optimized RMPC algorithm’s output power curve is closest to the rated power curve at different wind speeds, with a small fluctuating trend. Compared to the RMPC control results, the proposed method is significantly more stable. Within 0–5 s in Figure 7C, 0–7 S in Figure 7D, the output power fluctuates up and down considerably with the RMPC control strategy, while RMPC significantly reduces the output power fluctuation. As shown in Figure 7C, when the measured wind speed reaches the rated wind speed, the pitch angle is adjusted downwards to increase the capture of wind energy, so that the generator speed and power are stabilized at the rated value and constant power control is achieved. Taking the rated wind speed of 11.4 m/s as an example, this paper calculates the average parameter values under two different control results as shown in Table 1.

FIGURE 7

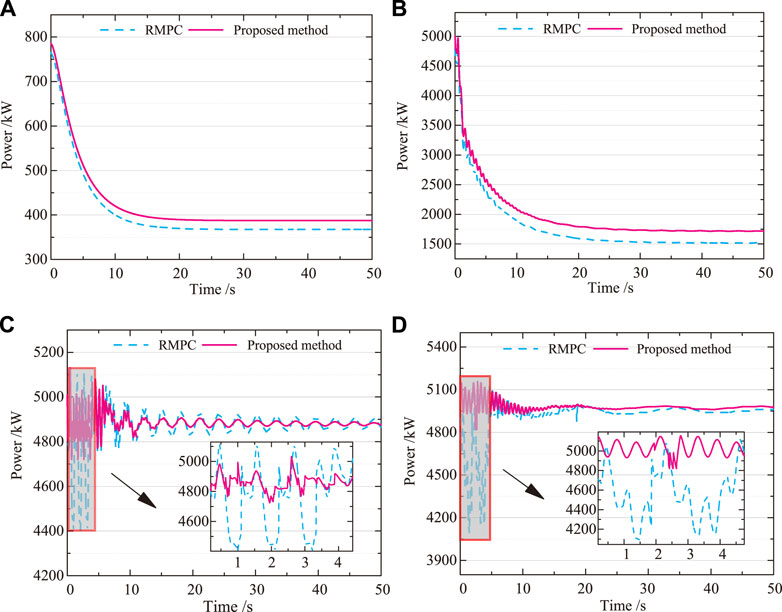
FIGURE 7. Power. (A) 5 m/s. (B) 8 m/s. (C) 11.4 m/s. (D) 12 m/s. The Bayesian optimized RMPC algorithm’s output power curve is closest to the rated power curve at different wind speeds, with a small fluctuating trend. Compared to the RMPC control results, the proposed method is significantly more stable.

TABLE 1

TABLE 1. Comparison of RMPC and Bayesian optimized RMPC results at 11.4 m/s.

In summary, at uniform wind speeds of 5 m/s, 8 m/s, 11.4 m/s and 12 m/s, the Bayesian optimized RMPC is capable of controlling the turbine to maximize power. It can be seen intuitively that the proposed method outperforms the RMPC at different uniform wind speeds. The proposed method exhibits small fluctuations in the active power of the generator, the torsion angle of the drive system and the pitch angle, effectively reducing the fluctuations at the stable operating point. The Bayesian optimized RMPC strategy is therefore superior for wind power system control, with significantly improved oscillations and high robustness. At the same time, the rationality and accuracy of the proposed approach is confirmed.

4.3 Results of turbulent wind control

The turbulent winds simulated in this paper are based on the most frequent wind conditions of varying turbulence intensity at a high altitude in the northwest. In order to verify the control performance of the designed robust model predictive controller under real turbulent wind conditions, the simulations are conducted through the use of the FAST software developed by NREL. Figure 8 shows the control results for each parameter at 5% turbulence intensity.

FIGURE 8

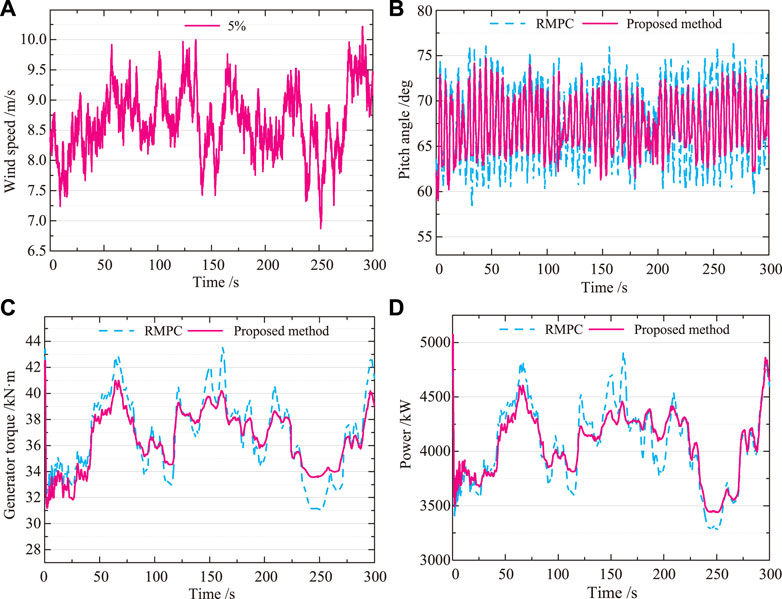
FIGURE 8. 5% turbulence intensity. (A) Wind speed. (B) Pitch angle. (C) Generator torque. (D) Power. At low turbulent wind speeds, the results of the proposed method are superior to RMPC. The output power is increased by an average of 2.6%, reducing output power fluctuations and improving the quality of power generation with the proposed control strategy.

It is clear from Figure 8 that the generator torque and output power fluctuate widely and become more unstable with time. When the turbine is in low turbulence intensity wind conditions, the RMPC control effect to improve the stable operation of the wind power system is not obvious enough, indicating that the RMPC control strategy needs to be improved. As can be seen in Figure 8C, the average generator torque is reduced by 1 kN ⋅ m, so that the proposed method drives the wind turbine with less force and achieves maximum wind power at low wind speeds. As can be seen from Figure 8D, the output power is increased by an average of 2.6%, reducing output power fluctuations and improving the quality of power generation with the proposed control strategy.

Figure 9 shows the control results for each parameter at 10% turbulence intensity. With turbulent wind speeds, the Bayesian optimized RMPC makes the wind turbine output power work around the rated value, effectively reducing the wind speed fluctuations on the WPGS. The generator speed is very close to the optimum speed at each moment, so that the proposed method can significantly suppress the effect of external wind speed disturbances on the system’s ability to capture wind energy. The results in Figures 9C,D show that the wind power system satisfies the input-output constraints, for both generator torque and output power. The output of the turbine increased by 1.3%. From the simulation results, the robust model predictive controller with self-optimizing parameters proposed in this paper can achieve maximum wind energy capture and reduce the fatigue of wind turbine components.

FIGURE 9

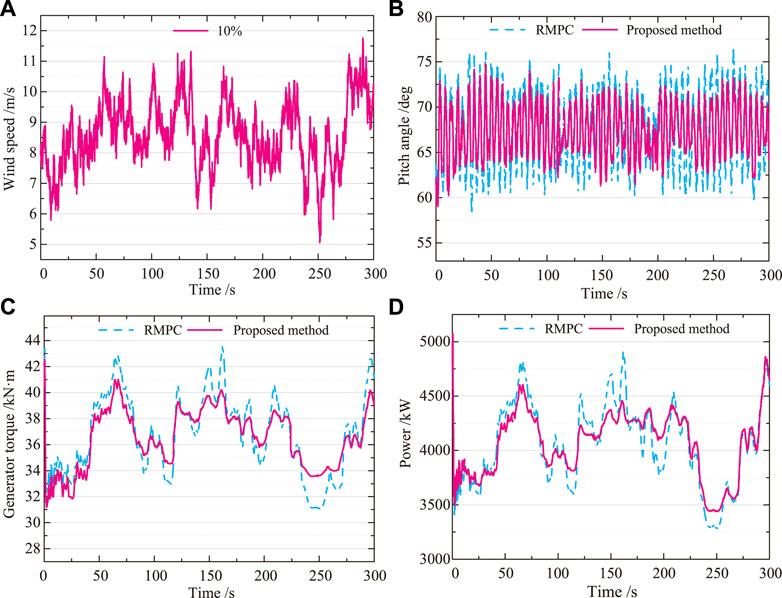
FIGURE 9. 10% turbulence intensity. (A) Wind speed. (B) Pitch angle. (C) Generator torque. (D) Power. At 10% turbulent wind speeds, the results of the proposed method are superior to RMPC. The output of the turbine increased by 1.3%. The robust model predictive controller with self-optimizing parameters proposed in this paper can achieve maximum wind energy capture and reduce the fatigue of wind turbine components.

Figure 10 shows a comparison of the control results at high turbulence intensities. The oscillations in the pitch angle and generator torque are much smaller with the Bayesian optimized RMPC controller compared to the RMPC controller. It can be concluded that Bayesian optimized RMPC allows a better trade-off between maximum generation rate and minimum fatigue losses. This is because the Bayesian optimized RMPC strategies introduce system dynamic processes into the decision-making hierarchy and aim to maximize economic efficiency, particularly in dynamic processes. As a result, it is possible to reduce fatigue losses in wind turbine components while producing generator power comparable to that of general RMPC. From Figure 10D, it can be seen that the output of the turbine increased by 1.5%. RMPC with Bayesian optimization can significantly enhance the capability of wind turbine in terms of increased generation efficiency, reduced mechanical losses and longer equipment life. The Bayesian optimized RMPC control strategy not only enables adaptive adjustment of controller parameters, but also achieves the control goal of stable operation of wind power systems.

FIGURE 10

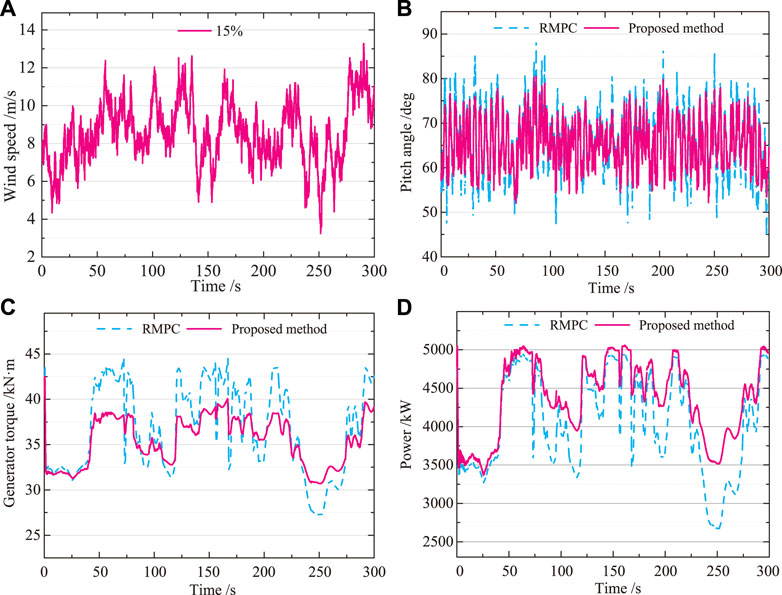
FIGURE 10. 15% turbulence intensity. (A) Wind speed. (B) Pitch angle. (C) Generator torque. (D) Power. At high turbulent wind speeds, the results of the proposed method are superior to RMPC. The output of the turbine increased by 1.5%. The Bayesian optimized RMPC control strategy not only enables adaptive adjustment of controller parameters, but also achieves the control goal of stable operation of wind power systems.

4.4 Industrial field verification

The proposed approach with adaptive optimization of parameters is validated using a wind power cluster at a wind power plant in north-western China. The wind power cluster is located in the high-altitude region of northwest China, which is rich in wind resources, and the construction of wind farms belongs to inland mountain wind farms. It has successfully realized grid-connected operation with obvious economic, social and environmental benefits. This wind power cluster is selected for the field validation, which can get the effectiveness of the proposed method more intuitively. The total installed capacity is 638.8 MW. This wind power plant contains 6 wind farms of different capacities. Moreover, all equipped with a wind power prediction control system. The installed capacity of each wind farm is shown in Table 2. The field situation is shown in Figure 11.

TABLE 2

TABLE 2. Installed capacity of wind farms.

FIGURE 11

FIGURE 11. Industrial field applications. The total installed capacity is 638.8 MW. It contains 6 wind farms of different capacities. Moreover, all equipped with a wind power prediction control system.

Figure 12 gives a typical wind farm power fluctuation response time, where the response time is defined as the time difference between the wind cluster active power fluctuation control device receiving the active power control command from the simulator and issuing the wind farm control command. As can be seen from Figure 12, the lowest response time for WF1 is 0.5 s, the highest response time for wind farm WF6 is 0.84 s, while the response times for the remaining wind farms are all within the value of 1 s. The analysis shows that the response times for power fluctuations vary from one wind farm to another, and all respond within a short period of time, further indicating that the proposed method can effectively suppress power fluctuations.

FIGURE 12

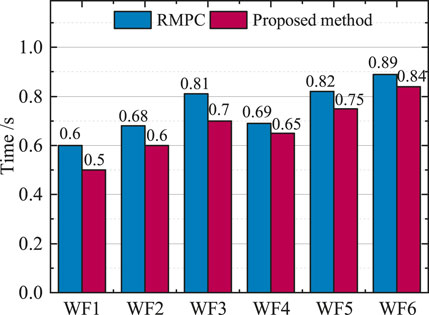
FIGURE 12. Optimal steady-state targets for different operating regions. The lowest response time for WF1 is 0.5 s, the highest response time for wind farm WF6 is 0.84 s, while the response times for the remaining wind farms are all within the value of 1s.

5 Conclusion

To enhance the control performance of wind power systems, an experimental study was conducted using Bayesian algorithms to optimize the parameters of the RMPC controller. This paper compares and analyses the RMPC and the Bayesian optimized RMPC algorithms using the classical 5 MW wind turbine model developed by NREL. A MATLAB/Simulink-based simulation platform is applied to simulate. The specific conclusions from the simulation analysis are as follows.

1) The field simulation experiments show that this paper uses the Bayesian optimization approach for parameter self-optimization of the cost function weight coefficients. The minimum response time for wind farms is 0.5 s, and the response time for each wind farm is within 1s, which improves the tracking performance and robustness of the RMPC controller.

2) The Bayesian optimized RMPC control strategy enables the control objectives of the turbine to be achieved at different wind speeds. The average power obtained by wind turbines at low wind speeds is 1.2 MW, an improvement of 1.9%. At high wind speeds, the output power is stable at 5 MW on average. This significantly achieves a stable transition of the turbine’s control objectives at different wind speeds. Moreover, fluctuations in output power are reduced and the quality of power generation is improved.

3) The proposed scheme can significantly increase the capability of wind power systems, including improving power generation efficiency, reducing mechanical losses and extending equipment life. The proposed control technique is adaptive, responsive, simple to implement and robust to various operating conditions and disturbance scenarios. The model has good robustness while addressing power deviations in wind power systems. However, the finer differential control of wind farms, the comprehensive wind speed simulation and the coordinated and optimized cooperation of conventional units under this framework need to be studied in greater depth in the future. And there was no the integration of microscale obstacle-resolving models.In future research issues related to the integration of the microscale barrier solution model will be addressed. Further optimization of wind turbine operating parameters to reduce the impact on control effectiveness. In addition, further research can be conducted to optimize the performance of robust model prediction controllers to improve control accuracy and system stability.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

MT: Conceptualization, Funding acquisition, Methodology, Project administration, Resources, Supervision, Writing–review and editing. WW: Data curation, Formal Analysis, Investigation, Methodology, Software, Visualization, Writing–original draft, YY: Investigation, Methodology, Supervision, Visualization, Writing–review and editing, Validation. YZ: Formal Analysis, Investigation, Resources, Validation, Writing–review and editing. BA: Formal Analysis, Investigation, Validation, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was funded by the National Natural Science Foundation of China [Grant Numbers 62363022, 61663021, 71763025, and 61861025]; Natural Science Foundation of Gansu Province [Grant Number 23JRRA886]; Gansu Provincial Department of Education: Industrial Support Plan Project [Grant Number 2023CYZC-35].

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alami, H. E., Badre, B., Mahfoud, M. E., Bouderbala, M., Majout, B. S., Paweł, M. S., et al. (2023). Robust finite control-set model predictive control for power quality enhancement of a wind system based on the dfig generator. Energies 16, 1422. doi:10.3390/en16031422

CrossRef Full Text | Google Scholar

Bernard, J., Lindberg, F., and Oswald, S. (2023). Urock 2023a: an open source gis-based wind model for complex urban settings. Geosci. Model. Dev. 16, 5703–5727. doi:10.5194/gmd-16-5703-2023

CrossRef Full Text | Google Scholar

Calaf, M., Meneveau, C., and Meyers, J. (2010). Large eddy simulation study of fully developed wind-turbine array boundary layers. Phys. fluids 22, 3095–3120. doi:10.1063/1.3291077

CrossRef Full Text | Google Scholar

Cao, L., Wang, L., and Zhao, L. (2021). Nonlinear control of maximum wind energy capture for variable-speed wind turbines. Control Eng. China 28, 1534–1539. doi:10.14107/j.cnki.kzgc.20180675

CrossRef Full Text | Google Scholar

Chen, S., Zheng, N., Luan, X., and Liu, F. (2022). Dynamic reference programming-based robust tube model predictive tracking control. Control Theory Appl. 39, 1725–1732.

Google Scholar

Cui, J., Liu, S., Liu, J., and Liu, X. (2018). A comparative study of mpc and economic mpc of wind energy conversion systems. Energies 11, 3127. doi:10.3390/en11113127

CrossRef Full Text | Google Scholar

Cui, J., and Liu, X. (2019). Economic model predictive control for variable speed wind turbines. Control Eng. 26, 431–439. doi:10.14107/j.cnki.kzgc.20180759

CrossRef Full Text | Google Scholar

David, E. C., Eduardo, M. N., and Javier, R. F. (2022). Model predictive control for optimal power flow in grid-connected unbalanced microgrids. Electr. Power Syst. Res. 209, 108000. doi:10.1016/j.epsr.2022.108000

CrossRef Full Text | Google Scholar

Dong, L., Chen, H., Pu, T., Chen, N., and Wang, X. (2016). Multi-time-scale dynamic optimal scheduling of active distribution network based on model predictive control. Chin. J. Electr. Eng. 36, 4609–4617. doi:10.13334/j.0258-8013.pcsee.151262

CrossRef Full Text | Google Scholar

Falugi, P., and Mayne, D. Q. (2014). Getting robustness against unstructured uncertainty: a tube-based mpc approach. IEEE Trans. Automation control 59, 1290–1295. doi:10.1109/tac.2013.2287727

CrossRef Full Text | Google Scholar

Gao, W., Zhang, Y., Zhang, L., Ai, C., and Chen, L. (2022). Research on a power smoothing control strategy for energy storage hydraulic wind turbines. Energy Sci. Eng. 11, 989–1004. doi:10.1002/ese3.1375

CrossRef Full Text | Google Scholar

Huang, C., Li, F., and Jin, Z. (2015). Maximum power point tracking strategy for large-scale wind generation systems considering wind turbine dynamics. IEEE Trans. Industrial Electron. 62, 2530–2539. doi:10.1109/tie.2015.2395384

CrossRef Full Text | Google Scholar

Hyacinthe, T. D., and Sun, Y. (2020). Predictive controller for interconnected microgrids. IET Generation, Transm. Distribution 14, 4273–4283. doi:10.1049/iet-gtd.2019.1257

CrossRef Full Text | Google Scholar

Jason, J., Sandy, B., Walter, M., and George, S. (2009). Definition of a 5-MW reference wind turbine for offshore system development. Tech. rep. Golden, CO, USA: National Renewable Energy Laboratory NREL.

Google Scholar

Kamel, O., Toufik, R., and Mohand, O. (2015). Real time simulation of nonlinear generalized predictive control for wind energy conversion system with nonlinear observer. ISA Trans. 53, 76–84. doi:10.1016/j.isatra.2013.08.004

CrossRef Full Text | Google Scholar

Krč, P., Resler, J., Sühring, M., Schubert, S., Salim, M. H., and Fuka, V. (2021). Radiative transfer model 3.0 integrated into the palm model system 6.0. Geosci. Model. Dev. 14, 3095–3120. doi:10.5194/gmd-14-3095-2021

CrossRef Full Text | Google Scholar

Kumar, D., Rotea, M. A., Aju, E. J., and Jin, Y. (2023). Wind plant power maximization via extremum seeking yaw control: a wind tunnel experiment. Wind Energy 26, 283–309. doi:10.1002/we.2799

CrossRef Full Text | Google Scholar

Lackner, M. A. (2011). An investigation of variable power collective pitch control for load mitigation of floating offshore wind turbines. Wind energy 16, 435–444. doi:10.1002/we.1502

CrossRef Full Text | Google Scholar

Lasheen, A., Saad, M. S., Emara, H. M., and Elshafei, A. L. (2017). Continuous-time tube-based explicit model predictive control for collective pitching of wind turbines. IEEE Trans. Automation control 118, 1222–1233. doi:10.1016/j.energy.2016.11.002

CrossRef Full Text | Google Scholar

Li, M., Jiang, X., Carroll, J., and Negenborn, R. R. (2022). A multi-objective maintenance strategy optimization framework for offshore wind farms considering uncertainty. Appl. Energy 321, 119284. doi:10.1016/j.apenergy.2022.119284

CrossRef Full Text | Google Scholar

Li, M., Jiang, X., Carroll, J., and Negenborn, R. R. (2023). A closed-loop maintenance strategy for offshore wind farms: incorporating dynamic wind farm states and uncertainty-awareness in decision-making. Renew. Sustain. Energy Rev. 18, 113535. doi:10.1016/j.rser.2023.113535

CrossRef Full Text | Google Scholar

Lio, W., Jones, B. L., and Rossiter, J. (2017). Preview predictive control layer design based upon known wind turbine blade-pitch controllers. Wind Energy 20, 1207–1226. doi:10.1002/we.2090

CrossRef Full Text | Google Scholar

Liu, J., Lv, Y., and Peng Guo, D. X. (2014). Intelligent model predictive control of wind power system maximum wind energy tracking. Comput. Eng. Appl. 47, 228–232.

Google Scholar

Liu, X., and Kong, X. (2014). Nonlinear model predictive control for dfig-based wind power generation. IEEE Trans. Automation Sci. Eng. 11, 1046–1055. doi:10.1109/tase.2013.2284066

CrossRef Full Text | Google Scholar

Maronga, B., Banzhaf, S., Burmeister, C., Esch, T., Forkel, R., Fröhlich, D., et al. (2020). Overview of the palm model system 6.0. Geosci. Model. Dev. 13, 1335–1372. doi:10.5194/gmd-13-1335-2020

CrossRef Full Text | Google Scholar

Moamed, A. B., Khaled, L., Sami, O., and Nida, S.-O. (2017). Fault tolerant control of wind turbine using robust model predictive min-max approach. IFAC Pap. Online 50, 9902–9907. doi:10.1016/j.ifacol.2017.08.1622

CrossRef Full Text | Google Scholar

Mosaad, M. I., Alenany, A., and Ahmed, A.-S. (2020). Enhancing the performance of wind energy conversion systems using unified power flow controller. IET Generation, Transm. Distribution 14, 1922–1929. doi:10.1049/iet-gtd.2019.1112

CrossRef Full Text | Google Scholar

Mulders, S., Brandetti, L., Spagnolo, F., Liu, Y., Christensen, P., and van Wingerden, J. (2023).A learning algorithm for the calibration of internal model uncertainties in advanced wind turbine controllers: a wind speed measurement-free approach, 2023 American Control Conference (ACC), 31 May 2023 - 02, USA. IEEE.

CrossRef Full Text | Google Scholar

Ping, X., Liu, S., Wu, Z., Liu, D., and Li, Z. (2022). Quasi-min-max optimization of dynamic output feedback robust mpc. J. Xidian Univ. 49, 164–176. doi:10.19665/j.issn1001-2400.2022.06.019

CrossRef Full Text | Google Scholar

Qin, S., Cheng, L., He, Z., and Chen, S. (2021). Review of research and application on the wind power-generation system. J. Mach. Des. 38, 1–8. doi:10.13841/j.cnki.jxsj.2021.08.001

CrossRef Full Text | Google Scholar

Rafael, R. S., and Darci, O. (2022). Robust cooperative distributed mpc: a multi-model approach. J. Process Control 117, 65–77. doi:10.1016/j.jprocont.2022.07.003

CrossRef Full Text | Google Scholar

Rezamand, M., Kordestani, M., Carriveau, R., Ting, D. S., Orchard, M. E., and Saif, M. (2020). Critical wind turbine components prognostics: a comprehensive review. IEEE Trans. Instrum. Meas. 69, 9306–9328. doi:10.1109/tim.2020.3030165

CrossRef Full Text | Google Scholar

Sahar, S. K., Khaled, M. A.-A.-E., and Tamer, F. M. (2017). Application of nonlinear model predictive control based on swarm optimization in power systems optimal operation with wind resource. Electr. Power Syst. Res. 143, 1415–1430. doi:10.1016/j.epsr.2016.09.013

CrossRef Full Text | Google Scholar

Salim, M. H., Schlünzen, K. H., and Grawe, D. (2015). Including trees in the numerical simulations of the wind flow in urban areas: should we care? J. Wind Eng. Industrial Aerodynamics 144, 84–95. doi:10.1016/j.jweia.2015.05.004

CrossRef Full Text | Google Scholar

Salim, M. H., Schlünzen, K. H., Grawe, D., Boettcher, M., Gierisch, A. M., and Fock, B. H. (2018). The microscale obstacle-resolving meteorological model mitras v2. 0: model theory. Geosci. Model. Dev. 11, 3427–3445. doi:10.5194/gmd-11-3427-2018

CrossRef Full Text | Google Scholar

Salim, M. H., Schubert, S., Resler, J., Krč, P., Maronga, B., Kanani-Sühring, F., et al. (2022). Importance of radiative transfer processes in urban climate models: a study based on the palm 6.0 model system. Geosci. Model. Dev. 15, 145–171. doi:10.5194/gmd-15-145-2022

CrossRef Full Text | Google Scholar

Shang, C., Chen, W., DuncanbStroock, A., and You, F. (2020). Robust model predictive control of irrigation systems with active uncertainty learning and data analytics. IEEE Trans. Control Syst. Technol. 28, 1493–1504. doi:10.1109/tcst.2019.2916753

CrossRef Full Text | Google Scholar

Soliman, M., Malik, O. P., and T Westwic, k D. (2011). Multiple model multiple-input multiple-output predictive control for variable speed variable pitch wind energy conversion systems. IET Renew. Power Gener. 5, 124–136. doi:10.1049/iet-rpg.2009.0137

CrossRef Full Text | Google Scholar

Song, D., Yang, J., Joo, M. D. Y. H., and Joo, Y. H. (2017). Model predictive control with finite control set for variable-speed wind turbines. Energy 126, 564–572. doi:10.1016/j.energy.2017.02.149

CrossRef Full Text | Google Scholar

Stanly, R., Martinez-Tossas, L. A., Frankel, S. H., and Delorme, Y. (2022). Large-eddy simulation of a wind turbine using a filtered actuator line model. J. Wind Eng. Industrial Aerodynamics 222, 104868. doi:10.1016/j.jweia.2021.104868

CrossRef Full Text | Google Scholar

Tanoe, V., Henderson, S., Shahirinia, A., and Bina, M. T. (2021). Bayesian and non-bayesian regression analysis applied on wind speed data. J. Renew. Sustain. Energy 13, 053303. doi:10.1063/5.0056237

CrossRef Full Text | Google Scholar

Usta, I., Arik, I., Yenilmez, I., and Kantar, Y. M. (2018). A new estimation approach based on moments for estimating weibull parameters in wind power applications. Energy Convers. Manag. 164, 570–578. doi:10.1016/j.enconman.2018.03.033

CrossRef Full Text | Google Scholar

Vali, M., Petrović, V., Steinfeld, G., Pao, L., and Kühn, M. (2018). Large-eddy simulation study of wind farm active power control with a coordinated load distribution. J. Phys. Conf. Ser. 1037, 2018. doi:10.1088/1742-6596/1037/3/032018

CrossRef Full Text | Google Scholar

Wang, D., Wang, W., and Cai, X. (2017). Research on control strategy of individual pitch control of wind turbine based on nmpc-pid. Acta Energiae Solaris Sin. 38, 2520–2526. doi:10.19912/j.0254-0096.2017.09.028

CrossRef Full Text | Google Scholar

Wang, J., Gong, H., and Chen, Y. (2011). Design and simulation of variable pitch control system for large wind turbines. Electr. Autom. 33, 18–20.

Google Scholar

Wu, J., and Wang, Y. (2014). Power conversion interface for small-capacity wind power generation system. IET Generation, Transm. Distribution 8, 689–696. doi:10.1049/iet-gtd.2013.0192

CrossRef Full Text | Google Scholar

Wu, Y.-T., and Porté-Agel, F. (2011). Large-eddy simulation of wind-turbine wakes: evaluation of turbine parametrisations. Boundary-layer Meteorol. 138, 345–366. doi:10.1007/s10546-010-9569-x

CrossRef Full Text | Google Scholar

Wurps, H., Steinfeld, G., and Heinz, S. (2020). Grid-resolution requirements for large-eddy simulations of the atmospheric boundary layer. Boundary-Layer Meteorol. 175, 179–201. doi:10.1007/s10546-020-00504-1

CrossRef Full Text | Google Scholar

Xie, L., Xie, L., and Su, H. (2017). A comparative study of robust and stochastic model predictive control algorithms for uncertain systems. J. Automation 43, 969–992. doi:10.16383/j.aas.2017.c170082

CrossRef Full Text | Google Scholar

Xie, Y., Yang, Z., Cai, S., Wang, D., Chen, M., and Zou, Y. (2021). Power supply restoration strategy of distribution network based on robust model predictive control. Power Syst. Autom. 45, 123–131.

Google Scholar

Xu, D., Wang, Q., and Li, Y. (2019). Robust control of uncertain linear systems based on reinforcement learning principles. IEEE Access 7, 16431–16443. doi:10.1109/access.2019.2894594

CrossRef Full Text | Google Scholar

Yang, W., Jia, L., Zhou, C., and Xu, Y. (2022). Dynamic just-in-time learning based model predictive control for variable pitch wind energy conversion system. J. Renew. Sustain. Energy 14, 063306. doi:10.1063/5.0121787

CrossRef Full Text | Google Scholar

Yang, X., Zhang, Y., Wang, S., and Chen, H. (2023). Improved model-free adaptive control considering wind speed and platform motion for floating offshore wind turbines. J. Renew. Sustain. Energy 15, 033309. doi:10.1063/5.0141656

CrossRef Full Text | Google Scholar

Ye, L., Wang, X., Zhang, X., and Bao, G. (2015). Multi-model predictive control of large-scale wind power generation systems. J. Lanzhou Univ. Technol. 41, 96–102. doi:10.13295/j.cnki.jlut.2015.02.020

CrossRef Full Text | Google Scholar

Yin, X., and Zhao, X. (2021). Deep neural learning based distributed predictive control for offshore wind farm using high-fidelity les data. IEEE Trans. Industrial Electron. 68, 3251–3261. doi:10.1109/tie.2020.2979560

CrossRef Full Text | Google Scholar

Zhang, H., Yang, Y., Wang, Y., Yuan, L., and Jiang, D. (2020). Tube robust model predictive control of load frequency for an interconnected power system with wind power based on pdnn. Power Syst. Prot. Control 48, 137–146. doi:10.19783/j.cnki.pspc.190892

CrossRef Full Text | Google Scholar

Zhang, J., Liu, L., Liu, Y., Zhu, Y., and Yan, J. (2022). Research on robust model predictive control strategy of wind turbines to reduce wind power fluctuation. Electr. Power Syst. Res. 213, 108809. doi:10.1016/j.epsr.2022.108809

CrossRef Full Text | Google Scholar

Zhang, J., Zhang, B., and Wang, C. (2018). Improved schemes for traditional current based phase selectors in wind power systems. IET Generation, Transm. Distribution 12, 5781–5788. doi:10.1049/iet-gtd.2018.5873

CrossRef Full Text | Google Scholar

Zhao, H., Wu, Q., Guo, Q., Sun, H., and Xue, Y. (2015). Distributed model predictive control of a wind farm for optimal active power control-part i: clustering -based wind turbine model linearization. IEEE Trans. Sustain. Energy 6, 831–839. doi:10.1109/tste.2015.2418282

CrossRef Full Text | Google Scholar

Zhu, J., Ma, K., and Guo, Q. (2014). Research on independent pitch control technology of wind turbine based on model predictive control. Electr. Appl. 33, 112–115.

Google Scholar

Zou, T., Pan, H., Ding, B., and Yu, H. (2014). Research progress of predictive control of double-layer structure. Control Theory Appl. 31, 1327–1337.

Google Scholar