Adaptive ADMM-based entire-process distributed restoration of transmission and distribution systems

In the event of a major power outage in the power systems, there is an urgent need to investigate entire-process coordinated restoration strategies for the transmission systems (TSs) and distribution systems (DSs), aiming to accelerate the restoration speed of generating units, network reconfiguration, and load restoration. Furthermore, it is imperative to address the multiple uncertainties that arise during the restoration process to mitigate potential security risks associated with the restoration. Hence, an adaptive ADMM-based entire-process distributed restoration method of TSs and DSs considering CVaR is proposed in this paper. Firstly, an entire-process distributed restoration model of TSs and DSs considering CVaR is proposed to maximize the total restoration benefits of TSs and DSs. Then, an adaptive ADMM-based distributed solving algorithm for the coordinated restoration model of the TSs and DSs is introduced, which incorporates adaptive penalty parameter adjustments, leading to faster convergence compared to the standard ADMM. Finally, case studies on an improved 179-bus transmission system are employed to verify that the proposed restoration method can achieve higher restoration benefits and faster convergence speed compared to existing restoration models.

1 Introduction

In recent years, power system blackouts have become increasingly frequent on a global scale, with various natural and man-made disasters affecting the security and stable operation of power systems (Chen et al., 2021). Power system blackouts have significant impacts on society and people, so it is necessary to investigate restoration strategies after blackouts to effectively guide the power systems restoration and reduce corresponding economic losses (Chen Y. et al., 2023).

Power systems can be divided into transmission systems (TSs) restoration and distribution systems (DSs) restoration (Chen et al., 2022a). So far, many studies have separately explored the restoration strategies for TSs and DSs. In terms of TSs restoration, an extended black-start restoration optimization approach for TSs is introduced in (Wang et al., 2017) to maximize the restored power and loads. A network reconfiguration methodology is presented in (Sun et al., 2019) to effectively balance the impacts of generators, transmission lines, and loads during the reconfiguration of the network. A loop-network reconfiguration optimization strategy for TSs is proposed in (Li et al., 2022), which establishes regional loop-network structures to alleviate transmission line overloads. In (Shen et al., 2018), a triple-stage TSs load restoration model is presented, formulating load restoration strategies based on TSs status and three-stage objective functions. A distributed and coordinated restoration technique for TSs with wind power integration is investigated in (Zhao et al., 2020a), and the robust method is incorporated into the wind power output uncertainty. Regarding DSs restoration, note that DSs typically lack large thermal power units, thus lacking a black-start stage. In (Sekhavatmanesh and Cherkaoui, 2020), a multi-step reconfiguration model for DSs is introduced, taking into account the startup strategy of distributed generators. The objective here is to maximize load restoration while minimizing switching operations. A network reconfiguration method for DSs is proposed in (Shi et al., 2021), which also considers the scheduling of distributed energy resources to expedite load restoration. A distributed load restoration optimization model for unbalanced active DSs is established in (Roofegari and Sun, 2019), utilizing convex triple-phase unbalanced power flow constraints to account for their inherent imbalance. A bi-level service restoration strategy for active DSs is proposed in (Li et al., 2020), considering the coordination of various energy supply sources, including distributed generators and energy storage systems, to maximize the number of restored blackout loads. A modified Viterbi algorithm is proposed in (Yuan et al., 2017) to derive an optimal and resilient restoration strategy for the DS, accompanied by a case study that analyzes the impact of integrating distributed energy sources and microgrids. A novel load restoration method for DSs is proposed in (Ghasemi et al., 2019), which employs a decision-making tree algorithm to maximize load restoration power while minimizing switching operations.

In practice, a tightly coupled relationship exists between transmission and distribution systems, necessitating coordinated restoration efforts rather than isolated approaches (Fan et al., 2022). Therefore, investigating coordinated restoration strategies for transmission and distribution systems is of paramount practical significance. In this context, a distributed black-start optimization model of coupled transmission and distribution systems is proposed in (Zhao et al., 2021), aiming to minimize blackout-related costs. An innovative distributed load restoration model of coupled transmission and distribution systems is proposed in (Zhao et al., 2019), establishing an iterative framework that bridges both systems using a modified triple-loop analytical target cascading algorithm. A load restoration approach for coupled transmission and distribution systems based on the conditional value at risk (CVaR) theory is proposed in (Zhao et al., 2020b), employing a receding horizon control algorithm to manage uncertainties arising during the restoration process. In (Zhao et al., 2020c), a novel load restoration optimization model designed for integrated transmission and distribution systems with wind power integration is proposed, employing the alternating direction method of multipliers (ADMM) algorithm to achieve a distributed solution.

The above-mentioned studies have made significant contributions to the research on power systems restoration. However, there are still some shortcomings in existing studies. Firstly, most existing research tends to separate the study of black-start, network restoration, and load restoration, whereas in reality, these aspects are interrelated. For instance, black-start procedures require network reconfiguration, and prioritizing the restoration of critical loads necessitates the restoration of certain parts of the power network. Furthermore, when gradually restoring the network, it is also essential to restore some loads to maintain the frequency stability of power systems (Hao et al., 2022). Therefore, there is a need to explore entire-process restoration strategies for power systems. Additionally, the TSs and DSs are under the jurisdiction of different dispatching entities, and due to incomplete data and information sharing, it is necessary to separately construct optimization models and perform distributed solving for the TSs and DSs. Most existing studies primarily employ traditional ADMM algorithms for distributed solving, and if the parameter settings are not appropriate, it may lead to convergence difficulties.

Hence, an adaptive ADMM-based entire-process distributed restoration method of TSs and DSs considering CVaR is proposed in this paper to address the abovementioned issues. The contributions of this paper are summarized as follows.

1) An entire-process restoration model of TSs and DSs considering CVaR is proposed. Firstly, the CVaR is employed to quantify the conditional value at risk of multiple uncertainties during the entire restoration process. Subsequently, an entire-process restoration strategy of TSs and DSs considering CVaR is formulated to maximize the total restoration benefits of TSs and DSs. The proposed model provides restoration strategies that enable the entire-process restoration of the TSs and DSs, achieving higher generated power and load restoration benefits.

2) An adaptive ADMM-based distributed solving algorithm for the coordinated restoration model of the TSs and DSs is introduced, in which the interacted power at coupling buses between the TS and DS is utilized as the interaction variable to realize distributed solving. This algorithm incorporates adaptive penalty parameter adjustments, leading to faster convergence speed compared to the standard ADMM.

The rest of this paper is organized as follows: Section 2 establishes the entire-process restoration model of TSs and DSs considering CVaR; Section 3 establishes an adaptive ADMM-based distributed solving algorithm for the coordinated restoration model of the TSs and DSs; case studies and corresponding conclusions are presented in Sections 4, 5, respectively.

2 Entire-process restoration model of TSs and DSs considering CVaR

In this section, the CVaR theory is first employed to quantify the conditional risk value of multiple uncertainties, i.e., wind and solar power output forecasts, load prediction, and buses and lines restoration failure probabilities, in the entire restoration process. Subsequently, an entire-process restoration model of TSs and DSs considering CVaR is established to maximize the total restoration benefits of TSs and DSs.

2.1 Quantifying the CVaR of multiple uncertainties during the entire restoration process

During the entire restoration process of TSs and DSs, various uncertainties such as wind and solar power output forecasts, load predictions, and buses and lines restoration failure probabilities exist. If these uncertainties are not addressed properly, it may lead to restoration strategies that do not meet the security requirements of the system’s restoration. Therefore, this paper employs CVaR theory to assess the conditional risk value of multiple uncertainties during the entire restoration process.

CVaR is defined as the average loss incurred when the risk loss of an investment portfolio exceeds the value at risk (VaR) at a given confidence level within a certain investment horizon (Rockafellar and Stanislav, 2002), whose specific expression is represented by

$V_{\text{CVaR}}=E\left[f_{\mathrm{R}}\left(Z,\lambda \right)\left|f_{\mathrm{R}}\left(Z,\lambda \right)>\right.V_{\text{VaR}}\right](1)$

where Z is the optimization variable matrix, which corresponds to the restoration strategy in this work; $V_{\text{CVaR}}$ and $V_{\text{VaR}}$ are the CVaR and VaR, respectively; $\lambda$ is continuous random variables that represent multiple uncertainties; $E\left[\cdot \right]$ is the mathematical expectation; $f_{\text{CVaR}}^{\mathrm{B}}$ is the net restoration benefit of the TSs and DSs considering CVaR of multiple uncertainties, whose specific expression is presented by

$f_{\text{CVaR}}^{\mathrm{B}}=f^{\mathrm{B}}-{\displaystyle \sum _{t=1}^{T_{\text{step}}}}\left(p_t^{\text{RES}}\left|\Delta P_t^{\text{RES}}\right|+p_t^{\mathrm{L}}\left|\Delta P_t^{\mathrm{L}}\right|+p_t^{\text{line}}{\displaystyle \sum _{l=1}^{N^{\text{line}}}}{\rho }_{l,t}^{\text{RF},\text{line}}+p_t^{\text{bus}}{\displaystyle \sum _{n=1}^{N^{\text{bus}}}}{\rho }_{l,t}^{\text{RF},\text{bus}}\right)(2)$

where $f^{\mathrm{B}}$ is the restoration benefit of TSs and DSs without considering CVaR, and its specific expression will be illustrated in Section 2.2; $T_{\text{step}}$ is the number of restoration time step; $p_t^{\text{RES}}$ and $p_t^{\mathrm{L}}$ are the unit restoration risk costs associated with wind and solar power output forecasts errors and load prediction errors, respectively; $\Delta P_t^{\text{RES}}$ and $\Delta P_t^{\mathrm{L}}$ are the errors in wind and solar power output forecasts and load predictions during the restoration process, respectively; $p_t^{\text{line}}$ and $p_t^{\text{bus}}$ are the unit restoration risk costs resulting from line and node restoration failures, respectively; ${\rho }_{l,t}^{\text{RF},\text{line}}$ and ${\rho }_{l,t}^{\text{RF},\text{bus}}$ are the restoration failure probabilities of lines and buses, respectively; $N^{\text{line}}$ and $N^{\text{bus}}$ are the total numbers of lines and buses, respectively.

On this basis, the CVaR and VaR for the multiple uncertainties during the restoration process can be simultaneously obtained by solving Eq. 3.

$\min V_{\text{CVaR}}=V_{\text{VaR}}+\frac{{\displaystyle \sum _{n=1}^{N^{\text{SCE}}}}{P}_{\mathrm{r},n}{\left[f_{\text{CVaR},n}^{\mathrm{B}}-V_{\text{VaR}},0\right]}^{+}}{1-\beta }(3)$

where ${\beta }_{\text{CVaR}}$ is the confidence level of CVaR; ${\left[f_{\text{CVaR},n}^{\mathrm{B}}-V_{\text{VaR}},0\right]}^{+}$ is the maximum between $f_{\text{CVaR},n}^{\mathrm{B}}-V_{\text{VaR}}$ and 0; N^SCE is the number of operation scenarios; P_r,n is the occurred probability of the nth scenario.

2.2 Objective function of the proposed model

The objective function of the proposed model is to maximize the entire-process generation and load power restoration benefits of the TSs and DSs, as shown in (4).

$f^{\mathrm{B}}=\max {\displaystyle \sum _{z=1}^{N^{\text{TDS}}}}{\displaystyle \sum _{n=1}^{N_{\text{bus}}^z}}\left({\int }_0^{T_{\text{step}}}{P}_{\text{NBS},n,t}^{z}dt+b_{\mathrm{L},n}^z{\displaystyle \sum _{t=1}^{T_{\text{step}}}}{P}_{\mathrm{L},n,t}^z\Delta t\right)(4)$

where $N^{\text{TDS}}$ is the number of TSs and DSs; $N_{\text{bus}}^z$ is the number of buses in the zth power system; $b_{\mathrm{L},n}^z$ is the unit restoration benefit of the nth bus in the zth power system; $P_{\text{NBS},n,t}^z$ and $P_{\mathrm{L},n,t}^z$ are the restored generation and load power of the nth bus in the zth power system at time step t; $\Delta t$ is the duration of each time step. Note that the linearization method for generation power restoration refers to reference (Zhao et al., 2018), and the linearized expression is represented by (5).

$\frac{P_{\text{NBS},n}^{z,\max }{T}_{\text{NBS},n}^{z,\text{rp}}-P_{\text{NBS},n}^{z,\text{st}}\left(T_{\text{NBS},n}^{z,\text{rp}}+T_{\text{NBS},n}^{z,\text{sp}}\right)}{2}+\left(P_{\text{NBS},n}^{z,\max }-P_{\text{NBS},n}^{z,\text{st}}\right)\left(T_{\text{step}}-T_{\text{NBS},n}^{z,\text{sp}}-T_{\text{NBS},n}^{z,\text{rp}}\right)-T_{\text{NBS},n}^{z,\text{st}}\left(P_{\text{NBS},n}^{z,\max }-P_{\text{NBS},n}^{z,\text{st}}\right)(5)$

where $P_{\text{NBS},n}^{z,\max }$ and $P_{\text{NBS},n}^{z,\text{st}}$ are the rated power and auxiliary consumption power of non-black-start units at the bus n in the zth power system, respectively; $T_{\text{step}}$ is the number of time steps; $P_{\text{NBS},n}^{z,\text{st}}$, $T_{\text{NBS},n}^{z,\text{sp}}$ and $T_{\text{NBS},n}^{z,\text{rp}}$ are the start time, start duration and ramp duration, respectively.

2.3 Constraints of the proposed model

The constraints of the proposed model consist of the entire-process restoration constraints for the TSs and DSs. The unique and general constraints for the TSs and DSs are described as follows.

1) Unique constraints of the TS

The TS typically includes large thermal power units that are not black-start capable, so when a major power outage occurs, these units need to be black-started initially using black-start units. Therefore, the unique constraints for the TSs encompass the black-start-related constraints. More specifically, the relationship between the restoration power and time step for non-black-start units is expressed as 6); the relationship between the start-up time step of non-black-start units and bus restoration status is presented as 7); the constraints on the start-up time step of non-black-start units concerning cold start and hot start time step are expressed as 8).

$P_{\text{NBS},n,t}^{\text{TS}}=\left\{\begin{array}{l}0,t<t_1\\ \left(t-t_1\right)R_{\text{NBS},n}^{\text{TS}}-P_{\text{NBS},n}^{\text{TS},\text{st}},t_1\le t<t_2\\ P_{\text{NBS},n}^{\text{TS},\max }-P_{\text{NBS},n}^{\text{TS},\text{st}},t\ge t_2\end{array}\right.(6)$

${\sum }_{t=1}^{T_{\text{step}}}\left(1-B_{\text{bus},n,t}^{\text{TS}}\right)\le T_{\text{NBS},n}^{\text{TS},\text{st}}(7)$

$T_{\text{NBS},n}^{\text{TS},\text{st},\min }\le T_{\text{NBS},n}^{\text{TS},\text{st}}\le T_{\text{NBS},n}^{\text{TS},\text{st},\max }(8)$

where $P_{\text{NBS},n,t}^{\text{TS}}$, $P_{\text{NBS},n}^{\text{TS},\text{st}}$, and $P_{\text{NBS},n}^{\text{TS},\max }$ are the restored generation power, auxiliary consumption power, and rated power of non-black-start units at the bus n in time step t, respectively; $R_{\text{NBS},n}^{\text{TS}}$ is the ramping rate of non-black-start units; t₁ and t₂ are the time steps when non-black-start units restart and reach their rated power, respectively; $B_{\text{bus},n,t}^{\text{TS}}$ is a binary variable indicating the restoration status of the bus where the non-black-start unit is located; $T_{\text{NBS},n}^{\text{TS},\text{st},\max }$ and $T_{\text{NBS},n}^{\text{TS},\text{st},\min }$ are the upper and lower bounds on the black-start time of non-black-start units.

2) Unique constraints of the DS

DSs typically do not have large non-black-start units, but they directly manage the loads connected to them. Therefore, the unique constraints for DSs encompass load restoration-related constraints. More specifically, restored non-flexible loads cannot be disconnected again, as represented by Eq. 9). Flexible loads can be subject to demand response and partial disconnection after being restored, as represented by Eq. 10). Considering practical factors like power flow limits and system frequency security, the load restored in each time step should not exceed a certain value, as expressed in Eq. 11). The load at bus n can only be restored after its bus has been restored, as expressed in Eq. 12). Note that some buses in the TS also have high-voltage level loads connected to them, so they also need to follow these load restoration constraints as well.

$0\le P_{n,t-1}^{\text{DS},\mathrm{L}}\le P_{n,t}^{\text{DS},\mathrm{L}}\le P_n^{\text{DS},\mathrm{L},\max },\forall n\in {\mathrm{\Omega }}_{\text{bus}}^{\text{DS},\text{NFL}}(9)$

$0\le P_{n,t}^{\text{DS},\mathrm{L}}\le P_n^{\text{DS},\mathrm{L},\max },\forall n\in {\mathrm{\Omega }}_{\text{bus}}^{\text{DS},\text{FL}}(10)$

$P_{n,t}^{\text{DS},\mathrm{L}}-P_{n,t-1}^{\text{DS},\mathrm{L}}\le \Delta P_{n,t}^{\text{DS},\mathrm{L},\max }(11)$

$B_{\text{bus},n,t}^{\text{DS},\mathrm{L}}\le B_{\text{bus},n,t-1}^{\text{DS}}(12)$

where $P_{n,t}^{\text{DS},\mathrm{L}}$ and $P_n^{\text{DS},\mathrm{L},\max }$ are the already restored load at bus n and the maximum load, respectively; ${\mathrm{\Omega }}_{\text{bus}}^{\text{DS},\text{NFL}}$ and ${\mathrm{\Omega }}_{\text{bus}}^{\text{DS},\text{FL}}$ are sets of non-flexible and flexible load buses; $\Delta P_{n,t}^{\text{DS},\mathrm{L},\max }$ is the upper limit of the restorable load for each time step, which is related to power flow limits and system frequency security; $B_{\text{bus},n,t}^{\text{DS},\mathrm{L}}$ is the load restoration state variable for the bus n.

3) General constraints for the TSs and DSs

The general constraints for the TSs and DSs include network restoration constraints and power balance constraints. More specifically, the restored buses and lines will not experience another power outage, as represented by Eqs 13, 14), respectively; the necessary but not sufficient condition for line restoration is that both of its start and terminal buses have been restored, as represented by Eq. 15); the necessary condition for bus restoration is that at least one connected line has been restored, as represented by Eq. 16); considering practical factors such as manual operations and line charging time, if the adjacent lines of a specific line have not been restored in a given time step, that line cannot be restored in that time step, as represented by (17); the operation constraints of energy storage systems refer to reference (Chen C. et al., 2023).

$B_{\text{bus},n,t}^{\mathrm{T}\left(\mathrm{D}\right)\mathrm{S}}\ge B_{\text{bus},n,t-1}^{\mathrm{T}\left(\mathrm{D}\right)\mathrm{S}}(13)$

$B_{\text{line},l,t}^{\mathrm{T}\left(\mathrm{D}\right)\mathrm{S}}\ge B_{\text{line},l,t-1}^{\mathrm{T}\left(\mathrm{D}\right)\mathrm{S}}(14)$

$B_{\text{bus},n,t}^{\mathrm{T}\left(\mathrm{D}\right)\mathrm{S}}\ge B_{\text{line},l,t}^{\mathrm{T}\left(\mathrm{D}\right)\mathrm{S}},\forall l\in {\mathrm{\Omega }}_{\text{line},\text{bus}n}^{\mathrm{T}\left(\mathrm{D}\right)\mathrm{S}}(15)$

$B_{\text{bus},n,t}^{\mathrm{T}\left(\mathrm{D}\right)\mathrm{S}}\le {\displaystyle \sum _{l\in {\mathrm{\Omega }}_{\text{line},\text{bus}n}^{\mathrm{T}\left(\mathrm{D}\right)\mathrm{S}}}}{B}_{\text{line},l,t}^{\mathrm{T}\left(\mathrm{D}\right)\mathrm{S}}(16)$

$B_{\text{line},p,t}^{\mathrm{T}\left(\mathrm{D}\right)\mathrm{S}}\le {\displaystyle \sum _{q\in {\mathrm{\Omega }}_{\text{line},\text{line}p}^{\mathrm{T}\left(\mathrm{D}\right)\mathrm{S}}}}{B}_{\text{line},q,t-1}^{\mathrm{T}\left(\mathrm{D}\right)\mathrm{S}}(17)$

where $B_{\text{bus},n,t}^{\mathrm{T}\left(\mathrm{D}\right)\mathrm{S}}$ and $B_{\text{line},l,t}^{\mathrm{T}\left(\mathrm{D}\right)\mathrm{S}}$ are Boolean variables reflecting the restoration status of bus n and line l, respectively, with a value of 1 indicating that the bus or line has been restored; ${\mathrm{\Omega }}_{\text{line},\text{bus}n}^{\mathrm{T}\left(\mathrm{D}\right)\mathrm{S}}$ is the set of lines connected to bus n, while ${\mathrm{\Omega }}_{\text{line},\text{line}p}^{\mathrm{T}\left(\mathrm{D}\right)\mathrm{S}}$ is the set of lines connected to line l.

Both TSs and DSs need to consider power balance constraints, as represented by Eqs 18, 19), respectively. It can be seen from Eqs 18, 19 that the power balance constraints in the DS are less complex than those in the TS, as they do not involve the power of black-start and non-black-start units. Besides, power interaction between TSs and DSs can occur through the transmission-distribution coupling buses.

${\displaystyle \sum _{n\in {\mathrm{\Omega }}_{\text{bus}}^{\text{TS}}}}\left(P_{\text{NBS},n,t}^{\text{TS}}+P_{\text{BS},n,t}^{\text{TS}}+P_{\text{RES},n,t}^{\text{TS}}+P_{\text{ES},n,t}^{\text{TS}}\right)={\displaystyle \sum _{n\in {\mathrm{\Omega }}_{\text{bus}}^{\text{TS}}}}\left(P_{\mathrm{L},n,t}^{\text{TS}}+P_{\text{DS},n,t}^{\text{TS}}\right)(18)$

$P_{\text{DS},n,t}^{\text{TS}}+{\displaystyle \sum _{x\in {\mathrm{\Omega }}_{\text{bus}}^{\text{DS},n}}}\left(P_{\text{RES},x,t}^{\text{DS},n}+P_{\text{ES},x,t}^{\text{DS},n}\right)={\displaystyle \sum _{x\in {\mathrm{\Omega }}_{\text{bus}}^{\text{DS},n}}}{P}_{\mathrm{L},x,t}^{\text{DS},n}(19)$

where ${\mathrm{\Omega }}_{\text{bus}}^{\text{TS}}$ and ${\mathrm{\Omega }}_{\text{bus}}^{\text{DS},n}$ are the sets of buses in the TS and its connected DS under bus n, respectively; $P_{\text{BS},n,t}^{\text{TS}}$, $P_{\text{RES},n,t}^{\text{TS}}$, and $P_{\text{ES},n,t}^{\text{TS}}$ are the power generation of black-start units, renewable energy units, and energy storage devices at bus n in the TS, respectively; $P_{\mathrm{L},n,t}^{\text{TS}}$ is the load power at bus n in the TS; $P_{\text{DS},n,t}^{\text{TS}}$ is the interaction power provided by the TS to the connected DS at its bus n, with positive values indicating supply from the TS to the DS; $P_{\text{RES},x,t}^{\text{DS},n}$, $P_{\text{ES},x,t}^{\text{DS},n}$, and $P_{\mathrm{L},x,t}^{\text{DS},n}$ are the power generation of renewable energy units and energy storage devices, as well as the load power at bus x in the TS connected under bus n in the TS.

Both TSs and DSs are subject to power flow constraints. More specifically, the TS typically has a meshed structure, so AC power flow constraints as shown in Eqs 20, 23) need to be considered. On the other hand, the DS is typically radial in structure, allowing the use of DistFlow DC power flow constraints as in Eqs 24–29). Since both TSs and DSs power flow constraints involve non-convex and non-linear terms, they are linearized separately using the approximate linearization methods proposed in references (Zhao et al., 2021; Chen et al., 2022b).

$P_{i,t}^{\text{TS}}={\displaystyle \sum _{\left(i,j\right)\in {\mathrm{\Omega }}_{\text{line}}^{\text{TS}}}}{P}_{i,j,t}^{\text{TS}}(20)$

$Q_{i,t}^{\text{TS}}={\displaystyle \sum _{\left(i,j\right)\in {\mathrm{\Omega }}_{\text{line}}^{\text{TS}}}}{Q}_{i,j,t}^{\text{TS}}(21)$

$P_{i,j,t}^{\text{TS}}={\left(U_{i,t}^{\text{TS}}\right)}^2{G}_{i,j,t}^{\text{TS}}-U_{i,t}^{\text{TS}}{U}_{j,t}^{\text{TS}}\left(G_{i,j,t}^{\text{TS}}\cos {\theta }_{i,j,t}^{\text{TS}}+B_{i,j,t}^{\text{TS}}\sin {\theta }_{i,j,t}^{\text{TS}}\right)(22)$

$Q_{i,j,t}^{\text{TS}}=-{\left(U_{i,t}^{\text{TS}}\right)}^2{B}_{i,j,t}^{\text{TS}}-U_{i,t}^{\text{TS}}{U}_{j,t}^{\text{TS}}\left(G_{i,j,t}^{\text{TS}}\sin {\theta }_{i,j,t}^{\text{TS}}-B_{i,j,t}^{\text{TS}}\cos {\theta }_{i,j,t}^{\text{TS}}\right)(23)$

${\displaystyle \sum _{p\in {\mathrm{\Omega }}_{\text{line},n+}^{\text{DS}}}}{P}_{p,t}^{\text{DS}}-{\displaystyle \sum _{q\in {\mathrm{\Omega }}_{\text{line},n-}^{\text{DS}}}}\left.{\left(P_{q,t}^{\text{DS}}-\left(I_{q,t}^{\text{DS}}\right)\right.}^2{R}_{q,j}^{\text{DS}}\right)=P_{n,t,\text{out}}^{\text{DS}}(24)$

$U_{j,t}^{\text{DS}}=U_{i,t}^{\text{DS}}-I_{i,j,t}^{\text{DS}}{R}_{i,j}^{\text{DS}}(25)$

$P_{i,j,t}^{\text{DS}}=U_{i,t}^{\text{DS}}{I}_{i,j,t}^{\text{DS}}(26)$

$\left|P_{i,j,t}^{\text{DS}}\right|\le P_{i,j}^{\text{DS},\max }(27)$

$\left|I_{i,j,t}^{\text{DS}}\right|\le I_{i,j}^{\text{DS},\max }(28)$

$0\le U_{i,t}^{\text{DS}}\le U_i^{\text{DS},\max }(29)$

where $P_{i,t}^{\text{TS}}$ and $Q_{i,t}^{\text{TS}}$ are the total injected active and reactive power at bus i, respectively; $P_{i,j,t}^{\text{TS}}$ and $Q_{i,j,t}^{\text{TS}}$ are the active and reactive power on line ij, respectively; ${\mathrm{\Omega }}_{\text{line}}^{\text{TS}}$ is the set of lines in the TS; $U_{i,t}^{\text{TS}}$ is the voltage at bus i. $G_{i,j,t}^{\text{TS}}$, $B_{i,j,t}^{\text{TS}}$, and ${\theta }_{i,j,t}^{\text{TS}}$ are the conductance, susceptance, and phase angle of line ij in the TS, respectively; ${\mathrm{\Omega }}_{\text{line},n+}^{\text{DS}}$ and ${\mathrm{\Omega }}_{\text{line},n-}^{\text{DS}}$ are the set of lines in the DS that start from and end at bus n, respectively; $P_{q,t}^{\text{DS}}$, $I_{q,t}^{\text{DS}}$, and $R_{q,j}^{\text{DS}}$ are the power, current, and resistance of bus i in the DS, respectively; $P_{n,t,\text{out}}^{\text{DS}}$ is the power flowing out of bus n in the DS; $U_{i,t}^{\text{DS}}$ is the voltage at bus i in the DS; $P_{i,j}^{\text{DS},\max }$, $I_{i,j}^{\text{DS},\max }$, and $U_i^{\text{DS},\max }$ are the upper limits for line power, current, and bus voltage in the DS, respectively.

3 Adaptive ADMM-based distributed solving algorithm for the coordinated restoration model of the TSs and DSs

Due to the separate jurisdiction of TSs and DSs and the incomplete sharing of data and information, it is challenging to directly establish the unified optimization model as presented in Section 2 and solve it in a centralized manner in practical applications. Therefore, the original optimization model is transformed into two distributed optimization models. Subsequently, by treating the power exchange between the TSs and DSs as coupling variables, an adaptive ADMM algorithm is employed for iterative convergence, enabling the distributed solving of the entire-process restoration of the TSs and DSs. Note that the solution time and optimal solution of the standard ADMM are significantly affected by the initial penalty factor. Inappropriately setting the initial penalty factor may lead to convergence to local optima and an increase in solution time. On the contrary, the utilized adaptive ADMM can adjust the step size dynamically according to the primal residue and dual residue during the iterative process, thereby achieving a faster convergence rate than that of standard ADMM.

3.1 Distributed restoration optimization models for TSs and DSs

Considering the objective function and constraints of the unified restoration optimization model for the TSs and DSs shown in Eq. 4), the augmented Lagrangian function is introduced to formulate the distributed restoration optimization models for the TSs and DSs, as represented by (30) and (31), respectively.

$f^{\text{TS}}=\max f_{\text{CVaR}}^{\text{TS},\mathrm{B}}+{\displaystyle \sum _{x=1}^{N_{\text{bus},\text{DS}}^{\text{TS}}}}{\displaystyle \sum _{t=1}^{T_{\text{step}}}}\left[{\lambda }_{\text{DS},x,t}^{\text{TS}}\left(P_{\text{DS},x,t}^{\text{TS}}-P_{\text{TS},t}^{\text{DS},x}\right)\right]+{\displaystyle \sum _{x=1}^{N_{\text{bus},\text{DS}}^{\text{TS}}}}\left[\frac{{\rho }_{\text{DS},x}^{\text{TS}}}{2}{\displaystyle \sum _{t=1}^{T_{\text{step}}}}{\left(P_{\text{DS},x,t}^{\text{TS}}-P_{\text{TS},t}^{\text{DS},x}\right)}^2\right](30)$

s.t. (6)–(8), (13)–(18), (20)–(23)

$f^{\text{DS},n}=\max f_{\text{CVaR}}^{\text{DS},n,\mathrm{B}}+{\displaystyle \sum _{t=1}^{T_{\text{step}}}}\left[{\lambda }_{\text{TS},t}^{\text{DS},n}\left(P_{\text{DS},n,t}^{\text{TS}}-P_{\text{TS},t}^{\text{DS},n}\right)\right]+\frac{{\rho }_{\text{TS}}^{\text{DS},n}}{2}{\displaystyle \sum _{t=1}^{T_{\text{step}}}}{\left(P_{\text{DS},n,t}^{\text{TS}}-P_{\text{TS},t}^{\text{DS},n}\right)}^2(31)$

s.t. (9)–(12), (13)–(18), (24)–(29).

where $f^{\text{TS}}$ and $f^{\text{DS},n}$ are the augmented objective functions for the TS and the nth DS, respectively; ${\lambda }_{\text{DS},x,t}^{\text{TS}}$ and ${\rho }_{\text{DS},x}^{\text{TS}}$ are the Lagrange multipliers and penalty factors for the TS, while ${\lambda }_{\text{TS},t}^{\text{DS},x}$ and ${\rho }_{\text{TS}}^{\text{DS},x}$ are the Lagrange multipliers and penalty factors for the nth DS, respectively; $f_{\text{CVaR}}^{\text{TS},\mathrm{B}}$ and $f_{\text{CVaR}}^{\text{DS},n,\mathrm{B}}$ are the restoration benefits for the TSs and DSs considering CVaR, and their specific expressions are represented by Eqs 32, 33), respectively.

$f_{\text{CVaR}}^{\text{TS},\mathrm{B}}={\displaystyle \sum _{n=1}^{N_{\text{bus}}^{\text{TS}}}}\left({\int }_0^{T_{\text{step}}}{P}_{\text{NBS},n,t}^{\text{TS}}dt+b_{\mathrm{L},n}^{\text{TS}}{\displaystyle \sum _{t=1}^{T_{\text{step}}}}{P}_{\mathrm{L},n,t}^{\text{TS}}\Delta t\right)(32)$

$f_{\text{CVaR}}^{\text{DS},n,\mathrm{B}}={\displaystyle \sum _{m=1}^{N_{\text{bus}}^{\text{DS},n}}}{b}_{\mathrm{L},m}^{\text{DS},n}{\displaystyle \sum _{t=1}^{T_{\text{step}}}}{P}_{\mathrm{L},m,t}^{\text{DS},n}\Delta t(33)$

3.2 Distributed solving process based on the adaptive ADMM

The adaptive ADMM-based distributed solving process for the previously constructed distributed optimization models for the TSs and DSs is utilized, as outlined below.

Step 1. Set the maximum iteration number $k^{\max }$, primal residual convergence threshold ${\delta }^{\mathrm{P}}$, dual residual convergence threshold ${\delta }^{\mathrm{D}}$, and initial iteration counter k = 1.

Step 2. The TS collects the desired transmission-distribution interaction power strategy matrix ${\mathit{P}}_{\text{TS},t}^{\text{DS},n,k}$ from each DS. Then, it solves the distributed restoration model for the TS as represented by (30) to obtain the desired transmission-distribution interaction power strategy matrix ${\mathit{P}}_{\text{DS},n,t}^{\text{TS},k+1}$ for the TS. Set n = 1.

Step 3. The nth DS receives ${\mathit{P}}_{\text{DS},n,t}^{\text{TS},k+1}$ from the TS. Then, it solves the distributed restoration model for the nth DS as represented by (31) to obtain the desired transmission-distribution interaction power strategy matrix ${\mathit{P}}_{\text{TS},t}^{\text{DS},n,k+1}$. n = n+1.

Step 4. Check if n > $N_{\text{bus},\text{DS}}^{\text{TS}}$? If yes, proceed to Step 5, otherwise, return to Step 3.

Step 5. According to the previous description, the utilized adaptive ADMM can adjust the step size dynamically according to the primal residue and dual residue during the iterative process, thereby achieving a faster convergence rate than that of standard ADMM. More specifically, according to the dual-update acceleration iteration strategy, if the primal residual is greater than a certain threshold, update the penalty factors according to (34)–(35) and update the Lagrange multipliers according to (36)–(37); otherwise, when the primal residual is equal to or less than a certain threshold at iteration $k^{*}$, keep the penalty factors unchanged and update the Lagrange multipliers according to (38)–(39).

${\rho }_{\text{DS},n}^{\text{TS},k+1}=\left\{\begin{array}{l}{\rho }_{\text{DS},n}^{\text{TS},k}/\left[1+\lg \left(\frac{d_{\text{DS},n}^{\text{TS},k,\mathrm{D}}}{p_{\text{DS},n}^{\text{TS},k,\mathrm{P}}}\right)\right],\left(\frac{d_{\text{DS},n}^{\text{TS},k,\mathrm{D}}}{{\delta }^{\mathrm{D}}}\right)\ge \frac{10p_{\text{DS},n}^{\text{TS},k,\mathrm{P}}}{{\delta }^{\mathrm{P}}}\\ {\rho }_{\text{DS},n}^{\text{TS},k}\left[1+\lg \left(\frac{p_{\text{DS},n}^{\text{TS},k,\mathrm{P}}}{d_{\text{DS},n}^{\text{TS},k,\mathrm{D}}}\right)\right],\left(\frac{p_{\text{DS},n}^{\text{TS},k,\mathrm{P}}}{{\delta }^{\mathrm{P}}}\right)\ge \frac{10d_{\text{DS},n}^{\text{TS},k,\mathrm{D}}}{{\delta }^{\mathrm{D}}}\\ {\rho }_{\text{DS},n}^{\text{TS},k},\text{otherwise}\end{array}\right.(34)$

${\rho }_{\text{TS}}^{\text{DS},n,k+1}=\left\{\begin{array}{l}{\rho }_{\text{TS}}^{\text{DS},n,k}/\left[1+\lg \left(\frac{d_{\text{TS}}^{\text{DS},n,k,\mathrm{D}}}{p_{\text{TS}}^{\text{DS},n,k,\mathrm{P}}}\right)\right],\left(\frac{d_{\text{TS}}^{\text{DS},n,k,\mathrm{D}}}{{\delta }^{\mathrm{D}}}\right)\ge \frac{10p_{\text{TS}}^{\text{DS},n,k,\mathrm{P}}}{{\delta }^{\mathrm{P}}}\\ {\rho }_{\text{TS}}^{\text{DS},n,k}\left[1+\lg \left(\frac{p_{\text{TS}}^{\text{DS},n,k,\mathrm{P}}}{d_{\text{TS}}^{\text{DS},n,k,\mathrm{D}}}\right)\right],\left(\frac{p_{\text{TS}}^{\text{DS},n,k,\mathrm{P}}}{{\delta }^{\mathrm{P}}}\right)\ge \frac{10d_{\text{TS}}^{\text{DS},n,k,\mathrm{D}}}{{\delta }^{\mathrm{D}}}\\ {\rho }_{\text{TS}}^{\text{DS},n,k},\text{otherwise}\end{array}\right.(35)$

${\lambda }_{\text{DS},n,t}^{\text{TS},k+1}={\lambda }_{\text{DS},n,t}^{\text{TS},k}+{\rho }_{\text{DS},n}^{\text{TS},k+1}\left(P_{\text{DS},n,t}^{\text{TS},k+1}-P_{\text{TS},t}^{\text{DS},n,k+1}\right)(36)$

${\lambda }_{\text{TS},t}^{\text{DS},n,k+1}={\lambda }_{\text{TS},t}^{\text{DS},n,k}+{\rho }_{\text{TS},t}^{\text{DS},n,k+1}\left(P_{\text{DS},n,t}^{\text{TS},k+1}-P_{\text{TS},t}^{\text{DS},n,k+1}\right)(37)$

$\begin{array}{l}{\lambda }_{\text{DS},n,t}^{\text{TS},k+1}={\lambda }_{\text{DS},n,t}^{\text{TS},k}+{\rho }_{\text{DS},n}^{\text{TS},k+1}\left(P_{\text{DS},n,t}^{\text{TS},k+1}-P_{\text{TS},t}^{\text{DS},n,k+1}\right)+\\ K^{\mathrm{D}}\left[\left(P_{\text{DS},n,t}^{\text{TS},k+1}-P_{\text{TS},t}^{\text{DS},n,k+1}\right)-\left(P_{\text{DS},n,t}^{\text{TS},k}-P_{\text{TS},t}^{\text{DS},n,k}\right)\right]+K^{\mathrm{I}}{\displaystyle \sum _{m=k^{*}}^k}\left(P_{\text{DS},n,t}^{\text{TS},m+1}-P_{\text{TS},t}^{\text{DS},n,m+1}\right)\end{array}(38)$

$\begin{array}{l}{\lambda }_{\text{TS},t}^{\text{DS},n,k+1}={\lambda }_{\text{TS},t}^{\text{DS},n,k}+{\rho }_{\text{TS},t}^{\text{DS},n,k+1}\left(P_{\text{DS},n,t}^{\text{TS},k+1}-P_{\text{TS},t}^{\text{DS},n,k+1}\right)+\\ K^{\mathrm{D}}\left[\left(P_{\text{DS},n,t}^{\text{TS},k+1}-P_{\text{TS},t}^{\text{DS},n,k+1}\right)-\left(P_{\text{DS},n,t}^{\text{TS},k}-P_{\text{TS},t}^{\text{DS},n,k}\right)\right]+K^{\mathrm{I}}{\displaystyle \sum _{m=k^{*}}^k}\left(P_{\text{DS},n,t}^{\text{TS},m+1}-P_{\text{TS},t}^{\text{DS},n,m+1}\right)\end{array}(39)$

where $K^{\mathrm{D}}$ and $K^{\mathrm{I}}$ are the integral and double residual control parameters, respectively; $p_{\text{DS},n}^{\text{TS},k,\mathrm{P}}$ = $p_{\text{TS}}^{\text{DS},n,k,\mathrm{P}}$ and $d_{\text{DS},n}^{\text{TS},k,\mathrm{D}}$ = $d_{\text{TS}}^{\text{DS},n,k,\mathrm{D}}$ are the primal and dual residuals for the kth iteration, whose specific expressions are represented by Eqs 40, 41).

$p_{\text{DS},n}^{\text{TS},k,\mathrm{P}}=p_{\text{TS}}^{\text{DS},n,k,\mathrm{P}}={\displaystyle \sum _{t=1}^{T_{\text{step}}}}{\left(P_{\text{DS},n,t}^{\text{TS},k+1}-P_{\text{TS},t}^{\text{DS},n,k+1}\right)}^2(40)$

$d_{\text{DS},n}^{\text{TS},k,\mathrm{D}}=d_{\text{TS}}^{\text{DS},n,k,\mathrm{D}}=\max \left[{\displaystyle \sum _{t=1}^{T_{\text{step}}}}{\left(P_{\text{DS},n,t}^{\text{TS},k+1}-P_{\text{DS},n,t}^{\text{TS},k}\right)}^2,{\displaystyle \sum _{t=1}^{T_{\text{step}}}}{\left(P_{\text{TS},t}^{\text{DS},n,k+1}-P_{\text{TS},t}^{\text{DS},n,k}\right)}^2\right](41)$

Step 6. Determine the convergence of the primal and dual residuals according to (42). If (42) is satisfied or k $\ge k^{\max }$, terminate the iterations. Otherwise, k = k+1 and return to Step 2.

$p_{\text{DS},n}^{\text{TS},k,\mathrm{P}}\le {\delta }^{\mathrm{P}}\cap d_{\text{DS},n}^{\text{TS},k,\mathrm{D}}\le {\delta }^{\mathrm{D}}=1(42)$

According to the above process, it can realize distributed solving for the TSs and DSs and obtain their respective optimal restoration strategies. The distributed optimization models are established using the YALMIP platform in MATLAB R2021a software and the distributed solving can be realized through the GUROBI 10.0 solver.

4 Case studies

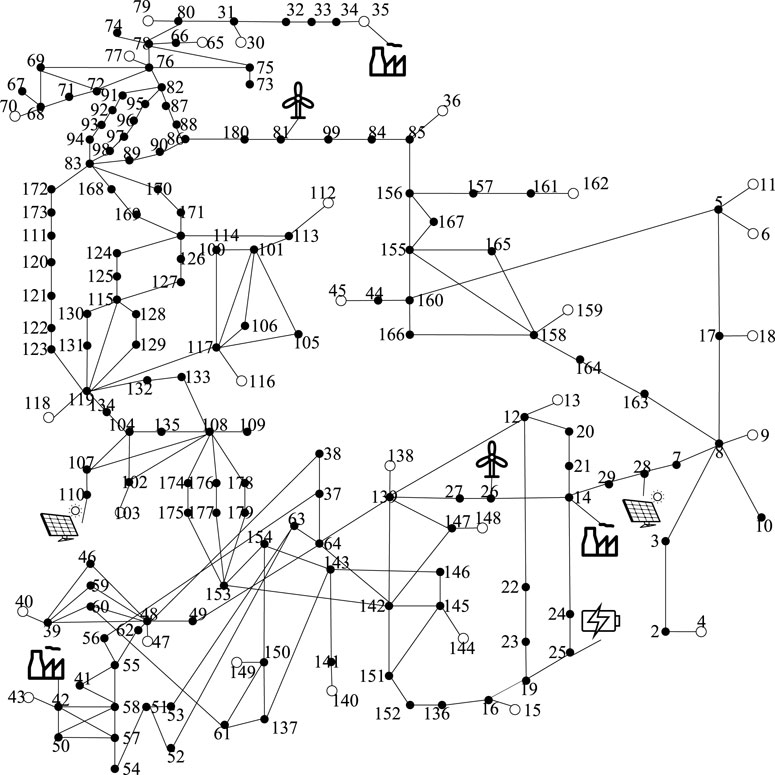
In this work, an improved 179-bus TS is employed for analysis, whose topology is shown in Figure 1. Some main technique parameters of this case are set as follows: $T_{\text{step}}$ = 30, $\Delta t$ = 5min, buses 14, 35, and 42 are equipped with black-start units, buses 26 and 81 are connected to wind power generators, and buses 28 and 110 have photovoltaic units. Each bus in the TS is connected to an IEEE 33-bus DS, and the feeders connected to each bus of the DS are not considered in this work. The bus voltages of the TS and DS are 220 kV and 110kV, respectively. The other technique parameters of this case refer to reference (Liu et al., 2023). Three blackout scenarios are considered as follows: Scenario 1 occurs at 2:00 with only wind power output; Scenario 2 occurs at 10:00 with both wind and photovoltaic power output, and Scenario 3 occurs under typhoon disasters with neither wind nor photovoltaic power output.

FIGURE 1

FIGURE 1. Topology of the improved 179-bus TS.

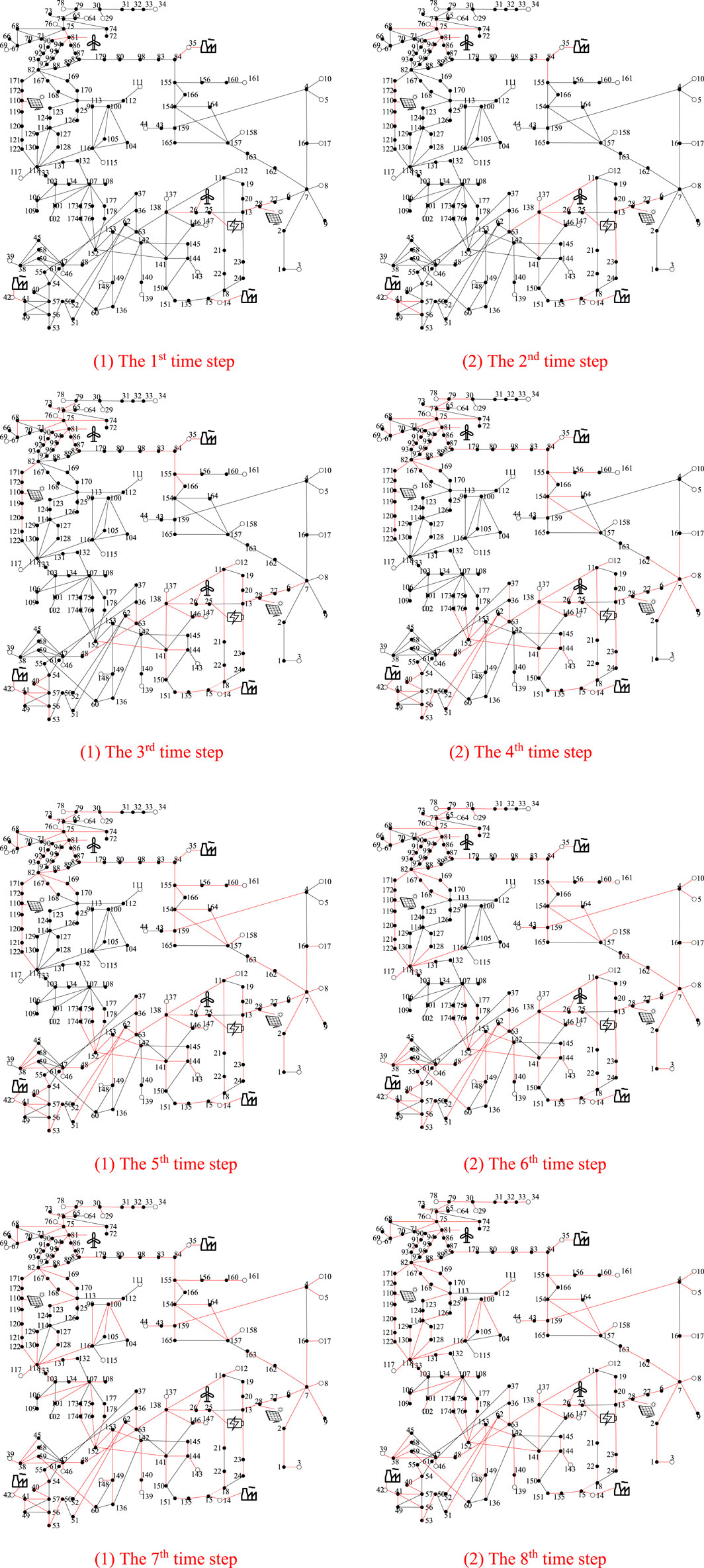
Taking Scenario 2 as an example, the black-start and network restoration process for the TS is illustrated in Figure 2. It can be seen from Figure 2 that in the first time step, black-start units from buses 14, 35, and 42, wind power generators at buses 26 and 81, a pumped hydro storage unit at bus 25, and photovoltaic units at buses 28 and 110 initiate the network reconfiguration process by expanding outward, gradually restoring non-black-start units. In the second and third time steps, non-black-start units located at buses 76 and 147 begin their black-start processes, respectively. During these time steps, it is also necessary to restore a portion of the load to maintain system frequency stability. By the fourth time step, 63.7% of the network has been reconfigured, 26.9% of non-black-start units have entered black-start status, and 61.4 p.u. of the load (representing 12.2% of the total load) has also been restored to maintain system frequency stability. The black-start and network reconfiguration processes for the TS are completed by the eighth time step.

FIGURE 2

FIGURE 2. Black-start and network restoration process for the TS.

Taking the DS under bus 66 as an example, its network reconfiguration strategy under three disaster scenarios is shown in Table 1. It can be seen from Table 1 that there is no photovoltaic output in Scenario 1, only the wind power and energy storage units at buses 12 and 16 serve as black-start units for the DS’s network restoration, taking a total of 9 time steps to complete the network reconfiguration. In Scenario 2, except for wind power and energy storage units, the photovoltaic power unit at bus 5 also acts as a black start unit to participate in the DS’s network reconfiguration. This accelerates the network reconfiguration process, which takes only 6 time steps to complete network reconfiguration. In Scenario 3, due to the typhoon disaster, both wind and photovoltaic power units have no output power, so only the energy storage unit can be used as a black-start unit for black-starting, completing the network reconfiguration in 10 time steps.

TABLE 1

TABLE 1. Network reconfiguration strategy of DS connected with bus 66 under three disaster scenarios.

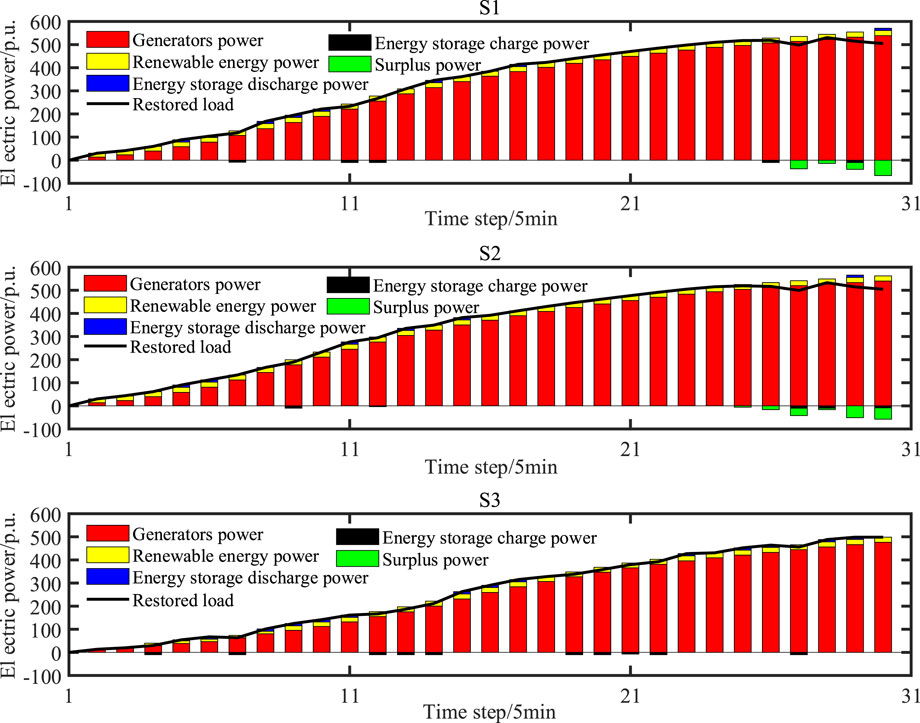
Figure 3 illustrates the power balance of the TS under three different disaster scenarios. It can be seen from Figure 3 that during the early restoration process, i.e., the first 5 time steps, non-black-start units have not fully restored to their rated power, as a result, the renewable energy output has a significant proportion of the total output power of the TS. Then, the system has also restored a portion of the load to maintain system frequency stability. In the mid to late restoration process (i.e., 6–25 time steps), as non-black-start units gradually restore their generated power, and the network undergoes reconfiguration, the loads also restore rapidly.

FIGURE 3

FIGURE 3. Power balance of the TS under three different disaster scenarios.

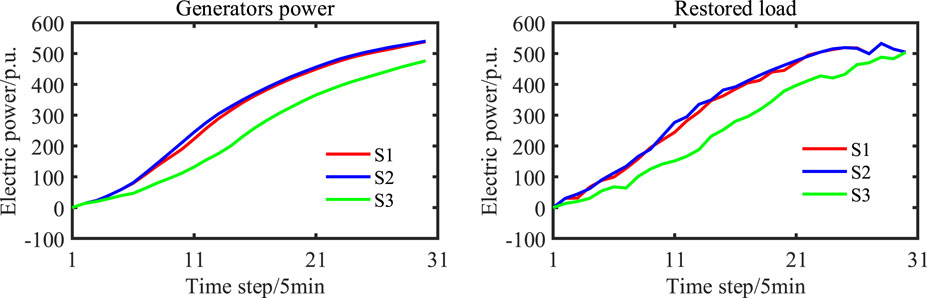
To better illustrate the impact of different disaster scenarios on the entire-process restoration of the TS, Figure 4 presents the power generation and load power restoration under the three scenarios. It can be seen from Figure 4 that Scenario 2 occurs at 10:00 when both wind and photovoltaic units are active, making them available as black-start units. Consequently, Scenario 2 exhibits the highest restoration rates of generated power and load among the three scenarios. Scenario 1, occurring at 2:00 with only wind power output and no photovoltaic output, has a slightly slower black-start process than Scenario 2, resulting in slightly lower rates of power generation and load power restoration. Scenario 3 represents a typhoon disaster where rainy conditions lead to no photovoltaic output, and the high wind speeds exceed the wind turbine cut-off power. Therefore, the wind power unit is also inactive. In this context, only the energy storage unit is available as black-start units, resulting in a 22.35% and 24.11% lower generated power restoration compared to Scenarios 1 and 2, respectively, and load restoration is 20.55% and 22.12% lower compared to Scenarios 1 and 2, respectively.

FIGURE 4

FIGURE 4. Power generation and load power restoration under the three scenarios.

To analyze the advantages of the proposed entire-process distributed restoration model of TSs and DSs considering CVaR (RM-TS-CVaR) compared to other restoration models, Table 2 presents a comparison among the proposed RM-TS-CVaR, the entire-process distributed restoration model that does not consider CVaR (RM-TS), and the entire-process restoration model that does not consider transmission-distribution systems coordination (RM-I-CVaR) under Scenario 2. It can be seen from Table 2 that the RM-TS tends to be optimistic when formulating restoration strategies, failing to account for the security risks posed by various uncertainties during the restoration process. Consequently, the restoration benefits of the RM-TS are 1.44 billion CNY and 1.09 billion CNY higher than those of the proposed RM-TS-CVaR, respectively. However, when there are deviations between the actual values of renewable energy output and load forecasts and their predicted values, the TSs and DSs may incur additional security risk costs due to the lack of reserved power in advance, potentially leading to over-limit system frequencies and voltages. As a result, after deducting the additional security risk costs, the total restoration benefits of the RM-TS are 3.93 billion CNY less than those of the proposed RM-TS-CVaR. In the RM-I-CVaR, the TSs and DSs independently conduct restoration, failing to fully exploit their energy mutual support capabilities. This may lead to situations where power-deficient systems do not receive power support, while power-surplus systems need to curtail wind and photovoltaic power. Consequently, the restoration benefits of the TS, DS, and the overall benefits of the RM-I-CVaR are 1.55%, 52.4%, and 10.61% less than those of the proposed RM-TS-CVaR, respectively. In summary, our proposed RM-TS-CVaR exhibits advantages in enhancing system restoration benefits.

TABLE 2

TABLE 2. Comparison among the proposed RM-TS-CVaR, RM-TS and RM-I-CVaR under Scenario 2.

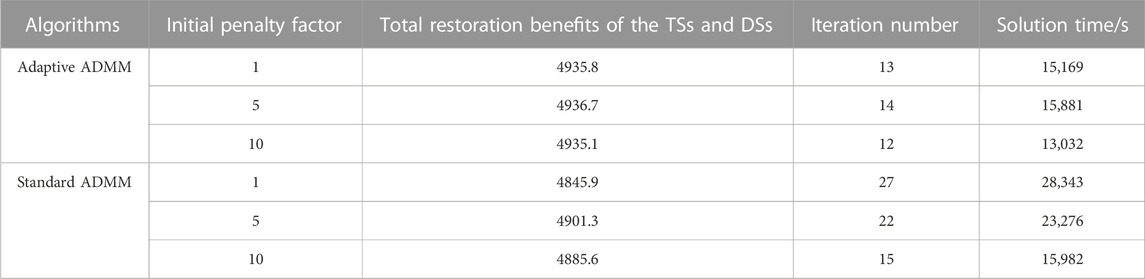
To verify the effectiveness of the adaptive ADMM algorithm employed in this paper, the results obtained by the adaptive ADMM are compared with those of a standard ADMM, as shown in Table 3. It can be seen from Table 3 that the solution time and optimal solution of the standard ADMM are significantly affected by the initial penalty factor. Inappropriately setting the initial penalty factor may lead to convergence to local optima and an increase in solution time. The average solution time for the adaptive ADMM used in three scenarios is 7,840 s shorter than that of the standard ADMM, while the maximum restoration benefits of the adaptive ADMM exceed those of the standard ADMM by 0.72%. This is because the ADMM algorithm employed in this paper can dynamically adjust penalty factors based on the results of each iteration, which accelerates the convergence rate of the distributed solution and enhances the practicality of the proposed RM-TS-CVaR.

TABLE 3

TABLE 3. Comparison between the adaptive ADMM and the standard ADMM.

5 Conclusion

An adaptive ADMM-based entire-process distributed restoration method of TSs and DSs considering CVaR is proposed in this work. The case study based on an improved 179-bus transmission system is conducted to test the effectiveness and advantages of the proposed method, and the following conclusions are drawn from the simulation.

1) The entire-process restoration strategy of TSs and DSs considering CVaR is formulated to maximize the total restoration benefits of TSs and DSs, which achieves higher generated power and load restoration benefits compared to the entire-process distributed restoration model that does not consider CVaR and the entire-process restoration model that does not consider transmission-distribution systems coordination.

2) The proposed adaptive ADMM achieves approximately equal restoration benefits of the TSs and DSs compared to the standard ADMM, while reducing by over 50% iteration number and corresponding 13,174 s of solution time compared to the standard ADMM. Hence, the proposed adaptive ADMM accelerates the convergence rate of the distributed solution and enhances the practicality of the proposed entire-process distributed restoration model of TSs and DSs considering CVaR.

The detailed restoration strategies for the feeders connected to each bus of DSs are not considered in this paper, which will be further studied in future work.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

QL: Methodology, Conceptualization, Software, Writing–original draft. CC: Methodology, Supervision, Writing–original draft. YZ: Investigation, Visualization, Writing–review and editing. YW: Writing–review and editing, Investigation. CL: Writing–review and editing, Validation. HL: Software, Writing–original draft. ZL: Software, Writing–review and editing. ZZ: Methodology, Writing–review and editing. LY: Supervision, Validation, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. We appreciate the support from the Key Technology Project of China Southern Power Grid Co., Ltd. (Project Code: 067600KK52222002; Technology Code: GZKJXM20222170) for this work.

Conflict of interest

Authors QL, YZ, ZL, and ZZ were employed by Guizhou Power Grid Co., Ltd.

The authors declare that this study received funding from the Key Technology Project of China Southern Power Grid Co., Ltd. The funder had the following involvement in the study: decision to publish and approval of the final version of the manuscript.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chen, C., Liang, H., Zhai, X., Zhang, J., Liu, S., Lin, Z., et al. (2022a). Review of restoration technology for renewable-dominated electric power systems. Energy Convers. Econ. 3, 287–303. doi:10.1049/enc2.12064

CrossRef Full Text | Google Scholar

Chen, C., Liu, C., Ma, L., Chen, T., Wei, Y., Qiu, W., et al. (2023b). Cooperative-game-based joint planning and cost allocation for multiple park-level integrated energy systems with shared energy storage. J. Energy Storage 73, 108861. doi:10.1016/j.est.2023.108861

CrossRef Full Text | Google Scholar

Chen, C., Qiu, W., Liu, C., Zhang, Q., Li, Z., Lin, Z., et al. (2022b). Cooperative-game-based day-ahead scheduling of local integrated energy systems with shared energy storage. IEEE Trans. Sustain. Energy 13 (4), 1994–2011. doi:10.1109/tste.2022.3176613

CrossRef Full Text | Google Scholar

Chen, C., Wu, Y., Cao, Y., Liu, S., Tan, Q., and Wang, W. (2021). Intending island service restoration method with topology-powered directional traversal considering the uncertainty of distributed generations. Front. Energy Res. 9, 762491. doi:10.3389/fenrg.2021.762491

CrossRef Full Text | Google Scholar

Chen, Y., Qi, D., Hui, H., Yang, S., Gu, Y., Yan, Y., et al. (2023a). Self-triggered coordination of distributed renewable generators for frequency restoration in islanded microgrids: a low communication and computation strategy. Adv. Appl. Energy 10, 100128. doi:10.1016/j.adapen.2023.100128

CrossRef Full Text | Google Scholar

Fan, R., Sun, R., Liu, Y., and Hassan, R. (2022). An online decision-making method based on multi-agent interaction for coordinated load restoration. Front. Energy Res. 10, 3389. doi:10.3389/fenrg.2022.992966

CrossRef Full Text | Google Scholar

Ghasemi, S., Khodabakhshian, A., and Hooshmand, R. (2019). New multi-stage restoration method for distribution networks with DGs. IET Generation, Transm. Distribution 13 (1), 55–63. doi:10.1049/iet-gtd.2018.5624

CrossRef Full Text | Google Scholar

Hao, L., Xue, Y., Li, Z., Wang, H., and Xu, Q. (2022). Decision support system for adaptive restoration control of distribution system. J. Mod. Power Syst. Clean Energy 10 (5), 1256–1273. doi:10.35833/mpce.2021.000528

CrossRef Full Text | Google Scholar

Li, S., Wang, L., Gu, X., Zhao, H., and Sun, Y. (2022). Optimization of loop-network reconfiguration strategies to eliminate transmission line overloads in power system restoration process with wind power integration. Int. J. Electr. Power & Energy Syst. 134, 107351. doi:10.1016/j.ijepes.2021.107351

CrossRef Full Text | Google Scholar

Li, Z., Khrebtova, T., Zhao, N., Zhang, Z., and Fu, Y. (2020). Bi-level service restoration strategy for active distribution system considering different types of energy supply sources. IET Generation, Transm. Distribution 14 (19), 4186–4194. doi:10.1049/iet-gtd.2020.0047

CrossRef Full Text | Google Scholar

Liu, S., Chen, C., Jiang, Y., Lin, Z., Wang, H., Waseem, M., et al. (2023). Bi-level coordinated power system restoration model considering the support of multiple flexible resources. IEEE Trans. Power Syst. 38 (2), 1583–1595. doi:10.1109/tpwrs.2022.3171201

CrossRef Full Text | Google Scholar

Rockafellar, R., and Stanislav, U. (2002). Conditional value-at-risk for general loss distributions. J. Bank. Finance 26 (7), 1443–1471. doi:10.1016/s0378-4266(02)00271-6

CrossRef Full Text | Google Scholar

Roofegari, R., and Sun, W. (2019). Distributed load restoration in unbalanced active distribution systems. IEEE Trans. Smart Grid 10 (5), 5759–5769. doi:10.1109/tsg.2019.2891419

CrossRef Full Text | Google Scholar

Sekhavatmanesh, H., and Cherkaoui, R. (2020). A multi-step reconfiguration model for active distribution network restoration integrating DG start-up sequences. IEEE Trans. Sustain. Energy 11 (4), 2879–2888. doi:10.1109/tste.2020.2980890

CrossRef Full Text | Google Scholar

Shen, C., Kaufmann, P., Hachmann, C., and Braun, M. (2018). Three-stage power system restoration methodology considering renewable energies. Int. J. Electr. Power & Energy Syst. 94, 287–299. doi:10.1016/j.ijepes.2017.07.007

CrossRef Full Text | Google Scholar

Shi, Q., Li, F., Olama, M., Dong, J., Xue, Y., Starke, M., et al. (2021). Network reconfiguration and distributed energy resource scheduling for improved distribution system resilience. Int. J. Electr. Power & Energy Syst. 124, 106355. doi:10.1016/j.ijepes.2020.106355

CrossRef Full Text | Google Scholar

Sun, R., Liu, Y., Zhu, H., Azizipanah-Abarghooee, R., and Terzija, V. (2019). A network reconfiguration approach for power system restoration based on preference-based multiobjective optimization. Appl. Soft Comput. 83, 105656. doi:10.1016/j.asoc.2019.105656

CrossRef Full Text | Google Scholar

Wang, D., Gu, X., Zhou, G., Li, S., and Liang, H. (2017). Decision-making optimization of power system extended black-start coordinating unit restoration with load restoration. Int. Trans. Electr. Energy Syst. 27 (9), e2367. doi:10.1002/etep.2367

CrossRef Full Text | Google Scholar

Yuan, C., Illindala, M., and Khalsa, A. (2017). Modified viterbi algorithm based distribution system restoration strategy for grid resiliency. IEEE Trans. Power Deliv. 32 (1), 310–319. doi:10.1109/tpwrd.2016.2613935

CrossRef Full Text | Google Scholar

Zhao, J., Liu, Y., Wang, H., and Wu, Q. (2020b). Receding horizon load restoration for coupled transmission and distribution system considering load-source uncertainty. Int. J. Electr. Power & Energy Syst. 116, 105517. doi:10.1016/j.ijepes.2019.105517

CrossRef Full Text | Google Scholar

Zhao, J., Wang, H., Hou, Y., Wu, Q., Hatziargyriou, N., Zhang, W., et al. (2020a). Robust distributed coordination of parallel restored subsystems in wind power penetrated transmission system. IEEE Trans. Power Syst. 35 (4), 3213–3223. doi:10.1109/tpwrs.2020.2971023

CrossRef Full Text | Google Scholar

Zhao, J., Wang, H., Liu, Y., Wu, Q., Wang, Z., and Liu, Y. (2019). Coordinated restoration of transmission and distribution system using decentralized scheme. IEEE Trans. Power Syst. 34 (5), 3428–3442. doi:10.1109/tpwrs.2019.2908449

CrossRef Full Text | Google Scholar

Zhao, J., Wang, H., Wu, Q., Hatziargyriou, N., and Shen, F. (2020c). Distributed risk-limiting load restoration for wind power penetrated bulk system. IEEE Trans. Power Syst. 35 (5), 3516–3528. doi:10.1109/tpwrs.2020.2973429

CrossRef Full Text | Google Scholar

Zhao, J., Zhang, Q., Liu, Z., and Wu, X. (2021). A distributed black-start optimization method for global transmission and distribution network. IEEE Trans. Power Syst. 36 (5), 4471–4481. doi:10.1109/tpwrs.2021.3056096

CrossRef Full Text | Google Scholar

Zhao, Y., Lin, Z., Ding, Y., Liu, Y., Sun, L., and Yan, Y. (2018). A model predictive control based generator start-up optimization strategy for restoration with microgrids as black-start resources. IEEE Trans. Power Syst. 33 (6), 7189–7203. doi:10.1109/tpwrs.2018.2849265

CrossRef Full Text | Google Scholar