
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res. , 08 January 2024
Sec. Sustainable Energy Systems
Volume 11 - 2023 | https://doi.org/10.3389/fenrg.2023.1283818
This article is part of the Research Topic Recent Advances in Energy Systems for Sustainable Development View all 11 articles
Solar energy is an attractive renewable energy option for countries located in the tropical region. Harvesting this energy using simple yet innovative technologies such as solar chimney power plants (SCPP) will help the developing countries in meeting their sustainable development goals. In an SCPP, air is heated under a greenhouse collector and the hot air is passed to a chimney, where it drives a turbine while rising up. Research efforts have been directed in the past at improving the performance and power output of an SCPP by varying its geometric parameters. The chimney height of a previously optimized solar chimney power plant, having a divergent chimney, was increased from 4 to 6 m and then to 8 m in this first experimental work of this kind. The temperature variations inside the collector, along the chimney height, the velocity at the turbine section, the power available and the output power of an air turbine, estimated by applying mechanical load, are compared for the three chimney heights. The temperature rise of the air inside the collector was the highest for the 4 m tall SCPP and reduced as the chimney height was increased to 6 and 8 m due to the lower time of stay of air in the collector for greater chimney heights. Along the height of the divergent chimney, the temperature dropped with the maximum drop occurring for the 8 m tall SCPP indicating a lower enthalpy loss at the chimney exit. The air velocity at the turbine section was found to increase with chimney height for given solar insolation/time of the day due to the higher driving force which is the buoyancy effect produced by the hot air. The maximum turbine output power for the 8 m tall SCPP increased by 252% compared to the 4 m tall SCPP indicating that significant improvement in the power output can be achieved by increasing the height of a divergent chimney SCPP. An average power of about 40 kW will be available for a chimney height of 100 m which will be extremely beneficial for the sustainable development of small islands.
The Pacific Islanders have a strong relationship with their ocean and their land. Any changes in climate directly impact their livelihood, culture, and customs (Hennessy et al., 2011). Climate change is caused mainly by burning fossil fuels such as oil and coal which release harmful gases to the environment. The impact of climate change on the environment includes cyclones, droughts, rising sea levels, extreme heat waves, bushfires, ocean acidification, and many more (Casule, 2020). An example of these impacts is the cyclone Winston that affected Fiji in 2016. Cyclone Winston was one of the strongest cyclones in the recorded history of the southern hemisphere which caused $470 million worth of damage to Fiji (Casule, 2020). To mitigate such issues, the energy sector over the last decade has been focusing on moving to renewable sources of energy including wind, solar, hydro, geothermal, biomass, etc. The consumption of renewable energy is now showing an increasing trend compared to all other sources with solar energy being one of the largest contributors in 2020 (Looney, 2021).
About 174 PW worth of solar energy falls onto the earth’s atmosphere which is 10,000 times the total energy consumed by humans on earth (Rhodes, 2010). Solar energy, being the largest source of energy available, can be directly used for processes like cooking, water and space heating, and agricultural dryers or it can be converted to electrical energy using a system such as a photovoltaic cell (Al Qubeissi and El-Kharouf, 2020).
One of the popular technologies for harvesting solar energy is a solar chimney power plant (SCPP). An SCPP is a very innovative yet simple technology comprising of three key components: the collector, the chimney and a power conversion unit which consists of the turbine-generator unit (Cao et al., 2018). The radiation from the Sun penetrates the collector cover which is transparent and heats up the air and the ground under the collector. Due to the greenhouse effect, the air in the collector becomes warmer, while the ambient temperature at the exit of the chimney is significantly lower. This temperature difference between the collector and the chimney exit causes the air in the collector to rise upwards in the chimney. This rising airflow is used to drive a turbine-generator unit which is usually located near the base of the chimney. Air moving out of the collector is replaced by the ambient air from the outside due to natural convection. This cycle continues as long as a sufficient temperature difference exists between the collector and the chimney exit. The SCPP does not require any fuel or cooling water and has a very simple operating principle; it does not require sophisticated and expensive materials for construction or maintenance, can be constructed in any geographic location if good amount of solar radiation is available and has a long operating life (Ming, 2016). Another major advantage of SCPPs is that they can be constructed on a smaller land area compared to PV panels; this is a very important factor in countries where land is not easily available. It can help in the sustainable development of Pacific Island countries and meet their sustainable development goals especially SDG 7. Regardless of its low efficiency, the advantages it offers has motivated several investigators to carry out further research on the SCPP.
The first ever prototype of a solar chimney power plant (SCPP) was proposed and fabricated by Schlaich and his colleagues in 1981 in Manzanares, Spain (Haaf et al., 1983; Haaf, 1984) with a height of 194.6 m, a radius of 5.08 m and a collector radius of 133 m. The characteristics of this SCPP and the technical issues are reported by Schlaich et al. (2005). The viability of SCPPs for rural areas was investigated by Padki et al. (1989). To investigate the theoretical and experimental performance characteristics of SCPPs, Pasumarthi and Sherif. (1998a) proposed a mathematical model and studied the effect of different geometric parameters on the temperature, velocity and power output of the plant. In a subsequent work, Pasumarthi and Sherif. (1998b) made further modifications to their plant and reported better performance. The collector radius and chimney height of their demonstration model were 9.15 and 7.92 m respectively. A model to evaluate the performance of SCPPs was developed by Ming et al. (2006). In a subsequent work, Ming et al. (2008) studied the heat storage characteristics of an energy storage layer under different solar insolations.
Esmail et al. (2021) identified the need for design theories for the SCPP turbine because existing design theories being utilized were initially formulated for gas and steam turbines. Operating gas and steam turbines under the operating conditions of an SCPP adversely affected the overall performance of an SCPP. Kasaeian et al. (2017) carried out CFD simulation to understand the effect of the number of turbine blades, rotational speed of the turbine, chimney height and collector diameter on the performance of the SCPP. A three-bladed turbine was reported to show the highest mass flow rate, whereas a five-blade turbine produced the maximum power. The study also reported that increasing the collector diameter while keeping the turbine rotational speed fixed, directly increased the air velocity, turbine torque and the output power. An axisymmetric mathematical model using the continuity equation, Navier-Stokes equations and the energy equation was developed by Xu et al. (2011). After validating their results, they presented results of static pressure, velocity, and temperature distributions for two turbine pressure drops. The effect of solar radiation was also studied in their work.
Experimental work under controlled conditions at three heat fluxes was carried out by Li and Liu (2014) with the use of a phase change material for energy storage and release. A CFD analysis of an SCPP of 10 m height with a divergent chimney was carried out by Patel et al. (2014), in which the effects of collector inlet opening, outlet height, outlet diameter, the chimney divergence angle, chimney inlet opening, and chimney diameter were studied in detail. Optimum values of these parameters were obtained and a chimney divergence angle of 2° (each side) was found to give the best performance. Ahmed and Patel (2017) reported results from further detailed experiments on a 4 m tall SCPP that was designed based on the findings of the previous optimization work carried out using CFD, including the temperature variations in the collector and the chimney, and the velocity of air at the turbine section at different solar insolations and at different times of the day. Similar to the findings of Patel et al. (2014), Motoyama et al. (2014) found that a diffuser tower gives higher velocity in the chimney from their experimental work on a 4 m high SCPP. An indoor SCPP was built by Guo et al. (2016) which was used to study the air temperature and velocity for different solar insolations and heights of the chimney. For a constant solar insolation, they reported an increasing air velocity in the chimney with a trend matching their theoretical results of velocity being proportional to 1/3 power of chimney height; however, the rate of increase of air velocity reduced with increasing chimney height. This was attributed to the heat losses through the chimney walls as well as the flow losses. Based on their findings, they suggested that there has to be an upper limit for the chimney height above which the air velocity does not increase much.
Singh et al. (2021) proposed the novel concept of a bell-mouth shaped collector inlet in a converging-diverging SCPP. They reported that an efficient bell-mouth shaped collector inlet can improve the air velocity by up to 270%. The improvement in air velocity was because of high or uniform static pressure recovery in the chimney which does not occur in a conventional system. Faisal et al. (2023) used ANSYS Fluent software to minimize flow losses by modifying the chimney inlet. The connection at the collector outlet and the chimney inlet was modified by rounding it rather than having a sharp bend. The available power improved by 55% when the ratio between the curvature radius and the chimney diameter was 0.45.
Habibollahzade et al. (2021) proposed a modified theoretical model which could be used to realistically simulate solar chimneys incorporating wind turbine power curves. It was concluded by these researchers that increasing the chimney height and collector radius to very high values can adversely affect the system performance. The multi-objective grey wolf optimization technique employed by them provided a range of most suitable design parameters for the locations studied. Patil et al. (2023) developed a machine learning model which could be used to vary dimensional parameters of the SCPP and understand their effect on the power output. They reported that increasing the chimney height and collector radius enhances the power production of an SCPP. Azad et al. (2021) also used multi-objective optimization to obtain the best design parameters by changing the geometric parameters such as collector diameter, collector height, chimney diameter, chimney height and the chimney wall curvature to achieve balance between power and water production for an SCPP combined with a water desalination plant. Considering the design parameters, chimney height and the collector diameter were identified as the most influential parameters. Cottam et al. (2019) developed a thermo-fluid based numerical model first presented by Cottam et al. (2016) to optimize the performance of solar chimney power plants by dimension matching. Optimum pressure drop in the system was found to be dependent on the collector and chimney radius only. Power output was seen to linearly increase before reaching a maximum by varying the collector and chimney radius. However, increasing the chimney height increased the power output quadratically. A simple cost model coupled with the thermodynamic model indicated that multiple plants with an optimum collector radius would be better compared to a single large power plant. Larger solar chimney power plants can be economical until the cost of the chimney increases more than quadratically with height.
Nia and Ghazikhani (2023) carried out experimental and numerical studies on an SCPP which had a chimney height of 4 m and a collector diameter of 5 m. Various parameters such as the collector height, collector radius and the chimney height were varied to optimize the power output of the SCPP. Maximum available power of 1.74 W was reported for the SCPP with the optimized parameters. Mandal et al. (2021) carried out a numerical study by varying the height of the collector inlet. They reported that reducing the collector inlet height from 10 cm to 5 cm increases the velocity of the air at the chimney inlet from 1.5 m/s to around 5.5 m/s which significantly improves the power generation of the SCPP. Cuce et al. (2020) analyzed the effect of chimney height on the various performance parameters of an SCPP using 3D axisymmetric CFD modelling. The mass flow rate of the air increased when the chimney height was increased. Similar to the findings of Guo et al. (2016), they concluded that there should be an optimum chimney height. Another important parameter studied was the temperature rise in the collector. It was found that increasing the chimney height reduced the air temperature in the collector. When the chimney height was increased 5 times, the temperature in the collector dropped by about 3°. Najm and Shaaban (2018) conducted numerical simulation and optimization of the SCPP performance with different geometric and operating conditions. The solar chimney height was increased keeping the solar insolation and the optimum collector radius fixed. Increasing the chimney height increased the turbine power. Shirvan et al. (2017) carried out 2D axisymmetric numerical simulation and sensitivity analysis on a prototype SCPP in Zanjan, Iran to determine the potential maximum power output. They concluded that the maximum power output reduces when the entrance gap of the collector is increased and increases when the chimney height and diameter are increased. Kebabsa et al. (2020) carried out a numerical investigation using 2D axisymmetric chimney model to investigate the effect of collector inlet geometry. Weli et al. (2021) studied the effect of ground slope, collector tilt angle and the collector inlet height using CFD simulations. They studied the above parameters against the temperature of the air at the chimney inlet, air velocity and pressure variations. They reported an optimum ground slope of 35° which enables the collector span to be reduced by 18% and chimney height by 36% having the same system volume as the flat ground collector.
In other studies, Mandal et al. (2023) used ANSYS Fluent to carry out a 3D study to understand the effect of modifying the absorber surface. Biswas et al. (2023) also used ANSYS Fluent to carry out 3D study by modifying the absorber surface. Guo et al. (2019) carried out a detailed review by focusing on the current understanding of the SCPPs in terms of the optimal arrangement of geometric parameters, effect of climate conditions, role of radiation heat transfer, maximizing power production, scaling of laboratory results to commercial plants, lack of large-scale power plants and current innovations in this area. Guo et al. (2017) carried out an economic analysis considering parameters such as the cost advantage of materials in China, low loan rates and low maintenance and operating cost. They reported that the levelized cost of electricity (LCOE) for a 10 MW SCPP in Yinchuan, China was 0.4174 Yuan/kWh. The LCOE is reported to be comparable with wind power and solar PV in China.
A 6 m tall SCPP was designed, fabricated and experimented upon by Balijepalli et al. (2020). They reported the absorber plate temperature, collector cover surface temperature and air temperature from 6.00 a.m. to 6.00 p.m. They reported a maximum air velocity of 4.7 m/s and 5.5 m/s before and after the turbine, respectively (the velocity before the turbine was measured in the collector). The theoretical power output of the SCPP was reported to be 1.37 W whereas the actual power output was reported to be 0.82 W. Bansod (2020) varied the chimney height from 0.5 to 2.0 m in an experimental SCPP with a collector diameter of 1.8 m and a constant chimney diameter of 38 mm. It was reported that the maximum air velocity increases from 0.953 to 1.645 m/s when the chimney height is increased from 0.5 to 1.5 m and then reduces slightly to 1.641 m/s when the height is further increased to 2.0 m. Ghalamchi et al. (2016) from their research concluded that, of the three chimney heights of 2, 3, and 4 m, the height of 3 m is optimum and gives the maximum air velocity in the chimney. It should, however, be noted that in some of these works, temperature inversion effect was observed. An experimental SCPP with a chimney height of 6 m and a collector diameter of 2.5 m was built and tested for performance by Mandal et al. (2022). For a maximum solar radiation of 750 W/m2, they reported a maximum velocity of 1.5 m/s. They performed a computational study and found that the air velocity increases to 2.7 m/s if the chimney height is increased to 8 m for the same collector diameter for a solar insolation of 600 W/m2. Das and Chandramohan (2019a) reported from their computational work that as the height of the constant diameter chimney is increased from 3 to 8 m, the air velocity increased up to 44%.
It can be seen that while some researchers, e.g., Cottam et al. (2019) and Pradhan et al. (2021) concluded that the dimensions of the main components of an SCPP should be matched well for optimum performance, other researchers such as Sivaram et al. (2018), Bansod (2020), Belkhode et al. (2020) and Mandal et al. (2022) concluded that the chimney height has a direct effect on the pressure difference and that the exit air velocity increases with chimney height. They argued that an SCPP with a smaller collector area and a greater chimney height could produce higher velocity and better efficiency compared to an SCPP with higher collector area. Some other researchers concluded that there will be an optimum chimney height above which the air velocity does not increase (Kasaeian et al., 2014; Ghalamchi et al., 2016). However, these works were carried out on constant diameter chimneys. In view of the above, the present work is intended to study the effect of chimney height on the performance characteristics of an SCPP having a divergent chimney by keeping the collector area constant.
In the present work, the effect of chimney height on the performance enhancement of an SCPP having a divergent chimney is experimentally investigated. A 4 m tall SCPP was initially fabricated and tested for performance by Ahmed and Patel (2017); two sections of 2 m each were then added to this SCPP one after the other to obtain total chimney heights of 6 m and 8 m and experiments were carried out under different conditions to investigate the effect of chimney height on the performance of the plant. No such experimental work on the effect of chimney height of a divergent chimney on the performance of an SCPP has been reported till now. The results of temperature distributions across the collector and along the chimney height, the air velocity at the turbine section, the available power and the turbine power recorded and estimated hourly at different solar insolations throughout a day are presented. As the experiments were performed up to solar insolations of 1,000 W/m2, the present work is expected to enhance the existing state of knowledge and understanding of the effect of chimney height on the SCPP performance. Moreover, the turbine power was directly measured by loading the air turbine mechanically at different solar insolations for the three chimney heights. Direct power measurements of an SCPP have not been reported in the literature so far.
An existing solar chimney power plant initially constructed for experimentation with a total height of 4 m (Ahmed and Patel, 2017) was refurbished and used for the present experimental work. Figure 1 shows the newer, completed 8 m tall SCPP while a photograph of the 4 m tall SCPP is shown in the inset. The collector diameter was 3.2 m. Further details on the dimensions of the SCPP are available in the work reported by Ahmed and Patel (2017).
The footing of the SCPP consisted of a 1,000 mm deep foundation to hold the solar chimney structure in place. The absorber around the foundation was created by pouring concrete and making a flat surface of 50 mm thickness. The area of the absorber was slightly larger than the diameter of the collector cover. The concrete was painted with black paint to improve the absorption capacity. A chimney bell-mouth was constructed to connect the solar collector to the solar chimney. The chimney bell-mouth acts as a nozzle accelerating the flow towards the turbine section, hence the inner surface was smoothened using Bondo body filler. The bell-mouth housing was 200 mm in height and 700 mm in diameter.
The construction details and a schematic of the 4 m tall SCPP used for experimentation earlier are reported in detail in ref. (Ahmed and Patel, 2017). For the present work, the SCPP height was firstly increased to 6 m and then finally another detachable 2 m unit was constructed to increase the SCPP height to 8 m above the ground. The detailed dimensions are shown in Figure 2. The ratio of chimney height to the collector diameter in the present experimental work ranged from 1.25 to 2.5 which is well within the acceptable range of 0.8–5.0 (Pasumarthi and Sherif, 1998a; Zhou et al., 2007a).
A turbine housing unit was constructed and installed in between the solar chimney and the bell housing. An axial flow turbine was placed in the turbine section of the chimney. An inspection glass was provided on the housing to allow for shaft rotational speed and power measurement.
The 4 m tall SCPP was initially tested in 2016 (Ahmed and Patel, 2017) for temperature and velocity variations whereas the 6 m and 8 m tall SCPPs were tested in 2022. The turbine installation and the associated measurements were carried out in 2022 as well.
PT-100 K type temperature sensors were placed across the radius of the collector and along the height of the chimney. The temperature sensors have a measurement range, resolution and accuracy of 0°C–700°C, 0.1°C, and ±0.5%, respectively. The locations of the temperature sensors are shown in Figure 2.
The temperature readings were logged onto a 16 port CR-1000 series data-logger with an accuracy of ±0.06% of the reading for the temperature range of 0°C–40°C, ±0.12% of the reading for the temperature range of -25°C–50°C and ±0.18% of the reading for the temperature range of -55°C–85°C. The data-logger has an external keyboard for taking instantaneous measurements. The data-logger requires a 12 V DC battery and suspends measurements when the voltage drops below 9.6 V. The temperature measurements were recorded onto the in-built 4 MB memory card of the data-logger from which a dongle was used to retrieve the data.
A pitot-static tube was fitted at the turbine location to measure the air velocity. The pitot-static tube was aligned perfectly parallel to the airflow to ensure that accurate velocity measurements were recorded. A Furness Controls (model FCO510) digital micromanometer was connected to the pitot-static tube to measure the dynamic pressure readings. The micromanometer has a range of −2,000 to + 2,000 mm of water and an accuracy of ±0.25%. The maximum error in the estimation of velocity was found to be 4.9% (Ahmed and Patel, 2017).
A Licor LI200S Pyranometer was used to measure the solar insolation. The absolute maximum error in the measurements of solar insolation was ±5% with a typical error of ±3%.
A photo-tachometer (model: DT-2234B) was used to measure the turbine rpm. The tachometer has a range of 0–99,999 rpm. The tachometer has a resolution of 0.1 rpm for measurements less than 1,000 rpm and a resolution of 1 rpm for measurements above 1,000 rpm. The accuracy of the Tachometer is ±0.05%.
The torque of the turbine was measured using a mass and string system along with a spring balance as shown in Figure 3. The string’s one end was loaded with a mass via a pulley and the other end was attached to a spring balance. For all the experiments, the spring balance did not show any deflection, but it was kept in place throughout the torque measurements to ensure that the shaft of the turbine did not bend. The mass on the other side was gradually varied and the rpm was noted. The torque was obtained by multiplying the net force with the radius. The torque was multiplied with the angular velocity to get the power output of the turbine. The maximum error in the estimation of power output was estimated to be 2.7% following the procedure described by Moffat (1988).
Figure 4 shows a photograph of the turbine housing and the turbine inside the housing (A) along with the instrumentation and the box containing the data acquisition system (B). The constant diameter turbine section between the two flanges can be seen in the figure.

FIGURE 4. A photograph of the turbine placed inside the turbine housing (A) and set-up for measurements in the turbine section (B).
To compare the present results with the previously reported results by Ahmed and Patel (2017), solar insolations and ambient temperatures over three typical days in February 2016 and February 2022 were measured. The solar insolations and ambient temperatures showed similar trends for 2016 and 2022. The solar insolation peaked at 1.00 p.m. with values of about 1000 W/m2 for both the years. The maximum deviation in the solar insolation trends was seen at 10.00 a.m. where the solar insolation for 2022 was 133 W/m2 higher than that of the year 2016. The ambient air temperature for both the years peaked at 3.00 p.m. even though the peak solar insolations were measured at 1.00 p.m. The ambient air temperatures for 2022 throughout the day, however, were slightly higher than that of 2016 with the greatest difference of 0.8°C recorded at 2.00 p.m. (31.94°C in 2022 and 31.13°C in 2016). A similar trend of ambient temperature peaking at 3.00 p.m. while the solar insolation peaking at 1.00 p.m. was reported by Mekhail et al. (2017). They attributed it to the time it takes for the heat to be absorbed by the ground and then transferring it to the air.
Variation of ground temperature at different solar insolations was also compared for the years 2016 and 2022. The maximum ground temperature for 2016 was recorded to be 68.75°C whereas the maximum ground temperature for 2022 was recorded to be 72.26°C. The variation of ground temperature with solar insolation was seen to be linear for both the years. A best fit straight line was drawn by Ahmed and Patel (2017) for the variation of ground temperature with solar insolation for 2016 and its equation was reported. The results presented in this work are based on the measurements performed in the months of January to April, during which the ambient temperatures varied between 27°C and 33°C. As Fiji is a tropical country, there are very little variations in the daytime temperature. The average temperatures in Fiji remain relatively constant throughout the year (World Bank, 2021).
The temperature rise in the collector for days which had relatively similar solar insolations was compared for the three chimney heights and the results are shown in Figure 5. A very interesting trend is observed in the temperature rise with solar insolation. The temperature rise in the collector is found to reduce as the chimney height is increased. The reduction in the temperature rise is apparently due to the increase in the air velocity with chimney height which shortens the time for which the air stays in the collector. Similar results were reported by Cuce et al. (2020) and Sivaram et al. (2018). At the (average) higher solar insolation of 846 W/m2 shown in Figure 5A, the average of the maximum temperature rise for the 4 m, 6 m and 8 m tall solar chimneys are recorded to be 18°, 17.5° and 16.4°, respectively. As the solar insolation reduces (shown in Figures 5B–D), the temperature rise in the collector also shows a reducing trend; however, the trend of lower temperature rise from collector inlet to outlet with increasing chimney height can be seen for all the solar insolations.
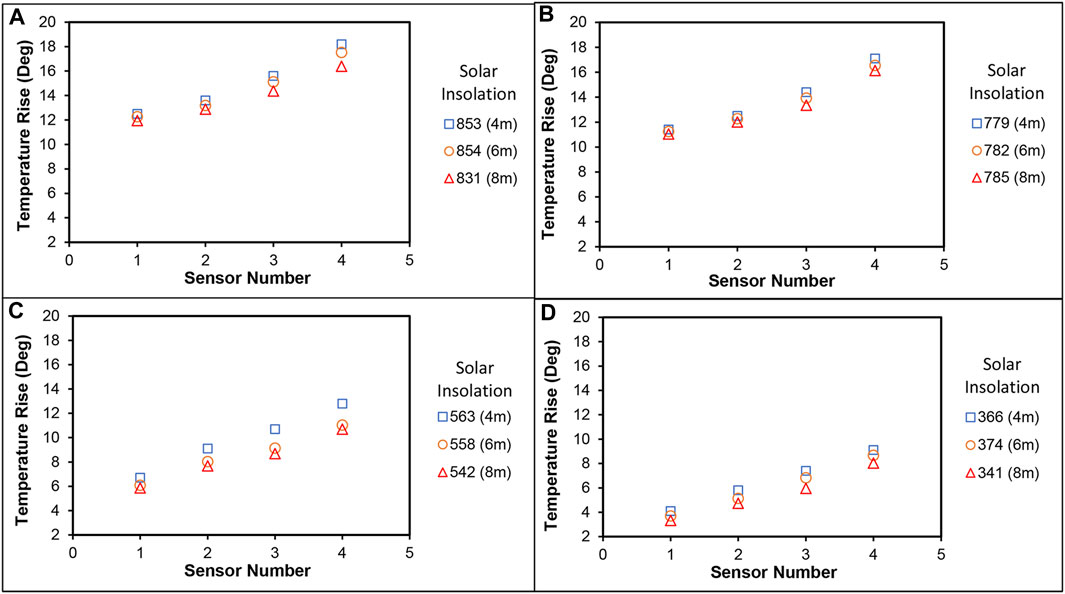
FIGURE 5. Temperature rise in the collector at solar insolation of: (A) 831–855 W/m2. (B) 779–785 W/m2. (C) 542–563 W/m2. (D) 341–374 W/m2.
The rise in the air temperature inside the collector from sensor 1 to sensor 4 for days which had relatively similar solar insolations was also compared from 9.00 a.m. to 9.00 p.m. for the three SCPP heights and the results are presented in Figure 6. At 9.00 a.m., the temperature rise in the collector from sensor 1 to sensor 4 for the three chimney heights is almost similar. There is a noticeable difference in the temperature rise between the three chimney heights from 11.00 a.m. onwards. The temperature rise peaked at 1.00 p.m., along with the solar insolation. Despite the solar insolation peaking at 1.00 p.m., the degree of temperature rise in the collector from sensor 1 to sensor 4 for the three chimney heights was the greatest at 2.00 p.m. This is due to the fact that it takes some time for the ground to absorb the solar heat, get heated up and then transfer the heat to the air that is entering the collector by convection and radiation. The difference (rise) in temperatures between sensor 1 and sensor 4 for the three chimney heights was also the highest at 2.00 p.m. followed by 3.00 p.m. At 9.00 p.m., the difference in the temperature rise reduces considerably between the three chimney heights although the effect of the heated ground is still felt with the air in the collector still at a higher temperature compared to the ground temperature thus causing an upward flow of air as can be seen in the variation of air velocity (Figure 13).
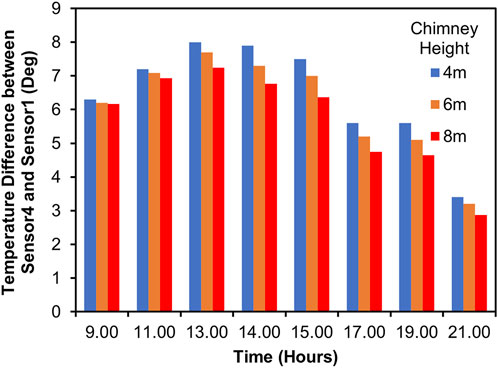
FIGURE 6. Temperature rise from sensor1 to sensor4 in the collector from 9.00 a.m. to 9.00 p.m. for the three chimney heights.
The temperature rise recorded by the 4 sensors placed across the collector (from inlet to outlet) at 9.00 a.m. on different days with similar solar insolations is shown in Figure 7, noting that the temperature rise right at the collector inlet would be zero. The temperatures gradually rise from the collector inlet to the outlet for all the three chimney heights. For the chimney height of 4 m, the temperature rise was found to be the highest, while it was the lowest for the maximum chimney height of 8 m.
The temperature rise measured by the 4 sensors placed across the collector at 1.00 p.m. at relatively similar solar insolations is shown in Figure 8. The temperature rise at 1.00 p.m. is considerably higher due to the high solar insolation at this time of the day which was about 1,000 W/m2 during these days. The 4 m tall SCPP showed the highest temperature rise with the first sensor recording a temperature rise of 16.7° and the last sensor close to the collector exit showed a temperature rise of 24.7°. The temperature rise was lower for the greatest chimney height of 8 m with the first sensor recording a temperature rise of 14.5° and the last sensor showing a rise of 21.74°. Similar trends were observed by Rishak et al. (2021) who reported the maximum temperature rise at 1.00 p.m. for two chimney heights of 3.3 and 4.5 m. Cuce et al. (2020) reported a reduction in the temperature rise in the collector as the chimney height is increased. Due to the increased velocity of air through the SCPP for greater chimney height, the air stays for less time inside the collector and hence absorbs less heat, which is the reason for lower temperature at the collector outlet for greater chimney height.
Figure 9 shows the temperature rise measured by the 4 sensors placed across the collector at 9.00 p.m. for the three chimney heights. All the three heights showed gradual increase at 9.00 p.m. and the temperature rise was the least compared to morning and afternoon times. The maximum temperature rise of 6.1° was recorded for the 4 m tall SCPP by sensor number 4 located close to the collector exit. At this time, the solar insolation is zero; however, the ground remains heated due to absorption of heat the whole day and transfers that heat to the air that enters the collector. The temperature of the air gradually rises till the exit of the collector. Due to the lower air velocities at this time (shown in Figure 13), the time for which air remains in the collector is longer causing the air to get heated; however, the temperature rise is significantly less compared to the rise at 1.00 p.m., as can be seen from a comparison of Figures 8, 9. Similar observations were made by Rishak et al. (2021) who recorded a reducing temperature difference after 1.00 p.m. Their last measurement was performed at 5.00 p.m. when a temperature rise of about 8° was recorded for a chimney height of 4.5 m.
The variations of the air temperature at the collector outlet were also plotted at different solar insolations and the results are shown in Figure 10. The exit air temperature is found to increase linearly as the solar insolation increased for all the three chimney heights. The outlet air temperatures for all the three chimney heights were measured to be almost identical at lower solar insolations of less than 300 W/m2. Similar trends were also reported by Sivaram et al. (2018). Zhou et al. (2007b) argued that this is due to the temperature inversion effect which starts clearing as the area close to the ground heats up with rising ambient temperature or solar insolation. At the insolation of about 360 W/m2, the difference in the collector outlet air temperature between the three chimney heights was recorded to be 1.8° which is very small. The difference starts to increase with increasing solar insolation, and at the highest insolation of about 1000 W/m2, the difference between the collector outlet temperatures was recorded to be 7.2° between the 4 m tall SCPP and the 8 m tall SCPP. As discussed earlier, the lower temperature for the 8 m tall SCPP is due to the smaller duration of time for which the air stays in the collector due to higher velocity, as will be shown later.
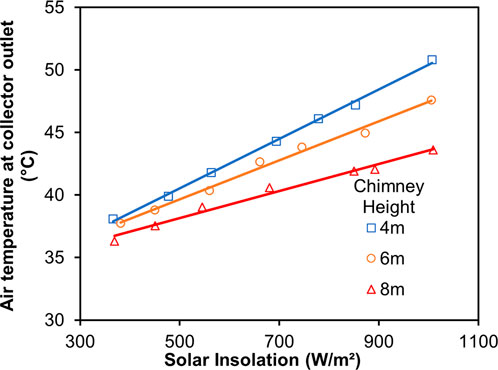
FIGURE 10. Variation of air temperature at the collector outlet with solar insolation for the three chimney heights.
Figure 11 shows the temperature drop along the chimney for the three chimney heights from 9.00 a.m. to 9.00 p.m. for days which had relatively similar solar insolations. This is the difference in air temperature between the chimney inlet and the outlet. As the air enters the chimney from the collector, the air pressure reduces while the velocity increases due to a reduction in area and the flow becoming predominantly uni-directional. As the air passes over the turbine blades, it transfers energy to the blades causing them to rotate. It was reported by Huang et al. (2007) that the temperature difference inside the collector as well as the pressure reduction during transition from the collector to the chimney increase with increasing solar insolation. The drop in temperature along the chimney height is due to the conversion of the enthalpy of air and the kinetic energy into pressure energy with the increasing area facilitating the pressure recovery from suction to atmospheric pressure at the chimney exit. The air velocity increases from zero at the collector inlet to its maximum at the location of minimum area in the chimney (Ming, 2016). The temperature drop in the 4 m tall chimney remained below 1.5° at all the times measurements were performed. The previous work also had similar trends (Ahmed and Patel, 2017). For the 6 m tall chimney, an increasing temperature drop from 9.00 a.m. to 2.00 p.m. was recorded along the chimney height, after which the drop reduced until 9.00 p.m. Similar trend was also observed for the 8 m tall chimney. The 8 m tall chimney produced the largest temperature drop of 9.2° at 2.00 p.m. The largest temperature drop for this case indicates a greater conversion of energy; at the same time, it also means that there is minimum loss of energy from the chimney outlet (loss of air enthalpy) as the temperature of air at the collector outlet (chimney inlet) was the lowest for this case. Das and Chandramohan (2019b) also reported the lowest air temperature at the chimney exit (maximum temperature drop) for the maximum chimney height of 8 m from their work on a constant diameter chimney. A similar level of temperature drop was also reported by Zhou et al. (2007a) for a chimney height of about 8 m although the solar insolations were not recorded in their work. Rishak et al. (2021) reported a temperature drop of about 8° at 12.00 p.m. and a drop of about 6° at about 2.00 p.m. for a chimney height of 3.3 m.
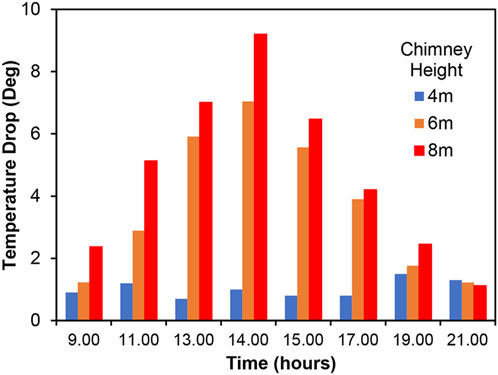
FIGURE 11. Temperature drop of air along the chimney height for the three chimney heights measured from 9.00 a.m. to 9.00 p.m.
The effect of chimney height on the air velocity was studied by plotting the variation of the air velocity at the turbine section at different solar insolations for the three chimney heights as shown in Figure 12. The air velocities were estimated on typical days with relatively similar solar insolations. The air velocities linearly increase for all the three chimney heights as the solar insolation increases. The air velocity increases with increasing chimney height because of the larger driving force which is the buoyancy effect due to the vertical column of hot air which has to link with the outside ambient air of the same height and lower temperature (Koonsrisuk et al., 2010; Ming, 2016). Thus, there is a larger pressure difference between the air entering the collector and the air entering the chimney for larger chimney height. Effect of changing the chimney height on the air velocity was also reported by Ghalamchi et al. (2016), Cuce et al. (2020), Sivaram et al. (2018) and Rishak et al. (2021) where similar trends were presented. Best fit straight lines are drawn to see the effect of chimney height on the air velocity more clearly. It can be seen from Figure 12 that the velocities for the lowest chimney height are lower and the difference between the velocities for 4 m and 6 m chimneys is larger than that between 6 m and 8 m chimney heights, indicating that after an optimum height, they may not be a significant increase in the air velocity. Some other researchers also made a conclusion that there will be an optimum chimney height above which the air velocity does not increase (Kasaeian et al., 2014; Ghalamchi et al., 2016). An optimization work by Dos Santos et al. (2017) based on constructal theory showed that there is an intermediate ratio of the chimney diameter at the exit and the chimney height that relates to the best performance of the device. In the present work, the loss due to friction in the chimney will be reduced as the velocity decreases in the divergent chimney. There is also a greater utilization of the enthalpy of air due to higher temperature drop along the chimney height. Ming. (2016) mentioned that the energy loss from the chimney outlet is the most significant loss and research efforts should be directed at reducing this loss. The present results show that the energy loss can be reduced by employing a divergent chimney and a suitable chimney height.
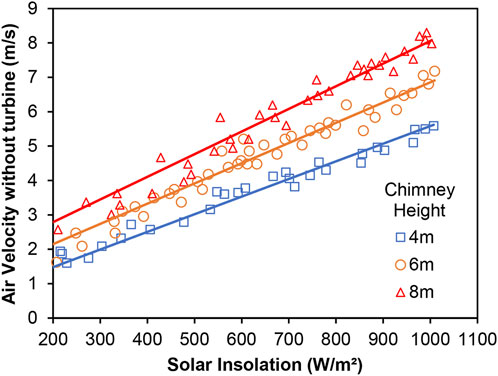
FIGURE 12. Variation of air velocity at the turbine section with solar insolation for the three chimney heights.
Figure 13 shows the variation of air velocity at the turbine section from 9.00 a.m. to 9.00 p.m. recorded on typical days with relatively similar solar insolations for the three chimney heights. The velocity trends for all the three chimney heights were similar. The air velocities were below 3 m/s for 9.00 a.m. and 10.00 a.m. for the three chimney heights. A substantial increase was observed from 10.00 a.m. until 1.00 p.m. for all the three heights. This correlates well with the significant increase in solar insolations during that time. Rishak et al. (2021) also reported the maximum air velocity at 1.00 p.m. for the two chimney heights of 3.3 and 4.5 m. The air velocities showed a decreasing trend from 1.00 p.m. to 4.00 p.m. The air velocities significantly reduced at 5.00 p.m. This is because the solar insolation at 5.00 p.m. starts to reduce significantly. From 5.00 p.m. to 9.00 p.m., the air velocities show a steady decline for all the three chimney heights. The air velocities for all the three chimney heights peaked at 1.00 p.m. with the 8 m tall chimney recording the highest velocity of 7.64 m/s corresponding to a solar insolation of about 1000 W/m2. The increments in air velocities as the chimney height increases are significant. The air velocity improves by 27% at the peak time when the chimney height is increased from 4 m to 6 m and further increases by 10% when the chimney height is increased to 8 m. Similar findings were reported by Al-Kayiem et al. (2014) who reported enhancement of velocity by 23% when the solar chimney height was increased from 5 m to 15 m. Das and Chandramohan (2019a) also studied the effect of solar chimney height on the air velocity and reported a 33% increase in air velocity when the chimney height was increased from 3 m to 8 m.
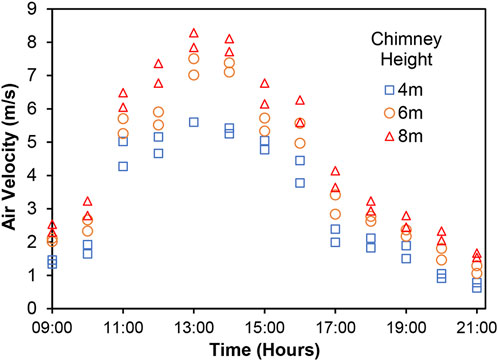
FIGURE 13. Variation of air velocity at the turbine section from 9.00 a.m. to 9.00 p.m. for the three chimney heights for typical days.
Figure 14 shows the maximum recorded air velocity at the turbine section as a function of chimney height. The maximum recorded air velocity was found to increase logarithmically as the chimney height is increased. This indicates that there exists a maximum chimney height after which the air velocity will not increase much. A very similar trend of air velocity increase was reported by Das and Chandramohan (2019b) when the chimney height was increased from 3m to 8 m. For a collector height of 50 mm, Rishak et al. (2021) reported an increase of 8.7% in the air velocity when the chimney height was increased from 3.3 to 4.5 m. Cuce et al. (2020) carried out performance studies taking into consideration geometrical parameters of the Manzanares pilot plant and reported the results. They also found that the maximum velocity tends to rise to a maximum. They presented a regression model which could be used to determine the optimum solar chimney height. Habibollahzade et al. (2021) also carried out parametric studies on the effect of geometric parameters on the performance of an SCPP and concluded that extreme values of collector diameter and chimney height reduce the power output of an SCPP. The findings of the present work support the above-mentioned findings.
The power available to the turbine at different solar insolations for the three chimney heights recorded on typical days with relatively similar solar insolations is shown in Figure 15. The power available was estimated using Eq. (1)
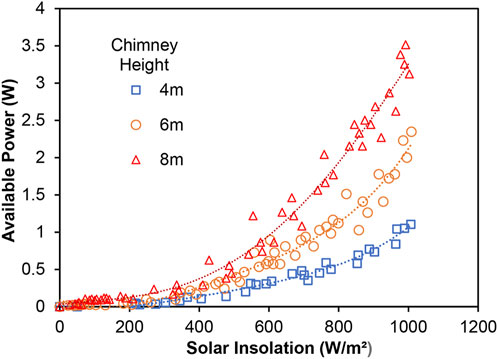
FIGURE 15. Variation of power available to the turbine with solar insolation for the three chimney heights.
For an SCPP of 6 m height with a constant diameter chimney, Mekhail et al. (2017) reported an available power of 3 W, while in the present work, it is 2.35 W. The power available at the turbine section at the solar insolation of 1000 W/m2 increased by 112% when the chimney height was increased from 4 m to 6 m and increased by 49% when the chimney height was increased from 6 m to 8 m, again indicating that the power will not keep increasing at the same rate with height. At the solar insolation of 1000 W/m2, the power available to the turbine for the 8 m tall SCPP is estimated to be about 3.5 W. For a collector height of 50 mm, Rishak et al. (2021) reported an increase of 25.2% in the available power when the constant diameter chimney height was increased from 3.3 to 4.5 m.
Figure 16 shows the free rpm of the turbine at a nearly constant solar insolation of 800 W/m2. About 150 measurements were taken within a short span of time during which the solar insolation did not change much. It can be seen that the free rotational speed varies between 650 rpm and 850 rpm. The free rpm of the turbine was found to generally increase with the solar insolation (not shown). The free rpm of a turbine is a direct indication of the energy transferred from the fluid to the rotor. Balijepalli et al. (2020) reported a speed range of 140–320 rpm from their SCPP of 6 m height and constant diameter chimney. Noting that the maximum air velocity in their case was 4.7 m/s, the lower range of rpm is expected as the lower air velocity results in lower transfer of energy to the turbine.
Figure 17 shows the power output from the turbine with respect to solar insolation for the three chimney heights. The turbine power output followed a trend similar to that of the available power at the turbine section for all the three cases. However, it is always lower than the available power due to the efficiency of the turbine which is lower at lower solar insolations due to the low air velocities. It should be noted that the power was measured fewer times compared to the velocity. The maximum measured powers for the 4 m, 6 m and 8 m tall SCPP are 0.79, 1.86, and 2.78 W, respectively. In the present work, the maximum power output increased by 135% when the SCPP height was increased from 4 m to 6 m and by 49% when the SCPP height was increased from 6 m to 8 m. For a chimney height of 6 m, Balijepalli et al. (2020) reported a theoretical power output of 1.37 W, which is lower than the power estimated in the present work. The higher power in the present work is due to the divergent chimney and a higher solar insolation. For a constant diameter chimney height increase of 33.3% (from 3.6 to 4.8 m), Belkhode et al. (2020) reported an electrical power output increase of 38.46%. Cuce et al. (2020) and Zhou et al. (2007b) presented a linear relationship between power output and solar chimney height. Li et al. (2012) however, reported a logarithmic trend between power output and chimney height. They suggested that as the chimney height increases, buoyancy weakens and the flow losses increase. They also suggested that there should be a maximum chimney height after which the power output will not increase much. It was reported from our previous work (Ahmed and Patel, 2017) that an average power of about 40 kW will be available for a chimney height of 100 m at a solar insolation of 800 W/m2 which will be extremely beneficial for meeting the energy needs of small islands.
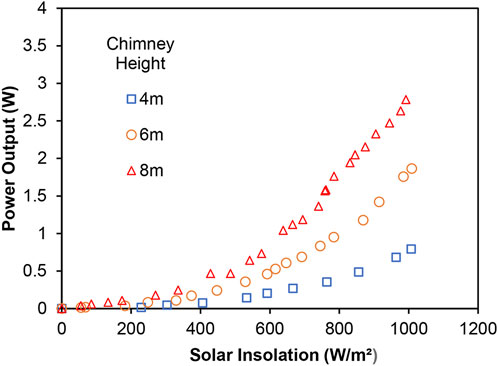
FIGURE 17. Power output from the turbine for the three chimney heights at different solar insolations.
The height of a solar chimney power plant having a divergent chimney was increased from 4 m to 6 m and then to 8 m in this experimental work. For all the three heights, the temperature variations inside the collector and along the chimney height, the air velocity at the turbine section, the power available and the power output from an axial flow turbine were measured/estimated. The main conclusions of the present work are:
• the temperature rise in the collector is the highest for the 4 m tall SCPP with an exit temperature of 50.8°C and the smallest for the 8 m SCPP with an exit temperature of 43.6°C due to the shorter stay of air in the taller chimney because of larger driving force and higher velocity in the chimney.
• the temperature drop along the chimney height was the maximum for the 8 m SCPP and minimum for the 4 m SCPP. The largest temperature drop for the 8 m SCPP indicates a lesser loss of energy from the chimney outlet.
• the air velocity at the turbine section increased with chimney height for all solar insolations and a maximum air velocity of 8.29 m/s was recorded for the 8 m SCPP; it was observed that the increase in the maximum air velocity is not linear but tends to be logarithmic.
• the free rpm of the turbine was measured to be in the range of 650 rpm–850 rpm at a solar insolation of 800 W/m2.
• the power output from the turbine was estimated by loading the turbine mechanically; the maximum power output increased from 0.79 W for the 4 m tall SCPP to 2.78 W for the 8 m SCPP at a solar insolation of 1000 W/m2, which is an increase of 252%.
• the output of the SCPP can be further enhanced by increasing the chimney height and a power of about 40 kW will be available at a solar insolation of about 800 W/m2.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
RP: Data curation, Formal Analysis, Investigation, Methodology, Writing–original draft. MRA: Conceptualization, Funding acquisition, Project administration, Supervision, Writing–review and editing.
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The student was provided funding from the University for his research work.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2023.1283818/full#supplementary-material
Ahmed, M. R., and Patel, S. K. (2017). Computational and experimental studies on solar chimney power plants for power generation in Pacific Island countries. Energy Convers. Manag. 149, 61–78. doi:10.1016/j.enconman.2017.07.009
Al-Kayiem, H. H., Sreejaya, K., and Gilani, S. I. U. H. (2014). Mathematical analysis of the influence of the chimney height and collector area on the performance of a roof top solar chimney. Energy Build. 68, 305–311. doi:10.1016/j.enbuild.2013.09.021
Al Qubeissi, M., and El-Kharouf, A. (2020). Renewable energy: resources, challenges and applications. London, United Kingdom: InTechOpen.
Azad, A., Aghaei, E., Jalali, A., and Ahmadi, P. (2021). Multi-objective optimization of a solar chimney for power generation and water desalination using neural network. Energy Convers. Manag. 238, 114152. doi:10.1016/j.enconman.2021.114152
Balijepalli, R., Chandramohan, V., and Kirankumar, K. (2020). Development of a small scale plant for a solar chimney power plant (SCPP): a detailed fabrication procedure, experiments and performance parameters evaluation. Renew. Energy 148, 247–260. doi:10.1016/j.renene.2019.12.001
Bansod, P. J. (2020). “Determination of optimum height of small prototype model of chimney operated solar power plant,” in Proceedings of ICRRM 2019 – system reliability, quality control, safety, maintenance and management (Singapore: Springer).
Belkhode, P., Sakhale, C., and Bejalwar, A. (2020). Evaluation of the experimental data to determine the performance of a solar chimney power plant. Mater. Today Proc. 27, 102–106. doi:10.1016/j.matpr.2019.09.006
Biswas, N., Mandal, D. K., Manna, N. K., and Benim, A. C. (2023). Novel stair-shaped ground absorber for performance enhancement of solar chimney power plant. Appl. Therm. Eng. 227, 120466. doi:10.1016/j.applthermaleng.2023.120466
Cao, F., Liu, Q., Yang, T., Zhu, T., Bai, J., and Zhao, L. (2018). Full-year simulation of solar chimney power plants in Northwest China. Renew. energy 119, 421–428. doi:10.1016/j.renene.2017.12.022
Casule, N. (2020). The state of the climate in the Pacific. Available at: https://apo.org.au/sites/default/files/resource-files/2020-12/apo-nid309955.pdf (Accessed July 22, 2023).
Cottam, P., Duffour, P., Lindstrand, P., and Fromme, P. (2016). Effect of canopy profile on solar thermal chimney performance. Sol. Energy 129, 286–296. doi:10.1016/j.solener.2016.01.052
Cottam, P., Duffour, P., Lindstrand, P., and Fromme, P. (2019). Solar chimney power plants–Dimension matching for optimum performance. Energy Convers. Manag. 194, 112–123. doi:10.1016/j.enconman.2019.04.074
Cuce, E., Sen, H., and Cuce, P. M. (2020). Numerical performance modelling of solar chimney power plants: influence of chimney height for a pilot plant in Manzanares, Spain. Sustain. Energy Technol. Assessments 39, 100704. doi:10.1016/j.seta.2020.100704
Das, P., and Chandramohan, V. (2019a). Computational study on the effect of collector cover inclination angle, absorber plate diameter and chimney height on flow and performance parameters of solar updraft tower (SUT) plant. Energy 172, 366–379. doi:10.1016/j.energy.2019.01.128
Das, P., and Chandramohan, V. (2019b). Effect of chimney height and collector roof angle on flow parameters of solar updraft tower (SUT) plant. J. Therm. Analysis Calorim. 136 (1), 133–145. doi:10.1007/s10973-018-7749-y
Dos Santos, E. D., Isoldi, L. A., Gomes, M. D. N., and Rocha, L. A. (2017). “The constructal design applied to renewable energy systems,” in Sustainable energy technologies. Editors E. Rincón-Mejía, and A. De Las Heras (Florida, United States: CRC Press), 55–61.
Esmail, M. F., A-Elmagid, W., Mekhail, T., Al-Helal, I., and Shady, M. (2021). A numerical comparative study of axial flow turbines for solar chimney power plant. Case Stud. Therm. Eng. 26, 101046. doi:10.1016/j.csite.2021.101046
Faisal, S. H., Aziz, B. S., Jabbar, T. A., and Hameed, R. S. (2023). Hydrodynamic study of a solar chimney power plant for better power production. Therm. Sci. 00, 42. doi:10.2298/TSCI220819042F
Ghalamchi, M., Kasaeian, A., Ghalamchi, M., and Mirzahosseini, A. H. (2016). An experimental study on the thermal performance of a solar chimney with different dimensional parameters. Renew. Energy 91, 477–483. doi:10.1016/j.renene.2016.01.091
Guo, P., Li, T., Xu, B., Xu, X., and Li, J. (2019). Questions and current understanding about solar chimney power plant: a review. Energy Convers. Manag. 182, 21–33. doi:10.1016/j.enconman.2018.12.063
Guo, P., Wang, Y., Meng, Q., and Li, J. (2016). Experimental study on an indoor scale solar chimney setup in an artificial environment simulation laboratory. Appl. Therm. Eng. 107, 818–826. doi:10.1016/j.applthermaleng.2016.07.025
Guo, P., Zhai, Y., Xu, X., and Li, J. (2017). Assessment of levelized cost of electricity for a 10-MW solar chimney power plant in Yinchuan China. Energy Convers. Manag. 152, 176–185. doi:10.1016/j.enconman.2017.09.055
Haaf, W. (1984). Solar chimneys: part ii: preliminary test results from the Manzanares pilot plant. Int. J. Sustain. Energy 2 (2), 141–161. doi:10.1080/01425918408909921
Haaf, W., Friedrich, K., Mayr, G., and Schlaich, J. (1983). Solar chimneys part I: principle and construction of the pilot plant in Manzanares. Int. J. Sol. Energy 2 (1), 3–20. doi:10.1080/01425918308909911
Habibollahzade, A., Fakhari, I., Mohsenian, S., Aberoumand, H., and Taylor, R. A. (2021). Multi-objective grey wolf optimization of solar chimneys based on an improved model incorporating a wind turbine power curve. Energy Convers. Manag. 239, 114231. doi:10.1016/j.enconman.2021.114231
Hennessy, K., Power, S., and Cambers, G. (2011). Climate change in the pacific: scientific assessment and new research. Volume 1. Canberra, Australia: Regional Overview.
Huang, H., Zhang, H., Huang, Y., and Lu, F. (2007). “Simulation calculation on solar chimney power plant system,” in Challenges of power engineering and environment (Hangzhou, China: Spinger), 1158–1161.
Kasaeian, A., Ghalamchi, M., and Ghalamchi, M. (2014). Simulation and optimization of geometric parameters of a solar chimney in Tehran. Energy Convers. Manag. 83, 28–34. doi:10.1016/j.enconman.2014.03.042
Kasaeian, A., Mahmoudi, A. R., Astaraei, F. R., and Hejab, A. (2017). 3D simulation of solar chimney power plant considering turbine blades. Energy Convers. Manag. 147, 55–65. doi:10.1016/j.enconman.2017.05.029
Kebabsa, H., Lounici, M. S., Lebbi, M., and Daimallah, A. (2020). Thermo-hydrodynamic behavior of an innovative solar chimney. Renew. Energy 145, 2074–2090. doi:10.1016/j.renene.2019.07.121
Koonsrisuk, A., Lorente, S., and Bejan, A. (2010). Constructal solar chimney configuration. Int. J. Heat Mass Transf. 53 (1-3), 327–333. doi:10.1016/j.ijheatmasstransfer.2009.09.026
Li, J. Y., Guo, P. H., and Wang, Y. (2012). Effects of collector radius and chimney height on power output of a solar chimney power plant with turbines. Renew. Energy 47, 21–28. doi:10.1016/j.renene.2012.03.018
Li, Y., and Liu, S. (2014). Experimental study on thermal performance of a solar chimney combined with PCM. Appl. Energy 114, 172–178. doi:10.1016/j.apenergy.2013.09.022
Looney, B. (2021). Statistical review of world energy. Bp. 70th Edn, 58. Available at: https://www.bp.com/content/dam/bp/business-sites/en/global/corporate/pdfs/energy-economics/statistical-review/bp-stats-review-2021-full-report.pdf
Mandal, D., Goswami, P., Pradhan, S., Chakraborty, R., Khan, N., and Bose, P. (2021). A Numerical experimentation on fluid flow and heat transfer in a SCPP. IOP Conf. Ser. Mater. Sci. Eng. 1080, 012027. doi:10.1088/1757-899X/1080/1/012027
Mandal, D. K., Biswas, N., Barman, A., Chakraborty, R., and Manna, N. K. (2023). A novel design of absorber surface of solar chimney power plant (SCPP): thermal assessment, exergy and regression analysis. Sustain. Energy Technol. Assessments 56, 103039. doi:10.1016/j.seta.2023.103039
Mandal, D. K., Pradhan, S., Chakraborty, R., Barman, A., and Biswas, N. (2022). Experimental investigation of a solar chimney power plant and its numerical verification of thermo-physical flow parameters for performance enhancement. Sustain. Energy Technol. Assessments 50, 101786. doi:10.1016/j.seta.2021.101786
Mekhail, T., Rekaby, A., Fathy, M., Bassily, M., and Harte, R. (2017). Experimental and theoretical performance of mini solar chimney power plant. J. Clean Energy Technol. 5 (4), 294–298. doi:10.18178/jocet.2017.5.4.386
Ming, T., Liu, W., Pan, Y., and Xu, G. (2008). Numerical analysis of flow and heat transfer characteristics in solar chimney power plants with energy storage layer. Energy Convers. Manag. 49 (10), 2872–2879. doi:10.1016/j.enconman.2008.03.004
Ming, T., Liu, W., and Xu, G. (2006). Analytical and numerical investigation of the solar chimney power plant systems. Int. J. Energy Res. 30 (11), 861–873. doi:10.1002/er.1191
Moffat, R. J. (1988). Describing the uncertainties in experimental results. Exp. Therm. Fluid Sci. 1, 3–17. doi:10.1016/0894-1777(88)90043-x
Motoyama, M., Sugitani, K., Ohya, Y., Karasudani, T., Nagai, T., and Okada, S. (2014). Improving the power generation performance of a solar tower using thermal updraft wind. energy power Eng. 6 (11), 362–370. doi:10.4236/epe.2014.611031
Najm, O. A., and Shaaban, S. (2018). Numerical investigation and optimization of the solar chimney collector performance and power density. Energy Convers. Manag. 168, 150–161. doi:10.1016/j.enconman.2018.04.089
Nia, E. S., and Ghazikhani, M. (2023). Dimensional investigation of solar chimney power plant based on numerical and experimental results. Therm. Sci. Eng. Prog. 37, 101548. doi:10.1016/j.tsep.2022.101548
Padki, M., Sherif, S., and Chan, A. (1989). “Solar chimney for power generation in rural areas,” in Seminar on energy conservation and generation through renewable resources (Ranchi, India: Spinger).
Pasumarthi, N., and Sherif, S. (1998a). Experimental and theoretical performance of a demonstration solar chimney model—Part I: mathematical model development. Int. J. Energy Res. 22 (3), 277–288. doi:10.1002/(sici)1099-114x(19980310)22:3<277::aid-er380>3.0.co;2-r
Pasumarthi, N., and Sherif, S. (1998b). Experimental and theoretical performance of a demonstration solar chimney model—Part II: experimental and theoretical results and economic analysis. Int. J. energy Res. 22 (5), 443–461. doi:10.1002/(sici)1099-114x(199804)22:5<443::aid-er381>3.0.co;2-v
Patel, S. K., Prasad, D., and Ahmed, M. R. (2014). Computational studies on the effect of geometric parameters on the performance of a solar chimney power plant. Energy Convers. Manag. 77, 424–431. doi:10.1016/j.enconman.2013.09.056
Patil, S., Dhoble, A., Sathe, T., and Thawkar, V. (2023). Predicting performance of solar updraught tower using machine learning regression model. Aust. J. Mech. Eng. 2023, 1–19. doi:10.1080/14484846.2023.2179134
Pradhan, S., Chakraborty, R., Mandal, D., Barman, A., and Bose, P. (2021). Design and performance analysis of solar chimney power plant (SCPP): a review. Sustain. Energy Technol. Assessments 47, 101411. doi:10.1016/j.seta.2021.101411
Rhodes, C. J. (2010). Solar energy: principles and possibilities. Sci. Prog. 93 (1), 37–112. doi:10.3184/003685010x12626410325807
Rishak, Q. A., Sultan, H. S., and Jawad, I. N. (2021). Experimental study of the performance of a solar chimney power plant model in Basrah city. J. Mech. Eng. Res. Dev. 44 (7), 340–351.
Schlaich, J. R., Bergermann, R., Schiel, W., and Weinrebe, G. (2005). Design of commercial solar updraft tower systems—utilization of solar induced convective flows for power generation. J. Sol. Energy Eng. 127 (1), 117–124. doi:10.1115/1.1823493
Shirvan, K. M., Mirzakhanlari, S., Mamourian, M., and Abu-Hamdeh, N. (2017). Numerical investigation and sensitivity analysis of effective parameters to obtain potential maximum power output: a case study on Zanjan prototype solar chimney power plant. Energy Convers. Manag. 136, 350–360. doi:10.1016/j.enconman.2016.12.081
Singh, A. P., Kumar, A., and Singh, O. (2021). A novel concept of integrating bell-mouth inlet in converging-diverging solar chimney power plant. Renew. Energy 169, 318–334. doi:10.1016/j.renene.2020.12.120
Sivaram, P. M., Harish, S., Premlatha, M., and Arunagiri, A. (2018). Performance analysis of solar chimney using mathematical and experimental approaches. Int. J. Energy Res. 42 (7), 2373–2385. doi:10.1002/er.4007
Weli, R. B., Atrooshi, S. A., and Schwarze, R. (2021). Investigation of the performance parameters of a sloped collector solar chimney model–An adaptation for the North of Iraq. Renew. Energy 176, 504–519. doi:10.1016/j.renene.2021.05.075
World Bank (2021). Fiji’s current Climatology. Available at: https://climateknowledgeportal.worldbank.org/country/fiji/ (Accessed November 30, 2023).
Xu, G., Ming, T., Pan, Y., Meng, F., and Zhou, C. (2011). Numerical analysis on the performance of solar chimney power plant system. Energy Convers. Manag. 52 (2), 876–883. doi:10.1016/j.enconman.2010.08.014
Zhou, X., Yang, J., Xiao, B., and Hou, G. (2007a). Experimental study of temperature field in a solar chimney power setup. Appl. Therm. Eng. 27 (11-12), 2044–2050. doi:10.1016/j.applthermaleng.2006.12.007
Keywords: solar chimney power plant, solar collector, experimental testing, air turbine, power output
Citation: Prasad R and Ahmed MR (2024) Experimental evaluation of the performance and power output enhancement of a divergent solar chimney power plant by increasing the chimney height. Front. Energy Res. 11:1283818. doi: 10.3389/fenrg.2023.1283818
Received: 27 August 2023; Accepted: 18 December 2023;
Published: 08 January 2024.
Edited by:
Sunday Olayinka Oyedepo, Covenant University, NigeriaReviewed by:
Agnimitra Biswas, National Institute of Technology, Silchar, IndiaCopyright © 2024 Prasad and Ahmed. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: M. Rafiuddin Ahmed, YWhtZWRfckB1c3AuYWMuZmo=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.