- Key Laboratory of Modern Power System Simulation and Control and Renewable Energy Technology, Ministry of Education (Northeast Electric Power University), Jilin, China
The problem of insufficient inertia and frequency security becomes a critical concern in generation maintenance scheduling due to the increasing penetration of renewable energy sources (RESs). To address the issue, this paper presents a stochastic generation maintenance scheduling with inertia-dependent primary frequency regulation constraints. First, inertia-dependent primary frequency regulation constraints consisting of the minimum inertia requirement, frequency nadir, and quasi-steady-state frequency deviation are formulated based on the dynamic frequency characteristic of power systems in response to large disturbances. Then, a two-stage stochastic optimization model for generation maintenance scheduling including frequency security constraints is proposed. Finally, a solution methodology based on Benders decomposition (BD) is used to promote the calculation speed of the proposed model. Numerical simulations demonstrate that the proposed generation maintenance scheduling could address the potential frequency security issues and promote integration of RESs associated with calculation speed.
1 Introduction
To cope with the climate crisis and reduce carbon dioxide emissions, the installed capacity of RESs represented by wind power has developed rapidly. In 2022, the global cumulative wind power capacity reached 906 GW (GWEC, 2023). Accordingly, dispatchable synchronous generations with high levels of rotational inertia are gradually being replaced. System operators face new challenges of insufficient inertia and high uncertainty to enhance frequency security and stability of power systems.
Generation maintenance scheduling (GMS) optimizes a range of time periods for generation maintenance based on the optimal power flow security constraints with the power load and renewable energy generation forecasting. The generator is unable to provide inertia support when it is outage for maintenance; thus, an improper GMS could weaken the power system’s ability to ensure sufficient inertia in response to large disturbances. A large power shortage disturbance interrupted with an improper GMS leads to the frequency security problem, which poses a serious threat to the stability of the power system (Doherty et al., 2010). In addition, renewable energy generation cannot provide inertia support without additional control, and the system inertia will continue to shrink with a sustainable increase in RESs in the future. Therefore, the frequency security problem, together with the corresponding inertia-dependent primary frequency regulation constraints, has become a critical concern in GMS for a low-inertia power system.
To address potential frequency security issues, several studies have incorporated inertia-dependent constraints in economic dispatch (ED) and unit commitment (UC) models. Gu et al. (2018) proposed a synchronous inertia-constrained ED model to meet the minimum synchronous inertia requirement for power systems. Lin et al. (2023) studied the inertia impact on power grid operation costs based on the frequency security-constrained UC model. Daly et al. (2019) proposed a rate of change of frequency (RoCoF)-constrained commitment-and-dispatch scheduling, including demand response. To evaluate the impact of frequency regulation on power system operation scheduling, primary frequency regulation constraints were formulated in a UC model proposed by Restrepo and Galiana (2005). Furthermore, a UC model that incorporates the RoCoF, frequency nadir, and quasi-steady-state frequency deviation constraints was proposed by Trovato et al. (2019). Regarding the computational burden caused by the high nonlinearity of the frequency nadir constraint in a UC model, Ahmadi and Ghasemi (2014) useda piecewise linearization technique to convert the frequency nadir expression into a linear formulation to improve the calculation time. However, the aforementioned papers studied the frequency security problem in power systems based on predicted values of load and renewable energy without uncertainties. To analyze the impact of renewable power uncertainties on scheduling, Pérez-Illanes et al. (2016) and Lagos and Hatziargyriou (2021) proposed a robust UC model with frequency security constraints. Lee and Baldick (2013) presented a stochastic frequency response-constrained ED model. Teng et al. (2016) proposed a stochastic optimization model with uncertainties of wind power and generation outage to optimize the power, reserve, and inertia response of generations. In addition, Ding et al. (2021) proposed a two-stage chance-constrained stochastic UC model incorporating security constraints to optimize the provision of virtual inertia.
Until now, the impact of frequency security on ED and UC problems has been thoroughly studied, but few papers consider the frequency security issue in GMS. Studies on security-constrained GMS mainly focus on system reliability and power flow security indicators (Marwali and Shahidehpour, 1998; Li and Korczynski, 2009). Wang et al. (2016a) and Wang et al. (2016b) proposed an integrated generation and transmission maintenance scheduling approach with N-1 contingencies. Then, Wang et al. (2016c) proposed a coordination mechanism for GMS to equalize the reliability indicator across the time horizon. Fu et al. (2007) proposed a short-term coordinated generation and transmission maintenance optimization model considering DC network constraints and achieved a compromise between the operational cost and power flow security. To analyze the impact of uncertainty on GMS, Wu et al. (2010) proposed a joint optimization model for generation and transmission maintenance scheduling with uncertainties. However, the impact of the inertia-dependent primary frequency regulation constraints on GMS has not been explicitly formulated, and hence, the frequency security problem is prone to arise in low-inertia systems with traditional GMS.
In this context, this paper proposes a mixed-integer linear programming (MILP) formulation for two-stage stochastic GMS with inertia-dependent primary frequency regulation constraints to enhance the frequency response security against large power shortage disturbances. Several methods, such as heuristic algorithms (Pellegrini et al., 2015; Shi et al., 2017) and mathematical programming solvers (Li et al., 2019; Hua et al., 2023), are widely used to solve the MILP problem. However, heuristic algorithms focus on improving computational efficiency at the expense of the optimality of the solution, and the solution is usually suboptimal. The computational efficiency of mathematical programming solvers such as CPLEX and GUROBI decreases rapidly as the size of the MILP problem increases. To overcome the shortcomings of the aforementioned methods, the BD method is used in this paper. The main contributions of this paper are summarized as follows:
1) A two-stage stochastic GMS optimization model with frequency security constraints, namely, RoCoF, frequency nadir, and quasi-steady-state frequency deviation, is proposed to ensure frequency security in the GMS horizon.
2) The proposed model is a multi-scenario, large-scale MILP complex problem. To diminish the calculation time, we use the BD method to divide the proposed problem into a master problem and several subproblems. In the master problem, binary decision variables associated with generation maintenance and UC are determined considering the RoCoF and frequency nadir constraints. The subproblems check the feasibility and optimality of the solution of the master problem based on the quasi-steady-state frequency-constrained ED.
The remainder of the paper is organized as follows: Section 2 describes inertia-dependent primary frequency regulation constraints. Section 3 formulates a two-stage stochastic GMS model incorporating the frequency security constraints. Section 4 provides the detailed solution methodology of the proposed model. Section 5 uses different test systems to analyze the proposed model and verifies the validity of the model. Section 6 outlines the conclusion.
2 Formulation of inertia-dependent primary frequency regulation constraints
According to the dynamic frequency characteristic of power systems in response to large disturbances (Lin et al., 2023), it can be found that the system frequency maintains a nominal value f0 under the steady-state condition, in which the generation and load are balanced. However, when a large power shortage disturbance occurs, the system frequency will experience a transient process of changing from the nominal frequency f0 to a new quasi-steady-state frequency f0-fss with inertia response and primary frequency regulation. At the beginning of the disturbance, sufficient inertia should be ensured to resist rapid frequency drop with the inertia response. Subsequently, the frequency nadir and quasi-steady-state frequency deviation limits in the dynamic frequency process should be maintained at an acceptable threshold with primary frequency regulation.
Regarding transient frequency, three key indicators, namely, RoCoF (fRoCoFM), frequency nadir (fnadir), and quasi-steady-state frequency deviation (∆fss), are often used to evaluate the frequency security of power systems.
2.1 RoCoF
In the inertia response stage immediately after the disturbance occurs, the generator governor lacks time for regulation, and the primary frequency regulation of the generator does not work. Therefore, a large RoCoF depending on the system inertia arises, as shown in Eq. 1.
Here, the disturbance ∆Pctg(t) is a normalized value.
The system inertia is provided by the synchronous generators, and its normalized value is shown in Eq. 2.
Here, SB is the base power of the synchronous generators, i.e., a sum of nominal powers of synchronous generators connected to the power system.
To resist the rapid droop in transient frequency during the initial stage of disturbance, fRoCoFM should be limited to an acceptable threshold as shown in (3).
Substituting (1) (2) into (3) and conducting a set of mathematical transformations yield an equivalent minimum inertia requirement constraint to the RoCoF as
2.2 Frequency nadir
The transient frequency security from the initial inertia response period to a new quasi-steady-state frequency period should also be considered to ensure that the frequency nadir of the system is greater than the trigger value of under-frequency load shedding.
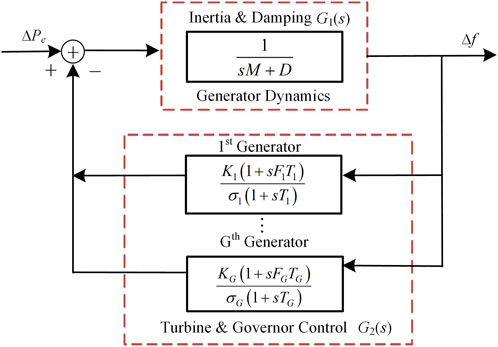
After a large power shortage disturbance, the system frequency begins to decline at a certain decay rate, and a simplified uniform frequency response model that satisfies the accuracy requirements can be established according to the synchronous generators’ swing equation (Markovic et al., 2019). The frequency response model is separated into system inertia response model G1(s) and primary frequency regulation response model G2(s), as shown in Figure 1. The input of the frequency response mode is the step disturbance ∆Pe, and the output is frequency deviation ∆f. In the model, M and D represent the normalized inertia constant and damping constant corresponding to the synchronous generators, respectively.
From Figure 1, the frequency response transfer function G(s) of a general-order system can be derived as
Since the frequency nadir of the power system is the least sensitive to the governor time constant Ti within its allowable range, it is reasonable to assume that the governor time constants of all turbines are approximated by the same value TR (Markovic et al., 2019). The transient frequency deviation ∆f can be obtained by simplifying (5) with the assumption as follows:
In Formula 6, the natural frequency wf and damping ratio ξ are calculated as follows:
where F and A are the expressions consisting of the parameters Ki, Fi, and σi; more details on the expressions of F and A can be found in Markovic et al. (2019).
Assuming a step disturbance in the electrical power ∆Pe(s) = −∆Pctg(t)/s, the system frequency deviation ∆f(t) in time-domain can be obtained as shown in (8) by the inverse Laplace transform of Eq. 6, where tnadir corresponds to d∆f(t)/dt = 0, and the maximum frequency deviation |∆fnadir| gives rise at the time instant t = tnadir as shown in (9).
2.3 Quasi-steady-state frequency deviation
When the system frequency reaches the quasi-steady-state after primary frequency regulation, the system frequency will maintain a stable value without secondary frequency regulation. The mathematical formula of quasi-steady-state frequency as shown in (10) can be derived according to (6) under the condition s = 0.
3 Stochastic GMS model considering inertia-dependent primary frequency regulation
The stochastic GMS with inertia-dependent primary frequency regulation constraints can be formulated as a two-stage optimization problem, as shown in Eq. 11. In the first stage, a GMS coupled with UC considering the minimum inertia and frequency nadir constraints is formulated to decide the generation maintenance schedules and unit status. The solutions of the given first stage need to be used by the second stage, a stochastic ED problem considering the quasi-steady-state frequency deviation constraints is modeled, and the decision variables are the generation output and wind power curtailment for each hour under different scenarios.
where F1 is the objective function at the first stage and represents the costs related to 0-1 decision variables of generation maintenance schedules and unit status against all representative scenarios; F2 is the objective function at the second stage and represents expected costs of generation and wind curtailment; and C1 and C2 are, respectively, the sets constrained by the first-stage and second-stage constraints.
3.1 Objective function
The specific mathematical expression of the objective function in Eq. 11 is stated as
3.2 First-stage constraints
3.2.1 Generation maintenance constraints
Here, constraint (13) describes the generator maintenance window limits, which indicates that the generation maintenance starts at time ei and ends at time li, and the generator maintenance needs to be scheduled within the windows. Constraints (14)–(15) present the relationship among Xi,t, ui,t, and vi,t; Constraints (16)–(17) ensure that the generator maintenance must be completed successively within the predefined duration. Constraint (18) represents generator maintenance resource and crew availability.
3.2.2 Unit commitment constraints
Here, constraints (19) and (20) describe the minimum start-up and shut-down time limits of generating units. Constraint (21) represents the start-up cost limitations for generator i at time t.
3.2.3 Minimum inertia requirement constraint
3.2.4 Coupling constraint between generation maintenance and unit status
where constraint (23) indicates that the generator cannot produce electricity when it is on maintenance (Xi,t = 0). Combining (22), it can be concluded that the generator on maintenance cannot provide inertia support to the system, and GMS is coupled with the inertia level of the system.
3.2.5 Frequency nadir constraints
The frequency nadir constraint shown in Formula 8 is a highly nonlinear function related to (A, F, M, and D) and will cause a significant calculation burden on the optimization of the model without any manipulation. To address this problem, we first obtain all possible values of A, F, M, and D at each time period in Eqs 25–28 by enumerating all states of UC in power systems (Matthieu et al., 2020). We then substitute these values into (8) to obtain the lower boundary values of A, F, M, and D at each time period that satisfy the requirement of the frequency nadir. Therefore, the frequency nadir constraint can be equally substituted with the lower boundary values of A, F, M, and D as shown in (29). It has been illustrated to be more effective and accurate to use (29) to represent the frequency nadir constraint compared to the piecewise linearization by Matthieu et al. (2020).
where constraints (25)–(28) are the expressions for the extracted boundary variables and constraint (29) represents their respective lower limits at each time period.
3.3 Second-stage constraints
The second stage is to solve the quasi-steady-state frequency-constrained ED problem against various uncertain wind power scenarios. The constraints of the second stage depend on the parameters (Xi,t and Ii,t) given in the first stage, and the feasible operation region constrained by these constraints exists for any wind power scenario only if Xi,t and Ii,t determined in the first stage are feasible. The second-stage constraints are as follows.
3.3.1 Active power balance constraint
3.3.2 Generator operation constraints
Here, constraint (31) ensures that the generation output is within the generation limits. Constraint (32) describes the ramping limits of each generator. Constraint (33) ensures that the primary frequency reserve (PFR) is imposed to not exceed the capacity limits. Furthermore, the corresponding dual variables of constraints (31) and (33) are
3.3.3 Wind power curtailment constraint
Constraint (34) ensures that the wind power curtailment in each wind farm cannot exceed the predicted value of each wind power scenario.
3.3.4 Transmission capacity limit constraint
Constraint (35) ensures that the transmission line power flow is within its capacity.
3.3.5 Quasi-steady-state frequency deviation constraints
Conducting a set of mathematical transformations for (36) yields
where the deployed frequency regulation reserve is limited by the maximum quasi-steady-state frequency deviation, as shown in Eq. 38. λi,t,s and αi,t,s are the corresponding dual variables of constraints (37) and (38), respectively.
4 Solution methodology
4.1 Formulation of subproblems and coordination strategies
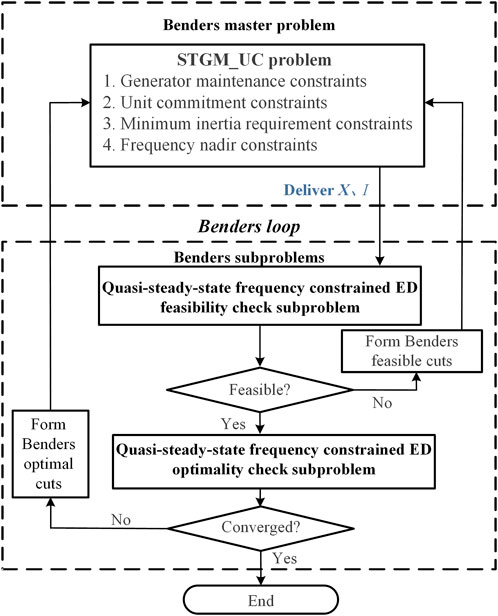
The proposed stochastic optimization model in Section 3 is a large-scale mixed-integer problem that is difficult to solve efficiently. Therefore, this paper divides the proposed model into a master problem and several subproblems based on the BD method. The master problem is to optimize short-term generation maintenance and UC (STGM_UC) considering minimum inertia requirement and frequency nadir constraints. The subproblems include quasi-steady-state frequency-constrained ED feasible and optimal check subproblems. The master problem and subproblems are coordinated through Benders feasible or optimal cuts. The decomposition and coordination framework of the proposed model is shown in Figure 2.
4.1.1 STGM_UC master problem
The master problem mainly considers the generation maintenance and UC constraints. To accelerate the calculation speed of the proposed model, we extract the constraints at work at the second stage into Benders cuts and remove the relaxed constraints instead. Thus, the master problem is formulated and is composed of constraints (13)–(29) and the supplementary formulas (39)–(41).
where ΩFSP and ΩOSP are the sets of Benders feasible and optimal cuts, respectively.
4.1.2 Quasi-steady-state frequency-constrained ED subproblems
Given the generation maintenance and UC solutions of the master problem, the quasi-steady-state frequency-constrained ED subproblems optimize the traditional generator power output and wind power curtailment of each scenario and are used to check the feasibility and optimality of GMS solved by the master problem. If the solution is not feasible or optimal, corresponding Benders cuts are formed and added to the master problem, thereby driving the solution of the master problem gradually toward the optimal solution. Therefore, it is necessary to construct the quasi-steady-state frequency-constrained ED feasibility and optimality check subproblems.
When the master problem gives a trial solution {I*i,t, X*i,t}, for any uncertain scenario s, slack variables are introduced to construct the quasi-steady-state frequency-constrained ED feasibility check subproblem as shown in (42).
where ηFSP(I*i,t, X*i,t) is the optimal objective value of the feasibility check subproblem. S1t,s and S2t,s are introduced non-negative slack variables in scenario s.
If ηFSP(I*i,t, X*i,t) > 0 for a certain scenario, which indicates that the subproblem is infeasible, then a Benders feasible cut, as shown in Eq. 43, needs to be formed and added to the master problem. If ηFSP(I*i,t, X*i,t) ≤ 0 for all scenarios, the subproblem is feasible and continues to check the solution optimality of the master problem.
The model of quasi-steady-state frequency-constrained ED optimality check subproblem is formulated as follows:
After solving the optimality check subproblem, the optimality criteria are given as follows:
where εOSP is a positive number close to zero. ηOSP* is the value of ηOSP in the last iterative solution of the master problem. If the optimality criteria cannot be satisfied, then a Benders optimal cut is constructed, as shown in Eq. 46, and added to the master problem.
4.2 Decomposition and coordination procedure
Figure 2 shows the solution procedure based on the decomposition and coordination strategy, which is summarized as follows:
Step 1:. Separate the original problem into a master problem and feasibility and optimality check subproblems based on Benders decomposition.
Step 2:. Solve the master problem to get the hourly generator maintenance schedule X*i,t and unit status I*i,t, and deliver I*i,t and ηOSP* to the subproblems.
Step 3:. Solve the quasi-steady-state frequency-constrained ED feasibility check subproblems. Once a violation that ηFSP(I* i,t, X*i,t) > 0 is detected in the subproblem, the corresponding Benders feasible cuts as shown in (43) should be generated and added into the master problem; then return to step 2; otherwise, go to step 4.
Step 4:. Solve the quasi-steady-state frequency-constrained ED optimality check subproblem. If (45) is not satisfied, the Benders optimal cut as shown in (46) is generated and added into the master problem; then return to step 2; otherwise, stop the iterative process and output the optimal generator maintenance schedule.
5 Case studies
In this section, two case studies including a six-bus system and the IEEE 118-bus system are considered to demonstrate the performance of the proposed model and approach.
5.1 Six-bus system
The six-bus test system consists of three synchronous generators, seven transmission lines, two wind farms, and three loads, and the test data of the system are slightly modified from Kargarian and Fu (2014). The generator operating parameters are shown in Table 1. Table 2 shows the generator maintenance data for the six-bus system. The parameters related to frequency response are set as follows: fRoCoFmax = 0.24 Hz/s (Ge et al., 2021), TR = 8s (Cai et al., 2021), ∆fnadir = 0.8 Hz, and ∆f lim ss = 0.2 Hz (Yang et al., 2022). The Monte Carlo sampling method is applied to generate 1,000 stochastic wind power scenarios for wind farms W1 and W2 according to wind power uncertain data in Zhou et al. (2015). The scenario reduction method is used to reduce the scenarios to five to trade off computational efficiency and accuracy. Figure 3 shows the hourly expected wind and load power profile. The power shortage disturbance is assumed to be a sudden 8% load increase and a 10% wind farm output decrease.
In order to show the effectiveness of the proposed approach, we analyze the following four cases for a 168-h period.
Case 1:. Without inertia-dependent primary frequency regulation constraints.
Case 2:. With the minimum inertia demand constraint.
Case 3:. With the minimum inertia demand and the frequency nadir constraints.
Case 4:. The proposed model with the minimum inertia requirement, frequency nadir, and quasi-steady-state frequency deviation constraints.
5.1.1 Analysis of generation maintenance schedule and system frequency stability
The schedules of generation maintenance and UC corresponding to Cases 1–4 are shown in Figures 4A–D, respectively. Figure 5–Figure 7 show the hourly system inertia, frequency nadir, and quasi-steady-state frequency deviation in the four cases. The generation maintenance schedule and frequency stability for the four cases are analyzed as follows.
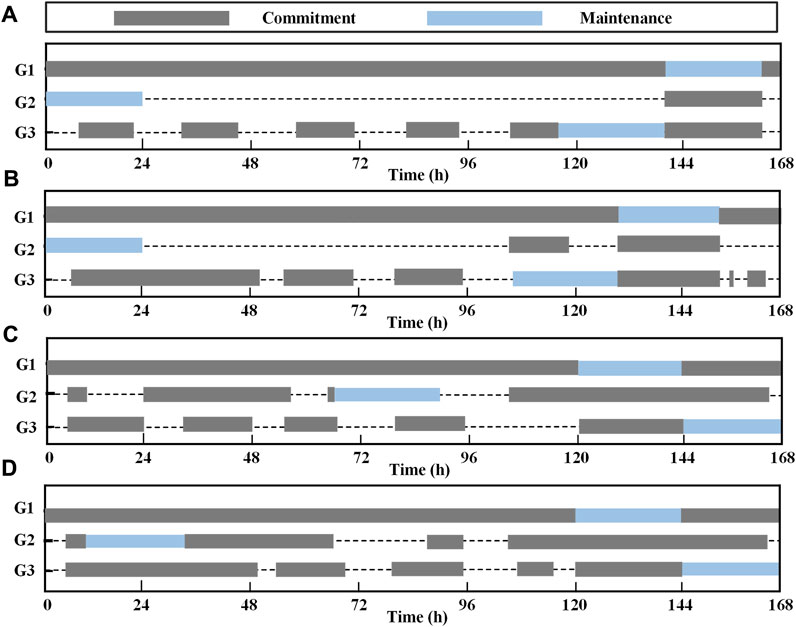
FIGURE 4. Schedules of generator maintenance and UC in four cases. (A) Case 1, (B) Case 2, (C) Case 3, and (D) Case 4.
The generator maintenance schedules are not coordinated with the frequency stability in Case 1. It can be found from Figure 4A that the maintenance of units G1 and G3 is scheduled at the minimum net load hours for maintaining the economy of the power system operation, and the more expensive unit G2 has to be committed to ensure the generation–demand balance during hours 141–164 when G1 is on maintenance. To minimize the penalty cost of the generator maintenance schedule deviating from the expected maintenance hours, G2 is scheduled for maintenance at hours 1–24. However, without considering inertia-dependent primary frequency regulation, the minimum inertia requirement is not satisfied at hours 7–8, 21–23, 25–27, 29–31, 45–50, 55, 95, 104, and 117–118 of low net load when only G1 is committed to provide system inertia. In addition, insufficient inertia also arises at hours 153–164 when G1 is on maintenance, as illustrated in Figure 5. To address the insufficient inertia issue, Case 2 schedules the unit G3 commitment at hours 7–8, 21–31, 45–50, 55, and 95; units G1 and G3 are committed to be online during hours 153–164, and the maintenance of G1 and G3 is scheduled at hours 129–152 and 105–128 in advance, respectively. To satisfy the system inertia requirement, unit G2 is also committed during hours 95–118 and 105–128.
As shown in Figure 6, the frequency nadir in Case 2 is below the minimum allowed frequency of 49.2 Hz at hours 5–9, 25–56, 67–68, and 148–166. The reason is that, on the one hand, fewer units are committed to enhance the frequency stability for hours with low load and high wind power output, and on the other hand, the power shortage disturbances at hours with high load and wind power are too large to resist frequency drop. To address the frequency nadir issue during these hours, unit G2 is committed to be online additionally in Case 3, which delays maintenance of G2 to hours 69–92 in proportion. As unit G1 has larger boundary values of A, F, M, and D and better performance on primary frequency regulation, units G1 and G2 are committed to be online in Case 3 to resist frequency drop during hours 148–166. Consequently, the maintenance of unit G1 is scheduled at hours 121–144 with minor disturbances, and the maintenance of unit G3 is scheduled at hours 145–168 of low load.
As shown in Figure 7, the quasi-steady-state frequency deviation in Case 3 is greater than 0.2 Hz at hours 58–66, 88–94, and 107–115, during which only two units are committed to be online, and the primary frequency regulation reserve is insufficient in response to the large power shortage disturbances. Specifically, at hours 58–66 with a minimum disturbance of 24.83 MW, the maximum frequency regulation reserve provided by units G1 and G3 is 24 MW, which is lower than the requirement, resulting in the quasi-steady-state frequency deviation of 0.216 Hz. To address this problem, Case 4 schedules unit G2 to be online additionally during hours 58–66 and 88–94 and schedules unit G3 to be committed additionally during hours 107–115 to ensure the quasi-steady-state frequency within the predefined threshold. Accordingly, the maintenance of unit G2 is shifted to hours 9–32, and unit G3 needs to be committed during hours 25–32 to enhance the quasi-steady-state frequency.
5.1.2 Analysis of the system economy
To illustrate the economic performance of the proposed scheduling model in this paper to cope with the frequency security problem, we fixed the maintenance status as the maintenance schedules of Cases 1–4 and then optimized the unit commitment, generation output, and wind power curtailment based on the proposed model in this paper. The total costs of the four cases are summarized in Table 3.
Case 1:. In this case, the inertia-dependent primary frequency regulation constraints are not considered in the given generator maintenance schedule, which would lead to frequency security issues. To address this problem, more units need to be committed additionally at frequency security violation hours. In addition, units G1 and G2 cannot be committed to provide frequency support during maintenance hours 5–9 and 148–164, respectively, and hence, wind power curtailment has to increase, and the power out of more expensive G3 increases to balance the load. In this case, the total cost is increased to $538,822 including the generator maintenance cost of $9,614 and operation cost of $529,208.
Case 2:. The given maintenance schedule of this case coordinates the system economy and the minimum inertia requirement, and it can reduce unnecessary unit commitment to meet frequency security requirements compared to Case 1. In addition, as there are no standby generators to be committed online to provide frequency support during 5–9, 107–115, and 148–152 hours, frequency nadir violation and wind power curtailment still occur. However, due to the earlier maintenance of unit G1 compared to Case 1, G1 can be committed at hours 153–164; therefore, the wind power curtailment and the power output of more expensive units G2 and G3 decrease. The total cost in this case is $524,819, which includes the generator maintenance cost of $9,374 and operation cost of $515,445. The total cost is reduced by $14,003 compared to case 1.
Case 3:. The maintenance schedule of this case considers the system inertia and frequency nadir requirement; therefore, we only need to adjust the UC schedule to meet the quasi-steady-state frequency requirement. However, wind power curtailment still occurs because unit G2 is on maintenance and cannot perform primary frequency regulation during hours 69–92. Moreover, both units G1 and G3 need to increase the power generation to meet the balance between the generation and demand during hours 88–94. Compared with Case 2, the wind power curtailment and the increased generation cost to meet the frequency security are decreased by optimizing the UC schedule. The total cost in this case is decreased to $517,247, which includes the generator maintenance cost of $10,354 and operation cost of $506,893.
Case 4:. In this case, the generator maintenance schedule coordinates the system frequency stability and economy. Compared to case 3, the maintenance of unit G2 is moved forward to hours 9–32, and the total cost is decreased to $514,342 including the generator maintenance cost of $9,754 and operation cost of $504,588.
5.2 IEEE 118-bus system
In this section, the IEEE 118-bus system is used to demonstrate the effectiveness of the proposed model in large-scale test systems. The system is composed of 54 synchronous generators, 186 transmission lines, and 91 loads. The peak load is 5,470 MW, and the load profile is the same as that in Figure 3. The test data are given at http://motor.ece.iit.edu/data, and the generator maintenance data are listed in Table 4. The frequency requirements are set as follows: fRoCoFmax = 0.5 Hz/s, ∆fnadir = 0.8 Hz, and ∆f lim ss = 0.2 Hz (Ding et al., 2021).
The generator maintenance schedule of the four cases is shown in Table 5. Table 6 shows the comparison of the total cost given the maintenance schedule in the four cases. Figure 8 compares the deviation of the worst system frequency indicators in the horizon with their respective thresholds in the four cases. A positive percentage in the frequency indicator deviation indicates that the threshold has been exceeded, while a negative percentage indicates that the frequency stability requirements are satisfied. The results shown in Figure 8 indicate that the proposed model can meet all frequency security constraints.
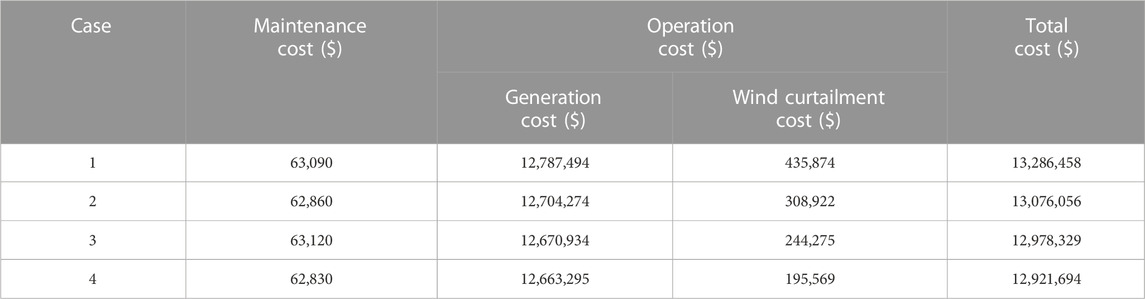
Table 6 indicates that the maintenance schedule of Case 1 will result in a high wind curtailment cost of $435,874 and a generation cost of $12,787,494. However, the system operation cost will be significantly decreased by considering frequency security constraints comprehensively. The maintenance schedule of Case 2 decreases the wind curtailment cost and generation cost by $126,952 and $83,220, respectively, compared to Case 1, and the maintenance schedule of Case 3 decreases by $64,647 and $33,340, respectively, compared to Case 2. However, compared to Case 3, the wind curtailment cost and generation cost of the maintenance schedule in Case 4 decided based on the proposed model can be further decreased by $48,706 and $7,639, respectively, which indicates that the proposed maintenance schedule has a better performance to maintain the system economic operation while ensuring frequency stability.
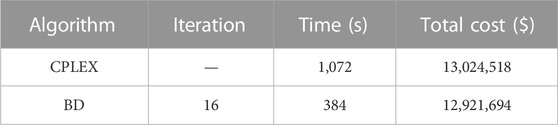
Table 7 compares the calculation time and iteration numbers of using the proposed BD algorithm with directly using CPLEX to centrally solve the model. The results show that the BD algorithm, which separates the complex original problem into several smaller subproblems and eliminates a large number of inactive constraints in the master problem, has a better computing performance, with a 64% reduction in solution time compared to CPLEX. Using CPLEX as a benchmark algorithm, the objective value of the BD algorithm is nearly the same as that of CPLEX, and the relative error is smaller than 1%, which verifies the accuracy of the proposed algorithm in this paper.
6 Conclusion
This paper proposes a two-stage stochastic optimization model for generation maintenance considering the inertia-dependent primary frequency regulation constraints against wind power uncertainty. Case studies on the six-bus system and IEEE 118-bus system demonstrate good performance of the proposed model and method, and the conclusions are as follows.
1) It is necessary to consider the impact of inertia-dependent primary frequency regulation constraints on generation maintenance scheduling in the high-proportion and low-inertia renewable energy power system.
2) The optimized generation maintenance schedule based on the proposed model in this paper not only improves the system inertia response and ensures the system frequency nadir and quasi-steady-state frequency deviation indicators within the safety threshold but also exhibits a good economic performance.
3) The BD method is used to separate the original problem into a master problem and several feasibility and optimality check subproblems, and the optimal solution is obtained by Benders cuts to coordinate the master problem and subproblems. Compared to the integrated solution method (CPLEX), the BD method not only ensures the solution accuracy but also significantly reduces the calculation time.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
BL: project administration, writing–review and editing, and supervision. JW: writing–original draft, conceptualization, formal analysis, methodology, and software. SL: investigation, visualization, and writing–original draft.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Jilin Province Science and Technology Development Project (20210508031RQ).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Ahmadi, H., and Ghasemi, H. (2014). Security-constrained unit commitment with linearized system frequency limit constraints. IEEE Trans. Power Syst. 29 (4), 1536–1545. doi:10.1109/TPWRS.2014.2297997
Cai, G., Zhong, C., Wu, G., Yang, D., and Wang, B. (2021). Unit commitment strategy of power system considering overspeed load reduction and inertia control of wind turbine. Automation Electr. Power Syst. 45 (16), 134–142. doi:10.7500/AEPS20200907005
Daly, P., Qazi, H. W., and Flynn, D. (2019). RoCoF-constrained scheduling incorporating non-Synchronous residential demand response. IEEE Trans. Power Syst. 34 (5), 3372–3383. doi:10.1109/TPWRS.2019.2903784
Ding, T., Zeng, Z., Qu, M., Catalão, J. P. S., and Shahidehpour, M. (2021). Two-stage chance-constrained stochastic thermal unit commitment for optimal provision of virtual inertia in wind-storage systems. IEEE Trans. Power Syst. 36 (4), 3520–3530. doi:10.1109/TPWRS.2021.3051523
Doherty, R., Mullane, A., Nolan, G., Burke, D., Bryson, A., and O’Malley, M. (2010). An assessment of the impact of wind generation on system frequency control. IEEE Trans. Power Syst. 25 (1), 452–460. doi:10.1109/TPWRS.2009.2030348
Fu, Y., Shahidehpour, M., and Li, Z. (2007). Security-constrained optimal coordination of generation and transmission maintenance outage scheduling. IEEE Trans. Power Syst. 22 (3), 1302–1313. doi:10.1109/TPWRS.2007.901673
Ge, X., Liu, Y., Fu, Y., and Jia, F. (2021). Distributed robust unit commitment considering the whole process of inertia support and frequency regulations. Proc. CSEE 41 (2), 4043–4057. doi:10.13334/j.0258-8013.pcsee.200974
Gu, H., Yan, R., and Saha, T. K. (2018). Minimum synchronous inertia requirement of renewable power systems. IEEE Trans. Power Syst. 33 (2), 1533–1543. doi:10.1109/TPWRS.2017.2720621
GWEC (2023). Website global wind energy council (GWEC). Available at: https://gwec.net/globalwindreport2023/.
Hua, H., Liu, T., Liu, X., He, C., Wu, L., Nan, L., et al. (2023). Optimal allocation and sizing of fault current limiters considering transmission switching with an explicit short circuit current formulation. IEEE Trans. Power Syst. 38 (2), 1322–1335. doi:10.1109/TPWRS.2022.3174870
Kargarian, A., and Fu, Y. (2014). System of systems based security-constrained unit commitment incorporating active distribution grids. IEEE Trans. Power Syst. 29 (5), 2489–2498. doi:10.1109/TPWRS.2014.2307863
Lagos, D. T., and Hatziargyriou, N. D. (2021). Data-driven frequency dynamic unit commitment for island systems with high RES penetration. IEEE Trans. Power Syst. 36 (5), 4699–4711. doi:10.1109/TPWRS.2021.3060891
Lee, Y., and Baldick, R. (2013). A frequency-constrained stochastic economic dispatch model. IEEE Trans. Power Syst. 28 (3), 2301–2312. doi:10.1109/TPWRS.2012.2236108
Li, W., and Korczynski, J. (2009). A reliability-based approach to transmission maintenance planning and its application in BC hydro system. IEEE Trans. Power Deliv. 19 (1), 303–308. doi:10.1109/TPWRD.2003.820183
Li, Y., Yang, Z., Zhao, D., and Tian, W. (2019). Optimal scheduling of an isolated microgrid with battery storage considering load and renewable generation uncertainties. IEEE Trans. Industrial Electron. 66 (2), 1565–1575. doi:10.1109/TIE.2018.2840498
Lin, Z., Wang, H., Wang, Y., Zhang, H., Li, W., and Li, R. (2023). Evaluation of the impact of inertia on system operation cost. Front. Energy Res. 8. doi:10.3389/fenrg.2023.1118349
Markovic, U., Chu, Z., Aristidou, P., and Hug, G. (2019). LQR-based adaptive virtual synchronous machine for power systems with high inverter penetration. IEEE Trans. Sustain. Energy 10 (3), 1501–1512. doi:10.1109/TSTE.2018.2887147
Marwali, M. L. C., and Shahidehpour, S. M. (1998). Integrated generation and transmission maintenance scheduling with network constraints. IEEE Trans. Power Syst. 13 (3), 1063–1068. doi:10.1109/59.709100
Matthieu, P., Delikaraoglou, S., Vrettos, E., Aristidou, P., and Hug, G. (2020). Stochastic unit commitment in low-inertia grids. IEEE Trans. Power Syst. 35 (5), 3448–3458. doi:10.1109/TPWRS.2020.2987076
Pellegrini, P., Marlière, G., Pesenti, R., and Rodriguez, J. (2015). RECIFE-MILP: an effective MILP-based heuristic for the real-time railway traffic management problem. IEEE Trans. Intelligent Transp. Syst. 16 (5), 2609–2619. doi:10.1109/TITS.2015.2414294
Pérez-Illanes, F., Álvarez-Miranda, E., Rahmann, C., and Campos-Valdés, C. (2016). Robust unit commitment including frequency stability constraints. Energies 9 (11), 957–972. doi:10.3390/en9110957
Restrepo, J. F., and Galiana, F. D. (2005). Unit commitment with primary frequency regulation constraints. IEEE Trans. Power Syst. 20 (4), 1836–1842. doi:10.1109/TPWRS.2005.857011
Shi, Z., Wang, L., Liu, P., and Shi, L. (2017). Minimizing completion time for order scheduling: formulation and heuristic algorithm. IEEE Trans. Automation Sci. Eng. 14 (4), 1558–1569. doi:10.1109/TASE.2015.2456131
Teng, F., Trovato, V., and Strbac, G. (2016). Stochastic scheduling with inertia-dependent fast frequency response requirements. IEEE Trans. Power Syst. 31 (2), 1557–1566. doi:10.1109/TPWRS.2015.2434837
Trovato, V., Bialecki, A., and Dallagi, A. (2019). Unit commitment with inertia-dependent and multispeed allocation of frequency response services. IEEE Trans. Power Syst. 34 (2), 1537–1548. doi:10.1109/TPWRS.2018.2870493
Wang, Y., Daniel, S. K., Zhong, H., Xia, Q., and Kang, C. (2016c). Coordination of generation maintenance scheduling in electricity markets. IEEE Trans. Power Syst. 31 (6), 4565–4574. doi:10.1109/TPWRS.2016.2514527
Wang, Y., Zhong, H., Xia, Q., Kang, C., Wang, T., and Cao, X. (2016b). Coordination of generation maintenance scheduling and long-term SCUC with energy constraints and N-1 contingencies. IET Gener. Transmission&Distribution 10 (2), 325–333. doi:10.1049/iet-gtd.2015.0183
Wang, Y., Zhong, H., Xia, Q., Kirschen, D. S., and Kang, C. (2016a). An approach for integrated generation and transmission maintenance scheduling considering N-1 contingencies. IEEE Trans. Power Syst. 31 (3), 2225–2233. doi:10.1109/TPWRS.2015.2453115
Wu, L., Shahidehpour, M., and Fu, Y. (2010). Security-constrained generation and transmission outage scheduling with uncertainties. IEEE Trans. Power Syst. 25 (3), 1647–1685. doi:10.1109/TPWRS.2010.2040124
Yang, L., Xu, Y., Zhou, Z., and Sun, H. (2022). Distributionally robust frequency constrained scheduling for an integrated electricity-gas system. IEEE Trans. Smart Grid 13 (4), 2730–2743. doi:10.1109/TSG.2022.3158942
Zhou, M., Xia, S., Li, Y., and Li, G. (2015). A joint optimization approach on monthly unit commitment and maintenance scheduling for wind power integrated power systems. Proc. CSEE 35 (7), 1586–1595. doi:10.13334/j.0258-8013.pcsee.2015.07.005
Nomenclature
Keywords: generation maintenance, unit commitment, minimum inertia requirement, primary frequency regulation, stochastic optimization
Citation: Li B, Wang J and Li S (2023) Stochastic generation maintenance scheduling with inertia-dependent primary frequency regulation constraints. Front. Energy Res. 11:1280678. doi: 10.3389/fenrg.2023.1280678
Received: 21 August 2023; Accepted: 04 October 2023;
Published: 19 October 2023.
Edited by:
Rakibuzzaman Shah, Federation University Australia, AustraliaReviewed by:
Xiaoming Liu, Xi’an Jiao Tong University, ChinaArshad Nawaz, Shanghai Jiao Tong University, China
Copyright © 2023 Li, Wang and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Benxin Li, YnhsaUBuZWVwdS5lZHUuY24=
 Benxin Li*
Benxin Li* Jiahui Wang
Jiahui Wang Shuguang Li
Shuguang Li