- 1Electrical Power Engineering, Egypt-Japan University of Science and Technology (E-JUST), New Borg El-Arab City, Alexandria, Egypt
- 2Electrical Engineering Department, Faculty of Engineering, Aswan University, Aswan, Egypt
- 3Electrical Engineering Department, Faculty of Engineering, Mansoura University, El-Mansoura, Egypt
- 4Electrical Power and Renewable Energy, University of Doha for Science and Technology, Doha, Qatar
- 5Faculty of Information Science and Electrical Engineering, Kyushu University, Fukuoka, Japan
A centralized secondary control is utilized in a DC islanded microgrid to fine-tune voltage levels following the implementation of droop control. This is done to avoid conflicts between current allocation and voltage adjustments. However, because it introduces a single point of failure, a distributed secondary control is preferred. This paper introduces a consensus-based secondary distributed control approach to restore critical bus voltages to their nominal values and properly distribute current among converters. The critical bus takes the lead in voltage adjustments, with only connected energy resources contributing to regulation. The microgrid is represented as an undirected graph to facilitate consensus building. Two adjustment terms, δv and δi, are generated to assist in returning voltage to its nominal level and correctly allocating current among energy resources. To enhance consistency and improve controller performance compared to those reported in existing literature, all buses are connected to a leader node. In the event of the failure of all converters except one, voltage can still be effectively restored. MATLAB-Simulink simulations are conducted on two medium-voltage DC (MVDC) microgrids to validate the efficiency of the proposed control method. The results confirmed that the proposed control method can effectively maintain voltage stability and enhance the precise distribution of current among agents by 8%.
1 Introduction
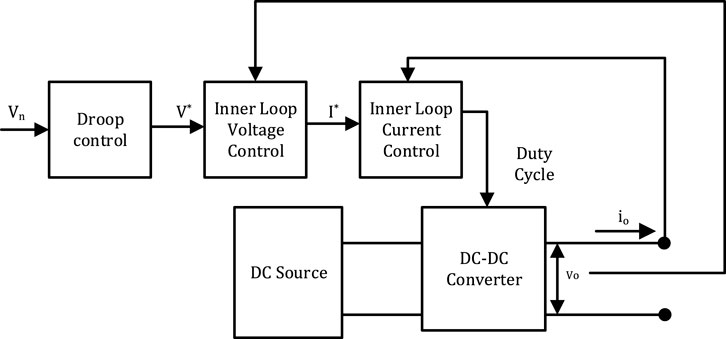
Certainly, microgrids (Meenual and Usapein, 2021; Abdel-Rahim et al., 2022) have gained considerable interest in the last few decades due to the flexible integration of distributed energy resources (DERs) (Liserre et al., 2010; Zhou and Francois, 2011; Abdel-Rahim et al., 2016; Ghiasi et al., 2019; Yousif et al., 2022a). Microgrids are classified into two main types: AC and DC (Abdel-Rahim et al., 2018; Oulis Rousis et al., 2018; Dasarathan et al., 2020). They could be distinguished by the voltage form at the common coupling point (Sharma et al., 2022). A DC microgrid (Wang et al., 2023) has many advantages over an AC microgrid (Zhang et al., 2023) as it handles the issues associated with reactive power, frequency control, power quality, enormous information processing, and complicated control system, which in turn enhances efficiency and reliability (Katiraei et al., 2008; Dragicevic et al., 2015; Yousif et al., 2022b; Ding et al., 2023). Moreover, it provides a smooth and natural incorporation of DC sources like PV and energy storage batteries (Bharath, Krishnan Mithun and Kanakasabapathy, 2019; Pires et al., 2023), which helps in reducing energy conversion levels (Chen et al., 2013; Abdel-Rahim and Wang, 2020; Nawaz et al., 2023). A DC microgrid operates in both islanded and grid-connected modes (Habibullah et al., 2021). So it includes a hierarchical control system, like AC microgrids (Chandorkar et al., 1993; Guerrero et al., 2011), to manage voltage regulation, shifting between the two modes of operation, supply of the critical load with fixed power, precise current sharing between converters, plug and play capability, economic operation, and optimal power flow. This structure consists of three layers: primary, secondary, and tertiary (Bidram and Davoudi, 2012; Albarakati et al., 2022; Ashok Kumar and Amutha Prabha, 2022; Faragalla et al., 2022; Kumar et al., 2022).
Tertiary control deals with optimal operation and power management in the grid-connected mode (Sun et al., 2011; Xu and Chen, 2011). Primary control, where droop control is implemented through the inner voltage and current control loops without any communication link (Zhang et al., 2018; Laribi et al., 2020; Sattianadan et al., 2020; Ashok Kumar and Amutha Prabha, 2022), maintains the voltage stability of the microgrid after islanding (Katiraei et al., 2005). It also solves the dilemma of power sharing (Batarseh et al., 1994; Sharma et al., 2021) from interfacing parallel converters (Lu et al., 2014; Huang et al., 2015; Tahim et al., 2015; Fang et al., 2019; Mohamed et al., 2021). After the droop control is applied, the voltage diverges slightly from the nominal value, particularly when the line resistance is negligible, which requires a secondary control to regulate the voltage (Anand et al., 2013; Peyghami et al., 2018; Aluko et al., 2022). This type of control must be coordinated to perform cooperative control purposes and extra functionalities besides the local functionalities. So communication links between energy resources are implemented. Depending on the type of connection between converters, it could be characterized as centralized, decentralized, or distributed (Meng et al., 2017). In centralized control (Wang et al., 2022), a central control unit is employed, and bidirectional digital communication connects it with the energy resources. Information from local controllers is collected and sent to a central unit, where it is processed and sent back through communication links (Rashad et al., 2018). Because the data are gathered and treated in a single controller, it appears to be the best mechanism to reach enhanced control functionalities, but it can experience a single point of failure in addition to the massive data processing, plug-and-play (PNP) unfeasibility, and other difficulties. The data will not be transmitted if the central control or one of the communication links is lost, and this type was proposed by Olivares et al. (2011). A redundancy in the communication links could solve critical applications, but cost analysis sho1uld be conducted. In decentralized control, which combines centralized and distributed control (Iyer et al., 2010; Kim et al., 2011), the data are sent through the power lines, which is the only communication method. It acts like a master and slave; one of the DERs acts as the master, and the other units follow it as slaves (virtual central unit) to achieve a common goal besides the local control. Anand et al. (2013) demonstrated a decentralized control to handle the limitation of local and centralized control. A mathematical model is derived, and stability analysis is illustrated using eigenvalues. Since the decentralized control does not have redundancy, it may also face a failure bottleneck. Therefore, distributed control is introduced. The power sources can exchange data with connected neighboring sources only via a spare communication network, and there is no central unit. In this case, failure occurs if any connection is lost, provided the network is still connected. This type of control has been proposed in the literature (Lu et al., 2013; Lu et al., 2013; Zha et al., 2019; Liu et al., 2020; Li and Zhao, 2021) where DC output voltage and current in each module could be transferred to the other modules through the low-bandwidth communication (LBC) network. Average voltage and current controllers are used locally as the distributed secondary controllers in each converter to enhance the current-sharing accuracy and restore the DC bus voltage simultaneously. In contrast to other developed algorithms of secondary control, Guo et al. (2018) illustrated a control relying only on the bus voltage’s feedback and a few neighbors’ data to determine the distributed secondary input and send it to the primary bus control. Further simplicity could be achieved by using a pinning control to send the bus voltage to only one bus. Wan and Zheng (2022) introduced a distributed cooperative secondary control scheme for DC microgrids controlled by a droop controller to ensure proper current sharing and voltage restoration. The voltage and current regulators include a PI controller and observer that use a reduced gain function. This helps eliminate the effect of communication noise on reaching consensus. Furthermore, Liu et al. (2023) demonstrated a distributed controller to justify the voltage drop and emphasize the current division between DERs in the case of load change. This secondary controller can effectively justify the droop coefficient and improve the altered voltage to handle the voltage sag resulting from the primary control. To study the system’s stability under several environmental circumstances, the authors presented the root locus and zero-pole diagram. In addition, a distributed secondary controller based on fuzzy logic was suggested by Onaolapo et al. (2023). By communicating with one another via a communication network, the proposed controller in each DS simultaneously provides balanced current sharing and maintains DC bus voltage at the reference value. The authors also presented stability analysis to properly select the control parameters. A novel distributed secondary control approach was presented by Xing et al. (2021) that can provide an adjustable current-sharing ratio among DC converters by imposing a time-varying droop gain and setting the “virtual voltage drop.” In addition, the impact of time delay on control performance is examined. Aluko et al. (2022) presented a distributed secondary control approach to regulate the voltage and reach accurate current sharing. If some portion of the communication link in the cyber layer breaks, the dispersed approach keeps the whole system’s reliability intact. The suggested controller employs type-II fuzzy logic to adaptively choose the secondary control settings for a better controller response. Poudel et al. (2020) utilized a distributed secondary control for critical bus voltage regulation in the recognition and relief of false data injection using a consensus algorithm. The voltage and current errors, generated to modify the voltage and current allocation exactitude after the primary control application, are established using the consensus meaning only. Furthermore, only one bus is linked to the crucial load to accomplish its regulation.
This paper proposes consensus-based distributed secondary control for proper current sharing between converters and voltage regulation for the critical bus in DC islanded microgrids. Consensus algorithms in multi-agent systems like microgrids enable the connected agents to reach a general target. Due to the absence of a central unit, the data of local controllers should be processed in a way that makes them aware of the global system. In other words, if two units are connected, they only receive their own data. Thus, the consensus algorithm is implemented in local controllers, where the algebraic differences between their data and the data of their neighboring controllers are continuously summed up (Spanos et al., 2005; Lashhab, 2020; Mosaad et al., 2023) to calculate an average value. This cooperation is maintained using a sparse communication graph, which helps reduce the messages passing through the converters. Each local controller includes voltage and current integral regulators to generate two correction terms,
The disadvantages of the proposed technique are as follows: due to the additional communication links, the system is more expensive than that reported in the literature. Each DER also includes current and voltage controls. Moreover, there should only be one essential load on the system, otherwise certain adjustments need to be made. Finally, cybersecurity needs to be researched and taken into account due to the implementation of communication links. The correction terms help effectively achieve fast convergence for all converters to the nominal voltage and proper current allocation between them, especially when the impedance of lines is very small compared to the virtual resistance and could be excluded.
The remainder of the paper is organized as follows: Section 2 explains the primary control using conventional droop control. Section 3 describes the dynamic consensus and graph theory. Section 4 describes the distributed secondary cooperative control. In Section 5, two medium-voltage DC microgrids are simulated, and the effectiveness of the control scheme is verified. Section 6 is devoted to final conclusion.
2 DER model and primary control
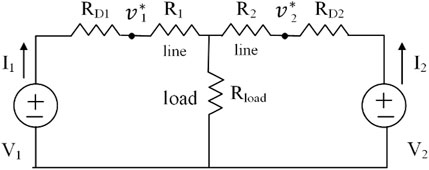
A DC microgrid enables renewable energy resources to be connected simply without cascaded conversions using DC–DC converters, as shown in Figure 1. The efficiency and reliability of the system operation are maintained by interface converters. If two sources of voltages, V1 and V2, with the same rating, are connected in parallel with lines R1 and R2 (as shown in Figure 2), it is assumed that the load Rload is shared equally between them. However, this does not happen due to the voltage difference, which causes unequal power sharing between them. Hence, appropriate coordination for current sharing respective to their ratings is required. Droop control can effectively achieve that by implementing a virtual resistance (Papadimitriou et al., 2015; GAO et al., 2019) to the PI inner voltage and current control loops as follows:
where
As the value of the droop coefficient increases, as depicted in Figure 3, the gap between the converter’s current reduces, and accurate sharing is enhanced, which is the primary objective. This resistance balances the difference between the voltage references, which may produce a circulating current between them. At no load, the voltage of reference is equal to the output voltage; however, when the load increases, the reference voltage decreases. As a result, the voltage deviates from the nominal value (Abbasi et al., 2023). So the design of virtual resistance is a compromise between high-voltage control and precise current sharing.
The virtual resistance is selected based on the current ratings of the converter, as shown in the following equation:
where
If the DC microgrid contains lines with low resistances that can be ignored, then
To ensure that the voltage at the boost converter’s terminals will not exceed the acceptable deviation limit, the droop coefficient must satisfy the following condition:
where
3 Graph theory and consensus algorithm
Graph theory is a mathematical form that could be used to demonstrate interactions between items. The graph consists of nodes (vertices) and edges (links) that connect the vertices with each other. A graph could be expressed as a pair, G = (V, E), where V is the nonempty finite vertices set, E is the edges set, and their pair is unordered. Therefore,
The microgrid is represented as an undirected graph with bidirectional communication links, allowing for cooperative control of DERs. In this graph, DERs are represented as vertices, and the connections between them are depicted as edges. Importantly, the cyber connection topology does not need to mirror the physical layout, indicating that not all distributed generators need to be directly linked.
Consensus algorithms, which are commonly employed in computer science and multi-agent systems like microgrids, play a vital role in enabling distributed energy resources to collaboratively reach agreements on shared data using the available communication network. It is worth noting that in this context, the dynamics of DERs on the communication graph are assumed to be scalar, first-order, and single integrators.
where
Each DER’s dynamics can be written as follows:
where
4 Distributed cooperative secondary voltage control
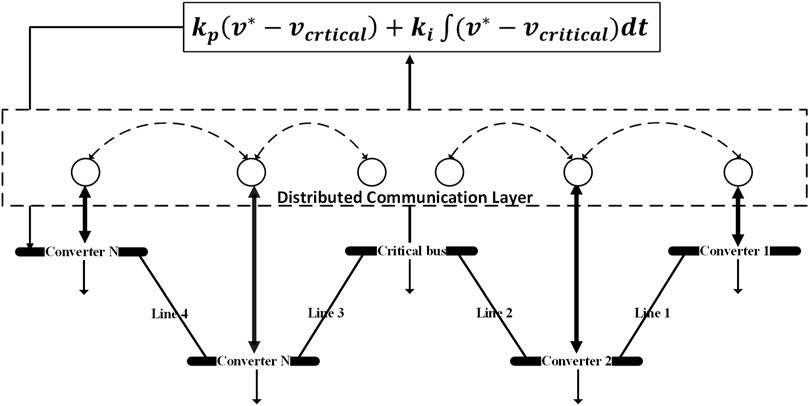
A centralized secondary control is employed to circumvent the dilemma between voltage regulation and the precision of current sharing. In this approach, local controllers interface with a centralized command center to relay measured data and receive control instructions after processing. However, if the communication links between these components are disrupted, it could lead to a catastrophic system failure. To address this concern, this study introduces a consensus-based distributed control approach. In distributed control, DERs communicate among themselves through a sparse communication network, which can be modeled as an undirected graph. The proposed control strategy focuses on regulating the critical or leader bus, which lacks a DER, by implementing a proportional–integral (PI) inner voltage control scheme, outlined as follows:
where
where
Cooperative control can be segmented into two primary challenges: consensus and tracking issues. The consensus problem entails devising a local control algorithm that enables all DERs to converge to a common steady-state value, especially when a spanning tree exists within the communication graph. On the other hand, the tracking problem is concerned with maintaining regulation over this consensus value.
The protocol for distributed voltage control, which determines the droop reference, is derived by taking its derivative to convert the grid into a first-order multi-agent system. This transformation process is detailed as follows:
As a result, the droop control reference is established using the DER neighboring tracing error for voltage and current ratio as follows:
where
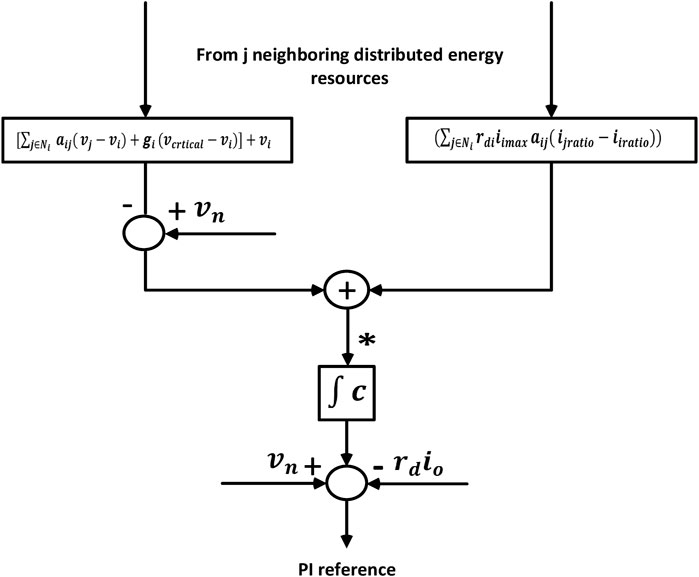
Instead of calculating the tracing error of voltage directly from the consensus algorithm, each DER estimates the average voltage using its measured voltage and the voltage of its linked neighbors as shown in the following equation (Shafiee et al., 2014):
where
Then the inaccuracy in neighboring voltage tracking is computed exactly by subtracting from the reference voltage, and the first correction term to adjust the converter’s terminal voltage is as follows:
The current ratio local consensus error will then be calculated to correct for current-sharing accuracy as follows:
where
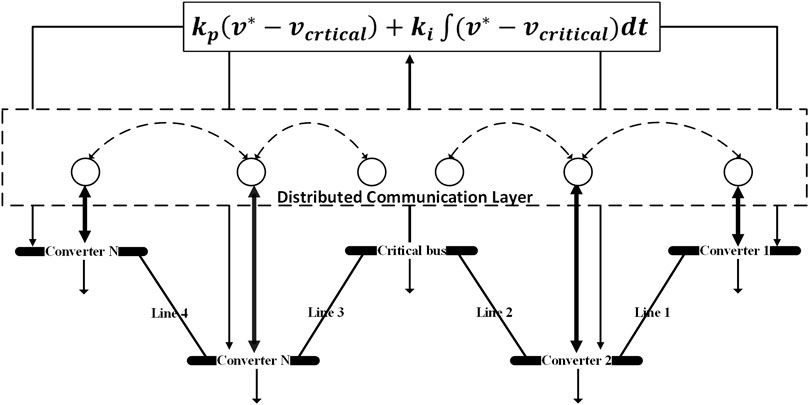
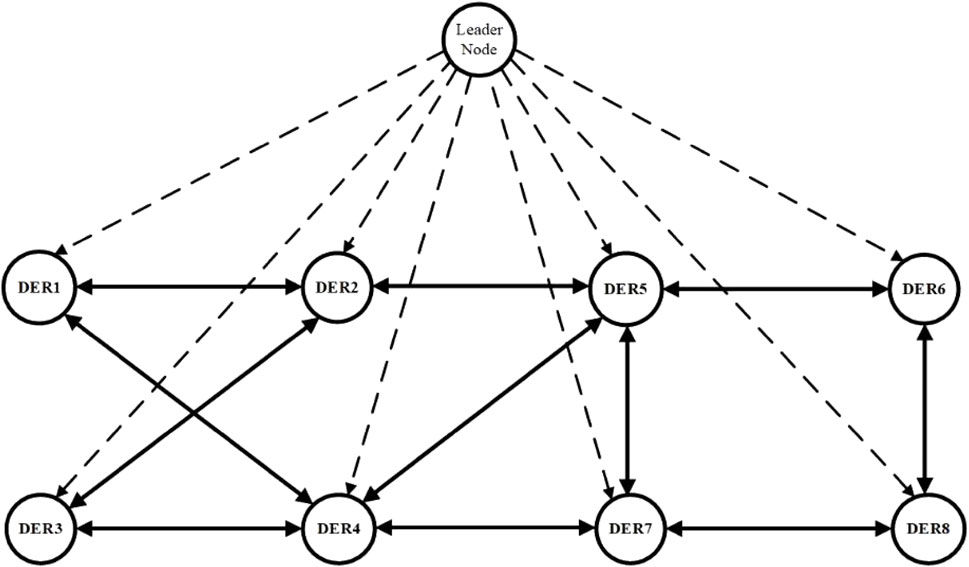
4.1 The leader node
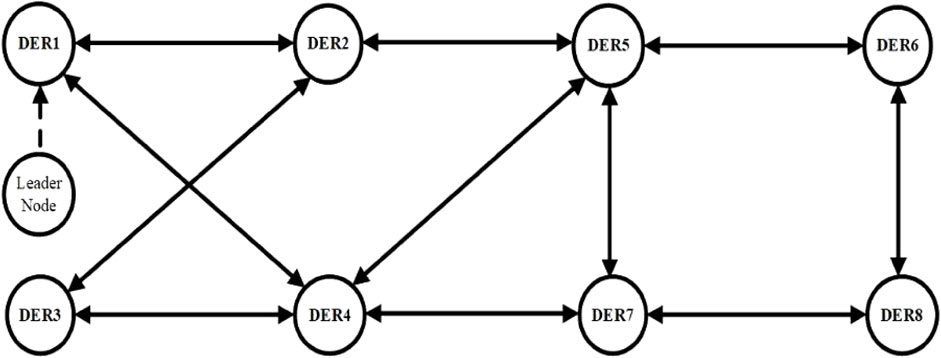
The leader node is not a physical converter, as shown in Figure 5. However, it is a virtual leader that leads the buses to regulate the voltage as it contains the critical load. This is an only method employed to show buses that contribute to voltage regulation. The nodes connected to the leader play a role in voltage control and vice versa for the unconnected nodes. If only one node is connected to the leader and it is missed, as depicted in Figure 6, the voltage adjustment will fail. So connecting the leader node to all other nodes, as depicted in Figure 5, maintains the highest reliability, which is introduced in this paper. In addition, if the leader is connected to one bus, the adequate current sharing will fail, and the efficiency of the regulation will decrease.
5 Results
In the following sections, two MVDC microgrids are simulated to verify the performance of the suggested secondary distributed cooperative control. The first microgrid consists of four DERs and five loads, including the critical load. The second microgrid includes eight DERs and nine loads, including the critical load. Two cases are introduced for each microgrid. Case A links only one converter to the leader, which already exists in the literature, and case B connects all converters to the critical bus, which is proposed in this paper.
5.1 The first microgrid
The power system shown in Figure 7 reproduces a standard MVDC ship. The loads and generators are selected according to IEEE (2018). This system, which involves four DERs and five loads, is simulated using MATLAB-Simulink. The reference voltage is tuned to 1,500 V, and
5.1.1 When only one bus knows about the critical bus voltage
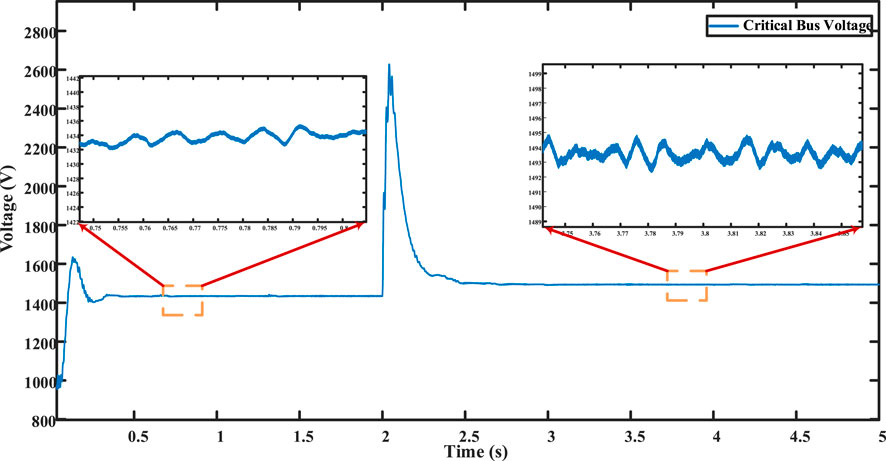
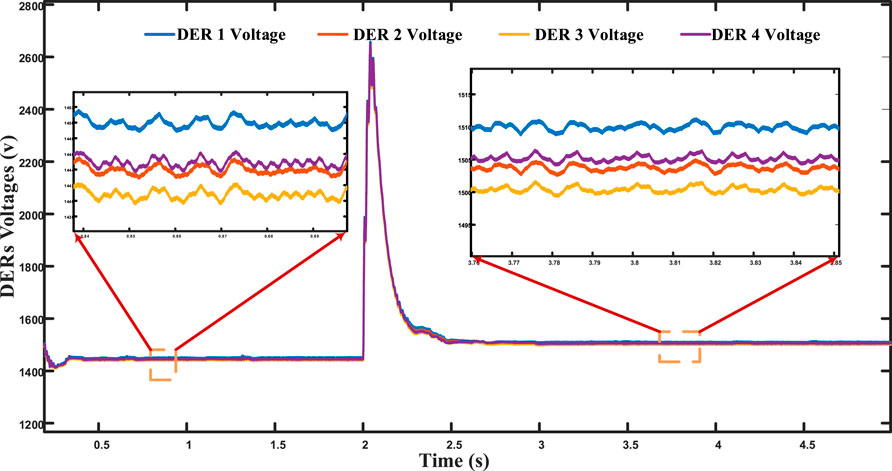
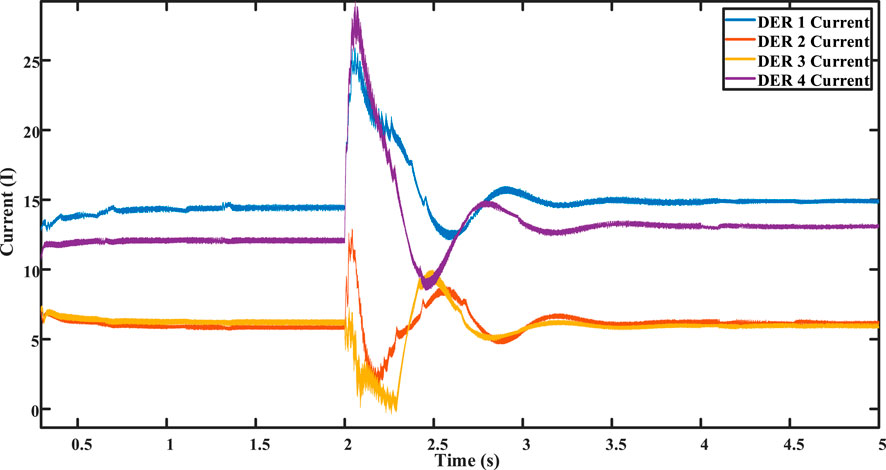
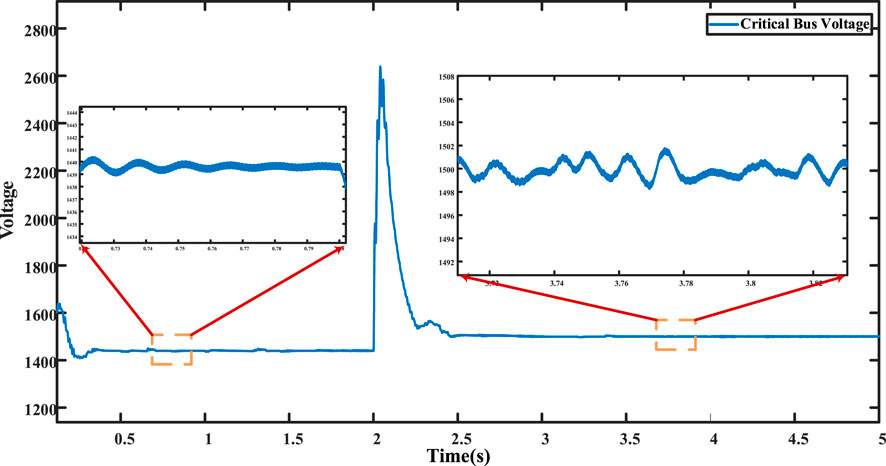
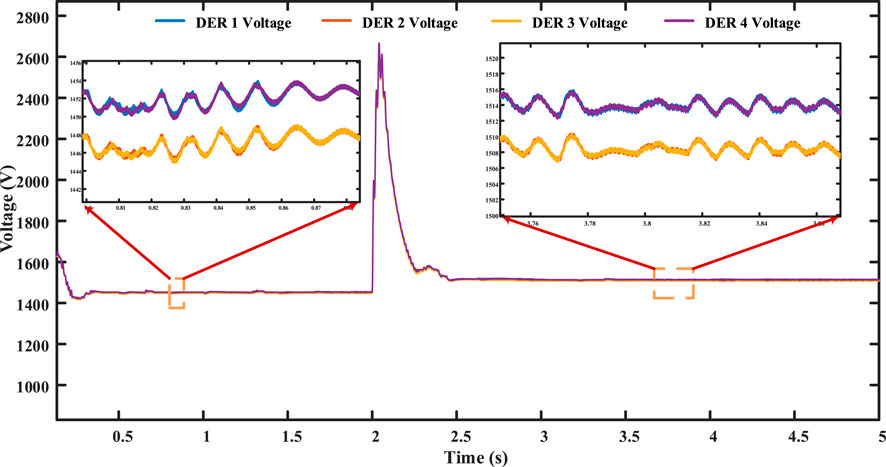
The DERs within the microgrid communicate according to the communication graph, as illustrated in Figure 8. Initially, when the microgrid is in islanded mode, the droop control is applied. While current distribution between converters is maintained, it is not extremely precise. DER 1 contributes approximately 0.357 of the total current, and DER 4 contributes approximately 0.306, as depicted in Figure 11. Simultaneously, DERs 2 and 3 share an equal amount of approximately 0.1667, as shown in Figure 11. Due to the influence of the droop coefficient, the voltage of all converters deviates from the nominal voltage, reaching approximately 1,440 V, as shown in the figures. Figure 9 shows the critical bus voltage, while Figure 10 displays individual DER voltages.
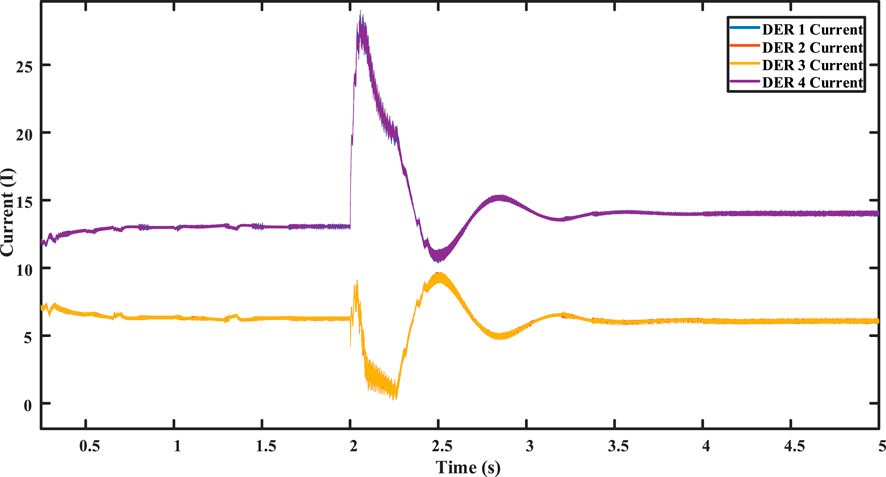
At t = 2 s, the distributed secondary cooperative control is implemented. Notably, the critical bus voltage is precisely adjusted to the nominal voltage, as shown in Figure 9, which is a key objective of the proposed control system. Furthermore, the voltage of all DERs successfully stabilizes at the nominal value of 1,500 V, as shown in Figure 10. The accurate division of current sharing between converters is achieved, as depicted in Figure 11, although not with absolute precision. There exists a slight disparity, particularly between DER 1’s current and DER 4’s current. DER 1 contributes approximately 14.6 A, while DER 4 provides 13 A. Meanwhile, DERs 2 and 3 equally share 6.9 A, as shown in Figure 11.
5.1.2 When all buses know about the critical bus voltage
In this scenario, the DERs establish communication through the communication graph, as shown in Figure 12. Initially, the microgrid is in an islanded state, and the droop control is applied. The droop control effectively maintains precise power sharing, with DER 1 and DER 4 sharing an equal current ratio of 0.33 of the total current. Figure 13 illustrates the current for DERs 1 and 4. Concurrently, DERs 2 and 3 equally share half the current ratio of DERs 1 and 4, which is 0.166, as indicated in the same figure. However, the voltage deviates from the nominal value due to virtual resistance, reaching 1,440 V for all buses, as shown in the figures. Figure 14 shows the critical bus voltage, while Figure 15 displays individual DER voltages.
At t = 2 seconds, the proposed distributed secondary cooperative control is activated. Consequently, the voltage of the critical bus, which carries the critical load, is precisely regulated to the nominal voltage of 1,500 V, fulfilling the primary objective of the control system, as depicted in Figure 16. Additionally, the voltages of all other buses, as shown in Figure 17, are adjusted to their normal values.
Ultimately, each agent contributes to the current sharing more accurately than in the previous case. The currents of DERs 1 and 4 are both 13.8 A, as shown in Figure 18, while the currents of DERs 2 and 3 are both 6.9 A, as shown in the same figure. This demonstrates the effective and enhanced performance of the proposed control scheme.
5.2 The second microgrid
The system (Figure 16), consisting of eight DERs and nine loads, including the critical load, is simulated using MATLAB-Simulink. The reference voltage is set to 1,500 V, and
The resistances of lines 1, 4, 5, and 8 are 0.21 Ω, whereas the resistances of lines 2, 3, 6, and 7 are 0.105 Ω. The rated power for DERs 1, 3, 6, and 8 is 60 kW, while that for DERs 2, 4, 5, and 7 is 30 kW. The rated current for DERs 1, 3, 6, and 8 is 40 A, while that for DERs 2, 4, 5, and 7 is 20 A. All DERs have a rated voltage of 1,500 V.
5.2.1 When only one bus knows about the critical bus voltage
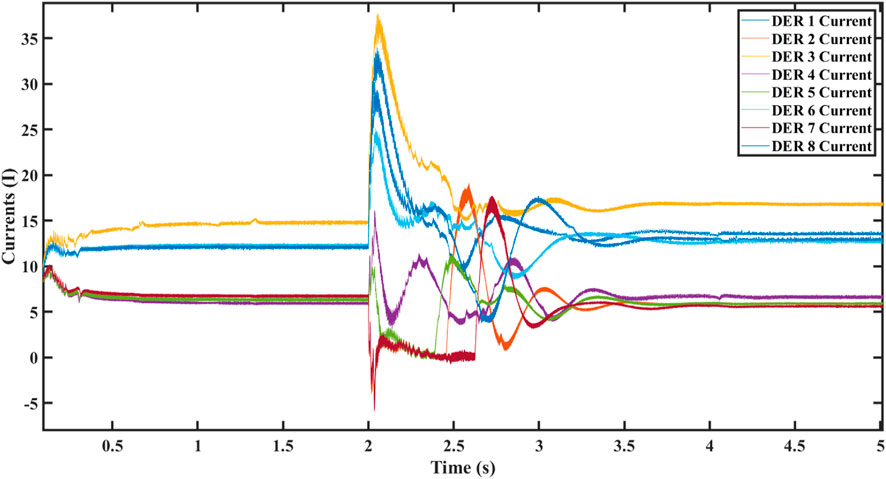
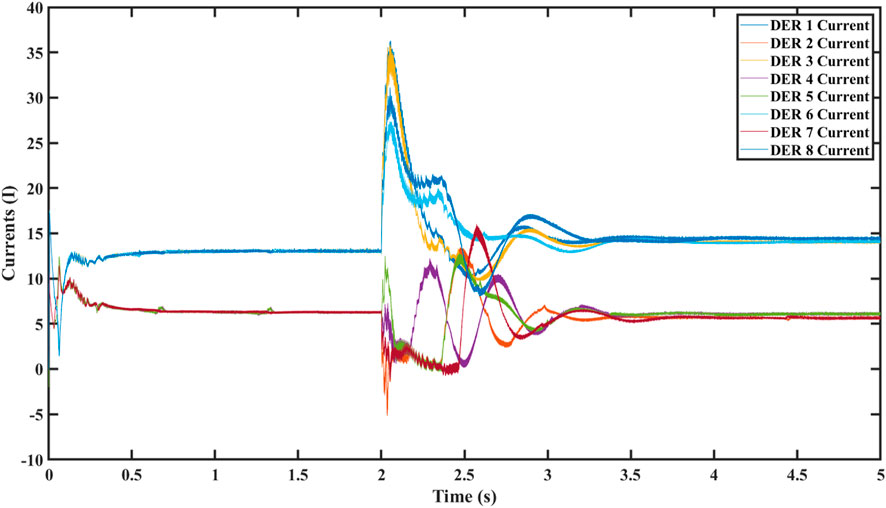
In this scenario, DERs communicate using the communication graph, as depicted in Figure 17. Initially, at t = 0, the microgrid is in an islanded state, and the droop control is implemented. The current participation ratio of each converter depends on its maximum capacity but cannot be achieved perfectly. Specifically, DERs 2, 4, 5, and 7 each share the same ratio of 0.083. DERs 1, 6, and 8 all share a ratio of 0.162 of the total current, as depicted in Figure 19. DER 3, however, slightly deviates from the expected sharing ratio, participating with 0.1811 of the total current, as shown in the same figure. These current disparities reflect a deviation from the ideal distribution based on maximum values.
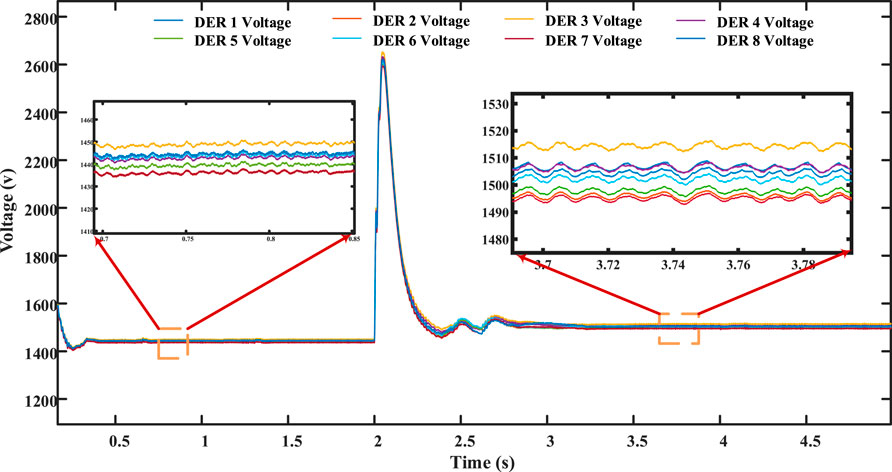
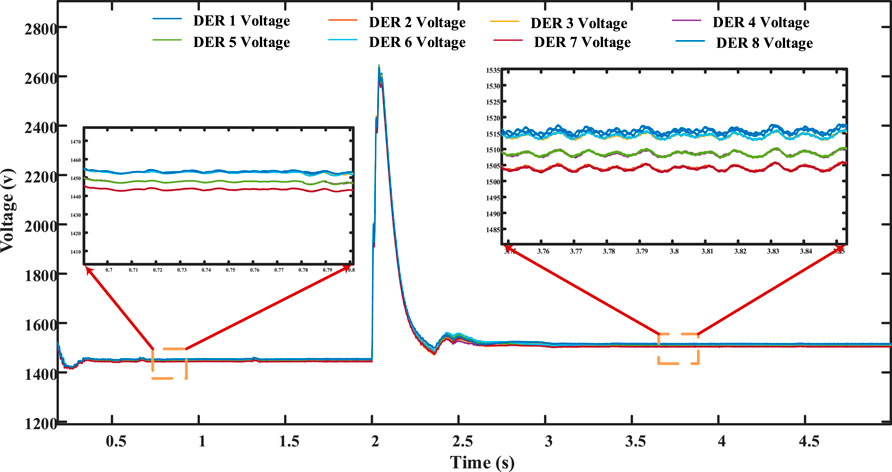
Additionally, due to the influence of the droop coefficient, the critical bus voltage cannot be precisely restored to the nominal voltage and instead reaches 1,440 V, as displayed in Figure 18. Furthermore, it was not possible to restore the voltages of all converters to the reference voltage. Figure 20 displays the following individual DER voltages: DER 1 voltage, DER 2 voltage, DER 3 voltage, DER 4 voltage, DER 5 voltage, DER 6 voltage, DER 7 voltage, and DER 8 voltage.
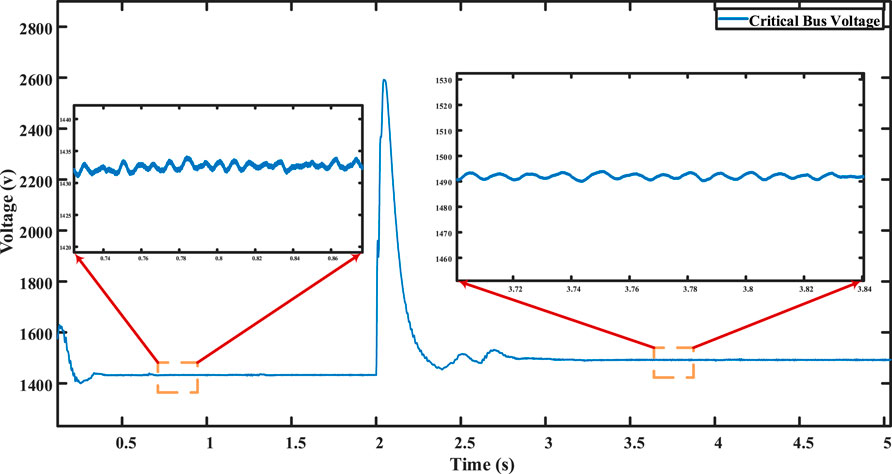
At t = 2 s, the distributed secondary cooperative control is activated. This results in the synchronization of the critical bus voltage to 1,500 V, as depicted in Figure 18, successfully achieving the primary objective of the proposed control technique. Furthermore, all other bus voltages are nearly regulated to the nominal value of 1,500 V, as shown in Figure 20. Finally, when it comes to the precise distribution of current among converters, there is a noticeable imbalance among DERs that have identical power ratings, as depicted in Figure 19.
5.2.2 When all buses know about the critical bus voltage
In this case, the DERs exchange data using the communication graph, as illustrated in Figure 21. Initially, the microgrid is in the islanded state, and the droop control is applied. The droop control could successfully maintain the exactness of power sharing. Each of DERs 2, 4, 5, and 7 shares a current ratio of 0.083, as shown in Figure 22, while each of DERs 1, 3, 6, and 8 shares a current ratio of 0.1667 of the total current, as depicted in the same figure. For voltages, there is a reduction of 60 V compared with the nominal value for the critical bus in addition to all other buses, as shown in Figures 23, 24.
At t = 2 seconds, the proposed distributed secondary cooperative control is employed. As a result, the voltage of the leader bus is restored to 1,500 V, as depicted in Figure 23. This meets the most important objective of the control structure. Additionally, the voltages, as shown in Figure 24, are adjusted to the normal voltage, which is 1,500 V. Finally, each DER participated in current sharing more accurately depending on its maximum current value than in the case of only one node connected to the leader, as depicted in Figure 22. Each of DERs 2, 4, 5, and 7 participates with 6.9 A, while each of DERs 1, 3, 6, and 8 participate with 13.8 A. This proves the effective performance of the proposed control arrangement. A comparison between both cases is provided in Table 1.
6 Conclusion
This paper introduces a novel approach to regulate the voltage of a critical bus and ensure precise power distribution among converters within an islanded DC microgrid. The critical bus plays a central role, guiding the control process, and agents connected to it actively participate in voltage regulation. A multi-agent system framework is employed for DERs in the microgrid, leveraging graph theory to facilitate consensus among these agents. The consensus algorithm is instrumental in achieving a steady-state global value across all DERs, leading to the creation of two crucial modification terms, namely, δv and δi. These terms are highly effective in restoring voltage to its nominal value and ensuring equitable power distribution among agents based on their power ratings.
In this approach, all DERs are interconnected with the leader, contributing to voltage adjustments. This design significantly enhances the reliability of the proposed control scheme and greatly improves the accuracy of current sharing among agents. To validate the effectiveness of the control strategy, simulations were conducted using MATLAB-Simulink on two distinct MVDC ship microgrids. The first microgrid comprised five buses, while the second had nine buses. Two scenarios were evaluated for each microgrid: case A, where only one converter was linked to the leader bus, and case B, where all converters were connected to the leader bus.
The findings revealed a notable improvement in performance when all buses were linked to the critical bus, with an 8% enhancement attributed to more precise and accurate current contributions from DERs compared to the single-bus connection scenario. Furthermore, the critical bus and all other buses swiftly converged to the reference voltage of 1,500 V, highlighting the effectiveness and efficiency of the proposed control approach.
The primary and distributed secondary cooperative control strategy demonstrates its capability to regulate critical bus voltage and ensure precise power distribution in an islanded DC microgrid. This approach offers enhanced performance, particularly when all converters are connected to the critical bus, showcasing its potential for practical application in microgrid systems.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
NM: conceptualization, formal analysis, methodology, validation, writing–original draft, and writing–review and editing. OA-R: conceptualization, formal analysis, methodology, supervision, validation, and writing–review and editing. TM: supervision and writing–review and editing. WR: data curation, resources, and writing–review and editing. TA: supervision and writing–review and editing. SA: conceptualization, formal analysis, methodology, supervision, and writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Qatar National Library (QNL).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abbasi, M., Abbasi, E., Li, L., Aguilera, R. P., Lu, D., and Wang, F. (2023). Review on the microgrid concept, structures, components, communication systems, and control methods. Energies 16, 484. doi:10.3390/en16010484
Abdel-Rahim, O., Chub, A., Vinnikov, D., and Blinov, A. (2022). DC integration of residential photovoltaic systems: a survey. IEEE Access 10, 66974–66991. doi:10.1109/ACCESS.2022.3185788
Abdel-Rahim, O., Funato, H., and Haruna, J. (2018). A comprehensive study of three high-gain DC-DC topologies based on Cockcroft-Walton voltage multiplier for reduced power PV applications. IEEJ Trans. Electr. Electron. Eng. 13 (4), 642–651. doi:10.1002/tee.22611
Abdel-Rahim, O., Funato, H., and Junnosuke, H. (November 2016). “Droop method based on model predictive control for DC microgrid,” in Proceedings of the 2016 19th international conference on electrical machines and systems (ICEMS), Chiba, Japan, 1–6.
Abdel-Rahim, O., and Wang, H. (2020). Five-level one-capacitor boost multilevel inverter. IET Power Electron. 13 (11), 2245–2251. doi:10.1049/iet-pel.2020.0033
Albarakati, A. J., Boujoudar, Y., Azeroual, M., Eliysaouy, L., Kotb, H., Aljarbouh, A., et al. (2022). Microgrid energy management and monitoring systems: a comprehensive review. Front. Energy Res. 10. doi:10.3389/fenrg.2022.1097858
Aluko, A., Buraimoh, E., Oni, O. E., and Davidson, I. E. (2022). Advanced distributed cooperative secondary control of islanded DC microgrids. Energies 15 (11), 3988. doi:10.3390/en15113988
Anand, S., Fernandes, B., and Guerrero, J. (2013). Distributed control to ensure proportional load sharing and improve voltage regulation in low-voltage DC microgrids. Power Electron. IEEE Trans. 28, 1900–1913. doi:10.1109/TPEL.2012.2215055
Ashok Kumar, A., and Amutha Prabha, N. (2022). A comprehensive review of DC microgrid in market segments and control technique. Heliyon 8 (11), e11694. doi:10.1016/j.heliyon.2022.e11694
Batarseh, I., Siri, K., and Lee, H. (1994). Investigation of the output droop characteristics of parallel-connnected DC-DC converters. Proc. 1994 Power Electron. Specialist Conf. - PESC’94 2, 1342–1351. doi:10.1109/PESC.1994.373859
Bharath, K. R., Krishnan Mithun, M., and Kanakasabapathy, P. (2019). A review on DC microgrid control techniques, applications and trends. Int. J. Renew. Energy Res. 9 (3), 1328–1338. doi:10.20508/ijrer.v9i3.9671.g7710
Bidram, A., and Davoudi, A. (2012). Hierarchical structure of microgrids control system. IEEE Trans. Smart Grid 3, 1963–1976. doi:10.1109/tsg.2012.2197425
Bidram, A., (2017). Cooperative synchronization in distributed microgrid control. Springer, Cham, Switzerland.
Chandorkar, M. C., Divan, D. M., and Adapa, R. (1993). Control of parallel connected inverters in standalone AC supply systems. IEEE Trans. Industry Appl. 29 (1), 136–143. doi:10.1109/28.195899
Chen, Y.-K., Wu, Y. C., and Song, C. C. (2013). Design and implementation of energy management system with fuzzy control for DC microgrid systems. Power Electron. IEEE Trans. 28, 1563–1570. doi:10.1109/TPEL.2012.2210446
Dasarathan, S., Kumar, G. R. P., Sridhar, R., Reddy, K. V., Reddy, B. S. U., and Mamatha, P. (2020). Investigation of low voltage DC microgrid using sliding mode control. Int. J. Power Electron. Drive Syst. (IJPEDS) 11, 2030. doi:10.11591/ijpeds.v11.i4.pp2030-2037
Ding, X., Wang, W., Zhou, M., Yue, Y., Chen, Q., Zhang, C., et al. (2023). Feedback control strategy for state-of-charge balancing and power sharing between distributed battery energy storage units in DC microgrid. IET Power Electron. 16, 1063–1076. doi:10.1049/pel2.12450
Dragicevic, T., Lu, X., Vasquez, J. C., and Guerrero, J. M. (2015). DC microgrids–Part II: a review of power architectures, applications and standardization issues. IEEE Trans. Power Electron. 31, 3528–3549. doi:10.1109/TPEL.2015.2464277
Fang, J., Shuai, Z., Zhang, X., Shen, X., and Shen, Z. J. (2019). Secondary power sharing regulation strategy for a DC microgrid via maximum loading factor. IEEE Trans. Power Electron. 34 (12), 11856–11867. doi:10.1109/TPEL.2019.2907551
Faragalla, A., Abdel-Rahim, O., Orabi, M., and Abdelhameed, E. H. (2022). Enhanced virtual inertia control for microgrids with high-penetration renewables based on whale optimization. Energies 15, 9254. doi:10.3390/en15239254
Gao, F., Kang, R., Cao, J., and Yang, T. (2019). Primary and secondary control in DC microgrids: a review. J. Mod. Power Syst. Clean Energy 7 (2), 227–242. doi:10.1007/s40565-018-0466-5
Ghiasi, M., Esmaeilnamazi, S., Ghiasi, R., and Fathi, M. (2019). Role of renewable energy sources in evaluating technical and economic efficiency of power quality. Technol. Econ. Smart Grids Sustain. Energy 5, 1. doi:10.1007/s40866-019-0073-1
Guerrero, J. M., Vasquez, J. C., Matas, J., de Vicuna, L. G., and Castilla, M. (2011). Hierarchical control of droop-controlled AC and DC microgrids - a general approach toward standardization. IEEE Trans. Industrial Electron. 58 (1), 158–172. doi:10.1109/TIE.2010.2066534
Guo, F., Xu, Q., Wen, C., Wang, L., and Wang, P. (2018). Distributed secondary control for power allocation and voltage restoration in islanded DC microgrids. IEEE Trans. Sustain. Energy 9 (4), 1857–1869. doi:10.1109/TSTE.2018.2816944
Habibullah, A. F., Padhilah, F. A., and Kim, K.-H. (2021). Decentralized control of DC microgrid based on droop and voltage controls with electricity price consideration. Sustainability 13, 11398. doi:10.3390/su132011398
Huang, P.-H., Liu, P. C., Xiao, W., and El Moursi, M. S. (2015). A novel droop-based average voltage sharing control strategy for DC microgrids. IEEE Trans. Smart Grid 6 (3), 1096–1106. doi:10.1109/TSG.2014.2357179
Ieee, (2018). IEEE recommended practice for 1 kV to 35 kV medium-voltage DC power systems on ships, IEEE std 1709-2018 (revision of IEEE std 1709-2010), Piscataway, NJ, USA, IEEE, 1–54. doi:10.1109/IEEESTD.2018.8569023
Iyer, S., Belur, M., and Chandorkar, M. (2010). A generalized computational method to determine stability of a multi-inverter microgrid. Power Electron. IEEE Trans. 25, 2420–2432. doi:10.1109/TPEL.2010.2048720
Katiraei, F., Iravani, M. R., and Lehn, P. W. (2005). Micro-grid autonomous operation during and subsequent to islanding process. IEEE Trans. Power Deliv. 20 (1), 248–257. doi:10.1109/TPWRD.2004.835051
Katiraei, F., Iravani, R., Hatziargyriou, N., and Dimeas, A. (2008). Microgrids management. IEEE Power Energy Mag. 6 (3), 54–65. doi:10.1109/MPE.2008.918702
Kim, J., Guerrero, J. M., Rodriguez, P., Teodorescu, R., and Nam, K. (2011). Mode adaptive droop control with virtual output impedances for an inverter-based flexible AC microgrid. Power Electron. IEEE Trans. 26, 689–701. doi:10.1109/TPEL.2010.2091685
Kumar, S., H. K., Y., Kumar Sharma, N., Bajaj, M., Naithani, D., and Maindola, M. (2022)“Classical secondary control techniques in microgrid systems–a review,” in 2022 2nd International Conference on Innovative Sustainable Computational Technologies (CISCT), Dehradun, India, 1–6. doi:10.1109/CISCT55310.2022.10046557
Laribi, R., Schaab, D. A., and Sauer, A. (July 2020). “Adaptive state of charge control for DroopControlled industrial DC-microgrids,” in Proceedings of the 2020 IEEE 14th international conference on compatibility, power electronics and power engineering (CPE-POWERENG), Setubal, Portugal, 187–193. doi:10.1109/CPE-POWERENG48600.2020.9161557
Lashhab, F. (2020)“Dynamic consensus networks: dynamic graph definitions and controllability analysis using the behavioral approach,” in 2020 IEEE International IOT, Electronics and Mechatronics Conference (IEMTRONICS), Vancouver, BC, 1–9. doi:10.1109/IEMTRONICS51293.2020.9216385
Li, D., and Zhao, D. (July 2021). An improved distributed secondary control to attain concomitant accurate current sharing and voltage restoration in DC microgrids’, in Proceedings of the 2021 40th Chinese control conference (CCC), Shanghai, China, 3834–3839. doi:10.23919/CCC52363.2021.9549431
Liserre, M., Sauter, T., and Hung, J. Y. (2010). Future energy systems: integrating renewable energy sources into the Smart power grid through industrial electronics. IEEE Ind. Electron. Mag. 4 (1), 18–37. doi:10.1109/MIE.2010.935861
Liu, S., Miao, H., Li, J., and Yang, L. (2023). Voltage control and power sharing in DC Microgrids based on voltage-shifting and droop slope-adjusting strategy. Electr. Power Syst. Res. 214, 108814. doi:10.1016/j.epsr.2022.108814
Liu, X.-K., Wang, Y. W., Lin, P., and Wang, P. (2020). Distributed supervisory secondary control for a DC microgrid. IEEE Trans. Energy Convers. 35 (4), 1736–1746. doi:10.1109/TEC.2020.2994251
Lu, X., Guerrero, J. M., and Sun, K. (May 2013). Distributed secondary control for dc microgrid applications with enhanced current sharing accuracy. Proceedings of the 2013 IEEE Int. Symposium Industrial Electron, Taipei, Taiwan, 1–6. doi:10.1109/ISIE.2013.6563742
Lu, X., Guerrero, J. M., Sun, K., and Vasquez, J. C. (2014). An improved droop control method for DC microgrids based on low bandwidth communication with DC bus voltage restoration and enhanced current sharing accuracy. IEEE Trans. Power Electron. 29 (4), 1800–1812. doi:10.1109/TPEL.2013.2266419
Macana, C. A., Mojica-Nava, E., Pota, H. R., Guerrero, J., and Vasquez, J. C. (2022). A distributed real-time energy management system for inverter-based microgrids. Electr. Power Syst. Res. 213, 108753. doi:10.1016/j.epsr.2022.108753
Meenual, T., and Usapein, P. (2021). Microgrid policies: a review of technologies and key drivers of Thailand. Front. Energy Res. 9. doi:10.3389/fenrg.2021.591537
Meng, L., Shafiee, Q., Trecate, G. F., Karimi, H., Fulwani, D., Lu, X., et al. (2017)“Review on control of DC microgrids and multiple microgrid clusters,” in IEEE Journal of Emerging and Selected Topics in Power Electronics 5 (3), 928–948. doi:10.1109/JESTPE.2017.2690219
Mohamed, M. A. A., Rashed, M., Lang, X., Atkin, J., Yeoh, S., and Bozhko, S. (2021). Droop control design to minimize losses in DC microgrid for more electric aircraft. Electr. Power Syst. Res. 199, 107452. doi:10.1016/j.epsr.2021.107452
Mosaad, N., Abdel-Rahim, O., Megahed, T. F., Asano, T., and Abdelkader, S. M.(2023)“Distributed cooperative secondary control for critical bus voltage regulation,” in 2023 IEEE International Conference on Environment and Electrical Engineering and 2023 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 1–6. doi:10.1109/EEEIC/ICPSEurope57605.2023.10194848
Nawaz, A., Wu, J., Ye, J., Dong, Y., and Long, C. (2023). Circulating current minimization based adaptive droop control for grid-connected DC microgrid. Electr. Power Syst. Res. 220, 109260. doi:10.1016/j.epsr.2023.109260
Olfati-Saber, R., and Murray, R. (2004). Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Automatic Control 49, 1520–1533. doi:10.1109/tac.2004.834113
Olivares, D., Canizares, C., and Kazerani, M. (2011). A centralized optimal energy management system for microgrids. Power and Energy Society General Meeting. Springer, Kannur, India, doi:10.1109/PES.2011.6039527
Onaolapo, A. K., Sharma, G., Bokoro, P. N., Aluko, A., and Pau, G. (2023). A distributed control scheme for cyber-physical DC microgrid systems. Energies 16, 5611. doi:10.3390/en16155611
Oulis Rousis, A., Tzelepis, D., Konstantelos, I., Booth, C., and Strbac, G. (2018). Design of a hybrid AC/DC microgrid using HOMER pro: case study on an islanded residential application. Inventions 3, 55. doi:10.3390/inventions3030055
Papadimitriou, C. N., Zountouridou, E. I., and Hatziargyriou, N. D. (2015). Review of hierarchical control in DC microgrids. Electr. Power Syst. Res. 122, 159–167. doi:10.1016/j.epsr.2015.01.006
Peyghami, S., Mokhtari, H., Loh, P. C., Davari, P., and Blaabjerg, F. (2018). Distributed primary and secondary power sharing in a droop-controlled LVDC microgrid with merged AC and DC characteristics. IEEE Trans. Smart Grid 9 (3), 2284–2294. doi:10.1109/TSG.2016.2609853
Pires, V., Pires, A. J., and Cordeiro, A. (2023). DC microgrids: benefits, architectures, perspectives and challenges. Energies 16, 1217. doi:10.3390/en16031217
Poudel, B. P., Mustafa, A., Bidram, A., and Modares, H. (2020). Detection and mitigation of cyber-threats in the DC microgrid distributed control system. Int. J. Electr. Power & Energy Syst. 120, 105968. doi:10.1016/j.ijepes.2020.105968
Rashad, M., Raoof, U., Ashraf, M., and Ashfaq Ahmed, B. (2018). Proportional load sharing and stability of DC microgrid with distributed architecture using SM controller. Math. Problems Eng. 2018, 1–16. doi:10.1155/2018/2717129
Sattianadan, D., Kumar, G. R. P., Sridhar, R., Reddy, K. V., Reddy, B. S. U., and Mamatha, P. (2020). Investigation of low voltage dc microgrid using sliding mode control. Int. J. Power Electron. Drive Syst. 11 (4), 2030–2037. doi:10.11591/ijpeds.v11.i4.pp2030-2037
Shafiee, Q., Dragicevic, T., Andrade, F., Vasquez, J. C., and Guerrero, J. M. (2014). “Distributed consensus-based control of multiple DC-microgrids clusters,” in IECON 2014 - 40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX, 2056–2062. doi:10.1109/IECON.2014.7048785
Sharma, S., Iyer, V. M., Das, P. P., and Bhattacharya, S. (2021). Protocol based management of common sports injuries by integrated approach of Sandhi Marmabhighata - an open labeled clinical trial. 2021 IEEE Appl. Power Electron. Conf. Expo. (APEC) 12, 119–125. doi:10.1016/j.jaim.2020.12.009
Sharma, S., Tripathy, M., and Wang, L. (2022). Transient power polarity based fault detection in DC microgrid with localized backup scheme. Electr. Power Syst. Res. 209, 108008. doi:10.1016/j.epsr.2022.108008
Spanos, D. P., Olfati-Saber, R., and Murray, R. M. (2005). Dynamic consensus for mobile networks, https://www.cds.caltech.edu/∼murray/papers/2005f_som05-ifac.html.
Sun, K., Zhang, L., Xing, Y., and Guerrero, J. M. (2011). A distributed control strategy based on DC bus signaling for modular photovoltaic generation systems with battery energy storage. IEEE Trans. Power Electron. 26 (10), 3032–3045. doi:10.1109/TPEL.2011.2127488
Tahim, A., Pagano, D. J., Lenz, E., and Stramosk, V. (2015). Modeling and stability analysis of islanded DC microgrids under droop control. Power Electron. IEEE Trans. 30, 4597–4607. doi:10.1109/TPEL.2014.2360171
Wan, Q., and Zheng, S. (2022). Distributed cooperative secondary control based on discrete consensus for DC microgrid. Energy Rep. 8, 8523–8533. doi:10.1016/j.egyr.2022.06.061
Wang, F., Shan, Q., Teng, F., He, Z., Xiao, Y., and Wang, Z. (2022). Distributed secondary control strategy against bounded FDI attacks for microgrid with layered communication network. Front. Energy Res. 10. doi:10.3389/fenrg.2022.914132
Wang, P., Zhao, J., Liu, K., Jin, C., and Chen, W. (2023). Mixed-potential-function-based large-signal stability analysis of DC microgrid with constant power loads. Front. Energy Res. 10. doi:10.3389/fenrg.2022.1052789
Xing, L., Guo, F., Liu, X., Wen, C., Mishra, Y., and Tian, Y. C. (2021). Voltage restoration and adjustable current sharing for DC microgrid with time delay via distributed secondary control. IEEE Trans. Sustain. Energy 12 (2), 1068–1077. doi:10.1109/TSTE.2020.3032605
Xu, L., and Chen, D. (2011). Control and operation of a DC microgrid with variable generation and energy storage. IEEE Trans. Power Deliv. - IEEE TRANS POWER Deliv. 26, 2513–2522. doi:10.1109/TPWRD.2011.2158456
Yousif, H., Abdel-Rahim, O., and Ali, Z. (2022a). High-gain seven-level switched-capacitor two-stage multi-level inverter. Front. Energy Res. 10. doi:10.3389/fenrg.2022.869662
Yousif, H., Abdel-Rahim, O., and Ali, Z. (2022b). New high-gain transformerless DC/DC boost converter system. Electronics 11, 734. doi:10.3390/electronics11050734
Zha, D., Wang, Q., Cheng, M., Deng, F., and Buja, G. (2019)“Distributed cooperative control for multiple DC electric springs with novel topologies applied in DC microgrid,” in 2019 IEEE 10th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Xi'an, China, 648–652. doi:10.1109/PEDG.2019.8807459
Zhang, L., Zhang, W., Zeng, F., and Yang, X. (2018). A review of control strategies in DC microgrid. J. Phys. Conf. Ser. 1087 (4), 042035. doi:10.1088/1742-6596/1087/4/042035
Zhang, Q., Song, Z., Ru, Q., Fan, J., Qiao, L., Li, M., et al. (2023). Coordinated control of distributed energy storage systems for DC microgrids coupling photovoltaics and batteries. Energies 16, 665. doi:10.3390/en16020665
Zhou, T., and Francois, B. (2011). Energy management and power control of a hybrid active wind generator for distributed power generation and grid integration. Industrial Electron. IEEE Trans. 58, 95–104. doi:10.1109/TIE.2010.2046580
Nomenclature
Keywords: DC microgrid, distributed secondary control, consensus algorithm, voltage stability, current sharing
Citation: Mosaad N, Abdel-Rahim O, Megahed TF, Rohouma W, Asano T and Abdelkader SM (2023) An enhanced consensus-based distributed secondary control for voltage regulation and proper current sharing in a DC islanded microgrid. Front. Energy Res. 11:1277198. doi: 10.3389/fenrg.2023.1277198
Received: 14 August 2023; Accepted: 03 November 2023;
Published: 29 November 2023.
Edited by:
Yunhe Hou, The University of Hong Kong, Hong Kong SAR, ChinaReviewed by:
Jianhang Zhu, The University of Hong Kong, Hong Kong SAR, ChinaZhaobin Du, South China University of Technology, China
Copyright © 2023 Mosaad, Abdel-Rahim, Megahed, Rohouma, Asano and Abdelkader. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wesam Rohouma, d2VzYW0ucm9ob3VtYUB1ZHN0LmVkdS5xYQ==; Omar Abdel-Rahim, by5hYmRlbHJhaGltQGFzd3UuZWR1LmVn
 Nada Mosaad
Nada Mosaad Omar Abdel-Rahim
Omar Abdel-Rahim Tamer F. Megahed1,3
Tamer F. Megahed1,3 Wesam Rohouma
Wesam Rohouma Sobhy M. Abdelkader
Sobhy M. Abdelkader