Precise emergency load shedding approach for distributed network considering response time requirements

Emergency load shedding (ELS) is a vital measure for power systems to manage extreme events, ensuring the safety, stability, and economic operation of the grid. The integration of distributed energy resources and controllable devices in modern power systems has bolstered grid flexibility. Consequently, developing precise load shedding strategies to balance economic and security goals has emerged as a prominent subject in power system optimization. However, existing methods exhibit inadequacies, including overlooking practical operability, privacy concerns, and a lack of adaptability to response time requirements. To address these gaps, this paper introduces a precise ELS approach for distributed networks with a focus on response time needs. Contributions encompass designing load shedding processes for various response times, integrating demand response, and partitioning networks for optimized load shedding. Through validation using standard test cases, the proposed approach effectively utilizes response time and demand-side resources for precise ELS control in distribution networks. It accommodates different scenarios, offering a robust solution for rapid and accurate load shedding during emergencies.

1 Introduction

Precise ELS is an essential measure for power systems to cope with extreme events, playing a crucial role in ensuring the safety, stability, and economic operation of the power grid. In modern power systems, the increasing integration of distributed energy resources and controllable devices has significantly enhanced the flexibility and responsiveness of the grid. Therefore, how to develop accurate load shedding control strategies to achieve a balance between economic and security objectives has become a hot topic in power system optimization and control research.

The approaches can be divided into two categories: optimization-based and AI-based approaches. The optimization-based approach models ELS as an optimization problem with nonlinear constraints or objectives. As to constraints, voltage/frequency deviation security is always considered a nonlinear constraint, which can lead to transient angle stability constraints (Xu et al., 2017), multi-operation modes constraints (Xu et al., 2019), voltage stability constraints (Al-Rubayi and Abd, 2020), stochastic correlation constraints (Jiang et al., 2019), etc. Some methods are used to enhance optimization efficiency, such as the constraint relaxation method (Li et al., 2017) and the parallel methods (Jiang, Wang and Geng, 2014; Gan et al., 2018). These approaches suffer from their slow reaction to the intense system state variation and require a specific to-decide time (Liu et al., 2022).

Artificial intelligence (AI) techniques have been identified as an effective and efficient data-driven tool for ELS problems and other power system applications, which can be divided into economic dispatch (Xu et al., 2017), operation (Mohandes et al., 2019) and planning (Deng and Lv, 2020). Its purpose is to find the approximation form of real electrical phenomena by learning the nonlinear mapping between operation features and targets from the offline or online database, in which the latter can update model parameters in a rolling manner. The neural networks (Zhang et al., 2015; Zhang et al., 2017) and deep learning methods (Yu et al., 2018) are proposed for the fast ELS problem. In (Wang et al., 2021), a load shedding contribution indicator is introduced as a load shedding criterion into the reward value function of dueling deep Q learning. In (Vu et al., 2021), a safe RL-based load shedding of power systems that can enhance the safe voltage recovery of the electric power grid after experiencing faults is proposed. In (Chen et al., 2023), An emergency load shedding method based on data-driven strategies and deep RL which constructs a typical mismatch scenario is proposed. Regarding ELS, the extreme learning machine (ELM) algorithm is applied in (Dai et al., 2012; Li et al., 2021) to maintain the frequency, which is further advanced in (Gomez-Exposito, Conejo and Caizares, 2008).

Although the reported methods show high effectiveness in solving ELS problems, they show the following inadequacies:

(1) The approach subdivides the load to be shed into precise-grained units and ideally treats users in low-voltage distribution areas as fully controllable entities. However, it overlooks the minimum units for load shedding and users’ controllable willingness based on cost, leading to a lack of practical operability.

(2) Using user-controllable cost as all known information for multi-objective optimization neglects the issue of information privacy. Moreover, this centralized solving approach may encounter infeasibility or excessive computation time when dealing with a large number of users, making it challenging to meet the time constraints for emergency load shedding.

(3) The methods lack a design to address the response time requirement of control instructions and apply a uniform direct optimization approach for all scenarios. This may result in situations where control decisions cannot be made within the required response time under high-speed response demands.

To fill the above gaps, this paper focuses on the precise ELS approach for distributed networks considering response time requirements. The main contributions of the proposed methods are as follows:

(1) Designing a precise emergency load shedding optimization process for distribution networks with different response time requirements; clarifying the load shedding control approach under various response time demands to ensure a rapid and effective response to load shedding instructions from the main station.

(2) Developing an emergency load shedding control method for distribution networks with low response time requirements, based on demand response; under high time requirements, giving priority to load shedding in regions with higher load importance to achieve fast load shedding in a short period.

(3) Building an emergency load shedding control method for distribution networks with low response time requirements, considering users’ willingness to respond; Incorporating the users’ winning demand response bid to mitigate the societal impacts of load shedding during emergencies and ensuring precise execution of main station instructions. Incorporate user-initiated response capabilities.

(4) Creating a fast load shedding control optimization method for distribution networks with low response time requirements, based on network partitioning; by equivalently dividing the distribution network into zones, reducing the complexity of load shedding optimization problems based on tie switches and supply switches, and achieving rapid load shedding with a certain level of accuracy.

Through verification with standard test cases, the proposed approach in this study effectively utilizes response time and demand-side resources to achieve precise emergency load shedding (ELS) control in distribution networks. The method is capable of providing fast load shedding with lower precision under high response time requirements, and appropriately balancing speed and accuracy for ELS under low response time requirements. These results demonstrate that the approach can adapt to different scenarios, offering an effective solution for rapid and accurate load shedding in distribution networks during emergencies.

2 Precise ELS optimization formulation

In actual load shedding control, to ensure the stability of the power system during extreme events, the most critical aspect is to execute the minimum load shedding commands within the required control time. However, the precise ELS control relies on the optimized consideration of discrete control objects such as power supply switches and tie switches between different branches. The resulting mixed-integer programming problem often requires lengthy optimization calculations and is not well-suited for load shedding commands with high response time requirements. Therefore, it is necessary to execute load shedding control commands differently for different response time requirements.

To address this, this study proposes two distinct methods for load shedding control based on different response time requirements. The first method is a fast ELS control based on the weighted method, suitable for high response time requirements. The second method is an optimal load shedding control considering demand response and network partitioning, specifically designed for low response time requirements. This approach achieves rapid load shedding control with lower accuracy for high response time requirements and appropriately paced load shedding control with higher accuracy for low response time requirements in the distribution network. The basic control logic is illustrated in the following flowchart Figure 1.

FIGURE 1

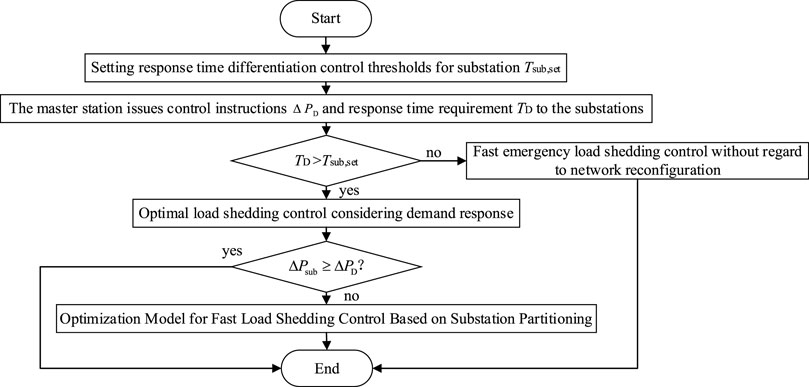
FIGURE 1. Optimization process for precise ELS at substations based on response time requirement differences.

2.1 Fast ELS control without regard to substation network reconfiguration

When the response time requirement issued by the master station is lower than the substation control threshold, the load shedding control process with a high response time requirement is activated. In the fast ELS control phase, to meet the response time requirement, the substation only performs disconnection operations on distribution line closing switches without regard to complex distribution network reconfiguration. Specifically, the substation determines the downstream load nodes that are affected by the resection of each closing switch and screen the switches to disconnect according to the control command and load importance ranking.

The specific process of the precise load shedding control strategy for the power grid without regard to network reconfiguration is shown in Figure 2. In this, offline phase before accepting the command, the substation computes the sets of downstream nodes supplied by different switches. This can usually be accomplished by graph-theoretic methods such as the shortest path method and does not take up command execution time. In the execution phase, the equivalent loss caused by the disconnection of each switch is calculated and sorted. The switches are added to the action switch set from smallest to largest until the control command is satisfied.

$K_s={\displaystyle \sum _{j\in {\mathcal{N}}_s}}{a}_j{p}_j(1)$

$\Delta P_{\text{sub}}={\displaystyle \sum _{s\in {\mathcal{S}}_{\mathrm{A}}}}{\displaystyle \sum _{j\in {\mathcal{N}}_s}}{p}_j(2)$

FIGURE 2

FIGURE 2. The specific process of the fast ELS control without regard to network reconfiguration.

Where, $K_s$ represents the equivalent loss after disconnecting switch s; ${\mathcal{N}}_s$ represents the set of downstream loads supplied by switch s; $a_j$ represents the importance of the $j$-th load (where higher values indicate greater significance); $p_j$ represents the active power of the $j$-th load; $\Delta P_{\text{sub}}$ represents the load shedding capacity of the substation; ${\mathcal{S}}_{\mathrm{A}}$ the set of switches to be disconnected;

2.2 Demand response-based ELS control method at substations under low response time requirement

When the response time requirement issued by the master station falls below the substation control threshold, the load shedding control process with a low response time requirement is activated. The demand response resources on the user side are abundant and can actively participate in the load shedding control process. Considering it can provide effective support for overall load control, this study incorporates the demand response resources that won bids in the ancillary service market and possesses fast response capabilities into the load shedding consideration.

Taking the common day-ahead solicitation type demand response as an example, the trading center collects the response volume and price reported by the user and determines the clearing price and the winning volume of the user. Then, the control substations and execution substations interact with the trading center to identify users’ specific adjustable boundaries. The control substations optimize the formulation of control instructions for adjustable resources at various nodes based on specific distribution network operation information and then proceed with the issuance. During the optimization control process of the controlling substations, the distribution network’s power flow constraints need to be considered, and the solution space for this optimization can be described as follows.

${\displaystyle \sum _{k:\left(j,k\right)\in \mathcal{L}}}{P}_{jk}={\displaystyle \sum _{i:\left(i,j\right)\in \mathcal{L}}}\left(P_{ij}-r_{ij}\frac{P_{ij}^2+Q_{ij}^2}{V_i^2}-p_j\right)(3)$

${\displaystyle \sum _{k:\left(j,k\right)\in \mathcal{L}}}{Q}_{jk}={\displaystyle \sum _{i:\left(i,j\right)\in \mathcal{L}}}\left(Q_{ij}-x_{ij}\frac{P_{ij}^2+Q_{ij}^2}{V_i^2}-q_j\right)(4)$

$V_j^2=V_i^2-2\left(r_{ij}{P}_{ij}+x_{ij}{Q}_{ij}\right)+\left(r_{ij}^2+x_{ij}^2\right)\frac{P_{ij}^2+Q_{ij}^2}{V_i^2}(5)$

$V_0=V_{\text{ref}}(6)$

$P_{ij}^2+Q_{ij}^2\le S_{ij}^2(7)$

$V_{i,\min }\le V_i\le V_{i,\max }(8)$

$P_{ij,\min }\le P_{ij}\le P_{ij,\max }(9)$

$Q_{ij,\min }\le Q_{ij}\le Q_{ij,\max }(10)$

Where,$\mathcal{L}$ represents the set of all branches in the distribution network, $P_{ij}$ and $Q_{ij}$ represent the active power flow and reactive power flow of the branch, respectively, $r_{ij}$ and $x_{ij}$ represent the resistance and reactance of the branch, respectively, $p_j$, $q_j$, $V_j$ represent the active and reactive power, and voltage at node $j$ , respectively, $V_{\text{ref}}$ represents the reference voltage at the upper-level grid connection point (node 0), in this study, the reference voltage per unit value is set to 1.05, $V_{i,\min }$ and $V_{i,\max }$ represents the upper and lower bounds of the voltage squared at node $i$, respectively, $P_{ij,\min }$, $P_{ij,\max }$, $Q_{ij,\min }$, $Q_{ij,\max }$ represent the active and reactive power limits of the branch $ij$, respectively, $S_{ij}$ represents the apparent power flowing through the branch.

Clearly, this constraint exhibits typical nonlinear non-convex characteristics, and solving it usually requires a considerable amount of time, with difficulty in guaranteeing optimality. This contradicts the requirement for load control to be fast and cost-effective. Therefore, this study considers introducing second-order cone relaxation to convexify the space of the aforementioned power flow constraints, and the results are as follows:

${\displaystyle \sum _{k:\left(j,k\right)\in \mathcal{L}}}{P}_{jk}={\displaystyle \sum _{i:\left(i,j\right)\in \mathcal{L}}}\left(P_{ij}-r_{ij}{l}_{ij}-p_j\right)(11)$

${\displaystyle \sum _{k:\left(j,k\right)\in \mathcal{L}}}{Q}_{jk}={\displaystyle \sum _{i:\left(i,j\right)\in \mathcal{L}}}\left(Q_{ij}-x_{ij}{l}_{ij}-q_j\right)(12)$

$U_j=U_i-2\left(r_{ij}{P}_{ij}+x_{ij}{Q}_{ij}\right)+\left(r_{ij}^2+x_{ij}^2\right)l_{ij}(13)$

$U_0=U_{\text{ref}}(14)$

$P_{ij}^2+Q_{ij}^2\le U_i{l}_{ij}(15)$

$U_{i,\min }\le U_i\le U_{i,\max }(16)$

$P_{ij,\min }\le P_{ij}\le P_{ij,\max }(17)$

$Q_{ij,\min }\le Q_{ij}\le Q_{ij,\max }(18)$

Where:$l_{ij}$ and $U_j$ represents the square of the current in branch $ij$ and the square of the voltage at node $j$, respectively.

For each node, its controllable resources on the load side can be aggregated (Lu et al., 2020), presenting clear controllable boundaries and participating in the demand response bidding market. Therefore, in the specific load shedding control process, the load-side resources can be simplified and considered as upper and lower limit constraints on node load regulation.

$p_{j,\text{base}}\ge p_j\ge p_{j,\text{base}}-\Delta p_{j,\max }(19)$

$q_{j,\text{base}}\ge q_j\ge q_{j,\text{base}}-\Delta q_{j,\max }(20)$

Where:$p_{j,\text{base}}$ and $q_{j,\text{base}}$ represent the pre-ELS reference active and reactive power at node $j$, respectively, $\Delta p_{j,\max }$ and $\Delta q_{j,\max }$ represent the total winning bid and corresponding reactive power in demand response for the users located at node j, respectively.

Furthermore, it is necessary to consider the response of substation load control to the master station. However, since even with the complete removal of demand response resources at the substations, it may still be challenging to ensure that the load shedding amount meets the master station’s control requirements. Therefore, it is difficult to include it directly as a constraint in the optimization model. In this regard, the constraint for the minimum response requirement is relaxed and formulated as a soft constraint in the optimization objective. Additionally, considering that the cost of load control under demand response is determined through market clearing, and the importance of load is not considered at this stage, the optimization objective is formulated as follows:

$\underset{\left\{p_j,q_j{U}_j{l}_{ij},P_{ij},Q_{ij}\right\}}{\min }{F}_1+F_2(21)$

$F_1={\displaystyle \sum _{j=1}^{n_{\mathrm{B}}}}\left(p_{j,\text{base}}-p_j\right)(22)$

$F_2=\alpha {\left(p_0-p_{0,\text{base}}-\Delta P_{\mathrm{D}}\right)}^2(23)$

Where:$F_1$ and $F_2$ represent the substation demand response compensation cost and penalty cost for instruction response deviation, respectively, $\alpha$ represents the penalty cost coefficient for instruction response deviation should be chosen as a relatively large constant (considered as 10,000 in this study) to ensure the priority fulfillment of the master station control instruction $\Delta P_D$, $n_{\mathrm{B}}$ represents the total number of nodes in the substation network, where node 0 is the connection point to the upper-level grid, $p_0$ represents the negative value of the power supplied by the upper-level grid.

Clearly, in this scenario, when there are sufficient demand response resources at the substations to respond to the master station’s control instructions, the optimization results will prioritize achieving response effectiveness and subsequently minimize the load shedding control. However, when it is not possible to fulfill the master station’s control instructions with the available resources, the optimization results will attempt to utilize all demand response resources as much as possible. Later on, the subsequent partitioned load shedding control model will provide support to compensate for any response shortfall.

2.3 Fast load shedding control optimization method based on substation partitioning under low response time requirement

As mentioned above, when the load shedding optimization at the substation based on demand response cannot fully meet the master station’s load shedding instruction, the load shedding control process described in this section will be activated. In this section, after fully utilizing the continuous adjustable demand-side resources, the focus will shift to consider the operation of tie switches and node supply substation switches in the substation grid. At this point, the problem will exhibit typical characteristics of a mixed-integer programming problem, and solving it will face difficulties due to the large-scale integer variables, making it challenging to fully satisfy the load shedding control time requirement.

In practice, it is often unnecessary to optimize load shedding for all global switch variables, as the control benefits gained from optimizing the entire system may not significantly improve compared to optimizing specific local regions. However, the computational cost required for solving the optimization for all global variables will substantially increase. Therefore, for engineering implementation purposes, this study adopts a partitioned optimization approach for load shedding control at the substations, aiming to narrow down the optimization scope as much as possible and achieve rapid switch actions within a short time. Specifically, by partitioning, the original large-scale problem is approximated into multiple small-scale problems. Each problem focuses on a part of integer variables, resulting in a decrease in time complexity for the problem. The control logic is illustrated in the Figure 3. The upper level optimization optimizes the contact switch state and subarea load-shedding commands to achieve coordination of the lower-level subregions.

FIGURE 3

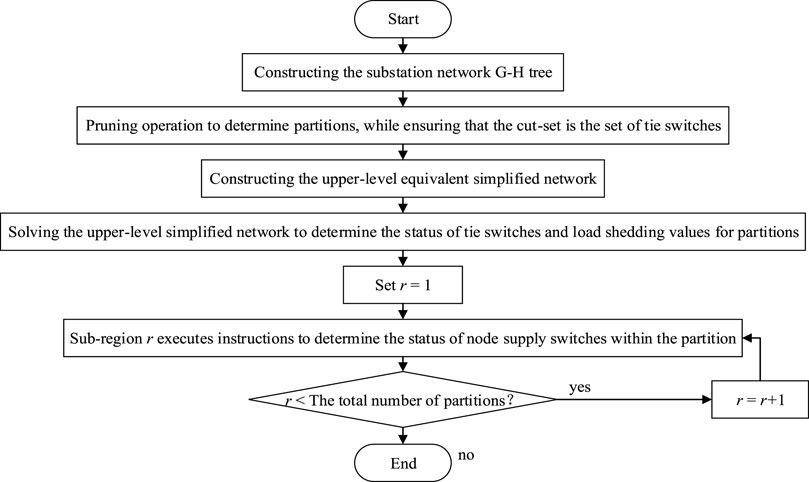
FIGURE 3. Fast load shedding control optimization method based on substation partitioning under low response time requirement.

2.3.1 Substation ELS global optimal control constraint model

After demand response, the controllable objects for ELS are all the controllable switches in the network. At this point, the network structure and the power supply to loads have changed, making it difficult to guarantee radial network constraints and power flow constraints. Therefore, in the optimal control at this stage, comprehensive considerations are necessary.

(1) Radial constraints in the distribution network

The current distribution network generally follows the principle of “closed-loop construction and open-loop operation” to ensure the effective operation of distribution network relay protection devices. Therefore, in reconstruction and other relevant optimization decisions after faults, the constraints of the radial network are usually crucial and cannot be ignored. Currently, many studies have focused on models related to commodity flow, but they have issues such as poor scalability and weak adaptability to large-scale networks. In contrast, the radial constraint method based on graph theory and maximum density has been proven to be a simpler and more general approach. Thus, this study adopts it as the radial network constraint model, and the expression is as follows:

$f_{ij}^{+}+f_{ij}^{-}=c_{ij},\forall \left(i,j\right)\in \mathcal{L}(24)$

${\displaystyle \sum _{j:\left(i,j\right)\in \mathcal{L}}}{f}_{ji}^{+}+{\displaystyle \sum _{j:\left(i,j\right)\in \mathcal{L}}}{f}_{ij}^{-}\le \frac{\left|\mathcal{N}\right|-\left|\mathcal{S}\right|}{\left|\mathcal{N}\right|-\left|\mathcal{S}\right|+1},\forall i\in \mathcal{N}/\mathcal{S}(25)$

${\displaystyle \sum _{i\in \mathcal{S}}}\left[{\displaystyle \sum _{j:\left(i,j\right)\in \mathcal{L}}}{f}_{ji}^{+}+{\displaystyle \sum _{j:\left(i,j\right)\in \mathcal{L}}}{f}_{ij}^{-}\right]\le \frac{\left|\mathcal{N}\right|-\left|\mathcal{S}\right|}{\left|\mathcal{N}\right|-\left|\mathcal{S}\right|+1}(26)$

$f_{ji}^{+},f_{ij}^{-}\ge 0,\forall \left(i,j\right)\in \mathcal{L}(27)$

Where:$\mathcal{N}$ and $\mathcal{S}$ represent the set of internal nodes in the distribution network and the set of supply nodes from the upper-level grid have the number of elements as $\left|\mathcal{N}\right|$ and $\left|\mathcal{S}\right|$, respectively, $c_{ij}$ is binary variable that represents the connectivity status of branch $ij$ (0 for disconnected, 1 for connected), $f_{ij}^{+}$ and $f_{ij}^{-}$ represents the auxiliary variable, with a value greater than or equal to 0.

(2) Distribution network power flow constraints considering line transfers and load supply constraints

In the previous section, this study has already introduced the second-order cone relaxation results for distribution network power flow constraints, which are applicable only to modeling power flow in a deterministic topology and not suitable for scenarios involving dynamic line transfers and load shedding. Therefore, this study introduces integer variables to describe load transfers and load shedding constraints separately and establishes their correlation with radial network constraints. The expressions Eqs 11–13) are rewritten as Eqs 28–30), and expressions (Eqs 17, 18) are rewritten as (Eqs 31, 32). Additionally, expressions (Eqs 33, 34) are included to implement faulted line constraints and their correlation with radial constraints. The resulting power flow constraints are as follows:

${\displaystyle \sum _{k:\left(j,k\right)\in \mathcal{L}}}{P}_{jk}={\displaystyle \sum _{i:\left(i,j\right)\in \mathcal{L}}}\left(P_{ij}-r_{ij}{l}_{ij}-w_j{p}_j\right)(28)$

${\displaystyle \sum _{k:\left(j,k\right)\in \mathcal{L}}}{Q}_{jk}={\displaystyle \sum _{i:\left(i,j\right)\in \mathcal{L}}}\left(Q_{ij}-x_{ij}{l}_{ij}-w_j{q}_j\right)(29)$

$\left\{\begin{array}{cc}{U}_j-U_i=-2\left(r_{ij}{P}_{ij}+x_{ij}{Q}_{ij}\right),& \text{if\hspace{0.17em}}{z}_{ij}=1\\ -\infty \le U_j-U_i\le \infty ,& \text{if\hspace{0.17em}}{z}_{ij}=0\end{array}\right.(30)$

$z_{ij}{P}_{ij,\min }\le P_{ij}\le z_{ij}{P}_{ij,\max }(31)$

$z_{ij}{Q}_{ij,\min }\le Q_{ij}\le z_{ij}{Q}_{ij,\max }(32)$

$z_{ij}=c_{ij}(33)$

$z_{ij}=1,\forall \left(i,j\right)\notin \mathcal{B}(34)$

Where:$z_{ij}$ is binary variable which represents the connectivity control status of branch $ij$, where 0 indicates that branch $ij$ is disconnected (open), and 1 indicates that branch $ij$ is connected (closed), $w_j$ is binary variable which represents the load shedding instruction for node j, where 0 indicates load shedding (cut-off), and 1 indicates no load shedding (not cut-off), $\mathcal{B}$ represents the set of branches with tie switches.

As can be seen, expression Eq. 30) is a significant logical constraint, which can be linearized as follows:

$\left\{\begin{array}{l}O-\left(1-z_{ij}\right)M\le U_j-U_i\le O+\left(1-z_{ij}\right)M\\ O=-2\left(r_{ij}{P}_{ij}+x_{ij}{Q}_{ij}\right)\end{array}\right.(35)$

Where:$O$ represents continuous auxiliary variable, $M$ represents a very large constant.

(3) Optimization objective

Different from the load shedding step in demand response where controllable resources are limited, the constraints on the response to the main station control instructions can be relaxed and converted into penalty terms in the optimization objective. This step is the final stage of precise load shedding, and it must strictly satisfy the constraints of the main station control instructions. Therefore, at this stage, load shedding should minimize its impact while meeting the requirements of the control instructions. The corresponding constraints and objectives are shown below.

$\underset{\left\{z_{ij},a_j,f_{ij}^{+},f_{ij}^{-},P_{ij},Q_{ij}\right\}}{\max }{\displaystyle \sum _{j\in \mathcal{N}}}\left(w_j{a}_j{p}_j\right)(36)$

$p_0\ge p_{0,\text{base}}+\Delta P_{\mathrm{D}}(37)$

2.3.2 Partitioning method for substation distribution network based on Gomory-Hu algorithm

As can be seen, to fully describe the network constraints and load shedding constraints in the distribution network, the load control model introduces a large number of integer variables. The overall optimization problem belongs to a complex mixed-integer problem, and its solution process will require a considerable amount of computation time, making it difficult to meet the requirements of load control speed. Therefore, this study considers partitioning the overall power grid, establishing an equivalent simplified network, determining the optimization results of the equivalent network, and then performing small-scale optimization control. One of the key aspects of partitioning is to ensure the consistency of distribution network constraints before and after partitioning. The distribution of tie switches should be an important basis for partitioning to avoid conflicts in radial network constraints between partitions. Please refer to the Figure 4 for more details.

FIGURE 4

FIGURE 4. Partitioning schematic diagram.

As can be seen in the schematic on the left side of the diagram, the partitioning includes branches with tie switches, and the equivalent simplified network with radial topology requires coordination of internal switches. This necessitates the design of an appropriate iterative method to achieve connectivity coordination. On the right side of the partitioning, there are no tie switches in the internal branches, so only ensuring the connectivity constraint of the optimized simplified network is required, making it an ideal partitioning method.

In practice, to achieve the ideal partitioning method mentioned above, the goal is to include tie switches in the cutting planes as much as possible. This problem can be transformed into a classic graph theory partitioning problem. Therefore, this study introduces the Gomory-Hu algorithm to achieve the ideal partitioning of the substation distribution network.

(1) Transformation of the minimum cut problem in an undirected weighted graph

First, transform the substation network into an undirected weighted graph $G=\left(V,E\right)$, where $V$ is the set of nodes, and $E$ is the set of edges formed by branches. The weight of each edge can be set based on the presence or absence of tie switches; if there is a tie switch, the weight of the edge is set to 1, and if there is no tie switch, it is set to a large value (determined based on the network size, usually set to 100), as follows:

$\left\{\begin{array}{cc}\omega \left(u,v\right)=1,& \text{if\hspace{0.17em}}\left(u,v\right)\in \mathcal{B}\\ \omega \left(u,v\right)=100,& \text{if\hspace{0.17em}}\left(u,v\right)\notin \mathcal{B}\end{array}\right.(38)$

Where:$u$ and $v$ represent the node $u$ and node $v$, respectively, $\left(u,v\right)$ and $\omega \left(u,v\right)$ represent the edge between nodes $u$ and $v$ and their corresponding weight values.

Consequently, the partitioning of the power grid can be viewed as a division of the node set $V$. All nodes in graph $G$ can be divided into two sets, denoted as $S$ and $T$. If nodes $u\in S$ and $v\in T$ are involved, this partition is referred to as a cut concerning $u$ and $v$. The edges $\left(u,v\right)\in E$ involved in this cut are known as cut edges, and the capacity of the cut is defined as the sum of all cut edges.

Based on this, the minimum cut for nodes $u$ and $v$ refers to the cut $\left(u,v\right)$ with the smallest capacity. Therefore, solving the problem of the optimal partitioning of the power grid is equivalent to finding the minimum cut of graph $G$. Assuming that the power grid is divided into $k$ disjoint sets $C_1,C_1,\dots ,C_k$, the minimum cut problem can be represented as follows:

$\min {\displaystyle \sum _{i=1}^{k-1}}{\displaystyle \sum _{j=i+1}^k}{\displaystyle \sum _{u\in C_i,v\in C_j}}\omega \left(u,v\right),k\in \left\{\mathrm{2,3},\cdots ,\left|V\right|\right\}(39)$

As shown in the above equation, the computational complexity is $\mathrm{O}\left({\left|V\right|}^2\right)$, which becomes impractical when the number of network nodes or $k$ is large. It is almost impossible to find the optimal solution through numerical simulations on a computer. Therefore, this study considers using the Gomory-Hu algorithm to solve the minimum cut problem and divide the power grid into different load shedding control regions.

(2) The Gomory-Hu algorithm

The Gomory-Hu algorithm is an effective method for solving graph partitioning problems, and it has the characteristic of providing the theoretically optimal solution.

The equivalent Gomory-Hu tree (G-H tree) of the graph is constructed by computing the maximum flow minimum cut problem $\left|V\right|-1$ times (with a computational complexity of $\mathrm{O}\left(\left|V\right|\right)$). The G-H tree can represent the minimum cut value between any adjacent pair of nodes in an undirected weighted graph and preserves the complete structural information of the original graph, making it easier to map the partitioning results back to the original graph. The steps to construct the equivalent G-H tree are as follows:

1) Initialization: Set the iteration count as the set of regions formed after the partitioning graph $G$. Initially, $Z=G$;

2) Arbitrarily choose one partition to obtain a subregion $Z_i\subset Z$, $\left|V_{Z_i}\cap V\right|>1$ from $Z$;

3) Arbitrarily select a pair of nodes $\left\{u,v\right\}\subset \left(V_{Z_i}\cap V\right)$ from the region $Z_i$;

4) Find the minimum cut between nodes $u$ and $v$, and divide $Z_i$ into two subregions $S_{Z_i}$ and $T_{Z_i}$; (the complexity of this minimum cut problem is only $\mathrm{O}\left(\left|V\right|\right)$);

5) Translation: Add a new edge $e_{S_{Z_i},T_{Z_i}}$ between regions $S_{Z_i}$ and $T_{Z_i}$, and set its weight to be the capacity of the minimum cut;

6) Update the edge weights between the nodes in regions $S_{Z_i}$ and $T_{Z_i}$, as well as between the nodes and the regions:

$\omega \left(u,T_{Z_i}\right)={\displaystyle \sum _{v\in T_{Z_i}}}\omega \left(u,v\right),\forall u\in S_{Z_i}(40)$

$\omega \left(v,S_{Z_i}\right)={\displaystyle \sum _{u\in S_{Z_i}}}\omega \left(u,v\right),\forall v\in T_{Z_i}(41)$

7) Update the set $Z$ to include the new regions $S_{Z_i}$ and $T_{Z_i}$.

8) If $i\le \left|V\right|-1$, go back to step 2); otherwise, proceed to step 9);

9) Obtain the equivalent Gomory-Hu tree $G^{\prime }=\left(V^{\prime },E^{\prime }\right)$, where $V^{\prime }=V\cap V_Z$, $E^{\prime }=W$.

On the equivalent Gomory-Hu tree $G^{\prime }=\left(V^{\prime },E^{\prime }\right)$, each edge weight represents the minimum cut value between two nodes. Arrange the edge weights in ascending order and select edges with weights less than 100 as the basis for partitioning. Remove these selected edges to obtain the final partitioning result. Map the partitioning result back to the original graph $G$ to obtain the optimal partitioning of the network.

2.3.3 Fast load shedding control optimization model based on substation partitioning

After completing the partitioning, the next step is to consider how to achieve simplified solutions to the above global optimization problem based on the partitioning. Taking the example of the diagram below, if the internal network structure within each partition is ignored (since the voltage drop in the distribution network sub-area is relatively small, ignoring the small-scale scope is in line with engineering requirements), the original 9-node distribution network topology can be simplified to a 3-node network.

At this point, the original global optimization problem can be approximately simplified into a two-level hierarchical problem. In the upper level, optimization is performed based on the obtained simplified network to determine the status of interconnecting switches and identify the subregions for load shedding tasks. Based on the upper-level optimization results, a precise-grained optimization of node load supply switches is conducted for the designated load shedding areas in the lower level. The optimization models for the upper and lower levels can be expressed as follows.

(1) Upper simplified model

In the upper simplified model, the control substations will optimize the partitioned equivalent network, and the discrete load-shedding commands are relaxed as continuous variables. In addition, the optimization objective is to minimize the impact of load shedding. And the importance of load shedding in each region is determined based on the average importance of unit load shedding within the region, as calculated by the following formula:

$a_i^{\prime }=\left({\displaystyle \sum _j^{n_i}}{a}_j{p}_j\right)/\left({\displaystyle \sum _j^{n_i}}{p}_j\right)(42)$

Where:$n_i$ represents the total load count in the equivalent node of region $i$, $a_i^{\prime }$ represents the average importance of the equivalent node load.

The overall optimization model can be listed as follows:

$\begin{array}{c}\underset{\left\{z_{ij}^{\prime },a_j^{\prime },f_{ij}^{’+},f_{ij}^{’-},P_{ij}^{\prime },Q_{ij}^{\prime }\right\}}{\min }{\displaystyle \sum _{j\in \mathcal{N}}}{\left(a_j^{\prime }\left(p_j^{\prime }-p_{j,\text{base}}^{\prime }\right)\right)}^2\\ s.t.\left(1\right)-\left(6\right),\left(14\right)-\left(17\right),\left(21\right)-\left(23\right),\left(25\right),\left(27\right)\end{array}(43)$

Where:${\left(•\right)}^{\prime }$ represents the equivalent network parameters.

The objective is set as the square of the load shedding impact to evenly distribute the load shedding instructions among the subregions as much as possible.

(2) Lower optimization model

At this point, the upper model publishes the obtained results to each subregion, and each subregion performs optimization control based on the received results. At this stage, the internal subregion no longer needs to consider the radial network constraints; it only needs to control the internal node supply switches to meet the control instructions from the upper layer. Here, the power of the corresponding branches is calculated based on the solution obtained from the upper layer model. The interconnection branches between region $r$ and other regions are abstracted as source nodes, and a certain upward adjustment range (set as 1 in this study) is defined to meet the power balance requirements. The control response constraint can be expressed as follows:

${\displaystyle \sum _{j\in \mathcal{S}\left(r\right)}}\left(-p_j\right)\le p_r^{\prime }(44)$

Where:$\mathcal{S}\left(r\right)$ represents the set of source nodes in region $r$.

In summary, the model can be expressed as follows:

$\begin{array}{c}\underset{\left\{a_j,w_j,P_{ij},Q_{ij}\right\}}{\max }{\displaystyle \sum _{\begin{array}{l}j\in \mathcal{N}\left(r\right)\\ j\notin \mathcal{S}\left(r\right)\end{array}}}\left(w_j{a}_j{p}_j\right)\\ s.t.\left(18\right)-\left(19\right),\left(4\right)-\left(7\right),\left(35\right)\end{array}(45)$

By now, the large-scale mixed-integer programming problem has been simplified into several small-scale mixed-integer programming problems within each subregion, significantly improving the overall efficiency of the solution. Taking Figure 5 as an example, the time complexity of the original problem is reduced from $O\left(2^{12}\right)$ to $3\times O\left(2^4\right)$. The time complexity of both the upper level problem and each lower level problem is $O\left(2^4\right)$. It ensures the response to the main station’s instructions and effectively addresses the speed issues related to precise-grained optimization.

FIGURE 5

FIGURE 5. Schematic diagram of network topology simplification.

3 Case study

3.1 Case setup

To validate the effectiveness of the load shedding control algorithm proposed in this study, we selected the IEEE-33 standard test case as the substation network for testing and verification. The network structure of the test case is shown in Figure 6 and Table 1. In this case, the distribution network has controllable telecommunication equipment deployed on the branch with the following numbered set $\left\{\mathrm{0,3,12,32,33,34,35,36}\right\}$, and the power supply of each node is determined by the status of a controllable switch. As shown in the diagram below, the first-level load node set is $\left\{\mathrm{3,8,9,15,18,20,25}\right\}$, and the second-level load node set is $\left\{\mathrm{4,7,10,11,14,16,17,26,30,31}\right\}$. The details of each line number and its associated nodes are shown in the table below (with impedance parameters as in the standard test case).

FIGURE 6

FIGURE 6. IEEE-33 topology.

TABLE 1

TABLE 1. Network line connection information.

Furthermore, the total load at each node in the substation network (normalized with a base voltage of 10 kV and a base capacity of 5.68 MW), the demand response adjustable amount, and their importance (calculated from the previous sections) can be summarized in the following Table 2.

TABLE 2

TABLE 2. Network line connection information.

Regarding the scenario settings, to verify the effectiveness of the proposed precise-grained ELS optimization method for different response time requirements, there are three emergency load control scenarios based on varying response time demands and main station load shedding instructions. The scenarios are as follows, with a time response gap threshold set at 5 s:

Scenario 1: The main station issues a control instruction to limit the substation’s power consumption to no more than 0.6 (per unit value) with a response time of 4 s.

Scenario 2: The main station issues a control instruction to limit the substation’s power consumption to no more than 0.6 (per unit value) with a response time of 6 s.

Scenario 3: The main station issues a control instruction to limit the substation’s power consumption to no more than 0.3 (per unit value) with a response time of 8 s.

All the examples in this chapter were simulated on a computer with an Intel(R) Core(TM) i7-7700 CPU, operating at a frequency of 3.60 GHz, and 8 GB of memory. The optimization problems were solved using the Gurobi solver in Python 3.7.

3.2 Simulation results and analysis of numerical examples

Scenario 1, 2, and 3 respectively represent the triggering of different load shedding control links in this project. The specific analysis is as follows.

3.2.1 Scenario 1 simulation result analysis

In scenario one, the response time requirement is 4 s, which is below the time response difference threshold. Therefore, the load shedding control enters the high time response control phase. In this case, the substation is also the executing station. It directly controls the normally closed switches for ELS control. The results are shown in Figure 7 and Figure 8.

FIGURE 7

FIGURE 7. Scenario 1 branch 12 contact switch action control result.

FIGURE 8

FIGURE 8. Scenario 1 branch 3 contact switch action control result.

In this control phase, the current power supply value from the upper-level grid is 0.6872 (the power injection at node 0, assuming it is obtained from the optimal power flow calculation with minimum line losses). In this control phase, the normally closed switch on branch 12 (between nodes 12 and 13) is opened, and the load at nodes 13 to 17 is shed, resulting in an overall load shedding of 0.0687. The load shedding action at this point is not sufficient to meet the main station’s load control instruction (0.6872–0.0687 > 0.6).

Therefore, the substation will make further decisions and open the interconnection switch at nodes 3 and 4 (branch 3–4), resulting in a total load shedding of 0.3724, which meets the main station’s control instruction requirement. The decision is then issued accordingly.

Overall, under high response time requirements, the decision-making time for fast load shedding actions can be negligible. The resulting unplanned load shedding impact on society is 0.065107 (obtained by multiplying the load shedding amount by its importance). It can be observed that load shedding actions in the distribution network under high time response requirements can effectively achieve load shedding in a short time and reliably execute main station instructions. However, there is a significant over-shedding in the control total, which will result in a certain impact on load control.

3.2.2 Scenario 2 simulation result analysis

In Scenario 2, the total load control from the main station is the same as in Scenario 1, but the response time requirement is 6 s, which is higher than the time response gap threshold. Therefore, the load control enters the low response time requirement phase based on demand response for substation ELS. At this time, the substation completes load shedding control by invoking demand response resources. The load values before and after load shedding for each node are shown in the Figure 9.

FIGURE 9

FIGURE 9. Adjustment results of demand response for each node in Scenario 2.

As seen, different nodes have been called to varying degrees in response to demand response resources. Nodes at the end of the power supply are prioritized for adjustment to reduce overall network losses, thereby compressing the total load shedding value under the load control command. The changes in upper-level power supply and user-side response before and after load shedding are further presented in Table 3. It is evident that the substation now closely adheres to the main station’s control instructions. Compared to Scenario 1, which exhibited significant over-shedding, the demand response resources are effectively utilized in this case, achieving precise load control with a solution time of 0.064 s, meeting the power grid’s load shedding response time requirements.

TABLE 3

TABLE 3. Result before and after control in Scenario 2.

3.2.3 Scenario 3 simulation result analysis

(1) Partition result

In this scenario, the main station’s response command is set to 0.3, which is lower than the adjustable capacity of the load-side demand response resources. Therefore, after fully utilizing the demand response resources, it will further enter the fast zone partition load shedding action stage. The connection relationships of the Gomory-Hu tree for the current substation network can be obtained through offline calculations, as shown in Table 4. The weight of branches with controllable tie switches is set to 1, while branches without controllable tie switches weight 100.

TABLE 4

TABLE 4. G-H tree connection relationships and weights.

Clearly, among the branches, the ones with weights lower than 100 are (1,0), (5,1), and (14,8). Resolving them visually, the partition is divided into 4 regions as follows:

1. Region 1: $\left\{0\right\}$ 2. Region 2: $\left\{\mathrm{1,2,3,22,23,24,18,19,20,21}\right\}$ 3. Region 3: $\left\{\mathrm{5,4,6,7,8,9,10,11,12,25,26,27,28,29,30,31,32}\right\}$ 4. Region 4: $\left\{\mathrm{14,13,15,16,17}\right\}$

After mapping it back to the original substation network, the specific partition is shown in the Figure 10 and Figure 11. The branches with controllable tie switches are all included in the cut set.

FIGURE 10

FIGURE 10. G-H characterization result.

FIGURE 11

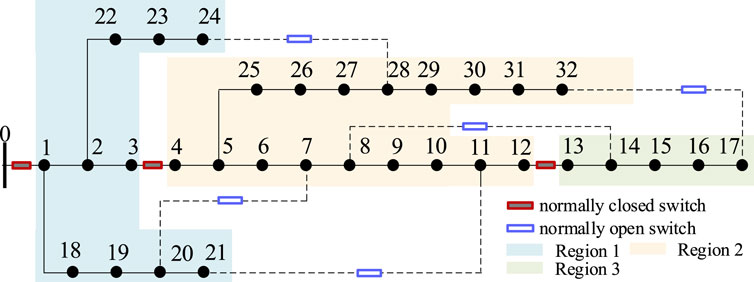
FIGURE 11. Substation network partition result. (2) Analysis of load control execution based on demand response

Based on the obtained partitioning results, rapid load control is executed. At this point, since the load control response time requirement is greater than the threshold, it enters the demand response load control stage first. The results are shown in the Table 5 and Figure 12. It can be seen that the demand response resources are fully activated, but the response results do not meet the requirements of the main station control instructions. Therefore, it will further enter the rapid partitioning load control stage.

FIGURE 12

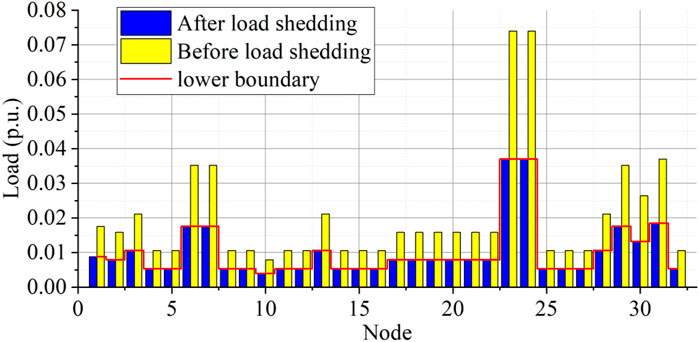
FIGURE 12. Adjustment results of demand response for each node in Scenario 3. (3) Analysis of load control execution based on fast partition action

TABLE 5

TABLE 5. Result before and after demand response control in Scenario 3.

Based on the results obtained from the load control response, the power grid status is updated, and the obtained results are fed into the optimization calculation of the upper simplified network. The equivalent simplified network, derived from the obtained partitioning results, is shown in Figure 13.

FIGURE 13

FIGURE 13. Equivalent simplified network topology.

By summing up the loads within each partition and considering each partition’s load as a continuous adjustable variable, we can obtain the model given in equations Eqs 32–34). With this, we complete the optimization calculation for the upper level. At this point, the upper-level problem needs to deal with integer variables for the status of the interlocking switches, with a total of 8 variables. The problem size is small, and the solution time is only 0.0788 s. The results are shown in Table 6 and Table 7.

TABLE 6

TABLE 6. Partition control upper layer contact switch branch results in Scenario 3.

TABLE 7

TABLE 7. Status before and after controlling each subregion in Scenario 3.

It can be observed that the upper-level optimization results distribute the load shedding branches as evenly as possible among the different regions, and the allocated results are consistent with the importance of each region’s load. Subregion 2 has low importance, and its control amount is the largest, which is 0.0101. On the other hand, Subregion 4 has the highest load importance, with a load shedding control amount of 0.0075, which is the smallest within the region. Subregion 3 has a load shedding instruction of 0.099.

After obtaining their respective control instructions, each region updates its network parameters and obtains the model Eqs 35–37) for solving independently. At this stage, the decision variables for each region are the states of the node supply switches, determining whether the load points are supplied or not. Compared to the global solution, the number of integer variables is greatly reduced. The load shedding results and solving time for each region are shown below.

Considering that the optimization of each subregion can be conducted in parallel, the overall optimization time for load control is the sum of the maximum computation time in the subregions and the solution time for the upper-level problem. It can be observed that the maximum optimization computation time for each subregion is 0.0598 s. When combined with the upper-level problem’s solution time of 0.0788 s, the overall computation time required is 0.1386 s. To demonstrate the necessity of subregion partitioning in this study, a comparison is made with the centralized optimization results without subregion partitioning. This refers to the optimization results obtained from the global optimal control model Eqs 14–27). The comparison between the optimization results of the centralized model and the subregion-based control model proposed in this study is shown in the Figure 14. The Tables 8, 9 illustrate the connection between upper-level instructions and lower-level decision outcomes. It shows the subregions’ accurate execution of the upper-level instructions.

FIGURE 14

FIGURE 14. Global optimal control model results. Fast partition optimal control model results.

TABLE 8

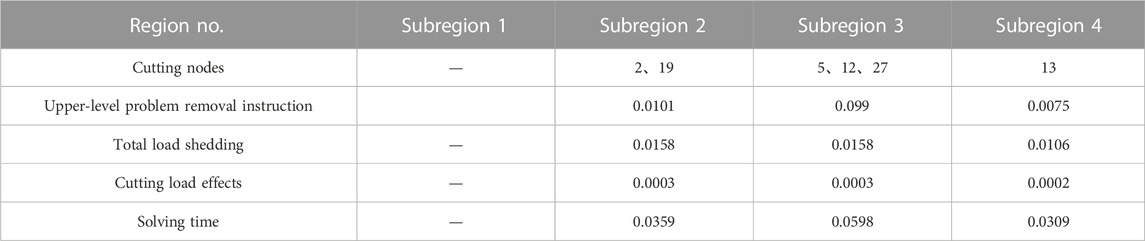
TABLE 8. Internal control actions in each subregion (subregion 1 as the upper-level grid injection node) in Scenario 3.

TABLE 9

TABLE 9. Internal control actions in each subregion (subregion 1 as the upper-level grid injection node) in Scenario 3.

As observed, the subregion-based control optimization exhibits some degree of over-shedding. However, the overall over-shedding is not significant and primarily occurs in less critical load nodes. Meanwhile, the corresponding computational time has significantly improved. The time it takes to solve the problem after partitioning is only 1/38th of the global control. This meets the requirement for rapid load shedding control effectively.

4 Conclusion

To achieve precise-grained ELS control in extreme events and ensure the safety, stability, and economy of the power system, avoiding excessive over-shedding which increases control costs, as well as issues related to unstable limits in under-shedding, overloaded tie lines, and bus voltage problems, this study focuses on effectively utilizing the adjustable capacity of distributed resources and formulating precise load shedding control strategies to achieve a balance between economic and safety objectives. In this section, the specific work of this study is as follows:

(1) A precise ELS approach for distributed networks considering response time requirements is proposed. For the differences in control instruction response time requirements, this study devised a fast load shedding control method based on the weight method for high response time requirements, and an optimal load shedding control method considering demand response and controllable switches for low response time requirements. Under high response time requirements, the main station’s instructions are rapidly responded to by controlling the tie-line switches simply and quickly. Under low response time requirements, the demand response resources are fully utilized for load shedding control, and for the portion exceeding the demand response adjustability, a hierarchical and partitioned control method is employed to achieve rapid response to the main station’s instructions.

(2) Through validation with standard test cases, the proposed method in this study effectively utilizes response time and demand-side resources, achieving fast ELS with lower precision under high response time requirements, and appropriate ELS with higher precision under low response time requirements for the distribution network.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

CL: Methodology, Writing–original draft. TP: Methodology, Writing–original draft. ZM: Methodology, Writing–original draft. XJ: Writing–review and editing. XC: Writing–review and editing. HL: Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. Supported by the National Key R&D Program of China for International S&T Cooperation Projects (2019YFE0118700). China Southern Power Grid Company Limited Science and Technology Project Support (Project Number: [036000KK52222004(GDKJXM20222117)]).

Conflict of interest

Authors CL, ZM, and XC were employed by Electric Power Dispatching Control Center of Guangdong Power Grid Co., Ltd. Authors TP, XJ, and HL were employed by China Southern Power Grid Company Ltd.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Al-Rubayi, R., and Abd, M. (2020). Emergency load shedding for voltage stability enhancement: with particular reference to the iraqi national power grid. Int. J. Intelligent Eng. Syst. 13 (2), 52–62. doi:10.22266/ijies2020.0430.06

CrossRef Full Text | Google Scholar

Chen, H., Zhuang, J., Zhou, G., Wang, Y., Sun, Z., and Levron, Y. (2023). Emergency load shedding strategy for high renewable energy penetrated power systems based on deep reinforcement learning. Energy Rep. 9, 434–443. doi:10.1016/j.egyr.2023.03.027

CrossRef Full Text | Google Scholar

Dai, Y., Xu, Y., Dong, Z. Y., Wong, K. P., and Zhuang, L. (2012). Real-time prediction of event-driven load shedding for frequency stability enhancement of power systems. Iet Generation Transm. Distribution 6 (9), 914–921. doi:10.1049/iet-gtd.2011.0810

CrossRef Full Text | Google Scholar

Deng, X., and Lv, T. (2020). Power system planning with increasing variable renewable energy: a review of optimization models. J. Clean. Prod. 246, 118962. doi:10.1016/j.jclepro.2019.118962

CrossRef Full Text | Google Scholar

Gan, G., Zhu, Z., Geng, G., and Jiang, Q. (2018). An efficient parallel sequential approach for transient stability emergency control of large-scale power system. IEEE Trans. Power Syst. 33 (6), 5854–5864. doi:10.1109/tpwrs.2018.2826534

CrossRef Full Text | Google Scholar

Gomez-Exposito, A., Conejo, A. J., and Caizares, C. (2008). Electric energy systems: analysis and operation. Boca Raton, Florida, United States: CRC Press.

Google Scholar

Jiang, Q., Wang, Y., and Geng, G. (2014). A parallel reduced-space interior point method with orthogonal collocation for first-swing stability constrained emergency control. IEEE Trans. Power Syst. 29 (1), 84–92. doi:10.1109/tpwrs.2013.2275175

CrossRef Full Text | Google Scholar

Jiang, Y., Chen, X., Peng, S., Du, X., Xu, D., Tang, J., et al. (2019). Study on emergency load shedding of hybrid AC/DC receiving-end power grid with stochastic, static characteristics-dependent load model. Energies 12 (20), 3912. doi:10.3390/en12203912

CrossRef Full Text | Google Scholar

Li, Q., Xu, Y., and Ren, C. (2021). A hierarchical data-driven method for event-based load shedding against fault-induced delayed voltage recovery in power systems. IEEE Trans. Industrial Inf. 17 (1), 699–709. doi:10.1109/tii.2020.2993807

CrossRef Full Text | Google Scholar

Li, Z., Yao, G., Geng, G., and Jiang, Q. (2017). An efficient optimal control method for open-loop transient stability emergency control. IEEE Trans. Power Syst. 32 (4), 2704–2713. doi:10.1109/tpwrs.2016.2629620

CrossRef Full Text | Google Scholar

Liu, J., Zhang, Y., Meng, K., Dong, Z. Y., Xu, Y., and Han, S. (2022). Real-time emergency load shedding for power system transient stability control: a risk-averse deep learning method. Appl. Energy 307, 118221. doi:10.1016/j.apenergy.2021.118221

CrossRef Full Text | Google Scholar

Lu, X., Li, K., Xu, H., Wang, F., Zhou, Z., and Zhang, Y. (2020). Fundamentals and business model for resource aggregator of demand response in electricity markets. Energy 204, 117885. doi:10.1016/j.energy.2020.117885

CrossRef Full Text | Google Scholar

Mohandes, B., Moursi, M. S. E., Hatziargyriou, N., and Khatib, S. E. (2019). A review of power system flexibility with high penetration of renewables. IEEE Trans. Power Syst. 34 (4), 3140–3155. doi:10.1109/tpwrs.2019.2897727

CrossRef Full Text | Google Scholar

Vu, T. L., Mukherjee, S., Yin, T., Huang, R., Tan, J., and Huang, Q. (2021). “Safe reinforcement learning for emergency load shedding of power systems,” in Proceedings of the 2021 IEEE Power & Energy Society General Meeting (PESGM), Washington, DC, USA, July, 2021.

CrossRef Full Text | Google Scholar

Wang, C., Yu, H., Chai, L., Liu, H., and Zhu, B. (2021). Emergency load shedding strategy for microgrids based on dueling deep Q-learning. IEEE Access 9, 19707–19715. doi:10.1109/access.2021.3055401

CrossRef Full Text | Google Scholar

Xu, T., Li, C., Liu, Y., Liu, C., Su, D., Xu, C., et al. (2019). “Optimization of emergency load shedding based on cultural particle swarm optimization algorithm,” in Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, June, 2019, 1208–1212. doi:10.1109/CEC.2019.8789990

CrossRef Full Text | Google Scholar

Xu, X., Zhang, H., Li, C., Liu, Y., Li, W., and Terzija, V. (2017). Optimization of the event-driven emergency load-shedding considering transient security and stability constraints. IEEE Trans. Power Syst. 32 (4), 2581–2592. doi:10.1109/tpwrs.2016.2619364

CrossRef Full Text | Google Scholar

Yu, J. J. Q., Hill, D. J., Lam, A. Y. S., Gu, J., and Li, V. O. K. (2018). Intelligent time-adaptive transient stability assessment system. IEEE Trans. Power Syst. 33 (1), 1049–1058. doi:10.1109/tpwrs.2017.2707501

CrossRef Full Text | Google Scholar

Zhang, R., Xu, Y., Dong, Z. Y., and Wong, K. P. (2015). Post-disturbance transient stability assessment of power systems by a self-adaptive intelligent system. IET Generation, Transm. Distribution 9 (3), 296–305. doi:10.1049/iet-gtd.2014.0264

CrossRef Full Text | Google Scholar

Zhang, Y., Xu, Y., Dong, Z. Y., Xu, Z., and Wong, K. P. (2017). Intelligent early warning of power system dynamic insecurity risk: toward optimal accuracy-earliness tradeoff. IEEE Trans. Industrial Inf. 13 (5), 2544–2554. doi:10.1109/tii.2017.2676879

CrossRef Full Text | Google Scholar