A runoff-based hydroelectricity prediction method based on meteorological similar days and XGBoost model

This paper proposes a runoff-based hydroelectricity prediction method based on meteorological similar days and XGBoost model. Accurately predicting the hydroelectricity supply and demand is critical for conserving resources, ensuring power supply, and mitigating the impact of natural disasters. To achieve this, historical meteorological and runoff data are analyzed to select meteorological data that are similar to the current data, forming a meteorological similar day dataset. The XGBoost model is then trained and used to predict the meteorological similar day dataset and obtain hydroelectricity prediction results. To evaluate the proposed method, the hydroelectricity cluster in Yunnan, China, is used as sample data. The results show that the method exhibits high prediction accuracy and stability, providing an effective approach to hydroelectricity prediction. This study demonstrates the potential of using meteorological similar days and the XGBoost model for hydroelectricity prediction and highlights the importance of accurate hydroelectricity prediction for water resource management and electricity production.

1 Introduction

In recent years, with the rapid development of distributed small hydropower, its position in the field of clean energy has become increasingly important (Li et al., 2021). However, the power transmission distance in distributed small hydropower-rich areas is far, and the channel resources of the main power grid are limited. Furthermore, large and small hydropower stations occupy the channel resources, which has an impact on the main power grid. The problem of small interference stability is prominent, and it is difficult for the power dispatching department to accurately grasp the power generation capacity of small hydropower stations, resulting in the frequent occurrence of large-scale power generation and water abandonment of small hydropower stations, which seriously affects the utilization efficiency of clean energy and the safe and stable operation of the power grid (Graciano-Uribe et al., 2021; Zhang et al., 2022). Therefore, it has become an urgent problem to carry out the distributed small hydropower generation capacity prediction and provide reference for the power dispatching department to carry out the coordinated dispatch of multiple power sources.

In recent years, the field of hydropower has become the focus of many experts and scholars in the new energy sustainable development industry (Kougias et al., 2019). The traditional runoff hydropower forecasting method is mainly based on the trend extrapolation method, which has fast calculation speed and is suitable for forecasting with small load fluctuations (Zhou et al., 2022). However, the modeling process of this method is relatively complex and requires high stability of the historical data trend, which has certain limitations.

Jung et al. (2021) predicted the potential of small hydropower in the future by building a neural network model using climate change scenarios and artificial simulations. The prediction results are generally optimistic, but they cannot directly guide the power dispatching department to carry out the coordinated dispatch of multiple power sources, and they need to be combined with hydropower output prediction. Demir et al. (2023) comprehensively analyzed the advantages of using the XGBoost algorithm in prediction from the aspects of samples, characteristics, index performance, and model robustness. Hanoon et al. (2023) verified the effective application of different machine learning algorithms in hydropower forecasting by modeling three different scenarios in quarterly, monthly, and daily dimensions with different machine learning methods. With the continuous development of artificial intelligence technology, application of some machine learning methods, such as XGBoost algorithm, is gradually becoming feasible for runoff hydropower prediction (Zhang et al., 2021; Kumar et al., 2021). These methods use the historical data as training samples, utilize the intelligent processing and self-learning mode of the algorithm, learn the mapping relationship between the historical data and the influencing factors, and apply the algorithm to predict the future load data after strengthening learning and improving the accuracy (Bordin et al., 2020; Bernardes et al., 2022; Lai et al., 2020). The XGBoost method shows the nonlinear mapping ability and strong self-adaptation ability and is expected to become an effective means to solve the problem of distributed small hydropower generation capacity prediction. Bilgili et al. (2022) introduced a deep learning method based on long short-term memory (LSTM) to predict the power generation of a run-of-the-river hydroelectric power plant 1 day in advance. In addition, in order to compare the prediction accuracy, the adaptive neural fuzzy inference system (ANFIS) and fuzzy C-means (FCM), ANIS and subtractive clustering (SC), and ANFIS grid partitioning (GP) methods were adopted, which shows that the LSTM neural network provides higher accuracy results in short-term energy production forecasting. Dehghani et al. (2019) combined the gray wolf method with ANFIS to predict hydroelectric power.

1.1 Research highlights

Forecasting the generation capacity of distributed small hydropower is an effective means to solve the problem of frequent large-scale water abandonment due to its long transmission distance, limited channel resources, unknown generation capacity, and other factors.

The XGBoost algorithm applied to runoff hydropower prediction has the ability of nonlinear mapping and strong self-adaptation, which can effectively improve the prediction accuracy and overall accuracy.

The artificial intelligence forecasting method takes historical data as training samples, and its intelligent processing and self-learning mode can learn the mapping relationship between historical data and the influencing factors and apply it to forecast future load data, which is an effective means to solve the problem of distributed small hydropower generation capacity forecasting.

2 Hydropower forecasting method

2.1 Principle of the XGBoost algorithm

The main problems of traditional runoff hydropower forecasting methods are as follows:

Complicated modeling process: Traditional runoff-based hydropower forecasting methods often involve complex modeling processes, which require specialized knowledge and skills, increasing the difficulty and cost of prediction.

High requirements for the stability of historical data trends: The effectiveness of these methods depends heavily on the stability of historical data. If the historical data trends change significantly, the accuracy of predictions based on these data may be affected.

Suitability for predictions with fewer load fluctuations: Due to the computational process and results of traditional methods being limited by the consistency and stability of historical data, they may be more suitable for predictions with fewer load fluctuations. For situations with greater load fluctuations, the accuracy of predictions may be reduced.

Limited adaptability to future changes in hydropower output: Traditional runoff-based hydropower forecasting methods are mainly based on extrapolating historical data, which may have limited the adaptability to future changes in hydropower output. If there are significant changes in hydropower output in the future, these methods may need to be adjusted or re-modeled.

Lack of handling of uncertainties: Traditional methods usually assume that the future hydropower output is deterministic, but in reality, the future hydropower output may be affected by many uncertain factors, such as climate change and fluctuations in the energy demand. Traditional methods lack effective handling of these uncertainties.

For the prediction of many quantities with uncertain characteristics, i.e., random variables, people often use the method of probability and statistic in engineering practice. The probability and statistic method requires finding statistical laws from a large number of data samples, and this statistical law must be easy to be processed by mathematical methods (Walpole et al., 1993). Different from probability and statistics, the gradient boosting decision tree (GBDT) is a type of machine learning algorithm (Ke et al., 2017); its good performance in the prediction and classification of problems has been widely observed by industry researchers (Charbuty et al., 2021). The algorithm is composed of multiple decision trees and uses the negative gradient value of the loss function in the current model as the approximate value of the residual in the lifting tree for the regression fit of the decision tree (Natekin et al., 2013). The general steps of the GBDT algorithm are as follows:

1) Input $n$ training samples $X$ and set relevant parameters. The number of iterations is $N$, $F$ is the function space composed of all trees, and $f_k$ is the single decision tree model; the initial value is $f_0=0$, and the expression of the GBDT algorithm is as follows:

${\widehat{y}}_i={\displaystyle {\sum }_{k=1}^K}{f}_k\left(x_i\right),(1)$

where $x_i$ is the eigenvector of the i-th sample; $K$ is the number of weak regression trees; $f_k\left(x_i\right)$ is the output value of the k-th weak regression tree; and ${\widehat{y}}_i$ is the final predicted value of the ith sample.

2) Define the objective function of the GBDT algorithm as

$Obj={\displaystyle {\sum }_{i=1}^n}l\left(y_i,{\widehat{y}}_i\right)+{\displaystyle {\sum }_{k=1}^K}\mathrm{\Omega }\left(f_k\right),(2)$

where $\mathrm{\Omega }$ is the complexity of the decision tree; $n$ is the total number of samples; $l$ is the loss function; and $y_i$ is the true value of the i-th sample.

The complexity is defined by the regular term:

$\mathrm{\Omega }\left(f_t\right)=\kappa T+\frac{1}{2}\lambda {\displaystyle {\sum }_{j=1}^T}{{\omega }_j}^2,(3)$

where $T$ is the number of nodes of the leaf; ${\omega }_j$ is the vector value corresponding to the leaf node; $\kappa$ is the minimum loss reduction required for leaf node splitting of the tree; and $\lambda$ is the penalty term coefficient.

3) According to the addition structure of the GBDT algorithm, we obtain

${{\widehat{y}}_i}^t={{\widehat{y}}_i}^{t-1}+f_t\left(x_i\right),(4)$

where ${{\widehat{y}}_i}^t$ is the sum of the outputs of the first $t$ trees of the i-th sample; ${{\widehat{y}}_i}^{t-1}$ is the sum of the outputs of the first $i$ trees of the (t-1)-th sample; and $f_t\left(x_i\right)$ is the output value of the tth tree of the ith sample.

Substituting Eq. 4 into the objective function and carrying out the Taylor expansion, we obtain

$Ob{j}^t={\displaystyle \sum _{i=1}^n}\left[g_i{f}_t\left(x_i\right)+\frac{1}{2}{h}_i{f_t}^2\left(x_i\right)+\kappa T+\frac{1}{2}\lambda {\displaystyle {\sum }_{j=1}^T}{{\omega }_j}^2\right]={\displaystyle {\sum }_{j=1}^T}\left[G_i{\omega }_j+\frac{1}{2}\left(H_i+\lambda \right){{\omega }_j}^2\right]+\kappa T,(5)$

where $G_i=\sum g_i,H_i=\sum h_i$ and $g_i$ and $h_i$ are the first and second derivatives of the loss function, respectively.

Let the first derivative of $Ob{j}^t$ be 0. Then the optimal value of leaf node ${{\omega }_j}^{*}$ can be obtained as follows:

${{\omega }_j}^{*}=-\frac{G_j}{H_j+\lambda }.(6)$

At this time, the objective function value is

$Ob{j}^t=-\frac{1}{2}{\displaystyle {\sum }_{j=1}^T}\frac{{G_j}^2}{H_j+\lambda }+\kappa T.(7)$

4) Generate a new decision tree through the greedy strategy to minimize the value of the objective function (Friedman et al., 2001), and obtain the optimal predictive value ${{\omega }_j}^{*}$ corresponding to the leaf node. Add the newly generated decision tree $f_t\left(x\right)$ to the model to obtain

${{\widehat{y}}_i}^t={{\widehat{y}}_i}^{t-1}+f_t\left(x_i\right).(8)$

5) Continue to iterate until the end of $N$ iterations, and output the GBDT algorithm composed of $N$ decision trees.

The GBDT algorithm has many effective implementations, such as the XGBoost algorithm and LightGBM algorithm, which are integrated learning algorithms of GBDT (Shi et al., 2018; Bentéjac et al., 2021).

XGBoost is an improved algorithm based on GBDT that uses multithreading parallelism to improve the accuracy and is suitable for classification and regression problems (Chen et al., 2016). The basic principle of XGBoost is the same as that of GBDT. The difference is that GBDT uses the first derivative of the loss function, while XGBoost uses the first and second derivatives to perform the second-order Taylor expansion of the loss function.

Experimentally, XGBoost is relatively faster than many other integrated classifiers, such as AdaBoost. The impact of the XGBoost algorithm has been widely recognized in many machine learning and data mining challenges, and it has become a more commonly used and popular tool among Kaggle’s competitors and industry data scientists. In addition to using different boosting algorithms, MART and XGBoost also provide different regularization parameters. In particular, XGBoost can provide additional parameters that are not available in GBDT. In addition, it provides the penalty for a single tree in the additive tree model. These parameters will affect the tree structure and the weighting of the leaves to reduce variance in each tree. In addition, XGBoost provides an additional randomization parameter that can be used to disassociate individual trees, thereby reducing the overall variance of the additive tree model (Nielsen, 2016).

The loss function of the XGBoost algorithm is

$Obj\left(\varphi \right)=l\left(y,f\left(x\right)\right)+{\displaystyle {\sum }_m}\mathrm{\Omega }\left(f_m\right),(9)$

where $y$ is the true value corresponding to the current sample $y$; $f\left(x\right)$ is the predicted value of sample $x$; $l\left(y,f\left(x\right)\right)$ is the loss function; $f_m$ is the mth classification tree model; $\mathrm{\Omega }\left(f_m\right)$ is the regularization term, which reflects the complexity of the algorithm; and $\varphi$ is the model parameter to be solved.

$Ob{j}^{\left(m\right)}={\displaystyle {\sum }_{i=1}^N}l\left(y_i,{{\widehat{y}}_i}^{\left(m\right)}\right)+{\displaystyle \sum _{i=1}^m}\mathrm{\Omega }\left(f_i\right)={\displaystyle {\sum }_{i=1}^N}l\left(y_i,{{\widehat{y}}_i}^{\left(m-1\right)}+f_m\left(x_i\right)\right)+\mathrm{\Omega }\left(f_m\right),(10)$

$Ob{j}^{\left(m\right)}\approx {\displaystyle {\sum }_{i=1}^N}\left[l\left(y_i,{{\widehat{y}}_i}^{\left(m-1\right)}\right)+g_i{f}_m\left(x_i\right)+\frac{1}{2}{h}_i{f_m}^2\left(x_i\right)\right]+\mathrm{\Omega }\left(f_m\right).(11)$

The Taylor expansion is used to approximate function $f_m\left(x_i\right)$. Substituting Eq. 10 into Eq. 11, we obtain

$g_i={\partial }_{{{\widehat{y}}_i}^{\left(m-1\right)}}l\left(y_i,{{\widehat{y}}_i}^{\left(m-1\right)}\right),(12)$

$h_i={\partial }_{{{\widehat{y}}_i}^{\left(m-1\right)}}^{2}l\left(y_i,{{\widehat{y}}_i}^{\left(m-1\right)}\right),(13)$

where ${\partial }_{{{\widehat{y}}_i}^{\left(m-1\right)}}$ and ${\partial }_{{{\widehat{y}}_i}^{\left(m-1\right)}}^2$ are the first and second derivatives of ${{\widehat{y}}_i}^{\left(m-1\right)}$ on the loss function, respectively.

The regularization term in the objective function is

$\mathrm{\Omega }\left(f_m\right)=\gamma T+\frac{1}{2}\lambda {‖\omega ‖}^2,(14)$

where $\gamma$ is the minimum loss reduction required for further splitting at the leaf node of the tree, representing the complexity of each leaf, and $\omega$ is the value of the leaf node.

2.2 Runoff hydropower forecasting method based on XGBoost

The runoff hydropower prediction based on XGBoost is mainly divided into five steps: data collection, preprocessing, characteristic engineering, model training, and model validation (Li et al., 2019). We collect historical hydropower generation data, runoff data, and meteorological data related to hydropower generation. Among them, runoff data refer to the flow data of the river, which can be obtained through hydrological stations. After screening, de-duplication, and checking the collected data, the duplicate, invalid, and abnormal data are removed. Second, we process the missing data and filled the missing data using the interpolation method. Then, we use the method based on an isolated forest to detect and process the outliers of the data. In runoff hydropower prediction, feature engineering is a very important step. It can process the data reasonably and improve the prediction performance of the model. In this paper, we use a variety of feature engineering methods, including lag characteristics, time characteristics, and statistical characteristics. Table 1 lists the specific functions:

TABLE 1

TABLE 1. Summary of characteristics.

Considering that meteorological data, which include multiple factors such as precipitation and temperature, have a great impact on runoff hydropower prediction, this paper proposes an XGBoost runoff hydropower prediction method based on “meteorological similar days.” Before model training, the meteorological data of the day to be predicted are first composed into a feature vector, and the similarity is then calculated by the feature vector composed of the feature vector of the forecast day and the historical meteorological data. This paper uses the reciprocal of Manhattan distance to measure the similarity between the two. The specific form is as follows:

$similarity=\frac{1}{{\displaystyle {\sum }_{i=1}^N}\left|x_i-y_i\right|}(15)$

where N represents the length of the meteorological vector, $y_i$ represents the ith element of the meteorological vector of the day to be predicted, and $x_i$ represents the ith element of the historical meteorological vector of a day. According to the above similarity, the XGBoost algorithm model is weighted by the loss function to increase the impact of similar samples on the forecast date. Finally, the model is verified based on this scheme.

3 Example analysis

We select the output data of the hydropower cluster in Yunnan area, which contains multistage runoff hydropower stations, as the sample data to evaluate the proposed method.

Hydropower prediction is a complex task. The industry usually uses capacity accuracy instead of RMSPE accuracy for the assessment of new energy. The formula is as follows:

$AC{C}_{new\_energy}=\left(1-\sqrt{\frac{1}{N}{\displaystyle {\sum }_{i=1}^N}{\left(\frac{y_i-\widehat{y_{\iota }}}{Cap}\right)}^2}\right)\times 100\%,(16)$

where N is the number of output points collected in a day, taken as N = 96, and $y_i$ is the actual output value at the i-th time point in a day. $\widehat{y_{\iota }}$ is the predicted output value at the i-th time point in a day, and Cap is the capacity of the station.

The gray theory model (GM) is considered a classic model in the field of hydropower prediction, which mainly solves the problems of lack of data and uncertainty. Therefore, the prediction experimental group in this paper adopts the similar-day weighted XGBoost, while the control experimental group selects the original XGBoost and GM, normalizes the historical data to the interval of [−1,1], and takes 80% of the data as the training data and the remaining 20% as the test data. The prediction results are shown in Table 2.

TABLE 2

TABLE 2. Comparison of prediction accuracy.

It can be seen from the above table that considering the same factors, the prediction accuracy of GM in the dry season is higher than that of the original XGBoost algorithm after sample screening according to our proposed similarity measure and allocating weights to the sample. The prediction accuracy of GM in the dry season is higher than that of the original XGBoost algorithm, but it is not ideal in the wet season. The effectiveness of the sample weight selection method based on similar days is demonstrated using the control experimental group. In addition, we found that the accuracy of the algorithm for winter data prediction is higher than that in the summer. This is because the summer weather changes violently, the unit output level fluctuates greatly, and the weather has an unbalanced effect. Therefore, it can be seen that the selection of meteorological data has a great impact on the prediction accuracy of small hydropower output.

An overall comparison shows that the similar-day weighted XGBoost has the highest prediction accuracy compared to original XGBoost and GM in both wet and dry periods.

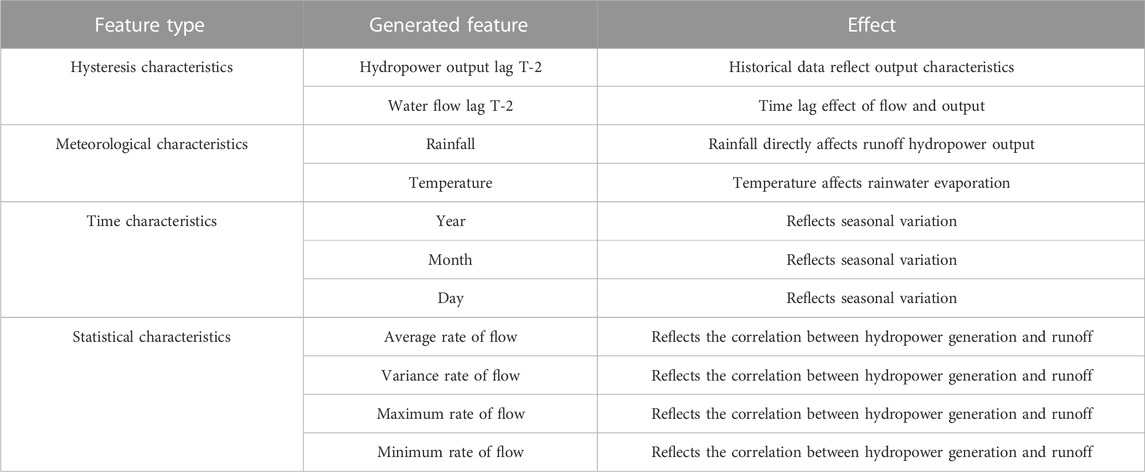
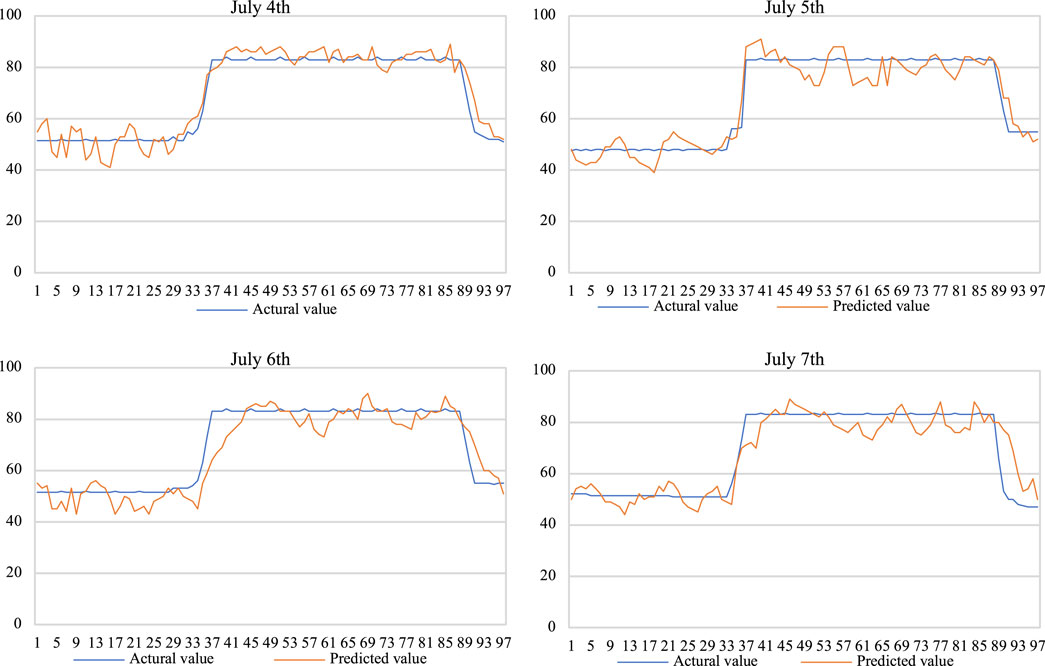
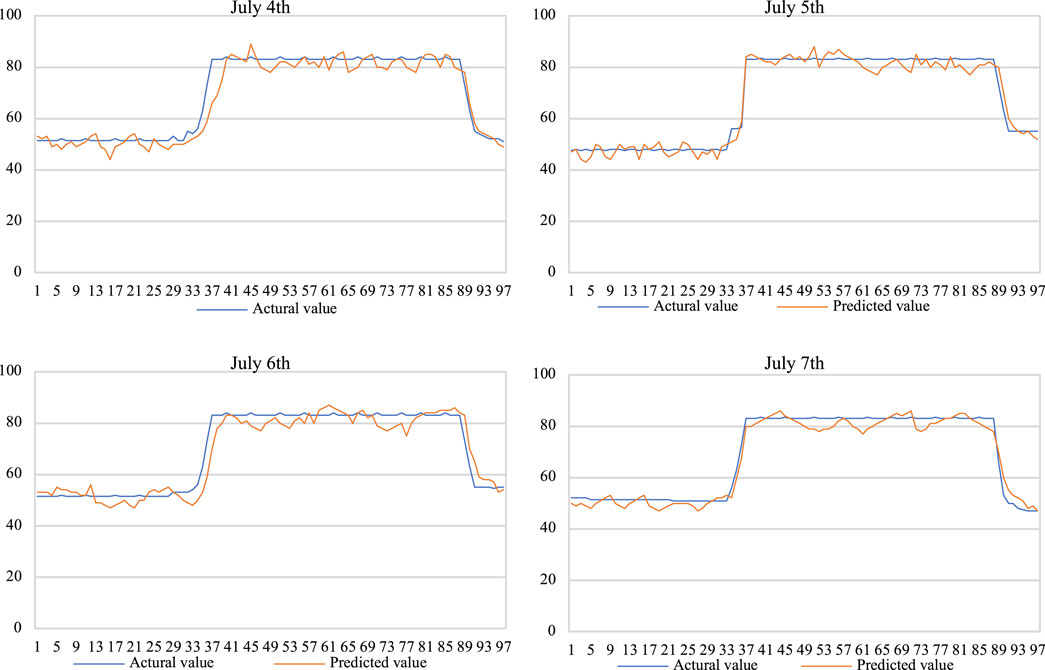
The prediction results using the similar-day weighted XGBoost algorithm are shown in Figure 1. It can be seen that the hydropower cluster has higher output and stable cycle in the wet season, and the prediction accuracy of this algorithm is higher.

FIGURE 1

FIGURE 1. Similar-day weighted XGBoost result prediction.

Figures 2, 3 show that the prediction accuracy of original XGBoost is higher than that of GM in the wet season. Through the comparison of Figures 1–3, it can be seen that similar-day weighted XGBoost has the best prediction effect in the wet season.

FIGURE 2

FIGURE 2. Original XGBoost result prediction.

FIGURE 3

FIGURE 3. GM result prediction.

4 Summary

In this paper, a novel hydropower forecasting method combining meteorological similar days and XGBoost model is proposed. By analyzing the historical meteorological and runoff data, this paper selected the meteorological similar days with meteorological conditions similar to the current data, which provided a valuable reference for the prediction of hydropower output. The XGBoost model not only shows its effectiveness in learning meteorological similar day datasets but also produces accurate and stable hydropower prediction results. The results show that the combination of meteorological similar days and XGBoost model is a promising method to improve the accuracy of hydropower prediction. The high prediction accuracy and stability of this method are particularly beneficial to water resource management and power production, which is conducive to better planning and utilization of hydropower resources, while ensuring a reliable power supply.

The application of this method in the Yunnan hydropower cluster in China has successfully demonstrated its practicability and the potential for promotion in other regions and power systems. However, it is worth noting that the universality of this method in different geographical locations and different climatic conditions needs further research and verification. The method proposed in this paper has made a valuable contribution to the field of hydropower prediction, and its effectiveness in improving the accuracy and stability of prediction highlights its importance in solving the challenges encountered in water resource and energy management. With continuous attention to water resources and energy, we believe that this method will help strengthen the management of sustainable water resources and energy, reduce the impact of natural disasters, and promote the development of green and sustainable energy in the future.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors without undue reservation.

Author contributions

YW: writing–review and editing. YX: writing–review and editing. FX: writing–original draft. XZ: conceptualization and writing–review and editing. SL: writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

Authors YW, YX, XZ, and SL were employed by Yunnan Power Grid Co., Ltd. Author FX was employed by Beijing Tsintergy Technology Co., Ltd.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bentéjac, C., Csörgő, A., and Martínez-Muñoz, G. (2021). A comparative analysis of gradient boosting algorithms. Artif. Intell. Rev. 54, 1937–1967. doi:10.1007/s10462-020-09896-5

CrossRef Full Text | Google Scholar

Bernardes, J., Santos, M., Abreu, T., Prado, L., Miranda, D., Julio, R., et al. (2022). Hydropower operation optimization using machine learning: a systematic review. AI 3 (1), 78–99. doi:10.3390/ai3010006

CrossRef Full Text | Google Scholar

Bilgili, M., Keiyinci, S., and Ekinci, F. (2022). One-day ahead forecasting of energy production from run-of-river hydroelectric power plants with a deep learning approach. Sci. Iran. 29 (4). doi:10.24200/sci.2022.58636.5825

CrossRef Full Text | Google Scholar

BordinSkjelbredKong, C. H. I. J., and Yang, Z. (2020). Machine learning for hydropower scheduling: state of the art and future research directions. Procedia Comput. Sci. 176, 1659–1668. doi:10.1016/j.procs.2020.09.190

CrossRef Full Text | Google Scholar

Charbuty, B., and Abdulazeez, A. (2021). Classification based on decision tree algorithm for machine learning. Appl. Sci. Technol. Trends 2 (01), 20–28. doi:10.38094/jastt20165

CrossRef Full Text | Google Scholar

Chen, T., and Guestrin, C. (2016). “XGBoost: a scalable tree boosting system,” in Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining, San Francisco, CA, USA, August 13-17, 2016, 785–794.

Google Scholar

Dehghani, M., Riahi-Madvar, H., Hooshyaripor, F., Mosavi, A., Shamshirband, S., Zavadskas, E. K., et al. (2019). Prediction of hydropower generation using grey wolf optimization adaptive neuro-fuzzy inference system. Energies 289 (12).

CrossRef Full Text | Google Scholar

Demir, S., and Sahin, E. K. (2023). An investigation of feature selection methods for soil liquefaction prediction based on tree-based ensemble algorithms using AdaBoost, gradient boosting, and XGBoost. Neural Comput. Appl. 35 (4), 3173–3190. doi:10.1007/s00521-022-07856-4

CrossRef Full Text | Google Scholar

Friedman, J. H. (2001). Greedy function approximation: a gradient boosting machine. Ann. Statistics 29 (5), 1189–1232. doi:10.1214/aos/1013203451

CrossRef Full Text | Google Scholar

Graciano-Uribe, J., Sierra, J., and Torres-Lopez, E. (2021). Instabilities and influence of geometric parameters on the efficiency of a pump operated as a turbine for micro hydro power generation: a review. Water Environ. Syst. 9 (4), 1–23. doi:10.13044/j.sdewes.d8.0321

CrossRef Full Text | Google Scholar

Hanoon, M. S., Ahmed, A. N., Razzaq, A., Oudah, A. Y., Alkhayyat, A., Huang, Y. F., et al. (2023). Prediction of hydropower generation via machine learning algorithms at three Gorges Dam, China. Ain Shams Eng. J. 14 (4), 101919. doi:10.1016/j.asej.2022.101919

CrossRef Full Text | Google Scholar

Jung, J., Han, H., Kim, K., and Kim, H. S. (2021). Machine learning-based small hydropower potential prediction under climate change. Energies 14 (12), 3643. doi:10.3390/en14123643

CrossRef Full Text | Google Scholar

Ke, G., Meng, Q., Finley, T., Wang, T., Chen, W., Ma, W., et al. (2017). Lightgbm: a highly efficient gradient boosting decision tree. Adv. neural Inf. Process. Syst. 30.

Google Scholar

Kougias, I., Aggidis, G., Avellan, F., Deniz, S., Lundin, U., Moro, A., et al. (2019). Analysis of emerging technologies in the hydropower sector. Renew. Sustain. Energy Rev. 113, 109257. doi:10.1016/j.rser.2019.109257

CrossRef Full Text | Google Scholar

Kumar, K., Singh, R. P., Ranjan, P., and Kumar, N. (2021). “Daily plant load analysis of a hydropower plant using machine learning,” in Applications of artificial intelligence in engineering, 819–826.

CrossRef Full Text | Google Scholar

Lai, J. P., Chang, Y. M., Chen, C. H., and Pai, P. F. (2020). A survey of machine learning models in renewable energy predictions. Appl. Sci. 10 (17), 5975. doi:10.3390/app10175975

CrossRef Full Text | Google Scholar

Li, A., Su, S., Han, T., Yin, C., Li, J., Chen, L., et al. (2021). “Energy demand forecast in yunnan province based on seq2seq model,” in E3S Web of Conferences 293, 02063, Strasbourg, France, May 5-7, 2021.

CrossRef Full Text | Google Scholar

Li, C., Zhu, L., He, Z., Gao, H., Yang, Y., Yao, D., et al. (2019). Runoff prediction method based on adaptive Elman neural network. Water 11 (6), 1113. doi:10.3390/w11061113

CrossRef Full Text | Google Scholar

Natekin, A., and Knoll, A. (2013). Gradient boosting machines, a tutorial. Front. Neurorobotics 7, 21. doi:10.3389/fnbot.2013.00021

PubMed Abstract | CrossRef Full Text | Google Scholar

Nielsen, D. (2016). Tree boosting with xgboost-why does xgboost win" every" machine learning competition? Trondheim, Norway: NTNU.

Google Scholar

Shi, Y., Li, J., and Li, Z. (2018). Gradient boosting with piece-wise linear regression trees. arXiv preprint arXiv:1802.05640 Available at: http://arxiv.org/abs/1802.05640.

Google Scholar

Walpole, R. E., Myers, R. H., Myers, S. L., and Ye, K. (1993). Probability and statistics for engineers and scientists, 5.

Google Scholar

Zhang, F., Zhang, Y., Qiu, Y., Wu, X., Tao, Y., and Ji, Q. (2022). Research review on hydropower-wind power-photovoltaic multi-energy coupling power prediction technology. Conf. Ser. 2354 (1), 012016. doi:10.1088/1742-6596/2354/1/012016

CrossRef Full Text | Google Scholar

Zhang, Y., Ma, H., and Zhao, S. (2021). Assessment of hydropower sustainability: review and modeling. Clean. Prod. 321, 128898. doi:10.1016/j.jclepro.2021.128898

CrossRef Full Text | Google Scholar

Zhou, F., Wang, Z., Zhong, T., Trajcevski, G., and Khokhar, A. (2022). HydroFlow: towards probabilistic electricity demand prediction using variational autoregressive models and normalizing flows. Intell. Syst. 37 (10), 6833–6856. doi:10.1002/int.22864

CrossRef Full Text | Google Scholar