Traceability analysis for low-voltage distribution network abnormal line loss using a data-driven power flow model

The abnormal behavior of end-users is one of the main causes of abnormal line loss in distribution networks. The integration of a large amount of distributed renewable energy into a low-voltage distribution network (LVDN) complicates line loss analysis. Traceability analysis for abnormal line loss aims to identify the specific end-user responsible for the anomaly in line loss. This paper proposes, for LVDNs with incomplete topology and line parameters, a practical traceability analysis approach using a data-driven power flow model. A data-driven power flow model based on a neural network is first established to capture the power flow mapping relationship without topology and line parameter information. A backpropagation algorithm is then presented to correct the actual power consumption data according to the measured voltage data. By comparing actual power consumption data with measured power data, users with abnormal behavior can be accurately identified and tracked. Finally, the effectiveness of the proposed approach is verified by actual data.

1 Introduction

A low-voltage distribution network (LVDN) is a terminal power grid that serves as a crucial component in delivering electricity to end-users (Li et al., 2021). With the increasing integration of distributed renewable energy resources (Xu et al., 2022) such as distributed photovoltaic energy and wind energy, the traditional consumption model of LVDNs has changed (Dou et al., 2023). The emergence of “prosumers,” who can both consume and produce electricity, has transformed the dynamics of power flow in the distribution network (Zhao et al., 2020). This bidirectional power flow will make distribution network line loss analysis more complex (Luo et al., 2020).

“Line loss” refers to energy loss during the transmission and distribution of electrical power (Zhang et al., 2022) and is an important indicator of the economical operation of LVDN. The management of abnormal line loss is crucial for improving the efficiency and economy of the power system (Enshaee et al., 2019). Abnormal line loss can result from factors such as inaccurate metering, power theft, and other user behaviors, leading to energy wastage and economic loss (Kong et al., 2021). Traceability analysis for abnormal line loss aims to identify the users causing these losses. By pinpointing the sources of line loss anomalies, targeted measures can be implemented to address and reduce these losses, ultimately improving the overall economy of power grid operation (Hu et al., 2022).

At present, analysis methods for abnormal line loss in LVDNs can be divided into three categories: state estimation, game theory, and data-driven. The first is based on state estimation (Xiao et al., 2018; Chen et al., 2019) and uses random matrix theory and other methods to estimate the LVDN state. It identifies abnormal line loss by comparing the state estimate results with the measured values. State estimation relies too much on the topology of the distribution network and the accuracy of line parameters (Zhang et al., 2020). In an LVDN, the network topology and line parameters are unknown due to the lack of intermediate measurement nodes, so the state estimation method is not applicable (Feng et al., 2022). Moreover, the actual operation of the distribution network may be nonlinear and complicated, and the state estimation method cannot fully reflect that, thus affecting the accuracy of the result (Zhao et al., 2020). The second category of analysis methods for abnormal line loss in LVDNs is based on game theory (Amin et al., 2015). Abnormal line loss is identified through the interaction game between the user and the power supply enterprise. However, such methods involve decisions and interactions by multiple players and can therefore lead to complex mathematical models and computational processes (Wang et al., 2023). This application of game theory has not been tested in practice but only through theoretical analysis (Mohammadi et al., 2019). The third analysis category is data-driven (Buzau et al., 2019; Lin et al., 2021; Pamir et al., 2022). XGBoost, LogitBoost, sparse random forest, and other supervised learning methods are proposed to extract features from manually labeled electricity datasets to identify abnormal electricity users. However, data-driven methods cannot provide a direct explanation of the cause of line loss anomalies and their physical mechanism.

Consequently, this paper proposes a neural network-based data-driven power flow model to locate the traceability of abnormal line losses in LVDN caused by users. The data-driven power flow model can adapt to LVDN. Because the middle node of the actual LVDN is not installed with measuring devices, its topology and line parameters are unknown. The trained data-driven power flow model calculates the voltage of each end-user directly from their measured power data without the need for topology and line parameters. First, a data-driven power flow model is established to fit the mapping relationship between power and voltage through the neural network. Second, voltage is calculated by the data-driven power flow model. The input power is updated by backpropagation. This process helps the calculated voltage to approximate the measured voltage. Then, by comparing the difference between the corrected and measured power of each user, the user causing the abnormal line loss is found. Finally, the accuracy and effectiveness of the proposed method are verified by combining the historical data and simulation of LVDNs.

The rest of the paper is organized as follows: Section 2 analyzes the feasibility of establishing a data-driven power flow model, and the data-driven power flow model based on neural networks is established. Section 3 uses the data-driven power flow model to trace the anomaly and find the user causing the abnormal line loss. Section 4 and Section 5 verify the validity and superiority of the proposed method and draw conclusions, respectively.

2 Neural network-based data-driven power flow model

This section first analyzes the functional relationship of the variables in the power flow constraint. It establishes that there is a unique mapping relation between the power flow variables. Then, the data-driven power flow model is established to fit the relationship using a neural network.

2.1 Analysis of variable function relations in power flow constraint

To build a data-driven power flow model, it is necessary to find the unique mapping relations among the power flow variables. Given some known power flow variables, this mapping relationship is used to derive other unknown power flow variables (Lyu et al., 2022).

In an LVDN with m nodes, 2m power flow constraint functions can be established. The relationship between active power P, reactive power Q, voltage V, and phase angle θ is expressed in polar coordinates:

$\left\{\begin{array}{l}{f}_1=P_1-V_1{\displaystyle \sum _{k=1}^m}{V}_k\left(G_{1k}\cos {\theta }_{1k}+B_{1k}\sin {\theta }_{1k}\right),\\ ⋮\\ f_m=P_m-V_m{\displaystyle \sum _{k=1}^m}{V}_k\left(G_{mk}\cos {\theta }_{mk}+B_{mk}\sin {\theta }_{mk}\right),\\ f_{m+1}=Q_1-V_1{\displaystyle \sum _{k=1}^m}{V}_k\left(G_{1k}\sin {\theta }_{1k}-B_{1k}\cos {\theta }_{1k}\right),\\ ⋮\\ f_{2m}=Q_m-V_m{\displaystyle \sum _{k=1}^m}{V}_k\left(G_{mk}\sin {\theta }_{mk}-B_{mk}\cos {\theta }_{mk}\right),\end{array}\right.(1)$

where V_i, P_i, and Q_i are the voltage, active power, and reactive power of node i, respectively; G_ij and B_ij are the conductance and susceptance between node i and j, respectively; and θ_ij is the phase angle difference between node i and node j, i,j∈{1,2, … ,m}.

Since the Jacobian matrix is invertible, a unique mapping relationship between the variables P, Q, V, and θ can be obtained according to the implicit function theorem. However, the value of θ is difficult to measure. The mapping relationship can be modified by removing θ:

$h\left(V_1,P_2,\cdots ,P_m,Q_2,\cdots ,Q_m\right)=\left[P_1,Q_1,V_2,\cdots ,V_m\right].(2)$

2.2 Data-driven power flow model

Based on the aforementioned discussion, this paper uses a neural network to fit the complex and nonlinear mapping relationship between power flow variables. Compared with traditional models, neural networks can learn and fit nonlinear mapping relationships between variables better. Additionally, they are capable of processing massive data in a short time by training for predictions. An L-layer neural network model can be divided into the following three layers:

$\left\{\begin{array}{l}x=g^{\left(0\right)}=\left[V_1,P_2,\cdots ,P_m,Q_2,\cdots Q_m\right],\\ g^{\left(l\right)}=\max \left(0,W^{\left(l\right)}{g}^{\left(l-1\right)}+b^{\left(l\right)}\right)l=1,\cdots ,L,\\ Y=F\left(x\right)=W^{\left(L+1\right)}{g}^{\left(L\right)}=\left[P_1,Q_1,V_2,\cdots ,V_m\right],\end{array}\right.(3)$

where x is the input of the neural network and the number of input neurons is 2m-1; Y is the final output result and the number of output neurons is m+1; g^(l) is the hidden layer in the middle; W^(l) is the weight matrix of the lth hidden layer; and b^(l) is the bias vector of the lth hidden layer. The mapping relationship between voltage and power can be obtained by fitting.

3 Traceability analysis considered abnormal line loss

3.1 Analysis of the relationship between abnormal user and power flow constraint

Abnormal users might exhibit instances where the measured voltage or power diverges from the actual value (Chen et al., 2023). Traditional analysis methods use the power flow constraint to identify the characteristic. When an anomaly occurs with a user, the measured power deviates from the actual value. Through power flow calculation, the calculated voltage is compared with the measured voltage. The user’s abnormality is then determined based on the magnitude of the deviation. Because the line parameters and topology of LVDNs are unknown, this method cannot be used. Consequently, a data-driven power flow model is pursued to address this challenge.

However, when the abnormal measured power is used as an input to the data-driven power flow model, multiple voltages will deviate simultaneously, making the identification of the abnormal user challenging.

Therefore, this paper consistently uses voltage to correct the power through backpropagation. The abnormal users are judged by comparing the corrected power with the measured power.

3.2 Backpropagation to correct the power

To keep the measured voltage constantly close to the calculated voltage, the power is constantly corrected by backpropagation. In this paper, FGSM (fast gradient sign method) is used to correct the power by calculating the difference between the voltage and the measured voltage without changing the parameters of the neural network (Duan et al., 2021; Li et al., 2022). The steps are as follows:

1) Select samples to be attacked: Select active and reactive power from the dataset as samples to be attacked, and these samples will be modified.

2) Calculate the loss function: Input the active and reactive power into the data-driven power flow model to calculate the loss function.

3) Calculate gradient: Calculate the gradient of the loss function with respect to the input sample.

4) Generate adversarial disturbance: Multiply the calculated gradient by the learning rate to obtain the disturbance vector in the direction of the fastest increase in the loss function.

5) Generate adversarial samples: Add the disturbance vector to the original sample.

The corrected formula is

$\left\{\begin{array}{l}{x}_{n+1}=x_n-\gamma ,\\ \gamma =\eta {\nabla }_x\mathrm{\Gamma }\left(\lambda ,x_n,V_{pre,n},V_{mea}\right),\\ \mathrm{\Gamma }\left(\lambda ,x_n,V_{pre,n},V_{mea}\right)={‖V_{pre,n}-V_{mea}‖}_2,\end{array}\right.(4)$

where n is the number of updates; x_n is power after the nth update; γ is the disturbance value; η is the learning rate; Γ(λ,x_n, V_pre, V_mea) is the loss function; λ is the neural network parameter; V_pre,n is the voltage value calculated by the data-driven power flow model for the nth time; and V_mea is the measured voltage value.

The power is constantly corrected by continuous backpropagation. The power of abnormal users exhibits the most conspicuous changes during the initial iterations. Concurrently, the power of the remaining users exhibits minimal variation during the iteration process. Therefore, abnormal users can be detected by examining the disparity between the corrected power and the measured power following iteration.

The process of backpropagation is shown in Figure 1.

FIGURE 1

FIGURE 1. The process of backpropagation.

3.3 Line loss abnormal user detection standard

Use the average correction distance to find the abnormal user:

$\left\{\begin{array}{l}{d}_{t,i}=\left|P_{cor}^{t,i}-P_{mea}^{t,i}\right|+\left|Q_{cor}^{t,i}-Q_{mea}^{t,i}\right|,\\ d_i=\frac{{\displaystyle \sum _{t=1}^T}{d}_{t,i}}{T},\end{array}\right.(5)$

where: Pt,i cor and Pt,i mea are the corrected active power and measured active power of the ith user at time t, respectively; Qt,i cor and Qt,i mea are the corrected and measured reactive powers of the ith user at time t, respectively; d_t,i is the corrected distance of the ith user at time t; and d_i is the average corrected distance of the ith user.

The calculated average correction distance of each user is compared with δ. If d_i>δ, it indicates that the ith user is the abnormal user.

4 Case studies

In this paper, data of an LVDN with clear ledger information in Zhejiang Province were selected. Some historical active power, reactive power, and voltage amplitude data were selected to train the model, 70% of which were training-set data and 30% of which were test-set data. Each sample includes active and reactive power injected by 32 user nodes and voltage amplitudes from distribution transformer nodes (1 × 65-dimensional vector). Each label includes voltage amplitudes for 32 user nodes and active and reactive power injected by distribution transformer nodes (1 × 34-dimensional vector). There are four layers in the neural network and 165 neurons in the hidden layer.

We also propose two evaluation indicators to verify the effectiveness of the proposed method. These are

$\left\{\begin{array}{l}{\alpha }_{\text{TPR}}=\frac{P_{\text{TP}}}{P_{\text{TP}}+P_{\text{FN}}},\\ {\alpha }_{\text{FPR}}=\frac{P_{\text{FP}}}{P_{\text{FP}}+P_{\text{TN}}},\end{array}\right.(6)$

where P_TP is the number of abnormal users detected as abnormal; P_FN is the number of abnormal users detected as normal; P_FP is the number of normal users detected as abnormal; P_TN is the number of normal users detected as normal; α_TPR is the precision of the method, representing the detection rate of abnormal users; and α_FPR is the false-positive rate of the method, representing the false detection rate of normal users.

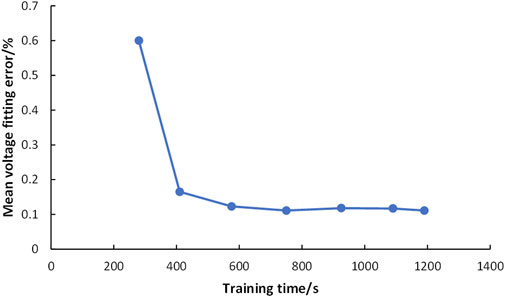
The training process of the neural network used in this paper is shown in Figure 2.

FIGURE 2

FIGURE 2. The training process of the neural network.

Figure 2 shows the relationship between the mean voltage fitting error and the training time of the neural network used in this paper during the training process. It can be seen that the neural network rapidly converges after 300 s, and the mean relative error between the neural network and the actual voltage measurement value drops to 0.165%, and that it takes 410 s to complete the training.

The traceability results of the data-driven power flow model in an LVDN with unknown constitutive parameters and the traceability results of the ordinary power flow method in the network with known parameters are shown in Table 1.

TABLE 1

TABLE 1. Method comparison.

From Table 1, the data-driven power flow model proposed in this paper is similar to the calculation results obtained by the ordinary power flow method, which proves the feasibility of the method used in this paper.

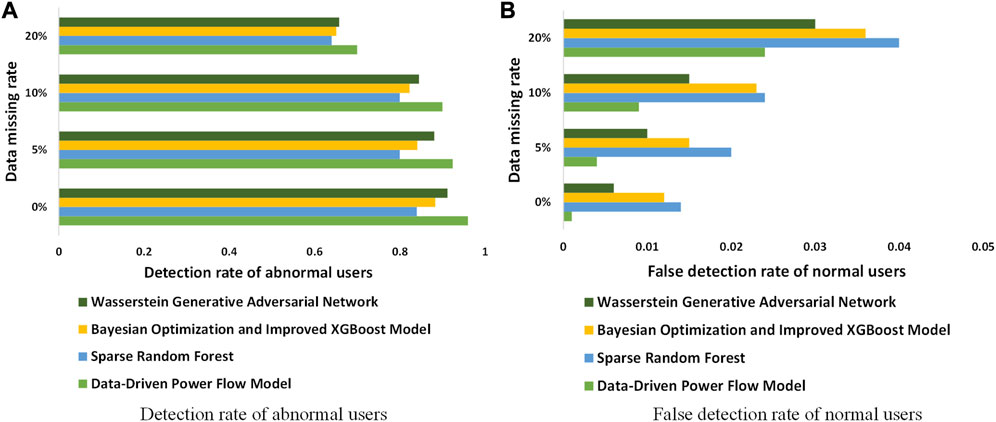
Under different data missing rates, the proposed indicators are used to compare the effectiveness of the proposed method with other methods.

From Figure 3, under different data missing rates, the detection rate and false-positive rate of the method used in this paper are superior to other methods, reflecting its effectiveness. When the missing data rate rises, its accuracy declines accordingly. When the missing data rate is 10% or less, the method maintains high accuracy.

FIGURE 3

FIGURE 3. Comparison of various methods.

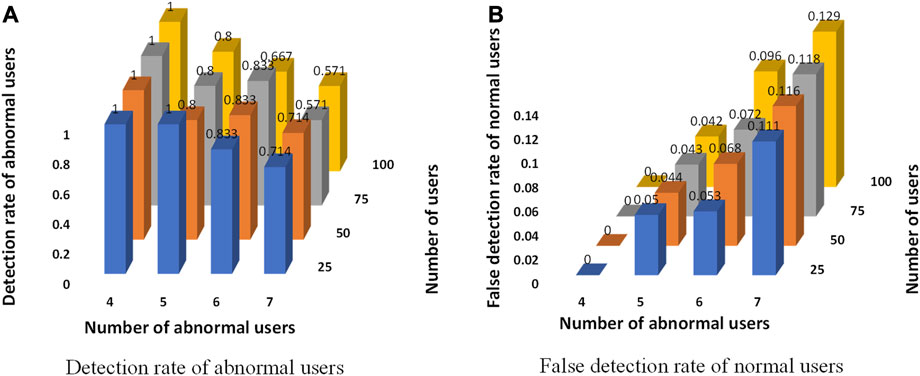
To test the detection ability of the method for multiple abnormal users, this method is used to detect an LVDN with a different number of users and abnormal users.

From Figure 4, regardless of the number of users, this method accurately detects anomalies in an LVDN containing four abnormal users. Furthermore, the method achieves a zero false-positive rate. In the LVDN with five or six abnormal users, most of the abnormal users are detected by this method. The false-positive rate is also low. However, the precision and false-positive rate of this method are poor for seven abnormal users.

FIGURE 4

FIGURE 4. Multi-target detection capability.

5 Conclusion

Given that it is currently difficult to obtain topology information and line parameters accurately and in a timely manner in LVDN, this paper proposes a data-driven traceability analysis approach to identify the specific end-user responsible for the anomaly in line loss. The proposed approach integrates the advantages of state estimation and data-driven methods. The main contributions of this paper are:

1) A practical traceability analysis approach is proposed to identify the specific end-user responsible for the anomaly in line loss for LVDN with incomplete topology and line parameters.

2) A data-driven power flow model based on a neural network is established to capture the power flow mapping relationship without topology and line parameter information.

3) A backpropagation algorithm is presented to correct the actual power consumption data according to the measured voltage data. By comparing the actual power consumption data with the measured power data, users with abnormal behavior can be accurately identified and tracked.

This method is suitable for anomaly tracing in most LVDNs. However, in cases where there are too many abnormal users in one LVDN, it is not able to accurately identify them and needs further improvement.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

ZS: writing—original draft. YX: data curation and writing—original draft. YH: writing—original draft. ZC: data curation and writing—original draft. JZ: writing—review and editing.

Funding

The authors declare that this study received funding from Science and Technology Projects of State Grid Zhejiang Electric Power Co. Ltd., grant number B311HZ230003. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.

Conflict of interest

Authors ZS and YX were employed by the Hangzhou Power Supply Company of the State Grid Zhejiang Electric Power Company, Author YH was employed by the State Grid Corporation of China, and Author JZ was employed by the State Grid Zhejiang Electric Power Company Ltd.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Amin, S., Schwartz, G., Cardenas, A., and Sastry, S. (2015). Game-theoretic models of electricity theft detection in Smart utility networks: providing new capabilities with advanced metering infrastructure. IEEE Control Syst. 35 (1), 66–81. doi:10.1109/MCS.2014.2364711

CrossRef Full Text | Google Scholar

Buzau, M. M., Tejedor-Aguilera, J., Cruz-Romero, P., and Gómez-Expósito, A. (2019). Detection of non-technical losses using Smart meter data and supervised learning. IEEE Trans. Smart Grid 10 (3), 2661–2670. doi:10.1109/TSG.2018.2807925

CrossRef Full Text | Google Scholar

Chen, H., Tao, X., Li, N., Xia, S., and Sui, T. (2019). Physical layer data analysis for abnormal user detecting: a random matrix theory perspective. IEEE Access. 7, 169508–169517. doi:10.1109/ACCESS.2019.2955103

CrossRef Full Text | Google Scholar

Chen, X., Yu, T., Pan, Z., Wang, Z., and Yang, S. (2023). Graph representation learning-based residential electricity behavior identification and energy management. Prot. Control Mod. Power Syst. 8 (2), 28–476. doi:10.1186/s41601-023-00305-x

CrossRef Full Text | Google Scholar

Dou, Y., Tan, S., and Xie, D. (2023). Comparison of machine learning and statistical methods in the field of renewable energy power generation forecasting: a mini review. Front. Energy Res. 11, 1218603. doi:10.3389/fenrg.2023.1218603

CrossRef Full Text | Google Scholar

Duan, L., Duan, F., Chapeau-Blondeau, F., and Abbott, D. (2021). Noise-boosted backpropagation learning of feedforward threshold neural networks for function approximation. IEEE Trans. Instrum. Meas. 70, 1–12. doi:10.1109/TIM.2021.3121502

PubMed Abstract | CrossRef Full Text | Google Scholar

Enshaee, A., and Yousefi, G. R. (2019). Tracing reactive power flows and allocating transmission lines losses: an analytical method. IEEE Syst. J. 13 (1), 783–791. doi:10.1109/JSYST.2017.2764631

CrossRef Full Text | Google Scholar

Feng, F., Zhang, P., and Zhou, Y. (2022). Authentic microgrid state estimation. IEEE Trans. Power Syst. 37 (2), 1657–1660. doi:10.1109/TPWRS.2022.3143362

CrossRef Full Text | Google Scholar

Hu, W., Guo, Q., Wang, W., Wang, W., and Song, S. (2022). Loss reduction strategy and evaluation system based on reasonable line loss interval of transformer area. Appl. Energy 306, 118123. doi:10.1016/j.apenergy.2021.118123

CrossRef Full Text | Google Scholar

Kong, X., Zhang, X., Lu, N., Ma, Y., and Li, Y. (2021). Online Smart meter measurement error estimation based on EKF and LMRLS method. IEEE Trans. Smart Grid 12 (5), 4269–4279. doi:10.1109/TSG.2021.3077693

CrossRef Full Text | Google Scholar

Li, C., Chen, G., Liang, G., and Dong, Z. (2022). A novel high-performance deep learning framework for load recognition: deep-shallow model based on fast backpropagation. IEEE Trans. Power Syst. 37 (3), 1718–1729. doi:10.1109/TPWRS.2021.3114416

CrossRef Full Text | Google Scholar

Li, Z., Liu, Y., Yan, Y., Wang, P., and Jiang, X. (2021). An identification method for asymmetric faults with line breaks based on low-voltage side data in distribution networks. IEEE Trans. Power Deliv. 36 (6), 3629–3639. doi:10.1109/TPWRD.2020.3045969

CrossRef Full Text | Google Scholar

Lin, G., Feng, X., Guo, W., Cui, X., Liu, S., Jin, W., et al. (2021). Electricity theft detection based on stacked autoencoder and the undersampling and resampling based random forest algorithm. IEEE Access 9, 124044–124058. doi:10.1109/ACCESS.2021.3110510

CrossRef Full Text | Google Scholar

Luo, E., Cong, P., Lu, H., and Li, Y. (2020). Two-stage hierarchical congestion management method for active distribution networks with multi-type distributed energy resources. IEEE Access 8, 120309–120320. doi:10.1109/ACCESS.2020.3005689

CrossRef Full Text | Google Scholar

Lyu, Z., Wei, H., and Wei, H. (2022). A method for directly extracting the jacobian matrix of the power flow equations of a power system in polar coordinates. Front. Energy Res. 10, 898943. doi:10.3389/fenrg.2022.898943

CrossRef Full Text | Google Scholar

Mohammadi, R., Mashhadi, H., and Shahidehpour, M. (2019). Market-based customer reliability provision in distribution systems based on game theory: a Bi-level optimization approach. IEEE Trans. Smart Grid 10 (4), 3840–3848. doi:10.1109/TSG.2018.2839598

CrossRef Full Text | Google Scholar

Pamir, N., Javaid, A., Almogren, M., Adil, M., Javed, U., and Zuair, M. (2022). RFE based feature selection and KNNOR based data balancing for electricity theft detection using BiLSTM-LogitBoost stacking ensemble model. IEEE Access 10, 112948–112963. doi:10.1109/ACCESS.2022.3215532

CrossRef Full Text | Google Scholar

Wang, Y., Chen, J., Zhao, M., Li, B., Shi, H., and You, H. (2023). Maximum energy penetration rate of PV in distribution network under security constraints based on game theory. IEEE Trans. Power Syst. 38 (4), 1–13. doi:10.1109/TPWRS.2022.3207512

CrossRef Full Text | Google Scholar

Xiao, F., and Ai, Q. (2018). Electricity theft detection in Smart grid using random matrix theory. IET Generation, Transm. Distribution 12 (2), 371–378. doi:10.1049/iet-gtd.2017.0898

CrossRef Full Text | Google Scholar

Xu, B., Zhang, G., Li, K., Li, B., Chi, H., Yao, Y., et al. (2022). Reactive power optimization of a distribution network with high-penetration of wind and solar renewable energy and electric vehicles. Prot. Control Mod. Power Syst. 7 (4), 51–813. doi:10.1186/s41601-022-00271-w

CrossRef Full Text | Google Scholar

Zhang, Y., and Wang, J. (2020). Towards highly efficient state estimation with nonlinear measurements in distribution systems. IEEE Trans. Power Syst. 35 (3), 2471–2474. doi:10.1109/TPWRS.2020.2967173

CrossRef Full Text | Google Scholar

Zhang, Z., Yang, Y., Zhao, H., and Xiao, R. (2022). Prediction method of line loss rate in low-voltage distribution network based on multi-dimensional information matrix and dimensional attention mechanism-long-and short-term time-series network. IET Generation Transm. Distribution 16 (20), 4187–4203. doi:10.1049/gtd2.12590

CrossRef Full Text | Google Scholar

Zhao, J., Zheng, Z., Wang, S., Huang, R., Bi, T., Mili, L., et al. (2020b). Correlation-aided robust decentralized dynamic state estimation of power systems with unknown control inputs. IEEE Trans. Power Syst. 35 (3), 2443–2451. doi:10.1109/TPWRS.2019.2953256

CrossRef Full Text | Google Scholar

Zhao, T., Chen, B., Zhao, S., Wang, J., and Lu, X. (2020a). A flexible operation of distributed generation in distribution networks with dynamic boundaries. IEEE Trans. Power Syst. 35 (5), 4127–4130. doi:10.1109/TPWRS.2020.3004765

CrossRef Full Text | Google Scholar