Abstract
Chinese electricity market reform poses huge challenges to hydropower operations and electricity trading. This study proposes a scheduling method coupling priority electricity and day-ahead trading for large hydropower plants. The study focuses on complex factors such as tariff uncertainty, different types of electricity settlement rules, and inter-provincial electricity transmission links. Spot market tariff scenarios are determined through the Latin hypercube and the K-means methods. A performance formulation of priority electricity deviation considering settlement assessment rules is established. A transmission description for different sub-plants and a triangular linear interpolation method based on binary independent branching mode are proposed to solve inter-regional transmission connections and hydraulic coupling in cascaded hydropower plants, respectively. Finally, the Big M method is employed to equivalently transform the complex non-linear problem into a mixed-integer linear programming (MILP) model. The method is verified with the day-ahead operation of four large hydropower plants downstream of the Jinsha River in China as a case study. Settlement assessment rules, inter-regional power transmission, and price uncertainty are analyzed in three different cases. Three conclusions are obtained: 1) the priority electricity performance rate and the price are positively correlated, which is useful to guide hydropower plants to actively participate in the market. 2) Introducing the prediction error of electricity price in the model can help avoid market decision risk and improve the expected return by approximately 1.2%. 3) Considering the settlement penalty rule is helpful for power generation enterprises to improve power allocation and thus seek higher revenue compared to traditional methods without considering it.
1 Introduction
In March 2015, China issued “Several Opinions on Further Deepening the Reform of the Electricity System,” kicking off the reform of China’s electricity (Chen et al., 2022; Cheng et al., 2023). The aim is to restore the commodity attributes of electric energy, establish a fully competitive, open, and orderly Chinese electricity market, and enable the market to play a decisive role in power resource allocation. There are significant advantages for hydropower to participate in the electricity market. Hydropower exhibits high regulation capacity (Pérez-Díaz et al., 2010; Gómez-Navarro and Ribó-Pérez, 2018; Shen et al., 2022) with low operating costs (Cheng et al., 2018; Rodríguez-Sarasty et al., 2021). At the same time, hydropower faces unprecedented challenges. In long-term operation, hydropower generation is strongly dependent on the water stored in the reservoir and inflow uncertainty in the future. In short-term generation scheduling, the electricity price in the day-ahead (Golmohamadi et al., 2021; Lago et al., 2021; Tschora et al., 2022) market is another important factor that is influenced by the load and nodal blockage in each receiving province. Currently, hydropower simultaneously faces long-term trading and short-term spot markets (Cai et al., 2020; Jia et al., 2022). The former involves both priority electricity and market trading, and the latter has to meet complex hydraulic connections and constraints, as well as market limitations (Guo et al., 2021). Such a complex situation inevitably poses severe challenges to hydropower scheduling, the decomposition of priority electricity, and the participation in the electricity market. Specifically, large hydropower plants with inter-provincial power transmission tasks must consider the multiple different markets, which further lead to additional complexities in market bidding and operations.
In the central dispatch mode, hydropower plants usually consider the results of medium- and long-term priority electricity decomposition, runoff forecast information, unit operating restrictions, transmission channel blockage, and other conditions to make day-ahead generation schedules (Avesani et al., 2022; Jiang et al., 2023; Zhang et al., 2023). However, in the electricity market environment with priority electricity and market trading, hydropower plants need to deal with three major day-ahead production tasks: 1) decomposing power curves of priority electricity for multiple power grids; 2) making day-ahead markets for declaration; and 3) determining day-ahead generation schedules for each hydropower unit.
As is known, the spot market price is affected by complex supply and demand relationships, bringing significant uncertainty to short-term trading decisions (Tang and Zhang, 2020; Guo et al., 2021; Wu et al., 2022). There have been many studies about hydropower operations and bidding in the electricity market. We summarize four main categories.
The first is market design and mechanism optimization (Fang et al., 2017; Shen et al., 2018; Stančin et al., 2020; Xinhong et al., 2020). These studies focused on the design and mechanism of hydropower marketing in order to facilitate effective supply and demand matching and optimize price discovery and transaction efficiency, for example, a trading decision-making method that uses the electricity market to promote established clean energy accommodation. Making full use of load difference, peak-to-valley difference, and time difference, a joint optimization model of clean energy purchasing–selling–transmission is established to promote clean energy accommodation. The second is cross-regional and inter-national hydropower trading (Lu et al., 2021). For instance, Lu et al. (2021) analyzed the types and channels of trans-provincial and trans-regional power transactions and then analyzed the mechanism of resource optimization allocation of trans-provincial and trans-regional power transactions. The third is cross-energy scheduling and trading (Merkert et al., 2015; Xiao et al., 2015; Wang and Huang, 2018). These studies focused on the collaborative scheduling and trading of hydropower with other energy sources (such as wind, solar, and storage) to optimize the overall utilization of renewable energy and the stability of the power system. This requires consideration of complementarities between different energy sources, coordinated dispatch, and market trading. For example, Wang and Huang (2018) studied the interactions among interconnected autonomous microgrids and developed a joint energy trading and scheduling strategy. The last aspect is uncertainty and risk management (Yuan et al., 2016; Carvajal et al., 2017; Kebede et al., 2022; Xu et al., 2022). These studies focused on investigating how to effectively deal with uncertainties and risks in hydropower dispatch (Kebede et al., 2022), such as water source changes, market price fluctuations, and external environmental changes. This may involve aspects such as uncertainty modeling, risk assessment, and risk management strategies. In particular, Carvajal et al. (2017) presented a method to assess the sensitivity of hydropower generation to uncertain water resource availability driven by future climate change.
Few of the aforementioned studies considered power defaults and hydropower flexibility in market trading, and even fewer studies involved both the complex actual operation constraints of hydropower units and power decomposition requirements for multiple power grids. In this paper, we propose a scheduling method coupling priority electricity and day-ahead trading for large hydropower plants, considering complex factors such as electricity price uncertainty, different types of power settlement rules, and inter-provincial power transmission connections. In this method, the spot market electricity price scenarios are determined using Latin hypercube sampling (Zhang et al., 2020; Bulut et al., 2021; Karolczuk and Kurek, 2022) and K-means clustering. A performance formulation of priority electricity deviation considering settlement assessment rules is established. A transmission description for different sub-plants and a triangular linear interpolation method based on binary independent branching mode are proposed to solve inter-regional transmission connections and hydraulic coupling in cascaded hydropower plants, respectively. Finally, the Big M method (Ding et al., 2014; Zhang et al., 2021) is employed to equivalently transform the complex non-linear problem into a mixed-integer linear programming (MILP) model (Krien et al., 2020; Zhao et al., 2021; Cao et al., 2022).
The remainder of the paper is organized as follows: the objective function and constraints are described in Section 2. Section 3 describes the tariff uncertainty approach and the associated linearization strategy. Section 4 shows the results of the demonstration calculation. Finally, Section 5 providesthe conclusion.
2 Mathematical models
2.1 Objective function
Taking into account the basic benefits of the medium- and long-term decomposition of planned electricity to day, the negative deviation penalty of the actual decomposition of day-ahead, and the day-ahead market time-of-use tariff settlement benefits, the model objective function is divided into the following three components:
Negative deviation penalty rule for planned electricity. Negative deviation power is penalized by planned electricity price.
Here, is the contract electricity revenue; is the planned electricity negative deviation penalty; is the day-ahead market revenue; is the penalty coefficient of planned electricity; is the planned electricity of power station i in province k; is the market price of power station i in province k at time t; is the planned electricity of power station i in province k at time t; and is the output of power station i in province k at time t;
2.2 Constraints
2.2.1 Hydroelectric power plant-related constraints
(1) Water balance constraint
where
is the reservoir capacity of power station i at time t, in billions;
is the interval inflow of power station i at time t;
is the set of upstream power stations with hydraulic connection of power station i; and
is the outflow of power station i at time t.
(2) Water level–reservoir capacity relationship and upper and lower limits of the water level
where
is the relationship between the water level and reservoir capacity of power station i and
and
are the upper and lower limits of the water level of power station i at time t, respectively.
(3) Flow balance and upper and lower limit constraints
where
is the outgoing flow of power station i at time t;
is the generation flow of power station i at time t;
is the disposal flow of power station i at time t;
and
are the minimum and maximum outgoing flows of power station i, respectively; and
and
are the minimum and maximum generation flows of power station i, respectively.
(4) The relationship between the flow rate and the tailwater level
where is the tailwater level of power station i at time t and is the tailwater level–discharge flow relationship of power station i.
2.2.2 Unit-related constraints
(1) Power generation characteristic curve relationship of the unit
where
is the output characteristic relationship of unit e power station i;
is the output of unit e power station i at time t;
is the generation flow of unit e power station i at time t; and
is the head of unit e power station i at time t.
(2) Unit stable output operation area
where
is the start–stop status of unit e power station i at time t, with 0 for off and 1 for on;
is the upper limit of stable operation output of unit e power station i; and
is the lower limit of stable operation output of unit e power station i.
(3) Stable flow constraint of the unit
where
is the upper limit of the quoted flow rate for the stable operation of unit e power station i and
is the lower limit of the quoted flow rate for the stable operation of unit e power station i.
(4) Head calculation constraint
where
is head loss of unit e power station i at time t.
(5) Start/stop-related constraints
Although hydro units can be adjusted quickly, frequent start-ups and shutdowns still have a negative impact on the unit’s service life and operating costs. To avoid frequent start-ups and shutdowns of hydro units, online and offline hourly constraints are introduced.
where
indicates whether unit e power station i performs start-up action at time t, where 0 represents no and 1 represents yes;
indicates whether unit e power station i performs shutdown action at time t, where 0 represents no and 1 represents yes.
(6) Correlation between power station and unit output
(7) Correlation between power station and unit generation flow
Here, is the output of unit e power station i at time t and is the generation flow of unit e power station i at time t.
2.2.3 Market power decomposition constraints
where is the proportional requirement of power delivery of power station i in province k and is the floatable proportional limit of marketed power (set at 0.2 in this paper)
3 Model processing strategy
3.1 Uncertainty description method of the price
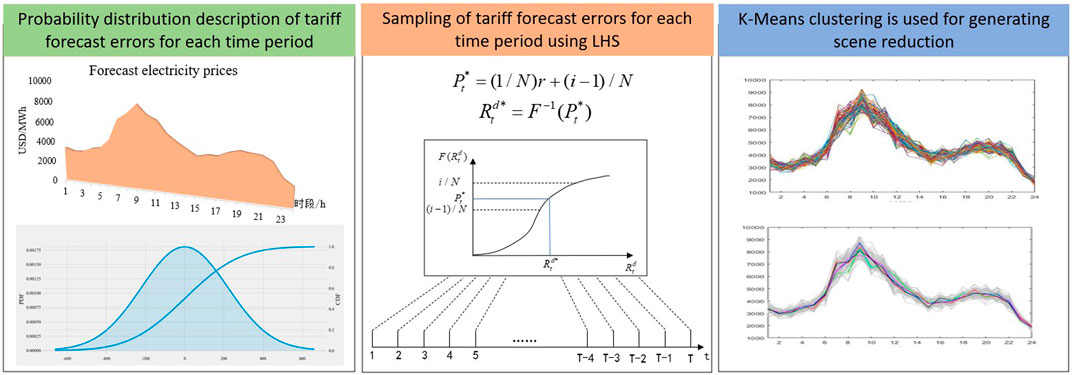
Since electricity prices are affected by multiple complex factors such as grid blockage (
Golmohamadi et al., 2021), market transactions (
Tschora et al., 2022), and weather conditions (
Lago et al., 2021), coupled with limitations in spot electricity price forecasting technology, there are bound to be certain deviations between the predicted and actual values of spot market electricity prices. Therefore, the uncertainty of the next day’s spot market electricity price should be fully considered when formulating short-term dispatching plans. In general, the forecast error distribution law of the electricity price is a finite skewed distribution at both ends, but generally the corresponding normal and skewed distributions do not differ much. Therefore, this model describes the electricity price uncertainty as follows (
Figure 1):
(1) Assume that the forecast error of the spot tariff for each time period follows a normal distribution with a mean of and a mean squared deviation of , where is the forecast tariff for time period t.
(2) The Latin hypercube sampling (LHS) method is used to generate multiple tariff simulation scenarios. The core technique of this method is to first stratify the probability distribution of the samples and then randomly select samples from each stratum in turn. The cumulative probability distribution function is calculated for each time period based on the mean and mean squared deviation assumed in (1), and is divided into non-overlapping subintervals, each with a spacing of . An integer is randomly selected from the set , representing the interval where the cumulative probability distribution lies. Subsequently, a random number in a range of is generated, which is denoted as corresponding to the interval . The cumulative probability function for is . Finally, the inverse function of the cumulative probability distribution function is substituted by to obtain the corresponding tariff data sampling value.
(3) In order to fully reflect the stochastic variation characteristics of the spot market clearing price, the LHS method in (2) is used to generate many electricity price scenarios. If all scenarios are considered in the model, it will significantly affect the computational efficiency, but if very few scenarios are considered, the computational accuracy will be lower. Therefore, in order to balance solution accuracy and efficiency, the K-means clustering algorithm based on the initial clustering centers and contour coefficients is used (Cheng et al., 2023) to reduce the number of scenarios as much as possible while maintaining the important features of the tariff scenarios.
FIGURE 1
3.2 Power station–substation difference regional outbound relationship processing
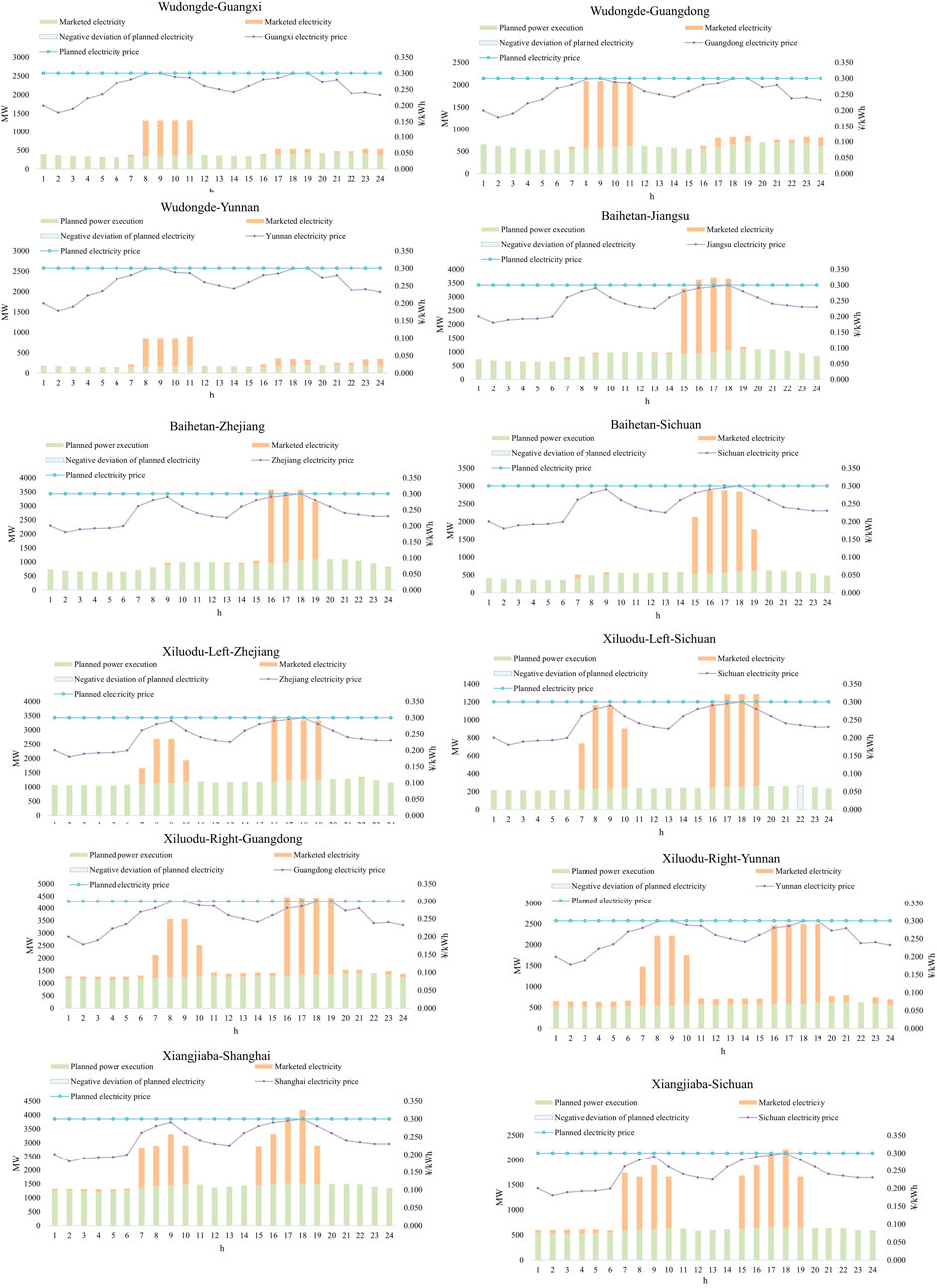
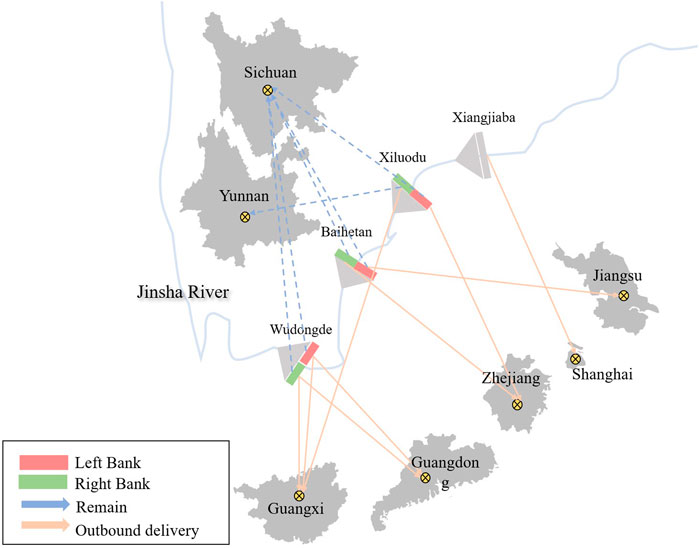
The Jinxia terraced power station contains various differential cases of outgoing transmission of sub-plants: (1) the power stations in the left and right banks represented by the Wudongde power station have the same outgoing and retained provinces. (2) The left and right bank outgoing provinces represented by Baihetan are different, but the retained provinces are the same. (3) In the case of Xiluodu, the power plants in both the left and right banks are different in terms of outgoing and retained provinces.
First, the aforementioned three cases require refined modeling of the outgoing power and the output of the corresponding substations, given K = 1, 2, 3, 4, 5, 6, and 7 corresponding to the provinces Guangdong, Guangxi, Jiangsu, Zhejiang, Shanghai, Sichuan, and Yunnan.
Case (1): No further refinement modeling is required because the sub-plant feeder areas are the same. Case (2): The following additional refinement modeling constraints are required.
➢ The output of the left bank unit is greater than or equal to the outgoing output to Jiangsu.
➢ The output of the right bank unit is greater than or equal to the outgoing output to Zhejiang.
Case (3): The following additional refinement modeling constraints are required.
➢ The output of the left bank unit is equal to outgoing output for Zhejiang and the retained output for Sichuan.
➢ The output of the right bank unit is equal to the outgoing output for Guangxi and the retained output for Yunnan.
3.3 Target linearization processing
Since Eq. 3 contains the max function, resulting in a non-linearly constrained objective, it needs to be linearized to transform the mixed-integer non-linear programming (MINLP) model into a MILP model. Then, a sophisticated and efficient optimization solver is used to solve the MILP model in order to obtain the optimal solution efficiently.
Variables 0–1, auxiliary variables (i represents whether there is a positive deviation in the power plant plan power), , and , and infinity value constant M are introduced, where in Eq. 3 and in Eq. 5 are transformed into the following mathematical expression:
3.4 Description of the flow curve under the tailwater level considering the top support of the return water
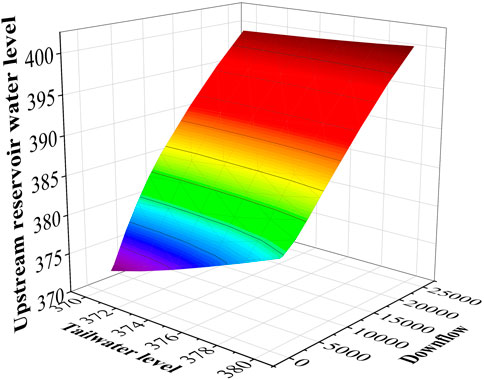
The backwater is a complex hydraulic connection between coupled reservoirs (Figure 2). Under normal conditions, there exists a stable relationship curve between the tailwater level and outflow. However, when the upstream and downstream dam sites of the reservoirs are closer, a high downstream reservoir level produces backwater. Furthermore, the stabilized water level–flow relationship curve will be disrupted, which is known as the backwater effect (Zhao et al., 2019). The requirements for short-term scheduling refinement of hydropower are becoming more stringent due to the gradual increase in the capacity of wind power and photovoltaic power. Addressing the influence of downstream backwater in the model and realizing an efficient solution is one of the key points and difficulties in current reservoir scheduling.
FIGURE 2
The example shows that if the optimal scheduling model is not constructed by taking into account the complex hydraulic coupling relationship between power stations, there will be deviations between the calculation results and the actual operation process, which does not meet the requirements of accuracy and practicality of hydropower scheduling. Therefore, this paper constructs the relationship between the upstream reservoir level, tailwater level, and downstream flow based on the triangular linear interpolation method in binary independent branching mode, as described in Cheng et al. (2022).
4 Example analysis
4.1 Calculation parameters
This paper takes Wudongde, Baihetan, Xiluodu, and Xiangjiaba (hereinafter referred to as Wu–Bai–Xi–Xiangba), the four mega power stations that have been put into operation in the lower Jinsha River gradient, as the research objects. The installed capacities are 10,200 MW, 16,000 MW, 12,600 MW, and 6,000 MW, respectively. Seven provinces (cities), namely, Guangdong, Guangxi, Jiangsu, Zhejiang, Shanghai, Sichuan, and Yunnan, are included in the grid at the receiving end of the gradient.
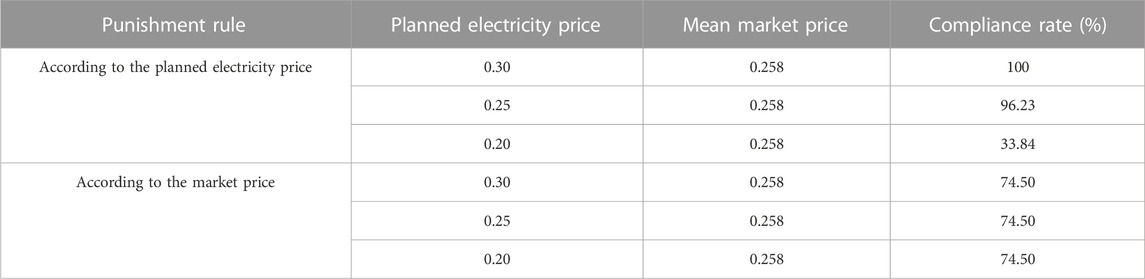
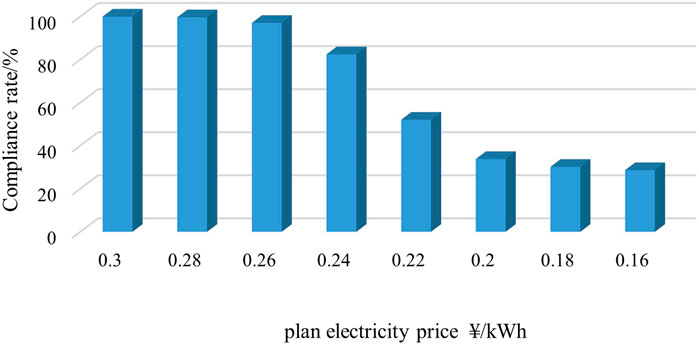
4.2 Analysis of penalty rules
As we can see from the aforementioned table (Table 1), according to the planned electricity price penalty (Figure 3), the planned electricity compliance rate decreases with the planned electricity price. According to the market price penalty (Figure 4), the planned electricity compliance rate does not change with the planned price. When the planned price is close to or much larger than the mean market price, the compliance rate of the punishment rule according to the planned electricity price is much larger than that according to the market price. In this case, the planned electricity price is higher than the market price during most periods. The punishment rule according to the planned electricity price can cause generators to suffer large revenue losses. According to the punishment rule based on the market price, power plants can seek higher revenue by defaulting on planned electricity during the period of low market price and participating in the day-ahead market during the high market price. Considering the policy specificity of planned power, grid companies use planned tariffs for compliance deviation penalties in order to ensure the compliance rate of planned power.
TABLE 1
| Punishment rule | Planned electricity price | Mean market price | Compliance rate (%) |
|---|---|---|---|
| According to the planned electricity price | 0.30 | 0.258 | 100 |
| 0.25 | 0.258 | 96.23 | |
| 0.20 | 0.258 | 33.84 | |
| According to the market price | 0.30 | 0.258 | 74.50 |
| 0.25 | 0.258 | 74.50 | |
| 0.20 | 0.258 | 74.50 |
Effect of punishment rules on the compliance rate.
FIGURE 3
FIGURE 4
From another perspective, if the planned power price is appropriately reduced, the willingness of hydropower plants to contract planned power will be weakened at the same time, so this paper tries to explore the correlation between planned power pricing and market performance, as shown in Figure 5.
FIGURE 5
4.3 Scheduling result analysis
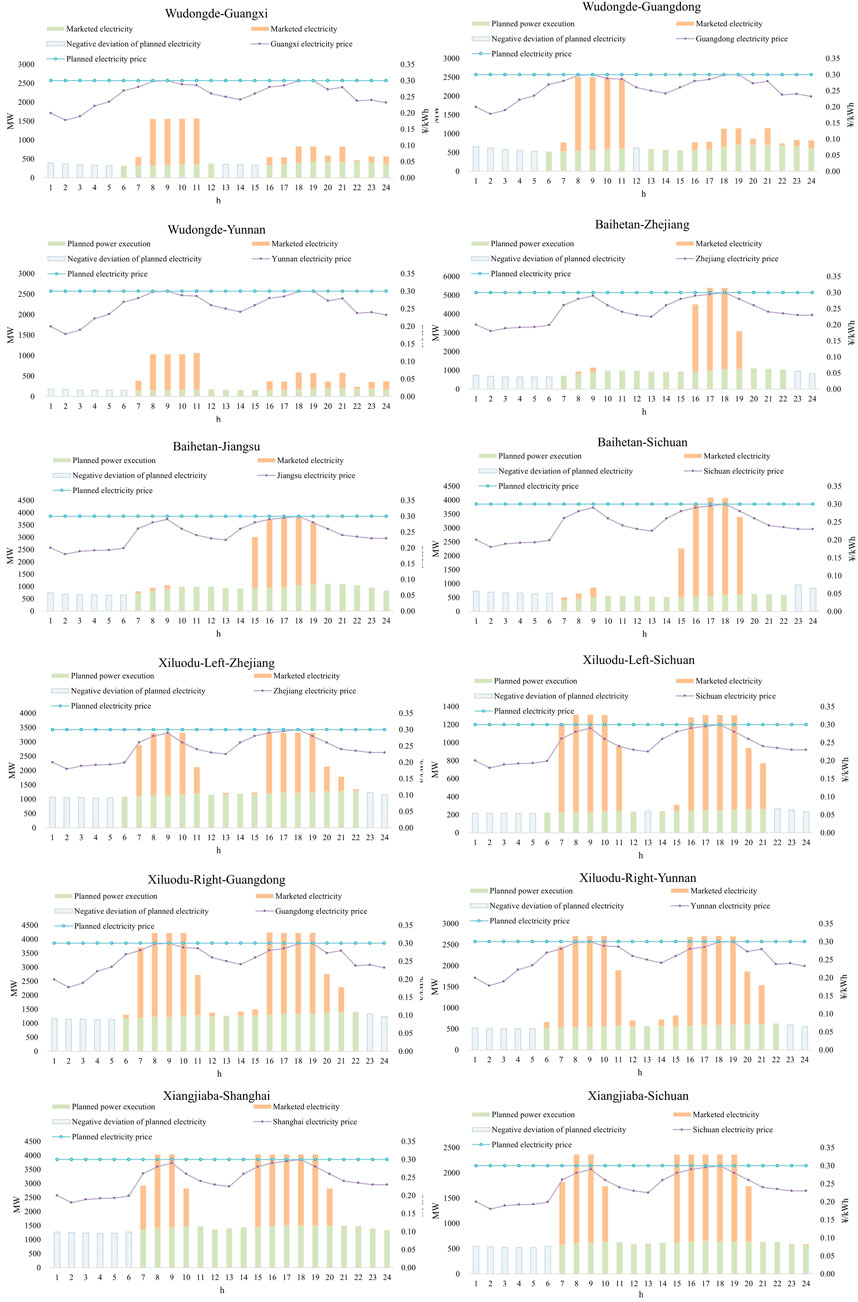
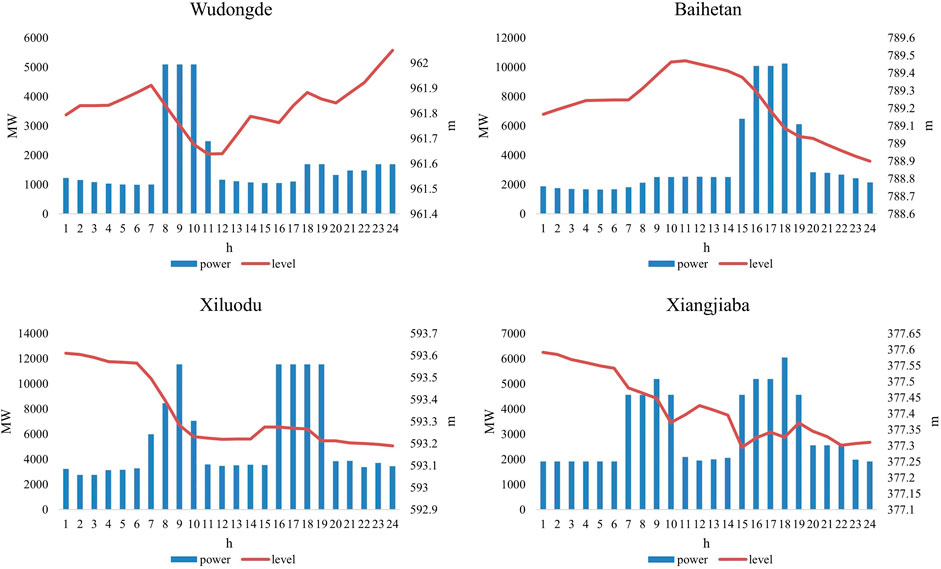
The model proposed in this paper can obtain the short-term dispatching scheme of cascade hydropower stations under the corresponding electricity price scenario. Figure 6 respectively, shows the changes in water level and output of each power station during the scheduling period, and their water levels and output meet the operation constraints and are within a reasonable range. It can be seen that the variation in the upstream water level is greater than that in the downstream water level, and the downstream power station can maintain stable high-head power generation as far as possible through the adjustment of upstream discharge flow so as to increase the overall power generation and benefits.
FIGURE 6
Further analysis of the overall output of cascade power stations shows that the electricity price is higher in the peak period and lower in the trough period. Under the guidance of the market price before the day, cascade hydropower stations give play to the spatial–temporal coupling characteristics and maximize the total revenue of the cascade hydropower station during the operation period through the spatial cooperation between its upstream and downstream and the coordination between different periods. It is consistent with the experience of hydropower optimal dispatching and the profit-seeking rule in the market environment and verifies the rationality of the dispatching results.
4.4 Analysis of the stable unit operation
As shown in Figure 7, power stations such as Baihetan and Xiluodu with different regions of the left and right bank sending provinces ( refer Section 3.2 Power station–substation difference regional outbound relationship processing) can be considered in the process of unit load distribution of the complex provinces of the sub-bank sending demand, at the peak of the two provinces, to increase the power allocation in a timely manner while taking into account the safe and stable operation of the unit (Table 2; Figure 8), to ensure the practicality of the power plan.
FIGURE 7
TABLE 2
| Hydropower station | Unit | Minimum power-on time/h | Minimum power-off time/h | Capacity up limit for stable operation | Capacity down limit for stable operation |
|---|---|---|---|---|---|
| Wudongde | #1∼#12 | 4 | 4 | 170 | 850 |
| Baihetan | #1∼#16 | 4 | 4 | 200 | 1000 |
| Xiluodu | #1∼#18 | 4 | 4 | 154 | 770 |
| Xiangjiaba | #1∼#8 | 4 | 4 | 160 | 800 |
Unit stabilization parameters.
FIGURE 8
4.5 Analysis of market price uncertainty
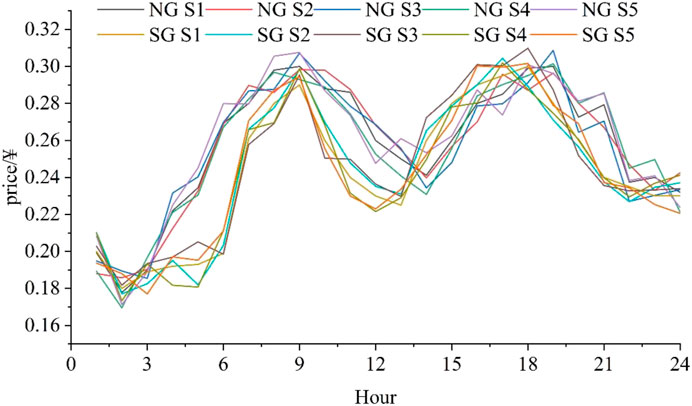
Using the methodology described in Section 4, five typical electricity price scenarios were generated based on the uncertainty of the forecast electricity price error (Figure 9). Two regional grids, the National Grid (NG) and the Southern Grid (SG), are included in the electricity price scenario. In this section, the planned electricity price is set to 0.3¥.
FIGURE 9
The aforementioned table shows the mean and maximum prices in different regions for different scenarios (Table 3). Overall, the average price in the SG region is higher than that in the NG region. Within the same region, the mean price for different scenarios does not vary much, but the maximum price difference accounts for approximately 4% of the mean price. Maximum tariffs are very important for market-based electricity allocation.
TABLE 3
| Area | SG | SG | SG | SG | SG | NG | NG | NG | NG | NG |
|---|---|---|---|---|---|---|---|---|---|---|
| Scenario | 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 |
| Mean price/¥ | 0.258 | 0.257 | 0.256 | 0.256 | 0.259 | 0.243 | 0.244 | 0.246 | 0.242 | 0.244 |
| Maximum price/¥ | 0.300 | 0.298 | 0.309 | 0.301 | 0.308 | 0.300 | 0.304 | 0.310 | 0.302 | 0.302 |
Multi-scenario electricity prices.
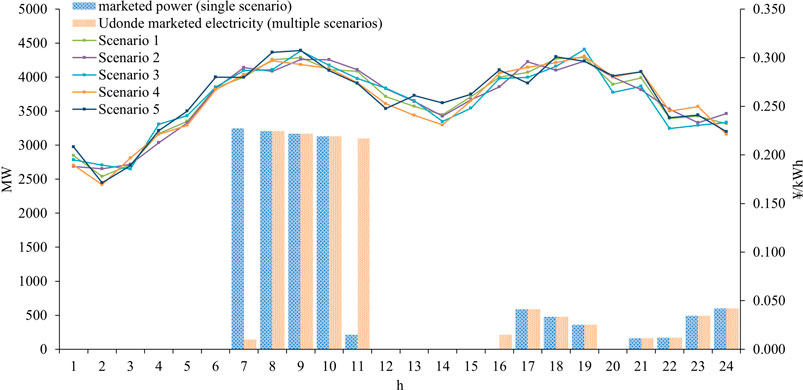
In order to facilitate the comparison between multiple scenarios of tariff uncertainty and single tariff scenarios, this subsection adopts “Plan Electricity Negative Deviation Penalty Rule II” and conducts a comparative analysis according to the principles of the plan tariff penalty.
The main difference between a single scenario and multiple scenarios (Figure 10) is observed in the seventh, 11th, and 16th time periods. The seventh and 11th time periods show a significant decrease in market decision power in the 11th time period with the single scenario. There was a significant increase in market decision power in the seventh time period compared with the single scenario, which is mainly due to the fact that only one scenario of price scenario 1 is considered in the single-scenario mode. The price in the seventh time period is lower than the tariff in the 11th time period in tariff scenario 1, while the other scenarios are the opposite. Therefore, in order to take into account the possibility of multiple tariffs and improve the expected revenue of the power plant, the power output in the seventh period is increased and the power output in the 11th and 16th periods is reduced in the multi-scenario decision to avoid the revenue risk. Using the decision results from scenario 1 to find the possible expected revenue for all price scenarios, there is a 3% reduction in revenue compared to the present expected return maximization model. It shows that expectation modeling is very important for risk aversion.
FIGURE 10
5 Conclusion
Currently, in the stage of market reform where planned electricity and marketed electricity coexist, hydropower taking on the task of delivering power to multiple-recipient provinces plays a decisive role. In the current market background, how to take into account the planned electricity and the cross-provincial market revenue is an important problem that cascade hydropower plants face. In this paper, taking the Jinsha River cascade hydropower plants as a relying project, we propose a day-ahead planned electricity compliance strategy and market electricity decision-making methods considering complex settlement rules and many end-user provinces. Finally, the expected revenue maximization model, considering the price uncertainty, is developed. The following conclusions were obtained:
(1) Hydropower plants have a much larger planned power compliance rate for the planned electricity compliance penalty rule based on the planned electricity price than based on the market price.
(2) The model proposed in this paper hedges the market decision risk by taking into account the tariff forecast error.
(3) While taking into account the demand for power delivery from complex provinces, the model can obtain an operation plan that meets the safe and stable operation of the units.
Statements
Author contributions
XH: software and writing–original draft. JS: writing–review and editing. CC: writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The National Natural Science Foundation of China (Nos 52079014 and 52039002) and the Fundamental Research Funds supported this research for the Central Universities (Nos DUT22QN224 and DUT22JC21).
Acknowledgments
The authors are very grateful to the reviewers and editors for their constructive comments.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1
AvesaniD.ZanfeiA.Di MarcoN.GallettiA.RavazzoloF.RighettiM.et al (2022). Short-term hydropower optimization driven by innovative time-adapting econometric model. Appl. Energy310, 118510. 10.1016/j.apenergy.2021.118510
2
BulutE.AlbakE. 0.SevilgenG.ÖztürkF. (2021). A new approach for battery thermal management system design based on Grey Relational Analysis and Latin Hypercube Sampling. Case Stud. Therm. Eng.28, 101452. 10.1016/j.csite.2021.101452
3
CaiZ.ZhangC.HuX.ZhangG.LuY. (2020). “Design of Hydropower Dominated Provincial Electricity Spot Markets in China,” in 2020 4th International Conference on Power and Energy Engineering (ICPEE), Xiamen, China, 19-21 November 2020 (IEEE), 206–212.
4
CaoY.ZhangZ.ChengF.SuS. (2022). Trajectory Optimization for High-Speed Trains via a Mixed Integer Linear Programming Approach. IEEE Trans. Intelligent Transp. Syst.23, 17666–17676. 10.1109/tits.2022.3155628
5
CarvajalP. E.AnandarajahG.MulugettaY.DessensO. (2017). Assessing uncertainty of climate change impacts on long-term hydropower generation using the CMIP5 ensemble—the case of Ecuador. Clim. Change144, 611–624. 10.1007/s10584-017-2055-4
6
ChenH.CuiJ.SongF.JiangZ. (2022). Evaluating the impacts of reforming and integrating China's electricity sector. Energy Econ.108, 105912. 10.1016/j.eneco.2022.105912
7
ChengC.ChenF.LiG.RistićB.MirchiA.QiyuT.et al (2018). Reform and renewables in China: the architecture of Yunnan's hydropower dominated electricity market. Renew. Sustain. Energy Rev.94, 682–693. 10.1016/j.rser.2018.06.033
8
ChengQ.LuoP.LiuP.LiX.MingB.HuangK.et al (2022). Stochastic short-term scheduling of a wind-solar-hydro complementary system considering both the day-ahead market bidding and bilateral contracts decomposition. Int. J. Electr. Power & Energy Syst.138, 107904. 10.1016/j.ijepes.2021.107904
9
ChengY.ChungM.TsangK. (2023). Electricity Market Reforms for Energy Transition: lessons from China. Energies16, 905. 10.3390/en16020905
10
DingT.BoR.GuW.SunH. (2014). Big-M Based MIQP Method for Economic Dispatch With Disjoint Prohibited Zones. IEEE Trans. Power Syst.29, 976–977. 10.1109/tpwrs.2013.2287993
11
FangW.HuangQ.HuangS.YangJ.MengE.LiY. (2017). Optimal sizing of utility-scale photovoltaic power generation complementarily operating with hydropower: A case study of the world’s largest hydro-photovoltaic plant. Energy Convers. Manag.136, 161–172. 10.1016/j.enconman.2017.01.012
12
GolmohamadiH.Guldstrand LarsenK.Gjøl JensenP.Riaz HasratI. (2021). Optimization of power-to-heat flexibility for residential buildings in response to day-ahead electricity price. Energy Build.232, 110665. 10.1016/j.enbuild.2020.110665
13
Gómez-NavarroT.Ribó-PérezD. (2018). Assessing the obstacles to the participation of renewable energy sources in the electricity market of Colombia. Renew. Sustain. Energy Rev.90, 131–141. 10.1016/j.rser.2018.03.015
14
GuoH.MaZ.ZhangH.ZhouQ.WangD.LvQ.et al (2021). “The Coordination Mechanism between Medium- and Long-term Market and Spot Market in China,” in 2021 3rd International Conference on Electrical Engineering and Control Technologies (CEECT), Macau, Macao, 16-18 December 2021 (IEEE), 14–18.
15
JiaZ.ShenJ.ChengC.ZhangY.LyuQ. (2022). Optimum day-ahead clearing for high proportion hydropower market considering complex hydraulic connection. Int. J. Electr. Power & Energy Syst.141, 108211. 10.1016/j.ijepes.2022.108211
16
JiangW.LiuY.FangG.DingZ. (2023). Research on short-term optimal scheduling of hydro-wind-solar multi-energy power system based on deep reinforcement learning. J. Clean. Prod.385, 135704. 10.1016/j.jclepro.2022.135704
17
KarolczukA.KurekM. (2022). Fatigue life uncertainty prediction using the Monte Carlo and Latin hypercube sampling techniques under uniaxial and multiaxial cyclic loading. Int. J. Fatigue160, 106867. 10.1016/j.ijfatigue.2022.106867
18
KebedeA. A.KalogiannisT.Van MierloJ.BerecibarM. (2022). A comprehensive review of stationary energy storage devices for large scale renewable energy sources grid integration. Renew. Sustain. Energy Rev.159, 112213. 10.1016/j.rser.2022.112213
19
KrienU.SchönfeldtP.LaunerJ.HilpertS.KaldemeyerC.PleßmannG. (2020). oemof.solph—A model generator for linear and mixed-integer linear optimisation of energy systems. Softw. Impacts6, 100028. 10.1016/j.simpa.2020.100028
20
LagoJ.MarcjaszG.De SchutterB.WeronR. (2021). Forecasting day-ahead electricity prices: A review of state-of-the-art algorithms, best practices and an open-access benchmark. Appl. Energy293, 116983. 10.1016/j.apenergy.2021.116983
21
LuY.MengF.HaoC.YangJ.SongL.TianZ. (2021). Mechanism and benefit analysis of resource optimal allocation of China’s trans-provincial and trans-regional power trading. IOP Conf. Ser. Earth Environ. Sci.827, 012017. 10.1088/1755-1315/827/1/012017
22
MerkertL.HarjunkoskiI.IsakssonA.SäynevirtaS.SaarelaA.SandG. (2015). Scheduling and energy – Industrial challenges and opportunities. Comput. Chem. Eng.72, 183–198. 10.1016/j.compchemeng.2014.05.024
23
Pérez-DíazJ. I.WilhelmiJ. R.ArévaloL. A. (2010). Optimal short-term operation schedule of a hydropower plant in a competitive electricity market. Energy Convers. Manag.51, 2955–2966. 10.1016/j.enconman.2010.06.038
24
Rodríguez-SarastyJ. A.DebiaS.PineauP. (2021). Deep decarbonization in Northeastern North America: the value of electricity market integration and hydropower. Energy Policy152, 112210. 10.1016/j.enpol.2021.112210
25
ShenJ.ChengC.JiaZ.ZhangY.LvQ.CaiH.et al (2022). Impacts, challenges and suggestions of the electricity market for hydro-dominated power systems in China. Renew. Energy187, 743–759. 10.1016/j.renene.2022.01.089
26
ShenJ.ChengC.ZhangX.ZhouB. (2018). Coordinated operations of multiple-reservoir cascaded hydropower plants with cooperation benefit allocation. Energy153, 509–518. 10.1016/j.energy.2018.04.056
27
StančinH.MikulčićH.WangX.DuićN. (2020). A review on alternative fuels in future energy system. Renew. Sustain. Energy Rev.128, 109927. 10.1016/j.rser.2020.109927
28
TangC.ZhangF. (2020). Study on the connection and settlement of forward electricity market and spot electricity market. IOP conference series. Earth Environ. Sci.508, 12061. 10.1088/1755-1315/508/1/012061
29
TschoraL.PierreE.PlantevitM.RobardetC. (2022). Electricity price forecasting on the day-ahead market using machine learning. Appl. Energy313, 118752. 10.1016/j.apenergy.2022.118752
30
WangH.HuangJ. (2018). Incentivizing Energy Trading for Interconnected Microgrids. IEEE Trans. Smart Grid9, 2647–2657. 10.1109/tsg.2016.2614988
31
WuY.SuC.LiuS.GuoH.SunY.JiangY.et al (2022). Optimal Decomposition for the Monthly Contracted Electricity of Cascade Hydropower Plants Considering the Bidding Space in the Day-Ahead Spot Market. Water14, 2347. 10.3390/w14152347
32
XiaoY.NiyatoD.HanZ.DaSilvaL. A. (2015). Dynamic Energy Trading for Energy Harvesting Communication Networks: A Stochastic Energy Trading Game. IEEE J. Sel. Areas Commun.33, 2718–2734. 10.1109/jsac.2015.2481204
33
XinhongS.YefeiZ.PanjiajiaZ.GaoqinW.JianhuL. (2020). Trans-regional power trading optimization for promoting clean energy accommodation. IOP Conf. Ser. Earth Environ. Sci.431, 012053. 10.1088/1755-1315/431/1/012053
34
XuB.SunY.HuangX.ZhongP. A.ZhuF.ZhangJ.et al (2022). Scenario‐Based Multiobjective Robust Optimization and Decision‐Making Framework for Optimal Operation of a Cascade Hydropower System Under Multiple Uncertainties. Water Resour. Res.58, 30965. 10.1029/2021wr030965
35
YuanL.ZhouJ.LiC.XieM.MoL. (2016). Benefit and Risk Balance Optimization for Stochastic Hydropower Scheduling. Water Resour. Manag.30, 3347–3361. 10.1007/s11269-016-1354-2
36
ZhangF.ChengL.WuM.XuX.WangP.LiuZ. (2020). Performance analysis of two-stage thermoelectric generator model based on Latin hypercube sampling. Energy Convers. Manag.221, 113159. 10.1016/j.enconman.2020.113159
37
ZhangL.ZhangQ.FanH.WuH.XuC. (2021). Big-M based MILP method for SCUC considering allowable wind power output interval and its adjustable conservativeness. Glob. Energy Interconnect.4, 193–203. 10.1016/j.gloei.2021.05.001
38
ZhangR.ZhangS.WenX.JingZ. (2023). Refined Scheduling Based on Dynamic Capacity Model for Short-term Hydropower Generation. Water Resour. Manag.37, 21–35. 10.1007/s11269-022-03352-5
39
ZhaoZ.LiuJ.ChengC. (2019). A MILP model for day-ahead peak operation of cascade hydropower stations considering. backwater ournal Hydraulic Eng.50, 925–935.
40
ZhaoZ.LiuS.ZhouM.AbusorrahA. (2021). Dual-Objective Mixed Integer Linear Program and Memetic Algorithm for an Industrial Group Scheduling Problem. IEEE/CAA J. Automatica Sinica8, 1199–1209. 10.1109/jas.2020.1003539
Summary
Keywords
electricity market, mixed-integer linear programming, electricity decomposition, day-ahead market, settlement rules
Citation
Han X, Shen J and Cheng C (2023) Market bidding method for the inter-provincial delivery of cascaded hydroelectric plants in day-ahead markets considering settlement rules. Front. Energy Res. 11:1271934. doi: 10.3389/fenrg.2023.1271934
Received
03 August 2023
Accepted
29 September 2023
Published
20 October 2023
Volume
11 - 2023
Edited by
Bin Zhou, Hunan University, China
Updates
Copyright
© 2023 Han, Shen and Cheng.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jianjian Shen, shenjj@dlut.edu.cn
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.