Mixed-integer second-order cone programming method for active distribution network

Developing a novel type of power system is an important means of achieving the “dual carbon” goals of achieving peak carbon emissions and carbon neutrality in the near future. Given that the distribution network has access to a wide range of distributed and flexible resources, reasonably controlling large-scale and adjustable resources is a critical factor influencing the safe and stable operation of the active distribution network (ADN). In light of this, the authors of this study propose a mixed-integer second-order cone programming method for an active distribution network by considering the collaboration between distributed, flexible resources. First, Monte Carlo sampling is used to simulate the charging load of electric vehicles (EVs), and the auto regressive moving average (ARMA) and the scenario reduction algorithms (SRA) based on probability distance are used to generate scenarios of the outputs of distributed generation (DG). Second, we establish an economical, low-carbon model to optimize the operation of the active distribution network to reduce its operating costs and carbon emissions by considering the adjustable characteristics of the distributed and flexible resources, such as on-load tap changer (OLTC), devices for reactive power compensation, and EVs and electric energy storage equipment (EES). Then, the proposed model is transformed into a mixed-integer second-order cone programming (SOCP) model with a convex feasible domain by using second-order cone relaxation (SOCR), and is solved by using the CPLEX commercial solver. Finally, we performed an arithmetic analysis on the improved IEEE 33-node power distribution system, the results show that ADN’s day-to-day operating costs were reduced by 47.9% year-on-year, and carbon emissions were reduced by 75.2% year-on-year. The method proposed in this paper has significant effects in reducing the operating cost and carbon emissions of ADNs, as well as reducing the amplitude of ADN node voltages and branch currents.

1 Introduction

With the development of technologies related to renewable energy and power distribution networks, such distributed and flexible resources as DG, electric vehicles, energy storage devices, and demand response have become more readily available in the power grid, and pose new challenges to the operation and maintenance of the distribution network (Kang and Huo, 2022). The traditional distribution network has gradually evolved into ADNs, which has the capacity for active regulation to control and manage these distributed and flexible resources (Jiang et al., 2022). Unlike the traditional distribution network, the ADN can take efficient and intelligent measures to actively manage distributed and flexible resources at all levels to enhance the flexibility and controllability of the grid, and improve the synergy and interactions among the source, network, load, and storage. Reasonably controlling the large amount of distributed and flexible resources in the ADN to ensure the low-carbon and economical operation of the power system is a key concern for researchers in the area.

Many researchers have investigated the problem of the optimal scheduling of the ADN. A robust and optimal model of operation of the active distribution network was proposed based on the minimum confidence interval of the beta distribution of distributed energy to deal with the inevitably uncertainty in it (Luo et al., 2021). This involves taking the minimum confidence interval of the output of distributed energy as the interval of uncertainty for the robust optimization of the ADN. This yields a robust two-stage model to optimize the ADN. The results of assessments showed that this model is more representative of the empirical scenario than the traditional robust optimization (TRO) model. Pu et al. (2017) proposed a method of optimal scheduling based on the consistency algorithm to improve the speed of convergence by setting the coefficients of node weights, in response to the problems of large amounts of data and complicated calculations when scheduling the distribution network. However, this method can analyze only the changes in the active power of the nodes without considering its effects on the other parameters, such as the current and voltage of the distribution network. Pamshetti et al. (2023) considered the effects of the reconfiguration of the distribution network as well as reductions in its energy consumption and voltage to develop a cooperative operational model of the ADN with Soft Open Points (SOP) and distributed energy. The results of calculations obtained by using this model showed that it can improve the reliability of the system and reduce carbon emissions in the distribution network. Ruan et al. (2020) proposed a model to control the distributed voltage of the ADN by automatically partitioning it in an optimal manner according to the number of decision variables and constraints in the model, thereby reducing the complexity of computations and improving the sensitivity of voltage control. Li et al. (2022) modeled the problem of day-ahead optimal dispatch in the ADN as a multi-level stochastic programming model, and used an improved deep reinforcement learning algorithm to solve the problem of fluctuations in the voltage brought about by uncertainty in the output of renewable energy to the active distribution network. Verma and Padhy, (2022) established a demand response-based optimal tide model of the ADN that uses the characteristics of components of the symmetric domain to combine the day-ahead dynamic tariff with constraints on the operation of the ADN to plan the distribution network by modifying the optimal tide. However, the model considers only DGs and generators, and loads due to the residential demand, and the types of energy supply equipment and the types of energy loads included in the ADN are relatively homogeneous. Mohd Azmi et al. (2022) talk about communication technologies, applications, and communication standards for ADNs, and analyze the issues and challenges faced in the development of ADNs from an ICT perspective.

In terms of second-order cone programming algorithms, Zhang et al. (2018) modeled and analyzed an integrated energy system consisting of a power system, a natural gas system, and an energy hub, and transformed the original nonconvex planning problem into a convex planning problem using SOCP. Finally, a simulation study is carried out on a modified IEEE 33 distribution network and a 15-node natural gas network. Xiao et al. (2018) illustrated the important role played by service restoration in improving the resilience and reliability of distribution networks, proposed a mixed integer second-order cone programming (MISOCP) model for distribution network service restoration, considered the minimization of disconnected loads and the total number of switching operations, and carried out simulations on three experimental systems to validate the effectiveness of the MISOCP method for distribution network service restoration. Kayacık and Kocuk (2021) proposed an alternative mixed-integer nonlinear programming formulation of the reactive optimal tidal flow (ROPF) problem, utilized MISOCP to find the globally optimal solution to the proposed formulation of the ROPF problem, strengthened the MISOCP relaxation by adding convex envelopes and cutting planes, and finally, through the design of experiments, the MISOCP-based approach yielded promising results as compared to the semi-deterministic programming-based approaches in the literature.

The above summary of the literature shows that most studies in the area have sought to control the active and reactive parameters of the ADN as well as its voltage by using a single device or model. They have neither adequately explored the potential of adjustable resources for regulating the distribution network, nor considered cooperation between different distributed and flexible resources for its optimal scheduling. Moreover, most of the existing studies only considered the active power of the distribution network without analyzing active and reactive power as well as multiple power quality parameters such as voltage and current at the same time. In addition, the objective functions formulated in past research have emphasized reducing the cost of the network while ignoring reductions in its carbon emissions.

To address the above issues, the authors of this paper propose a low-carbon, economical model of optimal dispatch for active distribution networks based on collaboration between distributed, flexible resources. The main contributions of this study are as follows: 1) We simulate changes in the load of the EV by using Monte Carlo simulations according to a probability distribution function of the travel habits of EV users. We also construct scenarios for the output of DG by using the autoregressive sliding-average method, and apply the probabilistic distance fast reduction method to reduce the number of scenarios. 2) In light of the adjustable characteristics of each distributed and flexible resource in the ADN, we construct a low-carbon, economical model to optimize the ADN, where the objective function is designed to reduce the cost of its operation as well as its carbon emissions. 3) We use the SOCR method to eliminate squared variables, such as those of current and voltage, in the model, transform the original problem into a mixed-integer second-order cone programming problem, perform tidal calculations on the IEEE 33-node distribution network, analyze changes in the parameters at each node of the ADN under different scenarios, and verify the impacts of its access to distributed and flexible resources on its operating cost and carbon emissions.

2 Related work

In the study of optimal scheduling of distribution networks, Zhang et al. (2021) proposed a research on two-level energy optimized dispatching strategy of microgrid cluster based on IPSO algorithm. The first level takes microgrids as the research object, and takes the highest economic benefit and the lowest operational risk as the optimization objectives, constructs the unit risk-economic benefit ratio screening solution set, and then formulates the microgrid internal scheduling candidate strategies. The second level determines the optimal internal scheduling strategy for each microgrid with the optimization objective of minimizing the interaction power between the microgrid cluster system and the distribution grid. The line loss of the microgrid cluster system is also considered to develop a microgrid cluster energy complementation scheme. The method simultaneously coordinates the economic benefits and operational risks of microgrids, reduces the interactive power and fluctuations between the microgrid cluster system and the distribution grid, and reduces the line losses.

In Zhang et al. (2022), considered the voltage fluctuations and stability problems caused by intermittent photovoltaic (PV) generation to the distribution network, a three-stage hierarchically-coordinated voltage/var control method based on PV inverters considering distribution network voltage stability has been proposed. In the first stage, the OLTC is dispatched 1 day in advance. In the second stage, the reactive output of the inverter is scheduled at 1 hour intervals. In the third stage, real-time local voltage drop control of the inverter is realized. In order to coordinate the interactions between these stages, the first two stages are coordinated by interval optimization. Meanwhile, the last two stages are coordinated hierarchically by simultaneously optimizing the inverter base reactive power output and sag control functions. Finally, the effectiveness of the method in reducing power losses and bus voltage deviation in distribution networks is verified through an arithmetic example.

Guo et al. (2019) proposed a model predictive control (MPC) -based coordinated voltage regulation method for distribution networks with distributed generation and energy storage system. In this method, equipment types such as DG units, energy storage systems, and on-load tap-changer are mainly considered. In order to better coordinate the economic operation and voltage regulation control of the distribution network, two control modes are designed according to the operating conditions: in the preventive mode, the DG units operates in the maximum power point tracking (MPPT) mode, while optimizing the power outputs of the DG units and the energy storage systems to keep the voltage within the specified range; in the corrective mode, the curtailment of active power from the distribution network is selected as an index for correcting the voltage deviation.

In order to optimize the active power of the distribution network, Li et al. (2018) proposed a three-layer cooperative scheduling system consisting of a distribution network scheduling layer, a microgrid centralized control layer and an energy Internet local control layer, and then solved the distribution network operation loss model by an improved branch current forward generation method and genetic algorithm to realize the optimal scheduling of active power in the distribution network.

In the distribution network robust optimization problem, in order to effectively reduce the conservatism of the traditional robust optimization model, Yang and Wu, (2019) proposed a distributionally robust real-time power scheduling model, which incorporates the two-phase scheme of economic scheduling and corrective control into the model, where the economic scheduling scheme optimizes the active power distribution of the distribution network, and generates the corrective control strategy of active and reactive power to eliminate the voltage overruns in the distribution network.

In order to achieve optimal power flow and power loss minimization in distribution networks, Zhang et al. (2016) proposed a coordinated day-ahead reactive power dispatch method in distribution network based on real power forecast errors. This method utilizes the active power prediction error of the DG units to estimate the probability distribution of the reactive power capacity of the DG units. Meanwhile, considering different output characteristics and constraints of reactive power sources, a dynamic preliminary-coarse-fine adjustment method is designed to optimize the outputs of the DG units and shunt reactive power compensator, which first obtains the initial value through preliminary optimization, and then iterates repeatedly between coarse optimization and fine optimization, so as to achieve the effect of reducing the power loss in the distribution network and realizing the optimal distribution of reactive power.

Uncertain and intermittent power output due to large-scale PV access in distribution networks can severely impair network operation, leading to unexpected power losses and voltage fluctuations. To solve the above problems, Li et al. (2023) proposed a multi-timescale affinely adjustable robust reactive power dispatch (MTAAR-RPD) method, In this approach, three levels of modeling covering multiple time scales of “hour-minute-second” are developed to coordinate the control of various devices in the distribution network. In the first stage, capacitor banks and OLTC are dispatched every hour; in the second stage, the basic reactive power output of PV inverters is dispatched every 15 min; and in the third stage, the reactive power output of inverters is adjusted in real time adaptively based on an optimized Q-P sag controller.

For the distribution network optimal dispatch problem, in terms of model solving methods, Sun et al. (2021) proposed a two-time scale robust optimization method for the multi-terminal soft open point (SOP). The operating points of the SOP are optimized by a semi-definite programming (SDP) model to minimize system losses and mitigate voltage imbalances, and an improved iterative cutting plane (ICP) method is utilized to enhance the accuracy of the SDP level 1 relaxation.

Han et al. (2022) proposed a novel decentralized operation strategy for a multi-terminal direct current (MTDC) link system to control the power flow between interconnected distribution networks. This strategy derives formulas for voltage and bus losses in the network by applying curve/surface fitting techniques to distribution network topology data. Subsequently, the active/reactive power setpoints of the MTDC links are optimized to minimize the network losses and balance the injected power from the upstream grid. Finally, the optimization model with a quadratically constrained quadratic problem is relaxed to a second-order constrained planning model for solution.

3 Analyzing uncertainty in the load of the source of ADN

Wind farms and photovoltaic power plants are connected to the distribution grid in the form of distributed sources of power, where this causes the distribution grid to gradually evolve into an active distribution grid. EV technology is quickly maturing, with new energy vehicles having garnered 23% of the market by 2022. As they are distributed and flexible resources, the output of DG and the charging load of EVs are highly random, fluctuating, and intermittent. An increase in DG and large-scale loads due to EVs will inevitably lead to new problems and challenges regarding the safe and stable operation of the distribution grid. Therefore, it is important to analyze the influence of uncertainties in the output of DG and the load due to EVs on dispatch in the ADN. We simulate the load of EVs here by using the Monte Carlo method, and represent uncertainty in the output of DG by using the ARMA and the SRA based on probability distance.

3.1 Simulating EV load using Monte Carlo method

The load of the EV is based on two factors: its daily mileage, and the time at which charging begins (Wang et al., 2023).

3.1.1 Daily driving range

Assuming that EV users have the same driving habits as drivers of vehicles that run on fossil fuels (Smadi and Shehadeh, 2023), the probability density function of their daily mileage can be expressed as:

$f\left(x\right)=\frac{1}{x}\frac{1}{{\sigma }_x\sqrt{2\pi }}\exp \left(-\frac{{\left(\ln x-{\mu }_x\right)}^2}{2{{\sigma }_x}^2}\right)(1)$

where x is the daily mileage of the EV, and σ_x and μ_x are its mean and variance, respectively.

3.1.2 Time of initiation of charging

The probability density function of the time at which the EV begins charging can be expressed as

$f\left(t\right)=\left\{\begin{array}{l}\frac{1}{{\sigma }_t\sqrt{2\pi }}\exp \left(-\frac{{\left(t-{\mu }_t\right)}^2}{2{{\sigma }_t}^2}\right){\mu }_t-12<t<24\\ \frac{1}{{\sigma }_t\sqrt{2\pi }}\exp \left(-\frac{{\left(t+24-{\mu }_t\right)}^2}{2{{\sigma }_t}^2}\right)0<t<{\mu }_t-12\end{array}\right.(2)$

where t is the time at which the EV begins charging, and σ_t and μ_t are its mean and variance, respectively.

The Monte Carlo simulation is used to solve a variety of problems (Li et al., 2021). We randomly chose the vehicle use-related behavior of a large number of EV users through the Monte Carlo method to simulate the load of EVs. The process is shown in Figure 1.

FIGURE 1

FIGURE 1. Load of EVs simulated by the Monte Carlo method.

3.2 Generating scenarios of DG based on ARMA and SRA

The output of DG is somewhat uncertain. We use the ARMA model to generate scenarios of this output (Dong et al., 2015):

$x_t={\displaystyle \sum _{i=1}^a}{\lambda }_i{x}_{t-i}+{\alpha }_t-{\displaystyle \sum _{j=1}^b}{\mu }_j{\alpha }_{t-j}(3)$

where x_t is the time series at time t, λ_i is the auto regressive parameter, μ_i is the moving average parameter, and α_t is normal white noise that has a mean of zero and a variance of σ².

Given that an excessively large number of scenarios may require significant computational resources and a long time, we use the SRA to reduce the size of the set of scenarios S generated by the ARMA model (Growe-Kuska et al., 2003). The process is shown in Figure 2.

FIGURE 2

FIGURE 2. Reducing the number of scenarios of outputs of DG based on the SRA.

4 Proposed model

Wind turbines (WT) and photovoltaic (PV) cells constitute the majority of sources of DG in the ADN. Distributed flexible resources involve active management equipment that can maintain the voltage and power of the ADN, including OLTC, EVs, switchable capacitor banks (SCBs), static var compensator (SVC), and EES. We establish the low-carbon, economical model of optimization of the ADN based on synergy between the distributed and flexible resources, and consider reductions in cost carbon emissions as the objectives of optimization.

4.1 Goals of optimization

4.1.1 Optimizing operating cost

The operating cost of the ADN includes the costs of power purchase, network loss, and EV regulation. The overall objective of optimizing its cost can be expressed as

$\min F_1=C_{\mathrm{g}\mathrm{r}\mathrm{i}\mathrm{d}}+C_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}+C_{\mathrm{e}\mathrm{v}}(4)$

where F₁ is the unit cycle operating cost of the ADN, C_grid is the cost of power purchase, C_loss is the cost of network loss, and C_ev is the cost of EV regulation.

1) Cost of power purchase:

$C_{\mathrm{g}\mathrm{r}\mathrm{i}\mathrm{d}}={\displaystyle \sum _{t=1}^T}{a}_{\mathrm{g}\mathrm{r}\mathrm{i}\mathrm{d},t}{p}_{\mathrm{g},t}(5)$

where a_grid,t is the price of power at time t and p_g,t is the power purchased at t.

2) Cost of network loss:

$C_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}=a_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}{\displaystyle \sum _{t=1}^T}{P}_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s},t}=a_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}{\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{\left(i,j\right)\in \phi }}{r}_{ij}{I}_{ij,t}^2(6)$

where a_loss is the coefficient of network loss, P_loss,t is the active power lost by the ADN at time t, r_ij is the resistance of branch (i,j), $I_{ij,t}^2$ is the square of the current in branch (i,j), and φ is the set of nodes of the ADN.

3) Cost of EV regulation

EV users participate in the optimal scheduling of the ADN in the form of flexible loads by signing an agreement with the operator. According to its mode of regulation, the load of the EV can be divided into a transferable load (TL) and a reducible load (RL). The TL can be transferred within the allowable transfer time, while the RL is more flexible, and can reduce its own power or interrupt its operation to relieve the pressure of supply on the system within the allowable time:

$C_{\mathrm{e}\mathrm{v}}=c_{\mathrm{T}\mathrm{L}}{p}_{\mathrm{T}\mathrm{L},t}^{\mathrm{e}\mathrm{v}}+c_{\mathrm{R}\mathrm{L}}{p}_{\mathrm{R}\mathrm{L},t}^{\mathrm{e}\mathrm{v}}(7)$

where c_TL and c_RL are the subsidies per unit of power for the transferable and the reducible loads, respectively, $p_{\mathrm{T}\mathrm{L},t}^{\mathrm{e}\mathrm{v}}$ is the magnitude of load of the EV transferred at time t, and $p_{\mathrm{R}\mathrm{L},t}^{\mathrm{e}\mathrm{v}}$ is the magnitude of reduced load of the EV at time t.

4.1.2 Optimizing carbon emissions

The carbon emissions of the ADN are mainly due to CO₂ emissions from the power purchased by it. We introduce a carbon emission penalty to formulate the objective of optimizing emissions:

$\min F_2={\displaystyle \sum _{t=1}^T}\omega \cdot a_{\mathrm{C}\mathrm{O}2}{p}_{\mathrm{g},t}(8)$

where F₂ is the daily cost of treating carbon emissions by the ADN, a_CO2 is the penalty per unit of CO₂ emissions, and ω is the carbon emissions factor of the power supply of the grid.

4.1.3 Overall goal of optimization

We combine the two objectives explained above to obtain the overall objective of optimization of the ADN:

$\min F_c=F_1+F_2(9)$

4.2 Constraints

4.2.1 Constraint on DG output

$P_{i,\min }^{\mathrm{D}\mathrm{G}}\le P_{i,t}^{\mathrm{D}\mathrm{G}}\le P_{i,\max }^{\mathrm{D}\mathrm{G}}i\in {\mathrm{D}\mathrm{G}}_i,t\in T(10)$

where $P_{i,t}^{\mathrm{D}\mathrm{G}}$ is the power output by the ith DG at time t, and $P_{i,\max }^{\mathrm{D}\mathrm{G}}$ and $P_{i,\min }^{\mathrm{D}\mathrm{G}}$ are the upper and lower limits on the power output by the ith DG, respectively.

4.2.2 EES constraint

$E_{s,t}=E_{s,t-1}+{\eta }_{\mathrm{c}\mathrm{h}}{P}_{\mathrm{c}\mathrm{h},t}-P_{\mathrm{d}\mathrm{i}\mathrm{s},t}/{\eta }_{\mathrm{d}\mathrm{i}\mathrm{s}}(11)$

$0⩽P_{\mathrm{c}\mathrm{h},t}⩽b_{\mathrm{c}\mathrm{h},t}{P}_{\mathrm{c}\mathrm{h}}^{\max }(12)$

$0⩽P_{\mathrm{d}\mathrm{i}\mathrm{s},t}⩽b_{\mathrm{d}\mathrm{i}\mathrm{s},t}{P}_{\mathrm{d}\mathrm{i}\mathrm{s}}^{\max }(13)$

${\lambda }_{\min }{E}_s⩽E_{s,t}⩽{\lambda }_{\max }{E}_s(14)$

$b_{c\mathrm{h},t}+b_{\mathrm{d}\mathrm{i}\mathrm{s},t}⩽1(15)$

$E_{s,0}=E_{s,T}(16)$

where E_s,t is the capacity of the EES at time t and its rated capacity is E_s. η_ch and η_dis are the efficiencies of charging and discharging of the EES, respectively, P_ch,t and P_dis,t are the powers of charging and discharging of the EES at time t, respectively, $P_{\mathrm{c}\mathrm{h}}^{\max }$ and $P_{\mathrm{d}\mathrm{i}\mathrm{s}}^{\max }$ are the maximum charging and discharging powers of the EES, respectively, and b_ch,t and b_dis,t are variables in the range of zero to one. b_ch,t = 1 means that the EES is charging while b_dis,t = 1 means that it is discharging. λ_max and λ_min are the maximum and minimum states of charge (SOC) of the EES, respectively. Eq. 14 indicates that the final power stored by the EES in a scheduling cycle is equal to the power at the initial time.

4.2.3 OLTC constraint

$\left\{\begin{array}{l}{U}_t^2={\left(U_{\mathrm{B}\mathrm{a}\mathrm{s}\mathrm{e}}\right)}^2{r}_t\\ r_t=r_{\min }+{\displaystyle \sum _s}{r}_s{\sigma }_{s,t}^{\mathrm{O}\mathrm{L}\mathrm{T}\mathrm{C}}\end{array}\right.(17)$

where U_Base is the voltage at the standard OLTC ratio, $U_t^2$ is the squared voltage at time t, r_t is the squared OLTC ratio at time t, r_min is the square of the lower limit of the ratio of variation in the OLTC, r_s is the difference between the ratios of variations of gear s and the square of gear s-1 of the OLTC, where this is an increase in adjacent regulation, and ${\sigma }_{s,t}^{\mathrm{O}\mathrm{L}\mathrm{T}\mathrm{C}}$ is a variable in the range of zero to one. ${\sigma }_{s,t}^{\mathrm{O}\mathrm{L}\mathrm{T}\mathrm{C}}$ = 1 means that the OLTC adjusts stall. In light of the life of the equipment and considerations of cost, the number of adjustments of the OLTC are limited. We thus set a limit on the total number of OLTC operations in multiple periods:

${\displaystyle \sum _{t\in T}}\left({\delta }_t^{\mathrm{O}\mathrm{L}\mathrm{T}\mathrm{C},\mathrm{I}\mathrm{N}}+{\delta }_t^{\mathrm{O}\mathrm{L}\mathrm{T}\mathrm{C},\mathrm{D}\mathrm{E}}\right)\le N_{\mathrm{O}\mathrm{L}\mathrm{T}\mathrm{C},\max }(18)$

where ${\delta }_t^{\mathrm{O}\mathrm{L}\mathrm{T}\mathrm{C},\mathrm{I}\mathrm{N}}$ and ${\delta }_t^{\mathrm{O}\mathrm{L}\mathrm{T}\mathrm{C},\mathrm{D}\mathrm{E}}$ are identifiers of the ratio of stall adjustment by the OLTC, and are in the range of zero to one. If ${\delta }_t^{\mathrm{O}\mathrm{L}\mathrm{T}\mathrm{C},\mathrm{I}\mathrm{N}}$ = 1, the stall value of the OLTC at time t is larger than that at time t-1. ${\delta }_t^{\mathrm{O}\mathrm{L}\mathrm{T}\mathrm{C},\mathrm{D}\mathrm{E}}$ has a similar meaning. $N_{\mathrm{O}\mathrm{L}\mathrm{T}\mathrm{C},\max }$ is the upper limit of the number of OLTC operations.

4.2.4 Constraints on powerless compensation device

1) SCB constraint

$\left\{\begin{array}{l}{Q}_t^{\mathrm{S}\mathrm{C}\mathrm{B}}=y_t^{\mathrm{S}\mathrm{C}\mathrm{B}}{Q}_{\mathrm{S}\mathrm{C}\mathrm{B},\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{p}}\\ y_t^{\mathrm{S}\mathrm{C}\mathrm{B}}\le Y_{\mathrm{S}\mathrm{C}\mathrm{B},\max }\end{array}\right.(19)$

where $Q_t^{\mathrm{S}\mathrm{C}\mathrm{B}}$ is the reactive power issued by the SCB at time t, and $y_t^{\mathrm{S}\mathrm{C}\mathrm{B}}$ is the number of SCB groups in operation. It is a discrete variable. $Y_{\mathrm{S}\mathrm{C}\mathrm{B},\max }$ is the upper limit of the number of SCB groups and $Q_{\mathrm{S}\mathrm{C}\mathrm{B},\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{p}}$ is the compensation power of each SCB group. Given such factors as the life of the equipment and economic considerations, the number of adjustment to discrete reactive power compensation is limited. We thus set a limit on the total number of SCB operations in multiple periods:

${\displaystyle \sum _{t\in T}}\left|y_t^{\mathrm{S}\mathrm{C}\mathrm{B}}-y_{t-1}^{\mathrm{S}\mathrm{C}\mathrm{B}}\right|\le N_{\mathrm{S}\mathrm{C}\mathrm{B},\max }(20)$

where $N_{\mathrm{S}\mathrm{C}\mathrm{B},\max }$ is the upper limit of the number of SCB operations.

(2) SVC constraint

$Q_{\mathrm{S}\mathrm{V}\mathrm{C},\min }\le Q_t^{\mathrm{S}\mathrm{V}\mathrm{C}}\le Q_{\mathrm{S}\mathrm{V}\mathrm{C},\max }(21)$

where $Q_t^{\mathrm{S}\mathrm{V}\mathrm{C}}$ is the reactive power emitted by the SVC at time t, and Q_SVC,max and Q_SVC,min are the upper and lower limits of its reactive power compensation, respectively.

4.2.5 EV constraint

1) Transferable load (TL) of EV

Let the period planned for the TL be $\left[t_{\mathrm{s}\mathrm{h}\mathrm{i}\mathrm{f}\mathrm{t}}^{-},t_{\mathrm{s}\mathrm{h}\mathrm{i}\mathrm{f}\mathrm{t}}^{+}\right]$. We then set the following constraint in order to ensure normal operating conditions for the TL.

${\displaystyle \sum _{t=t_{\mathrm{b}\mathrm{e}\mathrm{g}\mathrm{i}\mathrm{n}}}^{t_{\mathrm{b}\mathrm{e}\mathrm{g}\mathrm{i}\mathrm{n}}+t_{\mathrm{l}\mathrm{a}\mathrm{s}\mathrm{t}}-1}}\alpha =t_{\mathrm{l}\mathrm{a}\mathrm{s}\mathrm{t}}(22)$

$P_{\mathrm{T}\mathrm{L}}^t=\alpha L_{\mathrm{T}\mathrm{L}}(23)$

where t_begin and t_last are the start time of the transfer of load and its duration, respectively, and L_TL and $P_{\mathrm{T}\mathrm{L}}^t$ are the powers before and after transfer, respectively. α is a variable in the range of zero to one. α = 1 indicates the transfer of TL to time slot t.

2) Reducible load (RL) of EV

$P_{\mathrm{R}\mathrm{L}}^t=L_{\mathrm{R}\mathrm{L}}^t-\mu \cdot {\beta }_t{L}_{\mathrm{R}\mathrm{L}}^t(24)$

$0\le {\displaystyle \sum _{t=1}^T}{\beta }_t\le {\beta }_{\max }(25)$

$T_{\mathrm{R}\mathrm{L}}^{\min }\le {\displaystyle \sum _{\tau =t}^{t+T_{\mathrm{R}\mathrm{L}}-1}}{\beta }_t\le T_{\mathrm{R}\mathrm{L}}^{\max }(26)$

where $L_{\mathrm{R}\mathrm{L}}^t$ and $P_{\mathrm{R}\mathrm{L}}^t$ are the powers before and after reductions in load, respectively, μ is the coefficient of reduction of the RL, and β_t is a variable in the range of zero to one. β_t = 1 means that load reduction has occurred. τ is the period for which the load is reduced, β_max is the maximum number of reductions based on the RL, T_cut is the duration of load reduction, and $T_{\mathrm{R}\mathrm{L}}^{\min }$ and $T_{\mathrm{R}\mathrm{L}}^{\max }$ are the minimum and maximum durations of load reduction, respectively.

4.2.6 Trend-related constraint

The ADN usually has a radial structure. The Distflow tidal equation can be used to describe the tidal constraints on it:

${\displaystyle \sum _{i\in u\left(j\right)}}{P}_{ij}-r_{ij}{I}_{ij}^2={\displaystyle \sum _{k\in v\left(j\right)}}{P}_{jk}+P_j(27)$

${\displaystyle \sum _{i\in u\left(j\right)}}{Q}_{ij}-x_{ij}{I}_{ij}^2={\displaystyle \sum _{k\in v\left(j\right)}}{Q}_{jk}+Q_j(28)$

$V_j^2=V_i^2-2\left(r_{ij}{P}_{ij}+x_{ij}{Q}_{ij}\right)+I_{ij}^2\left(r_{ij}^2+x_{ij}^2\right)(29)$

$I_{ij}^2=\frac{P_{ij}^2+Q_{ij}^2}{V_i^2}(30)$

$P_j=P_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d},j}+P_{\mathrm{e}\mathrm{v},j}+P_{\mathrm{c}\mathrm{h},j}-P_{\mathrm{d}\mathrm{i}\mathrm{s},j}-P_{\mathrm{D}\mathrm{G},j}-P_{\mathrm{G},j}(31)$

$Q_j=Q_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d},j}-Q_{\mathrm{S}\mathrm{C}\mathrm{B},j}-Q_{\mathrm{S}\mathrm{V}\mathrm{C},j}-Q_{\mathrm{G},j}(32)$

where $i\in u\left(j\right)$ and $k\in v\left(j\right)$ are the set of branches with j as the end branch and the first node, respectively, P_ij and Q_ij are the active and the reactive powers flowing from node i to node j, respectively, r_ij and x_ij are the resistance and reactance of branch (i,j), respectively, P_j and Q_j are the equivalent active and reactive powers of node j, respectively, $V_i^2$ is the square of the magnitude of voltage at node i, $I_{ij}^2$ is the square of the current flowing through branch (i,j), and P_load,j, P_ev,j, P_ch,j, P_dis,j, P_DG,j, and P_G,j are the active power of the load at node j, the charging power of the electric vehicle, the charging and discharging powers of the energy storage device, respectively, the output of the distributed power source, and active power from the generator (power purchased from the grid), respectively. Q_load,j, Q_SCB,j, Q_SVC,j, and Q_G,j are the reactive power of the load at node j, the reactive power output of the SCBs, the reactive power output of the SVC, and the reactive power emitted by the generator, respectively.

4.2.7 Operational constraint

$\left\{\begin{array}{l}{V}_{\min }\le V_j\le V_{\max }\\ 0<I_{ij}\le I_{\max }\end{array}\right.(33)$

where V_max and V_min are the upper and lower limits of the voltage at nodes of the ADN, respectively, and I_max is the upper limit of the current allowed in the branch.

5 Low-carbon economical model of optimization of ADN

Because the constraints imposed by the tidal current and the safe operation of the ADN limit the squared terms, the proposed low-carbon economical model of its optimization is a non-convex non-linear programming model that cannot be directly solved. To address this issue, we used SOCR on Eq. 30 by using ${\stackrel{\sim }{I}}_{ij}$ = ${\stackrel{\sim }{I}}_{ij}$ and ${\stackrel{\sim }{V}}_j$ = $V_j^2$:

$P_{ij}^2+Q_{ij}^2\le {\stackrel{\sim }{I}}_{ij}{\stackrel{\sim }{V}}_{ij}(34)$

Further, the following equation can be derived:

${\left(2P_{ij}\right)}^2+{\left(2Q_{ij}\right)}^2+{\left({\stackrel{\sim }{I}}_{ij}-{\stackrel{\sim }{V}}_{ij}\right)}^2\le {\left({\stackrel{\sim }{I}}_{ij}+{\stackrel{\sim }{V}}_{ij}\right)}^2(35)$

The above equation can be rewritten as:

${‖\begin{array}{l}2P_{ij}\\ 2Q_{ij}\\ {\stackrel{\sim }{I}}_{ij}-{\stackrel{\sim }{V}}_{ij}\end{array}‖}_2\le {\stackrel{\sim }{I}}_{ij}+{\stackrel{\sim }{V}}_{ij}(36)$

Then, Eqs 27–29 and 33 can be transformed into:

${\displaystyle \sum _{i\in u\left(j\right)}}{P}_{ij}-r_{ij}{\stackrel{\sim }{I}}_{ij}={\displaystyle \sum _{k\in v\left(j\right)}}{P}_{jk}+P_j(37)$

${\displaystyle \sum _{i\in u\left(j\right)}}{Q}_{ij}-x_{ij}{\stackrel{\sim }{I}}_{ij}={\displaystyle \sum _{k\in v\left(j\right)}}{Q}_{jk}+Q_j(38)$

${\stackrel{\sim }{V}}_j={\stackrel{\sim }{V}}_i-2\left(r_{ij}{P}_{ij}+x_{ij}{Q}_{ij}\right)+{\stackrel{\sim }{I}}_{ij}\left(r_{ij}^2+x_{ij}^2\right)(39)$

$\left\{\begin{array}{l}{V}_{\min }^2\le {\stackrel{\sim }{V}}_j\le V_{\max }^2\\ 0<{\stackrel{\sim }{I}}_{ij}\le I_{\max }^2\end{array}\right.(40)$

The SOCR transforms the squared variables in the constraint into real variables, eliminates the phase angles of voltage and current, and converts the original model from a non-convex, non-linear programming model into a convex cone programming model. Moreover, the presence of discrete variables in the model changes the problem at hand into a mixed-integer second-order cone programming (MISOCP) problem, which can be solved by a commercial software or algorithm packages.

6 Examples for analysis

We programmed the proposed model by using the YALMIP modeling toolkit in the MATLAB 2020b environment, and called the Cplex 12.10 commercial algorithm for the calculations. The computational system was an Intel i7-4790CPU 3.60 GHz, with 16 GB of RAM, and the Windows 10 64-bit operating system.

6.1 Model parameters

We modified the IEEE 33-node distribution system to test the proposed model. Its network topology is shown in Figure 3. The standard active load of the ADN was 3.715 MW, the standard reactive load was 2.3 Mvar, the reference voltage was 12.66 kV the reference power was 10 MVA, the range of voltage of the nodes was 0.94–1.06 p. u., and the range of the square of the branch current was 0–10 A.

FIGURE 3

FIGURE 3. Improved IEEE 33-node active distribution grid.

The distributed power supply mainly consisted of power from the WT and the PV cell. The WT was connected to nodes 17 and 32, and the PV cell was connected to nodes 9 and 19. Both had a rated power of 1.5 MW and a cost of power generation of 0.1 RMB/kWh. The ADN was connected to the main network with the OLTC in the range of voltage regulation of 0.94–1.05 p. u., a step size of 0.01 p. u., a total of 11 adjustable steps, and a daily limit of five adjustments for load regulation. The cost of adjustment was 200 RMB each time. The SCBs were installed at nodes 5 and 15, had a capacity of 100 kvar × 5 groups, and its operating cost was 0.1 RMB/kvar-h. Nodes 5, 15, and 32 were connected to SVCs with a capacity of −0.1 to 0.3 Mvar, and an operating cost of 0.1 RMB/kvar-h. Nodes 15 and 32 were connected to an EES with a capacity of 1 M Wh, maximum charging and discharging powers of 0.3 MW and 0.2 MW, respectively, an efficiency of charging and discharging of 90%, and a cost of charging and discharging of 0.1 RMB/kWh. The EV loads were connected to node 22, and the adjustable EV load and the cost of compensation are shown in Table 1. The penalty for carbon emissions was set to the national average price used for carbon trading, 0.048 RMB/kg. The carbon emission factor of electricity from the grid was set to 0.581 kg/kWh.

TABLE 1

TABLE 1. Parameters of the adjustable load of the EV.

The ADN purchased electricity from the main grid at a time-of-use tariff, the specific values of which are shown in Table 2.

TABLE 2

TABLE 2. Time-of-use tariff for power purchase by the ADN.

We used the method detailed in Section 2.2, and applied the ARMA (3,2) model to sample the initial scenarios. The autoregressive parameters were set to φ₁ = 0.8, φ₂ = 0.15, and φ₃ = 0.15, the parameters of the sliding average were θ₁ = 0.8 and θ₂ = 0.2, σ = 2.5 was set for normal white noise, and the scenarios for the outputs of powers of the WT and the PV cell were generated as shown in Figures 4, 5, respectively.

FIGURE 4

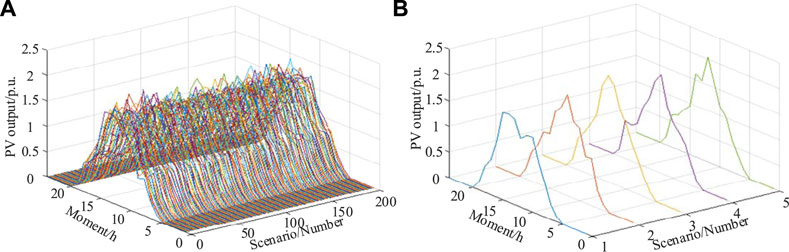
FIGURE 4. Generating and reducing the number of scenarios of the output of WT power. (A) Scenario generation of PV (B) Scenario reduction of PV

FIGURE 5

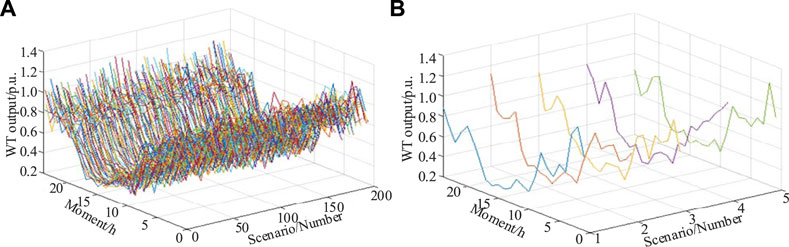
FIGURE 5. Generating and reducing the number of scenarios of the output of WT power. (A) Scenario generation of WT (B) Scenario reduction of WT

We used the method described in Section 1.1 to randomly choose 300 EVs. The battery capacity was set to 70 k Wh, the charging power to 4 kW, and the number of Monte Carlo simulations was set to 30. The curves of the load of the EV, equivalent output of DG, and variations in load during a day are shown in Figure 6. Where the equivalent outputs of the PV cell and the WT are averaged from Figures 5B, D, respectively.

FIGURE 6

FIGURE 6. Curves of the load, EV load, and distributed power output in a day.

The 24 h load distribution of each node of ADN is shown in Figure 7.

FIGURE 7

FIGURE 7. Load distribution at each node during the day. (A) Active load (B) Reactive load

6.2 Results and analysis

To verify the effectiveness of the proposed model of the active distribution network based on collaboration with distributed and flexible resources, we considered the following three scenarios:

Scenario 1: There was no DG, or any access to distributed and flexible resources. The load of the EV did not participate in grid regulation.

Scenario 2: While access to DG was available, the distributed and flexible resources were inaccessible. The load of the EV did not participate in grid regulation.

Scenario 3: Access to both DG, and the distributed and flexible resources was available. The load of the EV participated in grid regulation.

Curves of the amplitude of voltage at the nodes for all three scenarios are shown in Figure 8.

FIGURE 8

FIGURE 8. Curves of the amplitude of voltage of each node under different scenarios.

Figure 8 shows that the voltage of each node in the three scenarios was distributed in the range of 1–1.06 p. u., and no voltage overrun was noted. A comparison between scenario 2 and scenario 1 shows that the voltage at each node of the distribution network in the former improved significantly due to access to DG. The voltage of the system was smoother and deviations in it were significantly reduced, indicating that access to DG enhanced the system voltage and reduced the flow of reactive power. A comparison between scenario 3 and scenario 2 shows that the voltage of the distribution network improved even further in the former due to access to DG as well as the distributed and flexible resources. The system voltage was smoother in scenario 3, and deviations in it were further reduced. The ratios of the peak-to-valley difference in the magnitude of voltage at the nodes in scenarios 1, 2, and 3 were 4.24%, 2.34%, and 1.79%, respectively. Thus, the deviation in the peak-to-valley magnitude of the voltage of the distribution network decreased by 2.45% once DG as well as and the distributed and flexible resources had been connected to it.

Curves of the amplitude of current at the branches in the three scenarios are shown in Figure 9.

FIGURE 9

FIGURE 9. Curves of amplitude of current at each branch under different scenarios.

Figure 9 shows that the current at each branch in all three scenarios was distributed between 0 and 3.16 A, and there was no overcurrent. The amplitude of current at each branch was significantly lower in scenario 3 than in scenarios 1 and 2. This was because the ADN had access to DG as well as the distributed and flexible resources in this scenario, because of which fluctuations in voltage between nodes significantly decreased. This in turn reduced the current between branches and yielded the following advantages: 1) A reduction in the branch current reduced the loss of active power in the line. 2) A reduction in the amplitude of the branch current reduced the level of protection needed from the device to prevent overcurrent, and led to economic benefits for the network.

The daily operating costs of the ADN in the three scenarios are shown in Table 3.

TABLE 3

TABLE 3. Daily operating costs of the ADN under different scenarios.

Due to the lack of access to DG as well as the distributed and flexible resources in scenario 1, the distribution network could operate only by purchasing large amounts of electricity from the grid. Moreover, the low amplitude of voltage of each node in this scenario led to a significant loss of active power that yielded high costs due to power purchase, carbon emissions, and network loss for the distribution grid. As it could access DG in scenario 2, the distribution grid used clean energy generated by the PV cell and the WT. This reduced the costs due to power purchase and carbon emissions, but not the cost of network loss owing to the high amplitude of current in each branch. Access to DG further reduced the costs of power purchase and carbon emissions of the distributed network in Scenario 3. Moreover, its access to the distributed and flexible resources led to a significant increase in the system voltage owing to the reactive power provided by them, where this significantly reduced the cost of network loss in the distribution grid. However, the operating cost of each device was high owing to the large-scale commissioning of distributed and flexible resources.

By taking scenario 3 as an example, the output of DG in the ADN, and the 24-h operation of each distributed and flexible resource are shown in Figure 10.

FIGURE 10

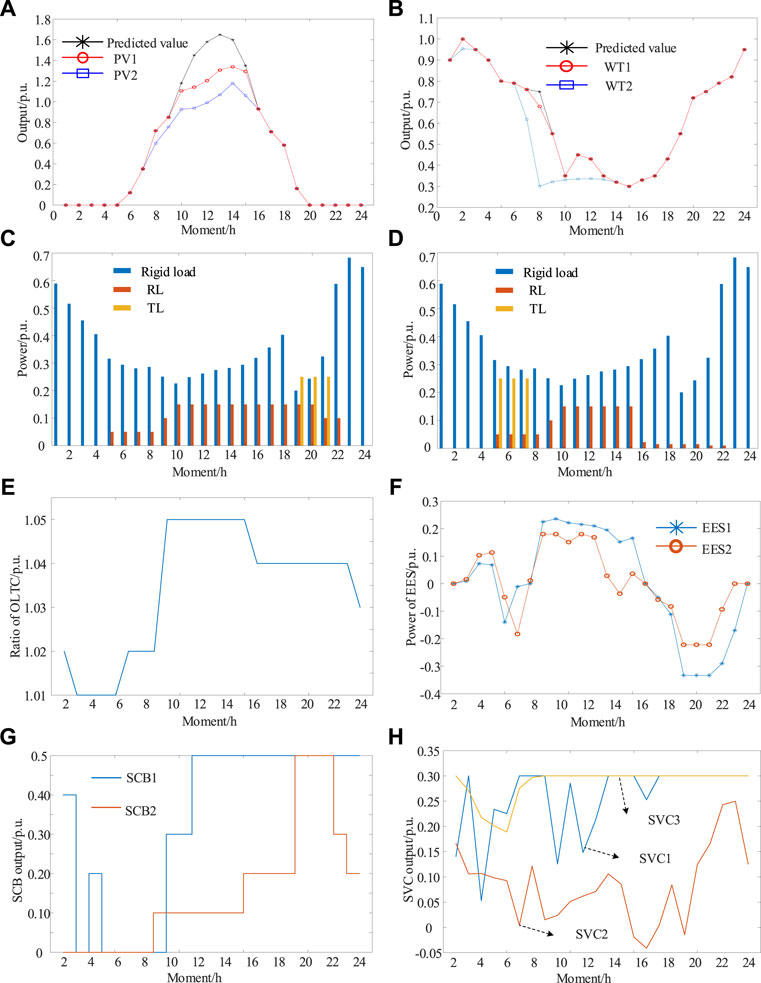
FIGURE 10. The 24-h operation of DG, and the distributed and flexible resources. (A) PV cell (B) WT (C) Before EV dispatch (D) After EV dispatch. (E) OLTC (F) EES. (G) SCB (H) SVC

The outputs of the PV cell and the WT are shown in Figures 10A, B, respectively, and compared to the predicted values, the actual energy utilization of the PV cell and the WT reached 83.8% and 96.1%, respectively. The participation of the EVs in dispatch in the distribution grid is shown in Figures 10C, D, where “rigid load” refers to the load of the EV that did not participate in dispatch. During the dispatch of EVs, the TL shifted from 19:00–21:00 to 05:00–07:00 h, and the RL underwent a significant reduction in the period 16:00–22:00 h. This is because the price of electricity peaked in the period of 19:00–21:00 h. To avoid consuming electricity in this period and reduce the operating cost of the ADN, the TL was shifted to the valley of the price of electricity. The price of electricity was normal in 16:00–22:00 h, the power of the WT was lower, and the power supplied by the PV cell gradually decreased to zero at night. At this time, RL performed peak shaving by reducing the power.

The ratios of operation of the OLTC and EES are shown in Figures 10E, F, respectively. The initial gear of the OLTC was at 1.02 p. u., and was adjusted at 02:00, 06:00, 09:00, 16:00, and 24:00 h. The range of voltage adjustment was 1.01–1.05 p. u., and is in line with the constraints of normal operation. The EES had a positive value while charging and a negative value while discharging. It was charged at noon, when the capacity of the PV cell to supply power was adequate, and was discharged at night when the load was at its peak to give full play to the scheme of “peak shaving and valley filling, and Store electricity when electricity prices are low and discharge them when electricity prices are high.” The ratios of operation of the SCB and SVC are shown in Figures 10G, H, respectively. Both the SCB and the SVC performed regulation based on reactive power compensation under a specified capacity and constraints on the gears. This mitigated the deviations in voltage, and reduced the network loss and the cost of operation.

7 Discussion and limitations

With the continuous breakthroughs in power line communication technology in recent years, it has gradually begun to be used in the field of smart grid, Internet of Things, power distribution network and so on. The communication architecture of the ADN proposed in this paper is shown in Figure 11.

FIGURE 11

FIGURE 11. ADN communication architecture.

Existing power communication protocols include IEC101/104, Modbus, DL/T645 and other protocols. IEC101/104 protocols are generally used in the higher configuration of power distribution terminals and automation masters, while Modbus and DLT645 protocols are generally used in the lower power distribution terminal equipment (Górski, 2022). The message queuing telemetry transport (MQTT) protocol is an instant communication protocol released by IBM in 1999, with the greatest advantage of providing reliable transmission to remote devices with limited computing power and low bandwidth (Zhao et al., 2023).

As can be seen in Figure 11, controller controls the reactive power output of SVC and SCB. The power output information of PV and wind power can be obtained through inverter. Converter controls the charging and discharging power of EES, and the charging power information of EV can be derived through charging post. The convergence terminal collects power information of various flexible resources in ADN through Modbus, DL/T645, RS485 and other communication protocols, and delivers the collected information to the ADN cloud platform through MQTT communication protocols, and generates the optimal operation plan and sends it to various types of equipments through the computation and analysis of the ADN cloud platform, so as to complete the low-carbon and economic operation of ADN.

In this paper, we propose a mixed-integer second-order cone programming model for active distribution network. By coordinating and complementing multiple distributed and flexible resources within the ADN, it serves to reduce the operating costs and carbon emissions of the ADN and improve the efficiency of energy utilization. The method proposed in this paper has the following advantages.

1) Wide range of application: Mixed-integer second-order cone programming can effectively deal with complex problems containing multiple types of constraints such as linear constraints, integer constraints, and second-order cone constraints, and thus has a wider scope of application.

2) Global optimization capabilities: In some cases, mixed-integer second-order cone programming can provide globally optimal solutions, especially for nonconvex and nonsmooth problems, where other intelligent optimization algorithms (e.g., genetic algorithms, simulated annealing algorithms, etc.) may fall into local optimality.

3) Solution efficiency: For specific types of problems, mixed-integer second-order cone programming algorithms can find the optimal solution efficiently by optimizing the solver, which may converge faster relative to some heuristic algorithms.

4) Algorithm stability: Compared with some intelligent optimization algorithms, the convergence and stability of mixed-integer second-order cone programming are theoretically better guaranteed.

However, although mixed-integer second-order cone programming has some advantages, it also has some limitations and drawbacks, especially in specific cases.

1) Complexity: Mixed-integer second-order cone programming is a complex mathematical problem whose solution process may be relatively complex and time-consuming, especially for large-scale problems, where the performance of the solver is degraded, resulting in a potentially significant increase in solution time.

2) Feasible solutions are difficult to find: For some problems, especially in the case of complex constraints or non-convex problems, finding feasible solutions may be challenging, or it may not even be possible to find feasible solutions, leading to ineffective optimization results.

3) Effectiveness depends on problem characteristics: the performance of mixed-integer second-order cone programming depends heavily on the characteristics and constraints of the problem, and may not work as well for some problems. In particular, when the problem involves nonlinear constraints, appropriate transformations and approximations are required, which may lead to complication of the problem.

4) Unique solutions are not guaranteed: not all cases of mixed-integer second-order cone programming provide a unique optimal solution; there may be multiple optimal solutions or unbounded solutions.

In summary, although mixed-integer second-order cone programming shows advantages in some aspects, it is not suitable for all types of optimization problems. In practical applications, it is necessary to consider the characteristics and scale of the problem and choose a suitable optimization algorithm to obtain better optimization results.

8 Conclusion

In this study, the authors proposed a mixed-integer second-order cone programming method to reasonably control large-scale distributed and flexible resources in active distribution networks by considering collaboration between flexible and distributed resources. We tested the proposed method on a modified IEEE 33-node distribution system. The following conclusions can be drawn.

1)Synergistic optimization, by using DG as well as the distributed and flexible resources, reduced the cost of daily operation of the ADN by 47.9% and its carbon emissions by 75.2% year on year.

2)The proposed model reduced the peak-to-valley difference in the magnitude of voltage at nodes of the ADN as well as the loss of active power of the system while ensuring its optimal economic performance.

3)The correlation between the powers of the PV cell and the WT influenced the results of analysis, and further research is needed on considering the correlation of outputs of the PV cell and the WT when analyzing the optimal operation of the ADN.

4)With the extensive access of massive and decentralized 5G base stations to the distribution grid, the self-provided energy storage of 5G base stations provides the grid with flexibility resources with considerable capacity and huge potential. How to synergistically control these adjustable idle resources is of great significance in promoting the consumption of distributed power sources and smoothing the peak-to-valley difference of the grid.

5)The soft open point (SOP) can exchange active power and compensate reactive power between connected distribution networks, realizing intelligent regulation of distribution network currents. How to control the SOPs to realize the complementary energy between multiple interconnected active distribution grids is an issue that needs to be focused on in the subsequent research.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be dfirected to the corresponding author.

Author contributions

DW: Writing–original draft, Conceptualization, Data curation. MZ: Writing–review and editing, Investigation. ZY: Writing–review and editing, Methodology, Software. FJ: Writing–review and editing, Investigation. QG: Writing–review and editing, Data curation, Investigation. QZ: Writing–review and editing, Investigation.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work is supported by State Grid Hunan Electric Power Company Science and Technology Project “Technology and Demonstration of Distributed Flexible Resource Cluster Autonomy and Provincial-Local-County Collaborative Dispatch in Active Distribution Networks” (5216A522000M).

Conflict of interest

Authors DW, MZ, and QZ were employed by State Grid Hunan Electric Power Company Limited Research Institute

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Dong, W., Wang, Q., and Yang, L. (2015). A coordinated dispatching model for a distribution utility and virtual power plants with wind/photovoltaic/hydro generators. Automation Electr. Power Syst. 39 (9), 75–81+207. doi:10.7500/AEPS20140719007

CrossRef Full Text | Google Scholar

Górski, T. (2022). UML profile for messaging patterns in service-oriented architecture, microservices, and Internet of Things. Appl. Sci. 12 (24), 12790. doi:10.3390/app122412790

CrossRef Full Text | Google Scholar

Growe-Kuska, N., Heitsch, H., and Romisch, W. (2003). Scenario reduction and scenario tree construction for power management problems. IEEE Bologna Power Tech. Conf. Proc. 3 (7). doi:10.1109/PTC.2003.1304379

CrossRef Full Text | Google Scholar

Guo, Y., Wu, Q., Gao, H., Chen, X., Østergaard, J., and Xin, H. (2019). MPC-based coordinated voltage regulation for distribution networks with distributed generation and energy storage system. IEEE Trans. Sustain. Energy 10 (4), 1731–1739. doi:10.1109/TSTE.2018.2869932

CrossRef Full Text | Google Scholar

Jiang, F., Peng, X., Tu, C., Guo, Q., Deng, J., and Dai, F. (2022). An improved hybrid parallel compensator for enhancing PV power transfer capability. IEEE Trans. Industrial Electron. 69 (11), 11132–11143. doi:10.1109/TIE.2021.3121694

CrossRef Full Text | Google Scholar

Kang, W., and Huo, Y. (2022). Analysis on the power flow characteristics considering uncertainty and correlation of wind power and photovoltaic station. Mod. Electr. Power 39 (02), 246–252. doi:10.19725/j.cnki.1007-2322.2021.0100

CrossRef Full Text | Google Scholar

Kayacık, S. E., and Kocuk, B. (2021). An MISOCP-based solution approach to the reactive optimal power flow problem. IEEE Trans. Power Syst. 36 (1), 529–532. doi:10.1109/TPWRS.2020.3036235

CrossRef Full Text | Google Scholar

Li, J., Shi, Y., Zhang, L., Yang, X., Wang, L., and Chen, X. (2021). Optimization strategy for the energy storage capacity of a charging station with photovoltaic and energy storage considering orderly charging of electric vehicles. Power Syst. Prot. Control 49 (07), 94–102. doi:10.19783/j.cnki.pspc.201296

CrossRef Full Text | Google Scholar

Li, P., Wu, Z., ZhangXu, C,Y., Dong, Z., and Hu, M. (2023). Multi-timescale affinely adjustable robust reactive power dispatch of distribution networks integrated with high penetration of PV. J. Mod. Power Syst. Clean Energy 11 (1), 324–334. doi:10.35833/MPCE.2020.000624

CrossRef Full Text | Google Scholar

Li, X., Han, X., and Yang, M. (2022). Day-ahead optimal dispatch strategy for active distribution network based on improved deep reinforcement learning. IEEE Access 10, 9357–9370. doi:10.1109/ACCESS.2022.3141824

CrossRef Full Text | Google Scholar

Li, Y., Fan, X., Cai, Z., and Yu, B. (2018). Optimal active power dispatching of microgrid and distribution network based on model predictive control. Tsinghua Sci. Technol. 23 (3), 266–276. doi:10.26599/TST.2018.9010083

CrossRef Full Text | Google Scholar

Luo, Y., Nie, Q., Yang, D., and Zhou, B. (2021). Robust optimal operation of active distribution network based on minimum confidence interval of distributed energy beta distribution. Mod. Power Syst. Clean Energy 9 (2), 423–430. doi:10.35833/MPCE.2020.000198

CrossRef Full Text | Google Scholar

Mohd Azmi, K. H., Mohamed Radzi, N. A., Azhar, N. A., Samidi, F. S., Thaqifah Zulkifli, I., and Zainal, A. M. (2022). Active electric distribution network: applications, challenges, and opportunities. IEEE Access 10, 134655–134689. doi:10.1109/ACCESS.2022.3229328

CrossRef Full Text | Google Scholar

Pamshetti, V. B., Singh, S., Thakur, A. K., Singh, S. P., Babu, T. S., Patnaik, N., et al. (2023). Cooperative operational planning model for distributed energy resources with soft open point in active distribution network. IEEE Trans. Industry Appl. 59 (2), 2140–2151. doi:10.1109/TIA.2022.3223339

CrossRef Full Text | Google Scholar

Pu, T., Liu, W., Chen, N., Wang, X., and Dong, L. (2017). Distributed optimal dispatching of active distribution network based on consensus algorithm. Proc. CSEE 37 (06), 1579–1590. doi:10.13334/j.0258-8013.pcsee.160937

CrossRef Full Text | Google Scholar

Ruan, H., Gao, H., Liu, Y., Wang, L., and Liu, J. (2020). Distributed voltage control in active distribution network considering renewable energy: a novel network partitioning method. IEEE Trans. Power Syst. 35 (6), 4220–4231. doi:10.1109/TPWRS.2020.3000984

CrossRef Full Text | Google Scholar

Smadi, I. A., and Shehadeh, L. I. (2023). An improved reactive power sharing in an isolated microgrid with a local load detection. Chin. J. Electr. Eng. 9 (2), 14–26. doi:10.23919/CJEE.2023.000021

CrossRef Full Text | Google Scholar

Sun, F., Ma, J., Yu, M., and Wei, W. (2021). Optimized two-time scale robust dispatching method for the multi-terminal soft open point in unbalanced active distribution networks. IEEE Trans. Sustain. Energy 12 (1), 587–598. doi:10.1109/TSTE.2020.3013386

CrossRef Full Text | Google Scholar

Verma, R., and Padhy, N. P. (2022). Optimal power flow based DR in active distribution network with reactive power control. IEEE Syst. J. 16 (3), 3522–3530. doi:10.1109/JSYST.2021.3106397

CrossRef Full Text | Google Scholar

Wang, Y., Qiu, D., Strbac, G., and Gao, Z. (2023). Coordinated electric vehicle active and reactive power control for active distribution networks. IEEE Trans. Industrial Inf. 19 (2), 1611–1622. doi:10.1109/TII.2022.3169975

CrossRef Full Text | Google Scholar

Xiao, J., Li, Y., Tan, Y., Chen, C., Cao, Y., and Lee, K. Y. (2018). “A robust mixed-integer second-order cone programming for service restoration of distribution network,” in 2018 IEEE Power and Energy Society General Meeting, Portland, OR, USA, 05-10 August 2018, 1–5. doi:10.1109/PESGM.2018.8585816

CrossRef Full Text | Google Scholar

Yang, Y., and Wu, W. (2019). A distributionally robust optimization model for real-time power dispatch in distribution networks. IEEE Trans. Smart Grid 10 (4), 3743–3752. doi:10.1109/TSG.2018.2834564

CrossRef Full Text | Google Scholar

Zhang, B., Sun, Y., Zhong, Y., and Shen, M. (2018). “Optimal energy flow of electricity-gas integrated energy system using second-order cone program,” in 2018 Chinese Control And Decision Conference, Shenyang, China, 09-11 June 2018, 5085–5089. doi:10.1109/CCDC.2018.8408012

CrossRef Full Text | Google Scholar

Zhang, C., Xu, Y., Wang, Y., Dong, Z., and Zhang, R. (2022). Three-stage hierarchically-coordinated voltage/var control based on PV inverters considering distribution network voltage stability. IEEE Trans. Sustain. Energy 13 (2), 868–881. doi:10.1109/TSTE.2021.3136722

CrossRef Full Text | Google Scholar

Zhang, L., Tang, W., Liang, J., Cong, P., and Cai, Y. (2016). Coordinated day-ahead reactive power dispatch in distribution network based on real power forecast errors. IEEE Trans. Power Syst. 31 (3), 2472–2480. doi:10.1109/TPWRS.2015.2466435

CrossRef Full Text | Google Scholar

Zhang, Z., Wang, Z., Cao, R., and Zhang, H. (2021). Research on two-level energy optimized dispatching strategy of microgrid cluster based on IPSO algorithm. IEEE Access 9, 120492–120501. doi:10.1109/ACCESS.2021.3108830

CrossRef Full Text | Google Scholar

Zhao, N., Zhang, H., Yang, X., Yan, J., and You, F. (2023). Emerging information and communication technologies for smart energy systems and renewable transition. Adv. Appl. Energy 9, 100125. doi:10.1016/j.adapen.2023.100125

CrossRef Full Text | Google Scholar