Research on dual lateral log simulation of shale bedding fractures under different influencing conditions

Micro scale fractures play a crucial role in facilitating the migration of oil and gas in low permeability shale reservoirs. However, the identification of such fractures is a complex task. The efficacy of the dual lateral log physical field changes as a means of identifying shale micro fractures remains uncertain. To address this issue, a three-layer shale bedding fracture model was developed using the finite element method and core and conventional logging data from eight wells, which was based on different shale reservoirs within the Yanchang Formation in the Ordos Basin. The present study examines the dual lateral log response characteristics resulting from distinct characteristics of horizontal bedding fractures, with a focus on the response mechanism. The simulation of logging response characteristics of shale and siltstone combination were utilized by core statistical data for verification purposes. The results indicate that under the lithology combination of shale and siltstone, the magnitude of the difference between the resistivity of the filled fracture and the formation resistivity, the greater the formation resistivity of the shale itself, the wider the fracture width, and the greater the difference between the apparent resistivity and the real formation resistivity. Furthermore, the suitable conditions for the detection of shale bedding fracture characteristics by dual lateral log are clarified. In the presence of effective filling, the dual lateral log has the capability to identify shale fractures at the micron scale. The findings of our study establish a theoretical framework for the identification and assessment of shale fractures, and furnish technical assistance for the optimal selection of “sweet spots” within shale reservoirs and the precise evaluation of reservoirs. This study lays a theoretical foundation for the identification and evaluation of shale fractures, and provides technical support for the optimal “sweet spot” selection of shale reservoirs and the accurate evaluation of reservoirs.

1 Introduction

Recent developments in shale oil and gas exploration in China have shown significant progress (Zou et al., 2023). Shale reservoirs are characterized by their high content of brittle minerals and the presence of multiple types of pores and fractures (Wang et al., 2016; Sun et al., 2022). Fractures serve as both reservoir spaces and seepage channels, enhancing the physical properties of the reservoir and facilitating the extraction of oil and gas. The presence of such fractures plays a crucial role in determining the potential for shale oil enrichment (Zeng et al., 2007; George et al., 1968; Fu H. J. et al., 2022; Fu et al., 2007). The identification and assessment of fractures in shale formations present several technical challenges owing to the intricate nature of their origin and classification of shale fracture systems (Yin et al., 2021; Shi et al., 2022). Consequently, it is imperative to devise a precise, practical, and flexible methodology for the detection and evaluation of fractured shale reservoirs (Wang et al., 2021; Ren et al., 2023; Gan et al., 2023).

The logging method serves as a valuable instrument for the quantitative depiction of fracture characteristics. Various logging techniques exhibit limitations in identifying fractures, with acoustic logging being susceptible to “cycle-skipping” phenomena and neutron porosity indicating high values for gas bearing fractures (Fan et al., 2008). While these methods are cost-effective, their indirect nature may result in inconsistent responses to fractures across different regions. Imaging logging provides accurate representation of fracture characteristics, but its detection range is limited and lacks data (Hadi et al., 2016; Dong et al., 2020). High resolution array induction logging struggles to interpret complex intrusion profiles (Tang, 2015). The cross dipole with high accuracy is only applicable to vertical fractures or high angle fractures near the wellbore (Wen et al., 2018). While new logging techniques have emerged that can extract detailed formation information, their widespread use is restricted by cost and application scope limitations (Wang et al., 2005; Tang et al., 2012; Xie et al., 2020; Lu, 2018; Liu, 2022; Liu et al., 2022). Nevertheless, the dual lateral log’s unique instrument structure, featuring a strong focusing effect, enables the detection of deeper formations. The fractured intervals’ logging response characteristics are distinctly apparent, as evidenced by the amplitude disparity between deep and shallow lateral resistivity curves. The positive difference is observed in the high dip angle fracture and vertical fracture, while the low dip angle fracture and horizontal fracture generally exhibit negative difference (Chen et al., 2005). Furthermore, the invasion difference ratio parameters, in conjunction with the response characteristics of dual lateral log, can aid in fracture identification (Zhou and Yang, 2003). The dual lateral log technology is an effective method for identifying fractures, characterized by good longitudinal continuity, moderate detection scale, low cost, and accurate description of fracture characteristics. Drawing upon the primary controlling factors of fractures, including lithology, structural, and stress control, geological data such as formation lithology and thickness are interpreted through logging curves to anticipate areas conducive to fracture development. The finite element numerical simulation method, a semi-quantitative approach to fracture prediction, amalgamates the benefits of other numerical simulation algorithms and can be implemented in complex 3D strata. (Zhang and Wang, 1996; Tan et al., 2007; Yang et al., 2009; Gao et al., 2010; Um et al., 2015; Tang et al., 2016; Huang et al., 2019; Xue et al., 2021; Yin et al., 2022). Scholars have conducted pertinent research on reservoirs utilizing the logging finite element method. Sibbit and Faivre (1985) developed a two-dimensional fracture model to simulate the dual lateral log response of fractures and assess fracture characteristics in vertical wells. Pezard and Anderson (1990) subsequently derived the relationship between fracture dip angle and dual lateral log response using a plate fracture model. Shi et al. (2004) computed the correlation between the dual lateral response of fractured formations and fracture porosity, mud resistivity, fracture dip angle, and bedrock resistivity. Deng et al. (2012); Zhao et al. (2015) simulated the dual lateral log response of fracture-cave formations. Subsequently, Tan et al. (2014); Su et al. (2015) gradually applied dual lateral log response simulation technology to shale fracture evaluation. Yong et al. (2022) used finite element to characterize nano scale shale fractures.

Currently, the identification and evaluation of fractures rely primarily on the analysis of curve changes and actual logging data calculations. The suitability of dual lateral logs cannot be assessed through the response mechanism based on physical field alterations. Additionally, there is a dearth of logging response simulations for shale fracture formation, resulting in a lack of theoretical foundation for the identification and evaluation of shale fractures through logging. Hence, utilizing logging data from eight wells and considering the prevailing formation conditions, a sophisticated wellbore-formation model of horizontal fractures is formulated. The logging response mechanism is scrutinized in light of the impact of fractures on electric field distribution under varying fracture conditions. To obtain more accurate fracture information, the fracture types and logging correction conditions that can be identified by dual lateral log are elucidated.

2 Methods

2.1 Establishment of the wellbore model of the fracture instrument

The dual lateral log tool comprises nine electrodes, consisting of a main electrode (A₀), two sets of monitoring electrodes (M₁, M₂ and M₁', M₂'), and two sets of shielding electrodes (A₁, A₂ and A₁', A₂'). The instrument has a diameter of 0.089 m, with the main electrode situated at the center. The remaining electrode pairs of the same type are symmetrically distributed and connected via wires to form a short circuit with identical potential. During operation, the main electrode A₀ emits a constant current I₀ for deep lateral logging, while the shielding electrode emits a current with the same polarity as the primary electrode. This results in the main current flowing vertically through the shielding electrode to the deeper formation, thereby obtaining an apparent resistivity that approximates the true resistivity of the formation. For shallow lateral log, the external shielding electrode is replaced by a loop electrode. The effect of the shielding current is reduced, the detection scale is reduced, so that the resistivity of the invasion zone can be measured. In order to obtain more accurate simulation experiment results, a fracture instrument wellbore model for horizontal fractures is established using the finite element interpolation method, based on the working principle of the dual lateral log tool and actual formation conditions. This model is depicted in Figure 1, where Rs represents wall rock resistivity, Rf represents fracture resistivity, Rt represents undisturbed formation resistivity, Rm represents mud resistivity and CAL represents the well diameter.

FIGURE 1

FIGURE 1. Horizontal fracture model of the dual lateral log.

2.2 Dual lateral logging finite element method

The essence of the finite element method of dual lateral logging is the calculation of the steady current electric field in the formation. The potential value in the monitoring electrode can be decomposed into the superposition result of the partial electric field generated by multiple emission electrodes. First, the problem of determining solution is transformed into the problem of determining solution of objective universal function through the constraint of boundary conditions. Then, the target area is discretizated. Finally, the target area is interpolated, and the interpolation function is substituted into the function to solve the equations. So that the apparent resistivity value of dual lateral logging can be obtained from the perspective physical field changes.

The distribution of the electrostatic field electromotive force in the 3D cylindrical coordinate system of double lateral measurement should satisfy:

$\frac{\partial }{\partial x}\left(\sigma \frac{\partial \varphi }{\partial x}\right)+\frac{\partial }{\partial y}\left(\sigma \frac{\partial \varphi }{\partial y}\right)+\frac{\partial }{\partial z}\left(\sigma \frac{\partial \varphi }{\partial z}\right)=0(1)$

In the context of dual lateral log numerical simulation, various boundary conditions are employed on the boundary and instrument surface in the x, y, z direction.

The first type of boundary condition is used for constant-pressure electrodes, where φ is a known constant.

The second boundary condition applies to the surface of the constant current electrode:

${\displaystyle \underset{\mathrm{\Gamma }}{\int }}{\sigma }_m\frac{\partial \varphi }{\partial n}\cdot \overrightarrow{n}d\tau =I_E(2)$

In the formula: Γ—the whole electrode surface; $\stackrel{\rightharpoonup }{n}$- Electrode direction; ${\mathrm{I}}_{\mathrm{E}}$ - Electrode current; ${\mathrm{\sigma }}_{\mathrm{m}}$- Drilling fluid resistivity.

On the insulation boundary surface:

$\frac{\partial \varphi }{\partial n}=0(3)$

The objective functional is constructed according to the above problem:

$F=\frac{1}{2}{\iiint }_{\mathrm{\Omega }}\sigma \left[{\left(\frac{\partial \varphi }{\partial x}\right)}^2+{\left(\frac{\partial \varphi }{\partial y}\right)}^2+{\left(\frac{\partial \varphi }{\partial z}\right)}^2\right]dxdydz-{\displaystyle \sum _E}{I}_E{\mathrm{\Phi }}_E(4)$

In the formula: Φ_E—Points on the electrode.

Thus, the problem of determining the definite solution is converted into an extreme value problem of the universal function. According to the boundary conditions obtained in the research process of dual lateral log, the universal function can be solved and the value to be solved can be obtained.

After discretization and interpolation of the objective function, we get:

${\mathrm{\Phi }}^e=\frac{1}{2}{\mathrm{\Phi }}^{eT}{G}^e{\mathrm{\Phi }}^e(5)$

In the formula: Φ—vector to be solved; Ge—Stiffness matrix of elements.

Ge is a symmetric real matrix of or 4 × 4 or 10 × 10. According to Ge, the total conductance matrix is obtained:

$\mathrm{\Phi }={\displaystyle \sum _{i=1}^M}{\mathrm{\Phi }}_i=\frac{1}{2}{{\mathrm{\Phi }}_i}^{T}G{\mathrm{\Phi }}_i={\left\{\begin{array}{c}{\varphi }_1\\ {\varphi }_2\\ ⋮\\ {\varphi }_N\end{array}\right\}}^T\left(\begin{array}{ccc}{G}_{11}& \dots & G_{1N}\\ ⋮& \ddots & ⋮\\ G_{N1}& \cdots & G_{NN}\end{array}\right)\left\{\begin{array}{c}{\varphi }_1\\ {\varphi }_2\\ ⋮\\ {\varphi }_N\end{array}\right\}(6)$

In the formula: M is the number of elements, N is the number of nodes, Φ is the vector at ϕ each node position to be solved, and G is the total Ge stiffness matrix obtained by N × N installation.

G is a large sparse symmetric matrix, and the matrix is a real number. Because of the extreme value of the functional, we must make each node satisfy the following conditions:

$\frac{\partial F}{\partial {\varphi }_i}=0(7)$

That is:

$G\mathrm{\Phi }=I_E(8)$

The value of each node can be obtained by solving Formula (5). Use formula (9) to calculate the apparent resistivity.

$R_a=k\frac{U_{M1}}{I_0}(9)$

It is important to note that multiple nodes will exist on each electrode after meshing, and each electrode can be treated as an equipotential body. Consequently, all nodes on the electrode possess the same electromotive force, and the electromotive force of all nodes on the boundary of the target area is also identical. The ratio of the electromotive force between the shielding electrodes A₁ and A₂ remains a fixed value, with a positive ratio observed in the deep lateral direction and a negative ratio in the shallow lateral direction. In the calculation of unknowns, the ratio of the electromotive force of the two shielding electrodes is positive, then the apparent resistivity is the deep lateral resistivity. If it is negative, then the apparent resistivity is the shallow lateral resistivity.

3 Analysis of fracture characteristics of typical shale oil reservoirs

Core samples and thin sections of 8 wells at Ordos basin were observed and samples were collected to study fracture typical growth and logging characteristics in Chang 9 shale. We statistics the Chang 9 shale oil reservoir includes black oil shale, grey‒black or black mud, silt-fine sandstone, sandstone and sand-mud interbeds. Based on the composition of sedimentary minerals and the characteristics of rock grain size, three types of lithological combinations, including shale and mudstone, shale and siltstone, and shale and sandstone, were divided. Five types of Structural fractures, including interlayer fractures, bedding fractures, and occasional abnormal fracturing fractures and reticular fractures were identified in work area, among which structural fractures (Figure 2A) and bedding fractures (Figure 2B) are dominant in mudstone (shale) fractures of 8 wells. Structural fractures are often developed in interlayer shales, and bedding fractures are often developed in bedding shale with high gas content (Gao et al., 2022). According to the mechanical causes, the structural fractures are divided into shear fracture and extension fracture (Gong et al., 2021). Shear fractures are the common ones in the Chang-9 Member mudstone (shale) fractures. Less extension fractures. The main length range of fracture observed by core is 0–10 cm, as shown in Figure 3, the main width range of fractures is mainly 0.1–1.5 mm, as shown in Figure 4. Calcite (Figure 2C), asphalt (Figure 2D) and carbon chip (Du et al., 2022) are seen in several of the fractures, unfilled fractures contain gas. As shown in Figure 5, vertical fractures and bedding fractures are the main ones. Horizontal bedding fracture is the most developed. Low angle fractures are not developed. Therefore, we mainly choose horizontal fractures for research. Through the analysis of conventional logging, the dual lateral log response characteristics of shale section in Ordos basin, the deep and shallow lateral resistivity almost coincide (Guo et al., 2023). When the fracture exists, the deep and shallow lateral resistivity will have amplitude difference (Wu, 2021).

FIGURE 2

FIGURE 2. Typical fracture types and filling characteristics in shale oil reservoir of Chang-9 Member. (A) Structural fracture. Well YY7 1,304.05 m. (B) Bedding fractures. Well YY7 1,141.14–1,141.3 m. (C) Structural fracture with filled with calcite. Well YY7 1,143.7–1,143.82 m. (D) Micro fractures are filled with organic matter. Well HH22.

FIGURE 3

FIGURE 3. Statistical graph of fracture lengths in the Chang 9 section of 8 coring wells.

FIGURE 4

FIGURE 4. Statistical graph of fracture widths in the Chang 9 section of 8 imaging wells.

FIGURE 5

FIGURE 5. Statistical graph of fracture dips in the Chang 9 section of 8 coring wells.

4 Results

The measurement results of the instrument can be influenced by the borehole, formation, and fracture when the borehole passes through the formation. To investigate the impact of various horizontal fracture characteristics on the response results of dual lateral log, it is assumed that the fracture is free from mud invasion, the well diameter remains constant, and each formation is uniform. A three-layer formation model is established, with a mud resistivity of 1.0 Ω·m, a sampling spacing of 0.1 m, a borehole radius of 0.1016 m, and a surrounding rock formation resistivity of 20 Ω·m. Based on the above determination of formation conditions and resistivity parameters, combined with the vertical fracture and horizontal fracture instrument wellbore models, the corresponding model parameters are established. By altering the fracture parameters, one can analyze the impact of various fracture fillings, fracture width, shale resistivity, and the conditions under which dual lateral log is applicable. The response characteristics of dual lateral log with different lithology combinations were analyzed by fixed formation conditions, mud resistivity, borehole radius and sampling spacing. In the following, the resulting calculation outcomes represent the apparent resistivity under distinct fracture characteristics, which are influenced by multiple factors, including formation. The target layer resistivity represents the true formation resistivity, unaffected by extraneous factors.

4.1 Influence of fracture filling

In instances where the fracture fillings differ, the response mechanism of dual lateral log remains unclear. The information of shale fracture fillings cannot be effectively accurately to evaluate the effectiveness of fractures. Hence, it is imperative to investigate the influence mechanism of fracture fillings on dual lateral log response, drawing upon statistical findings of actual shale reservoir fractures in the study region. Based on the analysis of fracture characteristics aforementioned, the fractures are commonly categorized as asphalt-filling fractures, calcite-filling fractures, unfilled gas-containing fractures, and carbon chip-filling fractures. The deep lateral resistivity of asphalt filled fracture is 156.988 Ω·m, and the shallow lateral resistivity is 163.086 Ω·m. The deep lateral resistivity of calcite-filled fracture is 45.444 Ω·m, and the shallow lateral resistivity is 43.481 Ω·m. The deep lateral resistivity of unfilled gas-bearing fracture is 51.73 Ω·m, and the shallow lateral resistivity is 45.33 Ω·m. The lateral resistivity of the carbon chip filling fracture resistivity is 62.645 Ω·m, and the shallow lateral resistivity is 50.004 Ω·m. Without considering the influence of mud intrusion, three-layer formation models of asphalt filling, calcite filling, gas filling and carbon chip filling were established. Under the condition of vertical well, the resistivity of the upper and lower surrounding rocks is 20 Ω·m. The resistivity of the target formation is 30 Ω·m. The fracture scale is 0.5 m, and the resistivities of the fracture with gas filling, asphalt filling, calcite filling and carbon filling are 100 Ω·m, 444 Ω·m, 266 Ω·m and 5 Ω·m, respectively. The findings depicted in Figure 6 illustrate that the dual lateral log response exhibits an abnormal “M-shaped” trend due to the disparity in resistivity between the fracture fillings and the surrounding rock. The anomalous segment corresponds to the fracture section that is filled with diverse materials, and the depth section of this segment represents the thickness of the fractured reservoir. Notably, the resistivity of the asphalt-filled fracture is the highest, while the carbon chip-filled fracture exhibits the lowest resistivity. When the fracture is filled, the greater the difference between the resistivity and the formation resistivity, the greater the difference between the apparent resistivity and the real resistivity of the formation.

FIGURE 6

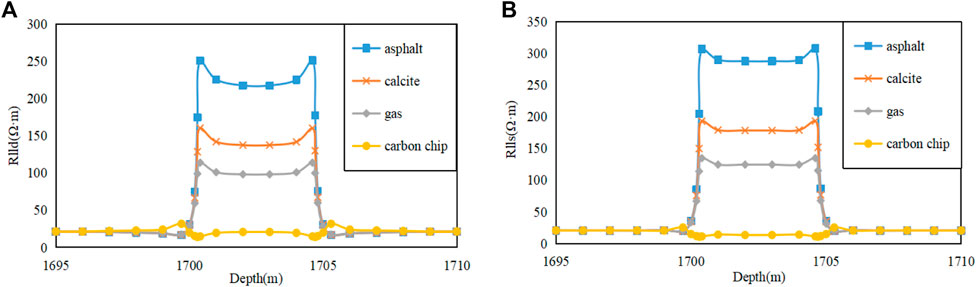
FIGURE 6. (A) Deep lateral response under different crack filling conditions; (B) Shallow lateral response under different crack filling conditions.

4.2 Influence of fracture scale

The impact of varying fracture scales on dual lateral log response remains uncertain, and the identification of micro-scale fractures is challenging. Consequently, it is imperative to investigate the influence of fracture scale on dual lateral log response by analysing statistical data on actual shale reservoir fractures in the study area. The scale of fractures within the work area undergoes a transition from centimeter to millimeter dimensions, with the primary range of fracture scales falling between 0.1 and 1.5 mm. When the fracture width is 0.01 m, the deep lateral resistivity is 35.917 Ω·m, and the shallow lateral resistivity is 40.75 Ω·m. When the fracture width is 0.03 m, the deep lateral resistivity is 34.454 Ω·m, and the shallow lateral resistivity is 37.402 Ω·m. Without considering the influence of mud invasion, a three-layer fracture width model is established: under the condition of a vertical well, the target formation resistivity is 45 Ω·m, and the fracture width is 0.05 m, 0.1 m, 0.2 m, 0.3 m, 0.4 m, and 0.5 m. Figure 7 illustrates that the resistivity of fractures differs from that of the surrounding rock due to variations in width. This discrepancy results in an anomalous dual lateral log response, with the abnormal portion representing the fracture section. The depth section of the abnormal part corresponds to the thickness of the fractured reservoir. The difference between the apparent resistivity and the real resistivity of the formation increases with the widening of fracture width. The shallow side is more affected than the deep side.

FIGURE 7

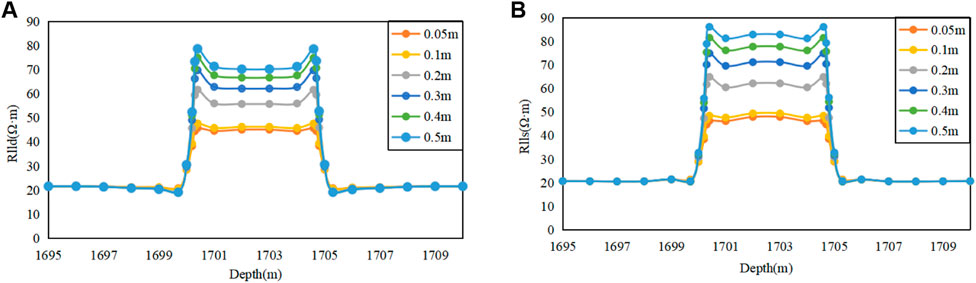
FIGURE 7. (A) Deep lateral response under different crack width conditions; (B) Shallow lateral response under different crack width conditions.

4.3 Influence of different shale resistivities

The dual lateral log response varies significantly when fractures occur in different shale reservoirs. The resistivity of the shale reservoirs within the study area is distributed between 20 Ω·m to 160 Ω·m. The deep lateral resistivity of the 1,383.75 m (mud) shale in Well X 45 is 20.29 Ω·m, and the shallow lateral resistivity is 22.927 Ω·m. The deep lateral resistivity of the (mud) shale in the 1,684.52 m–1693.52 m of the LP 171 well is 24.415 Ω·m, and the shallow lateral resistivity is 33.254 Ω·m; the deep lateral resistivity of Well YY6 shale is 33.611 Ω m, and the shallow lateral resistivity is 34.002 Ω·m. The deep lateral resistivity of the 859.1–859.6 m (mud) shale in the C109 well is 35.817 Ω·m, and the shallow lateral resistivity is 40.75 Ω·m. LP171 well 1,678.82–1,679.82 m deep lateral resistivity is 39.922 Ω·m, shallow lateral resistivity is 55.165 Ω·m; the deep lateral resistivity of 1853.22–1853.62 m shale in LP171 well is 47.025 Ω·m, and the shallow lateral resistivity is 60.381 Ω·m. Without considering the influence of mud invasion, a three-layer model is established: under the condition of a vertical well, the fracture scale is 0.5 m. The target formation resistivities are 25 Ω·m, 30 Ω·m, 35 Ω·m, 40 Ω·m and 50 Ω·m. Figure 8 illustrates that the dual lateral log response is anomalous due to the disparity between the resistivity of the shale and that of the surrounding rock. The fracture section is identified as the abnormal section, and the thickness of the fractured reservoir corresponds to the depth of the anomalous part. The greater the formation resistivity of shale itself, the greater the difference between the apparent resistivity and the true formation resistivity. The shallow side is more susceptible to the effects of the fracture than the deep side.

FIGURE 8

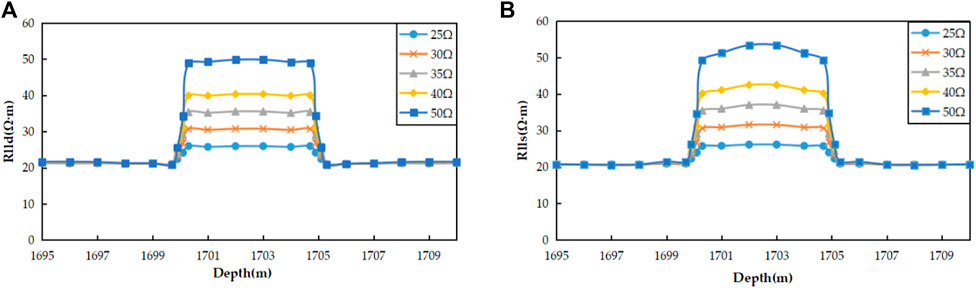
FIGURE 8. (A) Deep lateral response under different shale resistivity conditions; (B) Shallow lateral response under different shale resistivity conditions.

4.4 Response mechanism of dual lateral log in different lithologic assemblages

The dual lateral log response exhibits significant variation when fractures develop under distinct lithology combination conditions, necessitating an exploration of the statistical results of actual shale reservoir fractures in the work area to establish a law. To this end, we categorized the shale reservoirs in the work area into two groups, namely oil shale reservoirs and low-resistivity shale reservoirs, and investigated the dual lateral log response of different lithology combinations (shale-mudstone combination, shale-sandstone and shale-siltstone combination) in each group. The deep lateral resistivity of high resistivity shale is 51.730 Ω·m, and the shallow lateral resistivity is 45.337 Ω·m. The deep lateral resistivity of low resistivity shale is 24.261 Ω·m, and the shallow lateral resistivity is 27.632 Ω·m; mudstone resistivity deep lateral resistivity 44.971 Ω·m, shallow lateral resistivity 56.183 Ω·m; the deep lateral resistivity of sandstone is 35.540 Ω·m, and the shallow lateral resistivity is 37.720 Ω·m. The deep lateral resistivity of siltstone is 30.892 Ω·m, and the shallow lateral resistivity is 38.698 Ω·m. Without considering the influence of mud invasion, a three-layer formation model is established: under the condition of a vertical well, the fracture scale is 0.5 m, the resistivity of the target layer of the oil shale reservoir is 55 Ω·m, and the resistivity of the target layer of the low resistivity shale reservoir is 25 Ω·m. The analysis of different lithological combinations is shown in Figures 9, 10. The dual lateral log response is disrupted in the fracture section due to the influence of surrounding rock alterations. The thickness of the fractured reservoir is indicated by the depth of the abnormal section. While the dual lateral log response is minimally impacted by different lithological combinations in oil shale and low-resistivity shale reservoirs, distinctions still exist. It can be seen that the greater the difference between shale and surrounding rock is, the greater the error between the apparent resistivity and the real formation resistivity. The shallow lateral resistivity remains largely unaffected by varying lithological combinations.

FIGURE 9

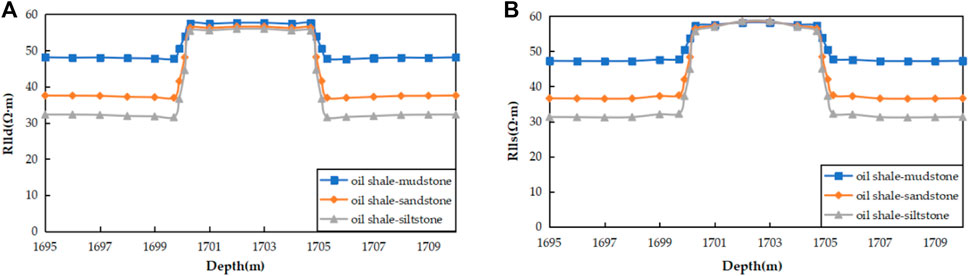
FIGURE 9. (A) Response characteristics of deep lateral logging under different lithologic combinations (oil shale); (B) Response characteristics of shallow lateral logging under different lithologic combinations (oil shale).

FIGURE 10

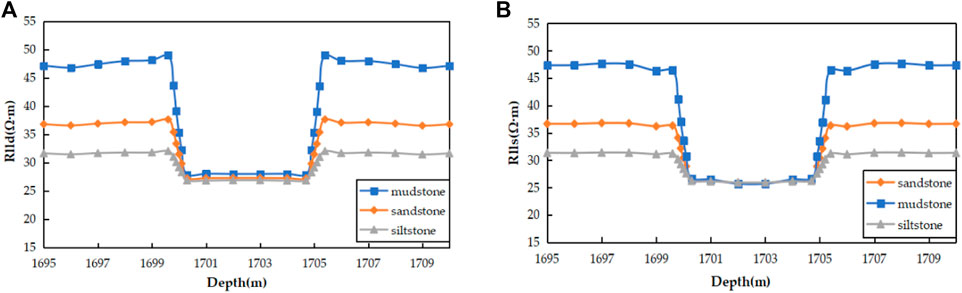
FIGURE 10. (A) Response characteristics of deep lateral logging under different lithologic combinations (low resistivity shale); (B) Response characteristics of shallow lateral logging under different lithologic combinations (low resistivity shale).

5 Discussion

5.1 Suitability analysis

In order to investigate the response properties of shale fractures containing effective filling, a three-layer model is constructed for a vertical well. The mud resistivity is 1 Ω·m. The resistivity of the upper and lower surrounding rocks is 20 Ω·m. The resistivity of the target layer is 35 Ω·m. The fracture width is 0.5 m–1 nm. As illustrated in Figure 11, it is apparent that fractures with a width of less than 0.1∼1 µm exhibit a linear response in both deep and shallow lateral directions, rendering them indistinguishable. Thus, the minimum dimension of a fracture is 0.1–1 µm.

FIGURE 11

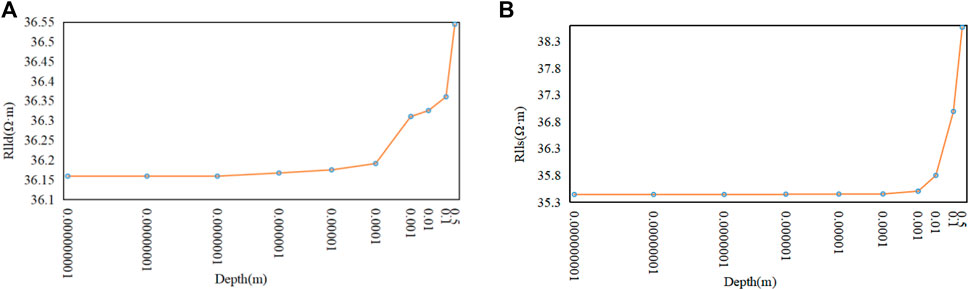
FIGURE 11. (A) Deep lateral response under effective filling conditions; (B) Shallow lateral response under effective filling conditions.

5.2 Application and effect

In order to validate the precision of the simulation, practical application was conducted using the measured data from Well YY7 in the work area, as depicted in Figures 12, 13. An unfilled horizontal bedding fracture section can be seen at a vertical depth of 1,139∼1,149 m. The deep lateral resistivity of the fracture at 1,141.14∼1,141.35 m is 38.531 Ω·m, and the shallow lateral resistivity is 32.729 Ω·m. The resistivity value of the dual lateral logging exhibits an overall decrease, while the core observation reveals the presence of horizontal bedding fractures, which is in agreement with the identification of fractures by lateral log. The response characteristics of the dual lateral log for vertical fractures are similar to those of horizontal fractures. To compare the difference of dual lateral log characteristics between horizontal and vertical fractures, two structural black oil shale fractures can be seen in the 1,299∼1,310 m well section. The deep lateral resistivity of the fracture at 1,308.5 m is 50.3 Ω·m, and the shallow lateral resistivity is 43.806 Ω·m. The dual lateral log shows a positive difference, and the acoustic interval transit time does not change much, which indicate a high angle fracture. The core observation shows that it is a high-angle tensile structural fracture without filling. The deep lateral resistivity of the fracture at 1,304.5 m is 51.638 Ω·m, and the shallow lateral resistivity is 45.142 Ω·m. The dual lateral log shows positive difference, indicating a vertical fracture. The core observation indicates the presence of unfilled vertical fractures. The identification conclusion of the fracture dual lateral log is consistent with the core observation statistics.

FIGURE 12

FIGURE 12. Comprehensive analysis of fractures in well section one139–1,149 m of the YY7 well.

FIGURE 13

FIGURE 13. Comprehensive analysis of fractures in well section one299–1,310 m of the YY7 well.

6 Conclusion

Based on geological and logging data, our study proposes reasonable parameters for shale bedding fracture formation models. Additionally, the study clarifies the conditions for applying dual-lateral logging methods under varying fracture characteristics and analyzes the minimum scale of fractures that can be characterized by this method. These findings provide a foundation for identifying and evaluating shale fractures.

The work area exhibits predominantly horizontal bedding fractures, with fracture lengths primarily ranging from 0–10 cm and widths ranging from 0.1 to 1.5 mm. Some fractures are filled with calcite, asphalt, and carbon chip.

The formation model with filling, fracture scale, different shale resistivity, and different lithological combinations is established and simulated in the forward direction. When the resistivity of the fracture is filled, the greater the difference between the resistivity and the formation resistivity, the greater the fracture scale, the greater the formation resistivity of the shale itself, the greater the difference between the resistivity of the surrounding rock and the target formation, and the greater the difference between the apparent resistivity value and the true resistivity value of the original formation. The horizontal fracture scale of shale identified by the dual lateral logging method under effective filling can reach the micron level or above.

In the future, it is recommended to conduct dual lateral log forward modelling of shale vertical fractures. On the basis of understanding the response law of forward simulation, combined with intelligent algorithm, the actual single well fracture identification is carried out, which lays a theoretical foundation for comprehensive reservoir evaluation.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

Conceptualization, KL and NW; methodology, NW, KL, and JS; formal analysis, NW, JS, and HL; resources, KL; data curation, NW, JS, and HL; writing—original draft preparation, NW; writing—review and editing, NW, JS, KL, XH, ZX and PW; funding acquisition, KL and DW. All authors contributed to the article and approved the submitted version.

Funding

This research was funded by the State Key Laboratory of Shale Oil and Gas Enrichment Mechanism and Effective Development and the National Energy Shale Oil Research and Development Center, grant number 33550000-20-FW2099-0153. The research was also supported by Science and Technology Department of Sichuan Province, grant number 2023NSFSC0765 and 2020JDJQ0058.

Acknowledgments

The authors are grateful to the State Key Laboratory of Shale Oil and Gas Enrichment Mechanism and Effective Development and the National Energy Shale Oil Research and Development Center for their founding (Grant No. 33550000-20-FW2099-0153). The author are also grateful from Science and Technology Department of Sichuan Province (Grant No. 2020JDJQ0058 and 2023NSFSC0765). They appreciate the guidance and help from the teachers of the Chengdu University of Technology and the Skate Key Laboratory of Oil and Gas Reservoir Geology and Exploitation.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chen, G. H., Wang, X. J., Wang, Y. G., Zhu, J. J., and Yang, H. X. (2005). Transversal prediction for reservoir parameters of fractured reservoirs in buried hills. J. China Univ. Petroleum(Edition Nat. Sci. (04), 26–29+34.

Google Scholar

Deng, S. G., Mo, X. X., Lu, C. L., Zhang, Y., and Liu, L. L. (2012). Numerical simulation of the dual laterolog response to fractures and caves in fractured-cavernous formation. Petroleum Explor. Dev. 39 (06), 751–757. doi:10.1016/s1876-3804(12)60100-1

CrossRef Full Text | Google Scholar

Dong, S. Q., Lyu, W. Y., Xia, D. L., Wang, S. J., Du, X. Y., Wang, T., et al. (2020). An approach to 3D geological modeling of multi-scaled fractures in tight sandstone reservoirs. Oil Gas Geol. 41 (03), 627–637. doi:10.11743/ogg20200318

CrossRef Full Text | Google Scholar

Fan, C. H., Qin, Q. R., Guo, X. S., Hu, D. F., Zhou, J. L., and Fan, Z. H. (2008). Fracture characterization and prediction of low permeability reservoir. Beijing: science press.

Google Scholar

Fu, H. J., Yan, D. t., Yao, C. P., Su, X. B., Wang, X. M., Wang, H., et al. (2022a). Pore structure and multi-scale fractal characteristics of adsorbed pores in marine shale: a case study of the lower silurian longmaxi shale in the sichuan basin, China. J. Earth Sci. 33 (05), 1278–1290. doi:10.1007/s12583-021-1602-0

CrossRef Full Text | Google Scholar

Fu, X. F., Gong, L., Su, X. C., Liu, B., Gao, S., Yang, J. G., et al. (2022b). Characteristics and controlling factors of natural fractures in continental tight-oil shale reservoir. Minerals 12 (12), 1616. doi:10.3390/min12121616

CrossRef Full Text | Google Scholar

Gao, J., Ke, S. Z., Wei, B. J., and Tan, M. J. (2010). Theoretical methods for identifying important functional genes in bacterial genomes. Well Logging Technol. 34 (01), 1–8. doi:10.1016/j.resmic.2009.10.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, L. J., Wu, P., Shi, X. F., Li, Y., Pang, J. D., and Yang, T. M. (2022). Logging interpretation and classification method of reservoir parameters of marine continental transitional shale based on source and reservoir type. Nat. Gas. Geosci. 33 (7), 1132–1143. doi:10.11764/j.issn.1672-1926.2022.01.007

CrossRef Full Text | Google Scholar

Gong, L., Gao, S., Liu, B., Yang, J. G., Fu, X. F., Xiao, F., et al. (2021). Quantitative prediction of natural fractures in shale oil reservoirs. Geofluids 2021, 1–15. doi:10.1155/2021/5571855

CrossRef Full Text | Google Scholar

Guo, H., Zhao, H. G., Li, Y., Lei, L. L., Wang, J., Li, J., et al. (2023). Fracture characteristics and hydrocarbon significance in the Chang 7 to Chang 9 members of triassic Yanchang Formation of gufengzhuang area, western Ordos Basin. Petroleum Geol. Exp. 45 (01), 109–121. doi:10.11781/sysydz202301109

CrossRef Full Text | Google Scholar

Hadi, S. J., Morteza, D., Chen, Z. X., and Peyman, P. (2016). Comprehensive evaluation of fracture parameters by dual laterolog data. J. Appl. Geophys. 131, 214–221. doi:10.1016/j.jappgeo.2016.06.005

CrossRef Full Text | Google Scholar

Huang, J. D., Hu, T. Y., Li, J. S., Li, Y. D., and Song, J. Y. (2019). Comparison between discontinuous finite element method and finite difference method. Beijing, China: Annual Meeting of Chinese Geoscience Union.

Google Scholar

Jiang, B., Xin, Z. X., Zhang, X. F., Deng, Y. S., Wang, M. Z., Li, S. D., et al. (2023). Mechanical properties and influence mechanism of confined concrete arches in high-stress tunnels. Int. J. Min. Sci. Technol. 33, 829–841. doi:10.1016/j.ijmst.2023.03.008

CrossRef Full Text | Google Scholar

Li, G., Zhu, C., He, M. C., Zuo, Y. J., Gong, F. Q., Xue, Y. G., et al. (2023). Intelligent method for parameters optimization of cable in soft rock tunnel base on longitudinal wave velocity. Tunn. Undergr. Space Technol. 133, 104905. doi:10.1016/j.tust.2022.104905

CrossRef Full Text | Google Scholar

Li, Y., Chen, J. Q., Elsworth, D., Pan, Z. J., and Ma, X. T. (2022). Nanoscale mechanical property variations concerning mineral composition and contact of marine shale. Geosci. Front. 13, 101405. doi:10.1016/j.gsf.2022.101405

CrossRef Full Text | Google Scholar

Liu, S. Q., Shi, Q., Tang, J. Z., Liu, T. Y., Zhao, W. J., and Chen, P. (2022). Novel evaluation of fracture-type reservoir based on optimization inversion of Sphere-Fracture Model. Chin. J. Geophys. 65 (04), 1451–1460. doi:10.6038/cjg2022P0481

CrossRef Full Text | Google Scholar

Liu, Y. J. (2022). Application of multi-resolution comprehensive evaluation of fracture logging to Asmari formation carbonate reservoir in a oilfield, southeastern Iraq. Mineralogy Petrology 42 (02), 101–111. doi:10.19719/j.cnki.1001-6872.2022.02.10

CrossRef Full Text | Google Scholar

Murray, George H. (1968). Quantitative fracture study—sanish pool, mckenzie county, north Dakota. AAPG Bull. 52 (1), 57–65.

CrossRef Full Text | Google Scholar

Pezard, P. A., and Anderson, R. N. (1990). “In situ measurements of electrical resistivity, formation anisotropy and tectonic context,” in SPWLA 31st Annual Logging Symposiu, Lafayette, Louisiana, June 24-27, 1990.

Google Scholar

Ren, F. Q., Zhu, C., He, M. C., Shang, J. L., Feng, G. L., and Bai, J. W. (2023). Characteristics and precursor of static and dynamic triggered rockburst: insight from multifractal. Rock Mech. Rock Eng. 56 (3), 1945–1967. doi:10.1007/s00603-022-03173-3

CrossRef Full Text | Google Scholar

Shi, G., He, T., Wu, Y. Q., Liu, J. H., and Ma, Y. (2004). A study on the dual laterologo response to fracture using the forward numerical modeling. Chin. J. Geophys., 359–363. doi:10.1002/cjg2.499

CrossRef Full Text | Google Scholar

Shi, Z. S., Zhao, S. X., Zhao, Q., Sun, S. S., Zhou, T. Q., Cheng, F., et al. (2022). Fractures in cores from the Lower Paleozoic Wufeng-Longmaxi shale in southern Sichuan Basin and their implications for shale gas exploration. Oil Gas Geol. 43 (5), 1087–1101. doi:10.11743/ogg20220507

CrossRef Full Text | Google Scholar

Sibbit, A. M., and Faivre, Q. (1985). “The dual laterolog response in fractured rocks,” in SPWLA 26st Annual Logging Symposium, Texas: Dallax, June 1985.

Google Scholar

Su, J. (2015). Study on numerical simulation of dual laterolog using finite element method in shale gas reservoir. Beijing, China: D. China University of Geosciences Beijing.

Google Scholar

Sun, Z. L., Li, Z. M., He, C. C., Zhu, F., Shen, B. J., and Lu, L. F. (2022). Characteristics of connected pores and evaluation of shale oil mobility in the qianjiang formation, qianjiang sag, jianghan basin, China. J. Earth Sci., 1–19.

Google Scholar

Tan, M. J., Wang, P., Liu, Q., and Yang, Q. (2014). Numerical simulation and fracture evaluation method of dual laterolog in organic shale. J. Appl. Geophys. 100, 1–13. doi:10.1016/j.jappgeo.2013.10.006

CrossRef Full Text | Google Scholar

Tan, M. J., Zhang, G. Y., Yun, H. Y., and Zhao, W. J. (2007). 3-D numerical mode-matching (NMM) method for resistivity logging responses in nonsymmetric conditions. Chin. J. Geophys. 50, 803–810. doi:10.1002/cjg2.1096

CrossRef Full Text | Google Scholar

Tang, S. B., and Tang, C. A. (2012). Numerical studies on tunnel floor heave in swelling ground under humid conditions. Int. J. Rock Mech. Min. Sci. 55, 139–150. doi:10.1016/j.ijrmms.2012.07.007

CrossRef Full Text | Google Scholar

Tang, S. B., Zhang, H., Tang, C. A., and Liu, H. Y. (2016). Numerical model for the cracking behavior of heterogeneous brittle solids subjected to thermal shock. Int. J. Solids Struct. 80, 520–531. doi:10.1016/j.ijsolstr.2015.10.012

CrossRef Full Text | Google Scholar

Tang, X. M., Chen, X., and Xu, X. (2012). A cracked porous medium elastic wave theory and its application to interpreting acoustic data from tight formations. Geophysics 77 (6), 245–D252. doi:10.1190/geo2012-0091.1

CrossRef Full Text | Google Scholar

Tang, X. Y. (2015). A review and perspective of logging evaluation technology for lower permeability reservoir. Prog. Geophys. 30 (02), 783–789.

Google Scholar

Um, E. S., Commer, M., Newman, G. A., and Hoversten, G. M. (2015). Finite element modelling of transient electromagnetic fields near steel-cased wells. Geophys. J. Int. 202 (2), 901–913. doi:10.1093/gji/ggv193

CrossRef Full Text | Google Scholar

Wang, J., Yang, C. C., Xyu, D. H., Chi, X. R., and Tan, M. J. (2005). Application and prospect of the formation microresistivity image well logging. Prog. Geophys. (02), 357–364.

Google Scholar

Wang, R. Y., Ding, W. L., Zhang, Y. Q., Wang, Z., Wang, X. H., He, J. H., et al. (2016). Analysis of developmental characteristics and dominant factors of fractures in lower cambrian marine shale reservoirs: a case study of niutitang Formation in cen’gong block, southern China. J. Petroleum Sci. Eng. 138, 31–49. doi:10.1016/j.petrol.2015.12.004

CrossRef Full Text | Google Scholar

Wang, R. Y., Hu, Z. Q., Dong, L., Gao, B., Sun, C. X., Yang, T., et al. (2021). Advancement and trends of shale gas reservior characterization and evaluation. Oil Gas Geol. 42, 54–65. doi:10.11743/ogg20210105

CrossRef Full Text | Google Scholar

Wen, R., Ji, C. L., Li, D., Li, N., Wang, Z. T., and Luo, J. (2018). “Comprehensive evaluation of fracturing effect by borehole micro-seismic and dipole acoustic logging,” in Proceedings of International Field Exploration and Development Conference, Xi’an, China, 18th September 2018.

Google Scholar

Wu, F. (2021). Research on fracture development and brittleness index of Chang 8 reservoir in Xiasiwan area. Xi’an, China: D. Xi’ an Shiyou University.

Google Scholar

Wu, P., Gao, L. J., Li, Y., Wu, J. G., Shi, X. F., Kang, H. N., et al. (2022). An evaluation method for shale gas potential of marine–continent transitional facies with frequent interbedded lithology: a case study on the lower permian shanxi Formation in linxing block of the Ordos Basin. Nat. Gas. Ind. 42 (2), 28–39. doi:10.3787/j.issn.1000-0976.2022.02.004

CrossRef Full Text | Google Scholar

Xie, Y., Liu, D. J., Li, C. F., Qyu, Y., and Sun, Y. (2020). Molecular mechanisms of the action of myricetin in cancer. Pet. Drill. Tech. 48 (02), 123–133. doi:10.2174/1389557519666191018112756

PubMed Abstract | CrossRef Full Text | Google Scholar

Xue, G. Q., Chang, J. H., Lei, K. X., and Chen, K. (2021). Review on three-dimensional simulations of transient electromagnetic field. J. Earth Sci. Environ. 43 (03), 559–567. doi:10.19814/j.jese.2020.11029

CrossRef Full Text | Google Scholar

Yang, S. W., Wang, H. N., Chen, G. B., and Yao, D. H. (2009). The 3-D finite difference time domain (FDTD) algorithm of response of multi-component electromagnetic well logging tool in a deviated and layered anisotropic formation. Chin. J. Geophys. 52 (03), 833–841+257. doi:10.1002/CJG2.1368

CrossRef Full Text | Google Scholar

Yin, Q., Wu, J. Y., Jiang, Z., Zhu, C., Su, H. J., Jing, H. W., et al. (2022). Investigating the effect of water quenching cycles on mechanical behaviors for granites after conventional triaxial compression. Geomechanics Geophys. Geo-Energy Geo-Resources 8 (2), 77. doi:10.1007/s40948-022-00388-0

CrossRef Full Text | Google Scholar

Yin, Q., Wu, J. Y., Zhu, C., He, M. C., Meng, Q. X., and Jing, H. W. (2021). Shear mechanical responses of sandstone exposed to high temperature under constant normal stiffness boundary conditions. Geomechanics Geophys. Geo-Energy Geo-Resources 7, 35. doi:10.1007/s40948-021-00234-9

CrossRef Full Text | Google Scholar

Zeng, L. B., Li, X. Z., Shi, C. E., Wang, Z. G., Zhao, J. Y., and Wang, Y. K. (2007). Characteristics and origin of fractures in the extra low-permeability sandstone reservoirs of the upper triassic Yanchang Formation in the Ordos Basin. Acta Geol. sin. 2, 174–180. doi:10.3321/j.issn:0001-5717.2007.02.005

CrossRef Full Text | Google Scholar

Zhang, G. J., and Wang, H. M. (1996). Numerical pattern matching solution of common resistivity logging. J. China Univ. Petroleum(Edition Nat. Sci. (02), 23–29.

Google Scholar

Zhao, J., Wang, D., and Gu, H. W. (2015). Numerical simulation of dual laterolog in cavernous carbonatite reservoir. J. Coast. Res. 73, 758–762. doi:10.2112/si73-130.1

CrossRef Full Text | Google Scholar

Zhou, C. C., and Yang, C. D. (2003). Contributing factor of sandstone fracture and its intgrated identifying technology for reugulae logging data. Oil Geophys. Prospect. 4, 425–430+462+9+98+100. doi:10.13810/j.cnki.issn.1000-7210.2003.04.016

CrossRef Full Text | Google Scholar

Zou, C. N., Ma, F., Pan, S. Q., Zhang, X. S., Wu, S. T., Fu, G. Y., et al. (2023). Formation and distribution potential of global shale oil and the developments of continental shale oil theory and technology in China. Earth Sci. Front. 30 (01), 128–142. doi:10.13745/j.esf.sf.2022.8.29

CrossRef Full Text | Google Scholar