Optimizing tight oil extraction from low permeability tight reservoirs: a study on stress sensitivity effects and applications in carbon capture, utilization, and storage

This paper takes into consideration the impact of stress sensitivity on bioenergy production from low permeability tight reservoirs, focusing on the post-fracturing phase. This paper established a trilinear flow model that effectively takes into account the dynamics of such reservoirs. This model incorporates stress sensitivity parameters and uses the perturbation transformation and Laplace transformation to solve the productivity prediction formula. The final productivity prediction curve post-fracturing is achieved through a numerical inversion method. This study shows that the stress sensitivity effect significantly diminishes the productivity of fractured horizontal wells used in bioenergy extraction. By introducing stress sensitivity effect parameters, this paper manages to uncover the influence law of mobility and artificial fracture parameters on productivity. Notably, as the reservoir mobility increases, the cumulative bioenergy production from fractured horizontal wells improves significantly. In addition to the above, this paper also scrutinizes the sensitivity of artificial fracture parameters and optimize both the quantity and length of these fractures. This plays a crucial role in enhancing the productivity and efficiency of bioenergy extraction from these tight reservoirs. The applicability and reliability of this method are extensively tested, thereby establishing its potential in guiding the development of low permeability reservoirs post-fracturing. Importantly, this research sets the groundwork for combining bioenergy production with Carbon Capture, Utilization, and Storage (CCUS) technologies. By focusing on optimization and stress management in tight reservoirs, this paper contributes to the sustainable production of bioenergy and reduce carbon emissions, moving a step closer to a cleaner and sustainable future.

1 Introduction

With the advancement of unconventional oil and gas production technology, low-permeability reservoirs have received more and more attention (Mahdaviara et al., 2022; Wang et al., 2023). In order to optimize the production of low permeability reservoirs, horizontal well fracturing in stages is the most important technical method to develop and exploit low permeability reservoirs (Kolawole et al., 2021; Xu et al., 2021). Therefore, the production prediction of low permeability reservoirs is beneficial for designing more suitable fracturing schemes and developing low permeability reservoirs in a scientific and rational manner (Vairogs et al., 1971; Hassan et al., 2021; Wang et al., 2022).

Experimentation is a common means of studying seepage mechanisms in low-permeability reservoirs (Parekh and Sharma, 2004; Sander et al., 2017). Chen introduces a new approach to characterizing microstructure through a combination of thin sectioning, scanning electron microscopy, pressure-controlled mercury injection, rate-controlled mercury injection, and nuclear magnetic resonance (Chen et al., 2019). Kuang proposes a new NMR-based method to determine the saturation index under wet conditions of water or oil (Kuang et al., 2018). These experiments include high-pressure mercury injection, constant-rate mercury injection, nuclear magnetic resonance, as well as microscopic analysis of casting thin sections and scanning electron microscopy. Wang et al. (2018) analyze the advantages and shortcomings of these commonly used experimental techniques. Liu et al. (2020) reported the pore structure and physical properties of a low-permeability stratigraphic sample. At present, studies on the modal pore-throat structure of low-permeability reservoirs are mainly focused on dense reservoirs with controlled genesis, while studies on weakly cemented reservoirs are limited (Zhong et al., 2022; Li et al., 2023). Other influential work includes (Wang et al., 2021; Yongshi et al., 2021; Li et al., 2022; Zhong et al., 2022). The mechanistic study of low-permeability reservoirs has been relatively well developed, but the study of capacity prediction methods for low-permeability reservoirs still needs to be improved.

Wang developed a comprehensive data mining process to evaluate well production performance in the Monee Formation of the Western Canadian Sedimentary Basin (Wang and Chen, 2019). Due to the presence of low-permeability conglomerate, its seepage characteristics are more complex and the capacity after volume fracturing is difficult to predict. To solve this problem. Considering the trigger pressure gradient, a two-media unsteady seepage model with matrix seepage and discrete fracture network seepage was developed by (Mahmoodi et al., 2019; Vishkai and Gates, 2019) investigated sand production in dense sandstone reservoirs in terms of seepage and in situ stress distribution based on data from the Daqing oil field in the Songliao basin. Dong et al. (2019) developed a new model to study the degree of well disturbance. The model is defined by a new and original mathematical expression on production. The model proposed by Wang et al. (2020) has shown potential practical use in predicting the productivity of multistage fractured horizontal wells and in analyzing the effect of certain factors on gas production from tight, low-permeability reservoirs. The prediction method proposed by Lu and Wang (2021) can accurately predict the production of volumetrically fractured horizontal wells in the experimental area, providing some guidance for the development and adjustment of low-permeability reservoirs. To investigate the contribution of microfractures to well productivity and the effect of dynamic capillary pressure on oil-water phase flow in low permeability reservoirs (Jiang et al., 2020a; Hu et al., 2020) introduced a semi-analytical model and solved it considering the disturbance between each hydraulic fracture (Jiang et al., 2020b). Although production prediction models for low-permeability reservoirs have been developed by previous authors from different aspects, the effect of stress sensitivity on them has rarely been considered.

This paper mainly predicts the productivity of staged fracturing horizontal wells in low permeability tight reservoirs by analytical solutions. Considering the influence of stress sensitivity on oil well production, a trilinear flow model is established. The productivity prediction formula considering stress sensitivity is solved by perturbation transformation and Laplace transformation. Finally, the productivity prediction curve after fracturing is obtained by numerical inversion method. The sensitivity analysis of stress sensitivity coefficient, reservoir mobility and artificial fracture parameters was carried out. This study lays the foundation for integrating bioenergy production with carbon capture, utilization and storage (CCUS) technology. By focusing on optimization and pressure management in tight reservoirs, this paper contributes to sustainable production of bioenergy and reduction of carbon emissions, a step towards a clean and sustainable future.

2 Mathematical model

2.1 Basic seepage model

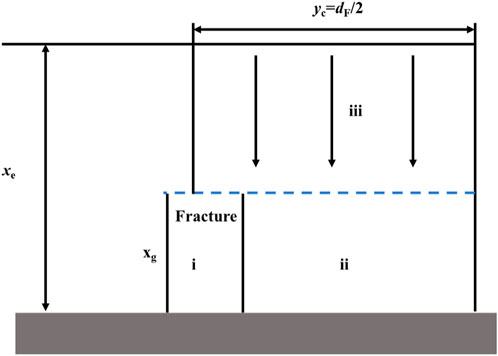
This paper assumes that the reservoir is horizontal equal thickness, homogeneous reservoir; reservoir top and bottom closed, only consider infinite boundary; the pressure drop caused by wellbore friction is not considered, and the pressure of each fracture is equal at the wellbore. The formation and fluid are slightly compressible, the fluid is single phase, and the flow in the formation conforms to Darcy’s law.

The coupled linear flow of the trilinear flow model in three continuous flow regions is shown in Figure 1: External reservoirs beyond the tip of hydraulic fractures, internal reservoirs between hydraulic fractures, and hydraulic fractures, each region has different characteristics. Internal reservoir matrix considered homogeneous.

FIGURE 1

FIGURE 1. Physical model of trilinear flow.

The state equation of reservoir is:

$\varphi ={\varphi }_i{e}^{-C_{\varphi }\left(P-P_i\right)},\rho ={\rho }_i{e}^{-C_{\rho }\left(P-P_i\right)}(1)$

Where $\varphi$, ${\varphi }_i$ are matrix porosity and original formation porosity, %; $C_{\rho }$, $C_{\varphi }$ represent the compression coefficient of fluid and pore, MPa-1; P_i is the original formation pressure, MPa; $\rho$, ${\rho }_i$ are the fluid density and the original fluid density, kg/m³.

The motion equation is generalized Darcy’s law:

$v=-\frac{k}{u}\left(\nabla P\right)(2)$

Among them: $v$ the seepage velocity of the fluid in the matrix, 10^–3 m/s; $u$ is the fluid viscosity, mPa s; $\nabla P$ is the reservoir pressure gradient, MPa/m; $k$ is the permeability, $\mu m^2$;

Formation permeability model considering stress sensitivity:

$k=k_a{e}^{c_k\left(p-p_i\right)}(3)$

Where k represents instantaneous formation permeability; $\mu m^2$; $k_a$ is the original formation permeability, $\mu m^2$; $c_k$ represents the stress sensitivity factor; p is formation pressure, MPa; P_i is the original formation pressure, MPa.

2.2 Reservoir seepage model

The seepage of the outer reservoir is assumed to be a one-dimensional single-phase flow along the x direction in the matrix, then the seepage differential equation and definite conditions of the outer reservoir are as follows:

$\left\{\begin{array}{l}{\nabla }^2{P}_o\left(x\right)=\frac{1}{{\eta }_o}\frac{\partial P_o\left(x\right)}{\partial t}\\ {\left.P_o\right|}_{t=0}=P_i\\ \begin{array}{l}{\left(\frac{\partial P_o}{\partial x}\right)}_{x=x_e}=0,on{\mathrm{\Gamma }}_q\\ {\left.P_o\right|}_{X=X_F}={\left.P_I\right|}_{X=X_F},\text{on }{\mathrm{\Gamma }}_p\end{array}\end{array}\right.(4)$

In the formula, $P_o$ is the pressure value of the external reservoir, MPa; $P_i$ is the initial pressure of the external reservoir, MPa; ${\eta }_o=\frac{k_o}{\varphi \mu C_f}$ is the conductivity coefficient of external reservoir, $\varphi$ is porosity, decimal. ${\mathrm{\Gamma }}_q$ represents the outer boundary and ${\mathrm{\Gamma }}_p$ represents the inner boundary.

The seepage of the internal reservoir is assumed to be a one-dimensional single-phase flow in the matrix along the y direction perpendicular to the hydraulic fracturing. The seepage differential equations and definite conditions of the internal reservoir are as follows:

$\left\{\begin{array}{l}\frac{k_{\mathrm{I}\mathrm{m}}}{\mu }\frac{{\partial }^2{P}_{\mathrm{I}\mathrm{m}}}{\partial y^2}+{\left.\frac{k_O}{x_F\mu }\frac{{\partial }^2{P}_o}{\partial x}\right|}_{x=x_F}=C_{mI}{\varphi }_{mo}\frac{\partial P_{\mathrm{I}\mathrm{m}}}{\partial t}\\ {\left.P_I\right|}_{t=0}=P_i\\ \begin{array}{l}{\left(\frac{\partial P_I}{\partial x}\right)}_{y=y_e}=0,on{\mathrm{\Gamma }}_q\\ {\left.P_I\right|}_{y=\frac{w_F}{2}}={\left.P_I\right|}_{y=\frac{w_F}{2}},\text{on }{\mathrm{\Gamma }}_p\end{array}\end{array}\right.(5)$

Where, $P_I$ is the pressure value of the internal reservoir, MPa; $P_i$ is the initial pressure of the external reservoir, MPa; $C_{mI}$ is the internal reservoir matrix permeability coefficient, MPa⁻¹; ${\varphi }_{mo}$ is internal reservoir porosity, decimal; $W_F$ is crack width, m.

2.3 Hydraulic fracture seepage model

The seepage assumption of hydraulic fracture is one-dimensional single-phase linear seepage along the x direction in the fracture. The seepage differential equation and definite solution condition of hydraulic fracture are:

$\left\{\begin{array}{l}\frac{k_F}{\mu }\frac{{\partial }^2{P}_{\mathrm{I}\mathrm{m}}}{\partial y^2}+{\left.\frac{k_{tm}}{\left(W_F/2\right)\mu }\frac{{\partial }^2{P}_o}{\partial y}\right|}_{y=\frac{W_F}{2}}=C_F{\varphi }_{Fo}\frac{\partial P_F}{\partial t}\\ {\left.P_F\right|}_{t=0}=P_i\\ \begin{array}{l}{\left(\frac{\partial P_F}{\partial x}\right)}_{x=x_F}=0,on{\mathrm{\Gamma }}_q\\ {\left.P_F\right|}_{X=0}=P_w,\text{on }{\mathrm{\Gamma }}_p\end{array}\end{array}\right.(6)$

Where $P_F$ is the pressure value of the internal reservoir, MPa; $P_i$ is the initial pressure value of the crack, MPa; $C_F$ is the fracture conductivity coefficient, MPa⁻¹; ${\varphi }_{Fo}$ is the fracture porosity, decimal.

3 Numerical method

3.1 Dimensionless quantization

Define dimensionless time, distance, pressure and permeability by:

$t_D=\frac{3.6K_{I}t}{{\left(\varphi c_t\right)}_I\mu x_F^2},x_D=\frac{x}{x_F},P_D=\frac{P_i-P}{P_i-P_w},C_{KD}=C_K\left(P_i-P_w\right)(7)$

where $t_D$ is dimensionless time, $x_D$ is dimensionless distance, and $P_D$ is dimensionless pressure.

The diffusivity ratio is defined as:

$\begin{array}{l}{\eta }_I=\frac{3.6K_I}{{\left(\varphi c_t\right)}_I\mu }\\ {\eta }_F=\frac{3.6K_F}{{\left(\varphi c_t\right)}_F\mu }\\ {\eta }_o=\frac{3.6K_o}{{\left(\varphi c_t\right)}_o\mu }\end{array}(8)$

In the above formula, ${\eta }_I$ is the diffusivity of the internal reservoir, ${\eta }_O$ is the diffusivity of the external reservoir, and ${\eta }_F$ is the diffusivity of the external reservoir.

Dimensionless seepage differential equation for external reservoir:

$\left\{\begin{array}{l}\frac{{\partial }^2{P}_{oD}}{{\partial }^2{x_D}^2}=e^{C_{KoD·PoD}}\frac{\partial P_{oD}}{\partial t_D}\\ \begin{array}{l}{\left.P_{oD}\right|}_{t_D=0}=0\\ {\left.\left(\frac{\partial P_{oD}}{\partial x_D}\right)\right|}_{x_D=x_{cD}}=0\end{array}\\ {\left.P_{oD}\right|}_{x_D=1}={\left.P_{ID}\right|}_{x_D=1}\end{array}\right.(9)$

The dimensionless transformation of seepage differential equations of internal reservoirs and hydraulic fractures is similar to that of external reservoirs, which is not summarized here.

3.2 Perturbation transform

Due to the strong nonlinearity of the differential equation, perturbation transformation is introduced, namely, (Khan and Wu, 2011).

$P_D=-\frac{1}{C_{KD}}\ln \left[{1-\mathrm{C}}_{KD}{\zeta }_D\right](10)$

The seepage differential equation after perturbation transformation of external reservoir is:

$\frac{{\partial }^2{\zeta }_{OD}}{\partial {x_D}^2}=\frac{1}{1-C_{KD}{\zeta }_{OD}}\frac{\partial {\zeta }_{OD}}{\partial t_D}(11)$

For low permeability reservoirs, C_KD is generally less than 0.2, the order of magnitude of the second-order term is much smaller than the first-order solution. Therefore, the seepage differential equation after $\frac{1}{1-C_{KD}{\zeta }_{OD}}\approx 1$ perturbation transformation can be written as:

$\frac{{\partial }^2{\zeta }_{OD}}{\partial {x_D}^2}=\frac{\partial {\zeta }_{OD}}{\partial t_D}(12)$

Perturbation transformation of internal reservoir seepage differential equation can be written as:

$\frac{{\partial }^2{\zeta }_{\mathrm{I}\mathrm{m}D}}{\partial {y_D}^2}+{\left.\frac{1}{y_{CD}{C}_{RD}}\frac{\partial {\zeta }_{OD}}{\partial x_D}\right|}_{x_D=1}=\frac{\partial {\zeta }_{\mathrm{I}\mathrm{m}D}}{\partial t_D}(13)$

Perturbation transformation of fracture seepage differential equation can be written as follows:

$\frac{{\partial }^2{\zeta }_{FD}}{\partial {x_D}^2}+{\left.\frac{2}{C_{FD}}\frac{\partial {\zeta }_{FD}}{\partial y_D}\right|}_{y_D=W_{FD}/2}=\frac{1}{{\eta }_{FD}}\frac{\partial {\zeta }_{FD}}{\partial t_D}(14)$

3.3 Laplace transform and equation solving

Laplace transform is performed on the seepage differential equations of these three parts, and the following three seepage differential equations are obtained:

$\frac{{\partial }^2{\overline{\zeta }}_{OD}}{\partial {x_D}^2}-s{\overline{\zeta }}_{OD}=0(15)$

$\frac{{\partial }^2{\zeta }_{\mathrm{I}\mathrm{m}D}}{\partial {y_D}^2}+{\left.\frac{1}{y_{CD}{C}_{RD}}\frac{\partial {\zeta }_{OD}}{\partial x_D}\right|}_{x_D=1}-s{\overline{\zeta }}_{\mathrm{I}\mathrm{m}D}=0(16)$

$\frac{{\partial }^2{\zeta }_{FD}}{\partial {x_D}^2}+{\left.\frac{2}{C_{FD}}\frac{\partial {\zeta }_{FD}}{\partial y_D}\right|}_{y_D=W_{FD}/2}-\frac{s}{{\eta }_{FD}}{\overline{\zeta }}_{FD}=0(17)$

For the seepage differential equation group (Eq. 14) of the external reservoir, after substituting its boundary conditions, the solution of Eq. 14 is:

${\overline{\zeta }}_{OD}={\left.{\overline{\zeta }}_{ID}\right|}_{x_D=1}\frac{\cosh \left|\sqrt{s}\left(x_{eD}-x_D\right)\right|}{\cosh \left|\sqrt{s}\left(x_{eD}-1\right)\right|}(18)$

The solution of the internal reservoir seepage equation is derived as:

${\overline{\zeta }}_{\mathrm{I}\mathrm{m}D}={\left.{\overline{\zeta }}_{FD}\right|}_{y_D=\frac{W_{FD}}{2}}\frac{\cosh \left[\sqrt{{\epsilon }_o}\left(y_{eD}-y_D\right)\right]}{\cosh \left[\sqrt{{\epsilon }_o}\left(y_{eD}-\frac{W_{FD}}{2}\right)\right]}(19)$

Where ${\epsilon }_o=\frac{\sqrt{s}\tanh \left[\sqrt{s}\left(x_{eD}-1\right)\right]}{C_{RD}{y}_{eD}}+s$.

The solution of fracture seepage equation is:

${\overline{\zeta }}_{FD}=\frac{1}{s}\frac{\cosh \left[\sqrt{{\epsilon }_F}\left(1-x_D\right)\right]}{\cosh \left(\sqrt{{\zeta }_F}\right)}(20)$

Dimensionless transformation yield formula

$q_D=\frac{B\mu x_F}{86.4k_F{A}_F\left(p_i-p_w\right)}q(21)$

Where B is the volume factor.

After Laplace and perturbation transformation, the solution of the yield is:

${\overline{q}}_D=\frac{1}{s-C_{KD}}\sqrt{{\epsilon }_F}\tanh \left(\sqrt{{\epsilon }_F}\right)(22)$

Where ${\epsilon }_F=\frac{2\sqrt{{\epsilon }_o}\tanh \left[\sqrt{{\epsilon }_o}\left(y_{eD}-W_{FD}/2\right)\right]}{C_{FD}}+\frac{s}{{\eta }_{FD}}$.

In this paper, the productivity prediction formula of trilinear flow simulation in Laplace space has been obtained. However, to solve the production capacity in the actual space, it is necessary to calculate the solution in the real-time domain by numerical inversion. This paper adopts the numerical inversion method of AWG method (Abate and Whitt, 1992). Compared with the Stehfest algorithm, the advantages of the AWG method are Higher computational accuracy and smaller numerical error, while Stehfest algorithm produces larger truncation error in high order cases. The AWG method can handle ordinary Laplace transform, while the Stehfest algorithm can only handle bilateral Laplace transform. The AWG method is more stable and accurate for computing the higher order derivatives of the Laplace transform. The AWG method can be easily computed in parallel, which is more conducive to engineering realization.

4 Sensitivity analysis

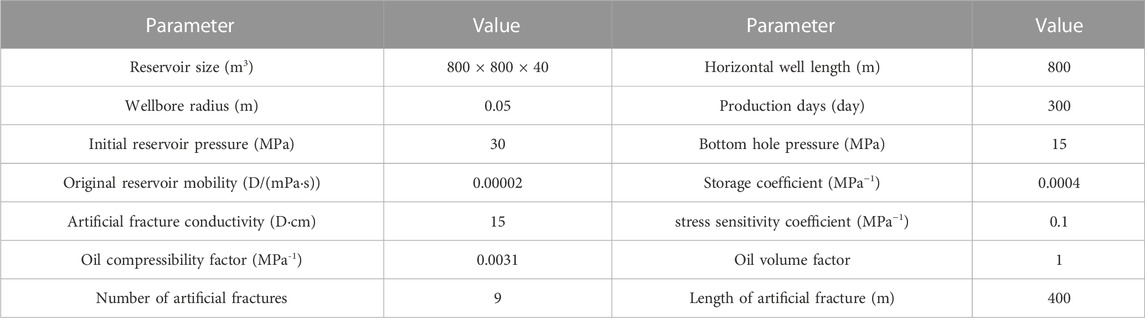
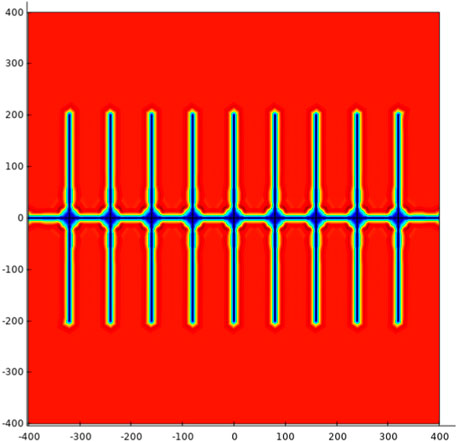
Firstly, the productivity curve obtained by the above derivation is compared and verified by actual reservoir. The basic parameters required for this reservoir are shown in the following Table 1. The model diagram can be seen in Figure 2. The size of the block is 800 m × 800 m × 40 m, and the production days are 350 days. The length of horizontal well is 800 m, the number of artificial fractures is 8, and the length of artificial fractures is 400 m. The original formation pressure is 30 MPa, and the fixed bottom hole flow pressure is 15 MPa. The stress sensitivity coefficient is considered to be 0.1 MPa⁻¹. In this paper, the productivity of fractured horizontal wells is calculated by considering the stress sensitivity coefficient and not considering the stress sensitivity coefficient, as shown in Figure 3.

TABLE 1

TABLE 1. Basic reservoir parameters.

FIGURE 2

FIGURE 2. Model diagram.

FIGURE 3

FIGURE 3. Field oil production total under different conditions.

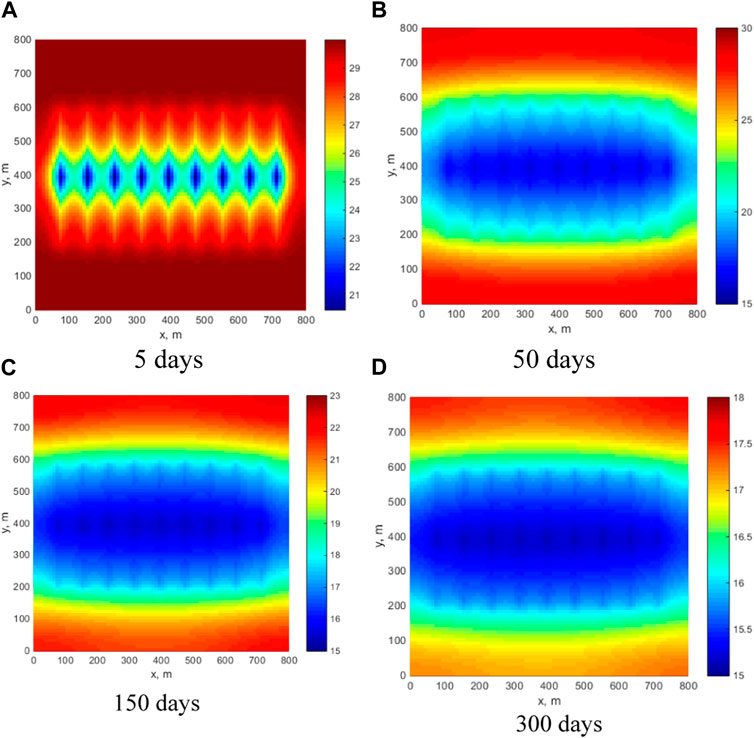
As shown in Figure 3, The red circle is the real data, the blue line is the result considering the stress sensitivity, and the black line is the result without considering the stress sensitivity. Considering stress sensitivity and not considering stress sensitivity have a great influence on productivity. In this paper, the calculation of stress sensitivity is more in line with the actual production capacity, which verifies the correctness of the method. Figure 4 shows the pressure distribution at different times. It can be seen that the pressure decreases as the production proceeds. From the initial 30 MPa, it drops to about 18 MPa at the end.

FIGURE 4

FIGURE 4. Pressure distribution. (A) 5 days, (B) 50 days, (C) 150 days, (D) 300 days.

4.1 Influence rule of stress sensitivity coefficient on production

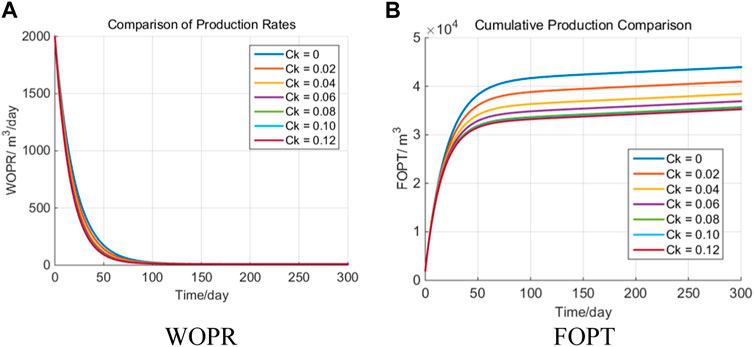
From the above analysis, stress sensitivity has a great influence on productivity. Therefore, this paper selects the stress sensitivity coefficient 0–1.2 MPa⁻¹ (interval 0.02) for productivity prediction analysis. Other parameters remain unchanged, as shown in the above example. The well oil production rate (WOPR) and field oil production total (FOPT) calculation results of the block are shown in Figure 5.

FIGURE 5

FIGURE 5. WOPR and FOPT with different stress sensitivity coefficients. (A) WOPR, (B) FOPT.

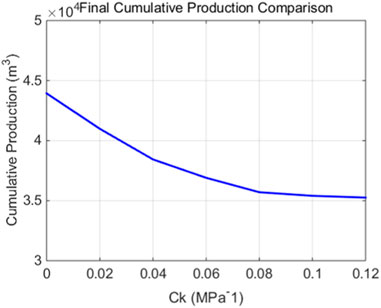
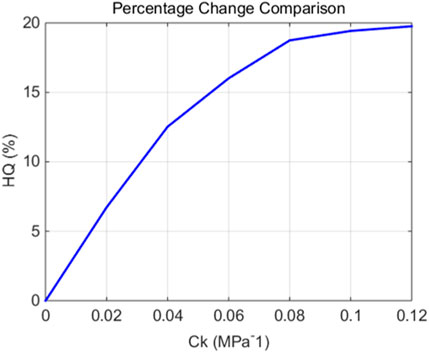
It can be seen from Figure 6 that as the stress sensitivity coefficient increases, the cumulative oil production of fractured horizontal wells shows a significant downward trend. When the stress sensitivity coefficient is 0, the field oil production total can reach 4.4 × 10⁴ m³. When the stress sensitivity coefficient is 0.12 MPa⁻¹, the field oil production total is only 3.58 × 10⁴ m³. This fully shows that the stress sensitivity coefficient has a very serious impact on productivity. Here, HQ is defined to represent the influence of stress sensitivity coefficient on productivity.

$HQ=100\%\times \frac{Q_o-Q}{Q_o}(23)$

FIGURE 6

FIGURE 6. Effect of stress sensitivity coefficients on field oil production total.

Figure 7 below shows the influence of stress sensitivity coefficient on HQ. It can be seen from Figure 7 that HQ increases with the increase of stress sensitivity coefficient.

FIGURE 7

FIGURE 7. Effect of different stress sensitivity coefficients on HQ.

4.2 Effect of mobility on production

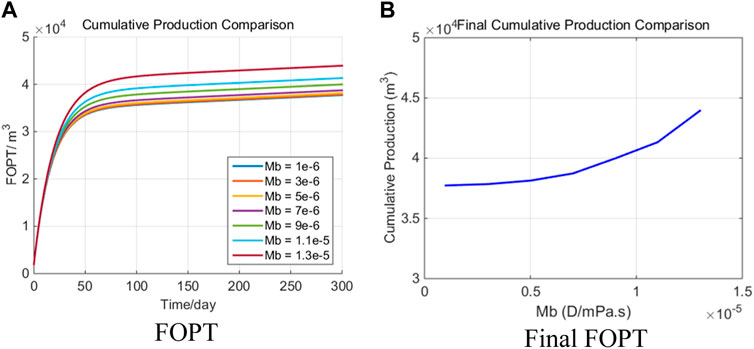
In this paper, the above examples are used. Other parameters are unchanged, and the mobility is changed to 1 × 10⁻⁶ and 1.3 × 10⁻⁵ D/(mPa·s).

It can be seen from Figure 8 that with the increase of reservoir mobility, the propagation velocity of pressure wave increases (the supply area increases), and the cumulative production of fractured horizontal wells will increase significantly. When the mobility is less than 10^–5 D/(mPa·s), the production capacity increases slowly. When the mobility is greater than 10^–5 D/(mPa·s), the production capacity increases linearly.

FIGURE 8

FIGURE 8. Effect of mobility on field oil production total. (A) FOPT, (B) Final FOPT.

4.3 Influence of artificial fracture parameters

4.3.1 Number of artificial fractures

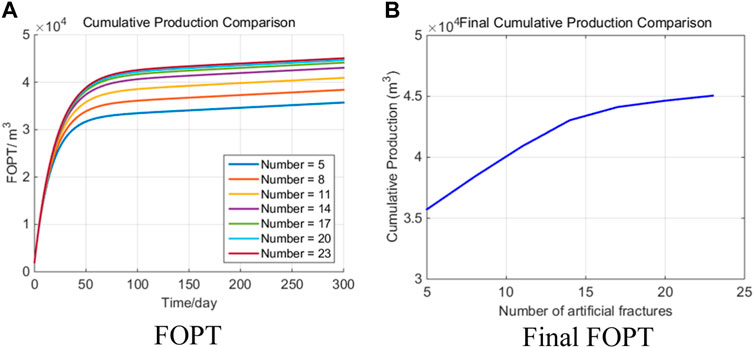
The stimulation effect of increasing artificial fracturing on fractured horizontal wells is determined by increasing contact area, flow channel and changing seepage form, but there is also the problem of interference between fractures. Due to multi-fracture interference work cannot be realized with the trilinear model. Here the dual medium model is utilized, which is different from the trilinear flow model. In this paper, 4, 5 artificial fracturing are selected for simulation. It can be seen from Figure 9, with the increase of the number of artificial fracturing, the production of fractured horizontal wells in the early stage (before the occurrence of inter-fracture interference) is higher. With the intensification of inter-fracture interference, the effect of increasing the number of artificial fractures will be gradually offset.

FIGURE 9

FIGURE 9. Effect of artificial fractures number on production. (A) FOPT, (B) Final FOPT.

For tight oil reservoirs with stress sensitivity effect, there are more areas affected by stress sensitivity effect before the occurrence of inter-fracture interference (the time of inter-fracture interference is not affected by stress sensitivity effect), which makes more areas produce at low permeability. Therefore, with the increase of the number of artificial fractures, the cumulative production of fractured horizontal wells increases rapidly and then becomes gentle. The effect of stress sensitivity on cumulative yield is also increased.

4.3.2 Half-length of artificial fracturing

Artificial fracturing half-length is the main factor to ensure the contact area with reservoir in y direction. Because the flow of crude oil between fractures is mainly linear flow, the increase of fracture length also increases the productivity almost linearly. Then it is also affected by the action of the outer boundary. The longer the crack length, the earlier the influence of the outer boundary appears. The effect of the outer boundary depends on the mobility of the reservoir. When the mobility is low, the outer boundary has little effect on the early and middle stages of production, and the seepage process of the fluid to the fractured horizontal well system in the area exceeding the fracture length is quasi-radial flow, and its seepage resistance is much larger than the linear flow process between fractures. Therefore, increasing the length of artificial fractures, the cumulative production of fractured horizontal wells also shows a process of rapid increase first and then slow increase. In addition, increasing the seam length can effectively weaken the negative effects of stress sensitivity (as shown in Figure 10).

FIGURE 10

FIGURE 10. Effect of artificial fracture length on production. (A) FOPT, (B) Final FOPT.

4.3.3 Artificial fracture flow conductivity

Artificial fracture conductivity mainly affects the early production process of fractured horizontal wells in tight oil reservoirs, and its influence degree is directly related to reservoir flow capacity. When the reservoir flow capacity is strong, the requirement for conductivity is high; when the reservoir flow capacity is weak, the demand for conductivity is also weak. In fractured horizontal wells in tight reservoirs, the effect of conductivity on cumulative production is not as great as that of fracture number and fracture length, but the trend is the same as before. And the greater the conductivity, the higher the initial production capacity, resulting in a stronger negative effect of stress sensitivity (see Figure 11).

FIGURE 11

FIGURE 11. Effect of Artificial fracture conductivity. (A) FOPT, (B) Final FOPT.

5 Conclusion

This paper presented a productivity prediction model for horizontal well staged fracturing in stress-sensitive tight reservoirs. The model demonstrates good adaptability in predicting the productivity of horizontal well staged fracturing. Our findings can be summarized as follows:

1. This paper developed a trilinear flow model to predict the productivity of segmented horizontal wells in tight oil reservoirs, accounting for the influence of stress sensitivity. Using mathematical methods such as perturbation transformation and Laplace transformation, this paper derived the productivity prediction formula and obtained the productivity prediction curve through numerical inversion.

2. By comparing the productivity of horizontal wells after staged fracturing with and without considering stress sensitivity, this paper found that stress sensitivity has a significant negative impact on the productivity of fractured horizontal wells.

3. This paper introduced stress-sensitive effect parameters and investigated the influence of reservoir mobility and artificial fracture parameters on productivity. Results show that as reservoir mobility increases, the cumulative production of fractured horizontal wells also increases significantly.

4. An increase in the number of artificial fractures and the length of fractures leads to a rapid increase in cumulative production, which then gradually levels off. Although conductivity does not have as substantial an impact on cumulative production as the number and length of fractures, higher conductivity results in higher initial productivity, exacerbating the negative effect of stress sensitivity.

In conclusion, this study provides valuable insights into the productivity of horizontal well staged fracturing in stress-sensitive tight reservoirs. The developed model and findings can be instrumental in optimizing hydraulic fracturing operations and enhancing oil recovery in tight reservoirs.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

XJ: conceptualization, data curation, writing original draft, investigation, project administration, writing—review and editing, project administration, and supervision. GY: project administration. All authors contributed to the article and approved the submitted version.

Acknowledgments

Thanks to the scholars in the references.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abate, J., and Whitt, W. (1992). The Fourier-series method for inverting transforms of probability distributions. Queueing Syst. 10, 5–87. doi:10.1007/bf01158520

CrossRef Full Text | Google Scholar

Chen, M., Dai, J., Liu, X., Kuang, Y., Qin, M., and Wang, Z. (2019). Contributions of pore-throat size distribution to reservoir quality and fluid distribution from NMR and MIP in tight sandy conglomerate reservoirs. Arabian J. Geosciences 12 (1), 9–12. doi:10.1007/s12517-018-4153-7

CrossRef Full Text | Google Scholar

Dong, X., Zhang, T., Yao, W., Hu, T., Li, J., Jia, C., et al. (2019). “A method to quantitatively characterize tight glutenite reservoir pore structure,” in Proceedings of the SPE Reservoir Characterisation and Simulation Conference and Exhibition, Abu Dhabi, UAE, September 2019.

CrossRef Full Text | Google Scholar

Hassan, A., Aljawad, M. S., and Mahmoud, M. J. A. o. (2021). An artificial intelligence-based model for performance prediction of acid fracturing in naturally fractured reservoirs. ACS Omega 6 (21), 13654–13670. doi:10.1021/acsomega.1c00809

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, J., Sun, R., and Zhang, Y. (2020). Investigating the horizontal well performance under the combination of micro-fractures and dynamic capillary pressure in tight oil reservoirs. Fuel 269, 117375. doi:10.1016/j.fuel.2020.117375

CrossRef Full Text | Google Scholar

Jiang, L., Liu, J., Liu, T., and Yang, D. (2020a). Semi-analytical modeling of transient pressure behaviour for a fractured vertical well with hydraulic/natural fracture networks by considering stress-sensitive effect. J. Nat. Gas Sci. Eng. 82, 103477. doi:10.1016/j.jngse.2020.103477

CrossRef Full Text | Google Scholar

Jiang, L., Liu, J., Liu, T., and Yang, D. (2020b). Semi-analytical modeling of transient rate behaviour of a horizontal well with multistage fractures in tight formations considering stress-sensitive effect. J. Nat. Gas Sci. Eng. 82, 103461. doi:10.1016/j.jngse.2020.103461

CrossRef Full Text | Google Scholar

Khan, Y., and Wu, Q. (2011). Homotopy perturbation transform method for nonlinear equations using He’s polynomials. Comput. Math. Appl. 61 (8), 1963–1967. doi:10.1016/j.camwa.2010.08.022

CrossRef Full Text | Google Scholar

Kolawole, O., Ispas, I., Kumar, M., Weber, J., Zhao, B. J. R. M., and Engineering, R. (2021). Time-lapse biogeomechanical modified properties of ultra-low permeability reservoirs. Rock Mech. Rock Eng. 54 (6), 2615–2641. doi:10.1007/s00603-021-02410-5

CrossRef Full Text | Google Scholar

Kuang, Y., Sima, L., Zhang, Z., Wang, Z., and Chen, M. (2018). A model for estimating the saturation exponent based on NMR in tight sandy conglomerate reservoirs. Arabian J. Sci. Eng. 43 (11), 6305–6313. doi:10.1007/s13369-017-3013-1

CrossRef Full Text | Google Scholar

Li, J., Zhang, K., Cheng, N., Xing, Z., Wang, S., Wang, B., et al. (2022). Optimization and evaluation of stabilizers for tight water-sensitive conglomerate reservoirs. ACS omega 7 (7), 5921–5928. doi:10.1021/acsomega.1c06140

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, S., Wang, P., Wang, Z., Cheng, H., and Zhang, K. (2023). Strategy to enhance geological CO2 storage capacity in saline aquifer. Geophys. Res. Lett. 50 (3), e2022GL101431. doi:10.1029/2022gl101431

CrossRef Full Text | Google Scholar

Liu, C., Yin, C., Lu, J., Sun, L., Wang, Y., Hu, B., et al. (2020). Pore structure and physical properties of sandy conglomerate reservoirs in the Xujiaweizi depression, northern Songliao Basin, China. J. Petroleum Sci. Eng. 192, 107217. doi:10.1016/j.petrol.2020.107217

CrossRef Full Text | Google Scholar

Lu, M., and Wang, Z. (2021). A new production forecasting method of the multifractured horizontal wells based on cluster analysis. Geofluids 2021, 1–8. doi:10.1155/2021/6631401

CrossRef Full Text | Google Scholar

Mahdaviara, M., Sharifi, M., and Ahmadi, M. J. F. (2022). Toward evaluation and screening of the enhanced oil recovery scenarios for low permeability reservoirs using statistical and machine learning techniques. Fuel (Lond). 325, 124795. doi:10.1016/j.fuel.2022.124795

CrossRef Full Text | Google Scholar

Mahmoodi, S., Abbasi, M., and Sharifi, M. (2019). New fluid flow model for hydraulic fractured wells with non-uniform fracture geometry and permeability. J. Nat. Gas Sci. Eng. 68, 102914. doi:10.1016/j.jngse.2019.102914

CrossRef Full Text | Google Scholar

Parekh, B., and Sharma, M. M. (2004). “Cleanup of water blocks in depleted low-permeability reservoirs,” in Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, Texas, September 2004.

CrossRef Full Text | Google Scholar

Sander, R., Pan, Z., and Connell, L. D. (2017). Laboratory measurement of low permeability unconventional gas reservoir rocks: A review of experimental methods. A Rev. Exp. methods 37, 248–279. doi:10.1016/j.jngse.2016.11.041

CrossRef Full Text | Google Scholar

Vairogs, J., Hearn, C., Dareing, D. W., and Rhoades, V. M. (1971). Effect of rock stress on gas production from low-permeability reservoirs. J. Pet. Technol. 23 (09), 1161–1167. doi:10.2118/3001-pa

CrossRef Full Text | Google Scholar

Vishkai, M., and Gates, I. (2019). On multistage hydraulic fracturing in tight gas reservoirs: montney Formation, Alberta, Canada. J. Petroleum Sci. Eng. 174, 1127–1141. doi:10.1016/j.petrol.2018.12.020

CrossRef Full Text | Google Scholar

Wang, L., Zhao, N., Sima, L., Meng, F., and Guo, Y. (2018). Pore structure characterization of the tight reservoir: systematic integration of mercury injection and nuclear magnetic resonance. Energy & Fuels 32 (7), 7471–7484. doi:10.1021/acs.energyfuels.8b01369

CrossRef Full Text | Google Scholar

Wang, Q., Wan, J., Mu, L., Shen, R., Jurado, M. J., and Ye, Y. (2020). An analytical solution for transient productivity prediction of multi-fractured horizontal wells in tight gas reservoirs considering nonlinear porous flow mechanisms. Energies 13 (5), 1066. doi:10.3390/en13051066

CrossRef Full Text | Google Scholar

Wang, S., and Chen, S. (2019). Insights to fracture stimulation design in unconventional reservoirs based on machine learning modeling. J. Petroleum Sci. Eng. 174, 682–695. doi:10.1016/j.petrol.2018.11.076

CrossRef Full Text | Google Scholar

Wang, Y., Mao, C., Li, Q., Jin, W., Zhu, S., Wang, X., et al. (2021). Pore throat characteristics of tight reservoirs by a combined mercury method: A case study of the member 2 of xujiahe formation in yingshan gasfield, north sichuan basin. Open Geosci. 13 (1), 1174–1186. doi:10.1515/geo-2020-0273

CrossRef Full Text | Google Scholar

Wang, Z., Li, S., Jin, Z., Li, Z., Liu, Q., and Zhang, K. (2023). Oil and gas pathway to net-zero: review and outlook. Energy Strategy Rev. 45, 101048. doi:10.1016/j.esr.2022.101048

CrossRef Full Text | Google Scholar

Wang, Z., Li, S., and Li, Z. (2022). A novel strategy to reduce carbon emissions of heavy oil thermal recovery: condensation heat transfer performance of flue gas-assisted steam flooding. Appl. Therm. Eng. 205, 118076. doi:10.1016/j.applthermaleng.2022.118076

CrossRef Full Text | Google Scholar

Xu, Y., Sheng, G., Zhao, H., Hui, Y., Zhou, Y., Ma, J., et al. (2021). A new approach for gas-water flow simulation in multi-fractured horizontal wells of shale gas reservoirs. J. Petroleum Sci. Eng. 199, 108292. doi:10.1016/j.petrol.2020.108292

CrossRef Full Text | Google Scholar

Yongshi, W., Yang, G. A. O., and Zhengwei, F. (2021). Pore throat structure and classification of Paleogene tight reservoirs in Jiyang depression, Bohai Bay Basin, China. Petroleum Explor. Dev. 48 (2), 308–322. doi:10.1016/s1876-3804(21)60025-3

CrossRef Full Text | Google Scholar

Zhong, X., Liu, L., Wang, H., Xu, Z., Chen, H., Wang, X., et al. (2022). Characteristics and origins of the modal pore throat structure in weakly cemented sandy conglomerate reservoirs. J. Petroleum Sci. Eng. 208, 109470. doi:10.1016/j.petrol.2021.109470

CrossRef Full Text | Google Scholar