Thermal and entropy behavior of sustainable solar energy in water solar collectors due to non-Newtonian power-law hybrid nanofluids

Introduction: Nanofluids, hybrid nanofluid possesses thermophysical features that boost the fluid performance. This research work is motivated by the utilization of water solar collectors that incorporate non-Newtonian, power-law hybrid nanofluid in a three-dimensional model, considering the two-phase model.

Method: The primary objective of this study is to transform the governing equations of the flow model into a set of ordinary differential equations by employing the three-parameters group technique. Based on the innovative discoveries, two models incorporating new associated functions have been successfully developed for two distinct scenarios characterized by the power-law index, n. The impact of physical factors on the velocity profile, temperature distribution, concentration field, and entropy output of the system is clearly illustrated through a variety of graphs.

Results: The results indicated that the inclination angle of 20° had the best thermal characteristics compared to other inclinations. The entropy generation reached its maximum value at temperature difference of 13 K due to irreversibility of the system, which indicates that the system is more efficient.

Discussion: Furthermore, the increasing percentage in Nusselt number is predicted to be 28.18% when the Prandtl number is taken a range. The Sherwood number enhanced up to 18.61% with a range of Brownian motion. A quantitative comparison is conducted between the present results and the literature in order to validate the superior efficiency of the used method.

1 Introduction

Solar energy is widely considered to be the most feasible solution for meeting the energy requirements of technical and industrial applications through the use of renewable sources. The world energy needs can be satisfied by solar energy that the Earth is exposed to. Solar radiation generates electricity or heat through chemical solar energy. Solar energy is well-recognized for its significant advantages, therefore making it suitable for various applications, including the utilization of solar collectors (SCs). Referring to Prado et al. (2016), a solar collector is a system comprising a heat exchanger, where solar radiation is absorbed and then converted into heat, which then transfers to a base fluid like water (H₂O) (Kalogirou, 2004; Ajeena et al., 2022). The base fluid travels through solar collectors to generate electrical energy for industrial applications. Industrial applications are space heating, refrigeration, and service hot water (Bellos et al., 2016). Solar energy application is classified into two categories: concentrated solar power and photovoltaics. The photovoltaic (PV) system utilizes solar cells to capture and convert solar radiation into electrical energy in a prompt manner (Jamshed et al., 2021a). The primary applications of photovoltaic systems encompass public lighting, such as billboards, highways, and parking lots (Slimene and Arbi Khlifi, 2020). Additionally, PV systems find utility in solar water pumps and the amplification of signals in wireless communication networks (Cano et al., 2021). On the other hand, concentrated solar power (CSP) systems utilize mirrors (reflectors and lenses) to collect Sun’s rays. As a result of this, a liquid substance is heated, causing a heat engine to work. High-power generation and decreases in the energy demand, consumption, and cost are only a few of the ways in which thermal energy storage technologies contribute to the efficiency of CSP systems (Freund et al., 2021).

Several nanoparticles are mixed together in a single fluid to create a hybrid nanofluid. Recently, the study of hybrid nanofluids have been deeply investigated to replace conventional base fluids (Qureshi, 2021; Jamshed et al., 2022a; Imran et al., 2022; Shahzad et al., 2022). A considerable proportion of researchers choose to focus their attention on the examination of heat transmission in hybrid nanofluids. The wide range of applications encompasses gas turbines, thermoplastic coatings, condensation, medical equipment, and computer storage systems (Dawar et al., 2022). Hybrid nanofluids (HNFs) exhibit high thermal conductivity that is helpful in improving the Solar System efficiency and optical properties (Tiwari et al., 2021). In contrast, magnetohydrodynamics (MHD) is an interdisciplinary field that integrates principles from the electromagnetic theory and fluid mechanics. The utilization of magnetohydrodynamics finds its application in diverse technical and industrial sectors, including but not limited to the petrol industry, MHD power generators, nuclear reactors, the control in aerodynamics, and magnetic mixers (Sheikholeslami et al., 2016). The investigation conducted by Imran focused on the analysis of the two-dimensional unsteady hybrid nanofluid around a deformable and horizontally moving porous plate (Imran et al., 2022). Jamshed et al. (2022a) studied unsteady hybrid nanofluids over a parabolic trough solar collector to enhance the activity of a solar aircraft. Dawar et al. (2022) adopted the homotopy analysis method to analyze the flow of the nanofluid for an inclined thin layer which is subjected to incident solar energy. Aljohani et al. (2023) employed a model to elucidate the behavior of an absorption solar collector. Their results led to the fact that an increase in the inclination angle γ resulted in a reduction of the velocity profile. Shahzad et al. (2022) used mathematical techniques to investigate the heat transmission phenomena in a solar-powered ship. Ghasemi and Hatami (2021) analyzed the effect of solar radiative energy on the two-dimensional model of a nanofluid around a sheet. Using a solar collector plate, Farooq et al. (2022) investigated the bioconvection flow performances of viscoelastic nanofluids in three dimensions (3D). Munir et al. (Farooq et al., 2020) presented the entropy generation of the 3D flow of the nanofluid over a moving plate subjected to an induced magnetic field. According to Sajid et al. (2021), solar aircraft wings show better performance in terms of heat production, viscous dissipative flowing, and thermal radiation. Ibrahim and Gizewu (2023) introduced an analysis of entropy generation over a curved stretching surface.

Krishnamurthy et al. (2016) investigated the effects of chemical reaction and radiation on nanofluids through a horizontal stretching sheet. Gireesha et al. concentrated, in his study, on the constant flow of nanofluids over a stretched surface in a two-dimensional setting, considering the influence of a magnetic field (Gireesha et al., 2016a). In another work, Mahanthesh et al. (2017) used the Eyring–Powell fluid to analyze the unsteady flow in a three-dimensional overheated surface in the existence of Joule heating. In their study, Mahanthesh et al. (2016) utilized a model to investigate the characteristics of the MHD nanofluid over a stretching surface, considering the impact of viscous dissipation. Gireesha et al. (2016b) examined the influence of Hall current and the thermal effect on the heat transfer characteristics of a dusty viscous fluid flowing over a permeable stretched sheet. Madhu et al. (2022) employed the finite element method to investigate the thermal analysis of an Eyring–Powell fluid within a microchannel. Khan et al. (2018) employed a two-dimensional model to obtain the entropy generation of the nanofluid flow on a stretching sheet in the existence of the magnetic field. Rehman et al. (2017) examined the MHD nanofluid in the 3D flow between the horizontal plates. Ijaz Khan et al. (2018) defined the entropy generation of the convective nanoliquid flow around a permeable surface. The same authors studied the heat and mass transfer of the Maxwell fluid toward the stretching plate in Khan et al. (2017a). Javed et al. (2018) used the shooting method to analyze the axisymmetric flow of a fluid over a cylinder. Azam et al., 2019) conducted numerical simulations to investigate the characteristics of the unsteady MHD fluid of a nanofluid subjected to thermal radiation. Rashed et al. (2022a) analyzed the axisymmetric forced flow of the $\left({\text{Al}}_2{\mathrm{O}}_3-\text{water}\right)$ nanofluid over a heated cylinder. Ghadikolaei et al. (2018) studied convection in the MHD flow of the Casson nanofluid over an inclined porous sheet. Khan et al. (2015) employed the shooting approach to examine the nanofluid flow in two orthogonal directions across a non-linearly stretched sheet. Rashed et al. (2021) investigated the characteristics of a nanofluid around a vertical plate, taking into account the variability of both the thermal and Brownian diffusion coefficients. Rashed et al. (2020a) scrutinized a mathematical model to analyze the different types of nanofluids over cylindrical solid pipes.

Ghadikolaei et al. (2018) obtained some results concerning the increase in the inclination angle which causes the decrease in the nanofluid velocity and the temperature profile to rise. Jamshed et al. (2021b) stated that when the power-law index $\left(\mathrm{n}\right)$ increases, the velocity of the nanofluid increases, while the temperature distribution decreases. Moreover, the same author proved that the temperature profile was enhanced for higher values of the radiation parameter $\left({\mathrm{R}}_{\mathrm{d}}\right)$. Ghasemi and Hatami (2021) reported that the thermophoresis parameter $\left({\mathrm{N}}_{\mathrm{t}}\right)$ has a tendency to enhance the concentration profile, while the parameter of Brownian motion $\left({\mathrm{N}}_{\mathrm{b}}\right)$ has an opposing effect on it. Imran et al. (2022) stated that entropy production increased with the enhancement of the Brinkmann parameter and Reynolds number for the (ZrO₂–Cu/engine oil) hybrid nanofluid. Qureshi (2021) reached the conclusion that increasing the magnetic field, Brinkman number, and Reynolds number for a nanofluid increases the entropy of the system. Sharma et al. (2023) mentioned that the rate of entropy enhances with the increment of the Prandtl number and diffusive variable. Sahoo and Nandkeolyar (2021) observed from the graphs that there is a significant increase in entropy generation for larger values of the concentration ratio parameter and diffusive variable. Furthermore, a contrary observation can be illustrated against the magnetic parameter and the temperature ratio parameter. The singular manifold approach and Lie infinitesimals, for example, are used to solve evolution equations (Saleh et al., 2021; Rashed et al., 2022b) and fluid dynamic applications (Rashed, 2019; Rashed et al., 2020b; Rashed et al., 2023), respectively.

This interest in a solar collector is because of its several applications, like in a solar power ship, collector storage, aircraft wings, solar furnaces, and thermal power systems (Kalogirou, 2004; Afzal and Aziz, 2016; Jamshed and Aziz, 2018). The non-Newtonian fluid has many applications, like biomedical flows, lubrication, fluid friction, and central cooling and heating systems (Hoyt et al., 1999). Furthermore, the hybrid nanofluid has various practical, technical, and technological uses, including its use in radiator systems, nuclear systems, and the cooling of electronic components (Jamil et al., 2020).The hybrid nanofluid incorporates copper (Cu) and ferro (Fe₃O₄) nanoparticles suspended in a water (H₂O) base fluid. Consequently, this research is more useful for the field of heating water, heat transfer, and thermal energy storage. Based on the aforementioned literature review (Afzal and Aziz, 2016; Jamshed and Aziz, 2018; Jamshed et al., 2021b; Farooq et al., 2022), the present study is focused on investigating the thermal and entropy behavior of a three-dimensional flow of a hybrid nanofluid within a solar collector, specifically under the influence of a magnetic field. The cases of operation are obtained by considering the effect of the power-law index. Therefore, this study could improve industrial production, particularly in a solar energy collector.

The novelty of the present study involves the following:

1) Obtaining two models with new related functions according to the power-law index $\left(n=2\text{\hspace{0.17em}and\hspace{0.17em}}n\ne 2\right)$ to cover different cases of operation.

2) Using a two-phase model of nanoparticle diffusion instead of a conventional single-phase model.

3) Using the data to fine-tune the entropy production parameters, the system’s performance is enhanced.

2 Mathematical formulation

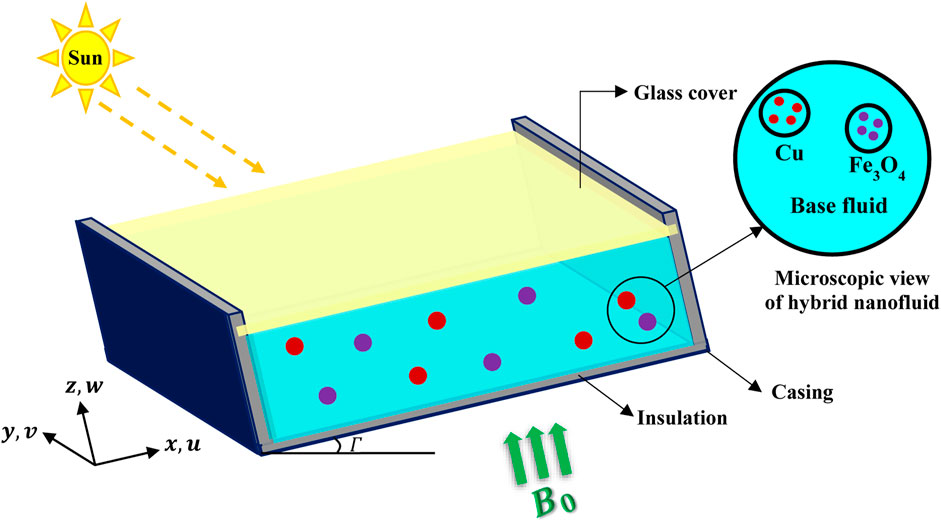
This study focuses on conducting a mathematical analysis of a non-homogeneous hybrid nanofluid within a solar collector. Owing to this study, it is assumed that the laminar boundary layer exhibits three-dimensional characteristics, is in an unstable condition, and possesses non-Newtonian behavior. Moreover, the inclusion of thermophoresis and Brownian motion is considered in order to address the limitations to the single-phase model. In order to optimize flow regulation, an external magnetic field has been implemented in the z-direction. The provided diagram, shown in Figure 1, illustrates the geometric configuration of the model. The mathematical model for the flow can be expressed by the following formula (Bhatti et al., 2016; Sheikholeslami and Ganji, 2016; Sheikholeslami and Rokni, 2017; Ghobadi and Hassankolaei, 2019; Jamshed et al., 2021c; Dawar et al., 2022; Algehyne et al., 2023; Sharma et al., 2023):

$u_x^{\ast }+v_y^{\ast }+w_z=0,(1)$

$u_t^{\ast }+u^{\ast }{u}_x^{\ast }+v^{\ast }{u}_y^{\ast }+w{u}_z^{\ast }-{\nu }_{hnf}{u_{zz}^{\ast }}^{n-1}+\left(\frac{{\sigma }_{hnf}{B}_0^2}{{\rho }_{hnf}}\right)\left(u^{*}-u_{\infty }\right){\mathit{sin}}^2\left(\Gamma \right)=0,(2)$

$v_t^{\ast }+u^{\ast }{v}_x^{\ast }+v^{\ast }{v}_y^{\ast }+w{v}_z^{\ast }-{\nu }_{hnf}{v_{zz}^{\ast }}^{n-1}+\left(\frac{{\sigma }_{hnf}{B}_0^2}{{\rho }_{hnf}}\right)\left(v^{\ast }-v_{\infty }\right){\mathit{sin}}^2\left(\Gamma \right)=0,(3)$

$T_t+u^{\ast }{T}_x+v^{\ast }{T}_y+w{T}_z-\left({\alpha }_{hnf}+\frac{16{\sigma }^{\ast }{T}_{\infty }^3}{3k^{\ast }{\left(\rho c_p\right)}_{hnf}}\right)T_{zz}-\frac{{\mu }_{hnf}}{{\left(\rho c_p\right)}_{hnf}}{w_z}^2=0,(4)$

$C_t^{\ast }+u^{\ast }{C}_x^{\ast }+v^{\ast }{C}_y^{\ast }+w{C}_z^{\ast }=D_B\left(C_{xx}^{\ast }+C_{yy}^{\ast }+C_{zz}^{\ast }\right)+\frac{D_T}{T_{\infty }}\left(T_{xx}+T_{yy}+T_{zz}\right),(5)$

where $\left(u^{*},v^{*},\text{and\hspace{0.17em}}w\right)$ denote the velocity components in the three dimensions, $T^{*}$ stands for the temperature, the concentration of nanoparticles is represented by ${\mathrm{C}}^{*}$, t refers to time, $D_B=\frac{K_{B}T}{3\pi \mu d_p}$ is the Brownian diffusion coefficient, and ${\mathrm{D}}_{\mathrm{T}}=\left(\frac{\mathrm{\mu }}{\mathrm{\rho }}\right)\frac{0.26{\mathrm{k}}_{\text{bf}}}{2{\mathrm{k}}_{\text{bf}}+{\mathrm{k}}_{\text{np}}}{\mathrm{C}}^{*}$ denotes the thermophoresis coefficient. Here, the related boundary conditions become the following (Khan et al., 2015; Khan et al., 2017b; Azam et al., 2019; Imran et al., 2022):

$\begin{array}{c}{u}^{*}\left(x,y,0,t\right)=u_w\left(x,y,t\right),v^{*}\left(x,y,0,t\right)=v_w\left(x,y,t\right),w\left(x,y,0,t\right)=0,\\ T^{*}\left(x,y,0,t\right)=T_w\left(x,y,t\right),{C^{*}\left(x,y,0,t\right)=C_w,u}^{*}\left(x,y,\infty ,t\right)=0,\\ v^{*}\left(x,y,\infty ,t\right)=0{,T}^{*}\left(x,y,\infty ,t\right)=T_{\infty },C^{*}\left(x,y,\infty ,t\right)=C_{\infty }.\end{array}(6)$

FIGURE 1

FIGURE 1. Physical representation of the study.

One of the typical solar collectors is used in this research, and the dimensions are given hereafter in Table 1 (Lakhdar et al., 2019; Dhaundiyal and Gebremicheal, 2022).

TABLE 1

TABLE 1. Dimensions and materials of the water solar collector.

The velocity components and temperature in the normalized form are introduced as follows (Sojoudi et al., 2014):

$u\left(x,y,z,t\right)=\frac{u^{*}\left(x,y,z,t\right)}{u_w\left(x,y,t\right)},v\left(x,y,z,t\right)=\frac{v^{*}\left(x,y,z,t\right)}{v_w\left(x,y,t\right)},(7)$

$\theta =\frac{T^{*}-T_{\infty }}{T_w-T_{\infty }},\hspace{1em}C=\frac{C^{*}-C_{\infty }}{C_w-C_{\infty }}.(8)$

As a result, Eqs 1–5 are rewritten as follows:

$u_x{u}_w+u{\left(u_w\right)}_x+v_y{v}_w+v{\left(v_w\right)}_y+w_z=0,(9)$

$u_t{u}_w+u{\left(u_w\right)}_t+u{u}_w\left(u_x{u}_w+u{\left(u_w\right)}_x\right)+v{v}_w\left(u_y{u}_w+u{\left(u_w\right)}_y\right)+w{u}_z{u}_w-{\nu }_{hnf}{u_{zz}}^{n-1}{u_w}^{n-1}+\left(\frac{{\sigma }_{hnf}{B}_0^2}{{\rho }_{hnf}}\right){\mathit{sin}}^2\left(\Gamma \right){uu}_w=0,(10)$

$v_t{v}_w+v{\left(v_w\right)}_t+u{u}_w\left(v_x{v}_w+v{\left(v_w\right)}_x\right)+v{v}_w\left(v_y{v}_w+v{\left(v_w\right)}_y\right)+w{v}_z{v}_w-{\nu }_{hnf}{v_{zz}}^{n-1}{v_w}^{n-1}+\left(\frac{{\sigma }_{hnf}{B}_0^2}{{\rho }_{hnf}}\right){\mathit{sin}}^2\left(\Gamma \right){vv}_w=0,(11)$

$∆T\left({\theta }_t+u{u}_w{\theta }_x+v{v}_w{\theta }_y+w{\theta }_z\right)-∆T\left({\alpha }_{hnf}+\frac{16{\sigma }^{*}{T}_{\infty }^3}{3k^{*}{\left(\rho c_p\right)}_{hnf}}\right){\theta }_{zz}-\frac{{\mu }_{hnf}}{{\left(\rho c_p\right)}_{hnf}}{w}_z^2=0,(12)$

$∆C\left(C_t+u{u}_w{C}_x+v{v}_w{C}_y+w{C}_z\right)-∆C{D}_B\left(C_{xx}+C_{yy}+C_{zz}\right)-\frac{∆T{D}_T}{T_{\infty }}\left({\theta }_{xx}+{\theta }_{yy}+{\theta }_{zz}\right)=0.(13)$

The related boundary conditions are as follows:

$u\left(x,y,0,t\right)=1,v\left(x,y,0,t\right)=1,w\left(x,y,0,t\right)=0,\theta \left(x,y,0,t\right)=1,C\left(x,y,0,t\right)=1,(14)$

$u\left(x,y,0,t\right)=1,v\left(x,y,\infty ,t\right)=0,\theta \left(x,y,\infty ,t\right)=0,C\left(x,y,\infty ,t\right)=0.(15)$

3 The group transformation method in three parameters

By employing group transformation, we proceed to examine the system of Equations 9–13. Upon a closer examination of the similarities, the governing PDEs undergo a transformation, resulting in a set of ODEs. One of the main benefits of the GTM approach is its ability to efficiently convert systems of PDEs with varying numbers of variables into systems of ODEs.

3.1 Group systematic formulation of the system

The definition of the group containing three parameters is given by the following:

$G:\overline{S}=Q^s\left(a_1,a_2,a_3\right)S+K^s\left(a_1,a_2,a_3\right),(16)$

where the symbol, S, refers to the variables of the system, $Q^s$ and $K^s$ denote the coefficient function to be differentiated, and the three parameters are, $a_1,a_2,$ and $a_3$. The partial derivatives are defined as follows:

$\left.\begin{array}{l}{\overline{S}}_{\overline{i}}=\left(\frac{Q^s}{Q^i}\right)S_i\\ {\overline{S}}_{\overline{i}\overline{j}}=\left(\frac{Q^s}{Q^i{Q}^j}\right)S_{ij}\end{array}\right\}i=x,y,zandj=x,y,z.(17)$

3.2 Invariance analysis of the system

The transformation of Equation 9,

${\overline{u}}_{\overline{x}}\overline{u_w}+\overline{u}{\left(\overline{u_w}\right)}_{\overline{x}}+{\overline{v}}_{\overline{y}}\overline{v_w}+\overline{v}{\left(\overline{v_w}\right)}_{\overline{y}}+{\overline{w}}_z=H_1\left(a_1,a_2,a_3\right)\left[u_x{u}_w+u{\left(u_w\right)}_x+v_y{v}_w+v{\left(v_w\right)}_y+w_z\right],(18)$

takes the form of equivalence, where $H_1\left(a_1,a_2,a_3\right)$ is an equivalence parameter.

Substituting (16) and (17) into (18) leads to the following:

$\begin{array}{c}\frac{Q^u}{Q^x}\left(Q^{u_w}{u}_w+K^{u_w}\right)u_x+\left(Q^{u}u+K^u\right)\frac{Q^{u_w}}{Q^x}{\left(u_w\right)}_x+\frac{Q^v}{Q^y}\left(Q^{v_w}{v}_w+K^{v_w}\right)v_y+\left(Q^{v}v+K^v\right)\frac{Q^{v_w}}{Q^y}{\left(v_w\right)}_y\hfill \\ +\frac{Q^w}{Q^z}{w}_z=H_1\left(a_1,a_2,a_3\right)\left[u_x{u}_w+u{\left(u_w\right)}_x+v_y{v}_w+v{\left(v_w\right)}_y+w_z\right],\hfill \end{array}(19)$

which is simplified as follows:

$\frac{Q^u{Q}^{u_w}}{Q^x}{u}_w{u}_x+\frac{Q^u{Q}^{u_w}}{Q^x}u{\left(u_w\right)}_x+\frac{Q^{v_w}{Q}^v}{Q^y}{v}_w{v}_y+\frac{Q^v{Q}^{v_w}}{Q^y}v{\left(v_w\right)}_y+\frac{Q^w}{Q^z}{w}_z+R_1\left(a_1,a_2,a_3\right)=H_1\left(a_1,a_2,a_3\right)\left[u_x{u}_w+u{\left(u_w\right)}_x+v_y{v}_w+v{\left(v_w\right)}_y+w_z\right].(20)$

The invariance of (9) reveals that $R_1\left(a_1,a_2,a_3\right)=0$ implies the following:

$K^{u_w}=K^u=K^{v_w}=K^v=0.(21)$

Similarly, Eq. 10 can be transformed into the following:

$\begin{array}{c}{\overline{u}}_{\overline{t}}\overline{u_w}+\overline{u}{\left(\overline{u_w}\right)}_{\overline{t}}+\overline{u}\overline{u_w}({\overline{u}}_{\overline{x}}\overline{u_w}+\overline{u}{\left(\overline{u_w}\right)}_{\overline{x}})+\overline{v}\overline{v_w}({\overline{u}}_{\overline{y}}\overline{u_w}+\overline{u}{\left(\overline{u_w}\right)}_{\overline{y}})\hfill \\ +\overline{w}{\overline{u}}_{\overline{z}}\overline{u_w}-{\nu }_{hnf}{\left({\overline{u}}_{\overline{z}\overline{z}}\overline{u_w}\right)}^{n-1}+\left(\frac{{\sigma }_{hnf}{B}_0^2}{{\rho }_{hnf}}\right){\mathit{sin}}^2\left(\Gamma \right)\overline{u}\overline{u_w}=H_2\left(a_1,a_2,a_3\right)\hfill \\ \left[u_t{u}_w+u{\left(u_w\right)}_t+u{u}_w\left(u_x{u}_w+u{\left(u_w\right)}_x\right)+v{v}_w\left(u_y{u}_w+u{\left(u_w\right)}_y\right)+w{u}_z{u}_w-{\nu }_{hnf}{u_{zz}}^{n-1}{u_w}^{n-1}+\left(\frac{{\sigma }_{hnf}{B}_0^2}{{\rho }_{hnf}}\right){\mathit{sin}}^2\left(\Gamma \right){uu}_w\right],\hfill \end{array}(22)$

Substituting (16) and (17) into (22) reveals the following:

$\begin{array}{c}\frac{Q^u}{Q^t}\left(Q^{u_w}{u}_w+K^{u_w}\right)u_t+\frac{Q^{u_w}}{Q^t}\left(Q^{u}u+K^u\right){\left(u_w\right)}_t+\left(Q^{u}u+K^u\right){\left(Q^{u_w}{u}_w+K^{u_w}\right)}^2\frac{Q^u}{Q^x}{u}_x+{\left(Q^{u}u+K^u\right)}^2\left(Q^{u_w}{u}_w+K^{u_w}\right)\hfill \\ \frac{Q^{u_w}}{Q^x}{\left(u_w\right)}_x+\left(Q^{v}v+K^v\right)\left(Q^{v_w}{v}_w+K^{v_w}\right)\left(Q^{u_w}{u}_w+K^{u_w}\right)\frac{Q^u}{Q^y}{u}_y+\left(Q^{v}v+K^v\right)\left(Q^{v_w}{v}_w+K^{v_w}\right)\left(Q^{u}u+K^u\right)\hfill \\ \frac{Q^{u_w}}{Q^y}{\left(u_w\right)}_y+\left(Q^{w}w+K^w\right)\left(Q^{u_w}{u}_w+K^{u_w}\right)\frac{Q^u}{Q^z}{u}_z{-\nu }_{hnf}{\left(\frac{Q^u}{{\left(Q^z\right)}^2}{u}_{zz}\left(Q^{u_w}{u}_w+K^{u_w}\right)\right)}^{n-1}\hfill \\ +\left(\frac{{\sigma }_{hnf}{B}_0^2}{{\rho }_{hnf}}\right){\mathit{sin}}^2\left(\Gamma \right)\left(Q^{u}u+K^u\right)\left(Q^{u_w}{u}_w+K^{u_w}\right)=H_2\left(a_1,a_2,a_3\right)\hfill \\ [u_t{u}_w+u{\left(u_w\right)}_t+u{u}_w\left(u_x{u}_w+u{\left(u_w\right)}_x\right)+v{v}_w\left(u_y{u}_w+u{\left(u_w\right)}_y\right)+w{u}_z{u}_w-{\nu }_{hnf}{u_{zz}}^{n-1}{u_w}^{n-1}+\left(\frac{{\sigma }_{hnf}{B}_0^2}{{\rho }_{hnf}}\right){\mathit{sin}}^2\left(\Gamma \right){uu}_w],\hfill \end{array}(23)$

Simplifying Eq. 23 implies the following:

$\begin{array}{c}\frac{Q^u{Q}^{u_w}}{Q^t}{u}_w{u}_t+\frac{Q^u{Q}^{u_w}}{Q^t}u{\left(u_w\right)}_t+\frac{{\left(Q^u\right)}^2{\left(Q^{u_w}\right)}^2}{Q^x}u{u_w}^2{u}_x+\frac{{\left(Q^{u_w}\right)}^2{\left(Q^u\right)}^2}{Q^x}{u}^2{u}_w{\left(u_w\right)}_x+\frac{Q^v{Q}^{v_w}{Q}^{u_w}{Q}^u}{Q^y}v{v}_w{u}_w{u}_y+\frac{Q^v{Q}^{v_w}{Q}^{u_w}{Q}^u}{Q^y}v{v}_{w}u{\left(u_w\right)}_y\hfill \\ +\frac{Q^{u_w}{Q}^w{Q}^u}{Q^z}w{u}_w{u}_z{-\nu }_{hnf}{\left(\frac{Q^u{Q}^{u_w}}{{\left(Q^z\right)}^2}{u}_{zz}{u}_w\right)}^{n-1}+\left(\frac{{\sigma }_{hnf}{B}_0^2}{{\rho }_{hnf}}\right){\mathit{sin}}^2\left(\Gamma \right)Q^u{Q}^{u_w}u{u}_w+R_2\left(a_1,a_2,a_3\right)=H_2\left(a_1,a_2,a_3\right)\hfill \\ [u_t{u}_w+u{\left(u_w\right)}_t+u{u}_w\left(u_x{u}_w+u{\left(u_w\right)}_x\right)+v{v}_w\left(u_y{u}_w+u{\left(u_w\right)}_y\right)+w{u}_z{u}_w-{\nu }_{hnf}{u_{zz}}^{n-1}{u_w}^{n-1}+\left(\frac{{\sigma }_{hnf}{B}_0^2}{{\rho }_{hnf}}\right){\mathit{sin}}^2\left(\Gamma \right){uu}_w],\hfill \end{array}(24)$

The invariance of Eq. 10 reveals that $R_2\left(a_1,a_2,{anda}_3\right),$ which ensures that

$k^w=0.(25)$

Similarly, Eqs 11–13 can be transformed into the following:

$\begin{array}{c}\frac{Q^v{Q}^{v_w}}{Q^t}{v}_w{v}_t+\frac{Q^v{Q}^{v_w}}{Q^t}v{\left(v_w\right)}_t+\frac{Q^{u_w}{Q}^u{Q}^v{Q}^{v_w}}{Q^x}u{u}_w{v}_x{v}_w+\frac{Q^{u_w}{Q}^u{Q}^v{Q}^{v_w}}{Q^x}u{u}_{w}v{\left(v_w\right)}_x+\frac{{\left(Q^{v_w}\right)}^2{\left(Q^v\right)}^2}{Q^y}v{v}_w^2{v}_y+\frac{{\left(Q^{v_w}\right)}^2{\left(Q^v\right)}^2}{Q^y}{v}^2{v}_w{\left(v_w\right)}_y\hfill \\ +\frac{Q^{v_w}{Q}^w{Q}^v}{Q^z}w{v}_w{v}_z-{-\nu }_{hnf}{\left(\frac{Q^v{Q}^{v_w}}{{\left(Q^z\right)}^2}{v}_{zz}{v}_w\right)}^{n-1}+\left(\frac{{\sigma }_{hnf}{B}_0^2}{{\rho }_{hnf}}\right){\mathit{sin}}^2\left(\mathrm{\Gamma }\right)Q^v{Q}^{v_w}v{v}_w+R_3\left(a_1,a_2,a_3\right)=H_3\left(a_1,a_2,a_3\right)\hfill \\ [v_t{v}_w+v{\left(v_w\right)}_t+u{u}_w\left(v_x{v}_w+v{\left(v_w\right)}_x\right)+v{v}_w\left(v_y{v}_w+v{\left(v_w\right)}_y\right)+w{v}_z{v}_w-{\nu }_{hnf}{v_{zz}}^{n-1}{v_w}^{n-1}+\left(\frac{{\sigma }_{hnf}{B}_0^2}{{\rho }_{hnf}}\right){\mathit{sin}}^2\left(\mathrm{\Gamma }\right){vv}_w],\hfill \end{array}(26)$

$\begin{array}{c}∆T\left(\frac{Q^{\theta }}{Q^t}{\theta }_t+\frac{Q^{\theta }{Q}^u{Q}^{u_w}}{Q^x}u{u}_w{\theta }_x+\frac{Q^{\theta }{Q}^v{Q}^{v_w}}{Q^y}v{v}_w{\theta }_y+\frac{Q^{\theta }{Q}^w}{Q^z}w{\theta }_z\right)\hfill \\ -{\left({\alpha }_{hnf}+\frac{16{\sigma }^{*}{T}_{\infty }^3}{3k^{*}{\left(\rho c_p\right)}_{hnf}}\right)∆T\frac{Q^{\theta }}{{\left(Q^z\right)}^2}\theta }_{zz}-\frac{{\mu }_{hnf}}{{\left(\rho c_p\right)}_{hnf}}\frac{Q^w}{{\left(Q^z\right)}^2}{w}_z^2+R_4\left(a_1,a_2,a_3\right)=H_4\left(a_1,a_2,a_3\right)\hfill \\ [∆T\left({\theta }_t+u{u}_w{\theta }_x+v{v}_w{\theta }_y+w{\theta }_z\right)-\left({\alpha }_{hnf}+\frac{16{\sigma }^{*}{T}_{\infty }^3}{3k^{*}{\left(\rho c_p\right)}_{hnf}}\right)∆T{\theta }_{zz}-\frac{{\mu }_{hnf}}{{\left(\rho c_p\right)}_{hnf}}{w}_z^2].\hfill \end{array}(27)$

$\begin{array}{c}∆C\left(\frac{Q^C}{Q^t}{C}_t+\frac{Q^C{Q}^u{Q}^{u_w}}{Q^x}u{u}_w{C}_x+\frac{Q^C{Q}^v{Q}^{v_w}}{Q^y}v{v}_w{C}_y+\frac{Q^C{Q}^w}{Q^z}w{C}_z\right)-D_B∆C\left({\frac{Q^C}{{\left(Q^x\right)}^2}C}_{xx}+{\frac{Q^C}{{\left(Q^y\right)}^2}C}_{yy}+{\frac{Q^C}{{\left(Q^z\right)}^2}C}_{zz}\right)\hfill \\ -\frac{D_T∆T}{T_{\infty }}\left({\frac{Q^{\theta }}{{\left(Q^x\right)}^2}\theta }_{xx}+{\frac{Q^{\theta }}{{\left(Q^y\right)}^2}\theta }_{yy}+{\frac{Q^{\theta }}{{\left(Q^z\right)}^2}\theta }_{zz}\right)+R_5\left(a_1,a_2,a_3\right)=H_5\left(a_1,a_2,a_3\right)\hfill \\ [∆C\left(C_t+u{u}_w{C}_x+v{v}_w{C}_y+w{C}_z\right)-∆C{D}_B\left(C_{xx}+C_{yy}+C_{zz}\right)-\frac{∆T{D}_T}{T_{\infty }}\left({\theta }_{xx}+{\theta }_{yy}+{\theta }_{zz}\right)].\hfill \end{array}(28)$

The invariance of Eqs 11–13 implies the following:

$Q^x=Q^y=\frac{{\left(Q^z\right)}^{2n-2}}{{\left(Q^{u_w}\right)}^{n-3}},\hspace{1em}{Q}^t=\frac{{\left(Q^z\right)}^{2n-2}}{{\left(Q^{u_w}\right)}^{n-2}},(29)$

$Q^w=\frac{{\left(Q^{u_w}\right)}^{n-2}}{{\left(Q^z\right)}^{2n-3}},\hspace{1em}{Q}^{\theta }=Q^C=\frac{{\left({\mathrm{Q}}^{{\mathrm{u}}_{\mathrm{w}}}\right)}^{2\mathrm{n}-4}}{{\left({\mathrm{Q}}^{\mathrm{z}}\right)}^{4\mathrm{n}-6}}.(30)$

The invariance of boundary conditions shows the following:

$K^z=K^{\theta }=K^t=0\text{\hspace{0.17em}and\hspace{0.17em}}{Q}^u=Q^v=1.(31)$

At the end of this analysis, the group of invariant transformations of systems (9)–(13) can be introduced in the following form:

$G:\left\{\begin{array}{c}{\mathrm{S}}^1\left\{\begin{array}{c}\begin{array}{c}\overline{x}=\frac{{\left(Q^z\right)}^{2n-2}}{{\left(Q^{u_w}\right)}^{n-3}}x+K^x\\ \overline{y}=\frac{{\left(Q^z\right)}^{2n-2}}{{\left(Q^{u_w}\right)}^{n-3}}x+K^y\\ \overline{z}=Q^{z}z\end{array}\\ \overline{t}=\frac{{\left(Q^z\right)}^{2n-2}}{{\left(Q^{u_w}\right)}^{n-2}}t\end{array}\right.\\ {\mathrm{S}}^2\left\{\begin{array}{c}\overline{u}=u\\ \overline{v}=v\\ \overline{w}=\frac{{\left(Q^{u_w}\right)}^{n-2}}{{\left(Q^z\right)}^{2n-3}}w\\ \overline{\theta }=\frac{{\left({\mathrm{Q}}^{{\mathrm{u}}_{\mathrm{w}}}\right)}^{2\mathrm{n}-4}}{{\left({\mathrm{Q}}^{\mathrm{z}}\right)}^{4\mathrm{n}-6}}\theta \\ \overline{C}=\frac{{\left({\mathrm{Q}}^{{\mathrm{u}}_{\mathrm{w}}}\right)}^{2\mathrm{n}-4}}{{\left({\mathrm{Q}}^{\mathrm{z}}\right)}^{4\mathrm{n}-6}}C\\ {\overline{u}}_w=u_w\\ {\overline{v}}_w=v_w\end{array}\right.\end{array}\right.(32)$

where ${\mathrm{S}}^1$ and ${\mathrm{S}}^2$ denote the group structures for independent and dependent variables.

3.3 The complete set of the invariant system

In this section, ODEs are derived from the governing equation by applying the Morgan theorem. Extending Morgan’s theorem (Moran and Gaggioli, 1969) results in achieving the invariant transformations of the system variables $x,y,z,t;u,v,w,\theta ,C,u_w,$ and $v_w$ for the three-parameter group that is listed as follows:

${\displaystyle \sum _{i=1}^{12}}\left({\beta }_i{s}_i+{\beta }_{i+1}\right)\frac{\partial {\overline{q}}_i}{\partial s_i}=0,(33)$

${\displaystyle \sum _{i=1}^{12}}\left({\gamma }_i{s}_i+{\gamma }_{i+1}\right)\frac{\partial {\overline{q}}_i}{\partial s_i}=0,(34)$

${\displaystyle \sum _{i=1}^{12}}\left({{\delta }_{i}s}_i+{\delta }_{i+1}\right)\frac{\partial {\overline{q}}_i}{\partial s_i}=0,(35)$

where $s_i$ refers to the initial system variables $\left(x,y,z,t;u,v,w,\theta ,C,u_{w,}\text{\hspace{0.17em}and\hspace{0.17em}}{v}_w\right)$ and $q_i$ refers to the group of transformed variables. The variables ${\beta }_i,{\gamma }_i,\text{and\hspace{0.17em}}{\delta }_i$ are defined by the following relations:

$\left\{\begin{array}{c}{\beta }_i=\frac{\partial Q^{S_i}\left(a_1,a_2,a_3\right)}{\partial a_1},\hspace{1em}{\beta }_{i+1}=\frac{\partial K^{S_i}\left(a_1,a_2,a_3\right)}{\partial a_1},\\ {\gamma }_i=\frac{\partial Q^{S_i}\left(a_1,a_2,a_3\right)}{\partial a_2},\hspace{1em}{\gamma }_{i+1}=\frac{\partial K^{S_i}\left(a_1,a_2,a_3\right)}{\partial a_2},\\ {\delta }_i=\frac{\partial Q^{S_i}\left(a_1,a_2,a_3\right)}{\partial a_3},\hspace{1em}{\delta }_{i+1}=\frac{\partial K^{S_i}\left(a_1,a_2,a_3\right)}{\partial a_3}.\end{array}\right.(36)$

3.3.1. Invariant transformation of the independent variables: x, y, z, and t

The transformation of the independent variables $\left(x,y,z,\text{and\hspace{0.17em}}t\right)$ to a single similarity variable can be achieved by applying Equations 33–35:

$\eta \left(x,y,z,t\right)=z\epsilon \left(x,y,t\right),(37)$

where $\epsilon \left(x,y,t\right)$ will be defined later. The transformation of the dependent variables helps in obtaining the following similarity variables:

$\left\{\begin{array}{c}u=U\left(x,y,t\right)E\left(\eta \right)\\ v=V\left(x,y,t\right)F\left(\eta \right)\\ w=W\left(\eta \right)\\ \theta =\xi \left(x,y,t\right)\mathrm{\Theta }\left(\eta \right)\\ C=\pi \left(x,y,t\right)\varphi \left(\eta \right)\\ u_w=u_w\left(x,y,t\right)\\ v_w=v_w\left(x,y,t\right).\end{array}\right.(38)$

By employing the aforementioned transformations, the system of Eqs. 9–13 can be simplified to the subsequent system:

$\epsilon w^{\prime }+\left({U_{x}u}_w+U{\left(u_w\right)}_x\right)E+u_{w}U{\epsilon }_{x}z{E}^{\prime }+\left(V{\left(v_w\right)}_y+v_w{V}_y\right)F+{Vv}_{w}z{\epsilon }_y{F}^{\prime }=0,(39)$

$\begin{array}{c}-{{\nu }_{hnf}{\epsilon }^{2n-2}\left(E^{″}\right)}^{n-1}+\left(\frac{{\left(u_w\right)}_t}{U^{n-2}{u_w}^{n-1}}+\frac{U_t}{U^{n-1}{u_w}^{n-2}}\right)E+\left(\frac{{z\epsilon }_t}{U^{n-2}{u_w}^{n-2}}\right)E^{\prime }+\left(\frac{{\left(u_w\right)}_x}{U^{n-3}{u_w}^{n-2}}+\frac{U_x}{U^{n-2}{u_w}^{n-3}}\right)E^2+\frac{z{\epsilon }_x}{U^{n-3}{u_w}^{n-3}}E{E}^{\prime }\hfill \\ +\left(\frac{V{v}_w{\left(u_w\right)}_y}{U^{n-2}{u_w}^{n-1}}+\frac{V{v}_w{U}_y}{U^{n-1}{u_w}^{n-2}}\right)EF+\frac{V{v}_{w}z{\epsilon }_y}{U^{n-2}{u_w}^{n-2}}F{E}^{\prime }+\frac{\epsilon }{U^{n-2}{u_w}^{n-2}}W{E}^{\prime }+\frac{1}{U^{n-2}{u_w}^{n-2}}\left(\frac{{\sigma }_{hnf}{B}_0^2}{{\rho }_{hnf}}\right){\mathit{sin}}^2\left(\Gamma \right)E=0,\hfill \end{array}(40)$

$\begin{array}{c}{{-\nu }_{hnf}{\epsilon }^{2n-2}\left(F^{″}\right)}^{n-1}+\left(\frac{{\left(v_w\right)}_t}{V^{n-2}{v_w}^{n-1}}+\frac{V_t}{V^{n-1}{v_w}^{n-2}}\right)F+\frac{{z\epsilon }_t}{V^{n-2}{v_w}^{n-2}}{F}^{\prime }+\left(\frac{{\left(v_w\right)}_y}{V^{n-3}{v_w}^{n-2}}+\frac{V_y}{V^{n-2}{v_w}^{n-3}}\right)F^2+\frac{z{\epsilon }_y}{V^{n-3}{v_w}^{n-3}}F{F}^{\prime }\hfill \\ +\left(\frac{U{u}_w{\left(v_w\right)}_x}{V^{n-2}{v_w}^{n-1}}+\frac{U{u}_w{V}_x}{V^{n-1}{v_w}^{n-2}}\right)FE+\frac{Uuz{\epsilon }_x}{V^{n-2}{v_w}^{n-2}}{EF}^{\prime }+\frac{\epsilon }{V^{n-2}{v_w}^{n-2}}W{F}^{\prime }+\frac{1}{V^{n-2}{v_w}^{n-2}}\left(\frac{{\sigma }_{hnf}{B}_0^2}{{\rho }_{hnf}}\right){\mathit{sin}}^2\left(\mathrm{\Gamma }\right)F=0,\hfill \end{array}(41)$

$\begin{array}{c}-\left({\alpha }_{hnf}+\frac{16{\sigma }^{*}{T}_{\infty }^3}{3k^{*}{\left(\rho c_p\right)}_{hnf}}\right)∆T{\mathrm{\Theta }}^{″}+∆T[\left(\frac{{\xi }_t}{\xi {\epsilon }^2}\right)\mathrm{\Theta }+{\left(\frac{z{\epsilon }_t}{{\epsilon }^2}\right)\mathrm{\Theta }}^{\prime }+\left(\frac{{\xi }_{x}U{u}_w}{\xi {\epsilon }^2}\right)E\mathrm{\Theta }+\left(\frac{{\xi }_{x}zU{u}_w}{{\epsilon }^2}\right)\mathrm{E}{\mathrm{\Theta }}^{\prime }\hfill \\ +\left(\frac{{\xi }_{y}V{v}_w}{\xi {\epsilon }^2}\right)F\mathrm{\Theta }+\left(\frac{{\xi }_{y}zV{v}_w}{{\epsilon }^2}\right)F{\mathrm{\Theta }}^{\prime }+\left(\frac{1}{\epsilon }\right)W{\mathrm{\Theta }}^{\prime }]-\frac{{\mu }_{hnf}}{{\left(\rho c_p\right)}_{hnf}}{\left(\frac{\xi }{\epsilon }\right)W}^{\prime }=0\hfill \end{array}(42)$

$-∆C{\varphi }^{″}+∆C[\left(\frac{{\pi }_t}{{\pi \epsilon }^2}\right)\varphi +\left(\frac{z{\epsilon }_t}{{\epsilon }^2}\right){\varphi }^{\prime }+\left(\frac{{\pi }_{x}U{u}_w}{{\pi \epsilon }^2}\right)E\varphi +\left(\frac{{\epsilon }_{x}zU{u}_w}{{\epsilon }^2}\right)E{\varphi }^{\prime }+\left(\frac{{\pi }_{y}V{v}_w}{{\pi \epsilon }^2}\right)F\varphi +\left(\frac{{\epsilon }_{y}zV{v}_w}{{\epsilon }^2}\right)F{\varphi }^{\prime }+\left(\frac{1}{\epsilon }\right)W{\varphi }^{\prime }]-∆T\frac{D_T}{T_{\infty }{D}_B}\left(\frac{\xi }{\pi }\right){\mathrm{\Theta }}^{″}=0(43)$

The functions $u_w,v_w,U\left(x,y,t\right),V\left(x,y,t\right),\xi \left(x,y,t\right),\pi \left(x,y,t\right),$ and $\eta \left(x,y,z,t\right)$ are precisely calculated to prove that Eqs 39–43 are defined by a similarity to the system of ODEs.

Two cases could be analyzed as follows:

Case-1: $\mathit{n}=\mathbf{2}$

As a result of this, the functions will be as follows:

$\begin{array}{c}{u}_w=ax{,v}_w=by,u=u_{0}E\left(\eta \right),v=v_{0}F\left(\eta \right),\\ \theta =c_1\sqrt{{\nu }_f}\Theta \left(\eta \right),C=c_2\sqrt{{\nu }_f}\varphi \left(\eta \right)and\eta =z\frac{1}{\sqrt{{\nu }_f}},\end{array}(44)$

where a, b, $c_1,$ and $c_2$ denote real-valued constants. Applying the attained results in (44), the systems of (39)–(43) can be written as follows:

$W^{\prime }+\sqrt{{\nu }_f}\left(a{u}_{0}E+{bv}_{0}F\right)=0,(45)$

$E^{″}-\left(\frac{{\epsilon }_2}{{\epsilon }_1}\right)\left({a{u}_{0}E}^2+\left(\frac{{\epsilon }_5}{{\epsilon }_2}\right)M{\mathit{sin}}^2\left(\Gamma \right)E+\frac{1}{\sqrt{{\nu }_f}}W{E}^{\prime }\right)=0,(46)$

$F^{″}-\left(\frac{{\epsilon }_2}{{\epsilon }_1}\right)\left({b{v}_{0}F}^2+\left(\frac{{\epsilon }_5}{{\epsilon }_2}\right)M{\mathit{sin}}^2\left(\Gamma \right)F+\frac{1}{\sqrt{{\nu }_f}}W{F}^{\prime }\right)=0,(47)$

${\mathrm{\Theta }}^{″}-\left(\frac{\mathit{Pr}}{R_d+{\epsilon }_4}\right)\left({\epsilon }_3\sqrt{{\nu }_f}W{\mathrm{\Theta }}^{\prime }-\frac{{\mu }_{hnf}}{{\left.\rho c_p\right)}_{hnf}}\frac{1}{\Delta T{c}_1\sqrt{{\nu }_f}}{W^{\prime }}^2\right)=0,(48)$

${\varphi }^{″}-\frac{Sc}{\sqrt{{\nu }_f}}W{\varphi }^{\prime }+\left(\frac{c_1}{c_2}\right)\frac{N_t}{N_b}{\Theta }^{″}=0.(49)$

Case-2: $\mathit{n}\ne \mathbf{2}$

The functions take the following form:

$\begin{array}{c}{u}_w=\frac{e^{-\left(\frac{n-2}{n}\right)c_{3}x}}{c_3},v_w=\frac{e^{-\left(\frac{n-2}{n}\right)c_{4}y}}{c_4},{U=e}^{+\left(\frac{n-2}{n}\right)c_{3}x},V=e^{+\left(\frac{n-2}{n}\right)c_{4}y}\\ \theta =\left(\frac{c_1}{{\left.{\nu }_f\right)}^{\frac{1}{n}}}\right)\mathrm{\Theta }\left(\eta \right),C=\left(\frac{c_2}{{\left.{\nu }_f\right)}^{\frac{1}{n}}}\right)\varphi \left(\eta \right)and\eta =z{\left({\nu }_f\right)}^{\frac{1}{n}}.\end{array}(50)$

From the obtained results in (50), the systems of (39)–(43) will be as follows:

$W^{\prime }+\left(\frac{n-2}{n}\right)\frac{1}{{\left({\nu }_f\right)}^{\frac{1}{n}}}\left(\left(1-c_3\right)E+\left(1-c_4\right)F\right)=0,(51)$

${\left(E^{″}\right)}^{n-1}-\left(\frac{1}{{\nu }_{hnf}}\right)\left(\frac{c_5}{{\left.{\nu }_f\right)}^{\frac{2n-2}{n}}}\right)\left(\left(\frac{n-2}{n}\right){\left(1-c_3\right)E}^2+\left(\frac{{\epsilon }_5}{{\epsilon }_2}\right)M{\mathit{sin}}^2\left(\Gamma \right)E+{\left({\nu }_f\right)}^{\frac{1}{n}}W{E}^{\prime }\right)=0,(52)$

${\left(F^{″}\right)}^{n-1}-\left(\frac{1}{{\nu }_{hnf}}\right)\left(\frac{c_6}{{\left.{\nu }_f\right)}^{\frac{2n-2}{n}}}\right)\left(\left(\frac{n-2}{n}\right){\left(1-c_4\right)F}^2+\left(\frac{{\epsilon }_5}{{\epsilon }_2}\right)M{\mathit{sin}}^2\left(\Gamma \right)F+{\left({\nu }_f\right)}^{\frac{1}{n}}W{F}^{\prime }\right)=0,(53)$

${\mathrm{\Theta }}^{″}-\left(\frac{\mathit{Pr}}{R_d+{\epsilon }_4}\right)\left(\frac{{\epsilon }_3}{{\left.{\nu }_f\right)}^{\frac{1}{n}-1}}W{\Theta }^{\prime }-\frac{{\mu }_{hnf}}{{\left.\rho c_p\right)}_{hnf}}\frac{{\left.{\nu }_f\right)}^{\frac{1}{n}+1}}{\Delta T{c}_1}{W^{\prime }}^2\right)=0,(54)$

${\varphi }^{″}-\frac{Sc}{{\left.{\nu }_f\right)}^{\frac{1}{n}+1}}W{\varphi }^{\prime }+\left(\frac{c_1}{c_2}\right)\frac{N_t}{N_b}{\Theta }^{″}=0,(55)$

with the related boundary conditions

$\left.\begin{array}{c}E\left(0\right)=1,F\left(0\right)=1,W\left(0\right)=0,\mathrm{\Theta }\left(0\right)=1,\varphi \left(0\right)=1\\ E\left(\infty \right)=0,F\left(\infty \right)=0,\mathrm{\Theta }\left(\infty \right)=0,\varphi \left(\infty \right)=0\end{array}\right\},(56)$

where the aforementioned parameters are the magnetic parameter, M; power-law index, $\mathrm{n};$ radiation parameter, ${\mathrm{R}}_{\mathrm{d}}$; the angle of inclination of the solar cell, $\mathrm{\Gamma }$; Prandtl number, $\mathrm{Pr}$; Brownian motion parameter, ${\mathrm{N}}_{\mathrm{b}}$; Schmidt number, $\text{Sc}$; and thermophoresis parameter, ${\mathrm{N}}_{\mathrm{t}}$, which are given in the following forms (Alaidrous and Eid, 2020; Sadiq, 2021):

$M=\frac{{\sigma }_f{B}_0^2}{{\rho }_f},\mathit{Pr}=\frac{{\nu }_f}{{\alpha }_f},R_d=\frac{16{\sigma }^{*}{T}_{\infty }^3}{3k^{*}{k}_f},Sc=\frac{{\nu }_f}{D_B},N_t=\frac{\tau D_T\Delta T}{{\nu }_f{T}_{\infty }},N_b=\frac{\tau D_B\Delta C}{{\nu }_f}.(57)$

The non-dimensional forms of the physical quantities are the Nusselt number, skin friction, and the Sherwood number, as shown as follows (Jamshed et al., 2021c; Jamshed et al., 2021d):

$\left.\begin{array}{c}{C}_f{Re}^{\frac{1}{2}}=-\left(\frac{{\epsilon }_1}{{\epsilon }_2}\right)E^{\prime }\left(0\right)\\ Nu{Re}^{-\frac{1}{2}}=-{\epsilon }_4\left[1+R_d\right]{\Theta }^{\prime }\left(0\right)\\ Sh{Re}^{-\frac{1}{2}}=-{\varphi }^{\prime }\left(0\right)\end{array}\right\}.(58)$

After that, the following correlations between the nanoparticle concentration in the base fluid and the hybrid nanofluid parameters are presented (Jamshed et al., 2022a):

$\left.\begin{array}{c}{\epsilon }_1=\frac{{\mu }_{hnf}}{{\mu }_f}={\left(1-{\phi }_{n1}\right)}^{-2.5}{\left(1-{\phi }_{n2}\right)}^{-2.5}\\ {\epsilon }_2=\frac{{\rho }_{hnf}}{{\rho }_f}=\left(1-{\phi }_{n2}\right)\left[\left(1-{\phi }_{n1}\right)+{\phi }_{n1}\left(\frac{{\rho }_{n1}}{{\rho }_f}\right)\right]+{\phi }_{n2}\left(\frac{{\rho }_{n2}}{{\rho }_f}\right)\\ {\epsilon }_3=\frac{{\left(\rho c_p\right)}_{hnf}}{{\left(\rho c_p\right)}_f}=\left(1-{\phi }_{n2}\right)\left[\left(1-{\phi }_{n1}\right)+\frac{{\phi }_{n1}{\left(\rho c_p\right)}_{n1}}{{\left(\rho c_p\right)}_{n2}}\right]+{\phi }_{n2}\left(\frac{{\left.\rho c_p\right)}_{n2}}{{\left.\rho c_p\right)}_f}\right)\\ {\epsilon }_4=\frac{k_{hnf}}{k_f}=\left(\frac{k_{n1}+\left(m-1\right)k_{bf}-\left(m-1\right){\phi }_{n1}\left(k_{bf}-k_{n1}\right)}{k_{n1}+\left(m-1\right)k_{bf}+{\phi }_{n1}\left(k_{bf}-k_{n1}\right)}\right)\\ \times \left(\frac{k_{n2}+\left(m-1\right)k_{bf}-\left(m-1\right){\phi }_{n2}\left(k_{bf}-k_{n2}\right)}{k_{n2}+\left(m-1\right)k_{bf}+{\phi }_{n2}\left(k_{bf}-k_{n2}\right)}\right)\\ {\epsilon }_5=\frac{{\sigma }_{hnf}}{{\sigma }_f}=1\\ +\frac{3\phi \left({\phi }_{n1}{\sigma }_{n1}+{\phi }_{n2}{\sigma }_{n2}-{\sigma }_f\left({\phi }_{n1}+{\phi }_{n2}\right)\right)}{{\phi }_{n1}{\sigma }_{n1}+{\phi }_{n2}{\sigma }_{n2}+2\phi {\sigma }_f-\phi {\sigma }_f\left({\phi }_{n1}{\sigma }_{n1}+{\phi }_{n2}{\sigma }_{n2}\right)-{\sigma }_f\left({\phi }_{n1}+{\phi }_{n2}\right)}\end{array}\right\}(59)$

Employing the MATLAB package, the obtained system of ODEs (45)–(49) is solved numerically with the same conditions as in (56). First, let

$y_1=E,y_2=E^{\prime },y_3=F,y_4=F^{\prime },y_5=W,y_6=\Theta ,y_7{=\Theta }^{\prime },y_8=\varphi ,y_9={\varphi }^{\prime }(60)$

Using Eq. 60, we find the following:

$\left.\begin{array}{c}{y}_1^{\prime }=y_2\\ y_2^{\prime }=\left(\frac{{\epsilon }_2}{{\epsilon }_1}\right)\left({a{u}_0{y}_1}^2+\left(\frac{{\epsilon }_5}{{\epsilon }_2}\right)M{\mathit{sin}}^2\left(\Gamma \right)y_1+\frac{1}{\sqrt{{\nu }_f}}{y}_5{y}_2\right)\\ y_3^{\prime }=y_4\\ y_4^{\prime }=\left(\frac{{\epsilon }_2}{{\epsilon }_1}\right)\left({b{v}_0{y}_3}^2+\left(\frac{{\epsilon }_5}{{\epsilon }_2}\right)M{\mathit{sin}}^2\left(\Gamma \right)y_3+\frac{1}{\sqrt{{\nu }_f}}{y}_5{y}_4\right)\\ y_5^{\prime }=\sqrt{{\nu }_f}\left(a{u}_0{y}_1+{bv}_0{y}_3\right)\\ y_6^{\prime }=y_7\\ y_7^{\prime }=\left(\frac{\mathit{Pr}}{R_d+{\epsilon }_4}\right)\left(\frac{{\epsilon }_3}{{\left.{\nu }_f\right)}^{\frac{1}{n}-1}}{y}_5{y}_7-\frac{{\mu }_{hnf}}{{\left.\rho c_p\right)}_{hnf}}\frac{{\left.{\nu }_f\right)}^{\frac{1}{n}+1}}{\Delta T{c}_1}{y_5^{\prime }}^2\right)\\ y_8^{\prime }=y_9\\ y_9^{\prime }=\frac{Sc}{\sqrt{{\nu }_f}}{y}_5{y}_9+\left(\frac{c_1}{c_2}\right)\frac{N_t}{N_b}{y}_7^{\prime }\end{array}\right\}(61)$

with the initial conditions

$\left.\begin{array}{c}{y}_1\left(0\right)=1,y_3\left(0\right)=1,y_5\left(0\right)=0,y_6\left(0\right)=1,y_8\left(0\right)=1\\ y_1\left(\infty \right)\to 0,y_3\left(\infty \right)\to 0,y_6\left(\infty \right)\to 0,y_8\left(\infty \right)\to 0\end{array}\right\}.(62)$

4 Analysis of entropy generation

The entropy outcome of the mathematical model can be characterized as follows (Farooq et al., 2020; Sahoo and Nandkeolyar, 2021):

$E_G=\frac{k_{hnf}}{{T_{\infty }}^2}\left(1+\frac{16{\sigma }^{*}{T}_{\infty }^3}{3k^{*}{\left(\rho c_p\right)}_f}\right){\left(\frac{\partial T^{*}}{\partial z}\right)}^2+\frac{R{D}_B}{C_{\infty }}{\left(\frac{\partial C^{*}}{\partial z}\right)}^2+\frac{{\sigma }_{hnf}{B}_0^2}{T_{\infty }}{\mathit{sin}}^2\left(\Gamma \right)\left[{\left(u^{*}\right)}^2\right]+\frac{{\mu }_{hnf}}{T_{\infty }}\left[{\left(\frac{\partial u^{*}}{\partial z}\right)}^2\right].(63)$

The entropy generation non-dimensional form, $N_G$, is defined as follows (Jamshed et al., 2021a):

$N_G=\frac{E_G}{E_{GO}}=\frac{{T_{\infty }}^2}{{k_f∆T}^2}{E}_{G.}(64)$

Entropy generation in the dimensionless form has been rewritten based on Eqs 63 and 64, as demonstrated in the subsequent expression:

$N_G={\epsilon }_4{c_1}^2\left(1+R_d\right){{\Theta }^{\prime }}^2+{c_2}^{2}L{\left(\frac{{\alpha }_2}{{\alpha }_1}\right)}^2{{\varphi }^{\prime }}^2+M{\mathit{sin}}^2\left(\Gamma \right){\epsilon }_5{\rho }_{f}aRe{E}^2+\left(\frac{{\mu }_{hnf}}{k_f{T}_{\infty }{{\alpha }_1}^2}\right)aRe{E^{\prime }}^2,(65)$

where diffusive variable $L=\frac{R{D}_B{C}_{\infty }}{k_f}$, dimensionless temperature ratio variable ${\alpha }_1=\frac{T_w-T_{\infty }}{T_{\infty }}$, and the dimensionless concentration ratio variable ${\alpha }_2=\frac{C_w-C_{\infty }}{C_{\infty }}$.

5 Results and discussion

Hereafter, the current model of the hybrid nanofluid flow inside water solar collectors is analyzed by using the GTM method. Two different novel models are obtained at two different cases of the power-law index $\left(n=2;n\ne 2\right)$. In the first model, the flow will be Newtonian at $n=2$, whereas in the second model, the flow will be non-Newtonian at $n\ne 2$. The influence of different parameters including $\left(4\le \mathit{Pr}\le 7\right)$, $\left(0.5\le M\le 2\right)$, $\left(2.5\le n\le 4.5\right)$, $\left(20°\le \Gamma \le 90°\right)$, $\left(0.1\le R_d\le 1\right)$, $\left(0.2\le N_t\le 0.8\right)$, and $\left({0.3\le N}_b\le 0.9\right)$ on the hybrid nanofluid characteristics is depicted graphically.

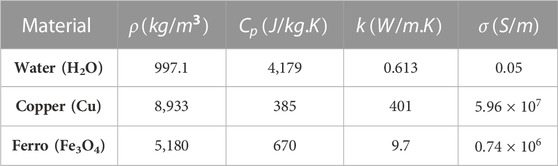
The applications of (Cu) and (Fe₃O₄) effective nanoparticles are demonstrated in solar thermal collectors, nanotechnology, and ferrofluids due to their physicochemical properties, such as high magnetic susceptibility and chemical stability (Jamshed and Aziz, 2018; Nezafat and Nasrollahzadeh, 2021; Nguyen et al., 2021). The properties of the (H₂O) base fluid and (Cu and Fe₃O₄) nanoparticles are shown in Table 2 (Jamshed and Aziz, 2018).

TABLE 2

TABLE 2. Thermophysical properties of H₂O, Cu, and Fe₃O₄.

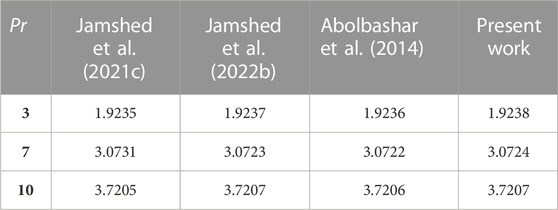
The accuracy of the used method is assessed as shown in Figure 2, which presents a comparison between our results and the results reported by Khan et al. (2015). Validation has been performed in a similar and limiting case as in Khan et al. (2015).These results have been achieved for the 3-D Newtonian flow under the influence of solar radiation, thermophoretic, and Brownian motion. As seen in Figure 2, the impact of the Prandtl number (Pr = 7) on the temperature profile is performed at ${n=2,M=\mathrm{\Gamma }=0,R}_d=1,Sc=1{,N}_t=0.6,$ and $N_b=0.5$. Moreover, the comparative analysis of the Nusselt number is compared to the accepted published data by Abolbashar et al. (2014), Jamshed et al. (2021c), and Jamshed et al. (2022b) in Table 3.

FIGURE 2

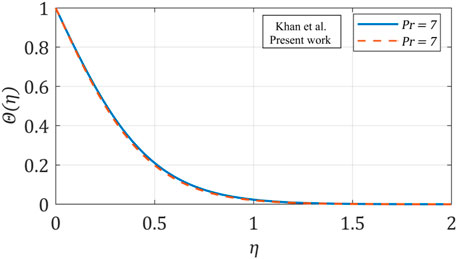
FIGURE 2. Comparison of the temperature profile between the present work with Khan et al. (2015).

TABLE 3

TABLE 3. Comparison of the Nusselt number values with variant $\mathit{Pr}$.

According to results in Figure 2 and Table 3, the current examination agrees with the published results.

Table 4 presents the quantitative values of skin friction, Nusselt number, and the Sherwood number.

TABLE 4

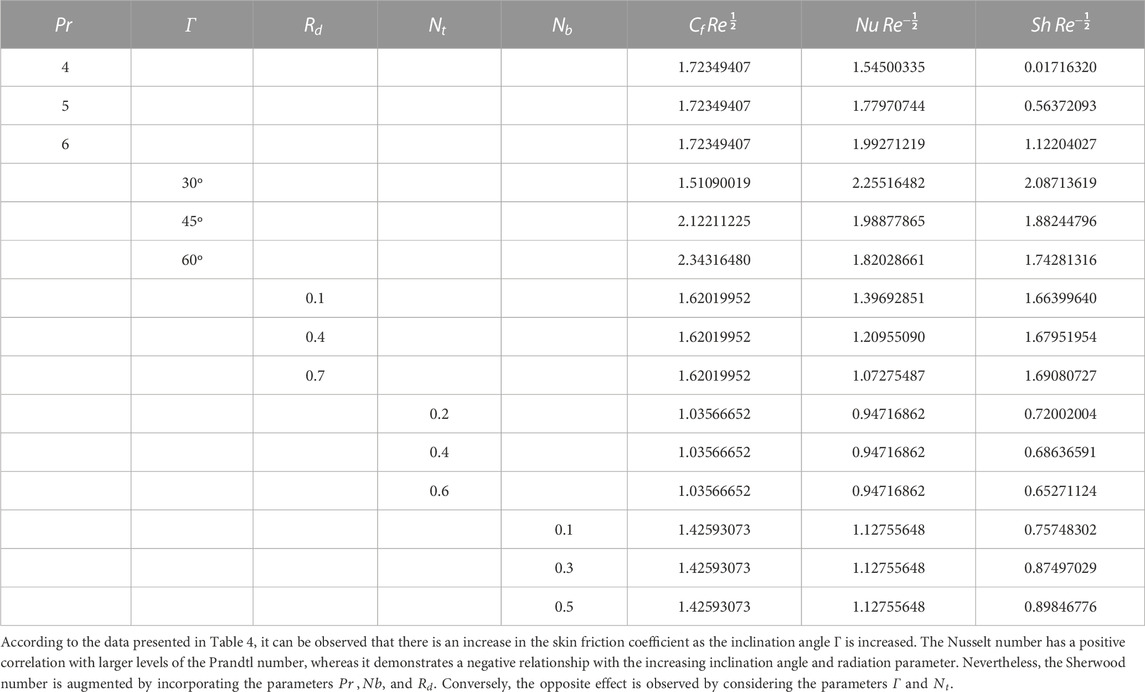
TABLE 4. Numerical values of the skin friction coefficient, Sherwood number, and the Nusselt number for different values of $\mathit{Pr},\mathbf{\Gamma },R_d,N_t,$ and $N_b$.

5.1 Influence of Prandtl number

Figures 3A, B demonstrates the influence of the Prandtl number on the fluid’s characteristics within a range $\left(4\le \mathit{Pr}\le 7\right)$. According to the definition of the Prandtl number, larger values of $\mathit{Pr}$ lead to the increase in the fluid viscosity; as a result of this, the horizontal velocity diminishes, as shown in Figure 3A. The Prandtl number exhibits an inverse relationship with thermal diffusivity, resulting in a decrease in the temperature field, as shown in Figure 3B.

FIGURE 3

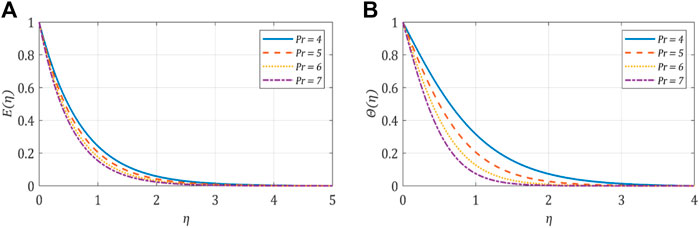
FIGURE 3. (A) Velocity profile against the Prandtl number; (B) temperature profile against the Prandtl number.

5.2 Effect of the magnetic field, M

The variation in fluid characteristics against the magnetic parameter $\left(0.5\le \mathrm{M}\le 2\right)$ is examined in Figures 4A, B. The application of a magnetic field to a fluid results in the generation of a resistive force known as the Lorentz force, which acts to impede the motion of the fluid. Hence, the reduction in the horizontal velocity is observed when the magnetic parameter M increases, as shown in Figure 4A. Based on the definition of the magnetic parameter, raising the magnetic field reduces the density. Consequently, the temperature field slightly increases, as shown in Figure 4B.

FIGURE 4

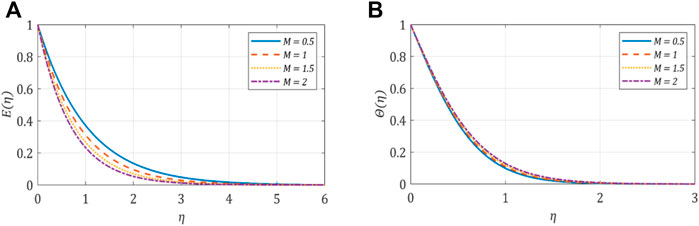
FIGURE 4. (A) Velocity profile against the magnetic parameter; (B) temperature profile against the magnetic parameter.

5.3 Effect of the power-law index, n

The performance of $\left(2.5\le n\le 4\right)$ on the velocity and temperature distribution is explained in Figures 5A, B. As the parameter $n$ increases, the horizontal velocity is raised to a higher value. Based on the findings shown in Figure 5B, there is a negative correlation between the power, n, and the temperature, indicating that an increase in power, n, leads to a drop in the temperature.

FIGURE 5

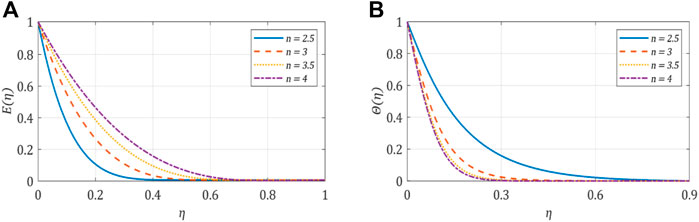
FIGURE 5. (A) Velocity profile against the power-law index; (B) temperature profile against the power-law index.

5.4 Effect of the inclination angle, Γ

The influence of the plate inclination from $20°$ to $90°$, on the fluid characteristics, is shown in Figures 6A–C. Moving away from the horizontal axis reduces the velocity because of the decrease in the gravity effect. The observations indicated a decrement in the velocity due to the increment in $\mathrm{\Gamma },$ as presented in Figure 6A. A reverse phenomenon is shown in Figures 6B, C; the temperature and concentration of nanoparticles increase for a large value of the inclination angle. The inclination affects the value of the net magnetic flux, which, in turn, is the reason for the previous results.

FIGURE 6

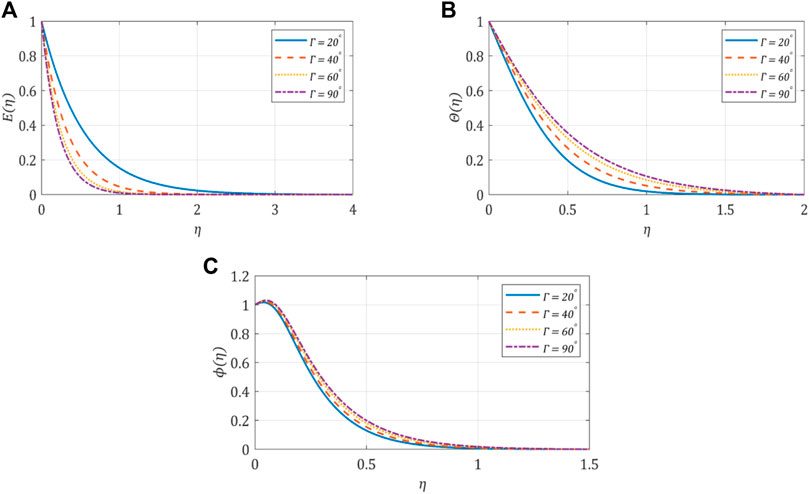
FIGURE 6. (A) Velocity profile against the inclined angle; (B) temperature profile against the inclined angle; (C) concentration profile against the inclined angle.

5.5 Effect of the radiation parameter, R_d

The thermal boundary layer thickness increases as the temperature of the hybrid nanofluid increases. Increasing $R_d$ acquires the system a large amount of heat, subsequently raising the hybrid nanofluid temperature. The temperature demonstrates a positive correlation with the radiation parameter $R_d$, as illustrated in Figure 7A. The inverse relationship is evident in the case of the heat flux and concentration, as illustrated in Figures 7B, C.

FIGURE 7

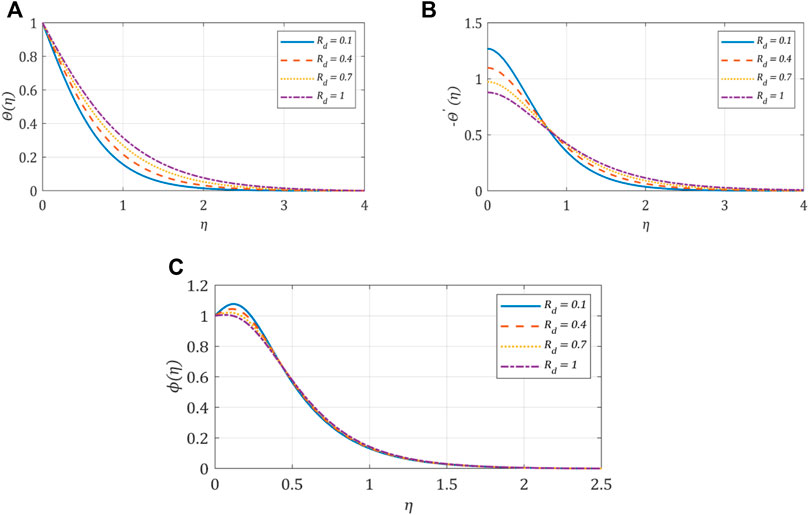
FIGURE 7. (A) Temperature profile against the radiation parameter; (B) heat flux profile against the radiation parameter; (C) concentration profile against the radiation parameter.

5.6 Effect of Brownian motion and the thermophoresis parameter, N_t

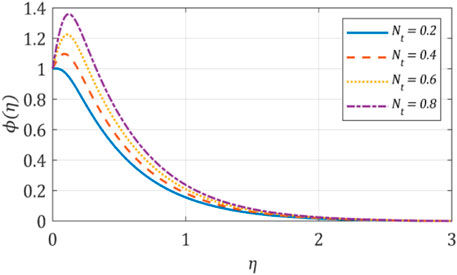
Figures 8, 9 are plotted to examine the effects in the fluid characteristics for a range of Brownian motion $N_b$ and the thermophoresis parameter $N_t$. Moreover, it is illustrated that the Brownian force rises for a larger $N_b$ value. This leads to a decrease in the concentration if $N_b$ increased, as illustrated in Figure 8. When the thermophoresis force rises, the concentration climbs to a peak value far away from the plate surface and then decreases to zero, establishing the boundary condition shown in Figure 9.

FIGURE 8

FIGURE 8. Concentration profile against the Brownian motion parameter.

FIGURE 9

FIGURE 9. Concentration profile against the thermophoresis parameter.

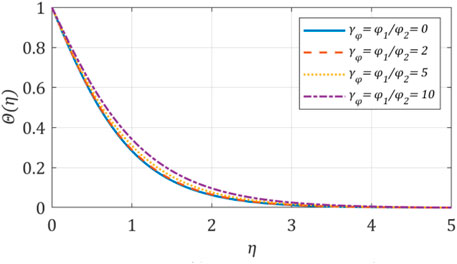
5.7 Effect of the nanoparticle ratio, γ_φ

The hybrid nanofluid contains the blend of two nanoparticles (NPs), including iron oxide $\left({\mathrm{F}\mathrm{e}}_3{\mathrm{O}}_4\right)$ and copper (Cu). The ratio of the volume fraction of magnetite particles to copper is defined as the nanoparticle ratio $\left({\gamma }_{\phi }={\phi }_{{Fe}_3{O}_4}/{\phi }_{cu}\right)$. An increase in the values of ${\gamma }_{\phi }$ leads to the enhancement in the temperature field due to an increase in thermal conductance, as shown in Figure 10. Notably, when ${\gamma }_{\varphi }=0,$ it means that only the nanoparticles of copper are used and the fluid is a mono-nanofluid. As the value of ${\gamma }_{\varphi }$ increases, this means that a hybrid mix of nanoparticles is used with different percentages. The resultant is an improvement in the thermal characteristics.

FIGURE 10

FIGURE 10. Temperature profile against the nanoparticle ratio parameter.

5.8 Effect of the studied parameters on the entropy output, N_G

Entropy generation $N_G$ is influenced by M, which is illustrated through Figure 11A. The large values of M generate more Lorentz force, which retards the fluid motion and decreases entropy generation. Physically, for the large values of the diffusive variable L, the mass diffusivity rises and leads to an increment in entropy generation, as seen in Figure 11B. The decrease in $N_G$ can be observed in Figure 11C as a result of the increase in the temperature ratio parameter ${\alpha }_1$, which is attributed to the presence of irreversible processes. The augmentation of $N_G$ is observed when the concentration ratio parameter is increased, which is attributed to the increase in mass transfer irreversibility, as shown in Figure 11D. The behavior of $N_G$ for various temperature differences $\Delta T$ is plotted in Figure 11E. The reduction of losses from heated components in a Solar System collector, with the purpose of improving the overall performance, is achieved by increasing the temperature differential $\Delta T$. This increase in $\Delta T$ corresponds to a minimum value of $N_G$ due to the irreversible nature of the process.

FIGURE 11

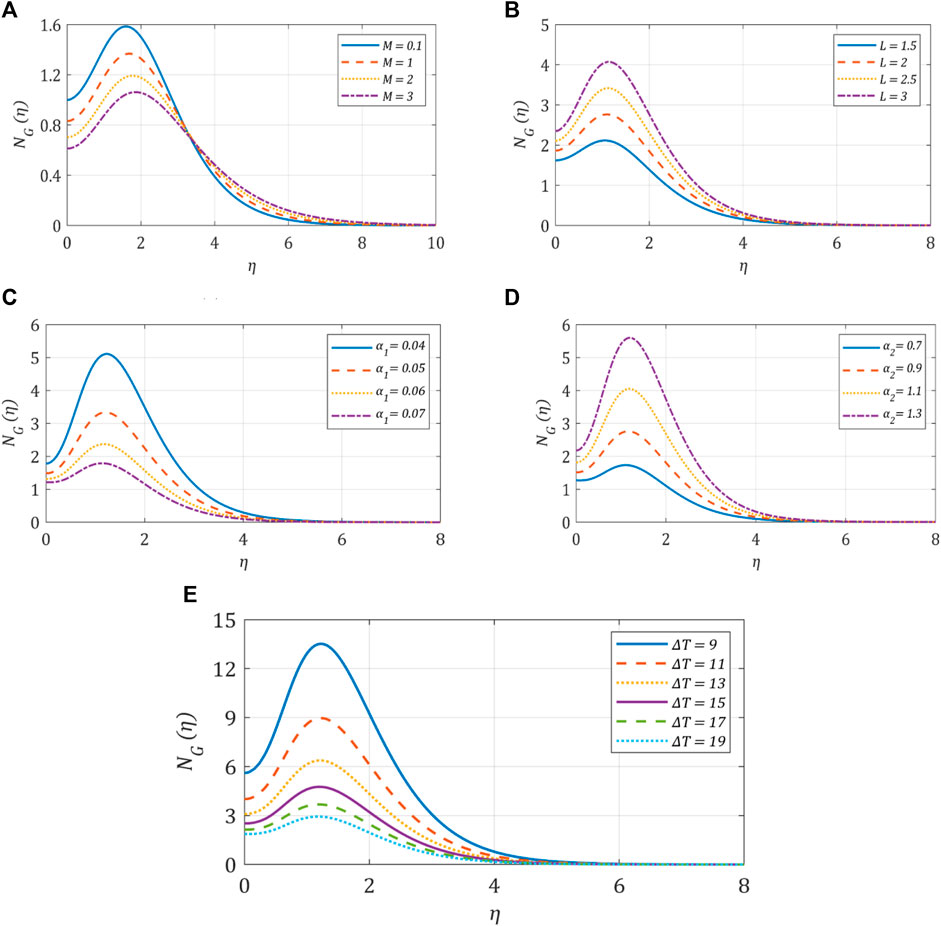
FIGURE 11. Variation in entropy for different studied parameters: (A) entropy against the magnetic parameter; (B) entropy against the diffusive variable; (C) entropy against the temperature ratio; (D) entropy against the concentration ratio; (E) entropy against the temperature difference.

6 Conclusion

In this paper, the GTM method is exploited to analyze the hybrid nanofluid behavior in a solar collector with an unsteady three-dimensional flow. A summary of the obtained results is listed as follows:

• Enhancing the values of the power-law index, n, results in increasing the fluid velocity, which decreases with the Prandtl number $\mathit{Pr}$, magnetic parameter $M,$ and inclination angle $\Gamma$.

• The temperature field exhibits an enhancement when the values of M, $\Gamma$, and the radiation parameter increase. In contrast, the temperature distribution diminishes as $\mathit{Pr}$ and the power-law index increase.

• An increase in the inclination angle and thermophoresis parameter $N_t$ results in the maximization of the concentration profile. Conversely, higher values of the radiation parameter and Brownian motion parameter $N_b$ lead to a decrease in the concentration.

• The increase in entropy generation is directly proportional to the increase in diffusivity length ($L$) and the concentration ratio parameter (${\alpha }_2$). The magnetic parameter ($M$) and the temperature ratio parameter (${\alpha }_1$) have a propensity for diminishing entropy generation ($N_G$), therefore suggesting a greater stability in the efficiency of the system.

• Skin friction reached the percentage of 54.96% when the inclination angle ranges from $30°$ to $60°$. The Prandtl number exhibits a propensity to augment the Nusselt number. In addition, it can be observed that the Sherwood number exhibits a positive correlation with the Prandtl number, Brownian motion parameter, and radiation parameter. Conversely, a negative relationship is shown between the Sherwood number and the thermophoresis parameter and the inclination angle.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abolbashari, M. H., Freidoonimehr, N., Nazari, F., and Rashidi, M. M. (2014). Entropy analysis for an unsteady mhd flow past a stretching permeable surface in nano-fluid. Powder Technol. 267, 256–267. doi:10.1016/j.powtec.2014.07.028

CrossRef Full Text | Google Scholar

Afzal, K., and Aziz, A. (2016). Transport and heat transfer of time dependent mhd slip flow of nanofluids in solar collectors with variable thermal conductivity and thermal radiation. Results Phys. 6, 746–753. doi:10.1016/j.rinp.2016.09.017

CrossRef Full Text | Google Scholar

Ajeena, A. M., Víg, P., and Farkas, I. (2022). A comprehensive analysis of nanofluids and their practical applications for flat plate solar collectors: fundamentals, thermophysical properties, stability, and difficulties. Energy Rep. 8, 4461–4490. doi:10.1016/j.egyr.2022.03.088

CrossRef Full Text | Google Scholar

Alaidrous, A. A., and Eid, M. R. (2020). 3-d electromagnetic radiative non-Newtonian nanofluid flow with joule heating and higher-order reactions in porous materials. Sci. Rep. 10 (1), 14513. doi:10.1038/s41598-020-71543-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Algehyne, E. A., Haq, I., Raizah, Z., Alduais, F. S., Saeed, A., and Galal, A. M. (2023). A passive control strategy of a micropolar hybrid nanofluid flow over a convectively heated flat surface. J. Magnetism Magnetic Mater. 567, 170355. doi:10.1016/j.jmmm.2023.170355

CrossRef Full Text | Google Scholar

Aljohani, A. F., Ebaid, A., Aly, E. H., Pop, I., Abubaker, A. O. M., and Alanazi, D. J. (2023). Explicit solution of a generalized mathematical model for the solar collector/photovoltaic applications using nanoparticles. Alexandria Eng. J. 67, 447–459. doi:10.1016/j.aej.2022.12.044

CrossRef Full Text | Google Scholar

Azam, M., Shakoor, A., Rasool, H. F., and Khan, M. (2019). Numerical simulation for solar energy aspects on unsteady convective flow of mhd cross nanofluid: a revised approach. Int. J. Heat Mass Transf. 131, 495–505. doi:10.1016/j.ijheatmasstransfer.2018.11.022

CrossRef Full Text | Google Scholar

Bellos, E., Tzivanidis, C., Antonopoulos, K. A., and Gkinis, G. (2016). Thermal enhancement of solar parabolic trough collectors by using nanofluids and converging-diverging absorber tube. Renew. Energy 94, 213–222. doi:10.1016/j.renene.2016.03.062

CrossRef Full Text | Google Scholar

Bhatti, M. M., Abbas, T., Rashidi, M. M., and Ali, M. E. (2016). Numerical simulation of entropy generation with thermal radiation on mhd carreau nanofluid towards a shrinking sheet. Entropy 18, 200. doi:10.3390/e18060200

CrossRef Full Text | Google Scholar

Cano, J. M., Martin, A. D., Herrera, R. S., Vazquez, J. R., and Ruiz-Rodriguez, F. J. (2021). Grid-connected pv systems controlled by sliding via wireless communication. Energies 14, 1931. doi:10.3390/en14071931

CrossRef Full Text | Google Scholar

Dawar, A., Wakif, A., Thumma, T., and Shah, N. A. (2022). Towards a new mhd non-homogeneous convective nanofluid flow model for simulating a rotating inclined thin layer of sodium alginate-based iron oxide exposed to incident solar energy. Int. Commun. Heat Mass Transf. 130, 105800. doi:10.1016/j.icheatmasstransfer.2021.105800

CrossRef Full Text | Google Scholar

Dhaundiyal, A., and Gebremicheal, G. H. (2022). The effect of psychrometry on the performance of a solar collector. Environ. Sci. Pollut. Res. 29 (9), 13445–13458. doi:10.1007/s11356-021-16353-5

CrossRef Full Text | Google Scholar

Farooq, U., Munir, S., Malik, F., Ahmad, B., and Lu, D. (2020). Aspects of entropy generation for the non-similar three-dimensional bioconvection flow of nanofluids. AIP Adv. 10. doi:10.1063/1.5142877

CrossRef Full Text | Google Scholar

Farooq, U., Waqas, H., Shah, Z., Kumam, P., and Deebani, W. (2022). On unsteady 3d bio-convection flow of viscoelastic nanofluid with radiative heat transfer inside a solar collector plate. Sci. Rep. 12 (1), 2952. doi:10.1038/s41598-022-06728-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Freund, S., Abarr, M., McTigue, J. D., Frick, K. L., Mathur, A., Reindl, D., et al. (2021). “Chapter 3 - thermal energy storage,” in Thermal, mechanical, and hybrid chemical energy storage systems. Editors K. Brun, T. Allison, and R. Dennis (Academic Press), 65–137.

CrossRef Full Text | Google Scholar

Ghadikolaei, S. S., Hosseinzadeh, K., Ganji, D. D., and Jafari, B. (2018). Nonlinear thermal radiation effect on magneto casson nanofluid flow with joule heating effect over an inclined porous stretching sheet. Case Stud. Therm. Eng. 12, 176–187. doi:10.1016/j.csite.2018.04.009

CrossRef Full Text | Google Scholar

Ghasemi, S. E., and Hatami, M. (2021). Solar radiation effects on mhd stagnation point flow and heat transfer of a nanofluid over a stretching sheet. Case Stud. Therm. Eng. 25, 100898. doi:10.1016/j.csite.2021.100898

CrossRef Full Text | Google Scholar

Ghobadi, A. H., and Hassankolaei, M. G. (2019). Numerical treatment of magneto carreau nanofluid over a stretching sheet considering joule heating impact and nonlinear thermal ray. Heat Transfer—Asian Res. 48 (8), 4133–4151. doi:10.1002/htj.21585

CrossRef Full Text | Google Scholar

Gireesha, B. J., Mahanthesh, B., Gorla, R. S. R., and Manjunatha, P. T. (2016b). Thermal radiation and hall effects on boundary layer flow past a non-isothermal stretching surface embedded in porous medium with non-uniform heat source/sink and fluid-particle suspension. Heat Mass Transf. 52 (4), 897–911. doi:10.1007/s00231-015-1606-3

CrossRef Full Text | Google Scholar

Gireesha, B. J., Mahanthesh, B., Shivakumara, I. S., and Eshwarappa, K. M. (2016a). Melting heat transfer in boundary layer stagnation-point flow of nanofluid toward a stretching sheet with induced magnetic field. Int. J. 19 (1), 313–321. doi:10.1016/j.jestch.2015.07.012

CrossRef Full Text | Google Scholar

Hoyt, J. W., "Some applications of non-Newtonian fluid flow," Rheology series, D. A. Siginer, D. De Kee, and R. P. Chhabra (Editors), vol. 8, Elsevier, 1999, pp. 797–826.

CrossRef Full Text | Google Scholar

Ibrahim, W., and Gizewu, T. (2023). Analysis of entropy generation of bio-convective on curved stretching surface with gyrotactic micro-organisms and third order slip flow. Int. J. Thermofluids 17, 100277. doi:10.1016/j.ijft.2022.100277

CrossRef Full Text | Google Scholar

Ijaz Khan, M., Ullah, S., Hayat, T., Waqas, M., Imran Khan, M., and Alsaedi, A. (2018). Salient aspects of entropy generation optimization in mixed convection nanomaterial flow. Int. J. Heat Mass Transf. 126, 1337–1346. doi:10.1016/j.ijheatmasstransfer.2018.05.168

CrossRef Full Text | Google Scholar

Imran, M., Yasmin, S., Waqas, H., Khan, S. A., Muhammad, T., Alshammari, N., et al. (2022). Computational analysis of nanoparticle shapes on hybrid nanofluid flow due to flat horizontal plate via solar collector. Nanomaterials 12, 663. doi:10.3390/nano12040663

PubMed Abstract | CrossRef Full Text | Google Scholar

Jamil, F., and Ali, H. M. (2020). “Chapter 6 - applications of hybrid nanofluids in different fields,” in Hybrid nanofluids for convection heat transfer. Editor H. M. Ali (Academic Press), 215–254.

CrossRef Full Text | Google Scholar

Jamshed, W., Alanazi, A. K., Suzilliana Putri Mohamed Isa, S., Banerjee, R., Eid, M. R., Sooppy Nisar, K., et al. (2022a). Thermal efficiency enhancement of solar aircraft by utilizing unsteady hybrid nanofluid: a single-phase optimized entropy analysis. Sustain. Energy Technol. Assessments 52, 101898. doi:10.1016/j.seta.2021.101898

CrossRef Full Text | Google Scholar

Jamshed, W., and Aziz, A. (2018). A comparative entropy based analysis of cu and fe3o4/methanol powell-eyring nanofluid in solar thermal collectors subjected to thermal radiation, variable thermal conductivity and impact of different nanoparticles shape. Results Phys. 9, 195–205. doi:10.1016/j.rinp.2018.01.063

CrossRef Full Text | Google Scholar

Jamshed, W., Eid, M. R., Aissa, A., Mourad, A., Nisar, K. S., Shahzad, F., et al. (2021b). Partial velocity slip effect on working magneto non-Newtonian nanofluids flow in solar collectors subject to change viscosity and thermal conductivity with temperature. PLOS ONE 16, e0259881. doi:10.1371/journal.pone.0259881

PubMed Abstract | CrossRef Full Text | Google Scholar

Jamshed, W., Eid, M. R., Al-Hossainy, A. F., Raizah, Z., Tag El Din, E. S. M., and Sajid, T. (2022b). Experimental and tddft materials simulation of thermal characteristics and entropy optimized of williamson cu-methanol and al2o3-methanol nanofluid flowing through solar collector. Sci. Rep. 12 (1), 18130. doi:10.1038/s41598-022-23025-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Jamshed, W., Eid, M. R., Azeany Mohd Nasir, N. A., Nisar, K. S., Aziz, A., Shahzad, F., et al. (2021c). Thermal examination of renewable solar energy in parabolic trough solar collector utilizing maxwell nanofluid: a noble case study. Case Stud. Therm. Eng. 27, 101258. doi:10.1016/j.csite.2021.101258

CrossRef Full Text | Google Scholar

Jamshed, W., Nasir, N. A. A. M., Isa, S. S. P. M., Safdar, R., Shahzad, F., Nisar, K. S., et al. (2021a). Thermal growth in solar water pump using Prandtl–eyring hybrid nanofluid: a solar energy application. Sci. Rep. 11 (1), 18704. doi:10.1038/s41598-021-98103-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Jamshed, W., Şirin, C., Selimefendigil, F., Shamshuddin, M. D., Altowairqi, Y., and Eid, M. R. (2021d). Thermal characterization of coolant maxwell type nanofluid flowing in parabolic trough solar collector (ptsc) used inside solar powered ship application. Coatings 11, 1552. doi:10.3390/coatings11121552

CrossRef Full Text | Google Scholar

Javed, M. F., Khan, M. I., Khan, N. B., Muhammad, R., Rehman, M. U., Khan, S. W., et al. (2018). Axisymmetric flow of casson fluid by a swirling cylinder. Results Phys. 9, 1250–1255. doi:10.1016/j.rinp.2018.04.015

CrossRef Full Text | Google Scholar

Kalogirou, S. A. (2004). Solar thermal collectors and applications. Prog. Energy Combust. Sci. 30 (3), 231–295. doi:10.1016/j.pecs.2004.02.001

CrossRef Full Text | Google Scholar

Khan, J. A., Mustafa, M., Hayat, T., and Alsaedi, A. (2015). Three-dimensional flow of nanofluid over a non-linearly stretching sheet: an application to solar energy. Int. J. Heat Mass Transf. 86, 158–164. doi:10.1016/j.ijheatmasstransfer.2015.02.078

CrossRef Full Text | Google Scholar

Khan, M. I., Khan, T. A., Qayyum, S., Hayat, T., Khan, M. I., and Alsaedi, A. (2018). Entropy generation optimization and activation energy in nonlinear mixed convection flow of a tangent hyperbolic nanofluid. Eur. Phys. J. Plus 133 (8), 329. doi:10.1140/epjp/i2018-12093-y

CrossRef Full Text | Google Scholar

Khan, M. I., Waqas, M., Hayat, T., Khan, M. I., and Alsaedi, A. (2017a). Chemically reactive flow of upper-convected maxwell fluid with cattaneo–christov heat flux model. J. Braz. Soc. Mech. Sci. Eng. 39 (11), 4571–4578. doi:10.1007/s40430-017-0915-5

CrossRef Full Text | Google Scholar

Khan, M., Malik, M. Y., and Salahuddin, T. (2017b). Heat generation and solar radiation effects on carreau nanofluid over a stretching sheet with variable thickness: using coefficients improved by cash and carp. Results Phys. 7, 2512–2519. doi:10.1016/j.rinp.2017.06.048

CrossRef Full Text | Google Scholar

Krishnamurthy, M. R., Prasannakumara, B. C., Gireesha, B. J., and Gorla, R. S. R. (2016). Effect of chemical reaction on MHD boundary layer flow and melting heat transfer of Williamson nanofluid in porous medium. Int. J. 19 (1), 53–61. doi:10.1016/j.jestch.2015.06.010

CrossRef Full Text | Google Scholar

Lakhdar, B., Azzouz, S., Mahfoud, B., and Mohamed, D. (2019). Exergetic analysis and optimization of a flat plate solar collector. J. Biodivers. Environ. Sci. 14, 1–12.

Google Scholar

Madhu, M., Shashikumar, N. S., Gireesha, B. J., and Kishan, N. (2022). Thermal analysis of mhd powell–eyring fluid flow through a vertical microchannel. Int. J. Ambient Energy 43 (1), 4454–4462. doi:10.1080/01430750.2021.1910566

CrossRef Full Text | Google Scholar

Mahanthesh, B., Gireesha, B. J., Gorla, R. S. R., Abbasi, F. M., and Shehzad, S. A. (2016). Numerical solutions for magnetohydrodynamic flow of nanofluid over a bidirectional non-linear stretching surface with prescribed surface heat flux boundary. J. Magnetism Magnetic Mater. 417, 189–196. doi:10.1016/j.jmmm.2016.05.051

CrossRef Full Text | Google Scholar

Mahanthesh, B., Gireesha, B. J., and Gorla, R. S. R. (2017). Unsteady three-dimensional mhd flow of a nano eyring-powell fluid past a convectively heated stretching sheet in the presence of thermal radiation, viscous dissipation and joule heating. J. Assoc. Arab Univ. Basic Appl. Sci. 23, 75–84. doi:10.1016/j.jaubas.2016.05.004

CrossRef Full Text | Google Scholar

Moran, M. J., and Gaggioli, R. A. (1969). A new systematic formalism for similarity analysis. J. Eng. Math. 3 (2), 151–162. doi:10.1007/bf01535519

CrossRef Full Text | Google Scholar

Nezafat, Z., and Nasrollahzadeh, M. (2021). Biosynthesis of cu/fe3o4 nanoparticles using alhagi camelorum aqueous extract and their catalytic activity in the synthesis of 2-imino-3-aryl-2,3-dihydrobenzo[d]oxazol-5-ol derivatives. J. Mol. Struct. 1228, 129731. doi:10.1016/j.molstruc.2020.129731

CrossRef Full Text | Google Scholar

Nguyen, M. D., Tran, H.-V., Xu, S., and Lee, T. R. (2021). Fe3o4 nanoparticles: structures, synthesis, magnetic properties, surface functionalization, and emerging applications. Appl. Sci. 11, 11301. doi:10.3390/app112311301

PubMed Abstract | CrossRef Full Text | Google Scholar

Prado, R. T. A., and Sowmy, D. S. (2016). “7 - innovations in passive solar water heating systems,” in Advances in solar heating and cooling. Editors R. Z. Wang, and T. S. Ge (Woodhead Publishing), 117–150.

CrossRef Full Text | Google Scholar

Qureshi, M. A. (2021). A case study of mhd driven Prandtl-eyring hybrid nanofluid flow over a stretching sheet with thermal jump conditions. Case Stud. Therm. Eng. 28, 101581. doi:10.1016/j.csite.2021.101581

CrossRef Full Text | Google Scholar

Rashed, A., Mahmoud, T., and Kassem, M. (2020a). Analysis of homogeneous steady state nanofluid surrounding cylindrical solid pipes. Egypt. Int. J. Eng. Sci. Technol. 31, 71–82. doi:10.21608/eijest.2020.38518.1003

CrossRef Full Text | Google Scholar

Rashed, A. S. (2019). Analysis of (3+1)-dimensional unsteady gas flow using optimal system of lie symmetries. Math. Comput. Simul. 156, 327–346. doi:10.1016/j.matcom.2018.08.008

CrossRef Full Text | Google Scholar

Rashed, A. S., Mabrouk, S. M., and Wazwaz, A.-M. (2022b). Forward scattering for non-linear wave propagation in (3 + 1)-dimensional jimbo-miwa equation using singular manifold and group transformation methods. Waves Random Complex Media 32 (2), 663–675. doi:10.1080/17455030.2020.1795303

CrossRef Full Text | Google Scholar

Rashed, A. S., Mabrouk, S. M., and Wazwaz, A.-M. (2023). Unsteady three-dimensional laminar flow over a submerged plate in electrically conducting fluid with applied magnetic field. Waves Random Complex Media 33, 505–524. doi:10.1080/17455030.2021.1883147

CrossRef Full Text | Google Scholar

Rashed, A. S., Mahmoud, T. A., and Kassem, M. M. (2021). Behavior of nanofluid with variable brownian and thermal diffusion coefficients adjacent to a moving vertical plate. J. Appl. Comput. Mech. 7 (3), 1466–1479.

Google Scholar

Rashed, A. S., Mahmoud, T. A., and Wazwaz, A.-M. (2022a). Axisymmetric forced flow of nonhomogeneous nanofluid over heated permeable cylinders. Waves in Random and Complex Media, 1–29.

CrossRef Full Text | Google Scholar

Rashed, A. S., Nasr, E. H., and Kassem, M. M. (2020b). Similarity analysis of mass and heat transfer of fhd steady flow of nanofluid incorporating magnetite nanoparticles (fe3o4).

Google Scholar

Rehman, F., Khan, M. I., Sadiq, M., and Malook, A. (2017). Mhd flow of carbon in micropolar nanofluid with convective heat transfer in the rotating frame. J. Mol. Liq. 231, 353–363. doi:10.1016/j.molliq.2017.02.022

CrossRef Full Text | Google Scholar

Sadiq, M. A. (2021). Non fourier heat transfer enhancement in power law fluid with mono and hybrid nanoparticles. Sci. Rep. 11 (1), 20919. doi:10.1038/s41598-021-00423-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Sahoo, A., and Nandkeolyar, R. (2021). Entropy generation and dissipative heat transfer analysis of mixed convective hydromagnetic flow of a casson nanofluid with thermal radiation and hall current. Sci. Rep. 11 (1), 3926. doi:10.1038/s41598-021-83124-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Sajid, T., Jamshed, D.-W., Shahzd, D., Eid, M., Akgül, E., and Nisar, K. (2021). Entropy analysis and thermal characteristics of reiner philippoff hybrid nanofluidic flow via a parabolic trough of solar aircraft wings. Keller box method.

Google Scholar

Saleh, R., Rashed, A. S., and Wazwaz, A.-M. (2021). Plasma-waves evolution and propagation modeled by sixth order ramani and coupled ramani equations using symmetry methods. Phys. Scr. 96 (8), 085213. doi:10.1088/1402-4896/ac0075

CrossRef Full Text | Google Scholar

Shahzad, F., Jamshed, W., Safdar, R., Hussain, S. M., Nasir, N. A. A. M., Dhange, M., et al. (2022). Thermal analysis characterisation of solar-powered ship using oldroyd hybrid nanofluids in parabolic trough solar collector: an optimal thermal application. Nanotechnol. Rev. 11 (1), 2015–2037. doi:10.1515/ntrev-2022-0108

CrossRef Full Text | Google Scholar

Sharma, B. K., Kumar, A., Gandhi, R., Bhatti, M. M., and Mishra, N. K. (2023). Entropy generation and thermal radiation analysis of emhd jeffrey nanofluid flow: applications in solar energy. Nanomaterials 13, 544. doi:10.3390/nano13030544

PubMed Abstract | CrossRef Full Text | Google Scholar

Sheikholeslami, M., and Ganji, D. D. (2016). “Chapter 1 - magnetohydrodynamic and ferrohydrodynamic,” in External magnetic field effects on hydrothermal treatment of nanofluid. Editors M. Sheikholeslami, and D. D. Ganji (William Andrew Publishing), 1–47.

CrossRef Full Text | Google Scholar

Sheikholeslami, M., and Ganji, D. D. (2016). Nanofluid convective heat transfer using semi analytical and numerical approaches: a review. J. Taiwan Inst. Chem. Eng. 65, 43–77. doi:10.1016/j.jtice.2016.05.014

CrossRef Full Text | Google Scholar

Sheikholeslami, M., and Rokni, H. B. (2017). Simulation of nanofluid heat transfer in presence of magnetic field: a review. Int. J. Heat Mass Transf. 115, 1203–1233. doi:10.1016/j.ijheatmasstransfer.2017.08.108

CrossRef Full Text | Google Scholar

Slimene, M. B., and Arbi Khlifi, M. (2020). Modelling and study of energy storage devices for photovoltaic lighting. Energy Explor. Exploitation 38 (5), 1932–1945. doi:10.1177/0144598720952894

CrossRef Full Text | Google Scholar

Sojoudi, A., Mazloomi, A., Saha, S. C., and Gu, Y. T. (2014). Similarity solutions for flow and heat transfer of non-Newtonian fluid over a stretching surface. J. Appl. Math. 2014, 1–8. doi:10.1155/2014/718319

CrossRef Full Text | Google Scholar

Tiwari, A. K., Kumar, V., Said, Z., and Paliwal, H. K. (2021). A review on the application of hybrid nanofluids for parabolic trough collector: recent progress and outlook. J. Clean. Prod. 292, 126031. doi:10.1016/j.jclepro.2021.126031

CrossRef Full Text | Google Scholar

Nomenclature