Impact characteristics and erosion mechanism of solid particles in a centrifugal pump

To study the impact and erosion mechanism of solid particles in centrifugal pumps, the standard k–ε turbulence model and SIMPLE algorithm are adopted in this paper. Based on the discrete phase model (DPM) of the Lagrange method and McLaury erosion model, the flow impact characteristics and erosion mechanism of solid particles impacting the surface of flow passage components in a single-stage centrifugal pump were numerically simulated, and the test data were compared with the numerical simulation results of the external characteristics of the pump in clean water. The results show that the erosion mechanism of the pressure surface of the blade is mostly the impact erosion caused by high-speed particles with large impact angles, and the impact angle and impact velocity are larger near the tail of the pressure surface. The impact angle of solid particles on the shroud and hub is relatively small, but the erosion mechanism is still impact erosion. The erosion mechanism of the volute wall is mostly the cutting friction erosion caused by the low-velocity particles with small impact angles, and it is only impacted by the particles with large angles near the volute tongue, which is impact erosion. Overall, the average impact angle and impact velocity of the particles on the pressure surface of the blade are higher than those on the volute, so the erosion of the pressure surface is more serious than that of the volute in theory. The research results have certain theoretical reference value for improving the wear resistance of a centrifugal pump.

1 Introduction

The pump is vital fluid transportation equipment that is widely used in petroleum, metallurgy, chemical industry, water conservation and drainage, irrigation, and other industrial and agricultural production fields (Shouqi et al., 2014; Li et al., 2023a). However, due to the actual application of the pump in the transport of media usually mixed with solid particles, it is easy to cause wear and tear of centrifugal pump overflow parts and lead to a decline in pump performance (Rennian et al., 2017; Li et al., 2023b). Therefore, it is of significant importance to study the impact characteristics and wear mechanism of solid particles in centrifugal pumps (Hebing and Yan, 2018).

In recent years, scholars at home and abroad have conducted a lot of in-depth studies on solid–liquid two-phase flow, particle motion, and wear inside centrifugal pumps using experimental methods and numerical calculations. Tan et al. (2018) observed the motion of large-size particles in a two-flow centrifugal pump using an impeller and volute made of transparent acrylic material with the help of high-speed photography, and the statistical experimental data found that with the increase in particle diameter, the average time of particles passing through the pump experienced a process of first decreasing and then increasing. In addition, the particle density also has a greater influence on the position of the impact volute tongue. Wenqi (2019) used a discrete-phase model combined with a standard k–ε turbulence model to study and analyze the effects of solid-phase particle parameters on the wear and hydraulic performance of a self-priming pump in a solid–liquid two-phase flow simulation of the full flow field of a self-priming pump. Yanping et al. (2021) studied and analyzed the distribution of fine particles in a centrifugal pump and found that with the increase in particle volume fraction and particle size, the particles tend to move from the working surface of the vane to the backside.

Zhengjing et al. (2019) analyzed the wear of a double suction pump used to pump Yellow River water for irrigation when conveying sandy water using a three-dimensional constant full flow field simulation based on the DPM model and the McLaury wear model and investigated the effects of particle size, volume fraction, and particle shape on wear and dissected the mechanism of action of wear in different regions. The wear rate increases with the increasing particle size and is positively correlated with the particle shape factor. Fen et al. (2021) analyzed the wear on the wall of a centrifugal pump by river sand-laden water based on the Lagrangian tracking particle trajectory method and predicted using the E/CRC wear model and found that the maximum wear rate occurred in the vane and rear cover area. Wang et al. (2022a) and Wang et al. (2022b) studied the effects of three factors—solid particle diameter, particle mass concentration, and impeller material—on the wear of a solid–liquid two-phase centrifugal pump through wear experiments. They also used a three-dimensional unsteady two-phase coupled Euler–Lagrange method to numerically simulate the internal characteristics of the centrifugal pump. The study found that as particle concentration and size increased, the wear zone extended to the leading edge and upper surface of the blade.

Regarding the comprehensive domestic and foreign research status, although research on the centrifugal pump solid–liquid two-phase flow is adequate, most of the research results are qualitative analysis of the wear position, while the study of the wear mechanism is relatively lacking, especially the lack of a quantitative analysis of particle collision and wear action in the pump under solid–liquid two-phase flow conditions. This paper analyzes the form of particle–wall collision and impact wear mechanisms in centrifugal pumps under solid–liquid mixed transport conditions and provides some theoretical reference for optimizing the hydraulic design of centrifugal pumps under solid–liquid two-phase flow and improving the wear resistance of centrifugal pumps.

2 Research model

2.1 Geometric models

In this paper, the HTJ100-80 single-stage centrifugal pump is selected as the object of interest. Its basic design parameters are as follows: Q = 100 m³/h, H = 19 m, and n = 2 900 r/min. The main geometric parameters of the impeller are inlet diameter D₁ = 89 mm, outlet diameter D₂ = 140 mm, outlet width b₂ = 27 mm, and the number of blades Z = 6. The pump was constructed in three dimensions using Pro/E modeling software. The software was also used to construct the pump in three dimensions, including the inlet extension, pump front chamber, pump back chamber, impeller, volute, and outlet extension, and the model is shown in Figure 1.

FIGURE 1

FIGURE 1. Geometric model of the computational domain.

2.2 Discrete phase model

In view of the small volume fraction of particles in the two-phase flow medium studied in this paper, the discrete phase model (DPM) based on the Lagrangian method is used to describe the motion of particles. The motion of the particles in the fluid is mainly constrained by their own gravity, interphase traction, flow resistance, pressure gradient force, Saffman lift, Magnus lift, and Basset force. To facilitate the analysis and discussion, the equilibrium equation of motion of a single particle with a particle size of d_p is taken as an example, which is expressed as follows:

$\frac{d{u}_{\mathrm{P}}}{dt}=F_{\mathrm{D}}\left(u-u_{\mathrm{p}}\right)+\frac{g\left({\rho }_{\mathrm{p}}-\rho \right)}{{\rho }_{\mathrm{p}}}+F,(1)$

where

$F_{\mathrm{D}}=\frac{18\mu }{{\rho }_{\mathrm{p}}{d}_{\mathrm{p}}^2}\frac{C_{\mathrm{D}}Re}{24},(2)$

where F_D (u-u_p) is the interphase traction force per unit mass of particles; u is the fluid phase velocity, m/s; u_p is the particle velocity, m/s; μ is the fluid dynamic viscosity, N·s/m²; ρ is the fluid density, kg/m³; ρ_p is the particle density, kg/m³; d_p is the particle diameter, mm; g is the acceleration of gravity, m/s²; Re is the relative Reynolds number; C_D is the traction coefficient; F is the combined force of other external forces per unit mass of particles, N; and t is the flow time, s.

2.3 Wear calculation model

In this paper, the McLaury wear model is used to simulate and calculate the wear rate and wear mechanism of solid-phase particles impacting the surface of overflow components, which fully considers the impact angle and impact velocity of the particles impacting the wall and the material hardness. The specific equations are as follows:

$E=A{V}^{\mathrm{n}}f\left(\theta \right),(3)$

where

$A=FB{h}^{\mathrm{k}},(4)$

where F denotes the empirical coefficient; V denotes the velocity of the solid-phase particles, m/s; Bh denotes the Brinell hardness of the material, N/mm²; and k denotes the empirical index related to the material. Eq. 5 gives the impact angle function f (θ):

$f\left(\theta \right)=\left\{\begin{array}{cc}x{\cos }^2\theta \sin \left(\theta \right)+y{\sin }^2\left(\theta \right)+z,& \theta >\frac{\pi }{12},\\ b{\theta }^2+c\theta ,& \theta \le \frac{\pi }{12},\end{array}\right.(5)$

where b, c, x, y, and z are empirical constants and θ is the transition angle, rad. When θ ≤ π/12, sliding wear predominates; when θ > π/12, impact wear predominates.

2.4 Particle impact model

The particle impact problem involves the motion of the particle itself and the motion of the wall, which is a complex relative motion relationship, as shown in Figure 2; the following discussion will treat the particle as a mass point. The impact of the particle on the volute wall can be regarded as the impact of the particle on the stationary wall, so the instantaneous absolute velocity of the particle touching the wall is the impact velocity of the particle. The impeller wall is a rotating wall, so the particle impact velocity should be understood as its motion velocity relative to the rotating wall of the impeller [13], as expressed in Eq. 6. The angle between the impact velocity and the tangential direction of the wall at the contact position is the impact angle, which is applicable to both the volute and the impeller wall surface, as expressed in Eq. 7.

$V_{\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{a}\mathrm{c}\mathrm{t}}=V\mathrm{p}-V_{\mathrm{b}\mathrm{l}\mathrm{a}\mathrm{d}\mathrm{e}},(6)$

$\alpha =\left|\arccos \left(\frac{V_{\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{a}\mathrm{c}\mathrm{t}}•N}{\left|V_{\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{a}\mathrm{c}\mathrm{t}}\right|\left|N\right|}\right)-\frac{\pi }{2}\right|,(7)$

FIGURE 2

FIGURE 2. Schematic diagram of particle impact on the wall.

where V_impact indicates the particle impact velocity, m/s; V_p indicates the absolute velocity of the particle in the flow field, m/s; V_blade indicates the circumferential velocity at the location of the particle contact point on the impeller, m/s; α indicates the impact angle, degree; and N is the normal vector of the wall at the contact location. The impact velocity and the wall normal angle both take values in the range [0, π], and the velocities are in the vector form. The particle velocity can be obtained by writing a user-defined function (UDF) macro and importing it into Fluent. The particle velocity macro is P_VEL(p)[i], where i is the vector direction; the normal vector of the pump inner wall surface is obtained by normal.

3 Numerical calculation method

3.1 Computational domain meshing and irrelevance verification

In this paper, a structured mesh grid for the entire flow field calculation domain was generated using Ansys ICEM software, with a relatively reasonable number of grids to obtain a fine mesh that meets the requirements of the selected simulation scheme on the solid wall surface. The mesh grids for the impeller and spiral casing calculation domain and the locally refined enlarged views are shown in Figure 3.

FIGURE 3

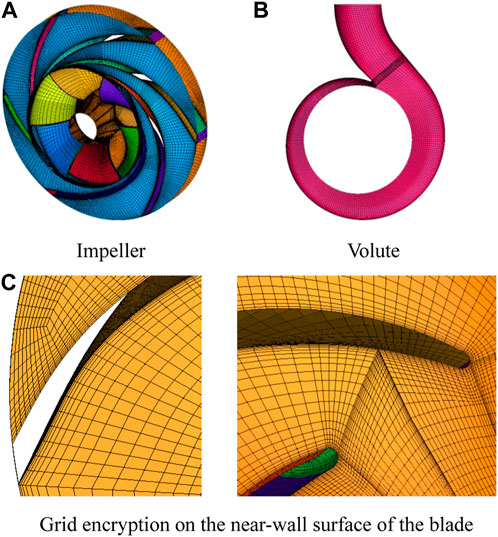
FIGURE 3. Grid generation and refinement of the key computing domain. (A) Impeller. (B) Volute. (C) Grid encryption on the near-wall surface of the blade.

To verify that the calculation results are not affected by changes in mesh density, six different computational schemes with varying numbers of mesh grids were selected for comparison analysis, with head and efficiency as the validation target variables. The verification results are shown in Figure 4. When the total grid number of the model is greater than 1.86 million, the calculated head and efficiency change little and tend to be stable, and the calculation error is less than 2%, which meets the requirements of the grid independence test. Taking into account the computation cost, the final mesh grid used for the analysis of single-phase clear water and two-phase mixed media flow was 1.86 million, with an overall y⁺ value controlled within 220, thereby meeting the requirements of the corresponding turbulence model and near-wall function.

FIGURE 4

FIGURE 4. Grid independence verification.

3.2 Turbulence model and boundary conditions

The standard k–ε turbulence model was selected based on the SIMPLE algorithm of the pressure–velocity coupling solution method, the inlet of the computational domain is a mass flow inlet, the outlet is a free flow outlet, the impeller domain uses Framer Motion to simulate rotational motion, and the rotational speed is set to 2,950 r/min. The coupling is set to be coupled with the continuous phase (liquid water), and the coupling iteration interval is 15 steps. In other words, the continuous phase is coupled with the discrete phase of particles once every 15 steps. The wear model is activated, and the coupling between the particle phase and the liquid phase is set to two-way turbulence. The influence of particle shape on the calculation is ignored, the default particle shape is a regular sphere, and the discrete random wandering model is used to describe the interaction between particles and turbulent vortices. The inlet and outlet surfaces of the computational domain are the particle-free entry and exit interfaces, and the rest of the walls are set as rebound walls. The impeller rotation of 2° is a single time step T (1.1299 × 10^-4 s); 180 time steps are calculated as one cycle, and a total of 10 cycles are calculated.

4 Experimental verification of external characteristics

To verify the accuracy of the numerical calculation results, the performance test of the HTJ100-80 centrifugal pump was conducted at the National Water Pump Center, and the actual photograph of the test is shown in Figure 5. The parameters of the measuring instrument are as follows: the power is less than or equal to 400 kW, the pressure range is −0.1–6.8 MPa, the flow range is 0–10,000 m³/h, and the total uncertainty of the measurement value is 0.68%.

FIGURE 5

FIGURE 5. Pump performance test site.

The external characteristics of the model pump numerical calculation and experimental results are shown in Figure 6. The figure shows that the simulated head and efficiency variation trends are in high agreement with the experimental values. At the rated operating point, the error between the simulated head and the experimental head is 3.06%, and the error between the simulated efficiency and the experimental efficiency is 2.81%. Under high flow conditions, only a small deviation between the simulated head and the experimental value occurs because the actual roughness in the experimental device is larger and the hydraulic loss is more significant due to the increase in flow velocity at high flow rates. Overall, the head and efficiency predicted by the numerical simulation are in good agreement with the experimental results, which proves the high reliability of the simulation results.

FIGURE 6

FIGURE 6. External characteristics of numerical and experimental results.

5 Calculation results and analysis

5.1 Monitoring point setting

Monitoring points are set on the blade surface and volute wall to obtain relevant data. The axis is located in the inlet side of the blade and the plane as the 0° section, around the axis interval of 10° for a total of 14 sections, and the blade surface intersection forms 14 radial intercept lines, with an exit side section angle of 130°. The blade monitoring points are obtained by taking five equidistant points on each radial section line, and the same equidistant points on each radial section line are connected as the axial section line. Considering the statistical calculation volume, seven of the radial cutoffs are selected for analysis in this paper, and the monitoring points on the volute wall are distributed along the spiral line of the volute mid-section; the location of each monitoring point is shown in Figure 7. The dotted line diagram in horizontal coordinates involve axial intercept line serial numbers 0–1 from the front cover to the rear cover direction, that is, the axial direction; radial intercept line angles 10°–130° are located from the blade inlet side to the exit side direction, that is, the radial direction. The average of the monitoring point data on the intercept line in each direction is the average of the data on the intercept line.

FIGURE 7

FIGURE 7. Monitoring points of the blade and volute.

5.2 Wear mechanism of each overcurrent component

According to Zhengjing S et al. [21] and Tarodiya R et al. [22], the wear pattern of surfaces subjected to erosion is related to the impact angle and impact velocity of the particles. Furthermore, Stachowiak W [24] proposed a mechanism of particle impact wear within hydromechanics, low impact angle frictional erosion, and large impact angle impact wear. According to reference [25], impact angles of less than 30° are referred to as “low impulse angles,” and impact angles greater than 30° are referred to as “large impulse angles.” Since the complex internal flow of centrifugal pumps when conveying two-phase flow media leads to different ways of particle impact on the wall within each overflow component, it is necessary to analyze the particle impact motion at different locations and derive the corresponding wear action mechanism. The centrifugal pump is analyzed as an example of conveying particles with a particle size of d_p = 1.0 mm and a volume fraction C_v = 1% under rated operating conditions. Figure 8 shows the impact angle distribution of the particles on the pressure surface of the blade. The overall impact angle on the pressure surface is large, and the impulse angle exceeds 30° in most areas. The impact angles in the inlet area and the middle area of the pressure surface are smaller compared with other areas of the pressure surface, and the large impact angles over 50° show a scattered distribution, while the impact angles in the tail area of the pressure surface are large, mostly over 50°. Thus, the pressure surface is mainly affected by the impact wear of particles with large impact angles.

FIGURE 8

FIGURE 8. Impact angle distribution of the blade pressure surface.

The impact angle distribution of the front and rear cover plates of the impeller is shown in Figure 9, and the shape of the particle impact angle distribution area is similar. The curvature of the runner against the inlet area of the inlet blade varies greatly, as does the trajectory of the particles, and the larger impact angle is primarily distributed in the front and middle areas of the impeller runner, where the radial size of the cover plate is small, and the impact angle does not exceed 30°. The curvature change in the front and rear cover plates at the back of the runner is smaller, and the impact angle near the blade exit area is smaller, not more than 10°, so the wear on the front and rear cover plates is mainly due to the impact wear caused by the lower impulse angle of the particles.

FIGURE 9

FIGURE 9. Impact angle distribution of the shroud and hub.

The impact angle distribution on the volute wall is shown in Figure 10, which is mainly distributed along the spiral section. The impact angle on the spiral section of the volute is small, not more than 25°, and the maximum impact angle appears at the location of the tongue, which is more than 50°. From the cloud distribution, most areas of the volute wall surface are subjected to small impact angles of the particles, and the mechanism of wear action is mainly frictional erosion caused by low impulse angles; the particles slide and cut on the volute surface. While the location of the tongue is mainly subjected to large angle impact wear of the particles, the analysis results are consistent with the results of the electron microscopy scan of Tarodiya R et al. [22] on the wear pattern of the volute wall surface.

FIGURE 10

FIGURE 10. Impact angle distribution of the volute wall.

The impact angle determines the wear mode of particles on the inner wall of the pump, and the impact speed determines the wear strength. When the impact speed is large, it shows a power exponential relationship with the wear rate, as shown in formula (8):

$-\frac{dm}{dt}=k{v}^{\mathrm{n}},(8)$

where m is the mass of the material, kg; t represents wear time, s; v is the particle impact velocity, m/s; and k is the empirical coefficient, which is generally related to the mass and shape of the particles. The value of index n is generally between 2 and 3.

The impact velocity distribution of the blade pressure surface is shown in Figure 11. The particle impact velocity on the inlet edge and front area of the blade is relatively low, approximately 15 m/s. With the increase in radial size, the circumferential linear velocity of the blade increases continuously. Accordingly, the velocity of particles under the action of centrifugal force also increases continuously. When the two collide in the middle area of the pressure surface, the impact velocity is approximately 20 m/s. The tail of the pressure surface is close to the outlet. Because the circumferential linear velocity of the blade is the largest and the particle movement velocity is also the largest, it is the area where the whole pressure surface is impacted by the particle with the largest impact velocity. The particle impact velocity in some positions exceeds 30 m/s. Therefore, these positions are most severely impacted by the particles, and the wear rate near the outlet edge of the blade pressure surface increases significantly.

FIGURE 11

FIGURE 11. Impact velocity distribution of the blade pressure surface.

The particle impact velocity distribution of the front and rear cover plates is shown in Figure 12. The high-speed impact area of the front cover plate particles is mainly distributed on the side close to the blade suction surface, and the middle area of the pressure surface and suction surface is less impacted by the high-speed impact of the particles. The high-speed impact area of particles in the rear cover plate is mainly distributed on the side close to the pressure surface of the blade. From the inlet to the outlet of the flow channel, the particle impact velocity of the front and rear cover plates increases but generally not more than 30 m/s.

FIGURE 12

FIGURE 12. Impact velocity distribution of the shroud and hub.

The distribution of particle impact velocity on the volute wall is shown in Figure 13. It can be seen that the area with the largest particle impact velocity is in the abdomen of the spiral section near the volute tongue, where the maximum impact velocity is 13 m/s, and the particle impact velocity in other areas is mostly 10 m/s. According to the analysis in Figure 8, the wear of other areas on the volute wall, except the tongue, is the friction erosion wear caused by the low angle of attack of approximately 20°. On the premise of the same wear mechanism, the spatial change in the wear rate of the volute wall mainly depends on the particle impact velocity. Therefore, theoretically, the area near the belly of the spiral section of the tongue should be the most seriously worn area on the whole volute wall. This conclusion is also confirmed in previous studies.

FIGURE 13

FIGURE 13. Impact velocity distribution of the volute wall.

5.3 The impact of particle volume fraction on impact characteristics

By changing the particle inlet flow rate under the conditions of particle size d_p = 1.0 mm, flow rate 1.0 Q, and speed 2950 r/min, the impact angle and impact velocity of particles and the impact data at each monitoring point are obtained under different particle volume fractions.

The impact angle data for pressure surfaces and monitoring points of the volute casing wall under different particle volume fractions are shown in Figure 14. The changing trends for average particle impact angles in both axial and radial directions on the pressure surface are consistent among the three volume fractions, with only a slight difference in the radial direction, which does not exceed 5°. There are significant differences in the impact angles at the cross-sectional position of the volute casing wall, and the impact angle at C_v = 4% is generally the highest, slightly higher than that at C_v = 2%. The impact angle at C_v = 1% is significantly lower than those under the other two volume fractions, especially in the lower surface of the exit diffusion section and the spiral section area, that is, monitoring points 1 to 10. The impact angles on the upper surface of the exit diffusion section gradually tend to be the same among the three volume fractions.

FIGURE 14

FIGURE 14. Average impact angle under different particle volume fractions.

The average impact velocity data of pressure surface and monitoring points of the volute casing wall under different particle volume fractions are shown in Figure 15. The impact velocity under different volume fractions is the closest in both axial and radial directions, and the changing trends are also consistent. In the axial direction, the average impact velocity first increases substantially and then decreases slightly, with the maximum average impact velocity occurring at the axial center of the pressure surface, which is approximately 16 m/s. In the radial direction, the average impact velocity impact angle (°) increases continuously from the inlet to the outlet of the pressure surface, with the maximum increase occurring in the middle of the pressure surface in the area where the radial sectional angle is 50°–110°, and the increase is significantly reduced near the outlet. The maximum average impact velocity is approximately 24 m/s. The particle volume fraction has a small effect on the impact velocity at the cross section of the volute casing wall, with little difference among the curves and similar changing trends. The maximum impact velocity on the cross section occurs near the baffle, at approximately 10 m/s. The impact velocity at other positions in the spiral section is approximately 8 m/s, and the impact velocity is generally the lowest in the outlet diffusion section. The particle impact velocity on the volute casing wall is generally lower than that on the blade pressure surface.

FIGURE 15

FIGURE 15. Average impact velocity under different particle volume fractions.

5.4 The impact of particle diameter on impact characteristics

Under conditions of particle volume fraction C_v = 1%, flow rate = 1.0 Q, and rotor speed = 2,950 r/min, the impact angles, impact velocities, and impact data at various monitoring points were obtained by varying the particle diameter to d_p = 0.5 mm, d_p = 1.0 mm, and d_p = 2.0 mm.

Based on the description and Figure 16, it can be observed that the smaller the particle diameter, the larger the average impact angle on the pressure surface. In the axial direction, the average impact angle difference between the three particle diameters is most noticeable in the area near the front cover plate, with d_p = 0.5 mm showing a significantly higher average impact angle, exceeding 25°. As the direction moves closer to the rear cover plate, the impact angle differences gradually decrease and tend to be consistent, approaching 35°. In the radial direction, the impact angle on the pressure surface generally increases with the increase in the blade radius under different particle size conditions, following the pattern that a smaller particle size corresponds to a larger impact angle, similar to the axial direction. On the casing wall, the impact angle at various positions of the cross section increases with the increase in particle diameter, while the variation in the impact angle under different particle diameter conditions is relatively consistent, showing a trend of reaching the maximum value at the tongue position, maintaining a steady oscillation in the spiral section, and rapidly declining at the lower wall of the exit section.

FIGURE 16

FIGURE 16. Average impact angle under different particle diameters.

The average impact velocity data on the pressure surface and casing wall under different particle diameters are shown in Figure 17. In the axial direction on the pressure surface, the average impact velocity under d_p = 0.5 mm is significantly higher near the front cover plate than in the other two particle size conditions and becomes more consistent as it approaches the rear cover plate. In the radial direction, the average impact velocity at different radial positions decreases with increasing particle diameter. Under the same particle diameter, the average impact velocity on the radial section line generally increases from the inlet side to the outlet side on the pressure surface. The average impact velocity under different particle diameters tends to be consistent at the outlet position. On the casing wall, the variation in particle diameter has a significant effect on the impact velocity at the intermediate cross-section position. With the increase in particle diameter, the impact velocity in most of the spiral sections shows a significant decreasing trend, and the impact velocity at each monitoring point is less than 10 m/s. Only the impact velocity of larger particle sizes is relatively greater at the casing outlet section. Overall, the particle impact on the casing under different particle diameter conditions is mainly low-speed impact.

FIGURE 17

FIGURE 17. Average impact velocity under different particle diameters.

5.5 Prediction of particle impact stress

To further investigate the impact characteristics of particle impact on the surface of pump flow components, a typical combination of particle impact angles and velocities was selected for predicting the stress changes on the material surface when impacted by particles. By inputting the particle impact model into Ansys Workbench and using the explicit dynamics analysis module to simulate and predict the particle impact on the target material, the maximum stress on the target material under different impact velocities and angles was obtained. The particle diameter was set to 1.0 mm, and considering the size of the pump flow components, a rectangular target material with dimensions of 20 mm × 20 mm × 5 mm was used, with the particle impact position at the center of the target material. The bottom of the target material was defined as a fixed constraint. The specific model is shown in Figure 18.

FIGURE 18

FIGURE 18. Particle impact target model.

The impact velocity can be decomposed into the normal component V_n and tangential component V_t, and the particle impact angle α can be determined using the relationship between the tangential component and the impact velocity, as shown in Eqs 9, 10.

$\left|V\right|=\sqrt{{\left|V_{\mathrm{t}}\right|}^2+{\left|V_{\mathrm{n}}\right|}^2},(9)$

$\alpha =\arccos \frac{\left|V_{\mathrm{t}}\right|}{\left|V\right|}.(10)$

The target material and particles were divided into adaptive grids, with a total of 137,995 nodes, as shown in Figure 19. The target material was selected from the Workbench material library as ductile iron, with a density of 7,300 kg/m³ and specific mechanical properties shown in Table 1. The particle material was gravel, with a density of 2,700 kg/m³.

FIGURE 19

FIGURE 19. Grid of the particle and target.

TABLE 1

TABLE 1. Mechanical properties of the target material.

Based on the previous study of impact angles and velocities, three impact angles (10°, 30°, and 60°) and three impact velocities (10 m/s, 20 m/s, and 30 m/s) were selected as the impact parameters, with the specific combination scheme shown in Table 2.

TABLE 2

TABLE 2. Combination scheme of impact angles and impact velocities.

The maximum equivalent stress of particle impact on the target material under different impact angles is shown in Figure 20. It can be seen from the figure that when the impact angle is 10°, the stress distribution on the target material is relatively dispersed, and the maximum equivalent stress is not located at the center of the impact, with a maximum value of 0.26308 MPa on the surface of the target material. As the impact angle increases, the stress distribution gradually concentrates in the center of the target material, with the maximum equivalent stress located in the center of the target material, and the equivalent stress in the impact center continues to increase. When the impact angle is 30°, the maximum equivalent stress is 0.65588 MPa; when the impact angle is 60°, the maximum equivalent stress is 0.86278 MPa. Therefore, it can be concluded that as the impact angle increases, the impact stress on the pump wall surface increases, which may cause more severe impact wear.

FIGURE 20

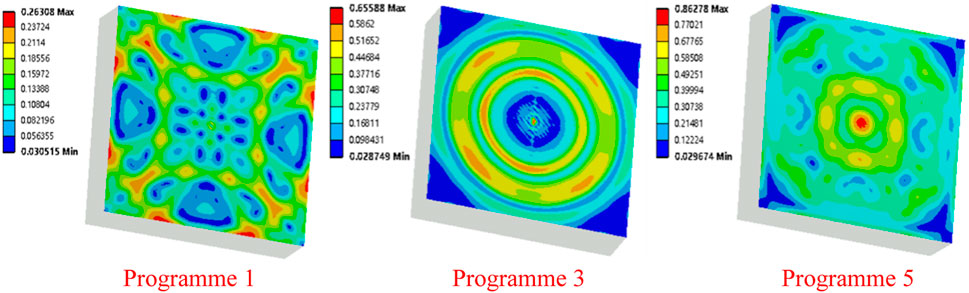
FIGURE 20. Equivalent stress distribution of the particle impacting the target under different impact angles.

The maximum equivalent stress of particle impact on the target material under different impact velocities is shown in Figure 21. When the impact velocity is 10 m/s, the equivalent stress in the center of the target material is relatively small, with a maximum equivalent stress of 0.26278 MPa. As the impact velocity increases, the maximum equivalent stress in the center of the target material also increases. When the impact velocity is 20 m/s, the maximum equivalent stress is 0.65588 MPa; when the impact velocity is 30 m/s, the maximum equivalent stress is 1.371 MPa. The impact velocity also has a significant impact on the impact energy on the wall surface, and as the impact velocity increases, the impact stress caused by particles on the wall surface also increases. Under the constant impact of particles, the pump wall surface is more likely to experience material failure, leading to wall surface wear.

FIGURE 21

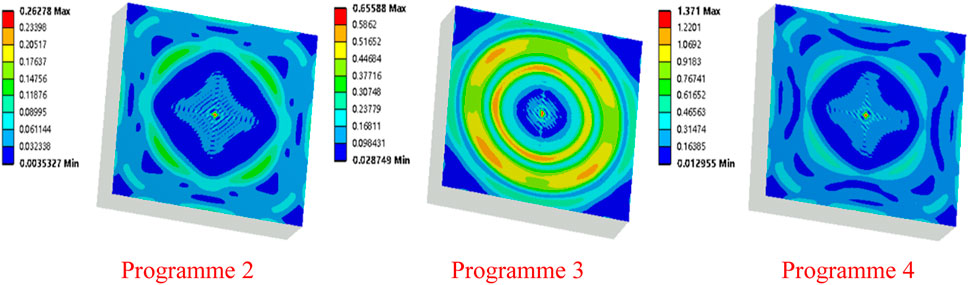
FIGURE 21. Equivalent stress distribution of the particle impacting the target under different impact velocities.

6 Conclusion

In this paper, through the analysis of the particle impact angle and impact velocity of the main flow components of the centrifugal pump, the mechanism of particle wear on the inner wall of the pump is clarified. The main conclusions are as follows:

(1) The pressure surface of the impeller is mainly subjected to high-speed particle impact wear at large angles. The impact angle and velocity are relatively large near the rear of the pressure surface, while the impact angles of particles on the front and rear cover plates are relatively small, but they still cause impact wear. However, the majority of the area of the spiral casing wall is subjected to low-impact angle and low-velocity frictional cutting wear, and only the impact angle at the baffle is relatively large.

(2) The effect of the change in the volume fraction on the impact angle and velocity of particles on the pump wall surface is relatively small, with only a slight increase in the impact angle of the spiral casing wall surface with an increase in the volume fraction. Particle size has a significant influence on the collision between particles and the wall surface. As the particle size increases, the impact angle and velocity of the pressure surface of the impeller under particle impact decrease significantly, and the impact velocity of the spiral casing also shows a decreasing trend. However, the impact angle of the spiral casing wall surface shows a significant increase with an increase in particle size, indicating a tendency toward impact wear.

(3) When the pump wall surface is subjected to high-speed impact from particles with large angles, the impact stress is relatively high, which increases the likelihood of wear on the wall surfaces of the pump flow components.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author contributions

WL: software, investigation, and writing—reviewing and editing. YY: validation and writing—original draft preparation. PW: conceptualization and methodology. LJ: writing—reviewing and editing. ML: software and visualization. HQ: methodology and supervision. SL: conceptualization and methodology. All authors contributed to the article and approved the submitted version.

Funding

This work was sponsored by the National Key R&D Program Project (No. 2020YFC1512405), the Key International Cooperative Research of the National Natural Science Foundation of China (No. 52120105010), the National Natural Science Foundation of China (No. 52179085), the Sixth “333 High Level Talented Person Cultivating Project” of Jiangsu Province, the Funded Projects of “Blue Project” in Jiangsu Colleges and Universities, the “Belt and Road” Innovation Cooperation Project of Jiangsu Province (No. BZ2020068), and the Independent Innovation Fund Project of Agricultural Science and Technology in Jiangsu Province (No. CX (20)2037).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Fen, L., Fengming, W., and Xiangyuan, Z. (2021). Erosion characteristics of centrifugal pumps based on E/CRC erosion model[J]. J. Harbin Eng. Univ. 42 (5), 719–728.

Google Scholar

Hebing, L., and Yan, L. (2018). Research status and prospect of solid liquid pump two phase flow and wear[J]. China South. Agric. Mach. 49 (23), 8–11.

Google Scholar

Li, W., Huang, Y., Ji, L., Ma, L., Agarwal, R. K., and Awais, M. (2023a). Prediction model for energy conversion characteristics during transient processes in a mixed-flow pump. Energy 271, 127082.

CrossRef Full Text | Google Scholar

Li, W., Liu, M., Ji, L., Li, S., Song, R., and Wang, C. (2023b). Study on the trajectory of tip leakage vortex and energy characteristics of mixed-flow pump under cavitation conditions. Ocean Engineering 267, 113225.

CrossRef Full Text | Google Scholar

Rennian, L., Hao, C., and Wei, H. (2017). Effect of particle size on flow in stator and rotor cascades of guide vane type centrifugal pump[J]. J. drainage irrigation Mach. Eng. (JDIME) 35 (12), 1018–1023.

Google Scholar

Shouqi, Y., Weidong, S., and Liu, H. (2014). Theory and technology of pump[M]. Beijing: China Machine Press.

Google Scholar

Tan, G., Lian, C., Liu, L., Wu, X., and Ding, R. (2018). Visualizing test on the pass-through and collision characteristics of coarse particles in a double blade pump. Int. J. Nav. Archit. Ocean Eng. 10 (1), 1–8. doi:10.1016/j.ijnaoe.2017.06.003

CrossRef Full Text | Google Scholar

Wang, Y., Li, W., and He, T. (2022b). Experimental study on the influence of particle diameter, mass concentration, and impeller material on the wear performance of solid–liquid two-phase centrifugal pump blade[J]. Front. Energy Res. 10, 893385.

CrossRef Full Text | Google Scholar

Wang, Y., Tao, R., Han, C., Li, W., He, T., and Zhu, Z. (2022a). Numerical study on flow and wear characteristics of dense fine particle solid–liquid two-phase flow in centrifugal pump. AIP Adv. 12 (4), 045109. doi:10.1063/5.0079425

CrossRef Full Text | Google Scholar

Wenqi, Z. (2019). Study on flow characteristics of solid-liquid two phase flow in selfpriming pump[D]. Zhejiang University of Technology.

Google Scholar

Yanping, W., Bozhou, C., Ye, Z., Ma, J., Zhang, X., Zhu, Z., et al. (2021). Numerical simulation of fine particle solid-liquid two-phase flow in a centrifugal pump. Shock Vib. 2021 (20), 1–10. doi:10.1155/2021/6631981

CrossRef Full Text | Google Scholar

Zhengjing, S., Wuli, C., Xiangjun, L., and Dong, W. (2019). Sediment erosion in the impeller of a double-suction centrifugal pump – a case study of the Jingtai Yellow River Irrigation Project, China. Wear 422 (1), 269–279. doi:10.1016/j.wear.2019.01.088

CrossRef Full Text | Google Scholar