Identification of cavitation state of centrifugal pump based on current signal

Centrifugal pump, which is widely used in water conservancy, electric power, petrochemical, ship, aerospace, and other technical fields, is the core equipment used to ensure all kinds of energy transfer. Cavitation not only affects the service life of the centrifugal pump but also seriously impacts the reliability of the process flow or device system. Due to the influence of the life, position and number of vibration sensors, the existing cavitation fault feature identification accuracy is not enough. The state analysis and characteristic recognition of the current signal under the cavitation state of the centrifugal pump are conducted in this paper based on soft sensing technology, and the signal component and judgment threshold representing the cavitation state are obtained. The following results are presented. Under different critical cavitation numbers, a small number of bubbles appeared near the suction surface of the inlet edge of the impeller, which verified the reliability of criterion for the critical cavitation number when the head coefficient decreased by 3%. The overall accuracy of binary classification cavitation recognition based on the current signal is 12.9% higher than that of three classification cavitation recognition. The recognition rate of VMD decomposition under different working conditions is higher than that of EMD, in design conditions, for example, overall accuracy improved by 7.3%, which also indicates that the obtained cavitation information of each component by VMD decomposition is richer than that obtained by EMD decomposition. Comparing different working conditions, a large flow rate easily leads to cavitation and high recognition current rate, compared with the flow of 0.75 Q and 1.25 Q, the overall accuracy is improved by 9.6%.

1 Introduction

As the main fluid conveying medium, centrifugal pump plays an important role in many industrial applications. Cavitation is one of the key factors affecting its performance. In traditional centrifugal pump cavitation monitoring, flow, and pressure data are measured, and a 3% drop in centrifugal pump head is taken as the occurrence standard of cavitation (ISO, 2010). However, in high and ultralow temperatures, conveying toxic and harmful or easy-to-wear medium and other extreme conditions and accurately measuring the centrifugal pump flow and pressure is difficult. Determining the centrifugal pump cavitation state using the head-down method is also complicated. Soft sensing technology uses relevant knowledge to build the mathematical relationship between the easy and difficult to measure quantities in the production process. The slightly measurable quantities are then predicted and estimated through these easy to measure quantities. At present, the soft sensing technology of centrifugal pump cavitation monitoring mainly includes the pressure pulsation, vibration, noise, and current methods. Among them, the vibration method is the most widely used in monitoring the cavitation state of a centrifugal pump (Sánchez et al., 2018; Wang and Wang, 2018), which has the advantages of avoiding research object damage and high signal sensitivity. However, in a complex environment, the location and number of monitoring points have a direct impact on the accuracy of cavitation identification, thus failing to meet the needs of some remote real-time monitoring due to the impact of sensor life and operating cost. With the continuous development of fluid dynamics, the fault diagnosis technology based on motor current signal is characterized by its simple, feasible, low cost, and remote real-time monitoring, which has attracted considerable attention (Wang et al., 2021). However, the current signal processing methods in the cavitation state are insufficient and comparative analysis of different signal processing methods is lacking. Second, the low sensitivity of the current signal leads to the unsatisfactory monitoring of the cavitation state of the centrifugal pump in some special cases. Therefore, other signals are also needed for multi-information fusion monitoring. Overall, the current signal has considerable potential advantages in the soft sensing field of the cavitation state of centrifugal pumps. However, research and application in related fields are still lacking.

In the existing cavitation research and monitoring methods, Mouleeswaran et al. (Senthilkumar et al., 2015) used the LabVIEW program and DAQ card as the interface to obtain vibration amplitude and frequency, respectively, on different axes of the pump with the help of an accelerometer. The vibration spectrum is then analyzed and the cavitation state of the centrifugal pump is determined by identifying the frequency whose vibration amplitude is higher than the dangerous limit. LIU et al. (2020) used the VMD algorithm to process and analyze the acoustic signals of centrifugal pump cavitation. Their results showed that the signal energy value at 50 and 100 KHz frequency bands decreased first and then increased with the intensification of cavitation degree. Izadeh and Yari (2017) classified the vibration signal data under the pump cavitation state and extracted the probability of cavitation recognition as features to build a classifier. The classifier is then used to determine the cavitation state by using Bayesian theory. Nazarov et al. (2018) proposed a high-speed cavitation test method, which can significantly shorten the test cycle and improve the accuracy of specified cavitation characteristics.

The current was first used to detect motor faults. Nazarychev et al. (2020) proposed a method for monitoring the rotor winding state of the asynchronous motor based on the current variation. The numerical simulation was conducted on the digital model of the induction motor developed in the ANSYS software package, and then the test was performed on the test bench. The results show that the amplitude of the high harmonic component of the current, which is consistent with the number of pole pairs of the motor, increases sharply at low frequency when the rotor rod is broken. Skowron et al. (2020) used a convolutional neural network (CNN) to detect and classify stator winding faults of induction motors. The feasibility of applying CNN to stator early winding fault detection and classification is proven by an online test. Siegler et al. (2010) used the motor current to monitor the impeller of a marine centrifugal pump and found the relationship between the current signal and the cavitation degree of the impeller through research. Casada et al. (1999) studied rotor misalignment faults of pump units, used instantaneous power spectrum analysis of motor current to characterize rotor misalignment faults, and obtained corresponding time- and frequency-domain characteristics of current signals under such faults. Welch et al. (2002) monitored the operating conditions of equipment by measuring current and power and the test results can be applied to most electromechanical equipment, realizing remote analysis and continuous monitoring. Perovic (Perovic, 2000) proved through experiments that the energy value of a specific frequency range of current signals could be used as the judgment value due to pump outlet blockage, blade damage, and cavitation. Kenull et al. (2003) studied the cavitation and inversion faults of centrifugal pumps, extracted fault features by using the motor current spectrum and energy distribution curve, and established a diagnostic model. Their results showed that current signals can effectively monitor the cavitation state of centrifugal pumps under certain circumstances. Schmalz and Schuchmann (2004) used the energy distribution diagram of the low-frequency band signal of motor current to monitor the cavitation state of the centrifugal pump under different working conditions. Harihara and Parlos (2008) utilized the centrifugal pump monitoring algorithm to determine cavitation faults, blade damage, and bearing failure. However, the signal classification basis has not been provided. Hu and Zhao (2007) analyzed the motor current signal in the frequency domain and found a corresponding relationship between the motor current signal and the pump medium pulsation information in the frequency domain. They also established the pump unit model for verification, and their results were consistent with the experimental conclusions.

Overall, the current signal-based soft sensing technology can be extended from motor fault diagnosis to centrifugal pump cavitation operating condition monitoring and fault diagnosis due to the electromagnetic coupling between the rotor system and windings. This technology is characterized by its simplicity, feasibility, and low cost; it can also realize the function of remote monitoring. However, overall research on the application of current soft sensing technology to the monitoring of centrifugal pump working conditions is limited. Particularly, the processing methods related to the extraction of minimal information containing cavitation state in the current signal are insufficient. The low sensitivity of the current signal also leads to the unsatisfactory monitoring of the cavitation primary state of the centrifugal pump. Therefore, further research is necessary to build an accurate identification model of the cavitation state of the centrifugal pump. Therefore, first of all, the current signal of the centrifugal pump model is obtained in this paper. Two methods of Empirical Mode Decomposition (EMD) and singular value decomposition (SVD) are adopted to analyze and identify the current signal in the cavitation state of the centrifugal pump. The signal component and the judgment threshold representing the cavitation state are obtained. Cavitation signals under different working conditions were identified and their applicability to the soft sensing technology was compared. The research results can provide reference for the soft sensing technology in the fault diagnosis of centrifugal pump cavitation.

2 Physical model

2.1 Geometric model

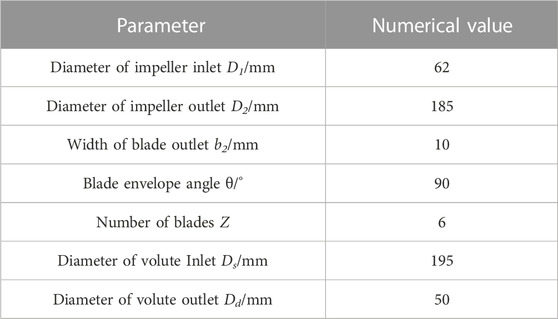
The model pump of this test is a single-stage single-suction centrifugal pump with a specific speed of 62, a rated head of 10 m, a rated flow of 13 m³/h, a motor power of 3.5 kw, and a speed of 1,450 r/min. The centrifugal pump in this test adopts a transparent plexiglass shell and impeller to facilitate the shooting of water conditions around the impeller during cavitation. The motor is a three-phase AC asynchronous motor. The parameters of the tested centrifugal pump are shown in Table 1 below.

TABLE 1

TABLE 1. Parameters of the model pump.

2.2 Experimental platform

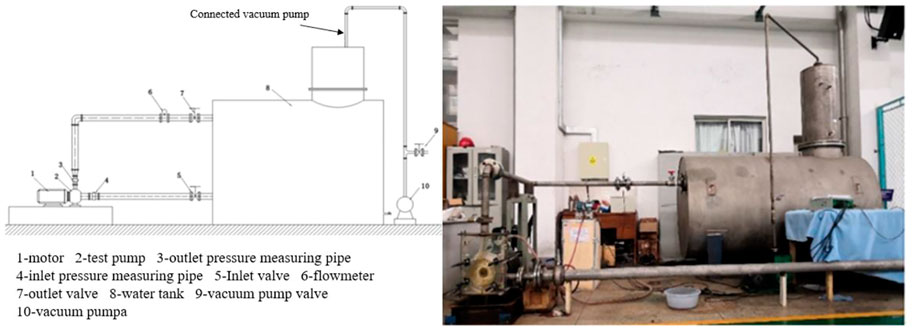
The test equipment mainly includes a closed test bench, a signal acquisition system, and high-speed photography equipment. The centrifugal pump test bed comprises the following: model pump, motor, water tank, flow meter, inlet pressure sensor, outlet pressure sensor, stainless steel tube, vacuum pump, valve, and bracket. The schematic and physical diagrams of the test are shown in Figure 1.

FIGURE 1

FIGURE 1. Schematic diagram and physical diagram of the test bed.

2.3 Data acquisition system

Data acquisition for this test included flow rate, inlet and outlet pressures, motor current voltage, speed, and vibration signal. The data acquisition system comprises a Graphical User interface (GUI) data acquisition system based on MATLAB and an NI data acquisition system based on LabVIEW. The GUI data acquisition system mainly collects traffic, import and export pressures, and current and voltage signals. The current signal is collected by the Hall sensor, and the sensor adopts the principle of the Roche coil probe, which has a fast response speed and no waveform distortion. High reliability, can work in 10 KV high-pressure environment, anti-interference ability to reach the national standard level two or above, precision level of 0.1. The pressure transmitter uses a piezoresistive sensor as a signal-measuring element with an accuracy class of 0.2% FS, as shown in Figure 2.

FIGURE 2

FIGURE 2. The physical picture of the sensor. (A) Hall sensor; (B) Pressure transmitter.

2.4 Cavitation performance test analysis

The cavitation condition of the test aims to vacuum the tank. Two important parameters in the cavitation test, namely, cavitation number and head coefficient, are respectively expressed as $\psi =H/\left(u_0^2/2g\right)$ and $\sigma =\left(P-P_v\right)/\left(0.5\rho u_0^2\right)$, where $\psi$ is the head coefficient, σ is the number of cavitation, H is the head of the centrifugal pump (the unit is m), u0 is the velocity of a fluid medium (the unit is m/s), P is the inlet static pressure (the unit is Pa), and Pv is the saturated vapor pressure of the medium at ambient temperature (the unit is Pa).

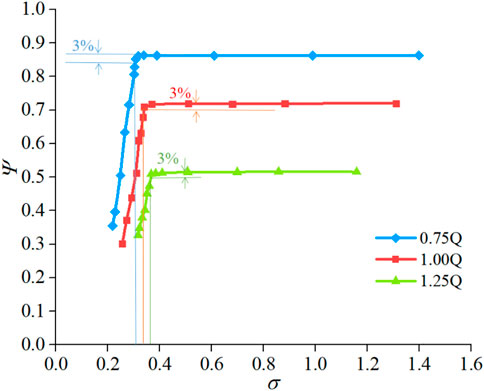
Using the above-closed test device, the cavitation performance curve as shown in Figure 3 is obtained. The figure shows that the head coefficient Ψ is unchanged at the beginning and then starts to decline with the decrease in the cavitation number. The reduction of the head coefficient by 3% is the critical cavitation point. When the pump cavitation occurs relatively early at high flow (1.25 Q), its corresponding critical cavitation σ is 0.36, the design condition (1.0 Q) critical cavitation σ is 0.34, and the low flow condition (0.75 Q) critical cavitation σ is 0.305. The cavitation state in each cavitation stage of a centrifugal pump is further accurately described and marked with cavitation σ to observe the changes in water flow in the cavitation stage of a centrifugal pump under different working conditions directly. Figure 4 shows that the high-speed camera technology was used to track and capture the internal cavitation of the pump to verify the accuracy of the above discrimination.

FIGURE 3

FIGURE 3. Cavitation performance curves of centrifugal pump under different working conditions.

FIGURE 4

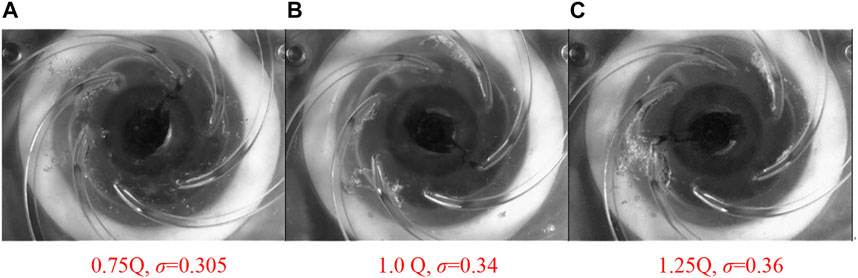
FIGURE 4. Birth of cavitation under the critical cavitation number in each working condition. (A) 0.75 Q, σ = 0.305 (B) 1.0 Q, σ = 0.34 (C) 1.25 Q, σ = 0.36.

Figure 4 also shows the existence of relatively few vacuoles inside the blade in the low flow condition (0.75 Q) and cavitation σ = 0.305, and these vacuoles are mainly distributed near the suction surface at the blade inlet. Vacuoles collapse and disappear in the middle of the blade with the fluid flow. When σ = 0.34 in the design condition and σ = 0.36 in the large flow condition (1.25 Q), a small number of cavitation also appears near the suction surface at the inlet edge of the blade, representing the birth of cavitation, which further verifies the accuracy of the above critical cavitation determination.

3 Identification of the cavitation state of the current signal

3.1 Current signal feature extraction

The empirical mode decomposition (EMD) method is used to decompose the signal according to the time scale characteristics of the data without setting any basis function in advance. This method can decompose complex signals into a finite number of intrinsic mode functions (IMFs), and each decomposed IMF component contains local characteristic information of the original signal at different time scales (Dragomiretskiy and Zosso, 2014; Li et al., 2021). Singular value decomposition (SVD) is similar considering the diagonalization of symmetric or Hermite matrices based on eigenvectors and is a generalization of spectral analysis theory on arbitrary matrices. In the scope of software filtering, SVD can remove strong interference signals and retain weak signals. Particularly, as a method of current power frequency filtering, the effect is satisfactory; thus, SVD is used to filter the current signal power frequency. Therefore, this paper mainly utilizes EMD and VMD to process and analyze current signals, respectively.

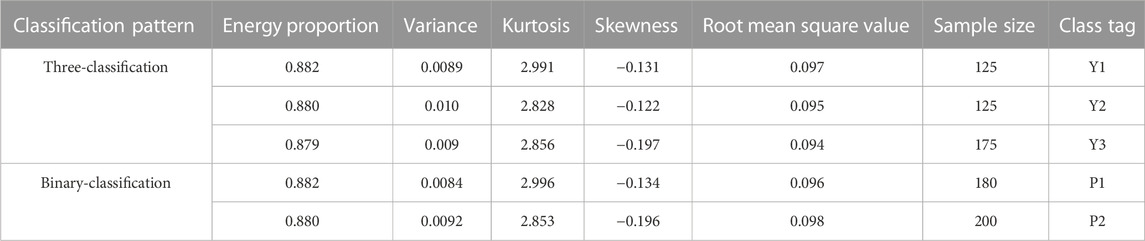
Each component of the current signal obtained by filtering can be effectively distinguished after the decomposition of EMD and VMD; particularly, the distinguishing effect of individual components is observed under the low flow condition. The obtained energy proportion of each component by different decomposition methods can also be used as a characteristic index to some extent. Therefore, in this paper, the energy ratio e_i, variance S_i, kurtosis k_i, skewness γ_i, and root mean square ε_i values of i components obtained by EMD and VMD decomposition are used in this paper as feature vectors T for current identification of cavitation state.

When current is used as the signal of cavitation state identification, the cavitation state can be divided into non-cavitation (σ > 0.358), cavitation birth (0.358 > σ > 0.302), severe cavitation (σ < 0.257), uncavitation (σ > 0.358), and cavitation (σ < 0.286) of the binary category. The sensitivity of the current signal to cavitation is lower than that of the vibration signal; thus, low differentiation may occur in the discrimination between non-cavitation and cavitation initiation. Distinguishing between cavitation and non-cavitation states is important for some practical engineering applications. Therefore, three classification [Y1, Y2, and Y3] and binary classification [P1 and P2] cases are respectively used in this paper for cavitation state identification and comparative analysis. Table 2 shows the characteristic data of the first component of the current signal at 1.0 Q after VMD decomposition.

TABLE 2

TABLE 2. BIMF each characteristic part data table.

3.2 Cavitation state prediction and result analysis of neural network based on current

The back propagation (BP) neural network is a multilayer feed-forward neural network trained in accordance with an error back propagation algorithm (Haykin, 1994; Sain, 1997). The structure of the multilayer feed-forward BP neural network is shown in Figure 5. Firstly, the obtained mixed current signals are estimated, and the independent component estimates of the completely separated source signals are obtained. Secondly, genetic algorithm is used to optimize the weight and threshold of BP neural network. Finally, the normalized energy of multiple independent component estimates is isolated and used as the input of neural grid for the training and prediction of optimized BP neural network.

FIGURE 5

FIGURE 5. Multilayer feedforward (BP) neural network.

The number of nodes in the BP network is determined. The choice of the number of nodes in each layer has a considerable influence on the performance of the network. The selection for the output node depends on the representation of the output and the number of categories of input vectors to be identified (or classified). Therefore, the choice of hidden junction points should be determined in accordance with the actual situation and experience. Node selection generally follows the equation $\mathrm{m}=\sqrt{n+l}+\alpha$, where n is the number of input nodes, l is the number of output nodes, and α is a number within 1–10.

After the decomposition of the filtered current signal by EMD and VMD, the cavitation representation components of different layers contain different cavitation information. This paper divides the sample data obtained under different decomposition methods of current signals into binary and triple classification and then establishes different neural network training models for cavitation pattern recognition to achieve the accuracy of sample classification and the comprehensiveness of comparative analysis to a considerable extent. EMD divides the filtered current signal into seven layers according to the analysis in Chapter 3. Therefore, the number of sample features is 5 × 7, and the number of hidden junctions of neural networks is 40. VMD was decomposed into seven layers; thus, the number of sample features is 5 × 7, and the number of hidden layer junctions of neural networks is 40. The training times are set to 1,000 and the learning rate is 0.02. The training of this model is based on the MATLAB pattern recognition module. The training results are represented by a confusion matrix and ROC curve. The confusion matrix is a direct representation of the accuracy rate of classification results and the category where the current classification results belongs to. The abscissa typically represents the real target category, and the ordinate is the obtained category by model classification. The “receiver operating characteristic,” which is also known as ROC curve, is used to determine the quality of the classification model and test results. The ROC curve is an essential and common statistical analysis method.

3.2.1 Three classifications of cavitation states

The training, validation, and test matrices comprised 75%, 10%, and 15% of the sample data of each training model, respectively. The classification results are shown in Figure 6.

FIGURE 6

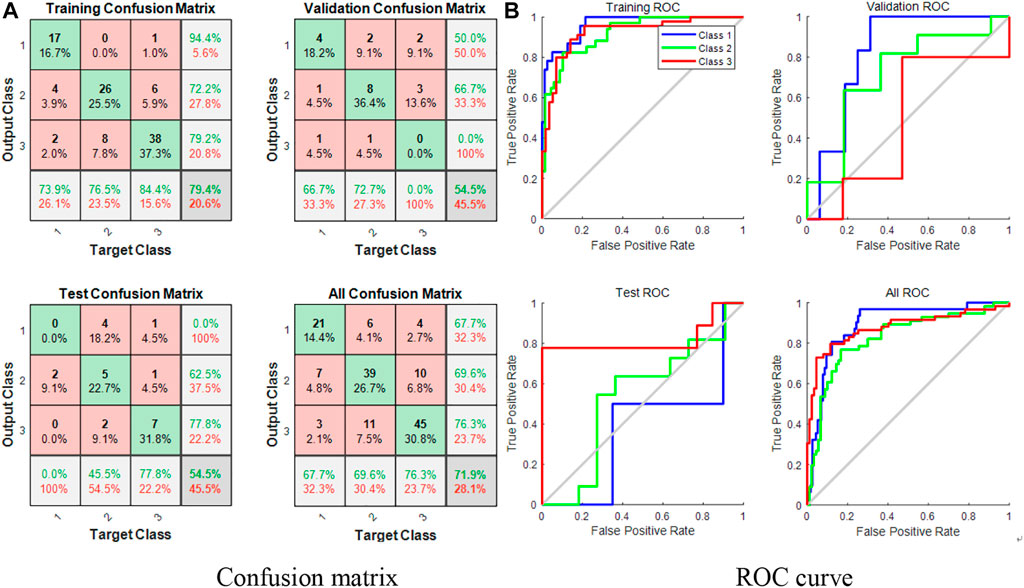
FIGURE 6. Three classification effects of EMD decomposition neural network cavitation state recognition. (A) Confusion matrix (B) ROC curve.

As shown in Figure 6, the accuracy of the neural network training set obtained by EMD decomposition is 79.4%, the verification set is 54.5%, the test set is 54.4%, and the overall accuracy is 71.9%. The ROC curve distribution is poor, the verification and test sets of the first and second classifications have a considerable uncertainty, and the recognition rate is the lowest. Overall, the accuracy of cavitation recognition and classification of the three classification neural network obtained by EMD decomposition is poor, and the classification model trained is not good.

As shown in Figure 7, the accuracy of the neural network training set obtained by VMD decomposition is 77.4%, the verification set is 83.0%, the test set is 80.9%, and the overall accuracy is 78.8%. In the ROC curve distribution diagram, the third classification has the best effect, while the first and second categories are partially confused. The current signal contains abundant cavitation information under serious cavitation. Overall, the classification accuracy of the three classification neural network obtained from VMD decomposition is universal, and the classification model is generally trained. The error distribution histogram of the recognition results is shown in the Figure 8.

FIGURE 7

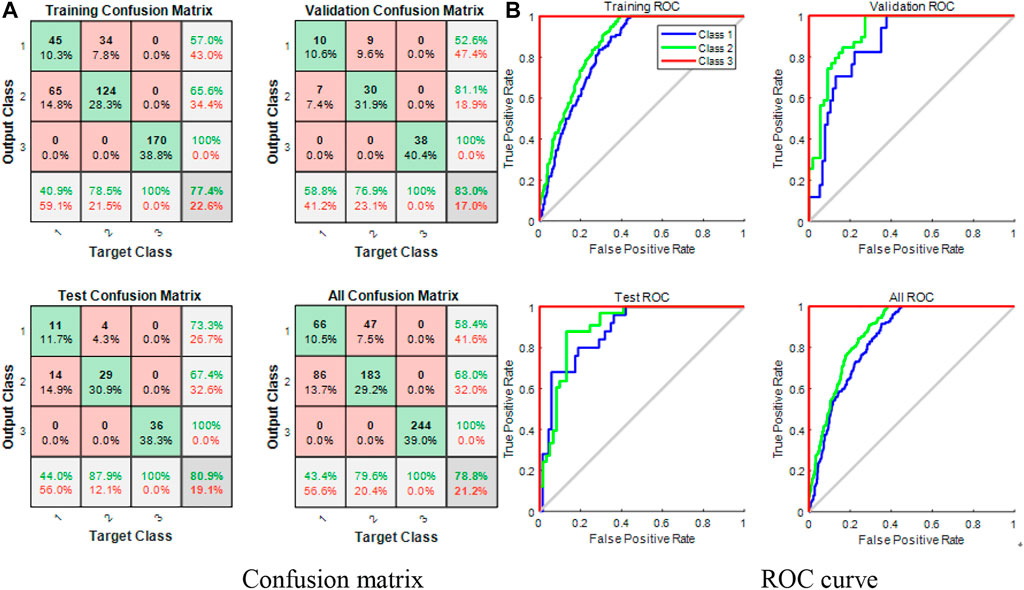
FIGURE 7. Effect of three classifications of VMD decomposition neural network cavitation state recognition. (A) Confusion matrix (B) ROC curve.

FIGURE 8

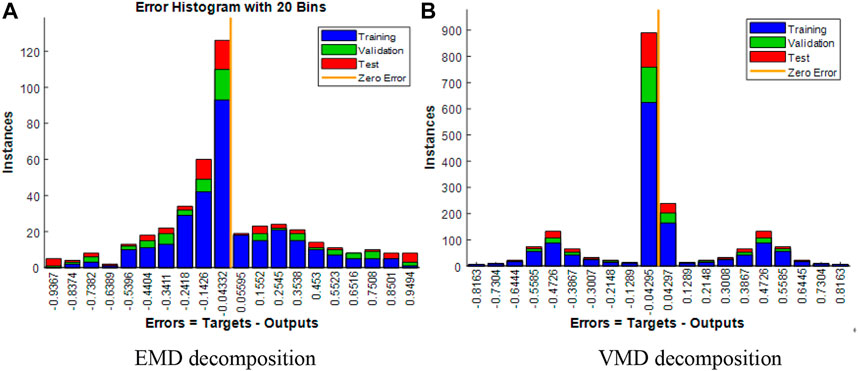
FIGURE 8. Error range distribution diagram of neural network training model based on current signal cavitation tri-classification. (A) EMD decomposition (B) VMD decomposition.

As shown in Figure 8, the error range distribution of the neural network training model obtained by three classification EMD and VMD decomposition is wide but that of VMD decomposition is relatively concentrated. The classification effect is slightly higher than that of EMD decomposition.

3.2.2 Cavitation state dichotomy

The effect of the three classifications is average based on the above analysis. Model training and prediction are conducted considering the requirement of cavitation state binary classification in practical engineering applications. For the sample data of the training model, the training, validation, and test matrices accounted for 75%, 15%, and 15% of the samples, respectively. The classification results are shown in the figure below.

As shown in Figure 9, the accuracy of the binary neural network obtained by EMD decomposition is 84.8% for the training set, 86.4% for the verification set, 83.1% for the test set, and 84.8% for overall accuracy. The ROC curve distribution is vertical, the distribution of the verification and test sets is similar, the resolution of the first and second classifications is also high, and the test performance of the model is satisfactory. Overall, the binary neural network obtained by EMD decomposition has high cavitation recognition and classification accuracies and the trained classification model is superior.

FIGURE 9

FIGURE 9. Effect of EMD binary classification. (A) Confusion matrix (B) ROC curve.

Table 3 is overall recognition accuracy table of current cavitation degree of the neural network under each decomposition method, where the “Q” is the flow of centrifugal pump. As shown in Figure 10, the accuracy of the neural network training set obtained by VMD decomposition is 93.8%, the verification set is 86.4%, the test set is 89.8%, and the overall accuracy is 92.1%. Meanwhile, the ROC curve distribution is approximately vertical, and the first and second classification accuracies are both high. Test set accuracy is also higher than EMD decomposition. Overall, the binary neural network obtained from VMD decomposition has high cavitation recognition and classification accuracy and trained classification model is superior.

TABLE 3

TABLE 3. Overall recognition accuracy table of current cavitation degree of the neural network under each decomposition method.

FIGURE 10

FIGURE 10. Effect of VMD binary classification. (A) Confusion matrix (B) ROC curve.

As shown in Table 3, the accuracy of binary cavitation recognition is generally higher than that of three-category cavitation recognition. Comparing the results under different working conditions, a large flow rate possibly leads to cavitation; therefore, the recognition rate of the current is high. The recognition rate of VMD decomposition under different working conditions is higher than that of EMD, indicating that each component obtained by VMD decomposition contains richer cavitation information than that obtained by EMD decomposition. Overall, in practical engineering applications, the neural network binary classification centrifugal pump cavitation recognition model based on VMD decomposition has high accuracy and has application value in general centrifugal pump cavitation monitoring applications when the cavitation state of the centrifugal pump is identified by current. This is consistent with the research conclusions obtained from the application of vibration signals in literature (Li et al., 2016) and literature (Ming et al., 2017). VMD decomposition can identify characteristic quantities with higher accuracy in centrifugal pump fault diagnosis. Therefore, the cavitation recognition technology based on current signal provided in this paper can still obtain the cavitation fault recognition rate of the same precision under complex and harsh environment. Therefore, the research results in this paper have obvious advantages, and also have significant value in the traditional centrifugal pump fault diagnosis application.

4 Conclusion

This paper mainly focuses on the soft sensing of the cavitation state of a centrifugal pump. In view of the difficulty of judging the cavitation state of centrifugal pump under complex working conditions, this paper analyzes the current and vibration signals in the cavitation state of centrifugal pump based on soft sensing technology. On this basis, based on the information fusion theory, a cavitation state recognition model combining the current and vibration signals is constructed to improve the cavitation state recognition rate and anti-interference performance, and the following conclusions are drawn:

(1) Testing results of the cavitation performance of the centrifugal pump showed that the head coefficient Ψ initially remains unchanged with the decrease in the cavitation number and the value of Ψ decreases rapidly when the cavitation number is reduced to a certain value. Comparison of the critical cavitation number under different conditions indicated the relatively early occurrence of cavitation under the high flow condition (1.25 Q). Thus, under the corresponding critical cavitation number, a small number of bubbles appear near the suction surface of the inlet edge of the impeller, which represents the beginning of cavitation.

(2) Comparison results of the neural network training obtained from EMD and VMD decompositions under the cavitation state classification revealed that the overall accuracy of EMD is 71.9%, which is lower than that of VMD (78.8%). The ROC curve distribution indicated that the first and second classifications of the verification and test sets obtained by EMD showed considerable uncertainty and the recognition rate was the lowest. The third classification obtained by VMD is the best, while the first and second categories are partially obscured.

(3) Comparison results of the neural network training obtained by EMD and VMD decompositions under cavitation state dichotomy demonstrated that the overall accuracy of the neural network training obtained by EMD decomposition is 84.8% while that of VMD can reach 93.8%. From the perspective of ROC curve distribution, the distribution obtained by VMD is approximately vertical, the resolution of the first and second classifications is high, and the accuracy of the test set is higher than that of EMD decomposition.

The current signal based centrifugal pump monitoring has a high application value for some low requirements of centrifugal pump cavitation state monitoring, especially for the monitoring equipment portability, low cost and accuracy has a great application demand. Therefore, the follow-up work can develop the corresponding portable monitoring equipment, focusing on the future 5G and Internet of things technology in the “cloud” development of the corresponding soft sensor model and database, to achieve the real-time monitoring of centrifugal pump cavitation state and pump operation stability.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

LC: Conceptualization, methodology, software; HY: Data curation, writing–original draft; TX: Visualization, investigation, supervision; ZL: Software, validation, writing–review editing. All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was supported by the Fundamental Research Funds for the Central Universities (No: JZ2021HGTB0090), the University Synergy Innovation Program of Anhui Province under Grant No. GXXT-2019-004, the financial support provided by the National Natural Science Foundation of China (51806053).

Acknowledgments

The authors are grateful for the support of the National Natural Science Foundation of China.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Casada, D., Tutterow, V., and Mckane, A. (1999). Screening pumping systems for energy savings opportunities. Energy Eng. 97 (2), 43–63.

Google Scholar

Dragomiretskiy, K., and Zosso, D. (2014). Variational mode decomposition. IEEE Trans. Signal Process. 62 (3), 531–544. doi:10.1109/tsp.2013.2288675

CrossRef Full Text | Google Scholar

Harihara, P. P., and Parlos, A. G. “Sensorless detection and isolation of faults in motor-pump systems,” in Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Boston, Massachusetts, USA, November 2008.

Google Scholar

Haykin, S. (1994). “Neural networks:A comprehensive foundation,” in Neural networks A comprehensive foundation (Upper Saddle River, NJ, United States: Prentice Hall PTR), 71–80.

Google Scholar

Hu, H. Y., and Zhao, H. P. (2007). The analysis of stator harmonic current when piston pump is driven by asynchronous motor. Ship Sci. Technol. 29 (1), 55–57.

Google Scholar

Iso, (2010). ISO 13709:2009 (identical). Centrifugal pumps for petroleum, petrochemical and natural gas industries. https://www.iso.org/standard/41612.html.

Google Scholar

Izadeh, S. A. .F., and Yari, B. (2017). Pump cavitation detection through fusion of support vector machine classifier data associated with vibration and motor current signature. Insight - Non-Destructive Test. Cond. Monit. 59 (12), 669–673. doi:10.1784/insi.2017.59.12.669

CrossRef Full Text | Google Scholar

Kenull, T., Canders, W. R., and Kosyna, G. (2003). Formation of self-excited vibrations in wet rotor motors and their influence on the motor current. Eur. Trans. Electr. Power 13 (2), 119–125. doi:10.1002/etep.4450130207

CrossRef Full Text | Google Scholar

Li, H., Yu, B., Qing, B., and Luo, S. (2016). Cavitation pulse extraction and centrifugal pump analysis. J. Mech. Sci. Technol. 31 (3), 1181–1188. doi:10.1007/s12206-017-0216-z

CrossRef Full Text | Google Scholar

Li, Z., Jiang, W., Zhang, S., and Sun, Y. (2021). A hydraulic pump fault diagnosis method based on the modified ensemble empirical mode decomposition and wavelet kernel extreme learning machine methods. Sensors 21 (8), 2599. doi:10.3390/s21082599

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Z., Zhang, X., Zou, S., and Li, Z. (2020). Feature extraction of cavitation acoustic emission signal of centrifugal pump based on improved variational mode decomposition. J. Drainage Irrigation Mach. Eng. 38 (12), 1196–1202.

Google Scholar

Ming, Z., Jiang, Z., and Feng, K. (2017). Research on variational mode decomposition in rolling bearings fault diagnosis of the multistage centrifugal pump. Mech. Syst. Signal Process. 93, 460–493. doi:10.1016/j.ymssp.2017.02.013

CrossRef Full Text | Google Scholar

Nazarov, V., Zuev, A., and Nazarov, L. (2018). Advancing methodology to specify cavitation characteristic of screw-type centrifugal pumps. Iop Conf. 450, 11–22.

CrossRef Full Text | Google Scholar

Nazarychev, A. N., Novoselov, E. M., Polkoshnikov, D. A., Strakhov, A. S., and Skorobogatov, A. A. (2020). A method for monitoring the condition of rotor windings in induction motors during startup based on stator current. Russ. J. Nondestruct. Test. 56 (8), 661–667. doi:10.1134/s1061830920080070

CrossRef Full Text | Google Scholar

Perovic, S. (2000). Diagnosis of pump faults and flow regimes. Brighton and Hove, England: University of Sussex.

Google Scholar

Sain, S. R. (1997). The nature of statistical learning theory. Technometrics 38 (4), 409. doi:10.1080/00401706.1996.10484565

CrossRef Full Text | Google Scholar

Sánchez, W., Carvajal, C., Poalacin, J., and Salazar, E. “Detection of cavitation in centrifugal pump for vibration analysis,” in Proceedings of the 4th International Conference on Control, Automation and Robotics (ICCAR), Auckland, New Zealand, April 2018, 460–464.

Google Scholar

Schmalz, S. C., and Schuchmann, R. P. (2004). “Method and apparatus of detecting low flow/cavitation in a centrifugal pump,”. US6709240B1 (Alexandria, Virginia, United States: United States Patent and Trademark Office).

Google Scholar

Senthilkumar, M., Yuvaraja, M., and Kok, M. (2015). fault diagnosis of centrifugal pump and vibration control using shape memory alloy based ATDVA. Appl. Mech. Mater. 787, 927–931. doi:10.4028/www.scientific.net/amm.787.927

CrossRef Full Text | Google Scholar

Siegler, J. A., Sark, Ad Y. A. A., and Nemarich, C. (2010). Motor current signal analysis for diagnosis of fault conditions in shipboard equipment. Nav. Eng. J. 107 (1), 77–98. doi:10.1111/j.1559-3584.1995.tb02576.x

CrossRef Full Text | Google Scholar

Skowron, M., Orlowska-Kowalska, T., and Wolkiewicz, M. (2020). Convolutional neural network-based stator current data-driven incipient stator fault diagnosis of inverter-fed induction motor. Energies 13 (6), 1–21.

CrossRef Full Text | Google Scholar

Wang, C., Wang, M., Yang, B., Song, K., Zhang, Y., and Liu, L. (2021). A novel methodology for fault size estimation of ball bearings using stator current signal. Measurement 171 (3), 108723. doi:10.1016/j.measurement.2020.108723

CrossRef Full Text | Google Scholar

Wang, J., and Wang, Y. (2018). Rotating corrected-based cavitation model for a centrifugal pump. J. Fluids Eng. Trans. Asme 140, 111301.

Google Scholar

Welch, D. E., Haynes, H. D., and Cox, D. F. (2002). Electrical signature analysis (ESA) as a diagnostic maintenance technique for detecting the high consequence fuel pump failure modes. Oak Ridge, TN, United States: Oak Ridge National Laboratory.

Google Scholar