Influence of fiber hollowness on the local thermo-electro-elastic field in a thermoelectric composite

The fiber geometry is one of the important parameters in the effective conversion performance and local strength of thermoelectric composites. In this study, the plane problem of a hollow fiber embedded within a non-linear thermoelectric medium in the presence of a uniform remote in-plane electric current and a uniform remote energy flux is investigated based on the complex variable method. Closed-form expressions for all the potential functions characterizing the thermoelectric field and the associated thermal stress field in both the matrix and fiber are obtained by solving the corresponding boundary value problem. Numerical examples are presented to illustrate the effect of hollowness ratio of the fiber on the local energy conversion efficiency and interfacial thermal stress concentration. It is found that a higher conversion efficiency and a lower amount of thermal stress concentration around a hollow fiber than that around a solid fiber could be achieved simultaneously by appropriate selection of the hollowness ratio of the fiber. The results can be directly used for performance optimization and reliability evaluation in design of thermoelectric composites in engineering.

1 Introduction

Thermoelectric material is a novel kind of functional material, which can directly convert heat into electricity and vice versa (Bell, 2008). A thermoelectric device is free of moving parts, noises, and environmentally harmful emissions, making it extremely attractive in renewable energy fields, such as waste heat recovery, solar power generation, carbon reduction, and Freon-free refrigeration (Zhang et al., 2016; He and Tritt, 2017; Mahmoudinezhad et al., 2018). The electric transport and thermal conduction in a thermoelectric material are intrinsically coupled, making it highly challenging to improve the conversion efficiency in a single-phase thermoelectric material (Yang et al., 2013). Therefore, a lot of effort in developing high-performance thermoelectric material is devoted to engineering hybrid composites by introducing inclusions/fibers into single-phase thermoelectric material to enhance the overall conversion efficiency (Wan et al., 2015; Guo et al., 2016; Srivastava et al., 2018).

From the point of view of solid mechanics, the existence of the inclusions/fibers may cause severe concentration of the temperature field and the associated thermal stress field in thermoelectric materials under in-service conditions. Most thermoelectric materials are semiconductors with poor mechanical properties, and excessive thermal stress may lead to the premature failure of the thermoelectric devices (Li et al., 2015; Song et al., 2019). The analysis of thermoelectric materials with the inclusions/fibers can further improve our understanding of the mechanical behavior of such new materials and thus is essential for optimal design and improved reliability of thermoelectric composites. Using complex variable methods, rigorous thermo-electro-mechanical analyses of thermoelectric materials containing elastic inhomogeneities have been carried out by several authors (Zhang et al., 2017; Wang et al., 2018; Yang et al., 2020). In the corresponding discussions of the inhomogeneity problem in thermoelectric materials, it has been assumed that the inclusion or fiber is assumed to have a solid cross-section. In engineering practice, hollow fibers or particles are often introduced into thermoelectric materials due to their distinct microstructures. To the best of our knowledge, the effect of a hollow particle/fiber on the thermoelectric and thermoelastic responses of a thermoelectric composite has never been thoroughly investigated. This motivates our current work.

The paper is organized as follows: basic equations of a non-linear thermoelectric material are presented in Section 2, followed by the detailed analysis of the plane problem of an infinite thermoelectric matrix containing a hollow fiber subjected to a uniform remote thermoelectric loading by using the complex variable technique in Section 3. In Section 4, we use the explicit results from Section 3 and present numerical examples to illustrate the influence of the hollowness ratio on the local energy conversion efficiency and thermal stress concentration around a hollow fiber in a thermoelectric composite. Finally, we summarize our conclusion in Section 5.

2 Basic equations for thermoelectric materials

In a homogenous thermoelectric medium wherein both electric charges and energy are conserved, the governing equations and transport equations for the non-linearly coupled electric and heat conduction are given as follows (Yang et al., 2013):

$\nabla \bullet \mathbf{I}=0,\hspace{0.17em}\nabla \bullet \mathbf{J}=0(1)$

together with

$\mathbf{I}=-\delta \nabla \varphi -\delta \epsilon \nabla T(2)$

$\mathbf{J}=\mathbf{q}+\varphi \mathbf{I}=\left(\varphi +\epsilon T\right)\mathbf{I}-\kappa \nabla T(3)$

where $\nabla$ is the Nabla operator, $\mathbf{I}={\left[I_x,I_y\right]}^{\mathrm{T}}$ is the electric current vector, $\mathbf{J}={\left[J_x,J_y\right]}^{\mathrm{T}}$ denotes the energy flux vector, and $\mathbf{q}={\left[q_x,q_y\right]}^{\mathrm{T}}$ represents the heat flux vector. In addition, $\varphi$ is the electric potential, $T$ is the temperature, $\delta$ is the electric conductivity, $\kappa$ is the thermal conductivity, and $\epsilon$ is the Seebeck coefficient. Inserting Eqs 2, 3 into the governing equations in Eq. 1 results in

${\nabla }^2\left(\varphi +\epsilon T\right)=0(4)$

${\nabla }^{2}T+\frac{\delta }{\mathit{\kappa }}\nabla \left(\varphi +\epsilon T\right)\bullet \nabla \left(\varphi +\epsilon T\right)=0(5)$

According to Eqs 4, 5, the electric potential $\varphi$ and temperature $T$ can be expressed in terms of two potential functions, namely, $h\left(z\right)$ and $g\left(z\right)$, of the complex variable $z=x+iy$ ($i=\sqrt{-1}$ is the imaginary unit) as follows (Yu et al., 2018):

$\varphi =\mathrm{R}\mathrm{e}\left[h\left(z\right)\right]-\epsilon \mathrm{R}\mathrm{e}\left[g\left(z\right)\right]+\frac{\delta \epsilon }{4\mathit{\kappa }}h\left(z\right)\overline{h\left(z\right)}(6)$

$T=\mathrm{R}\mathrm{e}\left[g\left(z\right)\right]-\frac{\delta }{4\mathit{\kappa }}h\left(z\right)\overline{h\left(z\right)}(7)$

where “Re” denotes the real part of a complex number and the overbar denotes the complex conjugate. It follows from Eqs 2, 3, 6, 7 that the electric current components $\left(I_x,I_y\right)$, the energy flux components $\left(J_x,J_y\right)$, and the heat flux components $\left(q_x,q_y\right)$ are expressed in terms of the two complex functions as follows (Yu et al., 2018):

$I_x-i{I}_y=-\delta h^{\prime }\left(z\right)(8)$

$J_x-i{I}_y=-\kappa g\prime \left(z\right)-\frac{\delta }{2}{h}^{\prime }\left(z\right)h\left(z\right)(9)$

$q_x-i{q}_y=-\kappa g\prime \left(z\right)+\frac{\delta }{2}{h}^{\prime }\left(z\right)\overline{h\left(z\right)}+\epsilon \delta h^{\prime }\left(z\right)\left\{\frac{\delta }{4\kappa }h\left(z\right)\overline{h\left(z\right)}-\mathrm{R}\mathrm{e}\left[g\left(z\right)\right]\right\}(10)$

where the prime ($\prime$) denotes the derivative of the complex variable $z$. In addition, the resultant electric current and energy flux on a certain directed curve $s$ can be expressed as follows (Yu et al., 2018):

$\mathit{\int }{I}_n\left(s\right)ds=-\delta \mathrm{I}\mathrm{m}\left[h\left(z\right)\right](11)$

$\mathit{\int }{J}_n\left(s\right)ds=-\kappa \mathrm{I}\mathrm{m}\left[g\left(z\right)+\frac{\delta }{4\kappa }{h}^2\left(z\right)\right](12)$

which can be used as the boundary conditions of the electric current and energy flux in the integral form. Here, “Im” denotes the imaginary part of a complex number.

For a steady thermal stress problem where the elastic constants are assumed to be temperature-independent, the three in-plane stresses (${\sigma }_x,{\sigma }_{y,}{\tau }_{xy}$) and the two in-plane displacements ($u_x,u_y$) caused by the uneven temperature distribution $T\left(x,y\right)$ given in Eq. 7 can be expressed in terms of two elastic potential functions, namely, $\phi \left(z\right)$ and $\psi \left(z\right)$, together with the aforementioned thermoelectric potential functions $h\left(z\right)$ and $g\left(z\right)$ as follows (Yu et al., 2018):

${\sigma }_y+{\sigma }_x=2\left[{\phi }^{\prime }\left(z\right)+\overline{{\phi }^{\prime }\left(z\right)}\right]+2\xi h\left(z\right)\overline{h\left(z\right)}(\mathrm{13a})$

${\sigma }_y-{\sigma }_x+2i{\tau }_{xy}=2\left[\overline{z}{\phi }^{″}\left(z\right)+{\psi }^{\prime }\left(z\right)\right]+2\xi h^{\prime }\left(z\right)\overline{H\left(z\right)}(\mathrm{13b})$

$2\mu \left(u_x+i{u}_y\right)=\beta \phi \left(z\right)-z\overline{{\phi }^{\prime }\left(z\right)}-\overline{\psi \left(z\right)}-\xi \overline{h\left(z\right)}H\left(z\right)+2\mu \lambda G\left(z\right)(\mathrm{14a})$

Here, $H\left(z\right)$ and $G\left(z\right)$ are two complex functions satisfying $H^{\prime }\left(z\right)=h\left(z\right)$ and $G^{\prime }\left(z\right)=g\left(z\right)$, $\mu$ is the shear modulus, $\xi =\mu {\lambda }_v\delta /4\kappa$ is a real constant, $\beta =3-4v_{*}$, $\lambda =\left(1+v_{*}\right){\lambda }_{*}$, and ${\lambda }_v=\left(1+v_{*}\right){\lambda }_{*}/\left(1-v_{*}\right)$ for plane strain, $\beta =\left(3-v_{*}\right)/\left(1+v_{*}\right)$, $\lambda ={\lambda }_{*}$, and ${\lambda }_v=\left(1+v_{*}\right){\lambda }_{*}$ for plane stress with ${\lambda }_{*}$ representing the thermal expansion coefficient and $v_{*}$ being the Poisson’s ratio. Additionally, the resultant forces ($f_x$, $f_y$) on a certain directed curve $s$ can be calculated as

$i\int \left(f_x+i{f}_y\right)ds=\phi \left(z\right)+z\overline{{\phi }^{\prime }\left(z\right)}+\overline{\psi \left(z\right)}+\xi \overline{h\left(z\right)}H\left(z\right)(\mathrm{14b})$

which will be used as the stress boundary condition in the integral form. To summarize, the mathematical formulation of the non-linearly coupled thermo-electro-mechanical problem is completed using the complex function theory with each unknown function determined by the corresponding boundary conditions.

3 Solutions of thermoelectric material with a hollow fiber

As illustrated in Figure 1, we consider the plane strain deformation of an infinite thermoelectric matrix enclosing a hollow fiber subjected to a uniform remote electric current $I_y^{\infty }$ and a uniform remote energy flux $J_y^{\infty }$. Let $S_1$ and $S_2$ denote the regions occupied by the surrounding matrix ($\left|z\right|\ge R_1$) and the hollow fiber ($R_2\le \left|z\right|\le R_1$), respectively. The fiber and matrix are assumed to be perfectly bonded, and both the electric and heat conduction can penetrate the interface $L_1$. The continuity conditions of the thermoelectric field across $L_1$ can be expressed as follows (Wang et al., 2018):

$h_1\left(z_1\right)+\overline{h_1\left(z_1\right)}=h_2\left(z_1\right)+\overline{h_2\left(z_1\right)}(\mathrm{15a})$

$h_1\left(z_1\right)-\overline{h_1\left(z_1\right)}=\frac{{\delta }_2}{{\delta }_1}\left[h_2\left(z_1\right)-\overline{h_2\left(z_1\right)}\right](\mathrm{15b})$

$g_1\left(z_1\right)+\overline{g_1\left(z_1\right)}-\frac{{\delta }_1}{{2\kappa }_1}{h}_1\left(z_1\right)\overline{h_1\left(z_1\right)}=g_2\left(z_1\right)+\overline{g_2\left(z_1\right)}-\frac{{\delta }_2}{{2\kappa }_2}{h}_2\left(z_1\right)\overline{h_2\left(z_1\right)}(\mathrm{16a})$

$g_1\left(z_1\right)-\overline{g_1\left(z_1\right)}+\frac{{\delta }_1}{{4\kappa }_1}\left({h_1\left(z_1\right)}^2-{\overline{h_1\left(z_1\right)}}^2\right)=\frac{{\kappa }_2}{{\kappa }_1}\left[g_2\left(z_1\right)-\overline{g_2\left(z_1\right)}+\frac{{\delta }_2}{{4\kappa }_2}\left({h_2\left(z_1\right)}^2-{\overline{h_2\left(z_1\right)}}^2\right)\right](\mathrm{16b})$

where $z_1=R_1{e}^{i\theta }$ represents those points on the interface $L_1$ with $\theta$ denoting the angle between the outer normal vector and the positive x-axis in the z-plane as shown in Figure 1; the index 1 or 2 indicates the corresponding quantity defined in either the matrix (region $S_1$) or the hollow fiber (region $S_2$), respectively. Furthermore, the inner surface of the hollow fiber is assumed to be electrically impermeable and thermally insulated

$h_2\left(z_2\right)-\overline{h_2\left(z_2\right)}=0(\mathrm{17a})$

$g_2\left(z_2\right)-\overline{g_2\left(z_2\right)}+\frac{{\delta }_2}{{4\kappa }_2}\left({h_2\left(z_2\right)}^2-{\overline{h_2\left(z_2\right)}}^2\right)=0(\mathrm{17b})$

where $z_2=R_2{e}^{i\theta }$ represents those points on the inner surface $L_2$. In ensuing analysis, we first solve the thermoelectric potentials $h_1\left(z\right)$ and $h_2\left(z\right)$ from the electric boundary conditions in Eqs 15a, 15b, 17a and then substitute them into the thermal boundary conditions in Eqs 16a, 16b, 17b to determine $g_1\left(z\right)$ and $g_2\left(z\right)$. Considering Eq. 8 and the far-field condition of the electric current, the potential function $h_1\left(z\right)$ takes the following form:

$h_1\left(z\right)=\frac{i{I}_y^{\infty }}{{\delta }_1}z+U_0+h_1^{*}\left(z\right)(18)$

where $U_0$ is a real constant related to the equilibrium thermoelectric potential and is set as zero (i.e., $U_0=0$) without loss of generality in this paper. The analytical function $h_1^{*}\left(z\right)$ satisfying $h_1^{*}\left(z\to \infty \right)=0$ represents the disturbance on the electric field caused by the fiber. The region occupied by the matrix is the exterior of contour $L_1$; thus, $h_1^{*}\left(z\right)$ can be expanded into Fourier series as $h_1^{*}\left(z\right)={\sum }_{n=1}^{+\infty }{a}_n{z}^n$, where $a_n$ is the complex coefficient to be determined. The region occupied by the fiber can be regarded as the intersection of the exterior of contour $L_2$ and the interior of contour $L_1$, and the potential function $h_2\left(z\right)$ then can be expanded as $h_2\left(z\right)={\sum }_{-\infty }^{+\infty }{b}_n{z}^n$ with $b_n$ being the unknown coefficients to be determined from the continuity conditions in Eqs 15a, 15b, 17a. Omitting details, the thermoelectric potential functions are finally determined as follows:

$h_1\left(z\right)=A_1\left(\frac{z}{R_1}\right)+A_{-1}{\left(\frac{z}{R_1}\right)}^{-1}(\mathrm{19a})$

$h_2\left(z\right)=C_1\left(\frac{z}{R_1}\right)+\alpha \overline{C_1}{\left(\frac{z}{R_1}\right)}^{-1}(\mathrm{19b})$

where $A_1=i{I}_y^{\infty }{R}_1/{\delta }_1$ and $\alpha$ is the hollowness ratio defined by the hollow area over the total area of the cross-section as $\mathrm{\alpha }={\left(R_2/R_1\right)}^2$. In addition, $A_{-1}$ and $C_1$ are two complex constants calculated by

$A_{-1}=\frac{\alpha \left(1+\frac{{\delta }_2}{{\delta }_1}\right)+\left(1-\frac{{\delta }_2}{{\delta }_1}\right)}{\left(1+\frac{{\delta }_2}{{\delta }_1}\right)+\alpha \left(1-\frac{{\delta }_2}{{\delta }_1}\right)}\overline{A_1},C_1=\frac{2}{\left(1+\frac{{\delta }_2}{{\delta }_1}\right)+\alpha \left(1-\frac{{\delta }_2}{{\delta }_1}\right)}{A}_1$

FIGURE 1

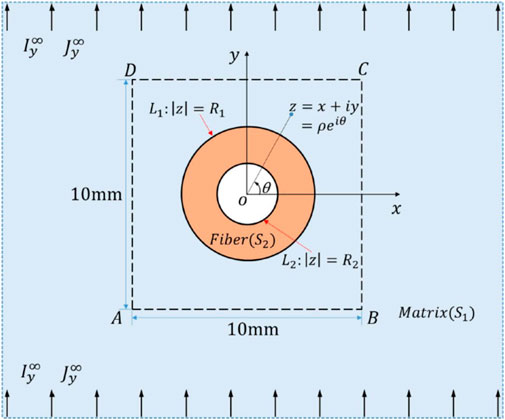
FIGURE 1. Hollow fiber embedded in a thermoelectric matrix under uniform remote in-plane thermoelectric loading.

Considering that the energy flux at infinity is uniform, according to Eqs 9, 18, the potential function $g_1\left(z\right)$ takes the form of

$g_1\left(z\right)=\frac{{I_y^{\infty }}^2}{{{4\kappa }_1\delta }_1}{z}^2+\frac{i{J}_y^{\infty }}{{\kappa }_1}z+T_0+g_1^{*}\left(z\right)(20)$

where the real constant $T_0$ denotes the uniform temperature field in the matrix and the analytical function $g_1^{*}\left(z\right)$ satisfying $g_1^{*}\left(z\to \infty \right)=0$ represents the disturbance on the thermal field caused by the fiber. The same argument applies to Eqs 16a, 16b, 17b, we obtain

$g_1\left(z\right)=B_2{\left(\frac{z}{R_1}\right)}^2+B_1\left(\frac{z}{R_1}\right)+T_0+B_{-1}{\left(\frac{z}{R_1}\right)}^{-1}+B_{-2}{\left(\frac{z}{R_1}\right)}^{-2}(\mathrm{21a})$

$g_2\left(z\right)=D_2{\left(\frac{z}{R_1}\right)}^2+D_1\left(\frac{z}{R_1}\right)+D_0+\alpha \overline{D_1}{\left(\frac{z}{R_1}\right)}^{-1}+{\alpha }^2\overline{D_2}{\left(\frac{z}{R_1}\right)}^{-2}(\mathrm{21b})$

where

$B_{-2}=\frac{\overline{D_2}}{2}\left[\left(1+\frac{{\kappa }_2}{{\kappa }_1}\right){\alpha }^2+\left(1-\frac{{\kappa }_2}{{\kappa }_1}\right)\right]+\frac{{\Delta }_{-2}}{2},B_{-1=}\frac{\overline{D_1}}{2}\left[\left(1+\frac{{\kappa }_2}{{\kappa }_1}\right)\alpha +\left(1-\frac{{\kappa }_2}{{\kappa }_1}\right)\right]$

$D_2=\frac{2B_2-{\Delta }_2}{\left(1+\frac{{\kappa }_2}{{\kappa }_1}\right)+\left(1-\frac{{\kappa }_2}{{\kappa }_1}\right){\alpha }^2},D_1=\frac{2B_1}{\left(1+\frac{{\kappa }_2}{{\kappa }_1}\right)+\left(1-\frac{{\kappa }_2}{{\kappa }_1}\right)\alpha }$

$D_0=T_0-\frac{{\delta }_1}{4{\kappa }_1}\left({\left|A_1\right|}^2+{\left|A_{-1}\right|}^2\right)+\frac{{\delta }_2}{4{\kappa }_2}\left({1+\alpha }^2\right){\left|C_1\right|}^2$

Here, the two complex constants, namely, ${∆}_2$ and ${∆}_{-2}$, are defined as

${\Delta }_2=\frac{{\delta }_1}{4{\kappa }_1}\left(2A_1\overline{A_{-1}}-A_1^2+{\overline{A_{-1}}}^2\right)-\frac{{\delta }_2}{4{\kappa }_2}\left[2\mathrm{\alpha }-\frac{{\kappa }_2}{{\kappa }_1}\left(1-{\alpha }^2\right)\right]C_1^2$

${\Delta }_{-2}=\frac{{\delta }_1}{4{\kappa }_1}\left(2A_{-1}\overline{A_1}-A_{-1}^2+{\overline{A_1}}^2\right)-\frac{{\delta }_2}{4{\kappa }_2}\left[2\mathrm{\alpha }+\frac{{\kappa }_2}{{\kappa }_1}\left(1-{\alpha }^2\right)\right]{\overline{C_1}}^2$

So far, the quantities related to the electric current and temperature fields in both the matrix and fiber can be determined from Eqs 6 to 10 together with Eqs 19, 21a. The following studies will deal with the analysis of the associated thermal stress problem. Considering the single-valued conditions of elastic displacement (Eq. 14) and the resultant force (Eq. 15), the elastic potential functions in both the matrix and fiber take the following form:

${\phi }_1\left(z\right)=P_0\mathit{ln}\left(\frac{z}{R_1}\right)+{\phi }_1^{*}\left(z\right)(\mathrm{22a})$

${\psi }_1\left(z\right)=Q_0\left(z\right)\mathit{ln}\left(\frac{z}{R_1}\right)+{\psi }_1^{*}\left(z\right)(\mathrm{22b})$

${\phi }_2\left(z\right)=Y_0\mathit{ln}\left(\frac{z}{R_1}\right)+{\phi }_2^{*}\left(z\right)(\mathrm{23a})$

${\psi }_2\left(z\right)=W_0\left(z\right)\mathit{ln}\left(\frac{z}{R_1}\right)+{\psi }_2^{*}\left(z\right)(\mathrm{23b})$

where ${\phi }_j^{*}\left(z\right)$ and ${\psi }_j^{*}\left(z\right)$ (j = 1, 2) are holomorphic functions in the respective regions. Taking Eqs 22, 23 into Eqs. 14, 15 and eliminating the multi-valued terms, we can obtain

$P_0=-\frac{2{\mu }_1{\lambda }_1}{{\beta }_1+1}{B}_{-1}{R}_1,\hspace{0.17em}{Q}_0\left(z\right)=\overline{P_0}+{\xi }_1\overline{A_{-1}}{R}_1{h}^{\left(1\right)}\left(z\right)$

$Y_0=-\frac{2{\mu }_2{\lambda }_2}{{\beta }_2+1}\alpha \overline{D_1}{R}_1,\hspace{0.17em}{W}_0\left(z\right)=\overline{Y_0}+{\xi }_2\alpha C_1{R}_1{h}^{\left(2\right)}\left(z\right)$

The analytical functions ${\phi }_j^{*}\left(z\right)$ and ${\psi }_j^{*}\left(z\right)$ (j = 1, 2) in Eqs 22, 23 will be determined by the following elastic boundary conditions:

${\phi }_1\left(z_1\right)+z_1\overline{{{\phi }_1}^{\prime }\left(z_1\right)}+\overline{{\psi }_1\left(z_1\right)}+{\xi }_1\overline{h_1\left(z_1\right)}{H}_1\left(z_1\right)={\phi }_2\left(z_1\right)+z_1\overline{{{\phi }_2}^{\prime }\left(z_1\right)}+\overline{{\psi }_2\left(z_1\right)}+{\xi }_2\overline{h_2\left(z_1\right)}{H}_2\left(z_1\right)(\mathrm{24a})$

$\frac{1}{{\mu }_1}\left[{\beta }_1{\phi }_1\left(z_1\right)-z_1\overline{{{\phi }_1}^{\prime }\left(z_1\right)}-\overline{{\psi }_1\left(z_1\right)}-{\xi }_1\overline{h_1\left(z_1\right)}{H}_1\left(z_1\right)+2{\mu }_1{\lambda }_1{G}_1\left(z_1\right)\right]=\frac{1}{{\mu }_2}\left[{\beta }_2{\phi }_2\left(z_1\right)-z_1\overline{{{\phi }_2}^{\prime }\left(z_1\right)}-\overline{{\psi }_2\left(z_1\right)}-{\xi }_2\overline{h_2\left(z_1\right)}{H}_2\left(z_1\right)+2{\mu }_2{\lambda }_2{G}_2\left(z_1\right)\right](\mathrm{24b})$

${\phi }_2\left(z_2\right)+z_2\overline{{{\phi }_2}^{\prime }\left(z_2\right)}+\overline{{\psi }_2\left(z_2\right)}+{\xi }_2\overline{h_2\left(z_2\right)}{H}_2\left(z_2\right)=0(25)$

Equations 24a, 24b describe the continuity of elastic stresses and displacements across the perfectly bonded interface $L_1$, and Eq. 25 indicates that the inner surface of the fiber $L_2$ is mechanically free. By enforcing the boundary conditions in Eqs 24, 25 with the aid of Eqs 19, 21b, we arrive at

${\phi }^{\left(1\right)}\left(z\right)=P_0\mathit{ln}\left(\frac{z}{R_1}\right)+\left({\omega }_2{Y}_{-1}+{\mathit{\Omega }}_{-1}\right){\left(\frac{z}{R_1}\right)}^{-1}(\mathrm{26a})$

${\psi }^{\left(1\right)}\left(z\right)=Q_0\left(z\right)\mathit{ln}\left(\frac{z}{R_1}\right)+\left({\omega }_1\overline{Y_1}+\overline{{\mathrm{\Omega }}_1}\right){\left(\frac{z}{R_1}\right)}^{-1}+\left({\omega }_1\overline{Y_2}+\overline{{\mathit{\Omega }}_2}\right){\left(\frac{z}{R_1}\right)}^{-2}+\left({\omega }_2{Y}_{-1}+{\mathit{\Omega }}_{-1}+{\omega }_1\overline{Y_3}+\overline{{\mathit{\Omega }}_3}\right){\left(\frac{z}{R_1}\right)}^{-3}(\mathrm{26b})$

${\phi }^{\left(2\right)}\left(z\right)=Y_0\mathit{ln}\left(\frac{z}{R_1}\right)+Y_{-1}{\left(\frac{z}{R_1}\right)}^{-1}+Y_1{\left(\frac{z}{R_1}\right)}^1+Y_2{\left(\frac{z}{R_1}\right)}^2+Y_3{\left(\frac{z}{R_1}\right)}^3(\mathrm{27a})$

${\psi }^{\left(2\right)}\left(z\right)=W_0\left(z\right)\mathit{ln}\left(\frac{z}{R_1}\right)+\left({\overline{{\mathrm{\Sigma }}_3}+Y_{-1}-\omega }_3\overline{Y_3}\right){\left(\frac{z}{R_1}\right)}^{-3}+\left({\overline{{\mathrm{\Sigma }}_2}-\omega }_3\overline{Y_2}\right){\left(\frac{z}{R_1}\right)}^{-2}+\left({\overline{{\mathrm{\Sigma }}_1}-Y_1-\omega }_3\overline{Y_1}\right){\left(\frac{z}{R_1}\right)}^{-1}+\left[\left({\omega }_2{\omega }_4-{\omega }_3\right)\overline{Y_{-1}}+{\overline{{\mathrm{\Sigma }}_{-1}}-3Y_3+\omega }_4\overline{{\mathit{\Omega }}_{-1}}\right]\left(\frac{z}{R_1}\right)(\mathrm{27b})$

where the four real dimensionless constants ${\omega }_1$, ${\omega }_2$, ${\omega }_3$, and ${\omega }_4$ are given as

${\omega }_1=\frac{{\beta }_2+1}{1-\frac{{\mu }_2}{{\mu }_1}}{\omega }_2=\frac{{\beta }_2+1}{1+{\beta }_1\frac{{\mu }_2}{{\mu }_1}}{\omega }_3=\frac{{\beta }_2+\frac{{\mu }_2}{{\mu }_1}}{\frac{{\mu }_2}{{\mu }_1}-1}{\omega }_4=\frac{{\mu }_2}{{\mu }_1}\frac{{\beta }_1+1}{\frac{{\mu }_2}{{\mu }_1}-1}$

and the four complex constants $Y_1$, $Y_2$, $Y_3$ and $Y_{-1}$ are identified as

$Y_1=\frac{{\mathrm{\Sigma }}_1-{\mathit{\Lambda }}_1}{\left({\omega }_3-\alpha \right)+\left(1-\alpha \right)}{Y}_2=\frac{{\mathrm{\Sigma }}_2+\alpha \overline{Y_0}}{{\omega }_3-{\alpha }^2}$

$Y_3=\frac{\alpha {\omega }_4\overline{{\mathit{\Omega }}_{-1}}+\alpha \overline{{\mathrm{\Sigma }}_{-1}}-{\mathit{\Lambda }}_2+\left[1-\alpha \left({\omega }_3-{{\omega }_2\omega }_4\right)\right]\overline{Y_{-1}}}{3\alpha \left(1-\alpha \right)}$

$Y_{-1}=\frac{\left({\alpha }^3-{\omega }_3\right)\left[{\mathit{\Lambda }}_2-\alpha \left({\omega }_4{\mathit{\Omega }}_{-1}+{\mathrm{\Sigma }}_{-1}\right)\right]+3\alpha \left(1-\alpha \right)\left(\overline{{\mathit{\Lambda }}_3}-\overline{{\mathrm{\Sigma }}_3}\right)}{\left({\alpha }^3-{\omega }_3\right)\left[1-\alpha \left({\omega }_3-{{\omega }_2\omega }_4\right)\right]+3\alpha {\left(1-\alpha \right)}^2}$

together with

${\mathit{\Lambda }}_3=-\frac{1}{2}{\alpha }^3{\xi }_2{R}_1{C_1}^2$

${\mathit{\Lambda }}_2=-{\alpha }^2{\xi }_2{R}_1{\left|\overline{C_1}\right|}^2$

${\mathit{\Lambda }}_1=-\left(\frac{1}{2}+\ln \left(\alpha \right)\right){\alpha }^2{\xi }_2{R}_1{\left|C_1\right|}^2$

${\mathit{\Omega }}_3=\frac{2{\mu }_2{R}_1}{3\left(1-\frac{{\mu }_2}{{\mu }_1}\right)}\left({\lambda }_2{D}_2-{\lambda }_1{B}_2\right)-\frac{{\xi }_1{R}_1}{2}{A}_1\overline{A_{-1}}$

${\mathit{\Omega }}_2=\frac{{\mu }_2{R}_1}{\left(1-\frac{{\mu }_2}{{\mu }_1}\right)}\left({\lambda }_2{D}_1-{\lambda }_1{B}_1\right)-\overline{P_0}$

${\mathit{\Omega }}_1=\frac{2{\mu }_2{R}_1}{\left(1-\frac{{\mu }_2}{{\mu }_1}\right)}\left({\lambda }_2{D}_0-{\lambda }_1{B}_0\right)-\frac{{\xi }_1{R}_1}{2}{\left|A_1\right|}^2$

${\mathit{\Omega }}_{-1}=\frac{2{\mu }_2{R}_1}{\left(1+{\beta }_1\frac{{\mu }_2}{{\mu }_1}\right)}\left({\lambda }_1{B}_{-2}-{\lambda }_2{\alpha }^2\overline{D_2}\right)$

${\mathrm{\Sigma }}_3=\frac{2{\mu }_2{R}_1}{3\left(1-\frac{{\mu }_2}{{\mu }_1}\right)}\left({\lambda }_2{D}_2-{\lambda }_1{B}_2\right)-\frac{{\xi }_2{R}_1}{2}\alpha C_1^2$

${\mathrm{\Sigma }}_2=\frac{{\mu }_2{R}_1}{\left(1-\frac{{\mu }_2}{{\mu }_1}\right)}\left({\lambda }_2{D}_1-{\lambda }_1{B}_1\right)-\overline{Y_0}$

${\mathrm{\Sigma }}_1=\frac{2{\mu }_2{R}_1}{\left(1-\frac{{\mu }_2}{{\mu }_1}\right)}\left({\lambda }_2{D}_0-{\lambda }_1{B}_0\right)-\frac{{\xi }_2{R}_1}{2}{\left|C_1\right|}^2$

${\mathrm{\Sigma }}_{-1}=\frac{2{\mu }_2{R}_1}{\left(1-\frac{{\mu }_2}{{\mu }_1}\right)}\left({\lambda }_1{B}_{-2}-{\lambda }_2{\alpha }^2\overline{D_2}\right)$

Up to here, the elastic stress components ${\sigma }_x$, ${\sigma }_y$, and ${\tau }_{xy}$ in both the matrix and fiber are determined from Eq. 13 with the aid of the two thermoelectric potential functions and two elastic potential functions, and the stress components in polar coordinates can be determined according to Eq. 13 and the following stress transformation formula:

${\sigma }_{tt}+{\sigma }_{nn}={\sigma }_x+{\sigma }_y(\mathrm{28a})$

${\sigma }_{tt}-{\sigma }_{nn}+2i{\tau }_{nt}=e^{2i\theta }\left({\sigma }_y-{\sigma }_x+2i{\tau }_{xy}\right)(\mathrm{28b})$

where ${\sigma }_{nn}$, ${\sigma }_{tt}$, and ${\tau }_{nt}$ are the normal stress, hoop stress, and shear stress, respectively.

4 Numerical examples

To illustrate the application of the analysis model, some numerical examples are presented. In the following examples, the matrix is set as a bismuth tellurium semiconductor, and the material constants are given as ${\delta }_1=1.67\times {10}^{5}S{\mathrm{m}}^{-1}$, ${\kappa }_1=2\mathrm{W}{\mathrm{m}}^{-1}{\mathrm{K}}^{-1}$, ${\epsilon }_1=2\times {10}^{-4}\mathrm{V}{\mathrm{K}}^{-1}$, ${\mu }_1=60GPa$, $v_1=0.3$, and ${\lambda }_1=4.2\times {10}^{-6}{\mathrm{K}}^{-1}$ (Huang et al., 2008). The imposed far-field loadings are $I_y^{\infty }=-2\times {10}^{4}A{\mathrm{m}}^{-2}$ and $J_y^{\infty }=8\times {10}^3\mathrm{W}{\mathrm{m}}^{-2}$, and the average temperature on the matrix is set as $T_0=350\mathrm{K}$. In addition, the Seebeck coefficient and Poisson’s ratio of the fiber are taken as the same with those of the matrix material.

In engineering practice, the thermoelectric conversion efficiency is a crucial parameter for the design of thermoelectric composites. Figure 2 shows the effect of the hollowness ratio $\mathrm{\alpha }$ on the local energy conversion efficiency $\mathrm{\eta }$ around a hollow fiber with different electric and thermal conductivity properties. A finite region ($10\mathrm{m}\mathrm{m}\times 10\mathrm{m}\mathrm{m}$) bounded by ABCD around the hollow fiber is selected to calculate the local thermoelectric conversion efficiency, as shown in Figure 1. The thermoelectric conversion efficiency in the area ABCD is given as follows (Liu, 2012):

$\mathrm{\eta }=\frac{q_{input}-q_{output}}{q_{input}}=\frac{\left|q_{CD}-q_{AB}\right|}{\mathit{max}\left(\left|q_{CD}\right|,\left|q_{AB}\right|\right)}$

where $q_{AB}={\int }_A^B{q}_y\left(x\right)dx$ and $q_{CD}={\int }_C^D{q}_y\left(x\right)dx$ denote the total heat flux on border AB and CD, respectively.

FIGURE 2

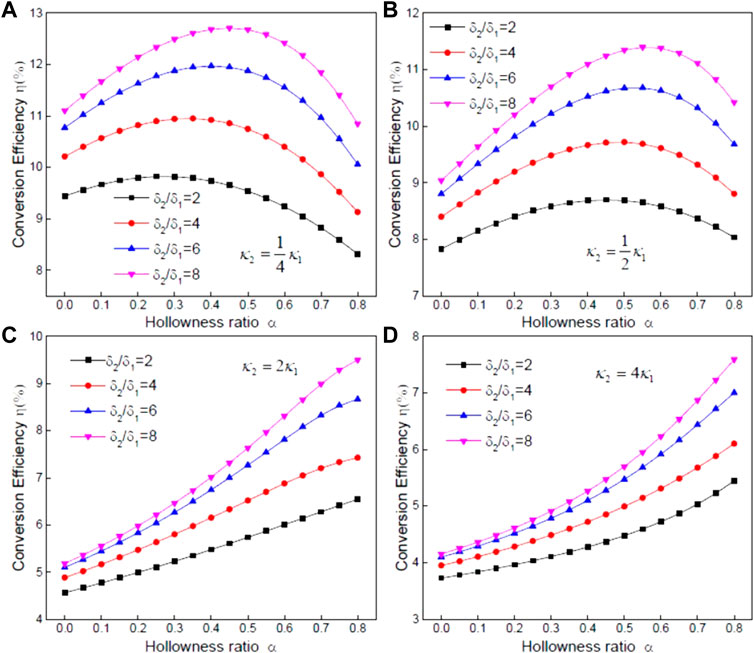
FIGURE 2. Effect of the hollowness ratio and conductivity properties of the fiber on the local energy conversion efficiency.

As shown in Figure 2, with specific fiber radius $R_1=4\mathrm{m}\mathrm{m}$, when the conductivity properties and hollowness ratio of the fiber are changed, different values of the local energy conversion efficiency are obtained. It can be found that the local energy conversion efficiency increased when the electric conductivity of the fiber increased and reduced when the thermal conductivity of the fiber increases. Thus, we can conclude that fibers with higher electric conductivity and lower thermal conductivity are desirable for the design of thermoelectric composites. By comparing Figure 2D with Figure 2A, we found that the thermal conductivity of the fiber has a more dominant effect on the local thermoelectric conversion efficiency than the electric conductivity when the hollowness ratio $\mathrm{\alpha }$ is relative small.

Figure 3 illustrates the variation of local energy conversion efficiency around a hollow fiber with desirable conductivity properties with respect to the hollowness ratio $\mathrm{\alpha }$. For all values of the fiber hollowness ratio, $\mathrm{\alpha }=0.45$ leads to the highest energy conversion efficiency, as shown in Figure 3A. We further compared the conversion efficiency around the hollow fiber with different $\mathrm{\alpha }$ values to that around a solid fiber (namely, $\mathrm{\alpha }=0$) under the same service conditions as shown in Figure 3B. As shown in this figure, compared with a solid fiber with radius of 4.5 mm, the highest conversion efficiency around a hollow fiber with $\mathrm{\alpha }=0.45$ is increased by 22.3%, showing the tremendous value of hollow fibers in improving the conversion performance of a thermoelectric composite material.

FIGURE 3

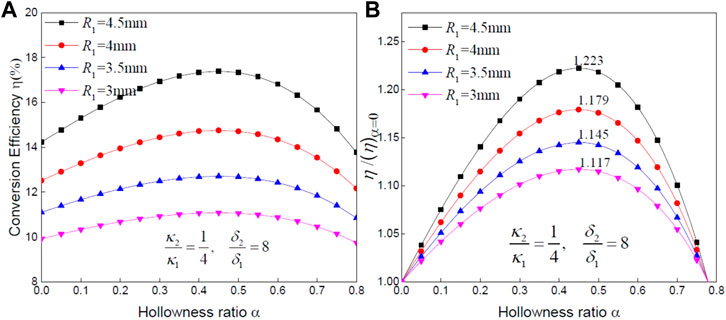
FIGURE 3. (A) Local energy conversion efficiency; (B) relative energy conversion efficiency around a desirable fiber with different hollowness ratios.

In addition to the conversion performance, the mechanical reliability also deserved further consideration when designing a thermoelectric composite. Figure 4 presents the variation of the interfacial normal stress distribution around a softer hollow fiber with desirable conductivity properties. Here, the soft fiber has a lower elastic modulus but a larger linear expansion coefficient than the matrix material. Since the thermal expansion of a softer fiber is greater than that of the matrix material, the matrix will prevent the fiber from expanding outward, and the interface is under compression, as shown in Figure 4A. In addition, the maximum compressive normal stress is achieved when $\mathrm{\theta }=1.5\mathrm{\pi }$ in this case, which may cause extrusion damage at this point and must be avoided in design. For given fiber–matrix system, as the fiber hollowness ratio $\mathrm{\alpha }$ increases, the maximum normal stress at the interface is reduced. The maximum normal stress in the vicinity of a hollow fiber is then compared to that of a solid fiber and the results are illustrated in Figure 4B. The relative concentration factor reaches 0.6 for a soft fiber of radius $R_1=3\mathrm{m}\mathrm{m}$, which means that the normal stress concentration around the hollow fiber is 40% lower than that around a solid fiber under the same service condition. In contrast to the soft fiber, the interfacial normal stress becomes tensile around a hollow fiber with harder elastic property, as shown in Figure 5A, which implies that the interface failure mode is more likely to be interface de-bonding in this case. Moreover, as shown in Figure 5B, we found that the concentration of interfacial normal stress can still be suppressed by increasing the fiber hollowness ratio in thermoelectric composites reinforced by hard fibers.

FIGURE 4

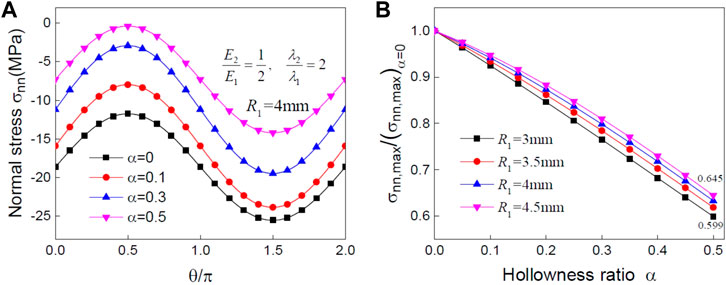
FIGURE 4. (A) Distribution of normal stress; (B) relative concentration factor of normal stress around a soft fiber with different hollowness ratios.

FIGURE 5

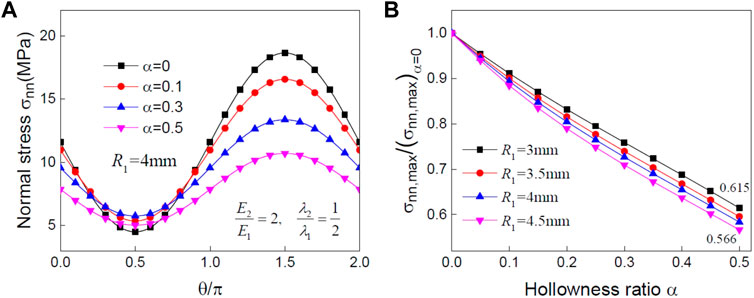
FIGURE 5. (A) Distribution of normal stress; (B) relative concentration factor of normal stress around a hard fiber with different hollowness ratios.

5 Concluding remarks

In this paper, the problem of a hollow fiber embedded in an infinite thermoelectric matrix under the remote uniform electric current and energy flux is investigated. The closed-form solutions of the electric field, temperature field, and associated thermal stress field in the entire composite are derived via the use of a complex variable technique. The following conclusions are summarized for designing and optimizing thermoelectric composites reinforced by hollow fibers/particles:

1. Fibers with lower thermal conductivity are helpful to improve the energy conversion efficiency of thermoelectric composites, but it may aggravate the interfacial thermal stress concentration.

2. A higher thermoelectric conversion efficiency and a lower amount of the normal stress concentration than that around a solid fiber could be achieved simultaneously by appropriate selection of the hollowness ratio of the fiber.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author contributions

CY and SX contributed to the conception and design of the study. CY performed the formal analysis, and wrote the first draft of the manuscript. HL and CD wrote sections of the manuscript. CY, HL, CD, and SX contributed to manuscript revision and supervision and read and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (grant no. 11802263&11902116), Natural Science Foundation of Jiangsu Province (grant no. BK20210787), Natural Science Foundation of Guangdong Province (grant no. 2022A1515011773), Natural Science Foundation of Guangzhou City (grant no. 202201010317), Qinglan Project of Yangzhou University, Provincial Natural Science Research of University of Anhui Province (KJ 2021A1058), and Key Laboratory of Construction Hydraulic Robots of Anhui Higher Education Institutes (grant no. TLXYCHR-O-21YB04).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bell, L. E. (2008). Cooling, heating, generating power, and recovering waste heat with thermoelectric systems. Science 321 (5895), 1457–1461. doi:10.1126/science.1158899

PubMed Abstract | CrossRef Full Text | Google Scholar

Guo, H., Xin, H., Qin, X., Zhang, J., Li, D., Li, Y., et al. (2016). Enhanced thermoelectric performance of highly oriented polycrystalline SnSe based composites incorporated with SnTe nanoinclusions. J. Alloy. Compd. 689, 87–93. doi:10.1016/j.jallcom.2016.07.291

CrossRef Full Text | Google Scholar

He, J., and Tritt, T. M. (2017). Advances in thermoelectric materials research: Looking back and moving forward. Science 357 (6358), eaak9997. doi:10.1126/science.aak9997

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, M. J., Chou, P. K., and Lin, M. C. (2008). An investigation of the thermal stresses induced in a thin-film thermoelectric cooler. J. Therm. Stress. 31 (5), 438–454. doi:10.1080/01495730801912512

CrossRef Full Text | Google Scholar

Li, G., An, Q., LiGoddard, W. A., Zhai, P., Zhang, Q., Snyder, G. J., et al. (2015). Brittle failure mechanism in thermoelectric skutterudite CoSb₃. Chem. Mat. 27 (18), 6329–6336. doi:10.1021/acs.chemmater.5b02268

CrossRef Full Text | Google Scholar

Liu, L. (2012). A continuum theory of thermoelectric bodies and effective properties of thermoelectric composites. Int. J. Eng. Sci. 55, 35–53. doi:10.1016/j.ijengsci.2012.02.003

CrossRef Full Text | Google Scholar

Mahmoudinezhad, S., Rezania, A., and Rosendahl, L. A. (2018). Behavior of hybrid concentrated photovoltaic-thermoelectric generator under variable solar radiation. Energy Convers. manage. 164, 443–452. doi:10.1016/j.enconman.2018.03.025

CrossRef Full Text | Google Scholar

Song, H., Song, K., and Gao, C. (2019). Temperature and thermal stress around an elliptic functional defect in a thermoelectric material. Mech. Mat. 130, 58–64. doi:10.1016/j.mechmat.2019.01.008

CrossRef Full Text | Google Scholar

Srivastava, D., Norman, C., Azough, F., Schäfer, M. C., Guilmeau, E., and Freer, R. (2018). Improving the thermoelectric properties of SrTiO₃-based ceramics with metallic inclusions. J. Alloy. Compd. 731, 723–730. doi:10.1016/j.jallcom.2017.10.033

CrossRef Full Text | Google Scholar

Wan, S., Huang, X., Qiu, P., Bai, S., and Chen, L. (2015). The effect of short carbon fibers on the thermoelectric and mechanical properties of p-type CeFe₄Sb₁₂ skutterudite composites. Mat. Des. 67, 379–384. doi:10.1016/j.matdes.2014.11.050

CrossRef Full Text | Google Scholar

Wang, P., Wang, B. L., Wang, K. F., and Cui, Y. J. (2018). Analysis of inclusion in thermoelectric materials: The thermal stress field and the effect of inclusion on thermoelectric properties. Compos. Part B-Eng. 166, 130–138. doi:10.1016/j.compositesb.2018.11.120

CrossRef Full Text | Google Scholar

Yang, H., Yu, C., Tang, J., Qiu, J., and Zhang, X. (2020). Electric-current-induced thermal stress around a non-circular rigid inclusion in a two-dimensional nonlinear thermoelectric material. Acta Mech. 231 (11), 4603–4619. doi:10.1007/s00707-020-02770-z

CrossRef Full Text | Google Scholar

Yang, Y., Ma, F. Y., Lei, C. H., Liu, Y. Y., and Li, J. Y. (2013). Nonlinear asymptotic homogenization and the effective behavior of layered thermoelectric composites. J. Mech. Phys. Solids 61 (8), 1768–1783. doi:10.1016/j.jmps.2013.03.006

CrossRef Full Text | Google Scholar

Yu, C., Zou, D., Li, Y., Yang, H., and Gao, C. (2018). An arc-shaped crack in nonlinear fully coupled thermoelectric materials. Acta Mech. 229 (5), 1989–2008. doi:10.1007/s00707-017-2099-6

CrossRef Full Text | Google Scholar

Zhang, A. B., Wang, B. L., Wang, J., and Du, J. K. (2017). Two-dimensional problem of thermoelectric materials with an elliptic hole or a rigid inclusion. Int. J. Therm. Sci. 117, 184–195. doi:10.1016/j.ijthermalsci.2017.03.020

CrossRef Full Text | Google Scholar

Zhang, Q. H., Huang, X. Y., Bai, S. Q., Shi, X., Uher, C., and Chen, L. D. (2016). Thermoelectric devices for power generation: Recent progress and future challenges. Adv. Eng. Mat. 18 (2), 194–213. doi:10.1002/adem.201500333

CrossRef Full Text | Google Scholar