State of charge estimation of lithium-ion battery based on extended Kalman filter algorithm

Due to excellent power and energy density, low self-discharge and long life, lithium-ion battery plays an important role in many fields. Directed against the complexity of above noises and the strong sensitivity of the common Kalman filter algorithm to noises, the state of charge estimation of lithium-ion battery based on extended Kalman filter algorithm is investigated in this paper. Based on the second-order resistor-capacitance equivalent circuit model, the battery model parameters are identified using the MATLAB/Simulink software. A battery parameter test platform is built to test the charge-discharge efficiency, open-circuit voltage and state of charge relationship curve, internal resistance and capacitance of the individual battery are tested. The simulation and experimental results of terminal voltage for lithium-ion battery is compared to verify the effectiveness of this method. In addition, the general applicability of state of charge estimation algorithm for the battery pack is explored. The ampere-hour integral method combined with the battery modeling is used to estimate the state of charge of lithium-ion battery. The comparison of extended Kalman filter algorithm between experimental results and simulation estimated results is obtained to verify the accuracy. The extended Kalman filter algorithm proposed in this study not only establishes the theoretical basis for the condition monitoring but also provides the safe guarantee for the engineering application of lithium-ion battery.

1 Introduction

Establishing the carbon-free alliance and developing new sustainable and high-efficiency energy storage device have become an effective method to come up with the ever-increasing energy problems (Chen et al., 2019; Hao et al., 2020a). The durability and safety are the key factors to ensure the smooth operation of energy storage device (Hao et al., 2020b; Hao et al., 2022; Lane et al., 2020). Lithium-ion battery is a kind of efficient green energy due to their excellent power density, high energy density, low self-discharge, wide temperature range and long lifetime. Due to these characteristics, lithium-ion battery plays an important role in many electronic products, such as electric automobile, notebook computer and mobile phone (Hao et al., 2019; Shi et al., 2022). At present, the technical bottleneck of lithium-ion battery is accompanied by the problems of high-performance battery development and maintenance caused by the increasing power demand. The battery management system (BMS) can be used to utilize the storage capacity rationally and monitor the working state precisely of the battery pack systems (Hao et al., 2018; Iurilli et al., 2019). The State of charge (SOC) estimation precisely in BMS not only improve the power transmission performance and increase the safety of the battery, but also decrease the over-charging and over-discharging and prolong the using life of the battery (Dang et al., 2022; Yang et al., 2022). Up to now, the determination of lithium-ion battery model is also needed to be studied. In addition, the SOC is indicated as the residual energy stored in the battery, but there is no uniform evaluation method of SOC estimation (Iurilli et al., 2019).

The lithium-ion battery model can be determined by three methods, including the electrochemical model (Hao and Xie, 2021; Liu et al., 2022; Wang et al., 2022), the machine learning model or data-driven model (Hong et al., 2023; Wang et al., 2023; Zhang et al., 2023) and the equivalent circuit model (Tran et al., 2021; Chang et al., 2022). For the electrochemical model, the internal reaction mechanism of battery is revealed from the electrochemical point of view. The advantage of the electrochemical model is that it can analyze the internal reactions of the lithium-ion battery during the operation process, and the physical significance of the model identification parameters is clear relatively. But the disadvantage of this model is that it is very difficult to establish and identify the battery model parameters, and the different material types of the battery needs to establish different electrochemical models (Xu L. et al., 2022). So this model is not suitable for battery management and is generally used in the battery design phase. For the machine learning model or data-driven model, the internal parameters of lithium-ion battery show high nonlinearity characteristics during the reaction process because the neural network has the advantages of good self-learning and high nonlinearity (Wang et al., 2021; Zhang et al., 2023). A clustering-based data partitioning method and a partitioned all-season coverage model established by the spiral self-attention neural network to perform real-time multi-forward-step temperature prediction for battery systems were presented by authors in (Hong et al., 2023). The results demonstrated that the partitioned training model has excellent online prediction performance for nondifferentiated real-world vehicle operation in all climates. This method requires a great amount of experimental data to support the construction of the battery model. For the equivalent circuit model, it can be used to describe the voltage features of lithium-ion battery in the charging and discharging processes. The battery can be equivalent to circuit configuration, and the variation between voltage and current is reflected by the combination of various electronic components. The dynamic and static characteristics of the battery can be well displayed by appropriate circuit configuration in the charging and discharging processes (Chen et al., 2021). Compared with the electrochemical model and machine learning model or data-driven model, the equivalent circuit model has obvious advantages: 1) It can be used in various types of batteries because of its strong adaptability; 2) it can be described by mathematical expression; 3) identification of this model parameters is much easier than that of other models.

Generally, the SOC estimation comprises the following techniques: coulomb counting technique (Jeong et al., 2014), open circuit voltage (OCV) technique (Tong et al., 2015), impedance spectroscopy technique (Qahouq and Xia, 2017), diverse intelligent technique (Hu et al., 2018) and Kalman filter (KF) technique (Wang et al., 2020). For the coulomb counting technique, the SOC of battery is estimated by integral approach, the coulomb-counting technique is the most commonly used approach for SOC estimation by integral approach due to its simplicity and ease of implementation (Li et al., 2017). But the precision is influenced by initial SOC and cumulative calculation error. For the impedance spectroscopy technique, the precision of SOC estimation is affected by the battery life, battery geometry, electrodes material and working temperature. The diverse intelligent technique was proposed in the literature by simulating the complicated nonlinear relationship between SOC and its influencing factors were based on artificial neural networks method (Hossain et al., 2017), support vector regression method (Hansen and Wang, 2005), fuzzy logic method (Salkind et al., 1999). In addition, the fractional-order method was attracted growing attention in the arena of BMS. The fractional-order method and its model parameter identification for LIBs based on the time-domain data was studied by authors in (Wang et al., 2015). A fractional-order equivalent circuit model was established and parameterized by authors in (Hu et al., 2018) to co-estimate the SOC and state-of-health (SOH) using a hybrid genetic algorithm/particle swarm optimization method. Comparative studies showed that it improves the modeling accuracy appreciably from its second- and third order counterparts. The diverse intelligent technique is highly dependent on the quality and quantity of training samples and data (Dang et al., 2022). The KF method generally has good path tracking performance and high accuracy, which is an effective online SOC estimation method (Meng et al., 2017; Dang et al., 2022). In addition, KF method also can be applied to SOC estimation for different dynamic lithium-ion battery models. Based on equivalent circuit model, the nonlinear properties of SOC estimation can be exhibited using KF method. Therefore, the nonlinear Kalman filter algorithms, such as extended Kalman filter algorithm and sigma point Kalman filter algorithm, are applied to estimate the SOC of battery (Wang et al., 2017; Rzepka et al., 2021). A dual fractional-order extended Kalman filter was put forward to realize simultaneous SOC and SOH estimation in the investigation by Hu et al. (2018). The probability distribution function is obtained through the determined sampling point in the sigma point Kalman filter algorithm. Compared with above algorithm, the extended Kalman filter algorithm uses the first order Taylor expansion to obtain the nonlinear function. This algorithm plays an important role in the SOC estimation of battery due to the accuracy and effectiveness (Chin et al., 2018; Yang et al., 2022). Firstly, the initial value estimation of lithium-ion battery using extended Kalman filter algorithm can significantly reduce the estimation error. Secondly, the extended Kalman filter algorithm can be corrected quickly and has good self-correcting ability when the estimation error is large. Finally, in early calibration stage of the battery, measurement error and Gaussian white noise error are occurred because of the measurement sensor itself, but extended Kalman filter algorithm can effectively eliminate these errors.

However, the established lithium-ion battery model determines the precision of the SOC estimation, which is closely associated with the parameter identification of the battery. In order to reduce the calculation time, the SOC estimation process of extended Kalman filter algorithm needs to be decreased, which may require a choice between computational accuracy and computational efficiency. In addition, the identification parameters of battery model are different due to the different conditions. The variation of identification parameters causes the battery model error, which affects SOC estimation results. However, the parameter identification of lithium-ion battery with the nonlinear time varying property is very complicated especially when the battery in different charging and discharging states. A linear SOC estimation model with a posterior measurement calibration based on the common KF algorithm was proposed by authors in (Wu et al., 2021). This algorithm not only needs the battery estimation model to have high precision, but also requires to exactly characterize the estimation process noise and measurement noise existed in the battery. But these noises cannot be characterized precisely using the common KF algorithm in the battery estimation model due to the randomness and complexity of these noises and the susceptibility of the common KF algorithm to noises.

In view of the complexity of above noises and the strong sensitivity of common KF algorithm to noises, a SOC estimation method of lithium-ion battery using an extended Kalman filter algorithm is proposed in this paper. Based on the second-order resistor-capacitance (RC) equivalent circuit model, the battery model parameters are identified using the MATLAB/Simulink software. A battery parameter test platform is built to test the charge-discharge efficiency, open-circuit voltage and SOC relationship curve, internal resistance and capacitance of individual battery are tested. The simulation and experimental results of the terminal voltage for lithium-ion battery are compared to verify the effectiveness of this method. In addition, the general applicability of SOC estimation algorithm for the battery pack is explored. The ampere-hour integral method combined with the battery modeling is used to estimate the SOC of lithium-ion battery. The comparison of extended Kalman filter algorithm between experimental results and simulation estimated results is obtained to verify the accuracy.

The main contributions of this paper can be summarized as: 1) We propose a SOC estimation method of lithium-ion battery using an extended Kalman filter algorithm. The ampere-hour integral method combined with the battery modeling can be used to estimate the SOC of lithium-ion battery. 2) Based on the second-order resistor-capacitance equivalent circuit model, we identify the battery model parameters by MATLAB/Simulink software. The fitting curves are obtained based on the curve between open circuit voltage and the state of charge. 3) We further verify the accuracy of extended Kalman filter algorithm between experimental and simulation results. The extended Kalman filter algorithm proposed in this study not only establishes the theoretical basis for the condition monitoring but also provides the safe guarantee for the engineering application of lithium-ion battery.

2 Methods and models

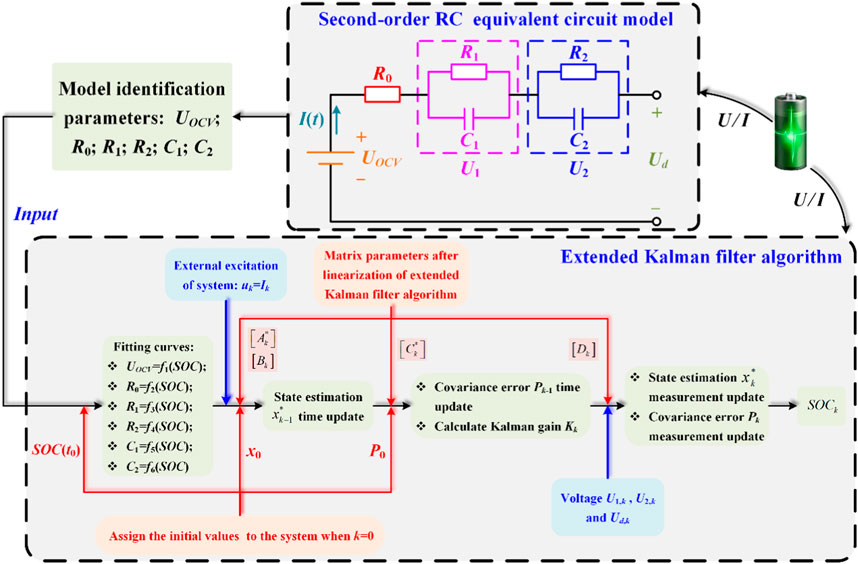
2.1 Second-order RC equivalent circuit model

In order to ensure the stability and accuracy of lithium-ion battery model, it is necessary to determine the mathematical relationship among battery characteristic parameters, including the capacity, internal resistance, OCV and SOC. Before establishing the mathematical relationship, the type of battery model is clarified. The second-order RC equivalent circuit model consisting of two RC circuits and a resistor in series is used to determine the lithium-ion battery model in this paper, which is shown in Figure 1. The two RC circuits in this model represent the influence factors caused by concentration polarization and the variation of battery parameters caused by electrochemical polarization. According to Kirchhoff’s law, the second-order RC equivalent circuit model (Ren et al., 2020) is given by

$\left\{\begin{array}{l}{U}_{OCV}=U_1+U_2+I{R}_0+U_d\\ I=\frac{U_1}{R_1}+C_1\frac{d{U}_1}{dt}\\ I=\frac{U_2}{R_2}+C_2\frac{d{U}_2}{dt}\end{array}\right.(1)$

where U_OCV, a function of SOC, is the OCV of the lithium-ion battery. U_d is the terminal voltage that can be measured directly. R₀ is the Ohmic internal resistance, R₁ is the concentration polarization resistance, R₂ is the electrochemical polarization resistance, C₁ is the concentration polarization capacitance, C₂ is the electrochemical polarization capacitance, I is the load current. Eq. 1 can be rewritten by

$\left\{\begin{array}{l}{U}_d=U_{OCV}-U_1-U_2-I{R}_0\\ \frac{d{U}_1}{dt}=\frac{I}{C_1}-\frac{U_1}{R_1{C}_1}\\ \frac{d{U}_2}{dt}=\frac{I}{C_2}-\frac{U_2}{R_2{C}_2}\end{array}\right.(2)$

FIGURE 1

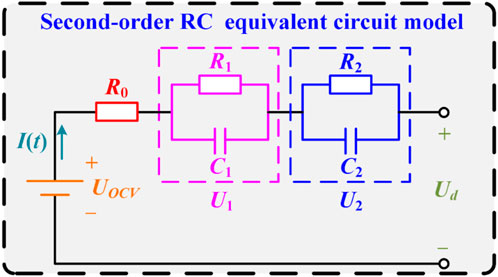
FIGURE 1. Second-order RC equivalent circuit model consisting of two RC circuits and a resistor in series of lithium-ion battery.

2.2 Battery model parameters identification method

In order to improve the SOC estimation precision of lithium-ion battery, the SOC estimation model is established by MATLAB/Simulink software. In addition, the characteristic parameters of battery model are identified by the Battery module in MATLAB/Simulink. The parameters identification method is to solve the problem of R₀, R₁, R₂, C₁, and C₂ parameters in the battery model based on OCV-SOC data collected in the simulation process. Then the parameters identification method can be applied to the measurement data of actual battery to realize the parameter identification of second-order RC equivalent circuit model. The battery model parameters identifications in the simulation process mainly include the capacity identification, the charging and discharging efficiency identification, the OCV-SOC curves identification, the resistance and capacitance identifications.

In order to predict the SOC of lithium-ion battery precisely, the maximum usable capacity of lithium-ion battery should be obtained to eliminate the influence of charging efficiency on the overall simulation process. It is assumed that the lithium-ion battery is considered fully charging when the current is less than 0.03 C. The two-stage charging method of battery is used, which is called the hybrid pulse capability characteristic experiment when the charging and discharging cycles number reaches a certain number. The charging and discharging processes are performed at the room temperature 25°C. Firstly, the lithium-ion battery is charged at constant current until the battery voltage reaches 4 V. Secondly, the lithium-ion battery is charged at constant voltage, so that the charging voltage of the battery is maintained at 4 V, and the charging is stopped when the charging current is lower than 0.03 C. Five charging and discharging repeatability experiments are performed and the average capacity of lithium-ion battery are obtained in this paper, as shown in Table 1. The maximum capacity of lithium-ion battery is 32.28 Ah.

TABLE 1

TABLE 1. Capacity of lithium-ion battery during the five charging and discharging repeatability experiments.

Due to the energy loss induced by electrochemical polarization, concentration polarization and other electrochemical phenomena, as well as the electric energy loss caused by the internal resistance and circuit of the battery in the charging and discharging processes, the energy cannot be 100% converted into chemical energy and stored in the battery in the charging process, and the stored energy cannot be 100% released to the load in discharging process. There is a problem of the energy conversion efficiency in the charging and discharging processes. Generally, capacity efficiency DOD_c or energy efficiency DOD_e can be used to evaluate the energy conversion and utilization in the charging and discharging process (Khaki and Das, 2023), which are shown by

$\left\{\begin{array}{l}DO{D}_c^{ch}=\frac{C_{ch}}{C_n}\\ DO{D}_c^{dis}=\frac{C_{dis}}{C_n}\\ DO{D}_e^{ch}=\frac{W_{ch}}{W_n}\\ DO{D}_e^{dis}=\frac{W_{dis}}{W_n}\end{array}\right.(3)$

where $DO{D}_c^{ch}$ and $DO{D}_c^{dis}$ are the charging capacity efficiency and the discharging capacity efficiency of lithium-ion battery, respectively. C_ch, C_dis, and C_n are the actual input capacity, the actual output capacity and the nominal capacity, respectively. $DO{D}_e^{ch}$ is the charging electrical energy efficiency, $DO{D}_e^{dis}$ is the discharging electrical energy efficiency. W_ch, W_dis, and W_n are the actual input electrical energy, the actual output electrical energy and the nominal electrical energy, respectively. The charging and discharging efficiency of battery in the current research is about 98.21%.

The OCV-SOC curve of the battery in charging and discharging process is obtained, as shown in Figure 2A. The quintic term fitting curves are obtained based on OCV-SOC curve and the conventional residual error is 0.82%, as shown in Figure 2B. The relationship between OCV and SOC of lithium-ion battery is given by

$OCV=4.5465+0.0161\cdot SOC-7.8443\cdot SO{C}^2+2.1203\cdot SO{C}^3-3.9585\cdot SO{C}^4+2.1945\cdot SO{C}^5(4)$

FIGURE 2

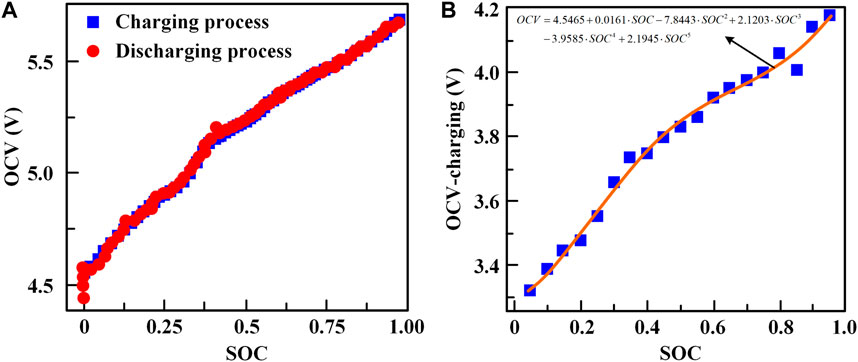
FIGURE 2. OCV-SOC curve of lithium-ion battery in the charging and discharging process: (A) OCV-SOC curve; (B) quintic term fitting curves.

2.3 MATLAB/Simulink method

The second-order RC equivalent circuit diagram for lithium-ion battery in MATLAB/Simulink software is shown in Figure 3. The circuit element is confirmed in Simulink Library Browser according to the second-order RC equivalent circuit diagram. Each controllable circuit element is controlled using the Lookup Table (1-D) module, which is used to load data directly associated with SOC into the module. The output ports of voltmeter and ammeter are connected with PS-Simulink module, which is a module that converts the physical signals into the digital signals on Simulink platform. In the outermost layer, the PMC_Port module is used to realize the contact between internal encapsulation and external physical signal. Finally, the current and terminal voltage are transmitted to the ammeter and voltmeter in real time, and then the data is transmitted out of the package through the Outport module.

FIGURE 3

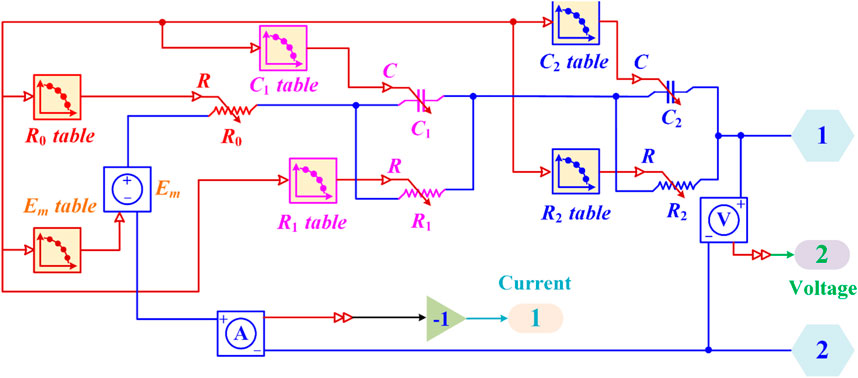
FIGURE 3. Second-order RC equivalent circuit diagram for lithium-ion battery in MATLAB/Simulink software.

In the conventional charging process of lithium-ion battery, the constant-current charging is generally adopted to reach the steady-state voltage designed by the target battery firstly, and then constant-voltage charging is adopted to continue charging. This is because constant-current charging with large current significantly improves the charging rate of the battery. Although high current charging can improve the charging efficiency of the battery, it cannot avoid the problem of virtual high voltage at the end of charging process due to the enhancement of the concentration polarization internal resistance of battery. Therefore, by using the constant voltage charging mode at the end of constant current charging process, the depth of discharge (DOD) of battery can be utilized to the maximum available capacity as much as possible by reducing the charging current. For the current charging and discharging strategy, the charging mode of constant current followed by constant voltage can not only increase the charging efficiency of the battery, but also reduce the damage to the system in charging process.

A lithium-ion battery model for most popular battery types in the MATLAB/Simulink software is adopted to simulate the charging and discharging processes of the battery. The nominal voltage, current and rated capacity are set to 47.84 V, 0.736 A and 23 Ah. The initial SOC is 95% and the battery response time is 1 × 10⁻⁴ s. The charging and discharging simulation model in the MATLAB/Simulink software of lithium-ion battery is shown in Figure 4. In addition, the load is set to 65 Ω during simulation process, the discharge mode is set to SOC from 95% to 90%, the simulation time is set to 10 min.

FIGURE 4

FIGURE 4. Charging and discharging simulation model in the MATLAB/Simulink software of lithium-ion battery.

2.4 Extended Kalman filter algorithm

The extended Kalman filter algorithm can not only handle with the problems of linear system, but also solve some problems of nonlinear system. The Kalman filter algorithm theory is a recursive method used to deal with the problem of discrete data linear filtering, it consists of the state equation and the observation equation (Yang et al., 2022), which can be expressed as

$x_{k+1}=A_k\cdot x_k+B_k\cdot u_k+w_k{w}_k\sim \left(0,Q_k\right)(5)$

$y_k=C_k\cdot x_k+D_k\cdot u_k+v_k{v}_k\sim \left(0,R_k\right)(6)$

where x_k, y_k and u_k are the state quantity, the observed quantity (the output quantity) and the external excitation at time k. A_k is the transfer matrix, which can reflect the influence of the previous moment on the current state. B_k and C_k are the input matrix and the output matrix, respectively. D_k is the feedforward matrix, which can reflect the influence of the state on the observation. w_k and v_k denote the stochastic process noise and the observation measurement noise respectively, which are Gaussian white noise with no correlation and zero mean (Hu et al., 2018). Q_k and R_k denote the stochastic process noise covariance and the observation measurement noise covariance, respectively,

The extended Kalman filter algorithm processing for SOC estimation can transform the nonlinear problem into the linear problem through the Gaussian reduced order (Hu et al., 2018). The state equation and the observation equation of extended Kalman filter algorithm are given by (Wu et al., 2021; Wu et al., 2022; Ge et al., 2022)

$x_k=f\left(x_{k-1},u_{k-1}\right)+w_k{w}_k\sim \left(0,Q_k\right)(7)$

$y_{k-1}=h\left(x_{k-1},u_{k-1}\right)+v_k{v}_k\sim \left(0,R_k\right)(8)$

where $f\left(x_{k-1},u_{k-1}\right)$ and $h\left(x_{k-1},u_{k-1}\right)$ are the nonlinear state function and the nonlinear measurement function related to system state, respectively. Since the extended Kalman filter algorithm can perform the second order Taylor series expansion of the nonlinear part, it could well describe the dynamic response of second-order RC equivalent circuit model (Xu X. D. et al., 2022). Consequently, for any observation point $x_{k-1}^{*},$ $f\left(x_{k-1},u_{k-1}\right)$ and $h\left(x_{k-1},u_{k-1}\right)$ are expanded by using Taylor series expansion and the higher order terms are ignored, which can be expressed as

$f\left(x_{k-1},u_{k-1}\right)\approx f\left(x_{k-1}^{*},u_{k-1}\right)+{\left.\frac{\partial f\left(x_{k-1},u_{k-1}\right)}{\partial x_{k-1}}\right|}_{x_{k-1}=x_{k-1}^{*}}\left(x_{k-1}-x_{k-1}^{*}\right)(9)$

$h\left(x_{k-1},u_{k-1}\right)\approx h\left(x_{k-1}^{*},u_{k-1}\right)+{\left.\frac{\partial h\left(x_{k-1},u_{k-1}\right)}{\partial x_{k-1}}\right|}_{x_{k-1}=x_{k-1}^{*}}\left(x_{k-1}-x_{k-1}^{*}\right)(10)$

Let ${\left.A_{k-1}^{*}=\frac{\partial f\left(x_{k-1},u_{k-1}\right)}{\partial x_{k-1}}\right|}_{x_{k-1}=x_{k-1}^{*}}$ and ${\left.C_{k-1}^{*}=\frac{\partial h\left(x_{k-1},u_{k-1}\right)}{\partial x_{k-1}}\right|}_{x_{k-1}=x_{k-1}^{*}},$ Eqs. 9, 10 can be rewritten as

$f\left(x_{k-1},u_{k-1}\right)\approx A_{k-1}^{*}{x}_{k-1}+\left[f\left(x_{k-1}^{*},u_{k-1}\right)-A_{k-1}^{*}{x}_{k-1}^{*}\right](11)$

$h\left(x_{k-1},u_{k-1}\right)\approx C_{k-1}^{*}{x}_{k-1}+\left[h\left(x_{k-1}^{*},u_{k-1}\right)-C_{k-1}^{*}{x}_{k-1}^{*}\right](12)$

The specific algorithm of extended Kalman filter is divided into six steps, which can be expressed as displayed in Table 2, where P_k-1 indicates the variance matrices of state estimation error. R_k represent the variance matrices for v_k. The general flow of first-order extended Kalman filter algorithm is shown in Figure 5. The voltage and current data are input into the second-order RC equivalent circuit model module. The model identification parameters R₀, R₁, C₁, R₂, and C₂ are inputted into the extended Kalman filter algorithm module after second-order RC equivalent circuit model parameter identification for SOC estimation.

TABLE 2

TABLE 2. Six steps of extended Kalman filter algorithm.

FIGURE 5

FIGURE 5. General flow of first-order extended Kalman filter algorithm.

The SOC estimation model based on the extended Kalman filter algorithm using MATLAB/Simulink software is shown in Figure 6. The input of the SOC estimation model is the _.mat file under different working conditions, which includes sampling step time, sampling voltage, sampling current and SOC measured value. The package model diagram of the extended Kalman filter algorithm based on MATLAB/Simulink software is shown in Figure 6A. The specific module of the extended Kalman filter algorithm is shown in Figure 6B. The charging and discharging data obtained by specific module as the main body is imported into extended Kalman filter algorithm package model. It should be noted that the sampling step time is 6.25 × 10⁻² s per step.

FIGURE 6

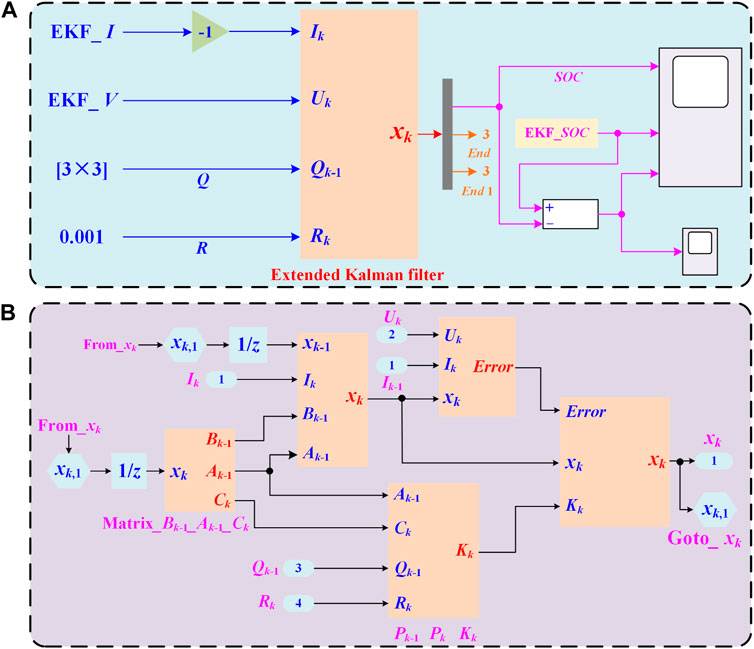
FIGURE 6. SOC estimation model based on the extended Kalman filter algorithm using MATLAB/Simulink software: (A) package model diagram; (B) specific module of the extended Kalman filter algorithm.

3 Results and discussion

3.1 Charging and discharging parameters identification

For the current charging and discharging strategy, the charging mode of constant current followed by constant voltage can not only increase the charging efficiency of the battery, but also reduce the damage to the battery in charging process. The changing curves of SOC, the current and terminal voltage with the time of lithium-ion battery are shown in Figure 7. The initial SOC of lithium-ion battery is about 95% and the simulation time is set to 10 min. The SOC of the battery in discharging process is set from 95% to 90%.

FIGURE 7

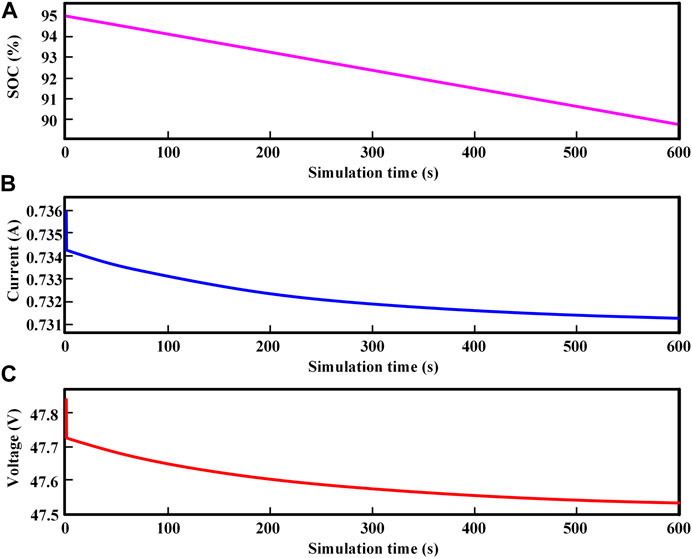
FIGURE 7. Changing curves of the SOC (A), the current (B) and the terminal voltage (C) with the time of lithium-ion battery.

The second-order RC equivalent circuit model of lithium-ion battery model in current research is shown in Figure 1. When the lithium battery is in constant current discharging, according to Eqs. 1, 2, the terminal voltage is expressed by

$U_d\left(t\right)=U_{OCV}-I{R}_0-I{R}_1\left(1-e^{-\frac{t}{R_1{C}_1}}\right)-I{R}_2\left(1-e^{-\frac{t}{R_2{C}_2}}\right)(13)$

It is assumed that the voltage across the capacitor is considered equal, then

$\left\{\begin{array}{l}{U}_1\left(0\right)=I{R}_1\left(1-e^{-\frac{t}{R_1{C}_1}}\right)\\ U_2\left(0\right)=I{R}_2\left(1-e^{-\frac{t}{R_2{C}_2}}\right)\end{array}\right.(14)$

The change of terminal voltage from U_d (t⁻) to U_d (t⁺) is mainly caused by the voltage drop on the Ohmic internal resistance R₀. The Ohmic internal resistance R₀ is given by

$R_0=\frac{U_{OCV}-U_d\left(t\right)}{I}(15)$

Let ${\tau }_1=R_1{C}_1$ and ${\tau }_2=R_2{C}_2$, Eq 13 can be rewritten by

$U_d\left(t\right)=U_{OCV}-I{R}_0-a\left(1-e^{-\frac{t}{{\tau }_1}}\right)-c\left(1-e^{-\frac{t}{{\tau }_2}}\right)(16)$

where the identification parameters of battery model are $R_1=\frac{a}{I}$, $R_2=\frac{c}{I}$, $C_1=\frac{I{\tau }_1}{a}$ and $C_2=\frac{I{\tau }_2}{c}$.

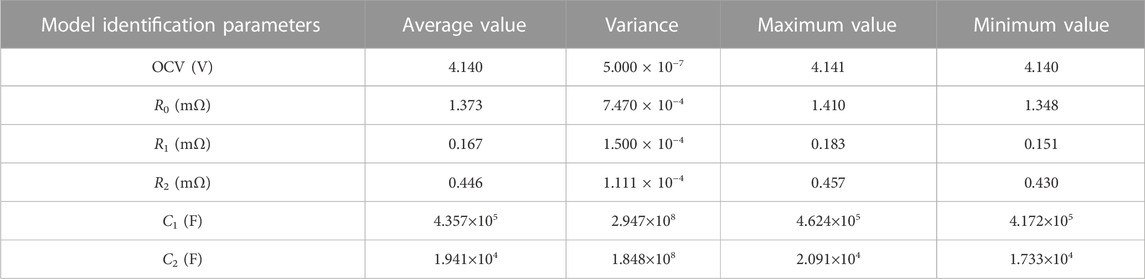
In order to identify above battery model parameters, these parameters are fitted using least squares method according to different SOC simulations. The identification parameters of the lithium-ion battery model described by second-order RC equivalent circuit model are shown in Table 3.

TABLE 3

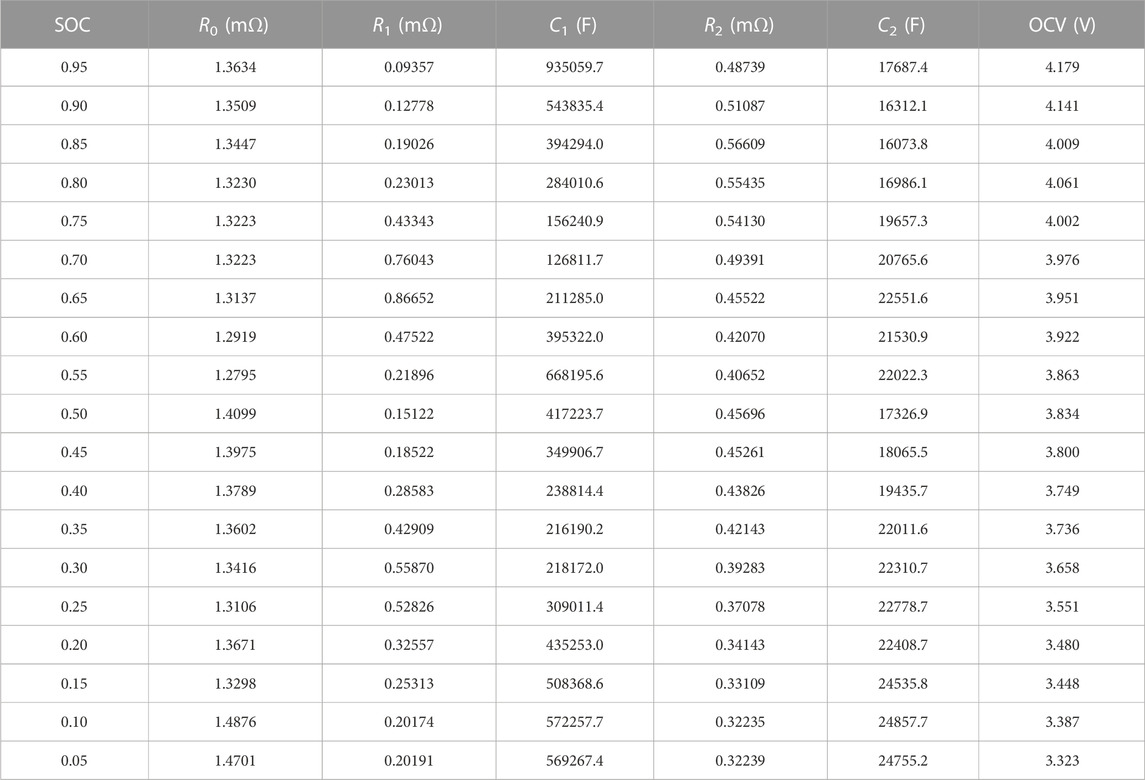
TABLE 3. Identification parameters of the lithium-ion battery model described by second-order RC equivalent circuit model.

3.2 Relationship between SOC and model identification parameters

Five individual lithium-ion battery samples are selected by normal distribution method. The model identification parameters of five individual lithium-ion battery samples are identified through the charging and discharging experiments. The comparison between simulation and experimental results of terminal voltage described by second-order RC equivalent circuit model is shown in Figure 8. The research results show that the terminal voltage of simulation results is in conformity with that of the experimental results, and the comparison error is 0.3%.

FIGURE 8

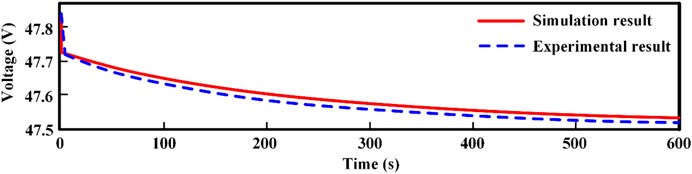
FIGURE 8. Comparison between the simulation and experimental results of the terminal voltage described by second-order RC equivalent circuit model.

The relationships between SOC and OCV, model identification parameters R₀, R₁, C₁, R₂, and C₂ of five individual lithium-ion battery samples are shown in Figure 9. According to results of SOC-OCV curves, the OCV of five individual lithium-ion battery samples has a good consistency with the variation of SOC from 0.10 to 1.00, as shown in Figure 9A.

FIGURE 9

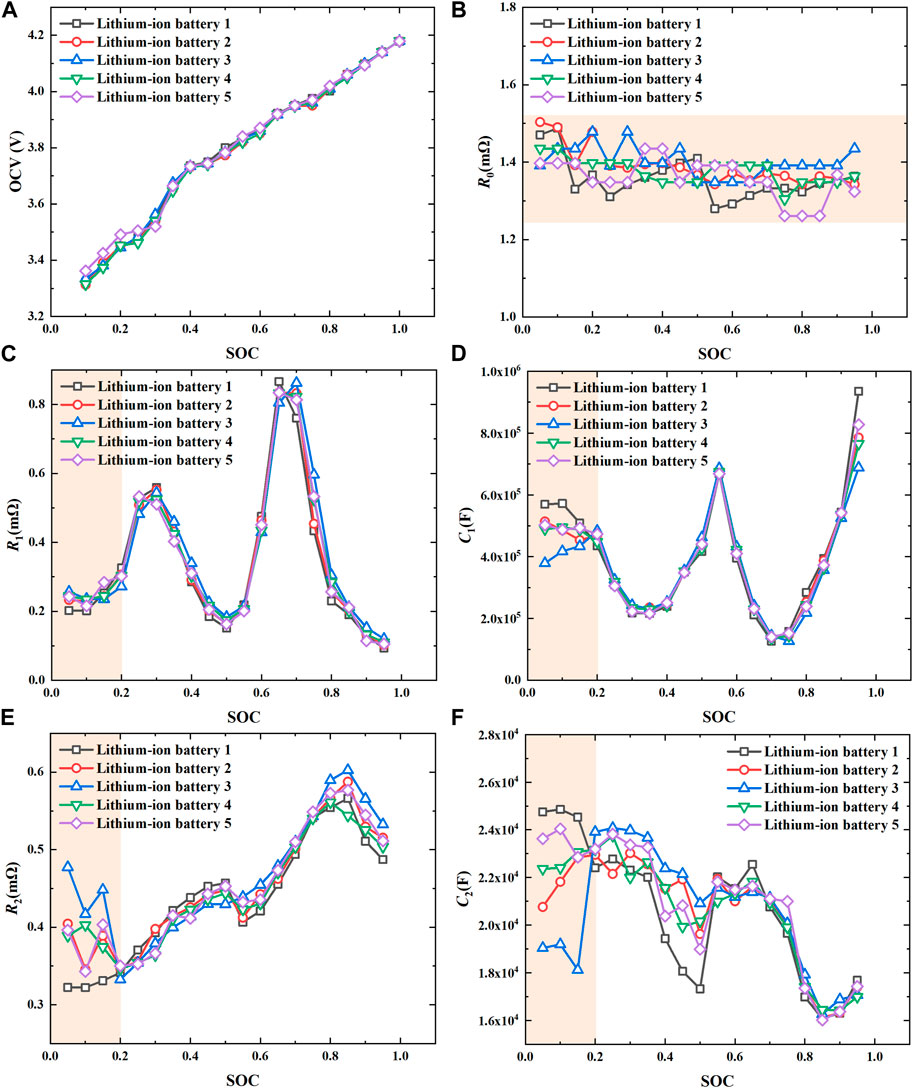
FIGURE 9. Relationships between the SOC (from 0.10 to 1.00 or from 0.05 to 0.95) and OCV, model identification parameters R₀, R₁, C₁, R₂, and C₂ of five individual lithium-ion battery samples: (A) SOC-OCV; (B) SOC-R₀; (C) SOC-R₁; (D) SOC-C₁; (E) SOC-R₂; (F) SOC-C₂.

The resistance to current flow is internal resistance when the lithium-ion battery is being charged and discharged, which is an important indicator of energy loss performance of the battery. In general, there are two kinds of internal resistance, the ohmic internal resistance and the polarized internal resistance, inside lithium-ion battery. On the one hand, the Ohmic internal resistance mainly consists of contact resistance among the positive and negative electrodes, the electrolytes and separator, which is relevant to the dimension and material of battery. On the other hand, the polarized internal resistance includes electrochemical polarization resistance induced by polarization in the electrochemical reaction and the concentration polarization resistance induced by the concentration difference in the polarization process. In addition, the internal resistance of battery varies with time in charging and discharging processes due to the electrode composition, lithium ions concentration and temperature changes with reaction time.

The Ohmic internal resistance R₀, which is instantaneous, varies from 1.29 mΩ to 1.49 mΩ, with the overall error of less than 15% (as shown in Figure 9B), which meets the engineering application demand of lithium-ion battery. It is assumed that the ohmic internal resistance obeys Ohm’s law as a whole. The concentration polarization resistance R₁ and the electrochemical polarization resistance R₂ are shown in Figures 9C, E. The concentration polarization resistance R₁ fluctuates with the increase of SOC. The concentration polarization resistance is maximum when SOC are 0.30 and 0.70, while the concentration polarization resistance is minimum when SOC are 0.10, 0.50, and 0.95. It is assumed that the concentration of lithium ions is uniform inside the battery before charging and discharging process. The diffusion rate of lithium ions is lower than electrochemical reaction rate in charging and discharging process, which causes the accumulation of electrical charge and then the concentration polarization. The concentration polarization time (microsecond range) is much less than the electrochemical polarization time (sub-millisecond range). So the concentration polarization resistance increases with SOC from 0.05 to 0.3. However, the accumulated electrical charge is consumed with electrochemical reaction of lithium-ion battery, and the concentration polarization resistance decreases with the increase of SOC from 0.30 to 0.50, as shown in Figure 9C. The variation trend of concentration polarization capacitance is opposite to that of concentration polarization resistance, as shown in Figure 9D. Since the electrochemical reaction time is in the order of microseconds, the electrochemical polarization resistance increases with the increase of SOC as a whole, as shown in Figure 9E. So the variation trend of electrochemical polarization capacitance is opposite to that of electrochemical polarization resistance, as shown in Figure 9F. The model identification parameters of five lithium-ion batteries have a certain error when SOC from 0.05 to 0.20, as shown in Figures 9C–F, which is mainly due to the redistribution of resistance and capacitance in the initial charging and discharging processes.

According to the data results in Figure 9, the OCV and model identification parameters R₀, R₁, C₁, R₂, and C₂ of lithium-ion battery when SOC = 0.50 are obtained, as shown in Table 4. The average values, variances and distribution intervals of OCV and model identification parameters also can be obtained. Take the OCV as an example, the average value is ${\overline{U}}_{OCV}=4.140V$, the variance is ${\sigma }^2=\frac{1}{4}\cdot {\displaystyle \sum _{i=1}^4}{\left(U_i-{\overline{U}}_{OCV}\right)}^2=5.000\times {10}^{-7}$, the maximum SOC and minimum SOC are $U_{\max }=4.141V$ and $U_{\min }=4.140V$. The simulation and experiment results between OCV and time of lithium-ion battery when SOC = 0.50 are shown in Figure 10A, which indicates that this battery model has good precision. The average error of OCV for simulation result is 0.023% when SOC = 0.50, as shown in Figure 10B.

TABLE 4

TABLE 4. Model identification parameters of lithium-ion battery when SOC = 0.50.

FIGURE 10

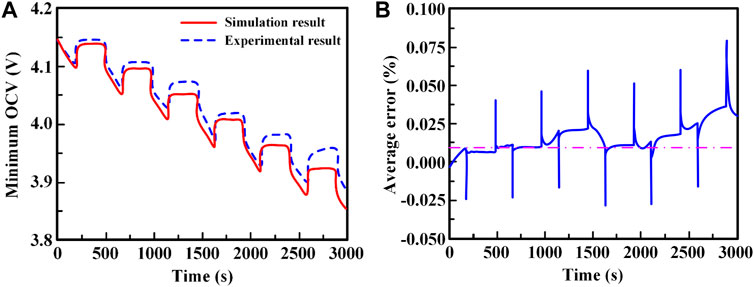
FIGURE 10. Relationships between the OCV and time of lithium-ion battery when SOC = 0.50: (A) comparison between the simulation and experimental results; (B) average error of OCV.

3.3 SOC estimation based on the extended Kalman filter algorithm

To make the evaluation more clarity, the comparison results of SOC estimation and corresponding error of lithium-ion battery between the current method and the previous method studied by authors in (Liu et al., 2016) are proposed, which is shown in Figure 11. The results of the experiment and SOC estimation results using current method and the previous method of fully charged lithium-ion battery are shown in Figure 11A with 1C discharging rate. It can also be seen that the SOC estimation results of the current model is consistent with the experiment results and the fractional order model (Liu et al., 2016). A certain error is existed between integer order model and other method. The error of SOC estimation between current method and previous method is shown in Figure 11B. The maximum relative errors of current estimation model, fractional order estimation model and integer order estimation model are 1.63%, 1.62% and 2.94%, respectively. The reason is that the SOC estimation method based on the extended Kalman filter algorithm can precisely describe the battery state and timely adjust the Kalman gain matrix according to the measurement information and the updated real-time battery information. Due to the significant hysteresis effect between fractional order model and integral order model, the inaccurate SOC estimated by the extended Kalman filter algorithm can be amended during the iteration process.

FIGURE 11

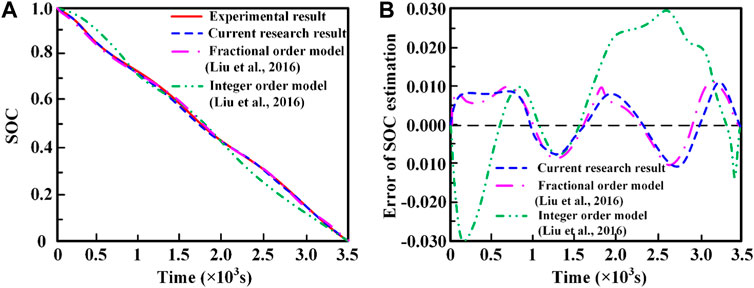
FIGURE 11. Comparison of SOC estimation and corresponding error of lithium-ion battery between the current result and the previous result studied by authors in (Liu et al., 2016): (A) SOC estimation; (B) error of SOC estimation.

The state variable of SOC estimation based on the extended Kalman filter algorithm for lithium-ion battery is $x_k={\left[\begin{array}{ccc}SO{C}_k& U_{1,k}& U_{2,k}\end{array}\right]}^T$. The external excitation of system is $u_k=I_k$. According to the ampere-hour integral method, The SOC is expressed as the ratio of the remaining capacity after a period of using time to the total capacity Q_n after fully charging of the battery. So the SOC can be expressed by coulomb counting as (Xu C. et al., 2022)

$SOC\left(t\right)=SOC\left(t_0\right)-\frac{{\int }_{t_0}^{t}I\left(t\right)\eta dt}{Q_n}(17)$

where SOC(t₀) indicates the state of charge at initial time t = t₀. Q_n is the total capacity after fully charging of the battery, η is the Coulomb efficiency relevant to the charging current, discharging current and working temperature. t) is the working current for the battery, which its forward direction is specified as the discharging direction.

The discretization form of Eq. 2 is

$\left\{\begin{array}{l}{U}_{d,k}=U_{OCV}\left(SO{C}_k\right)-U_{1,k}-U_{2,k}-I_k{R}_0\\ U_{1,k}=e^{\frac{-\Delta t}{{\tau }_1}}{U}_{1,k-1}+\left(1-e^{\frac{-\Delta t}{{\tau }_1}}\right)I_{k-1}{R}_1\\ U_{2,k}=e^{\frac{-\Delta t}{{\tau }_2}}{U}_{2,k-1}+\left(1-e^{\frac{-\Delta t}{{\tau }_2}}\right)I_{k-1}{R}_2\end{array}\right.(18)$

where k (k = 1, 2, … , n) denotes the discretization step with a sample interval of Δt. τ_i = R_iC_i (i = 1, 2). And Eq 17 can be written as

$SO{C}_k=SO{C}_{k-1}-\frac{\eta \Delta t}{Q_n}{I}_{k-1}(19)$

The state space model equation of the system was linearized by first-order Taylor series expansion, and the matrix parameters after linearization of first-order extended Kalman filter algorithm are expressed as follows

$\begin{array}{c}\left[A_k^{*}\right]=\left[{\left.\frac{\partial f\left(x_k,u_k\right)}{\partial x_k}\right|}_{x_k=x_k^{*}}\right]=\left[\begin{array}{ccc}1& 0& 0\\ 0& e^{\frac{-\Delta t}{{\tau }_1}}& 0\\ 0& 0& e^{\frac{-\Delta t}{{\tau }_2}}\end{array}\right],\left[B_k\right]=\left[\begin{array}{l}-\frac{\eta \Delta t}{Q_n}\\ R_1\left(1-e^{\frac{-\Delta t}{{\tau }_1}}\right)\\ R_2\left(1-e^{\frac{-\Delta t}{{\tau }_2}}\right)\end{array}\right],\\ \left[C_k^{*}\right]=\left[{\left.\frac{\partial h\left(x_k,u_k\right)}{\partial x_k}\right|}_{x_k=x_k^{*}}\right]={\left[\begin{array}{c}\frac{\partial U_{OCV}\left(SO{C}_k\right)}{\partial SO{C}_k}\\ -1\\ -1\end{array}\right]}^T,\left[D_k\right]=\left[-R_0\right]\end{array}(20)$

Combining Eqs. 18–20, the state-space equations by matrix form for SOC estimation of the battery can be concluded as

$\left\{\begin{array}{l}\left[\begin{array}{c}SO{C}_{k+1}\\ U_{1,k+1}\\ U_{2,k+1}\end{array}\right]=\left[\begin{array}{ccc}1& 0& 0\\ 0& e^{\frac{-\Delta t}{{\tau }_1}}& 0\\ 0& 0& e^{\frac{-\Delta t}{{\tau }_2}}\end{array}\right]\left[\begin{array}{c}SO{C}_k\\ U_{1,k}\\ U_{2,k}\end{array}\right]+\left[\begin{array}{l}-\frac{\eta \Delta t}{Q_n}\\ R_1\left(1-e^{\frac{-\Delta t}{{\tau }_1}}\right)\\ R_2\left(1-e^{\frac{-\Delta t}{{\tau }_2}}\right)\end{array}\right]\left[I_k\right]+\left[w_k\right]\\ \left[U_{d,k}\right]=\left[\begin{array}{ccc}\frac{\partial U_{OCV}\left(SO{C}_k\right)}{\partial SO{C}_k}& -1& -1\end{array}\right]\left[\begin{array}{c}SO{C}_k\\ U_{1,k}\\ U_{2,k}\end{array}\right]-\left[I_k\right]\left[R_0\right]+\left[v_k\right]\end{array}\right.(21)$

The linearized discrete equation of the nonlinear system is given by (Wu et al., 2021; Wu et al., 2022; Ge et al., 2022)

$\left[x_{k+1}\right]=\left[A_k^{*}\right]\cdot \left[x_k\right]+\left[B_k\right]\cdot \left[I_k\right]+\left[w_k\right](22)$

$\left[y_k\right]=\left[C_k^{*}\right]\cdot \left[x_k\right]+\left[D_k\right]\cdot \left[I_k\right]+\left[v_k\right](23)$

According to the general flow of first-order extended Kalman filter algorithm as shown in Figure 5, the parameters identified by the second-order RC equivalent circuit model are input into the program to fit the function expressions between each parameter and SOC firstly. Then, the circuit parameter values of each parameter under the SOC are input initially to obtain the initial value of state variable. The voltage, current, linearized parameter matrix and initial parameter data are put into the recursive method of extended Kalman filter algorithm, and the new SOC value and capacitance polarization voltage are obtained, that is, the first recursive process is completed.

The initial state variable of SOC estimation for the lithium-ion battery is assumed as $x_0={\left[\begin{array}{ccc}0.95& 0& 0\end{array}\right]}^T$ based on the extended Kalman filter algorithm. The Covariance error time update is $x_0={\left[\begin{array}{ccc}0.95& 0& 0\end{array}\right]}^T$. The stochastic process noise covariance and the observation measurement noise covariance are $Q=\left[\begin{array}{ccc}1\times {10}^{-6}& 0& 0\\ 0& 1\times {10}^{-6}& 0\\ 0& 0& 1\times {10}^{-6}\end{array}\right]$ and R = 0.001, respectively.

The SOC estimation results of lithium-ion battery based on the extended Kalman filter algorithm are shown in Figure 12. In order to verify the accuracy of battery estimation model, the simulation results based on extended Kalman filter algorithm are compared with the experimental results. The comparison between simulation results obtained by the extended Kalman filter algorithm based on MATLAB/Simulink and experimental results is shown in Figure 12A. The results show that the simulation results obtained by the extended Kalman filter algorithm based on MATLAB/Simulink are in good consistent with experimental results. The SOC error of simulation result is shown in Figure 12B. The SOC estimation results based on MATLAB/Simulink converge quickly and its error is about 0.02%, which reflects the precision of the extended Kalman filter algorithm.

FIGURE 12

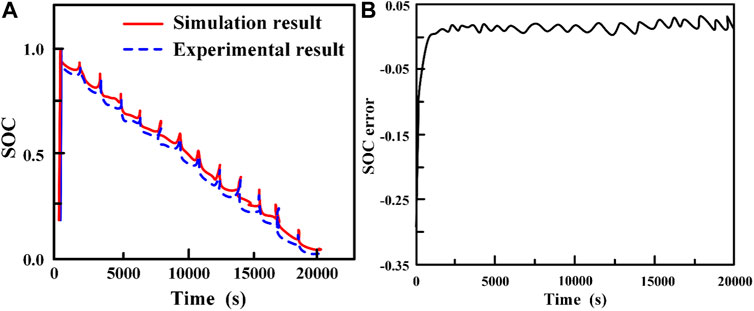
FIGURE 12. SOC estimation results of lithium-ion battery based on the extended Kalman filter algorithm: (A) comparison of SOC between the simulation results based on MATLAB/Simulink and experimental results; (B) SOC error of simulation result.

4 Conclusion

At present, the technical bottleneck of lithium-ion battery is accompanied by the problems of high-performance battery development and maintenance caused by the increasing power demand. Therefore, the state of charge estimation of battery management system has become a wide concern research topic in the field of lithium-ion battery. The state of charge estimation of lithium-ion battery based on extended Kalman filter algorithm is investigated in this paper. Based on the second-order resistor-capacitance equivalent circuit model, the battery model parameters are identified using the MATLAB/Simulink software. The quintic term fitting curves are obtained based on the curve between the open circuit voltage and the state of charge, and the conventional residual error is 0.82%. The variation trend of concentration polarization capacitance is opposite to that of concentration polarization resistance. The model identification parameters of five lithium-ion batteries have a certain error when state of charge from 0.05 to 0.20, which is mainly due to the redistribution of resistance and capacitance during the initial charging and discharging processes. The comparison of extended Kalman filter algorithm between experimental results and simulation estimated results is obtained to verify the accuracy. The results show that the simulation results obtained by the extended Kalman filter algorithm based on MATLAB/Simulink are in good agreement with previous experimental results. The extended Kalman filter algorithm proposed in this study has high effectiveness and accuracy to estimate SOC, which not only establishes the theoretical basis for the condition monitoring but also provides the safe guarantee for the engineering application of lithium-ion battery.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

JX, PZ, PC, and WH contributed to conception and design of this research. XW carried out the database and figures processing. JX, WH, and MY performed the MATLAB/Simulink results analysis. JX and WH wrote the first draft of the manuscript. XB, PZ, PC, and MY revised the finial manuscript. All authors contributed to manuscript revision, read, and approved the submitted version. All authors contributed to the article and approved the submitted version.

Funding

The authors acknowledge the contributions of the National Natural Science Foundation of China (Grant numbers: 12102399 and 12202407), Fundamental Research Program of Shanxi Province (Grant numbers: 20210302124263 and 20210302124383), Open Research Fund for Underground Target Damage Technology National Defense Key Discipline Laboratory (grant number: DXMBJJ 2021-03).

Acknowledgments

The authors acknowledge the contributions of North University of China, Underground Target Damage Technology National Defense Key Discipline Laboratory, and Northwestern Polytechnical University, that aided the efforts of the authors. The authors would like to gratefully acknowledge these funding.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chang, C., Wang, S. J., Tao, C., Jiang, J. C., Jiang, Y., and Wang, L. J. (2022). An improvement of equivalent circuit model for state of health estimation of lithium-ion batteries based on mid-frequency and low-frequency electrochemical impedance spectroscopy. Measurement 202, 111795. doi:10.1016/j.measurement.2022.111795

CrossRef Full Text | Google Scholar

Chen, D. D., Xiao, L., Yan, W. D., and Guo, Y. B. (2021). A novel hybrid equivalent circuit model for lithium-ion battery considering nonlinear capacity effects. Energy Rep. 7, 320–329. doi:10.1016/j.egyr.2021.06.051

CrossRef Full Text | Google Scholar

Chen, X., Lei, H., Xiong, R., Shen, W. X., and Yang, R. X. (2019). A novel approach to reconstruct open circuit voltage for state of charge estimation of lithium ion batteries in electric vehicles. Appl. Energy 255, 113758. doi:10.1016/j.apenergy.2019.113758

CrossRef Full Text | Google Scholar

Chin, C., Gao, Z., Chiew, J., and Zhang, C. (2018). Nonlinear temperature-dependent state model of cylindrical LiFePO₄ battery for open-circuit voltage, terminal voltage and state of charge estimation with extended Kalman filter. Energies 11, 2467. doi:10.3390/en11092467

CrossRef Full Text | Google Scholar

Dang, L. J., Huang, Y. L., Zhang, Y. G., and Chen, B. D. (2022). Multi-kernel correntropy based extended Kalman filtering for state of charge estimation. ISA T 129, 271–283. doi:10.1016/j.isatra.2022.02.047

CrossRef Full Text | Google Scholar

Ge, C., Zheng, Y., and Yu, Y. (2022). State of charge estimation of lithium-ion battery based on improved forgetting factor recursive least squares-extended Kalman filter joint algorithm. J. Energy Storage 55, 105474. doi:10.1016/j.est.2022.105474

CrossRef Full Text | Google Scholar

Hansen, T., and Wang, C. J. (2005). Support vector based battery state of charge estimator. J. Power Sources 141, 351–358. doi:10.1016/j.jpowsour.2004.09.020

CrossRef Full Text | Google Scholar

Hao, W. Q., Bo, X. Q., Xie, J. M., and Xu, T. T. (2022). Mechanical properties of macromolecular separators for lithium-ion batteries based on nanoindentation experiment. Polymers 14 (17), 3664. doi:10.3390/polym14173664

PubMed Abstract | CrossRef Full Text | Google Scholar

Hao, W. Q., Kong, D. C., Xie, J. M., Chen, Y. P., Ding, J., Wang, F. H., et al. (2020a). Self-polymerized dopamine nanoparticles modified separators for improving electrochemical performance and enhancing mechanical strength of lithium-ion batteries. Polymers 12 (3), 648. doi:10.3390/polym12030648

PubMed Abstract | CrossRef Full Text | Google Scholar

Hao, W. Q., and Xie, J. M. (2021). Reducing diffusion-induced stress of bilayer electrode system by introducing pre-strain in lithium-ion battery. J. Electrochem. En. Conv. Stor. 18 (2), 20909. doi:10.1115/1.4049238

CrossRef Full Text | Google Scholar

Hao, W. Q., Xie, J. M., Bo, X. Q., and Wang, F. H. (2019). Resistance exterior force property of lithium-ion pouch batteries with different positive materials. Int. J. Energy Res. 43 (9), 4976–4986. doi:10.1002/er.4588

CrossRef Full Text | Google Scholar

Hao, W. Q., Xie, J. M., and Wang, F. H. (2018). The indentation analysis triggering internal short circuit of lithium-ion pouch battery based on shape function theory. Int. J. Energy Res. 42 (11), 3696–3703. doi:10.1002/er.4109

CrossRef Full Text | Google Scholar

Hao, W. Q., Xie, J. M., Zhang, X., Wang, P., and Wang, F. H. (2020b). Strain rate effect and micro-buckling behavior of anisotropy macromolecular separator for lithium-ion battery. Express Polym. Lett. 14 (3), 206–219. doi:10.3144/expresspolymlett.2020.18

CrossRef Full Text | Google Scholar

Hong, J. C., Zhang, H. Q., and Xu, X. M. (2023). Thermal fault prognosis of lithium-ion batteries in real-world electric vehicles using self-attention mechanism networks. Appl. Therm. Eng. 226, 120304. doi:10.1016/j.applthermaleng.2023.120304

CrossRef Full Text | Google Scholar

Hossain, L., Hannan, M., Hussain, A., and Saad, M. (2017). Optimal BP neural network algorithm for state of charge estimation of lithium-ion battery using PSO with PCA feature selection. J. Renew. Sustain. Energy 9, 064102. doi:10.1063/1.5008491

CrossRef Full Text | Google Scholar

Hu, X. S., Yuan, H., Zou, C. F., Li, Z., and Zhang, L. (2018). Co-estimation of state of charge and state of health for lithium-ion batteries based on fractional-order calculus. IEEE Trans. Veh. Technol. 67, 10319–10329. doi:10.1109/tvt.2018.2865664

CrossRef Full Text | Google Scholar

Iurilli, P., Brivio, C., and Merlo, M. (2019). SoC management strategies in battery energy storage system providing primary control reserve. Sustain. Energy, Grids Netw. 19, 100230. doi:10.1016/j.segan.2019.100230

CrossRef Full Text | Google Scholar

Jeong, Y., Cho, Y., Ahn, J., Ryu, S., and Lee, B. (2014). “Enhanced Coulomb counting method with adaptive SOC reset time for estimating OCV,” in 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pennsylvania, United States, 14-18 September 2014, 1313–1318.

CrossRef Full Text | Google Scholar

Khaki, B., and Das, P. (2023). Definition of multi-objective operation optimization of vanadium redox flow and lithium-ion batteries considering levelized cost of energy, fast charging, and energy efficiency based on current density. J. Energy Storage 64, 107246. doi:10.1016/j.est.2023.107246

CrossRef Full Text | Google Scholar

Lane, B., Shaffer, B., and Samuelsen, S. (2020). A comparison of alternative vehicle fueling infrastructure scenarios. Appl. Energy 259, 114128. doi:10.1016/j.apenergy.2019.114128

CrossRef Full Text | Google Scholar

Li, Z., Huang, J., Liaw, B. Y., and Zhang, J. B. (2017). On state-of-charge determination for lithium-ion batteries. J. Power Sources 348, 281–301. doi:10.1016/j.jpowsour.2017.03.001

CrossRef Full Text | Google Scholar

Liu, C. Z., Liu, W. Q., Wang, L. Y., Hu, G. D., Ma, L. P., and Ren, B. Y. (2016). A new method of modeling and state of charge estimation of the battery. J. Power Sources 320, 1–12. doi:10.1016/j.jpowsour.2016.03.112

CrossRef Full Text | Google Scholar

Liu, K. L., Gao, Y. Z., Zhu, C., Li, K., Fei, M. R., Peng, C., et al. (2022). Electrochemical modeling and parameterization towards control-oriented management of lithium-ion batteries. Control. Eng. Pract. 124, 105176. doi:10.1016/j.conengprac.2022.105176

CrossRef Full Text | Google Scholar

Meng, J., Ricco, M., Luo, G., Swierczynski, M., Stroe, D., Stroe, A. I., et al. (2017). An overview and comparison of online implementable soc estimation methods for lithium-ion battery. IEEE Trans. Ind. Appl. 54, 1583–1591. doi:10.1109/tia.2017.2775179

CrossRef Full Text | Google Scholar

Qahouq, J. A. A., and Xia, Z. Y. (2017). Single-perturbation-cycle online battery impedance spectrum measurement method with closed-loop control of power converter. IEEE Trans. Ind. Electron. 64, 7019–7029. doi:10.1109/tie.2017.2686324

CrossRef Full Text | Google Scholar

Ren, B. Y., Xie, C. X., Sun, X. D., Zhang, Q., and Yan, D. (2020). Parameter identification of a lithium-ion battery based on the improved recursive least square algorithm. IET Power Electron 13, 2531–2537. doi:10.1049/iet-pel.2019.1589

CrossRef Full Text | Google Scholar

Rzepka, B., Bischof, S., and Blank, T. (2021). Implementing an extended kalman filter for SOC estimation of a Li-ion battery with hysteresis: A step-by-step guide. Energies 14, 3733. doi:10.3390/en14133733

CrossRef Full Text | Google Scholar

Salkind, A. J., Fennie, C., Singh, P., Atwater, T., and Reisner, D. E. (1999). Determination of state-of-charge and state-of-health of batteries by fuzzy logic methodology. J. Power Sources 80, 293–300. doi:10.1016/s0378-7753(99)00079-8

CrossRef Full Text | Google Scholar

Shi, H. T., Wang, L. P., Wang, S., Fernandez, C., Xiong, X., Dablu, B. E., et al. (2022). A novel lumped thermal characteristic modeling strategy for the online adaptive temperature and parameter co-estimation of vehicle lithium-ion batteries. J. Energy Storage 50, 104309. doi:10.1016/j.est.2022.104309

CrossRef Full Text | Google Scholar

Tong, S., Klein, M., and Park, J. (2015). On-line optimization of battery open circuit voltage for improved state-of-charge and state-of-health estimation. J. Power Sources 293, 416–428. doi:10.1016/j.jpowsour.2015.03.157

CrossRef Full Text | Google Scholar

Tran, M. K., Mathew, M., Janhunen, S., Panchal, S., Raahemifar, K., Fraser, R., et al. (2021). A comprehensive equivalent circuit model for lithium-ion batteries, incorporating the effects of state of health, state of charge, and temperature on model parameters. J. Energy Storage 43, 103252. doi:10.1016/j.est.2021.103252

CrossRef Full Text | Google Scholar

Wang, B., Li, S. E., Peng, H., and Liu, Z. (2015). Fractional-order modeling and parameter identification for lithium-ion batteries. J. Power Sources 293, 151–161. doi:10.1016/j.jpowsour.2015.05.059

CrossRef Full Text | Google Scholar

Wang, D. F., Zhang, Q., HuangYangDong, H. Q. B. W. H. S., Zhang, J. M., and Zhang, J. (2022). An electrochemical-thermal model of lithium-ion battery and state of health estimation. J. Energy Storage 47, 103528. doi:10.1016/j.est.2021.103528

CrossRef Full Text | Google Scholar

Wang, Q., Ye, M., Wei, M., Lian, G. Q., and Wu, C. G. (2021). Co-estimation of state of charge and capacity for lithium-ion battery based on recurrent neural network and support vector machine. Energy Rep. 7, 7323–7332. doi:10.1016/j.egyr.2021.10.095

CrossRef Full Text | Google Scholar

Wang, S., Fernandez, C., Shang, L., Li, Z., and Li, J. (2017). Online state of charge estimation for the aerial lithium-ion battery packs based on the improved extended Kalman filter method. J. Energy Storage 9, 69–83. doi:10.1016/j.est.2016.09.008

CrossRef Full Text | Google Scholar

Wang, S. L., Fan, Y. C., Jin, S. Y., Takyi-Aninakwa, P., and Fernandez, C. (2023). Improved anti-noise adaptive long short-term memory neural network modeling for the robust remaining useful life prediction of lithium-ion batteries. Reliab. Eng. Syst. Saf. 230, 108920. doi:10.1016/j.ress.2022.108920

CrossRef Full Text | Google Scholar

Wang, Y., and Chen, Z. (2020). A framework for state-of-charge and remaining discharge time prediction using unscented particle filter. Appl. Energy 260, 114324. doi:10.1016/j.apenergy.2019.114324

CrossRef Full Text | Google Scholar

Wu, M., Qin, L., Wu, G., Huang, Y., and Shi, C. (2021). State of charge estimation of power lithium-ion battery based on a variable forgetting factor adaptive Kalman filter. J. Energy Storage 41, 102841. doi:10.1016/j.est.2021.102841

CrossRef Full Text | Google Scholar

Wu, M., Qin, L., and Wu, G. (2022). State of charge estimation of power lithium-ion battery based on an affine iterative adaptive extended kalman filter. J. Energy Storage 51, 104472. doi:10.1016/j.est.2022.104472

CrossRef Full Text | Google Scholar

Xu, C., Zhang, E., Jiang, K., and Wang, K. L. (2022). Dual fuzzy-based adaptive extended Kalman filter for state of charge estimation of liquid metal battery. Appl. Energy 327, 120091. doi:10.1016/j.apenergy.2022.120091

CrossRef Full Text | Google Scholar

Xu, L., Lin, X., Xie, Y., and Hu, X. (2022). Enabling high-fidelity electrochemical P2D modeling of lithium-ion batteries via fast and non-destructive parameter identification. Energy Stor. Mat. 45, 952–968. doi:10.1016/j.ensm.2021.12.044

CrossRef Full Text | Google Scholar

Xu, X. D., Tang, S. J., Ren, H. H., Han, X. B., Wu, Y., Lu, L. G., et al. (2022). Joint state estimation of lithium-ion batteries combining improved equivalent circuit model with electrochemical mechanism and diffusion process. J. Energy Storage 56, 106135. doi:10.1016/j.est.2022.106135

CrossRef Full Text | Google Scholar

Yang, F., Shi, D. L., and Lam, K. H. (2022). Modified extended Kalman filtering algorithm for precise voltage and state-of-charge estimations of rechargeable batteries. J. Energy Storage 56, 105831. doi:10.1016/j.est.2022.105831

CrossRef Full Text | Google Scholar

Zhang, Z., Zhang, T., Hong, J., Zhang, H., and Yang, J. (2023). Energy management strategy of a novel parallel electric-hydraulic hybrid electric vehicle based on deep reinforcement learning and entropy evaluation. J. Clean. Prod. 403, 136800. doi:10.1016/j.jclepro.2023.136800

CrossRef Full Text | Google Scholar