AI-based voltage and power quality control of high-penetration grid-connected photovoltaic power plant

The importance of using renewable energy systems (RESs) worldwide has been consolidated. Moreover, connecting more RESs to the utility grid will lead to more technical problems. Photovoltaic (PV) and wind turbine (WT) based power plants are the most nonlinear sources of renewable energies contributing to the energy mix Electronic ballast and switching mode power supply in energy conservation of the PV and WT have caused power quality problems and less reliable output voltage. PV power plants are becoming increasingly integrated with the utility grid by onboarding certain superior power quality features. This grid integration drastically reduces the use of fossil fuels and prevents environmental hazards. This article presents the design of a 26 MWp grid-connected PV power plant, which is already tied to the Egyptian electrical network in Fares City, Kom Ombo Center, Aswan Governorate, Egypt The 26 MWp PV power plant consists of (11) blocks and the utility grid, which are simulated using Matlab/Simulink. Every block contains 2,376 kWp PV arrays connected directly to DC-DC boost converters to regulate the output DC power generated by each PV array. This output DC power is fed into a particular type of inverter called a “central inverter”, which converts it to AC power. In some cases, higher harmonic distortion at the grid and a greater negative impact on the power system performance occur when using this type of inverter. To optimize the gains of the proportional-integral (PI) controller for both the voltage and current regulators of this central inverter, meta-heuristic optimization techniques (MOTs) are used. During this article, Gray Wolf Optimization (GWO), Harris Hawks Optimization (HHO), and Arithmetic Optimization Algorithm (AOA) are applied as MOTs to enhance the quality of the power and voltage in addition to limiting the total harmonic distortions (THD) under the effect of different sunlight conditions and partial shading. As a result, the AOA-based controllers are found to show outstanding results and superior performance compared to GWO and HHO regarding solution quality and computational efficiency. Finally, MOTs are the best solution to most electrical problems regarding controlling nonlinear and high-penetration systems, such as PV power plants connected to the utility grid.

1 Introduction

Nowadays, conventional energy sources are being replaced with alternative RESs, such as solar, wind, and hydro energy due to problems related to climate conditions, environmental changes, and high liberation in traditional power systems. Therefore, it is also necessary to replace the conventional utility grid to accommodate the increased integration of renewable energy systems and to suit its conditions, especially nonlinear energy systems like photovoltaic, concentrated solar thermal, and wind power systems (Rakhshani et al., 2019). Although using RESs reduces harmful environmental pollution compared to traditional fossil fuels, it causes complex control problems with the utility grid, such as the occurrence of high fault current, low generation reserve, and low power quality. There is also a decrease in the inertia of these systems, which leads to a lack of synchronization, as it is in conventional energy systems. The power electronics built into the inverters are very important to integrate renewable energy systems with the utility grid according to power quality standards. Despite this, they can inject extra harmonics into the power systems because of the high-frequency switching of inverters, which leads to a reduction in power quality and an increase in power losses (Khadem et al., 2010).

The irregularity, intermittency, and nonlinearity of solar power generation can affect the utility grid voltage stability during peak load demand. As a result, it is important to understand the methodology of utility grid voltage stability during the high penetration of solar energy sources (Rahman et al., 2021). Based on the rapid increase in the adoption of renewable energy sources instead of conventional energy sources, there will be an impact on the stability and dynamic performance of power systems. One example of nonlinear renewable energy sources is PV power plants, whose high generation creates additional stability challenges during normal operation and abnormal disturbances in the electricity transmission network. These abnormal disturbances can be summarized in the disconnection of conventional generating stations from the grid, a sudden change of heavy loads, a major electrical transmission line being out of service, and the occurrence of various types of transmission line faults (three phase to ground fault, single phase to ground fault, phase to phase fault, etc.) (Sultan et al., 2019).

The large contribution of both PV and WT based power plants aims to attain eco-environmental benefits, but at the same time, many technical problems are raised due to their high variability and intermittent nature. Therefore, it is necessary to use the energy storage devices, fault current limiters and electrical gate devices to assist in tackling most of these technical problems (Shafiul Alam et al., 2020). Recently, it has been found that increasing the high penetration of PV power plants on the utility grid affects the performance of the protection system, the automatic voltage regulator (AVR), and the on-load tap changer (OLTC) of the power systems, so the proposed solution is to connect voltage controllers to these plants to reduce the voltage rise (Kenneth and Folly, 2014). Furthermore, the power systems have many technical problems, such as harmonic distortion, voltage transient, and spikes that lead to the process of overheating and increase power losses and disturbances in the utility grid (Kumar et al., 2021).

The wide distribution of PV generation units across the grid is one of the factors that increase the amount of harmonic distortion. So, the interference level of these units must not exceed the maximum capacity of the grid otherwise, voltage collapse, grid instability, and a partial or complete power grid outage will occur. Where the injection current and voltage of the generated PV energy will be with harmonics and poor quality as a result, voltage collapse occurs because of instability in the utility grid, which leads to a complete or partial power grid outage. Also, integrating the distributed PV generation units in the power systems cause different challenges, such as system reliability, power quality, voltage fluctuation, and reverse power flow. Thus, the high penetration level of PV distributed generation units in the utility grid can decrease the reliability of the power system and lead to more harmonic distortion in the power system network (Abdul Kadir et al., 2014). On the other hand, the protection of power systems with the high penetration level of PV is one of the critical challenges because the current protection methods are used for unidirectional, not bidirectional, power flow. Furthermore, power systems are affected by equipment overheating/failure, operation failure, system malfunction, voltage fluctuation, and equipment protection (Nkado and Franklin, 2021).

The incompatibility between the generated real power and the load profile characteristics of PV power plants causes major voltage imbalances, dangerous power flow reversal, and high-power losses during the load conditions. Furthermore, power quality is affected by several aspects, including generation, consumer, and network. As a result, the comparison between renewable energy technologies proves that PV power plants still face important difficulties and challenges that have harmful effects on power quality, such as overloading of the cables, harmonics, low efficiency, and dependability (Singh et al., 2018). Instability of the grid voltage depends on connecting the PV power plants to the utility grid suddenly, so it is necessary to control the stability of the voltage when connecting PV plants to the network. Based on all the challenges related to the connection of PV power plants to the utility grid, especially the high level of penetration, it is necessary to find possible technical solutions to overcome these challenges and improve and enhance the performance of the plants (Sujatha and Anitha, 2016).

There are several factors that affect PV Power System Performance, such as PV technology type, solar irradiation, tilt angle orientation, shading, dust, cell and ambient temperature. Furthermore, the optimal cleaning methods for each PV system can be determined through the PV size, design, location, dust type, and water availability (Aslam et al., 2022). Gallium arsenide (GaAs) has been employed on the surface of PV cells to eliminate the undesirable reflection losses of the solar irradiation using the graded refractive index properties in order to optimize PV cell design and diffraction Nano-gratings (Masouleh et al., 2016). Nowadays, machine learning and artificial intelligence (AI) processes are utilized for forecasting PV output power because of their comparatively high accuracy and ability to understand updated historical data, which has led to the existence of facilities for predicting PV output power (Iheanetu, 2022). Lately, using optimization techniques has achieved superior results in the sizing, power production, and capacity demand of PV systems such as increasing peak power integration, decreasing operational expenses and improving performance of the grid-connected PV systems (Soomar et al., 2022).

Electrical equipment can operate safely and effectively under the grid standard conditions of supply, which are represented in the power quality requirements (voltage and frequency regulation, power factor correction, and harmonics). Most power quality problems relating to grid-connected PV power plants can be summarized as harmonics, fast/slow voltage variations, overvoltage, flicker performance, voltage unbalance, sudden disconnection/reconnection, and inrush currents (Smith et al., 2017). Large-scale grid-connected PV plants have nonlinear factors, such as dead time and phase-locked loop (PLL), represented in the impedance model of the inverter output, and the diversity of PV capacity which affect the power quality and stability of the power system. PLL creates the asymmetric system, causes the frequency coupling effect, increases PV capacity in the utility grid, and also limits the influence of dead time on the system phase margin but may causes dangerous enlargement of certain dead-time harmonics (Zhang et al., 2018). Integration of the high penetration level of PV power plants must be according to the maximum carrying capacity of the utility grid because the high harmonic distortion level is increased as the penetration level of PV power plants is increased. So, it is recommended that the maximum penetration level of PV power plants must be in between this percentage rating (4.97%–14.98%) to allow only the agreeable limits of the harmonic distortion, total voltage harmonic distortion, and current demand distortion (Sharew et al., 2021). Harmonic reduction under nonlinear and unbalanced load conditions can be achieved by optimizing the hybrid shunt active power filter (HSHAPF) with the GWO method and fractional order proportional integral controller (FOPI), where the GWO method is used to tune the parameters of FOPI to decrease the harmonics effectively (Srikanth Goud et al., 2022). To achieve the overall power quality control and management represented in improving the power quality, grid security, stability, and efficiency, the cooperative power quality control strategy that integrates active power filter, reactive power compensation, and inverter functions is used. As a result, the power factor value is 0.99, reducing the current distortion rate to 2.71%, and improving the harmonics that grid-connected PV systems can obtain (Sun et al., 2022).

The efficiency of maximum power point tracking (MPPT) highly depends on its parameters, i.e., perturbation amplitude changing ΔD in what is called “duty cycle” and perturbation period Tp. To achieve the desired tracking speed and efficiency of MPPT, ΔD and Tp should be optimized accordingly (Dadkhah and Niroomand, 2021). There are different techniques; the Perturb and Observe (P&O) method and the Incremental conductance (IC) method are used to overcome nonlinear behavior, achieve MPPT, and improve the performance of PV power plants in cases of changing solar irradiation. Applying the P&O and IC methods on the PV power plants during Matlab simulation proved that the time response and performance of the P&O controller are better than those of the IC controller (Elbarbary and Alranini, 2021). The relationship between open-circuit voltage and maximum power voltage from partial open-circuit voltage is used to set a reduced and limited valid search space in what is called “an enhanced P&O”. This enhanced P&O method used for MPPT proved to significantly increase the efficiency of the PV system if compared with other methods (Harrison et al., 2022). Also, to overcome the nonlinearity of the PV modules and to produce the maximum power output from the PV arrays, a DC-DC Boost Converter with this enhanced P&O method is used to achieve efficient MPPT for the PV power plant (Raj and Praveen, 2022). There are various MPPT algorithms, but it requires in-depth information to select the best MPPT methods because each method has different advantages and disadvantages. The overview results of MPPT methods show that each algorithm’s advantages and limitations must be determined in order to choose the best solution to improve output power efficiency. Therefore, different intelligent algorithms must be added and combined with the MPPT algorithms to create high speed and processing ability in the presence of external factors (Le et al., 2022).

The optimal power flow (OPF) is one of the major arithmetical methods presently used for the best operation of power systems. The topical functions related to the power system that can be optimized are transmission line losses, total generation costs, flexible alternating current transmission system costs, voltage deviations, total power transfer capability, voltage stability, emission of generation units, and system security Furthermore, the performance of electrical power networks and resource planning effectiveness are enhanced by using OPF (Risi et al., 2022). The main aim of OPF optimization is to attain the optimal solution for the utility grid design variables that face the minimum value of the objective function, taking into consideration the restrictions of the electric power system. Applying Sun Flower Optimization (SFO), Harris Hawks Optimization (HHO), and Heap Optimization Algorithm (HOA) to solve the OPF problem of integrating PV and WT energy with the power system proves that HOA has higher speed and smoother convergence and is efficient in computations and implementation of the fitness function (Shaheen et al., 2021). Modified turbulent water flow-based optimization (MTFWO) is used effectively to solve the nonlinear and multi-objective OPF problems in power systems that integrate energy from WT and PV generators. MTFWO is a more flexible, computationally efficient, adaptive, and higher-quality method used to solve the OPF problem, especially multiple objective functions (Alghamdi, 2022).

The unsteady generated power from RESs affects the power flow of the whole utility grid, so it is important to optimize the power flow in order to achieve stable and dependable operation. Therefore, newly developed circle search algorithms (CSAs) are used and compared with other famous algorithms, such as the Genetic Algorithm (GA) and Particle Swarm Optimization (PSO) for improving OPF problems and reducing generation costs (Shaheen et al., 2022). Furthermore, the Gaussian bare-bones Levy-flight firefly algorithm (GBLFA) and its modified version, MGBLFA, are used for optimizing the various objective functions of the OPF problems (fuel costs, emission, power loss, and voltage deviation), whether with traditional power generators or interrupted RESs (Alghamdi, 2022). In addition, the hybrid optimization technique based on a machine learning approach and transient search optimization (ML-TSO) is also used to fix the ancient OPF and probabilistic OPF problems through examining the impact of sharing RESs (PV and WT) and time changing load profiles on generation costs. The convergence performance of the hybrid ML-TSO algorithm proves that applying it to solve OPF and POPF problems is better than using other optimization algorithms (Shaheen et al., 2022).

Several techniques can be used to control the voltage stability of photovoltaic generators, whether under normal or high load conditions, such as power flow, continuation power flow, and Q-V curve (Abdullah et al., 2021). Also, the synchronous power controllers of inverters used for the PV power plant have a beneficial impact on the power system because they work to limit frequency deviations, improve oscillation damping, and reduce the negative effect of the other generating units on the utility grid. Furthermore, PV power plants can be used to inject reactive power into the utility grid (Remon et al., 2017). The dynamic performance of PV power plants linked to the grid can be enhanced using the adaptive or self-tuning PI controllers of the central inverters. Many studies have employed this sort of control to enhance PV systems’ dynamic performance; however, its design is based on trial and error, which is not a reliable controller-design approach. Furthermore, the nonlinearity and fluctuation of PV plants in the power system are two problems faced by the PI controller (Hasanien, 2017). However, various optimization techniques, such as Particle Swarm Optimization (PSO), Gray Wolf Optimization (GWO), Harris Hawks Optimization (HHO), and the Arithmetic Optimization Algorithm (AOA) can be used to enhance the generated voltage and power quality and reduce electrical power losses under different operating conditions through optimizing the gains of this PI controller (Eltamaly et al., 2020). Voltage and current harmonics are also reduced according to the specified limits using these optimization techniques with RLC filters (Al-Shetwi et al., 2020).

The British Petroleum (BP) 71st edition report presents a statistical review of world energy, which contains the energy consumption and known reserves of 2022. As a positive development, RESs’ share of the power-generating market has increased to 13%, thanks mostly to the expansion of wind and solar power. Over the course of the previous 2 years, worldwide electricity output climbed by over 50%, but renewable generation increased by approximately 17% in 2021 (BP Statistical Review of World Energy Report, 2022). With its location in the so-called “solar belt,” an ideal area for solar power installations, Egypt is a veritable treasure trove of renewable energy potential. Based on 20-year averages, Atlas Egypt’s findings reveal that the country has excellent potential for investment in various solar energy industries (Moharram et al., 2022). The annual solar radiation average is 2000–3,200 kWh/m2, and daily sunlight hours vary between 9 and 11 h/day (Ministry of Electricity and Renewable Energy, 2022). By 2035, the Egyptian government plans to have generated energy from renewable sources accounting for 42% of Egypt’s total generated energy (Ministry of Electricity and Renewable Energy, 2022).

In line with this, a 26 MWp large-scale grid-connected PV power plant with modified inverters is designed and simulated by Matlab/Simulink. This PV power plant is already tied to the Egyptian electrical network in Fares City, Kom Ombo Center, Aswan Governorate, Egypt. It consists of (11) blocks and the utility grid, where every block contains 2,376 kWp PV arrays connected directly to DC-DC boost converters to regulate the output DC power generated by each PV array. The inverter used in this PV power plant is a central inverter, which can operate under normal conditions efficiently until any faults or abnormal conditions occur. It can change the mode of operation by using the PI controller to inject a reactive current based on the amount of these faults. Dynamic voltage and current regulators are built into this PI controller to control the inverter output and limit the voltage flicker, fluctuation, and unbalance injected from this large-scale PV power plant on the utility grid. Furthermore, the electrical filters can be used to enhance power quality, improve voltage stability, and compensate harmonic distortion by optimizing the amount of power extracted from the PV arrays to the central inverter under different sunlight conditions and in partial shade (Attia, 2018; Sameh et al., 2021).

This article aims to enhance the voltage and power quality of the high penetration level of PV power plants connected to the utility grid to reduce voltage flicker and total harmonic distortions using modern optimization methods and techniques. In this study, GWO, HHO, and AOA methods and filters are applied to the PI controller of the simulated inverter of the 26 MWp large-scale PV power plant. These optimization methods can improve the dynamic performance of this PV power plant interface system by optimizing the proportional gain (Kp) and the integral gain (Ki) of the proportional integral (PI) controller. The major contributions of this article can be summarized as follows. 1) Design of a realistic 26 MWp largescale grid-connected PV power plant, already tied to the Egyptian electrical network in Fares City, Kom Ombo Center, Aswan Governorate, Egypt is developed. 2) Several modern optimization techniques such as GWO, HHO, and AOA, are applied to enhance the power quality and voltage stability that is produced from this PV power plant under different sunlight conditions and in partially shaded conditions. 3) Intensive study is conducted and a solution is proposed for the high penetration level of PV power plants connected to the Egyptian electricity grid to control power quality, voltage stability, and total harmonic distortion issues.

2 Optimization methods

In this article, Gray Wolf, Harris Hawks, and Arithmetic algorithm optimization techniques are utilized. These optimization techniques are used to optimize the PI controller for every central inverter station by adjusting the proportional gain (Kp) and the integral gain (Ki) of the voltage regulator and the current regulator. Consequently, the dynamic performance of the interface system within the utility grid for PV power plants can be improved.

2.1 Gray Wolf Optimization (GWO)

Inspired by the intelligence and adaptability of gray wolves, or Canis lupus, a novel meta-heuristic dubbed Gray Wolf Optimization (GWO) has been developed (available online 21 January 2014). In Figure 1, we see a representation of the GWO algorithm as gray wolves’ natural hierarchy and hunting mechanism. The gray wolf social structure is modeled after that of an organization, using a pyramid of four wolf packs labeled alpha, beta, delta, and omega. Matlab/Simulink also incorporates the three primary phases of hunting: looking for prey, surrounding it, and attacking it. GWO mathematical equations can be represented by Eqs 1–7: (Mirjalili et al., 2014).

$\overrightarrow{\mathit{D}}=\left|\overrightarrow{\mathit{C}}.\overrightarrow{\mathit{X}}\mathit{p}\left(\mathit{t}\right)-\overrightarrow{\mathit{X}}\left(\mathit{t}\right)\right|(1)$

$\overrightarrow{\mathit{X}}\left(\mathit{t}+1\right)=\overrightarrow{\mathit{X}}\mathit{p}\left(\mathit{t}\right)-\overrightarrow{\mathit{A}}.\overrightarrow{\mathit{D}}(2)$

$\overrightarrow{\mathit{A}}=2\overrightarrow{\mathit{a}}.{\overrightarrow{\mathit{r}}}_1-\overrightarrow{\mathit{a}}(3)$

$\overrightarrow{\mathit{C}}=2.{\overrightarrow{\mathit{r}}}_2(4)$

${\overrightarrow{\mathit{X}}}_1={\overrightarrow{\mathit{X}}}_{\mathit{\alpha }}-{\overrightarrow{\mathit{A}}}_1.\left({\overrightarrow{\mathit{D}}}_{\mathit{\alpha }}\right),{\overrightarrow{\mathit{X}}}_2={\overrightarrow{\mathit{X}}}_{\mathit{\beta }}-{\overrightarrow{\mathit{A}}}_2.\left({\overrightarrow{\mathit{D}}}_{\mathit{\beta }}\right),{\overrightarrow{\mathit{X}}}_3={\overrightarrow{\mathit{X}}}_{\mathit{\delta }}-{\overrightarrow{\mathit{A}}}_3.\left({\overrightarrow{\mathit{D}}}_{\mathit{\delta }}\right)(5)$

${\overrightarrow{\mathit{D}}}_{\mathit{\alpha }}=\left|\overrightarrow{\mathit{C}}1.{\overrightarrow{\mathit{X}}}_{\mathit{\alpha }}-\overrightarrow{\mathit{X}}\right|,{\overrightarrow{\mathit{D}}}_{\mathit{\beta }}=\left|\overrightarrow{\mathit{C}}2.{\overrightarrow{\mathit{X}}}_{\mathit{\beta }}-\overrightarrow{\mathit{X}}\right|,{\overrightarrow{\mathit{D}}}_{\mathit{\delta }}=\left|\overrightarrow{\mathit{C}}3.{\overrightarrow{\mathit{X}}}_{\mathit{\delta }}-\overrightarrow{\mathit{X}}\right|(6)$

$\overrightarrow{\mathit{X}}\left(\mathit{t}+1\right)=\frac{\overrightarrow{\mathit{X}}1+{\overrightarrow{\mathit{X}}}_2+{\overrightarrow{\mathit{X}}}_3}{3}(7)$

Where, $\overrightarrow{\mathit{X}}\left(\mathit{t}+1\right)$: indicates the position vector of a gray wolf. t: indicates the current iteration. $\overrightarrow{\mathit{D}}$: encircling behavior. $\overrightarrow{\mathit{X}}\mathit{p}$: the position vector of the prey. $\overrightarrow{\mathit{A}}$ & $\overrightarrow{\mathit{C}}$: coefficient vectors. $\overrightarrow{\mathit{r}}$₁ & $\overrightarrow{\mathit{r}}$₂: random vectors in [0, 1]. $\overrightarrow{\mathit{a}}$: linearly decreased from 2 to 0 over the course of iterations.

FIGURE 1

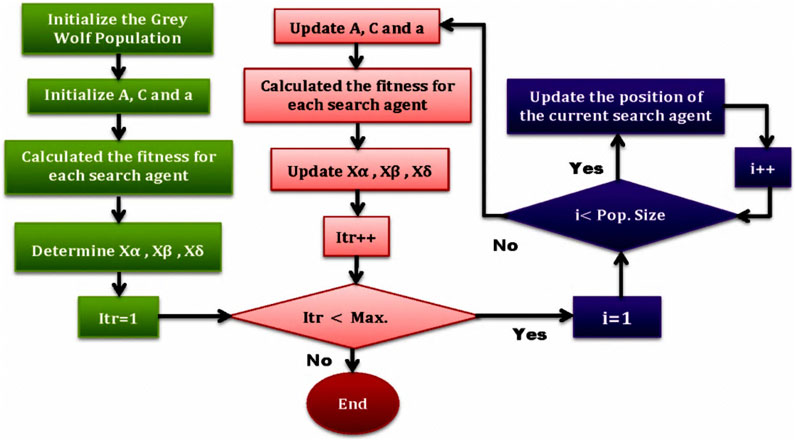
FIGURE 1. Flow chart of the GWO algorithm (Makhadmeh et al., 2018).

The new metaheuristic technique GWO is inspired by the gray wolf pack mentality during hunting. Gray wolves hunt as a pack and rely on their pack members to be in the right place at the right time. The pack of wolves receives the best-fitting answer in a mathematical model of the hunting process; the best solution is given to group α, followed by groups β, γ, and δ. When the wolves are ready to begin hunting, they circle the victim once (Mishra et al., 2020).

The benefit of GWO is that the method has few parameters and does not necessitate knowledge of the search space’s derivation. GWO is also simple to implement, adapt to new circumstances, and use. The algorithm achieves great convergence because it strikes a good balance between exploration and exploitation during the search process (Ghalambaz et al., 2021). However, GWO can quickly become stuck in a local optimum and has a poor convergence speed (Liu et al., 2021).

2.2 Harris Hawks Optimization (HHO)

HHO is based mainly on a natural hunting strategy used by Harris’s hawks, termed “surprise pounce,” which involves teamwork and cooperation (available online 28 February 2019). Several hawks will work together to surprise their target by swooping in from all sides (as depicted in Figure 2). Harris’s hawks have been observed to display a wide range of pursuit behaviors, which are in turn influenced by the circumstance and the prey’s tendency to either flee or be caught. Here, we model the HHO’s foraging and exploitative stages after the foraging, surprise pounce, and various attacking techniques of the Harris’s hawk. HHO mathematical equations can be represented by Eqs 8–18: (Heidari et al., 2019).

$\mathit{X}\left(\mathit{t}+1\right)=\left\{\begin{array}{cc}{\mathit{X}}_{\mathit{r}\mathit{a}\mathit{n}\mathit{d}}\left(\mathit{t}\right)-{\mathit{r}}_1\left|{\mathit{X}}_{\mathit{r}\mathit{a}\mathit{n}\mathit{d}}\left(\mathit{t}\right)-2{\mathit{r}}_2\mathit{X}\left(\mathit{t}\right)\right|& \mathit{q}\ge 0.5\\ \left({\mathit{X}}_{\mathit{r}\mathit{a}\mathit{b}\mathit{b}\mathit{i}\mathit{t}}\left(\mathit{t}\right)-{\mathit{X}}_{\mathit{m}}\left(\mathit{t}\right)\right)-{\mathit{r}}_3\left(\mathit{L}\mathit{B}+{\mathit{r}}_4\left(\mathit{U}\mathit{B}-\mathit{L}\mathit{B}\right)\right)& \mathit{q}<0.5\end{array}\right.(8)$

${\mathit{X}}_{\mathit{m}}\left(\mathit{t}\right)=\frac{1}{\mathit{N}}{\displaystyle {\sum }_{i=1}^N}{\mathit{X}}_{\mathit{i}}\left(\mathit{t}\right)(9)$

$\mathit{E}=2{\mathit{E}}_0\left(1-\frac{\mathit{t}}{\mathit{T}}\right)(10)$

$\mathit{X}\left(\mathit{t}+1\right)=∆\mathit{X}\left(\mathit{t}\right)-\mathit{E}\left|\mathit{J}{\mathit{X}}_{\mathit{r}\mathit{a}\mathit{b}\mathit{b}\mathit{i}\mathit{t}}\left(\mathit{t}\right)-\mathit{X}\left(\mathit{t}\right)\right|(11)$

$∆\mathit{X}\left(\mathit{t}\right)={\mathit{X}}_{\mathit{r}\mathit{a}\mathit{b}\mathit{b}\mathit{i}\mathit{t}}\left(\mathit{t}\right)-\mathit{X}\left(\mathit{t}\right)(12)$

$\mathit{X}\left(\mathit{t}+1\right)={\mathit{X}}_{\mathit{r}\mathit{a}\mathit{b}\mathit{b}\mathit{i}\mathit{t}}\left(\mathit{t}\right)-\mathit{E}\left|∆\mathit{X}\left(\mathit{t}\right)\right|(13)$

$\mathit{Y}={\mathit{X}}_{\mathit{r}\mathit{a}\mathit{b}\mathit{b}\mathit{i}\mathit{t}}\left(\mathit{t}\right)-\mathit{E}\left|\mathit{J}{\mathit{X}}_{\mathit{r}\mathit{a}\mathit{b}\mathit{b}\mathit{i}\mathit{t}}\left(\mathit{t}\right)-\mathit{X}\left(\mathit{t}\right)\right|(14)$

$\mathit{Z}=\mathit{Y}+\mathit{S}\times \mathit{L}\mathit{F}\left(\mathit{D}\right)\left(\mathrm{S}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{i}\mathrm{e}\mathrm{g}\mathrm{e}\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{n}\left|\mathrm{E}\right|\ge 0.5\mathrm{b}\mathrm{u}\mathrm{t}\mathrm{r}<0.5\right)(15)$

$\mathit{L}\mathit{F}\left(\mathit{x}\right)=0.01\times \frac{\mathit{u}\times \mathit{\sigma }}{{\left|\mathit{\upsilon }\right|}^{\frac{1}{\mathit{\beta }}}},\mathit{\sigma }={\left(\frac{\mathit{\Gamma }\left(1+\mathit{\beta }\right)\times \mathit{sin}\left(\frac{\mathit{\pi }\mathit{\beta }}{2}\right)}{\mathit{\Gamma }\left(\frac{1+\mathit{\beta }}{2}\right)\times \mathit{\beta }\times 2^{\left(\frac{\mathit{\beta }-1}{2}\right)}}\right)}^{\frac{1}{\mathit{\beta }}}(16)$

$\mathit{X}\left(\mathit{t}+1\right)=\left\{\begin{array}{c}\mathit{Y}\mathit{i}\mathit{f}\mathit{F}\left(\mathit{Y}\right)<\mathit{F}\left(\mathit{X}\left(\mathit{t}\right)\right)\\ \mathit{Z}\mathit{i}\mathit{f}\mathit{F}\left(\mathit{Z}\right)<\mathit{F}\left(\mathit{X}\left(\mathit{t}\right)\right)\end{array}\right.(17)$

$\mathit{Z}=\mathit{Y}+\mathit{S}\times \mathit{L}\mathit{F}\left(\mathit{D}\right)\left(\mathrm{H}\mathrm{a}\mathrm{r}\mathrm{d}\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{i}\mathrm{e}\mathrm{g}\mathrm{e}\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{n}\left|\mathrm{E}\right|<0.5\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{r}<0.5\right)(18)$

Where ${\mathit{X}}_{\mathit{r}\mathit{a}\mathit{b}\mathit{b}\mathit{i}\mathit{t}}\left(\mathit{t}\right)$: the rabbit’s position. $\mathit{X}\left(\mathit{t}+1\right)$: the next iteration’s (t) hawks position vector. $\mathit{X}\left(\mathit{t}\right)$: the hawk’s current position vector. A set of random numbers inside (0,1) are denoted by r₁, r₂, r₃, r₄, and q, which are updated in each iteration. ${\mathit{X}}_{\mathit{m}}$: the hawk’s current population’s average position. ${\mathit{X}}_{\mathit{r}\mathit{a}\mathit{n}\mathit{d}}\left(\mathit{t}\right)$: the current population of a randomly selected hawk ${\mathit{X}}_{\mathit{i}}\left(\mathit{t}\right)$: the hawk’s location in iteration t. $\mathit{L}\mathit{B}$ and $\mathit{U}\mathit{B}$: the upper and lower bounds of variables. $\mathit{N}$: the total hawks number. $\mathit{T}$: the maximum number of iterations. $\mathit{E}$: the prey’s escaping energy. ${\mathit{E}}_0$: the initial state of its energy. ${\mathit{r}}_5$: random number inside (0,1). $∆\mathit{X}\left(\mathit{t}\right)$: the difference between the position vector of the rabbit and the current location in iteration t. $\mathit{J}$ = 2 (1 − ${\mathit{r}}_5$): the random jump strength of the rabbit throughout the escaping procedure. $\mathit{S}$: random vector by size 1xD. $\mathit{D}$: the dimension of problem. $\mathit{L}\mathit{F}$: the levy flight function. $\mathit{\beta }$: default constant set to 1.5. $\mathit{u}$, $\mathit{\upsilon }$: random values inside (0,1). $\mathit{Y}$ and $\mathit{Z}$: obtained using Eqs 14, 15.

FIGURE 2

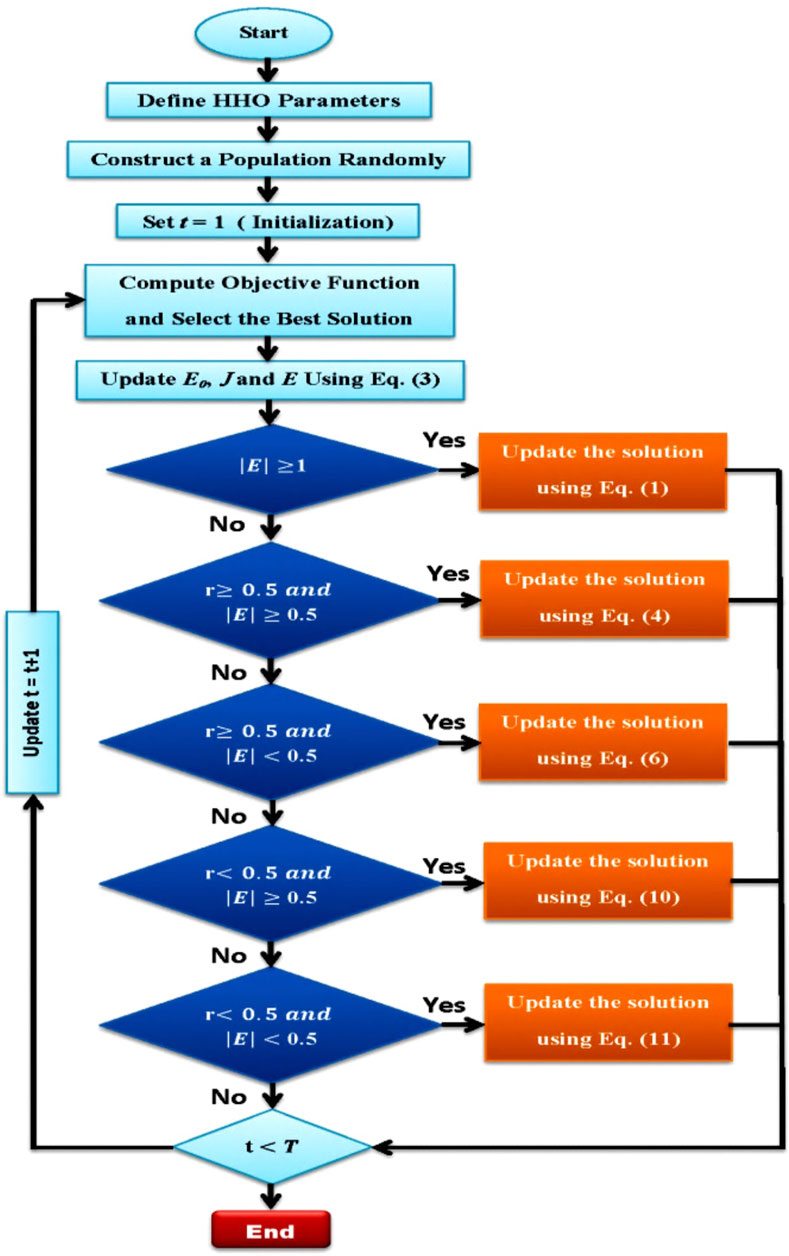
FIGURE 2. Flow chart of the HHO algorithm (Izci et al., 2020).

Compared to recognized metaheuristic methods, HHO’s results are often as good as or better than those obtained using the techniques. When compared to other highly recognized optimizers, HHO can produce superior solutions. The HHO has also outperformed competing optimizers in the context of six constrained engineering design challenges. However, HHO is a random optimization technique. Therefore, it has problems with high-dimensional datasets like population diversity and local optima (Mohamed Elgamal et al., 2020). In addition, HHO’s inaccuracy, slow convergence, and propensity to jump into a local optimum are also drawbacks (Song et al., 2022).

2.3 Arithmetic Optimization Algorithm (AOA)

The Arithmetic Optimization Algorithm (AOA) is a novel meta-heuristic approach that makes use of the statistical properties of the four basic arithmetic operations: multiplication (M), division (D), subtraction (S), and addition (A). To optimize across many different areas, mathematic models and code implementations of AOA are used (Available online on 11 January 2021). AOA mathematical equations can be represented by Eqs 19–26:

$\mathit{X}=\left[\begin{array}{c}{\mathit{x}}_{\mathrm{1,1}}\dots \dots {\mathit{x}}_{1,\mathit{j}}{\mathit{x}}_{1,\mathit{n}-1}{\mathit{x}}_{1,\mathit{n}}\\ {\mathit{x}}_{\mathrm{2,1}}\dots \dots {\mathit{x}}_{2,\mathit{j}}\dots {\mathit{x}}_{2,\mathit{n}}\\ \dots \dots \dots \dots \dots \dots \\ ......\\ ......\\ ......\\ {\mathit{x}}_{\mathit{N}-\mathrm{1,1}}\dots \dots {\mathit{x}}_{\mathit{N}-1,\mathit{j}}\dots {\mathit{x}}_{\mathit{N}-1,\mathit{n}}\\ {\mathit{x}}_{\mathit{N},1}\dots \dots {\mathit{x}}_{\mathit{N},\mathit{j}}{\mathit{x}}_{\mathit{N},\mathit{n}-1}{\mathit{x}}_{\mathit{N},\mathit{n}}\end{array}\right](19)$

$\mathit{M}\mathit{O}\mathit{A}\left({\mathit{C}}_{\mathit{I}\mathit{t}\mathit{e}\mathit{r}}\right)=\mathit{Min}+\left({\mathit{C}}_{\mathit{Iter}}\right)\times \left(\frac{\mathit{Max}-\mathit{Min}}{{\mathit{M}}_{\mathit{Iter}}}\right)(20)$

${\mathit{x}}_{\mathit{i},\mathit{j}}\left({\mathit{C}}_{\mathit{Iter}}+1\right)=\left\{\begin{array}{c}\mathit{b}\mathit{e}\mathit{s}\mathit{t}\left({\mathit{x}}_{\mathit{j}}\right)÷\left(\mathit{M}\mathit{O}\mathit{P}+\mathit{ϵ}\right)\times \left(\left(\mathit{U}{\mathit{B}}_{\mathit{j}}-\mathit{L}{\mathit{B}}_{\mathit{j}}\right)\times \mathit{\mu }+\mathit{L}{\mathit{B}}_{\mathit{j}}\right),\mathit{r}2<0.5\\ \mathit{b}\mathit{e}\mathit{s}\mathit{t}\left({\mathit{x}}_{\mathit{j}}\right)\times \mathit{M}\mathit{O}\mathit{P}\times \left(\left(\mathit{U}{\mathit{B}}_{\mathit{j}}-\mathit{L}{\mathit{B}}_{\mathit{j}}\right)\times \mathit{\mu }+\mathit{L}{\mathit{B}}_{\mathit{j}}\right)\mathit{o}\mathit{t}\mathit{h}\mathit{e}\mathit{r}\mathit{w}\mathit{i}\mathit{s}\mathit{e}\end{array}\right.(21)$

$\mathit{M}\mathit{O}\mathit{P}\left({\mathit{C}}_{\mathit{I}\mathit{t}\mathit{e}\mathit{r}}\right)=1-\frac{{{\mathit{C}}_{\mathit{Iter}}}^{\frac{1}{\mathit{\alpha }}}}{{{\mathit{M}}_{\mathit{Iter}}}^{\frac{1}{\mathit{\alpha }}}}(22)$

${\mathit{x}}_{\mathit{i},\mathit{j}}\left({\mathit{C}}_{\mathit{Iter}}+1\right)=\left\{\begin{array}{c}\mathit{b}\mathit{e}\mathit{s}\mathit{t}\left({\mathit{x}}_{\mathit{j}}\right)-\mathit{M}\mathit{O}\mathit{P}\times \left(\left(\mathit{U}{\mathit{B}}_{\mathit{j}}-\mathit{L}{\mathit{B}}_{\mathit{j}}\right)\times \mathit{\mu }+\mathit{L}{\mathit{B}}_{\mathit{j}}\right),\mathit{r}3<0.5\\ \mathit{b}\mathit{e}\mathit{s}\mathit{t}\left({\mathit{x}}_{\mathit{j}}\right)+\mathit{M}\mathit{O}\mathit{P}\times \left(\left(\mathit{U}{\mathit{B}}_{\mathit{j}}-\mathit{L}{\mathit{B}}_{\mathit{j}}\right)\times \mathit{\mu }+\mathit{L}{\mathit{B}}_{\mathit{j}}\right),\mathit{o}\mathit{t}\mathit{h}\mathit{e}\mathit{r}\mathit{w}\mathit{i}\mathit{s}\mathit{e}\end{array}\right.(23)$

$\mathit{L}{\mathit{B}}_{\mathit{j}}\le {\mathit{x}}_{\mathit{i}\mathit{j}}\le \mathit{U}{\mathit{B}}_{\mathit{j}},\mathit{j}=1,2,\dots ,\mathit{n}(24)$

$\mathit{min}\mathit{f}\left(\mathit{x}\right)$

$\begin{array}{c}\mathit{X}=\left\{{\mathit{x}}_{11},{\mathit{x}}_{1\mathit{j}},\dots ,{\mathit{x}}_{1\mathit{n}}\right\}\\ \mathit{s}.\mathit{t}.{\mathit{g}}_{\mathit{i}}\left(\mathit{X}\right)\le 0,\mathit{j}=1,2,\dots ,\mathit{m}\\ {\mathit{h}}_{\mathit{k}}\left(\mathit{X}\right)=0,\mathit{k}=1,2,\dots ,\mathit{l}\end{array}(25)$

$\mathit{L}{\mathit{B}}_{\mathit{j}}\le {\mathit{x}}_{\mathit{i}\mathit{j}}\le \mathit{U}{\mathit{B}}_{\mathit{j}},\mathit{j}=1,2,\dots ,\mathit{n}$

$\mathit{f}\left(\mathit{X}\right)=\mathit{f}\left(\mathit{X}\right){\displaystyle \sum _{\mathit{j}=1}^{\mathit{m}}}\mathit{P}{\mathit{e}}_{\mathit{j}}\mathit{max}\left\{{\mathit{g}}_{\mathit{i}}\left(\mathit{X}\right),0\right\}+{\displaystyle \sum _{\mathit{k}=1}^{\mathit{m}}}\mathit{P}{\mathit{e}}_{\mathit{k}}\mathit{max}\left\{\left|{\mathit{h}}_{\mathit{k}}\left(\mathit{X}\right)-\mathit{ϵ}\right|,0\right\}(26)$

The proposed AOA strategy demonstrates its mettle as a solution optimizer by consistently outperforming competing optimization algorithms across various test functions. Figure 3 shows that the proposed AOA converges steadily and accelerates its convergence on these test functions more slowly than the benchmark techniques (GA, FPA, BBO, BAT, PSO, and GWO). In addition, the AOA achieved faster convergence and better global search results for these test functions than any competing methods. Therefore, the AOA has a more rapid convergence rate and improved global search efficacy (Abualigah et al., 2021). Compared to competing algorithms, the proposed AOA may have a significantly lower required running time in seconds. Consequently, we concluded that the suggested AOA method has superior computing performance over the competing techniques.

FIGURE 3

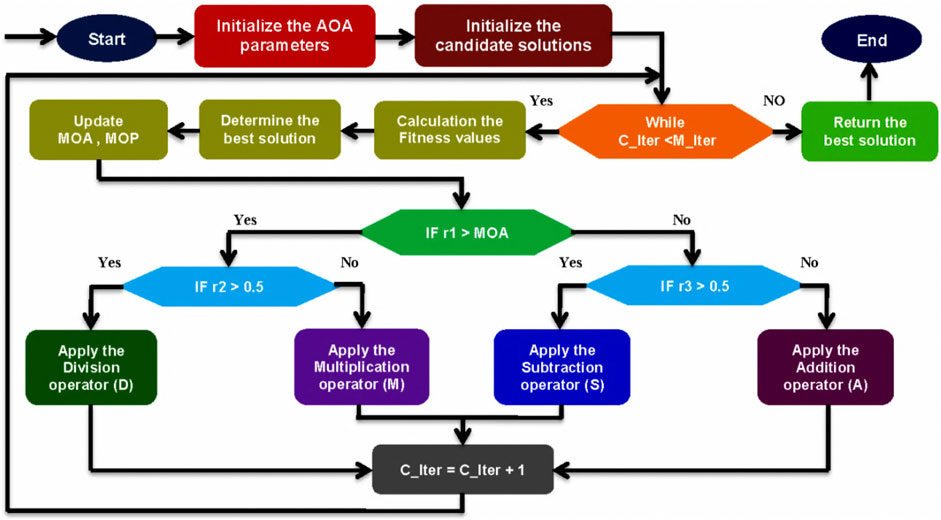
FIGURE 3. Flow chart of the AOA algorithm (Abualigah et al., 2021).

As a result of comparing the proposed AOA to a set of 12 benchmark optimization algorithms, we found that it holds its own against the industry’s best. There are still limitations to the original AOA. For instance, getting stuck in a local optimum is easily done because location updates based on the ideal value, premature convergence, and low solution accuracy must be addressed (Chen et al., 2022). When dealing with multi-dimensional optimization problems, the AOA suffers from insufficient investigation and premature convergence to sub-optimal solutions (Kaveh et al., 2021).

3 Designing of the simulated PV power plant

3.1 PV mathematical model

A photovoltaic (PV) solar cell’s P-N junction can be constructed from semiconductor material or other industrial alloys. This PV solar cell is capable of transforming solar energy into useable power. An integral part of a PV module is the series and parallel connection of PV solar cell sets, which together produce both the voltage and current that is needed. The PV solar cell is modeled as a current source coupled with other electrical elements. Following is a set of mathematical equations for a PV module (Eqs 27–30): (Natarajan et al., 2012).

${\mathit{I}}_{\mathit{p}\mathit{h}}=\frac{\left[{\mathit{I}}_{\mathit{s}\mathit{h}}+{\mathit{K}}_{\mathit{i}}\left(\mathit{T}-298\right)\mathit{x}\mathit{G}\right]}{1000}(27)$

${\mathit{I}}_{\mathit{r}\mathit{s}}=\frac{{\mathit{I}}_{\mathit{s}\mathit{h}}}{\left[\exp \left(\frac{\mathit{q}{\mathit{V}}_{\mathit{o}\mathit{c}}}{{\mathit{N}}_{\mathit{s}}\mathit{K}\mathit{A}\mathit{T}}\right)-1\right]}(28)$

${\mathit{I}}_{\mathit{O}}={\mathit{I}}_{\mathit{r}\mathit{s}}{\left[\frac{\mathit{T}}{{\mathit{T}}_{\mathit{r}}}\right]}^3\exp \left[\left(\frac{\mathit{q}{\mathit{E}}_{\mathit{g}}}{\mathit{A}\mathit{K}}\right)\left(\frac{1}{{\mathit{T}}_{\mathit{r}}}-\frac{1}{\mathit{T}}\right)\right](29)$

${\mathit{I}}_{\mathit{p}\mathit{v}}={\mathit{N}}_{\mathit{p}}{\mathit{I}}_{\mathit{p}\mathit{h}}-{\mathit{N}}_{\mathit{p}}{\mathit{I}}_{\mathit{o}}\left[\exp \left\{\frac{\left(\mathit{q}\left({\mathit{V}}_{\mathit{p}\mathit{v}}+{\mathit{I}}_{\mathit{p}\mathit{v}}{\mathit{R}}_{\mathit{s}}\right)\right)}{{\mathit{N}}_{\mathit{s}}\mathit{A}\mathit{K}\mathit{T}}\right\}-1\right](30)$

Where, ${\mathit{I}}_{\mathit{p}\mathit{h}}$: The PV module’s photo-current (A). ${\mathit{K}}_{\mathit{i}}$: The temperature coefficient of short current with PV solar cell (A/°C). ${\mathit{I}}_{\mathit{s}\mathit{h}}$: The short-circuit current (A) of a PV solar cell under standard test conditions (STC). ${\mathit{I}}_{\mathit{r}\mathit{s}}$: The current of PV module’s reverse saturation. $\mathit{G}$: The sun’s solar irradiance level (W/m2). ${\mathit{V}}_{\mathit{o}\mathit{c}}$: The PV solar cell open circuit voltage (V). $\mathit{K}$: The constant of Boltzmann (1.38 × 10⁻²³ J/K). ${\mathit{N}}_{\mathit{s}}$: The module’s number of series PV solar cells. $\mathit{T}$: Temperature in (K). $\mathit{A}$: Ideal factor. ${\mathit{I}}_{\mathit{o}}$: The PV module saturation current (A). $\mathit{q}$: Electron charge (1.6 × 10⁻¹⁹ C). ${\mathit{T}}_{\mathit{r}}$: The reference temperature (25°C). ${\mathit{I}}_{\mathit{p}\mathit{v}}$: The PV module output current (A). ${\mathit{E}}_{\mathit{g}}$: The silicon material band gap (1.1ev). ${\mathit{N}}_{\mathit{p}}$: The module’s number of parallel PV solar cells. ${\mathit{V}}_{\mathit{p}\mathit{v}}$: The PV module output voltage (V). ${\mathit{R}}_{\mathit{s}}$: The PV solar cell series resistance (Ω). ${\mathit{R}}_{\mathit{s}\mathit{h}}$: The PV solar cell shunt resistance (Ω).

3.2 Simulation of the proposed grid-connected PV power plant

This article presents the design of a 26 MWp grid-connected PV power plant, which is already tied to the Egyptian electrical network in Fares City, Kom Ombo Center, Aswan Governorate, in Egypt. This PV power plant consists of Eq. 11 inverter station blocks, which are simulated using Matlab Simulink, as shown in Figure 4A. Every block contains 2,376 kWp PV arrays connected directly to DC-DC boost converters that are used to regulate the output DC power generated by each PV array.

FIGURE 4

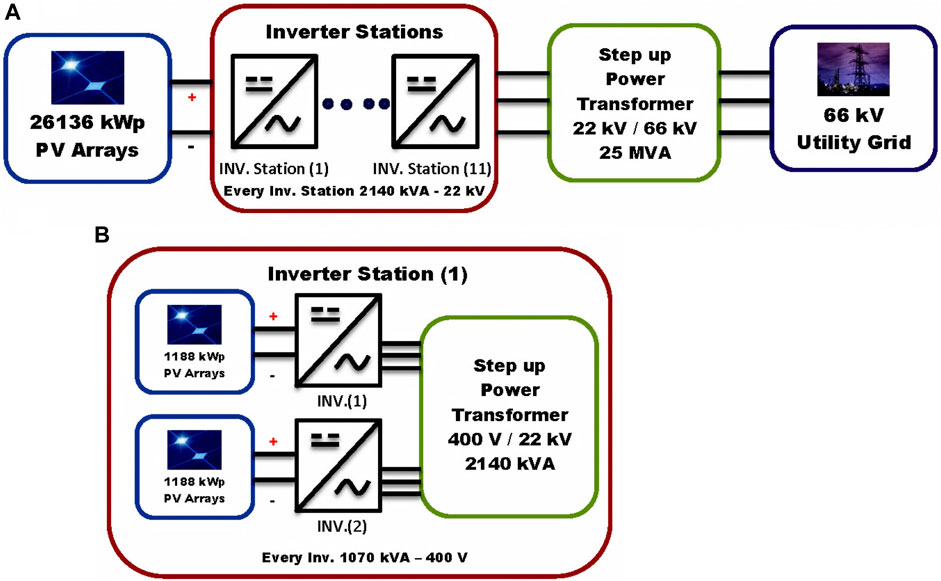
FIGURE 4. Block diagrams of the 26 MWp grid-connected PV power plant, (A) Main Parts of the plant, (B) Contents of every inverter station.

This regulated DC power is fed into a particular type of inverter called an “on-grid solar inverter” to convert it from DC power to AC power. The output AC voltage is stepped up to 66 kV through the power transformer to feed the utility grid, as shown in Figure 4B.

3.3 Maximum power point tracking algorithm

Since the Perturb & Observe algorithm (P&O) requires fewer measured parameters and is straightforward to execute, it finds widespread use in MPPT. Adjusting the output voltage up or down and monitoring the effect on the output power is essential for monitoring the MPP as the weather changes. If the output P_PV increases, the output V_PV regulates directly, as in the former cycle. If the output P_PV decreases, the output V_PV is perturbed in the inversion direction. When the MPP is found, the output V_PV will turn around the maximum operation voltage. In this study, the maximum power point tracking (MPPT) of PV arrays is controlled using the P&O algorithm. In addition, several optimization techniques are applied to enhance the quality of the power and voltage produced from the proposed PV power plant in different sunlight conditions and partial shading (GUIZA et al., 2019).

3.4 Voltage-current controller (PI)

The PI control is the main part of the central solar inverter, which is used to control the voltage and current values by adjusting the proportional gain (Kp) and the integral gain (Ki) of the voltage regulator and the current regulator. The measure and reference DC voltage will be the input to the voltage controller to find the reference current (Id_ref). Furthermore, the measure and reference current will be the input to the current controller to find the controlled voltage (VdVq_conv), which will feed the pulse width modulation (PWM). Finally, the output pulses of PWM are used to control the three-level IGBTs Bridge (Inverter).

4 Experimental simulation and analysis

4.1 Simulation environment and parameter settings

The performance of the proposed PV power plant during different sunlight conditions is validated and evaluated in this study by applying certain famous and recent optimization algorithms, such as GWO, HHO, and AOA. These techniques are used to optimize the PI parameters by adjusting the proportional gain (Kp) and the integral gain (Ki) of the voltage regulator and the current regulator to control the three-level IGBTs Bridge (Inverter). The PI control parameters (ki_VDCreg, kp_VDCreg, ki_Ireg, kp_Ireg) are obtained by GWO, HHO, and AOA to realize minimized voltage and power fluctuations. The experimental environment is Intel(R) Core (TM) i5-2430M CPU, 2.40GHz, 4GB, Windows 7 64-bit operating system, and all codes are programmed through Matlab (version: R2017b).

To achieve its goal, every optimization method requires some objective function. Each algorithm’s population size (N) is set to 20, and the maximum number of iterations (T) is set to 10. To prevent any unfair advantages from being gained, all experiments are conducted separately 20 times, and the mean of the 20 times is used as the metric of algorithm performance. Reducing the discrepancy between the actual and target values is the goal of this objective function. Integral of absolute error (IAE), integral of square error (ISE), integral of time and absolute error (ITAE), and integral of time square error (ITSE) are the four error benchmark objective functions.

Firstly, to select the best of the objective functions and gain values (ki_VDCreg, kp_VDCreg, ki_Ireg, kp_Ireg), GWO is applied to the proposed PV power plant under different sunlight conditions, with the four error benchmark objective functions (IAE, ISE, ITAE, and ITSE). Table 1 shows the best objective functions and gain values (ki_VDCreg, kp_VDCreg, ki_Ireg, kp_Ireg) generated using GWO for PI control of the proposed PV power plant, with each of the errors, through number of population = 20 and number of iteration = 10 By applying all of the gain values (ki_VDCreg, kp_VDCreg, ki_Ireg, kp_Ireg) in Table 1 to the proposed PV power plant under different sunlight conditions, the best value among them can be determined through comparisons between the power curves and voltage curves, as shown in Figure 5.

TABLE 1

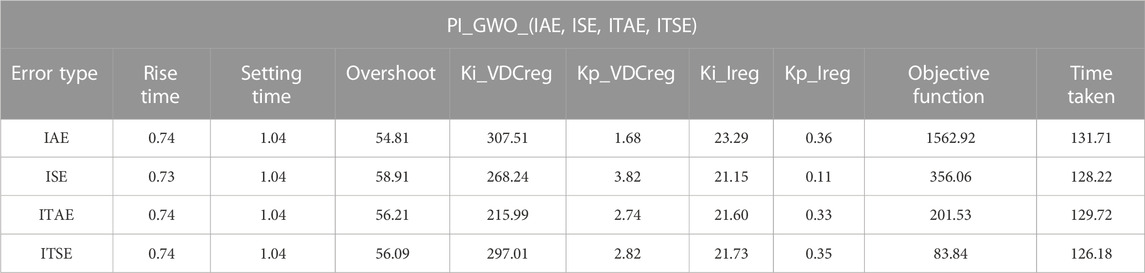
TABLE 1. Simulation results of the applied GWO for the PI controller of the PV power plant through the errors (IAE, ISE, ITAE, and ITSE).

FIGURE 5

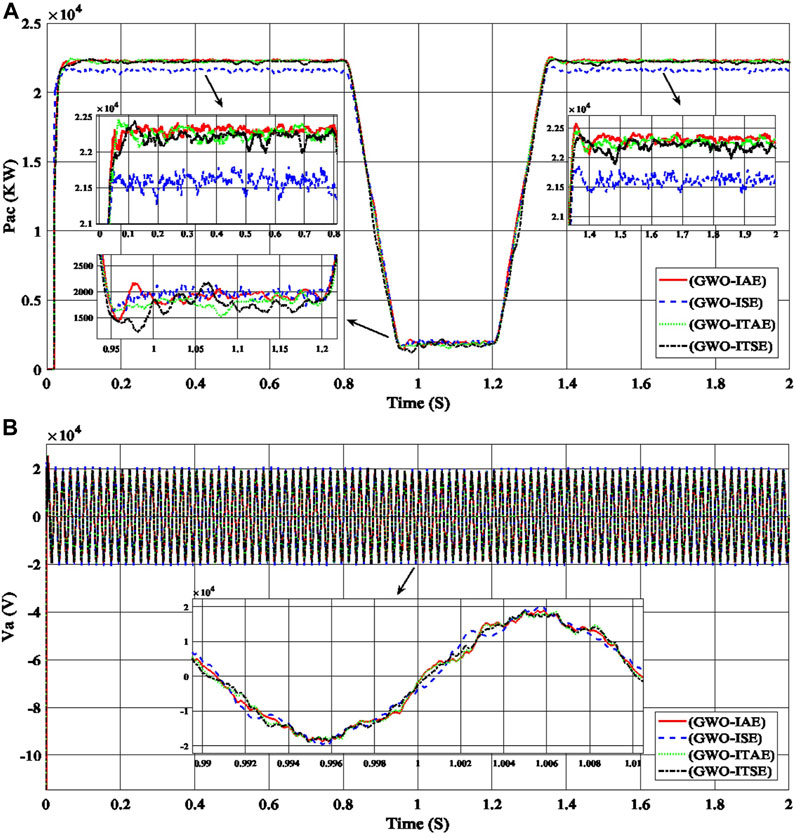
FIGURE 5. Performance of the PV power plant, (A) the output AC power curves (Pac), and (B) the output AC voltage curves for phase a (Va) with the time are produced using gain values (ki_VDCreg, kp_VDCreg, ki_Ireg, kp_Ireg) generated by GWO with the errors (IAE, ISE, ITAE, ITSE) for the PI controller of the PV power plant.

Secondly, to select the best of the objective functions and gain values (ki_VDCreg, kp_VDCreg, ki_Ireg, kp_Ireg), consequently, the AOA with ISE error is the best optimization technique and is recommended to be applied to the large-scale and high penetration level of grid-connected PV power plants to optimize and adjust the PI controller gains of the central inverter (IAE, ISE, ITAE, and ITSE). Table 2 shows the best objective functions and gain values (ki_VDCreg, kp_VDCreg, ki_Ireg, kp_Ireg) generated using HHO for PI control of the proposed PV power plant, with each of the errors, through number of population = 20 and number of iteration = 10. By applying all of the gain values (ki_VDCreg, kp_VDCreg, ki_Ireg, kp_Ireg) in Table 2 to the proposed PV power plant under different sunlight conditions, the best value among them can be determined through comparisons between the power curves and voltage curves, as shown in Figure 6.

TABLE 2

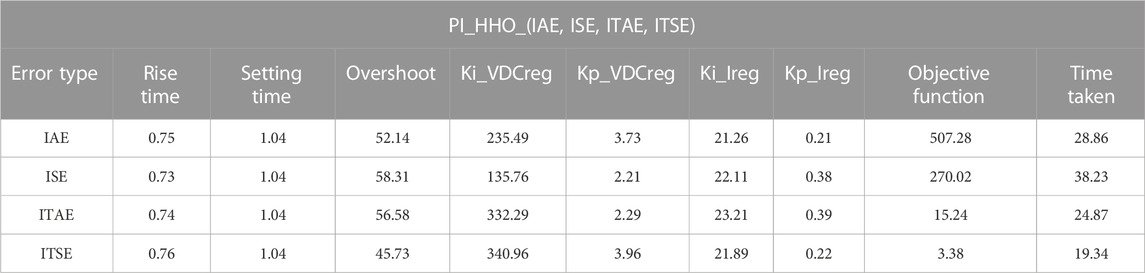
TABLE 2. Simulation results of the applied HHO for the PI controller of the PV power plant with the errors (IAE, ISE, ITAE, and ITSE).

FIGURE 6

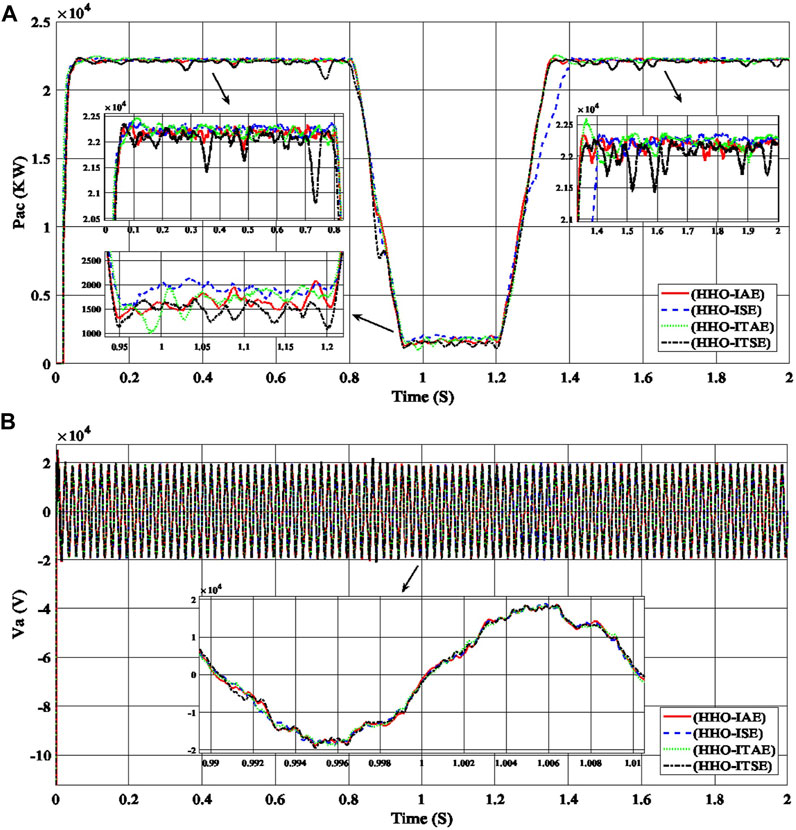
FIGURE 6. Performance of the PV power plant, (A) the output AC power curves (Pac), and (B) the output AC voltage curves for phase a (Va) with the time are produced using gain values (ki_VDCreg, kp_VDCreg, ki_Ireg, kp_Ireg) generated by HHO with the errors (IAE, ISE, ITAE, ITSE) for the PI controller of the PV power plant.

Thirdly, to select the best of the objective functions and gain values (ki_VDCreg, kp_VDCreg, ki_Ireg, kp_Ireg), the AOA is applied to the proposed PV power plant under different sunlight conditions with the four error benchmark objective functions (IAE, ISE, ITAE, and ITSE). Table 3 shows the best objective functions and gain values (ki_VDCreg, kp_VDCreg, ki_Ireg, kp_Ireg) generated using AOA for PI control of the proposed PV power plant, with each of the errors, through number of population = 20 and number of iteration = 10. By applying all of the gain values (ki_VDCreg, kp_VDCreg, ki_Ireg, kp_Ireg) in Table 3 to the proposed PV power plant during different sunlight conditions, the best value among them can be determined through comparisons between the power curves and voltage curves, as shown in Figure 7.

TABLE 3

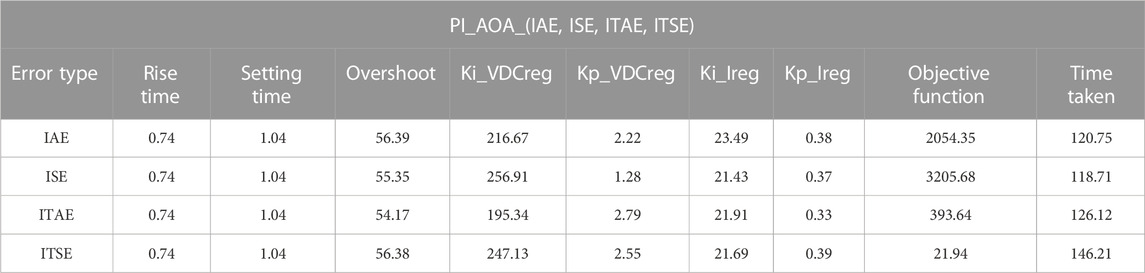
TABLE 3. Simulation results of the applied AOA for the PI controller of the PV power plant with the errors (IAE, ISE, ITAE, and ITSE).

FIGURE 7

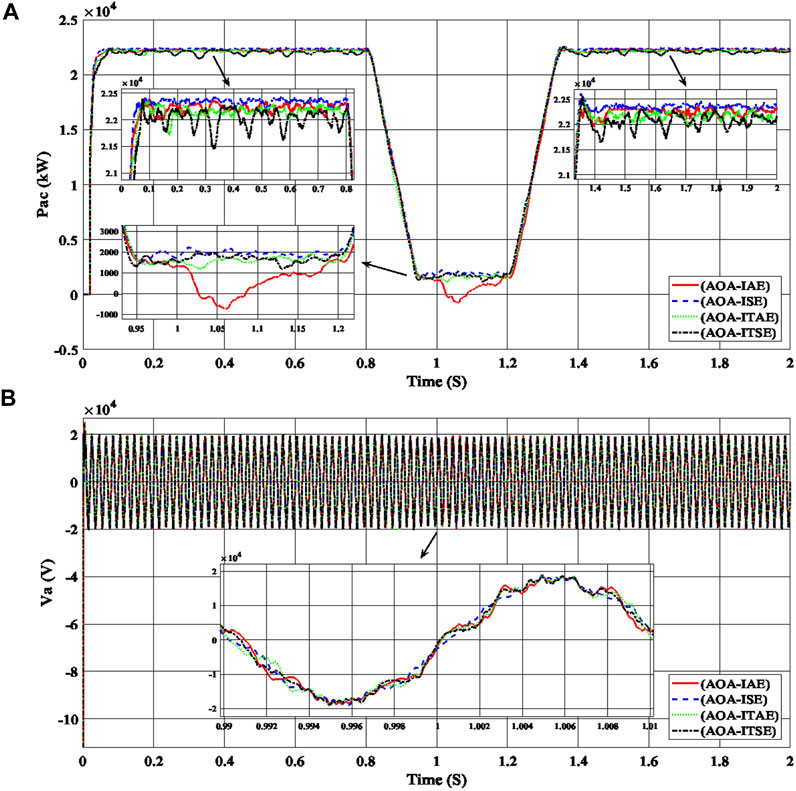
FIGURE 7. Performance of the PV power plant, (A) the output AC power curves (Pac), and (B) the output AC voltage curves for phase a (Va) with the time are produced using gain values (ki_VDCreg, kp_VDCreg, ki_Ireg, kp_Ireg) generated by AOA with the errors (IAE, ISE, ITAE, ITSE) for the PI controller of the PV power plant.

4.2 Analysis of results

By applying all the gain values (ki_VDCreg, kp_VDCreg, ki_Ireg, kp_Ireg) from the last three tables to the proposed PV power plant under different sunlight conditions, the best values among them can be determined. Table 4 shows the best gain values (ki_VDCreg, kp_VDCreg, ki_Ireg, kp_Ireg) produced using GWO, HHO, and AOA optimization techniques.

TABLE 4

TABLE 4. The best simulation results of the generated gains (Kp & Ki) using GWO with IAE error and HHO and AOA with ISE error for the PI controller of the PV power plant.

By applying IAE error with GWO and ISE error with the HHO and AOA optimization techniques, the best values (ki_VDCreg, kp_VDCreg, ki_Ireg, kp_Ireg) can be obtained, as shown in Table 4. To determine the best accurate gain value (ki_VDCreg, kp_VDCreg, ki_Ireg, kp_Ireg), which is generated from every one of these optimization techniques, comparisons can be made between the power curves and voltage curves produced by the proposed PV power plant under different sunlight conditions, as shown in Figure 8.

FIGURE 8

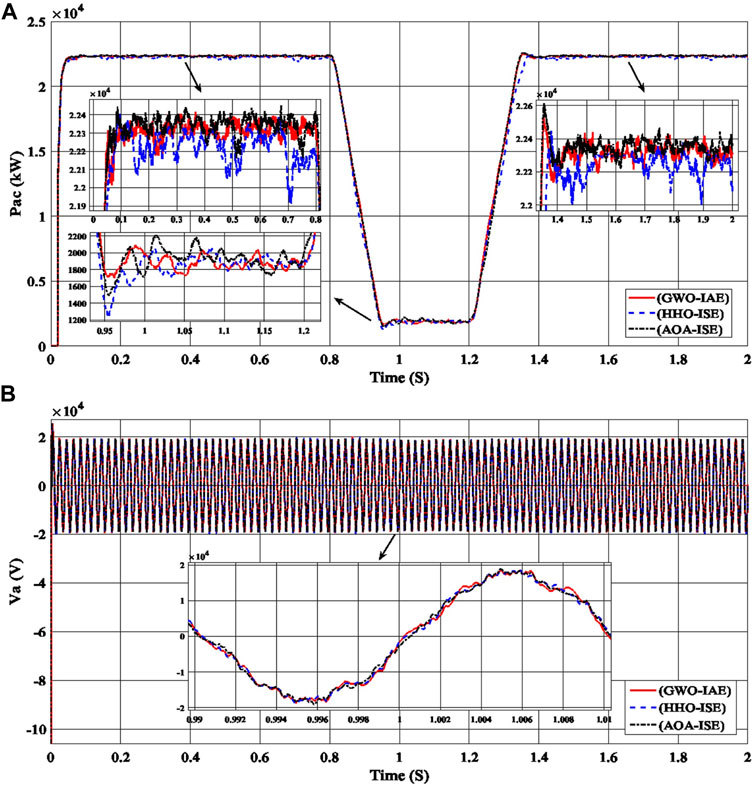
FIGURE 8. Performance of the PV power plant, (A) the output AC power curves (Pac), and (B) the output AC voltage curves for phase a (Va) with the time are produced using the best gain values (ki_VDCreg, kp_VDCreg, ki_Ireg, kp_Ireg) generated by GWO with IAE error and HHO and AOA with ISE error for the PI controller of the PV power plant.

Applying all the best gain values (ki_VDCreg, kp_VDCreg, ki_Ireg, kp_Ireg) in Table 4 to the PI control of the proposed PV power plant under different sunlight conditions, the total harmonic distortion values (THD) for voltage can be obtained for every error with GWO, HHO, and AOA. Finally, the AOA with ISE error produces the most accurate gain values (ki_VDCreg = 256.91, kp_VDCreg = 1.28, ki_Ireg = 21.43, kp_Ireg = 0.37) and a lower THD (7.25%). As a result, the AOA with ISE error is the best optimization technique and must be applied to the PI control of the proposed PV power plant so that the highest power quality and the lowest THD can be produced.

On the other hand, Table 5 presents the statistical evaluation of the results achieved in terms of the proposed optimization algorithm compared to the other algorithms. In this table, the results achieved by the proposed approach are superior and show promising performance. In addition, Tables 6, 7 show in-depth analysis of the results using the analysis of variance (ANOVA) (Abdelhamid et al., 2022a; El-Kenawy et al., 2022a; Khafaga et al., 2022; El-Kenawy et al., 2022b; El-Kenawy et al., 2022c; Eid et al., 2022) and the Wilcoxon signed rank tests (Abdel Samee et al., 2022; Alhussan et al., 2022; Abdelhamid et al., 2022b; Khafaga et al., 2022b; Khafaga et al., 2022; El-kenawy et al., 2022d; Khafaga et al., 2022d; El-Kenawy et al., 2022e). These tests proved the statistical difference between the proposed methodology and the other competing methods.

TABLE 5

TABLE 5. Statistical evaluation of the optimization algorithms results.

TABLE 6

TABLE 6. Analysis of variance test results.

TABLE 7

TABLE 7. Wilcoxon test results.

To visually highlight the performance of the proposed methodology, Figure 9 shows a histogram of the achieved results and a set of plots describing the residual error. In this figure, the results illustrated confirm the effectiveness of the proposed methodology.

FIGURE 9

FIGURE 9. Optimization algorithms, (A) Histogram of the results, (B) Visualizing of the results.

5 Conclusion

Connecting more RESs to the utility grid will lead to more technical problems. PV and WT based power plants are the most nonlinear sources of renewable energy contributing to the energy mix. Nowadays, the high penetration level of PV power plants connected to the Egyptian electricity grid is effective. The irregularity and intermittency of PV power generation can affect the voltage stability and power quality of the utility grid during peak load demand. This article presents a Matlab simulation of a 26 MWp large-scale grid-connected PV power plant, which is already tied to the Egyptian electrical grid in Fares City, Kom Ombo Center, Aswan Governorate, Egypt. This PV power plant consists of Eq. 11 blocks and the utility grid. Every block contains 2,376 kWp PV arrays connected directly to DC-DC boost converters. The output DC power is fed into a particular type of inverter called a “central inverter”, which is used to convert it to AC power. In this study, several optimization techniques, namely, GWO, HHO, and AOA, are applied to enhance the voltage stability and power quality produced by the proposed PV power plant under different sunlight conditions and in partial shade. These optimization techniques adjust Kp and Ki gains for the voltage regulator and the current regulator of the PI controller built into the central inverter of the proposed PV power plant. As a result, this PI controller increases the power quality, regulates the output voltage, and limits the THD for each block of this PV power plant. Simulation results confirm that using these optimization techniques led to enhanced power quality and decreased THD and made the output voltage of this PV power plant to the utility grid more stable. The AOA technique showed outstanding results and superior performance under shaded conditions when applied to this PV power plant compared to GWO and HHO in terms of solution quality and computational efficiency. Finally, the AOA with ISE error was found to produce the most accurate gain values (Ki_VDCreg = 256.91, Kp_VDCreg = 1.28, Ki_Ireg = 21.43, Kp_Ireg = 0.37) and the lower THD percentage (7.25%). Consequently, the AOA with ISE error is the best optimization technique and is recommended to be applied to the large-scale and high penetration level of grid-connected PV power plants to optimize and adjust the PI controller gains of the central inverter. This way, the highest power quality and voltage stability and the lowest THD can be produced from the high penetration level of PV power plants connected to the utility grid.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

Conceptualization, MME; methodology, ME-G, ME, and SW; software, ME-G and MAE; validation, DK; formal analysis, AA and DK; investigation, ME-G and SW; writing—original draft, ME-G and MAE; writing—review and editing, SW and MME. All authors contributed to the article and approved the submitted version.

Funding

Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R120), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Al-Shetwi, A. Q., Hannan, M. A., JernAmmar, K. P., and Pg Abas, A. E. (2020). Power quality assessment of grid-connected PV system in compliance with the recent integration requirements. MDPI, Electron. 9, 366. doi:10.3390/electronics9020366

CrossRef Full Text | Google Scholar

Abdel Samee, N., El-Kenawy, E. S. M., Atteia1, G., Jamjoom, M. M., Ibrahim, A., Abdelhamid, A. A., et al. (2022). Metaheuristic optimization through deep learning classification of COVID-19 in chest X-ray images. Comput. Mater. Continua 2022. doi:10.32604/cmc.2022.031147

CrossRef Full Text | Google Scholar

Abdelhamid, A., El-kenawy, E.-S. M., Alotaibi, B., Abdelkader, M., Ibrahim, A., et al. (2022). Robust speech emotion recognition using CNN+LSTM based on stochastic fractal search optimization algorithm. IEEE Access 10, 49265–49284. doi:10.1109/ACCESS.2022.3172954

CrossRef Full Text | Google Scholar

Abdelhamid, A., El-Kenawy, E.-S. M., Khodadadi, N., Mirjalili, S., Khafaga, D. S., Alharbi, A. H., et al. (2022). Classification of monkeypox images based on transfer learning and the Al-Biruni Earth radius optimization algorithm. MDPI, Math. 10, 3614. doi:10.3390/math10193614

CrossRef Full Text | Google Scholar

Abdul Kadir, A. F., Khatib, T., and Elmenreich, W. (2014). Integrating photovoltaic systems in power system: Power quality impacts and optimal planning challenges. Prog. Photovolt. Devices Syst. 2014, 1–7. doi:10.1155/2014/321826

CrossRef Full Text | Google Scholar

Abdullah, M. K., Hassan, L. H., and Moghavvemi, M. (2021). Voltage stability assessment of grid connected PV systems with FACTS devices. Res. Square 2021. doi:10.21203/rs.3.rs-1119382/v1

CrossRef Full Text | Google Scholar

Abualigah, L., Ali, D., Mirjalili, S., Abd Elaziz, M., and Amir, H. (2021). The arithmetic optimization algorithm. Comput. Methods Appl. Mech. Eng. 376, 113609. doi:10.1016/j.cma.2020.113609

CrossRef Full Text | Google Scholar

Alghamdi, A. S. (2022). Optimal power flow in wind–photovoltaic energy regulation systems using a modified turbulent water flow-based optimization. MDPI 14, 16444. doi:10.3390/su142416444

CrossRef Full Text | Google Scholar

Alghamdi, A. S. (2022). Optimal power flow of renewable-integrated power systems using a Gaussian bare-bones levy-flight firefly algorithm. Frontiers 10. doi:10.3389/fenrg.2022.921936

CrossRef Full Text | Google Scholar

Alhussan, A., Khafaga, D., El-Kenawy, E. -S. M., Ibrahim, A., Eid, M. M., and Abdelhamid, A. A. (2022). Pothole and plain Road classification using adaptive mutation dipper throated optimization and transfer learning for self-driving cars. IEEE Access 10, 84188–84211. doi:10.1109/ACCESS.2022.3196660

CrossRef Full Text | Google Scholar

Aslam, A., Ahmed, N., Ahmed Qureshi, S., Assadi, M., and Ahmed, N. (2022). Advances in solar PV systems; A comprehensive review of PV performance, influencing factors, and mitigation techniques. MDPI 15, 7595. doi:10.3390/en15207595

CrossRef Full Text | Google Scholar

Attia, M. A., (2018). Optimized controllers for enhancing dynamic performance of PV interface system, Electron. Res. Inst. (ERI), Elsevier. 2018. doi:10.1016/j.jesit.2018.01.003

CrossRef Full Text | Google Scholar

BP Statistical Review of World Energy Report (2022). BP statistical review of world energy report. Tech. rep. London: British Petroleum BP.

Google Scholar

Chen, M., Zhou, Y., and Luo, Q. (2022). An improved arithmetic optimization algorithm for numerical optimization problems. Mathematics 10, 2152. doi:10.3390/math10122152

CrossRef Full Text | Google Scholar

Dadkhah, J., and Niroomand, M. (2021). Optimization methods of MPPT parameters for PV systems: Review, classification, and comparison. MPCE 9, 225–236. doi:10.35833/MPCE.2019.000379

CrossRef Full Text | Google Scholar

Eid, M. M., El-Kenawy, E.-S. M., Khodadadi, N., Mirjalili, S., Khodadadi, , Abotaleb, M., et al. (2022). Meta-heuristic optimization of LSTM-based deep network for boosting the prediction of monkeypox cases. MDPI, Math. 10, 3845. doi:10.3390/math10203845

CrossRef Full Text | Google Scholar

El-Kenawy, E. -S. M., Albalawi, G., Ward, S. A., Ghoneim, S. S., Eid, M. M., Abdelhamid, A. A., et al. (2022). Feature selection and classification of transformer faults based on novel meta-heuristic algorithm. MDPI, Math. 10, 3144. doi:10.3390/math10173144

CrossRef Full Text | Google Scholar

El-Kenawy, E.-S. M., Khodadadi, N., Mirjalili, S., Makarovskikh, T., Abotaleb, M., Karim, F. K., et al. (2022). Metaheuristic optimization for improving weed detection in wheat images captured by drones. Mathematics 10, 4421. doi:10.3390/math10234421

CrossRef Full Text | Google Scholar

El-Kenawy, E.-S. M., Mirjalili, S., Abdelhamid, A. A., Ibrahim, A., Khodadadi, N., and Eid, M. M. (2022). Meta-heuristic optimization and keystroke dynamics for authentication of smartphone users. Mathematics 10, 2912. doi:10.3390/math10162912

CrossRef Full Text | Google Scholar

El-Kenawy, E. -S. M., Mirjalili, S., Alassery, F., Zhang, Y., Eid, M., El-Mashad, S. Y., et al. (2022). Novel meta-heuristic algorithm for feature selection, unconstrained functions and engineering problems. IEEE Access 10, 40536–40555. doi:10.1109/ACCESS.2022.3166901

CrossRef Full Text | Google Scholar

El-kenawy, E. S. M., Zerouali, B., Bailek, N., Bouchouich, K., Hassan, M. A., Almorox, J., et al. (2022). Improved weighted ensemble learning for predicting the daily reference evapotranspiration under the semi-arid climate conditions. Environ. Sci. Pollut. Res. 29, 81279–81299. doi:10.1007/s11356-022-21410-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Elbarbary, Z. M. S., and Alranini, M. A. (2021). Review of maximum power point tracking algorithms of PV system. Frontiers 1, 68–80. doi:10.1108/FEBE-03-2021-0019

CrossRef Full Text | Google Scholar

Eltamaly, A. M., Sayed Mohamed, Y., El-Sayed, A-H. M., Mohamed, M. A., and Elghaffar, A. N. A. (2020). Power quality and reliability considerations of photovoltaic distributed generation. Springer 5, 25. doi:10.1007/s40866-020-00096-2

CrossRef Full Text | Google Scholar

Ghalambaz, M., Yengejeh, R. J., and Davami, A. H. (2021). Building energy optimization using grey wolf optimizer (GWO). Case Stud. Therm. Eng. 27 (2021), 101250. doi:10.1016/j.csite.2021.101250

CrossRef Full Text | Google Scholar

Guiza, D., Djamel, O., Youcef, S., Abdelmalek, B., and Mahmoud, M. (2019). Implementation of modified Perturb and Observe based MPPT algorithm for photovoltaic system. IEEE Xplore 2019. doi:10.1109/ICSRESA49121.2019.9182483

CrossRef Full Text | Google Scholar

Harrison, A., Nfah, E. M., Jean de Dieu, N. N., and Henry Alombah, N. (2022). An enhanced P&O MPPT algorithm for PV systems with fast dynamic and steady-state response under real irradiance and temperature conditions. Hindawi 2022, 1–21. doi:10.1155/2022/6009632

CrossRef Full Text | Google Scholar

Hasanien, H. M. (2017). Performance improvement of photovoltaic power systems using an optimal control strategy based on whale optimization algorithm. Electr. Power Syst. Res. 157, 168–176. doi:10.1016/j.epsr.2017.12.019

CrossRef Full Text | Google Scholar

Heidari, A. A., Mirjalili, S., Faris, H., Aljarah, I., Mafarja, M., and Chen, H. (2019). Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 97, 849–872. doi:10.1016/j.future.2019.02.028

CrossRef Full Text | Google Scholar

Iheanetu, K. J. (2022). Solar photovoltaic power forecasting: A review. MDPI 14, 17005. doi:10.3390/su142417005

CrossRef Full Text | Google Scholar

Izci, D., Ekinci, S., Demirören, A., and Hedley, J. (2020). HHO algorithm based PID controller design for aircraft pitch angle control system. IEEE Xplore 2020. doi:10.1109/HORA49412.2020.9152897

CrossRef Full Text | Google Scholar

Kaveh, A., Biabani Hamedani, K., and Kamalinejad, M. (2021). Improved arithmetic optimization algorithm for structural optimization with frequency constraints. Int. J. Optim. Civ. Eng. 11 (4), 663–693.

Google Scholar

KennethFolly, A. P. K. (2014). Voltage rise issue with high penetration of grid connected PV. 19th IFAC World Congr. 47, 29. doi:10.3182/20140824-6-ZA-1003.01989

CrossRef Full Text | Google Scholar

Khadem, S. K., Basu, M., and Conlon, M. F. (2010). Power quality in grid connected renewable energy systems: Role of custom power devices. RE&PQJ 1, 878–881. doi:10.24084/repqj08.505

CrossRef Full Text | Google Scholar

Khafaga, D., Alhussan, A., El-Kenawy, E.-S. M., Ibrahim, A., Eid, M., and Abdelhamid, A. (2022a). Solving optimization problems of metamaterial and double T-shape antennas using advanced meta-heuristics algorithms. IEEE Access 10, 74449–74471. doi:10.1109/ACCESS.2022.3190508

CrossRef Full Text | Google Scholar

Khafaga, D. S., Alhussan, A. A., El-kenawy, E. S. M., Ibrahim, A., Said, H., Abd, E., et al. (2022b). Improved prediction of metamaterial antenna bandwidth using adaptive optimization of LSTM. Comput. Mater. Continua 2022. doi:10.32604/cmc.2022.028550

CrossRef Full Text | Google Scholar

Khafaga, D. S., Alhussan, A. A., El-kenawy, E. S. M., Takieldeen, A. E., Hassan, T. M., Hegazy, E. A., et al. (2022d). Meta-heuristics for feature selection and classification in diagnostic breast cancer. Comput. Mater. Continua 2022. doi:10.32604/cmc.2022.029605

CrossRef Full Text | Google Scholar

Khafaga, D. S., Ibrahim, A., El-Kenawy, E.-S. M., Abdelhamid, A. A., Karim, F. K., Mirjalili, S., et al. (2022c). An Al-Biruni Earth radius optimization-based deep convolutional neural network for classifying monkeypox disease. MDPI, Diagn. 12, 2892. doi:10.3390/diagnostics12112892

CrossRef Full Text | Google Scholar

Kumar, P., Mallappa, B., Martínez-García, H., and Velasco-Quesada, G. (2021). Power quality improvements in grid-connected PV system using hybrid technology. RE&PQJ 19, 316–320. doi:10.24084/repqj19.284

CrossRef Full Text | Google Scholar

Le, X. C., Duong, M. Q., and Le, K. H. (2022). Review of the modern maximum power tracking algorithms for permanent magnet synchronous generator of wind power conversion systems. MDPI 16, 402. doi:10.3390/en16010402

CrossRef Full Text | Google Scholar

Liu, J., Wei, X., and Huang, H. (2021). An improved grey wolf optimization algorithm and its application in path planning. IEEE Access 9, 121944–121956. doi:10.1109/ACCESS.2021.3108973

CrossRef Full Text | Google Scholar

Makhadmeh, S. N., Khader, A. T., Al-Betar, M. A., and Naim, S. (2018). Multi-objective power scheduling problem in smart homes using grey wolf optimiser. J. Ambient Intell. Humaniz. Comput. 10, 3643–3667. doi:10.1007/s12652-018-1085-8

CrossRef Full Text | Google Scholar

Masouleh, F. F., Das, N., and Rozati, S. M. (2016). Nano-structured gratings for improved light absorption efficiency in solar cells. MDPI 9, 756. doi:10.3390/en9090756

CrossRef Full Text | Google Scholar

Ministry of Electricity and Renewable Energy (2022). New and renewable energy authority (NREA), renewable energy targets. Egyptian Energy Strategy until 2035, Available online: http://www.nrea.gov.eg/test/en/About/Strategy.

Google Scholar

Mirjalili, S., Mirjalili, S. M., and Lewis, A. (2014). Grey wolf optimizer. Adv. Eng. Softw. 69, 46–61. doi:10.1016/j.advengsoft.2013.12.007

CrossRef Full Text | Google Scholar

Mishra, A. K., Das, S. R., Ray, P. K., Kumar Mallick, R., Mohanty, A., and Dillip, K. (2020). PSO-GWO optimized fractional order PID based hybrid shunt active power filter for power quality improvements. IEEE Access 8, 74497–74512. doi:10.1109/ACCESS.2020.2988611

CrossRef Full Text | Google Scholar

Mohamed Elgamal, Z., Yasin, N. B. M., Tubishat, M., Alswaitti, M., and Mirjalili, S. (2020). An improved Harris hawks optimization algorithm with simulated annealing for feature selection in the medical field. IEEE Access 8, 186638–186652. doi:10.1109/ACCESS.2020.3029728

CrossRef Full Text | Google Scholar

Moharram, N. A., Tarek, A., Gaber, M., and Bayoumi, S. (2022). Brief review on Egypt’s renewable energy current status and future vision. Elsevier 8, 165–172. doi:10.1016/j.egyr.2022.06.103

CrossRef Full Text | Google Scholar

Natarajan, P., Ramaprabha, R., and Muthu, R. (2012). Application of circuit model for photovoltaic energy conversion system. Hindawi 2012, 1–14. Article ID 410401. doi:10.1155/2012/410401

CrossRef Full Text | Google Scholar

Nkado, F., and Franklin, N. (2021). Power quality and performance assessment of grid connected photovoltaic distributed generation with compliance to stipulated grid integration requirements. Eur. J. Eng. Technol. Res. 6, 1–10. doi:10.24018/ejeng.2021.6.7.2628

CrossRef Full Text | Google Scholar

Rahman, S., Saha, S., Islam, S. N., Arif, M. T., Mosadeghy, M., Oo, A. M. T., et al. (2021). Analysis of power grid voltage stability with high penetration of solar PV systems. IEEE Trans. Industry Appl. 57, 2245–2257. doi:10.1109/TIA.2021.3066326

CrossRef Full Text | Google Scholar

Raj, A., and Praveen, R. P. (2022). Highly efficient DC-DC boost converter implemented with improved MPPT algorithm for utility level photovoltaic applications. Ain Shams Eng. J. 13, 101617. doi:10.1016/j.asej.2021.10.012

CrossRef Full Text | Google Scholar

Rakhshani, E., Rouzbehi, K., Adolfo, J., and Pouresmaeil, E. (2019). Integration of large scale PV-based generation into power systems. A Surv. MDPI, Energies 12, 1425. doi:10.3390/en12081425

CrossRef Full Text | Google Scholar

Remon, D., Cantarellas, A. M., Mauricio, J. M., and Rodriguez, P. (2017). Power system stability analysis under increasing penetration of photovoltaic power plants with synchronous power controllers. IET 11, 733–741. doi:10.1049/iet-rpg.2016.0904

CrossRef Full Text | Google Scholar

Risi, B. G., Fulginei, F. R., and Laudani, A. (2022). Modern techniques for the optimal power flow problem: State of the art. MDPI 15, 6387. doi:10.3390/en15176387

CrossRef Full Text | Google Scholar

Shafiul Alam, M., Saleh Al-Ismail, F., Salem, A., and MohammadAbido, A. (2020). High level penetration of renewable energy sources into grid utility: Challenges and solutions. IEE Access 8, 190277–190299. doi:10.1109/ACCESS.2020.3031481

CrossRef Full Text | Google Scholar

Shaheen, M. A. M., Hasanien, H. M., and Al-Durra, A. (2021). Solving of optimal power flow problem including renewable energy resources using HEAP optimization algorithm. IEEE Access 9, 35846–35863. doi:10.1109/ACCESS.2021.3059665

CrossRef Full Text | Google Scholar

Shaheen, M. A. M., Hasanien, H. M., Mekhamer, S. F., Qais, M. H., Alghuwainem, S., Ullah, Z., et al. (2022). Probabilistic optimal power flow solution using a novel hybrid metaheuristic and machine learning algorithm. MDPI 10, 3036. doi:10.3390/math10173036

CrossRef Full Text | Google Scholar

Shaheen, M. A. M., Ullah, Z., Qais, M. H., Hasanien, H. M., Chua, K. J., Tostado-Véliz, M., et al. (2022). Solution of probabilistic optimal power flow incorporating renewable energy uncertainty using a novel circle search algorithm. MDPI 15, 8303. doi:10.3390/en15218303

CrossRef Full Text | Google Scholar

Sharew, E. A., Kefale, H. A., and Werkie, Y. G. (2021). Power quality and performance analysis of grid-connected solar PV system based on recent grid integration requirements. Hindawi 2021, 1–14. doi:10.1155/2021/4281768

CrossRef Full Text | Google Scholar

Singh, B., Goyal, S. K., and Siddiqui, S. A. (2018). “Grid connected-photovoltaic system (GC-PVS): Issues and challenges,” in International Conference on Startup Ventures: Technology Developments and Future Strategies, Manipal University Jaipur, Rajasthan, India, 8–9 October 2018. doi:10.1088/1757-899X/594/1/012032

CrossRef Full Text | Google Scholar

Sameh, M. A., Marei, M. I., Badr, M. A., and Attia, M. A. (2021). An optimized PV control system based on the emperor penguin optimizer. Energies 14, 751. doi:10.3390/en14030751

CrossRef Full Text | Google Scholar

Srikanth Goud, B., Rami Reddy, Ch., Naga Sai kalyan, Ch., Udumula, R. R., Bajaj, M., Abdul Samad, B., et al. (2022). PV/WT integrated system using the gray wolf optimization technique for power quality improvement, Frontiers, 10. doi:10.3389/fenrg.2022.957971

CrossRef Full Text | Google Scholar

Smith, J., Rönnberg, S., Bollen, M., Meyer, J., Blanco, A., Koo, K., et al. (2017). Power quality aspects of solar power results from CIGRE JWG C4/C6.29. CIRED 2017, 809–813. doi:10.1049/oap-cired.2017.0351

CrossRef Full Text | Google Scholar

Song, M., Jia, H., Abualigah, L., Liu, Q., Lin, Z., Wu, D., et al. (2022). Modified Harris hawks optimization algorithm with exploration factor and random walk strategy. Comput. Intell. Neurosci. 2022, 1–23. Article ID 4673665, Hindawi. doi:10.1155/2022/4673665

CrossRef Full Text | Google Scholar

Soomar, A. M., Hakeem, A., Messaoudi, M., Musznicki, P., Iqbal, A., and Czapp, S. (2022). Solar photovoltaic energy optimization and challenges. Frontiers 10. doi:10.3389/fenrg.2022.879985

CrossRef Full Text | Google Scholar

Sujatha, B. G., and Anitha, G. S. (2016). Enhancement of PQ in grid connected PV system using hybrid technique. AinShams Eng. J. 9, 869–881. doi:10.1016/j.asej.2016.04.007

CrossRef Full Text | Google Scholar

Sultan, H. M., AhmedDiab, A. Z., KuznetsovAli, O. N. Z. M., and Abdalla, O. (2019). Evaluation of the impact of high penetration levels of PV power plants on the capacity, frequency and voltage stability of Egypt’s unified grid. MDPI, Energies 12, 552. doi:10.3390/en12030552

CrossRef Full Text | Google Scholar

Sun, Z., Liu, H., Ding, Y., Luo, H., Liu, T., and Tan, Q. (2022). Collaborative control strategy of power quality based on residual capacity of photovoltaic inverter. MDPI 15, 8049. doi:10.3390/en15218049

CrossRef Full Text | Google Scholar

Zhang, Q., Zhou, L., MaoXie, M. B., and Zheng, C. (2018). Power quality and stability analysis of large scale grid-connected photovoltaic system considering non-linear effects. IET 11, 1739–1747. doi:10.1049/iet-pel.2018.0063

CrossRef Full Text | Google Scholar