A solar irradiance estimation technique via curve fitting based on dual-mode Jaya optimization

Solar irradiance is a crucial environmental parameter for optimal control of photovoltaic (PV) systems. However, precise measurements of the solar irradiance are difficult since the irradiation sensors (i.e., pyranometer or pyrheliometer) are expensive and hard to calibrate. This paper proposes a cost-effective and accurate method for estimating the solar irradiance with a PV module via curve fitting. A dual-mode Jaya (DM-Jaya) optimization algorithm is introduced to extract the real-time value of solar irradiance from the measured PV characteristics data by using two search strategies. The step sizes of a random walk are taken from even and Lévy distribution distributions in different searching phases. Compared with the traditional irradiance sensors, the proposed estimator does not require additional circuit and obtains relatively lower error rates. A comparative study of seven population-based optimization algorithms for the optimal design of the estimator is presented. These algorithms include particle swarm optimization (PSO), cuckoo search (CS), Jaya, simulated annealing (SA), genetic algorithm (GA), supply-demand-based optimization (SDO), and the proposed DM-Jaya algorithm. Simulations and experimental results reveal that DM-Jaya outperforms the other optimization algorithms in terms of the estimation speed and accuracy.

1 Introduction

Solar energy is a renewable, clean and inexhaustible source of energy, making it one of the most promising alternatives to the traditional fossil fuel energy. Photovoltaic (PV) is a technique that directly converts the solar radiation to the electrical energy. Nowadays, owing to the simplicities of setting up, PV systems are applied in the city to power up public facilities such as streetlamps, traffic lights and weather detectors.

The output energy of PV modules is greatly affected by environmental conditions (e.g., the temperature and solar irradiance levels). Solar irradiance measurements provide essential information to calculate the efficiency of a power system, to determine possibilities for improvements of the PV plant setup, and to select a location for the construction of a PV power plant. Therefore, precise measurements of solar irradiance are of importance for the efficient operation of PV systems. It is easy to collect the temperature information with a relatively high accuracy by using commercial sensors, while this is not the case for the solar irradiance as the solar irradiation sensors are expensive and hard to calibrate (Hameed et al., 2019).

In the literature, the solar irradiance measurement methods can be roughly grouped into two categories: direct measurement and soft sensing. The former applies the conventional sensing devices like pyranometers (Matsumoto et al., 2017; Azouzoute et al., 2019), fisheye cameras (Baek and Choi, 2022; Mira et al., 2022), and smart devices (Al-Taani and Arabasi, 2018). Using pyranometer is the most direct approach to obtain the measurements of the solar irradiance. However, such sophisticated instruments are expensive and need to be properly calibrated from time to time in order to give the most possible accurate measurement results. The fish eye cameras were used in (Aakroum et al., 2017) to take the sky images from the ground. A deep neural network (DNN) was applied to estimate the solar irradiance from the cloud information in the sky images with an accuracy of 95%, but it is quite computationally expensive. In (Kawakami et al., 2018), the solar irradiance was estimated from the correlation between the brightness values derived from the color values by the image analysis. The average estimation error of this approach is around 90 W/m². Urbich et al. (Urbich et al., 2019) proposed a seamless solar radiation estimation method based on the optical flow of effective cloud albedo captured from satellite imagery. However, the sensitivity of the direct measurements needs to be properly controlled based on the reference value and the environment; otherwise, the observational data may be subject to a large error (Kim et al., 2018).

Data-driven soft sensor design has recently gained immense popularity due to advances in sensory devices, and a growing interest in data mining. Tan et al. (2013) developed a solar irradiance estimator based on a PV modeling equation. To obtain the required current data, the applied PV module will be short circuited during operation. Kang et al. (2022) developed a feature-enhanced gated recurrent unit (FEGRU) model, utilizing the time series data for predicting the solar radiation. No auxiliary data are required. Chen et al. (2022) proposed a modified Ineichen–Perez estimation model for the solar irradiance data. The peformance for estimating the clear-sky irradiance showed the proposed model has the potential for improving the physical methods. In (Ma et al., 2016b), an online support vector regression-based soft sensing model was presented. The model reconstruction was implemented to maintain the prediction accuracy even when the electrical characteristics of the solar cell vary with irradiance, temperature, and age. Ma et al. (2017) proposed a field-support vector regression (F-SVR)-based soft sensor to estimate the solar irradiance from the short-circuit current. Although interesting, these methods require a real-time measure of the short-circuit current. The applied PV module will be disconnected from the load, leading to the power generation losses. Besides, some estimation models without the dependence of measuring the short-circuit current have been proposed. Carrasco et al. (2014) proposed a solar irradiance estimator which was developed based on the principles of immersion and invariance. Simulation results demonstrated the estimated values are very close to those measured by a commercial irradiance sensor. In (Mancilla-David et al., 2014), the solar irradiance was predicted by a neural network from the operating voltage, current, and measured temperature. A big dataset for each specified PV module is required to be collected and trained before the use of this model. If the PV module is replaced or aging, the estimation result could be inaccurate. Moreover, the accurate measurement for the solar irradiance is hard to guarantee when establishing the dataset for training. The irradiance was computed utilizing the maximum power point (MPP) coordinates by the analytical model in (Abe et al., 2020). These soft-sensing approaches usually make use of the PV models to obtain the estimation values. The estimation accuracy cannot be guaranteed because the parameters in the model acquired from the manufacturer’s datasheet aren’t accurate in terms of the aging problem of PV cells.

With the aim of developing an accurate and cost-effective solar irradiance estimator, this paper proposes a real-time measuring method that extracts the value of irradiance from a series of measured current-voltage (I-V) data via curve fitting. The idea of this paper is similar to the work in (Batzelis et al., 2017) that applies curve fitting on voltage and current measurements obtained during operation to determine the MPP in real time. A dual-mode Jaya (DM-Jaya) optimization algorithm is introduced to balance searching space and speed for global optimization. The proposed irradiance estimation method does not need special installation prior to the measurement. In addition to the voltage and current sensors, only a commercial temperature sensor is required to measure the cell temperature. The computer simulations and experiments are conducted to evaluate its estimation performance under a variety of environmental conditions. The proposed estimator could serve as a quick tool to predict the irradiance levels in the preliminary stages of PV systems design.

The remainder of this paper is organized as follows. Section 2 introduces the electrical characteristics of a PV module and formulates the solar irradiance estimation problem. In Section 3, the estimation problem is addressed by a DM-Jaya algorithm. The results and discussions are presented in Section 4. Finally, Section 5 concludes this article.

2 Formulation of irradiance estimation problem

2.1 Single diode photovoltaic model

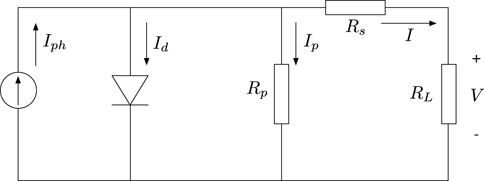
The electrical characteristics of a PV cell can be represented using an equivalent electrical circuit composing of linear and non-linear components. A single-diode equivalent circuit model defines the entire I-V curve of a PV cell for a given set of environmental conditions. Its circuit diagram is shown inFigure 1.

FIGURE 1

FIGURE 1. Equivalent single-diode circuit for a PV cell.

The output current of the PV cell I in Figure 1 can be expressed as Eq. 1.

$I=I_{ph}-I_d-I_p(1)$

where I_ph is the photocurrent, I_d is the current flowing through the antiparallel diode and I_p is the shunt current caused by the shunt resistor R_p.

On the basis of the Shockley diode representation, the expression for I_d is given in Eq. 2.

$I_d=I_o\left[\text{exp}\left(\frac{V+I{R}_s}{nT}\right)-1\right](2)$

where V is the PV output voltage, I_o is the diode saturation current and T is the cell temperature. n = ak/q, where a is the ideality factor, q is the electron’s electric charge (1.602 × 10⁻¹⁹ C), and k is the Boltzmann constant (1.38065 × 10⁻²³ J/K).

Therefore, by substituting Eq. 2 into Eq. 1, the I-V characteristic relation for a PV cell is as in Eq. 3.

$I=I_{ph}-I_o\left[\text{exp}\left(\frac{V+I{R}_s}{nT}\right)-1\right]-\frac{V+I{R}_s}{R_p}(3)$

Assuming that a PV module contains N_s PV cells connected in series. The I-V relation for a PV module is presented in Eq. 4.

$I=I_{ph}-I_o\left[\text{exp}\left(\frac{V+I{R}_s}{nT{N}_s}\right)-1\right]-\frac{V+I{R}_s}{R_p}(4)$

Brano et al. (2010) proposed an improved model as given in Eq. 5. Compared with the model in Eq. 2, the I-V characteristics presented by Lo Brano’s model is closer to the experimental one.

$\begin{array}{ll}\hfill I& ={\alpha }_G{I}_L\left(T\right)-I_o\left({\alpha }_G,T\right)\left[\text{exp}\left(\frac{{\alpha }_G\left(V+KI\mathrm{\Delta }T\right)+I{R}_s}{{\alpha }_{G}nT{N}_s}\right)-1\right]\hfill \\ \hfill & -\frac{{\alpha }_G\left(V+KI\mathrm{\Delta }T\right)+I{R}_s}{R_p}\hfill \end{array}(5)$

where α_G = G/G_STC denotes the ratio between the solar irradiance and the irradiance at standard test conditions (STC, 1000 W/m², 25°C). I_L is the photocurrent at 1000 W/m² and can be computed by Eq. 6. K is a thermal correction factor. ΔT = T − T_STC is the difference between the temperature and the value at STC. The saturation current I_o(α_G, T) can be obtained by Eq. 7 (Brano et al., 2012).

$I_L\left(T\right)=I_{ph,STC}+K_I\left(T-T_{\mathit{STC}}\right)(6)$

$I_o\left({\alpha }_G,T\right)=\exp \left(\frac{{\alpha }_G-0.2}{1-0.2}\text{ln}\frac{I_o\left(1,T\right)}{I_o\left(0.2,T\right)}+\text{ln}\left(I_o\left(0.2,T\right)\right)\right)(7)$

where I_ph,STC is the photocurrent at STC. K_I is the temperature coefficient of short-circuit current. The value of I_o(1, T) and I_o(0.2, T) are calculated by Eq. 8 as introduced in (Brano et al., 2012).

$I_o\left({\alpha }_G,T\right)={\alpha }_G\left(\frac{I_L\left(T\right)-V_{OC}\left({\alpha }_G,T\right)/R_p}{\text{exp}\left(V_{OC}\left({\alpha }_G,T\right)/\left(nT{N}_s\right)\right)-1}\right)(8)$

2.2 Objective function

In this paper, an estimator is proposed to predict the solar irradiance G from the measured I–V characteristics. The terminal current I, voltage V, and temperature T are used as inputs of the estimator.

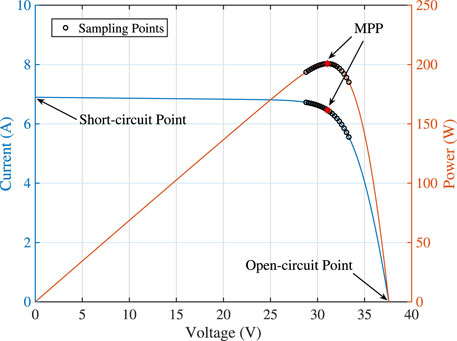
Figure 2 shows the I-V and power-voltage (P-V) characteristics of a PV module. At all operating points in between the short-circuit and open-circuit points, power is produced. The operating point delivering maximum possible power under a specific environmental condition is the MPP. As the operating point moves from the short-circuit point to the MPP, the corresponding I-V curve changes from flat to steep. When the operating point continually moves toward the open-circuit point, the current dramatically decreased. Therefore, the area around the MPP mainly reflects the curve shape, which is affected by several model parameters like R_s, R_p, and a. Assuming that G is constant in a sampling period, the I-V data are sampled as the black circles in Figure 2, which are in a voltage range V_range defined as Eq. 9.

$V_{\mathit{range}}=V_{\mathit{MPP}}\pm 0.35\times \left(V_{OC}-V_{\mathit{MPP}}\right)(9)$

where V_MPP is the voltage at the MPP. The distribution of sampling points is shown in Figure 2. Jiao et al. (2023) used the similar strategy in a real-time fault diagnosis system to determine normal or abnormal operations by sampling points.

FIGURE 2

FIGURE 2. Current-voltage and power-voltage characteristics of a PV module.

Ma et al. (2016a) extracted the parameters in the PV models through curve fitting by bio-inspired optimization algorithms. In this paper, the solar irradiance G is estimated by minimizing the difference between the measured data and the calculated current obtained by the single diode PV model. When the number of experimental data is up to N, the objective function can be formulated by RMSE as Eq. 10.

$\text{RMSE}=\sqrt{\frac{1}{N}\sum _{i=1}^N{\left(f_i\left(V,I,\mathbf{x}\right)\right)}^2}(10)$

where x = [R_s, R_p, a, K, G]. The f_i(V, I, x) can be expressed by Eq. 11, which is the equivalent form of Eq. 5.

$\begin{array}{ll}\hfill f_i\left(V,I,\mathbf{x}\right)& =I-{\alpha }_G{I}_L\left(T\right)+I_o\left({\alpha }_G,T\right)\hfill \\ \hfill & \times \left[\text{exp}\left(\frac{{\alpha }_G\left(V+KI\mathrm{\Delta }T\right)+I{R}_s}{{\alpha }_{G}nT{N}_s}\right)-1\right]\hfill \\ \hfill & +\frac{{\alpha }_G\left(V+KI\mathrm{\Delta }T\right)+I{R}_s}{R_p}\hfill \end{array}(11)$

3 Estimation of solar irradiance

3.1 Jaya algorithm

In 2016, Rao (2016) developed a new gradient-free optimization algorithm which is capable of solving both constrained and unconstrained optimization problems. In the literature, there exists a good number of gradient-free optimization algorithms, such as genetic algorithm (GA) (Holland, 1992), particle swarm optimization (PSO) (Kennedy and Eberhart, 1995), cuckoo search (CS) (Yang and Deb, 2009), simulated annealing (SA) (Kirkpatrick et al., 1983), supply-demand-based optimization (SDO) (Zhao et al., 2019), etc. The Jaya algorithm is distinguished since it does not contain any hyperparameter.

Suppose the objective function f(x) is with D dimensional variables, and $x_{i,j}^k$ is the estimation value of the jth (j = 1, 2, …, D) variable for the ith competitor solution in the kth iteration. In each iteration, the best and worst competitor solutions are identified among the n candidate solutions. The best competitor solution $x_{\mathit{best,j}}^k=(x_{best,1}^k,x_{best,2}^k,\dots ,x_{\mathit{best,D}}^k)$ obtains the minimum values of the objective function in the present populace and the worst competitor solution $x_{\mathit{worst,j}}^k=(x_{worst,1}^k,x_{worst,2}^k,\dots ,x_{\mathit{worst,D}}^k)$ obtains the maximum values of the objective function in the present populace. The new position $x_{i,j}^{k+1}$ is predicted based on the best and worst candidate solutions according to Eq. 12.

$x_{i,j}^{k+1}=x_{i,j}^k+ran{d}_1\times \left(x_{\mathit{best,j}}^k-|x_{i,j}^k|\right)-ran{d}_2\times \left(x_{\mathit{worst,j}}^k-|x_{i,j}^k|\right)(12)$

where the two random numbers rand₁ and rand₂ are in the range of [0,1]. The term “$x_{\mathit{best,j}}^k-|x_{i,j}^k|$” and “$x_{\mathit{worst,j}}^k-|x_{i,j}^k|$” drive the candidate solutions to the positions that are closed to the best solution and far from the worst solution. If the $x_{i,j}^{k+1}$ obtains a smaller function value than the current best value, it replaces the $x_{i,j}^k$. These updated solutions will become the input of the next iteration. In such a way, the Jaya algorithm seeks to achieve victory by forthcoming to the optimized result.

3.2 Dual-mode Jaya algorithm

As discussed in Section 2.2, the objective function is with five-dimensional factors, including series resistance R_s, shunt resistance R_p, ideality factor a, thermal correction factor K, and irradiance G. In the conventional Jaya algorithm, the random parameters rand₁ and rand₂ are two random numbers in the range of [0, 1]. The generated candidate solutions are with a certain distribution, which isn’t sufficient to balance searching space and speed for global optimization. In the local search phase, an intensive search is preferred to explore the feasible neighborhood space of the current best solutions. For a global search, more feasible solutions in the entire solution space can be evaluated to obtain the global optimum. In this sense, different random distributions can be applied in various search phrases.

Lévy flight is a random walk in which the step-lengths obey to the Lévy distribution named after the French mathematician Paul Lévy. In the real world, many animals spend most feeding time around a food source, and they will occasionally undertake long-distance movement to seek the next fool source (Viswanathan, 2010).

To generate random numbers with Lévy flights, the step length S can be determined by Eq. 13, known as Mantegna’s algorithm.

$S=\frac{u}{|v{|}^{1/\beta }}(13)$

where β is usually set to 1.5; u and v obey normal distributions, namely:

$u\sim N\left(0,{\sigma }_u^2\right),v\sim N\left(0,{\sigma }_v^2\right)(14)$

where

${\sigma }_u=\frac{\mathrm{\Gamma }\left(1+\beta \right)\times \sin \left(\pi \beta /2\right)}{\mathrm{\Gamma }\left(\left(1+\beta \right)/2\right)\times \beta \times 2^{\left(\beta -1\right)/2}},{\sigma }_v=1(15)$

And Γ denotes the gamma function. The detailed computation algorithm of gamma function is available is outlined in (Cody, 1976). In this paper, the new position $x_{i,j}^{k+1}$ is predicted based on the random numbers with uniform distribution and Lévy flights. Eq. 12 is modified as Eqs 16, 17.

$\begin{array}{ll}\hfill x_{i,j}^{k+1}& =x_{i,j}^k+\left(0.8+S*\alpha \right)\times \left(x_{\mathit{best,j}}^k-|x_{i,j}^k|\right)\hfill \\ \hfill & -\left(0.8+S*\alpha \right)\times \left(x_{\mathit{worst,j}}^k-|x_{i,j}^k|\right)\hfill \end{array}(16)$

$\begin{array}{ll}\hfill x_{i,j}^{k+1}& =x_{i,j}^k+\left(1-rand*\alpha \right)\times \left(x_{\mathit{best,j}}^k-|x_{i,j}^k|\right)\hfill \\ \hfill & -\left(1-rand*\alpha \right)\times \left(x_{\mathit{worst,j}}^k-|x_{i,j}^k|\right)\hfill \end{array}(17)$

Figure 3 shows the flowchart of the proposed dual-mode Jaya algorithm. Cosine similarity is used to measure the similarity between two non-zero vectors. In Eq. 18, the θ_gen is used to determine whether two candidate solutions in the same population are pointing in roughly the same direction.

${\theta }_{\mathit{gen}}=\frac{x_p^k\cdot x_q^k}{\Vert x_p^k\Vert \times \Vert x_q^k\Vert }(18)$

FIGURE 3

FIGURE 3. Flowchart of the proposed dual-mode Jaya algorithm: (A) Main program; (B) Update $x_{i,j}^k$.

The similarity between the two generations can be calculated by Eq. 19.

${\theta }_{\mathit{par}}=\frac{x^k\cdot x^{k-1}}{\Vert x^k\Vert \times \Vert x^{k-1}\Vert }(19)$

When the θ_gen < θ₁, the algorithm may fall into local optimum. The θ_par is used to further confirm the optimization status. If the θ_par is also greater than θ₂, it indicates that the candidate solutions in a population are similar. The α is then adjusted to α₁ to reduce the impact of the best and worst solutions. Otherwise, the α is set to α₂. If the situation cannot be improved, then the model switches the mode back to the one with uniform distribution. The algorithm attempts extraordinary endeavors to successfully discover the genuine result and solution on both modes, so it is named the DM-Jaya algorithm. In the validation part of the manuscript, the value for θ₁ is set to 10e-4, θ₁ is 0.99, α₁ is 0.5, and α₂ is 0.8. The selection of these values were verified through the experiments and can be tuned in terms of different applications.

4 Results and discussions

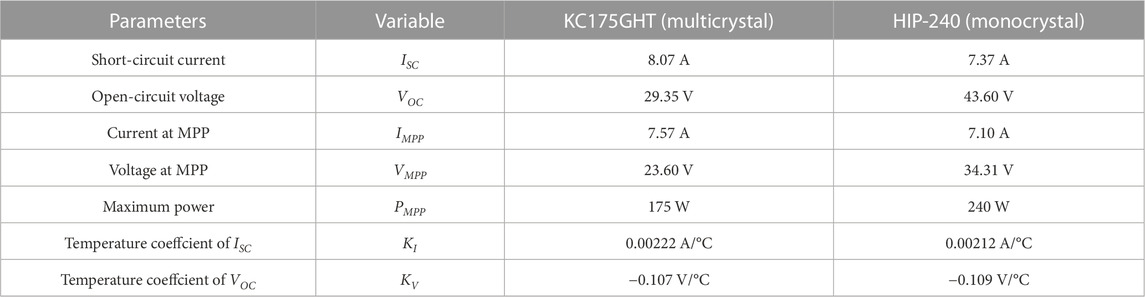
To provide a thorough evaluation of the proposed optimization algorithm, two solar panels that were manufactured using different PV technologies were tested in this paper: (a) a Kyocera KC175GHT module and (b) a Sanyo HIP-240 module. The former is a 1290*990 mm multicrystal PV module with 175 W maximum power at 1000 W/m². There are 48 cells bonded by 3 busbars in this module. The HIP-240 is a monocrystal PV module comprising 72 cells. Its rated output at STC is 240 W. The detailed specifications of the two PV modules are listed in Table 1.

TABLE 1

TABLE 1. Specifications of the PV modules used in this research under standard test condition.

The data collection comprises the data of these two modules operating under varied environmental conditions in the Simulink environment. Test temperature was varied from 0°C to 50°C in steps of 10°C. Test solar irradiance was varied from 100 W/m² to 1000 W/m² in steps of 100 W/m². A total of 60 test scenarios are available for evaluation for each PV module. The standard particle swarm optimization (PSO), cuckoo search (CS), Jaya, simulated annealing (SA), genetic algorithm (GA), and supply-demand-based optimization (SDO) algorithms were also tested in the same scenario with the proposed DM-Jaya. To make a fair comparison, the same objective function was used in all the involved optimization algorithms. Besides, the population size of all seven algorithms was set to 10. The parameter selection of the compared algorithms was as follows. For the PSO algorithm, the range of the inertia weight was [0.4, 0.9]. The initial temperature was set to 1 in the SA algorithm. For the GA algorithm, the crossover probability was set to 0.1 and the genetic probability was set to 0.9. The size of commodities in each market for SDO was set to 30. The Lévy distribution parameter β was set to 1.5 both in the CS and DM-Jaya algorithms.

Figure 4 depicts the comparative results of the root mean squared errors (RMSE) along with the number of iterations among the seven optimization algorithms based on the tested two PV modules. As shown in Figure 4A, for Kyocera KC175GHT PV module, it is observed that the at the iteration of 10,000, all the algorithms reach a low RMSE value below 0.01 A except for the SA algorithm, whose RMSE value is around 0.15 A. Among the seven algorithms involved in the comparative study, PSO has the slowest optimization speed. Although SDO could reach a low RMSE value similar to the proposed DM-Jaya algorithm, the optimization speed of the proposed DM-Jaya is much faster. Similar cases can be observed as in Figure 4B for Sanyo HIP-240 module, where the RMSE value of the final optimized result from the proposed DM-Jaya is around 0.0009 A and the best among all the tested optimization algorithms.

FIGURE 4

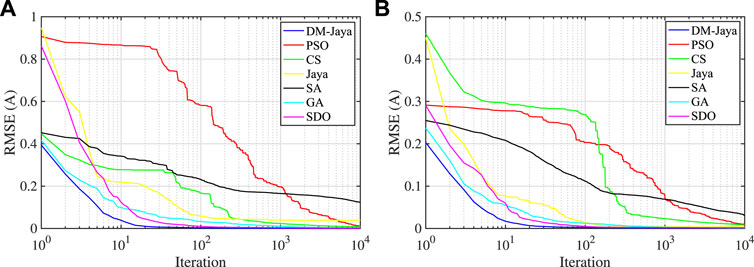
FIGURE 4. Comparison in RMSE values along with the number of iterations among seven optimization algorithms for (A) Kyocera KC175GHT and (B) Sanyo HIP-240.

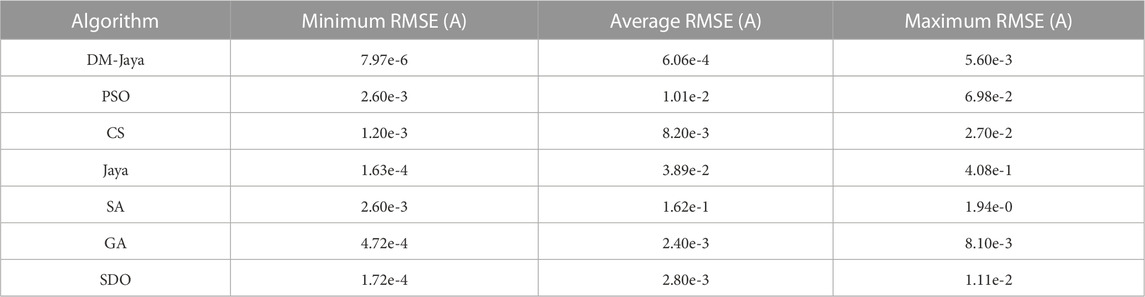
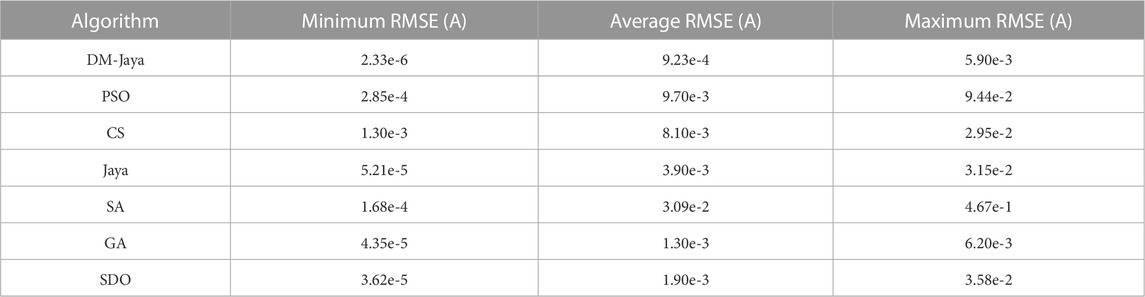
Tables 2, 3 list the statistical RMSE values within 10,000 iterations and 60 individual test scenarios from the seven optimization algorithms for Kyocera KC175GHT module and Sanyo HIP-240 module. In the comparative study, the SA algorithm shows the worst performance in terms of the maximum RMSE values. The difference between the maximum and minimum RMSE values of the SA algorithm are the largest on both PV modules, which indicates that the optimization performance of the SA algorithm is not stable. This can be also reflected from the results in Figure 4, where the final optimized RMSE values of SA algorithm are much larger than the other optimization algorithms. On the contrary, the minimum RMSE value of the proposed DM-Jaya algorithm is lower than the other six algorithms by at least 95%. Meanwhile, the maximum RMSE of DM-Jaya is also the best from the results in both Tables 2, 3.

TABLE 2

TABLE 2. Statistics of RMSE values in 60 test scenarios for Kyocera KC175GHT module.

TABLE 3

TABLE 3. Statistics of RMSE values in 60 test scenarios for Sanyo HIP-240 module.

The final estimation errors of the solar irradiance from the tested two PV panels are recorded in Tables 4, 5, respectively. Four mathematical indicators were used to analyze the accuracy of the irradiation estimators. They are RMSE, mean absolute errors (MAE), mean squared errors (MSE), and R-squared (R²). It is observed from the data that the proposed DM-Jaya algorithm significantly improves the performance in terms of the estimation accuracy. The DM-Jaya algorithm has the best estimation performance among the seven optimization algorithms. Although the GA algorithm has a similar estimation error to the proposed DM-Jaya, the convergence speed is slower than DM-Jaya based on the results shown in Figure 4. The GA algorithm converges to the vicinity of the optimum after the iteration of 10³ while the DM-Jaya algorithm achieves such value before the iteration of 10².

TABLE 4

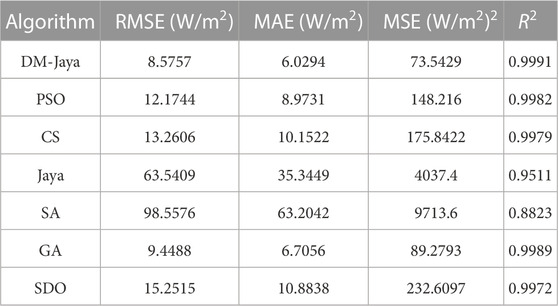
TABLE 4. Estimation errors of solar irradiance from different optimization algorithms for Kyocera KC175GHT module.

TABLE 5

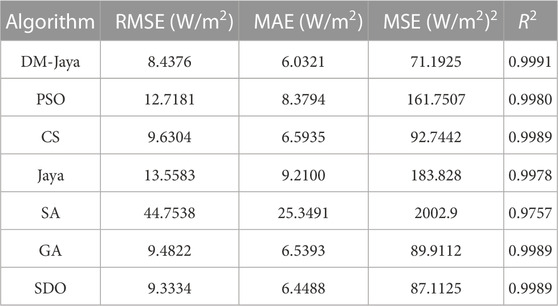
TABLE 5. Estimation errors of solar irradiance from different optimization algorithms for Sanyo HIP-240 module.

The performance of the proposed DM-Jaya algorithm under different environments (irradiation and temperature) is evaluated and the results are presented in Figures 5, 6. Figures 5A, B are respectively the box plots of the RMSE values in the 40 runs under different solar irradiances and temperatures for the PV module Kyocera KC175GHT, while Figure 6 is the result for Sanyo HIP-240 module. Based on the results in the box plots, it is observed that the median estimation RMSE values for KC175GHT multicrystal module fluctuate with different irradiation ranges. The median RMSE for the range 200–400 W/m² is lower than the other solar irradiances. Such a phenomenon does not exist for the HIP-240 monocrystal module. As shown in Figure 6A, the median RMSE values of different irradiation ranges are all around 5 × 10⁻⁵ A. In addition, the performance of the proposed DM-Jaya optimization algorithm is not affected too much by the temperature, the median RMSE values are around 5 × 10⁻⁴ A and 6 × 10⁻⁵ A for KC175GHT and HIP-240 module, respectively. Hence, the proposed DM-Jaya algorithm can remain a good optimization result under all the tested environments.

FIGURE 5

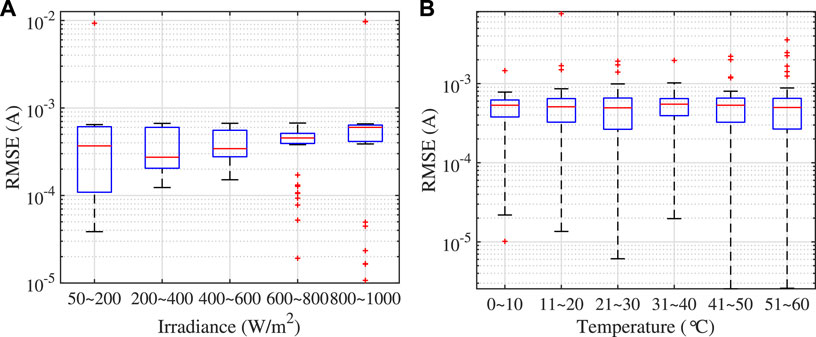
FIGURE 5. Statistics of the RMSE values in the 40 runs of the DM-Jaya optimization algorithm under (A) different solar irradiances at 25°C and (B) different temperatures at 1000 W/m² for Kyocera KC175GHT module.

FIGURE 6

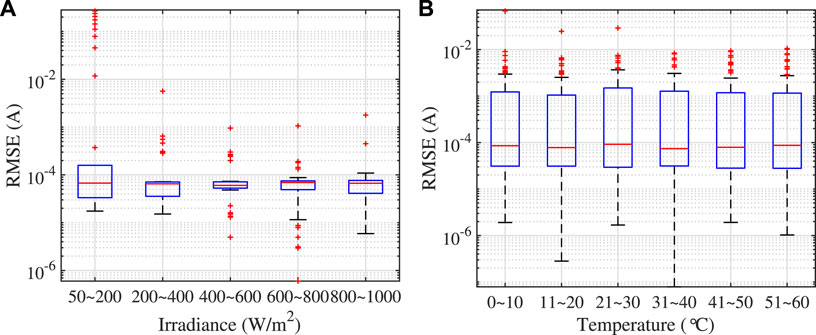
FIGURE 6. Statistics of the RMSE values in the 40 runs of the DM-Jaya optimization algorithm under (A) different solar irradiances at 25°C and (B) different temperatures at 1000 W/m² for Sanyo HIP-240 module.

Finally, the estimation results for the time-varied solar irradiance are shown in Figures 7, 8. The solid blue line is the measured irradiance values during day time from 8:00 to 16:00. The data in Figure 7A is measured on a sunny day, while the one in Figure 8A is for a cloudy day. The solar irradiance was sampled every 10 min by a calibrated pyranometer. The proposed solar irradiance estimation method is applied every 10 min. The red circles are used to represent the estimated solar irradiance values. Figures 7B, 8B present the absolute errors between the estimated values and experimental values. In average, the RMSE values in this test are 6.92 W/m² and 6.10 W/m² for the sunny day and cloudy day, respectively. It can be concluded that the proposed technique is capable of predicting the solar irradiance under changing irradiance conditions.

FIGURE 7

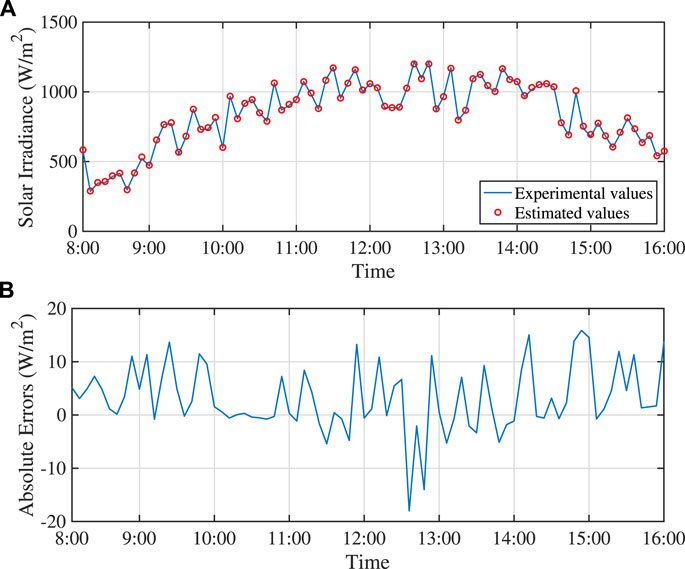
FIGURE 7. Estimation results of time-varied solar irradiance during day time on a sunny day: (A) comparison between experimental and estimated values; (B) absolute errors.

FIGURE 8

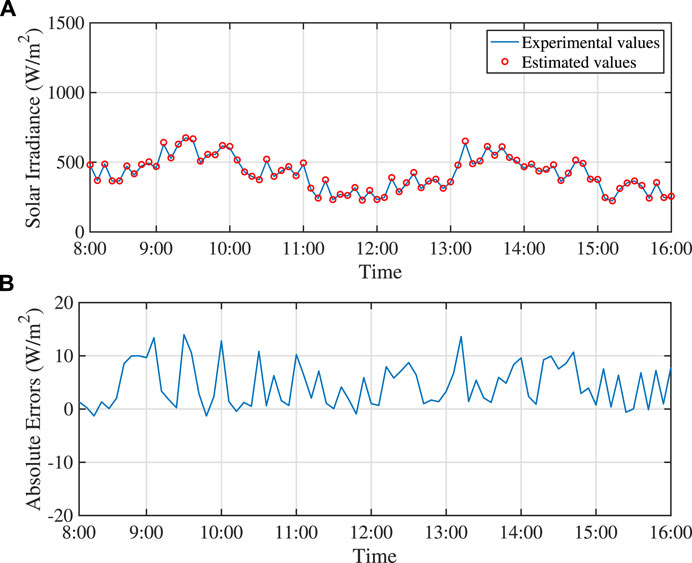
FIGURE 8. Estimation results of time-varied solar irradiance during day time on a cloudy day: (A) comparison between experimental and estimated values; (B) absolute errors.

5 Conclusion

This paper has proposed a novel estimation method for estimating the solar irradiance with a single PV module. The developed estimator is cost-effective and does not require any additional calibration process. By optimizing a single-diode PV mode, the proposed dual-mode Jaya (DM-Jaya) optimization algorithm can extract the current solar irradiance level from a series of measured I-V data. Six popular optimization algorithms, including particle swarm optimization (PSO), cuckoo search (CS), Jaya, simulated annealing (SA), genetic algorithm (GA), and supply-demand-based optimization (SDO) have been used to perform a comparative study in two modules manufactured by using different PV technologies. Simulation and experimental results show that the proposed DM-Jaya algorithm obtains a relatively lower error rate than other algorithms, and it is very reliable to estimate the solar irradiance and its variability under different environmental conditions.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author contributions

ZB wrote the manuscript. ZB, GC, XP, and JG implemented the experiments. MG and JB checked the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This research was supported by the Natural Science Foundation of the Jiangsu Higher Education Institutions of China under Grant No. 20KJB510026.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aakroum, M., Ahogho, A., Aaqir, A., and Ahajjam, A. A. (2017). “Deep learning for inferring the surface solar irradiance from sky imagery,” in 2017 International Renewable and Sustainable Energy Conference (IRSEC), Tangier, Morocco, 04-07 December 2017, 1–4.

CrossRef Full Text | Google Scholar

Abe, C. F., Dias, J. B., Notton, G., and Poggi, P. (2020). Computing solar irradiance and average temperature of photovoltaic modules from the maximum power point coordinates. IEEE J. Photovoltaics10, 655–663. doi:10.1109/jphotov.2020.2966362

CrossRef Full Text | Google Scholar

Al-Taani, H., and Arabasi, S. (2018). Solar irradiance measurements using smart devices: A cost-effective technique for estimation of solar irradiance for sustainable energy systems. Sustainability10, 508. doi:10.3390/su10020508

CrossRef Full Text | Google Scholar

Azouzoute, A., Merrouni, A. A., Bennouna, E. G., and Gennioui, A. (2019). Accuracy measurement of pyranometer vs reference cell for pv resource assessment. Energy Procedia157, 1202–1209. Technologies and Materials for Renewable Energy, Environment and Sustainability (TMREES). doi:10.1016/j.egypro.2018.11.286

CrossRef Full Text | Google Scholar

Baek, J., and Choi, Y. (2022). Comparative study on shading database construction for urban roads using 3d models and fisheye images for efficient operation of solar-powered electric vehicles. Energies15, 8228. doi:10.3390/en15218228

CrossRef Full Text | Google Scholar

Batzelis, E. I., Kampitsis, G. E., and Papathanassiou, S. A. (2017). Power reserves control for pv systems with real-time mpp estimation via curve fitting. IEEE Trans. Sustain. Energy8, 1269–1280. doi:10.1109/TSTE.2017.2674693

CrossRef Full Text | Google Scholar

Brano, V. L., Orioli, A., Ciulla, G., and Gangi, A. D. (2010). An improved five-parameter model for photovoltaic modules. Sol. Energy Mater. Sol. Cells94, 1358–1370. doi:10.1016/j.solmat.2010.04.003

CrossRef Full Text | Google Scholar

Brano, V. L., Orioli, A., and Ciulla, G. (2012). On the experimental validation of an improved five-parameter model for silicon photovoltaic modules. Sol. Energy Mater. Sol. Cells105, 27–39. doi:10.1016/j.solmat.2012.05.028

CrossRef Full Text | Google Scholar

Carrasco, M., Mancilla-David, F., and Ortega, R. (2014). An estimator of solar irradiance in photovoltaic arrays with guaranteed stability properties. IEEE Trans. Industrial Electron.61, 3359–3366. doi:10.1109/tie.2013.2281154

CrossRef Full Text | Google Scholar

Chen, S., Liang, Z., Guo, S., and Li, M. (2022). Estimation of high-resolution solar irradiance data using optimized semi-empirical satellite method and goes-16 imagery. Sol. Energy241, 404–415. doi:10.1016/j.solener.2022.06.013

CrossRef Full Text | Google Scholar

Cody, W. J. (1976). “An overview of software development for special functions,” in Numerical analysis. Editor G. A. Watson (Berlin, Heidelberg: Springer Berlin Heidelberg), 38–48.

CrossRef Full Text | Google Scholar

Hameed, W. I., Sawadi, B. A., Al-Kamil, S. J., Al-Radhi, M. S., Al-Yasir, Y. I. A., Saleh, A. L., et al. (2019). Prediction of solar irradiance based on artificial neural networks. Inventions4, 45. doi:10.3390/inventions4030045

CrossRef Full Text | Google Scholar

Holland, J. H. (1992). Genetic algorithms. Sci. Am.267, 66–72. doi:10.1038/scientificamerican0792-66

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiao, X., Li, X., Yang, T., Yang, Y., and Xiao, W. (2023). A novel fault diagnosis scheme for pv plants based on real-time system state identification. IEEE J. Photovoltaics2023, 1–9. doi:10.1109/JPHOTOV.2023.3262950

CrossRef Full Text | Google Scholar

Kang, T., Wang, H., Wu, T., Peng, J., and Jiang, H. (2022). Solar irradiance prediction based on self-attention recursive model network. Front. Energy Res.10. doi:10.3389/fenrg.2022.977979

CrossRef Full Text | Google Scholar

Kawakami, K., Takahashi, A., Imai, J., and Funabiki, S. (2018). “Measuring method for solar irradiance at multi-points with different color based on image analysis,” in 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23-27 September 2018, 2543–2548.

CrossRef Full Text | Google Scholar

Kennedy, J., and Eberhart, R. (1995). “Particle swarm optimization,” in Proceedings of ICNN’95 - International Conference on Neural Networks, Perth, WA, Australia, 27 November 1995 - 01 December 1995, 1942–1948.

Google Scholar

Kim, B.-Y., Lee, K.-T., Zo, I.-S., Lee, S.-H., Jung, H.-S., Rim, S.-H., et al. (2018). Calibration of the pyranometer sensitivity using the integrating sphere. Asia-Pacific J. Atmos. Sci.54, 639–648. doi:10.1007/s13143-018-0085-0

CrossRef Full Text | Google Scholar

Kirkpatrick, S., Gelatt, C. D., and Vecchi, M. P. (1983). Optimization by simulated annealing. Science220, 671–680. doi:10.1126/science.220.4598.671

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, J., Bi, Z., Shi, Y., Man, K. L., Pan, X., and Wang, J. (2016a). “Ol-svr based soft-sensor for real-time estimation of solar irradiance,” in 2016 IEEE Asia Pacific Conference on Circuits and Systems (APCCAS), Jeju, Korea (South), 25-28 October 2016, 448–451.

CrossRef Full Text | Google Scholar

Ma, J., Bi, Z., Ting, T. O., Hao, S., and Hao, W. (2016b). Comparative performance on photovoltaic model parameter identification via bio-inspired algorithms. Sol. Energy132, 606–616. doi:10.1016/j.solener.2016.03.033

CrossRef Full Text | Google Scholar

Ma, J., Jiang, H., Huang, K., Bi, Z., and Man, K. L. (2017). Novel field-support vector regression-based soft sensor for accurate estimation of solar irradiance. IEEE Trans. Circuits Syst. I Regul. Pap.64, 3183–3191. doi:10.1109/tcsi.2017.2746091

CrossRef Full Text | Google Scholar

Mancilla-David, F., Riganti-Fulginei, F., Laudani, A., and Salvini, A. (2014). A neural network-based low-cost solar irradiance sensor. IEEE Trans. Instrum. Meas.63, 583–591. doi:10.1109/tim.2013.2282005

CrossRef Full Text | Google Scholar

Matsumoto, Y., Antonio Urbano, J., Peña, R., de La Luz Olvera, M., Pitalúa, N., Luna, M. A., et al. (2017). “Performance comparisons of a pv system by monitoring solar irradiance with different pyranometers,” in 2017 IEEE 44th Photovoltaic Specialist Conference (PVSC), Washington, DC, USA, 25-30 June 2017, 632–637.

CrossRef Full Text | Google Scholar

Mira, D. A., Bartholomäus, M., Poessl, S., Poulsen, P. B., and Spataru, S. V. (2022). “Comparing the accuracy of horizon shade modelling based on digital surface models versus fisheye sky imaging,” in 2022 IEEE 49th Photovoltaics Specialists Conference (PVSC), Philadelphia, PA, USA, 05-10 June 2022, 060–065. doi:10.1109/PVSC48317.2022.9938715

CrossRef Full Text | Google Scholar

Rao, R. (2016). Jaya: A simple and new optimization algorithm for solving constrained and unconstrained optimization problems. Int. J. Industrial Eng. Comput.7, 19–34. doi:10.5267/j.ijiec.2015.8.004

CrossRef Full Text | Google Scholar

Tan, R. H. G., Tai, P. L. J., and Mok, V. H. (2013). “Solar irradiance estimation based on photovoltaic module short circuit current measurement,” in 2013 IEEE International Conference on Smart Instrumentation, Measurement and Applications (ICSIMA), Kuala Lumpur, Malaysia, 25-27 November 2013, 1–4.

CrossRef Full Text | Google Scholar

Urbich, I., Bendix, J., and Müller, R. (2019). The seamless solar radiation (sesora) forecast for solar surface irradiance—Method and validation. Remote Sens.11, 2576. doi:10.3390/rs11212576

CrossRef Full Text | Google Scholar

Viswanathan, G. M. (2010). Fish in Lévy-flight foraging. Nature465, 1018–1019. doi:10.1038/4651018a

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, X.-S., and Deb, S. (2009). “Cuckoo search via Lévy flights,” in 2009 World congress on nature & biologically inspired computing (NaBIC), Coimbatore, India, 09-11 December 2009, 210–214. IEEE.

Google Scholar

Zhao, W., Wang, L., and Zhang, Z. (2019). Atom search optimization and its application to solve a hydrogeologic parameter estimation problem. Knowledge-Based Syst.163, 283–304. doi:10.1016/j.knosys.2018.08.030

CrossRef Full Text | Google Scholar