Stackelberg equilibrium-based energy management strategy for regional integrated electricity–hydrogen market

This paper develops an optimal energy bidding mechanism for the regional integrated electricity–hydrogen system (RIEHS) considering complex electricity–hydrogen energy flow and further presents an electricity–hydrogen optimization management strategy based on Stackelberg game. The transaction mode of the RIEHS is first introduced, and the optimization models for the three market game participants are established. Then, the Stackelberg game-based bidding mechanism is formulated, where the electricity–hydrogen operator (EHO) is the leader and the regional electricity–hydrogen prosumer (REHP) and load aggregator (LA) are the followers. The EHO dominates the game through energy bidding, and REHP and LA respond to the bidding decision. The Stackelberg equilibrium of the formulation is obtained by applying the differential evolutionary algorithm combined with quadratic programming (DEA-QP). Finally, a demonstration case is studied to analyze the market behavior of the three market players and further validate the effectiveness of the proposed strategy. The proposed strategy is able to produce additional economic benefits to REHP and LA and improve the utilization of hydrogen.

1 Introduction

Exploitation of renewable energy is an important trend to reduce carbon emission and promote sustainable development of society and economy (Li et al., 2022). According to the prediction from the Hydrogen Council, hydrogen is becoming an important energy carrier, which will consume 18% of global energy by 2050 (Erdiwansyah et al., 2021). The commercial application of hydrogen energy is being subjected to increasing attention.

The regional integrated electricity–hydrogen system (RIEHS) is becoming a promising solution to promote the penetration of hydrogen energy due to high overall energy efficiency (Wen, et al., 2020), flexible multi-energy complementarity (Sharma et al., 2022), investment planning (Han, and Kim, 2019), and optimal scheduling operation (Liu, et al., 2021; Wang., et.al, 2022a). Optimal power management of the RIEHS is an important aspect.

Previous studies regarding optimization and control of the energy system integrated with hydrogen have been performed. El-Taweel et al. (2018) established a central scheduling model for an integrated electricity–hydrogen system to implement the capacity-based demand response. Fang et al. (2023), developed a convex–concave-based sequential convex approximation method to address the non-convexity optimization problem of hydrogen transmission in electricity–hydrogen scheduling. In He et al. (2021), hydrogen trucks and pipelines are additionally considered hydrogen storage units, and the economic performance and flexibility are analyzed in terms of electricity–hydrogen scheduling. A novel energy system architecture integrating the hydrogen production station, refueling station, and commercial electric vehicles is presented in Long and Jia (2021), where the hydrogen dispatch and EV charging are optimized to maximize the economic benefits. Fang et al. (2023) presented a study on the integrated charging stations of the hydrogen storage system and photovoltaic system and proposed a two-stage energy management strategy to improve the economic benefits through day-ahead scheduling optimization. However, the aforementioned work merely considers the impact of energy price on optimization of the energy system. Energy prices are critical to promote hydrogen trading. However, the buyers and sellers always compete with each other to maximize their utilities, making it difficult to obtain the desired economic benefits. Multiple bidding activities can result in market games among players.

1.1 Related work of game theoretical models

Game theoretical models were previously developed to perform optimal operation and management as well as energy bidding, such as the non-cooperative game (Liu, et al., 2018), Stackelberg game (Mediwaththe. et al., 2017), and the evolutionary game (Zhang. et al., 2021), which are methodologies to make a rational decision when there is a conflict of interest between multiple decision-makers (Luosong, et al., 2022; Smith. 1982). In the absence of utility intervention, the transaction between energy supply side and demand side is a game about energy price. Market participants can bid for economic benefits. A game equilibrium can be reached when all participants agree with the energy price.

Several energy trading strategies based on game theory are proposed to perform optimal operation of the traditional power system, microgrid, and hybrid energy system. Anoh et al. (2020) established a Stackelberg-game-based electricity trading model to optimize the prosumer’s benefits in a virtual microgrid. Liu et al. (2020) proposed a peer-to-peer trading method with an autonomous economic scheduling model based on the Stackelberg game to analyze the gaming relationship between sellers and buyers. An aggregative game approach for the pricing scheme is presented in Mishra and Parida (2020), where demand-side management is performed to consider the privacy and comfortability of customers. In addition, the different parties reach a Nash equilibrium. Bae and Park (2019) established the buyer pricing system and the seller pricing system in an electricity market by the Stackelberg duopoly game model and performed simulations to validate their stability and efficiency. However, the existing studies merely concern the operation characteristics of the hydrogen vector and energy conversion between electricity and hydrogen.

1.2 Main outcomes of this work

In this work, the system-level optimization is performed when the hydrogen energy vector is integrated into the RIEHS. The monetary-perspective-based energy management strategy can be improved to implement the marketization and to manage the unique internal equipment and loads. However, there exist critical challenges in the electricity–hydrogen market. First, the interests of certain entities may be sabotaged by a unified pricing mode. In addition, energy bidding, energy production, and load demand can be mutually constrained in a highly competitive market. For example, higher energy prices may incentivize energy production and suppress load demand, which further affects the management of the distributed generation in the RIEHS. A market involving the energy bidder, producer, and consumer can be adopted in the hierarchical game framework to solve the energy management problem with the leader–follower structure, which is a Stackelberg game. Therefore, it is urgent to develop a Stackelberg equilibrium-based energy management strategy with a flexible bidding mechanism to promote the marketability of hydrogen.

This paper presents a coordinated optimal management strategy for the RIEHS based on a Stackelberg game framework. The main contributions of this paper are explained as follows. 1) A novel electricity–hydrogen trading framework with the price bidding mechanism is developed to effectively analyze the market behavior of participants in the RIEHS. 2) A Stackelberg equilibrium-based electricity–hydrogen optimization model is formulated to optimize the economic benefits of different market stakeholders.

The rest of this paper is organized as follows. In Section 2, the models of the EHO, REHP, and LA are developed. In Section 3, the bidding mechanism based on Stackelberg game is established. A case study is provided to analyze market behaviors of the players in Section 4. The conclusions are drawn in Section 5.

2 Electricity–hydrogen market modeling of the RIEHS

2.1 Electricity–hydrogen trading mode

Figure 1 shows the proposed electricity–hydrogen trading mode in the RIEHS, where the energy bidding and business are performed within the three market game participants, namely, electricity–hydrogen operator (EHO), regional electricity–hydrogen prosumer (REHP), and load aggregator (LA). For the RIEHS, the electricity is supplied from the grid, renewable energy sources, and fuel cells. In addition, hydrogen can be supplied from hydrogen plants. The electricity subsystem and the hydrogen subsystem are integrated through the REHP and LA. The distributed units in RIEHS are operated by REHP.

FIGURE 1

FIGURE 1. Electricity–hydrogen trading mode of the RIEHS.

In this work, the EHO is proposed based on the concept of electricity sales companies in the electricity market. Hydrogen trading is considered in addition to electricity trading to meet the energy demand of customers. The EHO can provide a more flexible energy bidding strategy than the grid and coordinate the participation of distributed energy systems in the electricity–hydrogen market. As the middleman between energy suppliers and consumers, the EHO orders electricity and hydrogen supply and then earns revenue by electricity and hydrogen trading.

REHP has the ability to make autonomous decisions for supplying energy to the RIEHS. However, the limited generation capacity of REHP may cause energy shortage in the system. In addition, additional spare capacity will increase system operating costs and result in higher energy costs for customers. Figure 2 shows the electricity–hydrogen energy coupling relationship of REHP. Wind turbines (WTs) and photovoltaic (PV) panels provide electrical power to regional systems, and the battery system provides electrical power by storing redundant renewable energies according to the scheduling instructions. The hydrogen storage (HS) unit is a combination of multiple storage tanks, which collects hydrogen from the electrolyzer and provides hydrogen for fuel cell stacks and hydrogen load demand. Uncertainty in renewable energy can be mitigated by utilizing the surplus electricity–hydrogen stored, thereby compensating for potential generation shortfalls. Electric vehicles (EVs) are flexible loads that can participate in the dispatch of the electrical power system and are operated directly by REHP. In addition, hydrogen-driven vehicles (HVs) are considered flexible loads for hydrogen in the RIEHS.

FIGURE 2

FIGURE 2. Electricity–hydrogen coupling relationship of REHP.

Community customers have relatively low power ratings, and hence are not suitable to participate for business in the energy market. The LA aggregates a group of small and medium-sized customers with demand response capability to participate in market transactions. Apart from the sensitive electrical load (SEL) that ensures the normal life of consumers, the flexibility of electrical loads is considered with introducing a certain percentage of controllable insensitive electrical load (ISEL). Consumers receive information on the prices of electricity and hydrogen the next day from the EHO and optimize the hourly energy demand accordingly.

In the transaction process, all the players can optimize their own strategy according to the profit-driven objective, where conflicts exist among the players. Therefore, there exists a market game among the EHO, REHP, and LA. To establish the market game relationship, the global optimal solution should be modeled and obtained.

2.2 Modeling of the electricity–hydrogen market

In the electricity–hydrogen market, the optimization models are established to represent their market behaviors.

2.2.1 Modeling of the EHO

The EHO performs the optimal price bidding strategy. The optimal objective of the bidding strategy is to obtain maximum revenue, which can be represented as (Eq. 1).

$\max F^{\text{EHO}}=B^{\text{sell}}-C^{\text{pur}}-C^{\text{grid}}-C^{\mathrm{H},\text{src}},(1)$

where $B^{\text{sell}}$ is the economic income of the EHO for energy trading, $C^{\text{pur}}$ is the energy cost of the EHO from REHP, $C^{\text{grid}}$ is the cost of electricity exchange with the grid, and $C^{\mathrm{H},\text{src}}$ is the cost of hydrogen from the hydrogen source. The $B^{\text{sell}}$/ $C^{\text{pur}}$/ $C^{\text{grid}}$/ $C^{\mathrm{H},\text{src}}$ can be represented as Eqs 2–5.

$B^{\text{sell}}={\displaystyle \sum _{t=1}^T}\left({\lambda }_t^{\mathrm{e},\mathrm{s}}{P}_t^{\mathrm{L}}+{\lambda }_t^{\mathrm{H},\mathrm{s}}{H}_t^{\mathrm{L}}\right)\Delta t,(2)$

$C^{\text{pur}}={\displaystyle \sum _{t=1}^T}\left({\lambda }_t^{\mathrm{e},\mathrm{p}}{P}_t^{\text{RP}}+{\lambda }_t^{\mathrm{H},\mathrm{p}}{H}_t^{\text{RP}}\right)\Delta t,(3)$

$C^{\text{grid}}={\displaystyle \sum _{t=1}^T}\left({\lambda }_t^{\text{grid},\mathrm{p}}\cdot \max \left(P_t^{\text{grid}},0\right)+{\lambda }_t^{\text{grid},\mathrm{s}}\cdot \min \left(P_t^{\text{grid}},0\right)\right)\Delta t,(4)$

$C^{\mathrm{H},\text{src}}={\displaystyle \sum _{t=1}^T}{\lambda }_t^{\mathrm{H},\text{src}}\left(H_t^{\text{src}}\right)\Delta t,(5)$

where $\Delta t$ is the time interval, T is the total number of periods of the market game, ${\lambda }_t^{\mathrm{e},\mathrm{s}}$/ ${\lambda }_t^{\mathrm{H},\mathrm{s}}$ is the hourly electricity/hydrogen export price to the LA, ${\lambda }_t^{\mathrm{e},\mathrm{p}}$/ ${\lambda }_t^{\mathrm{H},\mathrm{p}}$ is the electricity/hydrogen import price from REHP, ${\lambda }_t^{\text{grid},\mathrm{p}}$ is the hourly real-time electricity price of the grid, ${\lambda }_t^{\text{grid},\mathrm{s}}$ is the hourly electricity collection price of the grid, ${\lambda }_t^{\mathrm{H},\text{src}}$ is the hourly hydrogen price from the hydrogen source, $P_t^{\mathrm{L}}$/ $H_t^{\mathrm{L}}$ is the electricity/hydrogen demand in the RIEHS, and $P_t^{\text{RP}}$/ $H_t^{\text{RP}}$ is the imported electricity/hydrogen from REHP. $P_t^{\text{grid}}$ is the exchanged power between the EHO and the grid and $H_t^{\text{src}}$ is the imported hydrogen from the hydrogen source, $t\in T$. In (Eq. 4), the positive $P_t^{\text{grid}}$ represents the EHO importing electricity from the grid, and a negative value represents the EHO exporting surplus electricity to the grid. $P_t^{\text{grid}}$ and $H_t^{\text{src}}$ can be calculated by (Eq. 6) with the constraints as shown in (Eq. 7).

$\left\{\begin{array}{c}{P}_t^{\text{grid}}=P_t^{\mathrm{L}}-P_t^{\text{RP}}\\ H_t^{\text{src}}=H_t^{\mathrm{L}}-H_t^{\text{RP}}\end{array}\right.,(6)$

$\left\{\begin{array}{c}{P}_{\min }^{\text{grid}}\le P_t^{\text{grid}}\le P_{\max }^{\text{grid}}\\ H_t^{\text{src}}\le H_{\max }^{\text{src}}\end{array}\right.,(7)$

where $P_{\min }^{\text{grid}}$ is the exported minimum electricity, which is a negative value; $P_{\max }^{\text{grid}}$ is the imported maximum electricity from the grid, which is a positive value; and $H_{\max }^{\text{src}}$ is the imported maximum hydrogen from the hydrogen source, $t\in T$.

To avoid REHP and LA trading directly with the grid, the EHO can offer a better bidding to REHP and LA (Liu. et al., 2017), as shown in (Eq. 8). Correspondingly, the hydrogen import/export price for the EHO can be specified between its upper and lower limits, as shown in (Eq. 9).

$\left\{\begin{array}{l}{\lambda }_t^{\text{grid},\mathrm{s}}<{\lambda }_t^{\mathrm{e},\mathrm{s}}<{\lambda }_t^{\text{grid},\mathrm{p}}\\ {\lambda }_t^{\text{grid},\mathrm{s}}<{\lambda }_t^{\mathrm{e},\mathrm{p}}<{\lambda }_t^{\text{grid},\mathrm{p},}\end{array}\right.(8)$

$\left\{\begin{array}{l}{\lambda }_{\min }^{\mathrm{H}}\le {\lambda }_t^{\mathrm{H},\mathrm{s}}\le {\lambda }_{\max }^{\mathrm{H}}\\ {\lambda }_{\min }^{\mathrm{H}}\le {\lambda }_t^{\mathrm{H},\mathrm{p}}\le {\lambda }_{\max }^{\mathrm{H}}\end{array}\right.,(9)$

where ${\lambda }_t^{\text{grid},\mathrm{s}}$ and ${\lambda }_t^{\text{grid},\mathrm{p}}$ are the electricity collection price and the real-time price of the grid and ${\lambda }_{\min }^{\mathrm{H}}$/ ${\lambda }_{\max }^{\mathrm{H}}$ is the lower/upper limit of hydrogen price, $t\in T$, respectively.

To avoid unaffordable energy prices for users in the EHO’s strategy, the bidding prices of electricity and hydrogen should meet the requirements given as follows (Eq. 10).

$\left\{\begin{array}{l}{\displaystyle \sum _{t=1}^T}{\lambda }_t^{\mathrm{e},\mathrm{s}}\le T\cdot {\lambda }_{\text{ave}}^{\mathrm{e},\mathrm{s}}\\ {\displaystyle \sum _{t=1}^T}{\lambda }_t^{\mathrm{h},\mathrm{s}}\le T\cdot {\lambda }_{\text{ave}}^{\mathrm{h},\mathrm{s}}\end{array}\right.,(10)$

where ${\lambda }_{\text{ave}}^{\mathrm{e},\mathrm{s}}$ and ${\lambda }_{\text{ave}}^{\mathrm{h},\mathrm{s}}$ are the average electricity price of electricity and hydrogen, $t\in T$, respectively.

2.2.2 Model of REHP

Based on the bidding strategy of the EHO, the REHP optimizes the electricity–hydrogen scheduling of the adjustable distributed units. The cost function to maximize economic benefits is represented as (Eq. 11).

$\max F^{\text{REHP}}={\displaystyle \sum _{t=1}^T}\left({\lambda }_t^{\mathrm{e},\mathrm{p}}{P}_t^{\text{RP}}+{\lambda }_t^{\mathrm{H},\mathrm{p}}{H}_t^{\text{RP}}\right)\Delta t-C^{\text{RP}},(11)$

where $C^{\text{RP}}$ is the operating cost of the facility of REHP, which can be represented as (Eq. 12).

$C^{\text{RP}}={\displaystyle \sum _{t=1}^T}{\displaystyle \sum }_{x,y}\left(C^x+C^y\right)\Delta t{|}_{x=\text{wt},\text{pv},\text{bt},\text{fc},\text{ev},\text{hv}\begin{array}{l}y=\text{elz},\text{hs},\end{array}}(12)$

where $C^x$/$C^y$ is the operating cost of the distributed unit in the RIEHS, including equipment maintenance cost and labor cost. The operation cost of each distributed unit can be represented as a primary or quadratic function on electrical power/hydrogen (He, et al, 2021; Yuan, et al, 2021; Xu. and Li, 2014), which is shown in Eqs 13–16 with constraints.

$\left\{\begin{array}{c}{C}^x={\displaystyle \sum _{t=1}^T}\left(a^x{\left(P_t^x\right)}^2+b^x{P}_t^x+c^x\right)\Delta t{|}_{x=\text{wt},\text{pv},\text{bt},\text{ev}}\\ C^x={\displaystyle \sum _{t=1}^T}\left(b^x{P}_t^x\right)\Delta t{|}_{x=\text{fc}}\\ C^y={\displaystyle \sum _{t=1}^T}\left(b^y{H}_t^y\right)\Delta t{|}_{y=\text{elz}}\\ C^y={\displaystyle \sum _{t=1}^T}\left(a^y{\left(H_t^y\right)}^2+b^y{H}_t^y+c^{\mathrm{y}}\right)\Delta t{|}_{y=\text{hv},}\end{array}\right.(13)$

$C^{\text{hs}}={\displaystyle \sum _{t=1}^T}\left(b^{\text{hs},\mathrm{d}}{H}_t^{\text{hs},\mathrm{d}}+b^{\text{hs},\mathrm{c}}{H}_t^{\text{hs},\mathrm{c}}\right)\Delta t,(14)$

$\left\{\begin{array}{c}0\le P_t^x\le P_{\max }^x{|}_{x=\text{wt},\text{pv},\text{fc}}\\ 0\le H_t^y\le H_{\max }^y{|}_{y=\text{elz}}\end{array}\right.,(15)$

$\left\{\begin{array}{c}{P}_{\min }^x\le P_t^x\le P_{\max }^x{|}_{x=\text{ev}}\\ H_{\min }^y\le H_t^y\le H_{\max }^y{|}_{y=\text{hv}}\end{array}\right.,(16)$

where $P_t^x$ is the electrical power output of distributed unit x (kW), $H_t^y$ is the hydrogen output of unit y (kg/h), $H_t^{\text{hs},\mathrm{d}}$/ $H_t^{\text{hs},\mathrm{c}}$ is the discharge/charge hydrogen mass of the HS tank (kg/h), $P_{\min }^x$/ $P_{\max }^x$ is the lower/upper adjustable electrical power limit for unit x, $H_{\min }^y$/ $H_{\max }^y$ is the lower/upper adjustable hydrogen limit for unit y, and $a^x$/ $b^x$/ $c^x$ and $a^y$/ $b^y$/ $c^y$ are the secondary/primary/zero cost coefficients of electricity and hydrogen, respectively. The hydrogen storage tank can be operated in the charging mode and discharging mode with primary cost coefficients of $b^{\text{hs},\mathrm{c}}$ and $b^{\text{hs},\mathrm{d}}$, $t\in T$.

The conversion facilities including electrolyzers and fuel cells are used to perform energy conversion in the dispatch strategy. In this work, hydrogen energy is represented in the form of mass. It is assumed that the density of hydrogen is 0.0899 kg/m³ at the standard atmospheric pressure.

The hydrogen mass $H_t^{\text{elz}}$ (kg) produced by the electrolyzer can be calculated as (Eq. 17).

$H_t^{\text{elz}}=\frac{{\eta }^{\text{elz}}{P}_t^{\text{elz}}}{LCV},(17)$

where ${\eta }^{\text{elz}}$ is the electrolyzer efficiency (%) and LCV is the lower calorific value of hydrogen (kW/kg), $t\in T$.

The electrical power generated by fuel cell stacks $P_t^{\text{fc}}$ can be calculated as (Eq. 18).

$P_t^{\text{fc}}={\eta }^{\text{fc}}{H}_t^{\text{fc}}\cdot LCV,(18)$

where ${\eta }^{\text{fc}}$ is the fuel cell stack efficiency (%), $t\in T$.

The model of the battery unit and the HS unit during a dispatch period are shown in Eqs 19–21. The amount of electricity and hydrogen in energy storage is constant during one cycle.

$\left\{\begin{array}{c}{P}_t^{\text{bt}}\cdot \Delta t=CA{P}^{\text{bt}}\left(SO{C}_t^{\text{bt}}-SO{C}_{t-1}^{\text{bt}}\right)\\ P_{\min }^{\text{bt}}\le P_t^{\text{bt}}\le P_{\max }^{\text{bt}},\\ SO{C}_0^{\text{bt}}=SO{C}_T^{\text{bt}}\\ SO{C}_{\min }^{\text{bt}}\le SO{C}_t^{\text{bt}}\le SO{C}_{\max }^{\text{bt}}\end{array}\right.(19)$

where $P_t^{\text{bt}}$ is the power output of the battery unit (kW), $CA{P}^{\text{bt}}$ is the battery capacity (kWh), and $SO{C}_t^{\text{bt}}$ is the state of charge (SoC) of the battery (%). In this work, a negative value of $P_t^{\text{bt}}$ means that the battery is operated under charging state, while a positive value means the battery is operated under discharging state. $P_{\min }^{\text{bt}}$ is the maximum charging power output of the battery unit and $P_{\max }^{\text{bt}}$ is the maximum discharging power output, $t\in T$.

$\left\{\begin{array}{c}{H}_t^{\text{hs}}=H_t^{\text{hs},\mathrm{d}}-H_t^{\text{hs},\mathrm{c}}\\ H_t^{\text{hs}}\cdot \Delta t=CA{P}^{\text{hs}}\left(SO{S}_t^{\text{hs}}-SO{S}_{t-1}^{\text{hs}}\right),\\ SO{S}_0^{\text{hs}}=SO{S}_T^{\text{hs}}\\ SO{S}_{\min }^{\text{hs}}\le SO{S}_t^{\text{hs}}\le SO{S}_{\max }^{\text{hs}}\end{array}\right.(20)$

$\left\{\begin{array}{c}{H}_t^{\text{hs},\mathrm{d}}=H_t^{\text{hsl}}+H_t^{\text{hv}}+H_t^{\text{fc}}\\ H_t^{\text{hs},\mathrm{c}}=H_t^{\text{elz}},\\ 0\le H_t^{\text{hs},\mathrm{d}}\le H_{\max }^{\text{hs},\mathrm{d}}\\ 0\le H_t^{\text{hs},\mathrm{c}}\le H_{\max }^{\text{hs},\mathrm{c}}\end{array}\right.(21)$

where $H_t^{\text{hs}}$ is the output of the HS unit (kg/h), $CA{P}^{\text{hs}}$ is the capacity of the HS tank (kg), $SO{S}_t^{\text{hs}}$ is the state level of storage (SoS) of the HS unit (%) (Pan et al., 2021), and $H_t^{\text{hsl}}$ is the hydrogen supplied to the system hydrogen load from the HS unit, $t\in T$.

The electricity and hydrogen sold by REHP to the EHO can be represented as (Eq. 22).

$\left\{\begin{array}{l}{H}_t^{\text{RP}}=H_t^{\text{hsl}}\\ P_t^{\text{RP}}=P_t^{\text{wt}}+P_t^{\text{pv}}+P_t^{\text{bt}}+P_t^{\text{fc}}-P_t^{\text{elz}}-P_t^{\text{ev}.}\end{array}\right.(22)$

2.2.3 Model of the LA

The LA optimizes the electrical power on ISEL based on the price given by the EHO. The objective function is to maximize the comprehensive benefits indicating the difference between the user utility and the energy cost, as shown in (Eq. 23).

$\max F^{\text{LA}}=U^{\text{LA}}-{\displaystyle \sum _{t=1}^T}\left({\lambda }_t^{\mathrm{e},\mathrm{s}}{P}_t^{\mathrm{L}}+{\lambda }_t^{\mathrm{H},\mathrm{s}}{H}_t^{\mathrm{L}}\right)\Delta t,(23)$

where $U_t^{\text{LA}}$ is the utility function indicating the satisfaction of the user in purchasing electrical power and hydrogen (Wei et al., 2017), which can be represented as (Eq. 24).

$U^{\text{LA}}={\displaystyle \sum _{t=1}^T}\left({\beta }^{\mathrm{e}}{P}_t^{\mathrm{L}}-\frac{{\alpha }^{\mathrm{e}}}{2}{\left(P_t^{\mathrm{L}}\right)}^2+{\beta }^{\mathrm{H}}{H}_t^{\mathrm{L}}-\frac{{\alpha }^{\mathrm{H}}}{2}{\left(H_t^{\mathrm{L}}\right)}^2\right)\Delta t,(24)$

where ${\beta }^{\mathrm{e}}$/ ${\alpha }^{\mathrm{e}}$/ ${\beta }^{\mathrm{H}}$/ ${\alpha }^{\mathrm{H}}$ is the co-efficient of user utility.

The electrical load ($P_t^{\mathrm{L}}$) is composed of SEL ($P_t^{\text{sel}}$) and ISEL ($P_t^{\text{isel}}$), as shown in (Eq. 25). The SEL is the mandatory power demand, such as that in data center, hospital, and critical industrial loads. Different from SEL, the ISEL can be flexibly controlled according to real-time price to improve the economic benefits. The total amount of ISEL in one scheduling cycle remains the same, as shown in (Eq. 26).

$P_t^{\mathrm{L}}=P_t^{\text{isel}}+P_t^{\text{sel}},(25)$

${\displaystyle \sum _{t=1}^T}{P}_t^{\text{isel}}\cdot \Delta t={\displaystyle \sum _{t=1}^T}\left(P_t^{\mathrm{L}}-P_t^{\text{sel}}\right)\cdot \Delta t.(26)$

The electricity consumption habits of users may be changed by the price-based demand response process. The adjustment in ISEL should be below its upper limit $P_{\max }^{\text{isel}}$, as shown in (Eq. 27).

$P_t^{\text{isel}}\le P_{\max }^{\text{isel}}.(27)$

2.3 Network transmission constraint

For any transmission branch m-n in the network, the power flow capacity constraint can be simplified and represented in DC power flow as shown in Eqs 28, 29. This simplification allows for efficient computation and analysis of power flows in a grid-connected regional system with different level load capacities.

$P_{\min }^{mn}\le B_t^{mn}\left({\delta }_t^m-{\delta }_t^n\right)\le P_{\max }^{mn},\forall m,n\in {\mathrm{\Lambda }}^N,(28)$

$P_{\min }^{mn}\le {\displaystyle \sum }_{x\in X}{Y}_{mn-x}{P}_t^x-{\displaystyle \sum }_{l\in L}{Y}_{mn-l}{P}_t^{\mathrm{L}}\le P_{\max }^{mn},\forall m,n\in {\mathrm{\Lambda }}^N,(29)$

where ${\mathrm{\Lambda }}^N$ identifies the set of buses of the electrical network, $B_t^{mn}$ is the line susceptance from bus m to bus n, ${\delta }_t^{\sim }$ is the nodal phase angle for node ∼, and $P_{\max }^{mn}$/$P_{\min }^{mn}$ is the upper/lower power transmission bound of branch m-n. In Eq. 29, $Y_{mn-\sim }$ is the power transfer distribution factor (PTDF) for the branch m-n, which can be calculated by the method in (Altomar and Passos Filho, 2022).

3 Stackelberg equilibrium of electricity–hydrogen market game

3.1 Development of Stackelberg games in the RIEHS

In a Stackelberg game, the followers perform decision-making processes in reaction to the leader’s decision based on their own objectives. As shown in Figure 3, the Stackelberg game-based energy trading involves the following two steps: 1) EHO sets the electricity–hydrogen bidding strategy to maximize its own benefits according to the market information and 2) based on the price decision from the EHO, REHP performs electricity–hydrogen optimal scheduling and LA performs ISEL optimization. The Stackelberg game model is formulated as (Eqs 30, 31)

$G=\left\{N,{\rho }^{\text{EHO}},{\delta }^{\text{REHP}},{\delta }^{\text{LA}},F^{\text{EHO}},F^{\text{REHP}},F^{\text{LA}}\right\},(30)$

$\left\{\begin{array}{c}N=\left\{\text{EHO},\text{REHP},\text{LA}\right\}\\ {\rho }^{\text{EHO}}=\left\{{\mathit{\lambda }}^{\mathrm{e},\mathrm{p}},{\mathit{\lambda }}^{\mathrm{H},\mathrm{p}},{\mathit{\lambda }}^{\mathrm{e},\mathrm{s}},{\mathit{\lambda }}^{\mathrm{H},\mathrm{s}}\right\}\\ {\delta }^{\text{REHP}}=\left\{{\mathit{P}}^x,{\mathit{H}}^y\right\}{|}_{x=\text{wt},\text{pv},\text{bt},\text{fc},\text{ev};y=\text{elz},\text{hsl},\text{hv}}\\ {\delta }^{\text{LA}}=\left\{{\mathit{P}}^{\text{isel}}\right\}\end{array}\right.,(31)$

FIGURE 3

FIGURE 3. Stackelberg equilibrium-based energy trading process.

which consists of the participants, strategies, and profits.

1) N is the set of market game participants (EHO, REHP, and LA).

2) ${\rho }^{\text{EHO}}$/ ${\delta }^{\text{REHP}}$/ ${\delta }^{\text{LA}}$ is the strategy set of EHO/REHP/LA, where the elements ${\mathit{\lambda }}^{\mathrm{e},\mathrm{p}}$/ ${\mathit{\lambda }}^{\mathrm{H},\mathrm{p}}$/ ${\mathit{\lambda }}^{\mathrm{e},\mathrm{s}}$/ ${\mathit{\lambda }}^{\mathrm{H},\mathrm{s}}$ in ${\rho }^{\text{EHO}}$ is the vector of electricity–hydrogen import and export price ${\lambda }^{\mathrm{e},\mathrm{p}}$/ ${\lambda }^{\mathrm{H},\mathrm{p}}$/ ${\lambda }^{\mathrm{e},\mathrm{s}}$/ ${\lambda }^{\mathrm{H},\mathrm{s}}$ of the EHO, the elements ${\mathit{P}}^x$/ ${\mathit{H}}^y$ in ${\delta }^{\text{REHSO}}$ is the response vector of the adjustable electrical/hydrogen distributed unit in the RIEHS, and the element ${\mathit{P}}^{\text{isel}}$ in ${\delta }^{\text{LA}}$ is the vector of ISEL.

3) $F^{\text{EHO}}$, $F^{\text{REHP}}$, and $F^{\text{LA}}$ are the profit functions of participants, as shown in (Eqs 1, 11, and 23).

By the chosen strategies, the objectives of EHO, REHP, and LA are to maximize the economic benefits, as shown in Eqs 1, 11, and the comprehensive benefits, as shown in Eq. 23, respectively. The Stackelberg equilibrium is one feasible solution to the game, where the EHO obtains its optimal bidding strategy with the best energy scheduling responses of REHP and LA. The set of strategies $\left\{{\rho }^{\text{EHO}*},{\delta }^{\text{REHP}*},{\delta }^{\text{LA}*}\right\}$ that constitutes Stackelberg equilibrium satisfies (Eq. 32), where any participant fails to gain more profits by unilaterally changing market decision (Lee. et al., 2015). The existence and uniqueness of Stackelberg equilibrium is proved in Appendix.

$\left\{\begin{array}{c}{F}^{\text{EHO}}\left({\rho }^{\text{EHO}},{\delta }^{\text{REHP}*},{\delta }^{\text{LA}*}\right)\le F^{\text{EHO}}\left({\rho }^{\text{EHO}*},{\delta }^{\text{REHP}*},{\delta }^{\text{LA}*}\right)\\ F^{\text{REHP}}\left({\rho }^{\text{EHO}*},{\delta }^{\text{REHP}},{\delta }^{\text{LA}*}\right)\le F^{\text{REHP}}\left({\rho }^{\text{EHO}*},{\delta }^{\text{REHP}*},{\delta }^{\text{LA}*}\right).\\ F^{\text{LA}}\left({\rho }^{\text{EHO}*},{\delta }^{\text{REHP}*},{\delta }^{\text{LA}}\right)\le F^{\text{LA}}\left({\rho }^{\text{EHO}*},{\delta }^{\text{REHP}*},{\delta }^{\text{LA}*}\right)\end{array}\right.(32)$

In addition, REHP and LA only need to collect the price data of the EHO and feedback their energy data, which effectively avoids the leakage of information and can protect the business privacy of the followers.

3.2 Establishment of the optimal bidding mechanism

The optimal bidding mechanism could be established by solving G in Eq. 30, and the energy management strategy can be further developed. Traditional centralized optimization methods require detailed information about all participants, such as equipment parameters and energy use preferences. However, in a competitive electricity–hydrogen market, the information of each participant is private. Each objective function should be optimized separately.

The bidding decision of the leader is a non-linear optimization problem, which can be solved by the differential evolutionary algorithm (DEA) (Yang, et al., 2008). If the optimization objectives of the followers are quadratic functions, the quadratic programming approach can be used to solve the problem. In this work, a differential evolutionary algorithm combining quadratic programming (DEA-QP) is employed to solve the proposed Stackelberg equilibrium model. The flowchart of the algorithm is shown in Figure 4.

FIGURE 4

FIGURE 4. Flowchart of the DEA-QP algorithm.

4 Case study

4.1 Case description

To analyze the effectiveness of the proposed energy management strategy, two comparative demonstration cases are studied.

• Case I: EHO, REHP, and LA all engage in energy trading and participate in the market game.

• Case II: EHO does not engage in energy trading, and there is no market game in the electricity–hydrogen market.

The tested RIEHS expanded combining the IEEE 6-bus power system and a 1-node hydrogen system is studied, as shown in Figure 5 (Fang et al., 2021a). The network data can be seen in (Peng et al., 2015). The forecasted output power for WT, PV, and electricity and hydrogen loads on a typical day are given in Figure 6 from (Energidataservice, 2022; Energinet, 2022). The electric load peak happens at 17:00–21:00, and the hydrogen load peak happens at 10:00–11:00 and 15:00–16:00. It is assumed that the ISEL is 20% of the total electrical load and the maximum adjustable amount of ISEL is 180 kW. The economic and technical parameters of the RIEHS are listed in Tables 1, 2. The time step is 1 h.

FIGURE 5

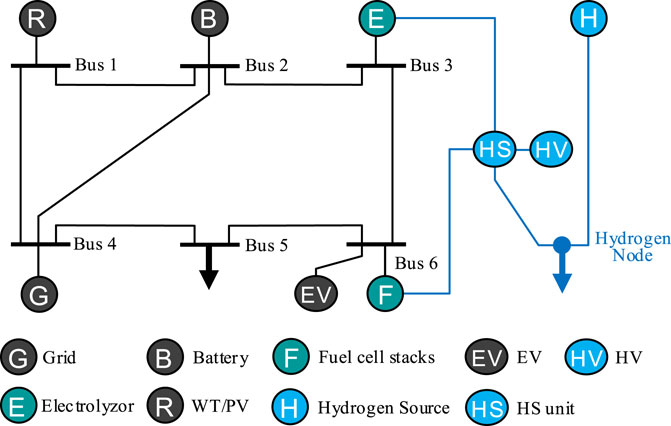
FIGURE 5. Network topology of the test system (Fang et al., 2021b).

FIGURE 6

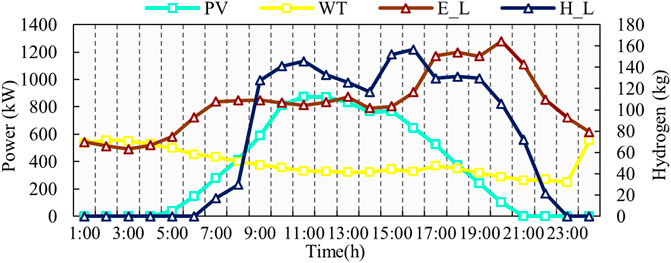
FIGURE 6. Power profile of renewable energies, electrical, and hydrogen load (Energidataservice, 2022; Energinet, 2022).

TABLE 1

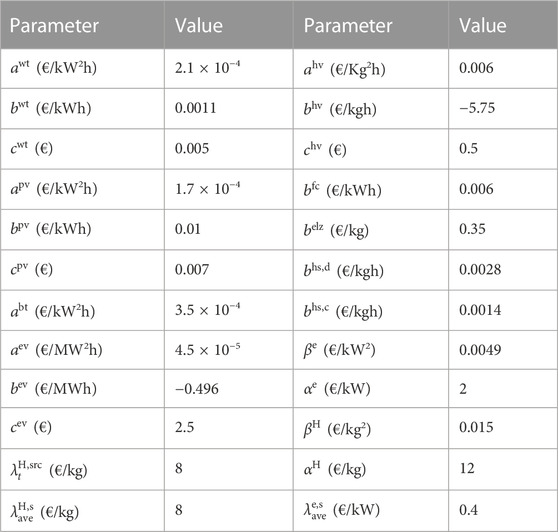
TABLE 1. Economic parameters of the RIEHS (Xu and Li, 2014; Binetti et al., 2014).

TABLE 2

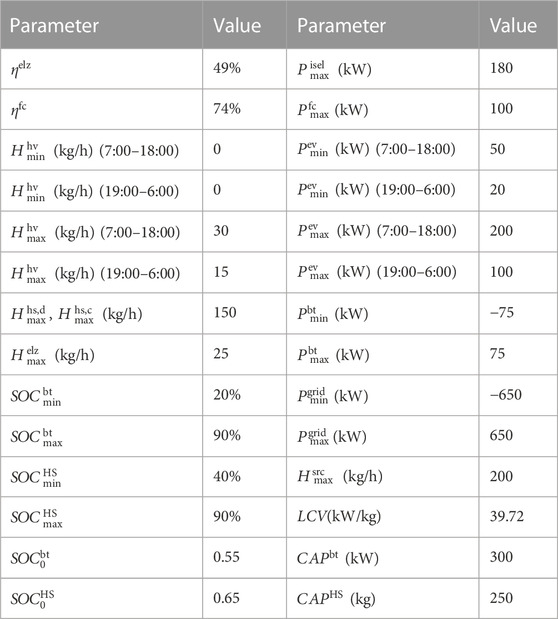
TABLE 2. Technical parameters of the RIEHS (Valverde et al, 2013; Xu and Li, 2014).

The computation is simulated in MATLAB by a workstation with an AMD Ryzen 4650 U CPU @ 2.60 GHz with 16.00 GB RAM. The total computation time is 3741.8 s.

4.2 Simulation analysis

4.2.1 Comparative analysis of tested cases

Table 3 shows the optimized results with and without the EHO. In case II, REHP and LA lose the flexible energy prices from the EHO and have to trade directly with the upper networks. It can be seen that the economic benefits of REHP is decreased from 2842.1€ to 2651.5€ without the EHO, and the comprehensive benefit of the LA is decreased from 13154.7€ to −2865.9€. The proposed energy management strategy produces extra 7.1% economic benefits to the REHP and increases the comprehensive benefit to the LA by 16,020.7€. In terms of retail prices, the 24-h average electricity purchased price of LA decreases by 17.3% and the 24-h average electricity sale price of REHP increases by 60% compared with Case I. It indicates that both REHP and LA can earn large amounts of benefits from electricity transactions. Different from electricity, the average hydrogen sales price for REHP decreases by 2%, and the average hydrogen purchase price for the LA increases by 6.5%. The total hydrogen production of the RIEHS for 24 h is 121.7 kg in Case I and decreases to 119.6 kg in Case II. Although the profits gained in the hydrogen transaction are lower, the bidding mechanism from the EHO incentivizes the RIEHS to increase hydrogen production by 1.8%. Correspondingly, the system hydrogen consumption is also incentivized.

TABLE 3

TABLE 3. RIEHS optimization comparison.

Table 4 shows the comparison of the percentage of renewable energies for hydrogen production ($P^{\text{elz}}/\left(P^{\text{wt}}+P^{\text{pv}}\right)$) during 24 h (Wang et al., 2022). By using the Stackelberg game model, the percentage of total renewable energies for hydrogen production (53.2%) is almost equal to that in the case with high hydrogen revenue (53.8%) and is higher than that in the case with moderate and low hydrogen revenue (22.7% and 12.1%). The proposed strategy can promote the penetration of clean energy.

TABLE 4

TABLE 4. Comparison of percentage of renewable energies for hydrogen production (Wang et al., 2022b).

4.2.2 Analysis of Stackelberg game

Figure 7 shows the DEA-QP iterative process that indicates the economic benefit obtained by the EHO, REHP, and LA. The optimization results validate the proposed model. Meanwhile, the Stackelberg equilibrium is reached, where all stakeholders obtain the optimal economic benefit with unchanged market decisions. The economic benefits of the EHO and REHP are 8173.7€ and 2842.1€, respectively. The comprehensive economic benefit of the LA is 13154.8€.

FIGURE 7

FIGURE 7. Economic benefit iteration of DEA-QP.

Figures 8A, B shows the electricity and hydrogen bidding strategy (blue curve) of the EHO. For the electricity pricing in Figure 8A, the export price (red curve) is not always higher than the import price (blue curve). It means that the EHO may obtain lower profits at a certain time window. The typical ones are 1:00 and 21:00 in Figure 8A. At 1:00, the export price for electricity is set at the lower limit due to lower demand. At 20:00, the import price reaches the upper limit, which means that the EHO supplies the load demand at the maximum cost. It incentivizes REHP to generate more power to obtain economic benefits. At 10:00 and 16:00, the EHO imports electricity at the lowest price and sells it to the LA at higher price to obtain the highest economic benefits. As shown in Figure 8B, the hydrogen bidding strategy shows similar commercial characteristics to the electricity market.

FIGURE 8

FIGURE 8. Hourly electricity–hydrogen bidding price of the EHO. (A) Electricity and (B) hydrogen.

Figure 9 shows the electrical load power profile of the LA based on dynamic electricity price from the EHO. Under the incentive of the electricity price, IESL moves to periods of low tariffs to reduce the total cost of electricity. Compared with the electrical load curve, the peak value of electricity demand during 17:00–21:00 is decreased significantly, while the valley value of electricity demand at 0:00–6:00 is increased due to LA optimization. Correspondingly, the fluctuation of the electrical load is smoothed.

FIGURE 9

FIGURE 9. Electrical load power profile of the LA with and without optimization.

Figures 10, 11 show the electricity–hydrogen scheduling of adjustable distributed units in the RIEHS. As shown in Figure 10, the electrolysis is operated during 1:00–17:00 and 23:00–24:00, except in the evening peak hours during 19:00–23:00. The fuel cell is operated only at 21:00 with power output 49.87 kW to supplement the power shortage due to PV shortage and load peak at night. Moreover, the additional benefits attract the EV unit to be operated continuously during the day. The energy consumption of EV loads is reduced at 20:00 and 21:00 due to relatively high load demands of the system and electricity prices. It can be seen from Figure 11 that the EHO can import hydrogen to supply hydrogen demands during the daytime. The HV unit is operated with minimum hydrogen consumption. At 24:00 a.m. and 1:00–6:00 a.m., the electrolyzer is operated to refuel the HS unit.

FIGURE 10

FIGURE 10. Optimal electricity scheduling in the RIEHS.

FIGURE 11

FIGURE 11. Optimal hydrogen scheduling in the RIEHS.

Figure 12 shows the SoC of the battery (%) and the SoS of the HS unit (%). To deal with the evening electricity peak, the battery is operated in a smooth charging state from 0:00–18:00. The battery reaches its maximum charging level at 18:00 and starts to supply power to the RIEHS until 22:00 (blue curve). The SoS of the HS unit is decreased at 8:00–19:00, which means that the hydrogen output of the HS unit is higher than electrolyzer hydrogen production. The HS unit is operated under storage state during 0:00–7:00 and 23:00–24:00 (red curve).

FIGURE 12

FIGURE 12. Storage state of the energy storage unit.

5 Conclusion

This paper presents an energy management strategy based on Stackelberg game for the RIEHS. The electricity–hydrogen transaction mode among the EHO, REHP, and LA is first proposed, and the optimization models of the three market participants are established. Then, the bidding mechanism of the electricity–hydrogen market is formulated based on the Stackelberg game to optimize the market strategy of all the players. The Stackelberg equilibrium solution for the proposed energy management strategy is derived by the DEA-QP approach. The algorithm has a good convergence considering the business privacy of REHP and LA. Simulation results show that the proposed bidding mechanism can adequately analyze the market behavior of EHO, REHP, and LA, which thus validates the effectiveness of the proposed energy management strategy. The proposed electricity–hydrogen management strategy with the EHO is able to optimize the bidding price and the energy scheduling in the RIEHS and produces economic benefits to REHP and LA. Moreover, the proposed strategy can increase the utilization of hydrogen through market-based mechanisms (He et al., 2019).

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

QW, YW, and ZC contributed to conception and design of the study. QW organized the database and performed the simulation. YW conceptualized this study and performed the statistical analysis. QW and YW wrote the first draft of the manuscript. ZC supervised this work and attributed to writing–reviewing and editing the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This study is supported by the State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources (Grant NO. LAPS21021).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Altomar, M. B., and Passos Filho, J. A. (2022). Maximizing wind power penetration through a new approach of the linear power transfer distribution factors. Electr. Eng. 104 (3), 1821–1829. doi:10.1007/s00202-021-01422-2

CrossRef Full Text | Google Scholar

Anoh, K., Maharjan, S., Ikpehai, A., Zhang, Y., and Adebisi, B. (2020). Energy peer-to-peer trading in virtual microgrids in smart grids: A game-theoretic approach. IEEE Trans. Smart Grid 11 (2), 1264–1275. doi:10.1109/TSG.2019.2934830

CrossRef Full Text | Google Scholar

Bae, S., and Park, S. (2019). Comparison between seller and buyer pricing systems for energy trading in microgrids. IEEE Access 7, 54084–54096. doi:10.1109/ACCESS.2019.2912758

CrossRef Full Text | Google Scholar

Binetti, G., Davoudi, A., Lewis, F. L., Naso, D., and Turchiano, B. (2014). Distributed consensus-based economic dispatch with transmission losses. IEEE Trans. Power Syst. 29 (4), 1711–1720. doi:10.1109/TPWRS.2014.2299436

CrossRef Full Text | Google Scholar

El-Taweel, N. A., Khani, H., and Farag, H. E. (2018). Hydrogen storage optimal scheduling for fuel supply and capacity-based demand response program under dynamic hydrogen pricing. IEEE Trans. Smart Grid 10 (4), 4531–4542. doi:10.1109/TSG.2018.2863247

CrossRef Full Text | Google Scholar

Energidataservice, dk (2022). Tso-electricity. Available:https://www.energidataservice.dk/(Accessed August 22, 2022).

Google Scholar

Energinet, dk (2022). Download of market data. Available:https://en.energinet.dk/(Accessed June 3, 2022).

Google Scholar

Erdiwansyah, M., Husin, H., Nasaruddin, M. Z., et al. (2021). A critical review of the integration of renewable energy sources with various technologies. Prot. Control Mod. Power Syst. 6 (1), 37–54. doi:10.1186/s41601-021-00181-3

CrossRef Full Text | Google Scholar

Fang, S., Zhang, S., Zhao, T., and Liao, R. (2021a). Optimal power-hydrogen networked flow scheduling for residential carpark with convex approximation. IEEE Trans. Ind. Appl. 58 (2), 2751–2759. doi:10.1109/TIA.2021.3095045

CrossRef Full Text | Google Scholar

Fang, S., Zhang, S., Zhao, T., and Liao, R. (2021b). Optimal power-hydrogen networked flow scheduling for residential carpark with convex approximation. IEEE Trans. Ind. Appl. 58 (2), 2751–2759. doi:10.1109/TIA.2021.3095045

CrossRef Full Text | Google Scholar

Fang, X., Wang, Y., Dong, W., Yang, Q., and Sun, S. (2023). Optimal energy management of multiple electricity-hydrogen integrated charging stations. Energy 262, 125624. doi:10.1016/j.energy.2022.125624

CrossRef Full Text | Google Scholar

Han, S., and Kim, J. (2019). A multi-period MILP model for the investment and design planning of a national-level complex renewable energy supply system. Renew. Energy 141, 736–750. doi:10.1016/j.renene.2019.04.017

CrossRef Full Text | Google Scholar

He, G., Mallapragada, D. S., Bose, A., Heuberger, C. F., and Gençer, E. (2021). Hydrogen supply chain planning with flexible transmission and storage scheduling. IEEE Trans. Sustain. Energy 12 (3), 1730–1740. doi:10.1109/TSTE.2021.3064015

CrossRef Full Text | Google Scholar

He, Y., Wang, W., and Wu, X. (2019). Multi-agent based fully distributed economic dispatch in microgrid using exact diffusion strategy. IEEE Access 8, 7020–7031. doi:10.1109/ACCESS.2019.2959600

CrossRef Full Text | Google Scholar

Kim, J., Lee, J., Park, S., and Choi, J. K. (2022). Power scheduling scheme for a charging facility considering the satisfaction of electric vehicle users. IEEE Access 10, 25153–25164. doi:10.1109/access.2022.3151355

CrossRef Full Text | Google Scholar

Lee, J., Guo, J., Choi, J. K., and Zukerman, M. (2015). Distributed energy trading in microgrids: A game-theoretic model and its equilibrium analysis. IEEE Trans. Ind. Electron. 62 (6), 3524–3533. doi:10.1109/TIE.2014.2387340

CrossRef Full Text | Google Scholar

Li, Y., Jin, X., Wang, G., Ren, Y., Tan, H., and Li, N. (2022). Construction and application of a carbon emission model for China’s coal production enterprises and result analysis. Front. Energy Res. 10, 889877. doi:10.3389/fenrg.2022.889877

CrossRef Full Text | Google Scholar

Liu, H., Li, J., Ge, S., He, X., Li, F., and Gu, C. (2020). Distributed day-ahead peer-to-peer trading for multi-microgrid systems in active distribution networks. IEEE Access 8, 66961–66976. doi:10.1109/ACCESS.2020.2983645

CrossRef Full Text | Google Scholar

Liu, N., He, L., Yu, X., and Ma, L. (2017). Multiparty energy management for grid-connected microgrids with heat-and electricity-coupled demand response. IEEE Trans. Ind. Inf. 14 (5), 1887–1897. doi:10.1109/TII.2017.2757443

CrossRef Full Text | Google Scholar

Liu, S., Zhou, C., Guo, H., Shi, Q., Song, T. E., Schomer, I., et al. (2021). Operational optimization of a building-level integrated energy system considering additional potential benefits of energy storage. Prot. Control Mod. Power Syst. 6 (1), 4–10. doi:10.1186/s41601-021-00184-0

CrossRef Full Text | Google Scholar

Liu, W., Gu, W., Wang, J., Yu, W., and Xi, X. (2018). Game theoretic non-cooperative distributed coordination control for multi-microgrids. IEEE Trans. Smart Grid 9 (6), 6986–6997. doi:10.1109/TSG.2018.2846732

CrossRef Full Text | Google Scholar

Long, T., and Jia, Q. S. (2021). Joint optimization for coordinated charging control of commercial electric vehicles under distributed hydrogen energy supply. IEEE Trans. Control Syst. Technol. 30 (2), 835–843. doi:10.1109/TCST.2021.3070482

CrossRef Full Text | Google Scholar

Luosong, J., Weidong, L., Cheng, C., Jingping, J., and Wei, W. (2022). Research on the internal and external monitoring mechanism of the electricity market in the spot market-from the perspective of evolutionary game theory. Front. Energy Res. 726. doi:10.3389/fenrg.2022.913032

CrossRef Full Text | Google Scholar

Mediwaththe, C. P., Stephens, E. R., Smith, D. B., and Mahanti, A. (2017). Competitive energy trading framework for demand-side management in neighborhood area networks. IEEE Trans. Smart Grid 9 (5), 4313–4322. doi:10.1109/TSG.2017.2654517

CrossRef Full Text | Google Scholar

Mishra, M. K., and Parida, S. K. (2020). A game theoretic approach for demand-side management using real-time variable peak pricing considering distributed energy resources. IEEE Syst. J. 16 (1), 144–154. doi:10.1109/JSYST.2020.3033128

CrossRef Full Text | Google Scholar

Pan, G., Gu, W., Lu, Y., Qiu, H., Lu, S., and Yao, S. (2020). Accurate modeling of a profit-driven power to hydrogen and methane plant toward strategic bidding within multi-type markets. IEEE Trans. Smart Grid 12 (1), 338–349. doi:10.1109/TSG.2020.3019043

CrossRef Full Text | Google Scholar

Pardalos, P. M., and Vavasis, S. A. (1991). Quadratic programming with one negative eigenvalue is NP-hard. J. Glob. Optim. 1 (1), 15–22. doi:10.1007/bf00120662

CrossRef Full Text | Google Scholar

Peng, J. C., Zhou, J., and Jiang, H. (2015). A liability division method for harmonic pollution based on line-transferred power components. J. Power Energy Eng. 3, 262–268. doi:10.4236/jpee.2015.34035

CrossRef Full Text | Google Scholar

Sharma, G., Narayanan, K., Adefarati, T., and Sharma, S. (2022). Frequency regularization of a linked wind–diesel system using dual structure fuzzy with ultra-capacitor. Prot. Control Mod. Power Syst. 7 (1), 12–19. doi:10.1186/s41601-022-00233-2

CrossRef Full Text | Google Scholar

Smith, J. M. (1982). Evolution and the theory of games. Cambridge, United Kingdom: Cambridge University Press.

Google Scholar

Valverde, L., Rosa, F., and Bordons, C. (2013). Design, planning and management of a hydrogen-based microgrid. IEEE Trans. Ind. Inf. 9 (3), 1398–1404. doi:10.1109/tii.2013.2246576

CrossRef Full Text | Google Scholar

Wang, C., Hao, Y., Han, G., Zhou, C., and Wang, C. July 2022b “Coordinated scheduling of integrated energy systems with hydrogen electrolyzer units,” in Proceedings of the 2022 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), Shanghai, China.

Google Scholar

Wang, Q., Wang, Y., and Chen, Z. (2022a). Day-ahead economic optimization scheduling model for electricity–hydrogen collaboration market. Energy Rep. 8, 1320–1327. doi:10.1016/j.egyr.2022.08.128

CrossRef Full Text | Google Scholar

Wei, F., Jing, Z. X., Wu, P. Z., and Wu, Q. H. (2017). A Stackelberg game approach for multiple energies trading in integrated energy systems. Appl. energy 200, 315–329. doi:10.1016/j.apenergy.2017.05.001

CrossRef Full Text | Google Scholar

Wen, T., Zhang, Z., Lin, X., Li, Z., Chen, C., and Wang, Z. (2020). Research on modeling and the operation strategy of a hydrogen-battery hybrid energy storage system for flexible wind farm grid-connection. IEEE Access 8, 79347–79356. doi:10.1109/access.2020.2990581

CrossRef Full Text | Google Scholar

Xu, Y., and Li, Z. (2014). Distributed optimal resource management based on the consensus algorithm in a microgrid. IEEE Trans. Ind. Electron. 62 (4), 2584–2592. doi:10.1109/TIE.2014.2356171

CrossRef Full Text | Google Scholar

Yang, G. Y., Dong, Z. Y., and Wong, K. P. (2008). A modified differential evolution algorithm with fitness sharing for power system planning. IEEE Trans. Power Syst. 23 (2), 514–522. doi:10.1109/tpwrs.2008.919420

CrossRef Full Text | Google Scholar

Yuan, W., Wang, Y., and Chen, Z. (2021). New perspectives on power control of AC microgrid considering operation cost and efficiency. IEEE Trans. Power Syst. 36 (5), 4844–4847. doi:10.1109/TPWRS.2021.3080141

CrossRef Full Text | Google Scholar

Zhang, B., Dou, C., Yue, D., Park, J. H., and Zhang, Z. (2021). Attack-defense evolutionary game strategy for uploading channel in consensus-based secondary control of islanded microgrid considering DoS attack. IEEE Trans. Circuits Syst. I Regul. Pap. 69 (2), 821–834. doi:10.1109/TCSI.2021.3120080

CrossRef Full Text | Google Scholar

Appendix

Theorem 1:. A unique Stackelberg equilibrium always exists in the proposed Stackelberg game G among EHO, REHP, and LA.

Proof:

1) It is obvious from (Eqs 1, 11, 25) that the problems of EHO, REHP, and LA all have strictly concave objective functions with continuous and non-empty solution set.

2) For a given bidding strategy $\left\{{\rho }^{\text{EHO},0}\right\}$, the optimization problem of REHP and LA is a quadratic programming process with concave functions, where a unique $\left\{{\delta }^{\text{REHP}*,0},{\delta }^{\text{LA}*,0}\right\}$ always exists (Pardalos, P. M., and Vavasis, S. A., 1991). Therefore, both REHP and LA will find a solution set that maximizes their benefit and utility.

3) As illustrated in Kim J. et al. (2022), by substituting an optimal strategy set $\left\{{P_t}^{x,0},{H_t}^{y,0},P_t^{\text{isel},0}\right\}$ in (1), the second-order partial derivative of $F_t^{\text{EHO}}$ with respect to ${\lambda }^{\mathrm{e},\mathrm{s}}$, ${\lambda }^{\mathrm{H},\mathrm{s}}$, ${\lambda }^{\mathrm{e},\mathrm{p}}$, and ${\lambda }^{\mathrm{H},\mathrm{p}}$ can be obtained, respectively. In addition, the Hessian matrix H of $F_t^{\text{EHO}}$ can be represented as follows (33), which is a negative definite matrix with positive $w^{\sim }$ and ${\mathrm{\Theta }}^{\sim }$. Then, we propose the optimal bidding strategy $\left\{{\rho }^{\text{EHO}*,0}\right\}$ is unique.

$H=\left\{\begin{array}{cccc}-\frac{1}{w^{\mathrm{e}.\mathrm{s}}\sum {\mathrm{\Theta }}^x}& 0& 0& 0\\ 0& -\frac{1}{w^{\mathrm{H}.\mathrm{s}}\sum {\mathrm{\Theta }}^y}& 0& 0\\ 0& 0& -\frac{1}{w_1^{\mathrm{e},\mathrm{p}}\sum {\mathrm{\Theta }}^x}& -\frac{1}{w_2^{\mathrm{e},\mathrm{p}}\sum {\mathrm{\Theta }}^y}\\ 0& 0& -\frac{1}{w_1^{\mathrm{H},\mathrm{p}}\sum {\mathrm{\Theta }}^x}& -\frac{1}{w_2^{\mathrm{H},\mathrm{p}}\sum {\mathrm{\Theta }}^x}-\frac{1}{w_3^{\mathrm{H},\mathrm{p}}\sum {\mathrm{\Theta }}^y}\end{array}\right\}.(33)$

Thus, there exists a unique Stackelberg equilibrium and Theorem 1 is proved.