A survey on voltage stability indices for power system transmission and distribution systems

Voltage stability is a critical aspect of power system operation, ensuring the reliable and efficient delivery of electrical energy to consumers. Recently, voltage stability in the power system has received much attention. The primary cause of voltage instability is the lack of real and reactive power generation to cope with the continuous demand increment. Maintaining voltage stability while planning, controlling, and assessing the system’s security is a difficult task for power system engineers. From knowledge of past incidents, a lack of reactive power is identified as the primary cause of voltage instability, which may further lead to the total collapse of the system. The importance of voltage stability assessment is essential to maintain the integrity of power systems. It helps prevent voltage instability, which can lead to cascading failures and widespread outages. This paper uses various parameters, including load demand, generator capacity, and system impedance, to develop voltage stability indices (VSIs). The paper mainly focuses on the idea of VSIs that have been developed in order to monitor and control the criticality of the power system. The voltage stability indices for transmission and distributed systems, as well as their subclasses, are thoroughly reviewed in this study. Furthermore, traditional voltage stability methods, as well as various software tools for monitoring the voltage stability problems, are also discussed. In addition, the development of VSIs and its related concepts are clearly described in this paper. This comprehensive survey provides a decent groundwork for future work in this area, and assists professionals in selecting the optimal VSI for various applications. Moreover, it provides a concise overview of methods and the importance of voltage stability assessment in both transmission and distribution systems.

1 Introduction

The present society needs an uninterruptable and reliable power supply as an essential resource. However, with an incessant growth in power demand, current power systems have been overstressed in delivering real and reactive power. Insufficient reactive power management may lead to voltage collapse and complete blackout of the system. Hence, continuous assessment of the voltage stability of the system should be carried out so as to take preventive measures to avoid voltage collapse. Comprehensive research on voltage stability assessment (VSA) has been performed (Ajjarapu, 1995; Ajjarapu and Lee, 1998; Amroune, 2021; Badru and Taylor, 2000; Boričić et al., 2021). In (Disturbance Analysis Working Group and others, 1979; Li et al., 2023; Liang et al., 2022; Mahseredjian and Alvarado, 1997; MathWorks and Inc, 1993), the cause for the blackouts that occurred in the past decades has been analyzed, and it was identified that reactive power deficiency is the major cause of the blackout. Moreover, sudden variations in atmospheric conditions, poor control over the voltage and frequency of the system, overloading on transmission networks, and transmission congestion were some of the other issues listed as influencing factors for the voltage collapse leading to blackout (Ajjarapu, 2007). Here, reactive power control and voltage limits in generators, the compensation devices that control reactive power and system load characteristics, were enumerated as the major causes for the voltage collapse.

As per IEEE/CIGRE, the definition of voltage stability and the theory on power system stability are well explained in (Kundur et al., 2004). During planning and control of the power system, voltage stability plays a key role in the stable operation of the system. A voltage stability toolbox for load flow and bifurcation analysis has been designed in (Ayasun et al., 2006). Simulation tools and MATLAB are the two software tools discussed here, which are used to analyze the power system stability. Simulation tools can be divided into two types: i) commercial tools such as Power System Simulator for Engineering (PSS/E), CYME Power Engineering, Power World Simulator, Power System Simulator (Simpow), LabVIEW, etc., and ii) customized toolboxes developed for academic and research purposes. Matlab, which is a programming platform widely used to obtain the solution for load flow studies and the VSA of large systems, is described in (Rao and Yuan, 2022; Salama and Vokony, 2022). This analysis was carried out with the help of several toolboxes and packages, such the Electromagnetic Transients Program (Mahseredjian and Alvarado, 1997), Educational Simulation Tool (Vournas et al., 2004), Power System Toolbox (Chow et al., 1992), Sim Power Systems (Sybille, 2004), Power System Simulation Package (Zimmerman, 2005), and Power Analysis Toolbox (Schoder, 2003).

In (Glavic et al., 2012), monitoring and control of system voltage based on supervisory control and data acquisition in the energy management system (EMS) were described. With the development and positioning of phasor measurement units (PMUs), effective online voltage monitoring in power systems is possible. Moreover, the wide-area monitoring system (WAMS) offers a base for online VSA in a large-scale power system (Modarresi et al., 2016; Pereira et al., 2023).

In this paper, different types of methods used in the literature for evaluating VSA have been elaborated. Here, both dynamic and static analyses have been presented clearly. Moreover, voltage stability analysis carried out on both transmission and distribution systems published in the literature has been reviewed. The analyses explored in this paper may help researchers to choose appropriate methods to evaluate VSA for the system considered.

The structural flow of the paper is as follows: in Section 2, the classifications of voltage stability and the cause for voltage instability are described. The traditional voltage stability methods to measure the stability margin from the present operating point to the collapse point are explained in Section 3. The line and bus indices presented in the literature are listed and elaborately explained in Section 4. Furthermore, the interdependence of the indices on the impedance of the system is well described in this section. Moreover, information about the index’s critical value and the network type for which the individual indices are most suitable are also presented here. The advantages, disadvantages, and applications of VSIs are explained in Section 5, and the discussion is concluded in Section 6.

2 Classification of voltage stability

Voltage stability, otherwise called load stability, is related to the transient stability of the power system. For a given operating condition, the power system is voltage stable if the voltage at the load side reaches an equilibrium value even after being subjected to a perturbation. However, voltage instability is a dynamic process that involves load and a means for voltage control. The process by which voltage instability leads to a shallow voltage profile is defined as voltage collapse. The voltage instability limit is not directly correlated to the network maximum power transfer limit. However, maximum power transfer is allied to voltage instability if the load is a constant power type. This can be briefly explained with a simple two-bus system, as shown in Figure 1A. The figure depicts a lossless transmission line transferring power from the generator to the load bus. If the generated voltage E and load voltage V are kept constant, at an angle (θ) of 90^o, the maximum power transfer occurs in the system. The relation between θ and P is shown in Figure 1B. Instead, if the terminal voltage at the load bus is considered as varying, then the relation between V and P is shown in Figure 1C. From this figure, it can be seen that the load bus voltage reduces with an increase in the load, and reaches a critical value that corresponds to P_max. Beyond this point there is no equilibrium. On top of a reduction in the load bus voltage, the critical value reached depends on the power factor of the load, as shown in Figure 1D (Ajjarapu, 2007).

FIGURE 1

FIGURE 1. (A) Simple two-bus system. (B) Relationship between P and θ. (C) Variation load bus voltage with P. (D) P vs. V curves with respect to power factor.

The voltage stability can be evaluated using two different methods of analysis. These are dynamic voltage stability and static voltage stability. In the first method, the dynamic behavior of the system components influences the voltage stability (Taylor, 1994). The second method is used to obtain the maximum loadability limit and the proximity to voltage instability. However, the computation time of the first method is greater than that of the second. Generally, voltage stability is categorized into four classes: large disturbance, small disturbance, short-term, and long-term stability. The causes of voltage stability and the threshold time limit of the perturbation, before which it has to be cleared, are tabulated in Table 1.

TABLE 1

TABLE 1. Categories of voltage stability and its causes.

3 Traditional voltage stability assessment methods

In recent years, the frequent occurrence of voltage stability problems is receiving special attention from power system engineers. These stability problems normally occur in heavily stressed systems. The analysis of voltage stability can be examined in the given system in terms of the following two aspects (Kundur, 1994).

i) Proximity to voltage instability: this involves how close the system is to voltage instability or the boundary, and it may be measured in terms of physical quantities, such as load levels, active power flow, and reactive power reserve.

ii) Mechanism of voltage instability: this deals with the cause and key factors influencing the instability. It also deals with the voltage-weak area and the various effective measures to enhance the voltage stability. The circumstances and their consequences leading to instability can be trapped by the time-domain simulations. However, as the time constants of the power system components differ on a large scale, the time-domain simulations are very slow and time-consuming. Moreover, this does not readily afford precise information about the degree of stability.

As the system dynamics affecting the voltage stability are generally slow, many aspects of the stability problem can be effectively investigated using static methods. The feasibility of the equilibrium point characterized by the specific operating conditions of a power system can be profoundly studied using this method. Alternatively, dynamic analysis is useful for a detailed study of the coordination of control and protection, exact voltage collapse situation, and testing of remedial measures. The way the steady-state equilibrium point is reached is also clearly analyzed by this method.

Traditional voltage stability methods such as the PV and QV curve method, sensitivity analysis, modal analysis, continuation power flow, singular value decomposition, and bifurcation analysis are discussed in the following subsections.

3.1 PV and QV curve method

The most common and conventional PV and QV curves used to evaluate the static voltage stability of the power system have allowed it to operate within the permissible load (Van et al., 2021; Vargas et al., 1999). The critical voltage is derived from Figure 1A and the quadratic voltage equation as given in Eq. 1, (Vournas, 2004; Vournas et al., 2000).

$v^2=-\left(2p\mathit{tan}\theta -1\right)\pm \frac{\sqrt{{\left(2p\mathit{tan}\theta -1\right)}^2-4p^2{\mathit{sec}}^2\varphi }}{2}(1)$

Voltage stability is determined by calculating the PV and QV curves at the particular load buses. In practice, these PV and QV curves are used as tools for evaluating the voltage stability at the Bonneville power administration centre. The drawback of this method is that it is more time-consuming and does not provide exact information. However, it can be used to evaluate the stability limit at every bus independently, irrespective of the system characteristics (Kamel et al., 2021).

In summary, the PV-QV curve method remains a fundamental tool in voltage stability assessment, offering valuable insights and aiding in the secure operation of power systems. As power grids continue to evolve, researchers and engineers will continue to refine and adapt this method to meet the demands of modern energy landscapes.

3.2 Sensitivity analysis

Sensitivity analysis can be used as an effective tool to estimate the static stability of the power system (Li and Jiang, 2012; Li and Wang, 2002) and is mainly related to the sensitivity matrix that must be extracted from the non-linear load flow equations given in Eqs. 2, 3.

$P\left(\theta ,V\right)=0(2)$

$Q\left(\theta ,V\right)=0(3)$

where P represents the system’s real power flow and Q denotes the system’s reactive power flow. The load flow equations under normal operating conditions can be written as

$\left[\begin{array}{c}\Delta P\\ \Delta Q\end{array}\right]=J\left[\begin{array}{c}\Delta \theta \\ \Delta V\end{array}\right]\left(\because J=\left[\begin{array}{cc}{J}_{P\theta }& J_{PV}\\ J_{Q\theta }& J_{QV}\end{array}\right]\right)(4)$

where J represents the Jacobian matrix of the system. An assessment of the sensitivity analysis is used for identifying the week bus, the loadability levels of the bus, and the system stability. However, the sensitivity index alone might not be adequate to evaluate week buses in an interconnected power system (Sinha and Hazarika, 2000). The effectiveness of the power system can become unstable if there is an increase in the sensitivity. The relationships between the node voltage to reactive power, node voltage to active power, load voltage to generator voltage, and the reactive power of the generator to a load of both active and reactive powers are regarded as commonly used sensitivity factors. These play vital roles in the prediction of critical buses in the system.

In summary, sensitivity analysis is a powerful method for voltage state assessment, providing essential insights for both real-time operation and long-term planning. This method provides a nuanced understanding of how variations in different system parameters impact voltage stability. Here are the key takeaways summarizing the significance of sensitivity analysis for voltage state assessment.

1. Granular insights: sensitivity analysis offers granular insights into the sensitivity of voltage-related parameters to changes in system conditions. This level of detail helps power system operators and planners identify critical factors affecting voltage stability.

2. Optimal operation: power system optimization benefits from sensitivity analysis by helping operators find the most efficient operating points while ensuring voltage stability. This is especially valuable in grids with variable renewable energy sources.

3. Planning and expansion: sensitivity analysis supports long-term planning and expansion of power systems. It aids in assessing the impact of new assets, such as generation units or transmission lines, on voltage stability, facilitating informed investment decisions.

4. Integration with advanced tools: modern power system analysis tools incorporate sensitivity analysis to enhance their capabilities. These tools integrate real-time data, advanced algorithms, and visualization techniques, further improving voltage state assessment.

3.3 Modal analysis

The modal analysis approach has been applied to the voltage stability analysis of practical systems. The advantage of this method is that it gives system-wide information related to voltage stability and clearly identifies critical areas in the power system. Moreover, it delivers information about the mechanism of instability. V-Q analysis is the primary step for estimating the modal analysis.

3.3.1 V-Q analysis

Voltage stability is a key factor that is always determined by both active and reactive power in the system. In accordance with this, Eq. 4 describes the relationship between the voltages of the efficient bus and the differences in power injection. Due to the incremental characteristics of V and Q, which are almost identical to the V-Q curve, the measurement of voltage stability is only possible if the real power is unchanged. In this case, in Eq. 4, by equating the value of ∆P with 0, the equation then becomes

$\left[\begin{array}{c}0\\ \Delta Q\end{array}\right]=J\left[\begin{array}{c}\Delta \theta \\ \Delta V\end{array}\right](5)$

By solving this Eq. 5, ΔQ is

$\Delta Q=J_R\Delta V\left(\because J_R=J_{QV}-J_{Q\theta }{J}_{P\theta }^{-1}{J}_{PV}\right)(6)$

where J_R denotes the reduced Jacobian matrix, and from Eq. 6, ΔV is

$\Delta V=J_R^{-1}\Delta Q(7)$

With respect to the reactive power injections, the V-Q sensitivity value at the ith bus varies (Van Cutsem and Vournas, 1998) so that the positive sensitivity value indicates that the voltage is stable and the negative sensitivity value indicates that the voltage is unstable.

3.3.2 Model sensitivity

In the power system, the physical characteristics of voltage stability can be calculated by the estimation of J_R eigenvalues and eigenvectors (Gao et al., 1992), which can be written as

$J_R=\xi \mathit{\Lambda }\eta \left(\because J_R^{-1}=\xi {\mathit{\Lambda }}^{-1}\eta \right)(8)$

where ξ = right eigenvector matrix, η = left eigenvector matrix, and Λ = diagonal eigenvalues matrix. Therefore, the V-Q response at the ith mode is given by

$v_i=\left(1/{\lambda }_i\right)q_i\left(or\right)=\Delta V={\displaystyle {\sum }_i}\left({\xi }_i{\eta }_i/{\lambda }_i\right)\Delta Q(9)$

From Eq. 9, the reactive power and modal voltage directions of variations are the same whenever λ_i > 0, which shows that the system voltage is under stable conditions. However, when λ_i < 0, the directions of variations in the reactive power and modal voltages will be in opposition, and this will lead the voltage at the ith bus to become unstable. Moreover, if λ_i = 0, modal reactive power changes can cause the modal voltage to change, which will lead to voltage collapse.

3.4 Continuation power flow (CPF) method

Continuation power flow (CPF) (Ajjarapu, 2007) is a numerical method used to analyze the steady-state behavior of power systems under varying operating conditions. It provides a systematic approach to track the behavior of the power system as load levels, generation levels, or control parameters change. The CPF method is particularly useful for studying voltage stability and identifying critical operating points that may lead to voltage collapse.

The CPF method extends the traditional power flow analysis, which solves a set of nonlinear algebraic equations to determine the steady-state conditions of the system. Instead of solving a single power flow equation, CPF solves a series of power flow equations in a sequential manner, gradually varying a continuation parameter. The following provides a comprehensive explanation of the CPF method.

3.4.1 Continuation parameter

The continuation parameter is a scalar parameter that is varied from an initial value to a final value. It represents a quantity of interest in the power system, such as load level, generation level, or control parameter like reactive power limits. The parameter is chosen such that the power system behavior significantly changes as it is varied.

3.4.2 Initialization

The CPF method starts with an initial power flow solution, usually obtained from a base case power flow analysis. This solution serves as the starting point for the continuation process.

3.4.3 Construction of jacobian matrix

The CPF method requires the construction of the Jacobian matrix, which describes the relationship between changes in power injections (P, Q) and voltage magnitudes and angles. The Jacobian matrix is typically sparse, and efficient techniques such as sparse matrix factorization are employed for its solution.

3.4.4 Tracking critical points

During the continuation process, the CPF method tracks critical points where the system behavior undergoes significant changes. These points can indicate voltage instability or voltage collapse conditions. Critical points are identified by analyzing the Jacobian matrix eigenvalues or other stability indicators.

3.4.5 Analysis of voltage stability

By varying the continuation parameter, the CPF method enables the identification of voltage stability limits, voltage collapse points, and the corresponding load/generation levels or control parameters. The method provides valuable insights into the system’s ability to maintain voltage within acceptable limits under different operating conditions.

In (Zhang and Zhang, 2005), an advanced version of the CPF method was implemented in which the theory of PQ decomposition was widely adopted to obtain the solution for the system’s power flow. In this connection, the simulation tool for a Lagrange two interpolation technique was developed to predict the process.

Continuation power flow is a powerful tool for voltage stability analysis as it allows for the systematic exploration of the steady-state behavior of power systems. It helps in understanding the impact of load changes, generation changes, and control parameter variations on voltage stability, ultimately aiding in effective system planning, operation, and control.

3.5 Singular value decomposition (SVD)

As seen in Eq. 4, one can transform the Jacobian matrix into a singular matrix if one of the J_R or J_Pθ matrices is singular. If |J_Pθ| ≠ 0 (which implies that there is no static angle problem), then it should be noted that under the defined conditions, the Jacobian matrix will become singular. Therefore, it is concluded that in the steady state voltage stability problem, the matrix J_R is a sub-matrix that is in turn associated with matrix J. Consider matrix A as a quadratic matrix (Lof et al., 1993), the SVD expression is defined in Eq. 10.

$A=U\sum V^T={\displaystyle {\sum }_{i=1}^n}{\sigma }_i{u}_i{v}_i^T(10)$

A new method for estimating the VSM is introduced (Ekwue et al., 1999) based on the closeness of the Jacobian matrix to become singular, which can be called the minimum singular value method. This is a new form of SVD. In connection with this, by correctly evaluating the lad values that can be modified in regular steps, a power flow Jacobian matrix can be calculated. If the Jacobian matrix’s singular value is almost equal to 0, the loadability limit of the system is reached. Eq. 11 provides the SVD solution for the linear system given in Eq. 10.

$x=A^{-1}b=\left(U\sum V^T\right)b={\displaystyle {\sum }_{i=1}^n}\frac{u_i^T{v}_i}{{\sigma }_i}b(11)$

It is therefore inferred that minor changes in both the value of A and the value of b would result in an enormous change in the value of x, given by a small value of n. Consequently, the small changes in both the active and reactive power injections impact ${\left[\begin{array}{cc}\Delta \theta & \Delta V\end{array}\right]}^T$. The equation can be written as

$\left[\begin{array}{c}\Delta \theta \\ \Delta V\end{array}\right]=V{\sum }^{-1}{U}^T\left[\begin{array}{c}\Delta P\\ \Delta Q\end{array}\right](12)$

Nevertheless, it is impossible to detect the specific reason for the voltage instability in the system. While this approach can be used to obtain a relative proximity value with respect to the voltage stability limit, it does not provide an exact or linear value for the given power system. This is because, after a given stable operating point that is defined by the system, it experiences a non-linear behavior up to the bifurcation point.

3.6 Bifurcation techniques

The bifurcation technique is a great tool that is widely applied in the study of power system voltage stability. Generally, the power system is expressed by highly nonlinear dynamical system equations, which include system parameters (Wu et al., 2017). If one of the parameters is varied, then the phase portrait of that system may deform slightly. These qualitative changes in the parameters of the dynamical system may lead to system instability. Poorly damped low-frequency oscillations, induction motor dynamics, and the dynamics of voltage collapse near the critical point are the main causes of the change in the dynamical behavior of the system.

The autonomous differential equation of a dynamical system is given in Eq. 13.

$\dot{x}=F\left(x,\lambda \right),x\in R^n,\lambda \in R^k(13)$

where f represents a differential equation and x denotes the state variables. Load voltage magnitudes or angles, generator angles, and generator angular velocities are the state variables of power system models. $\lambda$ denotes a vector of the time-invariant scalar parameter. At an equilibrium point $\left(x_0,{\lambda }_0\right)$, $\dot{x}$ the equation becomes zero, i.e., the steady-state solution of Eq. 13 satisfies Eq.14, representing a set of nonlinear algebraic equations.

$F\left(x_0,{\lambda }_0\right)=0(14)$

If the eigenvalues of the partial derivative of Eq.14 with respect to x, $\frac{\partial F}{\partial x}$ (i.e., Jacobian) become non-zero, then according to the implicit function theorem, the equilibria of Eq. 13 can be represented as a smooth function of $x=x\left(\lambda \right)$. The function $x\left(\lambda \right)$ is known as the branch of equilibria. However, if the eigenvalue of the Jacobian has zero real part occurring at some $\lambda$, say ${\lambda }_c$, the system $\dot{x}=F\left(x_c,{\lambda }_c\right)$ becomes structurally unstable, and several branches of $x=x\left(\lambda \right)$ can come together at $\left(x_c,{\lambda }_c\right)$ in $R^{n+k}$. The parameter set ${\lambda }_c$ where the system loses its stability is called a bifurcation set. The point $\left(x_c,{\lambda }_c\right)$ is called the bifurcation point.

Here, single-parameter bifurcation analysis can be successfully implemented for voltage stability analysis of the real-time system. Multi-parameter bifurcation analysis is too difficult due to the complexity of the electric power system itself. The different types of bifurcation techniques are briefly discussed below.

3.6.1 Saddle node bifurcation (SNB)

The bifurcations are known as a turning point or fold bifurcation and are usually defined by a couple of equilibrium points merging at the bifurcation point and then locally disappearing as the slowly varying parameter $\lambda$ changes. This bifurcation corresponds to an equilibrium point where the state matrix has a distinct zero eigenvalue, and certain transversal conditions are met (Dobson and Lu, 1993). The direct and continuation methods are two important types of SNB. The direct method is used to find the critical point where the Jacobian is singular by solving the power flow equations of the large power system in one step. The continuation method is described in (Seydel, 2009).

3.6.2 Holf bifurcation method

From Eq. 14, the state of the power system is asymptotically stable if the eigenvalues of the Jacobian have negative real parts at that point. If the real eigenvalue becomes zero or crosses the imaginary axis and moves into the right half-plane, the system can reach a critical point or oscillate with a small amplitude. This phenomenon is explained by the holf bifurcation theory. In this technique, the assumptions to make are (i) $f\left(x_c,{\lambda }_c\right)=0$, (ii) the Jacobian matrix has a simple pair of purely imaginary eigenvalues, $\mu \left({\lambda }_c\right)=\pm jw$, and (iii) $\frac{d\left(Re\left(\mu \left({\lambda }_c\right)\right)\right)}{d\lambda }\ne 0$ where ${\lambda }_c$ is the parameter at which bifurcation occurs (Hassard et al., 1981; Marsden and McCracken, 2012). The third assumption requires that there is a transversal crossing of the imaginary axis by the pair of complex conjugate eigenvalues. Numerical determination of the holf point involves estimation of the point $\left(x_c,{\lambda }_c\right)$. Evaluating all the eigenvalues of the Jacobian matrix is a costly way to identify the holf point. However, in the static approach, there are efficient ways to identify the holf point using both the direct and indirect methods (Ajjarapu and Lee, 1992; Rajagopalan et al., 1992; Venkatasubramanian et al., 1995; Seydel, 2009).

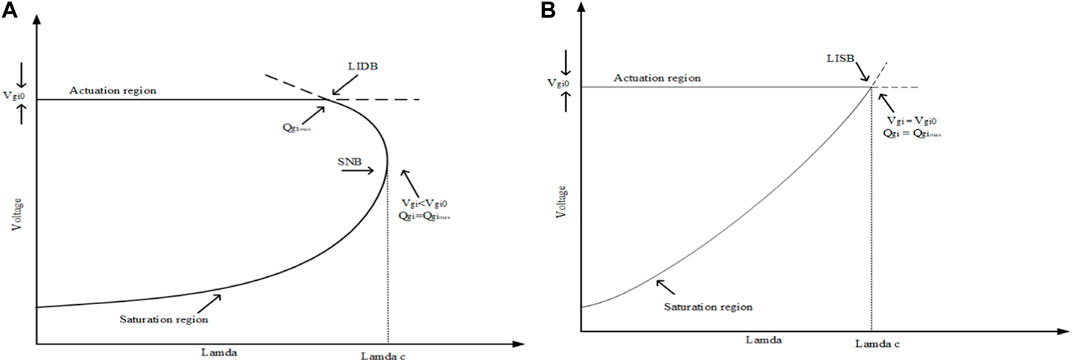
3.6.3 Limit-induced bifurcations (LIBs)

Mathematically, the solution points are the limit-induced bifurcations associated with load flow models, where all the eigenvalues of the resulting Jacobian have non-zero real parts, i.e., the Jacobian matrix is non-singular. The LIBs are broadly classified into two types, as follows.

i) limit-induced dynamic bifurcation (LIDBs): this refers to a sudden change in the dynamic behavior of a power system near a voltage stability limit. It occurs when a small change in system parameters or operating conditions causes a qualitative shift in the system’s stability and dynamic response. This bifurcation is associated with the onset of voltage instability or voltage collapse.

3.6.3.1 Significance

- Early warning of instability: limit-induced dynamic bifurcation provides an early warning sign of voltage instability and potential voltage collapse in the system. It helps identify critical operating points where small disturbances can lead to significant system disruptions.

- Impact on system dynamics: this type of bifurcation reveals changes in the system’s dynamic behavior, such as the appearance of oscillations, unstable voltage modes, or limit cycles. It indicates a shift from stable operation to a regime of unstable or oscillatory behavior.

3.6.3.2 Application

- System planning: understanding limit-induced dynamic bifurcation helps in determining the stability limits of a power system, guiding system planning and expansion decisions to avoid potential voltage collapse scenarios.

- Control strategies: by analyzing the bifurcation behavior, appropriate control strategies can be developed to mitigate voltage instability, enhance system damping, and improve the system’s dynamic performance.

ii) Limit-induced static bifurcations (LISBs): static bifurcation refers to the qualitative change in the steady-state behavior of a power system near a voltage stability limit. It occurs when there is a change in the number or type of steady-state solutions as system parameters or operating conditions are varied. Static bifurcations are associated with the appearance or disappearance of multiple equilibrium points or voltage collapse points (Avalos et al., 2009). In the case of LIDBs, the equilibrium points continue to exist after being reached as the bifurcation parameter $\lambda$ varies, as shown in Figure 2A. On the other hand, LISBs are approximately identical to SNBs, in that these correspond to the points at which two solutions converge and vanish as the bifurcation parameter $\lambda$ changes, as shown in Figure 2B. LISBs are often correlated with a maximum loadability margin.

FIGURE 2

FIGURE 2. (A) LIDB followed by SNB (B) LISB.

3.7 Limitations and challenges of traditional voltage stavility methods

Voltage stability analysis is an important aspect of power system analysis and operation. Several methods are employed to assess voltage stability, such as the PV and QV curve method, sensitivity method, modal analysis, continuation power flow analysis, singular value decomposition (SVD), and bifurcation analysis. While these methods provide valuable insights, they also have their limitations and challenges. The following is an overview of the limitations and challenges associated with each method.

3.7.1 PV and QV curve method

- Limited accuracy: the PV and QV curve method provides a simplified representation of the system, assuming a constant power factor or voltage magnitude. This simplification may lead to inaccuracies in representing the actual system behavior.

- Lack of dynamic information: this method does not capture dynamic phenomena and transient effects that can impact voltage stability.

- Limited applicability: it may not be suitable for analyzing complex systems with significant variations in load and generation conditions.

3.7.2 Sensitivity method

- Complexity: sensitivity analysis involves calculating derivatives and requires accurate system models, making it computationally intensive and complex.

- Model uncertainties: the sensitivity method is sensitive to model uncertainties, such as load models and parameter variations, which can affect the accuracy of the results.

- Limited scope: it may not provide a comprehensive assessment of voltage stability under large disturbances or system-wide events.

3.7.3 Modal analysis

- Linear approximation: modal analysis assumes linearity, which may not capture the non-linear behavior of power systems accurately.

- Modal truncation: the accuracy of modal analysis depends on the number of modes considered. Truncating the modal analysis may lead to the exclusion of important system dynamics.

- Assumptions: modal analysis often assumes decoupled modes, which may not hold true for all system conditions.

3.7.4 Continuation power flow analysis

- Computational requirements: continuation power flow analysis requires solving a series of power flow equations iteratively. It can be computationally demanding, particularly for large-scale systems.

- Convergence issues: the method may encounter convergence problems when dealing with ill-conditioned systems or in the presence of voltage collapse phenomena.

- Representation of dynamic effects: continuation power flow analysis typically focuses on steady-state conditions and may not capture transient or dynamic effects adequately.

3.7.5 Singular value decomposition (SVD)

- Limited applicability: SVD is primarily used for analyzing linearized models and may not fully capture the non-linear dynamics associated with voltage stability.

- Data requirements: SVD relies on system response data, and obtaining accurate and sufficient data for analysis can be challenging.

- Interpretability: interpreting the results of SVD and relating them to voltage stability issues can be complex and requires expertise.

3.7.6 Bifurcation analysis

- Computational complexity: bifurcation analysis involves exploring system behavior near critical points, which can be computationally intensive, particularly for large-scale systems.

- Non-linear system representation: bifurcation analysis assumes non-linear models, which may require accurate modelling of the system dynamics and associated parameters.

- Sensitivity to initial conditions: the results of bifurcation analysis can be sensitive to the initial conditions and small perturbations, making it necessary to carefully select the initial operating point.

It is worth noting that each method has its advantages and can provide valuable insights into voltage stability. However, it is essential to consider these limitations and challenges when applying these methods to ensure accurate and reliable results. Additionally, combining multiple methods and considering a holistic approach to voltage stability analysis can help mitigate some of these limitations.

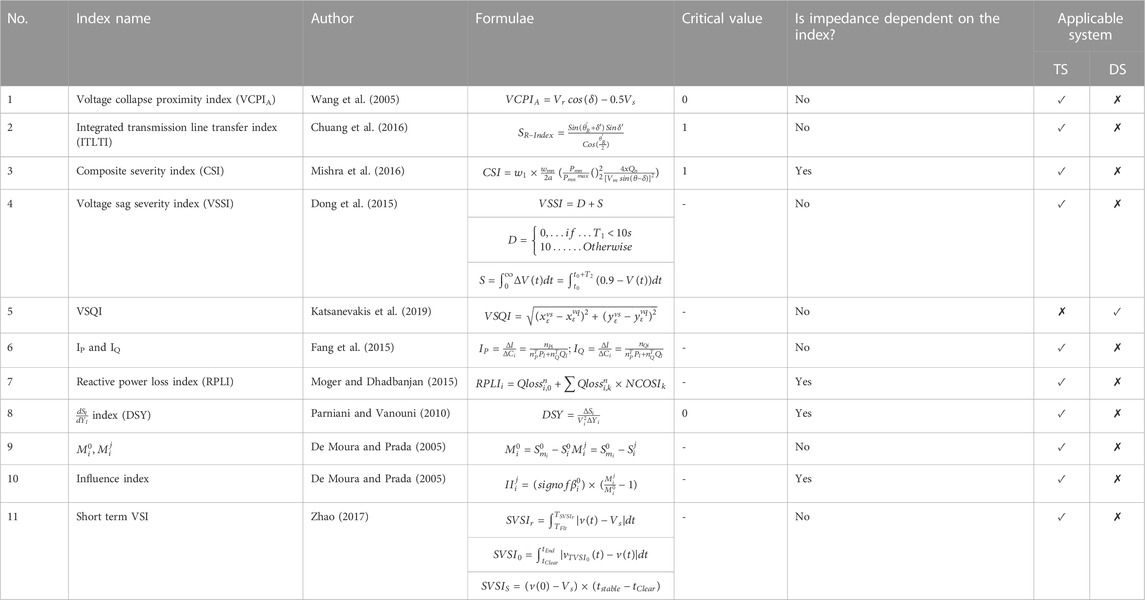
4 VSIs

In the study of power systems, voltage instability is a significant and challenging problem for electrical scientists and engineers. Numerous approaches and practices implemented on IEEE test systems are discussed in the following sections to assess voltage collapse prediction and voltage instability (Zambroni de Souza et al., 2011). Some of the conventional approaches were conferred in Section 3. Several VSIs are discussed to judge the dynamic problems for planning and controlling power systems. VSIs are categorized into two types.

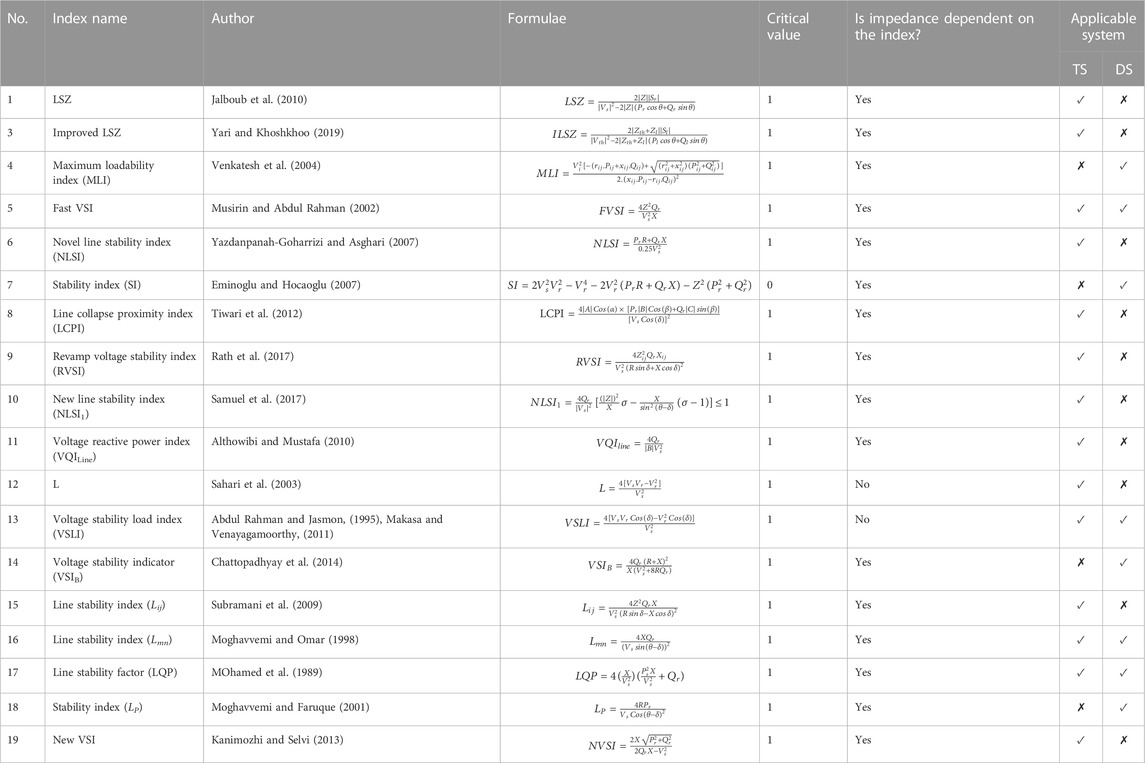
(i) Line VSIs: “The line VSIs are used to identify the capability of the TS to deliver power to the load area.” The value of these indices determined for each branch is used to find the gap between the current operating point and the maximum power transfer capability of the line.

(ii) Bus VSIs: “The bus indices have the ability to detect the margin between the present operating point of the buses and maximum loading of load buses."

In (Reis and Maciel Barbosa, 2009; Karbalaei et al., 2010; Zhao J and Yang, 2011; Lim et al., 2012; Ismail et al., 2014; Baleboina et al., 2017; Baleboina and Mageshvaran, 2018; Yuva Kishore and Guru Mohan, 2018; Yari and Khoshkhoo, 2019; Nageswa Rao et al., 2021), a comprehensive assessment of several line stability indices (LSIs) was carried out. Moreover, a modified LSI has been proposed to precisely measure the stability status of system networks at different conditions. The performance of nearly 17 indices was analyzed for the following conditions.

(i) Different ratios of R/X,

(ii) Different directions of load increment and load power factors, and

(iii) Different sending end bus voltages.

From the analysis, it is observed that indices such as LQP, LSZ, VSMI, VCPI (1), VCPI (3), MLI, and L were assessing the stability of the system properly in spite of the different direction of load increment and R/X ratios. Moreover, LQP, NVSI, VCPI (1), VCPI (3), Lsr, VSI, VSMI, L, LSZ, and MLI were the indices that have the ability to assess the stability during both low power factors (PF) and typical PFs (i.e., PF = 0.85 or higher) conditions. However, except for LSZ, the remaining indices did not perform well when P and Q flow in different directions. Furthermore, even the LSZ index is able to measure the stability of a simple two-bus system only and fails to analyze the stability stiffness of a real, large power system. In order to overcome this drawback, an improved LSZ has been proposed (Yari and Khoshkhoo, 2019).

4.1 Limitations of voltage stability indices and potential improvements

1. Simplified system representation: voltage stability indices often rely on simplified system models and assumptions, which may not capture all aspects of system behavior accurately. To address this limitation, improved models and algorithms can be developed that consider more detailed system representations, accounting for factors such as non-linear loads, voltage-dependent models, and more accurate representations of distributed energy resources.

2. Uncertain input data: voltage stability indices depend on accurate input data, including load models, system parameters, and real-time measurements. However, uncertainties in data can impact the accuracy of the indices. Advanced data estimation and assimilation techniques can be employed to enhance the quality and accuracy of input data, thus improving the reliability of voltage stability indices.

3. Lack of dynamic information: voltage stability indices primarily focus on steady-state conditions and may not capture transient or dynamic effects that can impact voltage stability. Incorporating dynamic models and considering dynamic stability analysis methods can provide a more comprehensive assessment of voltage stability, addressing the limitations of static indices.

4. Scalability: voltage stability indices should be applicable to large-scale systems with complex network topologies and various operational scenarios. Efficient computational algorithms and parallel computing techniques can be utilized to ensure scalability and computational efficiency of the indices.

5. Integration of control actions: voltage stability indices can be improved by incorporating control actions and their impact on voltage stability. This includes the integration of online monitoring systems, automated control schemes, and advanced control strategies to maintain voltage stability in real-time.

In this section, the VSIs were listed based on different concepts such as maximum power flow, PMU and local measurements, voltage equation, etc. Here, information about the critical value of the index, formulae, whether the index is impedance dependent or not, and the applicability of stability indices to the transmission system (TS) and distribution system (DS) (Nguyen et al., 2021) is clearly shown in all the tables.

4.2 Indices based on maximum power flow equations

A single line of an interconnected network and the parameters of a line are considered, as shown in Figure 1A (Balamourougan et al., 2004). The model of power flow analysis and the apparent power expressed at the sending end bus and receiving end bus can be given by Eqs. 15, 16.

$S_s=\frac{{\left|V_s\right|}^2}{Z}\angle \theta -\frac{\left|V_S\right|\left|V_r\right|}{Z}\angle \left(\theta +{\delta }_1-{\delta }_2\right)(15)$

$S_r=\frac{\left|V_s\right|\left|V_r\right|}{Z}\angle \left(\theta -{\delta }_1+{\delta }_2\right)-\frac{{\left|V_r\right|}^2}{Z}\angle \theta (16)$

From Eq. 15 and Eq. 16, separating the true and reactive power we obtain

$P_r=\frac{V_s{V}_r}{Z}\mathit{cos}\left(\theta -{\delta }_1+{\delta }_2\right)-\frac{V_r^2}{Z}\mathit{cos}\theta (17)$

$Q_r=\frac{V_s{V}_r}{Z}\mathit{sin}\left(\theta -{\delta }_1+{\delta }_2\right)-\frac{V_r^2}{Z}\mathit{sin}\theta (18)$

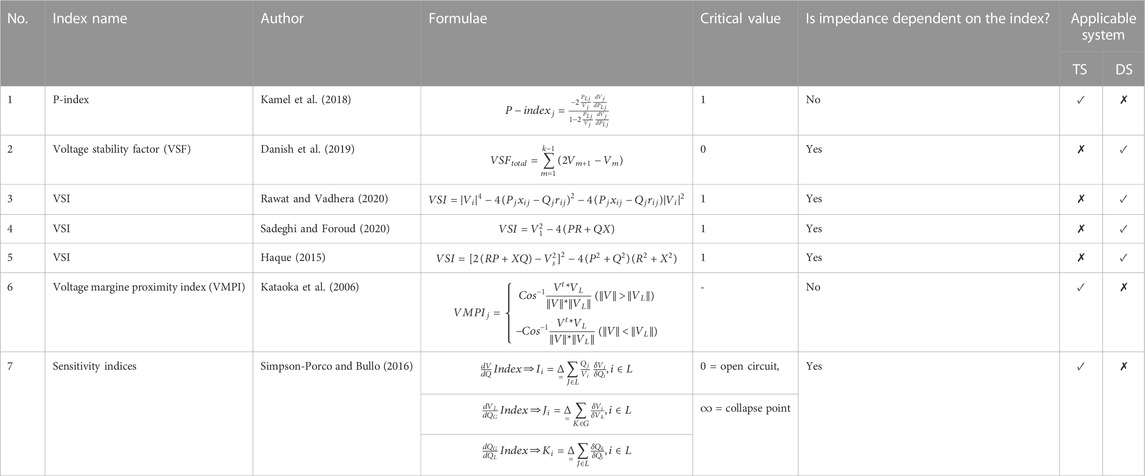
By using Eq. 15 to Eq. 18, the maximum power transfer through a line and the VSIs can be derived and are listed in Table 2 for the line and Table 3 for the bus.

TABLE 2

TABLE 2. Maximum power flow–based line indices.

TABLE 3

TABLE 3. Maximum power flow–based bus indices.

4.3 Indices based on PMU & local measurements

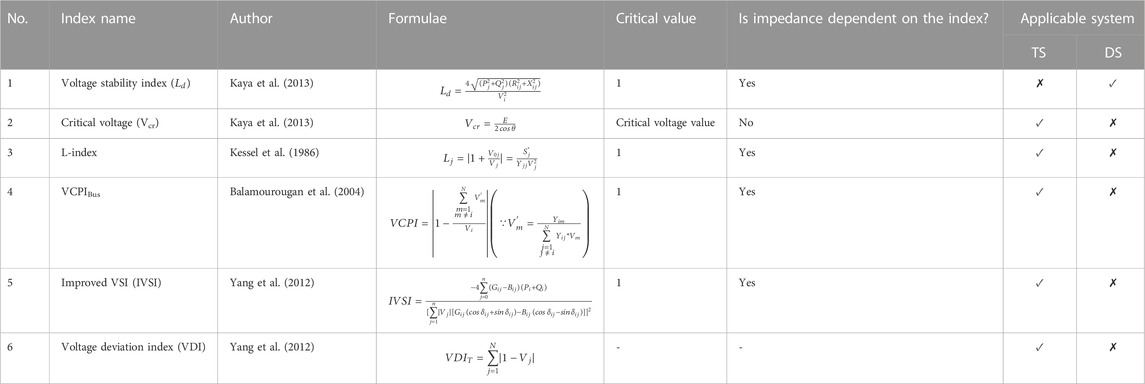
Advanced technology in smart devices such as PMU was introduced in the power system to monitor the power injections at all the buses and also to track the parameters of the system (i.e., current, voltage, etc.). Generally, PMUs are located on the generator side as well as on the load side. This smart device can measure the voltage and current phasor information, in discrete time intervals, of the system where it is installed. PMU measurements can be used to estimate the proximity of voltage collapse in the system. The VSI has been derived from load flow studies with the aid of data attained from PMUs, as given in Tables 4, 5. It provides an exact estimation of the strength/weakness of the system connected to the estimated capacity based on local measurements.

TABLE 4

TABLE 4. PMU and local measurement–based line indices.

TABLE 5

TABLE 5. PMU and local measurement–based bus indices.

4.4 Indices based on the voltage equation of a transmission line

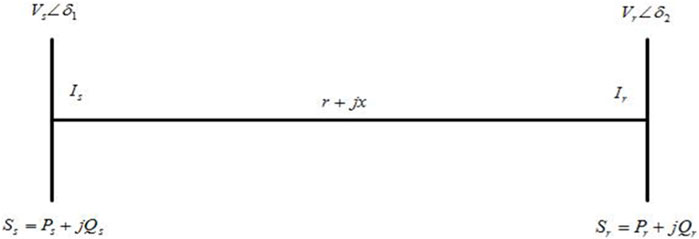
This section presents the indices based on the voltage equation of the transmission line (Ajjarapu, 2007). The bus voltage of the transmission system shown in Figure 3 is given in Eq. 19.

$V_s=\sqrt{\left(V_r+{\left(\frac{P_{r}r+Q_{r}x}{V_r}\right)}^2+{\left(\frac{P_{r}x-Q_{r}r}{V_r}\right)}^2\right)}(19)$

where V_s and V_r are the sending and receiving end voltages, respectively, P_r and Q_r are active and reactive power flowing from the sending end to the receiving end, respectively, and r and x are the equivalent resistance and reactance, respectively. Using the above equation, the various VSIs for lines and buses, along with their critical value and information about their dependency on the impedance, are elaborated in Tables 6, 7.

FIGURE 3

FIGURE 3. Two bus transmission network.

TABLE 6

TABLE 6. Voltage equation of transmission line–based line indices.

TABLE 7

TABLE 7. Voltage equation of transmission line–based bus indices.

4.5 Indices based on maximum power transfer theorem

In this section, a detailed list of indices derived from the well-known maximum power transfer theorem (MPTT) is given. In AC systems, the MPTT states that the maximum power will be delivered from source to load when the load impedance becomes equal to the complex conjugate of the source impedance. These indices were derived by applying the condition of MPTT on the power flow equations given in Eq. 15 to Eq.18. Table 8 provides a clear picture of these line and bus indices, along with their critical value and information about their dependency on the impedance. Moreover, Eq. 20 (Gong et al., 2006) and Eq. 21 (Gubina and Strmčnik, 1995) are developed for transmission systems to check the status of critical lines presented in the system.

$VS{I}_A=\mathit{Min}\left(\frac{P_{m\mathit{arg}in}}{P_{\mathit{max}}\frac{Q_{m\mathit{arg}in}}{Q_{\mathit{max}}\frac{S_{m\mathit{arg}in}}{S_{\mathit{max}}}}}\right)(20)$

$TPSI=0.5V_i-v_d(21)$

TABLE 8

TABLE 8. Maximum power transfer theorem–based bus indices.

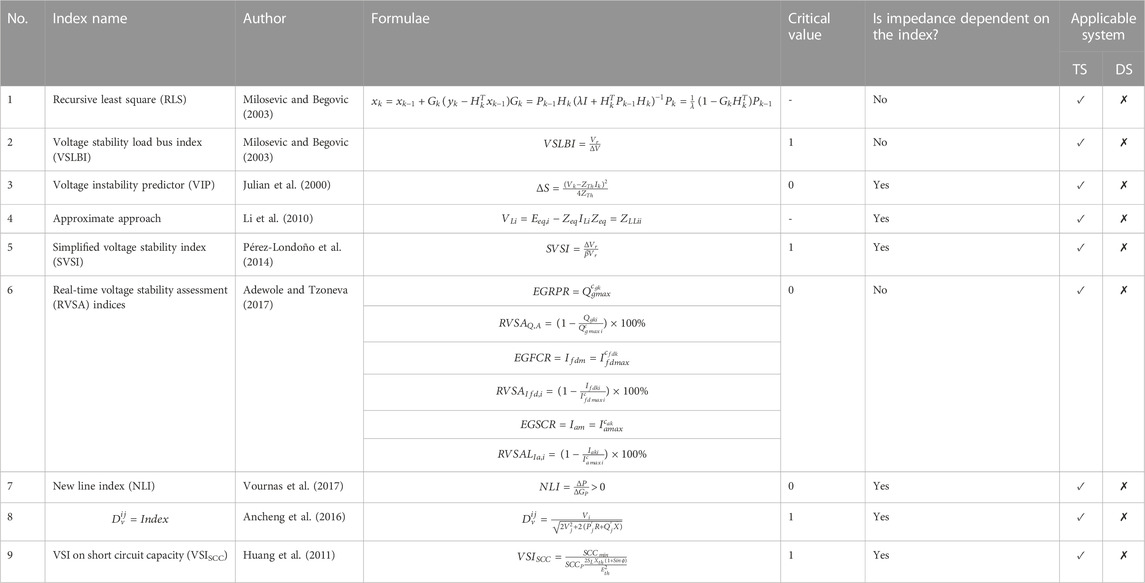
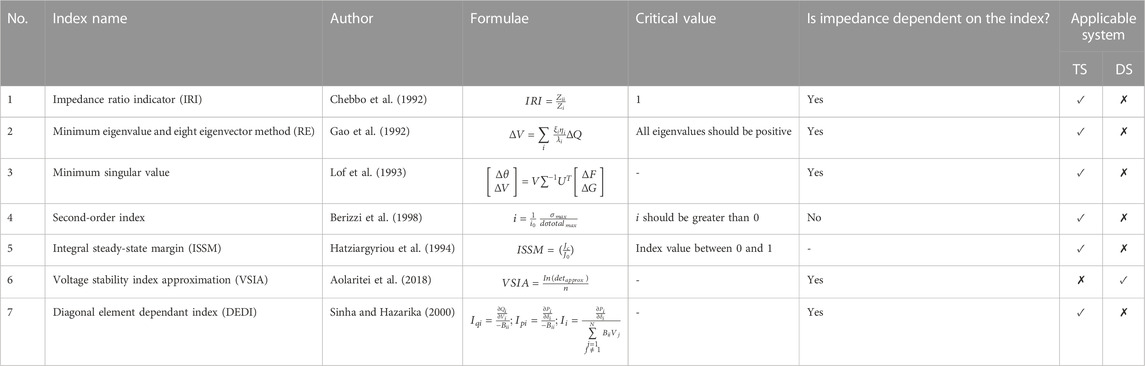
4.6 Indices based on the Jacobian matrix

This section deals with static voltage stability indices that are based on the Jacobian matrix of the power flow equations. These indices provide a clear view of the proximity to voltage instability and detail on the critical buses and areas. These VSIs are listed in Table 9. The critical value of these indices and the dependency on impedance are also mentioned in the table.

TABLE 9

TABLE 9. Jacobian matrix–based bus indices.

4.7 Indices based on the P-V curve

Using Eq. 1, the PV and QV curves can be drawn considering the constant power factor and constant real power, respectively (Ajjarapu, 2007). Moreover, the critical voltage and maximum power derived from the same equation are given in Eqs. 22, 23, respectively.

$v_{crit}=\frac{1}{\sqrt{2}*\sqrt{1+\mathit{sin}\varphi }}(22)$

${p\frac{\mathit{cos}\varphi }{2\left(1+\mathit{sin}\varphi \right)}}_{\mathit{max}}(23)$

At the unity power factor (UPF), the maximum permissible power can be obtained by substituting $\varphi =0$ into Eq. 22 ${p\frac{1}{2}}_{\mathit{max}}$. Similarly, the value of the critical voltage at UPF obtained from Eq. 21 is $v_{crit}=\frac{1}{\sqrt{2}}=0.707$. Various line and bus indices were derived based on the concept of the P-V curve and the maximum permissible power and critical voltage. Table 10 summarises the VSIs generated from the P-V curve. The rows 1–10 represent the bus indices and 11 and 12 represent line indices developed by the P-V curve.

TABLE 10

TABLE 10. P-V curve–based bus indices.

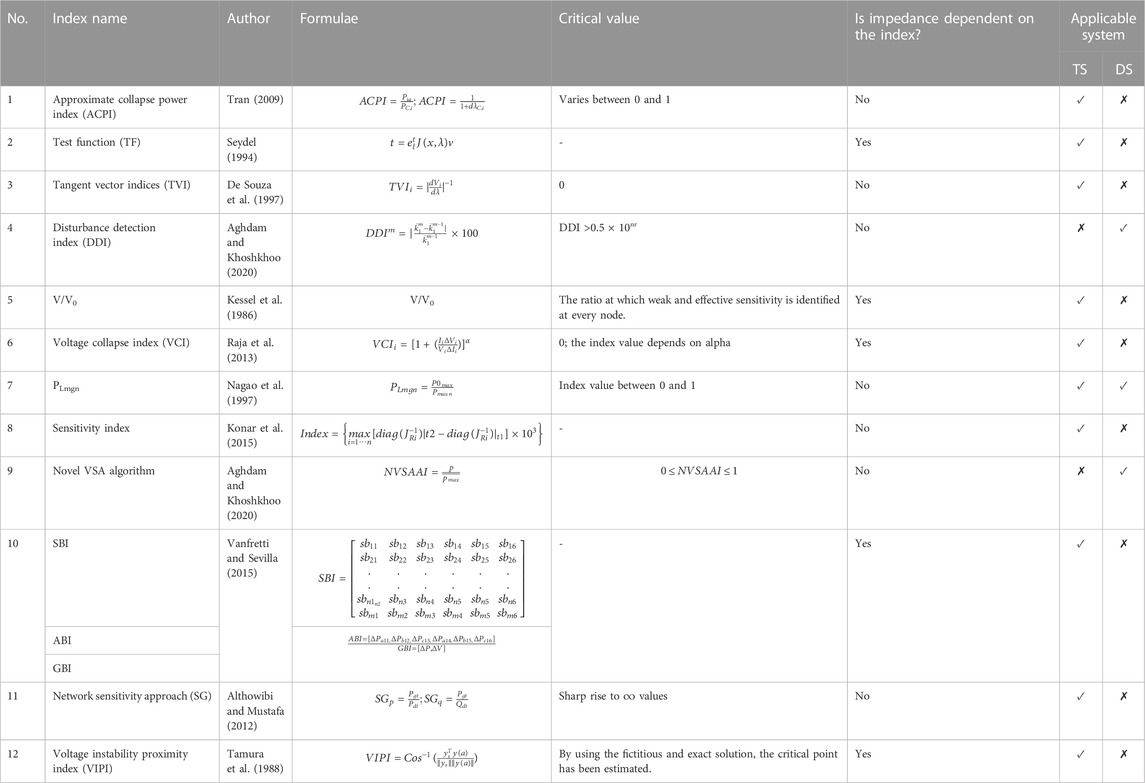
4.8 Miscellaneous indices

In this section, the line and bus indices based on ABCD parameters of the transmission line, the combination of two indices, reactive power loss, transmission paths, etc., other than those listed and described in the earlier sections, are discussed. The different types of miscellaneous line VSIs are listed in Table 11. The significant features of these indices are described in the following.

• The index VCPI_A tracks information about the weakest transmission paths and the reactive power reserve of the network (Wang et al., 2005).

• The integrated transmission line transfer index (ITLTI) is computed with the help of the power factor of the receiving end load and the power angle between sending and receiving ends. This index provides reliable information on the critical margin of voltage instability of the power system (Chuang et al., 2016).

• The CSI index is a combination of PI and Lmn indices, and provides information about the real power and voltage stability of the system (Mishra et al., 2016).

• VSSI can be used to evaluate the short-term VS. of the load bus. This index is obtained from the fault-induced voltage sag (Dong et al., 2015).

• VSQI is derived with the help of a voltage stability curve to examine the voltage stability and to check the quality of the system voltage (Katsanevakis et al., 2019).

TABLE 11

TABLE 11. Line indices.

The different miscellaneous bus indices are given in Table 11. Some important features of these indices are listed in the following.

• The index Ip and Iq is obtained from the bifurcation technique. It is used to find the critical nodes in the power system during abnormal operating and contingency conditions (Fang et al., 2015).

• RPLI is derived from the reactive power support and loss allocation algorithm using the Ybus method under both normal and severe contingency conditions (Moger and Dhadbanjan, 2015).

• The DSY index is a derivative of the apparent load power with respect to its admittance. As the apparent load power and admittance can be evaluated via the measurement of current and voltage, this index is easily determined via the locally measured scalar values of V and I. This index is used to find the loadability limit of the system (Parniani and Vanouni, 2010).

• The influence index, which is derived from the SV curve, is used to find the critical margin of the power system under contingency conditions (De Moura and Prada, 2005).

• Short-term VSI is computed with the help of three components: SVSIr, SVSIo, and SVSIs. These three components reflect transient voltage restoration, transient voltage oscillation, and the ability to reach a steady state, respectively (Zhao, 2017).

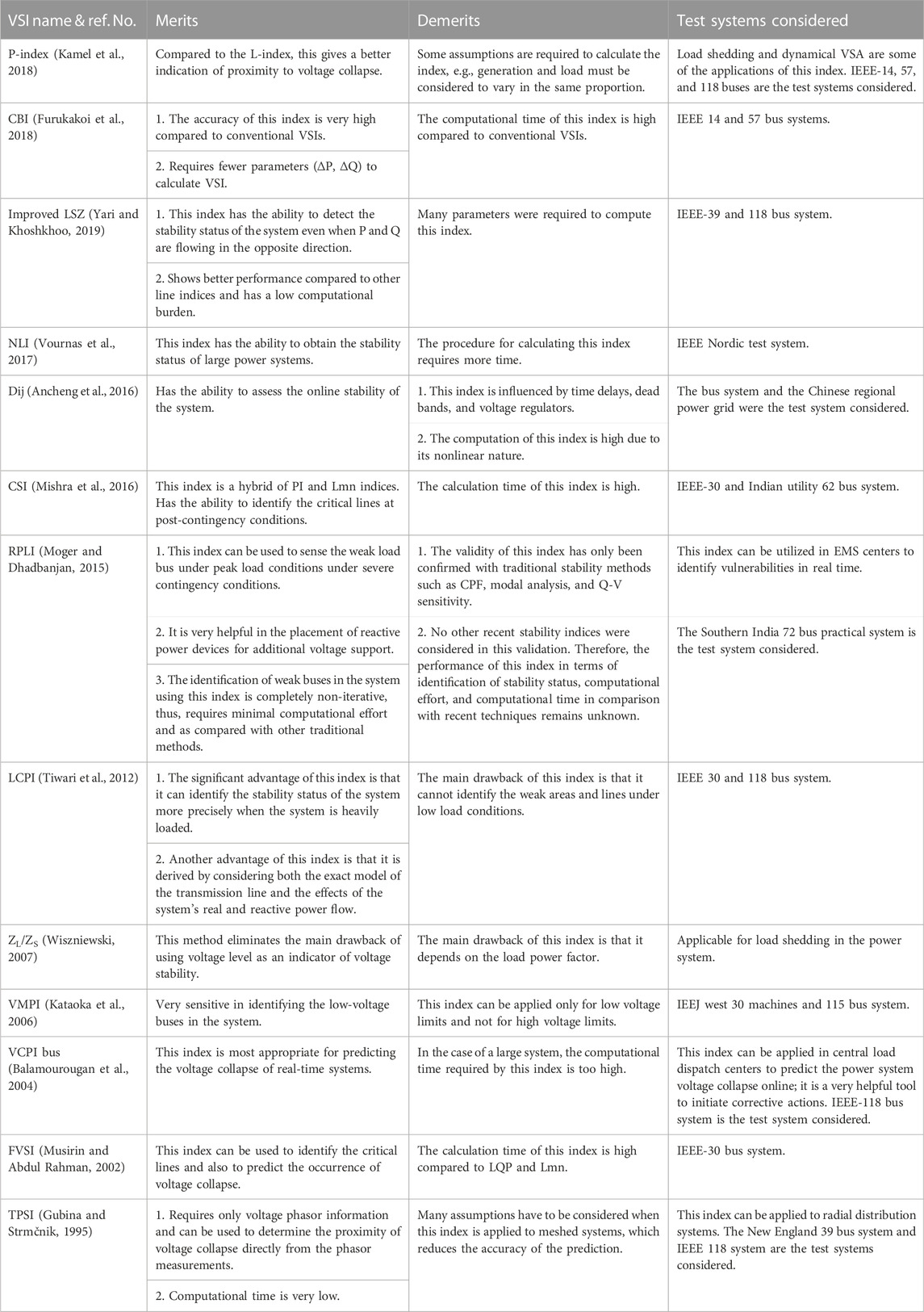
5 Merits and demerits of line and bus VSIs

In this section, the merits, demerits, and applications of various line and bus VSIs are described in Table 12. Reactive power planning, load shedding, power system planning and control, online stability monitoring, etc., are some of the different power system problems to which these indices can be applied in order to identify critical areas, buses, and lines. This may help power system engineers to operate the power system within safe limits. For further clarifications, readers may refer to (Furukakoi et al., 2018), in which a comparison based on the computation time taken by the indices was neatly described. Moreover (Yari and Khoshkhoo, 2019), provided a performance-based comparison of various VSIs.

TABLE 12

TABLE 12. Merits and demerits of VSIs.

6 Applications of VSIs

Voltage stability indices play a crucial role in assessing and managing voltage stability in real-world power systems. These indices provide quantitative measures of system stability and are used in various applications to ensure secure and reliable operation. The following are some common applications of voltage stability indices in real-world scenarios.

6.1 Voltage stability assessment

Voltage stability indices are employed to assess the voltage stability of power systems under different operating conditions. They provide a quantitative measure of the system’s proximity to voltage collapse or instability. By analyzing these indices, system operators and planners can identify critical operating points, voltage stability limits, and potential voltage collapse scenarios.

6.2 System planning and expansion

Voltage stability indices are used in system planning and expansion studies to ensure the long-term reliability and security of power systems. These indices help determine the maximum load or generation levels that the system can support without voltage stability issues. By incorporating voltage stability considerations into planning studies, system operators can make informed decisions regarding system reinforcements, network upgrades, and capacity expansion to mitigate voltage stability concerns.

6.3 Contingency analysis

Voltage stability indices are utilized in contingency analysis to evaluate the impact of contingencies, such as generator or transmission line outages, on voltage stability. By calculating these indices for different contingency scenarios, operators can identify critical contingencies that may lead to voltage instability and take appropriate preventive or corrective measures, such as load shedding or re-dispatching, to maintain system stability.

6.4 Online monitoring and control

Voltage stability indices are used for real-time monitoring and control of power systems. By continuously computing these indices based on real-time measurements, operators can detect and identify deteriorating voltage stability conditions in the system. This allows for timely implementation of control actions, such as reactive power control, voltage regulation, and load shedding, to maintain voltage stability within acceptable limits.

6.5 Remedial action schemes

Voltage stability indices are utilized in the design and operation of remedial action schemes (RAS). RAS are automatic control systems that respond to voltage instability conditions by taking predefined corrective actions. These indices serve as triggers for activating specific RAS, such as fast-acting voltage control devices, capacitor banks, or generator tripping, to prevent voltage collapse or mitigate voltage stability issues.

6.6 Dynamic security assessment

Voltage stability indices are integrated into dynamic security assessment tools to evaluate the system’s dynamic response under various disturbances or contingencies. These tools utilize real-time measurements and dynamic models to assess the system’s transient stability and voltage stability. Voltage stability indices provide valuable information to operators for making critical decisions during emergency situations or system restoration processes.

The voltage stability indices have diverse applications in real-world power systems, ranging from voltage stability assessment and system planning to online monitoring, control, and dynamic security assessment. These indices enable operators and planners to make informed decisions, implement preventive and corrective measures, and ensure the reliable and secure operation of power systems in the face of voltage stability challenges.

7 Conclusion

To analyze the evolution over time of some of the proposed different voltage stability methods and to identify voltage collapse, a detailed survey of these methods was carried out in this paper. An introduction, a brief literature survey of the different voltage stability methods, and indices proposed by various researchers were presented. The classification of indices based on the disturbances that occurred in the power system, traditional methods such as PV-QV curve, sensitivty, model analysis, CPF methods, and Bifurcation tecniques for voltage stability, and their limitations and applications as well as conclusions were described in the next sections.

A clear description of the various line and bus indices derived based on different voltage stability constraints such as PMU and local measurements, the Jacobian matrix, PV curve, and concepts such as the maximum power flow equations of the transmission line, voltage equation of the transmission line, and maximum power transfer theorem were presented in the subsequent sections. Moreover, the merits, demerits, and applications of the various VSIs were briefed in the last section. Finally, this paper gives a deep insight into most of the voltage stability methods and indices in the literature. This can assist researchers in the future in selecting the optimal VSI for various applications.

8 Future scope

The future scope of this article is as follows.

1. Integration of artificial intelligence (AI) and machine learning: the incorporation of AI and machine learning algorithms into voltage stability assessment will enable systems to learn from historical data and real-time measurements. This will enhance the accuracy of voltage stability predictions, especially in dynamic and complex grids with high renewable energy penetration.

2. Cyber-physical security: future research should focus on developing voltage stability assessment methods that account for cyber-physical security risks. This includes protecting systems from cyberattacks that can compromise voltage stability.

3. Advanced sensors and IoT: the deployment of advanced sensors and Internet of Things (IoT) devices in the grid will provide a wealth of real-time data. Future voltage stability assessments should harness this data to improve monitoring and control strategies.

4. Grid modernization: with the ongoing modernization of power grids, future voltage stability assessment methods must adapt to accommodate the increased complexity introduced by smart grids, microgrids, and distributed energy resources.

5. Multi-objective optimization: researchers can explore multi-objective optimization techniques to simultaneously optimize voltage stability, economic operation, and environmental impact, considering factors such as renewable energy generation and grid resiliency.

6. Energy storage integration: as energy storage systems become more prevalent, future assessments should incorporate the dynamic capabilities of energy storage devices to enhance voltage stability and grid reliability.

7. Real-time adaptive control: develop real-time adaptive control strategies that can dynamically respond to changing grid conditions, such as fluctuations in renewable generation, to maintain voltage stability.

8. Decentralized control: investigate decentralized control strategies that allow distributed energy resources, such as solar panels and batteries, to participate actively in voltage stability management.

9. Standardization and regulatory frameworks: future efforts should include the development of standardized methods for voltage stability assessment, facilitating consistent practices across utilities and regulatory bodies.

10. Cross-disciplinary collaboration: encourage collaboration between power system engineers, data scientists, cybersecurity experts, and policymakers to develop holistic approaches to voltage stability assessment, considering both technical and regulatory aspects.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdul Rahman, T. K., and Jasmon, G. B. (1995). “A New technique for voltage stability analysis in a power system and improved loadflow algorithm for distribution network,” in Proceedings 1995 International Conference on Energy Management and Power Delivery EMPD '95, Singapore, 21-23 November 1995, 714–719. doi:10.1109/empd.1995.500816

CrossRef Full Text | Google Scholar

Adewole, R., and Tzoneva, R. (2017). Extended synchrophasor-based online voltage stability assessment using synchronous generator-derived indices: PMU-Based Online Voltage Stability Assessment. Int. Trans. Electr. Energy Syst. 27 (1), e2236. doi:10.1002/etep.2236

CrossRef Full Text | Google Scholar

Aghdam, P. A., and Khoshkhoo, H. (2020). Voltage stability assessment algorithm to predict power system loadability margin. IET Generation, Transm. Distribution 14 (10), 1816–1828. doi:10.1049/iet-gtd.2019.0230

CrossRef Full Text | Google Scholar

Ajjarapu, B., and Lee, B. (1992). Bifurcation theory and its application to nonlinear dynamical phenomena in an electrical power system. IEEE Trans. Power Syst. 7 (1), 424–431. doi:10.1109/59.141738

CrossRef Full Text | Google Scholar

Ajjarapu, V. (1995). “Application of bifurcation and continuation methods for the analysis of power system dynamics,” in Proceedings of International Conference on Control Applications, Albany, NY, USA, 28-29 September 1995, 52–56.

Google Scholar

Ajjarapu, V. (2007). Computational techniques for voltage stability assessment and control. United States: Springer Science \& Business Media.

Google Scholar

Ajjarapu, V., and Lee, B. (1998). Bibliography on voltage stability. IEEE Trans. Power Syst. 13 (1), 115–125. doi:10.1109/59.651622

CrossRef Full Text | Google Scholar

Albuquerque, M. A., and Castro, C. A. (2003). “A contingency ranking method for voltage stability in real time operation of power systems,” in 2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 23-26 June 2003, 1–5.

Google Scholar

Althowibi, F. A., and Mustafa, M. W. (2010). “Line voltage stability calculations in power systems,” in 2010 IEEE International Conference on Power and Energy, Kuala Lumpur, Malaysia, 29 November 2010 - 01 December 2010, 396–401. doi:10.1109/PECON.2010.5697616

CrossRef Full Text | Google Scholar

Althowibi, F. A., and Mustafa, M. W. (2012). “Power system network sensitivity to voltage collapse,” in 2012 IEEE International Power Engineering and Optimization Conference Melaka, Malaysia, Melaka, Malaysia, 06-07 June 2012, 379–383. doi:10.1109/PEOCO.2012.6230893

CrossRef Full Text | Google Scholar

Amroune, M. (2021). Machine learning techniques applied to on-line voltage stability assessment: a review. Archives Comput. Methods Eng. 28 (2), 273–287. doi:10.1007/s11831-019-09368-2

CrossRef Full Text | Google Scholar

Ancheng, X., Ruihuang, L., Mingkai, L., Chow, J. H., Tianshu, B., Ting, Y., et al. (2016). On-line voltage stability index based on the voltage equation of transmission lines. IET Generation, Transm. Distribution 10 (14), 3441–3448. doi:10.1049/iet-gtd.2015.1544

CrossRef Full Text | Google Scholar

Aolaritei, L., Bolognani, S., and Dörfler, F. (2018). Hierarchical and distributed monitoring of voltage stability in distribution networks. IEEE Trans. Power Syst. 33 (6), 6705–6714. doi:10.1109/tpwrs.2018.2850448

CrossRef Full Text | Google Scholar

Avalos, R. J., Canizares, C. A., Milano, F., and Conejo, A. J. (2009). Equivalency of continuation and optimization methods to determine saddle-node and limit-induced bifurcations in power systems. IEEE Trans. Circuits Syst. I Regul. Pap. 56 (1), 210–223. doi:10.1109/TCSI.2008.925941

CrossRef Full Text | Google Scholar

Ayasun, S., Nwankpa, C. O., and Kwatny, H. G. (2006). Voltage stability toolbox for power system education and research. IEEE Trans. Educ. 49 (4), 432–442. doi:10.1109/te.2006.879798

CrossRef Full Text | Google Scholar

Badru, H., and Taylor, C. (2000). Voltage stability analysis: V-Q power flow simulation versus dynamic simulation. IEEE Trans. Power Syst. 15 (4), 1354–1359. doi:10.1109/59.898112

CrossRef Full Text | Google Scholar

Balamourougan, V., Sidhu, T. S., and Sachdev, M. S. (2004). Technique for online prediction of voltage collapse. IEEE Proceedings-Generation, Transm. Distribution 151, 453–460. doi:10.1049/ip-gtd:20040612

CrossRef Full Text | Google Scholar

Baleboina, G. M., Daram, S. B., Venkataramu, P. S., and Nagaraj, M. S. (2017). TCSC incorporated voltage stability assessment under contingency condition. Int. J. Grid Distributed Comput. 10 (7), 27–40. doi:10.14257/ijgdc.2017.10.7.03

CrossRef Full Text | Google Scholar

Baleboina, G. M., and Mageshvaran, R. (2018). Application of ANN technique for identification of critical bus and branch. Int. J. Control Automation 11 (9), 11–24. doi:10.14257/ijca.2018.11.9.02

CrossRef Full Text | Google Scholar

Berizzi, S., Finazzi, P., Dosi, D., Marannino, P., and Corsi, S. (1998). First and second order methods for voltage collapse assessment and security enhancement. IEEE Trans. Power Syst. 13 (2), 543–551. doi:10.1109/59.667380

CrossRef Full Text | Google Scholar

Boričić, A., Torres, J. L. R., and Popov, M. (2021). Comprehensive review of short-term voltage stability evaluation methods in modern power systems. Energies (Basel) 14 (14), 4076. doi:10.3390/en14144076

CrossRef Full Text | Google Scholar

Chakraborty, K., Deb, G., and Deb, S. (2016). “Voltage stability assessment in radial distribution system by line stability indicator (LSI) and its improvement using SVC,” in In 2016 IEEE 1st International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), Delhi, India, 04-06 July 2016, 1–5.

CrossRef Full Text | Google Scholar

Chattopadhyay, T. K., Banerjee, S., and Chanda, C. K. (2014). “Impact of distributed generator on voltage stability analysis of distribution networks under critical loading conditions for composite loads,” in International Conference on Electronics, Communication and Instrumentation (ICECI), kolkata, India, 16-17 January 2014, 288–291. doi:10.1109/ICONCE.2014.6808728

CrossRef Full Text | Google Scholar

Chebbo, A. M., Irving, M. R., and Sterling, M. J. H. (1992). Voltage collapse proximity indicator: behaviour and implications. IEE Proc. C (generation, Transm. distribution) 139 (3), 241–252. doi:10.1049/ip-c.1992.0037

CrossRef Full Text | Google Scholar

Chen, H., Jiang, T., Yuan, H., Jia, H., Bai, L., and Li, F. (2017). Wide-area measurement-based voltage stability sensitivity and its application in voltage control. Int. J. Electr. Power Energy Syst. 88, 87–98. Elsevier Ltd. doi:10.1016/j.ijepes.2016.12.011

CrossRef Full Text | Google Scholar

Chow, K. W., Joe, H., and Cheung, W. (1992). A toolbox for power system dynamics and control engineering education and research. IEEE Trans. Power Syst. 7 (4), 1559–1564. doi:10.1109/59.207380

CrossRef Full Text | Google Scholar

Chuang, S. J., Hong, C. M., and Chen, C. H. (2016). Improvement of integrated transmission line transfer index for power system voltage stability. Int. J. Electr. Power Energy Syst. 78, 830–836. doi:10.1016/j.ijepes.2015.11.111

CrossRef Full Text | Google Scholar

Danish, M. S. S., Senjyu, T., Danish, S. M. S., Sabory, N. R., Narayanan, K., and Mandal, P. (2019). A recap of voltage stability indices in the past three decades. Energies (Basel) 12 (8), 1544. doi:10.3390/en12081544

CrossRef Full Text | Google Scholar

Daram, S. B., Venkataramu, P. S., and Nagaraj, M. S. (2016). “Performance index based contingency ranking under line outage condition incorporating IPFC,” in 2016 International Conference on Electrical, Electronics, and Optimization Techniques (ICEEOT), Chennai, India, 03-05 March 2016, 2589–2593. doi:10.1109/ICEEOT.2016.7755161

CrossRef Full Text | Google Scholar

De Moura, R. D., and Prada, R. B. (2005). “Contingency screening and ranking method for voltage stability assessment,” in IEE proceedings-generation (Transmission and Distribution), 891–898.

CrossRef Full Text | Google Scholar

Deng, G., Sun, Y., and Xu, J. (2009). “A new index of voltage stability considering distribution network,” in Asia-Pacific Power and Energy Engineering Conference, APPEEC, Wuhan, China, 27-31 March 2009. doi:10.1109/APPEEC.2009.4918070

CrossRef Full Text | Google Scholar

De Souza, A. C. Z., Canizares, C. A., and Quintana, V. H. (1997). New techniques to speed up voltage collapse computations using tangent vectors. IEEE Power Eng. Rev. 17 (2), 1380–1387. doi:10.1109/59.630485

CrossRef Full Text | Google Scholar

Disturbance Analysis Working Group and others (1979). Review of selected electric system disturbances in North America. Princeton, New Jersey: NERC, 08540.

Google Scholar

Dobson, I., and Lu, L. (1993). New methods for computing a closest saddle node bifurcation and worst case load power margin for voltage collapse. IEEE Trans. Power Syst. 8 (3), 905–913. doi:10.1109/59.260912

CrossRef Full Text | Google Scholar

Dong, Y., Xie, X., Zhou, B., and Yao, W. (2015). “Voltage-sag-severity-index based size planning of shunt capacitor banks to improve short-term voltage stability,” in IEEE Power and Energy Society General Meeting, Denver, CO, USA, 26-30 July 2015, 1–5. doi:10.1109/PESGM.2015.7286441

CrossRef Full Text | Google Scholar

Ekwue, A. O., Wan, H. B., Cheng, D. T. Y., and Song, Y. H. (1999). Singular value decomposition method for voltage stability analysis on the National Grid system (NGC). Int. J. Electr. Power Energy Syst. 21 (6), 425–432. doi:10.1016/S0142-0615(99)00006-X

CrossRef Full Text | Google Scholar

Eminoglu, U., and Hocaoglu, M. H. (2007). “A voltage stability index for radial distribution networks,” in 2007 42nd International Universities Power Engineering Conference, Brighton, UK, 04-06 September 2007, 408–413. doi:10.1109/UPEC.2007.4468982

CrossRef Full Text | Google Scholar

Fang, S., Cheng, H., Song, Y., Zhou, Q., He, H., and Zeng, P. (2015). “A new type of MW and MVar dispatch index for meeting voltage stability margin criteria based on normal vector of limit surface,” in 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26-30 July 2015, 1–5. doi:10.1109/PESGM.2015.7285814

CrossRef Full Text | Google Scholar

Furukakoi, M., Adewuyi, O. B., Shah Danish, M. S., Howlader, A. M., Senjyu, T., and Funabashi, T. (2018). Critical Boundary Index (CBI) based on active and reactive power deviations. Int. J. Electr. Power Energy Syst. 100, 50–57. doi:10.1016/j.ijepes.2018.02.010

CrossRef Full Text | Google Scholar

Gao, B., Morison, G. K., and Kundur, P. (1992). Voltage stability evaluation using modal analysis. IEEE Power Eng. Rev. 12 (11), 41. doi:10.1109/MPER.1992.161430

CrossRef Full Text | Google Scholar

Glavic, M., Novosel, D., Heredia, E., Kosterev, D., Salazar, A., Habibi-Ashrafi, F., et al. (2012). See it fast to keep calm: real-time voltage control under stressed conditions. IEEE Power Energy Mag. 10 (4), 43–55. doi:10.1109/MPE.2012.2196332

CrossRef Full Text | Google Scholar

Gong, Y., Schulz, N., and Guzmán, A. (2006). “Synchrophasor-based real-time voltage stability index,” in 2006 IEEE PES Power Systems Conference and Exposition, Atlanta, GA, USA, 29 October 2006 - 01 November 2006, 1029–1036. doi:10.1109/PSCE.2006.296452

CrossRef Full Text | Google Scholar

Gu, W., and Wan, Q. (2010). Linearized voltage stability index for wide-area voltage monitoring and control. Int. J. Electr. power \& energy Syst. 32 (4), 333–336. doi:10.1016/j.ijepes.2009.09.003

CrossRef Full Text | Google Scholar

Gubina, F., and Strmčnik, B. (1995). Voltage collapse proximity index determination using voltage phasors approach. IEEE Trans. Power Syst. 10 (2), 788–794. doi:10.1109/59.387918

CrossRef Full Text | Google Scholar

Haque, M. H. (2008). Use of local information to determine the distance to voltage collapse. Int. J. Emerg. Electr. Power Syst. 9 (2), 407–412. doi:10.2202/1553-779X.1911

CrossRef Full Text | Google Scholar

Haque, M. H. (2015). “Voltage stability assessment of distribution systems with fixed speed wind generating systems,” in IEEE Innovative Smart Grid Technologies-Asia (ISGT ASIA), Bangkok, Thailand, 03-06 November 2015, 1–6.

CrossRef Full Text | Google Scholar

Hassard, B. D., Kazarinoff, N. D., and Wan, Y.-H. (1981). Theory and applications of Hopf bifurcation. CUP Archive.

Google Scholar

Hatziargyriou, N. D., van Hecke, J., and van Cutsem, T. (1994). Indices predicting voltage collapse including dynamic phenomena. CIGRE Task Force.

Google Scholar

He, T., Kolluri, S., Mandal, S., Galvan, F., and Rastgoufard, P. (2004). “Identification of weak locations in bulk transmission systems using voltage stability margin index,” in 2004 International Conference on Probabilistic Methods Applied to Power Systems, Denver, CO, USA, 06-10 June 2004, 1814–1819. doi:10.1007/0-387-23471-3_3

CrossRef Full Text | Google Scholar

Huang, L., Xu, J., Sun, Y., Cui, T., and Dai, F. (2011). “Online monitoring of wide-area voltage stability based on short circuit capacity,” in 2011 Asia-Pacific Power and Energy Engineering Conference, Wuhan, China, 25-28 March 2011, 1–5. doi:10.1109/APPEEC.2011.5747730

CrossRef Full Text | Google Scholar

Ismail, N. A. M., Zin, A. A. M., Khairuddin, A., and Khokhar, S. (2014). “A comparison of voltage stability indices,” in Proceedings of the international power engineering and optimization conference, Langkawi, Malaysia, 24-25 March 2014, 30–34.

CrossRef Full Text | Google Scholar

Jalboub, M. K., Rajamani, H. S., Liang, D. T. W., Abd-Alhameed, R. A., and Ihbal, A. M. (2010). “Investigation of voltage stability indices to identify weakest bus (TBC),” in In International Conference on Mobile Multimedia Communications, 682–687.

Google Scholar

Julian, D. E., Vu, K. T., and Quaintance, W. H. (2000). “Quantifying proximity to voltage collapse using the voltage instability predictor (VIP),” in 2000 Power Engineering Society Summer Meeting (Cat. No.00CH37134), Seattle, WA, USA, 16-20 July 2000, 931–936.

Google Scholar

Kamel, M., Karrar, A. A., Eltom, A. H., Member, S., Karrar, A. A., and Eltom, A. H. (2018). Development and application of a new voltage stability index for on-line monitoring and shedding. IEEE Trans. Power Syst. 33 (2), 1231–1241. doi:10.1109/TPWRS.2017.2722984

CrossRef Full Text | Google Scholar

Kamel, M., Li, F., Bu, S., and Wu, Q. (2021). A generalized voltage stability indicator based on the tangential angles of PV and load curves considering voltage dependent load models. Int. J. Electr. Power & Energy Syst. 127, 106624. doi:10.1016/j.ijepes.2020.106624

CrossRef Full Text | Google Scholar

Kanimozhi, R., and Selvi, K. (2013). A novel line stability index for voltage stability analysis and contingency ranking in power system using fuzzy based load flow. J. Electr. Eng. Technol. 8 (4), 694–703. doi:10.5370/JEET.2013.8.4.694

CrossRef Full Text | Google Scholar

Karbalaei, F., Soleymani, H., and Afsharnia, S. (2010). “A comparison of voltage collapse proximity indicators,” in 2010 Conference Proceedings IPEC, Singapore, 27-29 October 2010, 429–432.

CrossRef Full Text | Google Scholar

Kataoka, Y., Watanabe, M., and Iwamoto, S. (2006). “A new voltage stability index considering voltage limits,” in IEEE PES Power Systems Conference and Exposition, Atlanta, GA, USA, 29 October 2006 - 01 November 2006, 1878–1883.

CrossRef Full Text | Google Scholar

Katsanevakis, M., Stewart, R. A., and Lu, J. (2019). A novel voltage stability and quality index demonstrated on a low voltage distribution network with multifunctional energy storage systems. Electr. Power Syst. Res. 171, 264–282. doi:10.1016/j.epsr.2019.01.043

CrossRef Full Text | Google Scholar

Kaya, P., Chanda, C. K., Keşan, G., Alver, Ö., and Tursun, M. (2013). Vibrational spectroscopic investigation of 1-pyrrolidino-1-cyclohexene: a comparative density functional study. Int. J. Energy Environ. Eng. 4 (1), 1–9. doi:10.1016/j.saa.2013.04.100

PubMed Abstract | CrossRef Full Text | Google Scholar

Kessel, P., Glavitsch, H., and Kessel, H. G. P. (1986). Estimating the voltage stability of a power system. IEEE Trans. Power Deliv. 1 (3), 346–354. doi:10.1109/TPWRD.1986.4308013

CrossRef Full Text | Google Scholar

Konar, S., Chatterjee, D., and Patra, S. (2015). V–Q sensitivity-based index for assessment of dynamic voltage stability of power systems. IET Generation, Transm. Distribution 9 (7), 677–685. doi:10.1049/iet-gtd.2014.0710

CrossRef Full Text | Google Scholar

Kundur, P. (1994). Power system stability and control. New York: McGraw-Hill.

Google Scholar

Kundur, P., Paserba, J., Ajjarapu, V., Andersson, G., Bose, A., Canizares, C., et al. (2004). Definition and classification of power system stability IEEE/CIGRE joint task force on stability terms and definitions. IEEE Trans. Power Syst. 19 (3), 1387–1401. doi:10.1109/TPWRS.2004.825981

CrossRef Full Text | Google Scholar

Li, Q., and Jiang, T. (2012). Sensitivity analysis based on local voltage stability index margin and its application. J. Power Automation Equip. 32 (4), 1–5.

Google Scholar

Li, Q., Zhao, F., Zhuang, L., Wang, Q., and Wu, C. (2023). Steady-state risk prediction analysis of power system based on power digital twinning. Sustainability 15 (3), 2555. doi:10.3390/su15032555

CrossRef Full Text | Google Scholar

Li, W., Wang, Y., and Chen, T. (2010). Investigation on the Thevenin equivalent parameters for online estimation of maximum power transfer limits. IET Generation, Transm. Distribution 4 (10), 1180–1187. doi:10.1049/iet-gtd.2010.0342

CrossRef Full Text | Google Scholar

Li, W. J., and Wang, W. (2002). Voltage stability control method based on sensitivity of load margin. J. Electr. Mach. control 6 (2), 173–178.

Google Scholar

Liang, X., Chai, H., and Ravishankar, J. (2022). Analytical methods of voltage stability in renewable dominated power systems: a review. Electricity 3 (1), 75–107. doi:10.3390/electricity3010006

CrossRef Full Text | Google Scholar

Lim, Z. J., Mustafa, M. W., and Bt Muda, Z. (2012). “Evaluation of the effectiveness of voltage stability indices on different loadings,” in 2012 IEEE International Power Engineering and Optimization Conference, PEOCO 2012 - Conference Proceedings, Melaka, Malaysia, 06-07 June 2012, 543–547. doi:10.1109/PEOCO.2012.6230925

CrossRef Full Text | Google Scholar

Lof, P.-A., Andersson, G., and Hill, D. J. (1993). Voltage stability indices for stressed power systems. IEEE Trans. Power Syst. 8 (1), 326–335. doi:10.1109/59.221224

CrossRef Full Text | Google Scholar

Mahseredjian, J., and Alvarado, F. (1997). Creating an electromagnetic transients program in MATLAB: MatEMTP. IEEE Trans. Power Deliv. 12 (1), 380–388. doi:10.1109/61.568262

CrossRef Full Text | Google Scholar

Makasa, K. J., and Venayagamoorthy, G. K. (2011). “On-line voltage stability load index estimation based on PMU measurements,” in 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24-28 July 2011, 1–6. doi:10.1109/PES.2011.6039882

CrossRef Full Text | Google Scholar

Marsden, J. E., and McCracken, M. (2012). The Hopf bifurcation and its applications. New York, NY: Springer Science \& Business Media.

Google Scholar

Matavalam, A. R. R., and Ajjarapu, V. (2015). Calculating the long term voltage stability margin using a linear index. IEEE Power Energy Soc. General Meet. 2015 (2), 1–5. doi:10.1109/PESGM.2015.7285952

CrossRef Full Text | Google Scholar

MathWorks, Inc (1993). MATLAB, high-performance numeric computation and visualization software: user’s guide: for macintosh computers. United States: MathWorks.

Google Scholar

Milosevic, B., and Begovic, M. (2003). Voltage-stability protection and control using a wide-area network of phasor measurements. IEEE Trans. POWER Syst. 18 (1), 121–127. doi:10.1109/tpwrs.2002.805018

CrossRef Full Text | Google Scholar

Mishra, A., Gundavarapu, V. N. K., Bathina, V. R., and Duvvada, D. C. (2016). Real power performance index and line stability index-based management of contingency using firefly algorithm. IET Generation, Transm. Distribution 10 (10), 2327–2335. doi:10.1049/iet-gtd.2015.1001

CrossRef Full Text | Google Scholar

Modarresi, J., Gholipour, E., and Khodabakhshian, A. (2016). A comprehensive review of the voltage stability indices. Renew. Sustain. Energy Rev. 63, 1–12. doi:10.1016/j.rser.2016.05.010

CrossRef Full Text | Google Scholar

Moger, T., and Dhadbanjan, T. (2015). A novel index for identification of weak nodes for reactive compensation to improve voltage stability. IET Generation, Transm. Distribution 9 (14), 1826–1834. doi:10.1049/iet-gtd.2015.0054

CrossRef Full Text | Google Scholar

Moghavvemi, M., and Faruque, M. O. (2001). Technique for assessment of voltage stability in Ill-conditioned radial distribution network. IEEE Power Eng. Rev. 21 (1), 58–60. doi:10.1109/39.893345

CrossRef Full Text | Google Scholar

Moghavvemi, M., and Faruque, O. (1998). Real-time contingency evaluation and ranking technique. IEE Proc. Generation, Transm. Distribution 145 (5), 517–523. doi:10.1049/ip-gtd:19982179

CrossRef Full Text | Google Scholar

Moghavvemi, M., and Omar, F. M. (1998). Technique for contingency monitoring and voltage collapse prediction. IEE Proc. C (generation, Transm. distribution 145, 634–640. doi:10.1049/ip-gtd:19982355

CrossRef Full Text | Google Scholar

Mohamed, A., Jasmon, G. B., and Yusofand, S. (1989). A static voltage collapse indicator using line stability factors. J. industrial Technol. 7 (1), 73–85.

Google Scholar

Musirin, I., and Abdul Rahman, T. K. (2002). “Novel fast voltage stability index (FVSI) for voltage stability analysis in power transmission system,” in 2002 Student Conference on Research and Development: Globalizing Research and Development in Electrical and Electronics Engineering, SCOReD 2002 - Proceedings, Shah Alam, Malaysia, 17-17 July 2002, 265–268. doi:10.1109/SCORED.2002.1033108

CrossRef Full Text | Google Scholar

Nagao, T., Tanaka, K., and Takeriaka, K. (1997). Development of static and simulation programs for voltage stability studies of bulk power system. IEEE Trans. Power Syst. 12 (1), 273–281. doi:10.1109/59.574948

CrossRef Full Text | Google Scholar

Nageswa Rao, A. R., Vijaya, P., and Kowsalya, M. (2021). Voltage stability indices for stability assessment: a review. Int. J. Ambient Energy 42 (7), 829–845. doi:10.1080/01430750.2018.1525585

CrossRef Full Text | Google Scholar

Nguyen, T. T., Le, K. H., Phan, T. M., and Duong, M. Q. (2021). An effective reactive power compensation method and a modern metaheuristic algorithm for loss reduction in distribution power networks. Complexity 2021, 1–21. doi:10.1155/2021/8346738

CrossRef Full Text | Google Scholar

Nizam, M., Mohamed, A., and Hussain, A. (2006). “Dynamic voltage collapse prediction in power systems using power transfer stability index,” in 2006 IEEE International Power and Energy Conference, Putra Jaya, Malaysia, 28-29 November 2006, 246–250.

CrossRef Full Text | Google Scholar

Parniani, M., and Vanouni, M. (2010). A fast local index for online estimation of closeness to loadability limit. IEEE Power Eng. Rev. 25 (1), 584–585. doi:10.1109/tpwrs.2009.2036460

CrossRef Full Text | Google Scholar

Pereira, O., Rosés, R., and Giménez, M. D. C. (2023). QV analysis for the identification of vulnerable zones to voltage collapse: a study case. Rev. Técnica energía 19 (2), 32–41. doi:10.37116/revistaenergia.v19.n2.2023.545

CrossRef Full Text | Google Scholar

Pérez-Londoño, S., Rodríguez, L. F., and Olivar, G. (2014). A simplified voltage stability index (SVSI). Int. J. Electr. Power Energy Syst. 63, 806–813. doi:10.1016/j.ijepes.2014.06.044

PubMed Abstract | CrossRef Full Text | Google Scholar

Raja, P., Selvan, M. P., and Kumaresan, N. (2013). Enhancement of voltage stability margin in radial distribution system with squirrel cage induction generator based distributed generators. IET Generation, Transm. Distribution 7 (8), 898–906. doi:10.1049/iet-gtd.2012.0579

CrossRef Full Text | Google Scholar

Rajagopalan, C., Lesieutre, B. C., Sauer, P. W., and Pai, M. A. (1992). Dynamic aspects of voltage/power characteristics (multimachine power systems). IEEE Trans. Power Syst. 7 (3), 990–1000. doi:10.1109/59.207312

CrossRef Full Text | Google Scholar

Rao, S., and Yuan, Y. (2022). Online monitoring of power grid intelligent voltage stability considering potential factors. Mob. Inf. Syst. 2022, 1–9. doi:10.1155/2022/8760582

CrossRef Full Text | Google Scholar

Rath, A., Ghatak, S. R., and Goyal, P. (2017). “Optimal allocation of distributed generation (DGs) and static VAR compensator (SVC) in a power system using revamp voltage stability indicator,” in 2016 National Power Systems Conference (NPSC), Bhubaneswar, India, 19-21 December 2016, 1–6. doi:10.1109/NPSC.2016.7858877

CrossRef Full Text | Google Scholar

Ratra, S., Tiwari, R., and Niazi, K. R. (2018). Voltage stability assessment in power systems using line voltage stability index. Comput. Electr. Eng. 70, 199–211. doi:10.1016/j.compeleceng.2017.12.046

CrossRef Full Text | Google Scholar

Rawat, M. S., and Vadhera, S. (2020). Probabilistic approach to determine penetration of hybrid renewable DGs in distribution network based on voltage stability index. Arab. J. Sci. Eng. 45 (3), 1473–1498. doi:10.1007/s13369-019-04023-1

CrossRef Full Text | Google Scholar

Reis, C., and Maciel Barbosa, F. P. (2009). “Line indices for voltage stability assessmen,” in Proceedings of the IEEE Bucharest power tech conference, Bucharest, Romania, 28 June 2009 - 02 July 2009, 1–6.

Google Scholar

Sadeghi, S. E., and Foroud, A. A. (2020). A new approach for static voltage stability assessment in distribution networks. Int. Trans. Electr. Energy Syst. 30 (3). doi:10.1002/2050-7038.12203

CrossRef Full Text | Google Scholar

Sahari, S., Abidin, A. F., and Rahman, T. K. A. (2003). “Development of artificial neural network for voltage stability monitoring,” in Proceedings. National Power Engineering Conference, 2003. PECon 2003, Bangi, Malaysia, 15-16 December 2003, 37–42. doi:10.1109/PECON.2003.1437413

CrossRef Full Text | Google Scholar

Salama, H. S., and Vokony, I. (2022). Voltage stability indices–A comparison and a review. Comput. Electr. Eng. 98, 107743. doi:10.1016/j.compeleceng.2022.107743

CrossRef Full Text | Google Scholar

Samuel, I. A., Katende, J., Awosope, C. O. A., and Awelewa, A. A. (2017). Prediction of voltage collapse in electrical power system networks using a new voltage stability index. Int. J. Appl. Eng. Res. 12 (2), 190–199.

Google Scholar

Schoder, A. (2003). PAT: a power analysis toolbox for MATLAB/simulink. IEEE Trans. Power Syst. 18 (1), 42–47. doi:10.1109/tpwrs.2002.807117

CrossRef Full Text | Google Scholar

Seethalekshmi, K., Singh, S. N., and Srivastava, S. C. (2010). Adaptive scheme for minimal load shedding utilizing synchrophasor measurements to ensure frequency and voltage stability. Electr. Power Components Syst. 38 (11), 1211–1227. doi:10.1080/15325001003652884

CrossRef Full Text | Google Scholar

Selim, A., Kamel, S., Jurado, F., and Nasrat, L. (2020). Voltage stability assessment of radial distribution systems including optimal allocation of distributed generators. Int. J. Interact. Multimedia Artif. Intell. 6, 32–40. doi:10.9781/ijimai.2020.02.004

CrossRef Full Text | Google Scholar

Seydel, R. (1994). Practical bifurcation and stability analysis, from equilibirum to chaos. New York: Springer.

Google Scholar

Seydel, R. (2009). Practical bifurcation and stability analysis. New York, NY: Springer Science \& Business Media.

Google Scholar

Simpson-Porco, J. W., and Bullo, F. (2016). Distributed monitoring of voltage collapse sensitivity indices. IEEE Trans. Smart Grid 7 (4), 1979–1988. doi:10.1109/tsg.2016.2533319

CrossRef Full Text | Google Scholar

Sinha, A. K., and Hazarika, D. (2000). A comparative study of voltage stability indices in a power system. Int. J. Electr. power \& energy Syst. 22 (8), 589–596. doi:10.1016/s0142-0615(00)00014-4

CrossRef Full Text | Google Scholar

Smon, I., Member, S., and Verbiˇ, G. (2006). Local voltage-stability index using tellegen ’ s theorem. IEEE Trans. Power Syst. 21 (3), 1267–1275. doi:10.1109/tpwrs.2006.876702

CrossRef Full Text | Google Scholar

Subramani, C., Dash, S. S., Arun Bhaskar, M., Jagadeeshkumar, M., Sureshkumar, K., and Parthipan, R. (2009). “Line outage contingency screening and ranking for voltage stability assessment,” in 2009 International Conference on Power Systems, Kharagpur, India, 27-29 December 2009, 1–5. doi:10.1109/ICPWS.2009.5442743

CrossRef Full Text | Google Scholar

Sybille, G. (2004). Simpowersystems user’s guide, version 4, published under sublicense from hydro-qu{\’e}bec, and the mathworks. United States: inc. MathWorks.

Google Scholar

Tamura, Y., Sakamoto, K., and Tayama, Y. (1988). “Voltage instability proximity index (VIPI) based on multiple load flow solutions in ill-conditioned power systems,” in Proceedings of the 27th IEEE Conference on Decision and Control, Austin, TX, USA, 07-09 December 1988, 2114–2119.

Google Scholar

Taylor, C. W. (1994). Power system voltage stability. McGraw Hill.

Google Scholar

Tiwari, R., Niazi, K. R., and Gupta, V. (2012). Line collapse proximity index for prediction of voltage collapse in power systems. Int. J. Electr. Power Energy Syst. 41 (1), 105–111. doi:10.1016/j.ijepes.2012.03.022

CrossRef Full Text | Google Scholar

Tran, M. T. (2009). Definition and implementation of voltage stability indices in PSS{\textregistered} NETOMAC.

Google Scholar

Van, T. H., Le Van, T., Thi, T. M., Duong, M. Q., and Sava, G. N. (2021). Improving the output of dc-dc converter by phase shift full bridge applied to renewable energy. ROMANIAN J. Tech. Sci. — Electrotech. ENERGY Ser. 66 (3), 175–180.

Google Scholar

Van Cutsem, T., and Vournas, C. (1998). Voltage stability of electrical power systems. New York: Springer S.

Google Scholar

Vanfretti, L., and Sevilla, F. R. S. (2015). “A three-layer severity index for power system voltage stability assessment using time-series from dynamic simulations,” in IEEE PES Innovative Smart Grid Technologies, Europe, Istanbul, Turkey, 12-15 October 2014, 1–5. doi:10.1109/ISGTEurope.2014.7028788

CrossRef Full Text | Google Scholar

Vargas, V. H., Quintana, L., and Miranda D, R. (1999). Voltage collapse scenario in the Chilean interconnected system. IEEE Trans. Power Syst. 14 (4), 1415–1421. doi:10.1109/59.801905

CrossRef Full Text | Google Scholar

Venkatasubramanian, V., Schattler, H., and Zaborsky, J. (1995). Dynamics of large constrained nonlinear systems-a taxonomy theory [power system stability]. Proc. IEEE 83, 1530–1561. doi:10.1109/5.481633

CrossRef Full Text | Google Scholar

Venkatesh, B., Ranjan, R., and Gooi, H. B. (2004). Optimal reconfiguration of radial distribution systems to maximize loadability. IEEE Trans. Power Syst. 19 (1), 260–266. doi:10.1109/tpwrs.2003.818739

CrossRef Full Text | Google Scholar

Vournas, C. (2004). Technical summary on the Athens and southern Greece blackout. National Technical University of Athens.

Google Scholar

Vournas, C. D., Lambrou, C., and Mandoulidis, P. (2017). Voltage stability monitoring from a transmission bus PMU. IEEE Trans. Power Syst. 32 (4), 3266–3274. doi:10.1109/TPWRS.2016.2629495

CrossRef Full Text | Google Scholar

Vournas, C. D., Potamianakis, E. G., Moors, C., and Van Cutsem, T. (2004). An educational simulation tool for power system control and stability. IEEE Trans. Power Syst. 1, 48–55. doi:10.1109/tpwrs.2003.821016

CrossRef Full Text | Google Scholar

Vournas, T., Manos, G. A., Kabouris, J., and Van Cutsem, T. (2000). Analysis of a voltage instability incident in the Greek power system. IEEE Power Eng. Soc. Winter Meet. 2 (27), 1483–1488. doi:10.1109/PESW.2000.850198

CrossRef Full Text | Google Scholar

Wang, L., Liu, Y., and Luan, Z. (2005). “Power transmission paths based voltage stability assessment,” in 2005 IEEE/PES Transmission & Distribution Conference & Exposition: Asia and Pacific, Dalian, 18-18 August 2005, 1–5.

Google Scholar

Wang, Y., Li, W., and Lu, J. (2009). A new node voltage stability index based on local voltage phasors. Electr. Power Syst. Res. 79 (1), 265–271. doi:10.1016/j.epsr.2008.06.010

CrossRef Full Text | Google Scholar

Wiszniewski, A. (2007). New criteria of voltage stability margin for the purpose of load shedding. IEEE Trans. Power Deliv. 22 (3), 1367–1371. doi:10.1109/tpwrd.2006.886772

CrossRef Full Text | Google Scholar

Wu, Y.-K., Chang, S. M., and Hu, Y.-L. (2017). Literature review of power system blackouts. Energy Procedia 141, 428–431. doi:10.1016/j.egypro.2017.11.055

CrossRef Full Text | Google Scholar

Yang, C. F., Lai, G. G., Lee, C. H., Su, C. T., and Chang, G. W. (2012). Optimal setting of reactive compensation devices with an improved voltage stability index for voltage stability enhancement. Int. J. Electr. Power Energy Syst. 37 (1), 50–57. doi:10.1016/j.ijepes.2011.12.003

CrossRef Full Text | Google Scholar

Yari, S., and Khoshkhoo, H. (2019). A comprehensive assessment to propose an improved line stability index. Int. Trans. Electr. Energy Syst. 29 (4), e2806–e2825. doi:10.1002/etep.2806

CrossRef Full Text | Google Scholar

Yazdanpanah-Goharrizi, A., and Asghari, R. (2007). “A novel line stability index (NLSI) for voltage stability assessment of power systems,” in Proceedings of the 7th WSEAS International Conference on Power Systems, 164–167.

Google Scholar

Yuva Kishore, A., and Guru Mohan, B. (2018). Enhancement of voltage stability and transmission congestion management with UPFC. Int. J. Grid Distributed Comput. 11 (6), 15–26. doi:10.14257/ijgdc.2018.11.6.02

CrossRef Full Text | Google Scholar

Zambroni de Souza, A. C., Monn, F. W., Borges, I. F., and Ocariz, T. R. (2011). Using PV and QV curves with the meaning of static contingency screening and planning. Electr. Power Syst. Res. 81 (7), 1491–1498. doi:10.1016/j.epsr.2011.02.012

CrossRef Full Text | Google Scholar

Zhang, Y. Y., and Zhang, J.-S. (2005). An improved continuation power flow method for static voltage stability limit. J. t Power Syst. automation 17 (2), 21–25.

Google Scholar

Zhao, W. (2017). A short-term voltage stability index and case studies. arXiv preprint arXiv:1702.06697, Available at: https://arxiv.org/ftp/arxiv/papers/1702/1702.06697.pdf#:∼:text=Voltage%20Stability%20Index%20(SVSI)%2C%20case%20studies&text=CCORDING%20to%20the%20definition%20of,controlled%20loads%2C%20and%20HVDC%20converters.

Google Scholar

Zhao J, G. Z., and Yang, Y. (2011). “A review on on-line voltage stability monitoring indices and methods based on local phasor measurements,” in Proceedings of the power systems computation conference, 1–7.

Google Scholar

Zimmerman, D. (2005). RD and murrillo-S{\’a}nchez, CE and Gan, “MatPower, version 3.0. 0, user’s manual,” {power system engineering research center. Cornell University.

Google Scholar