A survey on parameters estimation of the proton exchange membrane fuel cells based on the swarm-inspired optimization algorithms

The main purpose of this study is to review various swarm-inspired optimization algorithms to discuss the significance of some established works in this area. Accurate parameter estimation is required to guarantee proper modeling of PEMFCs. However, because PEMFC models are complex, non-linear, and multivariate, parameter estimation is quite difficult. To estimate the linear and non-linear parameters of a PEMFC model in real time, this work investigates PEMFC model parameters estimation methods with a focus on online identification algorithms, which are thought of as the foundation of designing a global energy management strategy. Various PEMFC models with various classifications and objectives are initially addressed in this regard. The parameters of two well-known semi-empirical models in the literature, including 500 W BCS PEMFC and the 6 kW NedSstack PS6 PEMFC have then been identified using some potential swarm-inspired optimization algorithms for practical applications, such that the TSD error for the NedStack PS6 and BCS PEMFC based on the swarm-inspired optimization algorithms provide averagely 2.22 and 0.047, respectively. Finally, the obtained accomplishments and upcoming difficulties are highlighted.

1 Introduction

Today, population growth, growing demand for energy and the depletion of fossil resources, global environmental concerns, and the growing need to use energy have led researchers to look for more efficient and environmentally friendly methods of energy production (Abdelkareem, Elsaid, et al., 2021). In this context, renewable energy technologies have created new formats for the public use of renewable energy sources. A fuel cell is a suitable option for power generation due to its characteristics such as high efficiency, no noise, and no pollution (Wang, Wang et al., 2018). These batteries convert the chemical energy contained in gases such as hydrogen directly into electricity without a combustion process (Abdelkareem, Elsaid et al., 2021).

Fuel cells are widely used as environmentally friendly energy sources in the 21st century. Fuel cell research is associated with significant growth due to economic imperatives (Arshad, Ali et al., 2019). Fuel cells are one of the oldest energy conversion technologies. Fuel cells are good alternatives to conventional power generation methods for small applications (Shao, Dodelet et al., 2019). Hydrogen and hydrocarbons contain significant chemical energy compared to ordinary batteries. Therefore, fuel cells are currently being developed on a large scale to use multiple energies (Arshad, Ali et al., 2019). Fuel cells generate electricity and heat during the electrochemical reaction between oxygen and hydrogen in the form of water.

Fuel cell technology is a promising alternative to fossil fuels for providing energy in rural areas where there is no access to the public electricity grid or where electricity cabling and transmission costs are high (Ijaodola, El-Hassan et al., 2019).

These elements also are increasingly being used in grid-connected systems to improve efficiency and reduce emissions (Xu, Huang et al., 2022). By using the electricity produced by PEMFCs to supplement existing grid power, grid operators can reduce their reliance on traditional sources of energy while still meeting demand (Sun, Li et al., 2022). Additionally, PEMFCs offers a clean form of energy that emits zero carbon emissions, which can help reduce a region’s overall air pollution levels (Ge, Yan et al., 2022).

PEMFCs are highly efficient and cost-effective devices that are ideal for grid-connected systems as they offer both energy security and environmental benefits (Ge, Du et al., 2022). For instance, because PEMFCs use hydrogen fuel, an intermittent renewable resource, they can provide a reliable source of electricity even when the Sun is not shining or the wind is not blowing, helping to prevent brownouts or blackouts (Zhong, Zhou et al., 2022). Additionally, since the only byproduct of hydrogen fuel cells is water, they are one of the cleanest sources of energy available (Li, Deng et al., 2022). With their high efficiency, low emissions, and reliability, PEMFCs are rapidly becoming the preferred choice for grid-connected systems. Human:

In addition, applications with essential safety requirements for electrical energy, such as uninterruptible power supplies (UPS), power plants, and distributed systems, can use fuel cells as an energy source (Prasad and Tripathi, 2021). Currently, fuel cell systems are widely used in both small (Wang, Diaz et al., 2020) and large-scale (Arsalis, 2019) applications, such as combined cycle (CHP) power plants (Bornapour, Hemmati et al., 2020), mobile phone power systems (Shi, Dai et al., 2021), laptop computers (RavindranathTagore, Anuradha et al., 2019), and communications equipment (Li, Deng et al., 2020). Despite all the benefits of its use, there are some limitations to using fuel cells. For example, the short life of fuel cells corresponds to the pulse and impurity of the gas flow (Vichard, Harel et al., 2020). Fuel cells generate electricity and heat through an electrochemical reaction, which is a reverse electrolysis reaction (Zhang, Wang et al., 2023). The main difference between different fuel cell designs is the chemical properties of the electrolyte.

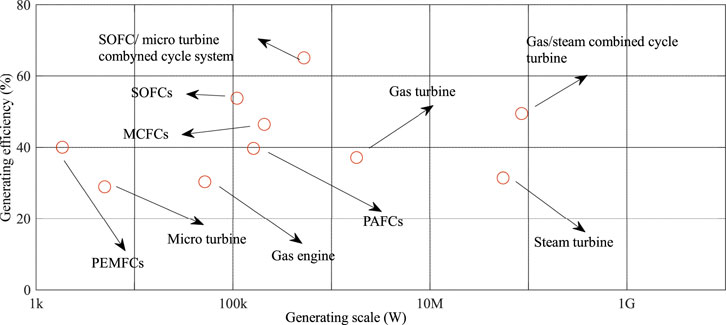
Fuel cells have different types according to temperature, efficiency, applications and costs. Which are divided into six main groups based on the choice of fuel and electrolyte: Alkaline fuel cell (AFC) (Sun, Lin et al., 2018), phosphoric acid fuel cell (PAFC) (Cheng, Zhao et al., 2021), Solid oxide fuel cell (SOFC) (Tian, Yan et al., 2020), Molten carbonate fuel cell (MCFC) (Salehi, Mousavi et al., 2019), and Proton exchange membrane fuel cell (PEMFC) (Yu, Wang et al., 2019). Figure 1 shows the performance of different fuel cells versus generating scale.

FIGURE 1

FIGURE 1. Efficiency of the different fuel cells vs. generating scale.

The main disadvantage of fuel cells is their high price. The high price of platinum catalysts is one of many obstacles to building a hydrogen infrastructure. The price of a fuel cell from a generator motor of the same power is more than three times higher (Zhao, Tu et al., 2021).

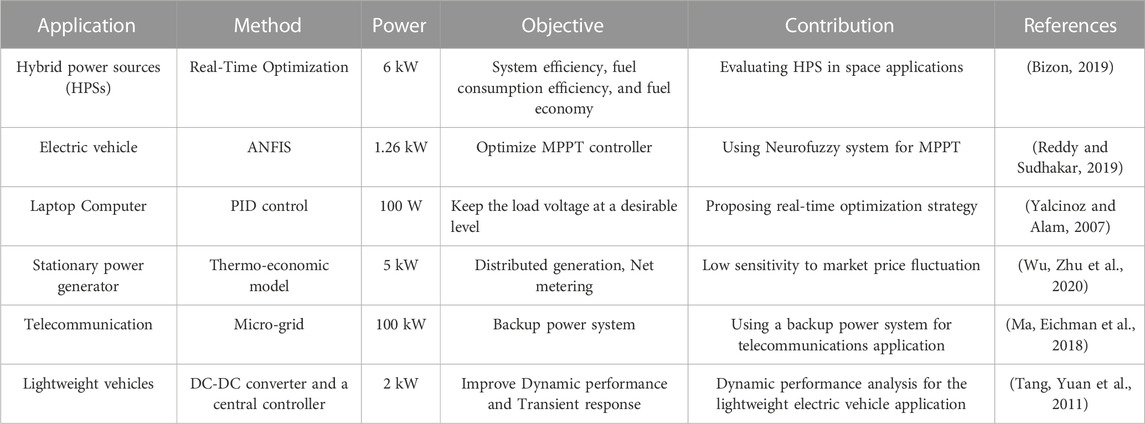
For specific applications, polymer electrolyte membrane fuel cells (PEMFCs) are preferable to other types. The reasons for their preference are their low operating temperature (60°C–80°C), which enables quick start-up and fast response to the load, and the use of solid polymer, which makes it easy to assemble and transport the fuel cell (Sapkota and Aguey-Zinsou, 2023). These advantages make the PEMFCs to become the best choice for an alternative power source for transportation and concentrated power systems. Therefore, achieving an optimal PEMFC design is an important issue in recent years (Fathy, Rezk et al., 2023). In the development of PEMFC technology, modeling is a key factor. Modeling of PEMFCs may be used for a variety of purposes. Table 1 indicates some applications of PEMFC onboard.

TABLE 1

TABLE 1. Some applications of PEMFC on-board.

Today, there are two methods for analyzing the performance of the PEMFC. One is the use of laboratory equipment and the other is mathematical modeling. It is very difficult to accurately measure the spatial and temporal concentration of elements, temperature, and current density for a better understanding of fuel cell performance (Zhao, Mao et al., 2020). In recent decades, many modeling improvements have been made, mainly in the form of numerical simulations, and fewer analytical studies have been conducted.

In recent years, many efforts have been made to achieve the optimal design of the PEMFC system. Although most of these studies have made a significant contribution to the description of PEMFC literature, e.g., the formulation of PEMFC models with different levels of complexity and the development of different optimization techniques, most of them limited to a single design goal (Blal, Benatiallah et al., 2019). Various studies have been conducted to optimize performance considering price, durability, and pollutant emission as design goals. In addition, some items aimed at optimizing a target for a specific part of the PEMFC system (Pashaki and Mahmoudimehr, 2023). The electrode-membrane assembly, electrode, bipolar plates, permeation layer, cathode and air diffuser, and a layer of catalyst presented (Lim, Majlan et al., 2021). However, the results of these studies can be misleading because the interaction between the different targets has not been taken into account (Zhang, Liu et al., 2019). Moreover, the incompatibility of the objectives can determine that the optimal solver is the most interesting.

By the way, it has been suggested to use identification algorithms to address the issues brought on by deterioration, aging, and changing operating conditions (Zakaria, Kamarudin et al., 2023). It should be noted that carefully selecting an identification method is just as crucial as selecting a model because it can enhance the model and even make up for its deficiencies in specifics and considerations (Chen, Badji et al., 2022).

In this review paper, the objective is to thoroughly evaluate the various methods and approaches used for parameter estimation of the PEMFCs based on the swarm-Inspired optimization algorithms. We will assess and compare the strengths and weaknesses of each approach and provide an overall assessment of the current literature on the subject. We aim to identify which methods are most effective for different applications and explain why, to provide valuable insights for practitioners.

2 Problem statement

The PEMFC systems convert chemical energy into electrical energy. The fuel is applied at a specific pressure to the anode part of the fuel cell until the catalytic layer is reached (Rezk, Olabi et al., 2022). The other part of the fuel cell is referred to as the cathode. The chemical reaction begins in the catalytic layer and produces both protons and electrons, but the electrolyte only allows for proton transport until it reaches the catalytic layer of the cathode (Zhao and Li, 2019). In another area of the fuel cell, up until the electrolyte, the flow of oxide allows for the production of liquid water, liquid oxygen, and residual heat. Figure 2 indicates the chemical reaction of the PEMFC (Ang, Salem et al., 2022).

FIGURE 2

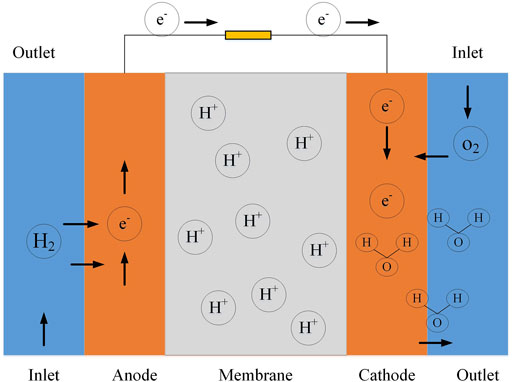
FIGURE 2. Chemical reaction of the PEMFC (Ang, Salem et al., 2022).

As can be observed from Figure 2, the overall chemical reaction can be defined as follows:

$O_2+2H_2\to 2H_{2}O+Heat+Electricity(1)$

Such that, on the anode side,

$H_2\to 2H^{+}+2e^{-}(\mathrm{2a})$

And in the cathode side,

$4H^{+}+O_2+4e^{-}\to 2H_{2}O(\mathrm{3a})$

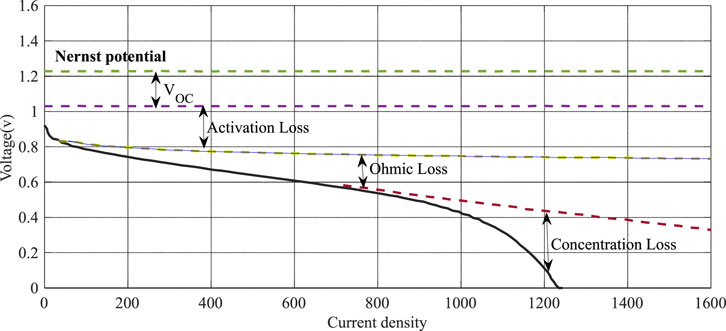
The Nernst-Plunk equation is used to determine the fuel cell voltage in the absence of voltage loss. However, after deducting the voltage losses from the output voltage, the terminal voltage will not match the open circuit voltage because of the voltage drops occurring in the fuel cell (Valdes-Lopez, Mason et al., 2020). They are the ohmic voltage drop (${\mathit{V}}_{\Omega }$), the activation voltage drop (${\mathit{V}}_{\mathit{a}\mathit{c}\mathit{t}}$), and the concentration voltage drop (${\mathit{V}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{s}}$). A typical polarization curve of a single cell operating at a temperature of about 70°C and normal atmospheric pressure is shown in Figure 3.

FIGURE 3

FIGURE 3. Single cell polarization curve.

The terminal voltage of a fuel cell can be obtained using the following equation by taking these voltage drops into account:

$E=E_{nernst}-V_{\Omega }-V_{act}-V_{cons}(\mathrm{2b})$

where, ${\mathit{E}}_{\mathit{n}\mathit{e}\mathit{r}\mathit{n}\mathit{s}\mathit{t}}$ specifies the cells’ mean thermodynamic potential which indicates the reversible voltage (Nernst voltage) and has been given below:

$E_{nernst}=0.5\times R\times T\times F^{-1}\left(P_{H_2}\times P_{O_2}^{\frac{1}{2}}\right)+E_0-{\lambda }_e\times {\tau }_{e}s\times {\left({\tau }_{e}s+1\right)}^{-1}\times I\left(s\right)-\delta T(\mathrm{3b})$

where, ${\mathit{E}}_{\mathrm{0}}$ describes the standard reference potential [${\mathit{E}}_{\mathrm{0}}=\mathrm{1.229}\mathit{V}$ (Lazarou, Pyrgioti et al., 2009)], $\mathit{\delta }$ signifies the experimental constant ($\mathit{V}/\mathit{K}$), $\mathit{T}$ determines the fuel cell temperature, $\mathit{F}$ describes the Faraday constant and is equal to $\mathrm{96.487}\mathit{k}\mathit{C}/\mathit{m}\mathit{o}\mathit{l}$, ${\mathit{\tau }}_{\mathit{e}}=\mathrm{80}\mathit{s}$ [Shakhshir, Gao et al., 2020), ${\mathit{\lambda }}_{\mathit{e}}$ defines a constant factor (here, ${\mathit{\lambda }}_{\mathit{e}}=\mathrm{3.3}\mathbf{\Omega }$ (Shakhshir, Gao et al., 2020)], and ${\mathit{P}}_{{\mathit{H}}_{\mathrm{2}}}$ and ${\mathit{P}}_{{\mathit{O}}_{\mathrm{2}}}$ determine, in turn, the partial pressures of hydrogen and oxygen ($\mathit{P}\mathit{a}$).

If the number of cells ($\mathit{n}$) is more than one, the voltage stack ($V_{\mathit{s}\mathit{t}\mathit{a}\mathit{c}\mathit{k}}$) has been achieved as follows:

$V_T=n\times E(4)$

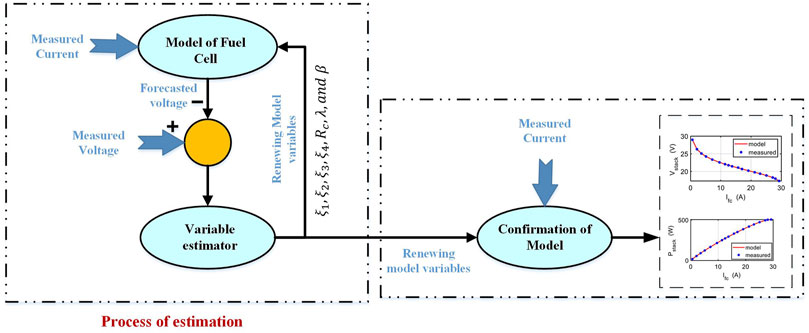
A fuel cell’s ideal operating voltage for all attracted currents from the cell is close to 1.2 V. In reality, the fuel cell can only receive a higher level of this voltage when there is no voltage drop in the system, which is not possible (Celik and Karagöz, 2020). To create an effective device design, all model parameters must be precisely set. The best estimate of the PEMFC model is a crucial task in general.

So, one of the main objectives of this work is to find the ideal value of the structure’s ${\mathit{E}}_{\mathrm{0}}$. Although the literature specifies the values of ${\mathit{\tau }}_{\mathit{e}}$ and ${\mathit{\lambda }}_{\mathit{e}}$, there is still a lot of room for interpretation. This served as further inspiration for us to focus on improving the estimate of these two variables. Electricity passing through a substance with low conductivity is related to ohmic resistance. In the word of Eq. 2a, it is possible to model the activation voltage drop of a PEMFC mathematically as follows:

$V_{act}={\beta }_1+{\beta }_2\times T+{\beta }_3\times T\times \ln \left(\mathit{C}{O}_2\right)+{\beta }_4\times T\times \ln \left(I\right)(5)$

where, $\mathit{i}$ stands for the coefficient number, an ${\mathit{\beta }}_{\mathit{i}}$ defines the coefficient number in the model that is usually achieved pseudo-empirically, $\mathit{I}$ dignifies the fuel cell’s current, and $\mathit{C}{\mathit{H}}_{\mathrm{2}}$ and $\mathit{C}{\mathit{O}}_{\mathrm{2}}$ are the concentration of hydrogen at the anode side ($\mathit{m}\mathit{o}\mathit{l}.\mathit{c}{\mathit{m}}^{-\mathrm{3}}$) and the cathode/gas interface concentration ($\mathit{m}\mathit{o}\mathit{l}.\mathit{c}{\mathit{m}}^{-\mathrm{3}}$) for oxygen and are achieved by the following equations:

$C{H}_2=\frac{P_{H_2}}{10.9\times e^{\left(\frac{77}{T}\right)}}\times {10}^{-7}(6)$

$C{O}_2=p_{O_2}\times {\left[5.08\times {10}^8\times e^{\left(\frac{-498}{T}\right)}\right]}^{-1}(7)$

That is accomplished with metaheuristic algorithms in the best possible way. The ohmic resistance has to do with electricity moving through a material with low conductivity. This can be stated as follows:

$R_{\Omega }=R_t+R_m(8)$

The equivalent resistance of the plate collector in this instance, which is passing protons and electrons over the membrane, is specified by ${\mathit{R}}_{\mathit{t}}$. The membrane resistance, ${\mathit{R}}_{\mathit{m}}$, is calculated using the formula below and is assumed in this study to be $\mathrm{300}\mathit{\mu }\mathit{\Omega }$.

$R_m=\frac{181.6\times l\times \left[1+0.03\times \frac{I}{A}+0.062\times {\left(\frac{I}{A}\right)}^{2.5}\times {\left(\frac{T}{303}\right)}^2\right]}{A\times \left(\phi -0.634-\frac{3I}{A}\right)\times e^{\left(4.18\times \frac{T^c-30}{T^c}\right)}}(9)$

where, $\phi$ denotes a variable quantity related to relative humidity, $l$ denotes the stack’s thickness (in millimeters) and the ratio of the positive electrode gas stoichiometry to membrane age was less than 23 (San Martin, Zamora et al., 2010). Due to the mass concentration drop, the reactant concentration on the surface of the electrodes is decreased. Below describes the formulation of the concentration loss model.

$R_{cons}=B\times I^{-1}\times \ln \left(\frac{I_l}{I_l-I}\right)(10)$

where, $B$ denotes an experimental coefficient that the cell’s operating circumstances allow it to achieve. Another term that is taken into account in this study as an optimization parameter is this value.

$V_C=\left(R_{act}+R_{cons}\right)\times \left(I-C\times \frac{d{V}_c}{dt}\right)(11)$

The non-linear nature of this component makes its value unclear. For optimal selection the best value for it, this parameter is therefore also taken into consideration.

Current limitation ($I_l$) is a further factor to take into account when enhancing the model. According to the (Spiegel, 2011), this parameter is defined as follows.

$I_l={\tau }^{-1}\times N_r\times F\times d\times C_b(12)$

where, $N_r$ signifies the needed value for the electrons in the reaction, $\tau$ specifies the diffusion layer thickness, $d$ defines the well-organized diffusion coefficient during the reaction, and $C_b$ represents the bulk concentration.

3 A survey of modeling of the PEMFCs

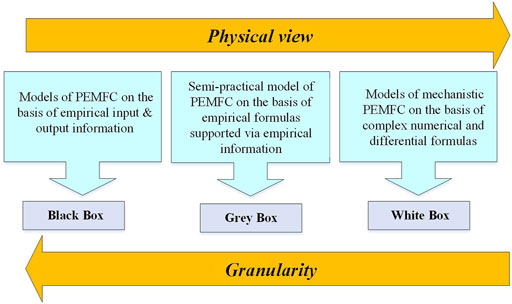
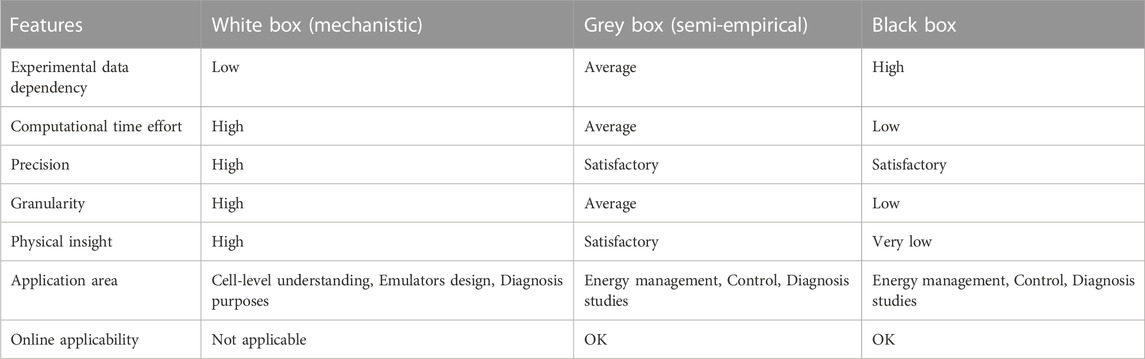
As illustrated in Figure 4, the existing PEMFC models in the literature may be divided into three groups: white box, black box, and grey box models (Tsalapati, Johnson et al., 2021), sometimes referred to as mechanistic or theoretical models, are made up of algebraic and differential equations that are based on the principles of fluid mechanics, electrochemistry, and thermodynamics.

FIGURE 4

FIGURE 4. PEMFC models categories.

They have diverse geographic dimensions and are intended to examine a variety of phenomena, like catalyst employment, polarization impacts, and water management. Blackbox models, in contrast to Whitebox models, are derived from observations and do not examine the specifics of physical interactions inside the PEMFC (Zhao, Mao et al., 2020). Blackbox models are extremely intriguing for online applications, such as cars, because of how little computing work is required. Yet, when faced with novel operational situations, these models’ uncertainties grow. Fuzzy logic, artificial neural networks, and their combinations are thought to be the most common methods for creating PEMFC black box models (Qaiser, Asghar et al., 2021). Greybox models, often referred to as quasi-models, present a respectable middle ground between complication and clarity.

These models illustrate the fundamental electrochemical properties of PEMFCs and are based on physical relationships that are confirmed by experimental evidence (polarization curve). Energy management design is one of the fascinating real-world uses for grey box PEMFC models. The physical understanding offers important details on polarization curve effects including cell reversible voltage, activation drop, ohmic loss, and concertation overvoltage, which are crucial for determining if the results are relevant. A quick synopsis of the PEMFC models addressed is provided in Table 2.

TABLE 2

TABLE 2. Different types of the PEMFC models.

Grey and black box models appear to be the most appropriate types for control and energy management reasons in light of the previously stated models. The next part offers a full analysis of the identification techniques used for PEMFC models’ parameter estimates, which are based on grey- and black-box models.

The accuracy of PEMFC models may be dramatically improved and the absence of details can be made up for by correctly identifying the parameters. However, due to their intricate characteristics, the PEMFC models’ parameter estimate is extremely difficult. To optimize and identify the parameters of a PEMFC model, various methods were reported in the literature. Due to the complexity of these systems, most of them are solved recently by metaheuristics algorithms. Some of these works can be considered as bird mating optimizer (Askarzadeh and Rezazadeh, 2013), flower pollination optimization algorithm (Askarzadeh and Rezazadeh, 2013), developed Krill herd optimization algorithm (Guo, Dai et al., 2020), improved seagull optimization algorithm (Cao, Li et al., 2019).

4 Model parameters estimation based on metaheuristic

The values of the model parameters, such as $R_c$, ${\zeta }_1$, ${\zeta }_2$, ${\zeta }_3$, ${\zeta }_4$, $B$, $\lambda$, $Q$, must be established to construct a mathematical model of PEMFC based on the electrochemical process described above. The key limitations are, however, that:

1. Model parameters are unknown

2. Model parameters differ significantly with each operating state and affect the quality of the V-I curves;

3. Model parameter values are not listed in the manufacturer’s datasheet.

Parameter identification is a crucial, challenging activity that is extremely complicated. As a result, to make things simpler, the choice of the fuel cell model parameter has been made as a numerical optimization issue that can be resolved using the optimization approach. The unknown PEMFC model parameters have been essentially determined using a variety of optimization approaches, including AI techniques. Additionally, the difficulty of estimating unknown model parameters using data from datasheets or experimental I-V data is known as the Fuel cell model parameter estimation problem. The objective function is often the Root Mean Square Error (RMSE) between the empirical and simulated data, i.e.,

$MSE=\frac{1}{N}{\displaystyle \sum }_{j=1}^N{\left(V_{out}^j-V_{\mathit{exp}}^j\right)}^2(13)$

where, $N$ describes the sample data quantity of the empirical data, and $V_{out}^j$ and $V_{\mathit{exp}}^j$ specify, in turn, the output voltage for empirical and model data. The PEMFC’s basic modeling procedure is depicted in Figure 5 as a representation.

FIGURE 5

FIGURE 5. Basic modeling of the parameter estimation for a PEMFC.

To identify the linear and non-linear parameters of an electrochemical PEMFC model without being trapped in local optima, many articles have presented metaheuristic-based optimization strategies (Yang, Wang et al., 2020). The bulk of the metaheuristic-based approaches is surprisingly based on the semi-empirical model presented by Amphlett et al., which can adequately mimic the behavior of the PEMFC (Wilberforce, Rezk et al., 2023). The central concept of all of this research is to study the impact of the metaheuristic approaches on estimating the physical parameters of the static semi-empirical PEMFC model.

5 A review of some newest swarm-inspired algorithms utilized for model parameters estimation

Finding the most suitable solution that satisfies the problem’s constraints and criteria is the basic goal of optimization [4; 26]. A function known as a fitness (cost) function is used to compare many possible solutions to a problem to choose the best one.

Depending on the problem’s nature will determine how to select a fitness function. One of the frequent objectives of improving transportation networks, for instance, is to reduce spent time or cost. The main goal of optimization is to choose the design parameters so that they minimize or maximize the objective function. Several optimization methods have been used for this purpose. In recent years, the use of metaheuristic algorithms as efficient optimization methods has been considered in various problems. Meta-heuristic algorithms show different efficiency in solving different problems. A meta-heuristic algorithm may perform better than other algorithms for solving a specific problem and show a weaker performance in another problem.

The idea behind a metaheuristic algorithm is to present an adequate solution to a problem in a reasonable amount of time, and an exploratory algorithm may not be the best solution to a problem, but it may be the closest solution. Metaheuristic algorithms can be combined with optimization algorithms to improve algorithm efficiency. A metaheuristic is a combination of heuristics designed to find, generate, or select each exploration at each step and provide a good solution to an optimizable problem. Metaheuristic algorithms assume some assumptions about the optimization problem to be solvable. Metaheuristic algorithms are algorithms that are usually inspired by nature, physics, and human life and are used to solve many optimization problems.

Swarm intelligence is inspired by the collective behavior of decentralized, self-organizing natural or artificial systems. This concept is used in work with artificial intelligence. Swarm intelligence systems usually consist of a set of simple agents or bodies that locally interact with each other and with the environment. Inspiration often comes from nature, especially biological systems. Agents follow very simple rules, and while there is no central control structure that dictates how individual agents should behave, local and somewhat random interactions between these agents lead to “intelligent” globally behaving agents. Include ant colonies, bee colonies, flocks of birds, eagle hunting, animal husbandry, bacterial growth, fish schools, and microbial intelligence.

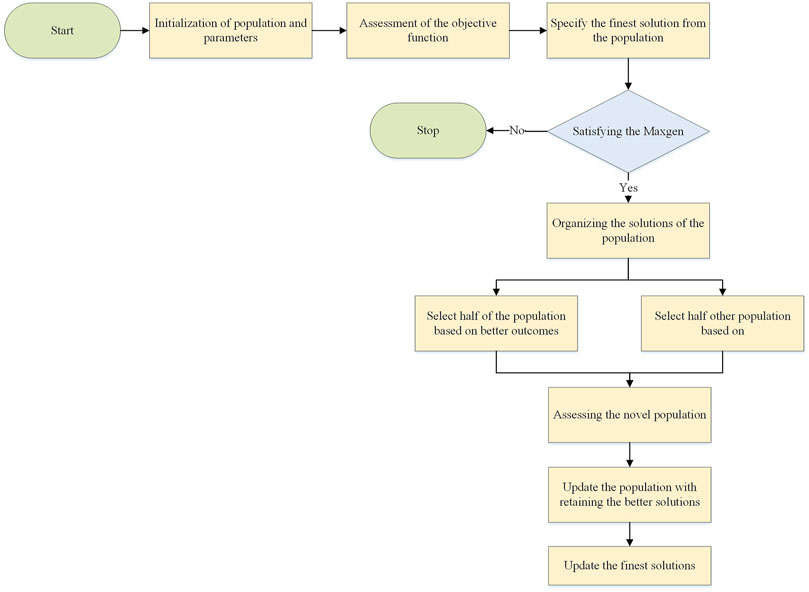
The candidates are considered as solutions in the search space of the objective problem in SI algorithms, and the candidates are varied and self-organizing during the evolutionary process and may learn from each other to update their solutions. Swarm intelligence algorithms are often used in combination with other algorithms to reach an optimal solution or to avoid a locally optimal solution. In the following, some newest swarm intelligence algorithms like the Bi-subgroup optimization algorithm (Chen, Pi et al., 2022), the improved Salp Swarm Algorithm (Sultan, Menesy et al., 2020), the improved chicken swarm optimization algorithm (Wang, Huang et al., 2022), artificial bee colony differential evolution optimizer (Hachana and El-Fergany, 2022), that were utilized for PEMFC stacks model identification, have been explained in details.

5.1 Bi-subgroup optimization algorithm

5.1.1 Flower pollination algorithm

The best individual and the best historical position in the swarm are the two vectors used in PSO’s population evolution to pull every individual for updating (Diab and El-Sharkawy, 2016). Everyone uses the same updating strategy. However, the majority of SI algorithms do not take into account the hierarchical organization of people. The flower pollination algorithm (FPA)’s search procedure is deliberately segmented, in comparison to the PSO’s.

The FPA is s swam intelligence global optimization algorithm that is inspired by the flower pollination process features. This process is divided into the following four ideal guidelines (Mohammadzadeh and Gharehchopogh, 2021).

Guideline 1: Cross-pollination by pollinators like birds is considered a phase of global pollination, and the pollinators fly with a gentle touch.

Guideline 2: Local pollination is considered to occur when neighboring flowers self-pollinate.

Guideline 3: The reproducing rate, which is directly correlated with the comparable level of the two concerned flowers, is considered the floral constancy.

Guideline 4: Using a switch probability, both global and local pollination is carried out.

The FPA has both a worldwide and local pollination operator, following the aforementioned requirements. Each pollen item is considered as a solution in the FPA, and the solutions are given random vector initializations in the search space that is possible. As an introductory formula, consider the following:

$x_i=\underset{-}{x}+\sigma \left(\overline{x}-\underset{-}{x}\right)i=\mathrm{1,2},\dots ,N(14)$

where, $\sigma$ describes a d-dimensional random value between 0 and 1, $N$ defines the population quantity.

Pollinators like birds, which have a very wide range of movement and can transport pollen over great distances, play an important role in the worldwide pollination process. Rules 1 and 3 are so developed as follows:

$x_i^{t+1}=x_i^t+\gamma L\left(\gamma \right)\left(gbest-x_i^t\right)(15)$

where, $x_i^t$ defines the $i^{th}$ solution for iteration $t$, $\gamma$ specifies a step factor, $L\left(\gamma \right)$ defines the flight feature of birds that can be assumed as a changing step factor, $gbest$ signifies the global best position.

By assuming $L$ bigger than 1, we have the:

$L\sim \frac{\lambda \mathrm{\Gamma }\left(\lambda \right)\sin \left(\pi \lambda /2\right)}{\pi }\frac{1}{s^{1+\lambda }},(16)$

where, $\mathrm{\Gamma }\left(\lambda \right)$ describes the conventional gamma function, $s\gg s_0>0$, and $s_0=0.1$ such that $s$ is defined by two gaussian distributions as follows:

$\begin{array}{c}s=\frac{U}{{\left|V\right|}^{\frac{1}{\lambda }}},U\sim N\left(0,{\sigma }^2\right),V\sim N\left(0,1\right)\\ {\sigma }^2={\left[\frac{\mathrm{\Gamma }\left(1+\lambda \right)}{\lambda \mathrm{\Gamma }\left[\frac{1+\lambda }{2}\right]}\frac{\sin \left(\pi \lambda /2\right)}{2^{\left(\lambda -1\right)/2}}\right]}^{\frac{1}{\lambda }}\end{array}(17)$

where, $N\left(0,{\sigma }^2\right)$ indicates the standard normal distribution and denotes the normal distribution with a mean value of 0 and variance ${\sigma }^2$.

Pollen is transmitted to a nearby neighbor if the pollination activities involve local pollination, and the model may be constructed using Guideline 2 and Guideline 3 as follows:

$x_i^{t+1}=x_i^t+\psi \left(x_j^t-x_k^t\right)j,k\in \left(\mathrm{1,2},\dots ,N\right)(18)$

where, $\psi$ specifies a d-dimension random variable between 0 and 1, $x_j^t$ and $x_k^t$ describes the pollen that was chosen at random from several flowers on the same plant.

The FPA’s primary disadvantage is that the precise transfer probability is determined manually, and this uncertainty significantly reduces the optimization impact.

5.1.2 Subgroup optimization algorithm

The BSOA uses a hierarchical framework to split all persons into two subgroups. Diverse methods were used to update these subgroups. Particularly, solution candidates are graded following how fit the general population is. The grouping made up of people who are more physically fit is known as the advanced subgroup, whereas the subgroup made up of those who are less physically fit is known as the backward subgroup (Chen, Pi et al., 2022). The backward subgroup is created, and it is updated using Eq. 15.

This means that individuals with low fitness should perform Levy flights to the population’s ideal positions and investigate novel solutions in objective space. By rewriting Eq. 18 as Eq. 19 for the advanced subgroup, we enhance it by adding the guidance of the random person and the difference vector between the ideal location and the present position. A uniformly distributed random number between 0 and 1 is represented by the symbol as follows:

$x_i^t=x_i^t+\left(1-ϵ\right)\left(gbest-x_i^t\right)+ϵ\left(x_j^t-x_k^t\right)(19)$

The goal of the advanced subgroup is to share knowledge and find fresh local solutions. Throughout the population’s cyclical history, members of these two subgroups have been in continual contact with one another, making it easier to focus on finding specific people and effectively ensuring the population’s variety.

The BSOA has been extended to include the step of leaping out of the local optimal solution to prevent the loss of population diversity and inefficient iterative search time. If the algorithm does not update the new solution at half the maximum number of iterations and the present solution is not the ideal solution to the cost function, we believe that the process looks to have converged prematurely.

Since we typically don't know what the theoretically ideal solution to the problem is, this strategy can efficiently employ the search resources to increase the population’s capacity for searching the solution space. We create new solutions at random in the space of possible solutions using the following equation:

$x_i=\overline{x}-\left(\overline{x}-\underset{-}{x}\right)r(20)$

where, $r$ is a random variable between 0 and 1.

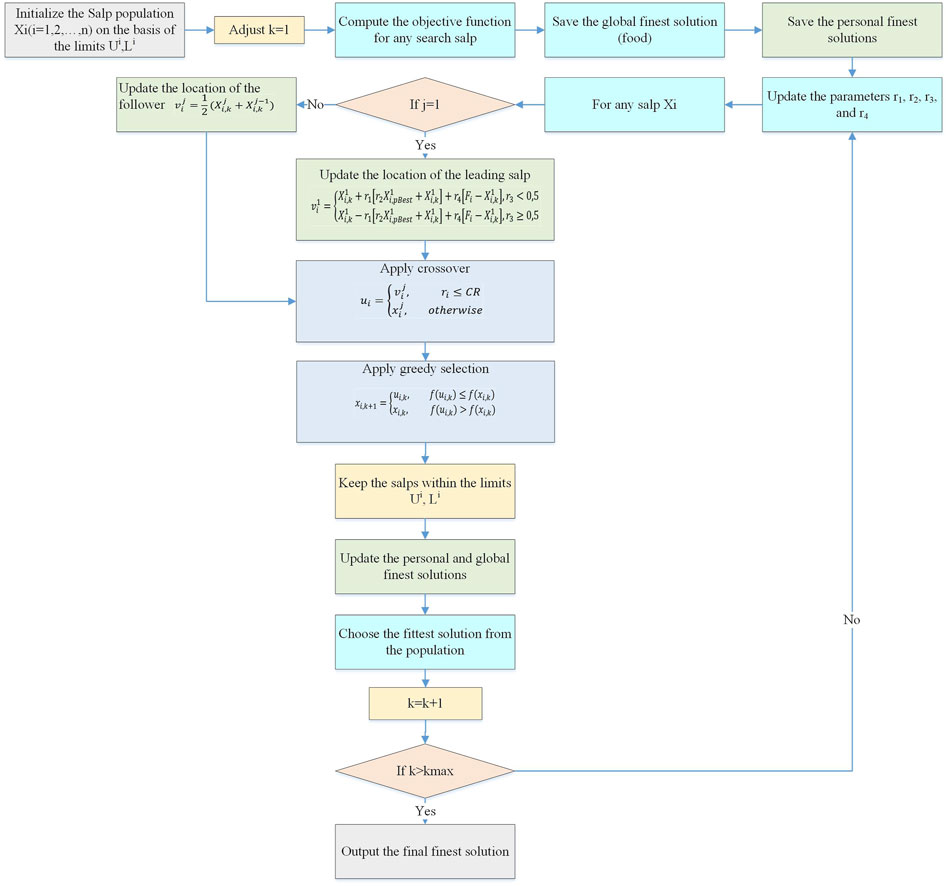
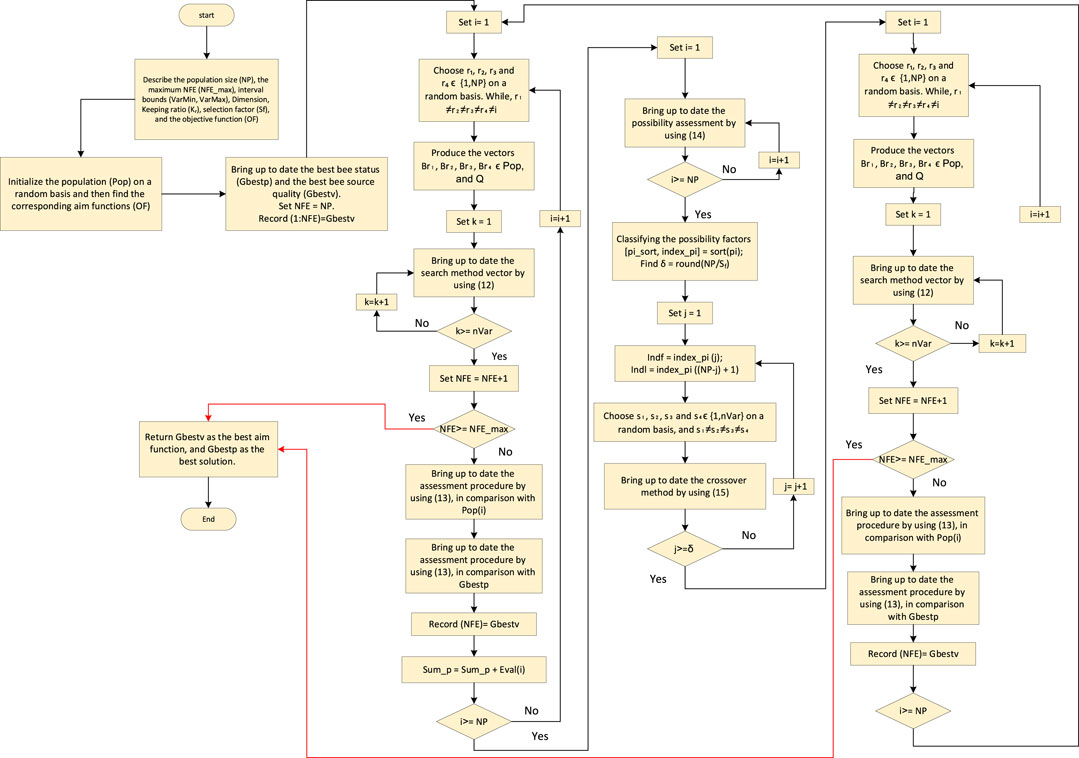
Figure 6 shows the flowchart of the BSO algorithm.

FIGURE 6

FIGURE 6. Flowchart of the BSO algorithm.

5.2 Improved salp swarm algorithm

5.2.1 Salp swarm algorithm

SSA mimics the salp chain’s technique for looking for prey (Al-Shabi, Ghenai et al., 2021). This behavior is mathematically expressed using two populations. The front of the chain is home to the first population, known as the leader, and the second group, known as the followers. The updating formula of the leading position is as follows:

$X_i^t=\left\{\begin{array}{c}{F}_i+r_1\left(L_i+r_2\left(U_i-L_i\right)\right),r_3<0.5\\ F_i-r_1\left(L_i+r_2\left(U_i-L_i\right)\right),r_3\ge 0.5\end{array}\right.(21)$

where $F_i$ describes the food location, which is the chain search’s primary objective, and $X_i^t$ specifies the leader’s current position in the ith dimension. The salps are kept within the search space using random values $r_1$, $r_2$, and $r_3$, and the lower and upper bounds are $L_i$ and $U_i$.

The balance between the stages of exploitation and exploration must be reached when using metaheuristic techniques; as a result, $r_1$ is used during the iterative process as follows:

$r_1=2e^{-{\left(\frac{4k}{k_{\mathit{max}}}\right)}^2}(22)$

where, $K$ is the current iteration, $k_{\mathit{max}}$ determines the number of iterations that may be made. $r_3$ specifies a random switching parameter, while $r_2$ is utilized to adapt the movement toward the meal. The leader uses the following formula to determine where the followers should stand:

$x_i^l=0.5\times \left(x_i^l-x_i^{l-1}\right)(23)$

Such that $l\ge 2$ and $x_i^l$ describes the $i$-dimensional slap position $l$,

5.2.2 Improved salp swarm algorithm

The SSA may experience various issues, much as any metaheuristic optimization approaches, such as overflow during the exploration phase, which may cause skipping a real solution and becoming trapped on local optima (Mirjalili, Gandomi et al., 2017). If the exploration and exploitation stages are not properly balanced, this issue arises.

In the conventional salp swarm algorithm, $r_1$ is in charge of maintaining equilibrium between the stages of exploitation and exploration, however, in the first iterations, the solutions are updated far from the optimal location (food), when $r_1$ should be assisting with exploration at this point. Additionally; $r_2$ aids in the search for the ideal result. As a result, the result changes positions and loses its characteristic throughout each iteration of the search. To get over these issues, a modified version of SSA using crossover and greedy selection is designed by Hamdy et al. (Sultan, Menesy et al., 2020). For the leader, a modified search equation is used as follows:

$v_i^1=\left\{\begin{array}{cc}{x}_{i,k}^l+r_1\left(r_2{x}_{i,pBest}^l+x_{i,k}^l\right)+r_4\left(F_i-x_{i,k}^l\right),& r_3<0.5\\ x_{i,k}^l-r_1\left(r_2{x}_{i,pBest}^l+x_{i,k}^l\right)+r_4\left(F_i-x_{i,k}^l\right),& r_3\ge 0.5\end{array}\right.(24)$

And:

$v_i^j=0.5\times \left(x_i^l-x_i^{l-1}\right)(25)$

where, $x_{i,pBest}^l$ denotes the individual’s best performance at iteration $k$, and $v_i^j$ denotes the recently updated vector.

Here, a crossover between the $x_i^j$ and $x_i^j$ is performed. This can be formulated as follows:

$u_i=\left\{\begin{array}{cc}{v}_i^j,& r_i\le CO\\ x_i^j,& otherwise\end{array}\right.(26)$

where, $r_i$ is an arbitrary number that ranges from 0 to 1, and $CO$ describes the crossover rate. The crossover CR probability is set at 0 points in this study.

The greedy selection is another improvement. The updated vector’s capacity to survive in the following iteration is tested using this. The following comparison of the fitness of updated and existing solution vectors can be used to complete this process:

$u_i=\left\{\begin{array}{cc}{u}_{i,k},& f\left(u_{i,k}\right)\le f\left(x_{i,k}\right)\\ u_{i,k},& f\left(u_{i,k}\right)>f\left(x_{i,k}\right)\end{array}\right.(27)$

where, $f$ defines the objective function. Figure 7 shows the flowchart of the ISS algorithm.

FIGURE 7

FIGURE 7. Flowchart of the ISS algorithm.

5.3 Artificial bee colony differential evolution optimizer

The artificial bee colony differential evolution (ABCDE) optimizer is a combination of the ABC algorithm and the differential evolution (DE) optimizers; it mimics bee behavior and their research technique to find the best honey source. The bees (elements) communicate information on the quality of the obtained sources using the DE mutation technique. Following the first navigation, the bees are categorized into 3 groups: scouts, observers, and leaders. The ABC optimizer’s probability evaluation is used to classify the data. The bystanders, who are directed by the leaders, utilize the honey sources.

Simultaneously, using ABC’s crossover technique, the scout bees investigate the remainder of the search space in search of more appropriate honey sources. As a result, when the swarm is formed, the bees begin exposing the search field using the search approach. The search vector of each bee based on the other bees can be given as follows:

$M_i=B_{best}+Q\left(B_{r1}-B_{r2}\right)+Q\left(B_{r3}-B_{r4}\right)(28)$

Where, $B_{r1}$, $B_{r2}$, $B_{r3}$, and $B_{r4}$ are the position of the honey sources for the bees with $r_1$, $r_2$, $r_3$, and $r_4$ indices, respectively. It should be noted that the indices of these bees vary from $i$. $B_{best}$ is the coordinates of the best source detected from the entire swarm, and $Q$ is a random factor between −1 and 1.

It is carried out whenever the search method for each bee is determined. It enables speedy evolution and rapid examination. In which $M_i$ is compared to the finest global source identified to date as judged by the following:

$B_i=\left\{\begin{array}{cc}{M}_i,& ifOF\left(M_i\right)<OF\left(B_i\right)\\ B_i,& otherwise\end{array}\right.(29)$

where, $OF\left(M_i\right)$ describes the objective function based on the $i^{th}$ bee. Likewise, $OF\left(M_i\right)$ corresponds to the $i^{th}$ bee mutation vector.

$P_i=\frac{OF\left(B_i\right)}{{\displaystyle \sum }_i^{NP}OF\left(B_i\right)}(30)$

The leaders share their data with the scouts in order to encourage them to conduct more accurate investigations. This is resolved by selecting four random dimensions as indicated by

$B_i^S=\left\{\begin{array}{cc}{B}_{NP+1-i}^S,& ifi\le \delta \\ B_i^S,& otherwise\end{array}\right.(31)$

where, $S$ describes the indices vector of the randomly chosen dimensions, and $S_1$, $S_2$, $S_3$, and $S_4$ describe the distinct elements from seven dimensions due to the fuel cell parameter extraction problem. $\delta$ defines the maximum number of leaders depending on the selection factor $S_f$.

The ABCDE approach is designed in such a way that the search vector ($M_i$) is run in a single independent loop for the whole swarm. The probability analysis and crossover approach are then implemented to optimize both the exploration and exploitation operations. Then after, the search strategy is conducted again in one other loop just as the first time. This approach allows the bees to be framed from the first search strategy, which could be called the test method, to the second search strategy, which could be termed the training procedure. Figure 8 represents the flowchart of the ABCDE algorithm.

FIGURE 8

FIGURE 8. Flowchart of the ABCDE algorithm.

6 Validation results of the comparative SI methods for model parameters estimation

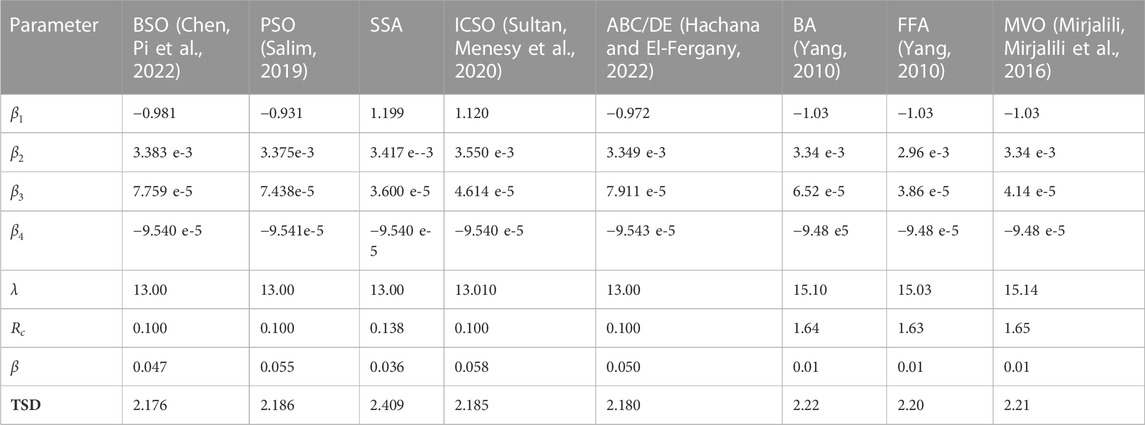
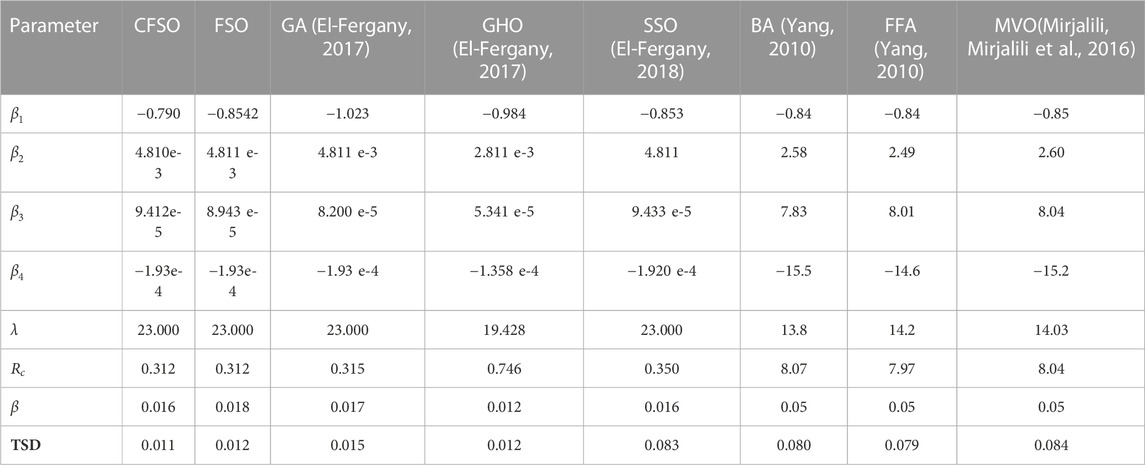
Different methods have produced a wide range of simulation results, which have been used to assess the viability and accuracy of each technique for obtaining the PEMFC parameters. To provide a proper verification among different swarm-based metaheuristic algorithms, some highly accurate approaches of this group, including the Bi-subgroup optimization algorithm (Chen, Pi et al., 2022), improved Salp Swarm Algorithm (SSA), improved chicken swarm optimization algorithm (ICSO) (Wang, Huang et al., 2022), artificial bee colony differential evolution optimizer (ABC/DE) (Hachana and El-Fergany, 2022), bat-inspired algorithm (BAT) (Yang, 2010), Firefly algorithm (FFA) (Yang, 2010), and Multi-verse optimizer (MVO) (Mirjalili, Mirjalili et al., 2016) are assessed.

To evaluate the effectiveness of the studied algorithms, two distinct fuel cell modules-500 W BCS PEMFC and the 6 kW NedSstack PS6 -are employed. The validation is performed into two standard benchmark functions, including 500 W BCS PEMFC and the 6 kW NedSstack PS6 PEMFC. MATLAB R2019b has been used to validate the swarm-based metaheuristic algorithms. 100 iterations are performed to all of the algorithms to get a fair estimation for the PEMFC. After 100 iterations, the objective function’s IAE optimal value is discovered. Table 5 shows the ideal PEMFC parameter values based on the comparative algorithms.

6.1 Case study 1: NedStack PS6

The NedSstack PS6 contains a 6 kW rated power. This benchmark primary data for the simulation is gathered from [7, 8], such that N_cells = 65, T_PEM = 343 K, A = 240 cm², l = 178 $\mu m$. Operating ranges for the output voltage and current are [0, 225] A DC and [32, 60]V DC and 0.5 bar–5 bar, respectively. The comparison results of the Bi-subgroup optimization algorithm (Chen, Pi et al., 2022), improved Salp Swarm Algorithm (SSA), improved chicken swarm optimization algorithm (ICSO) (Wang, Huang et al., 2022), artificial bee colony differential evolution optimizer (ABC/DE) (Hachana and El-Fergany, 2022), bat-inspired algorithm (BAT) (Yang, 2010), Firefly algorithm (FFA) (Yang, 2010), and Multi-verse optimizer (MVO) (Mirjalili, Mirjalili et al., 2016) are indicated in Table 3. The final optimal values for the determined PEMFC model based on the studied algorithms are provided here.

TABLE 3

TABLE 3. TSD assessment of the NedStack PS6.

Table 4 shows the Elapsed Time for the cutting-edge techniques on the 6 kW NedStack PS6. As can be seen, all of the swarm-based technique provides feasible results for the identification. However, there needs a balance between the accuracy and the elapsed time for this purpose.

TABLE 4

TABLE 4. The Elapsed time for the state-of-the-art methods on the NedS stack PS6.

6.2 Test case 2

The BCS PEMFC is another PEMFC benchmark system for the methods’ assessment. This benchmark provides a rated power of 500 W and a maximum current of 30 A. BCS Technologies is an American company, that manufactures this kind. The operational ranges for the partial pressures of hydrogen and oxygen are 1 atm and 0.2075 atm, respectively, and more information for an accurate simulation of this model may be found in (Corrêa, Farret et al., 2004), where $T_{PEM}=333K$, $A=64cm2$, $l=178$, and $Ncells=32$.

Table 5 shows the Elapsed Time for the cutting-edge techniques on the BCS PEMFC. As can be seen, all of the swarm-based technique provides feasible results for the identification. However, there needs a balance between the accuracy and the elapsed time for this purpose.

TABLE 5

TABLE 5. TSD validation for the BCS PEMFC.

Table 6 indicates the Elapsed Time for the cutting-edge techniques on the BCS PEMFC. As can be observed, all of the swarm-based technique provides feasible results for the identification. However, there needs a balance between the accuracy and the elapsed time for this purpose.

TABLE 6

TABLE 6. The Elapsed time for the state-of-the-art methods on the BCS PEMFC.

Similar to case study 1, the findings demonstrate a favorable fitting of the empirical voltage model and the data, which was accomplished using the swarm-based methods. They also demonstrate appropriate accuracy in locating the optimal values for the seven unknown parameters.

Figure 9 represents the TSD bar plot of the two benchmarks studied based on investigated swarm-based methods.

FIGURE 9

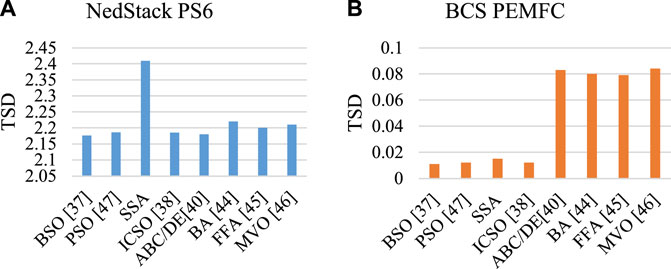
FIGURE 9. TSD bar plot of the two benchmarks, including (A) NedStackPS6 and (B) BCS PEMFC studied based on investigated swarm-based methods.

As can be observed from Figure 9, the superiority of the algorithms in two different cases are different. The reason is that due to the random nature of these swarm-based methods, the results in different runs can be changed. Unless a mean value of the methods is considered. Also, as can be observed, the efficiency of an algorithm for a case study is completely different from another one.

7 Conclusion

A PEMFC is an electrical generator that uses electrochemistry. To match its V-I and P-I characteristic curves under various operating situations, it has a non-linear model with seven parameters that characterize its performance and operation in governing equations. This study focuses on new swarm-based algorithms from BSO, PSO, SSA, ICSO, ABC/DE, BA, FFA, and MVO and enhances them such that they may be used to precisely extract seven unknown parameters from the PEMFC non-linear model. The fitness function is shown by the TSD between the actual and ideal models to confirm the proper values of unknown model parameters for addressing the optimization issue. The used methods verified excellent agreement between calculated and measured data under various operating situations, satisfying good performance for all investigated fuel cell stacks. Compared to the outcomes of other algorithms from the literature, the BSO, PSO, SSA, ICSO, ABC/DE, BA, FFA, and MVO have satisfied the most optimal solution in a better computing approach.

Author contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdelkareem, M. A., Elsaid, K., Wilberforce, T., Kamil, M., Sayed, E. T., and Olabi, A. (2021). Environmental aspects of fuel cells: A review. Sci. Total Environ. 752, 141803. doi:10.1016/j.scitotenv.2020.141803

PubMed Abstract | CrossRef Full Text | Google Scholar

Al-Shabi, M., Ghenai, C., Bettayeb, M., Ahmad, F. F., and Assad, M. E. H. (2021). Estimating PV models using multi-group salp swarm algorithm. IAES Int. J. Artif. Intell. 10 (2), 398. doi:10.11591/ijai.v10.i2.pp398-406

CrossRef Full Text | Google Scholar

Ang, T.-Z., Salem, M., Kamarol, M., Das, H. S., Nazari, M. A., and Prabaharan, N. (2022). A comprehensive study of renewable energy sources: Classifications, challenges and suggestions. Energy Strategy Rev. 43, 100939. doi:10.1016/j.esr.2022.100939

CrossRef Full Text | Google Scholar

Arsalis, A. (2019). A comprehensive review of fuel cell-based micro-combined-heat-and-power systems. Renew. Sustain. Energy Rev. 105, 391–414. doi:10.1016/j.rser.2019.02.013

CrossRef Full Text | Google Scholar

Arshad, A., Ali, H. M., Habib, A., Bashir, M. A., Jabbal, M., and Yan, Y. (2019). Energy and exergy analysis of fuel cells: A review. Therm. Sci. Eng. Prog. 9, 308–321. doi:10.1016/j.tsep.2018.12.008

CrossRef Full Text | Google Scholar

Askarzadeh, A., and Rezazadeh, A. (2013). A new heuristic optimization algorithm for modeling of proton exchange membrane fuel cell: Bird mating optimizer. Int. J. energy Res. 37 (10), 1196–1204. doi:10.1002/er.2915

CrossRef Full Text | Google Scholar

Bizon, N. (2019). Hybrid power sources (HPSs) for space applications: Analysis of PEMFC/Battery/SMES HPS under unknown load containing pulses. Renew. Sustain. Energy Rev. 105, 14–37. doi:10.1016/j.rser.2019.01.044

CrossRef Full Text | Google Scholar

Blal, M., Benatiallah, A., NeÇaibia, A., Lachtar, S., Sahouane, N., and Belasri, A. (2019). Contribution and investigation to compare models parameters of (PEMFC), comprehensives review of fuel cell models and their degradation. Energy 168, 182–199. doi:10.1016/j.energy.2018.11.095

CrossRef Full Text | Google Scholar

Bornapour, M., Hemmati, R., Pourbehzadi, M., Dastranj, A., and Niknam, T. (2020). Probabilistic optimal coordinated planning of molten carbonate fuel cell-CHP and renewable energy sources in microgrids considering hydrogen storage with point estimate method. Energy Convers. Manag. 206, 112495. doi:10.1016/j.enconman.2020.112495

CrossRef Full Text | Google Scholar

Cao, Y., Li, Y., Zhang, G., Jermsittiparsert, K., and Razmjooy, N. (2019). Experimental modeling of PEM fuel cells using a new improved seagull optimization algorithm. Energy Rep. 5, 1616–1625. doi:10.1016/j.egyr.2019.11.013

CrossRef Full Text | Google Scholar

Celik, E., and Karagöz, İ. (2020). Polymer electrolyte membrane fuel cell flow field designs and approaches for performance enhancement. Proc. Institution Mech. Eng. Part A J. Power Energy 234 (8), 1189–1214. doi:10.1177/0957650919893543

CrossRef Full Text | Google Scholar

Chen, K., Badji, A., Laghrouche, S., and Djerdir, A. (2022). Polymer electrolyte membrane fuel cells degradation prediction using multi-kernel relevance vector regression and whale optimization algorithm. Appl. Energy 318, 119099. doi:10.1016/j.apenergy.2022.119099

CrossRef Full Text | Google Scholar

Chen, Y., Pi, D., Wang, B., Chen, J., and Xu, Y. (2022). Bi-subgroup optimization algorithm for parameter estimation of a PEMFC model. Expert Syst. Appl. 196, 116646. doi:10.1016/j.eswa.2022.116646

CrossRef Full Text | Google Scholar

Cheng, S., Zhao, G., Gao, M., Shi, Y., Huang, M., and Marefati, M. (2021). A new hybrid solar photovoltaic/phosphoric acid fuel cell and energy storage system; Energy and Exergy performance. Int. J. Hydrogen Energy 46 (11), 8048–8066. doi:10.1016/j.ijhydene.2020.11.282

CrossRef Full Text | Google Scholar

Corrêa, J. M., Farret, F. A., Canha, L. N., and Simoes, M. G. (2004). An electrochemical-based fuel-cell model suitable for electrical engineering automation approach. IEEE Trans. industrial Electron. 51 (5), 1103–1112. doi:10.1109/tie.2004.834972

CrossRef Full Text | Google Scholar

Diab, N., and El-Sharkawy, E. (2016). Recent advances in flower pollination algorithm. Int. J. Comput. Appl. Technol. Res. 5 (6), 338–346. doi:10.7753/ijcatr0506.1003

CrossRef Full Text | Google Scholar

El-Fergany, A. A. (2017). Electrical characterisation of proton exchange membrane fuel cells stack using grasshopper optimiser. IET Renew. Power Gener. 12 (1), 9–17. doi:10.1049/iet-rpg.2017.0232

CrossRef Full Text | Google Scholar

El-Fergany, A. A. (2018). Extracting optimal parameters of PEM fuel cells using Salp Swarm Optimizer. Renew. energy 119, 641–648. doi:10.1016/j.renene.2017.12.051

CrossRef Full Text | Google Scholar

Fathy, A., Rezk, H., Alharbi, A. G., and Yousri, D. (2023). Proton exchange membrane fuel cell model parameters identification using chaotically based-bonobo optimizer. Energy 268, 126705. doi:10.1016/j.energy.2023.126705

CrossRef Full Text | Google Scholar

Ge, L., Du, T., Li, C., Li, Y., Yan, J., and Rafiq, M. U. (2022a). Virtual collection for distributed photovoltaic data: Challenges, methodologies, and applications. Energies 15 (23), 8783. doi:10.3390/en15238783

CrossRef Full Text | Google Scholar

Ge, L., Yan, J., Sun, Y., and Wang, Z. (2022b). Situational awareness for smart distribution systems. MDPI 15, 4164. doi:10.3390/en15114164

CrossRef Full Text | Google Scholar

Guo, Y., Dai, X., Jermsittiparsert, K., and Razmjooy, N. (2020). An optimal configuration for a battery and PEM fuel cell-based hybrid energy system using developed Krill herd optimization algorithm for locomotive application. Energy Rep. 6, 885–894. doi:10.1016/j.egyr.2020.04.012

CrossRef Full Text | Google Scholar

Hachana, O., and El-Fergany, A. A. (2022). Efficient PEM fuel cells parameters identification using hybrid artificial bee colony differential evolution optimizer. Energy 250, 123830. doi:10.1016/j.energy.2022.123830

CrossRef Full Text | Google Scholar

Ijaodola, O., El-Hassan, Z., Ogungbemi, E., Khatib, F., Wilberforce, T., Thompson, J., et al. (2019). Energy efficiency improvements by investigating the water flooding management on proton exchange membrane fuel cell (PEMFC). Energy 179, 246–267. doi:10.1016/j.energy.2019.04.074

CrossRef Full Text | Google Scholar

Lazarou, S., Pyrgioti, E., and Alexandridis, A. T. (2009). A simple electric circuit model for proton exchange membrane fuel cells. J. Power Sources 190 (2), 380–386. doi:10.1016/j.jpowsour.2009.01.065

CrossRef Full Text | Google Scholar

Li, D., Deng, L., Su, Q., and Song, Y. (2020). Providing a guaranteed power for the BTS in telecom tower based on improved balanced owl search algorithm. Energy Rep. 6, 297–307. doi:10.1016/j.egyr.2020.01.006

CrossRef Full Text | Google Scholar

Li, J., Deng, Y., Sun, W., Li, W., Li, R., Li, Q., et al. (2022). Resource orchestration of cloud-edge–based smart grid fault detection. ACM Trans. Sens. Netw. (TOSN) 18 (3), 1–26. doi:10.1145/3529509

CrossRef Full Text | Google Scholar

Lim, B. H., Majlan, E. H., Tajuddin, A., Husaini, T., Daud, W. R. W., Radzuan, N. A. M., et al. (2021). Comparison of catalyst-coated membranes and catalyst-coated substrate for PEMFC membrane electrode assembly: A review. Chin. J. Chem. Eng. 33, 1–16. doi:10.1016/j.cjche.2020.07.044

CrossRef Full Text | Google Scholar

Ma, Z., Eichman, J., and Kurtz, J. (2018). Fuel cell backup power system for grid-service and micro-grid in telecommunication applications. Energy Sustain. 51418.

CrossRef Full Text | Google Scholar

Mirjalili, S., Gandomi, A. H., Mirjalili, S. Z., Saremi, S., Faris, H., and Mirjalili, S. M. (2017). Salp swarm algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 114, 163–191. doi:10.1016/j.advengsoft.2017.07.002

CrossRef Full Text | Google Scholar

Mirjalili, S., Mirjalili, S. M., and Hatamlou, A. (2016). Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 27 (2), 495–513. doi:10.1007/s00521-015-1870-7

CrossRef Full Text | Google Scholar

Mohammadzadeh, H., and Gharehchopogh, F. S. (2021). A novel hybrid whale optimization algorithm with flower pollination algorithm for feature selection: Case study Email spam detection. Comput. Intell. 37 (1), 176–209. doi:10.1111/coin.12397

CrossRef Full Text | Google Scholar

Pashaki, M. K., and Mahmoudimehr, J. (2023). Performance superiority of an arc-shaped polymer electrolyte membrane fuel cell over a straight one. Int. J. Hydrogen Energy. doi:10.1016/j.ijhydene.2022.12.261

CrossRef Full Text | Google Scholar

Prasad, J., and Tripathi, R. K. (2021). Effect of sediment microbial fuel cell stacks on 9 V/12 V DC power supply. Int. J. Hydrogen Energy 46 (27), 14628–14638. doi:10.1016/j.ijhydene.2020.07.187

CrossRef Full Text | Google Scholar

Qaiser, M., Asghar, A., Jaffery, M., Javaid, M., and Khurram, M. (2021). Flow control of hydrogen fuel in pem fuel cell using soft computing techniques. J. Ovonic Res. 17 (1).

Google Scholar

RavindranathTagore, Y., Anuradha, K., Babu, A. R. V., and Kumar, P. M. (2019). Modelling, simulation and control of a fuel cell-powered laptop computer voltage regulator module. Int. J. Hydrogen Energy 44 (21), 11012–11019. doi:10.1016/j.ijhydene.2019.02.141

CrossRef Full Text | Google Scholar

Reddy, K. J., and Sudhakar, N. (2019). ANFIS-MPPT control algorithm for a PEMFC system used in electric vehicle applications. Int. J. Hydrogen Energy 44 (29), 15355–15369. doi:10.1016/j.ijhydene.2019.04.054

CrossRef Full Text | Google Scholar

Rezk, H., Olabi, A., Ferahtia, S., and Sayed, E. T. (2022). Accurate parameter estimation methodology applied to model proton exchange membrane fuel cell. Energy 255, 124454. doi:10.1016/j.energy.2022.124454

CrossRef Full Text | Google Scholar

Salehi, A., Mousavi, S. M., Fasihfar, A., and Ravanbakhsh, M. (2019). Energy, exergy, and environmental (3E) assessments of an integrated molten carbonate fuel cell (MCFC), Stirling engine and organic Rankine cycle (ORC) cogeneration system fed by a biomass-fueled gasifier. Int. J. Hydrogen Energy 44 (59), 31488–31505. doi:10.1016/j.ijhydene.2019.10.038

CrossRef Full Text | Google Scholar

Salim, R. I. (2019). The performance of aco in the parameter identification of a pem fuel cell model in comparison to ga and PSO, Proceedings of the 2019 International Conference on Power Generation Systems and Renewable Energy Technologies (PGSRET), Istanbul, Turkey, August 2019(IEEE). doi:10.1109/PGSRET.2019.8882690

CrossRef Full Text | Google Scholar

San Martin, J., Zamora, I., San Martin, J., Aperribay, V., Torres, E., and Eguia, P. (2010). Influence of the rated power in the performance of different proton exchange membrane (PEM) fuel cells. Energy 35 (5), 1898–1907. doi:10.1016/j.energy.2009.12.038

CrossRef Full Text | Google Scholar

Sapkota, P., and Aguey-Zinsou, K.-F. (2023). Iron and tin phosphide as polymer electrolyte membrane fuel cell cathode catalysts. Int. J. Hydrogen Energy 48 (1), 257–267. doi:10.1016/j.ijhydene.2022.09.230

CrossRef Full Text | Google Scholar

Shakhshir, S. A., Gao, X., and Berning, T. (2020). An experimental study of the effect of a turbulence grid on the stack performance of an air-cooled proton exchange membrane fuel cell. J. Electrochem. Energy Convers. Storage 17 (1). doi:10.1115/1.4044154

CrossRef Full Text | Google Scholar

Shao, Y., Dodelet, J. P., Wu, G., and Zelenay, P. (2019). PGM-free cathode catalysts for PEM fuel cells: A mini-review on stability challenges. Adv. Mater. 31 (31), 1807615. doi:10.1002/adma.201807615

CrossRef Full Text | Google Scholar

Shi, X., Dai, Y., Esan, O. C., Huo, X., An, L., and Zhao, T. (2021). A passive fuel cell fed with an electrically rechargeable liquid fuel. ACS Appl. Mater. Interfaces 13 (41), 48795–48800. doi:10.1021/acsami.1c14505

PubMed Abstract | CrossRef Full Text | Google Scholar

Spiegel, C. (2011). PEM fuel cell modeling and simulation using MATLAB. Amsterdam, Netherlands: Elsevier.

Google Scholar

Sultan, H. M., Menesy, A. S., Kamel, S., Selim, A., and Jurado, F. (2020). Parameter identification of proton exchange membrane fuel cells using an improved salp swarm algorithm. Energy Convers. Manag. 224, 113341. doi:10.1016/j.enconman.2020.113341

CrossRef Full Text | Google Scholar

Sun, B., Li, Y., Zeng, Y., Chen, J., and Shi, J. (2022). Optimization planning method of distributed generation based on steady-state security region of distribution network. Energy Rep. 8, 4209–4222. doi:10.1016/j.egyr.2022.03.078

CrossRef Full Text | Google Scholar

Sun, Z., Lin, B., and Yan, F. (2018). Anion-exchange membranes for alkaline fuel-cell applications: The effects of cations. ChemSusChem 11 (1), 58–70. doi:10.1002/cssc.201701600

PubMed Abstract | CrossRef Full Text | Google Scholar

Tang, Y., Yuan, W., Pan, M., and Wan, Z. (2011). Experimental investigation on the dynamic performance of a hybrid PEM fuel cell/battery system for lightweight electric vehicle application. Appl. Energy 88 (1), 68–76. doi:10.1016/j.apenergy.2010.07.033

CrossRef Full Text | Google Scholar

Tian, M.-W., Yan, S.-R., Han, S.-Z., Nojavan, S., Jermsittiparsert, K., and Razmjooy, N. (2020). New optimal design for a hybrid solar chimney, solid oxide electrolysis and fuel cell based on improved deer hunting optimization algorithm. J. Clean. Prod. 249, 119414. doi:10.1016/j.jclepro.2019.119414

CrossRef Full Text | Google Scholar

Tsalapati, E., Johnson, C., Jackson, T. W., Jackson, L., Low, D., Davies, B., et al. (2021). Enhancing polymer electrolyte membrane fuel cell system diagnostics through semantic modelling. Expert Syst. Appl. 163, 113550. doi:10.1016/j.eswa.2020.113550

CrossRef Full Text | Google Scholar

Valdes-Lopez, V. F., Mason, T., Shearing, P. R., and Brett, D. J. (2020). Carbon monoxide poisoning and mitigation strategies for polymer electrolyte membrane fuel cells–A review. Prog. Energy Combust. Sci. 79, 100842. doi:10.1016/j.pecs.2020.100842

CrossRef Full Text | Google Scholar

Vichard, L., Harel, F., Ravey, A., Venet, P., and Hissel, D. (2020). Degradation prediction of PEM fuel cell based on artificial intelligence. Int. J. Hydrogen Energy 45 (29), 14953–14963. doi:10.1016/j.ijhydene.2020.03.209

CrossRef Full Text | Google Scholar

Wang, J., Wang, H., and Fan, Y. (2018). Techno-economic challenges of fuel cell commercialization. Engineering 4 (3), 352–360. doi:10.1016/j.eng.2018.05.007

CrossRef Full Text | Google Scholar

Wang, T., Huang, H., Li, X., Guo, X., Liu, M., and Lei, H. (2022). Optimal estimation of proton exchange membrane fuel cell model parameters based on an improved chicken swarm optimization algorithm. Int. J. Green Energy, 1–20. doi:10.1080/15435075.2022.2131432

CrossRef Full Text | Google Scholar

Wang, Y., Diaz, D. F. R., Chen, K. S., Wang, Z., and Adroher, X. C. (2020). Materials, technological status, and fundamentals of PEM fuel cells–a review. Mater. today 32, 178–203. doi:10.1016/j.mattod.2019.06.005

CrossRef Full Text | Google Scholar

Wilberforce, T., Rezk, H., Olabi, A., Epelle, E. I., and Abdelkareem, M. A. (2023). Comparative analysis on parametric estimation of a PEM fuel cell using metaheuristics algorithms. Energy 262, 125530. doi:10.1016/j.energy.2022.125530

CrossRef Full Text | Google Scholar

Wu, Z., Zhu, P., Yao, J., Tan, P., Xu, H., Chen, B., et al. (2020). Thermo-economic modeling and analysis of an NG-fueled SOFC-WGS-TSA-PEMFC hybrid energy conversion system for stationary electricity power generation. Energy 192, 116613. doi:10.1016/j.energy.2019.116613

CrossRef Full Text | Google Scholar

Xu, S., Huang, W., Wang, H., Zheng, W., Wang, J., Chai, Y., et al. (2022). A simultaneous diagnosis method for power switch and current sensor faults in grid-connected three-level NPC inverters. IEEE Trans. Power Electron. 38 (1), 1104–1118. doi:10.1109/tpel.2022.3200721

CrossRef Full Text | Google Scholar

Yalcinoz, T., and Alam, M. S. (2007). “The dynamic performance of PEM fuel cells under various operating conditions of a laptop computer,” in Proceedings of the EUROCON 2007-The International Conference on" Computer as a Tool, Warsaw, Poland, September 2007 (IEEE).

CrossRef Full Text | Google Scholar

Yang, B., Wang, J., Yu, L., Shu, H., Yu, T., Zhang, X., et al. (2020). A critical survey on proton exchange membrane fuel cell parameter estimation using meta-heuristic algorithms. J. Clean. Prod. 265, 121660. doi:10.1016/j.jclepro.2020.121660

CrossRef Full Text | Google Scholar

Yang, X.-S. (2010b). A new metaheuristic bat-inspired algorithm. Nat. inspired Coop. strategies Optim. (NICSO 2010) 284, 65–74. doi:10.1007/978-3-642-12538-6_6

CrossRef Full Text | Google Scholar

Yang, X.-S. (2010a). Firefly algorithm, stochastic test functions and design optimisation. Int. J. bio-inspired Comput. 2 (2), 78–84. doi:10.1504/IJBIC.2010.032124

CrossRef Full Text | Google Scholar

Yu, D., Wang, Y., Liu, H., Jermsittiparsert, K., and Razmjooy, N. (2019). System identification of PEM fuel cells using an improved Elman neural network and a new hybrid optimization algorithm. Energy Rep. 5, 1365–1374. doi:10.1016/j.egyr.2019.09.039

CrossRef Full Text | Google Scholar

Zakaria, Z., Kamarudin, S. K., and Wahid, K. A. A. (2023). Polymer electrolyte membrane modification in direct ethanol fuel cells: An update. J. Appl. Polym. Sci. 140, e53383. doi:10.1002/app.53383

CrossRef Full Text | Google Scholar

Zhang, F., Wang, B., Gong, Z., Zhang, X., Qin, Z., and Jiao, K. (2023). Development of photovoltaic-electrolyzer-fuel cell system for hydrogen production and power generation. Energy 263, 125566. doi:10.1016/j.energy.2022.125566

CrossRef Full Text | Google Scholar

Zhang, Z., Liu, W., and Wang, Y. (2019). Three dimensional two-phase and non-isothermal numerical simulation of multi-channels PEMFC. Int. J. hydrogen energy 44 (1), 379–388. doi:10.1016/j.ijhydene.2018.05.149

CrossRef Full Text | Google Scholar

Zhao, J., and Li, X. (2019). A review of polymer electrolyte membrane fuel cell durability for vehicular applications: Degradation modes and experimental techniques. Energy Convers. Manag. 199, 112022. doi:10.1016/j.enconman.2019.112022

CrossRef Full Text | Google Scholar

Zhao, J., Tu, Z., and Chan, S. H. (2021). Carbon corrosion mechanism and mitigation strategies in a proton exchange membrane fuel cell (PEMFC): A review. J. Power Sources 488, 229434. doi:10.1016/j.jpowsour.2020.229434

CrossRef Full Text | Google Scholar

Zhao, Y., Mao, Y., Zhang, W., Tang, Y., and Wang, P. (2020). Reviews on the effects of contaminations and research methodologies for PEMFC. Int. J. Hydrogen Energy 45 (43), 23174–23200. doi:10.1016/j.ijhydene.2020.06.145

CrossRef Full Text | Google Scholar

Zhong, C., Zhou, Y., Chen, J., and Liu, Z. (2022). DC-side synchronous active power control of two-stage photovoltaic generation for frequency support in Islanded microgrids. Energy Rep. 8, 8361–8371. doi:10.1016/j.egyr.2022.06.030

CrossRef Full Text | Google Scholar