A hybrid discrete state transition algorithm for combinatorial optimization problems

The discrete state transition algorithm (DSTA) has been wildly applied to deal with combinatorial optimization problems. However, its low convergence accuracy limits its application in large-scale optimization problems. Aiming at the convergence performance and search intensity of the algorithm, a hybrid discrete state transition algorithm (HDSTA) is proposed in this work by introducing tabu search and elite solution set. Firstly, a searching mechanism with the integration of DSTA and tabu search (TS) is established, which allows moving to adjacent solutions at an increased cost to escape from the local optimum. Specifically, a tabu list as adaptive memory is adopted to avoid the loop when deviating from local optima. Secondly, an elite solution set is introduced to integrate the information of the previous optimal solution and the global optimal solution, and the search strategy is modified to expand the range and diversity of candidate solutions. Finally, the proposed HDSTA is verified according to the real data on two well-known optimization problems (staff assignment problem and traveling salesman problem) and the real data of an industrial case. The experimental results show the effectiveness of the proposed algorithm in large-scale optimization problems.

1 Introduction

Combinatorial optimization problems are encountered in almost all branches of engineering, including system control, process management, parameter setting, etc. Generally speaking, the combinatorial optimization problems are NP-hard. When the problem scale is small, accurate algorithms are adopted to obtain exact solutions step by step, for example, branch-and-cut approach (Lin and Tian, 2021) and Hooke-Jeeves pattern search (Tabassum et al., 2021). However, these methods mainly take exponential time to run. As the scale of the problem increases, more and more attention has been paid to stochastic algorithms which can obtain approximate solutions within the acceptable computation time. The existing stochastic methods mainly include evolutionary algorithms and metaheuristic algorithms. The evolutionary methods consist of evolution strategies (Hassanzadeh et al., 2021), genetic programming (Zhang et al., 2019a) and genetic algorithm (Wang and Sobey, 2020), while metaheuristic methods contain particle swarm optimization, simulated annealing, differential evolution algorithm (Abdel-Basset et al., 2021; Houssein et al., 2021; Wang et al., 2021), etc.

The state transition algorithm (STA) is originally proposed by Zhou et al., based on structuralist learning (Zhou et al., 2012). The concept of the STA is to treat the solution as a state and the process of updating as a state transition, through which a new state will be created. It generates candidate solutions by the cyclic utilization of four special operators. The greedy criterion is used to update the current optimal solution until the termination condition of the iteration is met. For PID control problem, (Zhang et al., 2018; Zhang et al., 2019b) fuzzy fractional order PID controller is adjusted by the state transition algorithm to achieve the optimal control of zinc powder addition. The traditional state transition algorithm is an unconstrained optimization method and applicable to continuous optimization problems. Therefore, a discrete state transfer algorithm (DSTA) is proposed to solve the discrete optimization problems (Zhou et al., 2016). The existing results show that DSTA is an effective and promising algorithm for combinatorial optimization problems. However, when the problem scale is large, the DSTA is excellent in convergence rate but poor in convergence accuracy, and it is easy to get trapped into local optima. Dong et al. (2016) proposed the concept of quadratic state transition to solve the assignment problems, which expanded the scope of candidate solutions and increased the diversity of candidate solutions. In (Wang et al., 2016), a quantum state transition algorithm is used to solve the job shop scheduling problems. It combines the shift decoding and position exchange coding to map the solution space, and the non-local optimal solution tolerance mechanism is proposed to improve the convergence accuracy. Unfortunately, in the above studies, the generation of the next population is only related to the optimal solution of the previous generation, which shows slow convergence rate and low convergence accuracy in the later search stage.

In this paper, a hybridization search framework which combines DSTA and tabu search (TS) is proposed to solve the combinatorial optimization problems. The DSTA is used to be the global search scheme, and the TS is introduced to act as a local search scheme. The primary contributions of this article can be summarized as follows:

(1) A hybrid discrete state transition algorithm is proposed by combining the tabu search process with discrete state transition algorithm. A search framework combining DSTA and tabu search is proposed. The tabu list is introduced as a short-term memory and can be updated based on the recently accessed solutions.

(2) A new approach for the population in DSTA is developed to produce feasible solutions, called elite solution set, which integrates the information of previous optimal solution and global optimal solution to speed up the search process.

(3) The effectiveness of HDSTA is verified on various combinatorial optimization problems, including the staff assignment problems, traveling salesman problems, and multi-AGV task assignment problems based on real-world industrial data.

The rest of the paper is organized as follows. Section 2 presents the principle of the discrete state transition algorithm. The hybrid discrete state transition algorithm is explained in Section 3. In Section 4, the results of various experiments are presented to evaluate the performance of the proposed method. Finally, the paper is summarized in Section 5.

2 The discrete state transition algorithm

In order to introduce the main principle of the discrete state transition algorithm, the following discrete optimization problems are considered:

$\underset{x_i\in K}{\mathit{min}}f\left(x\right)(1)$

where $x={\left[x_1,x_2,\cdots ,x_i,\cdots ,x_n\right]}^{\mathrm{T}}$, $K=\left\{{\kappa }_1,{\kappa }_2,\cdots ,k_m\right\}$ is the set of values for $x_i$.

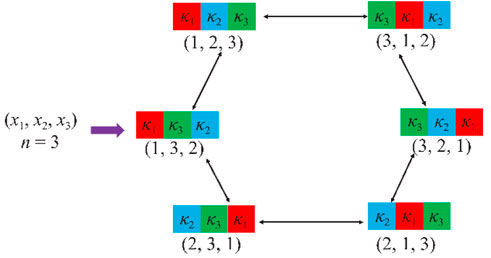
To facilitate solving the discrete optimization problems and accelerate the search rate, the subscript representation is usually used to encode the candidate solutions. The values of the n-dimensional decision variable $K=\left\{{\kappa }_1,{\kappa }_2,\cdots ,k_m\right\}$ correspond to the numbers $\left\{\mathrm{1,2},\cdots ,m\right\}$. A three-dimensional example of the subscript representation is shown in Figure 1, and the different values of $x$ correspond with six encoding methods. The subscript representation is expandable, which can make corresponding changes according to the specific form of the discrete optimization problems. Moreover, the subscript representation can also reduce the difficulty of solving the partial discrete optimization problems.

FIGURE 1

FIGURE 1. Illustration of subscript representation.

The DSTA designs four special geometric operators shown in Figure 2.

(1) Swap transformation operator

$x_{k+1}=A_k^{swap}{\left(m_a\right)x}_k(2)$

where, $A_k^{swap}\in {\mathbb{R}}^{n\times n}$ is a random Boolean matrix. It has the ability to exchange $m_a$ positions in $x_k$, and $m_a$ is the swap factor with the function of controlling the maximum number of exchangeable positions.

(2) Shift transformation operator

$x_{k+1}=A_k^{shift}\left(m_b\right)x_k(3)$

where, $A_k^{\mathrm{s}\mathrm{h}\mathrm{i}\mathrm{f}\mathrm{t}}\in {\mathbb{R}}^{n\times n}$ is called a shift transformation matrix. $m_b$ is the shift factor to control the number of positions to be shifted. The shift transformation operator can move $m_b$ positions behind another specified positions.

(3) Symmetry transformation operator

$x_{k+1}=A_k^{sym}{\left(m_c\right)x}_k(4)$

where, $A_k^{sym}\in {\mathbb{R}}^{n\times n}$ is called a symmetric transformation matrix. $m_c$ is a constant to determine the maximum length of subsequent positions. The symmetric transformation operator has ability to symmetrically exchange consecutive $m_c$ positions.

(4) Substitute transformation operator

$x_{k+1}=A_k^{sub}{\left(m_d\right)x}_k(5)$

where, $A_k^{sub}\in {\mathbb{R}}^{n\times n}$ is called a substitute transformation matrix, and $m_d$ is a constant to determine the maximum number of positions to be substituted. The substitute transformation operator can be regarded as global exploration, and the positions of substituted elements are created randomly.

FIGURE 2

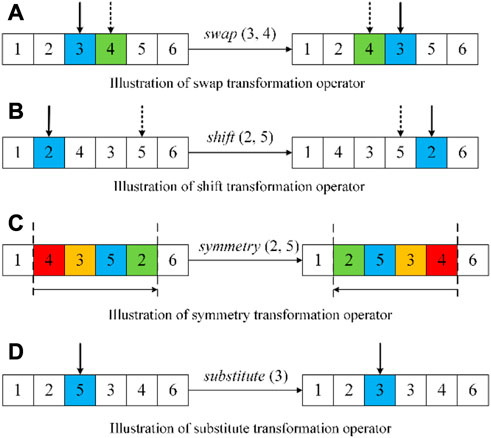
FIGURE 2. Operators of discrete state transformation. (A) illustration of swap transformation operator. (B) illustration of shift transformation operator. (C) illustration of symmetry transformation operator. (D) illustration of substitute transformation operator.

3 Hybrid discrete state transition algorithm

The state transition algorithm is wildly used in optimization problems because of its excellent performance in exploring complex solution space (global search). However, it is easily stuck in the optimum local area in large-scale problems. Contrarily, TS has superiority in local search (Ding et al., 2015) to help DSTA escape from the local optimum. TS allows transmitting from a better solution in the present iteration to a worse solution (Berlin´ska and Przybylski, 2021). Therefore, a hybrid state transition algorithm (HDSTA) is proposed by combining state transition algorithm with tabu search method. The HDSTA balances searches by combining DSTA and TS with the initialization scheme, resulting in higher quality solutions.

3.1 The main scheme of HDSTA

The algorithm starts with an initialization of the elite solution set ${\phi }_i$, and tentative multiple local optimal solutions are sorted in ascending order of the value of the objective function, where the solution in elite solution set is denoted by $p_n$. Candidate solutions are generated by four special geometric operators defined in Eqs 2–5, and then the update strategies based on TS are introduced to select optimal solutions. Hybridization is carried out by inserting the TS into the DSTA framework to explore a local search space.

The purpose of introducing TS here is to balance global decentralized search with local area capabilities. TS considers a worse solution, which increases the risk of falling into a cyclic search. The main challenge in avoiding cyclic search lies in how to establish a mechanism for relevant historical information. Therefore, a tabu list with short-term memory is used to prevent duplicate responses, and the current solution can be displaced to the next one only if the new solution is not on the tabu list and all conditions are satisfied. One solution from the elite solutions is selected and sets as the current solution, and a certain number of candidates are selected from the neighbors of the current solution. Only if the candidate solution is much more adaptive than the solution in current elite solution set will it be accepted by new elite solution set. Conversely, if there is no candidate solution that satisfies this type, the next solution is selected from the elite solution set and its corresponding move is added to the tabu list. By iterating the above steps until the termination condition is met, the algorithm will stop.

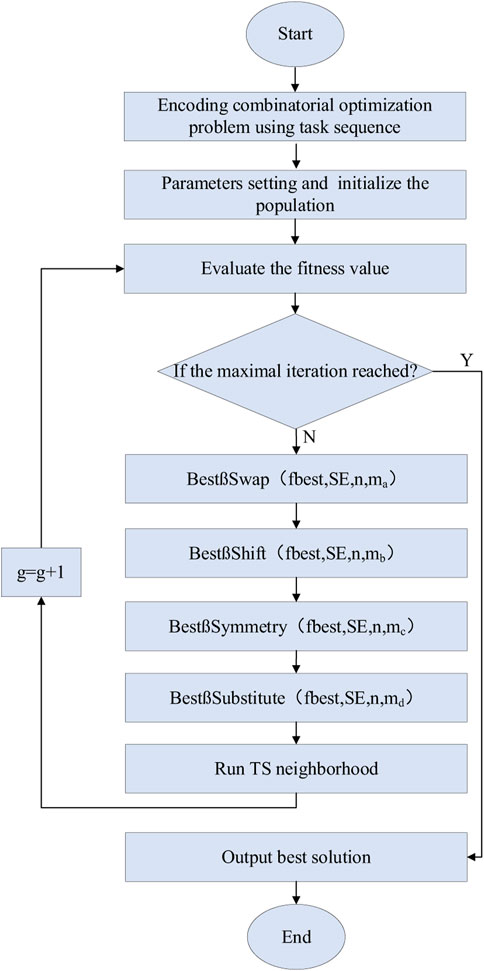
The flow chart of the proposed HDSTA is shown in Figure 3. The detailed steps are described below:

Detailed steps of HDSTA.

Step 1: encoding combinatorial optimization problem using task sequence

Step 2: setting parameters and generating the initialized population

Step 3: evaluate the fitness value

Step 4: is the maximal iteration reached? If reached, go to Step 7, else, go to Step 5

Step 5: reproduction using four special transformation operators defined in Eqs 2–5

Step 6: run TS neighborhood (insert, swapping), the go to Step 3

Step 7: output best solution

FIGURE 3

FIGURE 3. Flow chart of the hybrid discrete state transition algorithm.

3.2 The elite solution set

In the traditional DSTA, the population is only related to the optimal solution of the previous generation. It is excellent in convergence rate but its probability of falling into local optimum increases. To address the limitations, the elite solution set with the information of previous optimal solution is proposed.

In initial population of the traditional DSTA, all solutions are positioned at the one side of search space. When this side of search space is the property of local optima, the algorithm will converge faster. Therefore, the initialization method of elite solution set is proposed to generate solutions located in different search spaces. The solution set $Q_0$ is initialized and the upper limit of the number of solutions in the set is defined as m, which is stored in ascending order of the objective function value. After creating the initial population, the fitness evaluation is performed by an objective function. During the iteration process, all the elite solutions searched in each generation are compared with the solutions stored in $Q_0$. If there is a better solution, it will be replaced so as to ensure that the elite solution set $Q_0$ contains all the elite individuals in the search process. The initialization of the elite solution set is given in Algorithm 1. Here, $S_e$ is the number of solutions in the population, $S_{best}$ is the optimal solution in the population and $Q_0$ is the elite solution set.

Algorithm 1. Initialization of the elite solution set

1: The initialized solutions are generated $S_{best}$

2: $f_{best}$ ←fitness ($S_{best}$)

3: $k$ ←0

4: repeat

5: [$Q_0,f_{best},S_{best}$] ← swap ($Q_0,f_{best},S_{best},S_e$)

6: [$Q_0,f_{best},S_{best}$] ← shift ($Q_0,f_{best},S_{best},S_e$)

7: [$Q_0,f_{best},S_{best}$] ← symmetry ($Q_0,f_{best},S_{best},S_e$)

8: [$Q_0,f_{best},S_{best}$] ← substitute ($Q_0,f_{best},S_{best},S_e$)

9: $k$ ← $k+1$

10: until the maximum number is reached

Output: $Q_0$

3.3 Tabu search

TS is a widely used local search strategy based on the neighborhood search. Inspired by (Umam et al., 2022), the framework of this paper consists of the neighborhood structure, tabu list and move attribution. Firstly, the length of tabu list and the aspiration criteria are determined. Then, the maximum iteration of DSTA is taken as the termination condition. Next, using a neighborhood search with insertion and swapping methods makes a move. Finally, solutions are evaluated and updated with the best solution which is non-tabu of the search results till the termination condition is met.

The neighborhood structure determines the quality of the solution generated by the search, and also affects the search efficiency and convergence speed of the algorithm. In this paper, the state itself or the process of state transition is regarded as a tabu object. For example, when a state changes from $a$ to $b$, the state $b$ or the state transition $a$ → $b$ can be regarded as a tabu object, which is simple and easy to understand.

The tabu list affects the search process through the length of the list. The increase of list size causes a wider search scope, and more solutions are listed. The proposed HDSTA adopts the variable tabu list mode with the length of the list between the minimum and maximum values, and the length of tabu list increases from minimum to maximum gradually in the process. Whenever a better solution is obtained or the elite solution set is updated, the length of tabu list is increased to support deeper exploration in this area.

The candidate solution set consists of the better neighbor solutions in the neighbor solution set. The better neighbor solutions are selected by the fitness value function, then, the candidate solutions satisfying the forbidden and amnesty criteria are selected as the new current solutions in the candidate solution set. The mobility attribute is the key pillar for TS to find the optimum solution. The proposed algorithm defines two conditions. The first condition is that if a move of a member leads to a solution with higher cost than the best answer already obtained, then the member is removed from the tabu list. The second one is that if the structure of the method and tabu list in the stage of the algorithm is such that there is no possibility of moving to a member. In this case, the member closest to the exit is removed from the list.

4 Experimental results and discussion

The effectiveness of the proposed HDSTA is verified through three experiments, including the staff assignment problems, traveling salesman problems and a large-scale industry case using real-world data. All experiments are implemented on a computer with Intel Core i7-9700 CPU 4.8 GHz and 16 GB RAM. The population size is set to 50 for all experiments of different problems. The parameters, including elite solution set size, tabu list size and maximum iterations, are set to 30, 120 and 200 respectively. The best indicates the minimum value of results, the worst means the maximum value of results, and then it follows the mean (average value), st.dev (standard deviation) and time/s (computation time). These common statistics can indicate the convergence accuracy, search efficiency and stability of the algorithm.

4.1 Results analysis for staff assignment problem

Staff assignment problem is a well-known combinatorial optimization problem in human resources department (Mo et al., 2020), which can be described formally as follows: $n$ employees are assigned to $m$ locations, where the cost of the $i$ th employee traveling to the $k$ th location is defined by $c_{ik}$. The communication time between employee $i$ and employee $j$ is denoted by $t_{ij}$, and $f_{kg}$ represents the communication cost. It is required that each location must be assigned one employee, and each employee only travel to one location. The mathematical model can be expressed as follows:

$minQ\left(x\right)={\displaystyle \sum }_{i=1}^n{\displaystyle \sum }_{k=1}^n{c}_{ik}{t}_{ij}(6)$

The matrix coefficients of different dimensions are introduced. Both $c_{ik}$ and $t_{ij}$ are random integers ranging from 1 to 100, and $f_{kg}$ is a random decimal ranging from 0 to 1. To verify the performance of the proposed HDSTA, it is compared with the discrete state transfer algorithm (DSTA) and the simulated annealing algorithm (SA). The cases of 20, 30, 40 and 50 dimensions are generated, and each algorithm runs 20 times for each case independently.

The performance of the different methods is illustrated in Table 1. It can be seen that the best and average values of the results when solving the above assignment problems with four different dimensions using HDSTA are better than those of SA and DSTA. In addition, the HDSTA algorithm takes less time to solve each problem than the simulated annealing algorithm and is close to that of DSTA. The above results reflect the effectiveness of the algorithm proposed by HDSTA algorithm.

TABLE 1

TABLE 1. Comparison results of staff assignment problems.

4.2 Results analysis for traveling salesman problem

Traveling salesman problem (TSP) is another well-known combinatorial optimization problem. To test the performance of the HDSTA, the simulated annealing algorithm (SA) is compared with DSTA based on standard TSP data (Tagne Fute et al., 2022).

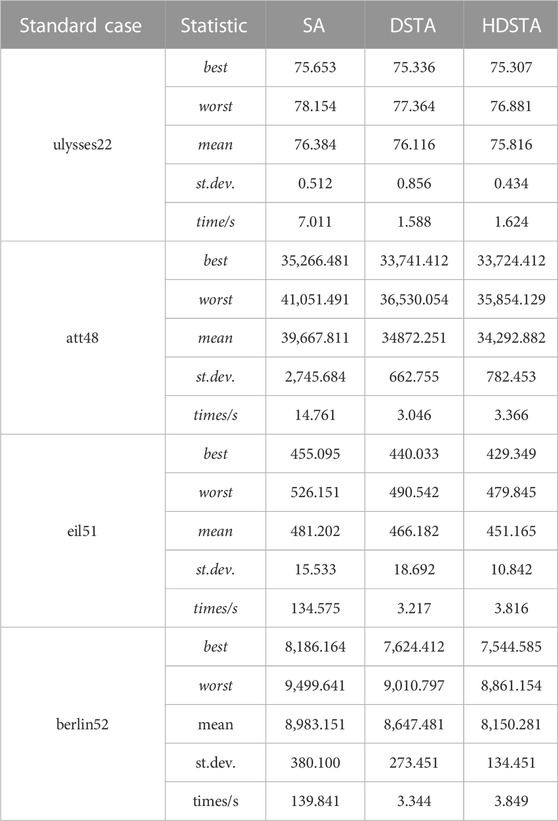
From the results shown in Table 2, it can be concluded that HDSTA outperforms SA and DSTA in almost all performances. HDSTA obtains better results in all four standard cases. Taking the att48.tsp standard case as an example, the best result is shown in Figure 4.

TABLE 2

TABLE 2. Comparison results of traveling salesman standard cases.

FIGURE 4

FIGURE 4. The best route of att48.tsp obtained by HDSTA.

Table 2 shows the results of different standard cases. The standard deviation of HDSTA is lower than that of SA and DSTA, which proves that the proposed algorithm has a relatively strong stability. In addition, both HDSTA and DSTA have better advantages in terms of computation time than SA.

4.3 Results analysis for real-world industrial cases

Automated guided vehicles (AGV) are widely used to improve warehouse transport efficiency (Cheikhrouhou and Khoufi, 2021). Multi-AGV task assignment problem is to assign and sequence tasks for each AGV, with the main objective of minimizing the sum of costs through efficient AGV fleet management. When all warehouses in the layout are fixed and the cost of using AGV is only related to the moving distance, the task assignment problem is a special traveling salesman problem, whose polynomial can be expressed as below (Li et al., 2020).

$\mathit{min}{\displaystyle \sum }_{k\in K}\mathit{min}{\displaystyle \sum }_{\left(i,j\right)\in A}{d}_{ij}{x}_{ijk}(7)$

where $K$ is the set of all vehicles with $\left|K\right|=m$. $i,j$ are nodes. $d_{ij}$ represents the distance from node $i$ to $j$. $x_{ijk},i,j\in V,k\in K$ is a binary variable used by vehicle k if the edge between node $i$ and node $j$ is 1, otherwise it is 0.

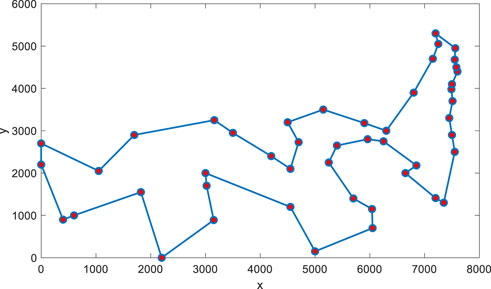
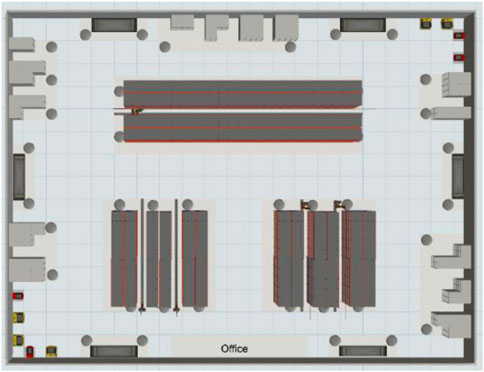
The real AGV system of a warehouse in Changsha, China is used as the experimental platform. The system consists of 15 AGV and 39 warehouses, and the layout of the warehouses is illustrated in Figure 5. Practitioner feedback indicates that periods of 50 requests using over 5 AGV are regarded as busy periods (Li et al., 2022). Taking the number of AGV and task distances into consideration, the objective can be transformed into obtaining a near-optimal solution in a reasonable amount of time and determining its degree of approximation according to its NP-hard property.

FIGURE 5

FIGURE 5. The layout of the warehouse.

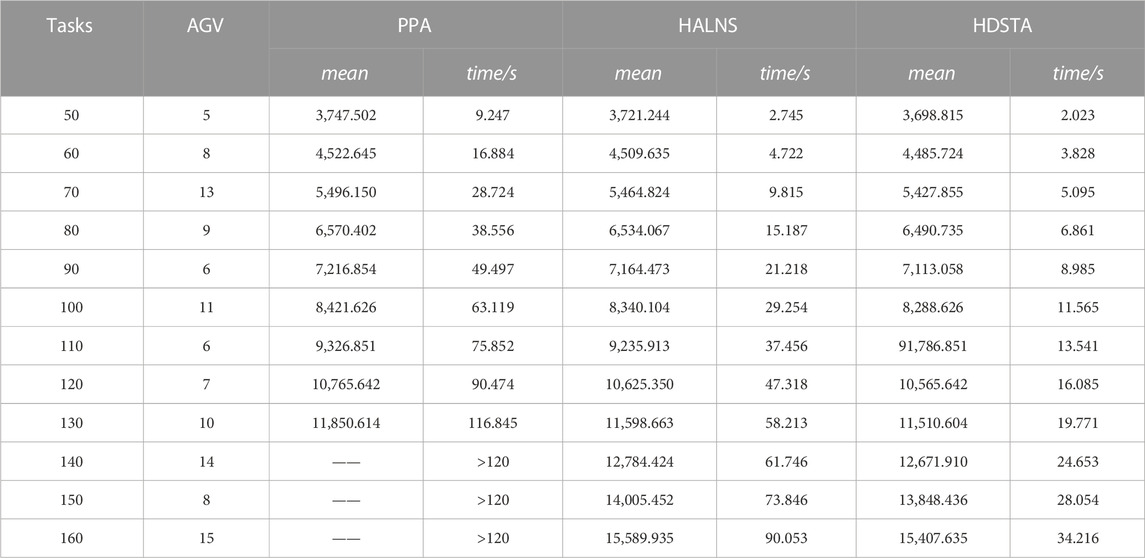
To verify the effectiveness of HDSTA, 50–160 tasks were randomly generated, and AGV numbers range from 5 to 15. In the experiments, 10 groups of tasks were generated and ran 10 times for each case, and the mean value and computation time were assessed. In industrial applications, the average value and computation time are the most important performance indicators. In each case, HDSTA is compared with the adaptive large neighborhood search algorithm (HALNS) (Singh et al., 2022), and the pre-programmed algorithm (PPA) (Maza and Castagna, 2005). The performance and computation time of HALNS, PPA and HDSTA for 120 sets of task assignments assigned by 20 case types are shown in Tables 3. Compared with PPA and HALNS, HDSTA has a lower mean value and less computation time.

TABLE 3

TABLE 3. Comparison results of multi-AGV task assignment problems.

5 Conclusion

HDSTA is proposed to solve the large-scale combinatorial optimization problems. The TS method is introduced to guide the local search of DSTA to achieve the balance between the exploration capabilities and the exploitation capabilities. Furthermore, a new approach for the population generation of DSTA has been adapted. It avoids that all solutions are positioned at one side of the search space, resulting in too fast convergence. The experimental results of three large-scale combinatorial optimization problems show that the proposed method has better solving accuracy than the other two algorithms. The HDSTA can be further applied to more industrial cases. In addition, this research can be expanded by combining the DSTA with another local search algorithm for future works under multiple objectives.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

EH and SS: Conceptualization and writing—original draft preparation. EH: Data curation. EH, SS, and JH: Methodology, validation, and formal analysis. JH: Writing—review and editing and funding acquisition. All authors contributed to the article.

Funding

This study was supported by National Natural Science Foundation of China under Grant No. 61873282.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdel-Basset, M., Ding, W., and El-Shahat, D. (2021). A hybrid Harris Hawks optimization algorithm with simulated annealing for feature selection. Artif. Intell. Rev. 54, 593–637. doi:10.1007/s10462-020-09860-3

CrossRef Full Text | Google Scholar

Berlin´ska, J., and Przybylski, B. (2021). Scheduling for gathering multitype data with local computations. Eur. J. Oper. Res. 294 (2), 453–459. doi:10.1016/j.ejor.2021.01.043

CrossRef Full Text | Google Scholar

Cheikhrouhou, O., and Khoufi, I. (2021). A comprehensive survey on the multiple traveling salesman problem: Applications, approaches and taxonomy. Comput. Sci. Rev. 40, 100369. doi:10.1016/j.cosrev.2021.100369

CrossRef Full Text | Google Scholar

Ding, J., Song, S., Gupta, J., Zhang, R., Chiong, R., and Wu, C. (2015). An improved iterated greedy algorithm with a Tabu-based reconstruction strategy for the no-wait flowshop scheduling problem. Appl. Soft Comput. J. 30, 604–613. doi:10.1016/j.asoc.2015.02.006

CrossRef Full Text | Google Scholar

Dong, T. X., Yang, C. H., Zhou, X. J., and Gui, W. H. (2016). A novel discrete state transition algorithm for staff assignment problem. Control Theory & Appl. 33 (10), 1378–1388.

Google Scholar

Hassanzadeh, A., Altajer, A. H., Rahman, H. S., Saleh, M. M., Bokov, D. O., Abdelbasset, W. K., et al. (2021). Mesenchymal stem/stromal cell-based delivery: A rapidly evolving strategy for cancer therapy. Front. Cell Dev. Biol. 9, 686453. doi:10.3389/fcell.2021.686453

PubMed Abstract | CrossRef Full Text | Google Scholar

Houssein, E. H., Gad, A. G., Hussain, K., and Suganthan, P. N. (2021). Major advances in particle swarm optimization: Theory, analysis, and application. Swarm Evol. Comput. 63, 100868. doi:10.1016/j.swevo.2021.100868

CrossRef Full Text | Google Scholar

Li, M., Hao, J. K., and Wu, Q. (2022). Learning-driven feasible and infeasible tabu search for airport gate assignment. Eur. J. Operational Res. 302 (1), 172–186. doi:10.1016/j.ejor.2021.12.019

CrossRef Full Text | Google Scholar

Li, Z., Barenji, A. V., Jiang, J., Zhong, R. Y., and Xu, G. (2020). A mechanism for scheduling multi robot intelligent warehouse system face with dynamic demand. J. Intelligent Manuf. 31 (2), 469–480. doi:10.1007/s10845-018-1459-y

CrossRef Full Text | Google Scholar

Lin, Y. H., and Tian, Q. (2021). Branch-and-cut approach based on generalized benders decomposition for facility location with limited choice rule. Eur. J. Operational Res. 293 (1), 109–119. doi:10.1016/j.ejor.2020.12.017

CrossRef Full Text | Google Scholar

Maza, S., and Castagna, P. (2005). A performance-based structural policy for conflict-free routing of bi-directional automated guided vehicles. Comput. industry 56 (7), 719–733. doi:10.1016/j.compind.2005.03.003

CrossRef Full Text | Google Scholar

Mo, Y., Zhao, D., Du, J., Syal, M., Aziz, A., and Li, H. (2020). Automated staff assignment for building maintenance using natural language processing. Automation Constr. 113, 103150. doi:10.1016/j.autcon.2020.103150

CrossRef Full Text | Google Scholar

Singh, N., Dang, Q. V., Akcay, A., Adan, I., and Martagan, T. (2022). A matheuristic for AGV scheduling with battery constraints. Eur. J. Operational Res. 298 (3), 855–873. doi:10.1016/j.ejor.2021.08.008

CrossRef Full Text | Google Scholar

Tabassum, M. F., Saeed, M., Chaudhry, N. A., Ali, J., Farman, M., and Akram, S. (2021). Evolutionary simplex adaptive Hooke-Jeeves algorithm for economic load dispatch problem considering valve point loading effects. Ain Shams Eng. J. 12 (1), 1001–1015. doi:10.1016/j.asej.2020.04.006

CrossRef Full Text | Google Scholar

Tagne Fute, E., Nyabeye Pangop, D. K., and Tonye, E. (2022). A new hybrid localization approach in wireless sensor networks based on particle swarm optimization and tabu search[J]. Appl. Intell. 2022, 1–16. doi:10.1007/s10489-022-03872-y

CrossRef Full Text | Google Scholar

Umam, M. S., Mustafid, M., and Suryono, S. (2022). A hybrid genetic algorithm and tabu search for minimizing makespan in flow shop scheduling problem. J. King Saud University-Computer Inf. Sci. 34 (9), 7459–7467. doi:10.1016/j.jksuci.2021.08.025

CrossRef Full Text | Google Scholar

Wang, C., Zhang, H. L., and Fan, W. H. (2016). Volterra series identification based on state transition algorithm with orthogonal transformation. Telkomnika 14 (1), 171–180. doi:10.12928/telkomnika.v14i1.2663

CrossRef Full Text | Google Scholar

Wang, K., Li, X., Gao, L., and Gupta, S. M. (2021). A genetic simulated annealing algorithm for parallel partial disassembly line balancing problem. Appl. Soft Comput. 107, 107404. doi:10.1016/j.asoc.2021.107404

CrossRef Full Text | Google Scholar

Wang, Z. Z., and Sobey, A. (2020). A comparative review between Genetic Algorithm use in composite optimisation and the state-of-the-art in evolutionary computation. Compos. Struct. 233, 111739. doi:10.1016/j.compstruct.2019.111739

CrossRef Full Text | Google Scholar

Zhang, F., Parayath, N. N., Ene, C. I., Stephan, S. B., Koehne, A. L., Coon, M. E., et al. (2019). Genetic programming of macrophages to perform anti-tumor functions using targeted mRNA nanocarriers. Nat. Commun. 10 (1), 3974. doi:10.1038/s41467-019-11911-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, F. X., Yang, C. H., Zhou, X. J., and Gui, W. H. (2019). Optimal setting and control strategy for industrial process based on discrete-time fractional-order PI$^{\lambda}$ D$^{\mu}$. IEEE Access 7, 47747–47761. doi:10.1109/access.2019.2909816

CrossRef Full Text | Google Scholar

Zhang, F., Yang, C., Zhou, X., and Gui, W. (2018). Fractional-order PID controller tuning using continuous state transition algorithm. Neural Comput. Appl. 29 (10), 795–804. doi:10.1007/s00521-016-2605-0

CrossRef Full Text | Google Scholar

Zhou, X., Gao, D. Y., Yang, C., and Gui, W. (2016). Discrete state transition algorithm for unconstrained integer optimization problems. Neurocomputing 173, 864–874. doi:10.1016/j.neucom.2015.08.041

CrossRef Full Text | Google Scholar

Zhou, X., Yang, C., and Gui, W. (2012). State transition algorithm. J. Industrial Manag. Optim. 8 (4), 1039–1056. doi:10.3934/jimo.2012.8.1039

CrossRef Full Text | Google Scholar