
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res., 10 April 2023
Sec. Hydrogen Storage and Production
Volume 11 - 2023 | https://doi.org/10.3389/fenrg.2023.1145978
This article is part of the Research TopicMicrobiology of Underground Hydrogen StorageView all 5 articles
Underground Hydrogen storage (UHS) is a promising technology for safe storage of large quantities of hydrogen, in daily to seasonal cycles depending on the consumption requirements. The development of UHS requires anticipating hydrogen behavior to prevent any unexpected economic or environmental impact. An open question is the hydrogen reactivity in underground porous media storages. Indeed, there is no consensus on the effects or lack of geochemical reactions in UHS operations because of the strong coupling with the activity of microbes using hydrogen as electron donor during anaerobic reduction reactions. In this work, we apply different geochemical models to abiotic conditions or including the catalytic effect of bacterial activity in methanogenesis, acetogenesis and sulfate-reduction reactions. The models are applied to Lobodice town gas storage (Czech Republic), where a conversion of hydrogen to methane was measured during seasonal gas storage. Under abiotic conditions, no reaction is simulated. When the classical thermodynamic approach for aqueous redox reactions is applied, the simulated reactivity of hydrogen is too high. The proper way to simulate hydrogen reactivity must include a description of the kinetics of the aqueous redox reactions. Two models are applied to simulate the reactions of hydrogen observed at Lobodice gas storage. One modeling the microbial activity by applying energy threshold limitations and another where microbial activity follows a Monod-type rate law. After successfully calibrating the bio-geochemical models for hydrogen reactivity on existing gas storage data and constraining the conditions where microbial activity will inhibit or enhance hydrogen reactivity, we now have a higher confidence in assessing the hydrogen reactivity in future UHS in aquifers or depleted reservoirs.
The limitation of natural resources and the climatic and environmental crisis led our societies to undertake an energy transition to meet the future energy needs. Hydrogen (H2) is an energy carrier that is identified as a possible substitute for fossil fuels1. The option of using hydrogen as an energy source on a large scale will depend on the availability of durable and reliable hydrogen storage when considering intermittent hydrogen generation from renewable energy. Underground Hydrogen Storage (UHS) is an attractive solution because large quantities of hydrogen can be stored, in a safe and economic way (Foh et al., 1979; Tarkowski, 2019; Londe, 2021; Aftab et al., 2022). Hydrogen as an energy carrier can be used to produce electricity, for transport when used as a fuel directly or for producing liquid fuels, for different industrial processes (refinery, metallurgy, production of electronics or glass or food-processing industry) and blended in the natural/town gas distribution network. Today, different UHS sites exist based on a seasonal storage of hydrogen for use in chemical or petrochemical industrial processes and for which rentability is proven.
UHS can be implemented in salt caverns, in porous media formations such as depleted oil and gas reservoirs or saline aquifers and in lined rock caverns (Londe, 2021). Hydrogen is a small molecule that requires high pressure storage to store large quantities of equivalent energy. As hydrogen is a reactive molecule, several questions specific to hydrogen have been raised for the development of UHS. These questions deal with the mechanical integrity of the storage, the salt or caprock tightness, the compatibility of materials (steel, elastomers, cement) with hydrogen and the biological and chemical reactions with in-situ fluids and minerals. Biological and chemical reactions in UHS and their consequences can potentially affect the performance or safety of the storage. Therefore, it is important to anticipate and assess the possible reactions of hydrogen before storing it in a reservoir. Recently, various review articles (Reitenbach et al., 2015; Beckingham and Winningham, 2020; Dopffel et al., 2021; Heinemann et al., 2021) identify the potential effects of hydrogen reactions within underground gas storages. These reviews point out the need for a better understanding and quantification of hydrogen reactivity in UHS.
The hydrogen injected in a reservoir will change the chemical equilibrium between the formation water, the dissolved gases and rock minerals. The resulting geochemical reactions may lead to:
i) loss of hydrogen.
ii) pollution of the hydrogen stored by produced gases - in particular hydrogen sulfide (H2S).
iii) precipitation/dissolution of minerals resulting in changes of injectivity in the reservoir.
iv) changes in the integrity of wells and installations (corrosion) due to the production of hydrogen sulfide.
v) dissolution of minerals altering the mechanical properties of the reservoir or the caprock.
vi) dissolution of minerals resulting in the formation of gas leakage pathways through the caprock.
Although geochemical processes may have a significant impact on technical and economic aspects of hydrogen storage, the extend and rates of reactions are subject to high uncertainties. There is currently no consensus on the effect or absence of effects of geochemical reactions in storage operations. This uncertainty lies in the complex kinetics of redox reactions involving hydrogen and its strong coupling with the bacterial dynamics. The uncertainty results from the low number of experimental studies in the laboratory and the scarce and often poorly documented feedback from the hydrogen storage operations. As a result, modelling approaches still need to be improved to account for the kinetics of hydrogen reactivity at the reservoir scale.
The goal of the work presented here is to progress in establishing a model to evaluate the gas/water/rock interactions during underground hydrogen storage. Although the processes involved in hydrogen reactions are complex, the modelling approach focusses on finding a simple way to describe the hydrogen reactions. After identifying the main reactions expected during hydrogen storage, different modeling approaches are tested to consider the reductive effect of hydrogen. The models are then applied to Lobodice gas storage, where hydrogen loss was monitored during seasonal storage (Smigan et al., 1990). These calculations allow for a discussion on the adequate ways to model hydrogen-induced redox reactions and on the associated uncertainties, in the light of the environmental conditions favorable to microbial activity.
Feedback from underground gas storage (UGS) operations of gas containing hydrogen is a priori a valuable source of information on the reactivity of hydrogen. Worldwide and in recent decades, about a dozen gas storage sites stored gas mixtures containing hydrogen in different proportions (Foh et al., 1979; MARCOGAZ, 2017; Tarkowski, 2019; Dopffel et al., 2021; Sambo et al., 2022), especially in town gas or manufactured gas storage. Monitoring the composition of the gas over time allows estimates of the losses of hydrogen, either related to flow, diffusion, capillary trapping or reactions. The concentration of hydrogen sulfide in the stored gas is a direct indicator of hydrogen reactivity. However, the publicly available information is often limited. Compilations of gas storage sites containing hydrogen have emerged in recent years, but use or refer to indirect studies. Thus, the technical note of MARCOGAZ, a European technical association of gas manufacturers, seems to be the most reliable source. However, the information remains fragmentary (MARCOGAZ, 2017).
The reviews show that there is very low hydrogen reactivity in storage in salt cavities (Dopffel et al., 2021; Réveillère et al., 2022). Several sites are referenced such as Teeside (United Kingdom), Clemens dome (United States), Moss Bluff (United States), Spindletop (United States), Yakshunovskoe (Russia), Kiel (Germany) in which gases containing up to 95% hydrogen have been stored since the 1970s, for some of these. No loss of hydrogen due to its reactivity was observed in these cavities and only a small associated production of hydrogen sulfide is reported for some cavities. The possible reasons which can explain this lack of reactivity are the low surface area of rock in a salt cavern exposed to stored gas which limits the formation of possible biofilms and the high salinity which strongly limits bacterial diversity and growth. However, the occurrence and growth of sulfate-reducing bacteria in the remaining brine, once the cavity is filled with gas, and the associated souring issues cannot be totally discarded (Bordenave et al., 2013; Hemme and Van Berk, 2017; Schwab et al., 2022).
Conversely, in storage sites in sandstone reservoirs, such as depleted oil and gas reservoirs or saline aquifers, a reactivity of hydrogen might be observed, resulting, sometimes, in very high consumption of stored hydrogen. However, these observations from town gas storage sites are not directly applicable to pure hydrogen storage, due to the large presence of co-injected carbon sources. The most emblematic case is that of the town gas storage of Lobodice (Czech Republic), documented in two scientific articles (Smigan et al., 1990; Buzek et al., 1994). In Lobodice, town gas containing 54% H2 was stored in a sandstone reservoir at a depth of 500 m (pressure of 4 MPa and temperature of 25°C–45°C). After 7 months of storage, 10%–20% of the gas volume was lost and the composition of the gas changed, with the formation of methane and decreases in hydrogen, carbon dioxide and carbon monoxide. At Ketzin (Germany), the Lower Jurassic sandstone reservoir (280 m deep; salinity of 50 g/L) was used for town gas storage from the 1960s up to 2004. 61% of the volume of hydrogen was lost, corresponding to 8 million m3/year, and significant changes in the composition of the stored town gas was observed, with the generation of hydrogen sulfide, pressure losses and temperature changes (MARCOGAZ, 2017). The Beynes saline aquifer (France) was used from 1956 to 1972 as a storage of town gas containing 40%–60% of hydrogen before its conversion to a storage of natural gas (Foh et al., 1979). The operator describes a proven, but still limited reactivity of hydrogen in the Beynes field (MARCOGAZ, 2017). Hydrogen sulfide was produced by reduction of sulfates, present in the in-situ brine, by hydrogen, leading to desulfurize the produced gas which contained up to 40 ppm hydrogen sulfide (Foh et al., 1979). Sulfate concentrations were also observed to decrease in the Beynes aquifer, associated with this hydrogen sulfide production. Interestingly, the microbial ecosystem was observed to change so that methanogenic archea became dominant compared to sulfate-reducing bacteria after the depletion of sulfate in the Beynes aquifer (Ranchou-Peyruse et al., 2019).
The bibliography on storage sites of hydrogen in sandstone reservoirs also includes the Underground Sun Storage, a pilot2 storage site of hydrogen (Austria) operated by RAG Austria AG (RAG, 2017; Hassannayebi et al., 2019). In 2016, 115,000 m3 of gas containing 10% H2 was injected into a sandstone formation at a depth of 1,200 m for 3 months. Following this injection, about 18% of hydrogen was not recovered, through diffusion, mixing, dissolution and conversion. Methanogenic archaea and sulphate-reducing bacteria were identified, but their effect seems limited with only 3% of the hydrogen converted into methane. The Hychico project (Argentina) of methanation in a sandstone reservoir at a depth of 815 m in the Diadema field also reports a consumption of hydrogen (Pérez et al., 2016).
Dihydrogen (H2) is a gas with a high energy density per mass (≈120 MJ/kg) but with a low density (0.081272 kg/m3 at 25°C and 1 bar). Compared to natural gas, a higher storage volume is required for hydrogen to store the same amount of energy. Its storage efficiency increases with depth due to an increase in the density of hydrogen with pressure that is higher than the decrease in density of hydrogen with temperature, within the range of pressure and temperature of common storages.
In an UHS, hydrogen will mainly be stored as a gas phase because its solubility in water is very low. Like other gases, the solubility of hydrogen increases with increasing pressure and temperature but decreases with increasing salinity (Chabab et al., 2020). The solubility of hydrogen is much lower than the solubility of carbon dioxide and in the range of the solubility of methane. At 1 bar and 25°C, the solubility of hydrogen is about half the solubility of methane and 5 times lower than the solubility of carbon dioxide. At higher pressure, the solubility of hydrogen becomes higher than the solubility of methane. The solubility of hydrogen determines the potential reactivity of hydrogen since the reactivity occurs in solution between water and rock. The reactivity of gases with rocks without the presence of water is negligible (Yekta et al., 2018).
Hydrogen can act as an electron donor for oxidized species present in the pore water, possibly leading to a depletion of hydrogen. In the subsurface, hydrogen can be oxidized by various electron acceptors such as carbonates species, sulfates and other sulfur species, nitrate and other oxidized forms of nitrogen, ferric iron or oxygen. Meaning that, in aquifers and reservoirs that could host an underground hydrogen storage, hydrogen is mainly expected to induce redox reactions: ferri-reduction, sulfate reduction, methanogenesis and acetogenesis (listed from energetically more favorable to less favorable). The sulfate reduction may lead to the formation of hydrogen sulfide (souring) depending on the pH conditions, a toxic and corrosive gas that requires gas treatment. Methane is formed during methanogenesis and changes the gas mixture composition. An overview of the main redox reactions consuming hydrogen in the subsurface is shown in Table 1. These reactions are sorted depending on their expected importance in an underground hydrogen storage (Dopffel et al., 2021). The negative of the free energy of formation
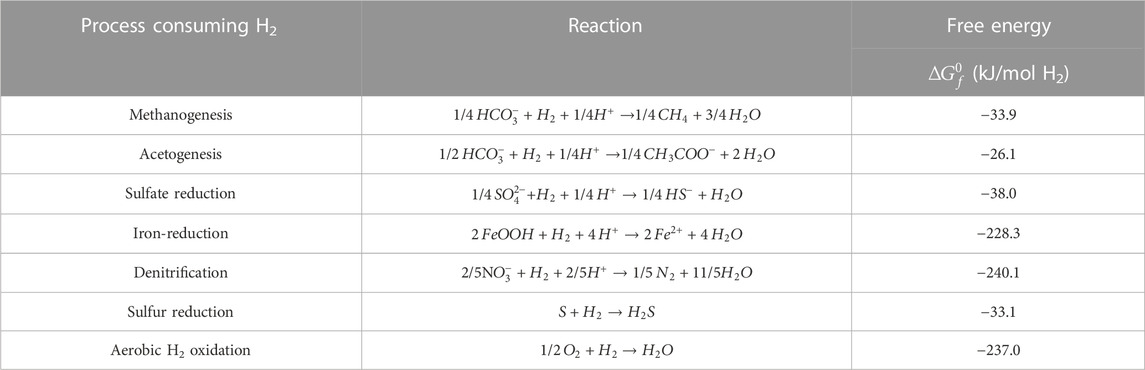
TABLE 1. Redox reactions involving oxidation of hydrogen relevant for underground hydrogen storage in sandstone reservoirs.
However, the redox reactions involving hydrogen are known to be restricted, because of the high energy barrier necessary to break the strong H-H bounds before the electron transfer can take place. In the absence of catalysts such as microorganisms or possibly metal and mineral surfaces, the extent of reactions induced by hydrogen are assumed to be minor under the temperature conditions expected in an underground hydrogen storage. Indeed, the experiments conducted by Truche et al. (2009) found a half-life of sulfate undergoing sulfate reduction, in the absence of bacteria, of 210,000 years at 90°C. Similarly, the same range of half-life (160,000 years) was measured under sterile conditions for oxidized carbon during methanogenesis at 100°C (Seewald et al., 2006).
Therefore, to have any significance during storage operations, the hydrogen consuming reactions such as sulfate-reduction, methanogenesis and acetogenesis need to be catalyzed by microbial activity. The microbial communities hosted in deep aquifers and reservoirs are dominated by sulfate-reducing bacteria, homoacetogenic bacteria, methanogenic bacteria and archea (Ranchou-Peyruse et al., 2019; Ranchou-Peyruse et al., 2021; Thaysen et al., 2021). Hydrogen is then necessary for the functioning of these ecosystems which are already present in reservoirs considered for UHS. The influence of microbial activity on reactions using hydrogen as electron donor is proven but its quantitative effect of this microbial activity on the reaction rates is uncertain. Relatively few experimental measurements of sulfate-reduction, methanogenesis or acetogenesis reaction rates are available for hydrogen-rich conditions (Berta et al., 2018). In addition, the upscaling of laboratory determined rates to storage scale rates is also poorly constrained.
Part of the uncertainties on the methanogenesis, acetogenesis and sulfate-reduction reaction rates could be related to the environmental conditions that change microbial activity and, then, hydrogen reactivity. Indeed, the growth and activity of each type of bacteria is optimal under a restricted range of environmental conditions, including temperature, pressure, salinity, pH and availability of nutrients. Beyond the optimum conditions, the microbial activity is reduced or inactive. Referring to the reviews addressed by Hoehler et al. (2010), Katz (2011) and Thaysen et al. (2021), it is possible to identify the optimum and limiting environmental conditions for sulfate-reduction, acetogenesis and methanogenesis in aquifers or reservoirs targeted for UHS. Temperature and salinity are the parameters with first order influence on the growth of sulfate-reducing, methanogenic and acetogenic microorganisms. Most cultured strains may grow at temperature up to 70°C, with optimum growth between 25 and 35C° for the most abundant mesophilic bacteria and between 50°C and 70°C for thermophilic bacteria. A critical temperature of 72°C is indicated for acetogens, 113°C for a sulfate-reducer strain and 122°C for a methanogenic strain. High salinity implies an adaptation of microorganisms. Most methanogens may grow at salinities up to 0.77 M NaCl and most sulfate-reducers and acetogens at between 0 and 0.4 M NaCl. Several strains can survive up to salinities of 4–5 M NaCl, but these extreme halophilic microorganisms are not necessarily resistant to elevated temperatures. Beside salinity, the modification of the activity of water because of changes in solution composition is also proposed as a factor of influence on bacterial activity. More commonly reported is a competition between microbial processes because of the chemical conditions, with, for example, an absence or a low concentration in sulfates favoring methanogenesis. An evolution of the microbial population is reported by Haddad et al. (2022) during a hydrothermal experiment of hydrogen consumption that showed a successive decrease and depletion of sulfates and carbonates. Methanogenic bacteria were observed to develop when sulfate concentration was lower than 0.08 mM. Bacterial growth is also sensitive to pH. Optimum pH for most microorganisms is 6.5–7.5, with an acceptable pH range of 4–9.5. Several sulfate-reducers and acetogens can grow at pH values slightly higher than 10. Pressure has less effect on microbial activity and increasing the pressure is often associated with the simultaneous increase of temperature. Although ceasing growth under aerobic conditions, methanogens are reported to present some tolerance to oxygen. It is also worth mentioning the importance of nutrient availability and the complexity related to the presence of hotspots or heterogeneously distributed reactions in pore networks or, at the reservoir scale, at the gas/water interfaces.
The chemical equilibrium between the formation pore water, the dissolved gases and the rock minerals is expected to be changed by the injection of large amounts of hydrogen. The dissolution of hydrogen induces redox reactions in solution that form species such as HS− or uses inorganic carbon that will impact the pH. Mineral dissolution and precipitation reactions that can occur because of hydrogen injection are driven both by redox and acid-base reactions.
In the literature, only few studies report interaction experiments between hydrogen and rocks in the context of underground hydrogen storage in porous reservoirs (Flesch et al., 2018; Yekta et al., 2018; Shi et al., 2020; Haddad et al., 2022; Hassanpouryouzband et al., 2022). A review of these experiments, their conditions and main results is given in Table 2. The observed changes in mineralogy are minor and consist in the dissolution of minerals of high solubility, located in the natural cementing minerals rather than in the rock matrix. These different experimental studies converge on their conclusion of a lack of abiotic reactivity or a very low reactivity of hydrogen with rock minerals.
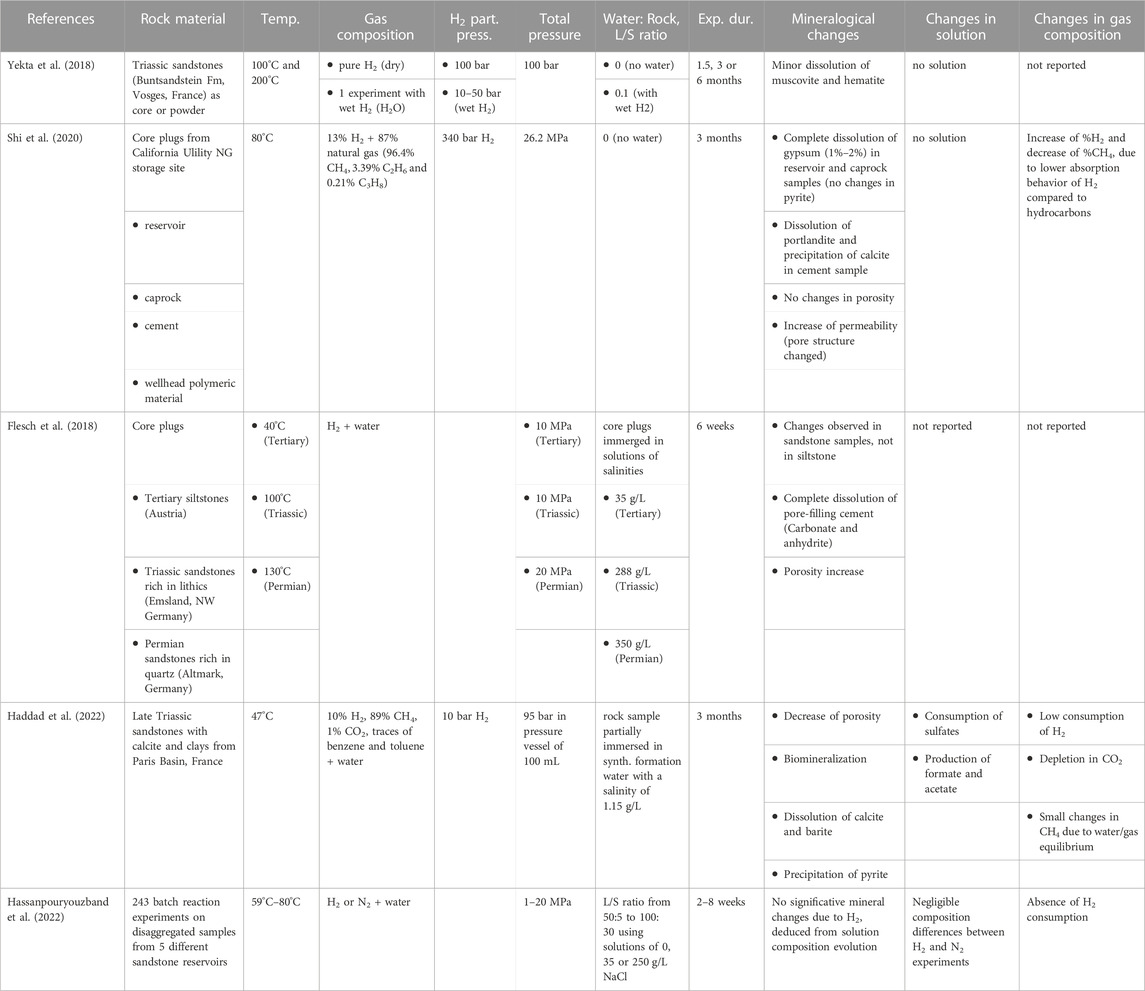
TABLE 2. Review of studies on the reactivity of hydrogen with rocks under conditions relevant for underground hydrogen storage in sandstone reservoirs.
The minerals potentially affected by redox reactions contain oxidized species that are destabilized by the on-going reduction due to hydrogen. This is the case of the Fe(III)-bearing minerals, such as Fe(III) oxides and oxi-hydroxides or clay minerals and micas containing Fe(III). A dissolution of hematite is suggested by Yekta et al. (2018) in the modelling of their experiments of interaction of hydrogen with a lithic-rich sandstone at 100 bar and 100 or 200°C. The dissolution of hematite was a result of their modelling when Fe(II) phases were considered as secondary phases, but was not clearly observed during the laboratory experiments. The reduction of Fe(III) contained in smectite, illite and mica has been reported by several authors as a potential mineral alteration induced by hydrogen (Libert et al., 2011; Hernsdorf et al., 2017; Heinemann et al., 2021; Thaysen et al., 2021). The evidence is provided by Esnault et al. (2010) that showed that, whether hydrogen was consumed or not in Fe(III)-smectite suspensions in laboratory experiments at 40°C and a partial pressure of H2 of 0.6 bar, depended on the presence or absence of iron-reducing bacteria.
The reduction of pyrite to pyrrhotite is a reaction involving hydrogen that may be significant at low or mid-hydrothermal temperatures (Bourgeois et al., 1979; Truche et al., 2010; Truche et al., 2013). The formation of pyrite from pyrrhotite corresponds to a coupled dissolution-precipitation reaction at the pyrite surface (Truche et al., 2010) and writes:
The hydrogen sulfide formed during the pyrite to pyrrhotite reaction will modify the redox potential and the pH of the formation water potentially destabilizing other minerals. Truche et al. (2010) observed that under pH conditions buffered by calcite, the kinetics of the pyrite to pyrrhotite reduction increased with temperature (from 90°C to 180°C), partial pressure of H2 (8–18 bar), mineral surface area and the water/solid ratio but decreased with the increase of hydrogen sulfide concentration. These authors established a kinetic rate law dependent on time, H2 partial pressure and temperature.
Carbonates and sulfate minerals can dissolve as a result of the removal of sulfate and the formation of acids such as H2S and HS− resulting in the displacement of chemical equilibria. In general, calcite and other carbonates may dissolve when the equilibrium of the carbonate system is changed. This can be due to variations in the partial pressure of carbon dioxide, e.g., due to consumption in the formation of methane, acetate, or variations in pH, temperature or calcium concentrations. In potential hydrogen storage reservoirs, calcite, anhydrite and gypsum are the minerals that can be dissolved due to methanogenesis and sulfate reduction (Flesch et al., 2018; Shi et al., 2020).
Well cements may also be subject to mineralogical changes due to the injection of hydrogen into a reservoir (Shi et al., 2020). In the presence of hydrogen sulfide, a more marked reactivity, related to acidic conditions, was observed resulting in degradation of cement minerals (portlandite, CSH.) and calcite precipitation (Jacquemet et al., 2012; Kiran et al., 2017). However, preliminary modeling results suggest that cement degradation is only expected to change slightly due to storage of a mixture of hydrogen and natural gas (Le Gallo et al., 2021; Zeng et al., 2022).
The modelling tool used is the widely used PHREEQC 3.0 (Parkhurst and Appelo, 2013) which include the relevant processes and their kinetics. The database used is a modified version of the phreeqc.dat database included in the installation. The phreeqc.dat database includes data to allow solubility computation of gases at high pressure with the Peng-Robinson equation of state. As considered in PHREEQC, without a calibration of binary interaction coefficients, hydrogen solubility in water can be slightly underestimated at increasing pressure (see Supplementary Material). Also, specific volumes of aqueous species are calculated as a function of the dielectric properties of water and the ionic strength of the solution, which allows calculation of pressure effects on chemical reactions and on solution density, potentially significant at the high pressures relevant for hydrogen storage.
The kinetic rate expressions for mineral dissolutions and precipitations are taken from the database of kinetic rates established by Marty et al. (2015).
The preceding review of hydrogen reactivity in UHS showed that the main and limiting reaction is the oxidation of hydrogen. Hence, the aqueous redox reactions of methanogenesis, sulfate-reduction and acetogenesis need to be correctly modeled. The occurrence of these reactions is not captured by assuming thermodynamic equilibrium but requires a description of the kinetic control. To explore the simulation of hydrogen reactivity, four different approaches of considering the aqueous redox reaction are implemented.
In its simplest form, water/rock interaction models usually consider the aqueous speciation reactions, including the oxidation and reduction reactions, occur so that thermodynamic equilibrium is obtained. As a first approach in the simulations evaluating hydrogen reactions, no constraints are considered on redox reactions so that they may occur to obtain thermodynamic equilibrium. Note that mineral dissolution and precipitation reactions are controlled by kinetics.
As highlighted by the literature review, if the redox reactions involving hydrogen are not catalyzed by bacterial activity, these reactions are almost negligible at the time scale of gas storage operations. Therefore, assuming abiotic conditions, it is reasonable to consider hydrogen as being non-reactive. Using PHREEQC, it is possible to have two separate, decoupled versions of hydrogen. The first type of hydrogen is the classical hydrogen system, involved in the water dissociation, pH and many chemical reactions. The second type of hydrogen is a chemically inert hydrogen that is only involved in gas-liquid dissolution equilibrium. In the phreeqc. dat thermodynamic database, the decoupled unreactive type of hydrogen is called “Hdg”.
Threshold energy models simulate the effect of bacterial activity on the redox reactions considering that thermodynamics and microbial kinetics are coupled near thermodynamic equilibrium (Jakobsen, 2007; Heimann et al., 2010; Bethke et al., 2011). Microbial activity induces an energy threshold on the reduction reaction consuming hydrogen, which correspond to differences in the hydrogen concentrations predicted by thermodynamics and the H2 concentrations necessary for the reaction to actually occur. This energy threshold corresponds to the production of biomolecules, heat and metabolic byproducts. For acetogenesis, methanogenesis and sulfate reduction, the energy thresholds range from −20 to −28 kJ/mol, −9 to −50 kJ/mol and −16 to −49 kJ/mol, respectively, according to Hoehler et al. (1998), when the reaction is written so that 1 mol of H2 reacts. Similar energy thresholds were obtained in a thermodynamic model of microbial community dynamics (Delattre et al., 2020).
In the threshold energy model used in this work, the kinetics of the redox reaction process is coupled to thermodynamic constraints. A 0-order kinetic law is considered, using reaction rates determined by Berta et al. (2018) or fitted to Lobodice gas composition evolution (Table 3). The metabolic energy thresholds for each terminal electron accepting process are considered by calculating effective equilibrium constants, adding the energy threshold to the Gibbs free energy of the reaction (Jakobsen, 2007). To simulate a kinetic control on the reactions of sulfate-reduction, methanogenesis and acetogenesis using PHREEQC, it is necessary to use a thermodynamic database where oxidized S (+VI) and reduced S (-II) sulphur as well as CH4, CO2 and acetate are uncoupled so that the transformations are controlled by kinetics. The phreeqc. dat, thermodynamic database was adapted for this context. Only the formation of methane from hydrogen and carbon dioxide was included in the model, but not from hydrogen and carbon monoxide.
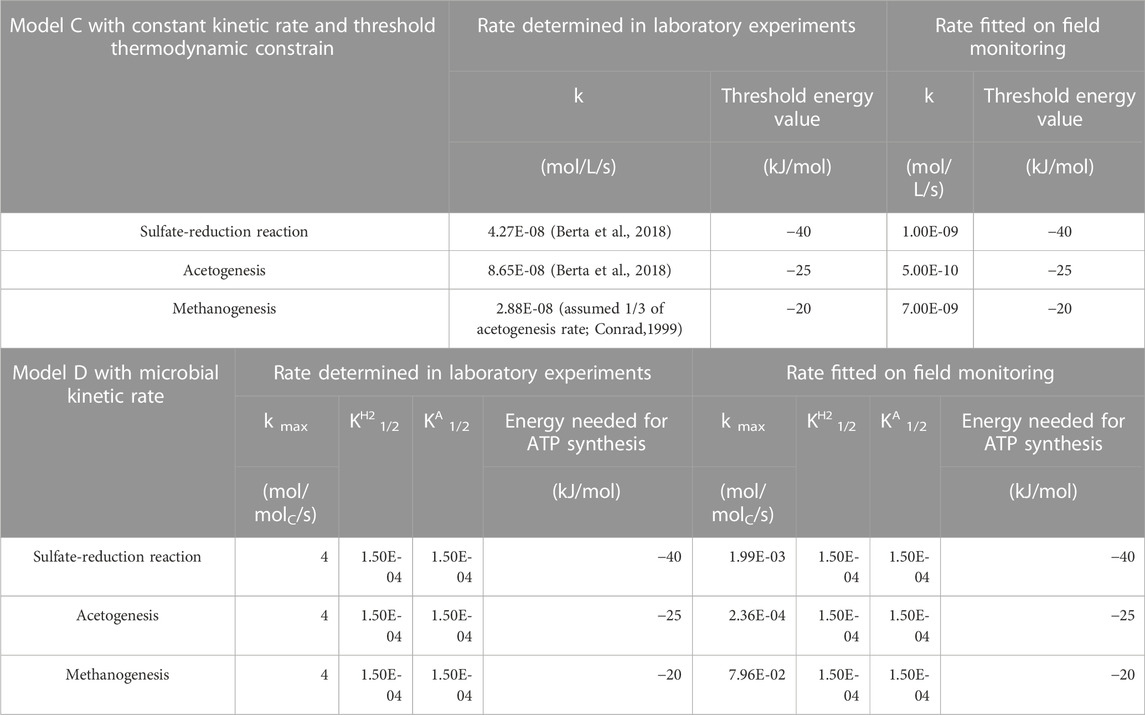
TABLE 3. Kinetic rates used for sulfate-reduction reaction, acetogenesis and methanogenesis in the different PHREEQC simulations. In Model D, a constant bacteria concentration of 104 cells/mL was considered, corresponding to 10−7 molC/L assuming 1 cell contains 10−14 mol of Carbon.
The study of Berta et al. (2018) reports kinetics for the consumption of hydrogen by the acetogenesis and sulphate-reduction reactions measured in the laboratory under conditions corresponding to UHS. Methanogenesis was not observed in this study. Under conditions where the H2 partial pressure is high (2–15 bar) and much higher than the natural H2 content in a reservoir, the kinetics of hydrogen consumption turn out to be similar, regardless of the H2 partial pressure or salinity of the solution. Although probably catalyzed by bacterial activity, the kinetics of consumption of hydrogen does not depend on bacterial dynamics in these experiments. These results can be simulated using a 0-order kinetic law, where only the reaction rate is considered, without any specific dependence on substrate concentrations, as long as the Gibbs thermodynamic energy available is above the threshold.
The fourth way of simulating aqueous redox reactions applied in this study is by considering a microbial kinetic control. A Monod-type rate equation, including cell concentration and a thermodynamic potential factor (Jin and Bethke, 2005) was used. The rate, Eq. 1, is defined as follows:
where, rate is the reaction rate (mol/L/s), kmax is the maximal rate (mol/molC/s, expressed per mol of Carbon in bacteria molC), B is the concentration of bacteria (molC/L), mA and mD are the concentrations of the electron acceptor and electron donor limiting substrates, KA1/2 and KD1/2 are the half-saturation constants for the electron acceptor and electron donor substrates, ΔGr is the Gibbs free energy of the reaction (J/mol/K), ΔGcrit is the critical energy used for ATP synthesis during the reaction (J/mol/K), χ is a stoichiometric number, R is the gas constant (8.314 J/mol/K) and T is the temperature (K).
In the Monod equation, Eq. 1, the reaction rate depends on the maximal rate and on the concentration of the reactants giving and accepting electrons and the half-saturation constants. The cell concentration is considered constant for the sake of simplicity, implying that the microbial ecosystem is already present at optimum concentration in the storage. The thermodynamic potential factor consists in an energetic drive of the process, where a critical energy yields is subtracted from the Gibbs free energy of the reaction. The main difference when comparing to the approach of Model C, described in Section 3.2.3 is that the rates specifically depend on the concentrations of the reactants. The reaction rates determined from laboratory experiments by (Smigan et al., 1990) and the rates fitted on Lobodice gas composition evolution used in the simulations are reported in Table 3.
The models of hydrogen reactions are applied to the case of Lobodice town gas storage, where conversion of hydrogen and carbon dioxide to methane was documented (Smigan et al., 1990; Buzek et al., 1994). The Lobodice reservoir is hosted in sediments of lower Badenian age (16.3–12.8 Ma B.P.) in the Carpathian Foredeep (Eastern part of The Czech Republic). The reservoir consists of water saturated strata in an anticline structure and is made of gravels and sandstones. It has a thickness of about 18 m and is overlain by about 300 m of a caprock formed by impermeable clay rocks and clayey sands. The reservoir was used as a town gas storage from 1965 to 1991 and has been used for natural gas storage since 1991. The temperature varies between 25°C and 45°C and the exploitation pressure was between 4.5 and 5.9 MPa. Before its conversion to a natural gas storage, the evolution of the town gas composition was monitored in the Lobodice reservoir (Smigan et al., 1990; Buzek et al., 1994). During 7 months of storage, 10%–20% of the gas volume was lost and the composition of the gas changed, with an increase in methane and decreases in hydrogen, carbon dioxide and carbon monoxide. The stored gas initially composed of 54% H2, 22% CH4, 12% CO2, 9% CO and 2.5% N2 evolved after being stored during 7 months to 40% CH4, 37% H2, 9% CO2, 9% N2 and 3% CO. The formation of methane observed at Lobodice was accompanied by growth of methanogens and a development in the isotopic signature of methane typical for microbially generated methane. Buzek et al. (1994) showed that some hydrogen losses are also linked to cap-rock heterogeneities and its tightness to hydrogen.
The mineral composition (Table 4) and the pore water composition used in the model were taken from Labus et al. (2016). These mineral and water composition data correspond to another reservoir of Badenian age in the Carpathian foredeep, deeper than the Lobodice reservoir, but they are used in the absence of site-specific data. A temperature of 35°C and a pressure of 50 bar are considered in the model. As an initial calculation, equilibrium is established between the initial gas phase at Lobodice and the chosen reservoir pore water (Table 4). Mineral dissolutions and precipitations are controlled by kinetics according to Marty et al. (2015).
Since the gas evolution (injected and produced) is the information available from Lobodice gas storage, the presentation of simulation results is primarily focused on the evolution of the gas composition. Comparison between the different model results and field data for hydrogen, methane and carbon dioxide contents and the evolution of the relative gas volume is shown in Figure 1.
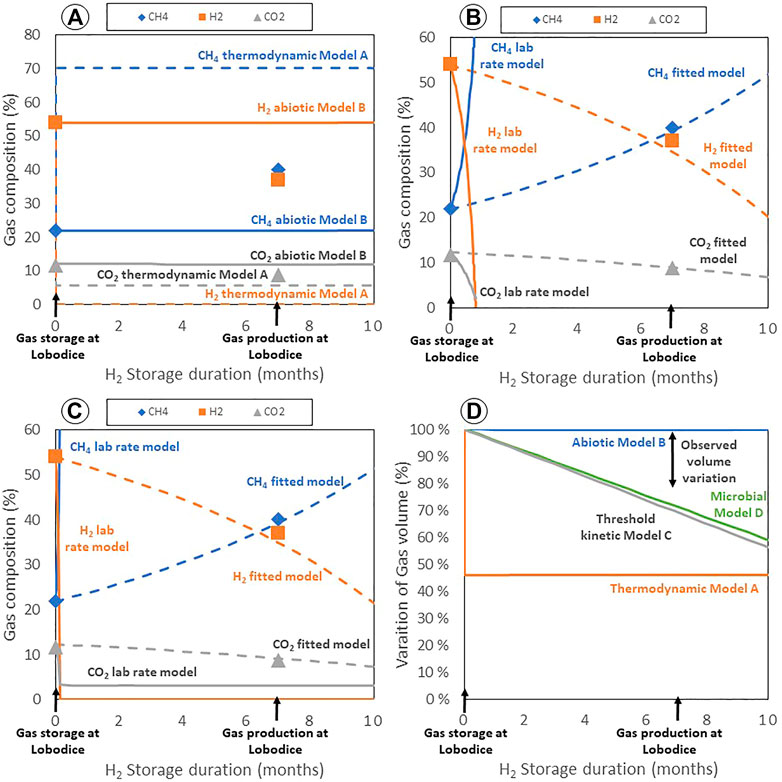
FIGURE 1. Gas composition evolution (A–C) and variation of gas volume (D) simulated and observed at Lobodice gas storage. Simulations made using the reactivity model for hydrogen assuming: (A) thermodynamic equilibrium for redox reactions (Model A), and assuming abiotic conditions (Model B); (B) a 0-order kinetic rate model with thermodynamic threshold limits (Model C); and (C) considering a kinetic model depending on substrate concentrations and thermodynamic energy yield and concentration of bacteria (Model D).
Using Model A, the reactive model considering redox reactions at thermodynamic equilibrium (Figure 1A), the gas composition evolves to its final composition during the first time-step, corresponding to a total consumption of hydrogen. The content of methane reaches 70% in this simulation, compared to 40% of methane at the end of the seasonal storage at Lobodice. The carbon dioxide content decreases to 5.9% in this simulation, while 8.8% was measured. This simulation leads to a decrease to less than the half of the gas volume (46%) (Figure 1D). Using the dissolved sulfate ions in solution, about 0.01% of hydrogen sulfide is forecasted when redox reactions occurs at thermodynamic equilibrium. The hydrogen sulfide content is then calculated to increase at about 1.25% after 7 months of storage, because of the progressive dissolution of gypsum, controlled by kinetics, reacting with the formed methane. No data on hydrogen sulfide is available at Lobodice (Smigan et al., 1990; Buzek et al., 1994).
The assumption made in the abiotic model (model B) is that redox reactions involving hydrogen are not catalyzed by microbial activity implying that hydrogen is inert. Accordingly, gas evolution simulated with the abiotic model shows no changes, with the hydrogen, methane and carbon dioxide contents remaining at their initial value (Figure 1A). This scenario is presumably only relevant for environments that are very hostile to microorganisms. This non-reactive hydrogen (model B) and the complete thermodynamic equilibrium (model A) simulations can be considered two extreme end-members, but do not fit the measured data.
The application of Model C, the kinetic model for the redox reactions implying threshold limits, consists in 2 different simulations (Figure 1B): one using the kinetic reaction rates determined in the Berta et al. (2018) experiments and the other using a rate fitted on Lobodice gas composition evolution. Using the experimental rates, dihydrogen is simulated to be entirely consumed in a little less than 1 month. The methane content is about 65% and carbon dioxide 2% of the reservoir gas when hydrogen is totally consumed. More carbon dioxide is consumed and less methane is produced in this simulation compared to the model with redox reactions at thermodynamic equilibrium because of the production of acetate which is now considered. The kinetic model (C) can reproduce the gas composition evolution at Lobodice by dividing the rate of methanogenesis by about 4, the rate of sulfate-reduction by about 40 and the rate of acetogenesis by about 150–200. With these kinetic rates, the simulated gas composition evolution after 7 months of interaction corresponds to the produced gas composition at Lobodice. A hydrogen sulfide content of 0.4% is also simulated. However, the simulated decrease of the gas volume (a little more than 30% after 7 months) is higher than the observed changes in the reservoir (10%–20% of volume loss) (Figure 1D). In this application of the kinetic model on methanogenesis, sulfate-reduction and acetogenesis, the reactions are taking place far from thermodynamic equilibrium, because of the high content in hydrogen, and the threshold limits have little influence on the reactions.
Model D, including microbial kinetic reactant constraints and thermodynamic limitations on the rates of methanogenesis, sulfate-reduction and acetogenesis is applied to Lobodice gas storage using the rate of methanogenesis measured on laboratory experiments by Smigan et al. (1990) and rates fitted to the gas composition evolution in the reservoir. The experiments reported by Smigan et al. (1990) consist in monitoring the production of methane in a Hungate tube at 37°C and 1.5 bar containing H2 and CO2 gas (proportion 80:20), starting from pore water which naturally contains methanogenic bacteria (104 cells/mL) and rock powder from Lobodice reservoir. The experiments are reproduced using the microbial kinetic model by fitting the rate of methanogenesis and the HCO3− and H2 half-saturation constants involved in the kinetic equation (Figure 2). These parameters determined on laboratory experiments on Lobodice water and rock were then used for the simulations at the gas storage scale. The simulation using the microbial kinetic model and the laboratory determined rates (Figure 1C) predicts a fast hydrogen consumption, that totally disappears in about 4 days. Together with hydrogen consumption, methane content increases to about 65% and carbon dioxide content decreases to about 2%. The evolution of the gas composition in the Lobodice gas storage can be reproduced using the microbial kinetic model and net rates divided by 50 for methanogenesis, by 2000 for sulfate-reduction and by 15,000–20,000 for acetogenesis. Since the resulting rate is derived from the product kmax and B (Eq. 1) it could also be that not kmax, but the concentration of bacteria is lower–or both. After 7 months of storage, a hydrogen sulfide content of 0.07% is simulated. The simulated volume variation of 30% is slightly higher than the observed volume loss (Figure 1D). The rate of methanogenesis is the fitting parameter of first order, while the rate of acetogenesis needs to be lowered to match the evolution of the H2/CH4 ratio. The coefficients multiplying the maximal reaction rate and the bacteria concentration remain at a value of 1, because the reactants remain in excess.
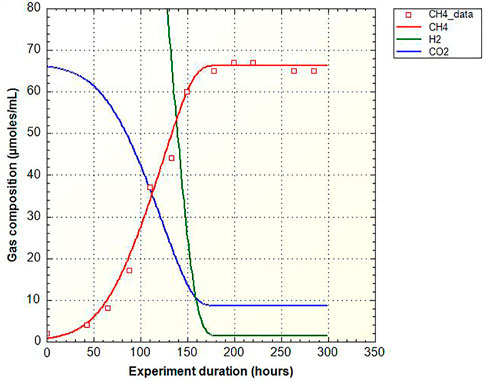
FIGURE 2. Simulation using the microbial kinetic model (Model D) on the experiment by Smigan et al. (1990) of methane production (squares) from hydrogen and carbon dioxide in presence of Lobodice rock and formation water containing bacteria (37°C, 1.5 bar).
The reservoir rock at Lobodice is a sandstone with about 60% quartz, 30% carbonate minerals (dolomite and calcite) and 10% aluminosilicate minerals (feldspars and micas). The mineralogical analysis available for the reservoir (Labus et al., 2016) also reports 0.2% of gypsum. Such a low content of gypsum in a sandstone suggests gypsum could have been formed from the porewater ions during the drying of the rock sample. However, gypsum is considered in the mineralogical assemblage of our simulations since it is not possible to discard its presence based on the available information.
The simulated mineral evolution is similar regardless of the models used to represent the redox reactions. No significant changes in mineral content are simulated (Figure 3). The main mineral reaction is a progressive dissolution of gypsum (0.1% in 7 months). Carbonate minerals obviously participate in the pH buffering and the presence of two carbonate minerals in the simulation leads to a minor conversion of dolomite to calcite. Quartz and aluminosilicate minerals remain stable during the duration of the simulation.
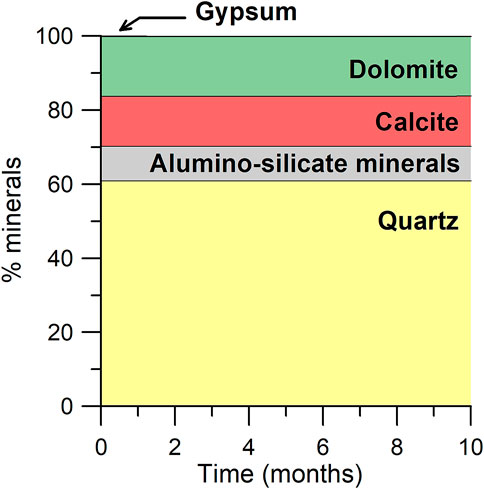
FIGURE 3. Mineral evolution simulated for the Lobodice reservoir during the seasonal storage of town gas.
pH values obtained using the different models range between 5.6 and 6 (Figure 4). It reflects that the pH initial value and evolution is mainly buffered by the carbonate system equilibrium, including the CO2 partial pressure and the carbonate minerals. The expected increase of pH because of the hydrogen consumption reactions is reflected by the initial pH increase from 5.7 to 6 simulated using the model with redox reactions at equilibrium (Model A). In this same model, pH then slightly decreases because of hydrogen sulfide production, from sulfate derived from kinetically controlled gypsum dissolution. In the models with a kinetic control of redox reactions (Models C and D), pH decreases during the first 2 months of the simulation and then increases. This pH decrease is due to gypsum dissolution which occurs at a higher rate in the first part of the simulation. Then, pH increases because of hydrogen consumption. Without gypsum in the simulation, pH only increases and tends towards a value of 6. In the abiotic Model B, considering inert H2, pH remains stable as it is not influenced by hydrogen consumption and hydrogen sulfide production.
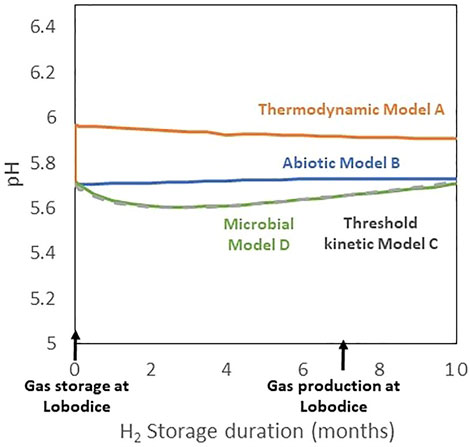
FIGURE 4. Simulated pH evolution during the seasonal storage of town gas at Lobodice, using the different models for describing redox reactions with the oxidation of hydrogen.
The bibliography review on expected reactivity of hydrogen in underground storage conditions and the models established here from this review help in evaluating the likely reactivity of hydrogen in Lobodice town gas reservoir. A very small reactivity of hydrogen is expected under abiotic conditions, confirming experiments of sulfate-reduction with H2 by Truche et al. (2009) or sterile interaction experiments between hydrogen, formation water and/or rock samples under storage (Yekta et al., 2018; Haddad et al., 2022; Hassanpouryouzband et al., 2022). When the redox reactions using hydrogen as electron donor for sulfate-reduction, methanogenesis and acetogenesis are catalyzed by microbes, a conversion of hydrogen to methane can be observed and simulated. Large quantities of hydrogen can be consumed by this methanogenesis reaction and it can result in non-negligible losses of hydrogen (Smigan et al., 1990). In addition to the crucial role of bacteria, methanogenesis also occurred at Lobodice town gas storage because of the presence of carbon dioxide and carbon monoxide in the stored gas. In absence of carbon dioxide or carbon monoxide, i.e., if pure hydrogen was stored, the methane formation rate would presumably be lowered when the dissolved carbonates had been used. The rate of methanogenesis would be limited by the rate of carbonate dissolution, which would presumably decrease as the Ca concentration and pH increased. Sulfate-reduction and formation of hydrogen sulfide appear to be less important than methanogenesis at Lobodice, mainly because of the small quantity of sulfate available for hydrogen consumption. Therefore, the production of hydrogen sulfide is not able to induce significant losses of hydrogen, but this “souring” may imply a need for anticorrosion treatments for the surface equipment or gas treatment after its seasonal storage. Iron-reduction was identified in the literature as a potential mechanism using hydrogen but, in absence of Fe-bearing minerals in Lobodice reservoir, its effect was not evaluated. With the exception of some geological formations, Fe(III) contents are low in most reservoirs and iron-reduction is not expected to lead to significant H2 consumption. Negligible amounts of minerals are simulated to precipitate or dissolve during the seasonal gas storage and therefore no impacts on general mineralogy nor on reservoir hydro-mechanical properties are expected if these minor amounts of dissolution and precipitation are extrapolated for longer time periods.
The calculations made to evaluate the reactivity of hydrogen in an underground gas storage and their application to Lobodice gas storage highlight the importance of considering a proper model to simulate the aqueous redox reactions involving hydrogen. Using a calibrated kinetic model for methanogenesis, sulfate-reduction and acetogenesis is fundamental to properly simulate the reactivity of hydrogen. We have seen that a model considering a thermodynamic control of these redox reactions highly exaggerates the reactivity of hydrogen, compared to the evolution in gas composition observed in the Lobodice case study. In an entirely abiotic situation, where the redox reactions are not catalyzed, considering an inert hydrogen leads to a complete absence of reactivity, which is also not expected. To reproduce the gas composition evolution observed at Lobodice, including the conversion of hydrogen and carbon dioxide to methane, it is necessary to consider the catalytic effect of microbial activity using a kinetic model for the aqueous redox reactions. Two kinetic models were used for this purpose: one that does not consider the bacteria explicitly but a constant 0-order reaction rate coupled with thermodynamic constraints (Model C) and a second model that introduces a dependency on the available energy as well as microbial effects of substrate levels (Model D). These two kinetic models can only reproduce the gas composition evolution at Lobodice after calibration to match the observations. Indeed, using kinetic rates for sulfate-reduction (Berta et al., 2018) or methanogenesis (Smigan et al., 1990) determined in laboratory experiments in hydrogen rich environments, the simulated hydrogen consumption is too fast compared to the reservoir data. To reproduce the gas composition evolution at Lobodice, it has been necessary to divide the laboratory rate of methanogenesis by 4–50, depending on the initial lab derived rate. Sulfate-reduction and acetogenesis appear to be secondary processes at Lobodice, as it was necessary to limit their rates far more than the rates of methanogenesis to achieve the simulation of the observed evolution of hydrogen, methane and carbon dioxide. This discrepancy, between kinetic rates of redox reactions determined in laboratory experiments and the rates fitted in order to simulate field observations (Jin et al., 2013; Thullner and Regnier, 2019) is explained by several factors; i) the fact that substrate enriched culture media are used in laboratory reactors, ii) differences in accessibility for microbes of water and reactants between a lab solution or suspension and an unsaturated porous media, and iii) differences in general physio-chemical conditions or iv) because of competition between processes and other microbes. These differences lead to differences in the activity of microbial communities, resulting in differences in the progress of terminal electron acceptor processes. Another point to mention regarding the models established for Lobodice is that they are all batch models applied to a reservoir that in reality is affected by gas and fluid dynamics. The simulation of the gas composition evolution gives acceptable results, most likely because the reservoir of Lobodice was already in operation for decades at the time of the gas sampling reported by Smigan et al. (1990), implying low levels of gas losses due to transport and other physical processes (Buzek et al., 1994).
The limitations of the thermodynamic models for redox reactions involving hydrogen have already been addressed (Lassin et al., 2011) and our calculations applied at Lobodice reservoir demonstrate that this modeling approach is inappropriate for simulating hydrogen reactions in UHS. When redox reactions are considered at thermodynamic equilibrium, reactivity is exaggerated, and some studies inappropriately reach conclusions of catastrophic effects of hydrogen storage in reservoirs, such as the dissolution of the reservoir carbonate cements leading to mechanical failure.
Only few studies have simulated the reactivity of hydrogen in UHS in porous media by considering the microbial catalysis and limitation of the redox reactions using hydrogen as electron donor through a kinetic control on these reactions (Hagemann et al., 2016; Hemme and Van Berk, 2018; Hassannayebi et al., 2019; Veshareh et al., 2022). Hagemann et al. (2016) simulated the storage of hydrogen in a fictive depleted reservoir that contains residual methane and carbon dioxide by considering biochemical reactions and hydrodynamics. Methanogenesis was simulated using a Monod-type microbial growth model and the associated consumption of hydrogen resulted in a slowing down the spreading of injected hydrogen in the reservoir. Hemme and Van Berk (2018) simulated the kinetic bacterial conversion of hydrogen to methane and hydrogen sulfide using a Monod-type equation in a gas/water/rock one-dimensional reactive mass transport model including a reservoir and a caprock domain. Sulfate-reduction was simulated to occur before and faster than methanogenesis, presumably because the high excess level of hydrogen, which removes the competitive advantage of sulfate reducers is not taken into account by the model. Despite uncertainties on the kinetic reaction rates, methanogenesis and hydrogen sulfide production were mainly limited by the availability of carbon dioxide and sulfates, respectively. Only small mineral changes were simulated, including anhydrite and calcite dissolutions. Hassannayebi et al. (2019) used batch simulations to simulate the reactivity of hydrogen in a reservoir corresponding to the formation hosting the injection of the Underground Sun Storage project in Austria. They considered a kinetic limitation on the rate of hydrogen dissolution in water rather than on the aqueous redox reactions. Focus was on sulfate reduction and pyrite to pyrrhotite reduction, as the reaction of methanogenesis and acetogenesis were decoupled in the thermodynamic database and, therefore not occurring. This study suggested that the reactions of hydrogen with minerals can only be relevant over time scales longer than the storage operations and that their estimation is strongly related to the uncertainty on the kinetic rates. Simulations by Veshareh et al. (2022) were dedicated to the evaluation of hydrogen reactivity if stored in Danish North Sea chalk reservoirs. Methanogenesis, sulfate-reduction and acetogenesis reactions were both controlled by kinetics, using a Monod-type equation. Their simulations indicate that methanogenesis is the main mechanism able to consume hydrogen, but it is difficult to conclude on the extent of this consumption because of the range of uncertainty on the methanogenesis kinetic rate. Formation of hydrogen sulfide appeared to be secondary in these simulations, with a small effect on hydrogen loss, but hydrogen sulfide could still reach concentrations implying corrosion or safety concerns. Under abiotic conditions, calcite dissolution was discarded. When triggered by methanogenesis and acetogenesis, small amounts of calcite were simulated to dissolve.
Hence, the results of these modeling studies on hydrogen storage in depleted reservoirs (Hagemann et al., 2016; Hemme and Van Berk, 2018; Hassannayebi et al., 2019; Veshareh et al., 2022) considering microbial kinetic control on the redox reactions using hydrogen as electron donor are in line with the results of our simulations applied to the gas composition evolution at Lobodice town gas storage. Namely, hydrogen can be reactive when catalyzed by microbial activity, leading to the formation of methane and hydrogen sulfide. Because of the reaction rates and of the availability of gaseous carbon dioxide, dissolved bicarbonates and dissolved and mineral sulfates, methanogenesis can lead to important losses of stored hydrogen. The formation of hydrogen sulfide appears to be small and is essentially an operational and safety concern. Only very small mineral changes are expected during hydrogen storage, both in sandstone reservoirs, according to this study, and carbonate reservoirs, according to Veshareh et al. (2022).
The main limitation of these simulations and predictions is the uncertainty on the rates of methanogenesis, acetogenesis and sulfate-reduction reactions in hydrogen rich environments since relatively few experimental data are available and none of these realistically reproduce the unsaturated conditions in a porous medium partially filled with gas. Related to this uncertainty, is the scale effect between rates determined in laboratory experiments and the rates to consider in a reservoir where effects of localized biofilms, localized mineral domains, heterogeneous water availability and limitations in transport must also play a role. The competition between redox processes, with different limitations of which some are coupled to the transport and availability of the involved substrates is also a source of uncertainty. In Section 2.3, it was noted that environmental factors such as temperature, pressure, salinity, pH and nutrients availability can significantly influence microbial activity. As a result, accurately quantifying hydrogen reactivity can be challenging due to the potential uncertainty introduced by these changing environmental conditions.
The summary of the many environmental factors that influence microbial activity illustrate that under reservoir temperature, salinity or composition conditions, the reactions using hydrogen as an electron donor may be very efficient or almost absent. For the gas storage of Lobodice, the high consumption of hydrogen and production of methane can be related to what is probably an optimal temperature between 25°C and 40°C and to the low pressure and salinity, including low sulfate content, in the reservoir. The adequacy of the Lobodice reservoir conditions and optimum conditions for microbial growth was already pointed out by Thaysen et al. (2021). Before envisaging a geochemical model of hydrogen reactivity accounting for the effects of the environmental conditions on the rates of sulfate-reduction, acetogenesis and methanogenesis reactions, it remains necessary to better understand and calibrate these effects. After that, it will also be necessary to put these processes and limitations in coherence to obtain a model sufficiently descriptive but simple enough to be implemented in reactive transport applications.
This study was devoted to the evaluation and the numerical simulation of hydrogen reactivity during underground hydrogen storage (UHS) in porous media such as saline aquifers or depleted reservoirs. Our conclusions can be summarized as follows:
• In abiotic conditions, negligible reactivity of hydrogen is predicted in the case of UHS.
• Hydrogen can be consumed in UHS when catalyzed by microbial activity by methanogenesis, sulfate-reduction and acetogenesis reactions. Under unfavorable conditions (microbially favorable), reactions induced by hydrogen will affect the gas composition and/or dissolved species but the effects on mineral dissolution and precipitation appear as minor.
• Methanogenesis can lead to losses in hydrogen when carbon dioxide, dissolved carbonates or carbonate minerals are available.
• Sulfate-reduction has few impacts on the hydrogen content but can lead to hydrogen sulfide production and associated corrosion issues, more so if sulfate minerals are present.
• Our study highlights the importance of considering the effect of microbial kinetics on the aqueous redox reactions using hydrogen as electron donor to properly simulate hydrogen reactivity. Different ways of considering methanogenesis, sulfate-reduction and acetogenesis were investigated through different reactive models and showed that a reasonable level of hydrogen reactivity could only be captured when kinetics controlled these reactions.
• There is a need of calibration of the kinetic rates and of the upscaling of the aqueous laboratory based redox reaction rates to the reservoir scale.
• Observational data from other hydrogen storage operations is necessary for better constraining the reactivity of hydrogen in UHS and how it relates to the environmental conditions.
The models of hydrogen reactivity were applied to Lobodice town gas storage that contained hydrogen but also large amount of carbon dioxide and carbon monoxide. In a storage of pure hydrogen, without carbon reactants for methanogenesis, a lower reactivity is expected. It needs to be confirmed by devoted simulations considering pure hydrogen. A next step could be the adaptation of the reactive model to a reactive transport model or reservoir model to more fully account for the hydrogen behavior and fate in reservoirs.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
JT: Conceptualization, methodology, software, writing–original draft; RJ: Conceptualization, methodology, software, writing–review and editing; YLG: Conceptualization, writing–review and editing.
This work was made within Hystories Project which received funding from the Fuel Cells and Hydrogen 2 Joint Undertaking (now Clean Hydrogen Partnership) under Grant Agreement No 101007176. This Joint Undertaking receives support from the European Union’s Horizon 2020 Research and Innovation program, Hydrogen Europe and Hydrogen Europe Research.
Nere Ruiz, Cyriane Fournier, and Arnaud Réveillère (Geostock) are acknowledged for fruitful discussions on the microbial risks for underground hydrogen storage. Three reviewers are thanked for their constructive comments that improved the manuscript.
Authors JT and YLG were employed by the company Geostock.
The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2023.1145978/full#supplementary-material
1https://www.iea.org/reports/the-future-of-hydrogen.
2https://www.underground-sun-storage.at/en/.
Aftab, A., Hassanpouryouzband, A., Xie, Q., Machuca, L. L., and Sarmadivaleh, M. (2022). Toward a fundamental understanding of geological hydrogen storage. Ind. Eng. Chem. Res. 61, 3233–3253. doi:10.1021/acs.iecr.1c04380
Beckingham, L. E., and Winningham, L. (2020). Critical knowledge gaps for understanding water-rock-working phase interactions for compressed energy storage in porous formations. ACS Sustain. Chem. Eng. 8, 2–11. doi:10.1021/acssuschemeng.9b05388
Berta, M., Dethlefsen, F., Ebert, M., Schäfer, D., and Dahmke, A. (2018). Geochemical effects of millimolar hydrogen concentrations in groundwater: An experimental study in the context of subsurface hydrogen storage. Environ. Sci. Technol. 52, 4937–4949. doi:10.1021/acs.est.7b05467
Bethke, C. M., Sanford, R. A., Kirk, M. F., Jin, Q., and Flynn, T. M. (2011). The thermodynamic ladder in geomicrobiology. Am. J. Sci. 311, 183–210. doi:10.2475/03.2011.01
Bordenave, S., Chatterjee, I., and Voordouw, G. (2013). Microbial community structure and microbial activities related to CO2 storage capacities of a salt cavern. Int. Biodeterior. Biodegrad. 81, 82–87. doi:10.1016/j.ibiod.2012.08.001
Bourgeois, J. P., Aupaix, N., Bloise, R., and Millet, J. L. (1979). Proposition d'explication de la formation d'hydrogène sulfuré dans les stockages souterrains de gaz naturel par réduction des sulfures minéraux de la roche magasin. Rev. l’Institut Français Pétrole 34, 371–386. doi:10.2516/ogst:1979013
Buzek, F., Onderka, V., Vančura, P., and Wolf, I. (1994). Carbon isotope study of methane production in a town gas storage reservoir. Fuel 73, 747–752. doi:10.1016/0016-2361(94)90019-1
Chabab, S., Théveneau, P., Coquelet, C., Corvisier, J., and Paricaud, P. (2020). Measurements and predictive models of high-pressure H2 solubility in brine (H2O+NaCl) for underground hydrogen storage application. Int. J. Hydrogen Energy 45, 32206–32220. doi:10.1016/j.ijhydene.2020.08.192
Conrad, R. (1999). Contribution of hydrogen to methane production and control of hydrogen concentrations in methanogenic soils and sediments. FEMS Microbiol. Ecol. 28, 193–202.
Delattre, H., Chen, J., Wade, M. J., and Soyer, O. S. (2020). Thermodynamic modelling of synthetic communities predicts minimum free energy requirements for sulfate reduction and methanogenesis. J. R. Soc. Interface 17, 20200053. doi:10.1098/rsif.2020.0053
Dopffel, N., Jansen, S., and Gerritse, J. (2021). Microbial side effects of underground hydrogen storage - knowledge gaps, risks and opportunities for successful implementation. Int. J. Hydrogen Energy 46, 8594–8606. doi:10.1016/j.ijhydene.2020.12.058
Esnault, L., Libert, M., Bildstein, O., Jullien, M., and Mustin, C. (2010). Clay-iron reducing bacteria interaction in deep geological environment: Experimental and modeling approach. 13th Congr. Water-Rock Interact. 13, 939–942.
Flesch, S., Pudlo, D., Albrecht, D., Jacob, A., and Enzmann, F. (2018). Hydrogen underground storage—petrographic and petrophysical variations in reservoir sandstones from laboratory experiments under simulated reservoir conditions. Int. J. Hydrogen Energy 43, 20822–20835. doi:10.1016/j.ijhydene.2018.09.112
Foh, S. E., Novil, M., Rockar, E. M., and Randolph, P. L. (1979). Underground hydrogen storage. Chicago, Illinois: Report. Institute of Gas Technology, Brookhaven National Laboratory.
Haddad, P. G., Ranchou-Peyruse, M., Guignard, M., Mura, J., Casteran, F., Ronjon-Magand, L., et al. (2022). Geological storage of hydrogen in deep aquifers – An experimental multidisciplinary study. Energy Environ. Sci. 15, 3400–3415. doi:10.1039/d2ee00765g
Hagemann, B., Rasoulzadeh, M., Panfilov, M., Ganzer, L., and Reitenbach, V. (2016). Hydrogenization of underground storage of natural gas. Comput. Geosci. 20, 595–606. doi:10.1007/s10596-015-9515-6
Hassannayebi, N., Azizmohammadi, S., De Lucia, M., and Ott, H. (2019). Underground hydrogen storage: Application of geochemical modelling in a case study in the molasse basin, upper Austria. Environ. Earth Sci. 78, 177. doi:10.1007/s12665-019-8184-5
Hassanpouryouzband, A., Adie, K., Cowen, T., Thaysen, E. M., Heinemann, N., Butler, I. B., et al. (2022). Geological hydrogen storage: Geochemical reactivity of hydrogen with sandstone reservoirs. ACS Energy Lett. 7, 2203–2210. doi:10.1021/acsenergylett.2c01024
Heimann, A., Jakobsen, R., and Blodau, C. (2010). Energetic constraints on H2-dependent terminal electron accepting processes in anoxic environments: A review of observations and model approaches. Environ. Sci. Technol. 44, 24–33. doi:10.1021/es9018207
Heinemann, N., Alcalde, J., Miocic, J. M., Hangx, S. J. T., Kallmeyer, J., Ostertag-Henning, C., et al. (2021). Enabling large-scale hydrogen storage in porous media – The scientific challenges. Energy Environ. Sci. 14, 853–864. doi:10.1039/d0ee03536j
Hemme, C., and Van Berk, W. (2018). Hydrogeochemical modeling to identify potential risks of underground hydrogen storage in depleted gas fields. Appl. Sci. 8, 2282. doi:10.3390/app8112282
Hemme, C., and Van Berk, W. (2017). Potential risk of H2S generation and release in salt cavern gas storage. J. Nat. Gas. Sci. Eng. 47, 114–123. doi:10.1016/j.jngse.2017.09.007
Hernsdorf, A. W., Amano, Y., Miyakawa, K., Ise, K., Suzuki, Y., Anantharaman, K., et al. (2017). Potential for microbial H2 and metal transformations associated with novel bacteria and archaea in deep terrestrial subsurface sediments. ISME J. 11, 1915–1929. doi:10.1038/ismej.2017.39
Hoehler, T., Gunsalus, R. P., and McInerney, M. J. (2010). “Environmental constraints that limit methanogenesis,” in Handbook of hydrocarbons and lipid microbiology. Editor K. N. Timmis (Berlin: Springer-Verlag), 635–654.
Hoehler, T. M., Alperin, M. J., Albert, D. B., and Martens, C. S. (1998). Thermodynamic control on hydrogen concentrations in anoxic sediments. Geochim. Cosmochim. Acta 62, 1745–1756. doi:10.1016/s0016-7037(98)00106-9
Jacquemet, N., Pironon, J., Lagneau, V., and Saint-Marc, J. (2012). Armouring of well cement in H2S–CO2 saturated brine by calcite coating – experiments and numerical modelling. Appl. Geochem. 27, 782–795. doi:10.1016/j.apgeochem.2011.12.004
Jakobsen, R. (2007). Redox microniches in groundwater: A model study on the geometric and kinetic conditions required for concomitant Fe oxide reduction, sulfate reduction, and methanogenesis. Water Resour. Res. 43. doi:10.1029/2006wr005663
Jin, Q., and Bethke, C. M. (2005). Predicting the rate of microbial respiration in geochemical environments. Geochim. Cosmochim. Acta 69, 1133–1143. doi:10.1016/j.gca.2004.08.010
Jin, Q., Roden, E. E., and Giska, J. R. (2013). Geomicrobial kinetics: Extrapolating laboratory studies to natural environments. Geomicrobiol. J. 30, 173–185. doi:10.1080/01490451.2011.653084
Katz, B. J. (2011). Microbial processes and natural gas accumulations. Open Geol. J. 5, 75–83. doi:10.2174/1874262901105010075
Kiran, R., Teodoriu, C., Dadmohammadi, Y., Nygaard, R., Wood, D., Mokhtari, M., et al. (2017). Identification and evaluation of well integrity and causes of failure of well integrity barriers (A review). J. Nat. Gas. Sci. Eng. 45, 511–526. doi:10.1016/j.jngse.2017.05.009
Labus, K., Bujok, P., Klempa, M., Porzer, M., and Matýsek, D. (2016). Preliminary geochemical modeling of water-rock-gas interactions controlling CO2 storage in the Badenian Aquifer within Czech Part of Vienna Basin. Environ. Earth Sci. 75, 1086. doi:10.1007/s12665-016-5879-8
Lassin, A., Dymitrowska, M., and Azaroual, M. (2011). Hydrogen solubility in pore water of partially saturated argillites: Application to callovo-oxfordian clayrock in the context of a nuclear waste geological disposal. Phys. Chem. Earth, Parts A/B/C 36, 1721–1728. doi:10.1016/j.pce.2011.07.092
Le Gallo, Y., Garcia Dominguez, A., and Gonzalez Cansado, B. (2021). “Hydrogen reactivity with a carbonated underground gas storage,” in Third EAGE geochemistry workshop (Muscat, Oman: European Association of Geoscientists & Engineers), 1–5.
Libert, M., Bildstein, O., Esnault, L., Jullien, M., and Sellier, R. (2011). Molecular hydrogen: An abundant energy source for bacterial activity in nuclear waste repositories. Phys. Chem. Earth, Parts A/B/C 36, 1616–1623. doi:10.1016/j.pce.2011.10.010
Londe, L. F. (2021). “Four ways to store large quantities of hydrogen,” in Abu Dhabi International Petroleum Exhibition and Conference, SPE-208178-MS.
MARCOGAZ (2017). Guidance: Injection of hydrogen/natural gas admixtures in underground gas storage (UGS). Report. Brussels, Belgium: Technical Association of the European Natural Gas Industry.
Marty, N. C. M., Claret, F., Lassin, A., Tremosa, J., Blanc, P., Madé, B., et al. (2015). A database of dissolution and precipitation rates for clay-rocks minerals. Appl. Geochem. 55, 108–118. doi:10.1016/j.apgeochem.2014.10.012
Parkhurst, D. L., and Appelo, C. A. J. (2013). Description of input and examples for PHREEQC Version 3–a computer program for speciation, batch-reaction, one-dimensional transport, and inverse geochemical calculations. Denver, Colorado: U.S. Geological Survey.
Pérez, A., Pérez, E., Dupraz, S., and Bolcich, J. (2016). “Patagonia wind-hydrogen project: Underground storage and methanation,” in 21st World Hydrogen Energy Conference 2016, Zaragoza, Spain.
Ranchou-Peyruse, M., Auguet, J.-C., Mazière, C., Restrepo-Ortiz, C. X., Guignard, M., Dequidt, D., et al. (2019). Geological gas-storage shapes deep life. Environ. Microbiol. 21, 3953–3964. doi:10.1111/1462-2920.14745
Ranchou-Peyruse, M., Guignard, M., Casteran, F., Abadie, M., Defois, C., Peyret, P., et al. (2021). Microbial diversity under the influence of natural gas storage in a deep aquifer. Front. Microbiol. 12, 688929. doi:10.3389/fmicb.2021.688929
Reitenbach, V., Ganzer, L., Albrecht, D., and Hagemann, B. (2015). Influence of added hydrogen on underground gas storage: A review of key issues. Environ. Earth Sci. 73, 6927–6937. doi:10.1007/s12665-015-4176-2
Réveillère, A., Fournier, C., Karimi-Jafari, M., and Courault, C. (2022). “Enabling large-scale hydrogen storage in salt caverns: Recent developments. Technical conference paper,” in Solution Mining Research Institute Spring 2022 Technical Conference, Rapid City, South Dakota.
Sambo, C., Dudun, A., Samuel, S. A., Esenenjor, P., Muhammed, N. S., and Haq, B. (2022). A review on worldwide underground hydrogen storage operating and potential fields. Int. J. Hydrogen Energy 47, 22840–22880. doi:10.1016/j.ijhydene.2022.05.126
Schwab, L., Popp, D., Nowack, G., Bombach, P., Vogt, C., and Richnow, H. H. (2022). Structural analysis of microbiomes from salt caverns used for underground gas storage. Int. J. Hydrogen Energy 47, 20684–20694. doi:10.1016/j.ijhydene.2022.04.170
Seewald, J. S., Zolotov, M. Y., and McCollom, T. (2006). Experimental investigation of single carbon compounds under hydrothermal conditions. Geochim. Cosmochim. Acta 70, 446–460. doi:10.1016/j.gca.2005.09.002
Shi, Z., Jessen, K., and Tsotsis, T. T. (2020). Impacts of the subsurface storage of natural gas and hydrogen mixtures. Int. J. Hydrogen Energy 45, 8757–8773. doi:10.1016/j.ijhydene.2020.01.044
Smigan, P., Greksak, M., Kozankova, J., Buzek, F., Onderka, V., and Wolf, I. (1990). Methanogenic bacteria as a key factor involved in changes of town gas stored in an underground reservoir. FEMS Microbiol. Lett. 73, 221–224. doi:10.1016/0378-1097(90)90733-7
Tarkowski, R. (2019). Underground hydrogen storage: Characteristics and prospects. Renew. Sustain. Energy Rev. 105, 86–94. doi:10.1016/j.rser.2019.01.051
Thaysen, E. M., McMahon, S., Strobel, G. J., Butler, I. B., Ngwenya, B. T., Heinemann, N., et al. (2021). Estimating microbial growth and hydrogen consumption in hydrogen storage in porous media. Renew. Sustain. Energy Rev. 151, 111481. doi:10.1016/j.rser.2021.111481
Thullner, M., and Regnier, P. (2019). Microbial controls on the biogeochemical dynamics in the subsurface. Rev. Mineral. Geochem. 85, 265–302. doi:10.2138/rmg.2019.85.9
Truche, L., Berger, G., Destrigneville, C., Guillaume, D., and Giffaut, E. (2010). Kinetics of pyrite to pyrrhotite reduction by hydrogen in calcite buffered solutions between 90 and 180°C: Implications for nuclear waste disposal. Geochim. Cosmochim. Acta 74, 2894–2914. doi:10.1016/j.gca.2010.02.027
Truche, L., Berger, G., Destrigneville, C., Pages, A., Guillaume, D., Giffaut, E., et al. (2009). Experimental reduction of aqueous sulphate by hydrogen under hydrothermal conditions: Implication for the nuclear waste storage. Geochim. Cosmochim. Acta 73, 4824–4835. doi:10.1016/j.gca.2009.05.043
Truche, L., Jodin-Caumon, M.-C., Lerouge, C., Berger, G., Mosser-Ruck, R., Giffaut, E., et al. (2013). Sulphide mineral reactions in clay-rich rock induced by high hydrogen pressure. Application to disturbed or natural settings up to 250°C and 30bar. Chem. Geol. 351, 217–228. doi:10.1016/j.chemgeo.2013.05.025
Veshareh, M. J., Thaysen, E. M., and Nick, H. M. (2022). Feasibility of hydrogen storage in depleted hydrocarbon chalk reservoirs: Assessment of biochemical and chemical effects. Appl. Energy 323, 119575. doi:10.1016/j.apenergy.2022.119575
Yekta, A. E., Pichavant, M., and Audigane, P. (2018). Evaluation of geochemical reactivity of hydrogen in sandstone: Application to geological storage. Appl. Geochem. 95, 182–194. doi:10.1016/j.apgeochem.2018.05.021
Keywords: hydrogen, geological storage, bio-geochemical modeling, gas/water/rock interaction, PHREEQC, sulfate-reduction, methanogenesis, Lobodice
Citation: Tremosa J, Jakobsen R and Le Gallo Y (2023) Assessing and modeling hydrogen reactivity in underground hydrogen storage: A review and models simulating the Lobodice town gas storage. Front. Energy Res. 11:1145978. doi: 10.3389/fenrg.2023.1145978
Received: 16 January 2023; Accepted: 28 March 2023;
Published: 10 April 2023.
Edited by:
Diana Z. Sousa, Wageningen University and Research, NetherlandsReviewed by:
Weijun Shen, Institute of Mechanics (CAS), ChinaCopyright © 2023 Tremosa, Jakobsen and Le Gallo. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Joachim Tremosa, am9hY2hpbS50cmVtb3NhQGdlb3N0b2NrLmZy
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.