Power system intelligent operation knowledge learning model based on reinforcement learning and data-driven

With the expansion of power grid scale and the deepening of component coupling, the operation behavior of power system becomes more and more complex, and the traditional function decoupling dispatching architecture is not available anymore. Firstly, this paper studies the corresponding relationship between reinforcement learning method and power system dispatching decision problem, and constructs the artificial intelligent dispatching knowledge learning model of power system based on reinforcement learning (AIDLM). Then, a data-driven intelligent dispatching knowledge learning method is proposed, and interpretable dispatching decision knowledge is obtained. Finally, a knowledge efficiency evaluation indexes is proposed and used to guide the extraction of original acquired knowledge. The intelligent economic dispatching problem of a regional power grid is analyzed. The results show that the AIDLM method can intelligently give the dispatching strategy of power generation according to the time series changing load, which effectively reduces the cost of power generation in the grid. The method proposed in this paper can make up for the shortcomings of traditional dispatching methods and provide strong support for modern power system dispatching.

1 Introduction

The power system is one of the most complex artificial large-scale systems, and its basic operation requirements are to maintain the real-time balance of generation, transmission, and consumption of electricity, meet the security constraints, and pursue the minimum operation cost.

Due to the limitations of existing methods and computing power, the traditional dispatching system divides the whole dispatching problem into different modules. Each module solves one sub-problem, such as active power economic dispatching (Li et al., 2021a), reactive power optimization (Ju and Chen, 2023), security check, and real-time control to form a dispatching problem-solving method system based on sub-problem solving, multi-module combination, and functional partition. Due to the effective reduction of sub-problem complexity, the existing dispatching method performs an important role in ensuring safety and quality of power system operation.

However, with the continuous expansion of the power grid and the great changes of the power supply structure, the operation mode is becoming variable and complicated. In the dispatching process, not only the complex temporal characteristics of the loads should be considered, but also the operation characteristics of different power sources should be coordinated. At the same time, the operation state of the modern power system tends to be critical, which leads to a significant increase in the probability of the operation mode close to the safety boundary, and the dispatching of power grid faces multidimensional security risks. The traditional dispatching architecture based on sub-problem solving method is not available anymore.

In recent years, the application of the new generation of artificial intelligence (AI) methods, represented by deep learning (DL) and reinforcement learning (RL), has made remarkable achievements in complex decision-making fields such as simulation (Francis et al., 2020), robot control (Johannink et al., 2019), Go game (Schrittwieser et al., 2020) and automatic driving. In 2017, NVIDIA took the human driving experience as prior knowledge and used DL and RL to achieve self-driving vehicles for long distances in a real road environment for the first time. This accomplishment fundamentally changed the situation that the previous intelligent driving technology could only be used as the human driving assistance. At the end of 2017, Google’s DeepMind reported in the journal Nature that its latest Go program, Alpha Zero based on RL (Silver et al., 2017), defeated AlphaGo, which had defeated the human world champion of Go with a score of 100:0. These achievements have shown the great potential and broad prospects of AI in solving complex decision-making problems.

The RL is a decision optimization method based on knowledge learning, unlike supervised and unsupervised learning in the traditional machine learning field (Wang et al., 2021; Luo et al., 2022). Therefore, the RL method is particularly suitable for solving highly complex decision-making problems (Zhang et al., 2019). The basic idea behind RL can trace back to the law of utility proposed by Thorndike in 1911 that in each situation, an agent can make the most appropriate behavior choice after learning experience through continuous trial and error. In 1989, Q-learning proposed by Watkins could solve the optimal policy without an instant reward and state transition functions and became a widely used RL method.

The RL method has been used for some applications in the electric power industry. In Literature (Zhang et al., 2017), the RL method is used to solve the decentralized optimization problem of dynamic power allocation of AGC in a large-scale complex power grid, which belongs to a nonlinear programming problem. The implementation of a power grid cutting machine control strategy based on deep reinforcement Q learning was presented in (Liu et al., 2018). Firstly, the generator’s electromagnetic and mechanical powers are taken as sample data to complete feature extraction. Then, the strategy is constantly modified according to the revenue value to complete the cutting optimization strategy. Literature (Bao et al., 2018) established a real-time supply and demand interaction model for power systems based on the Stackelberg game. Also, a new deep transfer RL algorithm was proposed to quickly obtain high-quality optimal solutions with the advantage of distributed computing. Literature (Yang et al., 2020) introduced deep reinforcement learning into the modeling of the relationship between wind power generation and the effect of electricity price uncertainty on generation revenue, and improves the revenue of wind farms using the proposed optimization and decision algorithms.

The above studies all adopt new AI methods to solve problems in different fields such as power system supply and demand balance (Li et al., 2022), generation control (Xi et al., 2019), power prediction, fault identification (Yang et al., 2018), and transient stability control (Huang et al., 2019). Also, some studies use supervised and unsupervised learning methods to solve the problems of pattern recognition and fault diagnosis in power systems (Xu and Yue, 2020; Parizad and Hatziadoniu, 2021). Currently, whether the knowledge learned by the agent is concise and efficient and whether it can be understood by the power grid operators have not attracted enough attention.

In this study, the basic idea of RL is applied to the power system dispatching problem by constructing the artificial intelligent dispatching knowledge learning model (AIDLM) for power systems. In this way, the agent can constantly explore and compare the rewards of different “actions” to learn and accumulate dispatching experience according to the different operating states of the power grid. To realize knowledge extraction and application, an ontology-oriented and data-driven knowledge validity assessment index is established. The AIDLM is a new attempt to solve the complex decision-making problem of power system dispatching. By “observing” the state of the power system, the optimal dispatching decision can be obtained directly by using “knowledge".

2 General description of intelligent dispatching and RL in power system

Before applying RL method to specific power system intelligent dispatching problems, the essential characteristics of intelligent dispatching problems should be clarified first, and a general framework for solving the target problem should be constructed.

2.1 Intelligent dispatching problem of power system

Because many power generation and loads are connected in the power system, the power transmission between power generation and load is realized through grid connection. Therefore, power grid operation requires meeting various constraints to ensure safety. The constraints are generally divided into equality and inequality constraints (Li et al., 2021b). Equality constraints come from conservation conditions, such as power flow equation constraints, while inequality constraints are more complicated, and some constrained boundaries can be given directly according to the system operation requirements, such as the upper and lower limits of node voltage and the upper limit of branch power. As many constraint boundaries are difficult to be given directly, they can only be given or approximately given by other special calculations, such as transient stability constraints and voltage stability constraints. Thus, the operation decision problem is extremely complex, and the number of power generation combinations that meet the demand of the same group of loads is huge or even inexhaustible. The above-mentioned analysis illustrates the power system dispatching complexity, which is also the reason and process for forming the current functional partition dispatching architecture.

The dispatching process can be abstracted as follow: among many feasible combinations of control variables, a set of optimal control decision schemes is determined in a certain physical environment. Hence, the performance of a specific aspect or some aspects of the power grid can reach the optimum.

In the traditional optimal power system dispatching methods, the optimal power flow (OPF) can directly achieve the optimal computation of dispatching schemes under various constraints. Moreover, the operational optimization with more controllable variables can also be considered in OPF (Bazrafshan et al., 2019; Nojavan and Seyedi, 2020; Davoodi et al., 2021).

However, when the whole dispatching problem is decomposed, different aspects of the problem adopt different description architecture, and even a variety of interrelated dispatching objectives cannot be considered simultaneously due to the inconsistent problem model architectures. Therefore, if the dispatching problem is regarded as a tightly coupled whole, a unified problem description model and a universal solution method will fundamentally provide feasible approaches to breaking the barriers of the current dispatching functional zones. The intelligent dispatching knowledge learning model established based on DL and RL in AI has the advantage of end-to-end. It means that with the current state given as the input, the optimized dispatching decision-making scheme will be continuously learned or directly output.

In this study, the power system dispatching problem with complex constraints is simplified to an economic dispatching problem with the goal of minimizing the generation cost to visually demonstrate the dispatching effect, verify and evaluate the power system dispatching “knowledge” validity acquired by agents, and facilitate the calculation of the potential generated “revenue” by intelligent dispatching. It is worth noting that an independent model can be designed without any specific dispatching objective by establishing a basic architecture of intelligent dispatching based on knowledge “learning”. The method of knowledge acquisition, knowledge application, and knowledge assessment can be applied to complex online dispatching processes undoubtedly.

2.2 General description of RL method

General RL modeling relies on Markov Decision Process (MDP), which is a quintuple < $S,A,P,R,\gamma$ >, in which S represents the state of the agent, with $S_t\in S$, where $S$ is the set of all possible states. $A$ represents the action executed by the agent, with $a_t\in A\left(S_t\right)$, where $A\left(S_t\right)$ indicates the set of all actions that can be executed under the state $S_t$. P is the state transition probability with $\left.P_{s{s}^{\prime }}^a={\mathrm{P}[\mathrm{S}}_{t+1}={\mathrm{s}}^{\prime }\left|S_t=s,A_t=a\right.\right]$, and R is revenue with $R_s^a=E\left[R_{t+1}\left|S_t=s,A_t=a\right.\right]$.

For the multi-step decision problem, the total revenue of subsequent actions is calculated by the discount factor $\gamma$ as $G_t={\displaystyle \sum }_{k=0}^{\infty }{\gamma }^k{R}_{t+k+1}$, where $\gamma$ is the discount factor, with $\gamma \in \left[\mathrm{0,1}\right]$. In terms of the agent policy $\pi$, the value of performing action $a$ in the state $s$ is $q_{\pi }\left(s,a\right)$, and $q_{\pi }\left(s,a\right)=E_{\pi }\left[G_t\left|S_t=s,A_t=a\right.\right]$.

The action value function records the value of performing each feasible action in the current state. The knowledge acquired by Q learning is stored as a Q table, with the basic form shown in Figure 1 as follows.

FIGURE 1

FIGURE 1. The Q table for knowledge describing.

In the knowledge learning process, the Q matrix is first initialized to an all-zero matrix, which means that there is no prior knowledge in the initial state of the agent, and the agent continues to explore the environment. The updating principle of the Q-learning algorithm is shown in Eq. 1, where $\alpha$ represents the learning rate; $\gamma$ is the revenue decay coefficient; s and a represent the current state and action taken; $s^{\prime }$ and $a^{\prime }$ represent the state and action at the next moment.

$\begin{array}{l}Q\left(s,a\right)=Q\left(s,a\right)+\\ \alpha \left(r+\gamma \underset{a^{\prime }\in A}{\max }Q\left(s^{\prime },a^{\prime }\right)-Q\left(s,a\right)\right)\end{array}(1)$

When decision-making is implemented by using the acquired knowledge, only by performing the most valuable action $a^{*}$ corresponding to the state $s_k$ can enter state $s_{k+1}$ and realize the optimal decision-driven state progression. The process of the agent applying knowledge is shown in Eq. 2.

${\pi }^{*}\left(s\right)=\underset{a\in A}{\mathrm{argmax}}{Q}^{\pi }\left(s,a^{*}\right)(2)$

3 AIDLM for power system based on RL

The AIDLM for power system based on reinforcement learning clarifies the basic elements of intelligent dispatching and the relationship between the elements from the architecture level. The data-driven AIDLM describes the basic process of how to refine data into knowledge. In order to improve the conciseness and effectiveness of knowledge, this chapter also explores the extraction and application of AI dispatching knowledge.

3.1 Establishment of AIDLM for power system

Due to the large scale of the power system, there are many variables related to the operation of the power system. The goal of power system dispatching is to adjust some controllable variables in which the system operation can meet the load demand and have acceptable technical and economic performances. According to this feature, the objective and control variables in the power system can be determined.

The objective variable set $O^{ps}$ is a set of variables that reflect the system’s operation goal or technical and economic performances, such as the load of each node, voltage of the load node, network loss rate, and transmission element load rate. Generally, the state $S$ in reinforcement learning method comes from the target variable set $O^{ps}$.

The control variable set $C^{ps}$ is a set of variables that can be used in power system dispatching and can change the value of the objective variable, such as the active power of the generator, nodal voltage of generator, the reactive power by the reactive compensation equipment, and the switching of components.

The environment $E^{ps}$ covers all operating variables obtained by sensing the practical power system, and it can also establish a mathematical model to reflect the correlation of all operating variables.

Accumulated reward $G^{ps}$ evaluates the technical and economic performance of an objective variables and the corresponding control. As the revenue assessment requires environment $E^{ps}$, all kinds of constraints can be tested in this module. Moreover, the violation and the impact of the violation on the control value can be corrected. The exploration reward of single-step actions to the environment is called immediate reward r, and in each episode, the agent will choose multi-step control actions to maintain a better economic and technical performance of the power system.

Since the problem of intelligent power system dispatch needs to meet both multiple operational objectives in time series and optimal decision making for multiple generation control variables. The knowledge of optimal dispatching under a single objective can be characterized as a Q table. However, Knowledge extraction is the process of dealing with the original knowledge formed by “target-control” to gain more refined knowledge expression (repository) $K^{ps}\left(i\right)$.

Based on the above analysis, the architecture of AIDLM in the power system is presented as shown in Figure 2. The above model architecture can achieve the learning and post-processing of power system AI dispatching knowledge.

FIGURE 2

FIGURE 2. The architecture of AIDLM in power system.

3.2 Data-driven AIDLM

As can be seen in Figure 1, the exhaustive method can be simply used as the way for agents to explore the environment and obtain the optimal decision knowledge, in terms of finite state and finite action discrete decision problems.

For general RL problems involving massive states and continuous actions, the Markov chain, $\epsilon -\mathrm{g}\mathrm{r}\mathrm{e}\mathrm{e}\mathrm{d}\mathrm{y}$, Monte Carlo decision tree, and other methods are usually used to select feasible actions. If the environment of the agent is complex, the state set S may face the problem of dimension explosion. At this time, the action evaluation Q under each state and action can be obtained by fitting a neural network with parameter $\omega$, which provides method support for the accumulation and application of complex intelligent dispatching knowledge. In this way, when the neural network reaches convergence, the optimal decision under a certain target $O^{ps}\left(i\right)$ can be achieved by comparing the values of neural network outputs among different actions.

The action value-based reinforcement learning method outputs the values of all possible actions within each iteration step. In addition, the convergence process of optimization decision can be observed when using the knowledge of agent for optimal dispatching, so the reinforcement learning method proposed in this paper has a better interpretability.

The power system has a relatively complete data acquisition system, including supervisory control and data acquisition (SCADA), to record the operation conditions of the system. The data reflect the relationship among the variables such as the environment, objective, and control in the past operation of the actual power system. The long-term accumulated historical operation data cover the steady-state operation behavior of the power system in conventional scenarios. Based on the historical data, a data-driven AI dispatching learning knowledge method for the power system can be constructed.

Supposing the historical data set {Data(i)} contains the operation data of n scenarios, the environment $E^{ps}\left(i\right)$ can be constructed from the data of scenario i. The objective vector $O^{ps}\left(i\right)$ and control vector $C^{ps}\left(i\right)$ can also be extracted from {Data(i)} to form the initial “objective-control".

During the whole training process of the agent, AIDLM sets the initial state of the agent to the initial control given by the historical data in each episode. However, due to the influence of time difference, the state faced by the agent in each episode of learning is uncertain, and the optimal dispatching knowledge to deal with $O^{ps}\left(i\right)$ needs to be updated through multiple episode cycles. In each episode, the agent will choose multi-step control actions to make the system’s operating state gradually converge. The learning process of each episode is shown in Figure 3.

FIGURE 3

FIGURE 3. Schematic diagram for the process of data-driven AIDLM.

Using the example of the economic dispatching problem, the key steps of the agent exploring the environment in Figure 3 are illustrated.

(1) Definition of state, action and reward

The state s is composed of the demand vector $\left\{P_L\right\}$ and the power supply vector $\left\{P_G\right\}$.

Each generator can be discrete into p actions at the current output level, and if there are l generators in the system, the total number of optional actions in the action set k = p×l. Since the agent can form the final optimal dispatching decision through multi-step actions, if the deviation between the optimal control ${C^{ps}}^{*}\left(i\right)$ and the initial control $C^{ps}\left(i\right)$ is large, the action steps required by the agent to explore the optimal control will increase. When defining an action set, coarse adjustment action with large step size and fine adjustment action with small step size can be defined at the same time. The knowledge learning process of the agent not only ensures high dispatching accuracy, but also takes into account high exploration efficiency.

The immediate reward r of agent consists of three components, i.e., r = r₁+r₂+r₃, where r₁ denotes the convergent performance evaluation. The agent needs to give positive rewards for performing excellent actions, conversely, negative rewards will be given for selecting poor actions.

$\begin{array}{l}{r}_1={\left.k_1\times \exp \left(-{\displaystyle \sum }_{i=1}^{l}f\left(P_{Gi}\right)/c_1\right)\right|}_{s=s_t}-\\ {\left.k_1\times \exp \left(-{\displaystyle \sum }_{i=1}^{l}f\left(P_{Gi}\right)/c_1\right)\right|}_{s=s_t,a=a_t}\end{array}(3)$

In Eq 3, $k_1$ and $c_1$ are the proportional factor and scaling adjustment factor, respectively. $f\left(P_{Gi}\right)$ represents the operating cost of generator i.

r₂ represents the penalty for exceeding the limit. The agent needs to continuously obtain the power flow information of the grid during the exploration of the environment. If the power flow does not meet the given operation constraints, the actions that do not meet the power grid operation constraints should be punished to reduce the probability of the agent making similar actions.

r₃ represents the penalty of exploration efficiency. In order to prevent the agent from repeatedly exploring around the local optimal solution, it is necessary to punish each adjustment action executed by the agent. r₃ is usually constant, but when the action selected by the agent is to maintain the output of the generator unchanged, r₃ = 0.

(2) Construction and training of deep neural networks

For deep Q learning, the main function of the neural network is to fit a Q table. Therefore, according to the difference in the complexity of the problem, the neural network structure can be composed of 2–5 fully connected layers. In order to solve the overestimation of action value by neural network, the estimation network and target network are used to jointly complete the iterative update of action value function Q in the process of agent training. The estimation network is used to fit the mapping relationship from states to Q values, and the target network is used to generate Q values for constructing learning targets. Therefore, in AIDLM, the target network Q values update formula is:

$Q=r_{t+1}+\gamma \max Q\left(s_{t+1},a^{\prime },{\omega }^{-}\right)(4)$

In Eq 4, ${\omega }^{-}$ represents the parameters to be trained for the target network, and $Q\left(s_{t+1},a^{\prime },{\omega }^{-}\right)$ is the Q values of the target network fitting in the next state.

The target network structure is the same as the estimation network structure. The target network is updated with the latest estimation network parameters after several steps and keeps the parameters constant during the interval, making the overall iterative process more stable. The update quantity of Q value in estimation network is as follows:

$\Delta Q\left(s_t,a_t\right)=\alpha \left[Q\left(s_t,a_t,{\omega }^{-}\right)-Q\left(s_t,a_t,{\omega }_t\right)\right](5)$

In Formula 5, ${\omega }_t$ is the network parameter of the estimated network, $\alpha$ is the learning rate of the neural network.

When the neural network converges, the optimal control $C^{ps*}\left(i\right)$ corresponding to the objective $O^{ps}\left(i\right)$ and the optimal dispatching knowledge $Q_i^{ps}\left(s,a,\omega \right)$ in the form of a deep neural network can be obtained.

For convenience, the optimal control accumulated reward of the objective $O^{ps}\left(i\right)$ is denoted as $G^{ps*}\left(i\right)$, and three column vectors are defined as follows:

$\begin{array}{l}{O}^{ps,vector}={\left[\begin{array}{cccc}{O}^{ps}\left(1\right)& O^{ps}\left(2\right)& \dots & O^{ps}\left(n\right)\end{array}\right]}^T\\ C^{ps*,vector}={\left[\begin{array}{cccc}{C}^{ps*}\left(1\right)& C^{ps*}\left(2\right)& \dots & C^{ps*}\left(n\right)\end{array}\right]}^T\\ G^{ps*,vector}={\left[\begin{array}{cccc}{G}^{ps*}\left(1\right)& G^{ps*}\left(2\right)& \dots & G^{ps*}\left(n\right)\end{array}\right]}^T\end{array}(6)$

where $O^{ps}\left(i\right)$ and $C^{ps}\left(i\right)$ themselves are vectors, and then the generalized n × 3 original knowledge repository matrix $K^{ps,ori}$ can be defined as:

$K^{ps,ori}=\left[O^{ps,vector}{C}^{ps*,vector}{G}^{ps*,vector}\right](7)$

The knowledge distribution of the original knowledge matrix $K^{ps,ori}$ is related to the data volume n and the distribution of the historical dataset. When the historical dataset is large and dense enough, $K^{ps,ori}$ will have much redundancy. Therefore, it is necessary to perform further post-processing.

3.3 Extraction and application of AI dispatching knowledge

In the original knowledge matrix of Eq. 6, each row of $O^{ps,vector}$ has a corresponding ${C^{ps}}^{*}\left(i\right)$, and the optimal control is associated with each specific objective. Therefore, the original knowledge can only deal with a specific problem but not a certain kind of problem. When the operational objective of the power system changes, the optimal control scheme cannot be obtained directly through the original knowledge matrix. In the field of machine learning, it generally adopts the method of additionally constructing a strongly nonlinear function. Thus, although it can approximately solve the problem without bringing significant performance loss, this method cannot reveal the relationship between knowledge validity and control results, and it is difficult to find the reasons for the poor effect of “control”. Hence, it is necessary to establish a knowledge validity assessment method to guide the knowledge extraction, and make the extracted knowledge expression concise and effective.

Clustering is used to calculate the “distance” between the data, in which the data in the same class have similar features. Moreover, the mentioned data are distinguished from the data with different features, simultaneously. By using the clustering method, the n elements of the first column (i.e., $O^{ps,vector}$) of the original knowledge matrix $K^{ps,ori}$ are divided into m classes. Accordingly, the original knowledge matrix $K^{ps,ori}$ is divided into m submatrices, i.e.,:

$K^{ps,ori}=\left[\begin{array}{c}{K}_1^{ps,ori}\\ K_2^{ps,ori}\\ ⋮\\ K_m^{ps,ori}\end{array}\right](8)$

Each sub-matrix corresponds to a knowledge subclass, and the elements in each the subclass have similar information. According to the definition of the original knowledge matrix $K^{ps,ori}$, its jth sub-matrix can be written as:

$K_j^{ps,ori}=\left[\begin{array}{ccc}{O}_j^{ps,vector}& C_j^{ps\ast ,vector}& G_j^{ps\ast ,vector}\end{array}\right](9)$

The number of its rows (the number of objective-control pairs containing) is ${\beta }_j$, and following can be obtained as follows:

${\displaystyle \sum }_{j=1}^{\alpha }{\beta }_j=n(10)$

For the objective set $O_j^{ps,vector}$ of the jth knowledge subclass, the cluster center $\overline{O_j}$ and relative standard deviation ${\epsilon }_j^O$ of the set are defined as:

$\overline{O_j}=\frac{1}{{\beta }_j}{\displaystyle \sum }_{\gamma =1}^{{\beta }_j}{O}_j^{ps,vector}\left(\gamma \right)(11)$

${\epsilon }_j^O=\frac{1}{‖\overline{O_j}‖}\sqrt{\frac{1}{{\beta }_j}{\displaystyle \sum }_{\gamma =1}^{{\beta }_j}‖O_j^{ps,vector}\left(\gamma \right)-\overline{O_j}‖}(12)$

Similarly, for the control set $C_j^{ps*,vector}$ of the jth subclass, the cluster center $\overline{C_j}$ and the relative standard deviation ${\epsilon }_j^C$ of the set are defined.

For the control set $C_j^{ps*,vector}$ of the jth subclass, the mean of all control values is defined as $\overline{G_j}$.

$\overline{G_j}=\mathrm{a}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{g}\mathrm{e}\left(G_j^{ps,vector}\right)(13)$

The maximum relative deviation ${\delta }_j^G$ of revenues in the subclass is:

${\delta }_j^G=\frac{\max \left(G_j^{ps,vector}\right)-\min \left(G_j^{ps,vector}\right)}{\overline{G_j}}(14)$

The final knowledge matrix $K^{ps}$ is formed after extraction:

$K^{ps}=\left[\begin{array}{c}{K}_1^{ps}\\ K_2^{ps}\\ ⋮\\ K_m^{ps}\end{array}\right](15)$

where $K^{ps}$ reduces from ${\beta }_j$ rows of original $K_j^{ps,ori}$ to one:

$K_j^{ps}=\left[\begin{array}{ccc}\overline{O_j}& \overline{C_j}& \overline{G_j}\end{array}\right](16)$

The knowledge validity assessment index $V_j^K$ of knowledge subclass j (or sub-matrix j) is defined as triplet:

$V_j^K=\left\{{\epsilon }_j^O,{\epsilon }_j^C,{\delta }_j^G\right\}(17)$

For a certain knowledge subclass j of a given classification, a smaller $V_j^K$ tripartite element means a better knowledge composition or a shallower knowledge compression. Relatively large ${\epsilon }_j^O$ and relatively small ${\epsilon }_j^C$ and ${\delta }_j^G$ mean that this control group has adaptability to wider objective requirements. The control shows a convergence trend to the objective. Moreover, relatively small ${\epsilon }_j^O$ and relatively large ${\epsilon }_j^C$ and ${\delta }_j^G$ mean that this group of controls is very sensitive to the objective. The control shows a divergency trend to the objective, which may face control errors with large fluctuation in the control implementation.

For different subclass partitioning schemes, it is evident that when the original repository $K^{ps,ori}$ is deeply compressed in the extraction process (fewer knowledge subclasses are retained), the triples in the knowledge validity assessment index should present large values. Conversely, if subclass compression is not carried out, i.e., m = n, all knowledge validity assessment indexes for the original repository $K^{ps,ori}$ are 0.

According to the knowledge validity assessment index $V_j^K$, the contradiction between knowledge simplification and guaranteeing control effect can be balanced in progressive knowledge extraction. For the divided knowledge subclasses, $V_j^K$ can be used to diagnose and compare the quality differences of each knowledge subclass.

When applying knowledge, for any new specified objective $O^{ps,spec}$, the $\overline{O_j}$ nearest to it in the first column of the knowledge matrix $Q^{ps}$ can be found. In this condition, control $\overline{C_j}$ can be adopted, and the loss in revenue will not be greater than ${\delta }_j^G$.

4 Case studies

In this paper, an actual regional power grid in Northeast China is taken as an example. The actual operation data collected by SCADA are used to learn the AI dispatching knowledge and evaluate the acquired dispatching knowledge validity. The mentioned knowledge is used to simulate dispatching and test the effect of intelligent dispatching.

4.1 Introduction of a practical power system

The practical power system is derived from Northeast of China, which has 22 loads, and the maximum total load is 2.283 million kW. There are five power plants, all of which have an installed capacity of 600 MW. The cost function of each power plant is as follows:

$\left\{\begin{array}{l}{f}_1\left(P_{G1}\right)=0.00011P_{G1}^2+0.005P_{G1}+0.15\\ f_2\left(P_{G2}\right)=0.000125P_{G2}^2+0.0011P_{G2}+0.7\\ f_3\left(P_{G3}\right)=0.0001225P_{G3}^2+0.001P_{G3}+0.335\\ f_4\left(P_{G4}\right)=0.00013P_{G4}^2+0.004P_{G4}+0.25\\ f_5\left(P_{G5}\right)=0.000085P_{G3}^2+0.0012P_{G3}+0.6\end{array}\right.(18)$

where $f_i\left(P\right)$ and $P_{Gi}$ are the generation cost (ten thousand yuan/hour) and active power (MW) of power plant i, respectively.

The topology is shown in Figure 4.

FIGURE 4

FIGURE 4. Topology diagram of an actual power system.

For this study, a total of 15 days on the regional power grid in the winter of 2015 were selected as the measured data, with a sampling interval of 15 min and a total of 1,440 sampling moments. The data of the first 14 days are used as the data set of AI dispatching knowledge learning. The total grid load and output curve of each generator in this period are shown in Figure 5.

FIGURE 5

FIGURE 5. The measured total load and the power of each generator for 14 days.

4.2 AI dispatching knowledge learning and intelligent dispatching based on AIDLM under lumped load

Loads of 22 nodes in the whole system are first accumulated into a lumped load, and the lumped load-multi-generation system dispatching is studied to display the results of the proposed method in this paper more clearly.

Data-driven AIDLM is used to learn intelligent dispatching knowledge. In this model, $O^{ps}\left(i\right)$ is selected as the total load to be allocated at scenario i, i.e., $O^{PS}\left(i\right)=P_{L\sum }\left(i\right)$. Due to the intelligent economic dispatch of lumped load-multiple generation, the objective variable has only one dimension at each moment.

The state s of the agent is defined as a 5-dimensional vector, including $s=\left[P_{G1},P_{G2},\cdots ,P_{GNg}\right]$ which is generated by each power plant at scenario i, and Ng is the number of power plants in the power grid. Ng takes the value of five because of there are five power plants in the grid. The operation status of each power plant should meet the following equation and inequality constraints:

$\left\{\begin{array}{l}{P}_{L\sum }\left(i\right)={\displaystyle \sum }_{j=1}^{ng}{P}_{Gj}\left(i\right)\\ P_{Gj\min }\le P_{Gj}\left(i\right)\le P_{Gj\max }\end{array}\right.(19)$

$P_{Gj\min }$ and $P_{Gj\max }$ are the minimum and maximum output of power plant j, which are set as 100 MW and 600MW, respectively.

Take the measured power generation scheme $C^{ps}\left(i\right)$ as the initial state of the agent exploration, and set five alternative actions for each power plant, corresponding to different operations for the current active output $P_{Gj}$ of power plant j, including increasing by 3%, increasing by 1%, keeping unchanged, decreasing by 1% and decreasing by 3%. According to the above definition, the dimension of total action space is 20.

When calculating the immediate reward of the agent, the proportional adjustment coefficient k₁ = 2, the scale adjustment coefficient c₁ = 6,000, and the penalty r₂ = −1 for the generator exceeding the operating limitation. The agent adjusts the output of the power plant at each step and obtains the exploration efficiency penalty r₃ = −0.05. Set the maximum number of control steps for each episode to 1,000, and the learning rate α = 0.0001. The agent is composed of four fully connected layers, and experience pool contains 10000 items.

After being sufficiently trained, the agent will output the optimal action $a_t^{*}$ corresponding to the state s = s_t. With the progression of the state, eventually the agent will stay in the execution of the action where the power plant output remains unchanged.

Accumulated reward G represents the total operating cost of all power plants in the grid after the optimal control actions are applied. Figure 6 shows the optimal control ${C^{ps}}^{*}\left(i\right)$ and optimal ${G^{ps}}^{*}\left(i\right)$ of the five generators.

FIGURE 6

FIGURE 6. AI dispatching schemes at the different load levels under lumped load case.

It can be seen that, after the full exploration of “control”, under 1,344 control objectives, the optimal control $C^{ps*,vector}$ has obtained different degrees of revenue improvement compared with the actual power generation method.

Currently, the average cost of the AI dispatching knowledge acquisition scheme is 851,000 yuan/h, and the cost of the measured operation mode is 902,000 yuan/h, in average. The unit price of power supply in the original scheme is 0.48 yuan/kWh, and that in the new scheme is 0.456 yuan/kWh, which is 5% lower.

Knowledge extraction is conducted on the original knowledge matrix $K^{ps,ori}$ (96 × 14 rows in total), and the compression ratios are taken as 14, 28, and 56 to extract the subclass 96, 48, and 24. Figures 7A, B show the average and maximum values of the triplet ${\epsilon }_j^O,{\epsilon }_j^C,{\delta }_j^G$ of knowledge validity assessment index when extracting subclass 96, 48, and 24, respectively. Statistical results indicate that the revenue loss ${\delta }_j^G$ of knowledge subclass increases with the decrease of the divided knowledge subclasses. For this example, subclass 48 shows a smaller deterioration than subclass 96, while subclass 24 shows a clear trend of deterioration.

FIGURE 7

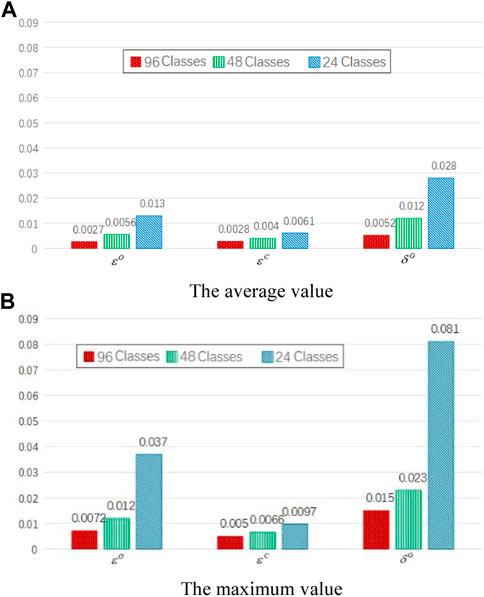
FIGURE 7. The statistics of knowledge validity indexes under different extraction depths in the lumped load case.

Regarding the test of AI dispatching knowledge, the measured total load data of the 15th day are taken as the objective $O^{PS}\left(i\right)$. The knowledge matrix Q ^ps of formed subclass 96 after extraction is used to simulate dispatching and obtain the intelligent dispatching curves of five generators in 15th day.

Figure 8 shows the comparison of the total generation cost between the knowledge-based intelligent dispatching scheme and the actual operation mode.

FIGURE 8

FIGURE 8. The generating cost curves of the AI dispatching and the real system in the lumped load case.

The cumulative daily generation cost of the actual operation mode is 23.536 million yuan, while this value for AI dispatching is 22 million yuan. Compared with the actual mode, the cumulative daily power generation cost of AI dispatching decreases by 1.536 million yuan or 6.52%. It shows that AI dispatching can reduce the power generation cost based on the actual operation mode of the system.

4.3 Intelligent dispatching of distributed load based on AIDLM

For the operation problem of the 22 loads and five power generators in the example system, the data of the first 14 days are used to train the AI dispatching knowledge, and then AI dispatching knowledge is used for dispatching the load of the 15th day.

In this case, the objective $O^{PS}\left(i\right)$ is the active power of each load in the network at scenario i, which is a 22-dimensional vector, with $O^{PS}\left(i\right)=\left[P_{L1}\left(i\right),P_{L2}\left(i\right),\cdots ,P_{L22}\left(i\right)\right]$. Table 1 shows load distributions at four typical moments. Although the total loads are similar, the distributions of the loads are quite different. Therefore, AI dispatching in this case requires agent to acquire oriented knowledge to more specific dispatching objectives.

TABLE 1

TABLE 1. Some distributed load illustration of the test system at several moments (MW).

$C^{ps}\left(i\right)$ is selected as the measured active power $C^{ps}\left(i\right)=\left[P_{G1}\left(i\right),\cdots ,P_{G5}\left(i\right)\right]$ generated by each power plant at moment i. Unlike the intelligent dispatching of a lumped load, here only the power of generator two to generator five can be directly controlled. Generator one is designated as the slack node of power flow calculation, and its power is determined by power flow calculation, but it does not affect its calculation of revenue.

Figure 9 presents the statistics of knowledge validity assessment indexes under different extraction schemes.

FIGURE 9

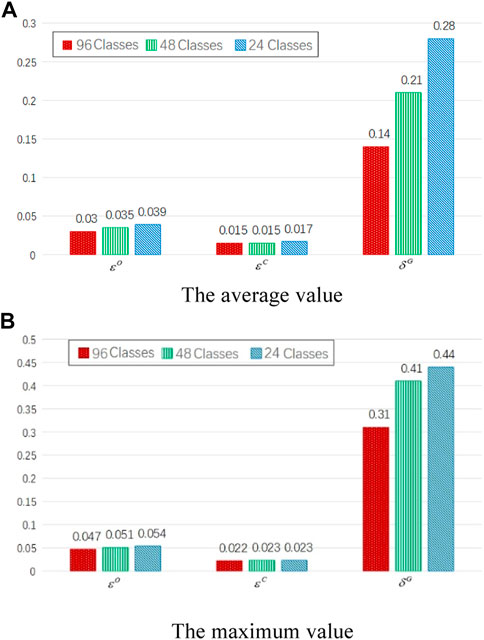
FIGURE 9. The statistics of knowledge validity indexes under different extraction depths in the distributed loads case.

The original knowledge is extracted and compressed into subclass 96. Table 2 compares the knowledge validity indexes under the dispatching modes of lumped and distributed loads. Compared with the case of lumped load, when the distributed load is taken as the objective, the dispersion degree of the objective set $O^{PS}$ increases and ${\epsilon }^{\mathrm{o}}$ becomes larger, and the dispersion ${\epsilon }^{\mathrm{c}}$ of the optimal control set also tends to improve.

TABLE 2

TABLE 2. Comparison of statistics of the knowledge validity index under lumped and distributed load cases.

In the training process of intelligent dispatching knowledge under lumped load, $O^{ps,vector}$ only contains a 1-dimensional feature quantity, and the mode is simplex when divided into different subclasses. However, under the dispatching mode of distributed load, $O^{ps,vector}$ contains 22-dimensional feature quantities, which can present more complex modes.

As the maximum relative deviation of the control value, the subset revenue deviation ${\delta }^{\mathrm{G}}$ reflects the effect of knowledge extraction from the value perspective. Therefore, with the same number of knowledge subclasses divided, the control value deviation under distributed load will be higher than that under centralized load.

Figure 10 compares the knowledge application effect of intelligent dispatching for lumped and distributed loads. The cumulative daily generation cost of AI dispatching under the distributed load case is 22.29 million yuan, which is 1.246 million yuan lower than the actual operation cost, with a decrease of 5.3%. The cumulative daily generation cost of AI dispatching in the scheme under the distributed load case is 290,000 yuan higher than the lumped load case, and the deterioration is 1.3%. Since the dispatching scheme under the distributed load case considers the network loss, the total power generation is slightly larger than the total load. The average network loss power is 11.69 MW, and the total daily network loss power is 280.5 MWh. Considering the average electricity price, the network loss value will be 132,700 yuan. After deducting the network loss, the dispatching scheme under the distributed load case has a net cost increase of 157,300 yuan compared with the lumped load case, and the actual deterioration is 0.7%.

FIGURE 10

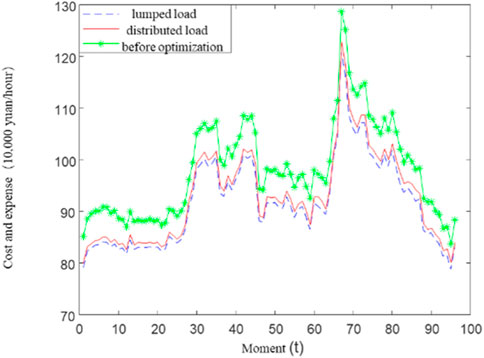
FIGURE 10. The generating cost curves of the AI dispatching and the real system in distributed load case.

5 Conclusion

Using the new progress of RL in AI, this paper has been investigated the modeling of intelligent dispatching knowledge learning in power systems, data-driven knowledge learning methods, and knowledge validity assessment. The main conclusions are as follows.

(1) The correspondence between reinforcement learning knowledge composition and power system operation problems is researched, and the reinforcement learning-based knowledge learning model AIDLM for AI dispatching of power systems is proposed.

(2) A data-driven AI dispatching knowledge learning method is proposed. Based on the interaction between agent and environment, the dispatching strategy under a given load objective can be learned, and then the optimal dispatching knowledge under different objectives can be continuously accumulated through Q-learning.

(3) Knowledge effectiveness evaluation indexes are proposed, which can analyze the performance of each knowledge subclass and guide the effective extraction of the acquired original knowledge.

(4) The example of a real power system shows that the AIDLM model and data-driven method can learn dispatching knowledge from operation data. The system operation cost can be reduced by more than 5% by applying the acquired intelligent dispatching knowledge. It has preliminarily demonstrated the feasibility of power system intelligent dispatching based on knowledge learning.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

YZ and GM: Conceptualization, Methodology, Writing—Original draft preparation. LZ: Writing, Methodology—Original draft preparation. JA: Translation and Validation.

Funding

This paper was supported in part by the National Natural Science Foundation of China (Key Project Number: 51877034).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bao, T., Zhang, X., Yu, T., and Liu, X. (2018). A Stackelberg game model of real-time supply-demand interaction and the solving method via reinforcement learning[J]. Proc. CSEE 38 (10), 2947–2955. doi:10.13334/j.0258-8013.pcsee.162388

CrossRef Full Text | Google Scholar

Bazrafshan, M., Gatsis, N., Taha, A. F., and Taylor, J. A. (2019). Coupling load-following control with OPF. IEEE Trans. Smart Grid 10 (3), 2495–2506. doi:10.1109/tsg.2018.2802723

CrossRef Full Text | Google Scholar

Davoodi, E., Babaei, E., Mohammadi-Ivatloo, B., Shafie-Khah, M., and Catalao, J. P. S. (2021). Multiobjective optimal power flow using a semidefinite programming-based model. IEEE Syst. J. 15 (1), 158–169. doi:10.1109/jsyst.2020.2971838

CrossRef Full Text | Google Scholar

Francis, A., Faust, A., Chiang, H. T. L., Hsu, J., Kew, J. C., Fiser, M., et al. (2020). Long-range indoor navigation with PRM-RL. IEEE Trans. Robotics 36 (4), 1115–1134. doi:10.1109/tro.2020.2975428

CrossRef Full Text | Google Scholar

Huang, Q., Huang, R., Hao, W., Tan, J., Fan, R., and Huang, Z. (2019). Adaptive power system emergency control using deep reinforcement learning. IEEE Trans. Smart Grid 11 (2), 1171–1182. doi:10.1109/tsg.2019.2933191

CrossRef Full Text | Google Scholar

Johannink, T., Bahl, S., Nair, A., Luo, J., Kumar, A., and Loskyl, M. (2019). “Residual reinforcement learning for robot control[C],” in 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20-24 May 2019, 6023–6029.

Google Scholar

Ju, Y., and Chen, Xi (2023). Distributed active and reactive power coordinated optimal scheduling of networked microgrids based on two-layer multi-agent reinforcement learning[J/OL]. Proceedings of the CSEE, 1-16 (in Chinese). Available at: http://kns.cnki.net/kcms/detail/11.2107.tm.20220316.1151.003.html (Accessed 01 29, 2023).

Google Scholar

Li, D., Yu, L., Li, N., and Lewis, F. (2021). Virtual-action-based coordinated reinforcement learning for distributed economic dispatch[J]. IEEE Trans. Power Syst. 36 (6), 5143–5152. doi:10.1109/TPWRS.2021.3070161

CrossRef Full Text | Google Scholar

Li, J., Yu, T., and Zhang, X. (2022). Coordinated load frequency control of multi-area integrated energy system using multi-agent deep reinforcement learning. Appl. Energy 306, 117900. doi:10.1016/j.apenergy.2021.117900

CrossRef Full Text | Google Scholar

Li, P., Yang, M., and Wu, Q. (2021). Confidence interval based distributionally robust real-time economic dispatch approach considering wind power accommodation risk. IEEE Trans. Sustain. Energy 12 (1), 58–69. doi:10.1109/tste.2020.2978634

CrossRef Full Text | Google Scholar

Liu, W., Zhang, D., and Wang, X. (2018). A decision making strategy for generating unit tripping under emergency circumstances based on deep reinforcement learning[J]. Proc. CSEE 38 (01), 109–119+347.

Google Scholar

Luo, G., Yuan, Q., Li, J., Wang, S., and Yang, F. (2022). Artificial intelligence powered mobile networks: From cognition to decision. IEEE Netw. 36 (3), 136–144. doi:10.1109/mnet.013.2100087

CrossRef Full Text | Google Scholar

Nojavan, M., and Seyedi, H. (2020). Voltage stability constrained OPF in multi-micro-grid considering demand response programs. IEEE Syst. J. 14 (4), 5221–5228. doi:10.1109/jsyst.2019.2961972

CrossRef Full Text | Google Scholar

Parizad, A., and Hatziadoniu, C. J. (2021). “Using prophet algorithm for pattern recognition and short term forecasting of load demand based on seasonality and exogenous features[C],” in 2020 52nd North American Power Symposium (NAPS), Tempe, AZ, USA, 11-13 April 2021, 1–6.

Google Scholar

Schrittwieser, J., Antonoglou, I., Hubert, T., Simonyan, K., Sifre, L., Schmitt, S., et al. (2020). Mastering Atari, Go, chess and shogi by planning with a learned model. Nature 588 (7839), 604–609. doi:10.1038/s41586-020-03051-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Silver, D., Schrittwieserh, J., Simonyan, K., Antonoglou, I., Huang, A., Guez, A., et al. (2017). Mastering the game of Go without human knowledge. Nature 550 (7676), 354–359. doi:10.1038/nature24270

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, L., Pan, Z., and Wang, J. (2021). A review of reinforcement learning based intelligent optimization for manufacturing scheduling. Complex Syst. Model. Simul. 1 (4), 257–270. doi:10.23919/csms.2021.0027

CrossRef Full Text | Google Scholar

Xi, L., Yu, L., and Fu, Y. (2019). Automatic generation control based on deep reinforcement learning with exploration awareness[J]. Proc. CSEE 39 (14), 4150–4162.

Google Scholar

Xu, J., and Yue, H. (2020). “Research on fault diagnosis method of power grid based on artificial intelligence[C],” in 2020 IEEE conference on telecommunications, optics and computer science (TOCS), Shenyang, China, 11-13 December 2020, 113–116.

Google Scholar

Yang, J. J., Yang, M., Wang, M. X., Du, P., and Yu, Y. (2020). A deep reinforcement learning method for managing wind farm uncertainties through energy storage system control and external reserve purchasing. Int. J. Electr. Power and Energy Syst. 119, 105928. doi:10.1016/j.ijepes.2020.105928

CrossRef Full Text | Google Scholar

Yang, T., Huang, J., and Kui, X. U. (2018). Diagnosis method of power transformer fault based on deep learning[J]. Power Syst. Big Data 21 (06), 23–30.

Google Scholar

Zhang, X., Qing, L. I., and Tao, Y. U. (2017). Collaborative consensus transfer Q-learning based dynamic generation dispatch of automatic generation control with virtual generation tribe[J]. Proc. CSEE 37 (5), 1455–1467. (in Chinese).

Google Scholar

Zhang, Z., Zhang, D., and Qiu, R. C. (2019). Deep reinforcement learning for power system applications: An overview[J]. CSEE J. Power Energy Syst. 6 (1), 213–225.

Google Scholar