- Faculty of Energy and Management, Komsomolsk-na-Amure State University, Komsomolsk-on-Amur, Russia
Purpose of the work: Researching possibility of creating a method for improving the energy efficiency of differentiated robotic technological process (RTP) in the food industry. The high rates of development of production processes robotization, including in the food industry, leading to increase the cost of electrical energy, determine the research tasks relevance in finding energy-efficient methods for controlling industrial robots.
Methodology: The proposed approach is based on principles of object-oriented design and possibility of classifying robotic technological process: Applying specific model sets and methods to improve energy efficiency to individual classes. The existing possibility of energy consumption synthesizing models of robots inside differentiated robotic technological process, such as stacking loads, in reduced form, made it possible to use neural network methods to identify non-linear dependencies. At the same time, training sample for intelligent modules was formed on the basis of classical experiment planning algorithms. The synthesis of methods, models and procedures was implemented on the basis of high-level programming languages C++, MATLAB.
Results: A mathematical model and automated algorithms for its synthesis are proposed, which make it possible to adjust robotic technological process simulation model taking into account its specifics and implement a method for finding the optimal parameters of its functioning. To confirm the effectiveness of proposed solution, the obtained neural network model and optimization method were tested on real robotic technological process, and the calculation of economic efficiency of proposed solution was also given.
Conclusion/recommendations: The application of this approach will significantly reduce energy costs for robotic operations in the food industry.
1 Introduction
In the conditions of an unstable world economy, increasing tensions at the geopolitical level and global climate change, the likelihood of emergency situations in the country is increasing. In order to reduce the impact of negative consequences, specialized services and structures are working to improve the national security systems of the country, including in the field of food security, which is one of the main goals of the agrarian and economic policy of the country. Thus, one of the important subsystems of ensuring food security is the warehousing and storage of products, essentials, devices, mechanisms, etc. At the same time, due to the constant correction of the nomenclature of stored objects towards its expansion, the issues of increasing the «productivity» of specialized warehouses are becoming more urgent. Qualitative indicators can be achieved by solving logistical problems inside a specialized room, as shown in (Ivanov et al., 2021), which can be achieved through the development of adequate mathematical models of processes and the use of modern automation tools, in particular, industrial robots (IR), sensor systems and intelligent control algorithms. Thus, the performance indicator of the removal, loading, reassembly subsystems, location changes, confirmation of the quality of objects and storage classes will be determined, among other things, at the stage of technological design processes at manufacturing enterprises, for example, the weight and size indicators of the combined cargo on a pallet, options for laying, packaging and fastening. Palletizing, packaging and fastening operations also make a significant contribution to the formation of the cost of storage of products. To date, the quality indicators of these operations are achieved through the use of automation tools—IR, which is confirmed by the results of work (Kaczmarek and Borys, 2016). Nevertheless, due to the specifics of their device, there is an increase in electric energy costs, which ultimately negatively affects the cost of product storage. Thus, the issues of searching for algorithms for optimizing the process of assembling cargo intended for the formation of a strategic reserve, in the direction of reducing the cost of storage by reducing the electric power costs of IR, are very relevant. The approach proposed in this paper is based on the results obtained earlier by the authors of the study of the processes of increasing the energy efficiency of robotic machining and welding (Efimov et al., 2021; Gorkavyy et al., 2021).
2 Materials and methods
A distinctive feature of robotic technological complex (RTC) from other technological complexes is their high versatility and the ability to quickly adapt to changing working environment conditions. In this regard, universal automated technological complexes in production can be used, among other things, for the execution of simple technological operations characterized by a limited set of complexes of movement trajectories. Examples of such processes are: palletizing/depalletization, loading/unloading of machines, contact welding (Kozhevnikov et al., 2016; Kozhevnikov et al., 2019), trimming of contours of parts (Kozhevnikov et al., 2020), various test operations. In such cases, the RTC functionality is redundant to perform the operation, and the complex itself can be described by a reduced model based on intelligent tools. The advantage of using a reduced model when describing the above simple technological operations is the ability to quickly adjust the model to the changed working conditions of the RTC.
Thus, a typical RTС of laying blocks can be described by a reduced model reflecting only the indicators of energy and time spent on performing a robotic operation. The developed models can be aggregated in the future to build models of more complex processes with the aim of further optimization due to modularity and the possibility of quick readjustment of models to the changed requirements of the technological task.
A typical technological process of robotic loading of pallets with loads passing through a conveyor belt is shown in the figure (see Figure 1).
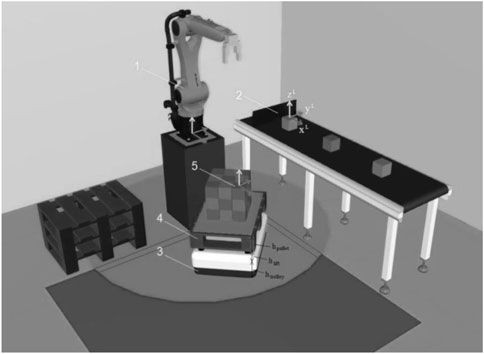
FIGURE 1. Robotized technological complex virtual model: 1—Industrial robot-manipulator, 2—Conveyor belt, 3—Robotic cart (RC), 4—Pallet, 5—Base unit in the loading zone. Source Compiled by the authors.
The main elements of RTP are: An industrial robot-manipulator, the working area of which is described by the set
Robotic cart 3 height
-
- For
- direction cosines
-
The last two functions are necessary if the RC does not position the pallet parallel to one of the planes of the global system
The set of all blocks on the pallet together with the set
Technological operations of placing loads (blocks) on pallets, as well as other operations of a similar class, such as conveyor assembly operations (for example, in the automotive industry, aircraft manufacturing), painting, radiography, etc., are characterized by a narrow range of changes and can be, in most restrictions, a small number of typical movements (Parisi et al., 2020), in contrast to the processes of machining and welding (Frolov, 2021a; Efimov et al., 2021; Gorkavyy et al., 2021). In such technological processes, the movements of the robot are carried out in a very limited segment of its working area. So for the considered RTP (see Figure 1), one of the typical complexes of REE movement trajectories for loading one block can be a complex of ten trajectories, shown in Figure 2A.
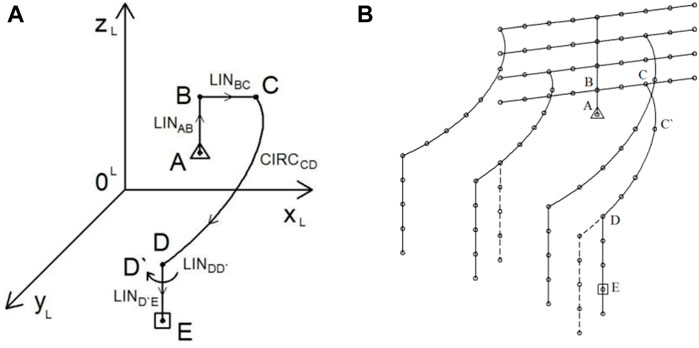
FIGURE 2. The REE trajectories. (A) Typical block movement trajectory, (B) Complex of trajectories for measurements. Source Compiled by the authors.
The set of trajectories consists of five trajectories
In order to be able to estimate the energy consumption of the robot associated with the trajectory of movement, it is necessary to have the function
In the KRL language, the REE movement commands would be:
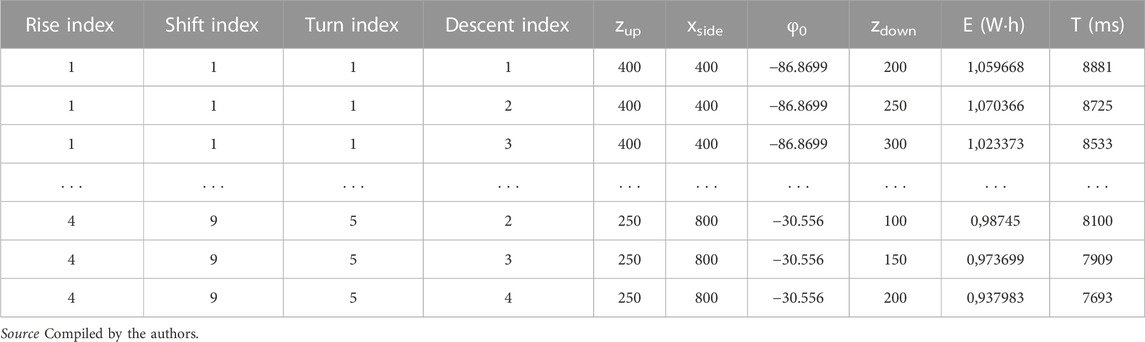
The number of trajectories required to form a training sample is determined empirically by setting the discreteness of changing parts of the trajectory. For example, Figure 2B defines the possibility of existence of 4·9·5·4 = 720 movement paths. The arguments
The KRL program for performing the necessary set of movements is formed automatically using specially developed software in C++ (Frolov, 2021b; Tretyak et al., 2021). Taking into account the specifics of the training sample, it is proposed to identify a non-linear dependence by a neural network of the feed-forward backprop type, as discussed in (Glorot and Bengio, 2010; Sozykin, 2017). An analysis of the effectiveness of using neural networks of different types in the framework of complex tasks is presented in (Martínez and Velásquez, 2011). After the dependence
if
After the array is completely calculated, it is necessary to search
It should be noted that as a result of the optimization, a set of trajectories of movement will be obtained only in the forward direction, while the trajectories of movement in the opposite direction are taken as “mirror” or return to point A using the PTP command. Energy consumption work when moving back is not taken into account in optimization algorithms, since the results of studies (Paesa et al., 2014; Qiu et al., 2021) showed a slight deviation in energy consumption in the forward and reverse directions.
In addition, it is possible, in case of energy expediency, to lay blocks by a robot in one layer, while the depth of laying is regulated by layer-by-layer lowering of RT pallets with cargo. At the same time, it is also necessary to take into account the difference between the saved energy for moving the REE to a depth and the energy required for the initial lifting of the pallet and its subsequent lowering.
3 Results
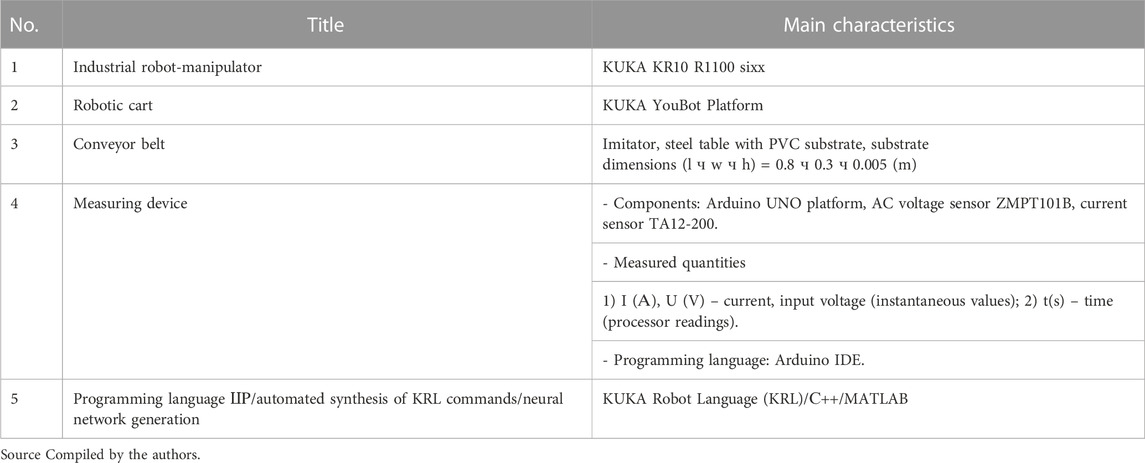
To confirm the effectiveness of the proposed solutions, an experiment was conducted under conditions close to industrial production using KUKA equipment (Table 2). Table 3 presents the initial data of experimental researches.
Figure 3 (a) shows a sweep of the graph of the function
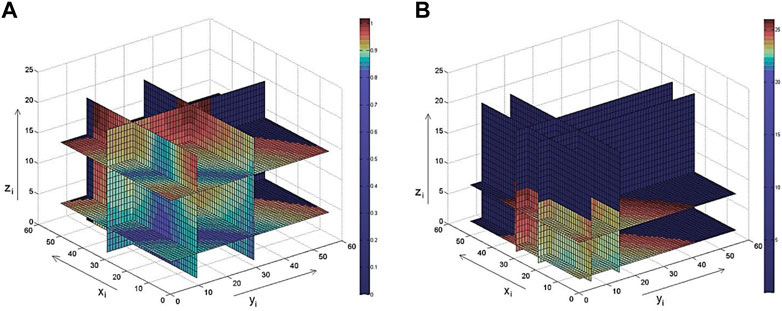
FIGURE 3. Graph of functions
Thus, as a result of the optimal choice of a set of movement trajectories, an effect is achieved, expressed in saving 1.56 W·h of electrical energy for laying one complete set of blocks.
Figure 4 shows in the form of a graph the energy values for assembling a complex of blocks relative to the base point with minimum and maximum costs.
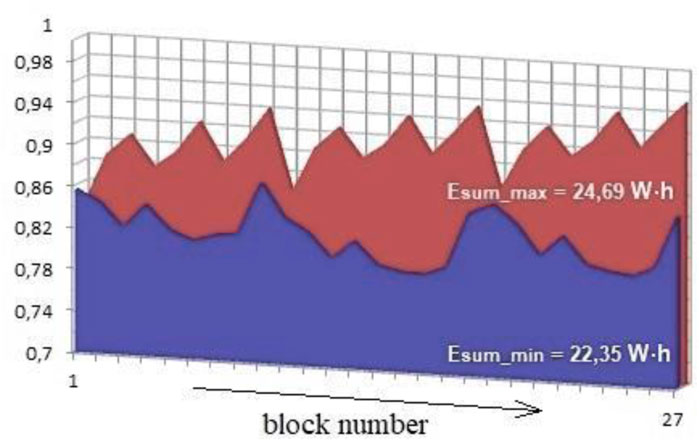
FIGURE 4. Energy values for the assembly of a complex of blocks relative to the base point. Source Calculated and built by the authors.
The energy value for the point selected by the operator is within the interval Esum_max - Esum_min, so the energy savings can reach
The total costs for the implementation of optimization measures can be found using the formula:
where Ealg is the total energy costs for the implementation of the algorithm; Eexp is the energy spent on conducting an experiment to measure the energy and time costs for each movement within a certain complex of movements; Eprogram is the energy spent on the operation of the software of an external device (user PC) that implements the developed optimization algorithms and forms the RTC control program optimized according to the selected criterion (minimum time or energy).
The cost of electrical energy for each movement (Table 1) in total with the cost of return movements to the home position amounted to
Since the time spent on the implementation of the optimization algorithm on a PC is 1 h, the cost of electrical energy for computing operations is equal to Eprogram = 250 W∙h (the average value is assumed).
Then the total cost of optimization measures is equal to
Since the obtained value of the cost of electrical energy for a single implementation of the proposed algorithm is comparable to the cost of conducting a robotic operation, the use of the algorithm seems to be the most profitable in conditions of continuous in-line production.
Because Esum_max = 24.69 W∙h, and Esum_min = 22.35 W∙h, the one-time energy costs for the implementation of the algorithm (Ealg) will pay off in
Thus, the implementation of the proposed algorithm will pay off after 689 technological cycles and then will bring net profit.
4 Conclusion
Thus, the presented research results demonstrate the possibility of a significant reduction in the energy intensity of the process of robotic stacking of blocks on a pallet, which ultimately reduces the cost of storing cargo in specialized premises within the strategic reserve, including through the use of the proposed solutions not only at the stage of primary assembly at the manufacturer, but also on robotic cargo sorting sites inside specialized storage locations. Thus, the potential for saving electrical energy with a typical variant of assembling cargo on a pallet can be up to 10%.
The proposed mathematical model and automated algorithms for its synthesis allow, with minimal time, information and intellectual costs, to set up a simulation model of RTP taking into account its specifics and implement a method for finding optimal parameters of its functioning: An optimal set of motion trajectories, energy consumption, execution time, RC positioning point.
As promising tasks for the development of the proposed topic, it seems appropriate to consider the influence of the rotation angle of the local coordinate system of the loading unit in the loading zone. In addition, it would be appropriate to ensure synchronization of RC consumption models and the robot in the case of laying a single layer by the robot with subsequent positioning of the RC of the local cargo base.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
The study was carried out as part of the activities of the Consortium for Sustainable Development and Technological Leadership and Research and Development Work No ВН002/2020, funded by Komsomolsk-na-Amure State University. The study was carried out using the equipment of the Scientific educational center «Industrial robotics and advanced industrial technologies».
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Anistrantsev, A. A., and Bespalova, O. N. (2021). Optimization of trajectories of robotic system manipulator for vegetable crop harvesting. Casp. Past. future, present 12, 75–80.
Cao, H. J., Zhou, J., Jiang, P., Hon, K. K. B., Yi, H., and Dong, C. Y. (2020). An integrated processing energy modeling and optimization of automated robotic polishing system. Robot. Comput. Integr. Manuf. 65, 101973. doi:10.1016/j.rcim.2020.101973
Efimov, A. Y., Gorkavyy, M. A., Egorova, V. P., and Gorkavyy, A. I. (2021). Optimization of technological parameters of robotized mechanical processing processes of aviation products. Current problems and ways of industry development: Equipment and technologies. Lect. Notes Netw. Syst. 200. doi:10.1007/978-3-030-69421-0_22
Frolov, A. V. (2021). Installation of automatic welding of elements of ship pipelines. Marine Intellectual Technologies, Т. 2. – № 2 (52), 91–96. doi:10.37220/MIT.2021.52.2.057
Frolov, A. V. (2021). The experience of the portal machine control system modernizing for automatic arc welding and surfacing in a shielded gas. Lect. Notes Netw. Syst. 200, 622–631. doi:10.1007/978-3-030-69421-0_66
Glorot, X., and Bengio, Y. (2010). “Understanding the difficulty of training deep feedforward neural networks,” in Proceedings of the International Conference on Artificial Intelligence and Statistics (AISTATS’10). Society for Artificial Intelligence and Statistics, venue, 249–256.
Gordin, S. A., Kozlova, O. V., and Zaychenko, I. V. (2020). Using the capabilities of neural networks to adapt the parameters of PID regulation in automatic control systems of low-power boilers. Int. Multi-Conference Industrial Eng. Mod. Technol. FarEastCon 2020, 9271418. doi:10.1109/FarEastCon50210.2020.9271418
Gorkavyy, M. A., Egorova, V. P., and Efimov, A. Y. (2021). Process automation for robot-based manufacturing components of prospective aviation complexes. Current problems and ways of industry development: Equipment and technologies. Lect. Notes Netw. Syst. 200. doi:10.1007/978-3-030-69421-0_20
Ivanov, Y. S., Zhiganov, S. V., and Ivanova, T. I. (2021). Intelligent deep neuro-fuzzy system of abnormal situation recognition for transport systems. Lect. Notes Netw. Syst. 200, 224–233. doi:10.1007/978-3-030-69421-0_24
Kaczmarek, W., and Borys, S. (2016). Wykorzystanie robotów przemysłowych w przemyśle spożywczym. Mechanik nr 07/2016 - XX międzynarodowa szkoła komputerowego wspomagania projektowania, wytwarzania i eksploatacji. China.
Kozhevnikov, M. M., Chumakov, O. A., Ilyushin, I. E., and Loboreva, L. A. (2019). Methods and algorithms for generating program trajectories of robotic manipulators in the process of arc welding. Rep. Belarusian State Univ. Inf. Radioelectron., № 1 (119)., 19–25.
Kozhevnikov, M. M., Chumakov, O. A., Shemenkov, V. M., Ilyushin, I. E., and Yurkina, A. A. (2020). Optimization of trajectories of industrial robotic manipulators for laser cutting. Bull. Belarusian-Russian Univ., № 2 (67)., 21–30.
Kozhevnikov, M. M., Ilyushin, I. E., Starovoitov, A. V., and Kosyrev, V. N. (2016). Planning the trajectories of robot manipulators in the technological process of point contact welding. Bull. Gomel State Tech. Univ. named after P.O. Sukhoi, № 2 (65)., 3–10.
Kuka Roboter GmbH, (2014). KUKA system software 8.3 operating and programming instructions for system integrators. Augsburg, Germany. (KSS 8.3 SI V3).
Kuka Roboter GmbH, (2016). KUKA System Software 8.3 Programming and operating instruction for end user. Augsburg, Germany. (KSS 8.3 END V5).
Marakhimov, M., Avazjon, A., and Khudaybergenov, K. (2018). Neuro-fuzzy identification of nonlinear dependencies. Bull. Natl. Univ. Uzbekistan Math. Nat. Sci. 1.
Martínez, C. A., and Velásquez, J. D. (2011). Analysis of nonlinear dependences using artificial neural networks. Rev. Fac. Ing. Univ. Antioquia, N. 60, 182–193.
Paesa, K., Dewulfa, W., Vander Elsta, K., Kellensb, K., and Slaetsa, P. (2014). Energy efficient trajectories for an industrial ABB robot. Procedia CIRP 15, 105–110. doi:10.1016/j.procir.2014.06.043
Parisi, F., Mangini, A. M., and Fanti, M. P. (2020). Optimal trajectory planning for a robotic manipulator palletizing tasks. Proceedings of the 2020 IEEE International Conference on Systems, Man, and Cybernetics (SMC), 2901–2906. Toronto, ON, Canada .
Qiu, B., Chen, S., Xiao, T., Gu, Y., Zhang, C., and Yang, G. (2021). “A feasible method for evaluating energy consumption of industrial robots,” in Proceedings of the 2021 IEEE 16th Conference on Industrial Electronics and Applications (ICIEA), Chengdu, China, 1073–1078. doi:10.1109/ICIEA51954.2021.9516218
Sozykin, A. V. (2017). Review of methods for training deep neural networks. Bull. South Ural State Univ. Ser. Comput. Math. Inf. 6 (3), 28–59.
Tretyak, A. V., Kapezkiy, I. O., and Vereschagina, E. A. (2021). Taking advantage of low-level programming languages for a new developing programming language. Mod. Sci. Actual Problems Theory Pract. Ser. Nat. Tech. Sci., № 2., 104–107.
Keywords: technological process, robotization, food industry, industrial robot, neural network model, energy efficiency, optimization
Citation: Gorkavyy MA, Gorkavyy AI, Egorova VP and Melnichenko MA (2023) Automated method based on a neural network model for searching energy-efficient complex movement trajectories of industrial robot in a differentiated technological process. Front. Energy Res. 11:1129311. doi: 10.3389/fenrg.2023.1129311
Received: 21 December 2022; Accepted: 07 March 2023;
Published: 04 October 2023.
Edited by:
Luis Puigjaner, Universitat Politecnica de Catalunya, SpainReviewed by:
Alaa Abdul-Ameer, British University in Dubai, United Arab EmiratesArunesh Kumar Kumar Singh, Jamia Millia Islamia, India
Copyright © 2023 Gorkavyy, Gorkavyy, Egorova and Melnichenko. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mikhail A. Gorkavyy, Z29ya2F2eXkubWlraGFpbEBiay5ydQ==
†ORCID: Mikhail A. Gorkavyy, orcid.org/0000-0001-8046-9906; Aleksandr I. Gorkavyy, orcid.org/0000-0001-7240-4264; Valeria P. Egorova, orcid.org/0000-0002-6749-6712; Markel A. Melnichenko, orcid.org/0000-0003-4498-6804
 Mikhail A. Gorkavyy
Mikhail A. Gorkavyy Aleksandr I. Gorkavyy†
Aleksandr I. Gorkavyy†