Prioritization of thermal energy storage techniques based on Einstein-ordered aggregation operators of q-rung orthopair fuzzy hypersoft sets

The capability to stock energy and manage consumption in the future is one of the keys to retrieving huge quantities of renewable energy on the grid. There are numerous techniques to stock energy, such as mechanical, electrical, chemical, electrochemical, and thermal. The q-rung orthopair fuzzy soft set (q-ROFSS) is a precise parametrization tool with fuzzy and uncertain contractions. In several environments, the attributes need to be further categorized because the attribute values are not disjointed. The existing q-rung orthopair fuzzy soft set configurations cannot resolve this state. Hypersoft sets are a leeway of soft sets (SSs) that use multi-parameter approximation functions to overcome the inadequacies of prevailing SS structures. The significance of this investigation lies in anticipating Einstein-ordered weighted aggregation operators (AOs) for q-rung orthopair fuzzy hypersoft sets (q-ROFHSSs), such as the q-rung orthopair fuzzy hypersoft Einstein-ordered weighted average (q-ROFHSEOWA) and the q-rung orthopair fuzzy hypersoft Einstein-ordered weighted geometric (q-ROFHSEOWG) operators, using the Einstein operational laws, with their requisite properties. Mathematical interpretations of decision-making constrictions are considered able to ensure the symmetry of the utilized methodology. Einstein-ordered aggregation operators, based on prospects, enable a dynamic multi-criteria group decision-making (MCGDM) approach with the most significant consequences with the predominant multi-criteria group decision techniques. Furthermore, we present the solicitation of Einstein-ordered weighted aggregation operators for selecting thermal energy-storing technology. Moreover, a numerical example is described to determine the effective use of a decision-making pattern. The output of the suggested algorithm is more authentic than existing models and the most reliable to regulate the favorable features of the planned study.

1 Introduction

Thermal energy storage (TES) is a technique for storing thermal energy by heating or cooling the storage medium so that the stockpiled energy can be used for consequent central heating and preservation solicitations and power generation. Energy storage systems are used primarily in construction and engineering practices. In these scenarios, almost half of the energy used is for heating, and its mandate can fluctuate daily. Thus, TES schemes can support stability mandates and daily, weekly, and periodic energy resources. They can also diminish ultimate declaration, energy ingestion, carbon dioxide releases, and expenditures while benefitting the whole productivity of energy schemes. Furthermore, the transformation and storing of adaptable renewable energy sources in the arrangement of thermal energy support increases the proportion of renewable energy in the energy mix. TES is mainly significant for power storing, combined with concentrated solar plants, which can stock solar heat to produce electricity without sunlight. TES is essential in several industrial scenarios. For example, one of the real-world problems related to solar energy schemes is the necessity for operational capital through which it can be stockpiled. Comparable difficulties exist in excess heat recovery schemes everywhere, and surplus heat accessibility and exploitation phases fluctuate. Heat storing can also be pragmatic for most kinds of construction where the heating system mandate is extraordinary and electrical energy notices permit heat storing to coexist with other arrangements of the heating system. There are numerous kinds of transaction systems, and several novel improvements are attracting interest in this area. Energy storage technology supports storing energy to avoid future energy complications. The thermal energy storage technique (TEST) is the most important energy technology. Dincer (2002) demonstrated in his study that the TEST is an essential energy storage skill for energy conversion. Monetary concerns act as a stimulus for energy transformation schemes, which makes the TEST even more important. Koçak et al. (2020) found that the TEST is a beneficial procedure with several uses in engineering. This TES solution can potentially escalate thermal energy apparatus usage on an elective foundation. There are commonly four different forms of TEST: sensible TEST, latent TEST, thermochemical TEST, and underground TEST. The prerequisite storage period typically affects the type of TEST used. It is anticipated that it will become one of the most effective thermal uses in this field.

Multi-criteria group decision-making (MCGDM) is the best way to manage suitable alternatives due to all the reliable assumptions, standards, or structures that come with it. A full assessment occurs when realistic intentions and confines are often unclear or imperfect. Zadeh (1965) initiated the notion of fuzzy sets (FSs) to demonstrate this incorrect and inconsistent information. It is imperative to compact with redundant and insecure decision-making (DM) matters. The FS model is used in various fields. Cavallaro (2010) established the fuzzy TOPSIS methodology to assess TES in concerted solar developments. Gumus et al. (2013) presented fuzzy AHP and fuzzy GRA approaches for choosing hydrogen energy systems. Contemporary FSs cannot handle cases when the regular consideration of membership degree (MD) and non-membership degree (NMD) by experts differs in the DM system. Atanassov (1986) addressed these limitations and demonstrated intuitionistic fuzzy sets (IFSs). Wang and Liu (2011) offered fundamental operations and aggregation operators (AOs) under their considered environment. Xu (2007a) furthered the theory of IFS and utilized the score and accuracy function to compute the relationship among two intuitionistic fuzzy numbers. Garg (2018) extended the cosine similarity measures (SMs), aiming to support DM proficiency. Lin et al. (2007) furthered the theory of IFS and demonstrated an advanced multi-criterion decision-making (MCDM) model. De et al. (2000) determined IFS concentration, normalization, and dilation operations. Garg and Kaur (2022) introduced the correlation measures for complex IFSs and utilized their developed measures to resolve MCDM obstacles. An IFS cannot apprehend unstable and confusing facts as it envisages a direct irregularity among MD and NMD. If the panel picks MD and NMD, such as $MD+NMD>1$, then existing IFS models fail to deal with this scenario.

Yager (2013) proposed that Pythagorean fuzzy sets (PFSs) overcome this deficiency by modifying the fundamental states $f+g\le 1$ to $f^2+g^2\le 1$. Xiao and Ding (2019) presented the divergence measures for PFSs and used their developed measures for medical diagnosis. Thao and Smarandache (2019) established an MCDM scheme built on entropy measures under the PFS setting. Mahmood et al. (2019) introduced T-spherical fuzzy sets (TSpFSs) with some fundamental operations and their properties. Khan et al. (2022a) developed a MADM system through the power of AOs for complex TSpFSs. Javed et al. (2022) extended the neutrality AOs for TSpFSs and presented a novel MAGDM technique to resolve DM obstacles. Zhang et al. (2019) introduced novel SMs for PFSs and proved that their use is more proficient compared to prevalent SMs. Hussain et al. (2022) established Aczel–Alsina AOs for PFSs and extended the MADM model to resolve DM complexities. Rahman et al. (2017) extended the multi-attribute group decision-making (MAGDM) model using Einstein-weighted geometric operators on PFSs. Zhang and Xu (2014) extended the TOPSIS method to remove MCDM constraints in PFSs. Jana et al. (2022) extended power Dombi AOs for PFSs and proposed an MADM approach to determine real-life obstacles. Wei and Lu (2018) developed the power AO for PFSs with its essential elements. Garg et al. (2022) developed Hamy mean AOs for complex PFSs and established the TOPSIS scheme to resolve MADM obstacles. Wang and Li (2020) extended Bonferroni mean AOs for PFSs considering the interaction among Pythagorean fuzzy numbers (PFNs). Kumar and Garg (2022) introduced some novel point operators for picture fuzzy sets and used their presented operators for DM. Ullah (2021) proposed Maclaurin symmetric mean operators for picture fuzzy sets and offered an MADM model using his developed operators. Zhang (2016) proposed a radical DM technique using SMs to solve the problem of MCGDM under PFS configuration. Yager (2016) established a generalized theory of IFS and PFS, known as a q-rung orthopair fuzzy set (q-ROFS). He developed numerous necessary operations for a q-ROFS and discussed their desirable elements. Sarkar et al. (2022) introduced Einstein AOs for q-ROFSs based on trapezoidal fuzzy numbers to resolve MCGDM issues. Khan et al. (2022b) proposed Aczel–Alsina AOs for q-ROFSs and extended the MADM approach to resolve DM difficulties. Akram et al. (2021a) presented Hamacher graphs for q-ROFSs and extended their proposed concept in DM. Riaz et al. (2020) developed hybrid AOs and a TOPSIS approach to resolve MADM problems considering the q-ROFS scenario.

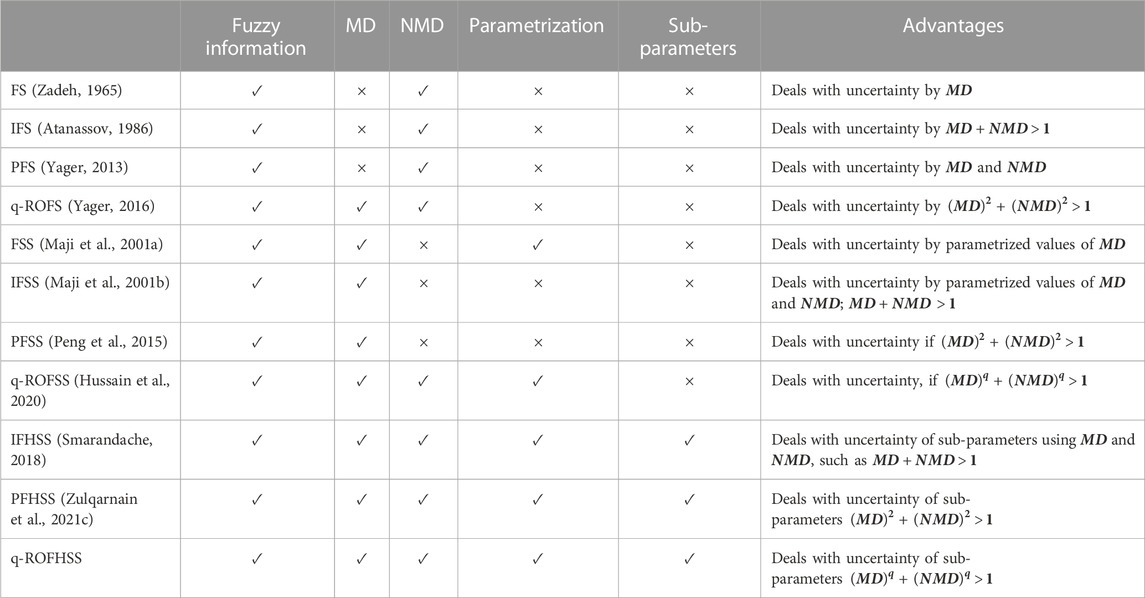
The aforementioned structures have a wide range of applications, but none of the above structures can handle alternative parameters. Molodtsov (1999) proposed the soft set (SS) notion to interact with the parametric standards of the alternatives. Maji et al. (2003) introduced several fundamental operations for SSs and discussed their significant properties. Cagman and Enginoglu (2011) extended the SS model to a fuzzy parametrized SS with some important tasks. They also extended the DM methodology to validate their established theory. Ali et al. (2009) introduced several fundamental operations for SSs. Maji et al. (2001a) fused two eminent models, FS and SS, and proposed the fuzzy soft set (FSS) theory. Roy and Maji (2007) extended a theoretical DM tool for FSSs to deal with obscure and invalid information. Maji et al. (2001b) developed the intuitionistic FSS (IFSS) with its complementary properties. Arora and Garg (2018) proposed an MCDM technique for IFSSs to resolve DM complications using their developed AOs. Çağman and Karataş (2013) extended the notion of IFSSs and presented their basic operations with a DM model to resolve real-life difficulties. Muthukumar and Krishnan (2016) proposed some novel SMs with important properties for IFSSs. Peng et al. (2015) constructed the Pythagorean fuzzy soft set (PFSS) with a mixture of PFSs and SSs. Athira et al. (2019) andAthira et al. (2020) extended the idea of PFSSs and introduced entropy and distance measures. Zulqarnain et al. (2022a) proposed Einstein operational laws for PFSSs and developed the Einstein AOs. They used their developed AOs to resolve MAGDM complications. Zulqarnain et al. (2021a) presented the Einstein-ordered averaging operator and developed a DM methodology to determine the supplier selection problem. They also introduced the Einstein-ordered geometric operator and used it to establish the MAGDM technique (Zulqarnain et al., 2022b). Athira et al. (2022) extended SMs for PFSSs with fundamental results and used their developed similarity measures for clustering analysis. Hussain et al. (2020) expanded the PFSS to a q-ROFSS and developed the AOs based on algebraic operational laws. Zulqarnain et al. (2022c) andZulqarnain et al. (2022d) extended the Einstein AOs for q-ROFSSs and established DM methodologies based on their developed operators. Akram et al. (2021b) introduced Yager AOs for q-ROFSSs and developed an MAGDM strategy to resolve DM issues. However, these AOs cannot resolve the MCGDM complexities where any expert considers the sub-parametric value of any parameter.

The models with SS configuration compact with single-parameter estimation functions, although hypersoft sets (HSSs), a leeway of SS, contract with multi-parameter approximation. The SS cannot grasp states wherever parameters are divided into further sub-attributes. To overcome such complications, Smarandache (2018) extended the SS to the HSS, the most generalized model to handle the multiple sub-attributes of the deliberated parameters. Rahman et al. (2022a) developed SMs for the possibility of an intuitionistic fuzzy supersoft set (IFHSS). Rahman et al. (2022b) introduced novel operations for fuzzy HSSs and established a MADM structure utilizing their developed operators. Zulqarnain et al. (2021b) presented AOs for IFHSSs engaging their algebraic operational laws. They also introduced the Pythagorean fuzzy hypersoft set (PFHSS) (Zulqarnain et al., 2021c) and discussed their significant properties. Siddique et al. (2021) delivered a creative MCDM system for PFHSSs using their developed AOs. Sunthrayuth et al. (2022) and Zulqarnain et al. (2022e) predicted the Einstein AOs for PFHSSs to obstinacy MCDM impediments and used them for agri-farming and material selection consistently. Zulqarnain et al. (2022f) developed Einstein-ordered AOs for PFHSSs and formulated an MCDM approach to resolve DM complexities.

Khan et al. (2021) extended the q-ROFSS to q-ROFHSS and introduced several fundamental operations. Gurmani et al. (2022) extended the TOPSIS method to q-ROFHSSs built on the correlation coefficient (CC). Khan et al. (2022c) presented the operational laws for q-ROFHSSs and developed the AOs. They also built a DM methodology using their proposed AOs and utilized it in the cryptocurrency market. Zulqarnain et al. (2022g) extended the interaction AOs of q-ROFHSSs to cryptocurrency analysis. A better-integrated organization is of interest to researchers with inadequate, incredible, and irregular facts to debate these flaws. They explained the importance of deliberation; q-ROFHSS is anticipated to play a dynamic role in DM by accumulating affluent cradles in a specific judgment.

1.1 Motivation

The q-ROFHSS is a mixed rational structure of HSSs and q-ROFSs, the basic mathematical tool for dealing with hesitancies, discrepancy, and imperfect details. AOs perform a vital role in DM, so facts concerning communal judgments from various causes can be ascribed to distinctive assessments. Einstein’s operational laws have no application in the literature with the hybridization of HSSs and q-ROFSs. Thus, the prevalent method neither has quantitative concise q-rung orthopair fuzzy hypersoft numbers (q-ROFHSNs) nor is it deliberately correlated with MD and NMD. The effect of MD (NMD) on the subsequent AOs does not interfere with the whole procedure. Furthermore, the model ranks the whole level of the MD (NMD) function, independent of the level of the NMD (MD) function. Therefore, by giving these AOs, the outcomes are obstructive, and consequently, the applicable partiality for alternatives is not determined. Therefore, it is necessary to know how to incorporate these q-ROFHSNs for Einstein operational laws. To resolve such queries, we introduce the q-rung orthopair fuzzy hypersoft Einstein-ordered weighted average (q-ROFHSEOWA) and the q-rung orthopair fuzzy hypersoft Einstein-ordered weighted geometric (q-ROFHSEOWG) operators for q-ROFHSSs. The prevalent Einstein-ordered AOs become the special cases of q-ROFHSSs. Therefore, it is determined that the proposed model is more competent than existing Einstein AOs. Thus, the consequence of the prevalent models is adverse, and the favoritism of the alternative cannot be configured appropriately. Therefore, incorporating these q-ROFHSNs into Einstein’s specification is an exciting subject. The methodologies proposed by Khan et al. (2022c) are inadequate to check the facts on flexible perspectives to achieve well-thought and specific outcomes. For example, we consider the set of two experts, such as $\mathcal{H}=\left\{{\mathcal{H}}_1,{\mathcal{H}}_2\right\}$, whose weights are given as ${\theta }_i={\left(.7,.3\right)}^T$; also, $d_1,d_2$ are two considered parameters. Let $d_1=\left\{d_{11},d_{12}\right\}$ and $d_2=\left\{d_{21}\right\}$ be the conforming sub-parameters of the deliberated parameters. Let ${\mathfrak{L}}^{\prime }$ be a 2-tuple Cartesian product of the considered attributes, which can be identified as ${\mathfrak{L}}^{\prime }=d_1\times d_2=\left\{d_{11},d_{12}\right\}\times \left\{d_{21}\right\}=$ $\left\{\left(d_{11},d_{21}\right),\left(d_{12},d_{21}\right)\right\}=\left\{{\mathit{ď}}_1,{\mathit{ď}}_2\right\}$ with weights ${\omega }_j={\left(0.4,.0.6\right)}^T$, and $\mathrm{\aleph }$ be an alternate. The preferences of the experts can be precise as $\mathrm{\aleph }=\left[\begin{array}{cc}\left(0.7,0.0\right)& \left(0.6,0.7\right)\\ \left(0.8,0.7\right)& \left(0.7,0.2\right)\end{array}\right]$ in q-ROFHSN form. Thus, we can overcome the $〈\begin{array}{c}0.6819,0\end{array}.0〉$ and $〈\begin{array}{c}0.6667,0.0\end{array}〉$ collective values using q-ROFHSWA and q-ROFHSWG (Khan et al., 2022c) operators. The aforementioned outcomes show that there is no influence on the communal outcome $g_{{\mathit{ď}}_k}$. Meanwhile, $g_{{\mathit{ď}}_{11}}$ = 0.0, $g_{{\mathit{ď}}_{12}}$ = 0.7, $g_{{\mathit{ď}}_{21}}$ = 0.7, and $g_{{\mathit{ď}}_{22}}$ = 0.2, which is unreasonable. Existing Einstein-ordered AOs (Zulqarnain et al., 2022f) for PFHSSs cannot handle the above-mentioned problem because $f_{{\mathit{ď}}_{21}}$ = 0.8 and $g_{{\mathit{ď}}_{21}}$ = 0.7, where ${\left(0.8\right)}^2+{\left(0.7\right)}^2>1$. Thus, the existing Einstein-ordered weighted AOs of PFHSSs cannot deal with such scenarios. To overcome these deficiencies, we propose an improved organizing methodology considering the Einstein operational laws under the q-ROFHSS setting to attract researchers to overcome inexplicable and deficient information. Deducing the investigation effects, q-ROFHSS plays an integral role in DM by accumulating numerous structures into a specific value.

1.2 Contribution

Einstein’s ordered weighted AOs are undoubtedly of interest in terms of the assessed AOs. It has been perceived that the general AO features do not respond to the finding of explicit effects by the DM scheme under apparent conditions. These AOs need to be reformed to eliminate these thorny problems. Therefore, to illuminate the current study of q-ROFHSSs and the aforementioned limitations, we assign Einstein-ordered weighted AOs founded on uncertain facts, with the primary purpose of the research given as follows:

⁃ The Einstein-ordered weighted AOs under q-ROFHSS settings are acquainted with attractive estimation AOs. It is believed that in some states, the main conceptual feature is the lack of sympathetic labeling of particular consequences of the DM process. To overcome such rigorous impairments, we extend both the idea of q-ROFHSSs and some novel AOs for q-ROFHSSs considering the Einstein operational laws.

⁃ q-ROFHSS expertly clarifies the obligation of the multiple sub-attributes of intellectual aspects in DM structures. To ensure this, we use Einstein’s ordered weighted AOs to represent q-ROFHSSs.

⁃ We present the q-ROFHSEOWA and q-ROFHSEOWG operators with their appropriate properties.

⁃ An excellent procedure with the projected AOs is presented to integrate MCGDM anxieties into the q-ROFHSS setting to assert DM negligence and to prioritize the TEST.

⁃ A comprehensive analysis of the advanced MCGDM methodology and predominant approaches is performed to confirm the validity and excellence of the proposed MCGDM approach.

The remainder of this paper is structured as follows: Section 2 contains some basic notions that sustain our organizational development follow-up study. Section 3 anticipates some Einstein operational laws for q-ROFHSNs, as well as introducing the q-ROFHSEOWA, with some significant results and properties. The q-ROFHSEOWG operator with its essential properties is presented in section 4. The MCGDM technique is developed with the proposed AOs, and a mathematical illustration is discussed to certify the practicality of the methodology in section 5. Moreover, a brief sensitivity exploration and comparative studies appear to highlight the advantages of the demonstrated approach in sections 6, 7, respectively.

2 Preliminaries

In the following section, we present some fundamental notions to construct this research.

Definition 2.1. (Molodtsov, 1999) Let $\mathcal{U}$ be a Universe of discourse and $\mathcal{E}$ be the set of attributes. Suppose $\mathcal{P}\left(\mathcal{U}\right)$ be the power set of $\mathcal{U}$ and $\mathcal{A}$ is any subset of attributes. Then, a pair ($\mathcal{F},\mathcal{A}$) is called a SS over $\mathcal{U}$, and its mapping is defined as follows:

$\mathcal{F}:\mathcal{A}\to \mathcal{P}\left(\mathcal{U}\right).$

It can also be defined as follows:

$\left(\mathcal{F},\mathcal{A}\right)=\left\{\mathcal{F}\left(\mathcal{e}\right)\in \mathcal{P}\left(\mathcal{U}\right):\mathcal{e}\in \mathcal{E},\mathcal{F}\left(\mathcal{e}\right)=\varnothing if\mathcal{e}\notin \mathcal{A}\right\}.$

Definition 2.2. (Smarandache, 2018) Let $\mathcal{U}$ be a Universe of discourse and $\mathcal{P}$ ($\mathcal{U}$) be a power set of $\mathcal{U}$ and $k$ = {$k_1$, $k_2$, $k_3$,..., $k_n$}, (n ≥ 1) and $K_i$ indicates the set of parameters and their equivalent sub-parameters, such as $K_i$ ∩ $K_j$ = φ, where i ≠ j for each n ≥ 1 and i, j ε {1,2,3 … n}. Assume $K_1$ × $K_2$ × $K_3$ × … × $K_n$ = $\stackrel{\dots }{\mathcal{A}}$ = $\left\{d_{1h}\times d_{2k}\times \cdots \times d_{nl}\right\}$ is a collection of sub-attributes, where 1 $\le$ $h$ $\le$ $\alpha$, 1 $\le$ $k$ $\le$ $\beta$, and 1 $\le$ $l$ $\le$ $\gamma$, and $\alpha$, $\beta$, $\gamma$ $\in$ ℕ. Then, the pair $\left(\mathcal{F},K_1\times K_2\times K_3\times \dots \times K_n\right)$ = $\left(\mathcal{F},\stackrel{\dots }{\mathcal{A}}\right)$ is called a HSS and is defined as follows:$\mathcal{F}$: $K_1$ × $K_2$ × $K_3$ × … × $K_n$ = $\stackrel{\dots }{\mathcal{A}}\to \mathcal{P}$ ($\mathcal{U}$).It can also be defined as follows:

$\left(\mathcal{F},\stackrel{\dots }{\mathcal{A}}\right)=\left\{\mathit{ď},{\mathcal{F}}_{\stackrel{\dots }{\mathcal{A}}}\left(\mathit{ď}\right):\mathit{ď}\in \stackrel{\dots }{\mathcal{A}},{\mathcal{F}}_{\stackrel{\dots }{\mathcal{A}}}\left(\mathit{ď}\right)\in \mathcal{P}\left(\mathcal{U}\right)\right\}$

Definition 2.3. (Zulqarnain et al., 2021c) Let $\mathcal{U}$ be a Universe of discourse and $\mathcal{P}$ ($\mathcal{U}$) be a power set of $\mathcal{U}$ and $k$ = {$k_1$, $k_2$, $k_3$,..., $k_n$}, (n ≥ 1) and $K_i$ signifies the set of parameters and their corresponding sub-parameters, such as $K_i$ ∩ $K_j$ = φ, where i ≠ j for each n ≥ 1 and i, j ε {1,2,3 … n}. Assume $K_1$ × $K_2$ × $K_3$ × … × $K_n$ = $\stackrel{\dots }{\mathcal{A}}$ = $\left\{d_{1h}\times d_{2k}\times \cdots \times d_{nl}\right\}$ is a collection of sub-parameters, where $1\le h\le \alpha$, $1\le k\le \beta$, and $1\le l\le \gamma$, and $\alpha ,\beta ,\gamma \in \mathbb{N}$, and ${PFS}^{\mathcal{U}}$ represents the collection of all subsets of Pythagorean fuzzy sets over $\mathcal{U}$. Then $\left(\mathcal{F},K_1\times K_2\times K_3\times \dots \times K_n\right)=\left(\mathcal{F},\stackrel{\dots }{\mathcal{A}}\right)$ is called a PFHSS and can be defined as follows:

$\mathcal{F}:K_1\times K_2\times K_3\times \dots \times K_n=\stackrel{\dots }{\mathcal{A}}\to {PFS}^{\mathcal{U}}$

It can also be defined as$\left(\mathcal{F},\stackrel{\dots }{\mathcal{A}}\right)=\left\{\left(\mathit{ď},{\mathcal{F}}_{\stackrel{\dots }{\mathcal{A}}}\left(\mathit{ď}\right)\right):\mathit{ď}\in \stackrel{\dots }{\mathcal{A}},{\mathcal{F}}_{\stackrel{\dots }{\mathcal{A}}}\left(\mathit{ď}\right)\in PF{S}^{\mathcal{U}}\in \left[0,1\right]\right\}$, where ${\mathcal{F}}_{\stackrel{\dots }{\mathcal{A}}}\left(\mathit{ď}\right)$ = $\left\{〈\delta ,f_{{\mathit{ď}}_{ij}}\left(\delta \right),g_{{\mathit{ď}}_{ij}}\left(\delta \right)〉:\delta \in \mathcal{U}\right\}$, where $f_{{\mathit{ď}}_{ij}}\left(\delta \right)$ and $g_{{\mathit{ď}}_{ij}}\left(\delta \right)$ signify the MD and NMD of the attributes, $f_{{\mathit{ď}}_{ij}}\left(\delta \right)$, $g_{{\mathit{ď}}_{ij}}\left(\delta \right)\in \left[0,1\right]$, and $0\le {\left(f_{{\mathit{ď}}_{ij}}\left(\delta \right)\right.}^2+{\left(g_{{\mathit{ď}}_{ij}}\left(\delta \right)\right)}^2\le 1$.For simplicity, the PFHSN ${\mathcal{F}}_{\stackrel{\dots }{\mathcal{A}}}\left(\mathit{ď}\right)$ = $\left\{〈\delta ,f_{\mathcal{F}\left(\mathit{ď}\right)}\left(\delta \right),g_{\mathcal{F}\left(\mathit{ď}\right)}\left(\delta \right)〉:\delta \in \mathcal{U}\right\}$ can be written as $J_{{\mathit{ď}}_{ij}}$ = $〈f_{{\mathit{ď}}_{ij}}\left(\delta \right),g_{{\mathit{ď}}_{ij}}\left(\delta \right)〉$. The score function (Sunthrayuth et al., 2022) for $J_{{\mathit{ď}}_{ij}}$ is stated as follows:

$S\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right)={{\mathit{f}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}}^2-{{\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}}^2,\hspace{1em}\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right)\in \left[-1,1\right].$

Occasionally, the scoring function does not deliver an appropriate result for calculating PFHSNs. It is challenging to draw conclusions about which alternative is informal. To overcome these barriers, accuracy functions are used:

$\mathit{A}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right)={\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\left(\mathit{\delta }\right)\right)}^2+{\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\left(\mathit{\delta }\right)\right)}^2,\hspace{1em}\mathit{A}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right)\in \left[-1,1\right]$

To compare the two PFHSNs ${\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}$ and ${\mathfrak{T}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}$, the comparison rules are given as follows:

1. If $\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right)$ $>$ $\mathit{S}\left({\mathfrak{T}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right)$, then ${\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}$ $>$ ${\mathfrak{T}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}$.

2. If $\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right)$ $=$ $\mathit{S}\left({\mathfrak{T}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right)$, then

• If $\mathit{A}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right)$ $>$ $\mathit{A}\left({\mathfrak{T}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right)$, then ${\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}$ $>$ ${\mathfrak{T}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}$

• If $\mathit{A}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right)$ $=$ $\mathit{A}\left({\mathfrak{T}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right)$, then ${\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}$ $=$ ${\mathfrak{T}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}$.

Definition 2.4. (Sunthrayuth et al., 2022) Let ${\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}$ = $\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}},{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}\right)$, ${\mathit{J}}_{{\mathit{ď}}_{11}}$ = $\left({\mathit{f}}_{{\mathit{ď}}_{11}},{\mathit{g}}_{{\mathit{ď}}_{11}}\right)$, and ${\mathit{J}}_{{\mathit{ď}}_{12}}$ = $\left({\mathit{f}}_{{\mathit{ď}}_{12}},{\mathit{g}}_{{\mathit{ď}}_{12}}\right)$ denote the PFHSNs, and $\mathit{\gamma }>0$. Then, the Einstein operational laws for PFHSNs are given as follows:

1. ${\mathit{J}}_{{\mathit{ď}}_{11}}{\oplus }_{\mathit{\epsilon }}{\mathit{J}}_{{\mathit{ď}}_{12}}=〈\frac{\sqrt{\left(1+{\mathit{f}}_{{\mathit{ď}}_{11}}^2\right)-\left(1-{\mathit{f}}_{{\mathit{ď}}_{12}}^2\right)}}{\sqrt{\left(1+{\mathit{f}}_{{\mathit{ď}}_{11}}^2\right)+\left(1-{\mathit{f}}_{{\mathit{ď}}_{12}}^2\right)}},\frac{\sqrt{2{\mathit{g}}_{{\mathit{ď}}_{12}}^2}}{\sqrt{\left(2-{\mathit{g}}_{{\mathit{ď}}_{11}}^2\right)+{\mathit{g}}_{{\mathit{ď}}_{12}}^2}}〉.$

2. ${\mathit{J}}_{{\mathit{ď}}_{11}}{\otimes }_{\mathit{\epsilon }}{\mathit{J}}_{{\mathit{ď}}_{12}}=〈\frac{\sqrt{2{\mathit{f}}_{{\mathit{ď}}_{11}}^2}}{\sqrt{\left(2-{\mathit{f}}_{{\mathit{ď}}_{11}}^2\right)+{\mathit{f}}_{{\mathit{ď}}_{12}}^2}},\frac{\sqrt{\left(1+{\mathit{g}}_{{\mathit{ď}}_{11}}^2\right)-\left(1-{\mathit{g}}_{{\mathit{ď}}_{12}}^2\right)}}{\sqrt{\left(1+{\mathit{g}}_{{\mathit{ď}}_{11}}^2\right)+\left(1-{\mathit{g}}_{{\mathit{ď}}_{12}}^2\right)}}〉.$

3. $\mathit{\gamma }{\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}=〈\frac{\sqrt{{\left(1+{{\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}}^2\right)}^{\mathit{\gamma }}-{\left(1-{{\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}}^2\right)}^{\mathit{\gamma }}}}{\sqrt{{\left(1+{{\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}}^2\right)}^{\mathit{\gamma }}+{\left(1-{{\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}}^2\right)}^{\mathit{\gamma }}}},\frac{\sqrt{2{\left({{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}}^2\right)}^{\mathit{\gamma }}}}{\sqrt{{\left(2-{{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}}^2\right)}^{\mathit{\gamma }}+{\left({{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}}^2\right)}^{\mathit{\gamma }}}}〉$.

4. ${{\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}}^{\mathit{\gamma }}=〈\frac{\sqrt{2{\left({{\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}}^2\right)}^{\mathit{\gamma }}}}{\sqrt{{\left(2-{{\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}}^2\right)}^{\mathit{\gamma }}+{\left({{\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}}^2\right)}^{\mathit{\gamma }}}},\frac{\sqrt{{\left(1+{{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}}^2\right)}^{\mathit{\gamma }}-{\left(1-{{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}}^2\right)}^{\mathit{\gamma }}}}{\sqrt{{\left(1+{{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}}^2\right)}^{\mathit{\gamma }}+{\left(1-{{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}}^2\right)}^{\mathit{\gamma }}}}〉$.

Zulqarnain et al. (2022f) defined the Einstein-ordered weighted AOs for PFHSNs by the previously deliberated Einstein operational laws with confident environments ${\mathit{\theta }}_{\mathit{i}}>0,{\displaystyle \sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}=1;{\mathit{\omega }}_{\mathit{j}}>0,{\displaystyle \sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}=1$, and $\mathfrak{r},\mathfrak{s}$ are permutations such that ${\mathit{J}}_{{\mathit{ď}}_{\mathfrak{r}\left(\mathit{i}-1\right)\mathfrak{s}\left(\mathit{j}\right)}}\ge {\mathit{J}}_{{\mathit{ď}}_{\mathfrak{r}\left(\mathit{i}\right)\mathfrak{s}\left(\mathit{j}\right)}}$ and ${\mathit{J}}_{{\mathit{ď}}_{\mathfrak{r}\left(\mathit{i}\right)\mathfrak{s}\left(\mathit{j}-1\right)}}\ge {\mathit{J}}_{{\mathit{ď}}_{\mathfrak{r}\left(\mathit{i}\right)\mathfrak{s}\left(\mathit{j}\right)}}$ $\forall \mathit{i},\mathit{j}$ given as follows:

$\mathbf{P}\mathbf{F}\mathbf{H}\mathbf{S}\mathbf{E}\mathbf{O}\mathbf{W}\mathbf{A}\left({\mathit{J}}_{{\mathit{ď}}_{11}},{\mathit{J}}_{{\mathit{ď}}_{12}},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}\right)$

$=\begin{array}{c}〈\begin{array}{c}\frac{\sqrt{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^2\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}-{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^2\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^2\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^2\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}\end{array},\end{array}$

$\times \frac{\sqrt{2{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^2\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(2-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^2\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^2\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}〉$(2.1)

$\mathbf{P}\mathbf{F}\mathbf{H}\mathbf{S}\mathbf{E}\mathbf{O}\mathbf{W}\mathbf{G}\left({\mathit{J}}_{{\mathit{ď}}_{11}},{\mathit{J}}_{{\mathit{ď}}_{12}},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}\right)=$

$=〈\frac{\sqrt{2{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^2\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(2-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^2\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^2\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}},$

$\times \frac{\sqrt{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^2\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}-{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^2\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^2\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^2\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}〉.$(2.2)

These existing AOs for PFHSSs were developed based on algebraic operational laws, and Einstein’s operational laws failed to handle the situation when ${\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right)}^2+{\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right)}^2>1$. To overcome these constraints, Khan et al. (2021) proposed the superior structure acknowledged as a q-ROFHSS, which adroitly contracts with the anxieties described previously.

Definition 2.5. (Khan et al., 2021) Let $\mathcal{U}$ be a Universe of discourse and $\mathcal{P}$ ($\mathcal{U}$) be a power set of $\mathcal{U}$ and $\mathit{k}$ = {${\mathit{k}}_1$, ${\mathit{k}}_2$, ${\mathit{k}}_3$,..., ${\mathit{k}}_{\mathit{n}}$}, (n ≥ 1) and ${\mathit{K}}_{\mathit{i}}$ show the set of parameters and their equivalent sub-parameters, such as ${\mathit{K}}_{\mathit{i}}$ ∩ ${\mathit{K}}_{\mathit{j}}$ = φ, where i ≠ j for each n ≥ 1 and $\mathit{i},\mathit{j}\in \left\{\mathrm{1,2,3}\dots \mathrm{n}\right\}$. Assume ${\mathit{K}}_1$ × ${\mathit{K}}_2$ × ${\mathit{K}}_3$ × … × ${\mathit{K}}_{\mathit{n}}$ = $\stackrel{\dots }{\mathcal{A}}$ = $\left\{{\mathit{d}}_{1\mathit{h}}\times {\mathit{d}}_{2\mathit{k}}\times \cdots \times {\mathit{d}}_{\mathit{n}\mathit{l}}\right\}$ is a collection of sub-parameters, where $1\le \mathit{h}\le \mathit{\alpha }$, $1\le \mathit{k}\le \mathit{\beta }$, and $1\le \mathit{l}\le \mathit{\gamma }$, and $\mathit{\alpha },\mathit{\beta },\mathit{\gamma }\in \mathbb{N}$, and ${\mathit{q}-\mathit{R}\mathit{O}\mathit{F}\mathit{S}}^{\mathcal{U}}$ represents the collection of all subsets of the q-ROFS over $\mathcal{U}$. Then $\left(\mathcal{F},{\mathit{K}}_1\times {\mathit{K}}_2\times {\mathit{K}}_3\times \dots \times {\mathit{K}}_{\mathit{n}}\right)=\left(\mathcal{F},\stackrel{\dots }{\mathcal{A}}\right)$ is called a q-ROFHSS and is defined as follows:

$\mathcal{F}:{\mathit{K}}_1\times {\mathit{K}}_2\times {\mathit{K}}_3\times \dots \times {\mathit{K}}_{\mathit{n}}=\stackrel{\dots }{\mathcal{A}}\to {\mathit{q}-\mathit{R}\mathit{O}\mathit{F}\mathit{S}}^{\mathcal{U}}$

It can also be defined as $\left(\mathcal{F},\stackrel{\dots }{\mathcal{A}}\right)=\left\{\left(\mathit{ď},{\mathcal{F}}_{\stackrel{\dots }{\mathcal{A}}}\left(\mathit{ď}\right)\right):\mathit{ď}\in \stackrel{\dots }{\mathcal{A}},{\mathcal{F}}_{\stackrel{\dots }{\mathcal{A}}}\left(\mathit{ď}\right)\in \mathit{P}\mathit{F}{\mathit{S}}^{\mathcal{U}}\in \left[0,1\right]\right\}$, where ${\mathcal{F}}_{\stackrel{\dots }{\mathcal{A}}}\left(\mathit{ď}\right)=〈\mathit{\delta },{\mathit{f}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\left(\mathit{\delta }\right),{\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\left(\mathit{\delta }\right)〉:\mathit{\delta }\in \mathcal{U}$, where ${\mathit{f}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\left(\mathit{\delta }\right)$ and ${\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\left(\mathit{\delta }\right)$ signify the MD and NMD of the sub-attributes, such as ${\mathit{f}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\left(\mathit{\delta }\right),{\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\left(\mathit{\delta }\right)\in \left[0,1\right]$ and $0\le {\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\left(\mathit{\delta }\right)\right)}^{\mathit{q}}+{\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\left(\mathit{\delta }\right)\right)}^{\mathit{q}}\le 1$.A q-ROFHSN can be stated as $\mathcal{F}=\left\{{\mathit{f}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\left(\mathit{\delta }\right),{\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\left(\mathit{\delta }\right)\right\}$, where $0\le {\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\left(\mathit{\delta }\right)\right)}^{\mathit{q}}+{\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\left(\mathit{\delta }\right)\right)}^{\mathit{q}}\le 1$.

Definition 2.6. (Khan et al., 2022c) Let ${\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}=\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}},{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}\right)$, ${\mathit{J}}_{{\mathit{ď}}_{11}}=\left({\mathit{f}}_{{\mathit{ď}}_{11}},{\mathit{g}}_{{\mathit{ď}}_{11}}\right)$, and ${\mathit{J}}_{{\mathit{ď}}_{12}}=\left({\mathit{f}}_{{\mathit{ď}}_{12}},{\mathit{g}}_{{\mathit{ď}}_{12}}\right)$ be the q-ROFHSNs, and $\mathit{\gamma }>0$. Then, the algebraic operational laws for q-ROFHSNs are given as follows:

1. ${\mathit{J}}_{{\mathit{ď}}_{11}}\oplus {\mathit{J}}_{{\mathit{ď}}_{12}}=〈\sqrt[\mathit{q}]{{{\mathit{f}}_{{\mathit{ď}}_{11}}}^{\mathit{q}}+{{\mathit{f}}_{{\mathit{ď}}_{12}}}^{\mathit{q}}-{{\mathit{f}}_{{\mathit{ď}}_{11}}}^{\mathit{q}}{{\mathit{f}}_{{\mathit{ď}}_{12}}}^{\mathit{q}}},{\mathit{g}}_{{\mathit{ď}}_{11}}{\mathit{g}}_{{\mathit{ď}}_{12}}〉.$

2. ${\mathit{J}}_{{\mathit{ď}}_{11}}\otimes {\mathit{J}}_{{\mathit{ď}}_{12}}=〈{\mathit{f}}_{{\mathit{ď}}_{11}}{\mathit{f}}_{{\mathit{ď}}_{12}},\sqrt[\mathit{q}]{{{\mathit{g}}_{{\mathit{ď}}_{11}}}^{\mathit{q}}+{{\mathit{g}}_{{\mathit{ď}}_{12}}}^{\mathit{q}}-{{\mathit{g}}_{{\mathit{ď}}_{11}}}^{\mathit{q}}{{\mathit{g}}_{{\mathit{ď}}_{12}}}^{\mathit{q}}}〉$.

3. $\mathit{\gamma }{\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}=〈\sqrt[\mathit{q}]{1-{\left(1-{{\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}}^{\mathit{q}}\right)}^{\mathit{\gamma }}},{{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}}^{\mathit{\gamma }}〉.$

4. ${\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{\gamma }}=〈{{\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}}^{\mathit{\gamma }},\sqrt[\mathit{q}]{1-{\left(1-{{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}}^{\mathit{q}}\right)}^{\mathit{\gamma }}}〉.$

For the multiplicity of q-ROFHSNs ${\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}$, where ${\mathit{\theta }}_{\mathit{i}}$ and ${\mathit{\omega }}_{\mathit{j}}$ represent the weight experts and sub-parameters, such as ${\mathit{\theta }}_{\mathit{i}}>0,{\displaystyle \sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}=1;{\mathit{\omega }}_{\mathit{j}}>0,{\displaystyle \sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}=1$, the AOs (Khan et al., 2022c) for the q-ROFHSSs are given as follows:

$\mathit{q}-\mathit{R}\mathit{O}\mathit{F}\mathit{H}\mathit{S}\mathit{W}\mathit{A}\left({\mathit{J}}_{{\mathit{ď}}_{11}},{\mathit{J}}_{{\mathit{ď}}_{12}},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}\right)=〈\sqrt[\mathit{q}]{1-{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{{\mathit{f}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}},{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}〉,$(2.3)

$\mathit{q}-\mathit{R}\mathit{O}\mathit{F}\mathit{H}\mathit{S}\mathit{W}\mathit{G}\left({\mathit{J}}_{{\mathit{ď}}_{11}},{\mathit{J}}_{{\mathit{ď}}_{12}},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}\right)=〈{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}},\sqrt[\mathit{q}]{1-{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{{\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}〉.$(2.4)

Remark 2.1.

1. If ${\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\left(\mathit{\delta }\right)\right)}^{\mathit{q}}+{\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\left(\mathit{\delta }\right)\right)}^{\mathit{q}}\le 1$ and ${\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\left(\mathit{\delta }\right)\right)}^2+{\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\left(\mathit{\delta }\right)\right)}^2\le 1$ hold, then the q-ROFHSS becomes a PFHSS (Zulqarnain et al., 2021c).

2. If ${\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\left(\mathit{\delta }\right)\right)}^{\mathit{q}}+{\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\left(\mathit{\delta }\right)\right)}^{\mathit{q}}\le 1$ and ${\mathit{f}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\left(\mathit{\delta }\right)+{\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\left(\mathit{\delta }\right)\le 1$ hold, then the q-ROFHSS becomes an IFHSS (Smarandache, 2018).

The q-ROFHSN ${\mathcal{F}}_{{\mathit{\delta }}_{\mathit{i}}}\left({\mathit{ď}}_{\mathit{j}}\right)$ = $\left\{\left({\mathit{f}}_{\mathcal{F}\left({\mathit{ď}}_{\mathit{j}}\right)}\left({\mathit{\delta }}_{\mathit{i}}\right),{\mathit{g}}_{\mathcal{F}\left({\mathit{ď}}_{\mathit{j}}\right)}\left({\mathit{\delta }}_{\mathit{i}}\right)\right)|{\mathit{\delta }}_{\mathit{i}}\in \mathcal{U}\right\}$ can be written as ${\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}$ = $〈{\mathit{f}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}},{\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}〉$. The score function for ${\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}$ is stated as follows:Let ${\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}$ = $〈{\mathit{f}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}},{\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}〉$ be a q-ROFHSN. Then,

$\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right)={\mathit{f}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{\mathit{q}}-{\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{\mathit{q}}+\left(\frac{{\mathit{e}}^{{\mathit{f}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{\mathit{q}}-{\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{\mathit{q}}}}{{\mathit{e}}^{{\mathit{f}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{\mathit{q}}-{\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{\mathit{q}}}+1}-\frac{1}{2}\right){\beth }_{{\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}}^{\mathit{q}},\mathrm{f}\mathrm{o}\mathrm{r}\mathit{q}\ge 3\mathrm{a}\mathrm{n}\mathrm{d}\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right)\in \left[-1,1\right].$(2.5)

Let ${\mathit{J}}_{{\mathit{ď}}_{11}}$ = $\left({\mathit{f}}_{{\mathit{ď}}_{11}},{\mathit{g}}_{{\mathit{ď}}_{11}}\right)$ and ${\mathit{J}}_{{\mathit{ď}}_{12}}$ = $\left({\mathit{f}}_{{\mathit{ď}}_{12}},{\mathit{g}}_{{\mathit{ď}}_{12}}\right)$ be two q-ROFHSNs. Then,If $\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{11}}\right)>\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{12}}\right)$, then ${\mathit{J}}_{{\mathit{ď}}_{11}}\succcurlyeq {\mathit{J}}_{{\mathit{ď}}_{12}}$.If $\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{11}}\right)<\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{12}}\right)$, then ${\mathit{J}}_{{\mathit{ď}}_{11}}\preccurlyeq {\mathit{J}}_{{\mathit{ď}}_{12}}$.If $\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{11}}\right)=\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{12}}\right)$, thenIf ${\beth }_{{\mathit{J}}_{{\mathit{ď}}_{11}}}>{\beth }_{{\mathit{J}}_{{\mathit{ď}}_{12}}}$, then ${\mathit{J}}_{{\mathit{ď}}_{11}}<{\mathit{J}}_{{\mathit{ď}}_{12}.}$If ${\beth }_{{\mathit{J}}_{{\mathit{ď}}_{11}}}^{\mathit{q}}$ = ${\beth }_{{\mathit{J}}_{{\mathit{ď}}_{12}}}^{\mathit{q}}$, then ${\mathit{J}}_{{\mathit{ď}}_{11}}={\mathit{J}}_{{\mathit{ď}}_{12}}.$For the comparison among two q-ROFHSNs ${\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}$ and ${\mathfrak{T}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}$, the comparison laws are defined as follows:

If $\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right)$ $>$ $\mathit{S}\left({\mathfrak{T}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right)$, then ${\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}$ $>$ ${\mathfrak{T}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}$.

If $\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right)$ $=$ $\mathit{S}\left({\mathfrak{T}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right)$, then

○ If $\mathit{A}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right)$ $>$ $\mathit{A}\left({\mathfrak{T}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right)$, then ${\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}$ $>$ ${\mathfrak{T}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}.$

○ If $\mathit{A}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right)$ $=$ $\mathit{A}\left({\mathfrak{T}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right)$, then ${\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}$ $=$ ${\mathfrak{T}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}$.

Definition 2.7. (Klement et al., 2004)Einstein operations comprise the Einstein product and Einstein sum, which are examples of t-norm and t-conorm, respectively, and can be defined as follows:

${\mathit{\alpha }}_1{\otimes }_{\mathit{\epsilon }}{\mathit{\alpha }}_2=\frac{{\mathit{\alpha }}_1{\mathit{\alpha }}_2}{1+\left(1-{\mathit{\alpha }}_1\right)\left(1-{\mathit{\alpha }}_2\right)}\mathrm{a}\mathrm{n}\mathrm{d}{\mathit{\alpha }}_1{\oplus }_{\mathit{\epsilon }}{\mathit{\alpha }}_2=\frac{{\mathit{\alpha }}_1+{\mathit{\alpha }}_2}{1+\left({\mathit{\alpha }}_1{\mathit{\alpha }}_2\right)}.$

The aforementioned Einstein product ${\otimes }_{\mathit{\epsilon }}$ (t-norm) and Einstein sum ${\oplus }_{\mathit{\epsilon }}$ (t-conorm) can be defined in a q-ROFHSS environment, such as${\mathit{\alpha }}_1{\otimes }_{\mathit{\epsilon }}{\mathit{\alpha }}_2=\frac{{\mathit{\alpha }}_1{\mathit{\alpha }}_2}{\sqrt[\mathit{q}]{1+\left(1-{{\mathit{\alpha }}_1}^{\mathit{q}}\right)\left(1-{{\mathit{\alpha }}_2}^{\mathit{q}}\right)}}$ and ${\mathit{\alpha }}_1{\oplus }_{\mathit{\epsilon }}{\mathit{\alpha }}_2=\frac{\sqrt[\mathit{q}]{{{\mathit{\alpha }}_1}^{\mathit{q}}+{{\mathit{\alpha }}_2}^{\mathit{q}}}}{\sqrt[\mathit{q}]{1+\left({{\mathit{\alpha }}_1}^{\mathit{q}}{{\mathit{\alpha }}_2}^{\mathit{q}}\right)}}$.The prevailing Einstein-ordered weighted AOs for a PFHSS only evaluate PFHSS influences and only contemplate the ordered positions of the PFHSS estimations, not the q-ROFHSS influences themselves. Similarly, from the aforementioned AOs for the q-ROFHSSs, it can be seen that, in assertive environments, these AOs convey some repulsive significance. To overcome these inadequacies, we offer innovative Einstein operational laws for q-ROFHSSs. In the next section, we introduce Einstein-weighted ordered AOs with their fundamental properties under a q-ROFHSS scenario based on these operational laws.

3 Einstein-ordered weighted average aggregation operator for q-rung orthopair fuzzy hypersoft sets

This section introduces a novel Einstein-ordered weighted average AO for q-ROFHSNs with the most necessary properties.

Definition 3.1. Let ${\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}=\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}},{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}\right)$, ${\mathit{J}}_{{\mathit{ď}}_{11}}=\left({\mathit{f}}_{{\mathit{ď}}_{11}},{\mathit{g}}_{{\mathit{ď}}_{11}}\right),$ and ${\mathit{J}}_{{\mathit{ď}}_{12}}=\left({\mathit{f}}_{{\mathit{ď}}_{12}},{\mathit{g}}_{{\mathit{ď}}_{12}}\right)$ represent the q-ROFHSNs, and $\mathit{\gamma }>0$. Then, the Einstein operational laws for q-ROFHSNs can be stated as follows:

1. ${\mathit{J}}_{{\mathit{ď}}_{11}}{\oplus }_{\mathrm{ℇ}}{\mathit{J}}_{{\mathit{ď}}_{12}}=〈\sqrt[\mathit{q}]{\frac{\left(1+{\mathit{f}}_{{\mathit{ď}}_{11}}^{\mathit{q}}\right)-\left(1-{\mathit{f}}_{{\mathit{ď}}_{12}}^{\mathit{q}}\right)}{\left(1+{\mathit{f}}_{{\mathit{ď}}_{11}}^{\mathit{q}}\right)-\left(1-{\mathit{f}}_{{\mathit{ď}}_{12}}^{\mathit{q}}\right)}},\sqrt[\mathit{q}]{\frac{2\left({\mathit{g}}_{{\mathit{ď}}_{12}}^{\mathit{q}}\right)}{\left(2-{\mathit{g}}_{{\mathit{ď}}_{11}}^{\mathit{q}}\right)+\left({\mathit{g}}_{{\mathit{ď}}_{12}}^{\mathit{q}}\right)}}.$

2. ${\mathit{J}}_{{\mathit{ď}}_{11}}{\oplus }_{\mathrm{ℇ}}{\mathit{J}}_{{\mathit{ď}}_{12}}=〈\sqrt[\mathit{q}]{\frac{2\left({\mathit{f}}_{{\mathit{ď}}_{12}}^{\mathit{q}}\right)}{\left(2-{\mathit{f}}_{12}^{\mathit{q}}\right)+\left({\mathit{f}}_{{\mathit{ď}}_{12}}^{\mathit{q}}\right)}},\sqrt[\mathit{q}]{\frac{\left(1+{\mathit{g}}_{{\mathit{ď}}_{11}}^{\mathit{q}}\right)-\left(1-{\mathit{g}}_{{\mathit{ď}}_{12}}^{\mathit{q}}\right)}{\left(1+{\mathit{g}}_{{\mathit{ď}}_{11}}^{\mathit{q}}\right)-\left(1-{\mathit{g}}_{{\mathit{ď}}_{12}}^{\mathit{q}}\right)}}.$

3. $\mathit{\gamma }{\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}=〈\sqrt[\mathit{q}]{\frac{{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}\right)}^{\mathit{\gamma }}-{\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}\right)}^{\mathit{\gamma }}}{{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}\right)}^{\mathit{\gamma }}+{\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}\right)}^{\mathit{\gamma }}}},\sqrt[\mathit{q}]{\frac{{2\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}\right)}^{\mathit{\gamma }}}{{\left(2-{\mathit{g}}_{\mathit{k}}^{\mathit{q}}\right)}^{\mathit{\gamma }}+{\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}\right)}^{\mathit{\gamma }}}}.$

4. ${\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{\gamma }}=〈\sqrt[\mathit{q}]{\frac{2{\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}\right)}^{\mathit{\gamma }}}{{\left(2-{\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}\right)}^{\mathit{\gamma }}+{\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}\right)}^{\mathit{\gamma }}}},\sqrt[\mathit{q}]{\frac{{\left(1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}\right)}^{\mathit{\gamma }}-{\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}\right)}^{\mathit{\gamma }}}{{\left(1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}\right)}^{\mathit{\gamma }}+{\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}\right)}^{\mathit{\gamma }}}}.$

Definition 3.2. Let ${\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}=\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}},{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}\right)$ be a collection of q-ROFHSNs; then, the q-ROFHSEOWA operator is defined as follows:

$\left.{\mathrm{q}-\mathrm{R}\mathrm{O}\mathrm{F}\mathrm{H}\mathrm{S}\mathrm{E}\mathrm{O}\mathrm{W}\mathrm{A}(\mathit{J}}_{{\mathit{ď}}_{11}},{\mathit{J}}_{{\mathit{ď}}_{12}},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}\right)={{\oplus }_{\mathrm{ℇ}}}_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}\left({{\oplus }_{\mathrm{ℇ}}}_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}{\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right)$(3.1)

In this manuscript, ${\mathit{\theta }}_{\mathit{i}}$ and ${\mathit{\omega }}_{\mathit{j}}$ indicate the weights for specialists and sub-attributes, respectively, such as ${\mathit{\theta }}_{\mathit{i}}>0$, ${\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}=1$, and ${\mathit{\omega }}_{\mathit{j}}>0,\mathrm{a}\mathrm{n}\mathrm{d}$ ${\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}=1$ and $\mathfrak{r},\mathfrak{s}$ are permutations such that ${\mathit{J}}_{{\mathit{ď}}_{\mathfrak{r}\left(\mathit{i}-1\right)\mathfrak{s}\left(\mathit{j}\right)}}\ge {\mathit{J}}_{{\mathit{ď}}_{\mathfrak{r}\left(\mathit{i}\right)\mathfrak{s}\left(\mathit{j}\right)}}$ and ${\mathit{J}}_{{\mathit{ď}}_{\mathfrak{r}\left(\mathit{i}\right)\mathfrak{s}\left(\mathit{j}-1\right)}}\ge {\mathit{J}}_{{\mathit{ď}}_{\mathfrak{r}\left(\mathit{i}\right)\mathfrak{s}\left(\mathit{j}\right)}}\forall \mathit{i},\mathit{j}.$

Theorem 3.1. Let ${\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}=〈{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}},{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}〉$ be a collection of q-ROFHSNs, then the aggregated value achieved by Eq. 3.1 is expressed as follows:

$\mathrm{q}-\mathrm{R}\mathrm{O}\mathrm{F}\mathrm{H}\mathrm{S}\mathrm{E}\mathrm{O}\mathrm{W}\mathrm{A}\left({\mathit{J}}_{{\mathit{ď}}_{\mathbf{11}}},{\mathit{J}}_{{\mathit{ď}}_{\mathbf{12}}},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}\right)$

$={{\oplus }_{\mathrm{ℇ}}}_{\mathit{j}=\mathrm{1}}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}\left({{\oplus }_{\mathrm{ℇ}}}_{\mathit{i}=\mathrm{1}}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}{\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right)$

$=〈\frac{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}-{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}},\times \frac{\sqrt[\mathit{q}]{2{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({{\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(2-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({{\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}.$(3.2)

Proof. We demonstrate this by mathematical induction.For $\mathit{n}=1,$ we get ${\mathit{\theta }}_{\mathit{i}}$ = 1

$\mathrm{q}-\mathrm{R}\mathrm{O}\mathrm{F}\mathrm{H}\mathrm{S}\mathrm{E}\mathrm{O}\mathrm{W}\mathrm{A}\left({\mathit{J}}_{{\mathit{ď}}_{\mathrm{11}}},{\mathit{J}}_{{\mathit{ď}}_{\mathrm{12}}},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}\right)={{\oplus }_{\mathrm{ℇ}}}_{\mathit{j}=\mathrm{1}}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}{\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathrm{1}\right)\mathit{s}\left(\mathit{j}\right)}}$

$=〈\begin{array}{c}\frac{\sqrt[q]{{\displaystyle \prod }_{j=1}^m{\left(1+f_{{ď}_{r\left(1\right)s\left(j\right)}}^q\right)}^{{\omega }_j}-{\displaystyle \prod }_{j=1}^m{\left(1-f_{{ď}_{r\left(1\right)s\left(j\right)}}^q\right)}^{{\omega }_j}}}{\sqrt[q]{{\displaystyle \prod }_{j=1}^m{\left(1+f_{{ď}_{r\left(1\right)s\left(j\right)}}^q\right)}^{{\omega }_j}+{\displaystyle \prod }_{j=1}^m{\left(1-f_{{ď}_{r\left(1\right)s\left(j\right)}}^q\right)}^{{\omega }_j}}},\\ \times \frac{\sqrt[q]{2{\displaystyle \prod }_{j=1}^m{\left(g_{{ď}_{r\left(1\right)s\left(j\right)}}^q\right)}^{{\omega }_j}}}{\sqrt[q]{{\displaystyle \prod }_{j=1}^m{\left(2-g_{{ď}_{r\left(1\right)s\left(j\right)}}^q\right)}^{{\omega }_j}+{\displaystyle \prod }_{j=1}^m{\left(g_{{ď}_{r\left(1\right)s\left(j\right)}}^q\right)}^{{\omega }_j}}}\end{array}〉$

$=〈\begin{array}{c}\frac{\sqrt[q]{{\displaystyle \prod }_{j=1}^m{\left({\displaystyle \prod }_{i=1}^1{\left(1+f_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}-{\displaystyle \prod }_{j=1}^m{\left({\displaystyle \prod }_{i=1}^1{\left(1-f_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}}}{\sqrt[q]{{\displaystyle \prod }_{j=1}^m{\left({\displaystyle \prod }_{i=1}^1{\left(1+f_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}+{\displaystyle \prod }_{j=1}^m{\left({\displaystyle \prod }_{i=1}^1{\left(1-f_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}}},\\ \times \frac{\sqrt[q]{2{\displaystyle \prod }_{j=1}^m{\left({{\displaystyle \prod }_{i=1}^1\left(g_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}}}{\sqrt[q]{{\displaystyle \prod }_{j=1}^m{\left({\displaystyle \prod }_{i=1}^1{\left(2-g_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}+{\displaystyle \prod }_{j=1}^m{\left({{\displaystyle \prod }_{i=1}^1\left(g_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}}}\end{array}〉.$

For $\mathit{m}=1$, we get ${\mathit{\omega }}_{\mathit{j}}$ = 1.q-ROFHSEOWA $\left({\mathit{J}}_{{\mathit{ď}}_{11}},{\mathit{J}}_{{\mathit{ď}}_{12}},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}\right)={{\oplus }_{\mathrm{ℇ}}}_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}{\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(1\right)}}$

$=〈\frac{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(1\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}-{\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(1\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}}}{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(1\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}+{\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(1\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}}},\times \frac{\sqrt[\mathit{q}]{2{\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(1\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}}}{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(2-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(1\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}+{\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(1\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}}}$

$=〈\begin{array}{c}\frac{\sqrt[q]{{\displaystyle \prod }_{j=1}^1{\left({\displaystyle \prod }_{i=1}^n{\left(1+f_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}-{\displaystyle \prod }_{j=1}^1{\left({\displaystyle \prod }_{i=1}^n{\left(1-f_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}}}{\sqrt[q]{{\displaystyle \prod }_{j=1}^1{\left({\displaystyle \prod }_{i=1}^n{\left(1+f_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}+{\displaystyle \prod }_{j=1}^1{\left({\displaystyle \prod }_{i=1}^n{\left(1-f_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}}},\\ \times \frac{\sqrt[q]{2{\displaystyle \prod }_{j=1}^1{\left({{\displaystyle \prod }_{i=1}^n\left(g_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}}}{\sqrt[q]{{\displaystyle \prod }_{j=1}^1{\left({\displaystyle \prod }_{i=1}^n{\left(2-g_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}+{\displaystyle \prod }_{j=1}^1{\left({{\displaystyle \prod }_{i=1}^n\left(g_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}}}\end{array}〉.$

So, Eq. 3.2 is true for $\mathit{n}=1$ and $\mathit{m}=1$.Assume that Eq. 3.2 holds for $\mathit{n}={\mathit{n}}_1\mathit{a}\mathit{n}\mathit{d}\mathit{m}={\mathit{m}}_1.$

${{\oplus }_{\mathrm{ℇ}}}_{\mathit{j}=\mathbf{1}}^{{\mathit{m}}_{\mathbf{1}}}{\mathit{\omega }}_{\mathit{j}}\left({{\oplus }_{\mathrm{ℇ}}}_{\mathit{i}=\mathbf{1}}^{{\mathit{n}}_{\mathbf{1}}}{\mathit{\theta }}_{\mathit{i}}{\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right)$

$=〈\begin{array}{c}\frac{\sqrt[q]{{\displaystyle \prod }_{j=1}^{m_1}{\left({\displaystyle \prod }_{i=1}^{n_1}{\left(1+f_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}-{\displaystyle \prod }_{j=1}^{m_1}{\left({\displaystyle \prod }_{i=1}^{n_1}{\left(1-f_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}}}{\sqrt[q]{{\displaystyle \prod }_{j=1}^{m_1}{\left({\displaystyle \prod }_{i=1}^{n_1}{\left(1+f_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}+{\displaystyle \prod }_{j=1}^{m_1}{\left({\displaystyle \prod }_{i=1}^{n_1}{{\left(1-f_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}}^{{\theta }_i}\right)}^{{\omega }_j}}},\\ \times \frac{\sqrt[q]{2{\displaystyle \prod }_{j=1}^{m_1}{\left({{\displaystyle \prod }_{i=1}^{n_1}\left(g_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}}}{\sqrt[q]{{\displaystyle \prod }_{j=1}^{m_1}{\left({\displaystyle \prod }_{i=1}^{n_1}{\left(2-g_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}+{\displaystyle \prod }_{j=1}^{m_1}{\left({{\displaystyle \prod }_{i=1}^{n_1}\left(g_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}}}\end{array}〉.$

For $\mathit{n}={\mathit{n}}_1+1$ and $\mathit{m}={\mathit{m}}_1+1$,

${{\oplus }_{\mathrm{ℇ}}}_{\mathit{j}=\mathrm{1}}^{{\mathit{m}}_{\mathrm{1}}+\mathrm{1}}{\mathit{\omega }}_{\mathit{j}}\left({{\oplus }_{\mathrm{ℇ}}}_{\mathit{i}=\mathrm{1}}^{{\mathit{n}}_{\mathrm{1}}+\mathrm{1}}{\mathit{\theta }}_{\mathit{i}}{\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right)$

$={{\oplus }_{\mathrm{ℇ}}}_{\mathit{j}=\mathrm{1}}^{{\mathit{m}}_{\mathrm{1}}+\mathrm{1}}{\mathit{\omega }}_{\mathit{j}}\left({{\oplus }_{\mathrm{ℇ}}}_{\mathit{i}=\mathrm{1}}^{{\mathit{n}}_{\mathrm{1}}}{\mathit{\theta }}_{\mathit{i}}{\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}{\oplus }_{\mathrm{ℇ}}{\mathit{\theta }}_{\mathit{i}+\mathrm{1}}{\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left({\mathit{n}}_{\mathrm{1}}+\mathrm{1}\right)\mathit{s}\left(\mathit{j}\right)}}\right)$

$=\left({{\oplus }_{\mathrm{ℇ}}}_{\mathit{j}=\mathrm{1}}^{{\mathit{m}}_{\mathrm{1}}+\mathrm{1}}{{\oplus }_{\mathrm{ℇ}}}_{\mathit{i}=\mathrm{1}}^{{\mathit{n}}_{\mathrm{1}}}{\mathit{\theta }}_{\mathit{i}}{\mathit{\omega }}_{\mathit{j}}{\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right)\left({{\oplus }_{\mathrm{ℇ}}}_{\mathit{j}=\mathrm{1}}^{{\mathit{m}}_{\mathrm{1}}+\mathrm{1}}{\mathit{\omega }}_{\mathit{j}}{\mathit{\theta }}_{\mathit{i}+\mathrm{1}}{\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left({\mathit{n}}_{\mathrm{1}}+\mathrm{1}\right)\mathit{s}\left(\mathit{j}\right)}}\right)$

$=〈\begin{array}{c}\frac{\sqrt[q]{{\displaystyle \prod }_{j=1}^{m_1+1}{\left({\displaystyle \prod }_{i=1}^{n_1}{\left(1+f_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}-{\displaystyle \prod }_{j=1}^{m_1+1}{\left({\displaystyle \prod }_{i=1}^{n_1}{\left(1-f_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}}}{\sqrt[q]{{\displaystyle \prod }_{j=1}^{m_1+1}{\left({\displaystyle \prod }_{i=1}^{n_1}{\left(1+f_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}-{\displaystyle \prod }_{j=1}^{m_1+1}{\left({\displaystyle \prod }_{i=1}^{n_1}{\left(1-f_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}}}\\ {\oplus }_{\mathrm{ℇ}}\frac{\sqrt[q]{{\displaystyle \prod }_{j=1}^{m_1+1}{\left({\left(1+f_{{ď}_{r\left(n_1+1\right)s\left(j\right)}}^q\right)}^{{\theta }_{n_1+1}}\right)}^{{\omega }_j}-{\displaystyle \prod }_{j=1}^{m_1+1}{\left({\left(1-f_{{ď}_{r\left(n_1+1\right)s\left(j\right)}}^q\right)}^{{\theta }_{n_1+1}}\right)}^{{\omega }_j}}}{\sqrt[q]{{\displaystyle \prod }_{j=1}^{m_1+1}{\left({\left(1+f_{{ď}_{r\left(n_1+1\right)s\left(j\right)}}^q\right)}^{{\theta }_{n_1+1}}\right)}^{{\omega }_j}-{\displaystyle \prod }_{j=1}^{m_1+1}{\left({\left(1-f_{{ď}_{r\left(n_1+1\right)s\left(j\right)}}^q\right)}^{{\theta }_{n_1+1}}\right)}^{{\omega }_j}}}\\ \times \frac{\sqrt[q]{2{\displaystyle \prod }_{j=1}^{m_1+1}{\left({{\displaystyle \prod }_{i=1}^{n_1+1}\left(2-g_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}}}{\sqrt[q]{{\displaystyle \prod }_{j=1}^{m_1+1}{\left({\displaystyle \prod }_{i=1}^{n_1+1}{\left(2-g_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}+{\displaystyle \prod }_{j=1}^{m_1+1}{\left(\begin{array}{c}{{\displaystyle \prod }_{i=1}^{n_1+1}\left(g_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\end{array}\right)}^{{\omega }_j}}}\\ {\oplus }_{\mathrm{ℇ}}\frac{\sqrt[q]{2{\displaystyle \prod }_{j=1}^{m_1+1}{\left({\left(g_{{ď}_{r\left(n_1+1\right)s\left(j\right)}}^q\right)}^{{\theta }_{\left(n_1+1\right)}}\right)}^{{\omega }_j}}}{\sqrt[q]{{\displaystyle \prod }_{j=1}^{m_1+1}{\left({\left(2-g_{d_{r\left(n_1+1\right)s\left(j\right)}}^q\right)}^{{\theta }_{\left(n_1+2\right)}}\right)}^{{\omega }_j}+{\displaystyle \prod }_{j=1}^{m_1+1}{\left(\begin{array}{c}{\left(g_{d_{r\left(n_1+1\right)s\left(j\right)}}^q\right)}^{{\theta }_{\left(n_1+1\right)}}\end{array}\right)}^{{\omega }_j}}}\end{array}〉$

$=〈\begin{array}{c}\frac{\sqrt[q]{{\displaystyle \prod }_{j=1}^{m_1+1}{\left({\displaystyle \prod }_{i=1}^{n_1+1}{\left(1+f_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}-{\displaystyle \prod }_{j=1}^{m_1+1}{\left({\displaystyle \prod }_{i=1}^{n_1+1}{\left(1-f_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}}}{\sqrt[q]{{\displaystyle \prod }_{j=1}^{m_1+1}{\left({\displaystyle \prod }_{i=1}^{n_1+1}{\left(1+f_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}+{\displaystyle \prod }_{j=1}^{m_1+1}{\left({\displaystyle \prod }_{i=1}^{n_1+1}{\left(1-f_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}}},\\ \times \frac{\sqrt[q]{2{\displaystyle \prod }_{j=1}^{m_1+1}{\left({{\displaystyle \prod }_{i=1}^{n_1+1}\left(g_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}}}{\sqrt[q]{{\displaystyle \prod }_{j=1}^{m_1+1}{\left({\displaystyle \prod }_{i=1}^{n_1+1}{\left(2-g_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}+{\displaystyle \prod }_{j=1}^{m_1+1}{\left(\begin{array}{c}{{\displaystyle \prod }_{i=1}^{n_1+1}\left(g_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\end{array}\right)}^{{\omega }_j}}}\end{array}〉$

$={{\oplus }_{\mathrm{ℇ}}}_{\mathit{j}=\mathrm{1}}^{{\mathit{m}}_{\mathrm{1}}+\mathrm{1}}{\mathit{\omega }}_{\mathit{j}}\left({{\oplus }_{\mathrm{ℇ}}}_{\mathit{i}=\mathrm{1}}^{{\mathit{n}}_{\mathrm{1}}+\mathrm{1}}{\mathit{\theta }}_{\mathit{i}}{\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right).$

So, it holds for $\mathit{m}={\mathit{m}}_1+1$ and $\mathit{n}={\mathit{n}}_1+1$; also, it is true $\forall \mathit{m},\mathit{n}\ge 0$.

Example 3.1. Let $\mathit{R}=\left\{{\mathit{R}}_1,{\mathit{R}}_2,{\mathit{R}}_3\right\}$ be a team of experts with weights ${\mathit{\theta }}_{\mathit{i}}$ = ${\left(0.3,0.4,0.3\right)}^{\mathit{T}}$. A team of experts will decide the most appropriate college for students at the intermediate level. First of all, a group of experts considers the five well-known colleges as follows: $\mathit{A}=\left\{{\mathit{A}}_1=\mathit{P}\mathit{u}\mathit{n}\mathit{j}\mathit{a}\mathit{b}\mathit{C}\mathit{o}\mathit{l}\mathit{l}\mathit{e}\mathit{g}\mathit{e},{\mathit{A}}_2=\mathit{S}\mathit{u}\mathit{p}\mathit{e}\mathit{r}\mathit{i}\mathit{o}\mathit{r}\mathit{C}\mathit{o}\mathit{l}\mathit{l}\mathit{e}\mathit{g}\mathit{e},{\mathit{A}}_3=\mathit{N}\mathit{i}\mathit{s}\mathit{a}\mathit{C}\mathit{o}\mathit{l}\mathit{l}\mathit{e}\mathit{g}\mathit{e},{\mathit{A}}_4=\mathit{A}\mathit{p}\mathit{e}\mathit{x}\mathit{C}\mathit{o}\mathit{l}\mathit{l}\mathit{e}\mathit{g}\mathit{e},{\mathit{a}\mathit{n}\mathit{d}\mathit{A}}_5=\mathit{l}\mathit{e}\mathit{a}\mathit{d}\mathit{e}\mathit{r}\mathit{s}\mathit{h}\mathit{i}\mathit{p}\mathit{C}\mathit{o}\mathit{l}\mathit{l}\mathit{e}\mathit{g}\mathit{e}\right\}$. The team of experts decides the set of parameters for the selection of the most appropriate college, such as ${\mathfrak{L}}^{\prime }$ = $\left\{{\mathit{d}}_1=\mathit{l}\mathit{a}\mathit{w}\mathit{n},{\mathit{d}}_2=\mathit{s}\mathit{e}\mathit{c}\mathit{u}\mathit{r}\mathit{i}\mathit{t}\mathit{y}\mathit{s}\mathit{y}\mathit{s}\mathit{t}\mathit{e}\mathit{m}\right\}$ with their conforming sub-attributes, Lawn = ${\mathit{d}}_1$ = $\left\{{\mathit{d}}_{11}=\mathit{w}\mathit{i}\mathit{t}\mathit{h}\mathit{g}\mathit{r}\mathit{a}\mathit{s}\mathit{s}\mathrm{a}\mathrm{n}\mathrm{d}{\mathit{d}}_{12}=\mathit{w}\mathit{i}\mathit{t}\mathit{h}\mathit{o}\mathit{u}\mathit{t}\mathit{g}\mathit{r}\mathit{a}\mathit{s}\mathit{s}\right\}$, and Security system = ${\mathit{d}}_2$ = $\left\{{\mathit{d}}_{21}=\mathit{g}\mathit{u}\mathit{a}\mathit{r}\mathit{d}\mathit{s}\mathrm{a}\mathrm{n}\mathrm{d}{\mathit{d}}_{22}=\mathit{c}\mathit{a}\mathit{m}\mathit{e}\mathit{r}\mathit{a}\mathit{s}\right\}$. Let ${\mathfrak{L}}^{\prime }$ = ${\mathit{d}}_1$ × ${\mathit{d}}_2$ be a set of multi sub-attributes:

${\mathfrak{L}}^{\prime }{\mathit{d}}_1\times d_2=\left\{{\mathit{d}}_{11},{\mathit{d}}_{12}\right\}\times \left\{{\mathit{d}}_{21},{\mathit{d}}_{22}\right\}=\left\{\begin{array}{c}\left({\mathit{d}}_{11},{\mathit{d}}_{21}\right),\left({\mathit{d}}_{11},{\mathit{d}}_{22}\right),\left({\mathit{d}}_{12},{\mathit{d}}_{21}\right),\left({\mathit{d}}_{12},{\mathit{d}}_{22}\right)\end{array}\right\}.$

${\mathfrak{L}}^{\prime }$ = $\left\{{\mathit{ď}}_1,{\mathit{ď}}_2,{\mathit{ď}}_3,{\mathit{ď}}_4\right\}$, with weights ${\mathit{\omega }}_{\mathit{j}}={\left(0.2,0.3,0.4,0.1\right)}^{\mathit{T}}$. The assumed rating values for each attribute in the form of q-ROFHSNs $\left({\mathit{J}}_{3\times 4},\mathit{A}\right)$ = ${\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}},{\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right)}_{3\times 4}$ are given as follows:

$\left({\mathit{J}}_{3\times 4},\mathit{A}\right)=\left[\begin{array}{cccc}\left(0.5,0.3\right)& \left(0.8,0.7\right)& \left(0.6,0.3\right)& \left(0.2,0.9\right)\\ \left(0.6,0.3\right)& \left(0.4,0.7\right)& \left(0.4,0.5\right)& \left(0.5,0.6\right)\\ \left(0.3,0.4\right)& \left(0.6,0.8\right)& \left(0.3,0.9\right)& \left(0.2,0.7\right)\end{array}\right].$

The associated ordered position matrix using Eq. 2.5 is given as follows:

$\left({\mathit{J}}_{3\times 4},\mathit{A}\right)=\left[\begin{array}{cccc}\left(0.6,0.3\right)& \left(0.8,0.7\right)& \left(0.5,0.3\right)& \left(0.2,0.9\right)\\ \left(0.6,0.3\right)& \left(0.4,0.5\right)& \left(0.5,0.6\right)& \left(0.4,0.7\right)\\ \left(0.3,0.4\right)& \left(0.6,0.8\right)& \left(0.2,0.7\right)& \left(0.3,0.9\right)\end{array}\right].$

As we know,

$\mathrm{q}-\mathrm{R}\mathrm{O}\mathrm{F}\mathrm{H}\mathrm{S}\mathrm{E}\mathrm{O}\mathrm{W}\mathrm{A}\left(J_{{ď}_{11}},J_{{ď}_{12}},\dots ,J_{{ď}_{nm}}\right)$

$〈\begin{array}{c}=\frac{\sqrt[q]{{\displaystyle \prod }_{j=1}^m{\left({\displaystyle \prod }_{i=1}^n{\left(1+f_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}-{\displaystyle \prod }_{j=1}^m{\left({\displaystyle \prod }_{i=1}^n{\left(1-f_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}}}{\sqrt[q]{{\displaystyle \prod }_{j=1}^m{\left({\displaystyle \prod }_{i=1}^n{\left(1+f_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}+{\displaystyle \prod }_{j=1}^m{\left({\displaystyle \prod }_{i=1}^n{\left(1-f_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}}},\\ \times \frac{\sqrt[q]{2{\displaystyle \prod }_{j=1}^m{\left({{\displaystyle \prod }_{i=1}^n\left(g_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}}}{\sqrt[q]{{\displaystyle \prod }_{j=1}^m{\left({\displaystyle \prod }_{i=1}^n{\left(2-g_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}+{\displaystyle \prod }_{j=1}^m{\left({{\displaystyle \prod }_{i=1}^n\left(g_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}}}.\end{array}$

For $\mathit{q}=3,$

$〈\begin{array}{c}=\frac{\sqrt[3]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^3\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}-{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^3\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[3]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^3\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^3\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}},\\ \frac{\sqrt[3]{2{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({{\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}\left({\mathit{g}}_{{\mathit{d}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^3\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[3]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(2-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^3\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({{\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^3\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}\end{array}〉$

$〈\begin{array}{c}=\frac{\sqrt[3]{\begin{array}{c}\left[\begin{array}{c}{\left\{\left(1.0604\right)\left(1.0604\right)\left(1.0080\right)\right\}}^{0.2}{\left\{\left(1.1320\right)\left(1.0251\right)\left(1.0604\right)\right\}}^{0.3}\\ {\left\{\left(1.0359\right)\left(1.0482\right)\left(1.0024\right)\right\}}^{0.4}{\left\{\left(1.0024\right)\left(1.0251\right)\left(1.0080\right)\right\}}^{0.1}\end{array}\right]\\ -\\ \left[\begin{array}{c}{\left\{\left(0.9296\right)\left(0.9072\right)\left(0.9918\right)\right\}}^{0.2}{\left\{\left(0.8064\right)\left(0.9739\right)\left(0.9296\right)\right\}}^{0.3}\\ {\left\{\left(0.9607\right)\left(0.9479\right)\left(0.9975\right)\right\}}^{0.4}{\left\{\left(0.9975\right)\left(0.9739\right)\left(0.9918\right)\right\}}^{0.1}\end{array}\right]\end{array}}}{\sqrt[3]{\begin{array}{c}\left[\begin{array}{c}{\left\{\left(1.0604\right)\left(1.0604\right)\left(1.0080\right)\right\}}^{0.2}{\left\{\left(1.1320\right)\left(1.0251\right)\left(1.0604\right)\right\}}^{0.3}\\ {\left\{\left(1.0359\right)\left(1.0482\right)\left(1.0024\right)\right\}}^{0.4}{\left\{\left(1.0024\right)\left(1.0251\right)\left(1.0080\right)\right\}}^{0.1}\end{array}\right]\\ +\\ \left[\begin{array}{c}{\left\{\left(0.9296\right)\left(0.9072\right)\left(0.9918\right)\right\}}^{0.2}{\left\{\left(0.8064\right)\left(0.9739\right)\left(0.9296\right)\right\}}^{0.3}\\ {\left\{\left(0.9607\right)\left(0.9479\right)\left(0.9975\right)\right\}}^{0.4}{\left\{\left(0.9975\right)\left(0.9739\right)\left(0.9918\right)\right\}}^{0.1}\end{array}\right]\end{array}}},\\ \frac{\sqrt[3]{2\left[\begin{array}{c}{\left\{\left(0.3384\right)\left(0.2358\right)\left(0.4384\right)\right\}}^{0.2}{\left\{\left(0.7254\right)\left(0.4353\right)\left(0.8181\right)\right\}}^{0.3}\\ {\left\{\left(0.3384\right)\left(0.5417\right)\left(0.7254\right)\right\}}^{0.4}{\left\{\left(0.9095\right)\left(0.6518\right)\left(0.9095\right)\right\}}^{0.1}\end{array}\right]}}{\begin{array}{c}\sqrt[3]{\begin{array}{c}\left[\begin{array}{c}{\left\{\left(1.2261\right)\left(1.3124\right)\left(1.2261\right)\right\}}^{0.2}{\left\{\left(1.1636\right)\left(1.2859\right)\left(1.1266\right)\right\}}^{0.3}\\ {\left\{\left(1.2261\right)\left(1.2605\right)\left(1.1636\right)\right\}}^{0.4}{\left\{\left(1.0746\right)\left(1.2239\right)\left(1.0746\right)\right\}}^{0.1}\end{array}\right]\\ +\\ \left[\begin{array}{c}{\left\{\left(0.3384\right)\left(0.2358\right)\left(0.4384\right)\right\}}^{0.2}{\left\{\left(0.7254\right)\left(0.4353\right)\left(0.8181\right)\right\}}^{0.3}\\ {\left\{\left(0.3384\right)\left(0.5417\right)\left(0.7254\right)\right\}}^{0.4}{\left\{\left(0.9095\right)\left(0.6518\right)\left(0.9095\right)\right\}}^{0.1}\end{array}\right]\end{array}}\end{array}}\end{array}〉$

$〈\begin{array}{c}\begin{array}{c}=\frac{\sqrt[3]{\begin{array}{c}\left[\left(1.0254\right)\left(1.0642\right)\left(1.0345\right)\left(1.0035\right)\right]\\ -\\ \left[\left(0.9649\right)\left(0.9099\right)\left(0.9623\right)\left(0.9963\right)\right]\end{array}}}{\sqrt[3]{\begin{array}{c}\left[\left(1.0254\right)\left(1.0642\right)\left(1.0345\right)\left(1.0035\right)\right]\\ +\\ \left[\left(0.9649\right)\left(0.9099\right)\left(0.9623\right)\left(0.9963\right)\right]\end{array}}},\\ \frac{\sqrt[3]{2\left[\left(0.5114\right)\left(0.6662\right)\left(0.4462\right)\left(0.9401\right)\right]}}{\begin{array}{c}\sqrt[3]{\begin{array}{c}\left[\left(1.1456\right)\left(1.1696\right)\left(1.2646\right)\left(1.0352\right)\right]\\ +\\ \left[\left(0.5114\right)\left(0.6662\right)\left(0.4462\right)\left(0.9401\right)\right]\end{array}}\end{array}}\end{array}\end{array}〉$

$=〈\begin{array}{c}\mathrm{0.5861,0.6859}\end{array}〉.$

3.1 Properties of the q-rung orthopair fuzzy hypersoft Einstein-ordered weighted average operator

3.1.1 Idempotency

Let ${\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}={\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}=〈{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}},{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}〉$ $\forall \mathit{i},\mathit{j}$. Then q-ROFHSEOWA $\left({\mathit{J}}_{{\mathit{ď}}_{11}},{\mathit{J}}_{{\mathit{ď}}_{12}},...,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}\right)={\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}$.

Proof. As

$\mathrm{q}-\mathrm{R}\mathrm{O}\mathrm{F}\mathrm{H}\mathrm{S}\mathrm{E}\mathrm{O}\mathrm{W}\mathrm{A}\left({\mathit{J}}_{{\mathit{ď}}_{11}},{\mathit{J}}_{{\mathit{ď}}_{12}},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}\right)=〈\begin{array}{c}\frac{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}-{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}},\\ \times \frac{\sqrt[\mathit{q}]{2{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({{\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(2-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({{\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}\end{array}〉$

$=〈\begin{array}{c}\frac{\sqrt[\mathit{q}]{{\left({\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}-{\left({\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[\mathit{q}]{{\left({\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}+{\left({\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}}},\\ \times \frac{\sqrt[\mathit{q}]{2{\left({\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[\mathit{q}]{\left({\left(2-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)+{\left({\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}}}\end{array}〉$

$=〈\frac{\sqrt[\mathit{q}]{\begin{array}{c}\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)-\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)\end{array}}}{\sqrt[\mathit{q}]{\begin{array}{c}\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)+\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)\end{array}}},\frac{\sqrt[\mathit{q}]{2\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}}{\sqrt[\mathit{q}]{\left(2-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)+\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}}〉$

$=〈{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}},{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}〉$

$={\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}={\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}$

3.1.2 Boundedness

Let ${\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}=〈{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}},{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}〉$ represent the collection of q-ROFHSNs and ${\mathit{J}}_{\mathit{min}}={\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}$, ${\mathit{J}}_{\mathit{max}}={\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}$. Then,

${\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}\le \mathrm{q}-\mathrm{R}\mathrm{O}\mathrm{F}\mathrm{H}\mathrm{S}\mathrm{E}\mathrm{O}\mathrm{W}\mathrm{A}\le \left({\mathit{J}}_{{\mathit{ď}}_{11}},{\mathit{J}}_{{\mathit{ď}}_{12}},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}\right)\le {\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}$

Proof. Let $\mathit{h}\left(\mathit{x}\right)=\sqrt[\mathit{q}]{\frac{1-{\mathit{x}}^{\mathit{q}}}{1+{\mathit{x}}^{\mathit{q}}}}$, $\mathit{x}\in \left[0,1\right]$, then $\frac{\mathit{d}}{\mathit{d}\left(\mathit{y}\right)}\mathit{h}\left(\mathit{x}\right)=-\frac{1}{\mathit{q}}{\left(\frac{1-{\mathit{x}}^{\mathit{q}}}{1+{\mathit{x}}^{\mathit{q}}}\right)}^{\frac{1}{\mathit{q}}-1}\left\{\frac{\mathit{q}{\mathit{x}}^{2\mathit{q}-1}+\mathit{q}{\mathit{x}}^{2\mathit{q}-1}}{{\left(1+{\mathit{x}}^{\mathit{q}}\right)}^2}\right\}<0$. So, $\mathit{h}\left(\mathit{x}\right)$ is a decreasing function on $\left[0,1\right]$. So,${\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}\le {\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\le {\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}$. Hence, $\mathit{h}\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)s\left(\mathit{j}\right)}\mathit{max}}\right)\le \mathit{h}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right)\le \mathit{h}\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}\right)$

$\sqrt[\mathit{q}]{\frac{\mathrm{1}-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}{\mathrm{1}+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}}\le \sqrt[\mathit{q}]{\frac{\mathrm{1}-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}{\mathrm{1}+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}}\le \sqrt[\mathit{q}]{\frac{\mathrm{1}-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}{\mathrm{1}+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}}$

$\Rightarrow \sqrt[\mathit{q}]{{\prod }_{\mathit{j}=\mathrm{1}}^{\mathit{m}}{\left({\prod }_{\mathit{i}=\mathrm{1}}^{\mathit{n}}{\left(\frac{\mathrm{1}-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}{\mathrm{1}+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}$

$\le \sqrt[\mathit{q}]{{\prod }_{\mathit{j}=\mathrm{1}}^{\mathit{m}}{\left({\prod }_{\mathit{i}=\mathrm{1}}^{\mathit{n}}{\left(\frac{\mathrm{1}-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}{\mathrm{1}+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}$

$\le \sqrt[\mathit{q}]{{\prod }_{\mathit{j}=\mathrm{1}}^{\mathit{m}}{\left({\prod }_{\mathit{i}=\mathrm{1}}^{\mathit{n}}{\left(\frac{\mathrm{1}-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}{\mathrm{1}+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}$

$\Rightarrow \sqrt[\mathit{q}]{{\left({\left(\frac{\mathrm{1}-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}{\mathrm{1}+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}\right)}^{{\displaystyle \sum }_{\mathit{i}=\mathrm{1}}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=\mathrm{1}}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}}$

$\le \sqrt[\mathit{q}]{{\prod }_{\mathit{j}=\mathrm{1}}^{\mathit{m}}{\left({\prod }_{\mathit{i}=\mathrm{1}}^{\mathit{n}}{\left(\frac{\mathrm{1}-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}{\mathrm{1}+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}$

$\le \sqrt[\mathit{q}]{{\left({\left(\frac{\mathrm{1}-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}{\mathrm{1}+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}\right)}^{{\displaystyle \sum }_{\mathit{i}=\mathrm{1}}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=\mathrm{1}}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}}$

$\Rightarrow \sqrt[\mathit{q}]{\mathrm{1}+\left(\frac{\mathrm{1}-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}{\mathrm{1}+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}\right)}\le \sqrt[\mathit{q}]{\mathrm{1}+{\prod }_{\mathit{j}=\mathrm{1}}^{\mathit{m}}{\left({\prod }_{\mathit{i}=\mathrm{1}}^{\mathit{n}}{\left(\frac{\mathrm{1}-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}{\mathrm{1}+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}$

$\le \sqrt[\mathit{q}]{\mathrm{1}+\left(\frac{\mathrm{1}-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}{\mathrm{1}+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}\right)}$

$\Rightarrow \sqrt[\mathit{q}]{\frac{\mathrm{2}}{\mathrm{1}+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}}\le \sqrt[\mathit{q}]{\mathrm{1}+{\prod }_{\mathit{j}=\mathrm{1}}^{\mathit{m}}{\left({\prod }_{\mathit{i}=\mathrm{1}}^{\mathit{n}}{\left(\frac{\mathrm{1}-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}{\mathrm{1}+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}$

$\le \sqrt[\mathit{q}]{\frac{\mathrm{2}}{\mathrm{1}+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}}$

$\Rightarrow \sqrt[\mathit{q}]{\frac{\mathrm{1}+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}{\mathrm{2}}}\le \sqrt[\mathit{q}]{\frac{\mathrm{1}}{\mathrm{1}+{\prod }_{\mathit{j}=\mathrm{1}}^{\mathit{m}}{\left({\prod }_{\mathit{i}=\mathrm{1}}^{\mathit{n}}{\left(\frac{\mathrm{1}-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}{\mathrm{1}+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}$

$\le \sqrt[\mathit{q}]{\frac{\mathrm{1}+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}{\mathrm{2}}}$

$\Rightarrow \sqrt[\mathit{q}]{\mathrm{1}+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}\le \sqrt[\mathit{q}]{\frac{\mathrm{2}}{\mathrm{1}+{\prod }_{\mathit{j}=\mathrm{1}}^{\mathit{m}}{\left({\prod }_{\mathit{i}=\mathrm{1}}^{\mathit{n}}{\left(\frac{\mathrm{1}-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}{\mathrm{1}+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}$

$\le \sqrt[\mathit{q}]{\mathrm{1}+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\begin{array}{c}\mathit{max}\end{array}}^{\mathit{q}}}$

$\Rightarrow {\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}\le \sqrt[\mathit{q}]{\frac{\mathrm{2}}{\mathrm{1}+{\prod }_{\mathit{j}=\mathrm{1}}^{\mathit{m}}{\left({\prod }_{\mathit{i}=\mathrm{1}}^{\mathit{n}}{\left(\frac{\mathrm{1}-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}{\mathrm{1}+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}-\mathrm{1}}\le {\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}$

$\Rightarrow {\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}\le \sqrt[\mathit{q}]{\frac{{\prod }_{j=1}^m{\left({\prod }_{i=1}^n{\left(1+f_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}-{\prod }_{j=1}^m{\left({\prod }_{i=1}^n{\left(1-f_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}}{{\prod }_{j=1}^m{\left({\prod }_{i=1}^n{\left(1+f_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}+{\prod }_{j=1}^m{\left({\prod }_{i=1}^n{\left(1-f_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}}}\le {\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}.$(3.3)

Let $\left(\mathit{y}\right)=\sqrt[\mathit{q}]{\frac{2-{\mathit{y}}^{\mathit{q}}}{{\mathit{y}}^{\mathit{q}}}}$, $\mathit{y}\in \left[0,1\right]$, then $\frac{\mathit{d}}{\mathit{d}\mathit{y}}\left(\mathit{k}\left(\mathit{y}\right)\right)=-\frac{1}{\mathit{q}}{\left(\frac{2-{\mathit{y}}^{\mathit{q}}}{{\mathit{y}}^{\mathit{q}}}\right)}^{\frac{1}{\mathit{q}}-1}\left(\frac{2}{{\left({\mathit{y}}^{\mathit{q}}\right)}^2}\right)$. So, $\frac{\mathit{d}}{\mathit{d}\mathit{y}}\left(\mathit{k}\left(\mathit{y}\right)\right)=-\frac{1}{\mathit{q}}{\left(\frac{2-{\mathit{y}}^{\mathit{q}}}{{\mathit{y}}^{\mathit{q}}}\right)}^{\frac{1}{\mathit{q}}-1}\left(\frac{2}{{\left({\mathit{y}}^{\mathit{q}}\right)}^2}\right)<0$, which shows that $\mathit{k}\left(\mathit{y}\right)$ is a decreasing function on $\left[0,1\right]$. So, ${\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\begin{array}{c}\mathit{min}\end{array}}\le {\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}$ ≤ ${\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}$ $\forall \mathit{i},\mathit{j}$. Hence, $\mathit{k}\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\begin{array}{c}\mathit{max}\end{array}}\right)\le \mathit{k}\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right)$ ≤ $\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}\right)$, $\forall$ $\mathit{i},\mathit{j}$.

$\sqrt[\mathit{q}]{\frac{2-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}}\le \sqrt[\mathit{q}]{\frac{2-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}}\le \sqrt[\mathit{q}]{\frac{2-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}}$

We have

$\sqrt[\mathit{q}]{{\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(\frac{2-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}$

$\le \sqrt[\mathit{q}]{{\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(\frac{2-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}$

$\le \sqrt[\mathit{q}]{{\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(\frac{2-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}$

$\Rightarrow \sqrt[\mathit{q}]{{\left({\left(\frac{2-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}\right)}^{{\displaystyle \sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}}$

$\le \sqrt[\mathit{q}]{{\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(\frac{2-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}$

$\le \sqrt[\mathit{q}]{{\left({\left(\frac{2-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}\right)}^{{\displaystyle \sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}}$

$\Rightarrow \sqrt[\mathit{q}]{1+\left(\frac{2-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}\right)}$

$\le \sqrt[\mathit{q}]{1+{\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(\frac{2-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}$

$\le \sqrt[\mathit{q}]{1+\left(\frac{2-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}\right)}$

$\Rightarrow \sqrt[\mathit{q}]{\frac{2}{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}}\le \sqrt[\mathit{q}]{1+{\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(\frac{2-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^3}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}$

$\le \sqrt[\mathit{q}]{\frac{2}{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}}$

$\Rightarrow \sqrt[\mathit{q}]{\frac{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}{2}}\le \sqrt[\mathit{q}]{\frac{1}{1+{\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(\frac{2-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}$

$\le \sqrt[\mathit{q}]{\frac{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}{2}}$

$\Rightarrow {\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}\le \sqrt[\mathit{q}]{\frac{2}{1+{\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(\frac{2-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}$

$\le {\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}$

$\Rightarrow {\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}$

$\le \sqrt[\mathit{q}]{\frac{2{\prod }_{j=1}^m{\left({\prod }_{i=1}^n{\left(g_{{\mathit{ď}}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}}{{\prod }_{j=1}^m{\left({\prod }_{i=1}^n{\left(2-g_{{ď}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}+{\prod }_{j=1}^m{\left({\prod }_{i=1}^n{\left(g_{{\mathit{ď}}_{r\left(i\right)s\left(j\right)}}^q\right)}^{{\theta }_i}\right)}^{{\omega }_j}}}\le {\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}.$(3.4)

Let q-ROFHSEOWA $\left({\mathit{J}}_{{\mathit{ď}}_{11}},{\mathit{J}}_{{\mathit{ď}}_{12}},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}\right)={\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}$. Then the inequalities (3.3) and (3.4) can be written as ${\mathit{f}}_{\begin{array}{c}{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}\end{array}}$ ≤ ${\mathit{f}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}$ ≤ ${\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}$ and ${\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\begin{array}{c}\mathit{min}\end{array}}$ ≤ ${\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}$ ≤ ${\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}$:

$\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}\right)={\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}-{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}+\left(\frac{{\mathit{e}}^{{\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}-{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}}}{{\mathit{e}}^{{\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}-{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}}+1}-\frac{1}{2}\right){\beth }_{{\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}}^{\mathit{q}}$

$\le {\left(\begin{array}{c}\mathit{max}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{max}\\ \mathit{i}\end{array}\left\{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}-{\left(\begin{array}{c}\mathit{min}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{min}\\ \mathit{i}\end{array}\left\{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}$

$+\left(\frac{{\mathit{e}}^{{\left(\begin{array}{c}\mathit{max}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{max}\\ \mathit{i}\end{array}\left\{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}-{\left(\begin{array}{c}\mathit{min}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{min}\\ \mathit{i}\end{array}\left\{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}}}{{\mathit{e}}^{{\left(\begin{array}{c}\mathit{max}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{max}\\ \mathit{i}\end{array}\left\{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}-{\left(\begin{array}{c}\mathit{min}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{min}\\ \mathit{i}\end{array}\left\{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}}+1}-\frac{1}{2}\right){{\beth }_{{{\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}}^{+}}}^{\mathit{q}}$

$=\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}\right).$

$\Rightarrow \mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}\right)\le \mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}\right)\mathrm{a}\mathrm{n}\mathrm{d}$

$\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_k}\right)={\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}-{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}+\left(\frac{{\mathit{e}}^{{\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}-{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}}}{{\mathit{e}}^{{\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}-{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}}+1}-\frac{1}{2}\right){\beth }_{{\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}}^{\mathit{q}}\ge {\left(\begin{array}{c}\mathit{min}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{min}\\ \mathit{i}\end{array}\left\{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}-{\left(\begin{array}{c}\mathit{max}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{max}\\ \mathit{i}\end{array}\left\{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}$

$+\left(\frac{{\mathit{e}}^{{\left(\begin{array}{c}\mathit{min}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{min}\\ \mathit{i}\end{array}\left\{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}-{\left(\begin{array}{c}\mathit{max}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{max}\\ \mathit{i}\end{array}\left\{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}}}{{\mathit{e}}^{{\left(\begin{array}{c}\mathit{min}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{min}\\ \mathit{i}\end{array}\left\{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}-{\left(\begin{array}{c}\mathit{max}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{max}\\ \mathit{i}\end{array}\left\{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}}+1}-\frac{1}{2}\right){{\beth }_{{{\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}}^{-}}}^{\mathit{q}}$

$=\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}\right).$

$\Rightarrow \mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}\right)\ge \mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}\right).$

From the aforementioned discussion, we have the following consequences.If $\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}\right)<\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}\right)\mathit{a}\mathit{n}\mathit{d}\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}\right)>\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}\right)$, then

$\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}\right)<\mathrm{q}-\mathrm{R}\mathrm{O}\mathrm{F}\mathrm{H}\mathrm{S}\mathrm{E}\mathrm{O}\mathrm{W}\mathrm{A}\left({\mathit{J}}_{{\mathit{ď}}_{11}},{\mathit{J}}_{{\mathit{ď}}_{12}},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}\right)<\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}\right).$

If $\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}\right)=\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\mathit{max}}\right),$ then${\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}-{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}+\left(\frac{{\mathit{e}}^{{\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}-{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}}}{{\mathit{e}}^{{\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}-{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}}+1}-\frac{1}{2}\right){\beth }_{{\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}}^{\mathit{q}}\le {\left(\begin{array}{c}\mathit{max}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{max}\\ \mathit{i}\end{array}\left\{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}-{\left(\begin{array}{c}\mathit{min}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{min}\\ \mathit{i}\end{array}\left\{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}+\left(\frac{{\mathit{e}}^{{\left(\begin{array}{c}\mathit{max}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{max}\\ \mathit{i}\end{array}\left\{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}-{\left(\begin{array}{c}\mathit{min}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{min}\\ \mathit{i}\end{array}\left\{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}}}{{\mathit{e}}^{{\left(\begin{array}{c}\mathit{max}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{max}\\ \mathit{i}\end{array}\left\{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}-{\left(\begin{array}{c}\mathit{min}\\ j\end{array}\begin{array}{c}\mathit{min}\\ \mathit{i}\end{array}\left\{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}}+1}-\frac{1}{2}\right){{\beth }_{{{\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}}^{+}}}^{\mathit{q}}$, using the aforementioned inequalities${\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}=\begin{array}{c}\mathit{max}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{max}\\ \mathit{i}\end{array}\left\{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}$, and ${\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}=\begin{array}{c}\mathit{min}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{min}\\ \mathit{i}\end{array}\left\{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}$.Hence, ${{\beth }_{{\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}}}^{\mathit{q}}={{\beth }_{{{\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}}^{+}}}^{\mathit{q}}$. Then q-ROFHSEOWA $\left({\mathit{J}}_{{\mathit{ď}}_{11}},{\mathit{J}}_{{\mathit{ď}}_{12}},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}\right)$ = ${\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}.}$If $\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}\right)=\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}\right),$ then ${\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}-{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}+\left(\frac{{\mathit{e}}^{{\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}-{\mathit{g}}_{{ď}_{\mathit{k}}}^{\mathit{q}}}}{{\mathit{e}}^{{\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}-{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}}+1}-\frac{1}{2}\right){\beth }_{{\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}}^{\mathit{q}}\le {\left(\begin{array}{c}\mathit{min}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{min}\\ \mathit{i}\end{array}\left\{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}-{\left(\begin{array}{c}\mathit{max}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{max}\\ \mathit{i}\end{array}\left\{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}+\left(\frac{{\mathit{e}}^{{\left(\begin{array}{c}\mathit{min}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{min}\\ \mathit{i}\end{array}\left\{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}-{\left(\begin{array}{c}\mathit{max}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{max}\\ \mathit{i}\end{array}\left\{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}}}{{\mathit{e}}^{{\left(\begin{array}{c}\mathit{min}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{min}\\ \mathit{i}\end{array}\left\{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}-{\left(\begin{array}{c}\mathit{max}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{max}\\ \mathit{i}\end{array}\left\{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}}+1}-\frac{1}{2}\right){{\beth }_{{{\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}}^{-}}}^{\mathit{q}}$, using the aforementioned inequalities${\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}=\begin{array}{c}\mathit{min}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{min}\\ \mathit{i}\end{array}\left\{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}$, and ${\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}=\begin{array}{c}\mathit{max}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{max}\\ \mathit{i}\end{array}\left\{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}$.Hence, ${{\beth }_{{\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}}}^{\mathit{q}}={{\beth }_{{{\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}}^{-}}}^{\mathit{q}}$. Thenq-ROFHSEOWA $\left({\mathit{J}}_{{\mathit{ď}}_{11}},{\mathit{J}}_{{\mathit{ď}}_{12}},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}\right)$ = ${\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}$.So, it is proven that${\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}\le$ q-ROFHSEOWA $\left({\mathit{J}}_{{\mathit{ď}}_{11}},{\mathit{J}}_{{\mathit{ď}}_{12}},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}\right)\le {\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}$.

3.1.3 Homogeneity

Prove that q-ROFHSEOWA $\left({\mathit{J}}_{{\mathit{ď}}_{11}},{\mathit{J}}_{{\mathit{ď}}_{12}},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}\right)=\mathit{\gamma }\mathrm{q}-\mathrm{R}\mathrm{O}\mathrm{F}\mathrm{H}\mathrm{S}\mathrm{E}\mathrm{O}\mathrm{W}\mathrm{A}\left({\mathit{J}}_{{\mathit{ď}}_{11}},{\mathit{J}}_{{\mathit{ď}}_{12}},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}\right)$ for $\mathit{\gamma }>0.$

Proof. Let ${\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}$ be a q-ROFHSN and $>0$. Then:

$\mathit{\gamma }{\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}$

$=\langle \sqrt[\mathit{q}]{\frac{{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{\mathit{\gamma }}-{\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{\mathit{\gamma }}}{{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{\mathit{\gamma }}+{\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{\mathit{\gamma }}}},\sqrt[\mathit{q}]{\frac{2{\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{\mathit{\gamma }}}{{\left(2-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{\mathit{\gamma }}+{\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{\mathit{\gamma }}}}\rangle .$

So, q-ROFHSEOWA $\left({\mathit{J}}_{{\mathit{ď}}_{11}},{\mathit{J}}_{{\mathit{ď}}_{12}},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}\right)$

$=\langle \begin{array}{c}\sqrt[\mathit{q}]{\frac{{\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}-{\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}{{\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}},\\ \sqrt[\mathit{q}]{\frac{{\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(2{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}{{\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(2-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}\end{array}\rangle$

$=〈\begin{array}{c}\sqrt[\mathit{q}]{\frac{{\left({\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}\right)}^{\mathit{\gamma }}-{\left({\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}\right)}^{\mathit{\gamma }}}{{\left({\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}\right)}^{\mathit{\gamma }}+{\left({\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}\right)}^{\mathit{\gamma }}}},\\ \sqrt[\mathit{q}]{\frac{{\left({\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(2{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}\right)}^{\mathit{\gamma }}}{{\left({\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(2-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}\right)}^{\mathit{\gamma }}+{\left({\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(2{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}\right)}^{\mathit{\gamma }}}}\end{array}〉$

$=\mathit{\gamma }\mathrm{q}-\mathrm{R}\mathrm{O}\mathrm{F}\mathrm{H}\mathrm{S}\mathrm{E}\mathrm{O}\mathrm{W}\mathrm{A}\left({\mathit{J}}_{{\mathit{ď}}_{11}},{\mathit{J}}_{{\mathit{ď}}_{12}},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}\right).$

3.1.4 Monotonicity

Let ${\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}=\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}},{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right)$ and ${\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{*}=\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{*},{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{*}\right)$ be the collection of q-ROFHSNs. Then,

$\mathrm{q}-\mathrm{R}\mathrm{O}\mathrm{F}\mathrm{H}\mathrm{S}\mathrm{E}\mathrm{O}\mathrm{W}\mathrm{A}\left({\mathit{J}}_{{\mathit{ď}}_{11}},{\mathit{J}}_{{\mathit{ď}}_{12}},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}\right)\le \mathrm{q}-\mathrm{R}\mathrm{O}\mathrm{F}\mathrm{H}\mathrm{S}\mathrm{E}\mathrm{O}\mathrm{W}\mathrm{A}\left({\mathit{J}}_{{\mathit{ď}}_{11}}^{*},{\mathit{J}}_{{\mathit{ď}}_{12}}^{*},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}^{*}\right)\mathrm{i}\mathrm{f}{\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\le {\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{*}\forall \mathit{i},\mathit{j}$

Proof. Let $\mathit{h}\left(\mathit{x}\right)=\sqrt[\mathit{q}]{\frac{1-{\mathit{x}}^{\mathit{q}}}{1+{\mathit{x}}^{\mathit{q}}}}$, $\mathit{x}\in \left[0,1\right]$, then $\frac{\mathit{d}}{\mathit{d}\left(\mathit{y}\right)}\mathit{h}\left(\mathit{x}\right)=-\frac{1}{\mathit{q}}{\left(\frac{1-{\mathit{x}}^{\mathit{q}}}{1+{\mathit{x}}^{\mathit{q}}}\right)}^{\frac{1}{\mathit{q}}-1}\left\{\frac{\mathit{q}{\mathit{x}}^{2\mathit{q}-1}+\mathit{q}{\mathit{x}}^{2\mathit{q}-1}}{{\left(1+{\mathit{x}}^{\mathit{q}}\right)}^2}\right\}$ < 0, so $\mathit{h}\left(\mathit{x}\right)$ is a decreasing function on $\left[0,1\right]$. If ${\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\le {\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{*}$, then $\mathit{h}\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{*}\right)\le \mathit{h}\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(i\right)\mathit{s}\left(\mathit{j}\right)}}\right)\forall \mathit{i},\mathit{j}$:

$1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{*}\le 1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}$

$\Rightarrow 1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}*}\le 1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}$

$\Rightarrow \left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)-\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)\le \left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}*}\right)-\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}*}\right)$

$\Rightarrow \frac{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)-\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)+\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}\le \frac{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}*}\right)-\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}*}\right)}{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}*}\right)+\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}*}\right)},$

where ${\mathit{\theta }}_{\mathit{i}}>0$, ${\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}=1$, and ${\mathit{\omega }}_{\mathit{j}}>0,$ ${\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}=1$. So,

$\Rightarrow \frac{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)-\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)+\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}\le \frac{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}*}\right)-\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}*}\right)}{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}*}\right)+\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}*}\right)}$

$\Rightarrow \frac{{\left({\left(\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)\right)}^{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}-{\left({\left(\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)\right)}^{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}}{{\left({\left(\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)\right)}^{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}+{\left({\left(\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)\right)}^{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}}$

$\le \frac{{\left({\left(\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}*}\right)\right)}^{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}-{\left({\left(\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}*}\right)\right)}^{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}}{{\left({\left(\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}*}\right)\right)}^{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}+{\left({\left(\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}*}\right)\right)}^{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}}$

$\Rightarrow \frac{{\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}-{\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}{{\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}$

$\le \frac{{\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}*}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}-{\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}*}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}{{\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}*}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}*}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}$

$\Rightarrow \frac{\sqrt[\mathit{q}]{{\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}-{\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[\mathit{q}]{{\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}$

$\le \frac{\sqrt[q]{{\prod }_{j=1}^m{\left({\prod }_{i=1}^n{\left(1+f_{{ď}_{r\left(i\right)s\left(j\right)}}^{q*}\right)}^{{\theta }_i}\right)}^{{\omega }_j}-{\prod }_{j=1}^m{\left({\prod }_{i=1}^n{\left(1-f_{{ď}_{r\left(i\right)s\left(j\right)}}^{q*}\right)}^{{\theta }_i}\right)}^{{\omega }_j}}}{\sqrt[q]{{\prod }_{j=1}^m{\left({\prod }_{i=1}^n{\left(1+f_{{ď}_{r\left(i\right)s\left(j\right)}}^{q*}\right)}^{{\theta }_i}\right)}^{{\omega }_j}+{\prod }_{j=1}^m{\left({\prod }_{i=1}^n{\left(1-f_{{ď}_{r\left(i\right)s\left(j\right)}}^{q*}\right)}^{{\theta }_i}\right)}^{{\omega }_j}}}$

Let $\mathit{k}\left(\mathit{y}\right)=\sqrt[\mathit{q}]{\frac{2-{\mathit{y}}^{\mathit{q}}}{{\mathit{y}}^{\mathit{q}}}}$, $\mathit{y}\in \left[0,1\right]$, then $\frac{\mathit{d}}{\mathit{d}\mathit{y}}\left(\mathit{k}\left(\mathit{y}\right)\right)=-\frac{1}{\mathit{q}}{\left(\frac{2-{\mathit{y}}^{\mathit{q}}}{{\mathit{y}}^{\mathit{q}}}\right)}^{\frac{1}{\mathit{q}}-1}\left(\frac{2}{{\left({\mathit{y}}^{\mathit{q}}\right)}^2}\right)$. So, $\frac{\mathit{d}}{\mathit{d}\mathit{y}}\left(\mathit{k}\left(\mathit{y}\right)\right)=-\frac{1}{\mathit{q}}{\left(\frac{2-{\mathit{y}}^{\mathit{q}}}{{\mathit{y}}^{\mathit{q}}}\right)}^{\frac{1}{\mathit{q}}-1}\left(\frac{2}{{\left({\mathit{y}}^{\mathit{q}}\right)}^2}\right)<0$. So, $\mathit{k}\left(\mathit{y}\right)$ is decreasing on $\left[0,1\right]$. If ${\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{*}\le {\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}$, then $\mathit{k}\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{*}\right)\ge \mathit{k}\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right)\forall \mathit{i},\mathit{j}$. There are two possibilities:

$\left(\mathrm{i}\right):{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{*}\le {\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\Rightarrow {\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}*}\le {\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}},$

where, ${\mathit{\theta }}_{\mathit{i}}>0$, ${\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}=1$, and ${\mathit{\omega }}_{\mathit{j}}>0,$ ${\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}=1$. So,

${\left({\left(\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}*}\right)\right)}^{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}\le {\left({\left(\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)\right)}^{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}$

$\Rightarrow 2{\left({\left(\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}*}\right)\right)}^{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}\le 2{\left({\left(\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)\right)}^{{{\displaystyle \sum }}_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{{\displaystyle \sum }}_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}.$(3.5)

(ii): ${\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{\mathit{q}*}\le {\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{\mathit{q}}$

$\Rightarrow 2-{\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{\mathit{q}}\le 2-{\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{\mathit{q}*}$

$\Rightarrow \left(2-{\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{\mathit{q}}\right)+{\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{\mathit{q}}\le \left(2-{\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{\mathit{q}*}\right)+{\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{\mathit{q}*}$

$\Rightarrow {\left({\left(\left(2-{\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{\mathit{q}*}\right)\right)}^{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}+{\left({\left(\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{\mathit{q}*}\right)\right)}^{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}\ge {\left({\left(\left(2-{\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{\mathit{q}}\right)\right)}^{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}+{\left({\left(\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{\mathit{q}}\right)\right)}^{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}.$(3.6)

From 3.5 and 3.6, we get

$\Rightarrow \frac{2{\left({\left(\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{\mathit{q}\ast }\right)\right)}^{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}}{{\left({\left(\left(2-{\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{\mathit{q}\ast }\right)\right)}^{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}+{\left({\left(\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{\mathit{q}*}\right)\right)}^{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}}$

$\le \frac{2{\left({\left(\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{\mathit{q}}\right)\right)}^{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}}{{\left({\left(\left(2-{\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{\mathit{q}}\right)\right)}^{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}+{\left({\left(\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{\mathit{q}}\right)\right)}^{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}}$

$\Rightarrow \frac{\sqrt[\mathit{q}]{2{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({{\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{\mathit{q}\ast }\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(2-{\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{\mathit{q}\ast }\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({{\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{\mathit{q}\ast }\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}$

$\le \frac{\sqrt[\mathit{q}]{2{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({{\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(2-{\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({{\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}.}}$

So, it proved that

$\mathrm{q}-\mathrm{R}\mathrm{O}\mathrm{F}\mathrm{H}\mathrm{S}\mathrm{E}\mathrm{W}\mathrm{A}\left({\mathit{J}}_{{\mathit{ď}}_{11}},{\mathit{J}}_{{\mathit{ď}}_{12}},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}\right)\le \mathrm{q}-\mathrm{R}\mathrm{O}\mathrm{F}\mathrm{H}\mathrm{S}\mathrm{E}\mathrm{W}\mathrm{A}\left({\mathit{J}}_{{\mathit{ď}}_{11}}^{*},{\mathit{J}}_{{\mathit{ď}}_{12}}^{*},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}^{*}\right)$

4 Einstein-ordered weighted geometric aggregation operator for q-rung orthopair fuzzy hypersoft sets

The following section will introduce the Einstein-ordered weighted geometric operator for q-ROPFHSSs with some important possessions.

Definition 4.1. Let ${\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}=\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}},{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}\right)$ be a collection of q-ROFHSNs. Then the q-ROFHSEOWG operator is defined as follows:

$\mathrm{q}-\mathrm{R}\mathrm{O}\mathrm{F}\mathrm{H}\mathrm{S}\mathrm{E}\mathrm{O}\mathrm{W}\mathrm{G}=\left({\mathit{J}}_{{\mathit{ď}}_{11}},{\mathit{J}}_{{\mathit{ď}}_{12}},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}\right)={{{\displaystyle \otimes }}_{\mathrm{ℇ}}}_{\mathit{j}=1}^{\mathit{m}}{\left(\left({{{\displaystyle \otimes }}_{\mathrm{ℇ}}}_{\mathit{i}=1}^{\mathit{n}}{\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)\right)}^{{\mathit{\omega }}_{\mathit{j}}},$(4.1)

where ${\mathit{\theta }}_{\mathit{i}}$ and ${\mathit{\omega }}_{\mathit{j}}$ are the weight vectors for experts and sub-attributes, respectively, such as ${\mathit{\theta }}_{\mathit{i}}>0$, ${\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}=1$, and ${\mathit{\omega }}_{\mathit{j}}>0,$ ${\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}=1$, and $\mathit{i}=\mathrm{1,2}\dots ..,\mathit{n}$, $\mathit{j}=\mathrm{1,2}\dots ..,\mathit{m}$. $\mathit{r},\mathit{s}$ are the permutations of $\mathit{i}$ and $\mathit{j}$, such as ${\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}-1\right)\mathit{s}\left(\mathit{j}\right)}}\ge {\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}$ and ${\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}-1\right)}}\ge {\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}$ $\forall \mathit{i},\mathit{j}.$

Theorem 4.1. Let ${\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}=\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}},{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right)$ represent the collection of q-ROFHSNs. Then, the aggregated value conquered by Eq. 4.1 is given as follows:

$\mathrm{q}-\mathrm{R}\mathrm{O}\mathrm{F}\mathrm{H}\mathrm{S}\mathrm{E}\mathrm{O}\mathrm{W}\mathrm{G}\left({\mathit{J}}_{{\mathit{ď}}_{11}},{\mathit{J}}_{{\mathit{ď}}_{12}},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}\right)$

$={{\otimes }_{\mathrm{ℇ}}}_{\mathit{j}=1}^{\mathit{m}}{\left({{\otimes }_{\mathrm{ℇ}}}_{\mathit{i}=1}^{\mathit{n}}{\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}$

$〈\begin{array}{c}=\frac{\sqrt[\mathit{q}]{2{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({{\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(2-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(1\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({{\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}},\\ \frac{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}-{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}\end{array}〉$(4.2)

where ${\mathit{\theta }}_{\mathit{i}}$ and ${\mathit{\omega }}_{\mathit{j}}$ represent the weight vectors such that ${\mathit{\theta }}_{\mathit{i}}>0,{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}$ = 1, and ${\mathit{\omega }}_{\mathit{j}}>0,$ ${\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}$ = 1, and $\mathit{r},\mathit{s}$ are permutations of $\mathit{i}$ and $\mathit{j}$ such that ${\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}-1\right)\mathit{s}\left(\mathit{j}\right)}}\ge {\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}$ and ${\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}-1\right)}}\ge {\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}$ $\forall \mathit{i},\mathit{j}.$

Proof. We use mathematical induction to demonstrate the aforementioned result.For $\mathit{n}=1$, we get ${\mathit{\theta }}_{\mathit{i}}=1.$q-ROFHSEOWG $\left({\mathit{J}}_{{\mathit{d}}_{\mathbf{11}}},{\mathit{J}}_{{\mathit{d}}_{\mathbf{12}}},\dots ,{\mathit{J}}_{{\mathit{d}}_{\mathit{n}\mathit{m}}}\right)={{\otimes }_{\mathrm{ℇ}}}_{\mathit{j}=\mathrm{1}}^{\mathit{m}}{\left({\mathit{J}}_{{\mathit{d}}_{\mathit{r}\left(\mathbf{1}\right)\mathit{s}\left(\mathit{j}\right)}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}$

$=〈\frac{\sqrt[\mathit{q}]{2{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(1\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left(2-{\mathit{f}}_{\left.{\mathit{ď}}_{\mathit{r}\left(1\right)\mathit{s}(\mathit{j}}\right)}^{\mathit{q}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(1\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}},$

$\frac{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left(1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(1\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}-{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(1\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left(1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(1\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(1\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}〉$

$〈\begin{array}{c}=\frac{\sqrt[\mathit{q}]{2{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({{\displaystyle \prod }_{\mathit{i}=1}^1\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^1{\left(2-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({{\displaystyle \prod }_{\mathit{i}=1}^1\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}},\\ \frac{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^1{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}-{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^1{\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^1{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^1{\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}\end{array}〉$

For $\mathit{m}=1$, we get ${\mathit{\omega }}_{\mathit{j}}$ = 1.q-ROFHSEOWG $\left({\mathit{J}}_{{\mathit{ď}}_{11}},{\mathit{J}}_{{\mathit{ď}}_{12}},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}\right)={{\otimes }_{\mathrm{ℇ}}}_{\mathit{i}=1}^{\mathit{n}}{\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(1\right)}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}$

$=〈\frac{\sqrt[\mathit{q}]{2{\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(1\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}}}{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(2-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(1\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}+{\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(1\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}}},\frac{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(1\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}-{\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(1\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}}}{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(1\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}+{\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(1\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}}}〉$

$=〈\frac{\sqrt[\mathit{q}]{2{\displaystyle \prod }_{\mathit{j}=1}^1{\left({{\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^1{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(2-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^1{\left({{\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}},\frac{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^1{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}-{\displaystyle \prod }_{\mathit{j}=1}^1{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^1{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^1{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}\rangle .$

Eq. 4.2 is true for $\mathit{n}=1$ and $\mathit{m}=1$.Suppose that the equation holds for $\mathit{n}={\mathit{n}}_1\mathit{a}\mathit{n}\mathit{d}\mathit{m}={\mathit{m}}_1{{\otimes }_{\mathrm{ℇ}}}_{\mathit{j}=1}^{{\mathit{m}}_1}{\left({{\otimes }_{\mathrm{ℇ}}}_{\mathit{i}=1}^{{\mathit{n}}_1}{({\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}=\langle \frac{\sqrt[\mathit{q}]{2{\displaystyle \prod }_{\mathit{j}=1}^{{\mathit{m}}_1}{\left({{\displaystyle \prod }_{\mathit{i}=1}^{{\mathit{n}}_1}\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{{\mathit{m}}_1}{\left({\displaystyle \prod }_{\mathit{i}=1}^{{\mathit{n}}_1}{\left(2-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^{{\mathit{m}}_1}{\left({{\displaystyle \prod }_{\mathit{i}=1}^{{\mathit{n}}_1}\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}},\frac{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{{\mathit{m}}_1}{\left({\displaystyle \prod }_{\mathit{i}=1}^{{\mathit{n}}_1}{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}-{\displaystyle \prod }_{\mathit{j}=1}^{{\mathit{m}}_1}{\left({\displaystyle \prod }_{\mathit{i}=1}^{{\mathit{n}}_1}{\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{{\mathit{m}}_1}{\left({\displaystyle \prod }_{\mathit{i}=1}^{{\mathit{n}}_1}{\left(1+{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^{{\mathit{m}}_1}{\left({\displaystyle \prod }_{\mathit{i}=1}^{{\mathit{n}}_1}{\left(1-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}〉.$ Now, we prove Eq. 4.2 for $\mathit{n}={\mathit{n}}_1+1$ and $\mathit{m}={\mathit{m}}_1+1.$

${{\otimes }_{\mathrm{ℇ}}}_{\mathit{j}=1}^{{\mathit{m}}_1+1}{\left({{\otimes }_{\mathrm{ℇ}}}_{\mathit{i}=1}^{{\mathit{n}}_1+1}{\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}={{\otimes }_{\mathrm{ℇ}}}_{\mathit{j}=1}^{{\mathit{m}}_1+1}{\left({{\otimes }_{\mathrm{ℇ}}}_{\mathit{i}=1}^{{\mathit{n}}_1}{{\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}}^{{\mathit{\theta }}_{\mathit{i}}}{\otimes }_{\mathrm{ℇ}}{{\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left({\mathit{n}}_1+1\right)\mathit{s}\left(\mathit{j}\right)}}}^{{\mathit{\theta }}_{\mathit{i}+1}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}$

$=\left({{\otimes }_{\mathrm{ℇ}}}_{\mathit{j}=1}^{{\mathit{m}}_1+1}{{\otimes }_{\mathrm{ℇ}}}_{\mathit{i}=1}^{{\mathit{n}}_1}{\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right)}^{{\mathit{\theta }}_{\mathit{i}}{\mathit{\omega }}_{\mathit{j}}}\right)\left({{\otimes }_{\mathrm{ℇ}}}_{\mathit{j}=1}^{{\mathit{m}}_1+1}{\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left({\mathit{n}}_1+1\right)\mathit{s}\left(\mathit{j}\right)}}\right)}^{{\mathit{\theta }}_{\mathit{i}+1}{\mathit{\omega }}_{\mathit{j}}}\right)$

$=〈\begin{array}{c}\frac{\sqrt[\mathit{q}]{2{\displaystyle \prod }_{\mathit{j}=1}^{{\mathit{m}}_1+1}{\left({\displaystyle \prod }_{\mathit{i}=1}^{{\mathit{n}}_1}{\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{{\mathit{m}}_1+1}{\left({\displaystyle \prod }_{\mathit{i}=1}^{{\mathit{n}}_1}{\left(2-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^{{\mathit{m}}_1+1}{\left({\displaystyle \prod }_{\mathit{i}=1}^{{\mathit{n}}_1}{\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}\\ {\otimes }_{\mathrm{ℇ}}\frac{\sqrt[\mathit{q}]{2{\displaystyle \prod }_{\mathit{j}=1}^{{\mathit{m}}_1+1}{\left({\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left({\mathit{n}}_1+1\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{{\mathit{n}}_1+1}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{{\mathit{m}}_1+1}{\left({\left(2-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left({\mathit{n}}_1+1\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{{\mathit{n}}_1+1}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^{{\mathit{m}}_1+1}{\left({\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left({\mathit{n}}_1+1\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{{\mathit{n}}_1+1}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}},\\ \frac{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{{\mathit{m}}_1+1}{\left({\displaystyle \prod }_{\mathit{i}=1}^{{\mathit{n}}_1}{\left(1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}-{\displaystyle \prod }_{\mathit{j}=1}^{{\mathit{m}}_1+1}{\left({\displaystyle \prod }_{\mathit{i}=1}^{{\mathit{n}}_1}{\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{{\mathit{m}}_1+1}{\left({\displaystyle \prod }_{\mathit{i}=1}^{{\mathit{n}}_1}{\left(1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^{{\mathit{m}}_1+1}{\left({\displaystyle \prod }_{\mathit{i}=1}^{{\mathit{n}}_1}{\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}\\ {\otimes }_{\mathrm{ℇ}}\frac{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{{\mathit{m}}_1+1}{\left({\left(1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left({\mathit{n}}_1+1\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{{\mathit{n}}_1+1}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}-{\displaystyle \prod }_{\mathit{j}=1}^{{\mathit{m}}_1+1}{\left({\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left({\mathit{n}}_1+1\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{{\mathit{n}}_1+1}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{{\mathit{m}}_1+1}{\left({\left(1+{\mathit{g}}_{{\mathit{ď}}_{\left({\mathit{n}}_1+1\right)\mathit{j}}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{{\mathit{n}}_1+1}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^{{\mathit{m}}_1+1}{\left({\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left({\mathit{n}}_1+1\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{{\mathit{n}}_1+1}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}\end{array}〉$

$=〈\begin{array}{c}\frac{\sqrt[\mathit{q}]{2{\displaystyle \prod }_{\mathit{j}=1}^{{\mathit{m}}_1+1}{\left({\displaystyle \prod }_{\mathit{i}=1}^{{\mathit{n}}_1+1}{\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{{\mathit{m}}_1+1}{\left({\displaystyle \prod }_{\mathit{i}=1}^{{\mathit{n}}_1+1}{\left(2-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^{{\mathit{m}}_1+1}{\left({\displaystyle \prod }_{\mathit{i}=1}^{{\mathit{n}}_1+1}{\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}},\\ \frac{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{{\mathit{m}}_1+1}{\left({\displaystyle \prod }_{\mathit{i}=1}^{{\mathit{n}}_1+1}{\left(1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}-{\displaystyle \prod }_{\mathit{j}=1}^{{\mathit{m}}_1+1}{\left({\displaystyle \prod }_{\mathit{i}=1}^{{\mathit{n}}_1+1}{\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{{\mathit{m}}_1+1}{\left({\displaystyle \prod }_{\mathit{i}=1}^{{\mathit{n}}_1+1}{\left(1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^{{\mathit{m}}_1+1}{\left({\displaystyle \prod }_{\mathit{i}=1}^{{\mathit{n}}_1+1}{\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\mathit{s}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}\end{array}〉$

$={{\otimes }_{\mathrm{ℇ}}}_{\mathit{j}=1}^{{\mathit{m}}_1+1}{\left({{\otimes }_{\mathrm{ℇ}}}_{\mathit{i}=1}^{{\mathit{n}}_1+1}{\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}.$

So, it holds for $\mathit{m}$ = ${\mathit{m}}_1+1$ and $\mathit{n}$ = ${\mathit{n}}_1+1$.

Example 4.1. Let $\mathit{R}=\left\{{\mathit{R}}_1,{\mathit{R}}_2,{\mathit{R}}_3\right\}$ be a team of experts with weights ${\mathit{\theta }}_{\mathit{i}}$ = ${\left(0.3,0.4,0.3\right)}^{\mathit{T}}$. A team of experts will decide the most appropriate college for students at the intermediate level. First of all, a group of experts considers the five well-known colleges as follows: $\mathit{A}=\left\{{\mathit{A}}_1=\mathit{P}\mathit{u}\mathit{n}\mathit{j}\mathit{a}\mathit{b}\mathit{C}\mathit{o}\mathit{l}\mathit{l}\mathit{e}\mathit{g}\mathit{e},{\mathit{A}}_2=\mathit{S}\mathit{u}\mathit{p}\mathit{e}\mathit{r}\mathit{i}\mathit{o}\mathit{r}\mathit{C}\mathit{o}\mathit{l}\mathit{l}\mathit{e}\mathit{g}\mathit{e},{\mathit{A}}_3=\mathit{N}\mathit{i}\mathit{s}\mathit{a}\mathit{C}\mathit{o}\mathit{l}\mathit{l}\mathit{e}\mathit{g}\mathit{e},{\mathit{A}}_4=\mathit{A}\mathit{p}\mathit{e}\mathit{x}\mathit{C}\mathit{o}\mathit{l}\mathit{l}\mathit{e}\mathit{g}\mathit{e},{\mathit{a}\mathit{n}\mathit{d}\mathit{A}}_5=\mathit{l}\mathit{e}\mathit{a}\mathit{d}\mathit{e}\mathit{r}\mathit{s}\mathit{h}\mathit{i}\mathit{p}\mathit{C}\mathit{o}\mathit{l}\mathit{l}\mathit{e}\mathit{g}\mathit{e}\right\}$. The team of experts decides the set of parameters for the selection of the most appropriate college, such as ${\mathfrak{L}}^{\prime }$ = $\left\{{\mathit{d}}_1=\mathit{l}\mathit{a}\mathit{w}\mathit{n}\mathrm{a}\mathrm{n}\mathrm{d}{\mathit{d}}_2=\mathit{s}\mathit{e}\mathit{c}\mathit{u}\mathit{r}\mathit{i}\mathit{t}\mathit{y}\mathit{s}\mathit{y}\mathit{s}\mathit{t}\mathit{e}\mathit{m}\right\}$ with their conforming sub-attributes, Lawn = ${\mathit{d}}_1$ = $\left\{{\mathit{d}}_{11}=\mathit{w}\mathit{i}\mathit{t}\mathit{h}\mathit{g}\mathit{r}\mathit{a}\mathit{s}\mathit{s}\mathrm{a}\mathrm{n}\mathrm{d}{\mathit{d}}_{12}=\mathit{w}\mathit{i}\mathit{t}\mathit{h}\mathit{o}\mathit{u}\mathit{t}\mathit{g}\mathit{r}\mathit{a}\mathit{s}\mathit{s}\right\}$, and Security system = ${\mathit{d}}_2$ = $\left\{{\mathit{d}}_{21}=\mathit{g}\mathit{u}\mathit{a}\mathit{r}\mathit{d}\mathit{s}\mathrm{a}\mathrm{n}\mathrm{d}{\mathit{d}}_{22}=\mathit{c}\mathit{a}\mathit{m}\mathit{e}\mathit{r}\mathit{a}\mathit{s}\right\}$. Let ${\mathfrak{L}}^{\prime }$ = ${\mathit{d}}_1$ × ${\mathit{d}}_2$ be a set of multi sub-attributes:

${\mathfrak{L}}^{\prime }={\mathit{d}}_1\times {\mathit{d}}_2=\left\{{\mathit{d}}_{11},{\mathit{d}}_{12}\right\}\times \left\{{\mathit{d}}_{21},{\mathit{d}}_{22}\right\}=\left\{\begin{array}{c}\left({\mathit{d}}_{11},{\mathit{d}}_{21}\right),\left({\mathit{d}}_{11},{\mathit{d}}_{22}\right),\left({\mathit{d}}_{12},{\mathit{d}}_{21}\right),\left({\mathit{d}}_{12},{\mathit{d}}_{22}\right)\end{array}\right\}.$

$\mathit{Let}{\mathfrak{L}}^{\prime }$ = $\left\{{\mathit{ď}}_1,{\mathit{ď}}_2,{\mathit{ď}}_3,{\mathit{ď}}_4\right\}$ be a collection of multi-sub-attributes with weights ${\mathit{\omega }}_{\mathit{j}}={\left(0.2,0.3,0.4,0.1\right)}^{\mathit{T}}$. Score values in the form of q-ROFHSNs $\left({\mathit{J}}_{3\times 4},\mathit{A}\right)$ = ${\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}},{\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right)}_{3\times 4}$ are given as follows:

$\left({\mathit{J}}_{3\times 4},\mathit{A}\right)=\left[\begin{array}{cccc}\left(0.5,0.3\right)& \left(0.8,0.7\right)& \left(0.6,0.3\right)& \left(0.2,0.9\right)\\ \left(0.6,0.3\right)& \left(0.4,0.7\right)& \left(0.4,0.5\right)& \left(0.5,0.6\right)\\ \left(0.3,0.4\right)& \left(0.6,0.8\right)& \left(0.3,0.9\right)& \left(0.2,0.7\right)\end{array}\right].$

The related ordered position matrix using Eq. 2.5 is as follows:

$\left({\mathit{J}}_{3\times 4},\mathit{A}\right)=\left[\begin{array}{cccc}\left(0.6,0.3\right)& \left(0.8,0.7\right)& \left(0.5,0.3\right)& \left(0.2,0.9\right)\\ \left(0.6,0.3\right)& \left(0.4,0.5\right)& \left(0.5,0.6\right)& \left(0.4,0.7\right)\\ \left(0.3,0.4\right)& \left(0.6,0.8\right)& \left(0.2,0.7\right)& \left(0.3,0.9\right)\end{array}\right].$

As we know,

$\mathrm{q}-\mathrm{R}\mathrm{O}\mathrm{F}\mathrm{H}\mathrm{S}\mathrm{E}\mathrm{O}\mathrm{W}\mathrm{G}\left({\mathit{J}}_{{\mathit{ď}}_{11}},{\mathit{J}}_{{\mathit{ď}}_{12}},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}\right)=〈\frac{\sqrt[\mathit{q}]{2{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({{\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(2-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({{\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}},\frac{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}-{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}\rangle .$

For $\mathit{q}=3$,

$=〈\frac{\sqrt[3]{2{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({{\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^3\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[3]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(2-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^3\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({{\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^3\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}},\frac{\sqrt[3]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^3\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}-{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^3\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[3]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^3\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^3\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}\rangle$

$=〈\begin{array}{c}\frac{\sqrt[3]{2\left[\begin{array}{c}{\left\{\left(0.6314\right)\left(0.5417\right)\left(0.3384\right)\right\}}^{0.2}{\left\{\left(0.8180\right)\left(0.3330\right)\left(0.6314\right)\right\}}^{0.3}\\ {\left\{\left(0.5359\right)\left(0.4353\right)\left(0.2349\right)\right\}}^{0.4}{\left\{\left(0.2349\right)\left(0.3330\right)\left(0.3384\right)\right\}}^{0.1}\end{array}\right]}}{\sqrt[3]{\begin{array}{c}\left[\begin{array}{c}{\left\{\left(1.1896\right)\left(1.2605\right)\left(1.2261\right)\right\}}^{0.2}{\left\{\left(1.1266\right)\left(1.3025\right)\left(1.1896\right)\right\}}^{0.3}\\ {\left\{\left(1.2075\right)\left(1.2421\right)\left(1.2297\right)\right\}}^{0.4}{\left\{\left(1.2297\right)\left(1.3025\right)\left(1.2261\right)\right\}}^{0.1}\end{array}\right]\\ +\\ \left[\begin{array}{c}{\left\{\left(0.6314\right)\left(0.5417\right)\left(0.3384\right)\right\}}^{0.2}{\left\{\left(0.8180\right)\left(0.3330\right)\left(0.6314\right)\right\}}^{0.3}\\ {\left\{\left(0.5359\right)\left(0.4353\right)\left(0.2349\right)\right\}}^{0.4}{\left\{\left(0.2349\right)\left(0.3330\right)\left(0.3384\right)\right\}}^{0.1}\end{array}\right]\end{array}}},\\ \frac{\sqrt[3]{\begin{array}{c}\left[\begin{array}{c}{\left\{\left(1.0080\right)\left(1.0107\right)\left(1.0188\right)\right\}}^{0.2}{\left\{\left(1.0925\right)\left(1.0482\right)\left(1.1320\right)\right\}}^{0.3}\\ {\left\{\left(1.0080\right)\left(1.0814\right)\left(1.0925\right)\right\}}^{0.4}{\left\{\left(1.1785\right)\left(1.1225\right)\left(1.1785\right)\right\}}^{0.1}\end{array}\right]\\ -\\ \left[\begin{array}{c}\left[{\left\{\left(0.9918\right)\left(0.9891\right)\left(0.9904\right)\right\}}^{0.2}\right.{\left\{\left(0.8816\right)\left(0.9479\right)\left(0.8816\right)\right\}}^{0.3}\\ {\left\{\left(0.9918\right)\left(0.9072\right)\left(0.6759\right)\right\}}^{0.4}{\left\{\left(0.6759\right)\left(0.8453\right)\left(0.6759\right)\right\}}^{0.1}\end{array}\right]\end{array}}}{\sqrt[3]{\begin{array}{c}\left[\begin{array}{c}{\left\{\left(1.0080\right)\left(1.0107\right)\left(1.0188\right)\right\}}^{0.2}{\left\{\left(1.0925\right)\left(1.0482\right)\left(1.1320\right)\right\}}^{0.3}\\ {\left\{\left(1.0080\right)\left(1.0814\right)\left(1.0925\right)\right\}}^{0.4}{\left\{\left(1.1785\right)\left(1.1225\right)\left(1.1785\right)\right\}}^{0.1}\end{array}\right]\\ +\\ \left[\begin{array}{c}\left[{\left\{\left(0.9918\right)\left(0.9891\right)\left(0.9904\right)\right\}}^{0.2}\right.{\left\{\left(0.8816\right)\left(0.9479\right)\left(0.8816\right)\right\}}^{0.3}\\ {\left\{\left(0.9918\right)\left(0.9072\right)\left(0.6759\right)\right\}}^{0.4}{\left\{\left(0.6759\right)\left(0.8453\right)\left(0.6759\right)\right\}}^{0.1}\end{array}\right]\end{array}}}\end{array}〉$

$=〈\begin{array}{c}\frac{\sqrt[3]{2\left[\begin{array}{c}\left(0.6496\right)\left(0.5897\right)\left(0.3129\right)\left(0.6955\right)\end{array}\right]}}{\sqrt[3]{\begin{array}{c}\left[\left(1.1295\right)\left(1.1819\right)\left(1.2774\right)\left(1.0698\right)\right]\\ +\\ \left[\begin{array}{c}\left(0.6496\right)\left(0.5897\right)\left(0.3129\right)\left(0.6955\right)\end{array}\right]\end{array}}},\\ \frac{\sqrt[3]{\begin{array}{c}\left[\left(1.0075\right)\left(1.0809\right)\left(1.0724\right)\left(1.0454\right)\right]\\ -\\ \left[\left(0.9942\right)\left(0.9124\right)\left(0.8196\right)\left(0.9092\right)\right]\end{array}}}{\sqrt[3]{\begin{array}{c}\left[\left(1.0075\right)\left(1.0809\right)\left(1.0724\right)\left(1.0454\right)\right]\\ +\\ \left[\left(0.9942\right)\left(0.9124\right)\left(0.8196\right)\left(0.9092\right)\right]\end{array}}}\end{array}〉$

$=〈\begin{array}{c}\mathrm{0.4474,0.6626}\end{array}〉.$

4.1 Properties of the q-rung orthopair fuzzy hypersoft Einstein-ordered weighted geometric operator

4.1.1 Idempotency

Let ${\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}={\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}=〈{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}},{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}〉$ $\forall \mathit{i},\mathit{j}.$ Then q-ROFHSEOWA $\left({\mathit{J}}_{{\mathit{ď}}_{11}},{\mathit{J}}_{{\mathit{ď}}_{12}},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}\right)$ = ${\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}$.

Proof. As we know that

$=〈\frac{\sqrt[\mathit{q}]{2{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({{\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(2-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({{\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}},\frac{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}-{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^q\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}〉$

$=〈\frac{\sqrt[\mathit{q}]{2{\left({\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[\mathit{q}]{\left({\left(2-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)+{\left({\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}}},\frac{\sqrt[\mathit{q}]{{\left({\left(1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}-{\left({\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[\mathit{q}]{{\left({\left(1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}+{\left({\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}}}〉$

$=〈\frac{\sqrt[\mathit{q}]{2\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}}{\sqrt[\mathit{q}]{\left(2-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)+\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}},\frac{\sqrt[\mathit{q}]{\begin{array}{c}\left(1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)-\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)\end{array}}}{\sqrt[\mathit{q}]{\begin{array}{c}\left(1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)+\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)\end{array}}}〉$

$=〈{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}},{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}〉={\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}.$

4.1.2 Boundedness

Let ${\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}=〈{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}},{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}〉$ be a collection of q-ROFHSNs and ${\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}\mathit{min}}={\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}$, ${\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}\mathit{max}}=$ ${\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}$. Then,

${\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}\le \mathrm{q}-\mathrm{R}\mathrm{O}\mathrm{F}\mathrm{H}\mathrm{S}\mathrm{E}\mathrm{O}\mathrm{W}\mathrm{G}\le \left({\mathit{J}}_{{\mathit{ď}}_{11}},{\mathit{J}}_{{\mathit{ď}}_{12}},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}\right)\le {\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}.$

Proof. Let $\mathit{h}\left(\mathit{x}\right)=\sqrt[\mathit{q}]{\frac{2-{\mathit{x}}^{\mathit{q}}}{{\mathit{x}}^{\mathit{q}}}}$, $\mathit{x}\in \left[0,1\right]$, then $\frac{\mathit{d}}{\mathit{d}\mathit{x}}\left(\mathit{h}\left(\mathit{x}\right)\right)=-\frac{1}{\mathit{q}}{\left(\frac{2-{\mathit{x}}^{\mathit{q}}}{{\mathit{x}}^{\mathit{q}}}\right)}^{\frac{1}{\mathit{q}}-1}\left(\frac{2}{{\left({\mathit{x}}^{\mathit{q}}\right)}^2}\right)$. So, $\frac{\mathit{d}}{\mathit{d}\mathit{x}}\left(\mathit{k}\left(\mathit{x}\right)\right)=-\frac{1}{\mathit{q}}{\left(\frac{2-{\mathit{x}}^{\mathit{q}}}{{\mathit{x}}^{\mathit{q}}}\right)}^{\frac{1}{\mathit{q}}-1}\left(\frac{2}{{\left({\mathit{x}}^{\mathit{q}}\right)}^2}\right)<0$. So, $\mathit{h}\left(\mathit{x}\right)$ is a decreasing function on $\left[0,1\right]$. So, ${\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\begin{array}{c}\mathit{min}\end{array}}\le {\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\le {\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}\forall$ $\mathit{i},\mathit{j}$. Hence, $\mathit{h}\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\begin{array}{c}\mathit{max}\end{array}}\right)\le \mathit{h}\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right)\le \mathit{h}\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}\right),\forall \mathit{i},\mathit{j}$. We have

$\iff \sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(\frac{2-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}\le \sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(\frac{2-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}$

$\le \sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(\frac{2-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}$

$\iff \sqrt[\mathit{q}]{{\left({\left(\frac{2-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}\right)}^{{\displaystyle \sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\displaystyle \sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}}$

$\le \sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(\frac{2-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}$

$\le \sqrt[\mathit{q}]{{\left({\left(\frac{2-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}\right)}^{{\displaystyle \sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\displaystyle \sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}}$

$\iff \sqrt[\mathit{q}]{\left(\frac{2-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}\right)}\le \sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(\frac{2-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}$

$\le \sqrt[\mathit{q}]{\left(\frac{2-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}\right)}$

$\iff \sqrt[\mathit{q}]{1+\left(\frac{2-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}\right)}\le \sqrt[\mathit{q}]{1+{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(\frac{2-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}$

$\le \sqrt[\mathit{q}]{1+\left(\frac{2-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}\right)}$

$\iff \sqrt[\mathit{q}]{\frac{2}{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}}\le \sqrt[\mathit{q}]{1+{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(\frac{2-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}$

$\le \sqrt[\mathit{q}]{\frac{2}{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}}$

$\iff \sqrt[\mathit{q}]{\frac{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}{2}}\le \frac{1}{\sqrt[\mathit{q}]{1+{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(\frac{2-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}$

$\le \sqrt[\mathit{q}]{\frac{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}{2}}$

$\iff {\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}\le \frac{2}{\sqrt[\mathit{q}]{1+{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(\frac{2-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}$

$\le {\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}$

${\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}$

$\le \frac{\sqrt[\mathit{q}]{2{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[\mathit{q}]{{\displaystyle \prod }_{j=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(2-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}$

$\le {\mathit{f}}_{{\mathit{d}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}.$(4.3)

Again, $\mathit{k}\left(\mathit{y}\right)=\sqrt[\mathit{q}]{\frac{1-{\mathit{y}}^{\mathit{q}}}{1+{\mathit{y}}^{\mathit{q}}}}$, $\mathit{y}\in \left[0,1\right]$, then $\frac{\mathit{d}}{\mathit{d}\left(\mathit{y}\right)}\mathit{h}\left(\mathit{y}\right)=-\frac{1}{\mathit{q}}{\left(\frac{1-{\mathit{y}}^{\mathit{q}}}{1+{\mathit{y}}^{\mathit{q}}}\right)}^{\frac{1}{\mathit{q}}-1}\left\{\frac{\mathit{q}{\mathit{y}}^{2\mathit{q}-1}+\mathit{q}{\mathit{y}}^{2\mathit{q}-1}}{{\left(1+{\mathit{y}}^{\mathit{q}}\right)}^2}\right\}<0$. So, $\mathit{h}\left(\mathit{y}\right)$ is a decreasing function on $\left[0,1\right]$.Hence,${\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}\le {\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\le {\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}$. Therefore, $\mathit{k}\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}\right)\le$ $\mathit{k}\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right)$ ≤ $\mathit{k}\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}\right)\forall \mathit{i},\mathit{j}$

$\Rightarrow \sqrt[\mathit{q}]{\frac{1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}{1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}}\le \sqrt[\mathit{q}]{\frac{1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}{1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}}\le \sqrt[\mathit{q}]{\frac{1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}{1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}}.$

We have

$\iff \sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(\frac{1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}{1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}$

$\le \sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(\frac{1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}{1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}$

$\le \sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(\frac{1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}{1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}$

$\iff \sqrt[\mathit{q}]{{\left({\left(\frac{1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}{1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}\right)}^{{\displaystyle \sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\displaystyle \sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}}$

$\le \sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(\frac{1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}{1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}$

$\le \sqrt[\mathit{q}]{{\left({\left(\frac{1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}{1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}\right)}^{{\displaystyle \sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\displaystyle \sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}}}$

$\iff \sqrt[\mathit{q}]{\left(\frac{1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}{1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}\right)}\le \sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(\frac{1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}{1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}$

$\le \sqrt[\mathit{q}]{\left(\frac{1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}{1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}\right)}$

$\iff \sqrt[\mathit{q}]{1+\left(\frac{1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}{1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}\right)}\le \sqrt[\mathit{q}]{1+{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(\frac{1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}{1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}$

$\le \sqrt[\mathit{q}]{1+\left(\frac{1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}{1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}\right)}$

$\iff \sqrt[\mathit{q}]{\frac{2}{1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}}\le \sqrt[\mathit{q}]{1+{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(\frac{1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}{1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}$

$\le \sqrt[\mathit{q}]{\frac{2}{1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}}$

$\iff \sqrt[\mathit{q}]{\frac{1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}{2}}\le \frac{1}{\sqrt[\mathit{q}]{1+{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(\frac{1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}{1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}$

$\le \sqrt[\mathit{q}]{\frac{1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}{2}}$

$\iff \sqrt[\mathit{q}]{1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}^{\mathit{q}}}\le \sqrt[\mathit{q}]{\frac{2}{1+{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(\frac{1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}{1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}$

$\le \sqrt[\mathit{q}]{1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}^{\mathit{q}}}$

$\iff {\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}\le \sqrt[\mathit{q}]{\frac{2}{1+{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(\frac{1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}{1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}-1}$

$\le {\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}$

$\iff {\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}$

$\le \frac{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}-{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}{\sqrt[\mathit{q}]{{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\displaystyle \prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\displaystyle \prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}$

$\le {\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}.$(4.4)

Let q-ROFHSEOWG $\left({\mathit{J}}_{{\mathit{ď}}_{11}},{\mathit{J}}_{{\mathit{ď}}_{12}},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}\right)={\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}$, then inequalities (4.3) and (4.4) can be written as ${\mathit{f}}_{{\mathit{d}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}$ ≤ ${\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}$ ≤ ${\mathit{f}}_{{\mathit{d}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}$ and ${\mathit{g}}_{{\mathit{d}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}$ ≤ ${\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}$ ≤ ${\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}$. Thus,

$\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}\right)={\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}-{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}+\left(\frac{{\mathit{e}}^{{\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}-{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}}}{{\mathit{e}}^{{\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}-{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}}+\mathrm{1}}-\frac{\mathrm{1}}{\mathrm{2}}\right){\beth }_{{\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}}^{\mathit{q}}$

$\le {\left(\begin{array}{c}\mathit{max}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{max}\\ \mathit{i}\end{array}\left\{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}-{\left(\begin{array}{c}\mathit{min}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{min}\\ \mathit{i}\end{array}\left\{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}$

$+\left(\frac{{\mathit{e}}^{{\left(\begin{array}{c}\mathit{max}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{max}\\ \mathit{i}\end{array}\left\{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}-{\left(\begin{array}{c}\mathit{min}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{min}\\ \mathit{i}\end{array}\left\{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}}}{{\mathit{e}}^{{\left(\begin{array}{c}\mathit{max}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{max}\\ \mathit{i}\end{array}\left\{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}-{\left(\begin{array}{c}\mathit{min}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{m}i\mathit{n}\\ \mathit{i}\end{array}\left\{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}}+\mathrm{1}}-\frac{\mathrm{1}}{\mathrm{2}}\right){{\beth }_{{{\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}}^{+}}}^{\mathit{q}}$

$=\mathit{S}\left({{\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}}_{\mathit{max}}\right)\mathrm{a}\mathrm{n}\mathrm{d}\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right)$

$={\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}+\left(\frac{{\mathit{e}}^{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}}{{\mathit{e}}^{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}}+\mathrm{1}}-\frac{\mathrm{1}}{\mathrm{2}}\right){\beth }_{{\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}}^{\mathit{q}}$

$\ge {\left(\begin{array}{c}\mathit{min}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{min}\\ \mathit{i}\end{array}\left\{{\mathit{f}}_{{\mathit{d}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}-{\left(\begin{array}{c}\mathit{max}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{max}\\ \mathit{i}\end{array}\left\{{\mathit{g}}_{{\mathit{d}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}$

$+\left(\frac{{\mathit{e}}^{{\left(\begin{array}{c}\mathit{min}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{min}\\ \mathit{i}\end{array}\left\{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}-{\left(\begin{array}{c}\mathit{max}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{max}\\ \mathit{i}\end{array}\left\{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}}}{{\mathit{e}}^{{\left(\begin{array}{c}\mathit{min}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{min}\\ \mathit{i}\end{array}\left\{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}-{\left(\begin{array}{c}\mathit{max}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{max}\\ \mathit{i}\end{array}\left\{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}}+\mathrm{1}}-\frac{\mathrm{1}}{\mathrm{2}}\right){{\beth }_{{{\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}}^{-}}}^{\mathit{q}}$

$=\mathit{S}\left({{\mathit{J}}_{{\mathit{d}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}}_{\mathit{min}}\right).$

$\Rightarrow \mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}\right)\le \mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}\right)\mathrm{a}\mathrm{l}\mathrm{s}\mathrm{o}$

$\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}\right)={\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}-{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}^q+\left(\frac{{\mathit{e}}^{{\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}-{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}}}{{\mathit{e}}^{{\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}-{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}}+1}-\frac{1}{2}\right){\beth }_{{\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}}^{\mathit{q}}\ge {\left(\begin{array}{c}\mathit{min}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{min}\\ \mathit{i}\end{array}\left\{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}-{\left(\begin{array}{c}\mathit{max}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{max}\\ \mathit{i}\end{array}\left\{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}+\left(\frac{{\mathit{e}}^{{\left(\begin{array}{c}\mathit{min}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{min}\\ \mathit{i}\end{array}\left\{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}-{\left(\begin{array}{c}\mathit{max}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{max}\\ \mathit{i}\end{array}\left\{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}}}{{\mathit{e}}^{{\left(\begin{array}{c}\mathit{min}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{min}\\ \mathit{i}\end{array}\left\{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}-{\left(\begin{array}{c}\mathit{max}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{max}\\ \mathit{i}\end{array}\left\{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}}+1}-\frac{1}{2}\right){{\beth }_{{{\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}}^{-}}}^{\mathit{q}}=\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}\right)$

$\Rightarrow \mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}\right)\ge \mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}\right)$

From the aforementioned procedure, we have the following consequences. If $\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}\right)<\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}\right)\mathit{a}\mathit{n}\mathit{d}\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}\right)>\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}\right)$, then

${\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}\mathit{min}}<\mathrm{q}-\mathrm{R}\mathrm{O}\mathrm{F}\mathrm{H}\mathrm{S}\mathrm{E}\mathrm{O}\mathrm{W}\mathrm{G}\left({\mathit{J}}_{{\mathit{ď}}_{11}},{\mathit{J}}_{{\mathit{ď}}_{12}},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}\right)<{\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}.$

If $\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}\right)=\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(j\right)}\mathit{max}}\right),$ then${\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}-{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}+\left(\frac{{\mathit{e}}^{{\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}-{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}}}{{\mathit{e}}^{{\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}-{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}}+1}-\frac{1}{2}\right){\beth }_{{\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}}^{\mathit{q}}\le {\left(\begin{array}{c}\mathit{max}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{max}\\ \mathit{i}\end{array}\left\{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}-{\left(\begin{array}{c}\mathit{min}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{min}\\ \mathit{i}\end{array}\left\{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}+\left(\frac{{\mathit{e}}^{{\left(\begin{array}{c}\mathit{max}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{max}\\ \mathit{i}\end{array}\left\{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}-{\left(\begin{array}{c}\mathit{min}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{min}\\ \mathit{i}\end{array}\left\{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}}}{{\mathit{e}}^{{\left(\begin{array}{c}\mathit{max}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{max}\\ \mathit{i}\end{array}\left\{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}-{\left(\begin{array}{c}\mathit{min}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{min}\\ \mathit{i}\end{array}\left\{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}}+1}-\frac{1}{2}\right){{\beth }_{{{\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}}^{+}}}^{\mathit{q}}$, using the aforementioned inequalities${\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}=\begin{array}{c}\mathit{max}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{max}\\ \mathit{i}\end{array}\left\{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}$, and ${\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}=\begin{array}{c}\mathit{min}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{min}\\ \mathit{i}\end{array}\left\{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}$. Hence, ${{\beth }_{{\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}}}^{\mathit{q}}={{\beth }_{{{\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}}^{+}}}^{\mathit{q}}$. Then q-ROFHSEOWG $\left({\mathit{J}}_{{\mathit{ď}}_{11}},{\mathit{J}}_{{\mathit{ď}}_{12}},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}\right)={\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}\mathit{max}}$.If $\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}\right)=\mathit{S}\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}\right),$ then ${\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}-{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}+\left(\frac{{\mathit{e}}^{{\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}-g_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}}}{{\mathit{e}}^{{\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}-{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}^{\mathit{q}}}+1}-\frac{1}{2}\right){\beth }_{{\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}}^{\mathit{q}}\le {\left(\begin{array}{c}\mathit{min}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{min}\\ \mathit{i}\end{array}\left\{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}-{\left(\begin{array}{c}\mathit{max}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{max}\\ \mathit{i}\end{array}\left\{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}+\left(\frac{{\mathit{e}}^{{\left(\begin{array}{c}\mathit{min}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{min}\\ \mathit{i}\end{array}\left\{{\mathit{f}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right\}\right)}^{\mathit{q}}-{\left(\begin{array}{c}\mathit{max}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{max}\\ \mathit{i}\end{array}\left\{{\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right\}\right)}^{\mathit{q}}}}{{\mathit{e}}^{{\left(\begin{array}{c}\mathit{min}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{min}\\ \mathit{i}\end{array}\left\{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}-{\left(\begin{array}{c}\mathit{max}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{max}\\ \mathit{i}\end{array}\left\{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}\right)}^{\mathit{q}}}+1}-\frac{1}{2}\right){{\beth }_{{{\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}}^{-}}}^{\mathit{q}}$, using the aforementioned inequalities,

${\mathit{f}}_{{\mathit{ď}}_{\mathit{k}}}=\begin{array}{c}\mathit{min}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{min}\\ \mathit{i}\end{array}\left\{{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\},\mathrm{a}\mathrm{n}\mathrm{d}{\mathit{g}}_{{\mathit{ď}}_{\mathit{k}}}=\begin{array}{c}\mathit{max}\\ \mathit{j}\end{array}\begin{array}{c}\mathit{max}\\ \mathit{i}\end{array}\left\{{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}\right\}.\mathrm{H}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{e},{{\beth }_{{\mathit{J}}_{{\mathit{ď}}_{\mathit{k}}}}}^{\mathit{q}}={{\beth }_{{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{-}}}^{\mathit{q}}.\mathrm{T}\mathrm{h}\mathrm{e}\mathrm{n}$

q-ROFHSEOWG $\left({\mathit{J}}_{{\mathit{ď}}_{11}},{\mathit{J}}_{{\mathit{ď}}_{12}},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}\right)={\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}$.So, it is proven that${\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{min}}\le$ q-ROFHSEOWG $\left({\mathit{J}}_{{\mathit{ď}}_{11}},{\mathit{J}}_{{\mathit{ď}}_{12}},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}\right)\le {\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}\mathit{max}}$.

4.1.3 Homogeneity

Prove that q-ROFHSEOWG $\left({\mathit{J}}_{{\mathit{d}}_{11},}{\mathit{J}}_{{\mathit{d}}_{12.}},\dots .,{\mathit{J}}_{{\mathit{d}}_{\mathit{n}\mathit{m}.}}\right)=\mathit{\gamma }\mathrm{q}-\mathrm{R}\mathrm{O}\mathrm{F}\mathrm{H}\mathrm{S}\mathrm{E}\mathrm{O}\mathrm{W}\mathrm{G}\left({\mathit{J}}_{{\mathit{d}}_{11},}{\mathit{J}}_{{\mathit{d}}_{12.}},\dots .,{\mathit{J}}_{{\mathit{d}}_{\mathit{n}\mathit{m}.}}\right)$ for any $\mathit{\gamma }>0.$

Proof. Let ${\mathit{J}}_{{\mathit{d}}_{\mathit{i}\mathit{j}}}$ be a q-ROFHSN and $>0$. Then we know that

$\mathit{\gamma }{\mathit{J}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}$

$=〈\sqrt[\mathit{q}]{\frac{2{\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{\mathit{\gamma }}}{{\left(2-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{\mathit{\gamma }}+{\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{\mathit{\gamma }}}},\sqrt[\mathit{q}]{\frac{{\left(1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{\mathit{\gamma }}-{\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{\mathit{\gamma }}}{{\left(1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{\mathit{\gamma }}+{\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{\mathit{\gamma }}}}〉.$

So, q-ROFHSEOWG $\left({\mathit{J}}_{{\mathit{d}}_{11},}{\mathit{J}}_{{\mathit{d}}_{12.}},\dots .,{\mathit{J}}_{{\mathit{d}}_{\mathit{n}\mathit{m}.}}\right)$

$=〈\sqrt[\mathit{q}]{\frac{{\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(2{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}{{\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(2-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}},\sqrt[\mathit{q}]{\frac{{\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}-{\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}{{\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}+{\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}}}\rangle 〉$

$=〈\sqrt[\mathit{q}]{\frac{{\left({\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(2{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}\right)}^{\mathit{\gamma }}}{{\left({\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(2-{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}\right)}^{\mathit{\gamma }}+{\left({\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(2{\mathit{f}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}\right)}^{\mathit{\gamma }}}},\sqrt[\mathit{q}]{\frac{{\left({\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}\right)}^{\mathit{\gamma }}-{\left({\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}\right)}^{\mathit{\gamma }}}{{\left({\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1+{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}\right)}^{\mathit{\gamma }}+{\left({\prod }_{\mathit{j}=1}^{\mathit{m}}{\left({\prod }_{\mathit{i}=1}^{\mathit{n}}{\left(1-{\mathit{g}}_{{\mathit{ď}}_{\mathit{r}\left(\mathit{i}\right)\mathit{s}\left(\mathit{j}\right)}}^{\mathit{q}}\right)}^{{\mathit{\theta }}_{\mathit{i}}}\right)}^{{\mathit{\omega }}_{\mathit{j}}}\right)}^{\mathit{\gamma }}}}\rangle$

$=\mathit{\gamma }$ q-ROFHSEOWG $\left({\mathit{J}}_{{\mathit{d}}_{11},}{\mathit{J}}_{{\mathit{d}}_{12.}},\dots .,{\mathit{J}}_{{\mathit{d}}_{\mathit{n}\mathit{m}.}}\right)$.

4.1.4 Monotonicity

Let ${\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}=\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}},{\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right)$ and ${\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{*}=\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{*},{\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{*}\right)$ be the collection of q-ROFHSNs. Then,

$\mathrm{q}-\mathrm{R}\mathrm{O}\mathrm{F}\mathrm{H}\mathrm{S}\mathrm{E}\mathrm{W}\mathrm{G}\left({\mathit{J}}_{{\mathit{ď}}_{11}},{\mathit{J}}_{{\mathit{ď}}_{12}},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}\right)\le \mathrm{q}-\mathrm{R}\mathrm{O}\mathrm{F}\mathrm{H}\mathrm{S}\mathrm{E}\mathrm{W}\mathrm{G}\left({\mathit{J}}_{{\mathit{ď}}_{11}}^{*},{\mathit{J}}_{{\mathit{ď}}_{12}}^{*},\dots ,{\mathit{J}}_{{\mathit{ď}}_{\mathit{n}\mathit{m}}}^{*}\right),\mathrm{i}\mathrm{f}{\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\le {\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{*}\forall \mathit{i},\mathit{j}$

Proof. Similar to 3.2.4.

5 Multi-criteria group decision model for q-rung orthopair fuzzy hypersoft sets

To substantiate the inference of the established Einstein-ordered weighted AOs, there is a DM method to eradicate MCGDM constraints. We also used the developed approach to select the most appropriate TEST.

5.1 Proposed multi-criteria group decision approach

Let $\mathrm{\aleph }=\left\{{\mathrm{\aleph }}^1,{\mathrm{\aleph }}^2,{\mathrm{\aleph }}^3,\dots ,{\mathrm{\aleph }}^{\mathit{s}}\right\}$ and $\mathcal{H}=\left\{{\mathcal{H}}_1,{\mathcal{H}}_2,{\mathcal{H}}_3,\dots ,{\mathcal{H}}_{\mathit{n}}\right\}$ be the collection of alternatives and group of experts with weights of experts $\mathit{\theta }={\left({\mathit{\theta }}_1,{\mathit{\theta }}_2,\dots ,{\mathit{\theta }}_{\mathit{n}}\right)}^{\mathit{T}}$ such as ${\mathit{\theta }}_{\mathit{i}}>0$ and ${\displaystyle \sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\theta }}_{\mathit{i}}=1$. Suppose $\mathfrak{L}=\left\{{\mathit{d}}_1,{\mathit{d}}_2,\dots ,{\mathit{d}}_{\mathit{m}}\right\}$ shows the set of parameters and ${\mathfrak{L}}^{\prime }=\left\{\left({\mathit{d}}_{1\mathit{\rho }}\times {\mathit{d}}_{2\mathit{\rho }}\times \dots \times {\mathit{d}}_{\mathit{m}\mathit{\rho }}\right)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}\mathit{\rho }\in \left\{1,2,\dots ,\mathit{t}\right\}\right\}$ be a collection of multi sub-attributes with weights $\mathit{\omega }={\left({\mathit{\omega }}_1,{\mathit{\omega }}_2,{\mathit{\omega }}_3,\dots ,{\mathit{\omega }}_{\mathit{m}}\right)}^{\mathit{T}}$, such as ${\mathit{\omega }}_{\mathit{j}}>0$, ${\displaystyle \sum }_{\mathit{j}=1}^{\mathit{m}}{\mathit{\omega }}_{\mathit{j}}=1$. The collection of sub-attributes can be designated as ${\mathfrak{L}}^{\prime }=\left\{{\mathit{d}}_{\partial }:\partial \in \left\{1,2,\dots ,\mathit{m}\right\}\right\}$. The group of experts $\left\{{\mathcal{H}}_{\mathit{i}}:\mathit{i}=1,2,\dots ,\mathit{n}\right\}$ evaluate the alternates $\left\{{\mathrm{\aleph }}^{\left(\mathit{z}\right)}:\mathit{z}=1,2,\dots ,\mathit{s}\right\}$ in the form of q-ROFHSNs beneath the chosen sub-parameters $\left\{{\mathit{ď}}_{\partial }:\partial =1,2,\dots ,\mathit{m}\right\}$, such as ${\left({\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{\left(\mathit{z}\right)}\right)}_{\mathit{n}\times \mathit{m}}={\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}},{\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right)}_{\mathit{n}\times \mathit{m}}$, where $0\le {\mathit{f}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}},{\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\le 1$ and $0\le {\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right)}^{\mathit{q}}+{\left({\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right)}^{\mathit{q}}\le 1\forall \mathit{i},\mathit{j}$. The group of experts conveys the verdict in q-ROFHSNs form for each alternate. A novel algorithm is developed under q-ROFHSS settings to compute the appropriate alternative.

Step 1. Compute the decision matrices for each alternate in terms of q-ROFHSNs $\left({\mathrm{\aleph }}^{\left(\mathit{z}\right)},{\mathfrak{L}}^{\prime }\right)={\left({\mathit{f}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}},{\mathit{g}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}\right)}_{\mathit{n}\times \mathit{m}}$:

${\left({\mathrm{\aleph }}^{\left(\mathit{z}\right)},{\mathfrak{L}}^{\prime }\right)}_{\mathit{n}\times \partial }=\begin{array}{c}{\mathcal{H}}_1\\ {\mathcal{H}}_2\\ ⋮\\ {\mathcal{H}}_{\mathrm{n}}\end{array}\left(\begin{array}{cccc}\left({\mathit{f}}_{{\mathit{ď}}_{11}}^{\left(\mathit{z}\right)},{\mathit{g}}_{{\mathit{ď}}_{11}}^{\left(\mathit{z}\right)}\right)& \left({\mathit{f}}_{{\mathit{ď}}_{12}}^{\left(\mathit{z}\right)},{\mathit{g}}_{{\mathit{ď}}_{12}}^{\left(\mathit{z}\right)}\right)& \cdots & \left({\mathit{f}}_{{\mathit{ď}}_{1\partial }}^{\left(\mathit{z}\right)},{\mathit{g}}_{{\mathit{ď}}_{1\partial }}^{\left(\mathit{z}\right)}\right)\\ \left({\mathit{f}}_{{\mathit{ď}}_{21}}^{\left(\mathit{z}\right)},{\mathit{g}}_{{\mathit{ď}}_{21}}^{\left(\mathit{z}\right)}\right)& \left({\mathit{f}}_{{\mathit{ď}}_{22}}^{\left(\mathit{z}\right)},{\mathit{g}}_{{\mathit{ď}}_{22}}^{\left(\mathit{z}\right)}\right)& \cdots & \left({\mathit{f}}_{{\mathit{ď}}_{2\partial }}^{\left(\mathit{z}\right)},{\mathit{g}}_{{\mathit{ď}}_{2\partial }}^{\left(\mathit{z}\right)}\right)\\ ⋮& ⋮& ⋮& ⋮\\ \left({\mathit{f}}_{{\mathit{ď}}_{\mathit{n}1}}^{\left(\mathit{z}\right)},{\mathit{g}}_{{\mathit{ď}}_{\mathit{n}1}}^{\left(\mathit{z}\right)}\right)& \left({\mathit{f}}_{{\mathit{ď}}_{\mathit{n}2}}^{\left(\mathit{z}\right)},{\mathit{g}}_{{\mathit{ď}}_{\mathit{n}2}}^{\left(\mathit{z}\right)}\right)& \cdots & \left({\mathit{f}}_{{\mathit{ď}}_{\mathit{n}\partial }}^{\left(\mathit{z}\right)},{\mathit{g}}_{{\mathit{ď}}_{\mathit{n}\partial }}^{\left(\mathit{z}\right)}\right)\end{array}\right).$

Step 2. Obtain the ordered position matrices for each alternative using the score function.

Step 3. Convert the cost type aspects into benefit types using the normalization rule.

${\left({\mathrm{\aleph }}^{\left(\mathit{z}\right)},{\mathfrak{L}}^{\prime }\right)}_{\mathit{n}\times \partial }=\left\{\begin{array}{c}{\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}}^{\mathit{c}};\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{t}\mathrm{t}\mathrm{y}\mathrm{p}\mathrm{e}\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{a}\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{e}\mathrm{r},\\ {\mathit{J}}_{{\mathit{ď}}_{\mathit{i}\mathit{j}}};\mathrm{b}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{f}\mathrm{i}\mathrm{t}\mathrm{t}\mathrm{y}\mathrm{p}\mathrm{e}\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{a}\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{e}\mathrm{r}.\end{array}\right.$

Step 4. With settled Einstein-ordered weighted AOs, compute the collective decision matrix ${\mathcal{L}}_{\mathit{k}}$.

Step 5. For the ranking of alternatives, find the score values using Eq. 2.5.

Step 6. Analyze the most apt TEST based on the maximum score value ${\mathcal{L}}_{\mathit{k}}$.

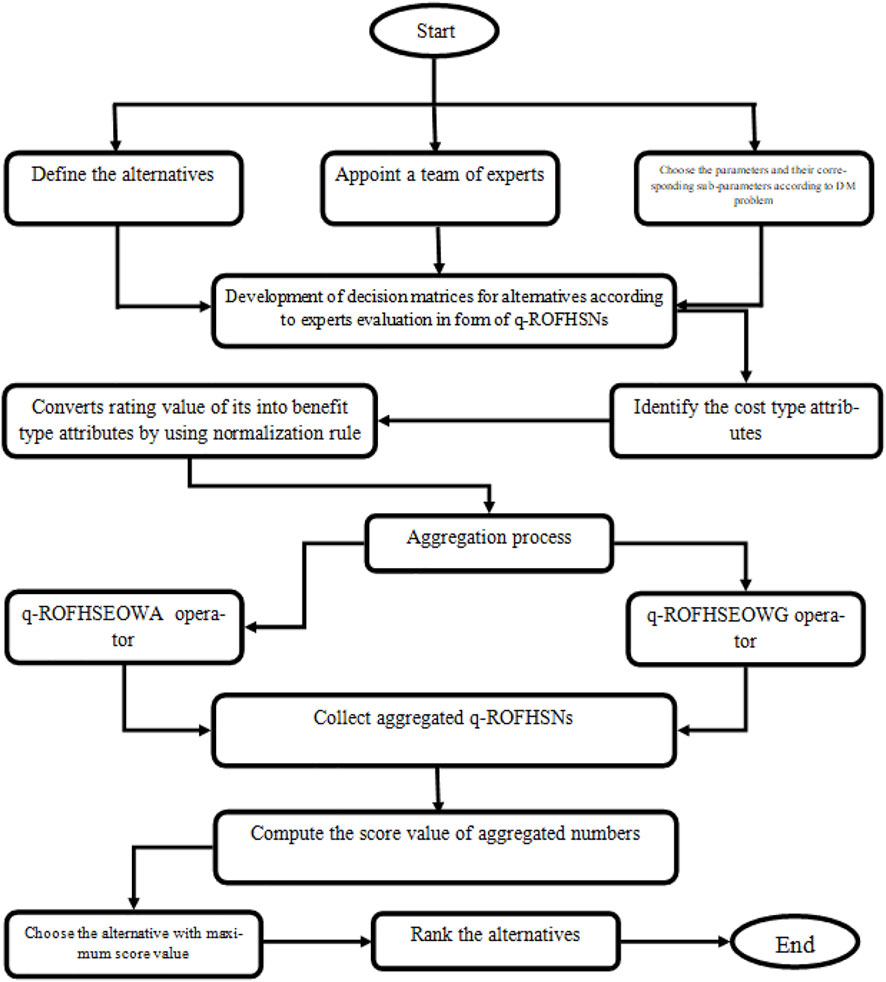
Step 7. Compute the ordering of the substitutes.The flowchart of the proposed algorithm is given in the following Figure 1.

FIGURE 1

FIGURE 1. Flowchart of the proposed MCGDM model.

5.2 Application of the proposed multi-criteria group decision approach

The energy storage method is intended to store energy when fabrication surpasses the mandate and to provide power according to consumers’ desires. They can easily conserve energy resources and overcome inconstant fabrication from renewable energy sources such as solar and wind, increase the productivity of energy systems, and decrease carbon dioxide emissions. It focuses on diminutive heat storage schemes. The purpose of energy storing is to apprehend energy and deliver it professionally for upcoming usage. Energy storage technology has numerous important advantages: enhanced solidity of power eminence, consistency of power quantity, etc. In the modern era, given the current energy crisis, energy storage has become the core focus of study in engineering and academia. The storing procedure is a necessary constituent of energy-proficient and justifiable energy systems. Energy storage is a cross-cutting problem that depends on several capabilities. Energy storage cooperation stimulates the widespread familiarity, management, and interdisciplinary organization of work agendas and exploration intentions. The energy storage technique generally supports accomplishing energy controlling on-demand sideways, addressing differences in power claims, power stock worth, and long-term dependability. Incorporating energy-storing classifications can clearly show the influence and energy experiments challenged by customary schemes. Energy storage types of machinery require a variety of forms, from large-scale power groups and transmission-based strategies to linkage circulation systems. Although different types of energy storing expertise exist, it can be seen that each storing method accomplishes its goal differently owing to its intrinsically different storing methods. Currently, people are gradually being attracted to the enlargement of energy-storing knowledge. Soon, storage capability intensities in established states can be amplified by 15–25%, although this rate may increase in emerging states. In this way, the important role of power engineering can be amended for better results. In the current circumstances, pushed hydro storage may be superior to other energy-storing arrangements that are not as effective in terms of large-scale energy storage. CAES schemes can participate with impelled hydropower schemes. However, their development may only be seen in states with high ethical values and auspicious geographical circumstances. Battery-operated expertise can support the energy market and storage, satisfying the need for electricity on demand.

Similarly, in recent years, in small and medium enterprises, flywheels, flow batteries, fuel cells, TES, etc., have become keys in the energy division. Their rapid payback makes them beneficial for several short- and long-term solicitations, particularly in terms of electrical superiority. In short, the energy productivity of extraordinary energy concentration and energy storing machinery, growing storage paybacks, solidity, dependability, energy preservation, and ecological sustainability predictions marks them consistently as the best choice for cumulative energy requirements. Due to the proliferation in heat, thermal energy is produced due to the pileup of atoms and spots. TES philosophy is used in several arenas of biological disciplines. Essentially, there are three skills for TES. The graphical representation of TES techniques is provided in Figure 2.

FIGURE 2

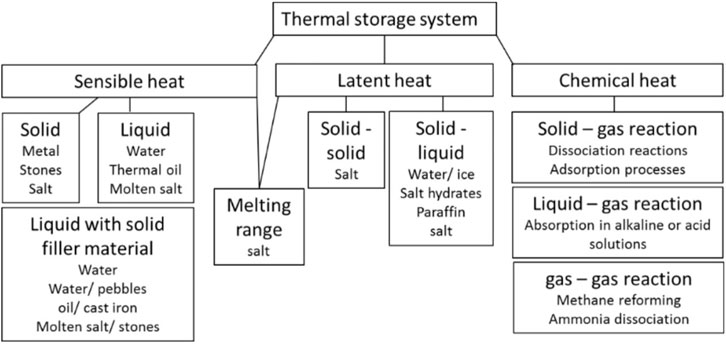
FIGURE 2. Thermal energy storage overview (Source: https://www.beilstein-journals.org/bjnano/content/figures/2190-4286-6-154-1.png?scale=2.0&max-width=1024&background=FFFFFF).

5.2.1 Sensible TEST

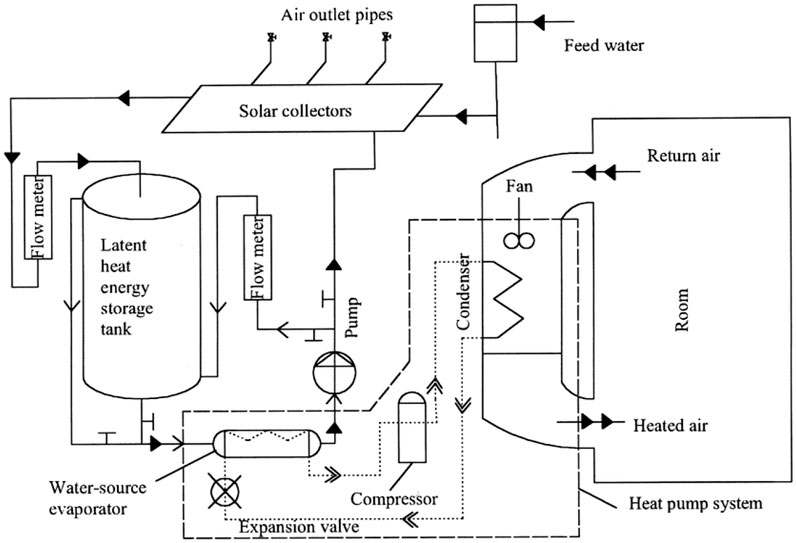
Sensible heat storage (SHS) is a system where energy is contained by increasing or reducing the heat of the stored substance. This storage medium can be a solid or a liquid. Water is economical and one of the most frequently used mediums. The graphical representation of the sensible TEST is displayed in Figure 3. Sensible thermal energy storage (STES) is used in numerous mechanisms, for example, construction and solar power plants. In solar preservation, solar food drying, and solar cooking, STES is the easiest and most established method of heat storage. Sensible thermal energy (STE) is stored by fluctuating the heat of STES ingredients, such as water, oil, rock beds, bricks, sand, or clay. There is no stage evolution through heat modifications in STES ingredients. SHS is easy to control and rationally exclusive. It is the best traditional, developed, and broadly used TES resolution. However, it achieves less energy-storing compactness than other TES alternatives, namely, latent heat storage (LHS) and thermochemical heat storage (TCHS) (Zhao et al., 2020). In this process, the transference of energy to storage liquids or solids suggests the identical alteration in the warmth of the medium. One of the benefits of this approach is that the storing and discharge of stored heat (charge and discharge phases) can be continually made easier through the accumulation of huge capacities to achieve this goal (Chandel and Agarwal, 2017).

FIGURE 3

FIGURE 3. Sensible thermal energy storage technique.

Furthermore, this scheme often benefits from specific features of the stockpiled substance, such as its particular high temperature (Rathore and Shukla, 2019). It is necessary to know two core features of SHS ingredients to increase the storing ability (MJ• ${\mathit{m}}^{-3}$) with extraordinary explicit temperature and compactness. Water has a moderately good particular temperature and solidity among the abundant materials available, so it is a frequently used storage material in numerous everyday uses. Regarding water with a thermal gradient of 60°C, the SHS capability is assessed to be 250 MJ• ${\mathit{m}}^{-3}$ (Lizana et al., 2017). This shows that high thermal ratings expedite heat discharge, enabling the transferral of low-temperature thermal energy to cooler areas during charging, resulting in more rapid generation of power from the warmest site for the duration of expulsion. Temperature stream restrictions are essential variables that disturb thermal inertia in reflexive systems (Borri et al., 2020). This parameter designates the degree to which the substance discharges or charges heat, with higher values increasing heat storage and reducing energy loss (Tarragona et al., 2020). Furthermore, obtainability, budget, harmfulness, and capacity variations are advanced standards for choosing justifiable SHS constituents. As stated earlier, the core shortcomings are limited energy compactness and device self-discharge. To estimate the efficacy of SHS schemes, Cárdenas-Ramírez et al. (2020) stated that the most useful properties are energy storing ability, influence, productivity, charge/discharge cycle time, and budget.

5.2.2 Latent TEST

The LHS system implies storing energy in phase change materials (PCMs). Thermal energy is stored and released when the storage material changes the segments. The benefit of LHS schemes is that they are usually condensed. For heat-storing, the PCM size is considerably smaller than the size of the SHS. This is essential since it affects the usage of fewer separations and is functional everywhere around the world. Other benefits of PCMs comprise the capability to stock huge volumes of heat with minor temperature alterations and being robust to severe operative temperatures since they can handle exertion under isothermal circumstances and have extraordinary storing compactness. Compared to SHS systems, LHS systems have almost five to ten times greater storing capacity. The stage alteration can be from solid to liquid, solid to gas, solid to solid, liquid to gas, and vice versa. In solid-stage alteration, heat is stockpiled as the substantial transmission from one sparkler organization to another. This stage conversion, i.e., solid-to-solid alteration, has less latent heat: high latent heat has issues and high capacity deviations connected with solid-to-gas and liquid-to-gas transformation. However, considerable variations in size can arise due to the requirement for a larger vessel. In several circumstances, this makes this method unrealistic. For the causes stated formerly, the best stage alteration is the transition from solid to liquid as it is associated with minor changes in volume, although the latent heat of the solid to liquid growth is lesser than that of liquid to gas. Solid to liquid material alteration is also economical as a thermal energy storing mode. The PCM itself cannot be reused as a heat transmission mode. An isolated heat transmission cause should be retrieved, with a heat exchanger in the interior, to transfer energy from the basis to the PCM and the PCM to the load. Assuming that the PCM’s thermal dispersal is usually small, consideration must be given to the role of the temperature exchanger (see Figure 4).

FIGURE 4

FIGURE 4. Latent heat energy storage technique (Source: latent heat storage TANK—Bing).

Compared to SHS, LHS systems have a moderately good energy solidity and have been used for low- and medium-temperature scenarios, for example, thermal regulation in buildings (De Gracia and Cabeza, 2015). Therefore, from the perspective of excessive heat, LHS systems aim to incorporate prodigious heat-concentrated solar power demonstrations. The low thermal conductivity, low thermal constancy, and restrained temperature of PCMs found in present LHS systems are critical barriers to their use, even if they have significant energy-storing strengths. In customary concealed storage systems, there are different methods to progress thermal enactment through organs, flowing unlike PCMs and embalmed PCMs (Jegadheeswaran and Pohekar, 2009). However, these approaches trade off PCMs’ retention capacity with their size, resulting in a reduction in the energy storage capability through the charging/discharge of the LHS system (Lin et al., 2018). One viable substitute is metal PCMs with unusual thermal conductivity, sentimental warmth, and abundant thermal solidity. Generally, the melt’s latent heat and the mixture material’s thermal constancy rise with the growth in the soppy heat (Bauer et al., 2012). Hence, there is an increasing need to understand PCMs in terms of unexpected melting point heats.

5.2.3 Thermochemical TEST

TCHS is one of the potential TES techniques in the procedure of revocable thermochemical reactions. The main significant benefit of TCHS is that the enthalpy of the reaction is considerably more than the heat. Thus, the storing compactness is superior in organic responses, with energy stockpiled in biochemical bonds among molecules forming fragments. At the atomic level, energy storage contains energy related to the orbital of electrons. In addition to whether the chemical captures or discharges the reaction energy, there is no global measurement of the quantity of energy through the reaction. The purpose of incorporating the TCHS technique used by the solar thermal system (STS) is to increase the amount of solar energy and thus increase the productivity of the STS. The excess heat delivered by the summer stock accumulation controls the TCHS. In the wintertime, stored heat can be reprocessed to overcome the excessive heat mandate of the system. Regarding the heat mandate of the system and the extent of the TCHS, a fossil-fuel-assisted STS using a proportion of more than 50% can be used, as well as a pure STS. Figure 5 displays a schematic diagram of TCHS combined with an STS. TCHS is linked to the water shield storage usually integrated in the STS through solar circuits and heat exchangers. The core component of TCHS is the heat and mass transfer that arises through the charge and discharge of the TCHS reactor. Dependent on the regulatory policy, the best reactor is a fixed bed reactor. The material comes into the reactor from above, and passage over the reactor is determined by gravity. Air moves in the reactor and passes moisture and heat to and from the reactor. For air-to-air heat alteration, entering fresh air is heated by hot air departure in TCHS, which controls the productivity of TCHS as heat damage by the gas stream is reduced. The heat entering the reactor is transmitted from the airflow to the solar circuit via air-to-water heat exchange in TCHS, releasing heat. For material preservation, the airflow is absorbed in the opposite way and reprocessed to transference reformative heat from the solar circuit to the reactor through the heat exchange airflow.

FIGURE 5

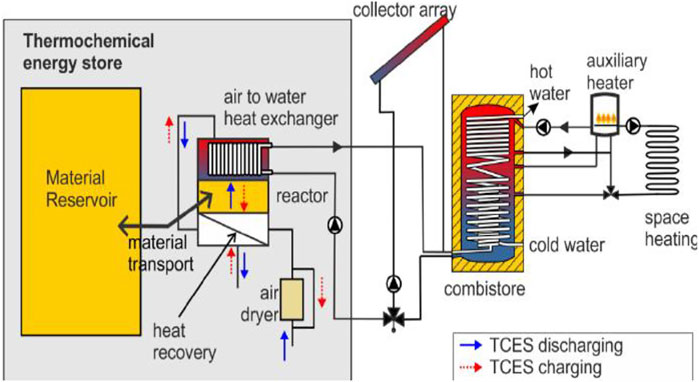
FIGURE 5. Thermochemical heat storage technique [Figure 1 (Mette et al., 2013)].

TCHS uses a series of reactions related to physical and chemical developments (for a provisional organization, see McNaught and Wilkinson, 1997). However, in this organization, adsorption is used to accumulate various physical properties and can lead to misinterpretations. We intentionally limit the organization development to out-of-phase reactions, including mechanisms of two or additional stages, as uniform responses are rarely used for TES. Prioritizing TES techniques is a significant initiative in this modern era. Industrial innovativeness is based on a vision, financial planning, environmental concerns, and the frequent lack of materials. The best design chooses the most appropriate TES technique by considering the most feasible financial plan. Several unreliable DM practices require prioritizing TES techniques, predominant AOs, and other DM methodologies in this context. These AOs need to be restructured to address these concerns. We recommend specific innovative ordered AOs considering the Einstein operational laws for accumulating helpful q-ROFHSNs. Considering that mentioned previously, DM discernment can characterize all configurations. Attention is first needed on prioritizing the TES technique and then on other features’ impacts to identify the multiple sub-parameters and ingredients for DM. The q-ROFHSS model and projected Einstein-ordered AOs can be used in this context.

Regarding the best features to contemplate when choosing an effective TES method in DM, it is necessary to select a process with a primary transmission of TES, focusing on rationalization configurations inherent to solicitation. MCGDM considers making decisions in the presence of several, often inconsistent, criteria. The different criteria can have a disparate scope and comparative weight. Some measures can be controlled scientifically, while others can only be intuitively determined. It is possible to use many methodologies to explain and overcome MCGDM obstacles. The MCGDM approach provides insights into numerous managerial difficulties. The primary aim of this study is to select the most appropriate TES technique based on Einstein-ordered weighted AOs under the q-ROFHSS environment.

5.3 Numerical example

Let $\left\{{\mathrm{\aleph }}^{\left(1\right)},{\mathrm{\aleph }}^{\left(2\right)},{\mathrm{\aleph }}^{\left(3\right)}\right\}$ be a collection of alternatives that represent the TES techniques, such as ${\mathrm{\aleph }}^{\left(1\right)}$: sensible thermal energy storage technique; ${\mathrm{\aleph }}^{\left(2\right)}$: latent thermal energy storage technique; and ${\mathrm{\aleph }}^{\left(3\right)}$: thermochemical energy storage technique. Let $\left\{{\mathcal{H}}_1,{\mathcal{H}}_2,{\mathcal{H}}_3\right\}$ be a team of experts with weights ${\mathit{\theta }}_{\mathit{i}}={\left(0.3,0.5,0.2\right)}^{\mathit{T}}$. The team of experts considers the set of parameters for the prioritization of the TES technique given as $\mathfrak{L}=\left\{{\mathit{d}}_1=\{\mathrm{E}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{g}\mathrm{y}\mathrm{s}\mathrm{t}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{g}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{p}\mathrm{a}\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{y},{\mathit{d}}_2=\mathrm{E}\mathrm{f}\mathrm{f}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{y},{\mathit{d}}_3=\mathrm{M}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{u}\mathrm{m}\mathrm{c}\mathrm{y}\mathrm{c}\mathrm{l}\mathrm{e}\mathrm{l}\mathrm{e}\mathrm{n}\mathrm{g}\mathrm{t}\mathrm{h}\right\}$. The multi sub-attributes of the deliberated factors are given as follows: Energy storage capacity = ${\mathit{d}}_1$ = $\left\{{\mathit{d}}_{11}=\mathrm{H}\mathrm{e}\mathrm{a}\mathrm{t}\mathrm{s}\mathrm{t}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{d}\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{m}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{a}\mathrm{l},{\mathit{d}}_{12}=\mathrm{H}\mathrm{e}\mathrm{a}\mathrm{t}\mathrm{s}\mathrm{t}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{d}\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{s}\mathrm{y}\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{m}\right\}$; Efficiency = ${\mathit{d}}_2$ = $\left\{{\mathit{d}}_{21}=\mathrm{h}\mathrm{e}\mathrm{a}\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{d}\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{h}\mathrm{e}\mathrm{a}\mathrm{t}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{k}\mathrm{d}\mathrm{u}\mathrm{r}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{c}\mathrm{h}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{i}\mathrm{n}\mathrm{g},{\mathit{d}}_{22}=\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{g}\mathrm{y}\mathrm{a}\mathrm{b}\mathrm{s}\mathrm{o}\mathrm{r}\mathrm{b}\mathrm{e}\mathrm{d}\mathrm{b}\mathrm{y}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{s}\mathrm{y}\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{m}\mathrm{d}\mathrm{u}\mathrm{r}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{c}\mathrm{h}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{i}\mathrm{n}\mathrm{g}\right\}$; Minimum cycle length = ${\mathit{d}}_3$ = $\left\{{\mathit{d}}_{31}=\mathit{s}\mathit{h}\mathit{o}\mathit{r}\mathit{t}\mathit{t}\mathit{e}\mathit{r}\mathit{m},{\mathit{d}}_{32}=\mathit{l}\mathit{o}\mathit{n}\mathit{g}\mathit{t}\mathit{e}\mathit{r}\mathit{m}\right\}$. Let ${\mathfrak{L}}^{\prime }$ = ${\mathit{d}}_1$ × ${\mathit{d}}_2$ × ${\mathit{d}}_3$ be a set of sub-attributes,

${\mathfrak{L}}^{\prime }={\mathit{d}}_1\times {\mathit{d}}_2\times {\mathit{d}}_3=\left\{{\mathit{d}}_{11},{\mathit{d}}_{12}\right\}\times \left\{{\mathit{d}}_{21},{\mathit{d}}_{22}\right\}\times \left\{{\mathit{d}}_{31},{\mathit{d}}_{32}\right\}$

$=\left\{\begin{array}{c}\left({\mathit{d}}_{11},{\mathit{d}}_{21},{\mathit{d}}_{31}\right),\left({\mathit{d}}_{11},{\mathit{d}}_{21},{\mathit{d}}_{32}\right),\left({\mathit{d}}_{11},{\mathit{d}}_{22},{\mathit{d}}_{31}\right),\left({\mathit{d}}_{11},{\mathit{d}}_{22},{\mathit{d}}_{32}\right),\\ \left({\mathit{d}}_{12},{\mathit{d}}_{21},{\mathit{d}}_{31}\right),\left({\mathit{d}}_{12},{\mathit{d}}_{21},{\mathit{d}}_{32}\right),\left({\mathit{d}}_{12},{\mathit{d}}_{22},{\mathit{d}}_{31}\right),\left({\mathit{d}}_{12},{\mathit{d}}_{22},{\mathit{d}}_{32}\right)\end{array}\right\}$ and ${\mathfrak{L}}^{\prime }$ = $\left\{{\mathit{ď}}_1,{\mathit{ď}}_2,{\mathit{ď}}_3,{\mathit{ď}}_4,{\mathit{ď}}_5,{\mathit{ď}}_6,{\mathit{ď}}_7,{\mathit{ď}}_8\right\}$ be a collection of multi-sub-attributes with weights ${\mathit{\omega }}_{\mathit{j}}={\left(0.2,0.1,0.15,0.05,0.1,0.1,0.18,0.12\right)}^{\mathit{T}}$. Experts provide their choices in q-ROFHSN form for each substitute considering the considered aspects.

5.3.1 Using the q-rung orthopair fuzzy hypersoft Einstein-ordered weighted average operator

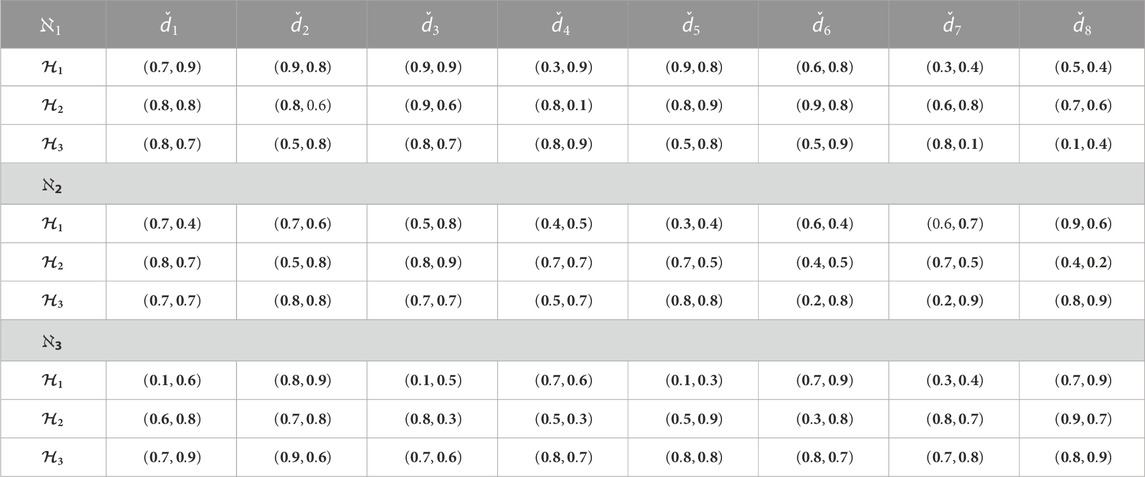
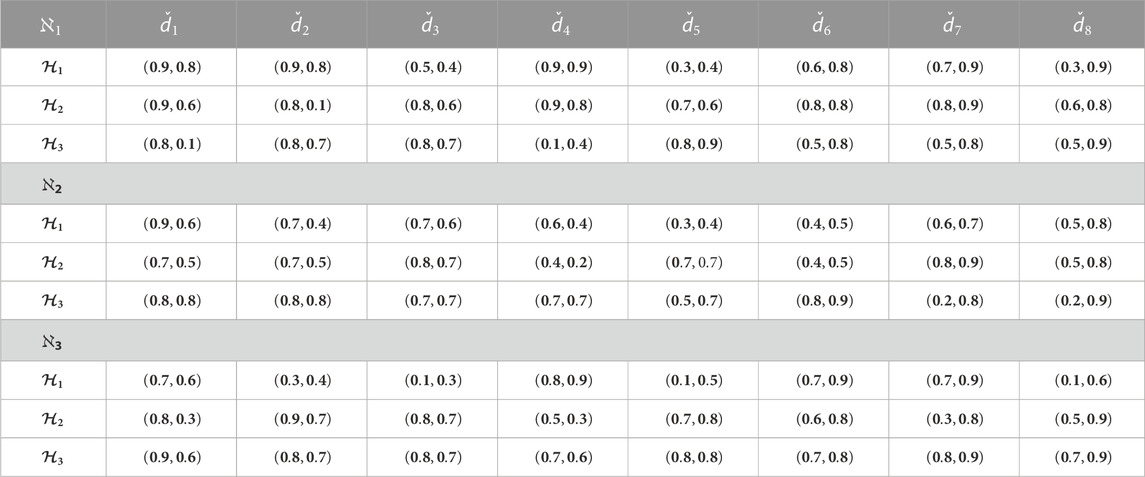
Step 1. Compute the decision matrices for each alternate in terms of q-ROFHSNs (their predilections are given in Table 1).

TABLE 1

TABLE 1. Decision matrices for alternatives.

Step 2. Using the score function, obtain the ordered position matrices for each alternative (Table 2).

TABLE 2

TABLE 2. Ordered decision matrix for alternatives.

Step 3. There is no need to normalize since the parameters are the same.

Step 4. Determine the collective aggregated values of alternatives from Table 2 using the q-ROFHSEOWA operator given as: ${\mathrm{\aleph }}_1$ = $〈0.6929,0.6197〉$; ${\mathrm{\aleph }}_2$ = $〈0.7401,0.6187〉$; ${\mathrm{\aleph }}_3$ = $〈0.7137,0.7019〉$.

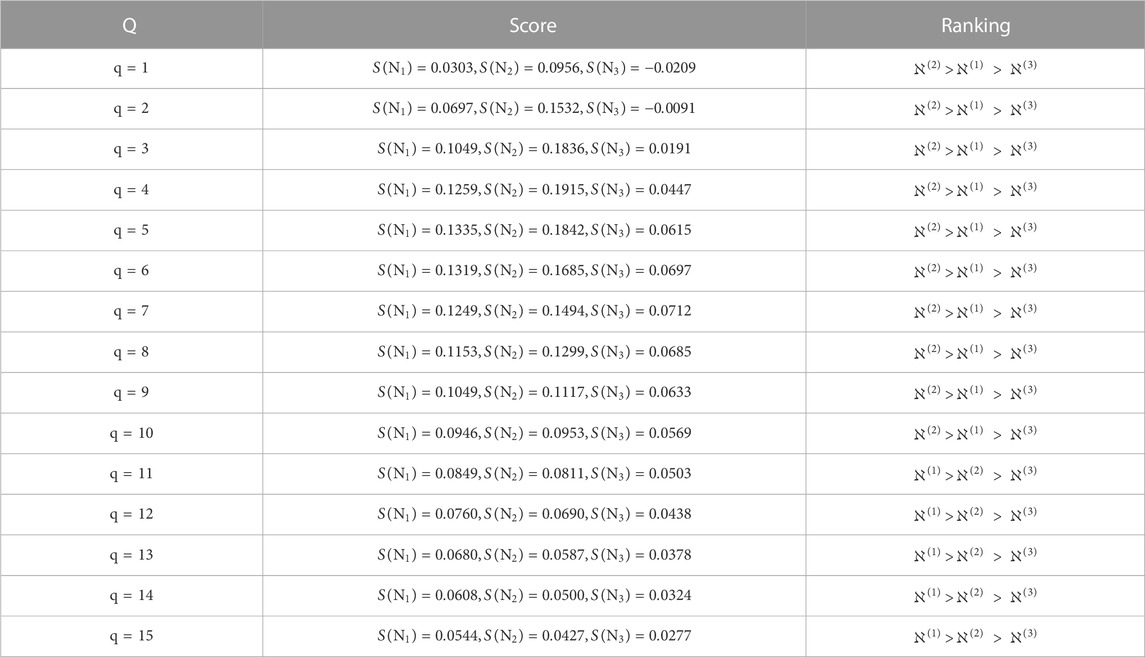
Step 5. From Eq. 2.5, find the score values, such as $\mathit{S}\left({\mathrm{\aleph }}_1\right)$ = 0.1049, $\mathit{S}\left({\mathrm{\aleph }}_2\right)$ = 0.1836, and $\mathit{S}\left({\mathrm{\aleph }}_3\right)$ = 0.0191.

Step 6. ${\mathrm{\aleph }}^2$ is the best TEST because of the maximum score value.

Step7. Investigate the ordering of the substitutes: $\mathit{S}\left({\mathrm{\aleph }}_2\right)>\mathit{S}\left({\mathrm{\aleph }}_1\right)>\mathit{S}\left({\mathrm{\aleph }}_3\right)$. So, ${\mathrm{\aleph }}^{\left(2\right)}>{\mathrm{\aleph }}^{\left(1\right)}>{\mathrm{\aleph }}^{\left(3\right)}$. It is perceived that the best applicable TEST is ${\mathrm{\aleph }}^{\left(2\right)}$. The influence of $\mathit{q}$ on assessment consequences for the q-ROFHSEOWA operator is specified in Table 3. The graphical demonstration of the influence of $\mathit{q}$ is displayed in Figure 6.

TABLE 3

TABLE 3. Effects on decision results by variation of $“\mathit{q}”$ under the q-ROFHSEOWA operator.

FIGURE 6

FIGURE 6. Score values of the alternatives for $\mathbf{1}\le \mathit{q}\le \mathbf{15}$ under q-ROFHSEOWA.

5.3.2 Using the q-rung orthopair fuzzy hypersoft Einstein-ordered weighted geometric operator

Steps 1–3. Similar to 5.3.1.

Step 4. Determine the collective aggregated values of alternatives from Table 2 using the q-ROFHSEOWG operator given as ${\mathrm{\aleph }}_1$ = $〈0.5392,0.7066〉$, ${\mathrm{\aleph }}_2$ = $〈0.6856,0.7228〉$, and ${\mathrm{\aleph }}_3$ = $〈0.5897,0.7879〉$.

Step 5. From Eq. 2.5, find the score values, such as $\mathit{S}\left({\mathrm{\aleph }}_1\right)$ = $-$0.2200, $\mathit{S}\left({\mathrm{\aleph }}_2\right)$ = $-$0.0595, $\mathit{S}\left({\mathrm{\aleph }}_3\right)$ = $-$0.3055.

Step 6. ${\mathrm{\aleph }}^2$ is the best TEST because of the maximum score value.

Step 7. Investigate the ordering of the substitutes: $\mathit{S}\left({\mathrm{\aleph }}_2\right)$ $>$ $\mathit{S}\left({\mathrm{\aleph }}_1\right)$ $>$ $\mathit{S}\left({\mathrm{\aleph }}_3\right)$. So, ${\mathrm{\aleph }}^{\left(2\right)}$ $>$ ${\mathrm{\aleph }}^{\left(1\right)}>{\mathrm{\aleph }}^{\left(3\right)}$. It is perceived that the best applicable TEST is ${\mathrm{\aleph }}^{\left(2\right)}$. The influence of $\mathit{q}$ on assessment consequences for the q-ROFHSEOWG operator is specified in Table 4. The graphical demonstration of the influence of $\mathit{q}$ is displayed in Figure 7.

TABLE 4

TABLE 4. Effects on decision results by variation of $“\mathit{q}”$ under the q-ROFHSEOWG operator.

FIGURE 7

FIGURE 7. Score values of the alternatives for $\mathbf{1}\le \mathit{q}\le \mathbf{15}$ under q-ROFHSEOWG.

6 Sensitivity analysis

This section evaluates the proposed approach and prevailing methodologies to confirm the practicality of the scheme.

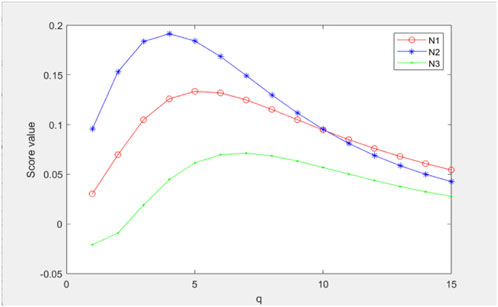
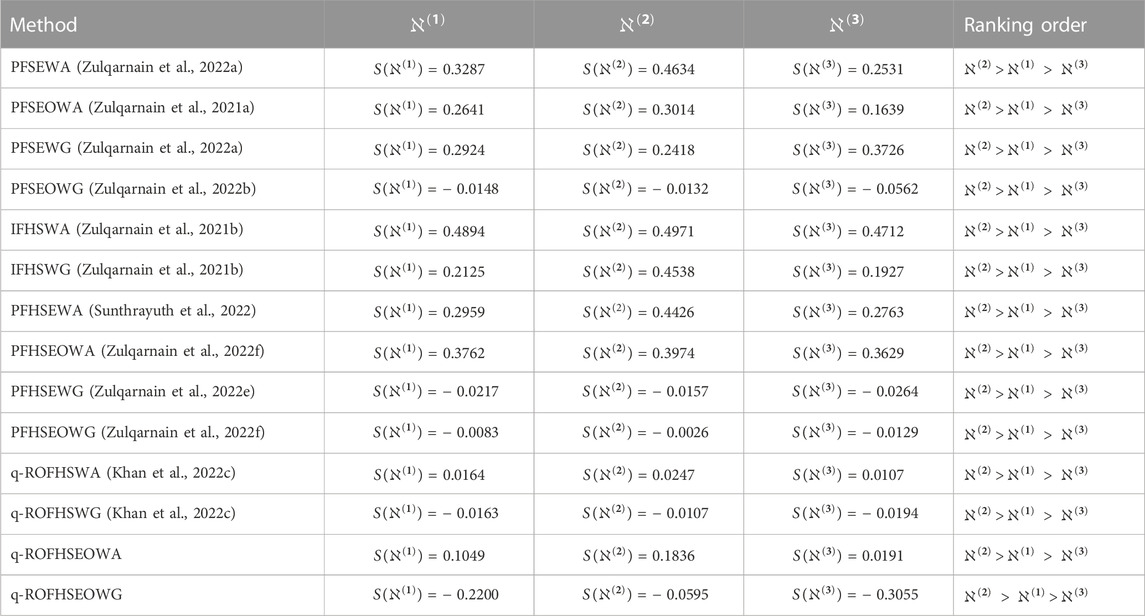
6.1 Influence on the alternatives’ rank of the deviancy of $\mathit{q}$ for the q-rung orthopair fuzzy hypersoft Einstein-ordered weighted average operator

The organization training shows that ${\mathrm{\aleph }}^{\left(2\right)}$ and ${\mathrm{\aleph }}^{\left(3\right)}$ are the optimum and poorest alternates, respectively. It can be observed from Table 3 that there is no variation in the alternatives’ ordering, while “$\mathit{q}$” is between 1 and 10, which is ${\mathrm{\aleph }}^{\left(2\right)}>{\mathrm{\aleph }}^{\left(1\right)}$ $>$ ${\mathrm{\aleph }}^{\left(3\right)}$. However, when the values of “$\mathit{q}$” are between 11 and 15, the raking of alternatives changes to ${\mathrm{\aleph }}^{\left(1\right)}>{\mathrm{\aleph }}^{\left(2\right)}$ $>$ ${\mathrm{\aleph }}^{\left(3\right)}$, and the best alternative is ${\mathrm{\aleph }}^{\left(1\right)}$ by replacing ${\mathrm{\aleph }}^{\left(2\right)}$. Additionally, it is observed that as the values of “$\mathit{q}$” increase, the score values of the alternatives decrease, which shows that the score values are dependent on the parameter “$\mathit{q}$.” Moreover, IFHSSs (Zulqarnain et al., 2021b) and PFHSSs (Siddique et al., 2021) fail to deal with the situation in the case of ${\left(\mathit{M}\mathit{D}\right)}^2+{\left(\mathit{N}\mathit{M}\mathit{D}\right)}^2>1$. It is thought that the method provided by Khan et al. (2022c) can designate fuzzy information. However, the parameter $“\mathit{q}”$ marks the fact-gathering procedure as more flexible. Through this analysis, it can be seen that a parameter’s presentation can make it easier for experts to assess any object. They are advised to set the parameter’s value according to their needs.

The proposed method makes fuzzy information easier to describe and makes it more flexible in combining facts with factors. When assembling some sequences, numerous amalgam structures of FS are converted into the special detail of q-ROFHSS (see Table 5). The parameter $″\mathit{q}″$ helps experts review any project more generally. Therefore, specialists are advised to choose $″\mathit{q}″$ to obtain the trend. Regarding this exploration and evaluation, we assert that the results achieved from the proposed model are more perfect than prevalent models.

TABLE 5

TABLE 5. Feature analysis of different models with a planned model.

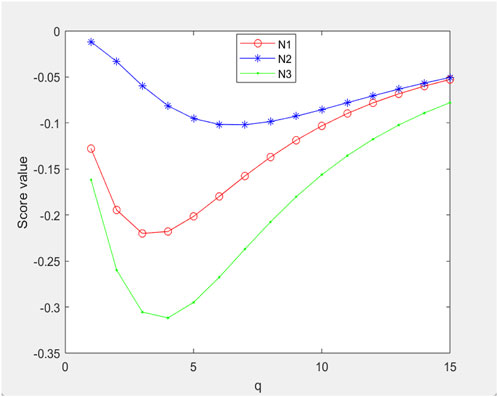
6.2 Influence on alternatives’ rank of the deviancy of $\mathit{q}$ for the q-rung orthopair fuzzy hypersoft Einstein-ordered weighted geometric operator

To minimize the impact of “$\mathit{q}$” judgment results, we tried disparate values of $\mathit{q}$ as an organizational mandate for alternatives. ${\aleph }^{\left(2\right)}$ is the most appropriate alternative when $\mathit{q}=1-15$, with the ranking ${\mathrm{\aleph }}^{\left(2\right)}>{\mathrm{\aleph }}^{\left(1\right)}$ $>$ ${\mathrm{\aleph }}^{\left(3\right)}.$ Moreover, it can be observed that as the values of $\mathit{q}$ increase, the score values of the alternatives also increase, which shows that the score values depend on the parameter $\mathit{q}$. The graphical description of Table 4 is presented in Figure 6. The aforementioned analysis shows that if we change $″\mathit{q},″$ it will disturb the hierarchical imperative of the alternatives. As a result, professionals can choose the value of $″\mathit{q}″$ to evaluate the most suitable object. It can be concluded that specialists should deliberate the value of $″\mathit{q}″$ when the alternative rating is stable.

7 Comparative analysis and discussion

This section compares the proposed model and predominant techniques to justify the practicality of our presented model.

7.1 Supremacy of the planned approach

The proposed scheme is effective and robust. We formulated an innovative MCGDM approach using q-ROFHSEOWA and q-ROFHSEOWG operators. The developed methodology in this research is more effective than prevalent methods and compatibility contracts for MCGDM problems. The proposed methodology is versatile and familiar, with disparities, accountabilities, and changes allowing for different outputs. Unlike models with explicit taxonomic comportment, there is a conventional alteration to the projected scheme classification to accommodate its perspective. Methodological studies and estimations consider that the consequences of prevalent approaches are similar to hybrid systems. Furthermore, after adding some suitable conditions, numerous amalgam configurations of FSs become the q-ROFHSS. Adding infrequent and blurred facts to the current practical plan is unexpected. Data concerning prosperity provide a more complete and reasonable description. Through the DM procedure, there are many fabricated and troubling details. Thus, our proposed methodology will be superior to several amalgam FS scenarios. Table 5 presents the feature analysis of our developed and prevalent approaches.

7.2 Comparative analysis

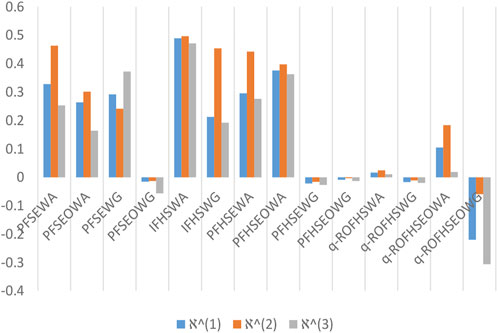
To demonstrate the efficacy of the established approach, we linked the inferences gained from some well-known systems. Table 6 summarizes the comparison between our developed model and existing AOs. Zulqarnain et al. (2022a) used the PFSEWA and PFSEWG operators to analyze the parametric values of the substitute. However, these Einstein AOs are ineffective in compacting with sub-parameters of the alternatives. Also, the Einstein-ordered AOs (Zulqarnain et al., 2021a; Zulqarnain et al., 2022b) for PFSSs cannot compute the alternatives’ multiple sub-attributes. The AOs presented in Zulqarnain et al. (2021b) under the IFHSS environment can diminish with the sub-parameters of substitutes. However, these AOs fail to deal with the decision outcomes when the sum of $\mathit{M}\mathit{D}+\mathit{N}\mathit{M}\mathit{D}>1$. Sunthrayuth et al. (2022) and Zulqarnain et al. (2022e) extended the Einstein weighted average and geometric AOs for PFHSSs and confirmed the novel MCDM techniques to solve MCDM obstacles because of the parameterization of sub-attributes. However, these AOs also fail when ${\left(\mathit{M}\mathit{D}\right)}^2+{\left(\mathit{N}\mathit{M}\mathit{D}\right)}^2>1$. Furthermore, the Einstein-ordered AOs (Zulqarnain et al., 2022f) for PFHSSs cannot address the above-mentioned concerns. Khan et al. (2022c) extended the algebraic operational laws and AOs for q-ROFHSS to overcome the aforementioned hurdles. However, these AOs cannot deliver the desirable outcomes in some situations. Therefore, to solve these composite issues, we introduce Einstein’s ordered weighted AOs for q-ROFHSS. The q-ROFHSS is an appropriate extension of a q-ROFSS and a generalized form of PFHSS. From the aforementioned facts, we assert that the proposed AOs are more competent, reliable, and valuable compared to prevalent AOs. The comparison between the developed AOs and some usual AOs is explored in Table 6.

TABLE 6

TABLE 6. Comparative analysis with existing operators.

Therefore, we have the right to be surprised by the exploitation and unreliability of the DM procedure for the prevailing operators we have recognized. Intentional sustenance for this method-related action has a slight influence on adverse reasons. In this way, it relaxes the organization of unreliable and assumed details in the amplification of DM. Figure 8 graphically demonstrates the comparison analysis.

FIGURE 8

FIGURE 8. Comparative analysis.

The aforementioned discussion and comparative studies show that the present study can play a significant role in the scientific community in terms of assessing better alternatives. It is the most generalized mathematical model to discuss the sub-parameters of the alternatives in DM problems.

7.3 Advantages of the proposed research

In the following section, we highlight the advantages of the proposed approach:

• The proposed technique takes into account the concept of parameterization in aggregation and discusses the importance of DM constraints with q-ROFHSS. The MD and NMD replication scenarios of constant parameterization have a certain degree of notation and rationality. This approach has an outstanding ability to demonstrate computational operations in an incredible world with these capabilities.

• Since the model highlights an in-depth investigation of the set of values of the parameter and its associated sub-parameters, it supports decision-makers in DM labeling combinations and making reliable decisions.

8 Conclusion

The lack of contemplation of complex conditions in the features can obstruct some of the multifaceted inferences of MCGDM. The mathematical demonstration in MCGDM exploits all special effects while being of interest under the limits of finance, superiority, and welfare boundaries. It is necessary to limit the investigation to make decisions at the highest level and capture the need for decisions. In factual DM, estimates of alternative details recognized by professionals are often inaccurate, asymmetrical, and insignificant, so q-ROFHSNs are used to calculate this impulsive information. The core objective of this research is to perform the Einstein operational laws for q-ROFHSS. Using our developed Einstein operational laws, we propose q-ROFHSEOWA and q-ROFHSEOWG operators with their preferred properties. In addition, the DM approach is expected to resolve MCGDM bottlenecks based on proven operators. To illustrate the strength of the presented methodology, we provide a mathematical description of the TES technique. This article also provides a comprehensive analysis of some contemporary models. Finally, based on the results obtained, it can be concluded that the approach proposed in this research is undeniably the most specific and feasible system to clarify MCGDM issues. Future investigations should focus on defining Bonferroni mean AOs, distance, and similarity measures with their conforming characteristics. Researchers could also integrate q-ROFHSNs with other MCGDM approaches and further practical solicitations in medical diagnosis, material selection, pattern recognition, information fusion, and supply chain management problems. Several configurations can be developed for q-ROFHSS, such as topological, algebraic, and ordered structures, with their DM techniques. Moreover, it can be extended to the T-spherical fuzzy hypersoft set, interval-valued T-spherical fuzzy hypersoft set, and interval-valued q-ROFHSS, with their algebraic and Einstein operations. Several other decision-making methodologies can be developed considering settings such as TOPSIS, VIKOR, AHP, and MABAC.

Data availability statement

The original contributions presented in the study are included in the article/supplementary materials; further inquiries can be directed to the corresponding author.

Author contributions

Conceptualization, RZ; methodology, RZ; validation, IS, SE, and MS; formal analysis, SE and JM; investigation, JM, SH, and MS; writing—original draft preparation, IM and RZ; visualization, IM and MS; supervision, RZ and SE; project administration, SE and JM; funding acquisition, JM and SE. All authors have read and agreed to the published version of the manuscript.

Acknowledgments

The author extends their appreciation to the deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number (IFP-2020-138).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akram, M., Alsulami, S., Karaaslan, F., and Khan, A. (2021). q-Rung orthopair fuzzy graphs under Hamacher operators. J. Intelligent Fuzzy Syst. 40 (1), 1367–1390. doi:10.3233/jifs-201700

CrossRef Full Text | Google Scholar

Akram, M., Shahzadi, G., Butt, M. A., and Karaaslan, F. (2021). A hybrid decision making method based on q-rung orthopair fuzzy soft information. J. Intelligent Fuzzy Syst. 40 (5), 9815–9830. doi:10.3233/jifs-202336

CrossRef Full Text | Google Scholar

Ali, M. I., Feng, F., Liu, X., Min, W. K., and Shabir, M. (2009). On some new operations in soft set theory. Comput. Math. Appl. 57 (9), 1547–1553. doi:10.1016/j.camwa.2008.11.009

CrossRef Full Text | Google Scholar

Arora, R., and Garg, H. (2018). A robust aggregation operators for multi-criteria decision-making with intuitionistic fuzzy soft set environment. Sci. Iran. 25 (2), 931–942.

Google Scholar

Atanassov, K. (1986). Intuitionistic fuzzy sets. Fuzzy Sets Syst. 20, 87–96. doi:10.1016/s0165-0114(86)80034-3

CrossRef Full Text | Google Scholar

Athira, T. M., John, S. J., and Garg, H. (2020). A novel entropy measure of Pythagorean fuzzy soft sets. AIMS Math. 5 (2), 1050–1061. doi:10.3934/math.2020073

CrossRef Full Text | Google Scholar

Athira, T. M., John, S. J., and Garg, H. (2019). Entropy and distance measures of Pythagorean fuzzy soft sets and their applications. J. Intelligent Fuzzy Syst. 37 (3), 4071–4084. doi:10.3233/jifs-190217

CrossRef Full Text | Google Scholar

Athira, T. M., John, S. J., and Garg, H. (2022). Similarity measures of Pythagorean fuzzy soft sets and clustering analysis. Soft Comput., 1–16. doi:10.1007/s00500-022-07463-4

CrossRef Full Text | Google Scholar

Bauer, T., Steinmann, W. D., Laing, D., and Tamme, R. (2012). Thermal energy storage materials and systems. Annu. Rev. Heat Transf. 15, 131–177. doi:10.1615/annualrevheattransfer.2012004651

CrossRef Full Text | Google Scholar

Borri, E., Tafone, A., Zsembinszki, G., Comodi, G., Romagnoli, A., and Cabeza, L. F. (2020). Recent trends on liquid air energy storage: A bibliometric analysis. Appl. Sci. 10 (8), 2773. doi:10.3390/app10082773

CrossRef Full Text | Google Scholar

Cagman, N., and Enginoglu, S. (2011). FP-soft set theory and its applications. Ann. Fuzzy Math. Inf. 2 (2), 219–226.

Google Scholar

Çağman, N., and Karataş, S. (2013). Intuitionistic fuzzy soft set theory and its decision making. J. Intelligent Fuzzy Syst. 24 (4), 829–836. doi:10.3233/ifs-2012-0601

CrossRef Full Text | Google Scholar

Cárdenas-Ramírez, C., Jaramillo, F., and Gómez, M. (2020). Systematic review of encapsulation and shape-stabilization of phase change materials. J. Energy Storage 30, 101495. doi:10.1016/j.est.2020.101495

CrossRef Full Text | Google Scholar

Cavallaro, F. (2010). Fuzzy TOPSIS approach for assessing thermal-energy storage in concentrated solar power (CSP) systems. Appl. Energy 87 (2), 496–503. doi:10.1016/j.apenergy.2009.07.009

CrossRef Full Text | Google Scholar

Chandel, S. S., and Agarwal, T. (2017). Review of current state of research on energy storage, toxicity, health hazards and commercialization of phase changing materials. Renew. Sustain. Energy Rev. 67, 581–596. doi:10.1016/j.rser.2016.09.070

CrossRef Full Text | Google Scholar

De Gracia, A., and Cabeza, L. F. (2015). Phase change materials and thermal energy storage for buildings. Energy Build. 103, 414–419. doi:10.1016/j.enbuild.2015.06.007

CrossRef Full Text | Google Scholar

De, S. K., Biswas, R., and Roy, A. R. (2000). Some operations on intuitionistic fuzzy sets. Fuzzy sets Syst. 114 (3), 477–484. doi:10.1016/s0165-0114(98)00191-2

CrossRef Full Text | Google Scholar

Dincer, I. (2002). Thermal energy storage systems as a key technology in energy conservation. Int. J. energy Res. 26 (7), 567–588. doi:10.1002/er.805

CrossRef Full Text | Google Scholar

Garg, H., Ali, Z., Mahmood, T., and Ali, M. R. (2022). TOPSIS-method based on generalized dice similarity measures with Hamy mean operators and its application to decision-making process. Alexandria Eng. J. 65, 383–397. doi:10.1016/j.aej.2022.10.043

CrossRef Full Text | Google Scholar

Garg, H. (2018). An improved cosine similarity measure for intuitionistic fuzzy sets and their applications to decision-making process. Hacettepe J. Math. Statistics 47 (6), 1578–1594.

Google Scholar

Garg, H., and Kaur, G. (2022). Algorithm for solving the decision-making problems based on correlation coefficients under cubic intuitionistic fuzzy information: A case study in watershed hydrological system. Complex and Intelligent Syst. 8 (1), 179–198. doi:10.1007/s40747-021-00339-4

CrossRef Full Text | Google Scholar

Gumus, A. T., Yayla, A. Y., Çelik, E., and Yildiz, A. (2013). A combined fuzzy-AHP and fuzzy-GRA methodology for hydrogen energy storage method selection in Turkey. Energies 6 (6), 3017–3032. doi:10.3390/en6063017

CrossRef Full Text | Google Scholar

Gurmani, S. H., Chen, H., and Bai, Y. (2022). Extension of TOPSIS method under q-rung orthopair fuzzy hypersoft environment based on correlation coefficients and its applications to multi-attribute group decision-making. Int. J. Fuzzy Syst., 1–14. doi:10.1007/s40815-022-01386-w

CrossRef Full Text | Google Scholar

Hussain, A., Ali, M. I., Mahmood, T., and Munir, M. (2020). q-Rung orthopair fuzzy soft average aggregation operators and their application in multi-criteria decision-making. Int. J. Intelligent Syst. 35 (4), 571–599. doi:10.1002/int.22217

CrossRef Full Text | Google Scholar

Hussain, A., Ullah, K., Alshahrani, M. N., Yang, M. S., and Pamucar, D. (2022). Novel Aczel–Alsina operators for Pythagorean fuzzy sets with application in multi-attribute decision making. Symmetry 14 (5), 940. doi:10.3390/sym14050940

CrossRef Full Text | Google Scholar

Jana, C., Garg, H., and Pal, M. (2022). Multi-attribute decision making for power Dombi operators under Pythagorean fuzzy information with MABAC method. J. Ambient Intell. Humaniz. Comput., 1–18. doi:10.1007/s12652-022-04348-0

CrossRef Full Text | Google Scholar

Javed, M., Javeed, S., Ullah, K., Garg, H., Pamucar, D., and Elmasry, Y. (2022). Approach to multi-attribute decision-making problems based on neutrality aggregation operators of T-spherical fuzzy information. Comput. Appl. Math. 41 (7), 310. doi:10.1007/s40314-022-01985-1

CrossRef Full Text | Google Scholar

Jegadheeswaran, S., and Pohekar, S. D. (2009). Performance enhancement in latent heat thermal storage system: A review. Renew. Sustain. energy Rev. 13 (9), 2225–2244. doi:10.1016/j.rser.2009.06.024

CrossRef Full Text | Google Scholar

Khan, M. R., Wang, H., Ullah, K., and Karamti, H. (2022). Construction material selection by using multi-attribute decision making based on q-rung orthopair fuzzy Aczel–Alsina aggregation operators. Appl. Sci. 12 (17), 8537. doi:10.3390/app12178537

CrossRef Full Text | Google Scholar

Khan, R., Ullah, K., Pamucar, D., and Bari, M. (2022). Performance measure using a multi-attribute decision-making approach based on complex T-spherical fuzzy power aggregation operators. J. Comput. Cognitive Eng. 1 (3), 138–146. doi:10.47852/bonviewJCCE696205514

CrossRef Full Text | Google Scholar

Khan, S., Gulistan, M., Kausar, N., Kousar, S., Pamucar, D., and Addis, G. M. (2022). Analysis of cryptocurrency market by using q-rung orthopair fuzzy hypersoft set algorithm based on aggregation operators. Complexity 2022, 1–16. doi:10.1155/2022/7257449

CrossRef Full Text | Google Scholar

Khan, S., Gulistan, M., and Wahab, H. A. (2021). Development of the structure of q-rung orthopair fuzzy hypersoft set with basic operations. Punjab Univ. J. Math. 53 (12), 881–892. doi:10.52280/pujm.2021.531204

CrossRef Full Text | Google Scholar

Klement, E. P., Mesiar, R., and Pap, E. (2004). Triangular norms. Position paper I: Basic analytical and algebraic properties. Fuzzy sets Syst. 143 (1), 5–26. doi:10.1016/j.fss.2003.06.007

CrossRef Full Text | Google Scholar

Koçak, B., Fernandez, A. I., and Paksoy, H. (2020). Review on sensible thermal energy storage for industrial solar applications and sustainability aspects. Sol. Energy 209, 135–169. doi:10.1016/j.solener.2020.08.081

CrossRef Full Text | Google Scholar

Kumar, S., and Garg, H. (2022). Some novel point operators and multiple rounds voting process based decision-making algorithm under picture fuzzy set environment. Adv. Eng. Softw. 174, 103274. doi:10.1016/j.advengsoft.2022.103274

CrossRef Full Text | Google Scholar

Lin, L., Yuan, X. H., and Xia, Z. Q. (2007). Multicriteria fuzzy decision-making methods based on intuitionistic fuzzy sets. J. Comput. Syst. Sci. 73 (1), 84–88. doi:10.1016/j.jcss.2006.03.004

CrossRef Full Text | Google Scholar

Lin, Y., Jia, Y., Alva, G., and Fang, G. (2018). Review on thermal conductivity enhancement, thermal properties and applications of phase change materials in thermal energy storage. Renew. Sustain. energy Rev. 82, 2730–2742. doi:10.1016/j.rser.2017.10.002

CrossRef Full Text | Google Scholar

Lizana, J., Chacartegui, R., Barrios-Padura, A., and Valverde, J. M. (2017). Advances in thermal energy storage materials and their applications towards zero energy buildings: A critical review. Appl. Energy 203, 219–239. doi:10.1016/j.apenergy.2017.06.008

CrossRef Full Text | Google Scholar

Mahmood, T., Ullah, K., Khan, Q., and Jan, N. (2019). An approach toward decision-making and medical diagnosis problems using the concept of spherical fuzzy sets. Neural Comput. Appl. 31 (11), 7041–7053. doi:10.1007/s00521-018-3521-2

CrossRef Full Text | Google Scholar

Maji, P. K., Biswas, R., and Roy, A. R. (2001). Fuzzy soft sets. J. Fuzzy Math. 9, 589–602.

Google Scholar

Maji, P. K., Biswas, R., and Roy, A. R. (2001). Intuitionistic fuzzy soft sets. J. Fuzzy Math. 9, 677–692.

Google Scholar

Maji, P. K., Biswas, R., and Roy, A. R. (2003). Soft set theory. Comput. Math. Appl. 45 (4-5), 555–562. doi:10.1016/s0898-1221(03)00016-6

CrossRef Full Text | Google Scholar

McNaught, A. D., and Wilkinson, A. (1997). IUPAC compendium of chemical terminology. 2nd ed. Hoboken, NJ, USA: Wiley Blackwell.

Google Scholar

Mette, B., Kerskes, H., Drück, H., Badenhop, T., Salg, F., and Gläser, R. (2013). “Thermochemical energy storage as an element for the energy turnaround,” in 8th int. Renew. Energy storage conf. Exhib.(IRES 2013 (Berlin, 1–10.

Google Scholar

Molodtsov, D. (1999). Soft set theory—First results. Comput. Math. Appl. 37 (4-5), 19–31. doi:10.1016/s0898-1221(99)00056-5

CrossRef Full Text | Google Scholar

Muthukumar, P., and Krishnan, G. S. S. (2016). A similarity measure of intuitionistic fuzzy soft sets and its application in medical diagnosis. Appl. Soft Comput. 41, 148–156. doi:10.1016/j.asoc.2015.12.002

CrossRef Full Text | Google Scholar

Peng, X. D., Yang, Y., Song, J., and Jiang, Y. (2015). Pythagorean fuzzy soft set and its application. Comput. Eng. 41 (7), 224–229.

Google Scholar

Rahman, A. U., Saeed, M., and Garg, H. (2022). An innovative decisive framework for optimized agri-automobile evaluation and HRM pattern recognition via possibility fuzzy hypersoft setting. Adv. Mech. Eng. 14 (10), 168781322211321. doi:10.1177/16878132221132146

CrossRef Full Text | Google Scholar

Rahman, A. U., Saeed, M., Khalifa, H. A. E. W., and Afifi, W. A. (2022). Decision making algorithmic techniques based on aggregation operations and similarity measures of possibility intuitionistic fuzzy hypersoft sets. AIMS Math. 7 (3), 3866–3895. doi:10.3934/math.2022214

CrossRef Full Text | Google Scholar

Rahman, K., Abdullah, S., Ahmed, R., and Ullah, M. (2017). Pythagorean fuzzy Einstein weighted geometric aggregation operator and their application to multiple attribute group decision making. J. Intelligent Fuzzy Syst. 33 (1), 635–647. doi:10.3233/jifs-16797

CrossRef Full Text | Google Scholar

Rathore, P. K. S., and Shukla, S. K. (2019). Potential of macroencapsulated PCM for thermal energy storage in buildings: A comprehensive review. Constr. Build. Mater. 225, 723–744. doi:10.1016/j.conbuildmat.2019.07.221

CrossRef Full Text | Google Scholar

Riaz, M., Farid, H. M. A., Karaaslan, F., and Hashmi, M. R. (2020). Some q-rung orthopair fuzzy hybrid aggregation operators and TOPSIS method for multi-attribute decision-making. J. Intelligent Fuzzy Syst. 39 (1), 1227–1241. doi:10.3233/jifs-192114

CrossRef Full Text | Google Scholar

Roy, A. R., and Maji, P. K. (2007). A fuzzy soft set theoretic approach to decision making problems. J. Comput. Appl. Math. 203 (2), 412–418. doi:10.1016/j.cam.2006.04.008

CrossRef Full Text | Google Scholar

Sarkar, A., Biswas, A., and Kundu, M. (2022). Development of q-rung orthopair trapezoidal fuzzy Einstein aggregation operators and their application in MCGDM problems. J. Comput. Cognitive Eng. 1 (3), 109–121.

Google Scholar

Siddique, I., Zulqarnain, R. M., Ali, R., Jarad, F., and Iampan, A. (2021). Multicriteria decision-making approach for aggregation operators of Pythagorean fuzzy hypersoft sets. London, United Kingdom: Computational Intelligence and Neuroscience.

Google Scholar

Smarandache, F. (2018). Extension of soft set to hypersoft set, and then to plithogenic hypersoft set. Neutrosophic Sets Syst. 22, 168–170.

Google Scholar

Sunthrayuth, P., Jarad, F., Majdoubi, J., Zulqarnain, R. M., Iampan, A., and Siddique, I. (2022). A novel multicriteria decision-making approach for Einstein weighted average operator under Pythagorean fuzzy hypersoft environment. J. Math. 2022, 1–24. doi:10.1155/2022/1951389

CrossRef Full Text | Google Scholar

Tarragona, J., de Gracia, A., and Cabeza, L. F. (2020). Bibliometric analysis of smart control applications in thermal energy storage systems. A model predictive control approach. J. Energy Storage 32, 101704. doi:10.1016/j.est.2020.101704

CrossRef Full Text | Google Scholar

Thao, N. X., and Smarandache, F. (2019). A new fuzzy entropy on Pythagorean fuzzy sets. J. Intelligent Fuzzy Syst. 37 (1), 1065–1074. doi:10.3233/jifs-182540

CrossRef Full Text | Google Scholar

Ullah, K. (2021). Picture fuzzy Maclaurin symmetric mean operators and their applications in solving multiattribute decision-making problems. Math. Problems Eng. 2021, 1–13. doi:10.1155/2021/1098631

CrossRef Full Text | Google Scholar

Wang, L., and Li, N. (2020). Pythagorean fuzzy interaction power Bonferroni mean aggregation operators in multiple attribute decision making. Int. J. Intelligent Syst. 35 (1), 150–183. doi:10.1002/int.22204

CrossRef Full Text | Google Scholar

Wang, W., and Liu, X. (2011). Intuitionistic fuzzy geometric aggregation operators based on Einstein operations. Int. J. Intelligent Syst. 26 (11), 1049–1075. doi:10.1002/int.20498

CrossRef Full Text | Google Scholar

Wei, G., and Lu, M. (2018). Pythagorean fuzzy power aggregation operators in multiple attribute decision making. Int. J. Intelligent Syst. 33 (1), 169–186. doi:10.1002/int.21946

CrossRef Full Text | Google Scholar

Xiao, F., and Ding, W. (2019). Divergence measure of Pythagorean fuzzy sets and its application in medical diagnosis. Appl. Soft Comput. 79, 254–267. doi:10.1016/j.asoc.2019.03.043

CrossRef Full Text | Google Scholar

Xu, Z. S. (2007a). Intuitionistic fuzzy aggregation operators. IEEE Trans. Fuzzy Syst. 15, 1179–1187. doi:10.1109/tfuzz.2006.890678

CrossRef Full Text | Google Scholar

Yager, R. R. (2016). Generalized orthopair fuzzy sets. IEEE Trans. Fuzzy Syst. 25 (5), 1222–1230. doi:10.1109/tfuzz.2016.2604005

CrossRef Full Text | Google Scholar

Yager, R. R. (2013). Pythagorean membership grades in multi-criteria decision making. IEEE Trans. Fuzzy Syst. 22 (4), 958–965. doi:10.1109/tfuzz.2013.2278989

CrossRef Full Text | Google Scholar

Zadeh, L. A. (1965). Fuzzy sets. Fuzzy Sets, Inf. Control 8, 338–353. doi:10.1016/s0019-9958(65)90241-x

CrossRef Full Text | Google Scholar

Zhang, Q., Hu, J., Feng, J., Liu, A., and Li, Y. (2019). New similarity measures of Pythagorean fuzzy sets and their applications. IEEE Access 7, 138192–138202. doi:10.1109/access.2019.2942766

CrossRef Full Text | Google Scholar

Zhang, X. (2016). A novel approach based on similarity measure for Pythagorean fuzzy multiple criteria group decision making. Int. J. Intelligent Syst. 31 (6), 593–611. doi:10.1002/int.21796

CrossRef Full Text | Google Scholar

Zhang, X., and Xu, Z. (2014). Extension of TOPSIS to multiple criteria decision making with Pythagorean fuzzy sets. Int. J. Intelligent Syst. 29 (12), 1061–1078. doi:10.1002/int.21676

CrossRef Full Text | Google Scholar

Zhao, Y., Zhao, C. Y., Markides, C. N., Wang, H., and Li, W. (2020). Medium-and high-temperature latent and thermochemical heat storage using metals and metallic compounds as heat storage media: A technical review. Appl. Energy 280, 115950. doi:10.1016/j.apenergy.2020.115950

CrossRef Full Text | Google Scholar

Zulqarnain, R. M., Ali, R., Awrejcewicz, J., Siddique, I., Jarad, F., and Iampan, A. (2022). Some Einstein geometric aggregation operators for q-rung orthopair fuzzy soft set with their application in MCDM. IEEE Access 10, 88469–88494. doi:10.1109/access.2022.3199071

CrossRef Full Text | Google Scholar

Zulqarnain, R. M., Rehman, H. K. U., Awrejcewicz, J., Ali, R., Siddique, I., Jarad, F., et al. (2022). Extension of Einstein average aggregation operators to medical diagnostic approach under q-rung orthopair fuzzy soft set. IEEE Access 10, 87923–87949. doi:10.1109/access.2022.3199069

CrossRef Full Text | Google Scholar

Zulqarnain, R. M., Siddique, I., Ahmad, S., Iampan, A., Jovanov, G., Vranješ, Đ., et al. (2021). Pythagorean fuzzy soft Einstein ordered weighted average operator in sustainable supplier selection problem. Math. Problems Eng. 2021, 1–16. doi:10.1155/2021/2559979

CrossRef Full Text | Google Scholar

Zulqarnain, R. M., Siddique, I., Ali, R., Awrejcewicz, J., Karamti, H., Grzelczyk, D., et al. (2022). Einstein ordered weighted aggregation operators for Pythagorean fuzzy hypersoft set with its application to solve MCDM problem. IEEE Access 10, 95294–95320. doi:10.1109/access.2022.3203717

CrossRef Full Text | Google Scholar

Zulqarnain, R. M., Siddique, I., Ali, R., Jarad, F., and Iampan, A. (2022). Einstein weighted geometric operator for Pythagorean fuzzy hypersoft with its application in material selection. Henderson, NV, United States: CMES-Computer Modeling in Engineering and Sciences. doi:10.32604/cmes.2023.023040

CrossRef Full Text | Google Scholar

Zulqarnain, R. M., Siddique, I., Ali, R., Pamucar, D., Marinkovic, D., and Bozanic, D. (2021). Robust aggregation operators for intuitionistic fuzzy hypersoft set with their application to solve MCDM problem. Entropy 23 (6), 688. doi:10.3390/e23060688

PubMed Abstract | CrossRef Full Text | Google Scholar

Zulqarnain, R. M., Siddique, I., and Ei-Morsy, S. (2022). Einstein-ordered weighted geometric operator for Pythagorean fuzzy soft set with its application to solve MAGDM problem. London, United Kingdom: Mathematical Problems in Engineering.

Google Scholar

Zulqarnain, R. M., Siddique, I., and Gurmani, S. H. (2022). Extension of interaction aggregation operators for the analysis of cryptocurrency market under q-rung orthopair fuzzy hypersoft set. IEEE Access 10, 126627–126650. doi:10.1109/access.2022.3224050

CrossRef Full Text | Google Scholar

Zulqarnain, R. M., Siddique, I., Jarad, F., Hamed, Y. S., Abualnaja, K. M., and Iampan, A. (2022). Einstein aggregation operators for Pythagorean fuzzy soft sets with their application in multiattribute group decision-making. J. Funct. Spaces 2022, 1–21. doi:10.1155/2022/1358675

CrossRef Full Text | Google Scholar

Zulqarnain, R. M., Xin, X. L., and Saeed, M. (2021). A Development of Pythagorean fuzzy hypersoft set with basic operations and decision-making approach based on the correlation coefficient. In Theory and application of hypersoft set. Belgium: Pons Publishing House Brussels, 85–106.

Google Scholar